EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 625 (May 2019) A&A, 625 (2019) A93 Full HTML
Free Access
Issue
A&A
Volume 625, May 2019
Article Number A93
Number of page(s) 9
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201834230
Published online 17 May 2019

© ESO 2019

1 Introduction

Supernova remnants (SNRs) are collisionally ionized emission nebulae that are formed soon after a supernova explosion. In fact, their evolution is closely related to a particular type of collisionless shock wave that is actually formed ahead of the ejected material (see Vink 2012). It turns out that SNRs strongly influence the interstellar medium through which they expand, and vice versa; furthermore, the ambient interstellar matter (ISM) plays a dominant role in dictating the evolution of an SNR.

These remarkable objects are believed to be primarily responsible for the production of the Galactic cosmic rays, that is, the high-energy, ultrarelativistic charged particles up to ~1015 eV (see, e.g. Bell 1978a,b; Blandford & Ostriker 1978). Of course, one should always bear in mind that such a collisionless shock formation, particle acceleration, and magnetic field amplification are all coupled processes that we still do not fully understand (see, e.g. Helder et al. 2012). In fact, we still do not fully understand all the processes, like various microinstabilities, which actually trigger collisionless shock formation.

The integrated radio continuum spectral energy distribution (SED) of SNRs are generally very well represented by a simple power law, reflecting the pure (non-thermal) synchrotron radiation from an SNR shell: 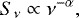Sν∝ν−α,\begin{equation*}S_{\nu}\propto\nu^{-\alpha}, \end{equation*}(1)

where Sν is the spatially integrated flux density and α is the radio spectral index. In that sense, astronomical observations of synchrotron emission, predominantly caused by the cosmic ray electrons accelerated via the diffusive shock acceleration (DSA) process, enable us to actually test and constrain all the known theoretical models that are believed to describe the physics behind the observed radiation from SNRs (see Urošević 2014, for a review). It is also easily verified that for a standard value of the mean Galactic magnetic field (several μG), gigaelectron volt cosmic ray electrons are mostly responsible for the observed synchrotron emission at radio, and teraelectron volt electrons at X-ray frequencies (Cherenkov Telescope Array Consortium 2019).

The mean value of the radio spectral indices, for some 300+ known Galactic and ~60 Large Magellanic Cloud (Bozzetto et al. 2017) SNRs, is around 0.5, which is in a good accordance with DSA theory (see, e.g. Helder et al. 2012; Dubner & Giacani 2015). However, our present knowledge of the SNR radio SED’s as well as of their overall shape is far from being precise, at least for the majority of known Galactic and Magellanic Cloud SNRs. It is therefore very important to obtain more reliable radio spectra, so that the analysis of the integrated continuum of SNRs could distinguish between various different theoretical models, particularly in the low-frequency domain.

After a brief review of the current knowledge on the Galactic SNR G5.9+3.1, we present the low-frequency (80–300 MHz) radio observations of this remnant, obtained with the Murchison Widefield Array (Lonsdale et al. 2009; Tingay et al. 2013, see Sects. 2 and 3). In Sect. 4, we will focus on the analysis of the integrated continuum spectrum and morphology of this remnant. In addition, in Sect. 5 we report the first detection of G5.9+3.1 in X-rays and analyse its X-ray spectrum, based on the archived XMM-Newton observations. Finally, in Sect. 6 we make a summary of our results.

2 Previous studies of SNR G5.9+3.1

The poorly studied Galactic SNR G5.9+3.1 was originally identified based on the radio continuum surveys of the Galactic plane with the Effelsberg 100-m telescope at λ = 11 cm (ν = 2.7 GHz) and λ = 21 cm (ν = 1.4 GHz) (Reich et al. 1988). Morphologically, it is an S-type remnant with an asymmetric shell and with an average angular radius of around 10′. Based on these early radio continuum observations, the radio spectral index of this remnant is found to be around 0.4 and flux density at 1 GHz around 3.3 Jy (Reich et al. 1988). Based on a revised radio surface brightness to diameter (Σ–D) relation, Pavlović et al. (2013, 2014) estimated the diameter of the SNR G5.9+3.1 and its distance, based on the method of orthogonal fitting, to be around 31.2 pc and 5.4 ± 2.8 kpc (average fractional error is 0.52), respectively.In addition, median distance, based on the so-called probability density function (PDF) method (Vukotić et al. 2014) is 5.1 ±2.2 kpc (average fractional error is 0.43).

G5.9+3.1 has been, so far, only observed at radio frequencies and has not been extensively analyzed in the current literature. Hewitt & Yusef-Zadeh (2009) included this remnant in the Very Large Array (VLA) 1720 MHz OH maser survey. No detection of interaction between radiative-phase shocks and molecular gas is reported, which is not unusual as the SNR is over 3° away from the bulk of the Galactic molecular clouds along the central plane.

We emphasize that the SNR G5.9+3.1 is also detected in the 1.4 GHz National Radio Astronomy Observatory (NRAO) VLA Sky Survey (NVSS; Condon et al. 1998) as well as in the Tata Institute of Fundamental Research (TIFR) alternative data release 1 (ADR1) Giant Metrewave Radio Telescope (GMRT) 150 MHz Sky Survey1 (TGSS ADR1; Intema et al. 2017). In addition, this remnant is also identified in the Parkes Radio Observatory – Massachusetts Institute of Technology (MIT) – NRAO 4850 MHz Southern Sky Survey (PMN; Griffith & Wright 1993). Unfortunately, because of the missing short spacings within the interferometer array configuration, we cannot extract precise flux values for an analysis of the G5.9+3.1 SED using these measurements.

We also note that a (isolated single-Gaussian) point source within the boundaries of G5.9+3.1 has already been detected and listed in the TGSS ADR1 150 MHz survey source catalog (J174711.9-221741, Intema et al. 2017) at approximately the same apparent location at which we find the central radio source inside the shell of the SNR (Stotal(150 MHz) = (263.0 ± 28.8) mJy, Speak (150 MHz) = (259.0 ± 26.8) mJy). In addition, this point radio source is also listed in the NVSS survey catalog at 1.4 GHz as NVSS J174711-221743 and with S(1.4 GHz) = (28.7 ± 1.0) mJy (Condon et al. 1998).

The SNR G5.9+3.1 has not been detected by the Fermi Large Area Telescope (LAT) team (Acero et al. 2016), as well as by any other γ-ray observations(see H. E. S. S. Collaboration 2018). Also, our extensive search at IR and optical frequencies (Stupar et al. 2008) did not reveal any detection despite G5.9+3.1 being positioned more than 3° above the Galactic plane where confusion is expected to be significantly reduced. Finally, G5.9+3.1 was not detected by the Infrared Astronomical Satellite (IRAS) survey of Galactic SNRs (Saken et al. 1992), nor in the Spitzer surveys (Reach et al. 2006; Andersen et al. 2011).

3 Murchison Widefield Array photometry

In this section we present the aperture photometry method we applied to Murchison Widefield Array (MWA) total intensity maps of the G5.9+3.1. The region containing G5.9+3.1 was observed with the MWA as a part of the GaLactic and Extragalactic All-sky Murchison Widefield Array (GLEAM) survey (Wayth et al. 2015). Following a similar strategy used to produce the extragalactic radio images in Hurley-Walker et al. (2017), but with improvements in the imaging and deconvolution strategy for the confused and complex regions of the Galactic plane, Hurley-Walker et al. (in prep.) produce GLEAM images over the Galactic longitude ranges 345° < l < 60° and 180° < l < 240°, which covers G5.9+3.1. Hurley-Walker et al. (in prep.) also provide flux density measurements for SNR and candidate SNRs within this region; a brief summary of the measurement method is provided here.

Through manual inspection, the region containing the SNR is marked out by the observer. An estimate of the background is made using the average flux density of the surrounding region, excluding regions with contaminating structures such as background radio galaxies. This background is subtracted from the total flux density of the area within the SNR region, and then the total flux density of the SNR is calculated.

GLEAM provides 20 × 7.68 MHz-bandwidth channels between 72 and 231 MHz. In these images, the object is resolved and clearly distinct from the relatively complicated environment. However, at frequencies above 162 MHz, the signal-to-noise ratio (S/N) becomes somewhat low and the flux density measurements less accurate. For G5.9+3.1, we therefore use the wideband GLEAM measurements of 72–103, 103–134, 139–170, and 170–231 MHz, for improved S/N.

Figure 1 shows the GLEAM measurements in these bands, with the highest resolution 170–231 MHz image in the top two panels and the three remaining bands as an red-green-blue (RGB) image in the lower two panels. The SNR is quite circularly symmetric, with a diameter of 18.5′.

4 Integrated radio continuum spectrum of the supernova remnant G5.9+3.1

Combining particular MWA wideband low-frequency observations with the Effelsberg 100-m Galactic plane survey at 1408 and 2695 MHz (Reich et al. 1990a,b) as well as with the Academy of Sciences Radio Telescope – 600 (RATAN-600) Galactic plane survey at 960 and 3900 MHz (Trushkin 1996, 1998), we present the SED of the SNR G5.9+3.1 (see Fig. 2 and Table 1). The integrated flux densities for Effelsberg data are estimated from the publicly available observations at Max Planck Institute for Radio Astronomy (MPIfR) Survey Sampler2, and for the RATAN-600, integrated flux densities are taken from Trushkin (1996, 1998).

Because of the steep radio spectral index (α = 0.99 ± 0.05 from TGSS and NVSS observations) and small values of the flux densities for the point radio source, which lay in the center of the SNR shell, we can actually use the MWA, Effelsberg, and RATAN-600 integrated flux densities assuming that the contribution of the central radio source is negligible.

No obvious SED turn-off is detected at the lowest observed continuum frequencies (see Fig. 2). In a similar fashion, a curvature at higher frequencies (up to 3.9 GHz) is also missing. The SNR SED is very well explained by a simple power-law relation.

In Fig. 2, we present the weighted least-squares fit of the integrated radio continuum (over the whole observable frequency range) of the SNR G5.9+3.1 using the simple power-law model for pure synchrotron emission (Eq. (1)). Circles correspond to the MWA data, diamond symbols indicate Effelsberg data and triangles depict RATAN observations. The best fitting radio synchrotron spectral index α is around 0.42 and the flux density at 1 GHz is estimated to be around 2.7 Jy.

The weighted least-squares fit is estimated with the MPFIT3 (Markwardt 2009) package written in IDL, with starting values estimated from the data. We note that MPFIT provides estimates of the 1σ uncertainties for each parameter.

Furthermore, because the spectral index of G5.9+3.1 is less than the value of 0.5 predicted by test-particle DSA, the so-called equipartition calculation, derived for α ≥ 0.5, cannot be used for magnetic field estimation for this SNR (Arbutina et al. 2012, 2013; Urošević et al. 2018). Bearing in mind the calculated parameter uncertainty, spectral indices less than 0.5 can be explained by a significant contributionof the stochastic Fermi acceleration (see Ostrowski 1999; Ostrowski & Schlickeiser 1993; Schlickeiser & Fürst 1989; Onić 2013).

This central point radio source is coincident (~20′′) with the position of the long-period variable (LPV) star known in the Optical Gravitational Lensing Experiment Galactic Bulge LPV star catalogue (OGLE BLG-LPV) as OGLE BLG-LPV 38416 (Soszyński et al. 2013). However, the non-thermal radio continuum of this point source is not in good accordance with the optically thick thermal free–free emission from a post-shock partially ionized layer in a stellar atmosphere, nor with thermal emission from the stellar photosphere, nor with non-thermal radio emission associated with stellar flare activity (see Estalella et al. 1983; Rudnitskij 1993; Reid & Menten 1997; Rudnitskij & Chapman 2007). Furthermore, the nearest known pulsar PSR+J1745-2229 (Hobbs et al. 2004) is about 20′ from the point source.

Additionally, in contrast to the radio spectral indices of SNRs (usually between 0.3 and 0.8), pulsar wind nebulae (PWNe) have spectral indices in the range of around 0–0.3 (Reynolds et al. 2012, and references therein). On the other hand, above100 MHz the spectra of the majority of detected pulsars can be described just by a simple power law with the average value of spectral index around 1.8 (Maron et al. 2000). Han et al. (2016) have found that spectral indices of 228 pulsars from their analysis are distributed in the range from 0.46 to 4.84. In that sense, we propose that this central object is possibly the compact remnant of the supernova explosion that gave rise to G5.9+3.1.

thumbnail Fig. 1

GLEAM images of G5.9+3.1. Top two panels: wideband image taken over 170–231 MHz. Lower two panels: an RGB image comprised of R = 72–103 MHz, G = 103–134 MHz, B = 139–170 MHz. The full width at half maximums (FWHMs) of the point spread functions (PSFs) of the images are, respectively: 2.4′, 5.2′, 3.9′, and 2.9′. Left panels: images without any annotations. Right panels: annotations indicating the GLEAM photometry measurement; the white lines show the region drawn by the observer that contains the SNR; the gray shaded region shows the area used to calculate the background; the blue dashed lines show a region excluded from the background measurement for containing contaminating background radio galaxies.
thumbnail Fig. 2

Weighted least-squares fit of the presently known integrated radio continuum spectrum of the SNR G5.9+3.1 using the simple power-law model (Eq. (1)) for pure synchrotron emission (solid line). Circles correspond to the MWA data, diamond symbols indicate Effelsberg data, and triangles depict RATAN observations.
Table 1

MWA, Effelsberg, and RATAN-600 integrated flux density measurements of SNR G5.9+3.1.

5 XMM-Newton observations of G5.9+3.1

The SNR G5.9+3.1 was the subject of a pointed observation made with the three European Photon Imaging Cameras (EPIC) Metal Oxide Semi-conductor (MOS) 1, MOS2, and p-n (PN) aboard the XMM-Newton Observatory on 1 March 2006 (PI: R. Bandiera; Obs. ID 0553110401). The archival datasets from the observations were downloaded from the XMM-Newton Science Archive and analyzed using standard tools in the High Energy Astrophysics Software (HEASOFT) Package (Version 6.22.1) and the Science Analysis Software (SAS) software package (Version 16.1.0). The SAS tools epchain and emchain were used to apply standard processing tools to the PN, MOS1, and MOS2 datasets while the tools pn-filter and mos-filter were used to filter the datasets for background flaring activity. After processing, the effective exposure times of the PN, MOS1, and MOS2 cameras were 6281, 11040, and 11080 s, respectively. Combined EPIC (PN+MOS1+MOS2) exposure-corrected and adaptively smoothed images of G5.9+3.1 were created using the Extended Source Analysis Software package (Snowden & Kuntz 2011).

In Fig. 3 we present an exposure-corrected and adaptively smoothed combined EPIC image of G5.9+3.1. The image depicts emission detected over the energy range from 0.4 to 1.0 keV. The dashed green ellipse is centered on RA (J2000.0) 17h 47m15.0s, Dec (J2000.0) −22°16′38.5′′ and has major and minor axes of 449.5′′ and 463.4′′, respectively.This ellipse corresponds to the region of extraction of the source spectrum for the entirety of G5.9+3.1 and the spectral properties of this region – along with smaller regions of the SNR – are discussed later in this section. A shell-like structure is clearly visible: the eastern rim (toward the left of the image) is particularly noticeable while the southwestern rim is readily detected as well. Fainter emission is detected along the northern rim and the interior of G5.9+3.1, while the southern portion of the SNR is not detected in the X-ray. We believe this result is the first published detection of X-ray emission from G5.9+3.1: we also note that the aimpoint of the observation (where the angular resolution capabilities and flux sensitivities of the imaging instruments attain their best values) was placed on the eastern rim of the SNR. Therefore, significant degradation in both angular resolution and flux sensitivity with increasing off-axis angle – particularly in the western direction toward the western edge of the radio shell of G5.9+3.1 – complicates the development of a detailed and accurate description of the X-ray morphology of this SNR. From inspection of the available image presented in Fig. 3, we conclude that the X-ray morphology of G5.9+3.1 is best described as more shell-like than center-filled. Additional X-ray observations of this SNR are needed to probe its X-ray morphology in a more rigorous manner. Finally, we note that the central radio point source discussed in detail in Sect. 4 is not detected in our X-ray image.

In Fig. 4 we present the same image given in Fig. 3 but with contours added to depict radio emission detected by MWA from G5.9+3.1. Inspection of this figure reveals that the bright X-ray emission from the eastern and western rims of this SNR appears to lie interior to the radio emission from these rims. We note that the eastern rim of the SNR is the brightest feature of the SNR in both the X-ray and the radio. The northern and southern rims of the SNR are weak in radio and essentially absent in the X-ray while little to no X-ray emission is seen along the southern radio rim.

Using the data collected by all three EPIC cameras aboard XMM-Newton during this observation, we conducted a spatially-resolved spectroscopic analysis of the X-ray emission from G5.9+3.1. This analysis was conducted using the standard X-ray spectroscopic analysis software package (XSPEC; Arnaud 1996) version 12.10.0c and can be described asfollows. Appropriate source regions (corresponding to the whole SNR along with the east rim, the north rim, and the west rim) and background regions were selected taking care to exclude the point sources. The locations of these regions of spectral extraction are indicated in Fig. 4 and the properties of these regions – including central RA (J2000) and Dec (J2000) values and dimensions – are listed in Table 2. As the background can have strong spatial variations, the region for extraction of background spectra was selected by averaging over several regions across the detector plane. Two spectra (source and background) were extracted per instrument (PN, MOS1, and MOS2) from each region: the first spectrum was extracted from the event list of the science observation and the second spectrum was extracted from the filter wheel closed (FWC) data. The FWC spectra were extracted at the same detector position as in the science observation because of the strong position dependency of the instrumental background for the PN, MOS1, and MOS2 cameras. The corresponding spectra from the FWC data were subtracted from the science spectra of the source and background regions to subtract the quiescent particle background component. Finally, in anticipation of a statistical analysis of the data using C-statistics (Cash 1979) the extracted spectra were all rebinned to a minimum of one count per bin.

The source spectra associated with emission from G5.9+3.1 (either from the whole SNR or from one of its rims) were fitted with the thermal model known as Astrophysical Plasma Emission Code (APEC; Foster et al. 2012): this model describes an optically thin thermal plasma in collision ionization equilibrium (CIE). For our purposes, the elemental abundances of the plasma were frozen to solar values. Furthermore, the source spectra for each region of interest of G5.9+3.1 and the background spectra from each camera (PN, MOS1, and MOS2) were fit simultaneously to constrain the source component as well as the astrophysical background (AXB) component. Following the example given by Kuntz & Snowden (2010), we used a three-component model for the AXB: the first component was an unabsorbed thermal component for the local hot bubble (LHB), while the second component was an absorbed thermal component for the Galactic halo emission. Both of these components were fit with the APEC model again with elemental abundances frozen to solar values. Lastly, the third component was an absorbed power law for the non-thermal unresolved extragalactic X-ray background. These three components will be denoted as the LHB component, the Halo component, and the DXB component, respectively, for the remainder of this paper. The full model applied in the spectral fitting can be denoted as CONSTANT × (APECLHB + TBABS × (APECHalo + Power LawDXB) + TBABS × APECSource. Here, “CONSTANT” refers to multiplicative constants used to account for variations in calibration between the different EPIC cameras and “TBABS” is the Tübingen–Boulder interstellar photoelectric absorption model (the interstellar elemental abundances given by Wilms et al. 2000 were used in our analysis). The intercalibration constants were determined from the spectrum with the highest statistical quality (west rim), and was fixed to these values for the rest of the spectral fits. The column densities forthe source spectra, the Halo component, and the DXB components were all tied together during the fitting. The temperature of the LHB component was allowed to vary during the fitting (its fitted value of kT ~ 0.30 keV is comparable to the fitted temperature of the component obtained by Kuntz & Snowden 2010) while the temperature of the Halo component was frozen to kT = 0.10 keV (which again is consistent with the results of Kuntz & Snowden 2010). Finally, the spectral index of the DXB component was fixed to 1.46 (Chen et al. 1997). We note that we excluded the extracted MOS2 spectra for the north rim and the west rim from our spectral analysis of those particular regions of G5.9+3.1 due to poor S/N.

In Table 3 we present the results of our spectral fitting with the model described above. In Fig. 5 we present plots of the extracted spectra for the whole SNR along with the three rims as fit with the model described above. We have obtained a statistically acceptable fit to this model based on the interpretation of Cash statistics. The fitted value of the column density toward G5.9+3.1 is NH~ 0.80 × 1022 cm−2 and the fitted values for the temperatures of the whole SNR and the three rims are approximately similar, ranging from kT ~ 0.14–0.23 keV. There is significant overlap in the error bounds on these fitted values: we therefore argue that there are no significant variations in the temperature of the X-ray emitting plasma across the angular extent of G5.9+3.1.

For comparison purposes with the results for fitting the spectra with the APEC model, we also fit the extracted spectra with a non-equilibrium ionization (NEI) plasma model (Borkowski et al. 2001). Our fitted results with the NEI model – when compared on the basis of the Cash statistics – do not differ in a significant way from our fitted results with the APEC model. Furthermore, our fits using the NEI model include a fitted value for the ionization timescale of τ ~ 1013 cm−3 s for the rims as well as the whole SNR. The lower limit on our fitted value for the ionization timescale (at the 90% confidence level) was 1012 cm−3 s, which is consistent with the interpretation that the X-ray emitting plasma of G5.9+3.1 is in CIE (Smith & Hughes 2010). This result is also consistent with our previous result where we obtained a statistically acceptable fit with the APEC model, which assumes CIE conditions for the plasma.

The fitted values of the normalizations using the APEC model for the different regions of G5.9+3.1 may be used to estimate the values of the electron number densities of the X-ray emitting gas at each rim. For the APEC model, the normalization is defined as 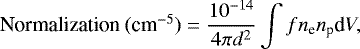Normalization(cm−5)=10−144πd2∫f nenpdV,\begin{equation*} \mbox{Normalization (cm$^{-5}$)} = \frac{10^{-14}}{4 \pi d^2} \int f n_{\textrm{e}} n_{\textrm{p}} \textrm{d}V, \end{equation*}(2)

where d is the distance to the SNR in cm, f is the volume filling factor, ne and np are the number densities of the electrons and protons of the region of spectral extraction in units of cm−3, and V = ∫ dV is the volume of the region of spectral extraction in units of cm3. Adopting a distance to G5.9+3.1 of 5.2 kpc based on arguments presented in Sect. 2, d is therefore 1.60 × 1022 cm. Furthermore, if we assume that the volumes of the regions of spectral extraction are ellipsoids with dimensions of semimajor axis × semiminor axis × semiminor axis, then the volumes of the whole SNR, the east rim, the north rim, and the west rim are 1.90 × 1059, 1.23 × 1058, 1.71 × 1058, and 2.05 × 1058 cm3, respectively. Finally, assuming that ne = 1.2 np and using our fitted values for the normalizations and the calculated volumes for each region, we estimate the electron densities associated with the whole SNR, the east rim, the north rim, and the west rim to be 0.29f−1∕2, 0.43f−1∕2, 0.21f−1∕2, and 0.21f−1∕2 cm−3, respectively.We physically interpret these results to indicate that G5.9+3.1 is expanding into an ambient interstellar medium with approximately constant density across its entire azimuth, though the electron density appears to be slightly elevated along the bright eastern rim of the SNR. Finally, based on the derived electron density for the whole SNR, we estimate the swept-up mass of the X-ray emitting plasma associated with G5.9+3.1 to be ~ 46f−1∕2 M⊙. Additional analysis is required to explore the X-ray properties of this SNR in more detail.

thumbnail Fig. 3

Adaptively smoothed exposure-corrected combined EPIC image of G5.9+3.1. The image depicts emission detected over the energy range 0.4–1.0 keV and the pixel range of the emission is 3–7.87 counts per second per square degree. The dashed green ellipse is centered on RA (J2000.0) 17h 47m15.0s, Dec (J2000.0) − 22°16′38.5′′ and has major and minor axes of 449.5′′ and 463.4′′, respectively. This ellipse corresponds to the region of extraction of the source spectrum for the whole SNR (see Sect. 5 and Table 2). We note the clear rim-brightened structure seen toward the eastern and southwestern rims of G5.9+3.1. Fainter emission is seen toward the northern rim and interior of the SNR. Emission from discrete sources has been flagged and excised in the creation of this image: voids of emission seen in this image correspond to artifacts from these excisions.
thumbnail Fig. 4

Same as Fig. 3 but with contours overlaid that depict radio emission detected by the MWA and regions of spectral extraction indicated and labeled. The contour levels correspond to 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.155, and 0.16 Jy beam−1. The X-ray emission along the eastern and western rims of G5.9+3.1 appears to lie interior to the radio rims, while X-ray and radio emission from the northern and southern rims are weak or absent. The source regions of spectral extraction for the northern, western, and eastern rims along with the entire SNR are indicated, as well as the accompanying regions of background spectral extraction.
Table 2

Properties of regions of extraction of source and background spectra for G5.9+3.1.

Table 3

Summary of fit to extracted XMM-Newton source and background spectra of G5.9+3.1 using TBABS × APEC model.

6 Summary

In this paper, we have discussed the properties of the poorly studied Galactic SNR G5.9+3.1. Here, we summarize our main findings.

  • 1.

    We have presented the low-frequency observations and flux density measurements of the Galactic SNR G5.9+3.1 using the MWA.

  • 2.

    Combining these new MWA observations with the surveys at higher radio continuum frequencies, we discussed the SED of this particular remnant. Synchrotron radio spectral index is estimated to be 0.42 ± 0.03 and the integrated flux density at 1 GHz to be around 2.7 Jy.

  • 3.

    We also propose that the central point radio source, located apparently inside the SNR shell, is possibly a compact remnant of the supernova explosion with typical steep pulsar SED of 0.99 ± 0.05.

  • 4.

    We have analyzed the X-ray properties of G5.9+3.1 using an archival pointed observation made of this SNR with XMM-Newton. We believe that our work describes the first detection and analysis of X-ray emission from G5.9+3.1. The spatial distribution of the X-ray emission of G5.9+3.1 as detected by XMM-Newton broadly matches the spatial distribution of the radio emission: the X-ray morphology of the SNR is shell-like rather than center-filled. The radio-bright eastern and western rims are also readily detected in the X-ray while the radio-weak northern and southern rims are weak or absent in the X-ray. We have extracted and fit MOS1+MOS2+PN spectra from the whole SNR as well as the northern, eastern, and western rims of the SNR: by the simultaneous fitting of source and background spectra along with accounting for the astrophysical X-ray background, we have successfully fit these extracted spectra with a single thermal model corresponding to an optically thin thermal plasma in collisional ionization equilibrium. The fitted column density toward the SNR is NH ~ 0.80 × 1022 cm−2 and the fitted temperatures for the spectra for the whole SNR as well as the bright rims are all comparable (kT ~ 0.14–0.23 keV). The derived electron number densities for the whole SNR and the rims are also roughly comparable (~ 0.20f−1∕2 cm−3), though the electron number density for the eastern rim is slightly larger (~0.43f−1∕2 cm−3). We also estimate the swept-up mass of the X-ray emitting plasma associated with G5.9+3.1 to be ~ 46f−1∕2 M⊙.

  • 5.

    New high-frequency radio continuum observations (i.e. using the Australia Telescope Compact Array (ATCA), the Australian Square Kilometre Array Pathfinder (ASKAP)) as well as the deeper X-ray observations (e.g. using XMM-Newton telescope) will presumably shed more light on the physical properties of this SNR.

thumbnail Fig. 5

Extracted PN, MOS1, and MOS2 spectra of the different regions of G5.9+3.1 as fit with the model and fit parameters given in Table 3. The residuals to the fits are also shown. In all panels, the PN source spectrum is shown in black, the PN FWC spectrum is shown in red, the MOS1 source spectrum is shown in green, the MOS1 FWC spectrum is shown in blue, the MOS2 source spectrum is shown in cyan, and the MOS2 FWC spectrum is shown in purple. Upper left: extracted spectra for the whole SNR. Upper right: extracted spectra for the east rim. Lower left: extracted spectra for the north rim. Lower right: extracted spectra for the west rim.

Acknowledgements

We thank the anonymous referee for useful comments that greatly improved the quality of this paper. This scientific work makes use of the Murchison Radio-astronomy Observatory, operated by CSIRO. We acknowledge the Wajarri Yamatji people as the traditional owners of the Observatory site. Support for the operation of the MWA is provided by the Australian Government (NCRIS), under a contract to Curtin University administered by Astronomy Australia Limited. We acknowledge the Pawsey Supercomputing Centre, which is supported by the Western Australian and Australian Governments. This work is part of the project 176005 “Emission nebulae: structure and evolution” supported by the Ministry of Education, Science, and Technological Development of the Republic of Serbia. T.G.P. would like to thank Dirk Grupe (Morehead State University), Aviv Brokman (University of Kentucky) and Eric Roemmele (University of Kentucky) for useful discussions about Cash statistics.

References

  1. Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 224, 8 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andersen, M., Rho, J., Reach, W. T., Hewitt, J. W., & Bernard, J. P. 2011, ApJ, 742, 7 [NASA ADS] [CrossRef] [Google Scholar]
  3. Arbutina, B., Urošević, D., Andjelić, M. M., Pavlović, M. Z., & Vukotić, B. 2012 ApJ, 746, 79 [NASA ADS] [CrossRef] [Google Scholar]
  4. Arbutina, B., Urošević, D., Vučetić, M. M., Pavlović, M. Z., & Vukotić, B. 2013, ApJ, 777, 31 [NASA ADS] [CrossRef] [Google Scholar]
  5. Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
  6. Bell, A. R. 1978a, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bell, A. R. 1978b, MNRAS, 182, 443 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beltrán, M. T., Estalella, R., Anglada, G., Rodríguez, L. F., & Torrelles, J. M. 2001, AJ, 121, 1556 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
  10. Borkowski, K. J., Lyerly, W. J., & Reynolds, S. P. 2001, ApJ, 548, 820 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bozzetto, L. M., Filipović, M. D., Vukotić, B., et al. 2017, ApJS, 230, 2 [NASA ADS] [CrossRef] [Google Scholar]
  12. Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cherenkov Telescope Array Consortium 2019, Science with the Cherenkov Telescope Array (Singapore: World Scientific Publishing Co. Pte. Ltd.) [Google Scholar]
  14. Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chen, L.-W., Fabian, A. C., & Gendreau, K. C. 1997, MNRAS, 285, 449 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dubner, G., & Giacani, E. 2015, A&ARv, 23, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Estalella, R., Paredes, J. M., & Rius, A. 1983 A&A, 124, 309 [NASA ADS] [Google Scholar]
  18. Foster, A. R., Ji, L., Smith, R. K., & Brickhouse, N. S. 2012, ApJ, 756, 128 [NASA ADS] [CrossRef] [Google Scholar]
  19. Griffith, M. R., & Wright, A. E. 1993, AJ, 105, 1666 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hales, C. A., Murphy, T., Curran, J. R., et al. 2012, MNRAS, 425, 979 [NASA ADS] [CrossRef] [Google Scholar]
  21. Han, J., Wang, C., Xu, J., & Han, J.-L. 2016, Res. Astron. Astrophys., 16, 159 [NASA ADS] [CrossRef] [Google Scholar]
  22. Helder, E. A., Vink, J., Bykov, A. M., et al. 2012, Space Sci. Rev., 173, 369 [NASA ADS] [CrossRef] [Google Scholar]
  23. H.E.S.S. Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Hewitt, J. W., & Yusef-Zadeh, F. 2009, ApJ, 694, L16 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hobbs, G., Faulkner, A., Stairs, I. H., et al. 2004, MNRAS, 352, 1439 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hurley-Walker, N., Callingham, J. R., Hancock, P. J., et al. 2017, MNRAS, 464, 1146 [NASA ADS] [CrossRef] [Google Scholar]
  27. Intema, H. T., Jagannathan, P., Mooley, K. P., & Frail, D. A. 2017, A&A, 598, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Kuntz, K. D., & Snowden, S. L. 2010, ApJS, 188, 46 [NASA ADS] [CrossRef] [Google Scholar]
  29. Lonsdale, C. J., Cappallo, R. J., Morales, M. F., et al. 2009, IEEE Proc., 97, 1497 [Google Scholar]
  30. Markwardt, C. B. 2009, ASP. Conf. Ser., 411, 251 [Google Scholar]
  31. Maron, O., Kijak, J., Kramer, M., & Wielebinski, R. 2000, A&AS, 147, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Onić, D. 2013, Ap&SS, 346, 3 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ostrowski, M. 1999, A&A, 345, 256 [NASA ADS] [Google Scholar]
  34. Ostrowski, M., & Schlickeiser, R. 1993, A&A, 268, 812 [NASA ADS] [Google Scholar]
  35. Pavlović, M. Z., Urošević, D., Vukotić, B., Arbutina, B., & Göker, U. D. 2013, ApJS, 204, 4 [NASA ADS] [CrossRef] [Google Scholar]
  36. Pavlović, M. Z., Dobardzić, A., Vukotić, B., & Urošević, D. 2014, Serb. Astron. J., 189, 25 [NASA ADS] [CrossRef] [Google Scholar]
  37. Reach, W. T., Rho, J., Tappe, A., et al. 2006, AJ, 131, 1479 [NASA ADS] [CrossRef] [Google Scholar]
  38. Reich, W., Fürst, E., Reich, P., & Junkes, N. 1988, Supernova Remnants and the Interstellar Medium, Proceedings of IAU Colloquium 101 (Cambridge: Cambridge University Press), 293 [NASA ADS] [Google Scholar]
  39. Reich, W., Reich, P., & Fuerst, E. 1990a, A&AS, 83, 539 [NASA ADS] [Google Scholar]
  40. Reich, W., Fuerst, E., Reich, P., & Reif, K. 1990b, A&AS, 85, 633 [NASA ADS] [Google Scholar]
  41. Reid, M. J., & Menten, K. M. 1997, ApJ, 476, 327 [NASA ADS] [CrossRef] [Google Scholar]
  42. Reynolds, S. P., Gaensler, B. M., & Bocchino, F. 2012, Space Sci. Rev., 166, 231 [NASA ADS] [CrossRef] [Google Scholar]
  43. Rudnitskij, G. M. 1993, Planetary Nebulae, Proceedings of the 155th Symposium of the IAU held in Innsbruck, Austria, July 13–17, 1992, eds. R. Weinberger & A. Acker (Dordrecht: Kluwer Academic Publishers), 155, 323 [NASA ADS] [Google Scholar]
  44. Rudnitskij, G. M., & Chapman, J. M. 2007, arXiv e-prints [arXiv:astro-ph/0703669] [Google Scholar]
  45. Saken, J. M., Fesen, R. A., & Shull, J. M. 1992, ApJS, 81, 715 [NASA ADS] [CrossRef] [Google Scholar]
  46. Schlickeiser, R., & Fürst, E. 1989, A&A, 219, 192 [NASA ADS] [Google Scholar]
  47. Smith, R. K., & Hughes, J. P. 2010, ApJ, 718, 583 [NASA ADS] [CrossRef] [Google Scholar]
  48. Snowden, S. L., & Kuntz, K. D. 2011, BAAS, 43, 344.17 [NASA ADS] [Google Scholar]
  49. Soszyński, I., Udalski, A., Szymański, M. K., et al. 2013, Acta Astron., 63, 21 [NASA ADS] [Google Scholar]
  50. Stupar, M., Parker, Q. A., Filipović, M. D. 2008, MNRAS, 390, 1037 [NASA ADS] [CrossRef] [Google Scholar]
  51. Tingay, S. J., Goeke, R., Bowman, J. D., et al. 2013, PASA, 30, 7 [Google Scholar]
  52. Trushkin, S. A. 1996, Bull. Spec. Astrophys. Obs., 41, 64 [NASA ADS] [Google Scholar]
  53. Trushkin, S. A. 1998, Bull. Spec. Astrophys. Obs., 46, 62 [NASA ADS] [Google Scholar]
  54. Urošević, D. 2014, Ap&SS, 354, 541 [NASA ADS] [CrossRef] [Google Scholar]
  55. Urošević, D., Pavlović, M. Z., & Arbutina, B. 2018, ApJ, 855, 59 [NASA ADS] [CrossRef] [Google Scholar]
  56. Vink, J. 2012, A&ARv, 20, 49 [Google Scholar]
  57. Vukotić, B., Jurković, M., Urošević, D., & Arbutina, B. 2014, MNRAS, 440, 2026 [NASA ADS] [CrossRef] [Google Scholar]
  58. Wayth, R. B., Lenc, E., Bell, M. E., et al. 2015, PASA, 32, 25 [Google Scholar]
  59. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
1

The GMRT is run by the National Centre for Radio Astrophysics of the TIFR.

All Tables

Table 1

MWA, Effelsberg, and RATAN-600 integrated flux density measurements of SNR G5.9+3.1.

In the text
Table 2

Properties of regions of extraction of source and background spectra for G5.9+3.1.

In the text
Table 3

Summary of fit to extracted XMM-Newton source and background spectra of G5.9+3.1 using TBABS × APEC model.

In the text

All Figures

thumbnail Fig. 1

GLEAM images of G5.9+3.1. Top two panels: wideband image taken over 170–231 MHz. Lower two panels: an RGB image comprised of R = 72–103 MHz, G = 103–134 MHz, B = 139–170 MHz. The full width at half maximums (FWHMs) of the point spread functions (PSFs) of the images are, respectively: 2.4′, 5.2′, 3.9′, and 2.9′. Left panels: images without any annotations. Right panels: annotations indicating the GLEAM photometry measurement; the white lines show the region drawn by the observer that contains the SNR; the gray shaded region shows the area used to calculate the background; the blue dashed lines show a region excluded from the background measurement for containing contaminating background radio galaxies.
In the text
thumbnail Fig. 2

Weighted least-squares fit of the presently known integrated radio continuum spectrum of the SNR G5.9+3.1 using the simple power-law model (Eq. (1)) for pure synchrotron emission (solid line). Circles correspond to the MWA data, diamond symbols indicate Effelsberg data, and triangles depict RATAN observations.
In the text
thumbnail Fig. 3

Adaptively smoothed exposure-corrected combined EPIC image of G5.9+3.1. The image depicts emission detected over the energy range 0.4–1.0 keV and the pixel range of the emission is 3–7.87 counts per second per square degree. The dashed green ellipse is centered on RA (J2000.0) 17h 47m15.0s, Dec (J2000.0) − 22°16′38.5′′ and has major and minor axes of 449.5′′ and 463.4′′, respectively. This ellipse corresponds to the region of extraction of the source spectrum for the whole SNR (see Sect. 5 and Table 2). We note the clear rim-brightened structure seen toward the eastern and southwestern rims of G5.9+3.1. Fainter emission is seen toward the northern rim and interior of the SNR. Emission from discrete sources has been flagged and excised in the creation of this image: voids of emission seen in this image correspond to artifacts from these excisions.
In the text
thumbnail Fig. 4

Same as Fig. 3 but with contours overlaid that depict radio emission detected by the MWA and regions of spectral extraction indicated and labeled. The contour levels correspond to 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.155, and 0.16 Jy beam−1. The X-ray emission along the eastern and western rims of G5.9+3.1 appears to lie interior to the radio rims, while X-ray and radio emission from the northern and southern rims are weak or absent. The source regions of spectral extraction for the northern, western, and eastern rims along with the entire SNR are indicated, as well as the accompanying regions of background spectral extraction.
In the text
thumbnail Fig. 5

Extracted PN, MOS1, and MOS2 spectra of the different regions of G5.9+3.1 as fit with the model and fit parameters given in Table 3. The residuals to the fits are also shown. In all panels, the PN source spectrum is shown in black, the PN FWC spectrum is shown in red, the MOS1 source spectrum is shown in green, the MOS1 FWC spectrum is shown in blue, the MOS2 source spectrum is shown in cyan, and the MOS2 FWC spectrum is shown in purple. Upper left: extracted spectra for the whole SNR. Upper right: extracted spectra for the east rim. Lower left: extracted spectra for the north rim. Lower right: extracted spectra for the west rim.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.