| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834952 | |
| Published online | 14 March 2019 | |
Detection and characterization of an ultra-dense sub-Neptunian planet orbiting the Sun-like star K2-292★
1
Instituto de Astrofísica de Canarias (IAC),
38205
La Laguna,
Tenerife,
Spain
e-mail: rluque@iac.es
2
Departamento de Astrofísica, Universidad de La Laguna (ULL),
38206
La Laguna,
Tenerife,
Spain
3
Department of Astrophysical Sciences, Princeton University,
4 Ivy Lane,
Princeton,
NJ
08544,
USA
4
Department of Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology,
Cambridge,
MA
02139,
USA
5
Landessternwarte, Zentrum für Astronomie der Universtät Heidelberg,
Königstuhl 12,
69117
Heidelberg,
Germany
6
Hamburger Sternwarte,
Gojenbergsweg 112,
21029
Hamburg,
Germany
7
Instituto de Astrofísica de Andalucía (IAA-CSIC),
Glorieta de la Astronomía s/n,
18008
Granada,
Spain
8
Institut de Ciències de l’Espai (ICE, CSIC),
C/Can Magrans, s/n, Campus UAB,
08193
Bellaterra,
Spain
9
Institut d’Estudis Espacials de Catalunya (IEEC),
08034
Barcelona,
Spain
10
Department of Astronomy, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo
113-0033,
Japan
11
Dipartimento di Fisica,
Università di Torino,
Via P. Giuria 1,
10125
Torino,
Italy
12
Department of Earth and Planetary Sciences, Tokyo Institute of Technology,
2-12-1 Ookayama,
Meguro-ku,
Tokyo
152-8551,
Japan
13
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala,
Sweden
14
Leiden Observatory, Leiden University,
2333CA
Leiden,
The Netherlands
15
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University,
Ny Munkegade 120,
8000
Aarhus C,
Denmark
16
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778 Tautenburg,
Germany
17
Centro de Astrobiología (CSIC-INTA),
ESAC campus, Camino Bajo del Castillo s/n,
28692
Villanueva de la Cañada,
Madrid,
Spain
18
Institute of Planetary Research, German Aerospace Center,
Rutherfordstrasse 2,
12489
Berlin,
Germany
19
Department of Astronomy and McDonald Observatory, University of Texas at Austin,
2515 Speedway, Stop C1400,
Austin,
TX
78712,
USA
20
Okayama Astrophysical Observatory, National Astronomical Observatory of Japan, NINS, Asakuchi,
Okayama
719-0232,
Japan
21
Rheinisches Institut für Umweltforschung an der Universität zu Köln,
Aachener Strasse 209,
50931
Köln,
Germany
22
Zentrum für Astronomie und Astrophysik, Technische Universität Berlin,
Hardenbergstr. 36,
10623
Berlin,
Germany
23
Astrobiology Center and National Astronomical Observatory of Japan, NINS,
2-21-1 Osawa,
Mitaka,
Tokyo
181-8588,
Japan
24
Department of Earth, Atmospheric and Planetary Sciences, MIT,
77 Massachusetts Avenue,
Cambridge,
MA
02139,
USA
25
Institute of Geological Sciences, Freie Universität Berlin,
Malteserstr. 74-100,
12249
Berlin,
Germany
26
Astronomy Department and Van Vleck Observatory, Wesleyan University,
Middletown,
CT
06459,
USA
27
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
28
JST, PRESTO,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo 113-0033,
Japan
29
National Astronomical Observatory of Japan,
2-21-1 Osawa,
Mitaka,
Tokyo 181-8588,
Japan
Received:
21
December
2018
Accepted:
25
January
2019
We present the discovery and characterization of a new transiting planet from Campaign 17 of the Kepler extended mission K2. The planet K2-292 b is a warm sub-Neptune on a 17 day orbit around a bright (V = 9.9 mag) solar-like G3 V star with a mass and radius of M⋆ = 1.00 ± 0.03 M⊙ and R⋆ = 1.09 ± 0.03 R⊙, respectively. We modeled simultaneously the K2 photometry and CARMENES spectroscopic data and derived a radius of Rp=2.63−0.10+0.12 R⊕ and mass of Mp=24.5−4.4+4.4 M⊕, yielding a mean density of ρp=7.4−1.5+1.6 g cm−3, which makes it one of the densest sub-Neptunian planets known to date. We also detected a linear trend in the radial velocities of K2-292 (γ˙RV = −0.40−0.07+0.07 m s−1 d−1) that suggests a long-period companion with a minimum mass on the order of 33 M⊕. If confirmed, it would support a formation scenario of K2-292 b by migration caused by Kozai-Lidov oscillations.
Key words: planetary systems / techniques: photometric / techniques: radial velocities / techniques: high angular resolution / stars: individual: HD 119130 / stars: individual: K2-292
The light curve is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/623/A114
© ESO 2019
1 Introduction
The synergybetween the first ground-based transit surveys and high-precision velocimeters aimed at detecting bona fide planets has been a first step toward comprehensive characterizations of exoplanets. The extended Kepler mission K2 (Howell et al. 2014) was the firstto provide the opportunity to search for transiting planets with radii smaller than Neptune and larger than Earth around a significant number of bright, solar-type stars amenable to high-precision radial velocity (RV) measurements. This opened the door to the precise determination of masses and, therefore, bulk densities of this new class of planets that have no counterparts in the solar system.
Results from the original Kepler mission (Borucki et al. 2010) showed that planets with radii smaller than Neptune are the most frequently occurring type within 1 au of solar-type stars (e.g., Petigura et al. 2018). Besides, a quarter of all Sun-like stars – up to 50% in the recent study of Petigura et al. (2018) – host planets smaller than 4 R⊕ with orbital periods shorter than 100 days (Batalha et al. 2013; Marcy et al. 2014; Silburt et al. 2015). Their radius distribution shows a bi-modal structure with a gap around 1.7 R⊕ that separates presumably rocky super-Earths, with radii centered at 1.2 R⊕, from gas-dominated sub-Neptunes, with radii centered at 2.4 R⊕ (Fulton et al. 2017; Fulton & Petigura 2018). The gap has also a potential slope as a function of orbital period and a possible decrease in the value of the critical radius with increasing period (Van Eylen et al. 2018).
While the shape of the bi-modal radius distribution can be understood with photoevaporation models (Owen & Wu 2013, 2017; López & Fortney 2013), it is still not clear how close-in planets are formed. Different mechanisms have been studied, andthey can be roughly divided into two categories: in-situ formation and migration. Hansen & Murray (2012), among others, suggested that low-mass super-Earths or sub-Neptunes formed close to their current orbital locations. On the other hand, disk-driven migration could also explain the formation of close-in planets (e.g., Mordasini et al. 2009a,b; Dawson & Chiang 2014). However, little is known for the rare population of ultra-dense sub-Neptunes without significant envelopes.
In this paper, we present the detection a thorough characterization in terms of radius, mass, and mean density of one such planet, along with a characterization of its host star, K2-292. Analysis of the K2 photometry presented in Sect. 2 reveals that K2-292 b has a radius typical of sub-Neptunian planets. In Sect. 3 we present high-resolution images that allow us to exclude a false-positive scenario due to the background, foreground or physically bound eclipsing binaries. In addition, we present CARMENES high-resolution spectroscopy, used in Sect. 4 for precise determination of the host star’s parameters that reveal its solar-like nature. A joint analysis of CARMENES’ high-precision RVs and K2 photometry performed to determine the planetary parameters is presented in Sect. 5. Finally, in Sect. 6 we discuss the implications of the high density of K2-292 b for planet composition models and formation scenarios.
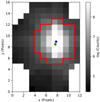 |
Fig. 1 Photometric aperture (red contour) used to construct the K2 light curve. The center of the flux distribution is depicted with a blue dot, while the position of the target in the EPIC catalog is marked in green. |
2 Candidate detection from K2 photometry
The K2 Field 17 was observed from March 1 until May 8 2018, in the direction of the constellation of Virgo. Among the 34 398 long-cadence (29.4-min integration time) targets was K2-292 (EPIC 212628254, HD 119130), proposed by several Guest Observer (GO) programs: GO-17003 (Cochran), GO-17032 (Buzasi), GO-17049 (Howard), and GO-17065 (Dressing). The star K2-292 is poorly investigated with few determined parameters (spectral type by Houk & Swift 1999; RAVE kinematics and metallicities by Boeche et al. 2011; Coşkunoǧlu et al. 2012; basic stellar parameters by Munari et al. 2014). We downloaded the target pixel files from the Mikulski Archive for Space Telescopes (MAST) and extracted the light curve using two methods.
Our first method (for details see Dai et al. 2017) attempts to reduce the brightness fluctuations associated with the rolling motion of the spacecraft using the observed motion of the center of light on the detector, similar to the one described by Vanderburg & Johnson (2014). For each image, we set a circular aperture around the brightest pixel and fit a two-dimensional Gaussian function to the flux distribution. In the case of K2-292, the aperture with the lowest levels of noise has a radius of ~4 pix, as seen in Fig. 1. Then, a piecewise linear function between the observed flux variation and the centroid coordinates of the Gaussian was fitted, which is used to detrend the observed intensity fluctuations. Secondly, to check the consistency in our results, we also built the light curve using an independent method based on the implementation of the pixel level decorrelation model (Deming et al. 2015) using a customized version of the Everest pipeline (Luger et al. 2018). The details of this procedure are described in Pallé et al. (2019).
We searched for transits in both light curves using the Box-fitting Least Squares algorithm (BLS; Kovács et al. 2002), improved to account for the expected scaling of transit duration with orbital period as pointed by Ofir (2014).Once a planetary signal is detected in the power spectrum, we remove such a transit feature and reapplythe BLS algorithm iteratively until no further signals are detected. The detrended light curve and transit detections by each method are shown in Fig. 2. Four transits with a depth of ~550 ppm are clearly detected, whose linear best-fit ephemeris analysis returns a planet candidate with a period of P ~ 17 d. The flux decrement seen at BJD −2 450 000 ≈ 8222 is related to K2 systematics and not to a single transit event.
In orderto check for the possibility of a binary scenario that is mimicking the observed transit signal, we searched the light curves for odd-even transit depth variations and secondary eclipse features. The depth of the odd-even transits agrees within 1σ and there is no hint of a secondary eclipse. As a result, we triggered a follow-up campaign to characterize precisely the K2-292 system.
 |
Fig. 2 Detrended K2 light curves of K2-292 using the two methods described in Sect. 2. Top panel: Dai et al. (2017) method à la Vanderburg & Johnson (2014). Bottom panel: Pallé et al. (2019) method based on the Everest pipeline (Luger et al. 2018). The vertical red lines mark the position of each detected transit. |
3 Ground-based follow-up observations
3.1 High-resolution imaging
We conducted speckle imaging observations of the host star using the NASA Exoplanet Star and Speckle Imager (NESSI; Scott et al. 2016, 2018), mounted on the WIYN 3.5-m telescope at Kitt Peak Observatory. The observations were conducted simultaneously in two narrow bands centered at 562 and 832 nm. Following Howell et al. (2011), we collected and reduced the data, resulting in 4.′′6 × 4.′′6 reconstructed images of the host star. We did not detect any secondary sources in the reconstructed images, and we produced 5σ background sensitivity limits from the reconstructed images using a series of concentric annuli (Fig. 3, top panel).
In addition, we observed K2-292 using the Infrared Camera and Spectrograph (IRCS; Kobayashi et al. 2000) and adaptive-optics system (AO188, Hayano et al. 2010) on the Subaru 8.2-m telescope. For K2-292, two sequences were implemented with a five-point dithering using the K′-band filter. The first sequence was for unsaturated frames for the absolute flux calibration, and we inserted a neutral-density filter with a transmittance of ~1% to avoid saturation. We also obtained saturated frames to look for faint nearby companions as the second sequence without the neutral-density filter. The total integration times for unsaturated and saturated frames were 120 and 12 s, respectively.
We reduced all the IRCS frames in the standard manner as described in Hirano et al. (2016), and obtained median-combined images for the saturated and unsaturated frames, respectively. The combined unsaturated image suggested a full width at half maximum (FWHM) of 0.′′078, which is close to the diffraction limit. No nearby companion is seen in the saturated image. In order to estimate the detection limit of such companions, we computed the flux contrast based on the scatter of flux counts within the annulus centered at the target star. The bottom panel of Fig. 3 shows a 5σ contrast curve as a function of angular separation from the central star, and its inset displays the target image with a field of view of 4′′ × 4′′.
 |
Fig. 3 Top panel: reconstructed images in the 562 and 832 nm narrow bands (inset panel) and their resulting 5σ contrast curves from WIYN/NESSI speckle interferometry. Bottom panel: Subaru/ IRCS+AO188 combined saturated image and 5σ contrast light curve of K2-292. |
3.2 High-resolution spectroscopy
We obtained a total of 24 measurements for K2-292 from June 10 to July 18 2018 with the CARMENES (Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical échelle Spectrographs) instrument (Quirrenbach et al. 2014, 2018), installed at the 3.5-m telescope at the Calar Alto Observatory in Spain. The instrument consists of two channels: the visual channel (VIS) obtains spectra at a resolving power of R = 94 600 in the wavelength range from 0.52 to 0.96 μm, while the near-infrared (NIR) channel yields spectra of R = 80 400 from 0.96 to 1.71 μm. CARMENES performance, data reduction, and wavelength calibration are described in Reiners et al. (2018) and Kaminski et al. (2018).
The dual-channel configuration of the CARMENES spectrograph is motivated by the desire to detect Earth-like planets around M dwarfs, whose redder spectral energy distribution requires red-optical and near-infrared coverage to derive precise RVs. However, due to the solar-like spectral type of K2-292, we only use the VIS observations to measure RVs. We used SERVAL (Zechmeister et al. 2018), a publicly available code based on least-squares fitting. SERVAL employs cross-correlation with a high signal-to-noise ratio (S/N) template that is constructed by coadding allavailable spectra of the star to derive RV values and several spectral indicators. In addition, we computed the cross-correlation function (CCF) using a weighted mask constructed from coadded CARMENES VIS spectra of K2-292. We determined the RV, full width at half maximum, contrast, and bisector velocity span by fitting a Gaussian function to the final CCF, following the method described in Reiners et al. (2018). The final RVs are corrected for barycentric motion, secular acceleration, and nightly zero-points (see Luque et al. 2018, for details).
Due to the low declination of the star, K2-292 was observed from Calar Alto at relatively high airmasses (ranging from 1.5 to 1.9), which has a high impact on the telluric contamination of the spectra. Therefore, we do not consider for the RV computation those spectra whose (S/N) per spectral sampling element, averaged over each order, is smaller than 40. Furthermore, to achieve the highest RV precision, we correct the spectra from telluric absorption using Molecfit (Smette et al. 2015; Kausch et al. 2015) following the method presented in Nortmann et al. (2018) and Salz et al. (2018).
The CARMENES RV measurements are listed in Table B.1. In total, 18 RVs were acquired using high (S/N) telluric-free spectra, covering a time span of 34 d and with a median internal RV precision of σRV = 3.1 m s−1. By computing the generalized Lomb-Scargle periodogram (GLS; Zechmeister & Kürster 2009) of the RVs (Fig. 4a), we find a single peak at the expected frequency of the planet at f = 0.06 d−1 (P =16.6 d). The peak is broad due to the short temporal baseline of our measurements, but consistent within the frequency resolution with the planet candidate atP ~ 17 d. Although the peak has a false alarm probability (FAP) higher than 10%, not enough to be claimed as a solid planet candidate from RVs alone, its consistency with the periodic signal detected in the K2 photometry confirms the planetary nature of the RV variation. We also checked for periodic signals at the expected planet frequency in the spectral indicators obtained with SERVAL and from the CCF, but find no evidence that the RV’s periodicity is due to stellar effects. A peak is seen in Hα and the CCF FWHM at P ~ 3.5 d that may be related to activity. The GLS periodogram of the spectral indicators is shown in the appendix (Fig. A.1) for completeness. We searched also for possible correlations between the RVs and the other spectral indicators but find no evidence of Doppler shifts induced by line distortions. Hence, we conclude that the 17 d-period transiting planet candidate from K2 photometry is a bona fide planet also present in our CARMENES RV measurements.
 |
Fig. 4 Top panel: GLS periodogram of the CARMENES RVs. Bottom panel: GLS periodogram of the residuals from the best-fit model. The vertical red line marks the period of the planet derived from K2 photometry. The dashed line corresponds to FAP = 10% level. The shaded blue area indicates the period space longer than the time span of the observations. |
4 Stellar properties
4.1 Photospheric parameters
We used the coadded high-resolution CARMENES VIS spectrum in order to determine the physical parameters of the host star using the spectral analysis package SME v5.22 (Valenti & Piskunov 1996; Valenti & Fischer 2005). SME is used to calculate, for a starting set of stellar parameters, a synthetic spectrum that is then fitted to the observed spectrum using a χ2 minimization procedure. SME makes use of a grid of recalculated stellar models, in our case the ATLAS12 model atmospheres (Kurucz 2013), which is a set of one-dimensional models applicable to solar-like stars.
In order to determine the effective temperature, Teff, the profile of either of the strong Balmer line wings is fitted to the appropriate stellar spectrum models (Fuhrmann et al. 1993, 1994, 1997a,b; Axer et al. 1994). This fitting procedure has to be carried out carefully since the determination of the level of the adjacent continuum can be difficult for modern high-resolution Echelle spectra where each order only contains a limited wavelength band (Fuhrmann et al. 1997b). The core of each Balmer line is excluded from the fitting process, since this part of the line profile originates above the photosphere and thus contributes at a different effective temperature.
We selected parts of the observed spectrum that contain spectral features that are sensitive to the required parameters. We used the empirical calibration equations for Sun-like stars from Bruntt et al. (2010) and Doyle et al. (2014) in order to determine the micro-turbulent (vmic = 1.0 ± 0.1 km s−1) and macro-turbulent (vmac = 3.1 ± 0.3 km s−1) velocities, respectively. The projected stellar rotational velocity, vsini⋆, and the metallicity, [Fe/H], were measured by fitting the profile of about 100 clean and unblended metal lines.
We find Teff = 5725 ± 65 K, log g = 4.30 ± 0.15, [Fe∕H] = 0.07 ± 0.05, and v sin i⋆ = 4.6 ± 1.0 km s−1. The effective temperatures derived from this work, as well as from Gaia Data Release 2 (DR2; Gaia Collaboration 2018), and the RAdial Velocity Experiment (RAVE; Kunder et al. 2017) are within 1σ. We chose to use the value from our work since it is derived from high-resolution spectroscopy and for homogeneity, while the other values are derived from either low-resolution spectroscopy (RAVE) or photometry based on few wide bands (Gaia). Only the surface gravity does not agree within 1σ with the results from Kunder et al. (2017). All derived values and previous ones reported in the literature can be found in Table 1.
Stellar parameters of K2-292.
4.2 Mass, radius, and age of the host star
To derive the physical parameters of K2-292, we used PARAM 1.31, a web interface for Bayesian estimation of stellar parameters using the PARSEC isochrones from Bressan et al. (2012). The required input is the effective temperature and metallicity of the star, together with its apparent visual magnitude and parallax. Following the method described in Gandolfi et al. (2008), we found that the interstellar reddening is zero and did not correct the apparent visual magnitude for extinction. We used the spectroscopically derived photospheric parameters obtained in the previous section and the values reported in Table 1. For the Gaia parallax, we added quadratically 0.1 mas to the nominal uncertainty to account for systematic uncertainties following Luri et al. (2018).
We derive a mass of M = 1.00 ± 0.03 M⊙, and a radius of R = 1.09 ± 0.03 R⊙, yielding a surface gravity of logg = 4.33 ± 0.04, in fairly good agreement with our spectroscopic value of 4.30 ± 0.15. The stellar models constrain the age of the star to be 6.8 ± 2.3 Gyr. We stress that the uncertainties on the derived parameters are internal to the stellar models used and do not include systematic uncertainties related to input physics. All derived values and previous ones reported in the literature can be found in Table 1.
5 Joint analysis
To derive precisely the parameters of the K2-292 system, we modeled simultaneously the photometric and spectroscopic data using the code pyaneti (Barragán et al. 2019). This software computes posterior distributions using Markov chain Monte Carlo methods based on Bayesian analysis. It uses the limb-darkened quadratic transit model by Mandel & Agol (2002) to fit the K2 light curves, and Keplerian orbits to model the RV data. We used for the joint fit the detrended K2 light curve obtained with the method of Pallé et al. (2019) described in Sect. 2. In order to account for the 30-min integration time of the photometric data, we re-sampled the model using ten iterations (see Kipping 2010). The fitted parameters are the systemic velocity γRV, the RV semi-amplitude K, the transit epoch T0, the period P, scaled semi-major axis a∕R⋆, planet-to-star radius ratio Rp∕R⋆, impact parameter b, eccentricity e, longitude of periastron ω, and the Kipping (2013) limb-darkening parametrization coefficients q1 and q2. We used wide-range non-informative uniform priors and the same likelihood as Barragán et al. (2016), except for the scaled semi-major axis, where we used Kepler’s third law to set a Gaussian prior based on the stellar mass and radius derived in Sect. 4.2. To explore the parameter space, we created 500 independent chains for each parameter and checked their convergence using the Gelman–Rubin statistic. Adequate convergence was considered when the Gelman–Rubin potential scale reduction factor dropped to within 1.03. Once all chains converged, we ran 25 000 more iterations with a thin factor of 50, leading to a posterior distribution of 250 000 independent samples for each fitted parameter.
A simple joint fit to the data reveals that the residuals of the RVs exhibit a long-term component, as seen also in the GLS periodogram of Fig. 4, where there is power at periods larger than the baseline of the observations. We considered two different scenarios regarding the nature of such long-term components: that it is physical and may be caused by a further companion and/or the rotation of the star, or that it is related to instrumental systematics.
Considering the first scenario, the photometry does not show evidence of a second transiting companion during the observed window, or variability attributable to the rotational period of the star that may induce a long-term component in the RVs. However, it is possible that the hypothetical long-period companion does not transit or that the transit occurred before or after the K2 observations. Alternatively, the long-term trend may be caused by systematic effects in the RVs, such as remaining effects from incomplete telluric decontamination. In either case, our data are not sufficient to infer the true nature of this long-term RV trend.
In orderto properly fit the current dataset, we tried different approaches to account for the RV long-term component described above. Thus, we performed the joint fit in two ways: (i) disregarding any long-term trend (M0) and (ii) including a linear trend term in the RV fit of the data (M1). Table 2 shows the goodness of the fit for each model. The preferred model is M1: a Keplerian orbit with a linear trend term, with the lowest 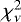 and Akaike information criterion (AIC; Akaike 1974). We used the AIC in spite of the widespread Bayesian information criterion because it performs better in selecting the “true model” when the number of parameters is small (Burnham & Anderson 2004), as is the case for our RV measurements.
and Akaike information criterion (AIC; Akaike 1974). We used the AIC in spite of the widespread Bayesian information criterion because it performs better in selecting the “true model” when the number of parameters is small (Burnham & Anderson 2004), as is the case for our RV measurements.
The orbital parameters and their uncertainties from the photometric and spectroscopic joint fit of such a model are listed in Table 3. The large uncertainties in the limb-darkening coefficients arise from the shallow transit depth (550 ppm) and the small number of data points and transits, especially during ingress and egress. Their posterior distributions are not symmetric and lean towards low values, but by fixing them interpolating the table of Claret & Bloemen (2011) we retrieve the same values within 1σ uncertainties as those derived by pyaneti using uniform priors. Therefore, following Csizmadia et al. (2013), we chose to fit them in our joint analysis to achieve the best precision in the planet radius, impact parameter, and scaled semi-major axis. Figure 5 shows the RV time series along with the best fitting transit and RV phase-folded models.
Model comparison.
Orbital parameters of the preferred model M1.
 |
Fig. 5 Top panel: time series of CARMENES RVs. Bottom left panel: phase-folded K2 light curve to the orbital period of K2-292 b and residuals. Bottom right panel: phase-folded RV curve to the same period and the linear trend subtracted. The solid black line in all panels indicates the preferred best-fit model M1. |
 |
Fig. 6 Mass–radius diagram for all known planets with masses between 0.5 and 30 M⊕ and radius 1–4 R⊕ determined with a precision better than 30%, comprising from Earth-like to sub-Neptunian regimes. K2-292 b is shown in black, while K2-66 b (Sinukoff et al. 2017) is shown in gray. Data are taken from the TEPCat database of well-characterized planets (Southworth 2011). Theoretical models for the planet’s internal composition are taken from Zeng et al. (2016). |
6 Discussion and summary
We determine that K2-292 b has a mass of 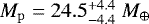 and a radiusof
and a radiusof 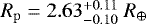 , which corresponds to a bulk density of
, which corresponds to a bulk density of 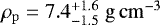 . Figure 6 shows the masses and radii of all confirmed planets whose precision in both parameter determinations is better than 30%. With such physical parameters, K2-292 b becomes one of the densest sub-Neptunian planets known to date, joining a rare population with only K2-66 b (Sinukoff et al. 2017) as a comparable case. For these planets, mass-radius relations such as the one presented by Weiss & Marcy (2014) do not apply. Instead, we see the remarkable differences in composition of planets with masses ranging from 10 to 30 M⊕.
. Figure 6 shows the masses and radii of all confirmed planets whose precision in both parameter determinations is better than 30%. With such physical parameters, K2-292 b becomes one of the densest sub-Neptunian planets known to date, joining a rare population with only K2-66 b (Sinukoff et al. 2017) as a comparable case. For these planets, mass-radius relations such as the one presented by Weiss & Marcy (2014) do not apply. Instead, we see the remarkable differences in composition of planets with masses ranging from 10 to 30 M⊕.
Planet K2-292 b is consistent with a pure silicate composition using Zeng et al. (2016) models. More complex three-layer models provide very similar results (Zeng & Sasselov 2013). Also, following López & Fortney (2014), we determine that if the planet has an H/He envelope atop the rocky-composition core, the former would represent less than 1% of the planet’s mass, which is in agreement with the statistical study of Wolfgang & López (2015) using sub-Neptunian planet candidates from Kepler. In the same study, the authors also stress the lack of a deterministic mass-radius relationship and the necessity of reliable mass measurements for the sub-Neptunian planet population.
The only other known ultra-dense sub-Neptune K2-66 b orbits very close to its host star and receives a high level of irradiation, placing it in the photoevaporation desert defined by Lundkvist et al. (2016). As a consequence, together with the fact that K2-66 is evolving up the subgiant branch, Sinukoff et al. (2017) concluded that photoevaporation stripped off the low-density volatiles in the planet envelope leading to the high density measured today. We investigated if the high density of K2-292 b could also be due to the absence of a substantial atmosphere caused by evaporation, as would be expected considering its location above the radius gap (Fulton & Petigura 2018; Van Eylen et al. 2018). Following the formulation in Lecavelier Des Etangs (2007), we derive a mass loss rate from extreme ultraviolet radiation of the star of only 0.005 M⊕ over the age of the star, which is insufficient to reduce significantly the radius of the planet. In addition, due to its period of 17 d and an incident flux of 67 F⊕, K2-292 b is far from the photoevaporation desert.
Consequently, K2-292 b likely formed with high density, similar to K2-110 b (ρp = 5.2 ± 1.2 g cm−3, Osborn et al. 2017). The remaining question is then how such a dense planet located at 0.13 au from its host star may have formed. Formation in situ can be ruled out, as a disk mass enhancement by a factor of ~ 40 above the minimum-mass solar nebula would be needed to form K2-292 b (Schlichting 2014). However, no significant enhancement is needed if the planet formed at larger distances (> 2 au), making inward migration a plausible explanation.
Kennedy et al. (2006) showed that the location of the snow line moves inward as a function of time. In the case of a solar-type star like K2-292, the current location of the snow line is at approximately 1 au, but it was as far as 5 au in the first Myr. Therefore, it is possible that the absence of volatiles can be explained by the fact that even though K2-292 b formed at large distances and migrated inward, it always did it inside the snow line (Kennedy & Kenyon 2008).
There are two main mechanisms to trigger inward migration: via interactions with the gaseous disk or dynamical interactions with another body. The latter type arises from the gravitational force exerted by a sufficiently massive body, which can also be expressed in terms of a torque. This torque alters the angular momentum of the planet’s orbit, resulting in a variation of the orbital elements, particularly, a decrease over time of the semi-major axis. Particularly, the migration could indeed be caused by Kozai-Lidov oscillations (Dawson & Chiang 2014; Mustill et al. 2017); these could be excited by the possible long-period companion suggested by a linear trend in the RV data. The derived slope, in case it is of a planetary nature, suggests a long-period companion with a minimum mass on the order of 33 M⊕ (see Eq. (1) in Feng et al. 2015).
Multiplanetary systems sculpted by Kozai-Lidov mechanisms are expected to exhibit significant mutual inclinations and this could be the reason why the further companion is not detected in the K2 light curve. The eccentricity of the transiting planet cannot be well constrained by the current RV data, but it is reasonable to assume that the eccentricity is small but non-zero, given that there is only one single transiting planet. Van Eylen et al. (2019) found that there is an eccentricity spread for this kind of system, and that they are well described by the positive half of a Gaussian, peaking at zero and with a width of 0.32 ± 0.06. However, to prove the proposed scenario, more measurements would be needed to constrain the eccentricity of the planet and reveal the nature of the slope in the RV time series.
Acknowledgements
This paper includes data collected by the K2 mission. Funding for the K2 mission is provided by the NASA Science Mission directorate. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC; https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain) funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas(CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium. R. L. has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 713673 and financial support through the “la Caixa” INPhINIT Fellowship Grant for Doctoral studies at Spanish Research Centres of Excellence, “la Caixa” Banking Foundation, Barcelona, Spain. This work is partly financed by the Spanish Ministry of Economics and Competitiveness through grants ESP2013-48391-C4-2-R and AYA2016-79425-C3, and supported by the Japan Society for Promotion of Science (JSPS) KAKENHI Grant Number JP16K17660, JP18H01265 and JP18H05439, and JST PRESTO Grant Number JPMJPR1775. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement no.: DNRF106). K.W.F.L acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Exoplanets in the Mass-Density Diagram” (RA 714/14-1). M.F. and C.M.P. gratefully acknowledge the support of the Swedish National Space Agency.
Appendix A Frequency analysis of spectral indicators
 |
Fig. A.1 GLS periodograms of CARMENES RVs (panel a) and their residuals (panel b) after removing the planet signal at f = 0.06 d−1 derived fromK2 photometry, marked in red. Panels c–e: periodograms of the chromatic index, differential line width, and Hα index. Panels f–h: periodograms for the cross-correlation function full-width half-maximum, contrast, and bisector velocity span. The horizontal dashed line shows the theoretical FAP level of 10%. The shaded blue area indicates the period range longerthan the time span of the observations. |
Appendix B Radial velocity measurements
Radial velocities and formal uncertainties of K2-292.
References
- Akaike, H. 1974, IEEE Trans. Automat. Contr., 19, 716 [Google Scholar]
- Axer, M., Fuhrmann, K., & Gehren, T. 1994, A&A, 291, 895 [NASA ADS] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Barragán, O., Grziwa, S., Gandolfi, D., et al. 2016, AJ, 152 [Google Scholar]
- Barragán, O., Gandolfi, D., & Antoniciello, G. 2019, MNRAS, 482, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Boeche, C., Siebert, A., Williams, M., et al. 2011, AJ, 142, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Burnham, K. P., & Anderson, D. R., eds. 2004, Model Selection and Multimodel Inference (New York: Springer) [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coşkunoǧlu, B., Ak, S., Bilir, S., et al. 2012, MNRAS, 419, 2844 [NASA ADS] [CrossRef] [Google Scholar]
- Csizmadia, S., Pasternacki, T., Dreyer, C., et al. 2013, A&A, 549, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dai, F., Winn, J. N., Gandolfi, D., et al. 2017, Masayuki Kuzuhara, 17, 16 [Google Scholar]
- Dawson, R. I., & Chiang, E. 2014, Science, 346, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, D., Knutson, H., Kammer, J., et al. 2015, ApJ, 805, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, A. P., Davies, G. R., Smalley, B., Chaplin, W. J., & Elsworth, Y. 2014, MNRAS, 444, 3592 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, Y. K., Wright, J. T., Nelson, B., et al. 2015, ApJ, 800, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1993, A&A, 271, 451 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1994, A&A, 285, 585 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M., Frank, C., Reetz, J., & Gehren, T. 1997a, A&A, 323, 909 [NASA ADS] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M. J., & Bernkopf, J. 1997b, A&A, 326, 1081 [NASA ADS] [Google Scholar]
- Fulton, B. J., & Petigura, E. A. 2018, AJ, 156, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gandolfi, D., Alcalá, J. M., Leccia, S., et al. 2008, ApJ, 687, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Murray, N. 2012, ApJ, 751, 158 [Google Scholar]
- Hayano, Y., Takami, H., Oya, S., et al. 2010, in Adaptive Optics Systems II, Proc. SPIE, 7736, 77360N [Google Scholar]
- Hirano, T., Fukui, A., Mann, A. W., et al. 2016, ApJ, 820, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Houk, N., & Swift, C. 1999, in Michigan Spectral Survey, (Ann Arbor, University of Michigan), 5 [Google Scholar]
- Howell, S. B., Everett, M. E., Sherry, W., Horch, E., & Ciardi, D. R. 2011, AJ, 142, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Kaminski, A., Trifonov, T., Caballero, J. A., et al. 2018, A&A, 618, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., Kenyon, S. J., & Bromley, B. C. 2006, ApJ, 650, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 408, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kobayashi, N., Tokunaga, A. T., Terada, H., et al. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye & A. F. Moorwood, Proc. SPIE, 4008, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kunder, A., Kordopatis, G., Steinmetz, M., et al. 2017, AJ, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 2013, Astrophysics Source Code Library [record ascl:1303.024] [Google Scholar]
- Lecavelier Des, A. 2007, A&A, 461, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luger, R., Kruse, E., Foreman-Mackey, D., Agol, E., & Saunders, N. 2018, AJ, 156, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Lundkvist, M. S., Kjeldsen, H., Albrecht, S., et al. 2016, Nat. Commun., 7, 11201 [Google Scholar]
- Luque, R., Nowak, G., Pallé, E., et al. 2018, A&A, 620, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López, E. D., & Fortney, J. J. 2013, ApJ, 776, 2 [NASA ADS] [CrossRef] [Google Scholar]
- López, E. D., & Fortney, J. J. 2014, ApJ, 792, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Weiss, L. M., Petigura, E. A., et al. 2014, Proc. Natl. Acad. Sci., 111, 12655 [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009a, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009b, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Henden, A., Frigo, A., et al. 2014, AJ, 148, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Mustill, A. J., Davies, M. B., & Johansen, A. 2017, MNRAS, 468, 3000 [NASA ADS] [CrossRef] [Google Scholar]
- Nortmann, L., Pallé, E., Salz, M., et al. 2018, Science, 362, 1388 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofir, A. 2014, A&A, 561, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osborn, H. P., Santerne, A., Barros, S. C. C., et al. 2017, A&A, 604, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Wu, Y. 2013, ApJ, 775, 105 [Google Scholar]
- Owen, J. E., & Wu, Y. 2017, ApJ, 847, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Pallé, E., Nowak, G., Luque, R., et al. 2019, A&A, 623, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petigura, E. A., Marcy, G. W., Winn, J. N., et al. 2018, AJ, 155, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471F [Google Scholar]
- Quirrenbach, A., Amado, P. J., Ribas, I., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, Proc. SPIE, 10702, 107020W [Google Scholar]
- Reiners, A., Ribas, I., Zechmeister, M., et al. 2018, A&A, 609, L5 [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A&A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichting, H. E. 2014, ApJ, 795, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, N. J., Howell, S. B., & Horch, E. P. 2016, in Optical and Infrared Interferometry and Imaging V, Proc. SPIE, 9907, 99072R [CrossRef] [Google Scholar]
- Scott, N. J., Howell, S. B., Horch, E. P., & Everett, M. E. 2018, PASP, 130, 054502 [Google Scholar]
- Silburt, A., Gaidos, E., & Wu, Y. 2015, ApJ, 799, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Sinukoff, E., Howard, A. W., Petigura, E. A., et al. 2017, AJ, 153, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A.,& Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Valenti, J. A.,& Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderburg, A., & Johnson, J. A. 2014, PASP, 126, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eylen, V., Agentoft, C., Lundkvist, M. S., et al. 2018, MNRAS, 479, 4786 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eylen, V., Albrecht, S., Huang, X., et al. 2019, AJ, 157, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, L. M., & Marcy, G. W. 2014, ApJ, 783, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfgang, A., & López, E. 2015, ApJ, 806, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
- Zeng, L., & Sasselov, D. 2013, PASP, 125, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, L., Sasselov, D. D., & Jacobsen, S. B. 2016, ApJ, 819, 127 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Photometric aperture (red contour) used to construct the K2 light curve. The center of the flux distribution is depicted with a blue dot, while the position of the target in the EPIC catalog is marked in green. |
| In the text | |
 |
Fig. 2 Detrended K2 light curves of K2-292 using the two methods described in Sect. 2. Top panel: Dai et al. (2017) method à la Vanderburg & Johnson (2014). Bottom panel: Pallé et al. (2019) method based on the Everest pipeline (Luger et al. 2018). The vertical red lines mark the position of each detected transit. |
| In the text | |
 |
Fig. 3 Top panel: reconstructed images in the 562 and 832 nm narrow bands (inset panel) and their resulting 5σ contrast curves from WIYN/NESSI speckle interferometry. Bottom panel: Subaru/ IRCS+AO188 combined saturated image and 5σ contrast light curve of K2-292. |
| In the text | |
 |
Fig. 4 Top panel: GLS periodogram of the CARMENES RVs. Bottom panel: GLS periodogram of the residuals from the best-fit model. The vertical red line marks the period of the planet derived from K2 photometry. The dashed line corresponds to FAP = 10% level. The shaded blue area indicates the period space longer than the time span of the observations. |
| In the text | |
 |
Fig. 5 Top panel: time series of CARMENES RVs. Bottom left panel: phase-folded K2 light curve to the orbital period of K2-292 b and residuals. Bottom right panel: phase-folded RV curve to the same period and the linear trend subtracted. The solid black line in all panels indicates the preferred best-fit model M1. |
| In the text | |
 |
Fig. 6 Mass–radius diagram for all known planets with masses between 0.5 and 30 M⊕ and radius 1–4 R⊕ determined with a precision better than 30%, comprising from Earth-like to sub-Neptunian regimes. K2-292 b is shown in black, while K2-66 b (Sinukoff et al. 2017) is shown in gray. Data are taken from the TEPCat database of well-characterized planets (Southworth 2011). Theoretical models for the planet’s internal composition are taken from Zeng et al. (2016). |
| In the text | |
 |
Fig. A.1 GLS periodograms of CARMENES RVs (panel a) and their residuals (panel b) after removing the planet signal at f = 0.06 d−1 derived fromK2 photometry, marked in red. Panels c–e: periodograms of the chromatic index, differential line width, and Hα index. Panels f–h: periodograms for the cross-correlation function full-width half-maximum, contrast, and bisector velocity span. The horizontal dashed line shows the theoretical FAP level of 10%. The shaded blue area indicates the period range longerthan the time span of the observations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


