| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201834464 | |
| Published online | 06 March 2019 | |
STiC: A multiatom non-LTE PRD inversion code for full-Stokes solar observations
1
Institute for Solar Physics, Dept. of Astronomy, Stockholm University, AlbaNova University Centre, 106 91 Stockholm, Sweden
e-mail: jaime@astro.su.se
2
National Solar Observatory, 3665 Discovery Drive, Boulder, CO 80303, USA
Received:
19
October
2018
Accepted:
16
January
2019
The inference of the underlying state of the plasma in the solar chromosphere remains extremely challenging because of the nonlocal character of the observed radiation and plasma conditions in this layer. Inversion methods allow us to derive a model atmosphere that can reproduce the observed spectra by undertaking several physical assumptions. The most advanced approaches involve a depth-stratified model atmosphere described by temperature, line-of-sight velocity, turbulent velocity, the three components of the magntic field vector, and gas and electron pressure. The parameters of the radiative transfer equation are computed from a solid ground of physical principles. In order to apply these techniques to spectral lines that sample the chromosphere, nonlocal thermodynamical equilibrium effects must be included in the calculations. We developed a new inversion code STiC (STockholm inversion Code) to study spectral lines that sample the upper chromosphere. The code is based on the RH forward synthesis code, which we modified to make the inversions faster and more stable. For the first time, STiC facilitates the processing of lines from multiple atoms in non-LTE, also including partial redistribution effects (PRD) in angle and frequency of scattered photons. Furthermore, we include a regularization strategy that allows for model atmospheres with a complex depth stratification, without introducing artifacts in the reconstructed physical parameters, which are usually manifested in the form of oscillatory behavior. This approach takes steps toward a node-less inversion, in which the value of the physical parameters at each grid point can be considered a free parameter. In this paper we discuss the implementation of the aforementioned techniques, the description of the model atmosphere, and the optimizations that we applied to the code. We carry out some numerical experiments to show the performance of the code and the regularization techniques that we implemented. We made STiC publicly available to the community.
Key words: Sun: chromosphere / radiative transfer / polarization / Sun: magnetic fields / stars: atmospheres
© ESO 2019
1. Introduction
The new generation of 4 m telescopes (DKIST, EST) aims at studying the chromosphere and its coupling to the underlying photosphere with unprecedented spatial resolution and signal-to-noise ratio. In the photosphere the local thermodynamical equilibrium approximation (LTE) can be adopted to model the observations in most spectral lines, but in the chromosphere collisional rates are in comparison very low, making this assumption generally not valid. Therefore the translation of the observed intensities to the underlying physical parameters of the plasma remains very challenging and the nonlocal character of the problem must be taken into account. From an observational perspective one of the most successful approaches to do so has been spectropolarimetric inversions (hereafter inversions; see reviews by del Toro Iniesta & Ruiz Cobo 2016 and de la Cruz Rodríguez & van Noort 2017).
Inversion codes allow the reconstruction of physical parameters from spectropolarimetric observations by assuming a model. Traditionally, the assumed model can be described by parameters of the radiative transfer equation directly (e.g., Milne–Eddington or constant slab model), or with thermodynamical variables from which the parameters of the radiative transfer equation can be calculated. The former does not allow the inclusion of a depth-varying line-of-sight velocity of magnetic field vector. Depth-varying LTE inversions were introduced by Ruiz Cobo & del Toro Iniesta (1992) under the assumption of LTE in the Stokes Inversion based on Reponse functions code (SIR). Under these conditions the atom populations are strictly set by the local conditions of the atmospheric plasma and the computation of the emerging intensity can be computed by calculating a formal solution of the polarized radiative transfer equation. These ideas were also used in the Stokes-Profiles-INversion-ORoutines (SPINOR; Frutiger et al. 2000). Perhaps the most popular photospheric lines used in Milne–Eddington (ME) and LTE inversions are Fe I lines such as the 525 nm dublet, 617 nm, 630 nm dublet, and 1565 nm dublet (some examples of recent studies are Scharmer et al. 2013; Jafarzadeh et al. 2014; Buehler et al. 2015; Martínez González et al. 2016; Esteban Pozuelo et al. 2016; Danilovic et al. 2016, 2017; Centeno et al. 2017; Borrero et al. 2017; Pastor Yabar et al. 2018).
The first attempts to perform such calculations under non-LTE conditions, where the rate equations are not dominated by collisional terms, were carried out by Socas-Navarro et al. (2000) in the Ca II infrared triplet lines (λ8498, λ8542, λ8662). Currently, the Non-LTE Inversion Code based on the Lorien Engine (NICOLE) allows us to perform such inversions assuming Zeeman-induced polarization (Socas-Navarro et al. 2015). Only recently a new non-LTE inversion code has been developed that includes for the first time non-LTE analytical response functions (Milić & van Noort 2018).
The Ca II infrared triplet lines sample the lower chromosphere (see Fig. 1) and they can be modeled assuming a complete redistribution of scattered photons (Uitenbroek 1989) and statistical equilibrium (Wedemeyer-Böhm & Carlsson 2011). Comparatively, the Na I D lines and Mg I 517 nm line have larger sensitivity to magnetic fields in the upper photosphere/lower chromosphere, but they form deeper than the Ca II IR triplet lines (Leenaarts et al. 2010; Rutten et al. 2011; Quintero Noda et al. 2018).
 |
Fig. 1. Vertical slice from a Bifrost radiation-MHD simulation, indicating the approximate formation height of different diagnostics. The solid lines indicate the τ = 1 layer at the core of the Mg II k line (purple), Ca II K line (navy) and Hα line (orange). The black solid line indicates the location where T = 20 kK and the dashed black line the plasma β = 1 layer. The gray shades illustrate the He I 10830 line opacity. We indicated the entire formation range of the Fe I 6301 line in green and the Ca II 8542 line in red. |
Unfortunately, the selection of lines that are sensitive to the upper chromosphere is not large; these are Mg II h& k, Ca II H&K, the Lyman alpha line, and the He I D3 and 10830 lines. With the exception of the He I lines, all the aforementioned diagnostics are strong resonance lines that are affected by partial redistribution effects of scattered photons, and these effects must be included in forward synthesis calculations. However, there are good reasons to attempt to include some of these lines simultaneously in one inversion, which has not been possible until now. These reasons are as follows:
-
By including information of the upper chromosphere, we can attempt to discriminate between physical processes that do not leave a clear imprint in the lower chromosphere (e.g., Kerr et al. 2016), or attempt to constrain opacity effects induced by the combined action of gas flows and temperature fluctuations (Scharmer 1984; de la Cruz Rodríguez et al. 2015; Henriques et al. 2017).
-
These upper chromosphere lines are also sensitive to the middle and lower chromosphere, providing valuable redundant information to constrain physical parameters in those layers (see Fig. 1).
-
If spectral lines from different atomic species can be processed simultaneously, some of the degeneracies that can arise between temperature (opacity broadening) and microturbulence (e.g., Shine & Linsky 1974; Carlsson et al. 2015) can be ameliorated because the thermal term present in the Doppler broadening of the line is divided by a different mass, whereas the turbulent velocity term is the same in all cases.
In this paper we present the STockholm inversion COde (STiC), which allows, for the first time, the processing of spectral lines from multiple atoms simultaneously, including partial redistribution effects (PRD) of scattered photons in angle and frequency. In the present paper, we discuss how the code operates and we present a new regularizing Levenberg–Marquardt algorithm (LM), which improves the convergence of the inversion process and allows for more degrees of freedom without loosing fidelity and unicity of the solution. Early versions of STiC have already been used in previous studies (de la Cruz Rodríguez et al. 2016; Leenaarts et al. 2018; Gošić et al. 2018; da Silva Santos et al. 2018).
2. Spectral synthesis module
The STiC code started as a modular LTE inversion code. In order to add non-LTE radiative transfer capabilities, we modified the 2014 version of RH (Uitenbroek 2001) to create a synthesis module that can be called efficiently from the main inversion code. The RH code can solve the non-LTE problem in multiple atoms at the same time, and it includes PRD effects in strong resonance lines.
The code STiC operates on a column-by-column basis, assuming plane-parallel geometry to solve the statistical equilibrium equations, usually referred to as the 1.5D approximation. Once the atom population densities are known for all atoms, a final formal solution is computed at the heliocentric angle of the observations. Unfortunately, horizontal radiative transfer cannot be included in these kinds of calculations as the computation of the derivatives of the intensity vector with respect to each physical parameter would be prohibitive, among other challenges such as radiative coupling that would be present among the different pixels.
Scattering is expected to be more dominant when collisional rates are low, and the latter are particularly low in the upper chromosphere. A number of recent studies have emphasized the importance of 3D radiative transfer when modeling strong scattering lines (e.g., Leenaarts et al. 2009; Sukhorukov & Leenaarts 2017; Bjørgen et al. 2018), especially for simulating observations toward the solar limb. However, those studies have made use of radiation 3D magnetohydrodynamics (MHD) simulations representative of quiet-Sun situations. In fact, the chromospheric gas density in those MHD simuilations seems to be lower than what observations indicate, even in the quiet-Sun (see details in Carlsson et al. 2016). The main target for our inversions are active regions, where the magnetic field is stronger and the ionization degree is higher than in the quiet-Sun. Furthermore, in active regions the transition region is usually pushed to higher mass densities and the local temperature is larger than in the quiet-Sun (Carlsson et al. 2015). All these effects would arguably lead to larger collisional rates in the chromosphere than the situation represented in those MHD simulations. For all these reasons we are compelled to speculate that the aforementioned studies that analyze 3D effects are representative of a worse case scenario when active regions are the main observational target.
2.1. Changes and optimizations to RH
This version of RH includes the fast PRD angle approximation proposed by Leenaarts et al. (2012), but we optimized the original algorithm with the following changes:
-
The algorithm originally implemented in RH by Leenaarts et al. (2012) computed the mean intensity in the comoving frame of the grid cell for all wavelengths, but that quantity is only used in calculations related to PRD or cross-redistribution lines (XRD). We changed the structure of the algorithm to ensure that these operations are only performed and stored for frequencies associated with PRD/XRD lines, rather than for the entire emerging spectrum.
-
We rearranged and restricted the extent of the loops where the interpolation coefficients are computed, saving between a factor two and three in the execution time of these calculations.
With this new implementation of the algorithm, the amount of time spent in the precomputation of interpolation coefficients is negligible in most applications.
RH can compute the van der Waals damping parameter (from collisions with neutral hydrogen) using the recent formalism of Barklem et al. (2000). Inside RH, this is done by interpolating the corresponding coefficients for the line under consideration from a table that is only valid for neutral species. For lines from ionized species these tables cannot be used. However, these coefficients have been computed for strong chromospheric lines like Ca II H&K, the Ca II IR triplet lines, and Mg II H&K (e.g., Barklem & O’Mara 1998) and they allow for a more accurate estimate of the damping wings. Therefore, we slightly modified the input atom format to allow for the feeding of those coefficients manually if needed.
Finally, since we need to compute response functions by finite differences during the inversion, we allow the code to store departure coefficients from LTE that can be used to initialize the atom populations during the inversions, a trick that was already introduced in the NICOLE code. This simple change allows the response functions at each node to be computed with very few iterations.
2.2. Formal solution of the radiative transfer equation
We included cubic DELO-Bezier formal solvers for polarized and unpolarized radiation (de la Cruz Rodríguez & Piskunov 2013), which allow us to accurately solve the radiative transfer equation in coarse depth grids. Given our choices in the definition of the Bezier interpolant control points used in the formal solver, the latter is exactly equivalent to a Hermite method (Auer 2003; Ibgui et al. 2013). The accuracy of these methods has been recently analyzed in great detail for the polarized case by Janett et al. (2017) and Janett & Paganini (2018).
The monochromatic unpolarized cubic Bezier integration scheme is given by
where the subindex u indicates quantities located in the upwind point, where both the intensity (Iu), the source function (Su) and the control point (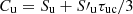 ) are known. The subindex c indicates quantities located in the central point, where only the source function Sc and the control point (
) are known. The subindex c indicates quantities located in the central point, where only the source function Sc and the control point (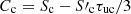 ) are known, but not the intensity (Ic) that we want to compute. The interpolation coefficients are
) are known, but not the intensity (Ic) that we want to compute. The interpolation coefficients are
In their analysis, Janett et al. (2017) also considered another Hermitian method, originally introduced by Bellot Rubio et al. (1998) (LBR hereafter), which seems to perform extremely well in their tests. We were encouraged by those results to try to implement polarized and unpolarized version of these solvers. The latter does not make use of the analytical formal solution of the transfer equation which, for unpolarized light, is
where Ic is the intensity at the central point, Iu is the already computed upwind intensity, S is the source function, and δτuc is the optical thickness of the medium between the upwind and central points. Normally, the integral of the source function in Eq. (3) is solved analytically by approximating the source function with a given depth-dependence: linear, parabolic, Bezier, Hermite. So these interpolants are only used to describe the source function.
In LBR’s method, the intensity vector at the central point of the interval is computed with a polynomial expansion around the upwind point. After some algebra, and using the transfer equation to provide the first and second derivatives of the intensity, they obtained a solution with Hermitian form.
A priori this method is very fast to compute and it does not require the computation of exponentials and vanishing small quantities. The latter may be a great asset when computing the mean intensities that are used to solve the non-LTE problem. But it does so by loosing some of the insights provided by the analytical form of the transfer equation in Eq. (3). The reason is that in this case, the polynomial expansion of the intensity must account for the exponential term in the optically thin regime, but it must also properly describe the behavior of the local contributions in optically thick cases.
If we apply the principles described in Bellot Rubio et al. (1998) to the unpolarized case, we recover the usual integration scheme that depends on the ensuing intensity, the source function values, and its derivatives as follows:
where the integration coefficients are similarly defined in terms of τuc. Defining k0 = τuc/2 and k1 = (τuc)2/12 we can express those coefficient as
Comparing Eq. (4) to Eq. (3), we would expect the coefficient A to behave like e−τuc. Figure 2 shows the comparison of these two quantities as a function of τuc. In fact, coefficient A coincides with a second order Padé approximant (Padé 1892) of the exponential function around τuc ≈ 0, which is usually considered to be a more accurate and somewhat better behaved approximant than the Taylor expansion (see Fig. 2), but it is still a polynomial approximation. For small optical thickness, coefficient A accurately follows the exponential, but from τuc > 0.1 the error is numerically noticeable and it starts to deviate from the exponential behavior and to even increase from τuc ⪆ 3.4, giving unrealistically high weight to the incoming radiation even when the medium is optically thick (where that part should be attenuated by the exponential).
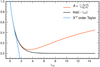 |
Fig. 2. Comparison of the integration coefficient A from LBR’s method (red) with an exponential (black). A is a good approximation to the exponential for small optical thickness, but it greatly deviates close to the optically thick regime. |
If the scheme presented in Eq. (4) is used to solve the non-LTE problem with strong scattering lines, the latter does not converge because the scheme is not accurate in the region of interest for these lines (τuc ⪅ 10). A similar conclusion may be applied to the polarized case, because it is also based on a polynomial expansion of the intensity vector around the upwind point, and that approximation is only supposed to work for small excursions from the point where the intensity is approximated.
Padé approximants can be more precise than a Taylor expansion of the same order for larger excursions from the origin point, as suggested by Fig. 2. In Appendix A we provide Padé polynomial approximations of the cubic Bezier interpolation coefficients, which are valid for small optical tickness regimes, where high-order schemes usually suffer from numerical errors.
3. Inversion engine
3.1. Equation of state
The STiC code works with depth-stratified atmospheres including the stratification of temperature, gas pressure, electron density, line-of-sight velocity, microturbulence, and the three components of the magnetic field vector as functions of column mass, optical depth or height. The magnetic field vector is decomposed in the longitudinal component (B∥), strength of the transverse component (|B⊥|) and azimuth of the transverse component (Bχ).
The inversion engine parameterizes the stratification of physical quantities as a function of optical depth or column mass. If the gas pressure and electron densities are not known, they can be derived assuming a gas pressure value at the upper boundary of the atmosphere and integrating the hydrostatic equilibrium equation. During the inversion, the gas pressure stratification and electron densities are derived assuming hydrostatic equilibrium, but in pure synthesis mode they can be provided externally. Similar to other inversion codes (e.g., SIR, NICOLE), we solve the equation of hydrostatic equilibrium to derive the gas pressure scale for any guessed model atmosphere (Mihalas 1970) as follows:
where p is gas pressure, τν is the optical depth, g is the value of gravity, κν is the mass absorption, and σλ is the scattering coefficient for continuum opacity. The subindex ν refers to a reference wavelength, typically 500 nm. The parameters κλ and σλ are computed assuming a LTE equation of state and background continuum opacity. This equation of state was adopted from the SME: evolution code (Piskunov & Valenti 2017). Equation (5) can be integrated numerically assuming linear dependence of βλ = κλ + σλ between consecutive grid cells. To simplify the notation we assume a discrete grid of k = 1, …, ndep values, where index 1 represents the upper boundary of the atmosphere and λ = 500 nm. Since βk depends on the value of pk, a few iterations are needed to get the values of βk and pk to be consistent. In that case, the solution is written as
If, on the contrary we decide to perform the inversion using column mass (ξ) as a depth variable, the hydrostatic equilibrium equations simplify greatly, no opacity calculations are involved, and no iterations are needed (see, e.g., Hubeny & Mihalas 2014), i.e.,
Working in any of these depth scales is somewhat equivalent to using a Lagrangian frame as the physical quantities follow density (not strictly in the case of optical depth, but very closely related). Working in column mass naturally sets the boundary condition at the top of the atmosphere pk = 0 = gξ. The main difference between working in column mass or optical depth is that the former stretches the chromosphere a bit more and greatly compresses the transition region, whereas the latter comparatively allows us to better resolve the transition region and photosphere (see Fig. 3). This figure gives some insight about how spicules would be squeezed in an optical depth or in a column-mass scale. They would appear as a localized bump in temperature because these scales are not sensitive to the coronal plasma that surrounds these cold material protrusions.
 |
Fig. 3. Vertical slice of a temperature snapshot from a publicly available 2.5D rMHD simulation (Martínez-Sykora et al. 2017). We adopted the original geometrical depth scale (top panel), an optical-depth scale (middle panel), and a column mass depth scale (bottom panel) to represent the same temperature slice. |
The electron pressure is tightly related to the local gas pressure and temperature. Once the gas pressure is known, we initialize the electron pressure under the assumption of LTE. Hydrogen is the main electron donor in the chromosphere. In principle, if hydrogen is included as an active non-LTE species in RH, the electron density can be iterated internally in RH to make it consistent with the non-LTE hydrogen ionization (in statistical equilibrium). We modified RH to allow us to solve the statistical equilibrium equations along with charge conservation (e.g., Leenaarts et al. 2007) for the hydrogen atom. With the modified equations, Newton–Raphson iterations are needed within each multi-level accelerated lambda iteration (MALI) to make the electron density and hydrogen ionization consistent with each other.
The penalty of including hydrogen as an active species is large. In that case, the whole process becomes up to three times slower compared to the LTE case. We only encourage the use of this setup for selected pixels, and we always recommend starting from a relatively converged atmosphere from an inversion with hydrogen in LTE.
3.2. Atmospheric parameterization
Ruiz Cobo & del Toro Iniesta (1992) introduced depth-stratified inversions based on nodes. These nodes represent the free parameters of our model. The inversion modifies the values of the nodes and generates a new fully stratified atmosphere that can be used to solve the (polarized) radiative transfer equation.
Radiative transfer calculations require a relatively dense grid of depth points to solve accurately the radiative transfer equation numerically. Ruiz Cobo & del Toro Iniesta (1992) showed that the inversion cannot be performed in such a fine grid because the observables would not constrain all these degrees of freedom. Therefore, they introduced a coarser grid (the nodes) for each physical parameter. They used piece-wise segments or splines to connect the nodes in the finer grid.
However, there is a fundamental difference in our implementation compared with the node approach introduced by Ruiz Cobo & del Toro Iniesta (1992). In the latter case, the nodes were used to describe corrections that are interpolated into the fine grid and added to an input model atmosphere. In our case, the nodes represent the actual value of the model atmosphere, that is directly interpolated into the fine depth grid. The Ruiz Cobo & del Toro Iniesta (1992) approach allows inversions to be performed with a relatively low number of nodes if the structuring of the input atmosphere is close to that of the final result. However, if the input model has a complex structure that does not correspond to the profiles that we are inverting, this approach struggles to remove such structuring, even with many nodes. Our approach is somewhat safer because the depth complexity is directly set by the number of nodes. We implemented both approaches in STiC, however we recommend using the scheme in which the nodes represent the actual value of the atmospheric parameter. The SPINOR2D, SPARSE and SNAPI codes also make use of this node scheme (van Noort 2012; Asensio Ramos & de la Cruz Rodríguez 2015; Milić & van Noort 2018), which also simplifies the implementation of spatial coupling and regularization that operate directly on the model parameters (see Sect. 3.4).
We allow the use of the following four types of nonovershooting interpolants:
-
Straight segments
-
Cuadratic Bezier splines
-
Cubic Bezier splines
-
Discontinuous grid-centered interpolation with linear slope delimiter
The exact implementation of these interpolants were described in detail in de la Cruz Rodríguez & Piskunov (2013) and in Steiner et al. (2016). Figure 4 illustrates an example showing fictitious node values and the interpolated curve using all these interpolants.
 |
Fig. 4. Example of node interpolation using quadratic Bezier (solid gray), cubic Bezier (solid orange), straight segments (blue), and discontinous with slope delimiter (green dots). The node values are indicated with black crosses. |
We allow the use of node parameterization in temperature, line-of-sight velocity, microturbulence, and the magnetic field vector (B∥, |B⊥|, Bχ).
We also noticed that when integrating Eq. (5), most inversion codes leave the boundary condition constant over the entire inversion. However, Shine & Linsky (1974) and Carlsson et al. (2015) used observations in the Ca II H&K lines and Mg II h&k lines, respectively, to derive ad hoc models that could produce similar spectra as in the observations. In both cases, they needed between one and two orders of magnitude higher gas pressure in the upper chromosphere and transition region than that in the FALC quiet-Sun model (Fontenla et al. 1993). We investigated the response of the aforementioned lines to changes in the boundary condition for the hydrostatic equilibrium equation.
Figure 5 illustrates the response of Ca II H&K, Ca II 854.2 nm, Fe I 630.2 nm, and Mg II k to perturbations in the gas pressure upper boundary. We used a plage model atmosphere that is very similar to that derived by Carlsson et al. (2015). For this model, increasing the gas pressure at the boundary increases the line core intensity of all chromospheric lines but photospheric lines remain unaffected. Figure 5 also illustrates the differences in opacity among these lines. Mg II k has more opacity than Ca II H&K and all of these lines have more opacity than the Ca II 854.2 nm line.
 |
Fig. 5. Normalized response function to perturbations to gas pressure at the upper boundary condition of the atmosphere. |
Figure 6 illustrates the results of several inversions of a plage (IRIS) Mg II h&k profile, using different values of the upper boundary gas pressure. For quiet-Sun values (Ptop = 0.3 dyn cm−2, in red) the inversion cannot reproduce the enhanced line-core intensity of the observation. But when the boundary condition is increased to higher values (Ptop ∼ 1.0 dyn cm−1), the line core intensity can be reproduced. By allowing the code to increase the gas pressure, the transition region can be moved to lower optical depth, where there is now more mass.
 |
Fig. 6. Inversions of one IRIS plage observation performed with various gas pressure values at the upper boundary of the model atmosphere. Top panel: fitted spectra (orange, green, navy and blue) and observed spectrum (black). Bottom panel: reconstructed stratification of temperature and turbulent velocity for each inversion, represented using the same color coding as in the upper panel. |
Figure 6 also illustrates that despite the degeneracy between the value of Ptop and the temperature gradient in the transition region, the inversion needs to have, at least, values that are one order of magnitude higher than in the quiet-Sun to reproduce the profile. We implemented the possibility of also adjusting the value of the upper boundary condition during the inversion as as free parameter. We found it more stable to implement it as a multiplicative factor to the upper boundary gas pressure. A good strategy to invert datasets that include quiet-Sun, sunspots and plage in the same field-of-view is to set the gas pressure to a value of approximately Ptop = 1.0 dyn cm−2 and let the code adjust the value to lower values if needed for the quiet-Sun areas. We discuss further how to do this and how this free parameter is regularized in Sect. 3.4.2.
3.3. Parallelization scheme and I/O
A C++ MPI-parallel code, STiC that follows a master-workers scheme. The parallelization is performed over pixels, assigning one worker to each vertical 1D model atmosphere. The master process performs I/O operations and distributes the workload among worker processes that are only used to process data. This scheme works particularly well when the time needed to process each package is not the same in all cases, allowing balancing of the load of each worker on the fly. A similar scheme was used in NICOLE (Socas-Navarro et al. 2015). We use the HDF5 library for data storage. This library is convenient because it allows storage of multiple named variables and metadata in one single file and it is supported by Python and IDL.
3.4. Regularizing Levenberg–Marquardt algorithm
The LM algorithm (Levenberg 1944; Marquardt 1963) facilitates a nonlinear least-squares fit of a model to observational data. The LM iteratively applies corrections to the parameters of a guessed model to minimize the difference between out synthetic and the measured data. This algorithm has been extensively used in solar inversion codes because it converges efficiently and it is particularly well suited for problems where the computation of derivatives is expensive.
In depth-stratified inversions finding the correct number of minimum number of free-parameters that allow the fitting of observations has been critical to avoid oscillatory behavior in the retrieved parameters. In this section we describe a regularizing LM algorithm that partly overcomes this issue.
We begin by defining the commonly used merit function χ2 that is minimized, but in this case including a generic regularization term,
where p is a vector containing the Npar parameters of the model, sk is the kth prediction of our model (computed at the abscissa points x), ok is the kth measured data point and σk is the error (or noise) of the kth measurement, α is a weight for the regularization term, and r(p) is a function that (in general) regularizes the problem by encouraging certain family of solutions that our algorithm prefers. In the following we work with normalized parameters, as these are numerically more stable.
In our application we assume that we defined a number of individual penalty functions that can depend on different combinations of parameters contained in p. That way the total penalty term is given by the sum of all (Npen) individual penalties rn(p) as
The problem of Eq. (9) is that now our figure to estimate the quality of the fits to the data also includes a term that depends on the model parameters themselves, while the standard definition of χ2 is normalized by the noise. Therefore it is particularly important to work with normalized model parameters within the LM part, which can be done by assuming a typical norm that scales the stratification of each physical parameter to values relatively close to unity (e.g., T = 5000 K, vl.o.s. = 6 km s−1, vturb = 6 km s−1, B∥ = 1000 G, B⊥ = 1000 G, Bχ = π rad). The idea behind the LM algorithm is that, in each iteration i, we can find corrections (Δpi = p − pi) to a set of model parameters (p) that decrease our merit function χ2, so that χ2(pi)> χ2(pi + Δpi).
At this point, one way to proceed would be linearizing Eq. (9), but that would assume that all dependences with the model parameter are linear (see Appendix B). Instead, it is more appropriate to consider a second order Taylor expansion of the merit function around the current estimate of the parameters (e.g., Press et al. 1992), i.e.,
where D is the Hessian matrix of dimension Npar × Npar. At the minimum, the derivative of Eq. (10) must be zero, i.e.,
The correction to our parameters at iteration i is therefore given by the solution to the linear system of equations,
and the new estimate of the model parameters is therefore given by
If we now expand Eq. (12) using Eq. (9), we only need to derive a formula for the Hessian and gradient of our merit function. Strictly speaking, the elements of the Hessian are given by
but in the LM method it is customary to assume that the differences between the observed and synthetic data points (ok − sk) are very small close to the minimum, and therefore to approximate that part of the Hessian with a linearized version that only depends on the first derivatives,
where we now denote the approximation to the Hessian matrix with A, as is usually done in the literature. In general we should not assume a similar linearization of the penalty term. However, when the regularizing function rn has a linear dependence with the parameters, then such linearization is exact and we can compute that contribution to the Hessian using only the product of its Jacobian matrix terms (which we show in Appendix B). The latter is the reason why this algorithm can also be derived assuming a linear model of χ2 under this assumption. Since all the penalty functions that we consider in this paper fulfill this requirement, we continue using the linearized case.
The gradient of the merit function (the right hand term in Eq. (12)) is trivially given by
Equation (12) can be written in matrix form as
where A is the Hessian matrix, J is the Jacobian of the synthetic spectra, and L is the Jacobian of the regularization functions. We included the division by σk in J and (o − s) and the a factor 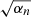 in the corresponding L and r. The linearized approximate Hessian matrix, assuming a linear dependence of the penalty functions with the parameters, can be written as
in the corresponding L and r. The linearized approximate Hessian matrix, assuming a linear dependence of the penalty functions with the parameters, can be written as
In some situations, the linear system in Eq. (16) can lead to unstable solutions. Following Marquardt’s insights, the diagonal of the Hessian matrix can be modified to stabilize the solution as
The λ parameter is a Lagrange multiplier that allows for switching between a steepest descent (when λ is large) and a conjugate gradient method (when λ is small). In our implementation we selected the value of λ by doing a simple line search that brackets the optimal value of λ and then we refined the optimal value with a parabola fit, which seems to work particularly well when regularization is included.
So the final (linearized) equation that we need to solve is written as
Comparing Eq. (19) with a traditional LM implementation, there is a new term that modifies the Hessian matrix and an additional residual on the right-hand side. We are effectively changing the way the Hessian maps a given solution into the right-hand term. The extra residual term in the right-hand term balances the equality and provides insight into how the parameter corrections must be driven to minimize the penalty term as well.
This kind of ℓ − 2 regularization has been extensively used to solve ill-posed problems in stellar applications (e.g., Piskunov & Kochukhov 2002). Other types of regularization have been included in the past in other inversion codes, and perhaps the closest implementation to our method can be found in NICOLE. However there are significant differences. Perhaps the main difference is that the penalty term in NICOLE is not squared in the definition of χ2, which changes completely the algebra of the problem from the beginning of the derivation, as the derivative of the penalty term respect to Δp is different from ours after using the parabolic approximation to solve the problem in Eq. (10). NICOLE must be applying ℓ − 1 regularization whereas our approach operates with ℓ − 2 norms. The regularization functions that we use are also rather different in nature than those in NICOLE (see Sect. 3.4.2).
To solve the linear system of equations in Eq. (19), we use singular value decomposition (SVD). The latter is used in most inversion codes that are currently available to get the correction to the model parameters. In situations where A is rank deficient, SVD provides a least-squares fit to the solution of that system of equations. Additionally, very small singular values can be avoided. This way of solving the linear system is also a regularization method but, unlike using the penalty function, it operates on the projected total Hessian matrix, not on individual physical parameters. Therefore it is harder to understand how it affects individual physical parameters.
Ruiz Cobo & del Toro Iniesta (1992) suggested checking the contribution of each singular value to the response of each physical parameter of the model and making sure that these contributions are filtered individually for each physical parameter. In our tests, the latter seems to mostly help with parameters that induce very small response in χ2 like the magnetic field azimuth, but proper weighting of the Stokes parameters can have a similar effect. Using SVD alone (without the other regularization terms) has the disadvantage that it does not particularly select any family of solutions, but instead filters the Hessian matrix in a way that removes unstable values in the system. In our experience both methods have slightly different effects and the combination of both methods greatly improves convergence. Our calculations of SVD decomposition are performed using the excellent C++ Eigen-3 library (Guennebaud & Jacob 2010).
3.4.1. Selection of the regularization weight αn
The real challenge in this approach is how to chose the regularization weights αn correctly. Too much weight affects the quality of the fits, as the problem is dominated by the penalty term. Too little regularization does not remove potential degeneracies in the solution. We surveyed the literature and there is a vast selection of different theoretical approaches to select the regularization weights, regardless of the fitting algorithm that is being employed (see, e.g., Kaltenbacher et al. 2008; Doicu et al. 2010).
Perhaps one of the best (practical) insights into how to choose the regularization weight is provided by Kochukhov (2017), based on the so-called L-curvature approach (Hansen & O’leary 1993). The idea is to assess how the value of the square of the residual 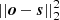 compares to the values of the penalty term
compares to the values of the penalty term 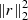 for different values of α in a log − log plot. Normally, for too small values of α, the quality of the fits remains rather constant. Once the order of magnitude of the penalty term approaches the same order of magnitude as
for different values of α in a log − log plot. Normally, for too small values of α, the quality of the fits remains rather constant. Once the order of magnitude of the penalty term approaches the same order of magnitude as 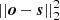 , then the quality of the fits usually begins to degrade rapidly. The idea is to choose a value of α very close to that turnover point.
, then the quality of the fits usually begins to degrade rapidly. The idea is to choose a value of α very close to that turnover point.
If we work with model parameters that are normalized to values around unity, for example by scaling the parameters by a norm, and if our estimate of the noise is adequate, then we should be able to choose α so that the penalty term remains slightly below unity. Now this is not exactly as straightforward as it sounds. The temperature and magnetic field strength, for example, have quite a large dynamic range compared to the other parameters. This is especially the case if our observations include lines that form under very different physical conditions because in that case, the model must accommodate all these regimes and the consequent gradients that connect them.
Kochukhov (2017) also indicates that some uncertainty in the choice of α cannot be avoided because we do not know the best fit a priori. However, we can perform test inversions on selected pixels to calibrate a good value. Normally we would need to be off by a factor ×10 in order to see significant errors.
3.4.2. Regularization functions
If the inversion is performed with many degrees of freedom, the solution can become unstable, introducing oscillatory behavior in the derived parameters as a function of depth. Regularization techniques provide a natural way to discourage certain families of solutions by adding a penalty term to the definition of χ2, as generally expressed in Eq. (8) with r(p).
We implemented Tikhonov’s regularization on the first derivative (Tikhonov & Arsenin 1977). Hereafter, the label phyc indicates that a given vector or constant is related to one physical parameter (e.g., temperature). In this case for each interval between two consecutive nodes in one physical parameter (k = 1, …, Nphyc, e.g., temperature) we define a regularization function (we note that the penalty function is not squared here, unlike in the definition of χ2) using the first derivative of the actual values of the physical parameter that we are considering (pphyc),
In this case, the derivatives of the regularization term relative to all parameters contained in p can be written as
where pj are the values of the nodes for a given physical parameter. In this case, the block in H corresponding to this physical variable only has nonzero terms in the diagonal and the band just below it. Alternatively, we could choose to penalize changes in the gradient of a variable, which is by definition what happens when we introduce wiggles in a curve. The latter can be attained by penalizing large values in the second derivative. For nonregular grids (nonequidistant node placement) we can define the penalty function as
where
are expressed in terms of the node separation Δxj + 1 = xj + 1 − xj and Δxj = xj − xj − 1. The derivative of this penalty function becomes trivially
Another useful form of regularization is to penalize deviations of the stratification of a parameter from a constant value v,
where v is a constant expected value. The derivative, which in this case is trivial, is written as
If v is taken to be mean of all elements in pphyc (denoted as 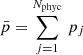 ), then the derivative must also account for the fact that changing one value pj also changes the value of p̅, by including the derivative of p̅ written as
), then the derivative must also account for the fact that changing one value pj also changes the value of p̅, by including the derivative of p̅ written as
Equation (23) obviously yields a diagonal block, whereas in Eq. (26) all block elements are nonzero because all nodes contribute to the mean value. We note that Eqs. (21), (23), (25), and (26) do not contain the constant factor α that multiplies each of the penalty functions.
Equations (21) and (22) are both capable of removing spurious oscillatory behavior and wiggles from the stratification of a parameter, but they operate in different ways. The former prefers to have small gradients in the solution whereas the latter only penalizes changes in the gradient itself. Similarly, the main difference between Eqs. (20) and (24) is that the former encourages smoothly varying solutions as a function of depth, whereas the latter does not necessarily encourage smoothness but discourages large deviations from the selected constant value. Equation (22) allows for a larger dynamic range in the stratification of a variable than Eq. (21) and it is particularly well suited for variables such as temperature, where we may have to include the transition region.
If the user decides to allow for adjustments in the gas pressure at the upper boundary (Ptop,) we allow for regularizing the multiplicative factor of Ptop with penalties to deviations from a value of 1. That way, if the input model assumes an upper chromosphere value of Ptop 1.0 dyn cm−2, the code only increases or decrease this value when it actually improves the value of χ2, but the algorithm will try to adjust the temperature gradient if possible. We are basically selecting to fit as much as we can with changes to the temperature stratification.
3.4.3. Numerical experiment
We performed a numerical test with a vertical slice extracted from snapshot 385 from a public 3D rMHD simulation (Carlsson et al. 2016). Snapshots from this simulation have been used extensively in recent years (Leenaarts et al. 2013, 2014; Pereira et al. 2013; de la Cruz Rodríguez et al. 2013; Štěpán et al. 2015; Rathore et al. 2015) as it was made publicly available as part of the NASA IRIS mission (De Pontieu et al. 2014). This simulation includes the solar photosphere, chromosphere, and corona, allowing us to prepare a meaningful test case for the code. In order to speed up our calculations, we selected a vertical cut of the snapshot, indicated in Fig. 7 with a black line over the field of view. This line connects two patches of opposite polarity and it is aligned with fibril-like structures that are visible in the magnetic field and line-of-sight velocity panels. In pixel coordinates, the slit extends from (x0, y0) = (69, 298) to (x1, y1) = (431, 165).
 |
Fig. 7. Physical parameters from a snapshot of a 3D rMHD BIFROST simulation (Carlsson et al. 2016). From left to right, temperature, line-of-sight velocity and the vertical component of the magnetic field. The upper row shows a horizontal cut in the chromosphere at z = 1.3 Mm and the lower row in the photosphere at z = 0 Mm. The black line illustrates the region that we extracted to perform our inversion tests. |
We synthesized spectra in the Mg II h&k, Ca II H&K, the Ca II 8542 Å line and Fe I 6301 & 6302 Å lines. This setup is representative of a co-observation between IRIS and the CRISP and CHROMIS instruments at the Swedish 1-m Solar Telescope (Scharmer 2006; Scharmer et al. 2008), which have been rather common since the launch of IRIS in 2014. Table 1 summarizes the wavelength coverage of each line and the assumed spectral resolution.
Synthetic observations from a 3D rMHD simulation.
In this test we want to show the usefulness of regularization, especially to dig more detail out of the model atmosphere. In this case the magnetic field information is retrieved only from the λ8542, λ6301, and λ6302 lines. In inversion runs, the depth resolution is set by the number of nodes that are being employed in a given physical parameter. The question however is how many nodes can we actually constrain during the inversion. Part of the answer is provided by the exact number of spectral lines that we observed, their sensitivities to different parts of the atmosphere and the spectral resolution of the observations. When the number of nodes is overestimated, the solution of the inversion shows oscillatory behavior and in extreme cases, the problem fails to converge at all. That is the reason why we normally must find a setup that allows for reproducing the observed spectra with the lowest number of degrees of freedom (de la Cruz Rodríguez & van Noort 2017).
An example of this effect is shown in Fig. 8, where we illustrated a number of inversions experiments that are summarized in Table 2. These results correspond to a single cycle inversion initialized with the same model atmosphere in all columns. Rows b and c represent an inversion with a very limited number of nodes (upper-middle) and a case where the code failed completely to converge when we used an unrealistically large number of nodes (row c). In the former case we used 7 nodes in temperature and 4 nodes in line-of-sight velocity, whereas in the latter case we used 22 nodes in temperature and line-of-sight velocity.
 |
Fig. 8. Inversion of a vertical slice from a 3D rMHD simulation. The panels illustrate from left to right the stratification in optical depth of temperature, line-of-sight velocity, and the vertical component of the magnetic field. Row a: original physical quantities from the MHD simulation. Row b: inversion computed without regularization and a small number of nodes. Row c: inversion computed without regularization and a very large number of nodes. Row d: inversion computed with understimated regularization and a very large number of nodes. Row e: inversion computed with a very large number of nodes and properly scaled regularization. The exact number of nodes of each experiment is indicated in Table 2. |
Number of nodes used in our inversion setups.
Adding regularization helps the convergence rate significantly and it removes the oscillations significantly. Row d illustrates what happens when we add regularization but the regularization term is heavily understimated. The code manages to converge to a solution that resembles the original model, but wiggles are present all over the three physical quantities. When the right amount of regularization is added (see Sect. 3.4.1), the problem converges to a solution that resembles the original model, as shown in row e. In this case we applied penalty terms to the second derivative of the stratification of temperature as well as to the first derivative of the line-of-sight velocity and magnetic field. In principle there is not much difference among these two types, except that when we applied the latter to the temperature stratification, the temperature of the transition region was lower because it did not have a sufficiently relevant impact in χ2 but it lowered the penalty term in that case. If we had included transition region lines, we think this effect would probably not be there, although we are not probing this point here.
Figure 9 shows the fits at x = 7.9, where the line profiles have similar shapes to those observed. The fits are good in most lines and in all cases, except in Stokes V where Mg II k and Ca II K were not included in full-Stokes mode in the inversion. All fits capture the global shape of the line, but the details are better fitted in the regularized cases. The differences between the blue and red curves and are harder to judge by looking at individual pixels, but the values of χ2 are statistically very similar.
 |
Fig. 9. Example fit of the different inversions (row (e), x = 7.9). We only fitted Stokes Q, U, and V in the λ8542, λ6301, and 6302 lines. The fits for the Ca II H, Fe Iλ6301, and Mg II h lines are not shown because they are virtually identical to those in their partnering lines. At the considered noise level, all Q and U signals are below the noise level in all chromospheric lines. |
The case that we tested in this work has perhaps way too many degrees of freedom for being a realistic case, but it serves to show the power of regularization. It also illustrates that the method does not always converge entirely. For example, in the photosphere at x ≈ 3.5 Mm the model has an artifact. At that location the Fe I lines are split due to the Zeeman effect and in this case the algorithm gets stuck in a local minimum where the magnetic field is small in the photosphere and the line is broadened by having wiggles in velocity. In our experience, these kind of artifacts usually appear when the initial guessed model is quite far from the real solution and there are a very large number of nodes. A good strategy to avoid these artifacts is to perform a first cycle with less nodes and then restart the inversion from the solution of the latter, but with more degrees of freedom. The latter approach was already introduced by Ruiz Cobo & del Toro Iniesta (1992) and it speeds up the whole inversion process considerably as the response functions of that first cycle are faster to compute because the inversion is re-initialized from a closer solution to the minimum.
4. Conclusions
We have developed a new inversion code that builds upon the ideas used in the SIR and NICOLE inversions codes. For the first time STiC allows us to consider lines from different atomic species while including PRD effects. The latter development allows the inclusion of lines that sample the upper chromosphere and that also set stronger physical constraints in the mid and lower chromosphere.
We implemented ℓ − 2 regularization in our LM algorithm. The latter is introduced in the approximation to the Hessian matrix directly, whereas other regularization techniques can be applied directly by projecting the parameters with a regularization operator (e.g., Asensio Ramos & de la Cruz Rodríguez 2015; Asensio Ramos et al. 2016). In this paper we show that regularization helps to dig more detail out of the inversion by allowing the inclusion of more degrees of freedom, while getting rid of erratic oscillatory behavior. It also improves the convergence rate of the algorithm, even when the regularization amount is underestimated. The gain is particularly large in problems with particularly large number of nodes and atoms.
A word of caution seems appropriate though, as inversions codes always provide a result. It is up to the user not to over interpret those results and to check the robustness of the inversions. A good way to do so is to have a clear idea of what aspect of our problem we want to solve with inversions.
In our opinion, future developments should focus on the elegant solutions shown by Milić & van Noort (2017), where the response functions are computed analytically instead of by finite differences, although at the moment their formalism is not mature enough to include PRD lines.
STiC is publicly available to the community1.
Acknowledgments
We are most thankful to N. Piskunov for sharing his LTE EOS with us. We thank J. Pires Bjørgen for his valuable help with the implementation of the non-LTE hydrogen ionization routines. We greatly appreciate the comments provided by I. Milic (the referee) who helped to improve the quality of this paper. JdlCR is supported by grants from the Swedish Research Council (2015-03994), the Swedish National Space Board (128/15). This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (SUNMAG, grant agreement 759548). SD and JdlCR are supported by a grant from the Swedish Civil Contingencies Agency (MSB). This research was supported by the CHROMATIC grant of the Knut and Alice Wallenberg foundation. Computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Centre for High Performance Computing (PDC-HPC) at the Royal Institute of Technology in Stockholm as well as recourses at the High Performance Computing Center North (HPC2N). This study has been discussed within the activities of team 399 “Studying magnetic-field-regulated heating in the solar chromosphere” at the International Space Science Institute (ISSI) in Switzerland. The Swedish 1-m Solar Telescope is operated on the island of La Palma by the Institute for Solar Physics of Stockholm University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. The Institute for Solar Physics is supported by a grant for research infrastructures of national importance from the Swedish Research Council (registration number 2017-00625).
References
- Asensio Ramos, A., & de la Cruz Rodríguez, J. 2015, A&A, 577, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asensio Ramos, A., de la Cruz Rodríguez, J., Martínez González, M. J., & Pastor Yabar, A. 2016, A&A, 590, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auer, L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 3 [NASA ADS] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1998, MNRAS, 300, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&A, 142, 467 [NASA ADS] [Google Scholar]
- Bellot Rubio, L. R., Ruiz Cobo, B., & Collados, M. 1998, ApJ, 506, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Bjørgen, J. P., Sukhorukov, A. V., Leenaarts, J., et al. 2018, A&A, 611, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Franz, M., Schlichenmaier, R., Collados, M., & Asensio Ramos, A. 2017, A&A, 601, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buehler, D., Lagg, A., Solanki, S. K., & van Noort, M. 2015, A&A, 576, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., Leenaarts, J., & De Pontieu, B. 2015, ApJ, 809, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J., & De Pontieu, B. 2016, A&A, 585, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centeno, R., Blanco Rodríguez, J., Del Toro Iniesta, J. C., et al. 2017, ApJS, 229, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., van Noort, M., & Rempel, M. 2016, A&A, 593, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Solanki, S. K., Barthol, P., et al. 2017, ApJS, 229, 5 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva Santos, J. M., de la Cruz Rodríguez, J., & Leenaarts, J. 2018, A&A, 620, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., & Piskunov, N. 2013, ApJ, 764, 33 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., & van Noort, M. 2017, Space Sci. Rev., 210, 109 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., De Pontieu, B., Carlsson, M., & Rouppe van der Voort, L. H. M. 2013, ApJ, 764, L11 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., Hansteen, V., Bellot-Rubio, L., & Ortiz, A. 2015, ApJ, 810, 145 [NASA ADS] [CrossRef] [Google Scholar]
- de la Cruz Rodríguez, J., Leenaarts, J., & Asensio Ramos, A. 2016, ApJ, 830, L30 [NASA ADS] [CrossRef] [Google Scholar]
- del Toro Iniesta, J. C., & Ruiz Cobo, B. 2016, Liv. Rev. Sol. Phys., 13, 4 [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [NASA ADS] [CrossRef] [Google Scholar]
- Doicu, A., Trautmann, T., & Schreier, F. 2010, Numerical Regularization for Atmospheric Inverse Problems, Springer Praxis Books (Berlin, Heidelberg: Springer) [CrossRef] [Google Scholar]
- Esteban Pozuelo, S., Bellot Rubio, L. R., & de la Cruz Rodríguez, J. 2016, ApJ, 832, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
- Gošić, M., de la Cruz Rodríguez, J., De Pontieu, B., et al. 2018, ApJ, 857, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Guennebaud, G., & Jacob, B. 2010, Eigen v3 http://eigen.tuxfamily.org [Google Scholar]
- Hansen, C. P., & O’leary, D. 1993, SIAM J. Sci. Comput., 14, 1487 [CrossRef] [MathSciNet] [Google Scholar]
- Henriques, V. M. J., Mathioudakis, M., Socas-Navarro, H., & de la Cruz Rodríguez, J. 2017, ApJ, 845, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Mihalas, D. 2014, Theory of Stellar Atmospheres (Princeton, NJ: Princeton University Press) [Google Scholar]
- Ibgui, L., Hubeny, I., Lanz, T., & Stehlé, C. 2013, A&A, 549, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Lagg, A., et al. 2014, A&A, 569, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janett, G., & Paganini, A. 2018, ApJ, 857, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Janett, G., Steiner, O., & Belluzzi, L. 2017, ApJ, 845, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenbacher, B., Neubauer, A., & Scherzer, O. 2008, Iterative Regularization Methods for Nonlinear Ill-Posed Problems, Radon Series on Computational and Applied Mathematics (Berlin: De Gruyter) [CrossRef] [Google Scholar]
- Kerr, G. S., Fletcher, L., Russell, A. J. B., & Allred, J. C. 2016, ApJ, 827, 101 [NASA ADS] [Google Scholar]
- Kochukhov, O. 2017, A&A, 597, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rutten, R. J. 2007, A&A, 473, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rouppe van der Voort, L. 2009, ApJ, 694, L128 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Rutten, R. J., Reardon, K., Carlsson, M., & Hansteen, V. 2010, ApJ, 709, 1362 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Pereira, T., & Uitenbroek, H. 2012, A&A, 543, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Pereira, T. M. D., Carlsson, M., Uitenbroek, H., & De Pontieu, B. 2013, ApJ, 772, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., de la Cruz Rodríguez, J., Kochukhov, O., & Carlsson, M. 2014, ApJ, 784, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., de la Cruz Rodríguez, J., Danilovic, S., Scharmer, G., & Carlsson, M. 2018, A&A, 612, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levenberg, K. 1944, Q. Appl. Math., 2, 164 [Google Scholar]
- Marquardt, D. 1963, J. Soc. Ind. Appl. Math., 11, 431 [Google Scholar]
- Martínez González, M. J., Pastor Yabar, A., Lagg, A., et al. 2016, A&A, 596, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., Hansteen, V. H., et al. 2017, Science, 356, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D. 1970, Stellar atmospheres (San Francisco: Freeman& Co.) [Google Scholar]
- Milić, I., & van Noort, M. 2017, A&A, 601, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milić, I., & van Noort, M. 2018, A&A, 617, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padé, H. 1892, On the Approximate Representation of a Function by Rational Fractions No. 740 (Gauthier-Villars and Son) [Google Scholar]
- Pastor Yabar, A., Martínez González, M. J., & Collados, M. 2018, A&A, 616, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Leenaarts, J., De Pontieu, B., Carlsson, M., & Uitenbroek, H. 2013, ApJ, 778, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N., & Kochukhov, O. 2002, A&A, 381, 736 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Quintero Noda, C., Uitenbroek, H., Carlsson, M., et al. 2018, MNRAS, 481, 5675 [NASA ADS] [CrossRef] [Google Scholar]
- Rathore, B., Pereira, T. M. D., Carlsson, M., & De Pontieu, B. 2015, ApJ, 814, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J., Leenaarts, J., Rouppe van der Voort, L. H. M., et al. 2011, A&A, 531, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B. 1984, in Accurate Solutions to non-LTE Problems Using Approximate Lambda Operators, ed. W. Kalkofen, 173 [Google Scholar]
- Scharmer, G. B. 2006, A&A, 447, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scharmer, G. B., Narayan, G., Hillberg, T., et al. 2008, ApJ, 689, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Scharmer, G. B., de la Cruz Rodriguez, J., Sütterlin, P., & Henriques, V. M. J. 2013, A&A, 553, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shine, R. A., & Linsky, J. L. 1974, Sol. Phys., 39, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Ruiz Cobo, B. 2000, ApJ, 530, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., de la Cruz Rodríguez, J., Asensio Ramos, A., Trujillo Bueno, J., & Ruiz Cobo, B. 2015, A&A, 577, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steiner, O., Züger, F., & Belluzzi, L. 2016, A&A, 586, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Štěpán, J., Trujillo Bueno, J., Leenaarts, J., & Carlsson, M. 2015, ApJ, 803, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhorukov, A. V., & Leenaarts, J. 2017, A&A, 597, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tikhonov, A. N., & Arsenin, V. Y. 1977, Solutions of Ill-posed Problems (New York: W.H. Winston) [Google Scholar]
- Uitenbroek, H. 1989, A&A, 213, 360 [NASA ADS] [Google Scholar]
- Uitenbroek, H. 2001, ApJ, 557, 389 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M. 2012, A&A, 548, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Carlsson, M. 2011, A&A, 528, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Approximation of the cubic Bezier interpolation coefficients with Padé interpolants
Most high order integration schemes can suffer from numerical precision issues for very small optical-depth values, even when the computations are performed in double precision. Therefore, most implementations switch to a third order Taylor expansion of the integration coefficients and of the exponential when τuc < 0.05 (e.g., Ibgui et al. 2013).
We tested a similar approach with Padé approximants and the resulting curve preserves five-digit accuracy up to τuc = 0.8 in all integration coefficients and in the exponential. The third order Taylor expansion can only keep the same accuracy in all parameters up to τuc = 0.046 in our tests. The latter could be used to restrict even more the range in which the (expensive) exponential term needs to be computed. For τuc < 0.8, the Padé approximation of the cubic Bezier coefficients are written as
It is not always clear that these equations are faster to compute than the actual interpolation, but at least the approximation of the exponential can be combined with the real coefficients for larger values of τuc.
Appendix B: An alternative derivation of the regularizing LM algorithm
An alternative way to derive the regularizing LM algorithm is to linearize the dependence of Eq. (9) respect to the model parameters. In order to find corrections (Δp) to a set of model parameters (p) that decrease our merit function χ2, so that χ2(p) > χ2(p + Δp), we perform a linear Taylor expansion of the merit function around the current value of the parameters. Given that we are assuming a nonlinear case and therefore we need to iterate the solution of our set of parameters, we can linearize the expression for χ2(p + Δp), assuming that Δp is sufficiently small in each iteration, i.e.,
where ji is the Jacobian (vector of Npar elements) of the synthetic spectrum si(p, xi) and hj is the Jacobian (vector of Npar elements) of a single rj(p). In principle, we can replace Eqs. (B.1) and (B.2) into Eq. (9) as follows:
We can rewrite Eq. (B.3) in matrix form, which simplifies enormously the algebraic manipulations and the notation. In that case, we define J as the full Jacobian matrix for all data points with dimensions (Npar, Ndat) and H is a matrix with dimensions (Npar, Npen). Each column of H contains the derivatives of one individual penalty function relative to all parameters in p. The penalty functions are contained in the components of vector r = (r1, r2, …, rNpen);
We implicitly hid the division by the noise in all relevant matrices, and we included the α factors in the vector r. If we equal to zero the derivative of Eq. (B.4) with respect to Δp and after performing some basic matrix algebra, we can find the corrections Δp that minimize our merit function.
Defining the modified approximate Hessian matrix,
then the corrections to our current estimate of the parameter are given by the following linear system of equations; these corrections include the effect of our regularizing functions r(p) and their derivatives as follows:
Equation (B.6) is very similar to the linear system usually considered in a standard LM algorithm. We simply modified the Hessian matrix and added an extra term to the residue on the right-hand side to account for the regularization terms. By definition, the linear approximation of the Hessian is automatically recovered, and the only limitation compared to the full algorithm in Sect. 3.4 is that the penalty terms must have a linear dependence with the model parameters.
All Tables
All Figures
 |
Fig. 1. Vertical slice from a Bifrost radiation-MHD simulation, indicating the approximate formation height of different diagnostics. The solid lines indicate the τ = 1 layer at the core of the Mg II k line (purple), Ca II K line (navy) and Hα line (orange). The black solid line indicates the location where T = 20 kK and the dashed black line the plasma β = 1 layer. The gray shades illustrate the He I 10830 line opacity. We indicated the entire formation range of the Fe I 6301 line in green and the Ca II 8542 line in red. |
| In the text | |
 |
Fig. 2. Comparison of the integration coefficient A from LBR’s method (red) with an exponential (black). A is a good approximation to the exponential for small optical thickness, but it greatly deviates close to the optically thick regime. |
| In the text | |
 |
Fig. 3. Vertical slice of a temperature snapshot from a publicly available 2.5D rMHD simulation (Martínez-Sykora et al. 2017). We adopted the original geometrical depth scale (top panel), an optical-depth scale (middle panel), and a column mass depth scale (bottom panel) to represent the same temperature slice. |
| In the text | |
 |
Fig. 4. Example of node interpolation using quadratic Bezier (solid gray), cubic Bezier (solid orange), straight segments (blue), and discontinous with slope delimiter (green dots). The node values are indicated with black crosses. |
| In the text | |
 |
Fig. 5. Normalized response function to perturbations to gas pressure at the upper boundary condition of the atmosphere. |
| In the text | |
 |
Fig. 6. Inversions of one IRIS plage observation performed with various gas pressure values at the upper boundary of the model atmosphere. Top panel: fitted spectra (orange, green, navy and blue) and observed spectrum (black). Bottom panel: reconstructed stratification of temperature and turbulent velocity for each inversion, represented using the same color coding as in the upper panel. |
| In the text | |
 |
Fig. 7. Physical parameters from a snapshot of a 3D rMHD BIFROST simulation (Carlsson et al. 2016). From left to right, temperature, line-of-sight velocity and the vertical component of the magnetic field. The upper row shows a horizontal cut in the chromosphere at z = 1.3 Mm and the lower row in the photosphere at z = 0 Mm. The black line illustrates the region that we extracted to perform our inversion tests. |
| In the text | |
 |
Fig. 8. Inversion of a vertical slice from a 3D rMHD simulation. The panels illustrate from left to right the stratification in optical depth of temperature, line-of-sight velocity, and the vertical component of the magnetic field. Row a: original physical quantities from the MHD simulation. Row b: inversion computed without regularization and a small number of nodes. Row c: inversion computed without regularization and a very large number of nodes. Row d: inversion computed with understimated regularization and a very large number of nodes. Row e: inversion computed with a very large number of nodes and properly scaled regularization. The exact number of nodes of each experiment is indicated in Table 2. |
| In the text | |
 |
Fig. 9. Example fit of the different inversions (row (e), x = 7.9). We only fitted Stokes Q, U, and V in the λ8542, λ6301, and 6302 lines. The fits for the Ca II H, Fe Iλ6301, and Mg II h lines are not shown because they are virtually identical to those in their partnering lines. At the considered noise level, all Q and U signals are below the noise level in all chromospheric lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



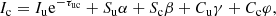
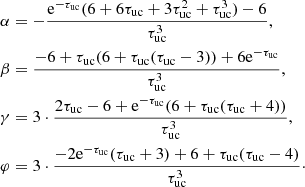
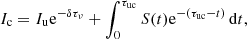
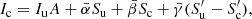
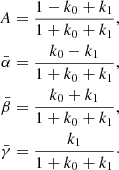
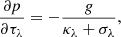
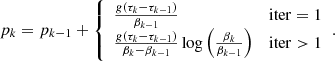
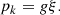
![$$ \begin{aligned} \chi ^2 ({\boldsymbol{p}}, {\boldsymbol{x}})= \frac{1}{N_{\rm dat}} \sum _{k=1}^{N_{\rm dat}} \bigg [\frac{o_k - s_k({\boldsymbol{p}},x_k)}{\sigma _k} \bigg ]^2 + \alpha r({\boldsymbol{p}})^2, \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq11.gif)
![$$ \begin{aligned} \chi ^2 ({\boldsymbol{p}}, {\boldsymbol{x}})= \frac{1}{N_{\rm dat}} \sum _{k=1}^{N_{\rm dat}}\bigg [\frac{o_k - s_k({\boldsymbol{p}}, x_k)}{\sigma _k}\bigg ]^2 + \sum _{n=1}^{N_{\rm pen}} \alpha _n r_n({\boldsymbol{p}})^2. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq12.gif)
![$$ \begin{aligned} \chi ({\boldsymbol{p}}, {\boldsymbol{x}})^2 = \chi ({\boldsymbol{p}}_i, {\boldsymbol{x}})^2 + {{\boldsymbol{\Delta {p}}}_{i}} \nabla \bigg [ \chi ({\boldsymbol{p}}_i, {\boldsymbol{x}})^2\bigg ] + \frac{1}{2}{{\boldsymbol{\Delta {p}}}_{i}} \mathbf D {{\boldsymbol{\Delta {p}}}_{i}}, \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq13.gif)
![$$ \begin{aligned} \nabla \bigg [ \chi ({\boldsymbol{p}}, {\boldsymbol{x}})^2 \bigg ] = \nabla \bigg [ \chi ({\boldsymbol{p}}_i, {\boldsymbol{x}})^2\bigg ] + \mathbf D {{\boldsymbol{\Delta {p}}}_{i}} = 0. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq14.gif)
![$$ \begin{aligned} \mathbf D {{\boldsymbol{\Delta {p}}}_{i}} = - \nabla \bigg [ \chi ({\boldsymbol{p}}_i, {\boldsymbol{x}})^2\bigg ], \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq15.gif)
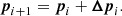
![$$ \begin{aligned}&D_{jz} = \frac{\partial ^2 \chi ^2}{\partial p_z \partial p_j}\nonumber \\&\quad \;=2\sum _k^{N_{\rm dat}} \frac{1}{\sigma _k^2}\bigg [ \frac{\partial s_k}{\partial p_z}\frac{\partial s_k}{\partial p_j} - (o_k-s_k) \frac{\partial ^2 s_k}{\partial p_z \partial p_j} \bigg ] + 2\sum _n^{N_{\rm pen}} \alpha _n \frac{\partial ^2 (r_n^2) }{\partial p_j \partial p_z}, \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq17.gif)
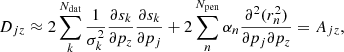
![$$ \begin{aligned} - \frac{\partial \chi ^2}{\partial p_j} = 2\sum _k^{N_{\rm dat}}\frac{1}{\sigma _k^2}\bigg [ (o_k-s_k) \frac{\partial s_k}{\partial p_j} \bigg ] - 2\sum _n^{N_{\rm pen}} \alpha _n r_n \frac{\partial r_n}{\partial p_j}\cdot \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq19.gif)
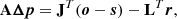
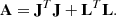
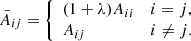
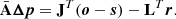
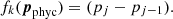
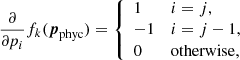
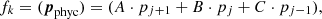
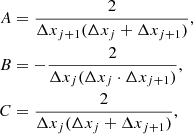
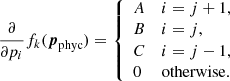
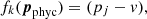
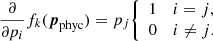
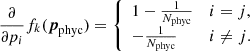
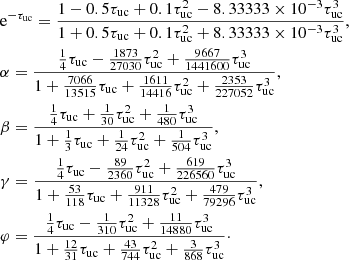
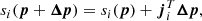
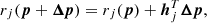
![$$ \begin{aligned} \chi ^2 ({\boldsymbol{p}}+{\boldsymbol{\Delta {p}}}, {\boldsymbol{x}}) = \frac{1}{N_{\rm dat}} \sum _{i=1}^{N_{\rm dat}} \bigg [\frac{o_i - s_i({\boldsymbol{p}},x_i) -{\boldsymbol{j}}_{i}^{T}{\boldsymbol{\Delta {p}}}}{\sigma _i}\bigg ]^2 + \sum _{j=1}^{N_{\rm pen}}\alpha _j \bigg [ r_j({\boldsymbol{p}})+ {{\boldsymbol{h}}^{T}}{\boldsymbol{\Delta {p}}}\bigg ]^2. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq40.gif)
![$$ \begin{aligned} \chi ^2 = \bigg [{{\boldsymbol{o}} - {\boldsymbol{s}}} - {J}^T{\boldsymbol{\Delta {p}}}\bigg ]^2 + \bigg [ {\boldsymbol{r}} + {H}^T{\boldsymbol{\Delta {p}}}\bigg ]^2 = \bigg [{{\boldsymbol{o}} - {\boldsymbol{s}}} - {J}^T{\boldsymbol{\Delta {p}}}\bigg ]^T \bigg [{{\boldsymbol{o}} - {\boldsymbol{s}}} - {J}^T{\boldsymbol{\Delta {p}}}\bigg ]+ \bigg [ {\boldsymbol{r}} + {H}^T{\boldsymbol{\Delta {p}}}\bigg ]^T \bigg [ {\boldsymbol{r}} + {H}^T{\boldsymbol{\Delta {p}}}\bigg ]. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq41.gif)
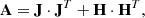
![$$ \begin{aligned} \mathbf A \cdot {\boldsymbol{\Delta {p}}} = \mathbf J \cdot ({{\boldsymbol{o}} - {\boldsymbol{s}}}) - \bigg [\mathbf H \cdot \mathbf r \bigg ]. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34464-18/aa34464-18-eq43.gif)