| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 15 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201833458 | |
| Published online | 19 March 2019 | |
Gaia DR 2 and VLT/FLAMES search for new satellites of the LMC⋆⋆⋆
1
Instituto de Astrofisica de Canarias, Calle Via Lactea s/n, 38205 La Laguna, Tenerife, Spain
e-mail: tfritz@iac.es
2
Universidad de La Laguna, Dpto. Astrofisica, 38206 La Laguna, Tenerife, Spain
3
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
Received:
20
May
2018
Accepted:
13
February
2019
A wealth of tiny galactic systems populates the surroundings of the Milky Way. However, some of these objects might have originated as former satellites of the Magellanic Clouds, in particular of the Large Magellanic Cloud (LMC). Examples of the importance of understanding how many systems are genuine satellites of the Milky Way or the LMC are the implications that the number and luminosity-mass function of satellites around hosts of different mass have for dark matter theories and the treatment of baryonic physics in simulations of structure formation. Here we aim at deriving the bulk motions and estimates of the internal velocity dispersion and metallicity properties in four recently discovered distant southern dwarf galaxy candidates, Columba I, Reticulum III, Phoenix II, and Horologium II. We combined Gaia DR2 astrometric measurements, photometry, and new FLAMES/GIRAFFE intermediate-resolution spectroscopic data in the region of the near-IR Ca II triplet lines; this combination is essential for finding potential member stars in these low-luminosity systems. We find very likely member stars in all four satellites and are able to determine (or place limits on) the bulk motions and average internal properties of the systems. The systems are found to be very metal poor, in agreement with dwarf galaxies and dwarf galaxy candidates of similar luminosity. Of these four objects, we can only firmly place Phoenix II in the category of dwarf galaxies because of its resolved high velocity dispersion (9.5 −4.4+6.8 km s−1) and intrinsic metallicity spread (0.33 dex). For Columba I we also measure a clear metallicity spread. The orbital pole of Phoenix II is well constrained and close to that of the LMC, suggesting a prior association. The uncertainty on the orbital poles of the other systems is currently very large, so that an association cannot be excluded, except for Columba I. Using the numbers of potential former satellites of the LMC identified here and in the literature, we obtain for the LMC a dark matter mass of M200 = 1.9 −0.9+1.3 × 1011 M⊙.
Key words: proper motions / stars: abundances / galaxies: dwarf / galaxies: kinematics and dynamics
Full Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/623/A129
© ESO 2019
1. Introduction
In the Λ cold dark matter (ΛCDM) framework, not only large galaxies, but also low-mass halos are expected to host their own systems of satellite sub-halos. How many of these will contain a luminous component depends on several variables, among which the mass of the host halo, the mass and build-up history of the sub-halos themselves, and various environmental factors, including the strength of the UV-ionizing background (see, e.g., the review by Bullock & Boylan-Kolchin 2017 and references therein).
Several low-luminosity galaxies have been detected that might be physically associated with stellar systems with masses similar to or lower than that of the LMC (e.g., Antlia A and the recently discovered Antlia B around NGC 3109, Sand et al. 2015; Scl-MM-Dw1 around NGC 253, Sand et al. 2014); in some cases, the “status” of satellite galaxy is guaranteed by the ongoing tidal disruption of such systems (e.g., Rich et al. 2012; Amorisco et al. 2014; Annibali et al. 2016; Toloba et al. 2016). This might be interpreted as a qualitative confirmation of one of the predictions of the ΛCDM hierarchical formation framework.
Recently, about two dozen low-luminosity candidate dwarf galaxies were discovered at projected locations in the sky close to the Magellanic Clouds (Drlica-Wagner et al. 2015; Koposov et al. 2015a, 2018; Martin et al. 2015; Bechtol et al. 2015; Laevens et al. 2015; Torrealba et al. 2018a; Kim & Jerjen 2015; Kim et al. 2015). This has of course raised the question whether some of these systems might be, or were before infall, part of a satellite system of the Clouds rather than of the Milky Way (MW). Determining how many and which of these dwarf satellites might have been brought in by the Clouds would give insights into several aspects of galaxy formation in a cosmological context: in addition to improving the current observational information on the properties of satellite systems around galaxies of lower mass than the MW, it would allow us to further consider the efficiency of galaxy formation at the low-mass end (see, e.g., Dooley et al. 2017), and might imply a revision of our understanding of the properties of the MW satellite system itself in terms of the number of its members as well as its luminosity and circular velocity function. Identifying which of these dwarf galaxies in particular might be or have been associated with the Clouds also provides a direct way to start addressing the effects of group preprocessing onto the observed properties of dwarf galaxies from the specific perspective of resolved stellar population studies.
The number of satellites that could be associated with systems with stellar masses similar to the Magellanic Clouds has been predicted, and in which stellar mass range they should be found (see, e.g., Dooley et al. 2017). Dooley and collaborators concluded that there is a dearth of “massive” satellites around the Large and Small Magellanic Clouds (LMC and SMC); this could imply a Magellanic Cloud “missing satellite problem”, although other solutions are possible, such as strong modifications to abundance-matching relations (which at the low-mass end are very uncertain, see, e.g., Garrison-Kimmel et al. 2017; Revaz & Jablonka 2018, and references therein) and strong tidal stripping.
Several studies have instead focused on predicting which of the dwarf galaxies found in the surroundings of the MW could have been brought in by the Magellanic system (Sales et al. 2011, 2017; Deason et al. 2015; Yozin & Bekki 2015; Jethwa et al. 2016). Of these, Deason et al. (2015) used the ELVIS N-body simulations to identify LMC-mass sub-haloes of MW/M31-like systems (considering virial masses in the range 1–3 × 1011 M⊙) and showed that the system of satellites rapidly disperses in phase-space unless the group has infallen recently. The sample of 25 LMC analogs included three dynamical analogs (with similar radial and tangential velocity as observed for the LMC): the expectations in these cases are that the sub-halos found at z = 0 within ∼50 kpc, or with a 3D velocity differing by less ∼50 km s−1, from the original host have a chance higher than 50% to have been part of an LMC-mass group. Nonetheless, for the whole sample considered together, systems within 50 kpc and 50 km s−1 of an LMC-mass dwarf at z = 0 would have a >90% probability of having been former group members.
Sales et al. (2017) used the LMC analog identified in Sales et al. (2011) in the Aquarius simulations, whose pericenter and velocity agree well with the measurements, to test whether any of the 20 dwarfs known at the time in the vicinity of the LMC and SMC are or were associated with the Clouds. Of the systems that had no kinematic information, they found that the positions and distances of Hor II, Eri III, Ret III, Tuc IV, Tuc V, and Phx II are consistent with a Magellanic origin, although the authors stressed that kinematic information was needed to confirm the association. This study concluded that several objects (among which all the classical dSphs except for the SMC) were not brought in by the Clouds. However, the LMC analog virial mass before infall (M200 = 3.6 × 1010 M⊙) is at the lower end of that expected from abundance-matching relations or measurements of the LMC circular velocity (van der Marel & Kallivayalil 2014); the satellite system of a more massive LMC analog would probably have had an intrinsically higher velocity dispersion and more extended spatial distribution; this would likely result in a wider distribution in velocity and distance space at z = 0 for the debris of accreted material with respect to those analyzed in that study.
Jethwa et al. (2016) have built a dynamical model of the Magellanic system that takes into account the dynamical influence of the SMC on the group satellites orbits, the dynamical friction exerted by the LMC onto the SMC and by the MW on the Magellanic Clouds, and a non-static MW. The LMC masses explored encompass the range of those in Deason et al. (2015) and Sales et al. (2017). Assuming isotropy for the MW sub-halo system, they found that half of the 14 dark energy survey (DES) dwarfs they were considering belonged to the LMC with a a probability >0.7.
An important general conclusion from these works is that knowledge of the systemic radial velocities, combined with sky position and distance, can greatly aid in the identification of previous Magellanic Cloud satellites. In particular, the most compelling evidence for association is expected to be provided by the additional information afforded by knowledge of systemic proper motions because the accreted galaxies are expected to share a similar direction of the orbital angular momentum of the LMC.
With the second Gaia mission (Gaia Collaboration 2016) data release (GDR2; Gaia Collaboration 2018a), the situation has dramatically improved: not only has the accuracy of the systemic proper motions of the classical MW dwarf spheroidal galaxies (dSphs)1 been significantly improved in several cases (Gaia Collaboration 2018b), but such determination has finally become possible for dozens of the ultra-faint dwarf galaxies (UFDs; Fritz et al. 2018a; Kallivayalil et al. 2018; Massari & Helmi 2018; Simon 2018), while before only Segue 1 had a systemic proper motion measurement (Fritz et al. 2018b). All of the above is in a common, absolute reference system.
Kallivayalil et al. (2018, hereafter K18) used the Sales et al. (2011, 2017) LMC analog to test a possible association with the LMC for 32 UFDs with MV ≳ −8. For the systems for which 3D velocities could be obtained, given the additional availability of published spectroscopic data, they concluded that four (Hor I, Car II, Car III, and Hyd I) were former satellites of the Clouds, while Hyd II and Dra II could be reconciled with a model allowing for a larger dispersion of the tidal debris properties in velocity and distance or sky location.
For the systems that lacked either systemic proper motion and/or radial velocity measurements at the times of the studies, predictions are provided in several of the works cited above under the assumption of a prior physical association to the Magellanic system. In particular, Jethwa et al. (2016) and K18 provided such predictions in the observable space of proper motion and/or radial velocity measurements, which has the advantage of not carrying the error propagation in the conversion to Galactocentric velocities.
Here we present results from unpublished Fibre Large Array Multi Element Spectrograph (FLAMES) GIRAFFE intermediate-resolution spectroscopic data available in the ESO archive for four faint and distant (70–190 kpc) candidate dwarf galaxies, whose location on the sky is close to the Clouds: Columba I (Col I), Horologium II (Horo II), Phoenix II (Phx II), and Reticulum III (Ret III). They were discovered in DES data (Koposov et al. 2015a; Bechtol et al. 2015; Drlica-Wagner et al. 2015; Kim & Jerjen 2015). Phx II was followed up with deeper Megacam imaging (Mutlu-Pakdil et al. 2018) and Col I with deeper Hyper Suprime-Cam imaging (Carlin et al. 2017). We use the FLAMES/GIRAFFE data in conjunction with GDR2 astrometric information to provide the first determination of the global properties (mean spectroscopic metallicity and line-of-sight velocity dispersion) and bulk motion of these systems, and discuss whether these four satellites might have been former LMC satellites.
The paper is structured as follows: in Sect. 2 we describe the datasets we used for the analysis and detail the data-reduction procedure and determination of line-of-sight (l.o.s.) velocities and metallicities from the spectroscopic data in Sect. 3, in Sect. 4 we describe the selection of star members to the target systems, and Sect. 5 contains the determination of their global properties and implications for their nature as galaxies or stellar clusters. In Sect. 6 we present the determination of space velocities and orbital properties of the objects in the sample and investigate a possible origin as LMC satellites. In Sect. 7 we discuss the LMC mass suggested by the number of potential satellites, and summarize and conclude in Sect. 8. In the appendix we carry out a detailed comparison with Pace & Li (2018).
2. Datasets
We analyzed four UF systems for which public FLAMES/GIRAFFE data exist in the ESO archive (program IDs: 096.B-0785 and 098.B-0419) with no associated publication to this date to the best of our knowledge: Col I, Phx II, Horo II, and Reticulum III (Ret III). We complemented the spectroscopic data with GDR2 (Gaia Collaboration 2016, 2018a) and public DECam photometry of individual point-sources from the first data release of the National Optical Astronomy Observatory (NOAO) source catalog (Nidever et al. 2018). This uses dark energy survey (DES) images.
We used the following distance moduli in the analysis: 21.31 ± 0.11 for Col I (Carlin et al. 2017), 19.46 ± 0.20 for Horo II (Kim & Jerjen 2015), 19.60 ± 0.10 for Phx II (Mutlu-Pakdil et al. 2018) and 19.82 ± 0.31 for Ret III (Drlica-Wagner et al. 2015). We also added in quadrature an additional error of 0.1 mag as safeguard against systematic errors, as in Fritz et al. (2018a).
3. Spectroscopic analysis
The observations were carried out with FLAMES mounted at Very Large Telescope (VLT) UT2 (Pasquini et al. 2002), together with the GIRAFFE spectrograph and the LR8 grating, which provides a resolution of ∼6500 in the region of the near-infrared Ca II triplet lines around 8500 Å. The data consist of 3x3000s exposures and one of 1980s for Phx II, 6 × 2775 s for Col I, 3 × 2775 s for Horo II, and 3 × 2775 s for Ret III.
3.1. Data reduction and extraction of spectra
The FLAMES/GIRAFFE data have been processed through the GIRAFFE data-reduction pipeline (Melo et al. 2009). This pipeline performs the bias, flat field, and scattered light corrections; finds, traces, and extracts the spectra; and obtains the wavelength calibration based on daytime calibration exposures. Our own software was used to subtract the sky emission following the procedure described in detail by Carrera et al. (2017, see also Battaglia et al. 2008). Briefly, a master sky is obtained by averaging all the spectra obtained from fibers located on sky positions. The resulting master sky spectrum and the spectra for each object are separated into two components: continuum and line. To obtain the continuum of both sky and object lines, we used a nonlinear median filter with 3σ clipping. The line spectrum was obtained by subtracting the continuum. The sky- and object-line components were compared to search for the scale factor that minimizes the sky line residuals. In practice, this optimum scaling factor is the value that minimizes the sum of the absolute differences between the object-line and the sky-line multiplied by the scale factor, known as L1 norm. The object-continuum was added back to the sky-subtracted object-line spectrum. Finally, the sky continuum was subtracted assuming that the scale factor is the same as for the sky-line component.
After applying the barycentric correction, individual spectra were averaged to obtain the combined spectrum for each star using the individual signal-to-noise ratio (S/N) as weight and an average sigma-clipping rejection algorithm to remove deviant pixels. Individual exposures with very low S/N, that is, S/N < 3 pixel, were rejected. This “combined” spectrum was then cross-correlated with each individual exposure to remove small shifts between them. This procedure was repeated until convergence.
3.2. Line-of-sight velocity and [Fe/H] determination
At this point, the combined spectrum was cross-correlated with a grid of 432 synthetic spectra. The details about the computation of this grid can be found in Allende Prieto et al. (2018). The grid has three dimensions: metallicity, [Fe/H]; effective temperature, Teff; and surface gravity, log g. Metallicity ranges from −5.0 to +1.0 dex with a step of 0.5 dex. Temperature extends from 3500 to 6000 K with a step of 500 K. Finally, the gravity covers from log g = 0.0 to 5.0 dex with a step of 1.0 dex. For the α-element abundances, the spectra were computed assuming [α/Fe] = 0.5 dex for [Fe/H] ≤ −1.5 dex, [α/Fe] = 0.0 dex for [Fe/H] ≥ +0.0 dex, and linear between them. The abundances of other elements were fixed to the solar values (Asplund 2005), and the microturbulence velocity was fixed to 1.5 km s−1. First, each spectrum was cross-correlated with a reference synthetic spectrum, which had the parameters of Arcturus, to obtain an initial shift. After we applied this initial shift, the observed spectrum was compared with the whole grid in order to identify the model parameters that best reproduced it through a χ2 minimization using FERRE2 (Allende Prieto et al. 2006). The best-fitting synthetic spectrum was again cross-correlated with the observed spectrum in order to refine the shift between the two. Of course, Arcturus is not the ideal template for some of the target stars. However, after the first initial determination of the shift with Arcturus, our procedure converged by itself to appropriate templates for these objects. For a few stars, this procedure yields temperatures close to the edge of the synthetic spectra grid, 6000 K, suggesting that they may be hotter. For these particular cases, we repeated the procedure using another synthetic spectrum grid covering a temperature range between 5500 and 8500 K also with a step of 500 K. The other features of this grid are the same as for the previous grid except for the log g, which starts at 1.0 dex. An example of the obtained fits is shown in Fig. 1.
 |
Fig. 1. Example of observed spectra (gray) with different S/N and the best synthetic models (black) found in the l.o.s. velocity determination analysis. Horologium II 8_184 is a hot star, likely a BHB star, and the continuum normalization is not optimized for these objects. |
The shifts obtained for each individual exposure were applied to the combined l.o.s. velocity to obtain individual values for each exposure. The final heliocentric l.o.s. velocity was obtained as the average of these using the individual S/N as weight. The procedure we followed also allowed us to determine the scatter between the multiple individual l.o.s. velocity determinations, Vscatter (see Fig. 2). This provides a better estimate of the internal precision than the typical uncertainty determined from the cross-correlation peak. For the Vscatter calculation, we excluded the short Phx II exposure because it clearly has a lower S/N than the rest. It has to be noted that the procedure can produce low Vscatter values by chance even at low S/N. Therefore, to better constrain the run of Vscatter as a function of S/N, we fit an exponential function to the individual Vscatter values. According to this, the typical uncertainty at ⟨S/N⟩∼10 pixel is ∼4 km s−1.
 |
Fig. 2. Run of Vscatter as a function of median S/N of the individual exposures for all observed stars with at least three individual measurements. An exponential function (solid line) has been fitted to parameterize the distribution. |
The procedure followed to derive the l.o.s. velocities might provide valuable information about the temperature, gravity, and metallicity of the observed stars. Unfortunately, the relatively small wavelength range covered, ∼1000 Å between 8200 and 9200 Å, and the spectral resolution, ∼6500, do not allow us to properly constrain the temperature and gravity of the observed stars, which are necessary to determine the stellar metallicity, however. We therefore used photometric information to constrain the stellar temperature and gravity. To that aim, we first transformed the Gaia magnitudes G, GBP, and GRP into V, I, J, H, and Ks using the relationships provided by Evans et al. (2018). The absolute magnitudes in these bandpasses were obtained using the distance moduli listed at the beginning of Sect. 2. Temperatures were derived using the relations described by Ramírez & Meléndez (2005) assuming an initial estimate of the metallicity of [M/H] = −2.0 dex. We derived temperatures for V − I, V − J, V − H, and V − Ks independently and obtained the corresponding uncertainties by propagating the errors throughout the whole procedure. The main sources of uncertainty are the relationships to transform magnitudes from the Gaia photometric system and the uncertainty in the distance. Altogether, our temperatures have a typical uncertainty of 100 K. The uncertainties are slightly higher for the hottest stars. Because the values obtained from the different colors agree within the uncertainties, we obtained the final temperature by averaging them together.
Surface gravities have been determined using the Bayesian estimation algorithm3 presented by da Silva et al. (2006) with PAdova and TRieste Stellar Evolution Code (PARSEC) evolutionary tracks (Bressan et al. 2012) and the temperatures above. The average uncertainty in the log g determination is 0.15 dex. Finally, the metallicity was determined from the combined spectra by comparing the observed spectra with the same synthetic grid used in the l.o.s. velocity determination, but fixing the temperatures and gravities to the photometric values. Our analysis confirms that one of the observed stars, Horo II 8_184, likely is a blue horizontal branch (BHB) star, as expected from its position on the color-magnitude diagram (CMD, see Fig. 4).
Because several of our observed stars have a low S/N, it was necessary to check the reliability of our results. To that aim, we selected synthetic models with metallicity [Fe/H] = −2.0 dex but with three different temperatures (4500, 5050, and 7500 K) and surface gravities (1.3, 2.0, and 3.5 dex), which covers the whole range of temperatures and gravities of the stars in our observed sample. Different levels of noise were injected in each spectrum in order to obtain spectra of different S/Ns. Fixing the temperature and gravity to their input values, the spectra were analyzed as the observed stars in order to determine their metallicity as a function of the S/N (Fig. 3). At S/N = 3 pixel, the recovered metallicity is underestimated with respect to the input metallicity for the three models. At S/N > 5 pixel, the input metallicity is recovered within the uncertainties for the two coldest models. For the coldest model, the method works slightly better than for the other model at a given S/N. For the hottest model, which represents the BHB star in Horo II (see Sect. 4), the recovered [Fe/H] is always underestimated, although the difference with the input value decreases as the S/N increases.
 |
Fig. 3. Recovered metallicities as a function of S/N for three different synthetic spectra with the input stellar parameters listed in the bottom right corner ([Fe/H]/effective temperature/log g). The S/N for each model has been slightly shifted to avoid superposition of the symbols. |
4. Search for member stars
4.1. Detection of the UF systems
In order to select potential member stars and detect the UF system in the l.o.s. velocity, we used a set of criteria making use of the photometric, astrometric, and spectroscopic information to progressively clean the sample (see Table 1 for the effect of each step on the selection).
Number of stars targeted in the FLAMES/GIRAFFE observations, retained after successive cleaning criteria.
We started by considering all the stars with a reliable l.o.s. velocity determination from the FLAMES/GIRAFFE spectra. We performed a broad selection on the CMD around the locus expected for red giant branch (RGB) and horizontal branch (HB) stars by using the DECam i magnitudes and the g − i color. Both were corrected for extinction using E(B − V) from Schlegel et al. (1998) and the band coefficient from Abbott et al. (2018). This retains nearly all FLAMES targets for Col I and Ret III because they were originally observed with a similar selection. In the case of Horo II and Phx II, the original selection did not appear to include a color cut, therefore the number of stars is clearly reduced.
We then concentrated on the stars with kinematic information from both GDR2 data and the FLAMES observations because they greatly complement each other in identifying signals in the low number regime. We used similar criteria as in Fritz et al. (2018a) to define a sample of halo stars. Because the the parallaxes of the stars at the distances of our targets are expected to be consistent with zero, we required that the parallax had a significance lower than 2σ; this also removed stars with artificially very negative parallaxes (Lindegren et al. 2018). We further selected stars by requiring them to be bound to the MW given their proper motion at the distance of the satellite. We used the same generous 2σ criterion as in Fritz et al. (2018a). This selection based on parallax and proper motion greatly cleans the sample (e.g., the number of stars for Ret III decreases from 43 to 10): as we show in Figs. 4–7, the disk component is essentially removed.
 |
Fig. 4. Plots for the identification of the Horo II members for targets with FLAMES spectroscopic observations. Stars consistent with a distant halo origin in Gaia parallax, proper motions, and color magnitude space are plotted in blue, and the non-halo stars are plotted in gray. Stars without Gaia proper motion information, but with a location on the CMD consistent with being an RGB or a BHB star at the distance of the object are plotted in red. The very likely members of the satellite are enclosed within a cyan square and the additional potential members within an orange square. Top left panel: spatial distribution of the targets. The semimajor axes of the ellipses are equal to 1.5 and 3 projected (elliptical) half-light radii and use ellipticity and PA from Kim et al. (2015). Top right panel: location in the proper motion plane; the proper motion selection box of halo stars given by the escape speed criterion is shown in gray. Bottom left panel: extinction-corrected CMD; the Parsec isochrones with [Fe/H] = −2.0 and −1.0 dex and age = 12 Gyr are overlaid. The isocrones have solar-scaled [α/Fe]; this might be a potential source for the discrepancy in the location of stars of a given spectroscopically determined metallicity with the isochrones of similar [Fe/H] because stars in such ancient systems are typically α-enhanced (e.g., Mashonkina et al. 2017, and references therein). Bottom right panel: distribution on the l.o.s. vhelio vs. distance from the satellite center in units of projected elliptical half-light radius. The velocity distribution of disk stars in the mock catalog (z < |1| kpc) is shown in gray; the horizontal lines indicate the central 1σ interval. |
 |
Fig. 5. Same as Fig. 4, but for Ret III. The structural parameters are from Drlica-Wagner et al. (2015). |
 |
Fig. 6. Same as Fig. 4, but for Col I. The structural parameters are from Drlica-Wagner et al. (2015). |
 |
Fig. 7. Same as Fig. 4, but for Phx II. The structural parameters are from Mutlu-Pakdil et al. (2018). |
We inspected the location of the stars that passed the selection criteria on the heliocentric l.o.s. velocity versus projected elliptical radius (R)/half-light radius (Rhalf) plane ( blue symbols in the bottom right panel of Figs. 4–7): in all cases some small group of stars clumps at fairly similar velocity, which we considered as our preliminary heliocentric l.o.s. systemic velocity for the satellites, vhelio, sat; this velocity spike consisted of six stars for Col I, three for Horo II, six for Phx II, and three for Ret III (see Sect. 4.2 for more details).
4.2. Testing the robustness of the detection
The first step was to determine whether the overall detection of a spike in heliocentric velocity is robust for each of the UF systems we analyzed. To that aim, we determined the density of contaminating objects at any velocity that passed the above CMD-based, parallax and proper motion-based selection criteria (ρcont) by applying the same cuts to GDR2 sources at distances 5 < R/Rhalf < 10. As before, we used stars in NSC catalogs that have measured motions in GDR2. When determining the amount of expected contaminants, we also took the completeness of the FLAMES observations into account, that is, not all potential targets had allocated FLAMES/GIRAFFE fibers. To do this, we selected potential member stars with our usual CMD selection from the NSC DR1 catalog. The faint limit was set by the faintest stars with Gaia kinematics, and the bright limit by the brightest star targeted with FLAMES. We also selected stars in the same way from the FLAMES catalog. We then counted in both catalogs how many stars lie within 3 Rhalf and obtained a rough number for the completeness: c = NFLAMES/NDECam, which means that c is between 67% and 85%.
Finally, considering c and the largest radius of the potential members for each system, we translated ρcont into the number of expected contaminating stars for each satellite in the area occupied by the potential member stars (Ncont). We obtain 2.1 stars for Col I, 5.4 for Horo II, 1.4 for Phx II, and 2.1 for Ret III. The larger number for Horo II is caused by a member star at 4.4 Rhalf and therefore the large area considered; when this rather bright star is omitted, only 1.2 contaminants would be expected in the correspondingly smaller area occupied by the remaining member stars. Thus, in most cases, the observed number of stars in the velocity spike is already somewhat larger than the expected number of contaminants. This indicates a detection.
We compared the number of expected contaminants at all velocities with the stars that can be considered clear contaminants from the FLAMES observations, that is, those that fall within the radius of the outermost candidate members and pass the CMD and GDR2-based cuts, but whose l.o.s. velocity lies outside of the velocity spike. Of these, there are two for Col I, none for Hor II, none for Phx II, and one for Ret III. The numbers are compatible with the expectations (given the small number statistics) for all cases, except for Horo II. The reason for this discrepancy might be that the expected number of contaminants is overestimated in Horo II because the outermost candidate lies clearly outside of the region of three half-light radii we used to calculate c.
The detection of the spike might be due to contaminants that cluster in a given velocity range rather than to the UF system. To determine this, we calculated the probability of observing a number of stars in the velocity range of the velocity spike of each UF system that was equal to or larger than the number of potential members, given a Poisson distribution with an expectation value equal to Ncont and the expected vhelio distribution of contaminant stars (which will be mostly halo stars because of our selection criteria).
Because no GDR2 l.o.s. velocity is available for sources as faint as those we studied here, we extracted the information on the expected heliocentric velocity distribution of contaminants at the location of the UF systems using the Gaia mock catalog of Rybizki et al. (2018). First, we selected objects within a 1° radius around the satellites in our sample and produced new estimates of their parallax, proper motion, and photometric properties by factoring in the measurement errors. Then we applied similar selection criteria as for the data4. The l.o.s. velocity distribution thus obtained is broad and shows no sign of a disk population, confirming that our approach is able to select halo stars. We then made the simplifying assumption that the velocity distribution of the contaminating stars is uniform, and focused around the velocity of the UF system to obtain a representative value, fhel, which can be used as the probability of observing a star at a given velocity5. From this we finally calculated the probability of observing a number of contaminants within the velocity range of the spike equal to or larger than that of the potential member stars, also accounting for that fact that we could have observed the spike at any velocity (i.e., we multiplied the values obtained by the approximate velocity range that is covered by the spectroscopically observed stars, 300 km s−1, and divided by the velocity range covered by stars in the spikes). For all satellites, the likelihood to observe a spike of these numbers by chance is lower than 0.1%, except for Horo II, for which it is small in any case (2.4%).
The reality of the spike of Horo II could be doubted because the two potential member stars are separated by 31.2 km s−1 or 2σ. However, one of the two stars has the color and magnitude of an BHB star exactly at the distance of the satellite (80 kpc). At that distance, the density of stars with BHB-like colors (which could also be blue straggler stars) is very low, about 0.05 stars per square degree per 0.2 mag bin, when QSOs and white dwarfs are excluded (Deason et al. 2014). The BHB candidate is found in the inner 0.017 square degree around the satellite position, which means that the probability is lower than 0.1% that the star is not associated with Horo II. Second, another brighter star lies within 5 km s−1 of the velocity of the BHB star at 4.4 half-light radii. As a result of its brightness, only 0.5 stars are expected even in this correspondingly larger area. Because now the velocity of system is already known even for a single star, the probability for a chance association at this vhelio is slightly lower than 1%. Therefore we included this star in our estimates of the mean properties of Horo II, although we also provide values when this object was excluded. The star also strengthens the detection of the systemic velocity of Horo II.
4.3. Membership
We now consider whether a certain star may be a contaminant or a member of the satellite. We again used the photometric data at large radii (split into different magnitude bins to account for different numbers of contaminants as a function of magnitude, i.e., mG < 19, 19 < mG < 20 and mG > 20) and the model for the heliocentric l.o.s. velocity distribution. We calculated the expected background level for each candidate star with the following formula:
The 3 (km s−1) accounts for the uncertainty in the value of the observed heliocentric velocity of the satellite, and the 10 (km s−1) removes the velocity range previously used to determine fhel. We used ncont, i to classify stars: those with ncont, i < 0.1 were treated as very likely members, and those with ncont, i between 0.1 and 1 are added as potential members.
The star located at 4.4 Rhalf in Horo II remains classified as only candidate member. A star in Phx II at 2.8 Rhalf is formally a member with ncont, i = 0.085, but has an unusually high metallicity (see Table 2), therefore we consider it as candidate member and not a very likely member.
Observed properties for potential member stars.
In total, we find 13 very likely members (3 in Col I, 2 in Horo II, 5 in Phx II, and 3 in Ret III), which are contained within 2.1 Rhalf (without the aforementioned BHB star, the largest distance would be at 1.8 Rhalf). In addition, we have 5 candidates: 3 for Col I, 1 for Horo II, and 1 for Phx II, usually at larger distances.
As a further step, we also considered the stars that have FLAMES spectroscopic measurements but no Gaia kinematic information (see the red symbols in Figs. 3–6). Only Col I has clearly promising candidates, therefore we ignored the other satellites. We used the NSC catalog to determine the background density between 5 Rhalf and 0.5° using the color box of Col I for mi between 20.4 and 21.5 and then used the l.o.s. velocity information as before: the probability of the two innermost stars is lower than 3% to be contaminants, and we therefore added them to our sample of likely members. The third innermost star has a ∼3% probability of being a contaminant, but it is also significantly redder than the other stars in the CMD; we therefore classify it as a candidate. We should note that whether these new members are included in the sample or are excluded from it does not significantly influence the overall properties of the system (determined taking into account error bars) given the low S/N and large measurement errors of these faint stars. In total, we have five very likely and four possible members for Col I.
Table 2 lists the classification of a given star as a very likely member or candidate, together to its l.o.s. heliocentric velocity, [Fe/H], and, when available, the proper motion information. We highlight an extremely metal poor star in Col I, col1_8_27, with mi = 19.1 and [Fe/H] = −3.36 dex.
Finally, we note that the location of the member stars in the CMD appears to be too red for the location expected from PARSEC isochrones of the same metallicity as the spectroscopic values. We have checked that the same effect is visible in NSC DR1 photometry of the globular cluster NGC 1904, which means that it is not intrinsic to our analysis; we also note that Dartmouth isochrones of the same metallicity and age would lead to slightly redder colors than the PARSEC isochrones. In addition, we checked that the DES DR1 catalog (used by Pace & Li 2018) also leads to a similar offset, see also Appendix A. All this suggests that the cause of the mismatch is more likely the isochrones and not the photometry.
5. Global properties and nature of the satellites
We now determine the global kinematic and metallicity properties of the objects, that is, their systemic l.o.s. velocity ⟨Vhel⟩, systemic proper motion in right ascension (⟨μα*⟩) and declination (⟨μδ⟩), the average correlation coefficient between μα* and μδ, mean metallicity (⟨[Fe/H]⟩), as well as the intrinsic spread in the l.o.s. velocity (σV, hel) and metallicity distribution (σ[Fe/H]). These latter two quantities are especially important for systems whose nature is uncertain, such as those in the luminosity and surface brightness regime of MW UF systems. The current thinking is that high dynamical mass-to-light ratios (as revealed by an intrinsic velocity dispersion significantly larger than accounted for by the baryonic component) and/or an intrinsic spread in metallicity can be used to classify the system as a galaxy (or defined to be, see Willman & Strader 2012).
Because of the large uncertainties in the individual proper motion measurements, we did not attempt to derive the intrinsic spread in the distribution of the proper motion values, and we performed a simple weighted average to determine ⟨μα*⟩, ⟨μδ⟩ and the correlation coefficient. On the other hand, we adopted a Bayesian approach to determine the other quantities, as in Taibi et al. (2018), by running the MultiNest code (Feroz et al. 2009; Buchner et al. 2014), which is a multi-modal nested sampling algorithm. The nested sampling (Skilling 2006) is a Monte Carlo method aimed at efficiently calculating the Bayesian evidence, which as a byproduct provides the posterior parameter estimate. We assumed that the metallicity and l.o.s. velocity distributions are Gaussian and took the measurement errors on the individual quantities into account in determining the intrinsic spread. We assumed flat priors between 0 and 100 km s−1 for σV, hel and between 0 and 3 dex for σ[Fe/H]. Table 3 summarizes the results for the sample of very likely members alone and for the sample that also includes potential members (we also highlight our preferred cases, as in the explanations below).
Average and global properties of the objects in our sample.
Figure 8 shows the posterior probability distribution functions (pPDF) obtained for σV, hel and σ[Fe/H]. In some cases the peak of the pPDF is found at a null spread, while the peak probability value in others is not much higher than the probability at σV, hel = 0 (and σ[Fe/H] = 0). It is important to resolve the intrinsic spread in these systems to ascertain their nature, therefore we complemented our analysis with mock datasets in order to understand whether the detection of an intrinsic spread might occur by chance because of the small number statistics and/or large measurement errors of the datasets, or if it is reliable. For each UF system, we produced 1000 mock samples of l.o.s. velocities and metallicities drawn from a Gaussian distribution with no intrinsic spread, which would mimic the case of the system being a stellar cluster, and with a size and error distribution as for the set of members being considered. As bin size we used a third of the lower 1σ error in the measured parameters everywhere. For each of these mock samples, we measured the ratio of the probability at σV, hel = 0 km s−1 (and σ[Fe/H] = 0 dex) over that of the probability at the peak of the PDF6: we considered that we resolved the intrinsic spread when the ratio of only 5% of the mock sets is as low as that given by the observations.
 |
Fig. 8. Posterior probability distribution function of the dispersion in l.o.s. velocity (left panel) and metallicity (right panel) for the four satellites. The blue line shows the results when all potential members are considers and the orange line represents the most probable members. |
While we resolved the intrinsic metallicity spread for all systems except for Hor II, the only system for which the current data allow us to resolve σV, hel is Phx II. For the cases where the intrinsic spreads are unresolved, we report in Table 3 the upper limits (defined as the values at the 90th percentile of the distributions). Figure 9 shows the object locations in the mass-metallicity plane with respect to UF systems studied in the literature.
 |
Fig. 9. Average metallicity and metallicity dispersion (the “error” bars) as a function of absolute magnitude for the four target satellites. Objects that have no dispersion measurement or only limits are plotted without an error bar, as for Horo II. The metallicities for the “other objects” are from Torrealba et al. (2016), Martin et al. (2007), Simon & Geha (2007), Simon et al. (2015, 2011, 2017), Koch et al. (2009), Carlin et al. (2009), Li et al. (2018a, 2017, 2018b), Kirby et al. (2015, 2013, 2017), Walker et al. (2016, 2009), Koposov et al. (2015b, 2018), Kim et al. (2016), Willman et al. (2011), Norris et al. (2010) and Longeard et al. (2018). The point at MV = −5.3/[Fe/H] = −1.68 is Laevens 1/Crater I, which is probably a globular cluster. |
Impact of different samples of members. We comment here on the set of values that we consider as the most reliable of those derived from the samples of very likely members alone and likely members + candidates. Only one star in Phx II has an uncertain membership. The metallicity ([Fe/H] = −1.1 ± 0.18 dex) of this star is significantly higher than that of the rest (see Table 2), therefore our preferred set of values was derived without this star. The spread in [Fe/H] alone is noticeably affected by the choice of including or excluding this star. It decreases from 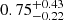 dex to
dex to 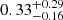 .
.
The candidate members in Col I are also on average somewhat more metal rich than the rest; but their metallicity values, [Fe/H] ≤ −1.65, are compatible with stars in dwarf galaxies of similar luminosity. We conservatively preferred values obtained from the sample of very likely members alone. We note that the properties of Col I in general do not significantly depend on the chosen sample because the candidates are faint (and therefore have large errors on the derived properties) and their properties are similar to those of the rest. In particular, the metallicity spread in this system is clear in both cases.
For both Col I and Phx II, the proper motion values do not depend much on the sample because the uncertain members have larger measurement errors and therefore have much less weight in the (weighted) average value. This is different for Horo II, for which the uncertain member is bright. Because it is difficult to adopt a preferred sets of values for Horo II, we retained both of them for the rest of the analysis.
Comparison with the literature. Our independent measurement of the proper motion of Phx II agrees excellently with that by K18, which was guided by the predictions from the model postulating an association with the LMC. Pace & Li (2018) have determined proper motions for a set of UF objects that also includes the four systems we studied here, without the aid of spectroscopic datasets. In Appendix A we compare the results from their work in detail. In summary, our preferred values differ by 1.6, 1.8, 0.9, and 1.9σ for Col I, Hor II, Phx II, and Ret III7. In all cases, the disagreement is small enough that it might have occurred by chance, although other reasons probably contribute, including underestimated errors. Independently of this, as we describe in Sect. 6, the current errors in systemic proper motions except for Phx II are large and further observations are necessary to obtain constrains on the orbit of these satellites.
Nature of the satellites. The only system for which we resolved the l.o.s. velocity dispersion is Phx II. Its value does not depend significantly on which set of members is considered, and it is based on at least five stars that are partly so bright that a chance association is very unlikely. Even though a robust determination would benefit from larger sample sizes and multiple observations with different time sampling, it was shown that undetected binaries usually cannot inflate the measured l.o.s. velocity dispersion to the values measured for Phx II (McConnachie & Côté 2010). The intrinsic metallicity spread in Phx II is 0.33 dex in the case of the preferred set of members. We consider this value as rather robust because it contains the brightest (highest S/N) stars. Overall, the values of the l.o.s. velocity and metallicity dispersion for Phx II are evidence that this satellite is a galaxy.
For Ret III we measure a formally robust metallicity dispersion of 0.35 dex, but because the stars are rather faint, we do not consider it as conclusive to classify the system as a galaxy.
The measurement for Col I (0.71 dex) is more robust since the two brightest certain members have a clearly different metallicity, [Fe/H] = −3.36 and −2.22. The large metallicity spread appears to indicate that Col I is a galaxy; this hypothesis is further supported by its rather large size (Carlin et al. 2017), which means that it is probably not a globular cluster.
For the case of Horo II our data are equally well consistent with a nature as globular cluster or galaxy because our limits on intrinsic spreads are unconstraining.
We note, however, that even if some of the UFs are globulars clusters, it is likely that they originated within a dwarf galaxy because halo globulars were very likely accreted (Zinn et al. 1993; Muratov & Gnedin 2010). Even in this case, we might therefore still learn about the orbital properties of their former hosts. We note that all our targets except maybe for Horo II have lower metallicities than most halo globulars, which is unlike Laevens 1 (Weisz et al. 2016; Kirby et al. 2015) and Pyxis (Fritz et al. 2017). This could very tentatively suggest an origin in a smaller system, although it is known that globular clusters can be much more metal-poor than the field stars of their host (as in the case of the Fornax dSph).
6. Velocities, orbital poles, and association with the LMC
We now use the systemic proper motions and l.o.s. velocities derived in the previous section to determine the Galactocentric velocities and orbital parameters of the systems in the sample (see Table 4 and Fig. 10). For the conversion into velocities and for the following analysis, we also added a systematic error that depended on the size of the system to the proper motions errors in both dimensions (see Fritz et al. 2018a, for the details), and we assumed it to be uncorrelated between α and δ. Because of the large random errors for our stars, the systematics are not important. We followed the same procedure as Fritz et al. (2018a) to convert the observed heliocentric velocities and proper motions into Galactocentric properties. This also accounts for uncertainties into the solar motion and distance of the satellite, but in our cases, the total uncertainties are dominated by the proper motion uncertainties. As discussed in Fritz et al. (2018a), in this situation, classical forward Monte Carlo simulations are still appropriate for orbital poles estimates, but backward Monte Carlo simulations are to be preferred to avoid biases in positive defined quantities such as the tangential velocity, Vtan.
Galactocentric distances and velocities for the satellites in our sample.
 |
Fig. 10. All-sky view of orbital poles for the objects in the sample; the open circles (or square) indicate the value that follows from the measurements, and the small points around each object plot the orbital poles from the individual Monte Carlo simulations. We show our preferred membership selection for all satellites; for Horo II, we also show the other option in light green, which covers nearly the full great circle. The two options lead to very similar results for the other satellites. |
Figure 10 shows the estimated orbital poles with their uncertainties, compared to the orbital pole of the LMC. Phx II has the best localized pole direction: l = 185 ± 9 and b = −18 ± 3 degree, which is at 16° from the pole of the LMC and close to the location of the pole of Hydra I, a galaxy considered to be a former LMC satellite in K18. In the other cases, the error in proper motion is large, which almost enables drawing a great circle. It appears unlikely, however, that Col I was once associated with the LMC because the direction of its orbital pole is always at least 32° from the pole of the LMC. An association of Horo II with the LMC becomes significantly more or less likely depending on whether the brightest (most distant in Rhalf) candidate member is truly a member or not. When this star is included, the most likely pole is formally determined with a higher accuracy, l = 156 ± 17 and b = −5 ± 12 degree, and it is at only 16 degree distance of the LMC. When it is excluded, the most likely pole direction changes very significantly (to l = 258 and b = 37) and the 1σ region spans nearly two-thirds of the sky, making a prior association with the LMC less likely (although it is not completely excluded). The inclusion/exclusion of this star also quite dramatically changes the values of the tangential and 3D velocity. Ret III is still an uncertain case because the LMC can be found within 3° from the great circle allowed by the Monte Carlo simulations, but only in a minority of cases.
The total velocity is very high for most galaxies, but the errors are too large for the measurement to be informative. The exception is Phx II (V3D = 258 ± 65 km s−1); its orbit would have an eccentricity of 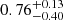 (
(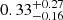 ) in a low- (high-) mass MW halo8; therefore Phx II might have been accreted on a high angular momentum orbit such as that of the LMC.
) in a low- (high-) mass MW halo8; therefore Phx II might have been accreted on a high angular momentum orbit such as that of the LMC.
We note in passing that the proper motion for Ret III by Pace & Li (2018) corresponds to a bias corrected 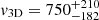 km s−1 with a pole similar to our determination, but better constrained, thus fully inconsistent with the LMC. If it is real, this velocity would be very interesting because it is more than 1σ larger than a generous escape speed of the MW9.
km s−1 with a pole similar to our determination, but better constrained, thus fully inconsistent with the LMC. If it is real, this velocity would be very interesting because it is more than 1σ larger than a generous escape speed of the MW9.
The determinations of the systemic proper motions and l.o.s. velocities, combined with the satellite distances, give a further opportunity of exploring a possible origin as former LMC satellites by comparing them with the predictions given by Jethwa et al. (2016) and K18 for these observables, which also avoids the issues of error propagation onto the Galactocentric velocities.
In the case of the generous membership sample, our measurements for Horo II match the predictions by K18 very well, but not those by Jethwa et al. (2016). On the other hand, the estimate from the sample of very likely members is compatible within 1–2σ with both studies because of the larger error bars.
Ret III matches the predictions by Jethwa et al. (2016) in all quantities within 1–2σ both for an association with the LMC or with the SMC. It also agrees well with the model in K18 in μδ and vhelio, but not in μα *.
For Col I the agreement is good in the proper motions with both models (mostly caused by the large errors of the observations), but it is entirely different in l.o.s. velocity for K18 and compatible with Jethwa et al. (2016) within 2σ. We point out, however, that the typical error bars in the l.o.s. heliocentric systemic velocity by the latter authors are very large for all satellites, at least ±70–80 km s−1. Because Col I is located outside the main track of LMC debris and the large distance does not fit its location, we deem it as very unlikely that it is a former member of the LMC cohort of satellites.
As mentioned in the previous section, we closely recovered the proper motion of Phx II deduced by K1810, but our systemic l.o.s. velocity is different by 45 km s−1, about 9σ away from their prediction, which is 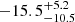 (here, σ is the error in the predicted l.o.s. velocity). Our proper motion measurements do not agree with the model predictions of Jethwa et al. (2016). The problems in K18 in predicting the properties exactly could be associated with the fact that they used a light-LMC analog (see, e.g., Sect. 7). Jethwa et al. (2016) considered a range of usually more massive analogs, whereby the predicted properties encompassed a much wider range of values than in K18. Still, the ranges given by Jethwa et al. (2016) and K18 differ, especially for the proper motions. There are several possible reasons for that. It might be that the difference in the LMC mass is the culprit, but it is also possible that other more subtle effects are responsible, such as differences in the conversion into the solar reference frame.
(here, σ is the error in the predicted l.o.s. velocity). Our proper motion measurements do not agree with the model predictions of Jethwa et al. (2016). The problems in K18 in predicting the properties exactly could be associated with the fact that they used a light-LMC analog (see, e.g., Sect. 7). Jethwa et al. (2016) considered a range of usually more massive analogs, whereby the predicted properties encompassed a much wider range of values than in K18. Still, the ranges given by Jethwa et al. (2016) and K18 differ, especially for the proper motions. There are several possible reasons for that. It might be that the difference in the LMC mass is the culprit, but it is also possible that other more subtle effects are responsible, such as differences in the conversion into the solar reference frame.
Because the orbital pole of Phx II is close to that of the LMC and because of the good agreement with the K18 predictions in most properties, we conclude that Phx II is the only object for which the case of a former association with the LMC can be made. The similarity of the LMC and vast polar structure of the orbital pole mean that this also implies that Phx II could be part of this structure (e.g., Pawlowski et al. 2012).
7. LMC mass
Currently, 42 galaxies close to the MW have sufficiently good proper motions and l.o.s. velocities to classify them as either LMC or MW satellites (all galaxies in Fritz et al. 2018a, except for Phoenix I, the SMC, Phx II, and Col I from this work and Antlia II from Torrealba et al. 2018b). The properties of five to eight UFDs are compatible with them having formed part of the satellite system of the LMC: the SMC (see, e.g., D’Onghia & Fox 2016), Hydrus I, Carina II, Carina III, Horologium I (Kallivayalil et al. 2018), and possibly Phx II (this work), Draco II, and Hydra II (Kallivayalil et al. 2018).
The number of LMC satellites might in principle be translated into a mass ratio of the LMC versus the MW, and then into a mass for the LMC, assuming the MW mass is known. In practice, there are a number of caveats. First of all, a scaling of the number of luminous satellites with the mass of the host needs to be assumed, which is not well known in the regime of hosts with low mass and which carries with it the uncertainties related to the formation of luminous components in the smallest sub-haloes. Moreover, the number of known satellites for both systems is incomplete to some extent. On the one hand, the completeness is likely slightly lower for the MW because the Galactic plane obscures less of the Magellanic system and because fewer of the Magellanic satellites are thought to lie at a larger distance from the Sun because less massive halos are less extended. On the other hand, the incomplete spectroscopy of recently discovered satellites acts in the opposite direction; to what extent the two effects compensate for each other is open to question. Finally, the mass of the MW itself is still subject of debate, with values varying by up to a factor of 2.
We assume that the number of luminous satellite galaxies scales with the host halo mass as the sub-haloes in Gao et al. (2004) and Wetzel et al. (2015). We then consider four options by varying the number of LMC satellites, NLMC, between 5 and 8 (and the number of MW satellites as 42 – NLMC), and adopt a Gaussian error given by the square-root of the number of satellites. This yields a median mass ratio of 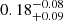 , similar to that obtained by Peñarrubia et al. (2016) from the timing argument (0.2) and by Erkal et al. (2018) using the Orphan stream (0.15). When we take 1.1 ± 0.3 × 1012 M⊙ as M200 of the MW (Bland-Hawthorn & Gerhard 2016) and assume that the mass ratio and the MW mass are independent of each other, we obtain a M200 mass for the LMC of
, similar to that obtained by Peñarrubia et al. (2016) from the timing argument (0.2) and by Erkal et al. (2018) using the Orphan stream (0.15). When we take 1.1 ± 0.3 × 1012 M⊙ as M200 of the MW (Bland-Hawthorn & Gerhard 2016) and assume that the mass ratio and the MW mass are independent of each other, we obtain a M200 mass for the LMC of 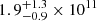 M⊙.
M⊙.
The error bar on our estimate of the LMC mass is large, but at least from the point of view of reasonable values for the MW mass, it seems unlikely that the LMC M200 was as low as 3.6 × 1010 M⊙ before infall, as for the analog used in Kallivayalil et al. (2018). Qualitatively, potential satellites such as Phx II and Hydrus II are found at large distances from the LMC, which also points in a similar direction. More models exploring high-mass LMC analogs are necessary to test whether they would produce tidal debris spread at large distances similar to those of Draco II, Hydra II, and Phx II.
Finally, we note that the increasing number of satellites around the MW that are being classified as former LMC satellites has the effect of decreasing the number of dwarf galaxies that are considered luminous satellites of the MW.
8. Summary and conclusions
We presented results from FLAMES/GIRAFFE intermediate-resolution spectroscopy in the region 8200–9200Å for individual stars in the l.o.s. to four of the newly discovered MW satellites that are lacking spectroscopic information in the literature: Col I, Hor II, Phx II, and Ret III. This implies that their nature as globular clusters or dwarf galaxies was not established and even basic properties such as their systemic l.o.s. velocity were unknown. Horo II and Ret III also lack determinations of their systemic proper motion, while for Col I and Phx II, the only existing determination was obtained by K18 by searching the proper motion space assuming that these objects would have been prior satellites of the LMC, guided by a “light LMC” N-body model.
We extracted the l.o.s. velocity and metallicity of the target stars through a spectral fitting analysis, assuming photometric estimates of the effective stellar temperature and gravity. The information from the spectroscopy was used together with GDR2 astrometric data and photometry (also from the DECam NSC DR1 catalog) to search for stars that are probable members of these systems. All the velocity peaks that we associated with detection of member stars in these systems are found to be highly unlikely to be due to polluter stars passing our selection criteria.
When the systemic velocity of the system was known, we searched for additional members among the stars targeted by FLAMES/GIRAFFE that had no GDR2 kinematic information. In total, we find 15 very likely members (5 in Col I, 2 in Horo II, 5 in Phx II, 3 in Ret III) at most within 2.1 Rhalf. In addition, we have 6 candidate member stars (4 for Col I, 1 for Horo II, and 1 for Phx II), usually at larger projected radii.
The system with the most strongly constrained properties is Phx II; we resolved the l.o.s. velocity dispersion (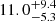 km s−1) for the preferred membership selection and also found an intrinsic metallicity spread of at least
km s−1) for the preferred membership selection and also found an intrinsic metallicity spread of at least 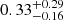 dex. These properties suggest that it is a dwarf galaxy. Col I also has a robust metallicity spread because the two brightest members have a metallicity difference of 1.1 dex. The results on the nature of Horo II and Ret III are inconclusive because they are more sensitive to the adopted sample, and we cannot robustly place the objects in one category or another. Nonetheless, if these objects are globular clusters, being in the outer halo, they might have formed within an accreted dwarf system and therefore still provide information on their former host, such as its orbital properties.
dex. These properties suggest that it is a dwarf galaxy. Col I also has a robust metallicity spread because the two brightest members have a metallicity difference of 1.1 dex. The results on the nature of Horo II and Ret III are inconclusive because they are more sensitive to the adopted sample, and we cannot robustly place the objects in one category or another. Nonetheless, if these objects are globular clusters, being in the outer halo, they might have formed within an accreted dwarf system and therefore still provide information on their former host, such as its orbital properties.
Along the great circle track allowed by the measurement errors, the Col I orbital pole always remains at least 32° from the LMC, making an association unlikely. On the other hand, we cannot firmly exclude an association between the LMC and Horo II or Ret III, although the latter appears rather unlikely due to the small fraction of Monte Carlo realizations that could bring its orbital pole close to that of the LMC.
The orbital pole of Phx II is about 16° away from the pole of the LMC, and its systemic proper motion agrees well with the predictions by Kallivayalil et al. (2018), although the l.o.s. systemic velocity is 9σ away. However, it is possible that an LMC analog producing a larger spread in the tidal debris properties would lead to a better agreement in this observable as well. Therefore Phx II appears as a promising system for having been a former LMC satellite. Because the LMC and the vast polar structure orbital pole are similar, this also implies that Phx II could be part of this structure (e.g., Pawlowski et al. 2012). Bar the caveats discussed, the number of potential LMC former satellites (Phx II and those from works in the literature) would suggest a high mass before infall for the LMC, on the order of 2 × 1011 M⊙.
Even though they might be the same class of objects in most cases, we refer to the typically brighter, passively evolving dwarf galaxies known before the Sloan Digital Sky Survey (SDSS) as “classical” dwarf spheroidal galaxies and to those discovered later as UFDs when their nature as dwarf galaxy has been established, or as ultra-faint (UF) systems or satellites when it is still uncertain.
Available at https://github.com/callendeprieto/ferre
Available at http://stev.oapd.inaf.it/cgi-bin/param_1.3
In practice, we modeled the heliocentric velocity distribution of contaminants within ±50 km s−1 from the preliminary velocity of the UF system with a quadratic function and took as the representative f10 km s−1 that given by the ratio of the number of contaminants within ±5 km s−1 from the UF system velocity over the total. f10 km s−1 was then scaled to the fhel of the satellite by multiplying by the velocity range of the satellite divided by 10 km s−1.
See Fritz et al. (2018a) for the definition of the halos.
For the escape velocity we used an MW halo of 1.6 × 1012 M⊙, as in Fritz et al. (2018a).
Acknowledgments
This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. G.B. gratefully acknowledges financial support by the Spanish Ministry of Economy and Competitiveness (MINECO) under the Ramon y Cajal Programme (RYC-2012-11537); G.B. and S.T. both acknowledge support by MINECO under the grants AYA2014-56795-P and AYA2017-89076-P.
References
- Abbott, T. M. C., Abdalla, F. B., Allam, S., et al. 2018, ApJS, 239, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., Koesterke, L., Hubeny, I., et al. 2018, A&A, 618, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amorisco, N. C., Evans, N. W., & van de Ven, G. 2014, Nature, 507, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Annibali, F., Nipoti, C., Ciotti, L., et al. 2016, ApJ, 826, L27 [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, G., Irwin, M., Tolstoy, E., et al. 2008, MNRAS, 383, 183 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bechtol, K., Drlica-Wagner, A., Balbinot, E., et al. 2015, ApJ, 807, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bullock, J. S., & Boylan-Kolchin, M. 2017, ARA&A, 55, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Carlin, J. L., Grillmair, C. J., Muñoz, R. R., Nidever, D. L., & Majewski, S. R. 2009, ApJ, 702, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Carlin, J. L., Sand, D. J., Muñoz, R. R., et al. 2017, AJ, 154, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, R., Rodríguez Espinosa, L., Casamiquela, L., et al. 2017, MNRAS, 470, 4285 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deason, A. J., Belokurov, V., Koposov, S. E., & Rockosi, C. M. 2014, ApJ, 787, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Deason, A. J., Wetzel, A. R., Garrison-Kimmel, S., & Belokurov, V. 2015, MNRAS, 453, 3568 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., & Fox, A. J. 2016, ARA&A, 54, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Dooley, G. A., Peter, A. H. G., Carlin, J. L., et al. 2017, MNRAS, 472, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Drlica-Wagner, A., Bechtol, K., Rykoff, E. S., et al. 2015, ApJ, 813, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Erkal, D., Belokurov, V., Laporte, C. F. P., et al. 2018, MNRAS, submitted [arXiv:1812.08192] [Google Scholar]
- Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, T. K., Linden, S. T., Zivick, P., et al. 2017, ApJ, 840, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, T. K., Battaglia, G., Pawlowski, M. S., et al. 2018a, A&A, 619, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fritz, T. K., Lokken, M., Kallivayalil, N., et al. 2018b, ApJ, 860, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Helmi, A., et al.) 2018b, A&A, 616, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, L., White, S. D. M., Jenkins, A., Stoehr, F., & Springel, V. 2004, MNRAS, 355, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Garrison-Kimmel, S., Bullock, J. S., Boylan-Kolchin, M., & Bardwell, E. 2017, MNRAS, 464, 3108 [NASA ADS] [CrossRef] [Google Scholar]
- Jethwa, P., Erkal, D., & Belokurov, V. 2016, MNRAS, 461, 2212 [NASA ADS] [CrossRef] [Google Scholar]
- Kallivayalil, N., Sales, L. V., Zivick, P., et al. 2018, ApJ, 867, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., & Jerjen, H. 2015, ApJ, 808, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Jerjen, H., Milone, A. P., Mackey, D., & Da Costa, G. S. 2015, ApJ, 803, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Jerjen, H., Geha, M., et al. 2016, ApJ, 833, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Boylan-Kolchin, M., Cohen, J. G., et al. 2013, ApJ, 770, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Simon, J. D., & Cohen, J. G. 2015, ApJ, 810, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. N., Cohen, J. G., Simon, J. D., et al. 2017, ApJ, 838, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A., Wilkinson, M. I., Kleyna, J. T., et al. 2009, ApJ, 690, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Belokurov, V., Torrealba, G., & Evans, N. W. 2015a, ApJ, 805, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Casey, A. R., Belokurov, V., et al. 2015b, ApJ, 811, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Walker, M. G., Belokurov, V., et al. 2018, MNRAS, 479, 5343 [NASA ADS] [CrossRef] [Google Scholar]
- Laevens, B. P. M., Martin, N. F., Bernard, E. J., et al. 2015, ApJ, 813, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T. S., Simon, J. D., Drlica-Wagner, A., et al. 2017, ApJ, 838, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T. S., Simon, J. D., Pace, A. B., et al. 2018a, ApJ, 857, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Li, T. S., Simon, J. D., Kuehn, K., et al. 2018b, ApJ, 866, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longeard, N., Martin, N., Starkenburg, E., et al. 2018, MNRAS, 480, 2609 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., Ibata, R. A., Chapman, S. C., Irwin, M., & Lewis, G. F. 2007, MNRAS, 380, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., Nidever, D. L., Besla, G., et al. 2015, ApJ, 804, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Jablonka, P., Sitnova, T., Pakhomov, Y., & North, P. 2017, A&A, 608, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massari, D., & Helmi, A. 2018, A&A, 620, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McConnachie, A. W., & Côté, P. 2010, ApJ, 722, L209 [NASA ADS] [CrossRef] [Google Scholar]
- Melo, C., Primas, F., Pasquini, L., Patat, F., & Smoker, J. 2009, The Messenger, 135, 17 [NASA ADS] [Google Scholar]
- Muratov, A. L., & Gnedin, O. Y. 2010, ApJ, 718, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Mutlu-Pakdil, B., Sand, D. J., Carlin, J. L., et al. 2018, ApJ, 863, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Dey, A., Olsen, K., et al. 2018, AJ, 156, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Wyse, R. F. G., Gilmore, G., et al. 2010, ApJ, 723, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Pace, A. B., & Li, T. S. 2018, ApJ, submitted [arXiv:1806.02345] [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Pawlowski, M. S., Pflamm-Altenburg, J., & Kroupa, P. 2012, MNRAS, 423, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Peñarrubia, J., Gómez, F. A., Besla, G., Erkal, D., & Ma, Y.-Z. 2016, MNRAS, 456, L54 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Revaz, Y., & Jablonka, P. 2018, A&A, 616, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rich, R. M., Collins, M. L. M., Black, C. M., et al. 2012, Nature, 482, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Rybizki, J., Demleitner, M., Fouesneau, M., et al. 2018, PASP, 130, 074101 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L. V., Navarro, J. F., Cooper, A. P., et al. 2011, MNRAS, 418, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L. V., Navarro, J. F., Kallivayalil, N., & Frenk, C. S. 2017, MNRAS, 465, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Crnojević, D., Strader, J., et al. 2014, ApJ, 793, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Spekkens, K., Crnojević, D., et al. 2015, ApJ, 812, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D. 2018, ApJ, 863, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., & Geha, M. 2007, ApJ, 670, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., Geha, M., Minor, Q. E., et al. 2011, ApJ, 733, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., Drlica-Wagner, A., Li, T. S., et al. 2015, ApJ, 808, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D., Li, T. S., Drlica-Wagner, A., et al. 2017, ApJ, 838, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 2006, Bayesian Anal., 1, 833 [CrossRef] [MathSciNet] [Google Scholar]
- Taibi, S., Battaglia, G., Kacharov, N., et al. 2018, A&A, 618, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toloba, E., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 816, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Torrealba, G., Koposov, S. E., Belokurov, V., & Irwin, M. 2016, MNRAS, 459, 2370 [NASA ADS] [CrossRef] [Google Scholar]
- Torrealba, G., Belokurov, V., Koposov, S. E., et al. 2018a, MNRAS, 475, 5085 [NASA ADS] [CrossRef] [Google Scholar]
- Torrealba, G., Belokurov, V., Koposov, S. E., et al. 2018b, MNRAS, submitted [arXiv:1811.04082] [Google Scholar]
- van der Marel, R. P., & Kallivayalil, N. 2014, ApJ, 781, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Belokurov, V., Evans, N. W., et al. 2009, ApJ, 694, L144 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. G., Mateo, M., Olszewski, E. W., et al. 2016, ApJ, 819, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Weisz, D. R., Koposov, S. E., Dolphin, A. E., et al. 2016, ApJ, 822, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzel, A. R., Deason, A. J., & Garrison-Kimmel, S. 2015, ApJ, 807, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Willman, B., & Strader, J. 2012, AJ, 144, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Willman, B., Geha, M., Strader, J., et al. 2011, AJ, 142, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Yozin, C., & Bekki, K. 2015, MNRAS, 453, 2302 [NASA ADS] [Google Scholar]
- Zinn, R. 1993, ASP Conf. Ser., 48, 38 [NASA ADS] [Google Scholar]
Appendix A: Comparison with Pace and Li
Pace & Li (2018) have determined systemic proper motions for UF systems in the DES with a method that uses photometric information from the first public data release of DES data and proper motions from GDR2. The set of objects includes the four satellites analyzed in this work, and as mentioned in the main text, we differ in our mean proper motions by 1.6, 1.8, 0.9, and 1.9σ for Col I, Hor II, Phx II, and Ret III, respectively.
To determine the reason for this small disagreement, we first checked the membership classification on a star-by-star basis. In total, the Pace & Li (2018) catalog (hereafter, PL18) contains 26 of our stars with measured l.o.s. velocities. Of these, all the stars that we classified as highly likely members have at least a membership probability p of 82% in the PL18 catalog (except for the BHB candidate in Hor II, which has p = 68%). We found matches only for Col I, which have p between 10% and 70%.
Seven of our stars are missing from the PL18 list, of which four with measured proper motions (hor2_2_48, phx2_8_24, phx2_5_46, and ret3_2_70). Not surprisingly, this includes a larger fraction of candidate members. phx2_8_24, phx2_5_46, and ret3_2_70 might be missing either because they are too red for the PL18 selection or because of their red-HB-like location in the CMD, a region that was excluded by the authors; hor2_2_48 is likely missing because of its large distance from the satellite center. We included hor2_2_48 in the set of members because of our preferred value: it is so bright that an interloper origin is less likely. Because of its high spectroscopic metallicity, phx2_8_24 instead was not part of the sample of members used for the preferred set of values. phx2_5_46 is bright and its properties agree well with those of the other members in the three components of the motion, therefore it very likely belongs to Phx II.
Only one of our non-members has a probability higher than 10% of membership in the PL18 catalog (col1_8_1,5 with 77%).
For 2, 3, 5, and 3 of the PL18 member stars (for the four satellites) with constraining properties (p > 50%, the majority of which have p > 90% and δμ < 4 mas/yr in Pace & Li (2018) do we have no l.o.s. velocity information. All but one of these stars would have passed our selection criteria, but either no FLAMES/GIRAFFE spectrum was available for these stars or their l.o.s. velocity determination was unreliable, and they were therefore excluded from our analysis.
In the following we discuss how the systemic motion would be affected when stars would be included in or excluded from one of the two samples. If col1_8_15 (vhelio = 82 km s−1) were excluded from the PL18 sample, their proper motion determination would change toward our values, but not enough to make it compatible within 1σ. We find that the main difference for Col I is caused by one bright star at (α, δ) = (49.1666, −50.0469) that is among the PL18 members but was not targeted in the FLAMES/GIRAFFE observations. For Hor II we give only a slight preference to our preferred membership selection; the other choice leads to agreement in proper motion within 1σ, but at the cost of a clearly larger error. The agreement was already good for Phx II. When we exclude ret3_2_70, our motion still disagrees to 1.6σ with the motion of Pace & Li (2018). Such a difference occurs with a probability of 26%.
This shows that we do not find clear-cut reasons in general to explain the slight disagreement. Because the disagreement is small, it might have occurred by chance. Underestimated errors could be another possible cause: for instance, we treated the stars with a binary membership classification rather than deriving the properties that factor in the membership probability. PL18 provided continuous probabilities, but the CMD information was treated in a binary way. Moreover, the spatial cut in Pl18 is rather close to the center of the satellite, which might exclude possible tidally affected stars.
Finally, because both studies adopted a photometric preselection of targets but on different catalogs (NSC DR1 versus DES DR1), we used the stars in common to test for systematic shifts that might affect the selection and found that these were very small (0.02 mag in g, r, i band). Overall, the stars that are identified in PL18 alone tend to be bluer than the stars for which we have l.o.s. velocity information. This is partly due to increased difficulties to obtain l.o.s. velocities for very blue stars and partly due to a possibly too restrictive (on the red side) selection box in PL18.
Regardless of which photometric catalog is used, both our members and the members of PL18 span a wider range in color (also reaching the location of a [Fe/H] = −1 isocrone) than expected for red giant branch stars on the basis of the measured spectroscopic metallicities and of the rareness of metal-rich stars in ultra-faint galaxies.
On the other hand, we confirm the finding of PL18 that the g − r/r − i color-color diagram can select metal-poor stars, see Fig. A.1. In our case, it only works for stars brighter than mi = 20, probably because of the increasingly larger errors in the colors. The majority of our members are above the foreground-star sequence as in Pace & Li (2018) and close to the [Fe/H] = −2 curve. We therefore confirm that the location of metal-poor stars in the color-color diagram is more according to expectations than that in the color-magnitude diagram. The reason for this is unclear.
 |
Fig. A.1. Color-color diagram of all our (potential) members for metallicity estimation following PL18 (filled circles: highly likely members; open circles: candidates). The members of Pace & Li (2018; p > 0.5) are indicated by crosses. The member of Pace & Li (2018) that is not confirmed by spectroscopy is indicated with a plus. Foreground stars are selected by requiring that they do not pass our halo selection based on Gaia kinematics. Larger symbols are stars brighter than mi = 20. The Parsec isochrones we used here only have evolutionary stages brighter than the turnoff. |
Similarly to PL18, we find that the location of Ret III members in the color-color plot would suggest a higher metallicity than for the rest of the UF systems we analyzed (even though the spectroscopic metallicities here derived do not confirm the suggestion from the color-color plot).
All Tables
Number of stars targeted in the FLAMES/GIRAFFE observations, retained after successive cleaning criteria.
All Figures
 |
Fig. 1. Example of observed spectra (gray) with different S/N and the best synthetic models (black) found in the l.o.s. velocity determination analysis. Horologium II 8_184 is a hot star, likely a BHB star, and the continuum normalization is not optimized for these objects. |
| In the text | |
 |
Fig. 2. Run of Vscatter as a function of median S/N of the individual exposures for all observed stars with at least three individual measurements. An exponential function (solid line) has been fitted to parameterize the distribution. |
| In the text | |
 |
Fig. 3. Recovered metallicities as a function of S/N for three different synthetic spectra with the input stellar parameters listed in the bottom right corner ([Fe/H]/effective temperature/log g). The S/N for each model has been slightly shifted to avoid superposition of the symbols. |
| In the text | |
 |
Fig. 4. Plots for the identification of the Horo II members for targets with FLAMES spectroscopic observations. Stars consistent with a distant halo origin in Gaia parallax, proper motions, and color magnitude space are plotted in blue, and the non-halo stars are plotted in gray. Stars without Gaia proper motion information, but with a location on the CMD consistent with being an RGB or a BHB star at the distance of the object are plotted in red. The very likely members of the satellite are enclosed within a cyan square and the additional potential members within an orange square. Top left panel: spatial distribution of the targets. The semimajor axes of the ellipses are equal to 1.5 and 3 projected (elliptical) half-light radii and use ellipticity and PA from Kim et al. (2015). Top right panel: location in the proper motion plane; the proper motion selection box of halo stars given by the escape speed criterion is shown in gray. Bottom left panel: extinction-corrected CMD; the Parsec isochrones with [Fe/H] = −2.0 and −1.0 dex and age = 12 Gyr are overlaid. The isocrones have solar-scaled [α/Fe]; this might be a potential source for the discrepancy in the location of stars of a given spectroscopically determined metallicity with the isochrones of similar [Fe/H] because stars in such ancient systems are typically α-enhanced (e.g., Mashonkina et al. 2017, and references therein). Bottom right panel: distribution on the l.o.s. vhelio vs. distance from the satellite center in units of projected elliptical half-light radius. The velocity distribution of disk stars in the mock catalog (z < |1| kpc) is shown in gray; the horizontal lines indicate the central 1σ interval. |
| In the text | |
 |
Fig. 5. Same as Fig. 4, but for Ret III. The structural parameters are from Drlica-Wagner et al. (2015). |
| In the text | |
 |
Fig. 6. Same as Fig. 4, but for Col I. The structural parameters are from Drlica-Wagner et al. (2015). |
| In the text | |
 |
Fig. 7. Same as Fig. 4, but for Phx II. The structural parameters are from Mutlu-Pakdil et al. (2018). |
| In the text | |
 |
Fig. 8. Posterior probability distribution function of the dispersion in l.o.s. velocity (left panel) and metallicity (right panel) for the four satellites. The blue line shows the results when all potential members are considers and the orange line represents the most probable members. |
| In the text | |
 |
Fig. 9. Average metallicity and metallicity dispersion (the “error” bars) as a function of absolute magnitude for the four target satellites. Objects that have no dispersion measurement or only limits are plotted without an error bar, as for Horo II. The metallicities for the “other objects” are from Torrealba et al. (2016), Martin et al. (2007), Simon & Geha (2007), Simon et al. (2015, 2011, 2017), Koch et al. (2009), Carlin et al. (2009), Li et al. (2018a, 2017, 2018b), Kirby et al. (2015, 2013, 2017), Walker et al. (2016, 2009), Koposov et al. (2015b, 2018), Kim et al. (2016), Willman et al. (2011), Norris et al. (2010) and Longeard et al. (2018). The point at MV = −5.3/[Fe/H] = −1.68 is Laevens 1/Crater I, which is probably a globular cluster. |
| In the text | |
 |
Fig. 10. All-sky view of orbital poles for the objects in the sample; the open circles (or square) indicate the value that follows from the measurements, and the small points around each object plot the orbital poles from the individual Monte Carlo simulations. We show our preferred membership selection for all satellites; for Horo II, we also show the other option in light green, which covers nearly the full great circle. The two options lead to very similar results for the other satellites. |
| In the text | |
 |
Fig. A.1. Color-color diagram of all our (potential) members for metallicity estimation following PL18 (filled circles: highly likely members; open circles: candidates). The members of Pace & Li (2018; p > 0.5) are indicated by crosses. The member of Pace & Li (2018) that is not confirmed by spectroscopy is indicated with a plus. Foreground stars are selected by requiring that they do not pass our halo selection based on Gaia kinematics. Larger symbols are stars brighter than mi = 20. The Parsec isochrones we used here only have evolutionary stages brighter than the turnoff. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} n_{\mathrm{cont, i} }=f_{\mathrm{hel} }\,\rho _{\mathrm{cont} }\, \pi \,R_{\mathrm{star} }^2\,/10\sqrt{[{ v}_{\rm hel,\,star ,\,i}-{ v}_{\rm hel,\,sat }]^2+3^2}. \end{aligned} $$](/articles/aa/full_html/2019/03/aa33458-18/aa33458-18-eq3.gif)