| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832587 | |
| Published online | 12 March 2019 | |
Magnetic field at a jet base: extreme Faraday rotation in 3C 273 revealed by ALMA★
1
Tuorla Observatory, University of Turku,
Väisäläntie 20,
21500 Piikkiö,
Finland
e-mail: talvikki.hovatta@utu.fi
2
Aalto University Metsähovi Radio Observatory,
Metsähovintie 114,
02540 Kylmälä,
Finland
3
Finnish Centre for Astronomy with ESO, University of Turku,
20014 University of Turku,
Finland
4
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112,
21029 Hamburg, Germany
5
Department of Earth and Space Sciences, Chalmers University of Technology, Onsala Space Observatory,
439 92,
Onsala,
Sweden
6
Aalto University Department of Electronics and Nanoengineering,
PL 15500,
00076 Aalto,
Finland
7
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121 Bonn,
Germany
8
Center for Interdisciplinary Exploration & Research in Astrophysics (CIERA), Physics & Astronomy, Northwestern University,
Evanston,
IL 60202, USA
9
Departments of Astronomy and Physics, Theoretical Astrophysics Center, University of California Berkeley,
Berkeley,
CA 94720-3411, USA
Received:
3
January
2018
Accepted:
27
March
2018
Aims. We studied the polarization behavior of the quasar 3C 273 over the 1 mm wavelength band at ALMA with a total bandwidth of 7.5 GHz across 223–243 GHz at 0.8′′ resolution, corresponding to 2.1 kpc at the distance of 3C 273. With these observations we were able to probe the optically thin polarized emission close to the jet base, and constrain the magnetic field structure.
Methods. We computed the Faraday rotation measure using simple linear fitting and Faraday rotation measure synthesis. In addition, we modeled the broadband behavior of the fractional Stokes Q and U parameters (qu-fitting). The systematic uncertainties in the polarization observations at ALMA were assessed through Monte Carlo simulations.
Results. We find the unresolved core of 3C 273 to be 1.8% linearly polarized. We detect a very high rotation measure (RM) of (5.0 ± 0.3) × 105 rad m−2 over the 1 mm band when assuming a single polarized component and an external RM screen. This results in a rotation of >40° of the intrinsic electric vector position angle, which is significantly higher than typically assumed for millimeter wavelengths. The polarization fraction increases as a function of wavelength, which according to our qu-fitting could be due to multiple polarized components of different Faraday depth within our beam or to internal Faraday rotation. With our limited wavelength coverage we cannot distinguish between the cases, and additional multifrequency and high angular resolution observations are needed to determine the location and structure of the magnetic field of the Faraday active region. Comparing our RM estimate with values obtained at lower frequencies, the RM increases as a function of observing frequency, following a power law with an index of 2.0 ± 0.2, consistent with a sheath surrounding a conically expanding jet. We also detect ~0.2% circular polarization, although further observations are needed to confirm this result.
Key words: polarization / quasars: individual: 3C 273 / galaxies: jets / radio continuum: galaxies
Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/623/A111
© ESO 2019
1. Introduction
Magnetic fields are thought to play a significant role in the formation of relativistic jets in active galactic nuclei (AGN). Magnetic fields can extract energy from the spinning supermassive black hole via the Blandford–Znajek mechanism (Blandford & Znajek 1977), launching a magnetically dominated outflow. In recent years, a major leap forward has been achieved through general relativistic magnetohydrodynamic (GRMHD) simulations of black hole accretion that show how this process can efficiently launch jets (e.g., McKinney & Gammie 2004; De Villiers et al. 2005; Hawley & Krolik 2006; McKinney & Blandford 2009; Tchekhovskoy et al. 2011).
Polarization observations, especially observations of Faraday rotation, can be used to probe the magnetic fields and magnetized plasma around relativistic jets, providing the means to connect observations to the theory of jet formation. When synchrotron emission passes through magnetized plasma, it undergoes Faraday rotation due to an induced phase offset between the velocities of the orthogonal plasma modes (Burn 1966). The amount of Faraday rotation, the rotation measure (RM), is proportional to the electron density ne of the plasma (in cm−3) and the magnetic field component B (in μG) along the line of sight (in parsecs), given by
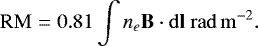 (1)
(1)
In the simplest case, Faraday rotation results in a linear dependence between the observed electric vector position angle (EVPA, χobs) and wavelength squared (λ2) so that χobs = χ0 + RMλ2, where χ0 is the intrinsic electric vector position angle of the emission region. This allows us to estimate the amount of Faraday rotation by observing the EVPA at multiple frequencies.
Centimeter-band Faraday rotation observations give us information about the magnetic field structure around the jets on parsec scales. The RM of the cores of AGN at centimeter wavelengths are typically up to a few thousand rad m−2 (e.g., Taylor 1998; Hovatta et al. 2012), indicating magnetic field strengths of a few μG if the Faradayrotating screen is the narrow line region of the source (Zavala & Taylor 2004). In order to study the plasma close to the black hole, millimeter-band observations are required to probe the jet base in the optically thin regime (e.g., Lobanov 1998). Plambeck et al. (2014) detected a high rotation measure of 9 × 105 rad m−2 in the radio galaxy 3C 84 using observations from SMA and CARMA. In the low-luminosity AGN M 87, a high rotation measure of RM < 2 × 105 rad m−2 was detected in the SMA observations by Kuo et al. (2014). These observations were interpreted by assuming that the Faraday rotation occurs in the radiatively inefficient accretion flow, and both studies estimated the mass accretion rate onto the black hole. Recently, Mościbrodzka et al. (2017) showed that in the case of M 87, the polarized emission and Faraday rotation is most likely dominated by the forward jet instead of the accretion flow, which limits the use of the RM to probe the accretion rate even in the low-luminosity sources.
The highest RM detected so far, 2 × 107 rad m−2 (~ 108 rad m−2 in the source frame), was seen in the high-power gravitationally lensed quasar PKS 1830−211 in dual-polarization ALMA observations by Martí-Vidal et al. (2015). Based on the frequency-dependence of the rotation measure, they argued that the Faraday rotation must originate in the jet from a region located 0.01 parsec from the black hole. Their result implies that the electron density and/or magnetic field is high, on the order of tens of Gauss at least, in the jet launching region.
In this paper we present the first full polarization ALMA observations of the nearest high-power quasar 3C 273 (z = 0.158; Strauss et al. 1992) over the 1 mm wavelength range. We selected 3C 273 for our pilot study because earlier observations of it in the 7–3mm range have shown indications of |RM| > 2 × 104 rad m−2 (Attridge et al. 2005; Hada et al. 2016, Savolainen, in prep.), making it a good candidate for high-RM studies in the 1 mm band.
Our paper is organized as follows. The observations and data reduction are described in Sect. 2. Section 3 contains our Faraday rotation and polarization modeling results. We present our discussion in Sect. 4, and list our conclusions in Sect. 5. We define the spectral index α such that the total intensity I at frequency ν follows the relation Iν ∝ να.
2. ALMA observations and data reduction
The Cycle 4ALMA observations at band 6 (1.3 mm) were taken on December 20, 2016, using 44 of the 12 m antennas. The observations lasted from 09:32 UTC until 12:05 UTC with a total integration time of about 73 min on 3C 2731. Our observations were taken in full polarization mode using the recommended continuum setup for band 6, where the four 1.875 GHz spectral windows (spw), each consisting of 64 channels that are 31.25 MHz wide, are placed at 224, 226, 240, and 242 GHz. The total bandwidth in our observations was then 7.5 GHz. The angular resolution (size of the synthesized beam) was 0.8′′. The quasar 3C 279 was observed as a bandpass and polarization calibrator and J1224+0330 as the gain calibrator.
The data reduction was done using Common Astronomical Software Applications (CASA) version 4.7.0. The amplitude scale of the observations was set using 3C279, assuming a flux density of 5.86 Jy at 233 GHz with a spectral index of − 0.63. Calibration of the cross-hand delay, cross-hand phase, and instrumental polarization (D-terms) was done using 3C279. For details of the standard data reduction and polarization calibration steps, see Nagai et al. (2016).
From these data with the standard calibration applied, we detect an inconsistency between spw 3 and the rest of the spectral windows, with a discontinuity in fractional polarization and EVPA that is very likely of instrumental origin. Since this window is the most affected by atmospheric opacity (see, e.g., the system temperature plots in Fig. A.1), the amplitudes and phases may be affected by differential atmospheric transmission between the phase calibrator and the target, we have performed an additional calibration step to minimize atmospheric and instrumental biases at the highest frequencies of our observations.
First, we self-calibrated the visibilities of our target using the CASA task gaincal in the so-called “T” mode, which ensures thatthe same corrections are found and applied to both polarization channels. Next, we ran a bandpass calibration using the target’s visibilities, also averaging the solutions to T mode, so that the same correction is applied to both polarizations. After this extra calibration, we found an increase in the signal-to-noise ratio (S/N) of the visibilities, as well as a more continuous behavior of fractional polarization and EVPA across all spectral windows.
In our analysis, we assume that the emission in 3C 273 is dominated by the central point source at the phase center of the image. In order to obtain Stokes parameters of each 31.25 MHz wide spectral channel, we use the external CASA library UVMULTIFIT (Martí-Vidal et al. 2014) to fit the visibility data. We fit a centered delta component to each channel individually to obtain the Stokes I, Q, U, and V values. These are listed in Table 1 along with the derived polarization fraction and EVPA.
Following Vlemmings et al. (2017), we perform Monte Carlo (MC) simulations to assess the uncertainties in the Stokes parameters. These simulations, accounting especially for the systematic calibration uncertainties, are described in detail in Appendix A. We find that the uncertainty in each channel is on average 8.4 mJy in Stokes I, 8.2 mJy in Stokes Q, and 8.2 mJy in Stokes U. This results in a high accuracy in the fractional polarization (~0.18%), while the EVPA uncertainty is on the order of 2.8circ. We report the standard deviation of the 100 MC simulations as the uncertainty for each parameter in Table 1.
3. Results
In this section we describe the methods used to analyze the polarization data over the ALMA 1 mm band. Thanks to the wide ALMA bandwidth of 7.5 GHz spread over a wide frequency range from 223 to 243 GHz, we were able to study the polarization over the single observing band. We first determined the RM using multiple methods and then modeled the Stokes I, Q, and U behavior as a function of wavelength squared using the broadband polarization modeling technique known as qu-fitting (e.g., Farnsworth et al. 2011; O’Sullivan et al. 2012, 2017; Farnes et al. 2014; Anderson et al. 2016; Schnitzeler 2018). In addition to the RM, this method can provide an estimate of the depolarization in the Faraday medium.
 |
Fig. 1 Top panel: EVPAs as a function of wavelength squared for 3C 273 over the ALMA 1 mm band. The uncertainties in the EVPA are obtained through MC simulations described in Appendix A. The dashed line is a linear fit to the data giving RM = (5.01 ± 0.04) × 105 rad m−2 and intrinsic EVPA of −108°. Bottom panel: residuals of the fit with MC uncertainties shown in gray. |
3.1. RM determination
The simplest way to estimate the RM is to directly fit the EVPAs as a function of wavelength squared. The underlying assumption is that the RM is caused by a single external Faraday screen, which results in a linear relation between the EVPAs and wavelength squared. This fit is shown in Fig. 1, and from the slope we obtain an RM = (+5.01 ± 0.04) × 105 rad m−2. The intrinsic EVPA given by the intercept is −108°, meaning that the Faraday rotation has a significant effect on the observed EVPAs, contrary to what is typically assumed at mm wavelengths.
While the advantage of this method is its simplicity, we need to manually adjust for any possible nπ ambiguities in the EVPAs. Looking at the residuals in Fig. 1, we can see that all the spectral windows do not fall exactly on this line. This may indicate that the EVPAs do not follow a simple λ2 law and highlights that the simple method does not give correct results if there are multiple polarized components that undergo different amounts of Faraday rotation. These problems can potentially be overcome by using Faraday rotation measure synthesis (Brentjens & de Bruyn 2005), where we coherently search for polarized emission as a function of Faraday depth.
The nominal RM resolution of our observation is ~ 1.3 × 107 rad m−2, estimated from the FWHM of the rotation measure spread function (RMSF)2. The maximum RM that can be measured from our data is ~ ± 4 × 109 rad m−2 and the maximum scale3 in RM is approximately 2 × 106 rad m−2 (meaning that RM structures broader than this will be heavily depolarized). By applying RM synthesis to the full dataset, we find an RM of (+4.8 ± 0.2) × 105 rad m−2 with a degree of polarization of (1.81 ± 0.01)% (~ 84 mJy beam−1 at 233 GHz). We also apply RM CLEAN (Heald et al. 2009) to deconvolve the RM spectrum, but find no additional peaks in the RM spectrum significantly above the band-averaged noise level of ~ 0.3 mJy beam−1 (Fig. 2).
3.2. Polarization modeling
As described in Sect. 1, in the simplest case, the Faraday rotation is due to an external screen that does not cause depolarization. If the Faraday rotating medium is mixed with the emitting region, or if there are variations in the RM screen over the finite resolution of the observations, depolarization towards longer wavelengths may be seen (Burn 1966). If the Faraday rotating medium is mixed with the emitting region (internal Faraday rotation), it is also possible to obtain inverse depolarization where the polarization increases as a function of wavelength (Sokoloff et al. 1998; Homan 2012). Inverse depolarization can also result from multiple emitting RM components (O’Sullivan et al. 2012).
In order to investigate the Faraday depolarization properties of the data in a quantitative manner, we used the qu-fitting technique. We first considered the simplest model, i.e., a model of a polarized component in the presence of Faraday rotation, as shown in (Eq. (2); Sokoloff et al. 1998; O’Sullivan et al. 2012),
 (2)
(2)
where q = Q∕I, u = U∕I, p0 is the intrinsic polarization fraction, χ0 is the intrinsic polarization angle, and λ is the wavelength. This results in RM = (4.95 ± 0.25) × 105 rad m−2 with a constant p0 = (1.81 ± 0.01)% and χ0 = (−107.1 ± 2.3)deg, consistent with the values obtained from the simple linear fit shown in Fig. 1. This fit is shown as a black solid line overlaid on the q, u, p, and χ values in Fig. 3.
However, the behavior of the polarization fraction we observe, where the polarization increases with wavelength, is not consistent with the constant polarization of the simple model. Nor can any single-component model with external Faraday screen explain the behavior (Sokoloff et al. 1998; O’Sullivan et al. 2012). Instead, a more complex model with either multiple emission components or internal Faraday rotation is needed to explain the polarization behavior.
In the case of multiple emission components, the model can simply be constructed as P = P1 + P2 + ⋯ + PN (O’Sullivan et al. 2012), where Pi is as defined in Eq. (2). This kind of a two-component model is shown in Fig. 3 as red dotted lines. The fit shown here gives the parameters p01 ~ 5.5%, p02 ~ 4.2%, RM1~ +1.26 × 105 rad m−2, RM2~−1.45 × 105 rad m−2, and χ01 ~ 88.6deg, χ02 ~ 16.7deg for the two components. Noteworthy is the smaller absolute RM value and different sign of the two components. However, it is possible that also other combinations of the parameters, or more than two components give equally good fits.
For the internal Faraday rotation model, we use the equation (Sokoloff et al. 1998; O’Sullivan et al. 2012)
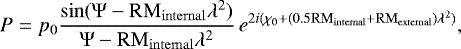 (3)
(3)
where p0 and χ0 are as in Eq. (2), Ψ is the twist of the uniform magnetic field through the jet, RMinternal is the amount of internal Faraday rotation, and RMexternal is the amount of external Faraday rotation. This model, shown in Fig. 3 as green dashed lines, gives us p0 ~ 17%, RMexternal ~ +3.6 × 105 rad m−2, RMinternal ~ +2.9 × 105 rad m−2, Ψ ~ 190deg, χ0 ~ 72deg. This is again one plausible set of parameters that fit the data, but it is not necessarily a unique solution. With these parameters, RMexternal + 0.5RMinternal ~ 5 × 105 rad m−2, which is consistent with the simple external screen-only value.
However, we emphasize that our current wavelength-squared coverage is not sufficient to uniquely distinguish between these two models, or between other possible solutions to the models. Moreover, the change in polarization across the band is not very large, and although our MC simulations indicate that it is significant, given the clear atmosphericsignal in spw 3 before the additional calibration steps, these trends should be confirmed with further data.
 |
Fig. 2 Amplitude of the Faraday dispersion function (FDF) after applying RM synthesis. The Faraday depth (ϕ) varies from − 2 × 108 to + 2 ×108 rad m−2 sampled at intervals of 104 rad m−2. The dirty FDFs are shown for q = Q∕I (green dotted line), u = U∕I (magenta dot-dashed line), and p (blue dashed line); the FDF after applying RM CLEAN is also shown (solid black line). The inset panel in the top right is a zoom-inof the main lobe of the FDF, while the bottom right is further zoomed-in to highlight the non-zero Faraday depth of the peak polarized emission (vertical dotted line in both cases). |
 |
Fig. 3 Example fits from the qu-fitting overlaid on the data as a function of wavelength squared. Top left panel: Stokes Q/I. Top right panel: Stokes U/I. Bottom left panel: fractional polarization. Bottom right panel: EVPA. In all panels Model 1 (no depolarization) is shown as a black solid line, Model 2 (2 RM components) is shown as a red dotted line, and Model 3 (internal Faraday rotation) is shown as a green dashed line. |
4. Discussion
In the previous section we show that we detected a Faraday rotation measure of RMobs ~ +5 × 105 rad m−2 in 3C 273 over the 1 mm band (224–242 GHz) of ALMA. Recently, Bower et al. (2017) reported 1 mm RM observations of the low-luminosity galaxies M 81 and M 84 obtained at SMA and CARMA. In their SMA observations, 3C 273 was used as a calibrator, and they report a value of RM consistent with zero in their observations. However, they only used a bandwidth of 4 GHz in the RM calculation, which is not wide enough to reveal an RM of + 5× 105 rad m−2 because of their larger uncertainties.
The value we obtain is about an order of magnitude higher than |RM| > 2 × 104 rad m−2, reported for 3C 273 in observations between 3 and 7 mm (Attridge et al. 2005; Hada et al. 2016, Savolainen, in prep.), suggesting adenser Faraday screen or a higher magnetic field strength over the 1 mm emission region. Savolainen et al. (2008) estimated the magnetic field strength as a function of distance from the jet apex in 3C 273 using multifrequency Very Long Baseline Interferometry (VLBI) observations. They found the magnetic field to be ~ 2 G in their 3 mm core, at a distance of ≤0.06 mas from the jetapex. Assuming that the jet is conical and that the magnetic field follows the relation B ∝ r−1 as expected for the toroidal component of the field (which could be expected to correspond to the line-of-sight component of the field), we would expect the magnetic field strength to be about 6 G in our observations. Using Eq. (1) we can then estimate the electron density in the Faraday rotating medium. If the path length through the medium is 1 pc, we obtain ne = 10 × 10−2cm−3, which is close to the central density of 6 × 10−2cm−3 found in the X-ray observations of Röser et al. (2000).
Alternatively, we can estimate the required magnetic field strength by assuming a value for the electron density. A higher electron density of 1000 cm−3, possibly typical of narrow line region clouds (Zavala & Taylor 2004), over a path length of 10 pc would result in a much lower magnetic field strength of 62 μG. In order to constrain this further, we need to compare our observation to simulations similar to those of Mościbrodzka et al. (2017), which we plan to do in a forthcoming publication.
We find that no simple model can explain the polarization behavior across the band. Instead, the inverse depolarization could be due to two (or more) RM components, or internal Faraday rotation. The former case can occur if there are multiple strongly polarized components within our beam. The synthesized beam size of our observations is 0.8′′, which at a distance of 3C 273 translates to 2.1 kpc, and includes the entire parsec-scale jet as observed by VLBI. Casadio et al. (2017) observed 3C 273 at 86 GHz with the Global Millimeter VLBI Array (GMVA) at 50 μas angular resolution in May 2016, about seven months before our observation. They saw only a single dominating polarized component down the jet. However, earlier 3 mm VLBI observations showed multiple polarized jet components in 3C 273 (Hada et al. 2016, Savolainen, in prep.), which means that due to possible variability in the source, we cannot exclude the possibility of multiple polarized components.
In the case of internal Faraday rotation, an increasing polarization as a function of wavelength can be obtained, for example, if there is a helical magnetic field within the jet (Homan 2012). This kind of inverse depolarization has also been observed in the pc-scale jet of 3C 273 (Hovatta et al. 2012). A helical field is also supported by observations of a parsec-scale transverse Faraday rotation measure gradient transverse to the jet direction in 3C 273 (e.g., Asada et al. 2002; Zavala & Taylor 2005; Hovatta et al. 2012). An ordered, helical magnetic field would be expected, for example, if the black hole is surrounded by dynamically important poloidal magnetic fields (Tchekhovskoy et al. 2011) that wind up in a tight helix due to the rotation of the black hole–accretion disk system (e.g., Meier et al. 2001).
We note that because of the limited wavelength coverage and angular resolution, our observations cannot distinguish between the two cases, and further observations with improved angular resolution such as observations with the Event Horizon Telescope (Doeleman et al. 2009) and the GMVA + ALMA (e.g., Boccardi et al. 2017) are needed to help determine the origin and properties of this Faraday rotation medium. Alternatively, observations at multiple bands will constrain the qu-fitting better, providing more strict constraints for the models.
4.1. RM as a function of frequency
The behavior of RM as a function of frequency can tell us about the underlying conditions in the jet as both the electron density and magnetic field strength change as a function of distance from the black hole, which under certain assumptions can be translated to observing frequency. As derived in Jorstad et al. (2007), in a conical jet under equipartition the RM is expected to follow a relation |RM|∝ νa, where the value of a depends on the power-law change in the electron density ne as a function of distance r from the black hole, ne ∝ r−a. For example, a = 2 would implythat the Faraday rotation is occurring in a sheath around a conically expanding jet, while lower values could be explained with a more highly collimated jet (e.g., O’Sullivan & Gabuzda 2009). The typical values for a obtained in the literature vary in the range 0.9–4 with average or median values around 2 (Jorstad et al. 2007; O’Sullivan & Gabuzda 2009; Kravchenko et al. 2017).
In order to look for the frequency dependency in 3C 273, we gathered from the literature previously reported values for the core RM at different frequency ranges. As the core in 3C 273 at lower frequencies is typically depolarized, we selected the value nearest to the core, so that these should formally be considered as lower limits. If multiple values are reported in the literature, we take their mean as the RM value and use the range as an uncertainty in the calculation of the slope. We used the range RM= 250–450 rad m−2 in the frequency range 4.7–8 GHz from Asada et al. (2002). This value is taken about 5 mas from the core and therefore is probably much lower than expected for the core. For the frequency range 8–15 GHz we use the range of near-core RM values of RM = 1000–3000 rad m−2 reported in Zavala & Taylor (2005) and Hovatta et al. (2012). For the 43–86 GHz range we use the range of lower limits 2.1– 2.4 × 104 rad m−2 from Attridge et al. (2005) and Hada et al. (2016).
The linear fit to these data is shown in Fig. 4. We obtain a = 2.0 ± 0.2, consistent with the mean value of a = 1.8 ± 0.2 by Jorstad et al. (2007), and as expected for a sheath surrounding a conically expanding flow. However, this slope should be considered as an upper limit because the RM values at the lower frequencies are most certainly lower limits. Our result is also consistent with the analysis presented in Plambeck et al. (2014), who found the extrapolation from lower frequencies with a slope of a = 2 to agree with with their high RM of 9 × 105 rad m−2 detected at 1.3 mm in 3C 84.
At 1 mm wavelength, the emission in 3C 273 is already optically thin (e.g., Courvoisier 1998; Planck Collaboration XV 2011) so that we may be viewing the polarized emission very close to the black hole. For example, in the models by Marscher (1980) and Potter & Cotter (2012), the emission at optically thin millimeter-band frequencies originates from the region where the jet transitions from a parabolic, magnetically dominated jet to a conical jet in equipartition (referred to as the transition region later in the text). This is supported by simulations of Porth et al. (2011), who show that at higher, optically thin frequencies the polarized flux from the unresolved core (jet base in case of optically thin emission) begins to dominate the RM signal, which can reach values up to 106 rad m−2, similar to what we detect.
However, it is also possible that the polarized emission is dominated by a single polarized jet component farther down the jet as seen in a 86 GHz VLBI image of 3C 273 taken in May 2016 (Casadio et al. 2017). In their image, the core is depolarized, possibly due to opacity, because at 86 GHz, 3C 273 is in the transition phase to becoming optically thin. The image of Casadio et al. (2017) was taken 3 months after a peak of a large total flux density flare4, and the polarized component may be related to this flaring activity. The peak polarized flux density detected by Casadio et al. (2017) is about 200 mJy beam−1. Assuming a spectral index of − 0.9 (as seen over our 1 mm band), we would expect to see about 80 mJy of polarized flux in our 1 mm observations, which is very close to the mean polarized flux density of 83 mJy we observe. Thus, it is possible that we are seeing a polarized component farther down the jet. However, our observationswere taken 7 months after the VLBI observations during a dip in the total flux density curve, and just before a new flare startedto rise; it is thus also possible that we are seeing emission related to the new flaring activity closer to the transition region or multiple emission components, as suggested by our qu-fitting results.
If at 1 mm wavelength we are seeing the optically thin emission in the jet transition region, observations at even higher frequencies should result in similar RM values to those we have now obtained, assuming that the Faraday screen is stable. Simultaneous observations at multiple frequencies will help to answer this question.
Our observed RMobs of 5.0 × 105 rad m−2 corresponds to RM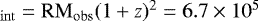 rad m−2 in the frame of the source, at an emitted frequency of νem = νobs(1 + z) = 270 GHz when using the central observed frequency νobs = 234 GHz. This is still much lower than the intrinsic RM of 108 rad m−2 seen in the quasar PKS 1830−211 by Martí-Vidal et al. (2015). This could partially be explained with the higher redshift (z = 2.5) of PKS 1830−211, which makes the emitted frequency over which the RM was detected correspond to 875−1050 GHz, and which could possibly originate from closer to the black hole where the electron density and magnetic field is expected to be higher. If we estimate the expected RM at these high frequencies using the slope 2.0 from above, we obtain an intrinsic RM of ~ 7 × 106 rad m−2, suggesting that the reason for the lower RM in 3C 273 is due to intrinsic differences in the electron density and/or magnetic field strength in these two sources. Studying a larger number of sources will allow us to establish whether this type of difference is common between various AGN.
rad m−2 in the frame of the source, at an emitted frequency of νem = νobs(1 + z) = 270 GHz when using the central observed frequency νobs = 234 GHz. This is still much lower than the intrinsic RM of 108 rad m−2 seen in the quasar PKS 1830−211 by Martí-Vidal et al. (2015). This could partially be explained with the higher redshift (z = 2.5) of PKS 1830−211, which makes the emitted frequency over which the RM was detected correspond to 875−1050 GHz, and which could possibly originate from closer to the black hole where the electron density and magnetic field is expected to be higher. If we estimate the expected RM at these high frequencies using the slope 2.0 from above, we obtain an intrinsic RM of ~ 7 × 106 rad m−2, suggesting that the reason for the lower RM in 3C 273 is due to intrinsic differences in the electron density and/or magnetic field strength in these two sources. Studying a larger number of sources will allow us to establish whether this type of difference is common between various AGN.
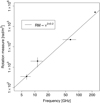 |
Fig. 4 Rotation measure as a function of frequency for 3C 273. The RM values at lower than ALMA 224– 242 GHz frequency from this study are taken from the near-core region in VLBA observations from the literature (see text for references). Apart from the ALMA observation, the uncertainty in RM is a range of reported values, not an uncertainty in a single measurement. Similarly, the frequency range of the observations over the which the RM was estimated is shown by a solid line. |
4.2. Circular polarization
Although circular polarization observations are not yet officially offered by the ALMA Observatory, our Monte Carlo uncertainty assessment, described in Appendix A, allows us to investigate the Stokes V signal in our data. Assuming that we have accounted for all the possible errors in the data, we find that the instrumental contribution to the total Stokes V is about 2– 3 mJy, while there seems to be an intrinsic signal of about 10 mJy across the band (see Appendix A for details). This would indicate a fractional circular polarization of ~0.2%. This result should be treated with caution, and we would need additional ALMA observations (with properly supported circular polarimetry) to verify the detection. However, the value we obtain is consistent with the 1.3 mm circular polarization observations by the POLAMI group (Thum et al. 2018) who typically do not detect significant circular polarization from 3C 273, which is then expected as their uncertainties are typically higher than 0.2%.
Assuming a magnetic field strength of ~6 G in the region dominating the mm emission and a Doppler factor of ~ 5 (Savolainen et al. 2008), an intrinsic circular polarization as high as 1.8% can be obtained for a completely uniform jet magnetic field. Alternatively, if Faraday rotation-driven conversion is dominating the production of circular polarization, then the observed Stokes V level of ~ 0.2% could be obtained from 5% linear polarization with a low-energy relativistic electron energy spectrum cutoff of ~ 4.5 (e.g., Homan et al. 2009; O’Sullivan et al. 2013). This would only provide an internal Faraday depth on the order of tens of rad m−2, and thus indicates that the majority of the Faraday rotating material we detect is likely in a boundary layer or wind external to the jet.
5. Conclusions
We have studied the quasar 3C 273 at 1 mm wavelength with ALMA in full polarization mode at 0.8 mas resolution, corresponding to 2.1 kpc atthe distance of 3C 273. We detect about 1.8% linear polarization in the unresolved core of the source, and model the polarization as a function of wavelength over the 1 mm band. Our main conclusions can be summarized as follows:
- 1.
We detect a very high Faraday rotation measure (RM) of (5.0 ± 0.3) × 105 rad m−2 over the band, which implies a magnetic field of several Gauss or a high electron density of ~1000 cm−3 in the Faraday rotating medium probed by the polarized emission. This amount of Faraday rotation rotates the EVPAs in the 1 mm wavelength by over 40circ, showing that it cannot be ignored when studying the intrinsic EVPA and magnetic field direction.
- 2.
By modeling the Stokes parameters as a function of wavelength, we find that no model with a single polarized component and an external screen can explain the inverse depolarization we observe. Instead, a model with at least two polarized components or with internal Faraday rotation is needed. Additional multifrequency and high angular resolution observations are required to distinguish between the models.
- 3.
Comparing the RM at 1 mm to values obtained at lower frequencies, we find that the RM increases as a function of observing frequency, following a power law with an index of <2.0 ± 0.2, consistent with a sheath surrounding a conically expanding jet.
- 4.
Through careful Monte Carlo assessment of the systematic uncertainties in the polarization observations, we are able to detect about 0.2% of circular polarization. Additional dedicated circular polarization observations are needed to confirm the result.
Acknowledgements
We thank Prof. Seiji Kameno for providing us with the independently calibrated polarization measurements for cross-checking our results. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2016.1.01073.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. This publication has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 730562 [RadioNet]. T.H. was supported by the Turku Collegium of Science and Medicine and the Academy of Finland project 317383. T.S. was funded by the Academy of Finland projects 274477, 284495, and 312496. A.T. was supported by the TAC fellowship.
Appendix A: Assessment of the polarization calibration
Based on the standard calibration and the quality assurance products provided by the ALMA Arc node, we detect an inconsistency between spw 3 and the rest of the frequency windows, with a discontinuity in fractional polarization and EVPA that is very likely of instrumental origin. This window is the most affected by atmospheric opacity, as shown in Fig. A.1, which is why we perform additional calibration steps, as described in Sect. 2.
 |
Fig. A.1 System temperature Tsys as a function of spectral window channel for all the spectral windows. |
The accuracy of the ALMA polarimetry, which may be affected by an imperfect polarization calibration, has been assessed via a Monte Carlo analysis, following a procedure similar to that explained in Vlemmings et al. (2017; see their Appendix A). These simulations are specially designed to account for the systematic uncertainties arising from the polarization calibration.
In our Monte Carlo analysis, each gain contribution to the full calibration (i.e., bandpass, amplitude and phase gains, polarization leakage, amplitude ratio between polarizers, and phase spectrum between the polarizers at the reference antenna) was perturbed with random noise. For each realization of the noise, the complete set of Stokes parameters of the target was derived by fitting a point source located at the phase center. This translated into a distribution of Stokes parameters, which reflect the posterior probability density of the target parameters, as given from the assumed noise distribution of the antenna gains. The parameters of the gain-noise distributions are summarized in Table A.1. In addition to the noise added to the calibration tables, an extra contribution of thermal noise was added to each Stokes parameter at each iteration to reflect the effects of the finite ALMA sensitivity.
The noise parameters given in Table A.1 are based on an educated guess, from our experience with ALMA polarimetry calibration (with the exception of the baseline sensitivity, which is taken from the thermal noise at ALMA, as estimated from the residuals of the Stokes V image, which is free of dynamic range limitations). The gains of each spectral window were perturbed with independent gain noises, with the exception of the X-Y phase (which is fitted by CASA using the same polarization model for all spws).
A.1. Monte Carlo results I: linear polarization
We show in Fig. A.2 the distributions of the differences (averaged over all frequency channels) between the polarization properties derived from the Monte Carlo iterations and the polarization properties derived from the original ALMA calibration tables. The accuracy in the estimate of the fractional linear polarization (which we estimate from the dispersion of m differences) is very high, on the order of 0.02%. The gain-noise contribution to the polarization angle, χ, is on the order of 0.5°.
 |
Fig. A.2 Distributions of the difference between polarization properties and the RM from the Monte Carlo iterations and those derived from the calibration. |
Parameters of the Gaussian noise distributions used to perturb the ALMA data in our Monte Carlo polarimetry assessment.
We have also computed the rotation measure (RM) from each Monte Carlo iteration. The distribution of RM deviations with respect to the value estimated from the original calibration is also shown in Fig. A.2. The standard deviation is ~ 3 × 104 rad m−2, consistent with the uncertainty estimate from the Faraday rotation synthesis and simple qu-fitting procedures.
A.2. Monte Carlo results II: circular polarization
The uncertainty in Stokes V, as estimated from Fig. A.2 (standard deviation of 0.9 mJy), is a large fraction of the total Stokes V derived from the original calibration (continuum average of ~10 mJy). This indicates that part of the detected V may be due to gain noise (in particular to inaccuracies in the estimate of the cross-polarization phases at the reference antenna). However, we note that any spurious Stokes V caused by this kind of calibration errors would depend on the source parallactic angle since the spurious V would be related to leakage from the linear polarization in the frame solidary to the antenna mounts. In particular, a calibration-related spurious circular polarization, Vsp, would be given by
![\begin{equation*} V^{\mathrm{sp}} = V^{\mathrm{true}}\,\textrm{cos}{\Delta} + I\,m\,\sin{\left(2[\chi - \psi]\right)}\,\sin{\Delta},\end{equation*}](/articles/aa/full_html/2019/03/aa32587-18/aa32587-18-eq5.png) (A.1)
(A.1)
where Δ is an uncalibrated instrumental phase offset between the X and Y polarizers of the reference antenna, χ is the EVPA of the source, ψ is the feed angle (i.e., parallactic angle plus rotation of the band 6 feed in the antenna frame5), Vtrue is the Stokes V intrinsic to the source, I is the total source intensity, and m is the fractional linear polarization.
In Fig. A.3, we show the Stokes V recovered from the original ALMA calibration (averaged over all the spectral channels) as a function of parallactic angle. A sinusoidal dependence of V is seen as a function of parallactic angle, which cannot be related to emission intrinsic to the source.
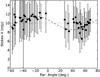 |
Fig. A.3 Frequency-averaged Stokes V, recovered from the original ALMA calibration, as a function of parallactic angle. The sinusoidal curve corresponds to Eq. (A.1). |
This dependence can be explained as being due to calibration artifacts (Eq. (A.1)), i.e., introduced by leakage from the linear polarization due to an error in the cross-polarization phase, Δ.
Given that the average EVPA is χ approximately − 60°, we would indeed expect the sinusoid to have a null close to a parallactic angle 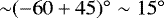 (i.e., when the EVPA is parallel tothe Y -axis of the polarizers, hence resulting in a null U Stokes in the antenna frame). This seems to be the case, according to Fig. A.3.
(i.e., when the EVPA is parallel tothe Y -axis of the polarizers, hence resulting in a null U Stokes in the antenna frame). This seems to be the case, according to Fig. A.3.
Using Eq. (A.1), we estimate that the observed dependence of V with parallactic angle can be produced by a cross-polarization phase offset of Δ ~ 1.5°, given a fractional linear polarization of ~1.8%. The uncertainty level in Stokes V derived from our Monte Carlo simulations (Fig. A.2) is indeed on the order of the amplitude in the sinusoid seen in the calibrated data (Fig. A.3), which indicates that our Monte Carlo estimates of polarimetric uncertainties are realistic.
We notice, though, that there is another contribution to Stokes V (at a level of about 10 mJy) that is independent of the parallactic angle and may be related to intrinsic Stokes V from the source (i.e., Vtrue in Eq. (A.1)). This conclusion should, however, be taken with care. Circular polarization is still not officially supported by the ALMA observatory, and even though we do account for all the residual gain factors in our Monte Carlo analysis (see Table A.1), we would need further ALMA observations (with a properly supported circular polarimetry) for the re-assessment of these results.
In short, the conclusion from the assessment of the circular polarization is that there is evidence of spurious contribution from gain noise (via the dependence of V with parallactic angle), but also evidence of intrinsic Stokes V from the source. In any case, the low level of Stokes V, together with other contributions from the gain noise, make the flux-density estimate of such an intrinsic V component difficult.
References
- Anderson, C. S., Gaensler, B. M., & Feain, I. J. 2016, ApJ, 825, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Asada, K., Inoue, M., Uchida, Y., et al. 2002, PASJ, 54, L39 [NASA ADS] [Google Scholar]
- Attridge, J. M., Wardle, J. F. C., & Homan, D. C. 2005, ApJ, 633, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Boccardi, B., Krichbaum, T. P., Ros, E., & Zensus, J. A. 2017, A&ARv, 25, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, G. C., Dexter, J., Markoff, S., Rao, R., & Plambeck, R. L. 2017, ApJ, 843, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Casadio, C., Krichbaum, T., Marscher, A., et al. 2017, Galaxies, 5, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Courvoisier, T. J.-L. 1998, A&ARv, 9, 1 [NASA ADS] [CrossRef] [Google Scholar]
- De Villiers, J.-P., Hawley, J. F., Krolik, J. H., & Hirose, S. 2005, ApJ, 620, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S., Agol, E., Backer, D., et al. 2009, astro2010: The Astronomy and Astrophysics Decadal Survey [Google Scholar]
- Farnes, J. S., Gaensler, B. M., & Carretti, E. 2014, ApJS, 212, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Farnsworth, D., Rudnick, L., & Brown, S. 2011, AJ, 141, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hada, K., Kino, M., Doi, A., et al. 2016, ApJ, 817, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F.,& Krolik, J. H. 2006, ApJ, 641, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Heald, G., Braun, R., & Edmonds, R. 2009, A&A, 503, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Homan, D. C. 2012, ApJ, 747, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Lister, M. L., Aller, H. D., Aller, M. F., & Wardle, J. F. C. 2009, ApJ, 696, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Hovatta, T., Lister, M. L., Aller, M. F., et al. 2012, AJ, 144, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Stevens, J. A., et al. 2007, AJ, 134, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Kravchenko, E. V., Kovalev, Y. Y., & Sokolovsky, K. V. 2017, MNRAS, 467, 83 [NASA ADS] [Google Scholar]
- Kuo, C. Y., Asada, K., Rao, R., et al. 2014, ApJ, 783, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&AS, 132, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marscher, A. P. 1980, ApJ, 235, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Martí-Vidal, I., Vlemmings, W. H. T., Muller, S., & Casey, S. 2014, A&A, 563, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martí-Vidal, I., Muller, S., Vlemmings, W., Horellou, C., & Aalto, S. 2015, Science, 348, 311 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., & Blandford, R. D. 2009, MNRAS, 394, L126 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., & Gammie, C. F. 2004, ApJ, 611, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, D. L., Koide, S., & Uchida, Y. 2001, Science, 291, 84 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mościbrodzka, M., Dexter, J., Davelaar, J., & Falcke, H. 2017, MNRAS, 468, 2214 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, H., Nakanishi, K., Paladino, R., et al. 2016, ApJ, 824, 132 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., & Gabuzda, D. C. 2009, MNRAS, 393, 429 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Brown, S., Robishaw, T., et al. 2012, MNRAS, 421, 3300 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., McClure-Griffiths, N. M., Feain, I. J., Gaensler, B. M., & Sault, R. J. 2013, MNRAS, 435, 311 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, S. P., Purcell, C. R., Anderson, C. S., et al. 2017, MNRAS, 469, 4034 [NASA ADS] [CrossRef] [Google Scholar]
- Plambeck, R. L., Bower, G. C., Rao, R., et al. 2014, ApJ, 797, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XV. 2011, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porth, O., Fendt, C., Meliani, Z., & Vaidya, B. 2011, ApJ, 737, 42 [Google Scholar]
- Potter, W. J., & Cotter, G. 2012, MNRAS, 423, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Röser, H.-J., Meisenheimer, K., Neumann, M., Conway, R. G., & Perley, R. A. 2000, A&A, 360, 99 [NASA ADS] [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., & Tornikoski, M. 2008, in Extragalactic Jets: Theory and Observation from Radio to Gamma Ray, eds. T. A. Rector & D. S. De Young, ASP Conf. Ser., 386, 451 [NASA ADS] [Google Scholar]
- Schnitzeler, D. H. F. M. 2018, MNRAS, 474, 300 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Huchra, J. P., Davis, M., et al. 1992, ApJS, 83, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, G. B. 1998, ApJ, 506, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy,A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Thum, C., Agudo, I., Molina, S. N., et al. 2018, MNRAS, 473, 2506 [NASA ADS] [CrossRef] [Google Scholar]
- Vlemmings, W. H. T., Khouri, T., Marti-Vidal, I., et al. 2017, A&A, 603, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zavala, R. T.,& Taylor, G. B. 2004, ApJ, 612, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Zavala, R. T.,& Taylor, G. B. 2005, ApJ, 626, L73 [NASA ADS] [CrossRef] [Google Scholar]
See the ALMA Calibrator Source Catalogue at https://almascience.eso.org/sc/ for the total flux density evolution of the source.
All Tables
Parameters of the Gaussian noise distributions used to perturb the ALMA data in our Monte Carlo polarimetry assessment.
All Figures
 |
Fig. 1 Top panel: EVPAs as a function of wavelength squared for 3C 273 over the ALMA 1 mm band. The uncertainties in the EVPA are obtained through MC simulations described in Appendix A. The dashed line is a linear fit to the data giving RM = (5.01 ± 0.04) × 105 rad m−2 and intrinsic EVPA of −108°. Bottom panel: residuals of the fit with MC uncertainties shown in gray. |
| In the text | |
 |
Fig. 2 Amplitude of the Faraday dispersion function (FDF) after applying RM synthesis. The Faraday depth (ϕ) varies from − 2 × 108 to + 2 ×108 rad m−2 sampled at intervals of 104 rad m−2. The dirty FDFs are shown for q = Q∕I (green dotted line), u = U∕I (magenta dot-dashed line), and p (blue dashed line); the FDF after applying RM CLEAN is also shown (solid black line). The inset panel in the top right is a zoom-inof the main lobe of the FDF, while the bottom right is further zoomed-in to highlight the non-zero Faraday depth of the peak polarized emission (vertical dotted line in both cases). |
| In the text | |
 |
Fig. 3 Example fits from the qu-fitting overlaid on the data as a function of wavelength squared. Top left panel: Stokes Q/I. Top right panel: Stokes U/I. Bottom left panel: fractional polarization. Bottom right panel: EVPA. In all panels Model 1 (no depolarization) is shown as a black solid line, Model 2 (2 RM components) is shown as a red dotted line, and Model 3 (internal Faraday rotation) is shown as a green dashed line. |
| In the text | |
 |
Fig. 4 Rotation measure as a function of frequency for 3C 273. The RM values at lower than ALMA 224– 242 GHz frequency from this study are taken from the near-core region in VLBA observations from the literature (see text for references). Apart from the ALMA observation, the uncertainty in RM is a range of reported values, not an uncertainty in a single measurement. Similarly, the frequency range of the observations over the which the RM was estimated is shown by a solid line. |
| In the text | |
 |
Fig. A.1 System temperature Tsys as a function of spectral window channel for all the spectral windows. |
| In the text | |
 |
Fig. A.2 Distributions of the difference between polarization properties and the RM from the Monte Carlo iterations and those derived from the calibration. |
| In the text | |
 |
Fig. A.3 Frequency-averaged Stokes V, recovered from the original ALMA calibration, as a function of parallactic angle. The sinusoidal curve corresponds to Eq. (A.1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


