| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833402 | |
| Published online | 25 January 2019 | |
The ALHAMBRA survey: tight dependence of the optical mass-to-light ratio on galaxy colour up to z = 1.5⋆
1
Centro de Estudios de Física del Cosmos de Aragón, Unidad Asociada al IAA-CSIC, Plaza San Juan 1, 44001 Teruel, Spain
e-mail: clsj@cefca.es
2
Instituto de Física de Cantabria (CSIC-UC), 39005 Santander, Spain
3
Unidad Asociada Observatorio Astronómico (IFCA-UV), 46980 Paterna, Spain
4
Universidade de São Paulo, Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Rua do Matão 1226, 05508-090 São Paulo, Brazil
5
Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la astronomía s/n, 18008 Granada, Spain
6
Observatori Astronòmic, Universitat de València, C/Catedrático José Beltrán 2, 46980 Paterna, Spain
7
Departament d’Astronomia i Astrofísica, Universitat de València, 46100 Burjassot, Spain
8
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
9
Institut of Space Sciences (ICE, CSIC), Campus UAB, Carrer Can Magrans, s/n, 08193 Barcelona, Spain
10
Institut d’Estudis Espacials de Catalunya (IEEC), 08193 Barcelona, Spain
11
Centro de Astrobiología (CSIC/INTA), 28850 Torrejón de Ardoz, Madrid, Spain
12
Instituto de Astrofísica de Canarias, Vía Láctea s/n, La Laguna, 38200 Tenerife, Spain
13
Ethiopian Space Science and Technology Institute (ESSTI), Entoto Observatory and Research Center (EORC), Astronomy and Astrophysics Research Division, PO Box 33679, Addis Ababa, Ethiopia
Received:
9
May
2018
Accepted:
20
September
2018
Aims. Our goal is to characterise the dependence of the optical mass-to-light ratio on galaxy colour up to z = 1.5, expanding the redshift range explored in previous work.
Methods. From the redshifts, stellar masses, and rest-frame luminosities of the ALHAMBRA multi-filter survey, we derive the mass-to-light ratio versus colour relation for quiescent and for star-forming galaxies. The intrinsic relation and its physical dispersion are derived with a Bayesian inference model.
Results. The rest-frame i-band mass-to-light ratio of quiescent and star-forming galaxies presents a tight correlation with the rest-frame (g − i) colour up to z = 1.5. The mass-to-light ratio versus colour relation is linear for quiescent galaxies and quadratic for star-forming galaxies. The intrinsic dispersion in these relations is 0.02 dex for quiescent galaxies and 0.06 dex for star-forming ones. The derived relations do not present a significant redshift evolution and are compatible with previous local results in the literature. Finally, these tight relations also hold for g- and r-band luminosities.
Conclusions. The derived mass-to-light ratio versus colour relations in ALHAMBRA can be used to predict the mass-to-light ratio from a rest-frame optical colour up to z = 1.5. These tight correlations do not change with redshift, suggesting that galaxies have evolved along the derived relations during the last 9 Gyr.
Key words: galaxies: fundamental parameters / galaxies: statistics / galaxies: stellar content
© ESO 2019
1. Introduction
Stellar mass is a fundamental parameter in galaxy evolution studies, presenting correlations with several galaxy properties such as star formation rate (e.g. Noeske et al. 2007; Chang et al. 2015), gas-phase metallicity (e.g. Tremonti et al. 2004; Mannucci et al. 2009; Lara-López et al. 2010), stellar content (e.g. Gallazzi et al. 2005; Gallazzi et al. 2014; Díaz-García et al. 2018), galaxy size (e.g. Shen et al. 2003; Trujillo et al. 2007; van der Wel et al. 2014), morphology (e.g. Moffett et al. 2016; Huertas-Company et al. 2016), and nuclear activity (e.g. Kauffmann et al. 2003; Bongiorno et al. 2016).
The measurement of stellar mass in modern photometric and spectroscopic surveys is mainly performed by comparing either an empirical or a theoretical library of templates with the observed spectral energy distributions (SEDs) of galaxies. The mass-to-light ratio associated with the templates, combined with the flux normalisation, provides the stellar mass of a given source (see Courteau et al. 2014 for a recent review on galaxy mass estimation). Thus, understanding and characterising the mass-to-light ratio of different galaxy populations is important in order to derive reliable stellar masses and to minimise systematic differences between data sets and template libraries.
Mass-to-light ratio versus colour relations (MLCRs) have been studied theoretically and observationally (Tinsley 1981; Jablonka & Arimoto 1992; Bell & de Jong 2001; Bell et al. 2003; Portinari et al. 2004; Gallazzi & Bell 2009; Zibetti et al. 2009; Taylor et al. 2011; Into & Portinari 2013; McGaugh & Schombert 2014; Zaritsky et al. 2014; van de Sande et al. 2015; Roediger & Courteau 2015; Herrmann et al. 2016) in the optical, the ultraviolet (UV), and the near-infrared (NIR). These studies focus on the low-redshift Universe (z ≲ 0.5) and find well-defined linear MLCRs with low scatter (< 0.2 dex).
We highlight the work of Taylor et al. (2011, hereafter T11). It is based on SED-fitting to the ugriz broad bands of the Sloan Digital Sky Survey (SDSS DR7, Abazajian et al. 2009) available for the Galaxy And Mass Assembly (GAMA; Driver et al. 2011) survey area. They find a remarkably tight relation (0.1 dex dispersion) between the mass-to-light ratio in the i band, denoted M⋆/Li, and the rest-frame colour (g − i) at z < 0.65, with a median redshift of ⟨z⟩ = 0.2 for the analysed global population. These authors argue that this small dispersion is driven by (i) the degeneracies of the galaxy templates in such a plane, which are roughly parallel to the MLCR, implying from the theoretical point of view ∼0.2 dex errors in the mass-to-light ratio even with large errors on the derived stellar population parameters; and (ii) the galaxy formation and evolution processes, which are encoded in the observed galaxy colours and only allow a limited set of solutions, making the observed relation even tighter than the theoretical expectations.
In the present work, we expand the results from T11 with the multi-filter Advanced, Large, Homogeneous Area, Medium-Band Redshift Astronomical1 (ALHAMBRA) survey (Moles et al. 2008). ALHAMBRA provides stellar masses and rest-frame luminosities thanks to the application of the MUlti-Filter FITing (MUFFIT, Díaz-García et al. 2015) code to 20 optical medium-band and 3 NIR photometric points. In addition, ALHAMBRA covers a wide redshift range, reaching z = 1.5 with a median redshift of ⟨z⟩ =0.65, and permits the MLCR of quiescent and star-forming galaxies to be studied separately.
We also refine the statistical estimation of the MLCRs. Instead of performing an error-weighted fit to the data, we applied a Bayesian inference model that accounts for observational uncertainties and includes intrinsic dispersions in the relations (see also Taylor et al. 2015; Montero-Dorta et al. 2016).
The paper is organised as follows. In Sect. 2 we present the ALHAMBRA photometric redshifts, stellar masses, and luminosities. The derived i-band MLCRs for quiescent and star-forming galaxies and their modelling are described in Sect. 3. Our results are presented and discussed in Sect. 4. The summary and conclusions are in Sect. 5. Throughout this paper we use a standard cosmology with Ωm = 0.3, ΩΛ = 0.7, Ωk = 0, H0 = 100h km s−1 Mpc−1, and h = 0.7. Magnitudes are given in the AB system (Oke & Gunn 1983). The stellar masses, M⋆, are expressed in solar masses (M⊙) and the luminosities, L, in units equivalent to an AB magnitude of 0. The derived mass-to-light ratios can be transformed into solar luminosities L⊙ by subtracting 2.05, 1.90, and 1.81 from the presented MLCRs for the g, r, and i bands, respectively. With the definitions above, stellar masses can be estimated from the reported mass-to-light ratios as
where M is the absolute AB magnitude of the galaxy.
2. ALHAMBRA survey
The ALHAMBRA survey provides a photometric data set over 20 contiguous, equal-width (∼300 Å), non-overlapping, medium-band optical filters (3500 Å–9700 Å) plus 3 standard broad-band NIR filters (J, H, and Ks) over eight different regions of the northern sky (Moles et al. 2008). The final survey parameters and scientific goals, as well as the technical properties of the filter set, were described by Moles et al. (2008). The survey collected its data for the 20 plus 3 optical-NIR filters with the 3.5 m telescope at the Calar Alto observatory, using the wide-field camera Large Area Imager for Calar Alto (LAICA) in the optical and the OMEGA–2000 camera in the NIR. The full characterisation, description, and performance of the ALHAMBRA optical photometric system was presented in Aparicio-Villegas et al. (2010). A summary of the optical reduction can be found in Molino et al. (2014), while that of the NIR reduction is in Cristóbal-Hornillos et al. (2009).
2.1. Bayesian photometric redshifts in ALHAMBRA
The Bayesian photometric redshifts (zb) of ALHAMBRA were estimated with BPZ2, a new version of the Bayesian photometric redshift (BPZ, Benítez 2000) code. The BPZ2 code is a SED-fitting method based in Bayesian inference, where a maximum likelihood is weighted by a prior probability. The main novelties of BPZ2 with respect to its previous version are an updated prior and a new template library that comprises 11 SEDs, with four ellipticals, one lenticular, two spirals, and four starbursts. Further details about BPZ2 can be found in Molino et al. (2014). The ALHAMBRA photometry used to compute the photometric redshifts is PSF-matched, aperture-corrected, and based on isophotal magnitudes (Molino et al. 2014). In addition, a recalibration of the zero point of the images was performed to enhance the accuracy of the photometric redshifts. Sources were detected in a synthetic F814W filter image defined to resemble the HST/F814W filter. The total area covered by the current release of the ALHAMBRA survey after masking low signal-to-noise areas and bright stars is 2.38 deg2 (Arnalte-Mur et al. 2014). The full description of the photometric redshift estimation is detailed in Molino et al. (2014).
The photometric redshift accuracy, as estimated by comparison with spectroscopic redshifts (zs), is σNMAD = 0.012 at F814W ≤ 23, where σNMAD is the normalised median absolute deviation of the photometric versus spectroscopic redshift distribution (e.g. Ilbert et al. 2006; Molino et al. 2014). The fraction of catastrophic outliers with |zb − zs|/(1 + zs) > 0.2 is 2.1%. We refer the reader to Molino et al. (2014) for a more detailed discussion.
2.2. MUFFIT: stellar masses and rest-frame colours
The BPZ2 template library discussed above is empirical, and the different templates do not have mass-to-light ratios assigned a priori. Hence, an alternative methodology is needed to compute the stellar mass of the ALHAMBRA sources.
The MUFFIT code is specifically performed and optimised to deal with multi-photometric data, such as the ALHAMBRA data set, through the SED-fitting (based in a χ2-test weighted by errors) to mixtures of two simple stellar populations (SSPs; a dominant “old” component plus a posterior star formation episode, which can be related with a burst or a younger/extended tail in the star formation history). MUFFIT includes an iterative process for removing those bands that may be affected by strong emission lines so as to carry out a detailed analysis of the galaxy SEDs even when strong nebular or active galactic nuclei (AGN) emission lines are present, which may be especially troublesome for intermediate- and narrow-band surveys. The two SSPs involved in the modelling share the same initial mass function (IMF) and extinction, but have independent ages and metallicities. The final number of free parameters in the fitting is eight (two ages, two metallicities, one extinction, the total stellar mass, the mass fraction in the older component, and the redshift), with a fixed IMF. ALHAMBRA sources with F814W ≤ 23 are analysed with MUFFIT by Díaz-García et al. (2017, hereafter DG17), retrieving ages, metallicities, stellar masses, rest-frame luminosities, and extinctions. MUFFIT also provides photometric redshifts, using the BPZ2 solutions presented in the previous section as a prior to minimise degeneracies. This improves the photometric redshift accuracy by ∼20% and decreases the fraction of outliers by ∼10% (DG17). The retrieved parameters are in good agreement with both spectroscopic diagnostics from SDSS data and photometric studies in the COSMOS survey, where the galaxy samples overlap (Díaz-García et al. 2015, DG17).
To study the MLCR of ALHAMBRA galaxies and its redshift evolution, we used the redshifts, stellar masses, and rest-frame luminosities in the gri broad bands derived by MUFFIT. These parameters were estimated assuming Bruzual & Charlot (2003, BC03) stellar population models, Fitzpatrick (1999) extinction law, and Chabrier (2003) IMF. We refer the reader to Díaz-García et al. (2015, 2018), and DG17 for further details about MUFFIT and the quantities derived.
2.3. Selection of quiescent and star-forming galaxies
Throughout this paper, we focus our analysis on the galaxies in the ALHAMBRA gold catalogue2. This catalogue comprises ∼100 k sources with F814W ≤ 23 (Molino et al. 2014).
We split our galaxies into quiescent and star-forming with the dust-corrected version of the UVJ colour–colour plane presented in DG17, adapted to the ALHAMBRA medium-band filter system: we used F365 instead of the filter U and F551 instead of the filter V; the ALHAMBRA filter J is the standard one. As shown by DG17, quiescent and star-forming galaxies with F814W ≤ 23 define two non-overlapping populations in the colour–colour plane after removing dust effects, with the selection boundary located at (F365 − F551) = 1.5. We refer the reader to DG17 for a detailed description of the selection process and the study of the stellar population properties of quiescent galaxies in the UVJ colour–colour plane. We show the observed (i.e. reddened by dust) rest-frame distribution of the 76642 ALHAMBRA gold catalogue galaxies with z < 1.5 in Fig. 1. The quiescent population is enclosed by the common colour–colour selection box (Williams et al. 2009), but a population of dusty star-forming galaxies is also located in this area. DG17 show that a significant fraction (∼20%) of these red galaxies are indeed dusty and star-forming, and are contaminating the quiescent population. Thanks to the low-resolution spectral information from ALHAMBRA, the MUFFIT code is able to provide a robust quiescent versus star-forming classification.
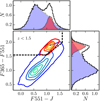 |
Fig. 1. Rest-frame colour–colour plane F365 − F551 versus F551 − J for the 76642 ALHAMBRA galaxies with F814W ≤ 23 at z < 1.5. This plane is equivalent to the commonly used UVJ diagram, and the quiescent selection box from the literature (Williams et al. 2009) is delimited by dashed lines. The coloured lines show level contours in the density of galaxies, starting at 0.1 galaxies dex−2 and increasing in 0.6 galaxies dex−2 steps. Red contours show the quiescent population, and blue contours show the star-forming population, as defined by DG17. The side panels show the normalised distribution in F365 − F551 (right panel) and F551 − J (top panel). In both panels the total distribution is presented in black, the quiescent population in filled red, and the star-forming population in filled blue. |
The final sample, having z < 1.5 and F814W ≤ 23, comprises 12905 quiescent and 63737 star-forming galaxies. The stellar masses covered by our data span the 8 < log10 M⋆/M⊙ < 11.5 range. Further details about the stellar mass completeness and the redshift distribution of the sample are presented in DG17. We study the MLCR of these samples in the next section.
3. Mass-to-light ratio versus colour relation at z < 1.5
3.1. Observed relation for quiescent and star-forming galaxies
In this section, we study the relation between the mass-to-light ratio in the i-band and the observed rest-frame (g − i) colour of the ALHAMBRA galaxies with z < 1.5. In some cases, we denote Υ = log10(M⋆/Li) and 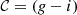 for the sake of clarity. The redshift, stellar masses, and observed rest-frame (i.e. reddened by dust) luminosities were derived by the MUFFIT code (Sect. 2.2).
for the sake of clarity. The redshift, stellar masses, and observed rest-frame (i.e. reddened by dust) luminosities were derived by the MUFFIT code (Sect. 2.2).
We present the M⋆/Li versus (g − i) colour plane for both quiescent and star-forming galaxies in the top panel of Fig. 2. We find that for both populations, the mass-to-light ratio increases for redder colours, in agreement with the literature (see references in Sect. 1). We describe the modelling of this dependence in Sect. 3.2. In the figure, we also present the MLCR found by T11 in the GAMA survey. Their relation is in excellent agreement with our observed values: the comparison between our measurements and their predictions, 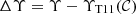 , has no bias, ⟨ΔΥ⟩ = 0.01 dex, and a small dispersion of σΔΥ = 0.1 dex (bottom panel in Fig. 2). We note that T11 use BC03 stellar population models and a Chabrier (2003) IMF, as we did, but different extinction laws (cf. Calzetti et al. 2000 and Fitzpatrick 1999) and star formation histories (SFHs; e-fold tau models versus two stellar populations mix) were assumed.
, has no bias, ⟨ΔΥ⟩ = 0.01 dex, and a small dispersion of σΔΥ = 0.1 dex (bottom panel in Fig. 2). We note that T11 use BC03 stellar population models and a Chabrier (2003) IMF, as we did, but different extinction laws (cf. Calzetti et al. 2000 and Fitzpatrick 1999) and star formation histories (SFHs; e-fold tau models versus two stellar populations mix) were assumed.
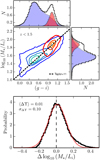 |
Fig. 2. Top panel: mass-to-light ratio M⋆/Li as a function of the rest-frame colour g − i for the 76642 ALHAMBRA galaxies with F814W ≤ 23 at z < 1.5. The coloured lines show level contours in the density of galaxies, starting at 0.1 galaxies dex−2 and increasing in 1.5 galaxies dex−2 steps. Red contours show the quiescent population, and blue contours the star-forming one. The side panels show the normalised distribution in g − i (upper panel) and log10 (M⋆/Li) (right panel). In both panels the total distribution is presented in black, the quiescent population in filled red, and the star-forming population in filled blue. The black dashed line marks the relation derived by Taylor et al. (2011) at z < 0.65 using GAMA galaxies and SDSS five-band photometry. Bottom panel: comparison between the observed ALHAMBRA mass-to-light ratio and that expected from the Taylor et al. (2011) relation. The red solid line is the best Gaussian fit with median ⟨ΔΥ⟩ = 0.01 dex and dispersion σΔΥ = 0.10 dex. |
The T11 study is performed using a sample of z < 0.65 galaxies with a median redshift of ⟨z⟩ = 0.2, and our data covers a wider redshift range (z ≤ 1.5) with a median redshift of ⟨z⟩ = 0.65. This suggests that the low-redshift relation measured by T11 in GAMA has not evolved significantly with redshift. We assume this redshift independence in the following and test it in Sect. 4.2.
3.2. Modelling the intrinsic mass-to-light versus colour relation
The measurements presented in the previous section are affected by observational errors, blurring the information and biasing our analysis. We are interested in the intrinsic distribution of our measurements in the mass-to-light ratio versus colour plane, and in this section we detail the steps to estimate it. The results are presented in Sect. 4.
The intrinsic distribution of interest is noted by D, and provides the real values of our measurements for a set of parameters θ,
where Υ0 and 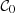 are the real values of the mass-to-light ratio and the colour unaffected by observational errors. We derive the posterior of the parameters θ that define the intrinsic distribution D for both quiescent and star-forming galaxies with a Bayesian model. Formally,
are the real values of the mass-to-light ratio and the colour unaffected by observational errors. We derive the posterior of the parameters θ that define the intrinsic distribution D for both quiescent and star-forming galaxies with a Bayesian model. Formally,
where σΥ and 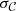 are the uncertainties in the observed mass-to-light ratio and (g − i) colour, respectively,
are the uncertainties in the observed mass-to-light ratio and (g − i) colour, respectively, 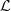 is the likelihood of the data given θ, and P(θ) the prior in the parameters. The posterior probability is normalised to one.
is the likelihood of the data given θ, and P(θ) the prior in the parameters. The posterior probability is normalised to one.
The likelihood function associated with our problem is
where the index k spans the galaxies in the sample, and Pk traces the probability of the measurement k for a set of parameters θ. This probability can be expressed as
where the real values Υ0 and 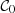 derived from the model D are affected by Gaussian observational errors,
derived from the model D are affected by Gaussian observational errors,
providing the likelihood of an observed value given its real value and uncertainty. We have no access to the real values Υ0 and 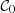 , so we marginalised over them in Eq. (5) and the likelihood is expressed therefore with known quantities; the marginalisation ranges were
, so we marginalised over them in Eq. (5) and the likelihood is expressed therefore with known quantities; the marginalisation ranges were ![$ {\cal{C}}_0 \in [-0.5,2.5] $](/articles/aa/full_html/2019/02/aa33402-18/aa33402-18-eq14.gif) and Υ0 ∈ [0.5, 3.0]. We assumed no covariance between Υ and
and Υ0 ∈ [0.5, 3.0]. We assumed no covariance between Υ and 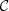 , although they share the i-band luminosity information. We checked by Monte Carlo sampling of the M⋆, Li, and Lg distributions that the covariance is small, with
, although they share the i-band luminosity information. We checked by Monte Carlo sampling of the M⋆, Li, and Lg distributions that the covariance is small, with 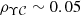 . Hence, we disregard the covariance term for simplicity.
. Hence, we disregard the covariance term for simplicity.
We explore the parameters posterior distribution with the emcee code (Foreman-Mackey et al. 2013), a Python implementation of the affine-invariant ensemble sampler for Markov chain Monte Carlo (MCMC) proposed by Goodman & Weare (2010). The emcee code provides a collection of solutions in the parameter space, denoted θMC, with the density of solutions being proportional to the posterior probability of the parameters. We obtained central values of the parameters as the median, denoted ⟨θMC⟩, and their uncertainties as the range enclosing 68% of the projected solutions around the median.
We define in the following the distributions assumed for the quiescent and star-forming populations, and the prior imposed to their parameters. The quiescent (Q) population is described as
where μQ and sQ describe the intrinsic Gaussian (g − i) colour distribution, AQ and BQ are the coefficients that define the MLCR, and σQ the intrinsic (i.e. related to physical processes) dispersion of the relation. We have a set of five parameters to describe the distribution of quiescent galaxies: θQ = {μQ, sQ, AQ, BQ, σQ}. We used flat priors, P(θQ)=1, except for the dispersions sQ and σQ, that we imposed as positive.
The star-forming (SF) population presents a more complex behaviour (Fig. 2), and we modelled it as
where μSF, sSF, and αSF describe the intrinsic (g − i) colour distribution; ASF, BSF, and CSF are the coefficients that define the MLCR for star-forming galaxies; and σSF the intrinsic dispersion of the relation. Important differences are present compared with the quiescent population. The distribution of 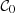 is not symmetric (Fig. 2), and we accounted for this asymmetry by adding the error function term and the parameter αSF, which controls the skewness of the distribution (Azzalini 2005). In addition, a second-order polynomial is preferred over a first-order one to describe the dependence of Υ0 on colour. This is motivated by the apparent curvature present at the redder colours in Fig. 2. To choose between the linear or the parabolic MLCR, we used the Bayesian information criterion (BIC, Schwarz 1978), defined as
is not symmetric (Fig. 2), and we accounted for this asymmetry by adding the error function term and the parameter αSF, which controls the skewness of the distribution (Azzalini 2005). In addition, a second-order polynomial is preferred over a first-order one to describe the dependence of Υ0 on colour. This is motivated by the apparent curvature present at the redder colours in Fig. 2. To choose between the linear or the parabolic MLCR, we used the Bayesian information criterion (BIC, Schwarz 1978), defined as
where N is the number of parameters in the model and n the number of galaxies in the sample. We find ΔBIC = BICpar − BIClin = −750, favouring the inclusion of CSF in the modelling. For consistency, we checked the application of a parabolic MLCR for quiescent galaxies. We found ΔBIC = BICpar − BIClin = 1.5, thus favouring the simpler linear model. Figure 2 also suggests an asymmetric distribution in Υ0, instead of the assumed Gaussian. We also studied the inclusion of an additional skew parameter for Υ0, but it was consistent with zero and in this case the BIC favours the simpler Gaussian model without the extra skew parameter. Thus, we have a set of seven parameters to describe the distribution of star-forming galaxies, θSF = {μSF, sSF, αSF, ASF, BSF, CSF, σSF}. We used flat priors, P(θSF)=1, except for the dispersions sSF and σSF, which we imposed as positive.
We note that the redshift dimension is not included in our analysis because we are assuming that the MLCRs do not depend on redshift. This was initially motivated by the excellent agreement with the local relation from T11 shown in Fig. 2, and we further test this assumption in Sect. 4.2.
4. Results
We present the derived i-band MLCRs for both quiescent and star-forming galaxies in Sect. 4.1, and explore the redshift dependence of the relations in Sect. 4.2. The g- and r-band MLCRs are presented in Sect. 4.3, and we compare our results with the literature in Sect. 4.4.
4.1. Mass-to-light ratio versus colour relation for quiescent and star-forming galaxies
In this section, we present the results of our modelling. They are summarised in Fig. 3 for quiescent galaxies and in Fig. 4 for the star-forming galaxies. The derived parameters are compiled in Table 1. In both cases we find that the assumed model satisfactorily describes the observed distributions in colour and mass-to-light ratio spaces.
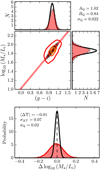 |
Fig. 3. Top panel: mass-to-light ratio M⋆/Li as a function of the rest-frame colour g − i for the 12905 ALHAMBRA quiescent galaxies with F814W ≤ 23 at z < 1.5. The solid lines show level contours in the density of galaxies as in Fig. 2. The grey scale shows the median fitting model to the data, |
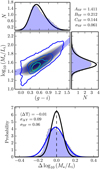 |
Fig. 4. Top panel: mass-to-light ratio M⋆/Li as a function of the rest-frame colour g − i for the 63737 ALHAMBRA star-forming galaxies with F814W ≤ 23 at z < 1.5. The solid lines show level contours in the density of galaxies as in Fig. 2. The grey scale shows the median fitting model to the data, |
ALHAMBRA mass-to-light ratio versus (g − i) colour relation.
We start by presenting the results for quiescent galaxies. We estimate
with a small intrinsic dispersion of σQ = 0.02 dex. The observed dispersion, which includes the observational errors, was estimated from a Gaussian fit to the distribution of the variable ΔΥ = Υ − ΥQ, yielding σΔΥ = 0.07 dex (bottom panel in Fig. 3). This value is lower than the 0.1 dex obtained with the local MLCR from T11.
For star-forming galaxies, we find
with an intrinsic dispersion of σSF = 0.06 dex. The observed dispersion in this case is σΔΥ = 0.09 dex (bottom panel in Fig. 4), similar to the 0.1 dex obtained with the T11 relation. The higher complexity of the star-forming population is not surprising, due to the combination of an underlying old population that dominates the stellar mass, a young population dominating the emission in the bluer bands, and the presence of different dust content. Even so, a well-defined MLCR with a small dispersion is inferred from our data.
We conclude that the encouraging 0.1 dex precision in the mass-to-light ratio estimation from the optical colour (g − i) found by T11 is even tighter after the observational uncertainties are accounted for. The dispersion derived with ALHAMBRA data at z < 1.5 is 0.02 dex for quiescent galaxies and 0.06 dex for star-forming galaxies. These small dispersions refer to the statistical analysis of the data, and systematic uncertainties related with the assumed stellar population models, IMF, SFHs, extinction law, etc., are not included in the analysis (see Portinari et al. 2004; Conroy et al. 2009; Barro et al. 2011, and Courteau et al. 2014, for a detailed discussion about systematics in stellar mass estimations). The similarity between the T11 values and ours suggests that the assumed extinction law and the SFHs are not an important source of systematics, with stellar population models and the IMF being the main contributors. The application of different stellar population models, such as those from Vazdekis et al. (2016), Maraston (2005), or Conroy & Gunn (2010), is beyond the scope of the present work.
4.2. Redshift evolution of the mass-to-light ratio versus colour relation
The results presented in the previous section imply a tight relation of the mass-to-light ratio with the optical colour (g − i). In our analysis, we assumed such a relation as redshift independent, motivated by the nice agreement with the z ∼ 0.2 results from T11 (Fig. 2).
We present the redshift evolution of ΔΥ in Fig. 5, both for quiescent and star-forming galaxies. We found no evidence of redshift evolution for either galaxy population, with the median |ΔΥ| at any redshift always below 0.02 dex. We performed a linear fit to constrain the possible residual evolution of Υ with redshift, finding ΔΥQ ∝ 0.04z for quiescent galaxies and ΔΥSF ∝ 0.01z for star-forming galaxies. We conclude therefore that the relations presented in Eqs. (10) and (11) have not changed appreciably during the last 9 Gyr of the Universe, with quiescent and star-forming galaxies evolving along the derived relations since z = 1.5.
 |
Fig. 5. Comparison between the observed ALHAMBRA mass-to-light ratio and the expected ratio from our median relation as a function of redshift for quiescent (top panel) and star-forming (bottom panel) galaxies with F814W ≤ 23 (grey dots). The solid contours show levels in the number of galaxies, starting at one galaxy and increasing in steps of five galaxies for quiescent galaxies, and in steps of 15 galaxies for star-forming galaxies. The dashed lines mark null difference. The solid lines show the linear fit to the mass-to-light ratio residuals, ΔΥQ ∝ 0.04z (top panel) and ΔΥSF ∝ 0.01z (bottom panel). |
4.3. Mass-to-light ratio versus colour relation in the r and g bands
We complement the results in the previous sections with the estimation of the intrinsic relation between the mass-to-light ratio in the r and g bands with (g − i) colour, both for quiescent and star-forming galaxies. We confirm the tight relations found with the i-band luminosity and the curvature for the star-forming population. We present the estimated relations in Table 1 for future reference.
We find that the normalisation of the MLCRs is similar in the gri bands at the 0.05 dex level. This occurs because our luminosities are expressed in AB units, so a null colour implies the same luminosity in all the bands which share a common stellar mass.
Regarding the slope for the quiescent population, it is larger for bluer bands. This implies that at the median colour of the quiescent population, ⟨(g − i)⟩ = 1, the mass-to-light ratio decreases from log10(M⋆/Lg)=2.26 to log10(M⋆/Li)=1.86, reflecting the larger contribution to the stellar mass budget of redder low-mass stars.
In the case of the star-forming galaxies, the parameter BSF is larger at bluer bands, but the parameter CSF is smaller. This implies a lower curvature of the MLCR in the g band. We checked that the quadratic model is still favoured by the data even in the g-band case, with Δ BIC = −190 (Table 1).
The intrinsic dispersion in the MLCRs is still low and similar to the i-band values, with σQ ∼ 0.02 dex and σSF ∼ 0.06 dex. Finally, the observed dispersion, affected by observational errors, are also similar to the fiducial i-band values, as summarised in Table 1.
We conclude that the MLCR holds in the optical range covered by the gri bands, confirming the tight correlation between optical mass-to-light ratios and the rest-frame colour (g − i).
4.4. Comparison with the literature
In addition to the T11 work, several studies in the literature have tackled the problem of the MLCR, both theoretically and observationally (see references in Sect. 1). We present the i-band mass-to-light ratio versus (g − i) colour from previous work in Fig. 6. We only present the colour range imposed by the ALHAMBRA data, 0 < (g − i) < 1.5 (Fig. 2). All the MLCRs have been scaled to a Chabrier (2003) IMF and referred to BC03 stellar population models to minimise systematic differences.
 |
Fig. 6. Comparison of the observed mass-to-light ratio versus (g − i) colour in ALHAMBRA with MLCRs from the literature. The contours are the same as in Fig. 2. The dashed green line is from the observational study of T11. The other black lines are from theoretical expectations: Zibetti et al. (2009, dotted) and Roediger & Courteau (2015, solid). All the MLCRs have been scaled to a Chabrier (2003) IMF and referred to BC03 models. |
We find a reasonably good agreement with the theoretical results from Roediger & Courteau (2015) and Zibetti et al. (2009). The comparison of these predictions with our values yields a bias of ⟨ΔΥ⟩ = − 0.01 and 0.08, and a dispersion of σΔΥ = 0.17 and 0.19, respectively. We highlight the predictions from Roediger & Courteau (2015), which have no bias and a dispersion only a factor of two larger than our optimal MLCRs.
From the observational point of view, we recall the agreement with the results from T11 (Fig. 2). Their relation provides no bias and a dispersion of σΔΥ = 0.1. We also compare our results with the popular work by Bell et al. (2003). Their relation yields a bias of ⟨ΔΥ⟩ = − 0.12 and again a dispersion of σΔΥ = 0.1. We note that the MLCR of Bell et al. (2003) was estimated with the PEGASE (Fioc & Rocca-Volmerange 1997) stellar populations models and a “diet Salpeter” IMF. Hence, we applied a −0.10 dex offset to the relations in Bell et al. (2003) to account for the difference in the stellar population models3, and a −0.15 dex offset to scale the IMF.
Following T11, we conclude that the range of colours covered by the observed galaxies, which are a consequence of their formation and evolution, restrict the parameter space of the models and provide tighter MLCRs than expected from theory. The bias with respect to previous work is at the ∼0.1 dex level, supporting the tight relations derived from ALHAMBRA data.
5. Summary and conclusions
We used the redshifts, stellar masses and rest-frame colours derived with MUFFIT for 76642 ALHAMBRA sources at z ≤ 1.5 to explore the i-band mass-to-light ratio relation with the rest-frame (g − i) colour. As shown by T11, there is a tight (0.1 dex) MLCR in the GAMA survey at z ∼ 0.2, and we expand their study up to z = 1.5.
We found that the i-band MLCR is also present in ALHAMBRA at z ≤ 1.5, for both quiescent and star-forming galaxies. The data suggests a linear MLCR for quiescent galaxies and a quadratic one for star-forming systems, as summarised in Table 1, and also holds for g and r luminosities.
The derived relations present an intrinsic dispersion, after accounting for observational uncertainties, of σQ = 0.02 dex and σSF = 0.06 dex. These dispersions are intrinsic and must be accounted for in addition to the colour error when deriving the mass-to-light ratio uncertainty. We also note that they refer to statistical dispersions, and the final error budget in mass-to-light ratio predictions should account for systematic uncertainties (σsys ∼ 0.3 dex; e.g. Barro et al. 2011) related to the assumed stellar population models, IMF, SFHs, extinction law, etc. Finally,
Our measurements suggest that the estimated MLCRs are redshift-independent, at least since z ∼ 1.5. That is, quiescent and star-forming galaxies have evolved along the MLCRs in the last 9 Gyrs of the Universe, preserving the observed relations with time.
We compare our data with other proposed MLCRs in the literature. The observational relation of T11, based on GAMA survey data, reproduces our values with no bias and dispersion σΔΥ = 0.1 dex. Regarding theoretical studies, the MLCR from Roediger & Courteau (2015) matches our measurements most closely; the bias is below 0.1 dex and the dispersion is σΔΥ = 0.17 dex.
Our results could be expanded in several ways. The analysis could be made by using different stellar population models to test the redshift independence of the relations and the curvature of the star-forming MLCR. The study of the MLCR at higher redshifts will provide extra clues about the absence of redshift evolution, for which a NIR-selected ALHAMBRA sample is needed (Nieves-Seoane et al. 2017). Finally, the study at masses lower than log10 M⋆ ∼ 8 will test the robustness of the results at the bluer end of the relation, where intense star-forming episodes could compromise the stellar masses estimated with our current techniques.
The derived relations can be used to estimate stellar masses with photometric redshift codes based on a limited set of empirical templates, such as BPZ2. The intrinsic MLCRs, unaffected by observational errors, are the needed priors to define the probability distribution function (PDF) of the stellar mass. The PDF-based estimator of the luminosity function was presented by López-Sanjuan et al. (2017) as part of the PROFUSE4 project, which uses PRObability Functions for Unbiased Statistical Estimations in multi-filter surveys, and has been successfully applied to estimate the B-band luminosity function at z < 1 (López-Sanjuan et al. 2017) and the UV luminosity function at 2.5 ≤ z < 4.5 (Viironen et al. 2018) in ALHAMBRA. The present paper is a fundamental step towards a PDF-based estimator of the stellar mass function.
To estimate this offset, we directly compared the stellar masses computed by Barro et al. (2011) with PEGASE and BC03 for a set of galaxies in the Extended Groth Strip (available at rainbowx.fis.ucm.es).
Acknowledgments
We dedicate this paper to the memory of our six IAC colleagues and friends who met with a fatal accident in Piedra de los Cochinos, Tenerife, in February 2007, with a special thanks to Maurizio Panniello, whose teachings of python were so important for this paper. We thank the anonymous referee for the comments and suggestions that improved the quality of the results and the readability of the manuscript. We thank R. Angulo, S. Bonoli, A. Ederoclite, C. Hernández-Monteagudo, A. Marín-Franch, A. Orsi, and all the CEFCA staff, post-docs, and students for the useful and productive discussions. This work has been mainly funded by the FITE (Fondos de Inversiones de Teruel) and the Spanish MINECO/FEDER projects AYA2015-66211-C2-1-P, AYA2012-30789, AYA2006-14056, and CSD2007-00060. We also acknowledge the financial support from the Aragón Government Research Groups E96, E103, and E16_17R. We acknowledge support from the Spanish Ministry for Economy and Competitiveness and FEDER funds through grants AYA2010-15081, AYA2010-22111-C03-01, AYA2010-22111-C03-02, AYA2012-39620, AYA2013-40609-P, AYA2013-42227-P, AYA2013-48623-C2-1, AYA2013-48623-C2-2, AYA2016-76682-C3-1-P, AYA2016-76682-C3-3-P, ESP2013-48274, Generalitat Valenciana project Prometeo PROMETEOII/2014/060, Junta de Andalucía grants TIC114, JA2828, P10-FQM-6444, and Generalitat de Catalunya project SGR-1398. K.V. acknowledges the Juan de la Cierva incorporación fellowship, IJCI-2014-21960, of the Spanish government. A.M. acknowledges the financial support of the Brazilian funding agency FAPESP (Post-doc fellowship - process number 2014/11806-9). B.A. has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 656354. M.P. acknowledges financial support from the Ethiopian Space Science and Technology Institute (ESSTI) under the Ethiopian Ministry of Science Science and Technology (MoST). This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013), and Matplotlib, a 2D graphics package used for Python for publication-quality image generation across user interfaces and operating systems (Hunter 2007).
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Aparicio-Villegas, T., Alfaro, E. J., Cabrera-Caño, J., et al. 2010, AJ, 139, 1242 [NASA ADS] [CrossRef] [Google Scholar]
- Arnalte-Mur, P., Martínez, V. J., Norberg, P., et al. 2014, MNRAS, 441, 1783 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Azzalini, A. 2005, Scand. J. Stat., 32, 159 [CrossRef] [Google Scholar]
- Barro, G., Pérez-González, P. G., Gallego, J., et al. 2011, ApJS, 193, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Bongiorno, A., Schulze, A., Merloni, A., et al. 2016, A&A, 588, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Y.-Y., van der Wel, A., da Cunha, E., & Rix, H.-W. 2015, ApJS, 219, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & Gunn, J. E. 2010, ApJ, 712, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Gunn, J. E., & White, M. 2009, ApJ, 699, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Cappellari, M., de Jong, R. S., et al. 2014, Rev. Mod. Phys., 86, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Cristóbal-Hornillos, D., Aguerri, J. A. L., Moles, M., et al. 2009, ApJ, 696, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2015, A&A, 582, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2017, A&A, submitted, [arXiv:1711.10590] [Google Scholar]
- Díaz-García, L. A., Cenarro, A. J., López-Sanjuan, C., et al. 2018, A&A, submitted, [arXiv:1802.06813] [Google Scholar]
- Driver, S. P., Hill, D. T., Kelvin, L. S., et al. 2011, MNRAS, 413, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gallazzi, A., & Bell, E. F. 2009, ApJS, 185, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Bell, E. F., Zibetti, S., Brinchmann, J., & Kelson, D. D. 2014, ApJ, 788, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Comm. App. Math. Comp. Sci., 5, 65 [Google Scholar]
- Herrmann, K. A., Hunter, D. A., Zhang, H.-X., & Elmegreen, B. G. 2016, AJ, 152, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Bernardi, M., Pérez-González, P. G., et al. 2016, MNRAS, 462, 4495 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Lauger, S., Tresse, L., et al. 2006, A&A, 453, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Into, T., & Portinari, L. 2013, MNRAS, 430, 2715 [NASA ADS] [CrossRef] [Google Scholar]
- Jablonka, J., & Arimoto, N. 1992, A&A, 255, 63 [NASA ADS] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2010, A&A, 521, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Tempel, E., Benítez, N., et al. 2017, A&A, 599, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Moffett, A. J., Ingarfield, S. A., Driver, S. P., et al. 2016, MNRAS, 457, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Moles, M., Benítez, N., Aguerri, J. A. L., et al. 2008, AJ, 136, 1325 [Google Scholar]
- Molino, A., Benítez, N., Moles, M., et al. 2014, MNRAS, 441, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Montero-Dorta, A. D., Bolton, A. S., Brownstein, J. R., et al. 2016, MNRAS, 461, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Nieves-Seoane, L., Fernandez-Soto, A., Arnalte-Mur, P., et al. 2017, MNRAS, 464, 4331 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Oke, J. B., & Gunn, J. E. 1983, ApJ, 266, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Portinari, L., Sommer-Larsen, J., & Tantalo, R. 2004, MNRAS, 347, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Roediger, J. C., & Courteau, S. 2015, MNRAS, 452, 3209 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Statist., 6, 461 [Google Scholar]
- Shen, S., Mo, H. J., White, S. D. M., et al. 2003, MNRAS, 343, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, E. N., Hopkins, A. M., Baldry, I. K., et al. 2011, MNRAS, 418, 1587 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, E. N., Hopkins, A. M., Baldry, I. K., et al. 2015, MNRAS, 446, 2144 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1981, MNRAS, 194, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Conselice, C. J., Bundy, K., et al. 2007, MNRAS, 382, 109 [NASA ADS] [CrossRef] [Google Scholar]
- van de Sande, J., Kriek, M., Franx, M., Bezanson, R., & van Dokkum, P. G. 2015, ApJ, 799, 125 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Koleva, M., Ricciardelli, E., Röck, B., & Falcón-Barroso, J. 2016, MNRAS, 463, 3409 [Google Scholar]
- Viironen, K., López-Sanjuan, C., Hernández-Monteagudo, C., et al. 2018, A&A, 614, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., van Dokkum, P., & Labbé, I. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., de Gil Paz, A., & Bouquin, A. Y. K. 2014, ApJ, 780, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, H.-W. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Rest-frame colour–colour plane F365 − F551 versus F551 − J for the 76642 ALHAMBRA galaxies with F814W ≤ 23 at z < 1.5. This plane is equivalent to the commonly used UVJ diagram, and the quiescent selection box from the literature (Williams et al. 2009) is delimited by dashed lines. The coloured lines show level contours in the density of galaxies, starting at 0.1 galaxies dex−2 and increasing in 0.6 galaxies dex−2 steps. Red contours show the quiescent population, and blue contours show the star-forming population, as defined by DG17. The side panels show the normalised distribution in F365 − F551 (right panel) and F551 − J (top panel). In both panels the total distribution is presented in black, the quiescent population in filled red, and the star-forming population in filled blue. |
| In the text | |
 |
Fig. 2. Top panel: mass-to-light ratio M⋆/Li as a function of the rest-frame colour g − i for the 76642 ALHAMBRA galaxies with F814W ≤ 23 at z < 1.5. The coloured lines show level contours in the density of galaxies, starting at 0.1 galaxies dex−2 and increasing in 1.5 galaxies dex−2 steps. Red contours show the quiescent population, and blue contours the star-forming one. The side panels show the normalised distribution in g − i (upper panel) and log10 (M⋆/Li) (right panel). In both panels the total distribution is presented in black, the quiescent population in filled red, and the star-forming population in filled blue. The black dashed line marks the relation derived by Taylor et al. (2011) at z < 0.65 using GAMA galaxies and SDSS five-band photometry. Bottom panel: comparison between the observed ALHAMBRA mass-to-light ratio and that expected from the Taylor et al. (2011) relation. The red solid line is the best Gaussian fit with median ⟨ΔΥ⟩ = 0.01 dex and dispersion σΔΥ = 0.10 dex. |
| In the text | |
 |
Fig. 3. Top panel: mass-to-light ratio M⋆/Li as a function of the rest-frame colour g − i for the 12905 ALHAMBRA quiescent galaxies with F814W ≤ 23 at z < 1.5. The solid lines show level contours in the density of galaxies as in Fig. 2. The grey scale shows the median fitting model to the data, |
| In the text | |
 |
Fig. 4. Top panel: mass-to-light ratio M⋆/Li as a function of the rest-frame colour g − i for the 63737 ALHAMBRA star-forming galaxies with F814W ≤ 23 at z < 1.5. The solid lines show level contours in the density of galaxies as in Fig. 2. The grey scale shows the median fitting model to the data, |
| In the text | |
 |
Fig. 5. Comparison between the observed ALHAMBRA mass-to-light ratio and the expected ratio from our median relation as a function of redshift for quiescent (top panel) and star-forming (bottom panel) galaxies with F814W ≤ 23 (grey dots). The solid contours show levels in the number of galaxies, starting at one galaxy and increasing in steps of five galaxies for quiescent galaxies, and in steps of 15 galaxies for star-forming galaxies. The dashed lines mark null difference. The solid lines show the linear fit to the mass-to-light ratio residuals, ΔΥQ ∝ 0.04z (top panel) and ΔΥSF ∝ 0.01z (bottom panel). |
| In the text | |
 |
Fig. 6. Comparison of the observed mass-to-light ratio versus (g − i) colour in ALHAMBRA with MLCRs from the literature. The contours are the same as in Fig. 2. The dashed green line is from the observational study of T11. The other black lines are from theoretical expectations: Zibetti et al. (2009, dotted) and Roediger & Courteau (2015, solid). All the MLCRs have been scaled to a Chabrier (2003) IMF and referred to BC03 models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



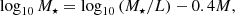
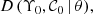
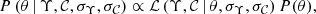
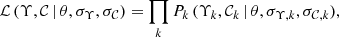
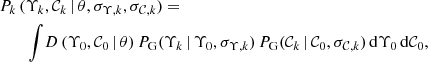
![$$ \begin{aligned} P_{\rm G}\,(x\,|\,x_0, \sigma _x) = \frac{1}{\sqrt{2 \pi } \sigma } \exp \bigg [-\frac{(x - x_0)^2}{2\sigma ^2}\bigg ], \end{aligned} $$](/articles/aa/full_html/2019/02/aa33402-18/aa33402-18-eq12.gif)
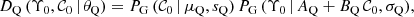
![$$ \begin{aligned} D_{\rm SF}\,(\Upsilon _0, \mathcal{{C}}_0\,|\,\theta _{\rm SF}) =&\,P_{\rm G}\,(\mathcal{{C}}_0\,|\,\mu _{\rm SF}, s_{\rm SF})\,\bigg [1 + \mathrm{erf}\,\bigg (\alpha _{\rm SF}\,\frac{C_0 - \mu _{\rm SF}}{\sqrt{2}s_{\rm SF}}\bigg )\bigg ]\nonumber \\&P_{\rm G}\,(\Upsilon _0\,|\,A_{\rm SF} + B_{\rm SF}\,\mathcal{{C}}_0 + C_{\rm SF}\,\mathcal{{C}}_0^2, \sigma _{\rm SF}), \end{aligned} $$](/articles/aa/full_html/2019/02/aa33402-18/aa33402-18-eq18.gif)
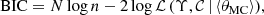
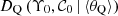
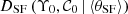
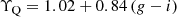
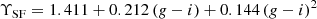
![$$ \begin{aligned} \sigma _{\Upsilon }^2 = [B + 2C\,({ g}-i)]^2\,\sigma _{({ g}-i)}^2 + \sigma _{\rm int}^2 + \sigma _{\rm sys}^2. \end{aligned} $$](/articles/aa/full_html/2019/02/aa33402-18/aa33402-18-eq25.gif)