| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 11 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834456 | |
| Published online | 08 January 2019 | |
Letter to the Editor
The angular momentum of disc galaxies at z = 1
1
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: marasco@astro.rug.nl
2
ASTRON, Netherlands Institute for Radio Astronomy, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
3
Research School of Astronomy and Astrophysics – The Australian National University, Canberra, ACT 2611, Australia
Received:
18
October
2018
Accepted:
20
December
2018
We investigate the relation between stellar mass (M⋆) and specific stellar angular momentum (j⋆), or “Fall relation”, for a sample of 17 isolated, regularly rotating disc galaxies at z ∼ 1. All galaxies have rotation curves determined from Hα emission-line data; HST imaging in optical and infrared filters; and robust determinations of their stellar masses. We use HST images in f814w and f160w filters, roughly corresponding to rest-frames B and I bands, to extract surface-brightness profiles for our systems. We robustly bracket j⋆ by assuming that rotation curves beyond the outermost Hα rotation point stay either flat or follow a Keplerian fall-off. By comparing our measurements with those determined for disc galaxies in the local universe, we find no evolution in the Fall relation in the redshift range 0 < z < 1, regardless of the band used and despite the uncertainties in the stellar rotation curves at large radii. This result holds unless stellar masses at z = 1 are systematically underestimated by ≳50%. Our findings are compatible with expectations based on a ΛCDM cosmological framework and support a scenario where both the stellar Tully–Fisher and mass-size relations for spirals do not evolve significantly in this redshift range.
Key words: galaxies: kinematics and dynamics / galaxies: evolution / galaxies: high-redshift / galaxies: photometry
© ESO 2019
1. Introduction
The stellar mass M⋆ and angular momentum J⋆ of a galaxy are two fundamental properties that are related qualitatively to the amount of material in the system, its rotational speed, and its size. Observationally, as first derived by Fall et al. (1983), M⋆ and specific angular momentum j⋆ = J⋆/M⋆ are related as 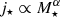 (α ∼ 2/3) with a normalisation that depends on the galaxy morphological type, increasing from early- to late-type systems (Romanowsky & Fall 2012; Fall & Romanowsky 2013).
(α ∼ 2/3) with a normalisation that depends on the galaxy morphological type, increasing from early- to late-type systems (Romanowsky & Fall 2012; Fall & Romanowsky 2013).
This “Fall” relation represents a key benchmark for models of galaxy evolution in a ΛCDM framework. While tidal torque theory (Peebles 1969; Efstathiou & Jones 1979) defines precise relations between the virial mass of halos and their specific angular momentum, which is also that of the baryonic matter, the mode by which the latter is redistributed within the stellar disc with time depends on the uncertain details of the galaxy evolution process (e.g. Mo et al. 1998; Dutton & van den Bosch 2012; Kravtsov 2013; Posti et al. 2018a). Early numerical studies suffered from dramatic angular momentum losses and strongly underpredicted the j⋆ of galaxies at all M⋆ (e.g. Katz & Gunn 1991; Navarro & Steinmetz 2000), but the situation has steadily improved in the years thanks to a better numerical resolution and to more effective stellar feedback implementations (Governato et al. 2010; Genel et al. 2015; Lagos et al. 2017). It still holds, though, that realistic models of galaxy evolutions - analytical or numerical – must aim at reproducing the Fall relation in the local universe as well as its evolution with cosmic time.
The j⋆ − M⋆ relation in the local universe was recently re-studied by Posti et al. (2018b) using a sample of 92 isolated, regularly rotating disc galaxies from the Spitzer Photometry and Accurate Rotation Curves (SPARC; Lelli et al. 2016) database, revealing a remarkably tight relation between the two quantities over four orders of magnitude in M⋆. The advent of modern IFU, like the KMOS and MUSE instruments on ESO/VLT, unveiled gas and stellar kinematics for galaxies at higher redshifts and opened the possibility to determine the evolution of the j⋆ − M⋆ relation with time. Harrison et al. (2017) studied a sample of 586 Hα-detected star-forming galaxies at 0.6 < z < 1 from the KMOS Redshift One Spectroscopic Survey (KROSS, Stott et al. 2016), finding a power-law j⋆ − M⋆ relation with the same slope as in the local universe, but with an offset of 0.2 − 0.3 dex towards lower j⋆ which they explained as due to the smaller disc sizes. Similar results were obtained by Swinbank et al. (2017) using KMOS and MUSE data for a sample of 405 galaxies at z ∼ 0.84, and by Burkert et al. (2016) for 360 galaxies at 0.8 < z < 2.6. In contrast, Contini et al. (2016) studied a smaller sample of 28 galaxies at 0.2 < z < 1.4 with MUSE, finding no evolution in the Fall relation in this redshift range for galaxies with large enough rotational support.
The reliability of j⋆ measurements depends on how accurately rotation curves and surface-brightness profiles can be determined. Di Teodoro et al. (2016, hereafter TFM16) selected 18 isolated, main-sequence disc galaxies at z ∼ 1 with intermediate inclination and high-quality Hα data from the KROSS and the KMOS3D (Wisnioski et al. 2015) surveys, and derived their Hα rotation curve and velocity dispersion profiles using the tilted-ring code 3DBAROLO (Di Teodoro & Fraternali 2015). This approach, based on the modelling of the entire emission-line data cube, virtually bypasses any beam-smearing problem associated to low spatial resolution of the data and thus allows us to break the degeneracy between rotation velocity and velocity dispersion. TFM16 concluded that the Hα kinematical properties of these z ∼ 1 systems are analogous to those measured at z = 0, with no evidence for additional dispersion support as previously claimed (e.g. Epinat et al. 2012; Kassin et al. 2012).
In this Letter, we determine the j⋆ − M⋆ relation for the galaxy sample of TFM16 by combining their accurate Hα kinematical measurements with surface-brightness profiles that we extract from HST images.
2. Method
In an axisymmetric disc, the specific stellar angular momentum enclosed within a given radius R is defined as
where Σ⋆(R′) and υ⋆(R′) are the surface density and the azimuthal velocity radial profiles of the stellar component.
In what follows, we focus on the task of computing j⋆ via Eq. (1) for the galaxy sample of TFM16 and do not attempt our own determination of M⋆. Instead, we use the stellar masses listed in Table 1 of TFM16, which come either from the Cosmic Assembly Near-infrared Deep Extragalactic Legacy Survey (CANDELS; Grogin et al. 2011; Koekemoer et al. 2011) as average values based on different techniques (Santini et al. 2015), or (for 5 galaxies) from the COSMOS (Scoville et al. 2007) and 3D-HST (Brammer et al. 2012) catalogues, which are derived by fitting stellar population synthesis templates to broad band photometry with the Fitting and Assessment of Synthetic Templates (FAST, Kriek et al. 2009) code.
The main properties of the galaxies studied in this work are reported in Table A.1. We note that we follow the same galaxy name and IDs as in Table 1 of TFM16. For consistency with TFM16, throughout this work we adopt a flat ΛCDM cosmology with Ωm, 0 = 0.27, ΩΛ, 0 = 0.73 and H0 = 70 km s−1 Mpc−1.
2.1. Surface-brightness profiles
We use optical/infrared surface-brightness profiles I(R) as a proxy for Σ⋆(R) in Eq. (1) under the assumption that light traces stellar mass. We determine I(R) using publicly available HST images from CANDELS or, for systems 3, 8, and 17, from COSMOS. No images were found for system 7 (zcos_z1_192), which we left out of our analysis. We focus on two different filters, f160w and f814w, which at the redshift of 1 roughly correspond to rest-frames I- and B-bands, respectively. According to Skelton et al. (2014), images in f160w (f814w) filter have an angular resolution of ∼0.19″ (∼0.10″), corresponding to about 1.5 kpc (0.8 kpc) in physical units, approximately three (six) times better than the KMOS IFU data. In spite of the fact that the B-band is not the best tracer for stellar mass, we show below that our results are nearly independent of the band used, which strengthens our conclusions.
The procedure used to extract I(R) from the images consists of several steps. We first compute the central value Ibkg and width σbkg of the background noise distribution. This is a crucial step, as an incorrect estimate for Ibkg affects the outer regions of the light profile, which may contain a significant fraction of j⋆. We focus on the pixel intensity distribution in a region of the image outside the main galaxy and fit a Gaussian function to a window encompassing the mode of such a distribution. The mean and the standard deviation of the best-fit Gaussian give Ibkg and σbkg respectively. Ibkg is then subtracted from the image before any further analysis.
We then define an “optical” centre by using an iterative approach on the f160w image: we compute an initial intensity-weighted centroid using all pixels within a circle centred at the galaxy coordinates given by TFM16 and with a radius of ∼5″, and progressively shrink the circle and re-centre it to the newly computed centroid until convergence is reached. The final centre coordinates are used for both bands and are reported in Table A.1. We notice that optical and kinematic centres are in good agreement with each other (see Fig. 2 in TFM16) and that our results are fairly robust against small (≲0.3″) off-centring, given that most j⋆ is locked in the galaxy outskirts.
To extract I(R), we consider a series of concentric annuli, centred on the optical centre, spaced out by one resolution element (∼3 pixels) and with constant axis-ratio and orientation given by the inclination and position angle determined by TFM16. As in Schombert (2007), a sigma-rejection algorithm is used to find and mask pixels contaminated by foreground stars or external galaxies. The surface brightness of each ring is computed as the mean intensity of the unmasked pixels, while the uncertainty associated to such a measurement, δI, is given by max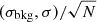 , σ being the rms intensity of the unmasked pixels and N the number of resolution elements in that ring. We proceed ring by ring until the signal-to-noise ratio I/δI drops below a value of 2.5. Finally, we fit the profile with an exponential function in order to derive the scale length Rd of the disc. In order to avoid contamination from bars/bulges, we exclude from the fit a region with R < Rsph. We obtain satisfying fits by choosing Rsph = 3.5 kpc for all galaxies but we stress that, contrary to other works (e.g. Swinbank et al. 2017; Harrison et al. 2017), in this analysis Rd does not enter directly into the computation of j⋆. We find 2 ≲ Rd ≲ 6 kpc, as reported in Table A.1.
, σ being the rms intensity of the unmasked pixels and N the number of resolution elements in that ring. We proceed ring by ring until the signal-to-noise ratio I/δI drops below a value of 2.5. Finally, we fit the profile with an exponential function in order to derive the scale length Rd of the disc. In order to avoid contamination from bars/bulges, we exclude from the fit a region with R < Rsph. We obtain satisfying fits by choosing Rsph = 3.5 kpc for all galaxies but we stress that, contrary to other works (e.g. Swinbank et al. 2017; Harrison et al. 2017), in this analysis Rd does not enter directly into the computation of j⋆. We find 2 ≲ Rd ≲ 6 kpc, as reported in Table A.1.
The first three panels in Fig. 1 demonstrate our procedure for system zmus_z1_119. We note that the optical profiles extend much further than the Hα emission, as shown by the outermost solid and dashed ellipses in the leftmost panels of Fig. 1. We also note the similarity between the normalised profiles in the two bands considered (third panel). The cumulative light profiles flatten out in both bands, which corroborates the validity of our procedure. This is the case for all the galaxies in our sample, as we show in Fig. A.1.
 |
Fig. 1. Photometry and kinematics of galaxy zmus_z1_119. First panel: HST image in f160w band (rest-frame I band). The concentric ellipses show the annuli where the surface brightness is computed. The green dashed ellipse shows the radius of the outermost Hα rotation velocity point. The blank region in the f814w image has been masked by our sigma-rejection algorithm (see text). Second panel: as in the first panel, but for the f814w band (rest-frame B band). Third panel: surface-brightness profiles in bands f160w (red circles) and f814w (blue triangles), normalised to the total light within the outermost ring. The thin dashed lines show exponential fits for R > 3.5 kpc, the solid thick lines show the cumulative light profile. Fourth panel: rotation curves. Points with error bars show υHα as determined by TFM16. The black and the red solid (dashed) lines show our fiducial profiles for υcirc and υ⋆ respectively, assuming a flat (Keplerian) extrapolation for the circular velocity. |
2.2. Stellar rotation curves
The computation of Eq. (1) requires measurements for the stellar rotation curves, υ⋆(R), that cover the full extent of the stellar discs. At z = 1, such measurements are very challenging (for a recent attempt, see Bezanson et al. 2018). Fortunately, from the study of TFM16 we have access to Hα rotation curves, υHα(R), although limited to the innermost (star-forming) regions. Therefore, we must convert υHα to υ⋆ via an asymmetric drift correction and then make assumptions for the shape of the rotation curve beyond the outermost measured velocity point.
The computation of υ⋆ is made in three steps: we first convert υHα to a circular velocity υcirc up to the outermost Hα radius, we subsequently extrapolate υcirc up to the outermost optical radius (see below), and finally we convert the whole υcirc profile to a υ⋆ profile. More quantitatively, we have
with υAD, Hα and υAD, ⋆ being the asymmetric drift corrections for the gas and the stellar components. Following Meurer et al. (1996), and assuming that galaxies have constant scale heights, these can be generically written as
where Σ(R) is the surface density profile of the component considered, and β is defined as σz/σR, σz and σR being the vertical and radial components of the velocity dispersion1.
To determine υAD, Hα we assume isotropy (β = 1) and a constant σz set to the values listed by TFM16 in their Table 1. For further simplification, we assume ΣHα to follow an exponential profile with scale-length equal to that of the stellar disc determined in the f814w band (see Sect. 2.1). For υAD, ⋆ we use the surface-brightness profiles determined in the f160w and f814w bands as a proxy for Σ, as well as an exponentially decreasing σz profile with e-folding length given by 2Rd and central dispersion given by σz(0) = (0.248 ± 0.038)×υ2.2Rd, with υ2.2Rd being the circular velocity measured at R = 2.2Rd (Martinsson et al. 2013). In order to avoid unrealistically small values for σz at large radii, we further impose a stellar-velocity dispersion floor2 of 15 km s−1. Finally, we assume 0.5 < β < 1.0 in order to account for the uncertainty in the velocity anisotropy in the error budget (see Sect. 2.3).
For the extrapolation of υcirc we consider two scenarios: either the rotation velocity remains constant at the value set by the last measured point, or it follows a Keplerian fall-off. The former represents a typical case for a late-type galaxy at z = 0, while the latter is extreme and sets a conservative lower limit on j⋆.
As an example, in the rightmost panel of Fig. 1 we show the “fiducial” υcirc and υ⋆ profiles derived for system zmus_z1_119. As we discuss in Sect. 2.3, several realisations contribute to produce these fiducial profiles, each may differ markedly from those shown here. Clearly, the type of extrapolation adopted dominates the uncertainty on the rotation curve (difference between solid and dashed lines), while the overall impact of the asymmetric drift corrections is small (difference between black and red lines). For this reason, the two types of extrapolation will be treated separately in our study.
2.3. Fiducial values and error budget
Given the many sources of uncertainty, we adopt a Monte-Carlo approach to estimate “fiducial” values and associated errors on j⋆. Our approach consists of producing 5 × 104 random realisations of the following quantities for any given galaxy: the Hα rotation curve υHα(R), the Hα velocity dispersion σHα, the stellar surface-brightness profile I(R), the central vertical dispersion for the stars σz(0), and the stellar dispersion anisotropy β. For the randomisation of υHα(R) and σHα we adopt Gaussian uncertainties based on the error bars determined by TFM16. For I(R) we use Gaussian uncertainties, δI, computed as discussed in Sect. 2.1. For σz(0) we use the formal (Gaussian) error determined by Martinsson et al. (2013) on their relation σz(0) = (0.248 ± 0.038)×υ2.2Rd, where both Rd and υ2.2Rd are now random quantities depending on the realisation of the brightness and velocity profiles. Finally, β is randomly extracted from a uniform distribution between 0.5 and 1.
For each galaxy we compute Eqs. (2) and (1) in all random realisations, and use the median and half the difference between the 84th and the 16th percentiles as our fiducial measurements and 1σ uncertainties associated to them, respectively. The computation is done four times in total: once for each band separately and, for a given band, once for each extrapolation of the rotation curve (flat or Keplerian).
3. Results
Figure 2 shows the cumulative j⋆ computed via Eq. (1) for all systems in our sample assuming a flat extrapolation for υcirc. All profiles shown are normalised by 2Rdυf, ⋆ (where υf, ⋆ is maximum υ⋆ in the extrapolated region of the curve), corresponding to the integrated j⋆ for an exponential disc with scale-length Rd and constant rotational speed υf, ⋆. The left (right) panel shows the results for the f160w (f814w) band. As expected, profiles in the f160w band show less scatter and a more uniform behaviour with respect to those in the f814w band, with a cleaner convergence towards unity. Following Posti et al. (2018b), we verified that all 17 systems satisfy in both bands the criteria for a “converging” j⋆ profile, Δj⋆/j⋆ < 0.1 and Δlogj⋆/ΔlogR < 0.5, where Δ is measured using the last two annuli of the profile. Trivially, convergence is ensured also for the Keplerian extrapolation. We note that none of the systems would pass the convergence test if we limited our study to their innermost regions traced by the Hα emission, represented by the coloured portion of the curves shown in Fig. 2.
 |
Fig. 2. Cumulative j⋆ profiles for our 17 galaxies in the f160w (left panel) and f814w (right panel) bands. Coloured solid lines show the innermost regions where rotation velocities from Hα data are available, while solid black lines show the extrapolation for a flat rotation curve. All profiles are either converging or have fully converged. |
The Fall relation for our z = 1 galaxies is presented in Fig. 3 (points with error bars) and compared to that determined in the local universe by Posti et al. (2018b3; grey-shaded region) for the SPARC sample (log(j⋆) = 0.55(log(M⋆/ M⊙)−11)+3.34, with a perpendicular scatter of 0.17 dex. Squared symbols (upwards triangles) represent the median j⋆ computed for a flat (Keplerian) extrapolation for the rotation curves. Upwards triangles have been further shifted downwards by 1σ in order to represent strict lower limits. Remarkably, all z = 1 measured points sit comfortably on the z = 0 relation of Posti et al. (2018b) with little dependence on the band adopted. We reiterate that corrections for asymmetric drift (Sect. 2.2) have a very small impact on our measurements, and stress that even our lower limits are typically enclosed within the scatter of the z = 0 relation.
 |
Fig. 3. Fall relation for our sample of disc galaxies at z ∼ 1. Left (right) panel: results derived using the f160w (f814w) HST band. The squared symbols show the j⋆ determined for a flat rotation curve extrapolation, while the upwards triangles represent lower limits derived from the assumption of a Keplerian fall-off. Numbers correspond to galaxy IDs from Table A.1. The black-dashed line and the grey-shaded region show the Fall relation and its intrinsic scatter, respectively, as determined by Posti et al. (2018b) for disc galaxies in the local universe from the SPARC data of Lelli et al. (2016). |
By assuming that the slope of the Fall relation does not vary in the redshift range considered, from our fiducial j⋆ measurements in f160w (f814w) band we infer a growth in the zero-point of the relation by 0.05 (0.03) dex from z = 0 to z = 1. This positive offset is mainly driven by systems 4, 17 and 18. We test whether this measurement is compatible with zero offset by randomly extracting 105 sets of 17 points in the (j⋆, M⋆) plane using the relation of Posti et al. (2018b) as a probability distribution, taking into account both the intrinsic scatter and the typical error-bars of our z = 1 data. We then compute the zero-point for each set, obtaining a distribution with a standard deviation of ∼0.05 dex, similar to the offset in the data. This indicates that our measurements are compatible with no evolution in the zero-point of the Fall relation for disc galaxies in the redshift range considered.
4. Discussion
Our findings indicate that disc galaxies move along a well defined j⋆ − M⋆ sequence while evolving from z = 1 to z = 0. As stellar mass grows, j⋆ increases by an amount defined by the Fall relation.
We stress that, while stellar masses for our z = 1 sample come from broadband SED fitting, the SPARC sample (on which the z = 0 Fall relation is based) adopts a constant M⋆/L[3.6] of 0.5 M⊙/L⊙ (Lelli et al. 2016). It is unclear whether or not these two methods are compatible: while SED fitting techniques applied to nearby galaxies give masses corresponding to lower M⋆/L[3.6] (∼0.1–0.3 M⊙/L⊙; see Ponomareva et al. 2018; Hunt et al. 2019), at a higher z this may no longer be the case. An in-depth analysis of these methods is beyond the purpose of this work, but a hint may come from the fact that our z = 1 galaxies follow the same stellar Tully–Fisher (TF) relation as those in the local universe (TFM16): were our stellar masses significantly underestimated, the zero-point of the TF would increase with redshift, against all theoretical expectations (e.g Somerville et al. 2008; Übler et al. 2017; Ferrero et al. 2017). Our measurements remain compatible with no evolution in the Fall relation unless stellar masses at z = 1 (z = 0) are systematically under(over)-estimated by ≳0.15–0.20 dex (∼50%).
Our results appear to be in tension with those of Harrison et al. (2017), who studied the Hα kinematics of 586 star-forming galaxies at z = 0.6 − 1 from the KROSS survey and concluded that, at a given M⋆, these galaxies have a deficiency of ∼0.2–0.3 dex in j⋆ with respect to their local counterpart. To understand this discrepancy we cross-matched our sample with that of Harrison et al. (2017), finding 12 systems in common. These galaxies do not occupy a preferred position in the (M⋆, j⋆) plane, thus are well representative for the overall population of rotationally dominated systems at z = 1. This excludes that our sample is biased towards high-j⋆ systems and indicates that the difference between the two works lies in the method. We derive rotation velocity and velocity dispersion profiles via a 3D modelling of the Hα datacubes, while Harrison et al. (2017) use major-axis υHα and σHα profiles, an approach that often leads to underestimation of the former and overestimation of the latter (e.g. Di Teodoro & Fraternali 2015). Also, they adopt an approximate estimator for j⋆ which relies on accurate measurements of disc sizes (see their Eq. (5)). By comparing the properties of the 12 galaxies in common we found that, while stellar masses are similar, our velocities and disc sizes are larger by about 0.08 and 0.14 dex, respectively, leading to a 0.2-dex larger j⋆, similar to the quoted deficiency with respect to the z = 0 spirals. Analogous arguments apply to the results of Swinbank et al. (2017).
One may wonder whether our results must be expected on the basis of simple, first-principles models. A straightforward, empirical approach is to consider j⋆ ∝ Rd υf and relate the evolution of j⋆ with that observed in the mass-size (MS) relation M⋆ − Rd and in the stellar TF relation M⋆ − υf. Observationally, the evolution of both these relations is highly debated. Our results support a scenario where both relations do not significantly change between z = 0 and z = 1, in agreement with the findings of Conselice et al. (2005), Miller et al. (2011), and TFM16 for the TF relation and with those of Barden et al. (2005) for the MS relation of disc galaxies. More recent measurements (van der Wel et al. 2014; Huang et al. 2017; Somerville et al. 2018) have reported only a modest evolution (∼0.1 dex) in the MS relation of late-type galaxies for the (M⋆, z) range of interest.
A more theoretical approach is to consider galaxy evolution models in a cosmological framework. Following Obreschkow et al. (2015), the j⋆ of a galaxy with stellar mass M⋆ that reside in a virialized spherical halo at a given redshift z can be written as
where λ is the halo spin parameter (∼constant in a ΛCDM universe), fm ≡ M⋆/Mh is the stellar-to-halo mass ratio, fj ≡ j⋆/jh is the stellar-to-halo specific angular momentum ratio, H(z) is the Hubble parameter and Δc(z) is the halo over-density relative to the mean density of the universe. Both fm and fj are, in principle, functions of M⋆ and z. Equation (4) leads immediately to
where we have explicitly written the dependence on (M⋆, z) of the various quantities.
The fm(M⋆, z) in Eqs. (4) and (5) is fully determined by assuming a stellar-to-halo mass relation (SHMR). Here we use the SHMR of Moster et al. (2013), which is well defined at all redshifts and is thought to be well representative for the local universe (e.g. Katz et al. 2017). If we ignore for a moment any evolution in fj, the right-hand term of Eq. (5) computed at z = 0.9 (the mean redshift of our sample) gives values ranging from ∼ + 0.08 dex at log(M⋆/ M⊙) = 9.5 to ∼−0.08 dex at log(M⋆/ M⊙) = 10.7. Adopting the SHMR of Behroozi et al. (2013) leads to a slightly larger range (±0.1 dex). Alternatively, we can assume 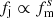 as in a “biased collapse” formation model where stars form inside-out according to the cooling time of the available gas reservoir, meaning that the angular momentum retention efficiency fj correlates with the star-formation efficiency fm (see van den Bosch 1998; Fall et al. 2002; Romanowsky & Fall 2012; Posti et al. 2018a) at all redshifts. If we adopt s = 0.68 as determined by Posti et al. (2018a), then in Eq. (4)
as in a “biased collapse” formation model where stars form inside-out according to the cooling time of the available gas reservoir, meaning that the angular momentum retention efficiency fj correlates with the star-formation efficiency fm (see van den Bosch 1998; Fall et al. 2002; Romanowsky & Fall 2012; Posti et al. 2018a) at all redshifts. If we adopt s = 0.68 as determined by Posti et al. (2018a), then in Eq. (4) 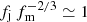 and j⋆(0.9)/j⋆(0)≃0.79 (−0.10 dex), constant over the interested M⋆ range. These predicted values, although uncertain, are within the scatter of the Fall relation, indicating that the lack of a strong variation in the relation between z = 0 and ∼1 is consistent with simple galaxy-evolution models.
and j⋆(0.9)/j⋆(0)≃0.79 (−0.10 dex), constant over the interested M⋆ range. These predicted values, although uncertain, are within the scatter of the Fall relation, indicating that the lack of a strong variation in the relation between z = 0 and ∼1 is consistent with simple galaxy-evolution models.
Finally, conclusions similar to ours have been drawn by Lagos et al. (2017) from the analysis of the EAGLE cosmological simulations in a full ΛCDM framework (Schaye et al. 2015). They found that the mean j⋆ computed within the half-M⋆ radius of star-forming galaxies with 10 < log(M⋆/ M⊙)< 10.5 decreases only marginally (∼0.05 dex, see their Fig. 7) in the redshift range considered, while differences become more marked at higher z. We plan to test this prediction in the near future by applying our technique to galaxies at z ∼ 2.
5. Conclusions
In this Letter we have studied the j⋆ − M⋆ “Fall” relation for a sample of 17 regularly rotating disc galaxies at z ∼ 1. For all galaxies in our sample there exist resolved Hα kinematics from KMOS IFU data, Hα rotation curves from Di Teodoro et al. (2016), HST images in optical and infrared bands from CANDELS, and robust stellar masses determinations. We have determined their surface-brightness profiles from HST images in f160w and f814w filters (rest-frame I and B bands, respectively), corrected the Hα rotation curves for asymmetric drift, and computed j⋆ by assuming that either rotation velocities stay constant beyond the outermost Hα data point or follow a Keplerian fall-off. The latter scenario provides a lower limit on j⋆. All systems show converging j⋆ profiles, which makes them suitable for our study.
We have found that the Fall relation at this redshift is compatible with that determined by Posti et al. (2018b) for spirals in the local universe, unless z = 1 stellar masses derived via SED fitting have been underestimated by more than ∼50%. This implies that the Fall relation for disc galaxies has not evolved significantly in the last ∼8 Gyr. Our findings are in line with expectations based on simple galaxy evolution models and with cosmological simulation in a ΛCDM framework, and support a scenario where both the stellar Tully–Fisher relations and the mass–size relations of disc galaxies do not evolve significantly between redshifts of 1 and 0.
As shown by Fall & Romanowsky (2018), this relation is in excellent agreement with those determined previously by Fall & Romanowsky (2013) and Obreschkow & Glazebrook (2014) for disc-dominated galaxies.
Acknowledgments
The authors thank the referee for an insightful report, and are grateful to M. Fall for his comments and insights. A.M. thanks F. Lelli for useful discussions. L.P. acknowledges financial support from a VICI grant from the Netherlands Organisation for Scientific Research (NWO). E.D.T. acknowledges the support of the Australian Research Council (ARC) through grant DP160100723.
References
- Barden, M., Rix, H.-W., Somerville, R. S., et al. 2005, ApJ, 635, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Wechsler, R. H., & Conroy, C. 2013, ApJ, 770, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Bezanson, R., van der Wel, A., Pacifici, C., et al. 2018, ApJ, 858, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., Franx, M., et al. 2012, ApJS, 200, 13 [Google Scholar]
- Burkert, A., Förster Schreiber, N. M., Genzel, R., et al. 2016, ApJ, 826, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bundy, K., Ellis, R. S., et al. 2005, ApJ, 628, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Contini, T., Epinat, B., Bouché, N., et al. 2016, A&A, 591, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [NASA ADS] [CrossRef] [Google Scholar]
- Di Teodoro, E. M., Fraternali, F., & Miller, S. H. 2016, A&A, 594, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutton, A. A., & van den Bosch, F. C. 2012, MNRAS, 421, 608 [NASA ADS] [Google Scholar]
- Efstathiou, G., & Jones, B. J. T. 1979, MNRAS, 186, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Tasca, L., Amram, P., et al. 2012, A&A, 539, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fall, S. M. 1983, in Internal Kinematics and Dynamics of Galaxies, ed. E. Athanassoula, IAU Symp., 100, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M. 2002, in Disks of Galaxies: Kinematics, Dynamics and Peturbations, eds. E. Athanassoula, A. Bosma, & R. Mujica, ASP Conf. Ser., 275, 389 [NASA ADS] [Google Scholar]
- Fall, S. M., & Romanowsky, A. J. 2013, ApJ, 769, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., & Romanowsky, A. J. 2018, ApJ, 868, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrero, I., Navarro, J. F., Abadi, M. G., et al. 2017, MNRAS, 464, 4736 [NASA ADS] [CrossRef] [Google Scholar]
- Genel, S., Fall, S. M., Hernquist, L., et al. 2015, ApJ, 804, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Brook, C., Mayer, L., et al. 2010, Nature, 463, 203 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Johnson, H. L., Swinbank, A. M., et al. 2017, MNRAS, 467, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, K.-H., Fall, S. M., Ferguson, H. C., et al. 2017, ApJ, 838, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., De Looze, I., Boquien, M., et al. 2019, A&A, 621, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kassin, S. A., Weiner, B. J., Faber, S. M., et al. 2012, ApJ, 758, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, N., & Gunn, J. E. 1991, ApJ, 377, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Lelli, F., McGaugh, S. S., et al. 2017, MNRAS, 466, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V. 2013, ApJ, 764, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., van Dokkum, P. G., Labbé, I., et al. 2009, ApJ, 700, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. D. P., Theuns, T., Stevens, A. R. H., et al. 2017, MNRAS, 464, 3850 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016, AJ, 152, 157 [Google Scholar]
- Martinsson, T. P. K., Verheijen, M. A. W., Westfall, K. B., et al. 2013, A&A, 557, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meurer, G. R., Carignan, C., Beaulieu, S. F., & Freeman, K. C. 1996, AJ, 111, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, S. H., Bundy, K., Sullivan, M., Ellis, R. S., & Treu, T. 2011, ApJ, 741, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., & Steinmetz, M. 2000, ApJ, 538, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Obreschkow, D., & Glazebrook, K. 2014, ApJ, 784, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Obreschkow, D., Glazebrook, K., Bassett, R., et al. 2015, ApJ, 815, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1969, ApJ, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Ponomareva, A. A., Verheijen, M. A. W., Papastergis, E., Bosma, A., & Peletier, R. F. 2018, MNRAS, 474, 4366 [NASA ADS] [CrossRef] [Google Scholar]
- Posti, L., Pezzulli, G., Fraternali, F., & Di Teodoro, E. M. 2018a, MNRAS, 475, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Posti, L., Fraternali, F., Di Teodoro, E. M., & Pezzulli, G. 2018b, A&A, 612, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romanowsky, A. J., & Fall, S. M. 2012, ApJS, 203, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Ferguson, H. C., Fontana, A., et al. 2015, ApJ, 801, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schombert, J. 2007, ArXiv e-prints [arXiv:astro-ph/0703646] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Somerville, R. S., Barden, M., Rix, H.-W., et al. 2008, ApJ, 672, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Behroozi, P., Pandya, V., et al. 2018, MNRAS, 473, 2714 [NASA ADS] [CrossRef] [Google Scholar]
- Stott, J. P., Swinbank, A. M., Johnson, H. L., et al. 2016, MNRAS, 457, 1888 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Harrison, C. M., Trayford, J., et al. 2017, MNRAS, 467, 3140 [NASA ADS] [Google Scholar]
- Übler, H., Förster Schreiber, N. M., Genzel, R., et al. 2017, ApJ, 842, 121 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C. 1998, ApJ, 507, 601 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Wisnioski, E., Förster Schreiber, N. M., Wuyts, S., et al. 2015, ApJ, 799, 209 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Supplementary material
Table A.1 lists the main properties of the 17 galaxies at z ∼ 1 analysed in this work. Galaxy names, IDs, redshifts, and stellar masses are the same as those reported in Table 1 of TFM16, while the other properties have been determined in this work. As in Fig. 1 for the case of zmus_z1_119, in Fig. A.1 we present the photometric and kinematic analysis for the other 16 galaxies of our sample.
Properties of the 17 galaxies at z ∼ 1 analysed in this work.
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
All Tables
All Figures
 |
Fig. 1. Photometry and kinematics of galaxy zmus_z1_119. First panel: HST image in f160w band (rest-frame I band). The concentric ellipses show the annuli where the surface brightness is computed. The green dashed ellipse shows the radius of the outermost Hα rotation velocity point. The blank region in the f814w image has been masked by our sigma-rejection algorithm (see text). Second panel: as in the first panel, but for the f814w band (rest-frame B band). Third panel: surface-brightness profiles in bands f160w (red circles) and f814w (blue triangles), normalised to the total light within the outermost ring. The thin dashed lines show exponential fits for R > 3.5 kpc, the solid thick lines show the cumulative light profile. Fourth panel: rotation curves. Points with error bars show υHα as determined by TFM16. The black and the red solid (dashed) lines show our fiducial profiles for υcirc and υ⋆ respectively, assuming a flat (Keplerian) extrapolation for the circular velocity. |
| In the text | |
 |
Fig. 2. Cumulative j⋆ profiles for our 17 galaxies in the f160w (left panel) and f814w (right panel) bands. Coloured solid lines show the innermost regions where rotation velocities from Hα data are available, while solid black lines show the extrapolation for a flat rotation curve. All profiles are either converging or have fully converged. |
| In the text | |
 |
Fig. 3. Fall relation for our sample of disc galaxies at z ∼ 1. Left (right) panel: results derived using the f160w (f814w) HST band. The squared symbols show the j⋆ determined for a flat rotation curve extrapolation, while the upwards triangles represent lower limits derived from the assumption of a Keplerian fall-off. Numbers correspond to galaxy IDs from Table A.1. The black-dashed line and the grey-shaded region show the Fall relation and its intrinsic scatter, respectively, as determined by Posti et al. (2018b) for disc galaxies in the local universe from the SPARC data of Lelli et al. (2016). |
| In the text | |
 |
Fig. A.1. Same as Fig. 1, but for the other 16 galaxies in our sample. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





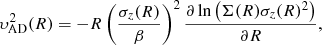
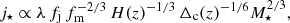
![$$ \begin{aligned} \frac{j_\star (M_\star ,z)}{j_\star (M_\star ,0)} = \left[\frac{f_{\rm j}(M_\star ,z)}{f_{\rm j}(M_\star ,0)}\right] \left[\frac{f_{\rm m}(M_\star ,z)}{f_{\rm m}(M_\star ,0)}\right]^{-2/3} \left[\frac{H(z)}{H(0)}\right]^{-1/3} \left[\frac{\Delta _{\rm c}(z)}{\Delta _{\rm c}(0)}\right]^{-1/6} , \end{aligned} $$](/articles/aa/full_html/2019/01/aa34456-18/aa34456-18-eq7.gif)