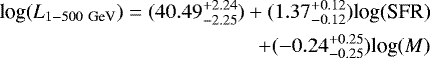EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 621 (January 2019) A&A, 621 (2019) A70 Full HTML
Free Access
Issue
A&A
Volume 621, January 2019
Article Number A70
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201833859
Published online 10 January 2019

© ESO 2019

1 Introduction

Several nearby star-forming and starburst galaxies have been identified to be GeV to TeV gamma-ray sources (e.g., Acero et al. 2009; VERITAS Collaboration 2009; Abdo et al. 2010a; Ackermann et al. 2012a; Tang et al. 2014; Peng et al. 2016; Griffin et al. 2016; Ackermann et al. 2017). Cosmic rays (CRs) accelerated by supernova remnants (SNRs) or the stellar wind of massive stars interact with the interstellar medium (ISM) and produce neutron pions (schematically written as p + p → p + π0+ other products), which in turn decay into high-energy gamma-rays (π0 → γ + γ). Interestingly, with the early Fermi Large Area Telescope (LAT) data, Abdo et al. (2010a) found a correlation between the gamma-ray (>100MeV) luminosity (Lγ) and star formation rate (SFR) for nearby star-forming galaxies. Based on three years of Fermi-LAT data, a tight correlation between the gamma-ray luminosity and total infrared luminosity (8–1000 μm) over 4–5 orders of magnitudes has been reported for star-forming galaxies by Ackermann et al. (2012a). Since the total infrared luminosity is an indicator of the SFR of star-forming galaxies and galaxies that are not yet detected in gamma-rays are also taken into account to reduce sample selection effects, this then suggests that the positive correlation between the gamma-ray luminosity and SFR (Lγ–SFR) is robust. Lately, this correlation has been extended to ultra-luminous infrared galaxies, with the detection of gamma-ray emission from Arp 220 (Peng et al. 2016; Griffin et al. 2016). This strengthens the connection between star formation process and gamma-ray emission on a larger luminosity scale.

Molecular clouds, which are the sites of star formation in our Galaxy, are also sources of gamma-ray emission (e.g., Ackermann et al. 2012b,c,d). The widely accepted explanation of the gamma-ray emission of molecular clouds is that the clouds are passive targets for interaction with diffuse Galactic CRs (e.g., Aharonian 2001; Grenier et al. 2005; Gabici et al. 2007). The passive-target scenario assumes that Galactic cosmic rays can freely penetrate the clouds and enter into the core region. This scenario has gained support from the fairly uniform distribution of gamma-ray emissivity per gas nucleon in the Gould Belt clouds and in the Local Arm (Abdo et al. 2009, 2010b; Ackermann et al. 2011a, 2012c,d; Casandjian 2012).

On the other hand, there have been suggestions that molecular clouds contain active sources of CRs. Embedded young stellar objects (YSOs) in giant molecular clouds are proposed to be sources of high-energy cosmic rays (e.g., Araudo et al. 2007; Bosch-Ramon et al. 2010; Maurin et al. 2016). The strong stellar wind activity in these objects generates large bubbles and induces collective effects that could accelerate particles up to high energy and produce gamma-rays (e.g., Ackermann et al. 2011b; Yang & Aharonian 2017; Yang et al. 2018; Aharonian et al. 2018). For low-mass YSOs such as T Tauri protostars, their jets and winds should be unimportant. However, these objects have bubbles and outflows that seem to sustain turbulence (Li et al. 2015). This would mean that particles could also be accelerated to relativistic energies by turbulence or a magnetic reconnection process (del Valle et al. 2011).

It has been clear that stars are born in the molecular gas, especially in regions with dense molecular gas, rather than those primarily with atomic hydrogen. The dense region within molecular clouds collapses and then forms new stars. The SFR of molecular clouds estimated from the far-infrared emission correlates well with the dense molecular gas mass traced by HCN for galaxies (e.g., Gao & Solomon 2004). This correlation continues to dense Galactic cores over a large scale of magnitude in SFR (e.g., Wu et al. 2005; Lada et al. 2010). As molecular clouds are ascaled down version of star-forming galaxies in some sense, the question arises whether the Lγ –SFR correlation can extend to the scale of Galactic molecular clouds.

To study whether the SFR plays an important role in producing gamma-ray emission in molecular clouds, we here conduct a comparative study of the correlation between gamma-ray luminosity and SFR for Galactic molecular clouds and star-forming galaxies. Furthermore, we systematically investigate the correlations among Lγ, SFR, and gas mass M to study the relative dependence of Lγ on SFR and gas mass. We analyzed the Fermi-LAT data of eight Galactic molecular clouds in the Gould Belt. We noted that the Fermi-LAT data of local molecular clouds of the Gould Belt had been used to probe the CR properties by several groups (Neronov et al. 2012, 2017; Yang et al. 2014; Shen et al. 2018). However, these works focused on deriving the spectrum of the parent CRs through the resolved gamma-ray spectral analysis and compared it with the measurements of local Galactic CRs. Their relatively large offsets from the Galactic plane ensure little contamination from the diffuse Galactic gamma-ray emission. The close distances lead to a high detection significance of the gamma-ray emission. These make them good candidates for our study. The structure of the paper is as follows. In Sect. 2, we describe the data reduction and results of the Fermi-LAT observations. In Sect. 3, we study whether the Lγ – SFR correlation of galaxies can extend to the scale of Galactic molecular clouds. In Sect. 4, we present the study on the correlation among gamma-ray luminosity Lγ, SFR, and the gas mass M. In Sect. 5, we discuss the implications of these two-parameter and three-parameter correlations. Finally, we conclude in Sect. 6.

2 Fermi-LAT data reduction

The LAT on board the Fermi mission is a pair-conversion instrument that is sensitive to GeV emission (Atwood et al. 2009). We accumulated data events from the start (MET 239557417) to 2017 April 6 (MET 513164606) to study gamma-ray emission from the Galactic molecular clouds. The basic information of the clouds, including the position, size, mass, and distance, is listed in Tables 1 and 2. The current Fermi-LAT Pass 8 SOURCE data (P8R2 Version 6) and the standard Fermi science tools version v10r0p5 were used. All FRONT+BACK converting photons with energies higher than 0.3 GeV were taken into consideration to reduce the contamination from poor angular resolution events at lower energies. To limit the gamma-rays produced by CR interactions in the upper atmosphere, the maximum zenith-angle cut zmax = 90° was required. The expression of (DATA_QUAL > 0) & & (LAT_CONFIG ==1) was used to further filter the data in the gtmktime. We performed the binned maximum likelihood analysis on a region of interest (ROI) with a radius of 10° centered on the position of each Galactic molecular cloud. We used the 3FGL (Acero et al. 2015) to generate the source model containing the position and spectral definition for all the point sources and diffuse emission within 15° of the ROI center. The extragalactic diffuse model iso_P8R2_SOURCE_V6_v06.txt was also included.

All molecular clouds in our sample extend several degrees above the Galactic plane on the sky. A comparison of the gamma-ray counts map with CO intensity reveals a good correlation between the gamma-ray and CO emission. The CO distribution in the direction of sight was reduced to a single peak by integrating the CO cube in the spatial dimension (Dame et al. 2001). We particularly focused on the integral gamma-ray flux of each molecular cloud for the correlation studies. Because the Galactic diffuse gamma-ray emission in the ROI is dominated by the interaction between CRs and molecular clouds and neutral hydrogen is distributed diffusively in our Galaxy, we adopted the following method. The templates for modeling the spatial and spectral distribution of molecular clouds were extracted from the standard Galactic diffuse emission model, that is, a cube file named as gll_iem_v06.fits, provided by the Fermi-LAT Collaboration. We selected one region nearby with the same size for each molecular cloud as the background without significant CO emission. In each energy band, we obtained the average value in the background region, which was also used to model the residual Galactic diffuse emission of the molecular cloud. Then we obtained the molecular cloud templates by subtracting the above value from the standard gll_iem_v06.fits. After the source model was created, the standard commands gtbin, gtltcube, gtexpcube2, and gtsrcmaps were successively executed, then a maximum likelihood analysis was performed in binned mode using the tool gtlike1.

Cosmic rays generate diffuse gamma-ray emission by interacting with interstellar gas and magnetic fields during their propagation through the Galaxy. One way to derive the spatial and spectral information of the diffuse gamma-ray emission templates is to use the GALPROP code2. We therefore checked the results on a diffuse emission model that did not include a gas component with the help of GALPROP. We used models for the predicted Galactic diffuse gamma-ray emission obtained from the Fermi-LAT collaboration work (Ackermannet al. 2012d), which provides 128 sets of maps corresponding to different model parameters. We tested 16 of these 128 templates and chose two each for the CR source distribution (Lorimer pulsars; Lorimer et al. 2006), SNRs (Case & Bhattacharya 1998), vertical boundaries (4 and 10 kpc), spin temperature for the optical depth correction (150 and 105 K), and E(B–V) magnitude cut (2 and 5 mag). We did not include the H2 component in these Galprop simulations. We used the spatial templates for pion-decay, bremsstrahlung radiation, and inverse Compton gamma-rays generated by GALPROP3 (Vladimirov et al. 2011) to replace the background model. The gamma-ray emissions of molecular clouds using the above 16 background models are consistent with those in Table 2, and the fluxes change at most by ~ 15% in these models; see Table 3. These small differences do not affect our statistical results and conclusion.

The integral gamma-ray fluxes of molecular clouds are presented in Table 2. To conform with the energy range of the data for the star-forming galaxies, we extrapolated the flux in 0.3– 100 GeV to that in the energy range of 0.1–100 GeV. The statistical error is small due to the high-significance detection. The data of gamma-ray emission in 0.1– 100 GeV from star-forminggalaxies were taken from previous publications (Ackermann et al. 2012a; Tang et al. 2014; Peng et al. 2016).

In order to reduce the possible contribution from leptonic emission, such as inverse Compton scatter and bremsstrahlung radiation at low energies, which would overestimate the flux due to hadronic CRs interaction, we also considered the Fermi-LAT data in 1– 500 GeV. Moreover, the possible gamma-ray contamination emission from unresolved sources such as pulsars was also suppressed by increasing the threshold energy for the data analysis (Abdo et al. 2013). To obtain the gamma-ray luminosity in 1–500 GeV (L1−500 GeV), we performed a likelihood analysis of the latest Fermi-LAT data following a method that was similar to the previously used method. The results are shown in Tables 2 and 4.

Table 1

Basic information on Galactic molecular clouds.

Table 2

Parameters and gamma-ray fluxes of Galactic molecular clouds.

Table 3

Change in gamma-ray flux of the first three molecular clouds for different background models.

thumbnail Fig. 1

Relation between gamma-ray emissivity (left panel: 0.1–100 GeV; right panel: 1–500 GeV) and SFR per unit mass for molecular clouds and star-forming galaxies. The best-fit lines together with their 1σ dispersion regions are shown with solid and dashed lines, respectively.

3 Do molecular clouds follow the Lγ–SFR correlation of star-forming galaxies?

As molecular clouds are a scaled-down version of star-forming galaxies in some sense, we first studied whether the Lγ – SFR correlation of galaxies can extend to the scale of Galactic molecular clouds. To do this, we checked whether the Galactic molecular clouds fall onto the correlation line in the Lγ – SFR diagram of star-forming galaxies. Since Lγ and SFR of molecular clouds and star-forming galaxies span 7–8 orders of magnitude, we reduced the dynamic range from clouds to star-forming galaxies by dividing the gamma-ray luminosity and SFR by the gas mass M. We compared the gamma-ray emissivity (Lγ∕M) and SFR per unit mass for molecular clouds and star-forming galaxies. Although the methods for determining the gas masses for molecular clouds and star-forming galaxies are different, it has been proved that the molecular-line-derived masses and the extinction-derived masses accurately reflect the same material (Lada et al. 2012). We computed the average integral > 100 MeV gamma-ray emissivity per hydrogen atom of molecular clouds using the following form: 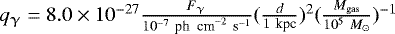, where the emissivity qγ is in unit of ph s−1 sr−1 H−1, Fγ is the integral photon flux, Mgas is the total gas content of the molecular cloud, and d is the distance to Earth. The mean value of the ratio between the measured integral gamma-ray emissivity of local atomic hydrogen (Abdo et al. 2009) and that of the sample molecular clouds in our work is 1.13 ± 0.69, and the median value is 0.90, indicating that the gamma-ray emissivities of molecular clouds are quite close to the emissivity of local atom hydrogen.

The results are reported in Fig. 1. A correlation is evident between the gamma-ray emissivity (Lγ ∕M) and SFR per unit mass for star-forming galaxies, but the molecular clouds significantly deviate from this correlation. The Pearson correlation coefficient of star-forming galaxies is r > 0.9 and the chance probability is p < 10−4. The derived total dispersions, including the intrinsic scatter of the data set and the statistic scatter, are 0.45 and 0.24 for the gamma-ray emissivity (Lγ∕M) in 0.1–100 GeV and 1–500 GeV, respectively. The gamma-ray emissivities (Lγ ∕M) of molecular clouds are distributed in a narrow space and are comparable to the mean value of the Milky Way, which contains a great variety of different molecular clouds with different star-forming activities. The different scalings imply that the gamma-ray emission of molecular clouds and star-forming galaxies has a different origin. The roughly constant gamma-ray emissivity among the clouds as well as the Milky Way supports the hypothesis that the gamma-ray emission of clouds is due to passive interactions by the diffuse Galactic CRs. This wide range of SFR/M may reflect the variations in the fractions of dense gas. The physical interpretation behind it could be due to the cloud evolution. The evolution of molecular clouds is controlled by a complex interplay of large-scale phenomena and microphysics, such as turbulence, magnetic field, outflow of young stellar objects, far-ultraviolet radiation, CR radiation, gas, and dust (e.g., Vázquez-Semadeni et al. 2011, and reference therein).

4 Multiple-variable regression analysis

In this section, we conduct a multiple-variable regression analysis to study the correlations among the parameters of gamma-ray luminosity, SFR, and M for molecular clouds and star-forming galaxies, respectively. The underlying theory for this statistical analysis is that gamma-ray emission should depend on both the sources of CRs and the target gases. The sources of Galactic CRs could be SNRs and/or young stellar objects, which are indicated by the SFR. We therefore studied the correlation between gamma-ray luminosity and SFRs for molecular clouds and star-forming galaxies. Furthermore, we systematically investigated the correlations among gamma-ray luminosity, SFR, and gas mass M to study the relative dependence of gamma-ray emission on SFR and gas mass. Through a comparative and statistic analysis, we examine whether the SFR plays an important role in producing gamma-ray emission in molecular clouds, and we study the difference of gamma-ray emission processes in molecular clouds and star-forming galaxies.

Generally speaking, the results of the regression analysis depend on the choice of dependent and independent variables (Isobe et al. 1990; Feigelson & Babu 1992), especially in our case, where the sample size is small and the intrinsic data scatter is large. The bisector or orthogonal method could be adopted to solve the problem from the point of view of mathematics. However, from a physical point of view, the independent and dependent variables are believed to be clear. For the given data set, SFR stands for the sources of CRs, the gas mass M stands for the target material, and Lγ is the result of CR interaction between sources and target. Therefore, Lγ was chosen as the independent variable in the following analysis.

The two-parameter correlation between Lγ and SFR fornearby star-forming galaxies has been found for the first time by Abdo et al. (2010a), and it has been confirmed by follow-up studies (Ackermann et al. 2012a; Tang et al. 2014; Peng et al. 2016; Griffin et al. 2016). This discovery is linked to the relation between CRs and SFR, although its origin is not yet fully understood. Here we explore the two-parameter correlations between gamma-ray luminosity and SFR (or gas mass) for star-forming galaxies and clouds to determine the roles that the SFR plays in producing gamma-ray emission and to understand the physical nature behind the scaling relations.

We modeled the two-parameter correlation using the form z = a + b × x. To obtain the best-fitting parameters to the observational data with the two-parameter correlation analysis, we used the maximum likelihood approach. The joint likelihood function for two-parameter analysis is 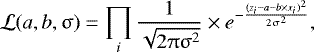(1)

where i is the corresponding serial number of molecular clouds or star-forming galaxies in our sample, z is Lγ, and x is SFR (or M). They all are derived in logarithmic space. Since no error bars for SFR and M are available, and very small statistic errors in Lγ for some molecular clouds (see Table 2) would lead to relatively large weights, no measurement errors were considered. σ is introduced to accommodate intrinsic scatter and measurement errors. The coefficients of a,   b, and σ are constrained simultaneously by maximizing the joint likelihood function.

For each sample of molecular clouds and star-forming galaxies, we used the Python Markov chain Monte Carlo module EMCEE (Foreman-Mackey et al. 2013) to explore the posterior distributions of parameters of a,   b, and σ. We derived the dispersion (δ) of a regression model with standard deviation of zr from z, where r marks the z value derived from the regression model.

We applied this two-parameter correlation analysis to molecular clouds and star-forming galaxies using the forms log Lγ = a + blog(SFR) or log Lγ = a + blog(M). The results of the correlations are shown in Tables 5 and 6. The results in Tables 5 and 6 show at first glance that all correlations between L1−500 GeV and SFR or M are significant from the statistical point of view, even though there is some difference in the correlation coefficients and the dispersion of the fit. Particularly, stronger dependences of L1−500 GeV on gas mass M for molecular clouds and L1−500 GeV on SFR for star-forming galaxies are indicated by the Pearson correlation coefficient r > 0.9 and the chance probability p < 10−4. Figure 2 shows the correlation between gamma-ray luminosity and mass M of the molecular cloud sample.

As described above, the gamma-ray emission from star-forming regions originates from CR interactions. In principle, Lγ may depend not only on the number of CR sources denoted by the SFR, but also on the mass of the target gas that is denoted by M. Therefore, it is interesting to investigate the possible multi-parameter correlation among Lγ, SFR, and M. The likelihood function can also be conveniently applied to the three-parameter correlation case by introducing an additional term of c × yi, that is, log Lγ = a + blog(SFR) + clog(M). The relative dependence of Lγ on SFR or M is shown clearly through this three-parameter correlation analysis, which is helpful to reveal the mechanism of gamma-ray emission.

The results of three-parameter correlations among Lγ, SFR, and M for molecular clouds and star-forming galaxies are reported in Table 7. The best-fit correlations are 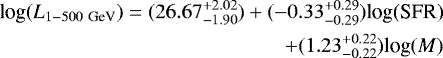(2)

for molecular clouds and (3)

for star-forming galaxies, respectively. The derived 1σ errors of these coefficients are listed in Table 7. The Pearson correlation coefficient r > 0.9 and chance probability p < 10−4 suggest strong correlations among L1−500 GeV, SFR, and M. For molecular clouds, the weak dependence on SFR, as indicated by b ~ 0 within the error box, shows that the 1–500 GeV gamma-ray luminosity is principally proportional to the gas mass M. However, the results for galaxies are the opposite. 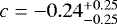means that the gamma-ray luminosity of galaxies depends little on the total gas mass M. There is a clear trend that L1−500 GeV increases with SFR. These results are consistent with the two-parameter correlations analysis. The dispersion and linear coefficient for the three-parameter correlation are almost the same as those of the two-parameter fit of L1−500 GeV–M for molecular clouds and L1−500 GeV–SFR for star-forming galaxies, respectively. Introducing the third parameter into the three-parameter correlation does not improves the fit significantly, which implies a weak dependence of Lγ on SFR for molecular clouds, and on M for star-forming galaxies. The regression lines together with 1σ dispersion regions are also presented in Fig. 3. For a comparison with previous works, we also performed amulti-parameter correlation analysis for molecular clouds and star-forming galaxies using a 0.1– 100 GeV gamma-ray luminosity. The results are reported in Table 8

thumbnail Fig. 2

Two-parameter correlation between L1−500 GeV and total gas mass (left panel) and dense gas mass (right panel) for molecular clouds. The best-fit lines together with their 1σ dispersion regions are shown with solid and dashed lines, respectively.
Table 4

Parameters and gamma-ray luminosities of star-forming galaxies.

Table 5

Results of the two-parameter correlation for L1−500 GeV and SFR in our sample.

thumbnail Fig. 3

Three-parameter correlation among L1−500 GeV, SFR, and M for molecular clouds (left panel) and star-forming galaxies (right panel). The best-fit lines together with their 1σ dispersion regions are shown with solid and dashed lines, respectively.
Table 6

Results of the two-parameter correlation for L1−500 GeV and M in our sample.

Table 7

Results of the three-parameter correlation for L1−500 GeV, SFR, and M in our sample.

Table 8

Results of the three-parameter correlation for L0.1−100 GeV, SFR, and M in our sample.

5 Discussion

The correlation among Lγ, SFR, and M is of theoretical interest in understanding the mechanism of GeV emission in molecular clouds and star-forming galaxies. The formula for estimating the gamma-ray emission quantitatively (Aharonian et al. 2018) reads 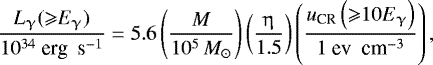(4)

where M is the mass of the relevant region, η accounts for the presence of nuclei higher in mass than hydrogen in CRs and interstellar matter, and uCR is the CR density.

If the molecular clouds in our sample are an active source of CR acceleration, similar to star-forming galaxies, or if the embedded YSOs can contribute CRs at a comparable level of the Galactic CR sea, gamma-ray emission should also show a correlation with CR density (denoted as SFR), smoothly connecting the Lγ – SFR relationship of star-forming galaxies. Correspondingly, the dependence of Lγ on the SFR in three-parameters correlation should be much stronger. However, this is not supported by our data analysis. The data set of molecular clouds and star-forming galaxies is located in different regions in the diagram of gamma-ray emissivity (Lγ ∕M) and SFR per unit mass (Fig. 1). The gamma-ray emissivity (Lγ ∕M) remains to be a constant for different SFR∕M for Galactic molecular clouds. This is consistent with the gamma-ray’s being produced outside of the cloud and with the recent study of diffuse Fermi gamma-ray emission, which seems to trace the total molecular gas content on a global scale (Remy et al. 2018). The nice linear correlation between Lγ and total mass for molecular clouds is demonstrated by the slope of 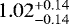. In other words, the CRs that produce the dominant part of the gamma-ray emission in molecular clouds may be accelerated outside, as expected from the passive-cloud scenario. These molecular clouds float in the sea of the Galactic CRs, and the produced gamma-ray emission is proportional to the total gas mass under the hypothesis that the non-violent change CRs flux penetrates the clouds. The embedded massive stars may contribute to CRs secondarily or account for some CR hot spots around clusters of young stellar objects (e.g., Marchili et al. 2018). The Pearson correlation coefficient of Lγ – SFR for molecular clouds is also good from a statistical point of view, but it may simply reflect the Lγ – Mdense correlation, as Mdense is a proxy of SFR. It could be naturally explained by the combination of an only mildly varying fraction of dense gas mass (see Table 1) and a tight Lγ–M correlation.

For star-forming galaxies, the Pearson correlation coefficient and dispersion of Lγ – M correlation demonstrates that the two-parameter relationship is poor, which is consistent with results of the three-parameter correlation. The gamma-ray luminosity of star-forming galaxies can be parameterized by Lγ ~ fcalLCR, where LCR is the CR luminosity in galaxies, which is proportional to the SFR, and fcal is the calorimetric factor denoting the fraction of the energy of CRs converted into secondary pions. Star-forming galaxies with an SFR > 10 M⊙ yr−1 are close to the calorimetric limit (e.g., Lacki et al. 2011; Wang & Fields 2018), that is, fcal ≃ 1. If the CR calorimetry hypothesis were to hold, the slope of the relation between the gamma-ray luminosity and SFR would be unity. The observed slope of the relation is steeper than unity, however (Abdo et al. 2010a; Ackermann et al. 2012a; Tang et al. 2014; Peng et al. 2016), indicating that galaxies with lower SFRs may have smaller fcal. Pfrommer et al. (2017) reproduced the observed relation between far-infrared and gamma-ray emission using magnetohydrodynamical galaxy formation simulations with self-consistent CR physics. They found that the calorimetric factor fcal decreases smoothly toward lower SFRs due to the increasing adiabatic losses of CRs.

6 Conclusions

We have analyzed the Fermi-LAT data of eight Galactic molecular clouds in the Gould Belt. Through a comparative study of the correlations among the gamma-ray luminosity, SFR, and gas mass M, we found that the gamma-ray luminosity of molecular clouds is strongly dependent on the total gas mass M and weakly dependent on SFR. The SFR inside molecular clouds makes minor contribution to the gamma-ray emission. The results of star-forming galaxies are just the opposite. A tight dependence between the gamma-ray luminosity and SFR is found, with little dependence on M. The different empirical correlations found in molecular clouds and star-forming galaxies indicates that different mechanisms produce the gamma-ray emission, with Galactic clouds being more of a passive target to interact with CRs. The gamma-ray emission in molecular clouds originates predominantly from the interaction of diffuse galactic CRs. Star-forming galaxies are effective reservoirs for CRs, and a significant fraction of CR energy is transferred into secondary gamma-rays, at least for those with GeV emission that are observed by Fermi-LAT.

Acknowledgments

This work is partially supported by the National Key R & D program of China under the grant 2018YFA0404203 and 2017YFA0402600, and the NSFC grants 11625312, 11851304, U1731238, 11565010, and 11725313. F.K.P acknowledges support from the Doctoral Starting up Foundation of Guizhou Normal University 2017 (GZNUD[2017] 33) and the open project of Guangxi Key Laboratory for Relativistic Astrophysics. Q.J.Z. acknowledges support from the science and technology innovation talent team (grant (2015)0415), the High Level Creative Talents (grant (2016)-4008) and Innovation Team Foundation of the Education Department (grant [2014]35) of Guizhou Province. D.L. acknowledges support from the International Partnership Program of Chinese Academy of Sciences, Grant No.114A11KYSB20160008 and the CAS Strategic Priority Research Program No. XDB23000000. We thank R.Z. Yang, R.-Y. Liu, J.Z. Wang, K.P. Qiu and H. Chen for useful discussions. This work has made use of data and software provided by the Fermi Science Support Center.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 703, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, A&A, 523, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 710, A133 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
  5. Acero, F., Aharonian, F., Akhperjanian, A. G., et al. 2009, Science, 326, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  6. Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
  7. Ackermann, M., Ajello, M., Baldini, L., et al. 2011a, ApJ, 726, 81 [NASA ADS] [CrossRef] [Google Scholar]
  8. Ackermann, M., Ajello, M., Allafort, A., et al. 2011b, Science, 334, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Ackermann, M., Ajello, M., Allafort, A., et al. 2012a, ApJ, 755, 164 [NASA ADS] [CrossRef] [Google Scholar]
  10. Ackermann, M., Ajello, M., Allafort, A., et al. 2012b, ApJ, 755, 22 [NASA ADS] [CrossRef] [Google Scholar]
  11. Ackermann, M., Ajello, M., Allafort, A., et al. 2012c, ApJ, 756, 4 [NASA ADS] [CrossRef] [Google Scholar]
  12. Ackermann, M., Ajello, M., Atwood, W. B., et al. 2012d, ApJ, 750, 3 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ackermann, M., Ajello, M., Albert, A., et al. 2017, ApJ, 836, 208 [NASA ADS] [CrossRef] [Google Scholar]
  14. Aharonian, F. A. 2001, Space Sci. Rev., 99, 187 [NASA ADS] [CrossRef] [Google Scholar]
  15. Aharonian, F., Yang R., & de Oña Wilhelmi, E. 2018, ArXiv e-prints [arXiv:1804.02331] [Google Scholar]
  16. Araudo, A. T., Romero, G. E., Bosch-Ramon, V., & Paredes, J. M. 2007, A&A, 476, 1289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bosch-Ramon, V., Romero, G. E., Araudo, A. T., & Paredes, J. M. 2010, A&A, 511, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Braun, R., Thilker, D. A., Walterbos, R. A. M., & Corbelli, E. 2009, ApJ, 695, 937 [Google Scholar]
  20. Carpenter, J. M., & Hodapp, K. W. 2008, Handbook of Star Forming Regions, Volume I (San Francisco: ASP), 4, 899 [Google Scholar]
  21. Casandjian, J.-M. 2012, AIP Conf. Ser., 1505, 37 [NASA ADS] [Google Scholar]
  22. Case, G. L., & Bhattacharya, D. 1998, ApJ, 504, 761 [Google Scholar]
  23. Cillis, A. N., Torres, D. F., & Reimer, O. 2005, ApJ, 621, 139 [NASA ADS] [CrossRef] [Google Scholar]
  24. Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
  25. del Valle, M. V., Romero, G. E., Luque-Escamilla, P. L., Martí, J., & Ramón Sánchez-Sutil J. 2011, ApJ, 738, 115 [NASA ADS] [CrossRef] [Google Scholar]
  26. Feigelson, E. D., & Babu, G. J. 1992, ApJ, 397, 55 [NASA ADS] [CrossRef] [Google Scholar]
  27. Förster Schreiber, N. M., Genzel, R., Lutz, D., & Sternberg, A. 2003, ApJ, 599, 193 [NASA ADS] [CrossRef] [Google Scholar]
  28. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
  29. Fukui, Y., Kawamura, A., Minamidani, T., et al. 2008, ApJS, 178, 56 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gabici, S., Aharonian, F. A., & Blasi, P. 2007, Ap&SS, 309, 365 [CrossRef] [Google Scholar]
  31. Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
  32. Grenier, I. A., Casandjian, J.-M., & Terrier, R. 2005, Science, 307, 1292 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  33. Griffin, R. D., Dai, X., & Thompson, T. A. 2016, ApJ, 823, L17 [NASA ADS] [CrossRef] [Google Scholar]
  34. Heiderman, A., Evans, N. J., II, Allen, L. E., Huard, T., & Heyer, M. 2010, ApJ, 723, 1019–37 [NASA ADS] [CrossRef] [Google Scholar]
  35. Hughes, A., Staveley-Smith, L., Kim, S., Wolleben, M., & Filipović, M. 2007, MNRAS, 382, 543 [NASA ADS] [CrossRef] [Google Scholar]
  36. Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Knude, J. 2010, ArXiv e-prints [arXiv:1006.3676] [Google Scholar]
  38. Lacki, B. C., Thompson, T. A., Quataert, E., Loeb, A., & Waxman, E. 2011, ApJ, 734, 107 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lada, C. J., Forbrich, J., Lombardi, M., & Alves, J. F. 2012, ApJ, 745, 190 [NASA ADS] [CrossRef] [Google Scholar]
  41. Lenc, E., & Tingay, S. J. 2006, AJ, 132, 1333 [NASA ADS] [CrossRef] [Google Scholar]
  42. Leroy, A., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]
  43. Li, H., Li, D., Qian, L., et al. 2015, ApJS, 219, 20 [NASA ADS] [CrossRef] [Google Scholar]
  44. Lombardi, M., Lada, C. J., & Alves, J. 2008, A&A, 480, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Lombardi, M., Lada, C. J., & Alves, J. 2010, A&A, 512, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Lombardi, M., Alves, J., & Lada, C. J. 2011, A&A, 535, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] [Google Scholar]
  48. Luhman, K. L. 2008, Handbook of Star Forming Regions, Volume II (San Francisco: ASP), 5, 169 [Google Scholar]
  49. Marchili, N., Piano, G., Cardillo, M., et al. 2018, A&A, 615, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Maurin, G., Marcowith, A., Komin, N., Krayzel, F., & Lamanna, G. 2016, A&A, 591, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Mizuno, A., Hayakawa, T., Tachihara, K., et al. 1999, PASJ, 51, 859 [NASA ADS] [CrossRef] [Google Scholar]
  52. Neronov, A., Semikoz, D. V., & Taylor, A. M. 2012, Phys. Rev. Lett., 108, 051105 [Google Scholar]
  53. Neronov, A., Malyshev, D., & Semikoz, D. V. 2017, A&A, 606, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Nieten, C., Neininger, N., Guélin, M., et al. 2006, A&A, 453, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Paladini, R., Montier, L., Giard, M., et al. 2007, A&A, 465, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Peng, F.-K., Wang, X.-Y., Liu, R.-Y., Tang, Q.-W., & Wang, J.-F. 2016, ApJ, 821, L20 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pfrommer, C., Pakmor, R., Simpson, C. M., & Springel, V. 2017, ApJ, 847, L13 [NASA ADS] [CrossRef] [Google Scholar]
  58. Pokhrel, R., Gutermuth, R., Ali, B., et al. 2016, MNRAS, 461, 22 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  59. Remy, Q., Grenier, I. A., Marshall, D. J., & Casandjian, J. M. 2018, A&A, 611, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Shen, Z.-Q., Liang, Y.-F., Duan, K.-K., et al. 2018, ArXiv e-prints [arXiv:1801.06075] [Google Scholar]
  61. Stanimirovic, S., Staveley-Smith, L., Dickey, J. M., Sault, R. J., & Snowden, S. L. 1999, MNRAS, 302, 417 [NASA ADS] [CrossRef] [Google Scholar]
  62. Staveley-Smith, L., Kim, S., Calabretta, M. R., Haynes, R. F., & Kesteven, M. J. 2003, MNRAS, 339, 87 [NASA ADS] [CrossRef] [Google Scholar]
  63. Strong, A. W., Porter, T. A., Digel, S. W., et al. 2010, ApJ, 722, L58 [NASA ADS] [CrossRef] [Google Scholar]
  64. Tang, Q.-W., Wang, X.-Y., & Tam, P.-H. T. 2014, ApJ, 794, 26 [NASA ADS] [CrossRef] [Google Scholar]
  65. Vázquez-Semadeni, E., Banerjee, R., Gómez, G. C., et al. 2011, MNRAS, 414, 2511 [NASA ADS] [CrossRef] [Google Scholar]
  66. VERITAS Collaboration (Acciari, V. A., et al.) 2009, Nature, 462, 770 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  67. Vladimirov, A. E., Digel, S. W., Jóhannesson, G., et al. 2011, Comput. Phys. Commun., 182, 1156 [NASA ADS] [CrossRef] [Google Scholar]
  68. Wang, X., & Fields, B. D. 2018, MNRAS, 474, 4073 [NASA ADS] [CrossRef] [Google Scholar]
  69. Wilke, K., Klaas, U., Lemke, D., et al. 2004, A&A, 414, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Wu, J., Evans, N. J., II, Gao, Y., et al. 2005, ApJ, 635, L173 [NASA ADS] [CrossRef] [Google Scholar]
  71. Yang, R.-z., & Aharonian, F. 2017, A&A, 600, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Yang, R.-z., de Oña Wilhelmi, E., & Aharonian, F. 2014, A&A, 566, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Yang, R.-z., de Oña Wilhelmi, E., & Aharonian, F. 2018, A&A, 611, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Basic information on Galactic molecular clouds.

In the text
Table 2

Parameters and gamma-ray fluxes of Galactic molecular clouds.

In the text
Table 3

Change in gamma-ray flux of the first three molecular clouds for different background models.

In the text
Table 4

Parameters and gamma-ray luminosities of star-forming galaxies.

In the text
Table 5

Results of the two-parameter correlation for L1−500 GeV and SFR in our sample.

In the text
Table 6

Results of the two-parameter correlation for L1−500 GeV and M in our sample.

In the text
Table 7

Results of the three-parameter correlation for L1−500 GeV, SFR, and M in our sample.

In the text
Table 8

Results of the three-parameter correlation for L0.1−100 GeV, SFR, and M in our sample.

In the text

All Figures

thumbnail Fig. 1

Relation between gamma-ray emissivity (left panel: 0.1–100 GeV; right panel: 1–500 GeV) and SFR per unit mass for molecular clouds and star-forming galaxies. The best-fit lines together with their 1σ dispersion regions are shown with solid and dashed lines, respectively.
In the text
thumbnail Fig. 2

Two-parameter correlation between L1−500 GeV and total gas mass (left panel) and dense gas mass (right panel) for molecular clouds. The best-fit lines together with their 1σ dispersion regions are shown with solid and dashed lines, respectively.
In the text
thumbnail Fig. 3

Three-parameter correlation among L1−500 GeV, SFR, and M for molecular clouds (left panel) and star-forming galaxies (right panel). The best-fit lines together with their 1σ dispersion regions are shown with solid and dashed lines, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.