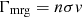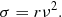| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201833485 | |
| Published online | 17 January 2019 | |
Letter to the Editor
The origin of the two populations of blue stragglers in M30
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
e-mail: spz@strw.leidenuniv.nl
Received:
23
May
2018
Accepted:
31
October
2018
We analyze the position of the two populations of blue stragglers in the globular cluster M30 in the Hertzsprung–Russell diagram. Both populations of blue stragglers are brighter than the cluster’s turn-off, but one population, the blue blue-stragglers, aligns along the zero-age main sequence whereas the other, red population is elevated in brightness (or color) by ∼0.75 mag. Based on stellar evolution and merger simulations we argue that the red population, which composes about 40% of the blue stragglers in M 30, has formed at a constant rate of ∼2.8 blue stragglers per gigayear over the last ∼10 Gyr. The blue population on the other hand formed in a burst that started ∼3.2 Gyr ago at a peak rate of 30 blue stragglers per gigayear with an e-folding time scale of 0.93 Gyr. We speculate that the burst resulted from the core collapse of the cluster at an age of about 9.8 Gyr, whereas the constantly formed population is the result of mass transfer and mergers through binary evolution. In this scenario, about half the binaries in the cluster effectively result in a blue straggler.
Key words: methods: numerical / blue stragglers / globular clusters: general / stars: evolution
© ESO 2019
1. Introduction
The blue stragglers (Sandage 1953) in M30 appear to be split into two distinct populations (Ferraro et al. 2009). Both populations are brighter than the current cluster turn-off point in the Hertzsprung–Russel diagram, but they can be distinguished from one another due to the fact that one population is positioned along the zero-age main sequence (which Ferraro et al. 2009 call the blue population) and the second, red population is brighter by about 0.75 mag. Both populations are centrally concentrated. The majority (90%) of the blue blue stragglers and all of the red blue stragglers are within the projected half-mass radius of the cluster. Ferraro et al. (2009) conclude that the blue population formed only 1–3 Gyr ago in a relatively short burst triggered by the core collapse of the cluster. The red population (60%) has been attributed to binary mass transfer (Xin et al. 2015), in which case it should be mainly composed of W UMa contact binaries (Jiang et al. 2017).
We test these hypotheses by conducting a series of stellar-merger simulations. We adopt the hypothesis that a blue straggler is the product of a merger between two stars that merge into a single star (with mass Mtot) at some moment in time tmrg. Such a merger can either result from a direct collision during the dynamical evolution of the star cluster or from an unstable phase of type A (Kippenhahn & Weigert 1967) mass transfer (Bailyn 1992; Knigge et al. 2009); we do not make a distinction in our models between these two scenarios, as both result in a single blue straggler.
The moment of merger is determined by finding a merger product that is consistent with the blue straggler’s position in the Hertzsprung–Russell diagram. From a theoretical perspective we determine the position of a blue straggler in the Hertzsprung–Russell diagram by evolving two stars to a certain age tmrg, perform the merger calculation, and continue to evolve the merger product for the remaining age of the cluster (13 Gyr according to Harris 1996). As we explain in the following section, the position of a blue straggler in the Hertzsprung–Russell diagram is sensitive to the total mass of the merger product as well as to the moment of the merger, but rather insensitive to the individual masses of the two stars at birth.
2. The experimental setup
We adopted the MESA Henyey stellar-evolution code (Paxton et al. 2011) to model the evolution of the stars with [Fe/H] = −2.33 (which according to their Table 1 is consistent with the cluster’s metallicity; Carretta et al. 2009). Both stars are initialized at the zero-age main sequence and evolved to tmrg. At that moment we merge the two stars using Make-Me-A-Massive-star (Gaburov et al. 2008), which uses the Archimedes’ principle to calculate the structure of the star resulting from a merger between two stars. After this we continue to evolve the merger product using MESA to the age of the cluster M30.
The numerical setup is realized with the Astronomical Multipurpose Software Environment (AMUSE, Portegies Zwart et al. 2013, 2018; Pelupessy et al. 2013). Our analysis is comparable to the method described in Lombardi et al. (2002), but then our procedure is completely automated. We tentatively limit ourselves to head-on collisions, such a described in Sills et al. (1997) because, apart from some additional mass loss, off-center collisions do not seem to result in qualitative differences in the merger product (Sills et al. 2001, see also Chapter 5.3.3 of Portegies Zwart & McMillan 2018).
We initialize a grid of primary masses between 0.5 M⊙ and the turn-off mass of 0.85 M⊙ in steps of 0.05 M⊙ and secondary masses between 0.2 M⊙ and the same upper limit in steps of 0.005 M⊙. The merger time is chosen between 0.1 Gyr and the age of the cluster with steps of 0.98 Gyr. The evolutionary state of the merger product at any time after the collision is predominantly determined by the total mass of the merger product Mtot. Small variations in the mass lost during the collision therefore have little effect on our determination of the merger time, because the location in the Hertzsprung–Russell diagram then depends on the total mass of the merger product and the moment of collision, rather than on the masses of the two stars that participate in the merger.
In Appendix A we present the AMUSE script to reproduce the calculations in this paper.
3. Results
The Hertzsprung–Russell diagram of the blue stragglers is presented in Fig. 1. Overplotted in color is the total mass of the merger products that remain on the main sequence until an age of 13 Gyr.
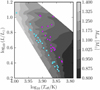 |
Fig. 1. Hertzsprung–Russell diagram of the M30 blue stragglers. The original data from Ferraro et al. (2015) were convoluted to the temperature-luminosity plane. With effective temperature and luminosity from Ferraro et al. (2009). The blue and red blue stragglers are indicated as such. |
Information about the masses of the two stars is largely lost in the merger process, and cannot be used for diagnostics (see also Lombardi et al. 2002). We, therefore, use the total blue straggler mass and the merger time as a diagnostic tool.
In Fig. 2 we present the same data as in Fig. 1, but with the time since collision overplotted in color. The lightest shades indicate the most recent mergers. The blue blue stragglers tend to cluster around a time since collision between 1 and 3 Gyr ago (in light green), whereas the red blue stragglers span a much wider range of merger times. We quantify this statement in Fig. 3, where we present the cumulative distribution of merger times for the blue and red blue stragglers together (colors) and separately (solid curves).
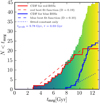 |
Fig. 3. Cumulative distribution of merger times (tmrg) for all the blue stragglers (blue plus red as the color-shaded area where the color corresponds to that in Fig. 2). The solid blue and solid red curves give the cumulative distribution for the blue and red blue stragglers, respectively. The dashed and dotted blue curves give the fit to the blue blue stragglers (the dotted curve gives the linear component and dashes give the sum of the exponential and the linear fits). The red dashed curve gives the linear fit to the red blue stragglers. The color coding is identical to that used in Fig. 2, here indicating the time since the merger occurred. |
We fitted both distributions with a constant blue straggler formation rate combined with a burst and exponential decay. The best fits are obtained using the Nelder–Mead simplex optimization (Nelder & Mead 1965) to find the minimum Kolmogorov–Smirnov (KS) statistic over the free parameters tmrg, and e-folding timescale τ, in combination with a line describing the constant formation rate.
The best fit (with KS statistics D = 0.10, p = 0.24) to the blue blue stragglers is obtained for tmrg = 9.8 Gyr and τ = 0.93 Gyr with a peak formation rate of 30 blue stragglers per gigayear and an additional constant formation rate of 1.8 ± 0.6 Gyr−1.
Fitting the red blue straggler formation rate with the same set of functions (a constant rate plus a power law) did not result in a satisfactory fit, but a single linear formation rate did produce the KS statistic of D = 0.19 (p = 0.23) with a constant formation rate of only 2.8 ± 0.5 Gyr−1 between an age of 3 Gyr and 10 Gyr. It is interesting to note that the formation rate for the red population levels off when the blue population reaches its maximum rate.
4. Interpretation
The majority of the blue stragglers in star clusters are thought to originate from either stellar collisions (Leonard 1989) or from mass transfer in a close binary system (Collier & Jenkins 1984). We would argue here that the two distinct populations found in M30 can be attributed to these different formation channels (see also Ferraro et al. 2009). We argue that the red population is consistent with being formed continuously and through mass transfer and mergers in binary systems, whereas the blue population is mainly the result of collisions during the core collapse of the star cluster. In that perspective, we attribute the burst population to the collision scenario, whereas the continuously formed population is the result of binary evolution.
4.1. The burst population of blue stragglers
According to our analysis about one third (15) of the blue stragglers in M30 are formed in a rather short burst that started at 9.8 Gyr with power-law decay with a characteristic timescale of 0.9 Gyr. At the peak the blue stragglers in the burst formed at a rate of about 30 blue stragglers per gigayear. Due to the exponential however we conclude that (and satisfactorily fitted) this burst lasts only a short while, long enough to produce some 20 blue stragglers.
We estimate the expected formation rate through stellar mergers during core collapse. This is realized by calculating the collision rate:
where n is the stellar number density, v the velocity dispersion, and the approximate gravitational-focused cross-section σ is
Here ν ≡ v/v∞ is the stellar velocity dispersion as a fraction of the stellar escape speed (Binney & Tremaine 1987).
Davies et al. (2004) derived a formation rate of blue stragglers for a star cluster through direct stellar collisions using the above arguments. We can adopt their Eq. 4 to calculate the expected number of blue stragglers formed through collisions. By adopting the current observed cluster parameters (n ≃ 3.8 × 105 pc−3, N = 1.6 × 105 stars, rcore ≃ 0.2 pc and adopting a mean stellar mass of 0.5 M⊙ from Harris 1996) we arrive at the current average blue-straggler production-rate through collisions of 20 Gyr−1.
4.2. The continuously formed blue stragglers
Mass transfer in binary systems are less likely to depend strongly on the cluster core density because binaries are present in the halo as well as in the cluster center, which causes them to be more homogeneously distributed across the cluster (Hut et al. 1992), whereas direct stellar collisions are predominantly occurring at the very center of the cluster (Portegies Zwart et al. 1997a). The binary merger rate is also not expected to be particularly affected by the cluster density profile. We therefore argue that the constant rate is a result of binary mass transfer and coalescence.
We can constrain the underlying binary semi-major axis distribution and mass ratio distribution that produces a constant blue straggler formation rate (or a constant rate of binaries that engage in a phase of mass transfer). Mass transfer in a binary system is typically initiated by the primary star, which overfills its Roche lobe when it either ascends the giant branch or, for very tight binaries, along the main sequence. Since the timescale between the terminal-age main sequence and the post-AGB phase is only a small fraction (≲0.15) of the main-sequence lifetime, we adopt the main-sequence lifetime as the limiting factor between zero age and the start of Roche-lobe overflow.
The lifetime of a main-sequence star scales as tms ∝ m2.5 (Spitzer 1962). A primary mass distribution of f(m)∝m−2.35 (Salpeter 1955) then produces a roughly constant rate at which stars leave the main sequence, consistent with the observed constant rate of blue-straggler formation.
M30 has a binary fraction of about 3% (Romani et al. 1991; Milone et al. 2012), so with 1.6 × 105 stars the cluster has 4800 binaries. A standard Salpeter mass function has about 5.8% of the stars between 0.5 M⊙ and ∼0.85 M⊙. A 0.5 M⊙ star requires an equal mass secondary star to evolve into a blue straggler in an unstable phase of mass transfer, whereas a 0.85 M⊙ star only requires a companion with a mass of ≳0.1 M⊙ (Portegies Zwart et al. 1997a). On average about half the binaries in the appropriate mass range then produce blue stragglers, totalling a potential number of 280. Because the mass-ratio distribution in cluster binaries tends to be flat (Kouwenhoven et al. 2007), roughly half of these binaries have a total mass that upon a merger results in a blue straggler. The binaries with small mass ratios do not form blue stragglers directly upon merger because the total mass of the merger product does not exceed the turn-off mass, but these stars pop up later when their rejuvenation causes them to stay behind in their evolution (Portegies Zwart et al. 1997b). The orbital separations of primordial binaries range from a few R⊙ to a maximum of ∼104 AU at the Heggie (1975) limit for hard-soft binaries. Roche-lobe overflow on the main sequence is most favorable for the formation of blue stragglers. This process is effective for binaries with an orbital separation of ≲10 R⊙. With a flat distribution in the logarithm of the semi-major axis (Zinnecker et al. 2004; Kouwenhoven et al. 2007), only about one in four binaries will effectively produce a blue straggler (Chen & Han 2009). The entire binary reservoir then produces ∼35 blue stragglers through mass transfer or coalescence.
5. Discussion
The 13 Gyr-old globular cluster M30 has a rich population of blue stragglers, which appear to be distributed bimodally in the Hertzsprung–Russell diagram (Ferraro et al. 2009). We tested the hypothesis that all these blue stragglers are the result of a merger due to an unstable phase of mass transfer in a binary system or a stellar collision. We simulate the current population of blue stragglers that could have resulted from the coalescence of two stars at some time tmrg with a total mass of mtot. The stellar merger product was subsequently evolved to the current age of the cluster of 13 Gyr. For each point in the Hertzsprung–Russell diagram we then obtain a unique solution for the mass of the blue straggler and the moment of merger tmrg. The two masses of the stars that merge are not well discriminated in the results because the memory of the two stellar masses is lost in the merger process due to the mixing in the merger process (Benz & Hills 1987; Glebbeek et al. 2013, and much more recent literature).
The merger time distribution for the blue blue stragglers is best described by a peak of formation of approximately 30 Gyr−1 at tmrg ≃ 9.8 Gyr and an e-folding timescale of 0.93 Gyr superposed with an additional constant formation rate of 1.8 Gyr−1 between tmrg ≃ 8 Gyr and the age of the cluster. This is consistent with the conclusions by Ferraro et al. (2009) that these blue stragglers were born in a burst during the core-collapse phase of the cluster some 2–3 Gyr ago. The population of red blue stragglers is best described with a constant formation rate of 2.8 Gyr−1 between an age of tmrg ≃ 3 and 11 Gyr (between 11 and 2 Gyr ago).
About 10% of the total number of blue and red blue stragglers appear to be missed in the observational data. We interpret this bimodality of blue stragglers with two distinct channels through which they form, much in the same way as Ferraro et al. (2009) argued based on the observations. The continuously formed population is consistent with originating from mass transfer in primordial binaries. In this scenario, about 10–15% (∼35/280) of all the binaries in M30 lead to the formation of a blue straggler at a constant rate. The burst, with an exponential decay, in the formation of blue stragglers is the result of direct stellar mergers during the core collapse of the star cluster.
We attribute the start of the blue-straggler formation burst to the moment of core collapse in the star cluster, at an age of ∼9.8 Gyr. This is consistent with the inverse cluster-evolution analysis by Pijloo et al. (2015, for details of the analysis, but the results adopted here were presented at the IAU conference in 2015), which leads to a core collapse at 9.5 ± 0.4 Gyr and which is consistent with the start of the blue-straggler formation burst.
We conclude that the core collapse of the cluster was associated with a burst in the formation of blue stragglers. The exponential decay is a result of the relatively extended period during which the cluster remains in a collapsed – or post-collapsed – state following the primary collapse (Heggie & Ramamani 1989). This could indicate a prolonged period of gravothermal oscillations following the primary collapse of the cluster core (Heggie et al. 1994). We argue that the post-collapse phase lasted for about 1 Gyr. The current cluster has a relatively low density consistent with the late stages of post-collapse (Bettwieser & Sugimoto 1984).
Acknowledgments
It is a great pleasure to thank Alex Rimoldi for the preliminary analysis and making the figures for this paper and Tjibaria Pijloo for reconstructing the cluster’s moment of core collapse. This work was in part done at the Canadian Institute for Theoretical Astronomy and I am grateful for their support, in particular to Norm Murray who made this possible. In this work we use the matplotlib (Hunter 2007), numpy (Oliphant 2006) and amuse (Portegies Zwart & McMillan 2018) packages.
References
- Bailyn, C. D. 1992, ApJ, 392, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., & Hills, J. G. 1987, ApJ, 323, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Bettwieser, E., & Sugimoto, D. 1984, MNRAS, 208, 493 [NASA ADS] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton NJ: Princeton University Press), 747 [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S. 2009, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, X., & Han, Z. 2009, MNRAS, 395, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Collier, A. C., & Jenkins, C. R. 1984, MNRAS, 211, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, M. B., Piotto, G., & de Angeli, F. 2004, MNRAS, 349, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Beccari, G., Dalessandro, E., et al. 2009, Nature, 462, 1028 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ferraro, F. R., Lanzoni, B., Dalessandro, E., Mucciarelli, A., & Lovisi, L. 2015, in Blue Straggler Stars in Globular Clusters: A Powerful Tool to Probe the Internal Dynamical Evolution of Stellar Systems, eds. H. M. J. Boffin, G. Carraro, & G. Beccari (Berlin, Heidelberg: Springer), 99 [Google Scholar]
- Gaburov, E., Lombardi, J. C., & Portegies Zwart, S. 2008, MNRAS, 383, L5 [NASA ADS] [Google Scholar]
- Glebbeek, E., Gaburov, E., Portegies Zwart, S., & Pols, O. R. 2013, MNRAS, 434, 3497 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, VizieR Online Data Catalog: VII/195 [Google Scholar]
- Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C., & Ramamani, N. 1989, MNRAS, 237, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C., Inagaki, S., & McMillan, S. L. W. 1994, MNRAS, 271, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P., McMillan, S., & Romani, R. W. 1992, ApJ, 389, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, D., Chen, X., Li, L., & Han, Z. 2017, ApJ, 849, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1967, Z. Astrophys., 65, 251 [NASA ADS] [Google Scholar]
- Knigge, C., Leigh, N., & Sills, A. 2009, Nature, 457, 288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leonard, P. J. T. 1989, AJ, 98, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, J., & Sawyer Warren, J. 2014, Astrophysics Source Code Library, [record ascl:1412.010] [Google Scholar]
- Lombardi, Jr., J. C., Warren, J. S., Rasio, F. A., Sills, A., & Warren, A. R. 2002, ApJ, 568, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, A&A, 540, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelder, J., & Mead, R. 1965, The Computer Journal, 7, 4 [Google Scholar]
- Oliphant, T. E. 2006, A Guide to NumPy (Trelgol Publishing USA), 1 [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2010, Astrophysics Source Code Library, [record ascl:1010.083] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Pelupessy, F. I., van Elteren, A., de Vries, N., et al. 2013, A&A, 557, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pijloo, J. T., Portegies Zwart, S. F., Alexander, P. E. R., et al. 2015, MNRAS, 453, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S., & McMillan, S. 2018, Astrophysical Recipes: the Art of AMUSE, (Institute of Physics Publishing) [Google Scholar]
- Portegies Zwart, S. F., Hut, P., & Verbunt, F. 1997a, A&A, 328, 130 [NASA ADS] [Google Scholar]
- Portegies Zwart, S. F., Hut, P., McMillan, S. L. W., & Verbunt, F. 1997b, A&A, 328, 143 [NASA ADS] [Google Scholar]
- Portegies Zwart, S., McMillan, S. L. W., van Elteren, E., Pelupessy, I., & de Vries, N. 2013, Comput. Phys. Commun., 183, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S., van Elteren, A., Pelupessy, I., et al. 2018, AMUSE: the Astrophysical Multipurpose Software Environment [CrossRef] [Google Scholar]
- Romani, R. W., & Weinberg, M. D. 1991, in The Formation and Evolution of Star Clusters, eds. K. Janes, ASP Conf. Ser., 13, 443 [NASA ADS] [Google Scholar]
- Sandage, A. R. 1953, AJ, 58, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sills, A., Lombardi, Jr., J. C., Bailyn, C. D., et al. 1997, ApJ, 487, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Sills, A., Faber, J. A., Lombardi, Jr., J. C., Rasio, F. A., & Warren, A. R. 2001, ApJ, 548, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1962, Physics of Fully Ionized Gases (North Chelmsford, MA: Courier Corporation) [Google Scholar]
- Xin, Y., Ferraro, F. R., Lu, P., et al. 2015, ApJ, 801, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., Köhler, R., & Jahreiß, H. 2004, in Rev. Mex. Astron. Astrophys. Conf. Ser., eds. C. Allen, & C. Scarfe, 21, 33 [NASA ADS] [Google Scholar]
Appendix A: Minimal AMUSE script for the runs
In the listing (Script A.1) we present an AMUSE (Portegies Zwart & McMillan 2018; Portegies Zwart et al. 2018) script to calculate the evolution of two stars that undergo a merger, and that continue to evolve to some late time. This script is tuned for M30 to limit the number of input parameters. The script starts by initializing the MESA stellar-evolution code (Paxton et al. 2010, 2011), and then declares the two stars and submits them to the stellar evolution code. In the subsequent block of lines, the stars are evolved to an age of 9 Gyr, and the resulting stellar models are merged using MakeMeAMassiveStar (Gaburov et al. 2008; Lombardi & Sawyer Warren 2014). In the last block of lines, the merger product is submitted again to the stellar-evolution code and is allowed to evolve to an age of 13 Gyr. For a more thorough explanation of the script we refer to Chapter 4 (List. 4.7) of the AMUSE book (Portegies Zwart & McMillan 2018) or amusecode.org for the complete source.
import numpy
from amuse.lab import *
def merge_stars(Mprim=0.8|units.MSun,
Msec=0.6|units.MSun,
t_coll=11|units.Gyr):
code = MESA()
p = Particles(mass=Mprim)
primary = code.particles.add_particle(p)
s = Particles(mass=Msec)
secondary = code.particles.add_particle(s)
code.evolve_model(t_coll)
stars = code.particles
print "Pre merger:\n", stars
n_zones = stars.get_number_of_zones()
code.merge_colliding(primary.copy(),
secondary.copy(),
MakeMeAMassiveStar,
dict(),
dict(target_n_shells_mixing=max(n_zones)),
return_merge_products=["se"])
code.evolve_model(13|units.Gyr)
print "Post merger stellar parameters:",\
"T=", stars.temperature,\
"L=", stars.luminosity.in_(units.LSun)
code.stop()
All Figures
 |
Fig. 1. Hertzsprung–Russell diagram of the M30 blue stragglers. The original data from Ferraro et al. (2015) were convoluted to the temperature-luminosity plane. With effective temperature and luminosity from Ferraro et al. (2009). The blue and red blue stragglers are indicated as such. |
| In the text | |
 |
Fig. 2. As in Fig. 1, but for the time since collision, which is color-coded here. |
| In the text | |
 |
Fig. 3. Cumulative distribution of merger times (tmrg) for all the blue stragglers (blue plus red as the color-shaded area where the color corresponds to that in Fig. 2). The solid blue and solid red curves give the cumulative distribution for the blue and red blue stragglers, respectively. The dashed and dotted blue curves give the fit to the blue blue stragglers (the dotted curve gives the linear component and dashes give the sum of the exponential and the linear fits). The red dashed curve gives the linear fit to the red blue stragglers. The color coding is identical to that used in Fig. 2, here indicating the time since the merger occurred. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.