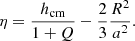| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833780 | |
| Published online | 30 November 2018 | |
Understanding the orbital periods of CEMP-s stars
1
Argelander-Institut für Astronomie der Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail cabate@uni-bonn.de
2
Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
Received:
5
July
2018
Accepted:
26
September
2018
The chemical enrichments detected in carbon- and s-element-enhanced metal-poor (CEMP-s) stars are believed to be the consequence of a past episode of mass transfer from a now extinct asymptotic-giant-branch primary star. This hypothesis is borne out by the evidence that most CEMP-s stars exhibit radial-velocity variations suggesting that they belong to binary systems in which the companion is not directly visible. We used the orbital-period distribution of an unbiased sample of observed CEMP-s stars to investigate the constraints it imposes on our models of binary evolution and on the properties of the metal-poor binary population in the Galactic halo. We generated synthetic populations of metal-poor binary stars using different assumptions about the initial period distribution and about the physics of the mass-transfer process, and we compared the predicted period distributions of our synthetic CEMP-s stars with the observed one. With a set of default assumptions often made in binary population-synthesis studies, the observed period distribution cannot be reproduced. The percentage of observed CEMP-s systems with periods shorter than about 2000 days is underestimated by almost a factor of three, and by about a factor of two between 3000 and 10 000 days. Conversely, about 40% of the simulated systems have periods longer than 104 days, which is approximately the longest measured period among CEMP-s stars. Variations in the assumed stability criterion for Roche-lobe overflow and the efficiency of wind mass transfer do not alter the period distribution enough to overcome this discrepancy. To reconcile the results of the models with the orbital properties of observed CEMP-s stars, one or both of the following conditions are necessary: (i) the specific angular momentum carried away by the material that escapes the binary system is approximately two to five times higher than currently predicted by analytical models and hydrodynamical simulations of wind mass transfer, and (ii) the initial period distribution of very metal-poor binary stars is significantly different from that observed in the solar vicinity and weighted towards periods shorter than about ten thousand days. Our simulations show that some, perhaps all, of the observed CEMP-s stars with apparently constant radial velocity could be undetected binaries with periods longer than 104 days, but the same simulations also predict that twenty to thirty percent of detectable binaries should have periods above this threshold, much more than are currently observed.
Key words: stars: chemically peculiar / stars: Population II / Galaxy: halo / binaries: general / stars: winds, outflows / stars: kinematics and dynamics
© ESO 2018
1. Introduction
A significant proportion of the low-metallicity stars observed in the Galactic halo are found to have abundances of carbon relative to iron more than ten times larger than in the Sun, that is1 [C/Fe] > 1.0. These so-called carbon-enhanced metal-poor (CEMP) stars are a significant fraction of the metal-poor population of the halo and their proportion increases with decreasing metallicity, making up more than 20% of all metal-poor stars at [Fe/H] < −3 (e.g. Cohen et al. 2005; Frebel et al. 2006; Lucatello et al. 2006; Carollo et al. 2012; Lee et al. 2013; Yong et al. 2013; Placco et al. 2014). At [Fe/H] > −3.5 the majority of these carbon-rich stars also have strong enhancements in the element barium, which is predominantly produced by the slow neutron-capture process. These objects are therefore classified as CEMP-s stars. The main site of nucleosynthesis of s-elements is the intershell region of thermally-pulsing asymptotic giant branch (TP-AGB) stars (e.g. Gallino et al. 1998; Busso et al. 1999; Herwig 2005; Romano et al. 2010; Prantzos et al. 2018). However, the luminosities and surface gravities of observed CEMP-s stars prove that most of these objects, if not all, have not yet reached the AGB phase. On the other hand, the majority of CEMP-s stars are found in binary systems (Aoki et al. 2007; Hansen et al. 2016), suggesting that the origin of the chemical enrichment is mass transfer from a binary companion that was once a TP-AGB star.
Insight into the nature of the mass-transfer mechanism can be gained from the study of the orbital properties of these systems. However, information on orbital periods is hard to come by, particularly for long-period systems for which an accurate orbital solution cannot be achieved without observations spanning many years. Lucatello et al. (2005) were the first to suggest that all CEMP-s stars are members of binary systems, based on a sample of 19 stars with radial-velocity variations. They were able to calculate orbital solutions for ten of these systems. With the exception of HE 0024–2523, which has a very short period of just 3.41 days, all the systems have periods between a few hundred and a few thousand days. With this same data, and additional radial-velocity data from many sources, Starkenburg et al. (2014) perform a maximum-likelihood analysis and concluded that the binary fraction of the CEMP-s stars is consistent with unity. They also place a maximum period of around 104 days on such systems, with an average period of around 500 days. In addition, they show that CH stars (the higher metallicity analogues of the CEMP-s stars) have a similar, if not tighter, period distribution.
In their analysis of 13 low-metallicity carbon stars, Jorissen et al. (2016) provide orbital solutions for an additional four CEMP-s stars, finding periods of 400–3000 days in line with those determined for previous systems. They also note the similarity of the period range occupied by the CH and CEMP-s stars, and in addition point out that the two groups have a similar distribution in period-eccentricity space. Similar orbital properties and a binary fraction consistent with 100% have been determined for barium stars, a class of G and K barium-rich giants at solar metallicity, which are believed to form by the same mass-transfer mechanism as CH and CEMP-s stars (e.g. Boffin & Jorissen 1988; McClure & Woodsworth 1990; Jorissen et al. 1998; Van der Swaelmen et al. 2017).
Hansen et al. (2016) build a sample of 22 CEMP-s stars, selected only based on their enhanced abundances of carbon and barium, and they monitored the radial velocities of these systems monthly over a period of about 3000 days. They determine 17 orbits independently of other work, adding twelve CEMP-s stars to the set of those with known orbital parameters. Because this sample was chosen regardless of any previous detection of radial-velocity variations, it is not expected to be biased towards any period range and it should be representative of the orbital properties of the overall CEMP-s population. Hansen et al. (2016) find periods between 20 and 10 000 days for 17 out of 22 systems (shown as blue-filled circles in Fig. 1). Four stars are apparently single, while one further system exhibits clear radialvelocity variations but it was impossible to determine its orbit (the point at negative eccentricity in Fig. 1), indicating that the orbital period is probably very long.
 |
Fig. 1. Period-eccentricity diagram of the binary systems detected by Hansen et al. (2016, blue-filled circles) and of all other known binary CEMP-s stars in the literature (Suda et al. 2008, 2011; Jorissen et al. 2016, black crosses). |
Model predictions from binary population synthesis (Abate et al. 2015c) show that the observed fraction of CEMP stars among the very metal-poor stars of the SDSS/SEGUE survey can be reproduced at [Fe/H] ≲ −2.0, but only with the contribution of binaries in a wide range of initial periods, up to a few times 105 days. This also yields a wide distribution of current orbits, mostly in the range 103 up to almost 106 days (Izzard et al. 2009; Abate et al. 2013, 2015c). In particular, Abate et al. (2015c) demonstrated that the orbital-period distribution of the simulated binaries is shifted towards periods longer by a factor of ten (on average) compared to the observed distribution. Because the data available at the time was an inhomogeneous collection of orbital periods from the literature, the authors could not draw any definite conclusions from this comparison. Either the models should produce more CEMP stars in binary systems below a few thousand days, or, alternatively, the observed sample was biased towards short periods and most observed CEMP stars without an orbit determination should have periods longer than 104 days. The comparison with the unbiased sample of Hansen et al. (2016), which has periods in a range consistent with previous results, has the potential to provide tighter constraints on the simulations, in particular on the modelling of the mass-transfer process.
The nature of mass transfer in binary systems containing AGB stars is not well understood. Because mass transfer by Rochelobe overflow (RLOF) from stars with deep convective envelopes is in many cases unstable, it is likely an inefficient mechanism of mass transfer. Hence, systems with AGB donors have to be wide to avoid RLOF and the secondary stars accrete material from the AGB winds. Unfortunately, our understanding of wind mass transfer is rather uncertain. In situations where the wind speed is much faster than the orbital speed of the binary, the accretion can be described by the model of Bondi, Hoyle and Lyttelton (Hoyle & Lyttleton 1939; Bondi & Hoyle 1944), which results in low accretion efficiencies. However, AGB stars typically have slow winds of not more than around 15 km s−1 (Vassiliadis & Wood 1993), making the situation much more complex. Much effort has gone into modelling this type of mass transfer (e.g. Mohamed & Podsiadlowski 2007; de Val-Borro et al. 2009, 2017; Chen et al. 2017, 2018; Liu et al. 2017; Saladino et al. 2018), which has led to the discovery of a new mode of mass transfer, dubbed wind Rochelobe overflow (WRLOF, Mohamed & Podsiadlowski 2007). This mode relies on the fact that AGB winds require the formation of dust to efficiently accelerate their winds. If the dust formation radius lies sufficiently close to the Roche lobe, then the AGB wind moves very slowly and material can be efficiently transferred to the companion through the inner Lagrangian point, with perhaps up to half the ejected material being accreted (Mohamed & Podsiadlowski 2007; Abate et al. 2013).
Coupled with the issue of mass transfer and mass loss from binary systems is the issue of angular-momentum loss and transfer. While the latter is most important for the subsequent evolution of the secondary, angular-momentum loss from the system as a whole will alter the binary orbit. In the Jeans approximation of a spherically symmetric wind, the ejected material has the same specific angular momentum as the orbit of the wind-losing star and consequently the system widens in response to mass loss. However, in the case of a dense AGB outflow with velocity comparable to or lower than the orbital velocity of the binary the situation is certainly more complicated and both observations and hydrodynamical simulations show that the matter is not ejected isotropically (see e.g. Karovska et al. 2005 for the observations of Mira AB, the prototypical detached binary system with an AGB donor star, and de Val-Borro et al. 2009; Mohamed 2010; Liu et al. 2017 for the simulations). Jahanara et al. (2005) and, more recently, Chen et al. (2018) and Saladino et al. (2018) have performed hydrodynamical simulations to determine the amount of angular momentum carried by the ejected material for different binary separations and mass ratios and a variety of assumptions about the input physics, such as the wind acceleration mechanism, chemical composition of the outflowing gas and its cooling efficiency. However, because of the complexity of the problem, a reliable model of how the amount of angular momentum lost by the binary system depends on all these parameters has yet to be developed.
In this work we use our binary population-synthesis model to investigate how different assumptions about the accretion efficiency, angular-momentum loss, stability of Roche-lobe overflow and the initial binary-parameter distributions modify the period distributions of synthetic CEMP-s stars. In particular, we assume that the sample of CEMP-s stars observed by Hansen et al. (2016) is representative of the overall population and we use the period distribution determined from this sample as a case study to address the following questions:
-
What mechanism is responsible for mass transfer in binary systems and how efficient is it?
-
How much angular momentum is carried away by the material that leaves the binary system?
-
Is there a set of assumptions with which our binary-population-synthesis model reproduces the orbital-period distribution observed in CEMP-s stars?
2. Models
In this study we use the binary population synthesis code binary_c/nucsyn2 developed by Izzard et al. (2004, 2006, 2009, 2018). The starting point of our analysis is the default model set A of Abate et al. (2015c), of which we describe the basic properties, assumptions, and selection criteria in Sect. 2.1. We introduce several modifications in the input physics of this model set and we investigate their consequences for the orbital-period distribution of the synthetic CEMP-s population. These modifications are discussed in Sects. 2.2–2.5. Table 1 presents a list of all adopted model sets, together with the CEMP fractions they produce and a few numbers characterising their period distributions (which will be discussed in Sect. 3).
Input physics adopted in our calculated binary-population models and predicted fraction of CEMP stars.
2.1. Population-synthesis models
Following Abate et al. (2015c), in our simulated populations of binary stars the primary masses and separations (M1,i and ai) are logarithmically spaced over the intervals [0.5, 8.0] M⊙ and [5, 5 × 106] R⊙, respectively, while the secondary masses, M2,i, are linearly distributed in [0.1, 0.9] M⊙. Our grid resolution is N = NM1 × NM2 × Na, with NM1 = 100, NM2 = 32, Na = 80, giving a total grid of 256 000 systems. In most of our simulations we consider circular orbits, although ten observed CEMP-s stars have eccentricities greater than zero. The results of modelling eccentric systems are discussed in Sect. 4.4. The mass of the partial mixing zone, a parameter that determines the abundances of neutron-capture elements synthetised in the AGB phase (Karakas 2010; Lugaro et al. 2012; Abate et al. 2015a), is set to be equal to MPMZ = 2 × 10−3 M⊙, which is the default of Karakas (2010). This assumption has negligible effects on the total fraction of CEMP stars or the period distribution of synthetic CEMP stars. This is because the populations of simulated CEMP stars are dominated by binary systems with initial primary masses smaller than about 2 M⊙ (cf. Fig. 1 of Abate et al. 2015c), and the amount of s-elements produced at these low masses does not depend much on the mass of the partial-mixing zone (Lugaro et al. 2012; Abate et al. 2015c). The wind velocity and mass-loss rate on the AGB are computed according to the empirical relations determined by Vassiliadis & Wood (1993). Wind velocities vary between 5 and 15 km s−1, as in the paper of Abate et al. (2013), except in our model set M7 in which we adopt a maximum of 7.5 km s−1.
The primary masses in our populations are initially distributed according to the solar-neighbourhood initial mass function (IMF) proposed by Kroupa et al. (1993). In most of our models the distribution of initial mass ratios qi = M2,i/M1,i is flat in the interval [0, 1], and the separation distribution is flat in log ai. The total binary fraction, fbin, is assumed to be unity in the considered range of ai, [5, 5 × 106] R⊙. Following the approach of Moe & Di Stefano (2017), these assumptions translate into a constant binary fraction per decade of orbital period, d f /dlog P ≡ flog P = 0.11, because our separation distribution spans a range of 109 days in orbital periods and the sum over all log P-bins adds up to the total binary fraction, ΣP flog P = fbin. Alternative separation distributions are explored in Sect. 2.5.
As initial composition we adopt the solar abundance distribution of Asplund et al. (2009) scaled down to metallicity 10−4 (that is [Fe/H] ≈ −2.2). We assume that the transferred material is mixed throughout the accreting star (hereinafter, the accretor) to mimic the effect of non-convective mixing processes, such as thermohaline mixing, which is expected to be efficient in lowmass stars (Stancliffe et al. 2007; Stancliffe & Glebbeek 2008). Our assumption will overestimate the dilution effect of these non-convective processes (see e.g. Matrozis et al. 2017) but it has a small impact on the final properties of the CEMP population, partly because most of our synthetic CEMP stars have undergone first dredge-up, which efficiently mixes the accreted material anyway (Abate et al. 2015c).
We evolve our binary systems with these initial conditions and we select the stars that after ten billion years have not yet become white dwarfs. We determine which of these stars are visible with a criterion based on their luminosity following the method described by Abate et al. (2015c, Sect. 2.3) with V-magnitude limits at 6 and 16.5. According to the selection criteria of Hansen et al. (2016), we flag a star as CEMP-s when its carbon and barium surface abundances are [C/Fe] > 1 and [Ba/Fe] > 0.5, respectively.
2.2. Stability of Roche-lobe overflow
Roche-lobe overflow from AGB donors is believed to be generally unstable, except in some cases when the donor is less massive than its companion or the mass of the convective envelope is small compared to that of the core (Hjellming & Webbink 1987). This is because AGB stars expand in response to mass loss because of their large convective envelopes (Paczyński 1965), whereas the Roche-lobe radius shrinks in response to mass transfer when the donor is more massive than its companion (Paczyński 1965, 1971). Favourable conditions for stable RLOF are rarely met in the formation process of CEMP-s stars. Low-metallcitity AGB stars of initial masses above 0.9 M⊙ efficiently dredge up nuclear-processed material to the surface (Stancliffe 2009; Karakas 2010; Lugaro et al. 2012). By contrast, their binary companions need to be low in mass, M2,i ≤ 0.85 M⊙ (Abate et al. 2015c), otherwise after accreting a few hundredths of a solar mass of material they rapidly evolve and become white dwarfs before 10–12 Gyr, which is approximately the age of the Galactic-halo population. In that case they would not be observable today as CEMP-s stars. Consequently, the mass ratio in most potential progenitors of CEMP-s stars is M2/M1 < 1 during the whole evolution and therefore the RLOF is in most cases unstable. The binary system is then believed to evolve into a common-envelope phase (Paczyński 2011) during which there is no significant accretion of material on to the companion star (Ricker & Taam 2008).
Our binary population-synthesis model determines whether RLOF is stable by comparing the mass ratio between the donor and the accretor, Q = Mdon/Macc, with a critical value, Qcrit: if Q > Qcrit during RLOF, the systems undergo common-envelope evolution. When the donor star is a giant, Qcrit is calculated with Eq. (57) of Hurley et al. (2002, Sect. 2.6.1) and scales with the fifth power of the ratio between the core and total masses of the donor. When the RLOF process is unstable, we model the common-envelope evolution according to Eqs. (69)–(78) of Hurley et al. (2002, Sect. 2.7), in which we assume αCE = 1.0, λion = 0.0, and λCE is computed as in Eq. (A.1) of Claeys et al. (2014, Appendix A).
In recent years, the response of giant stars to mass loss has been investigated by several authors who have argued that stars with convective envelopes may expand less, and less rapidly, than previously derived with simplified models (e.g. Chen & Han 2008; Ge et al. 2010, 2015; Woods & Ivanova 2011; Passy et al. 2012a,b; Pavlovskii & Ivanova 2015). Chen & Han (2008, Tables 1 and 2) provide critical mass ratios for stable RLOF for different primary masses, stellar radii, and mass accretion efficiencies. These values are generally higher than the Qcrit implemented in our code, which implies that RLOF from AGB donors may be more stable than, for example, in the simulations of Abate et al. (2015c). Therefore, we use the results of Chen & Han (2008) to construct a table (R.G. Izzard, priv. comm.) which can be interpolated by our population-synthesis code to determine the stability of RLOF in binary systems with an alternative criterion to that of Hurley et al. (2002). Hereinafter we will refer to the former as the “CH08 criterion” of RLOF stability and to the latter as the “H02 criterion”. The CH08 criterion is adopted in most of our model sets (see Table 1).
As we discuss in Sect. 3.1, models with more stable RLOF from AGB donors predict a larger number of CEMP-s stars with orbital periods between a few hundred and a few thousand days. To test the maximum possible effect of increased RLOF stability on the period distribution of synthetic CEMP-s stars, in our model set M3 we impose that RLOF from AGB stars is always stable by setting an arbitrarily high Qcrit (namely, Qcrit = 106).
2.3. Accretion efficiency of wind mass transfer
Because of the above-mentioned constraints on the stability of the RLOF process, mass transfer from AGB donors and the consequent formation of CEMP-s stars is generally considered to occur by accretion of stellar winds. The efficiency of this process as a function of the masses of the two stars and of the orbital separation is not well understood. Population-synthesis studies often use the Bondi–Hoyle–Lyttleton model (Hoyle & Lyttleton 1939; Bondi & Hoyle 1944; Bondi 1952; Edgar 2004) to determine the accretion efficiency of wind mass transfer. This prescription is adopted in our model sets labelled with BHL in Table 1, which compute the wind accretion rate using Eq. (6) of Boffin & Jorissen (1988):
where G is the gravitational constant, υw and υorb are the wind and orbital velocities, respectively, e is the eccentricity, and BHL is a numerical constant between one and two (by default it is equal to 1.5 in our models).
The BHL model is appropriate under the assumption that the orbital velocity of the accretor is much smaller than the wind velocity. AGB winds do not usually fulfil this condition. Their detected velocities vary between approximately 3 and 30 km s−1 (e.g. Vassiliadis & Wood 1993; van Loon et al. 2005; Goldman et al. 2017), which are comparable to the orbital velocities of binary stars of total mass in the range 1−3 M⊙ and periods up to about 30 000 days. In wider systems AGB winds are typically faster than the orbital velocities of the donor stars.
Abate et al. (2013) use the results of detailed hydrodynamical calculations (Mohamed & Podsiadlowski 2007, 2012; Mohamed 2010) to develop a simplified model of wind Rochelobe overflow (WRLOF), a mode of mass transfer in which it is the slow and dense wind of the donor star, rather than the star itself, that fills the Roche lobe and is transferred on to the binary companion. We refer to Abate et al. (2013) for a complete description of their WRLOF model and here we summarise the basics. AGB winds are attributed to a combination of stellar pulsations, which create the conditions for dust condensation at some distance Rd from the surface of the AGB star, and radiation pressure on dust grains. These are accelerated beyond the escape velocity and, by dynamical collisions with the gas, transfer a net outward momentum to the wind particles (e.g. Freytag & Höfner 2008; Nowotny et al. 2010; Bladh & Höfner 2012; Bladh et al. 2015; Höfner 2015). If Rd is greater than or comparable to the Roche-lobe radius RRL of the donor, the AGB wind is slow inside the Roche lobe and is gravitationally focused through the inner Lagrangian point L1 and transferred with high efficiency to the secondary star. The dust-formation radius, Rd, is a function of the effective temperature of the star and of the condensation temperature of the dust (Höfner 2007). The latter depends on the chemical composition of the dust and it is assumed to be 1500 K and 1000 K for carbon- and oxygen-rich dust, respectively (Höfner 2009). Because the dust composition of low-metallicity AGB stars is complex and often very uncertain (e.g. Boyer et al. 2015a,b), in our model the condensation temperature, Tcond, is treated as a free parameter.
In their hydrodynamical calculations of WRLOF, Mohamed & Podsiadlowski (2007) originally adopt Tcond = 1000 K, which is also the value used by Abate et al. (2015c) to maximise the fraction of CEMP stars in their synthetic populations of metal-poor stars. Indeed, a low dust-condensation temperature implies that the range in which WRLOF takes place is shifted towards longer separations compared to the case of a higher Tcond, because dust forms further away from the star and hence Rd is larger. Consequently, the number of binary systems that undergo efficient wind mass transfer at long separations increases and so does the CEMP fraction3. However, a large proportion of these systems are formed at much longer periods than observed (Abate et al. 2015c). Following Abate et al. (2013), here we choose to assume Tcond = 1500 K because after about five thermal pulses our model AGB stars have C/O > 1 at the surface and hence the dust formed in their outflow is also likely carbon rich.
2.4. Angular-momentum-loss model
The variation in orbital angular momentum caused by mass loss in a binary system can be parameterised as
where Ωorb and a are the orbital angular velocity and separation of the binary, respectively, ˙Mdon and ˙Macc are the mass-loss and mass-accretion rates of the donor and the accretor, respectively, hence their difference is the total mass lost by the system per unit time, and η is a parameter identifying the specific angular momentum carried away by the expelled material per unit mass.
In our model sets M1–M5, M13 and M14, the variations of orbital angular momentum because of wind mass loss are computed according to the Jeans approximation of an isotropic, spherically-symmetric wind, as for example in Eq. (4) of Abate et al. (2013). This is a valid approximation in the case of fast winds, with velocities much larger than the orbital velocity of the binary. In this approach the specific angular momentum of the ejected material is
This mode of mass loss always results in expansion of the orbit.
In contrast with the isotropic-wind approximation, a variety of observations (e.g. Karovska et al. 1997, 2005, 2010; Castro-Carrizo et al. 2002) and hydrodynamical simulations (e.g. Theuns & Jorissen 1993; Nagae et al. 2004; Mohamed & Podsiadlowski 2007; Chen et al. 2017; de Val-Borro et al. 2017; Liu et al. 2017) show that the geometry of the wind lost in binary systems with AGB donor stars is in many cases not spherical, but focussed into the orbital plane. As a consequence, the angular momentum carried away by the ejected material may be larger than predicted by the Jeans mode. This in turn can cause the binary orbit to shrink rather than expand (Chen et al. 2018; Saladino et al. 2018). Taking into account such enhanced angular-momentum loss may therefore help to explain the short orbital periods of CEMP-s binaries and related systems. For example, Izzard et al. (2010) find that the observed period-eccentricity distribution of barium stars, which are often considered the solar-metallicity analogues of CEMP-s stars, can be reproduced if the ejected material carries away at least two times the average specific orbital angular momentum of the binary system. Abate et al. (2015a) reach a similar conclusion in their effort to simultaneously model the chemical composition and the orbital period of 15 observed CEMP-s stars.
By including the formalism of Izzard et al. (2010, Eq. (2)) into our Eq. (2), we obtain the following
from which follows the relation η = γ Q (1 + Q)−2. Izzard et al. (2010) and Abate et al. (2015a) adopt γ = 2. In this work, we test different values of the constant γ, namely γ = 2, 3, and 6, to qualitatively investigate how strong the angular-momentum loss has to be in order to reproduce the period distribution of CEMP-s stars4.
The choice of a constant γ in Eq. (4) implies that the specific angular momentum of the ejected material does not depend on the orbital period of the system. Hence, a binary system so wide that the gravitational influence of the companion star on the wind of the donor is negligible loses the same amount of angular momentum as a close binary, if the total ejected mass in the two cases is the same. A step towards a more physical description of the process is to include a dependence of γ on the orbital properties of the binary system. For this purpose we use the results of the hydrodynamical simulations of Jahanara et al. (2005), Chen et al. (2018) and Saladino et al. (2018), in which the angular-momentum loss rates from binaries interacting via stellar winds are computed explicitly. Chen et al. (2018) and Saladino et al. (2018) present simulations of low-mass binaries interacting via the winds of their AGB donor stars. Despite the different assumptions made in these studies, the specific orbital angular momentum of matter lost from the system in both studies is very similar when it is expressed as a function of the ratio of the terminal wind velocity and the orbital velocity, υw/υorb (see Saladino et al. 2018). Jahanara et al. (2005) present more generic simulations of wind mass transfer, of which those labelled as “radiatively driven” are the most applicable to AGB winds. They also find that the specific angular momentum of the ejected matter depends on the ratio of the wind velocity and the orbital velocity.
Saladino et al. (2018) find that the results of all three sets of simulations can be represented fairly well by a simple relation,
where υw and υorb are the wind and orbital velocities, respectively, and ηiso is the specific angular momentum for isotropic mass loss given by Eq. (3). The second term in Eq. (5) gives ηhydro a dependence on the separation through υorb. In binary systems with very long orbital periods the ratio υw/υorb is large, consequently the first term of Eq. (5) dominates and the angular momentum lost by the system is the same as in the isotropicwind model. By contrast, for shorter orbital separations the ratio υw/υorb decreases (because υw is constant while υorb increases) and consequently the contribution of the second term in Eq. (5) becomes stronger.
Alternatively, we can use the results of Brookshaw & Tavani (1993) who studied the angular-momentum loss from binary systems in which the wind is modelled by ballistic calculations of test particles. These calculations ignore the effects caused by gas pressure and radiative acceleration. This is permissible for fast winds, but it is a poor representation of slow and dense AGB winds. Because both these phenomena will tend to make the outflow more isotropic, the results of this ballistic study can be taken to give an upper limit to the amount of angular momentum lost by a stellar wind. We fit the results of Brookshaw & Tavani (1993) as a function of the mass ratio and υw/υorb (see Appendix A), similarly to Eq. (5):
With Eq. (6) wide binary systems evolve as for an isotropic outflow, whereas in closer binaries the angular momentum lost is significantly higher. The transition between these two regimes is considerably steeper than in Eq. (5), as shown by Fig. 2, in which we plot the specific angular momentum of the ejected material for different models and mass ratios (Q = 1.05 and 2 in the left and right panels, respectively) as a function of the orbital period in binary systems with primary mass Mdon = 0.9 M⊙. Figure 2 also shows that in the models with constant γ and with an isotopic wind, η does not depend on the orbital period and consequently the variations of angular momentum are only determined by the total mass that is lost by the system.
 |
Fig. 2. Specific angular momentum, (in units of a2Ωorb), as a function of the orbital period of binary systems with fixed primary mass, Mdon = 0.9 M⊙, and mass ratios Q = 1.05, 2 (left and right panels, respectively). The solid, dashed, dot-dashed and dotted lines show, respectively, the profiles of η as computed with Eqs. (2) and (3) with γ = 2, (4) and (5). |
The angular-momentum loss rates given by Eqs. (3)–(6) represent only the angular-momentum loss from the orbit, and do not include a possible contribution from the loss of rotational angular momentum in the wind of the AGB donor star. The latter is accounted for separately in our code. In case the spin of the mass-losing star is tidally locked to the orbit, this rotational angular-momentum loss is effectively also taken out of the orbit. This is important in binaries that are close enough for tidal friction to occur on a timescale shorter than the mass-loss timescale, and can result in additional orbital shrinkage. In our binary population synthesis code, tidal friction and angular momentum transfer between the stars and the orbit is calculated explicitly (Hurley et al. 2002) and the effect of spin angular-momentum loss on the evolution of the orbit is thus taken into account as well.
2.5. Initial distribution of orbital periods and separations
In our model sets it is assumed by default that the initial distribution of separations is flat in log ai over the range [5, 5 × 106] R⊙, with a constant binary fraction per decade of orbital period, flog P, of approximately 0.11 in this interval. This choice has the advantage of being easy to implement and to compare with previous results of population synthesis studies. Furthermore, it is broadly consistent with the observed orbital separations of binary systems in the young stellar association Scorpius OB2 (Kouwenhoven et al. 2007) and with the data of Moe & Di Stefano (2017, Fig. 37) for the orbits of A/late-B-type binaries with primary masses in the range 2–5 M⊙. However, solartype stars with masses between 0.8 and 1.2 M⊙, which are the most frequent primary masses of the progenitor systems of our synthetic CEMP-s stars, have a rather different orbital-period distribution and a lower overall binary frequency (Raghavan et al. 2010; Moe & Di Stefano 2017). In addition, by default we assume in our models that the initial distributions of period and mass ratios are independent, hence the joint probability of forming a binary system with initial period P and mass ratio Q, p(P, Q), is the product of the individual probabilities p(P) and p(Q). By contrast, Moe & Di Stefano (2017) find that the period and mass-ratio distributions of observed binary stars are not separable, but closely interconnected. Moe & Di Stefano (2017) determine a set of equations to calculate the joint probability function of forming a binary system with primary mass M1, mass ratio Q, and orbital period P. We implement this set of equations in our model set M13.
Anticipating the results of Sect. 3, our simulations in general form CEMP-s stars at much longer orbital periods than observed, unless angular momentum is removed from the system with extremely high efficiency. For the sake of comparison, in our model set M14 we assume that all binary systems are formed with orbital periods in the range [10, 2 × 104] days, which is approximately the range in which the CEMP-s stars are observed by Hansen et al. (2016), and that the total binary fraction is 50% over this interval. Although we have little information about the initial binary and orbital properties of very metal-poor halo stars, in particular for relatively wide binaries, the resulting value of flog P = 0.15 is in approximate agreement with the results of Gao et al. (2014) for metal-poor F, G, and K stars in binary systems with P ≲ 1000 d. Figure 3 shows the three different initial period distributions adopted in our simulations.
 |
Fig. 3. Initial period distributions adopted in our models. The vertical axis represents the binary fraction in each period bin, i.e. flog P. The solid black line represents our default initial distribution of separations, which is flat in log10 ai between 5 R⊙ and 5 × 106 R⊙, with flog P = 0.11 over this interval. The dashed brown line shows the prescription of Moe & Di Stefano (2017), adopted in set M13, for a 1.0 M⊙ primary and mass ratio M2,i/M1,i > 0.1. The shape and maximum of the distribution of Moe & Di Stefano (2017) depend on the primary mass and mass ratio. The dotted green line shows a period distribution flat in log10 Pi and with flog P = 0.15 in the period range [10, 2 × 104] days, which we adopt in our model set M14. The integral of each curve represents the total binary fraction over the period interval. |
2.6. Detection probability of the orbits
In order to compare our simulations to the observed distribution of systems, we need to take account of the likelihood of a given synthetic binary to be detected by the observing campaign of Hansen et al. (2016), whose strategy consisted of taking observations roughly every 30 days for around 3000 days. We compute this likelihood using a Monte Carlo method. For a given set of system parameters (primary and secondary masses, orbital period and eccentricity), we randomly select an angle between the orbit’s major axis and the line of nodes, a value for the cosine of the inclination of the orbital plane of the binary to the plane of the sky5, and a starting point in the orbit. We compute the line-of-sight velocity at this point and at every 30 days for 3000 days, recording the maximum and minimum velocity. The difference between these is compared to the threshold radialvelocity amplitude of the observations, and if it is above this threshold, the system is deemed to have been detected. In their study, Hansen et al. (2016) achieve a 0.1 km s−1 precision in their radial-velocity measurements, and we consider this value to be our detection threshold, Kmin.
We repeat this for 105 choices of the orientation of the major axis, the inclination, and starting point in the orbit. The detection probability is then given by the number of systems that exceed the detection threshold, divided by the total number of iterations. We compute detection probabilities for a grid of potential binaries. To limit the number of systems we need to compute, we first determine the relevant parameter range of systems, as explained below. We then interpolate in this grid to find the detection probability of any CEMP-s system returned by the population-synthesis calculations.
In the binary systems of our simulated CEMP-s population, the primary is the carbon-rich star which would be observed. Its mass should be higher than 0.5 M⊙, or its luminosity would be so low (L⋆ ≲ 0.08 L⊙) that the V-magnitude would typically not satisfy our selection criteria (see Sect. 2.1), and lower than about 0.95 M⊙, otherwise the star would have become a white dwarf before ten billion years (see e.g. Fig. 7 of Abate et al. 2015c). The secondary star is a white dwarf of mass that depends on the initial progenitor mass, and in our simulations varies mostly in the range [0.5, 0.8] M⊙. CEMP-s systems at periods longer than 106 days are not found in our simulations. For binary systems with periods shorter than 3000 days the full radial-velocity curve would be sampled by the observing campaign of Hansen et al. (2016). Such a binary would still go undetected if observed close to face-on (i ≲ 1[openbullet] for a detection limit of Kmin = 0.1 km s−1), but the probability of such an unfavourable inclination is less than about 1%. We therefore assume a detection probability of 100% for P < 3000 d. In conclusion, our grid of detection probabilities covers total system masses in the range [0.7, 2.0] M⊙, secondary masses in the range [0.5, 1.0] M⊙, and orbital periods in the range [103, 106] days. Because all our synthetic systems are circular, we do not account for the detectability of eccentric orbits (but see the discussion in Sects. 4.1 and 4.4).
Figure 4 illustrates the effect of different radial-velocity detection thresholds on the period distribution of the synthetic CEMP-s systems computed with our default model set M2. In the top panel of Fig. 4, the black-dashed line shows the differential period distribution of all our synthetic CEMP-s stars. The blue-dot-dashed and orange-dotted lines show the CEMP-s stars that would be detected as binary systems with threshold radial-velocity amplitudes of 0.1 and 0.5 km s−1, respectively. Figure 4b shows the period distributions of CEMP-s systems that would be detected as single stars with the observation strategy and thresholds described above. In Fig. 4c the same three models as in panel (a) are compared to the observed cumulative period distribution (grey-solid line). Only 18 out of the 22 CEMP-s stars observed by Hansen et al. (2016, ≈82% of the sample) are confirmed binaries, 17 of which have a determined period while the binary with an as yet undetermined period is tentatively plotted at P = 15 000 d in Fig. 4. We make the assumption that the other four stars also belong to binary systems but have periods too long to be detected (indicatively Porb > 15 000 days). As expected, the proportion of CEMP-s stars detected as binary systems in our simulations decreases with increasing radial-velocity threshold Kmin. A binary fraction among simulated CEMP-s stars consistent with the observations is found adopting Kmin = 0.5 km s−1 in our model set M2. Nonetheless, to be consistent with the precision achieved in the work of Hansen et al. (2016) we adopt Kmin = 0.1 km s−1.
 |
Fig. 4. Panel a: period distributions of synthetic CEMP-s stars computed with our model set M2 and with different adopted detection thresholds for radial-velocity variations. The dashed black line shows the period distribution of all the CEMP-s stars in our simulation. The dot-dashed blue and dotted orange lines show the period distributions of the simulated CEMP-s stars with detection thresholds of Kmin = 0.1 and 0.5 km s−1, respectively. Panel b: same as in panel a for synthetic CEMP-s stars that would be detected as singles with the above thresholds. Panel c: the cumulative orbital-period distributions corresponding to the models in panel a are compared with the observed distribution calculated with the data of Hansen et al. (2016, solid grey line). |
3. Results
We evolve a population of very metal-poor binary stars for each set of initial assumptions described in the previous sections. We select the CEMP-s stars and we calculate the orbitalperiod distribution for these systems, which we subsequently compare with the observations of Hansen et al. (2016). Columns 7–9 of Table 1 characterise the resulting period distribution of each model set by providing the logarithmic orbital periods at 2.5, 50 and 97.5 percentiles of the synthetic CEMP-s population (i.e. the orbital period at which the cumulative period distribution is equal to 0.025, 0.5 and 0.975, respectively).
For each model set, we perform a Kolmogorov–Smirnov (K–S) test to evaluate the likelihood that the observed period distribution is drawn from the corresponding synthetic distribution. Column 10 in Table 1 shows the resulting p-values6, which give an indication of the relative goodness-of-fit of each model. We note that eleven of our model sets have p-values less than 0.05, which is the threshold often used as a criterion to reject a model with statistical significance. While this result suggests that most of our models are incompatible with the observed period distribution, in the following we will discuss in detail how different model assumptions modify the theoretical orbitalperiod distributions and why many of these fail to reproduce the data.
All figures in this section consist of two panels, as in Fig. 4. In the top panel we show the differential period distributions predicted with our models, before accounting for the detection probability of the orbit. The results are normalised such that the integral of each curve is equal to the total CEMP fraction computed with that model, fC, which is reported in the top-right corner of the plot and in Table 1. The bottom panels show the corresponding cumulative period distributions, after applying a radial-velocity detection threshold of Kmin = 0.1 km s−1. These are compared to the observed cumulative period distribution, shown as a thick, solid grey line. Each cumulative distribution is normalised to the total CEMP-s population, either observed or modelled, such that the value at P = 106 days corresponds to the detected (or detectable) binary fraction in the population. Our default model set M2 is always shown as a reference with a black-solid line.
3.1. Changes in the stability criterion of Roche-lobe overflow
Figure 5 shows the period distributions of the models sets M1, M2 and M3, with different stability criteria for RLOF from AGB donors. As expected, if the value of Qcrit increases, meaning that RLOF is stable for a larger range of binary systems, the number of CEMP stars with periods between approximately a few hundred and a few thousand days is increased. This is roughly the interval at which the primary stars avoid filling their Roche lobes on the first giant branch so that the RLOF phase can occur when the donors have reached the AGB. In this period range we find systems in which the secondary star accretes enough material to become carbon-enriched through stable RLOF. This is best seen in the top panel of Fig. 5, where the distributions of sets M2 and M3 have a peak at periods between about 300 and 1000 days, as a result of the increased stability of RLOF.
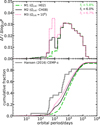 |
Fig. 5. As Fig. 4 for models with different RLOF stability criteria. Model set M1 adopting the H02 criterion is shown by the dashed green line. Model set M2 (thin, solid black line) uses the CH08 criterion. Model set M3 with Qcrit = 106 (i.e. RLOF from AGB stars is always stable) is indicated by the dotted magenta line. The top panel shows the entire simulated populations, while in the the bottom panel only CEMP-s stars detectable as binary systems are shown (Kmin = 0.1 km s−1 is adopted). |
The proportion of CEMP stars with periods less than 2500 days is 15% and 24% in model sets M1 and M2, respectively, whereas it is 32% in set M3 in which RLOF is always stable. This implies that at least two thirds of our synthetic CEMP stars, most realistically more, are formed by accretion of stellar winds. Were RLOF the only efficient mechanism to transfer material in low-mass binary stars, the fraction of CEMP stars in our metal-poor population would therefore be at most 2%, even if RLOF is always stable, that is, at least a factor of three lower than the fraction determined from the observed SDSS/SEGUE sample (≈6.1% for stars with [Fe/H] ≈ −2.0, Lee et al. 2013).
In addition, Fig. 5 shows that at any value of the cumulative fraction the synthetic distributions overestimate the observed periods approximately by a factor of between two and ten. The mismatch is also reflected in the small p-values in Table 1. While set M3 has a marginally acceptable p-value of 0.05, this model lacks physical realism. Furthermore, a large proportion of simulated CEMP stars have periods above 15 000 days, most of which should be detectable with the observing strategy of Hansen et al. (2016). In their sample, only one CEMP-s star out of 22 (about 5%) is detected as a binary with an as yet undetermined period that is presumably at least 15 000 days, while four stars (about 18% of the sample) have apparently constant radial velocity. By contrast, the proportion of detectable synthetic CEMP binaries with periods above 15 000 days is about 26% in model set M3, and it is 29% and 32% in the more realistic sets M2 and M1, respectively. The expected fraction of undetected binaries, with radial-velocity amplitude less than 0.1 km s−1, is only about 7% for all three models. This confirms that, regardless of the assumptions about RLOF stability, a significant fraction of systems form at very long separations. We therefore conclude that, while a better understanding of the RLOF process is necessary to reproduce the proportion of observed CEMP-s systems with periods up to a few thousand days, it is not sufficient to solve the discrepancy between models and observations. To reproduce at the same time the fraction of observed CEMP-s stars and their period distribution it is necessary to correctly account for wind mass transfer.
3.2. Varying the accretion efficiency of wind mass transfer
Figure 6 compares the period distributions of model sets M2 and M5 (dashed blue line), in which the wind accretion efficiency is computed with the WRLOF and BHL models, respectively. The WRLOF model predicts higher accretion efficiencies than the BHL prescription over a large range of separations, also in wide systems (Abate et al. 2013). Consequently set M2 produces CEMP stars at longer periods than set M5. However, the BHL model set M5 is only marginally closer to reproducing the observed period distribution than the WRLOF model. Furthermore, this comes at the expense of a predicted CEMP fraction of 4.6%, which underestimates the results of the SDSS/SEGUE survey (≈6.1% Lee et al. 2013), and a predicted fraction of undetected binaries of only about 4%, even lower than in model set M2.
 |
Fig. 6. As Fig. 5 for model sets M2 and M5 (dashed blue line) in which the wind accretion efficiency is computed with the WRLOF and BHL prescriptions, respectively. |
3.3. Changes in the adopted angular-momentum loss
Figures 7 and 8 show the period distributions obtained with model sets adopting different assumptions about the angular-momentum loss. In all models shown, the WRLOF prescription of wind accretion efficiency and the CH08 criterion of RLOF stability are used. Model sets M9, M11 and M12 in Fig. 7 are computed using γ = 2, 3, 6 in Eq. (4), whereas set M2 assumes the wind is expelled isotropically by the binary system. The CEMP fraction increases with increasing γ because the enhanced angular-momentum loss causes the binary systems to shrink more and therefore the range of separations at which the stars can interact is larger. Also the number of systems that produce a CEMP star after experiencing a common envelope increases with γ. Many of these had a relatively large initial separation, and hence the accretor had the time to accrete material and become carbon-rich before the onset of unstable RLOF. These systems appear at P ≲ 400 days in Fig. 7.
 |
Fig. 7. As Fig. 5 for different for angular-momentum-loss prescriptions. Model set M2 assumes isotropic wind mass loss. Model sets M9, M11, and M12 (dotted red, dot-dashed orange, and dashed violet lines, respectively) are computed with Eq. (4) and γ = 2, 3, 6, respectively. |
 |
Fig. 8. As Fig. 7 with model sets M6 (dashed line) and M7 (dot-dashed line), in which the angular-momentum loss is computed with Eq. (5) and υw = 15 and 7.5 km s−1, respectively, and set M8 (dotted line), in which Eq. (6) is adopted. |
For γ = 2 and 3, the increased angular-momentum loss compared to the isotropic wind model does not correspond to a significant shift of the period distributions towards shorter periods. To understand this result it is convenient to sub-divide the entire range of orbital periods of the synthetic CEMP populations into smaller intervals and subsequently compare the initial periods of the progenitor binary systems which, with different model sets, end up in the same interval. This exercise shows, for example, that model sets M2, M9 and M11 form the same proportion (approximately 36–38%) of CEMP stars with orbital periods between 103 and 104 days, but the progenitor binary systems in the three model sets had different initial-period ranges. In the isotropic-wind assumption (set M2) CEMP stars come from systems that had initial periods in the interval 1000–8000 days. Using Eq. (4) with = 2 (set M9) the progenitor binary systems had initial periods mostly between 2000 and 20 000 days, with a tail up to about 105 days. With model set M11 (γ = 3), the initial periods of these CEMP stars span between about 2000 and 50 000 days, with a tail up to a few hundred thousand days.
With model set M12 the cumulative period distribution of CEMP stars is roughly consistent with the observations (p = 0.28, see also Fig. 7) because of the combined effect of a strong angular momentum loss by stellar winds and the increased number of systems undergoing a common envelope. It should be remembered, however, that the assumption of a constant γ is not supported by physical arguments and it is unrealistic. In fact, it implies that the specific angular momentum expelled by the binary system does not depend on the masses of the stars and their distance, which is at odds with the results of hydrodynamical simulations (e.g. Jahanara et al. 2005; Chen et al. 2018; Saladino et al. 2018). Considering for example a 1 M⊙ primary star and a 0.6 M⊙ companion in a 105-day orbit, with γ = 6 the ejected material has a specific angular momentum ten times higher than in the isotropic-wind approximation, despite the fact that at wide separations the outflow from the donor star is expected to be essentially spherical (e.g. Mohamed & Podsiadlowski 2011, 2012).
The distributions computed with the orbit-dependent angular-momentum loss prescriptions of model sets M6, M7 and M8 are shown in Fig. 8 with dashed, dot-dashed, and dotted lines, respectively. Model M6 uses Eq. (5) based on hydrodynamical simulations from the literature and predicts an increased proportion of CEMP-s stars at periods shorter than about 2500 days compared to default set M2, at the expense of systems with periods between about 2500 and 30 000 days (see top panel of Fig. 8). Binaries with P ≲ 30 000 d lose more angular momentum than in the isotropic-wind model and thus evolve into closer orbits. This results in a larger fraction of CEMP-s stars formed through stable RLOF (with 300 d ≲ P ≲ 2500 days) as well as systems experiencing a common envelope after accreting enough material to become CEMP-s stars (ending up with P ≲ 300 d). With model sets M2 and M6 the proportion of CEMP-s stars with periods up to 2500 days is 24% and 31%, respectively. At periods longer than about 10 000 days the cumulative distributions of M2 and M6 are essentially identical, and the mismatch with the observations discussed in Sect. 3.1 therefore persists (p < 0.05, see Table 1).
A critical parameter in Eq. (5) is the terminal velocity of AGB winds, υw, because a lower wind velocity implies that, for the same orbital period, a larger amount of specific angular momentum is carried away by the ejected material. This parameter is uncertain, as observed wind velocities range between a few and a few tens of km s−1 (e.g. Vassiliadis & Wood 1993; Danilovich et al. 2015; Goldman et al. 2017). For the sake of comparison, in model set M7 we assume υw = 7.5 km s−1, which is half of our default value and consistent with the lowest velocity detected by Goldman et al. (2017) among high-luminosity, high-mass-loss stars in the Large Magellanic Cloud. Consequently, in set M7 the proportion of CEMP-s stars with periods below 2500 days increases even more, to about 34%. A low υw also affects the number of CEMP-s stars in very wide orbits (P ≳ 50 000 days). These systems do not enter the WRLOF regime and consequently the mass-transfer efficiency is calculated according to the BHL prescription (Eq. (6) of Boffin & Jorissen 1988), which is proportional to 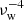 (for υorb ≤ υw). With a low υw also very wide systems accrete enough material to form a carbon-rich star. As a consequence, about 15% of the detectable synthetic CEMP-s stars have periods longer than 50 000 days (4% have P > 105 days), whereas it is only about 10% in model M6 (≈2% at P > 105 days). Thus, while the correspondence with observations improves somewhat at the short-period end of the distribution, it becomes worse at the long-period end.
(for υorb ≤ υw). With a low υw also very wide systems accrete enough material to form a carbon-rich star. As a consequence, about 15% of the detectable synthetic CEMP-s stars have periods longer than 50 000 days (4% have P > 105 days), whereas it is only about 10% in model M6 (≈2% at P > 105 days). Thus, while the correspondence with observations improves somewhat at the short-period end of the distribution, it becomes worse at the long-period end.
The results of model set M8, based on the ballistic simulations of Brookshaw & Tavani (1993), are roughly consistent with the observed cumulative distribution up to about 104 days, although the fraction of undetectable binaries is much smaller than the observed fraction of apparently single CEMP-s stars. This is not surprising because Eq. (6) predicts large angularmomentum loss for systems with υw ≤ υorb, much larger than both the isotropic-wind model and the hydrodynamics-based prescription up to periods of about 50 000 days. However, as we mentioned in Sect. 2.4, it should be kept in mind that this model overestimates the amount of angular momentum carried by the ejected winds and consequently the effect on the period distribution of CEMP stars, because it ignores the effects caused by gas pressure and radiative acceleration. Nevertheless, model set M8 is a useful test case to estimate how much angular momentum binary systems would need to lose in order to reconcile the results of our simulations with the observed CEMP-s population.
We note that in model sets M6 and M8 the total fraction of CEMP stars (5.8% and 5.5%, respectively) is somewhat lower than in set M2 (6.0%). This is because some binary systems that are just wide enough to avoid unstable RLOF and form CEMP stars in the isotropic-wind case, which widens their orbits, instead become tighter with the larger angular-momentum loss of model sets M6 and M8. Many of these undergo commonenvelope evolution before sufficient chemical pollution of the accretor has taken place. Unlike in the models with constant γ, this is not compensated by very wide systems evolving into close enough orbits to become CEMP stars.
In conclusion, Eq. (5) used in sets M6 and M7, which derives from the results of hydrodynamical simulations, is at present the only prescription for orbital angular-momentum loss with a physical basis. The evidence that, despite the uncertainty on υw, these model sets do not reproduce the observed period distribution very well suggests that other physical aspects in our models may have to be reconsidered.
3.4. Changes in the range of initial periods
Our model sets M13 and M14 adopt the same assumptions as the default set M2 except for the initial distribution of orbital periods and mass ratios. In model M13 we implement the set of fitting equations to observed binary stars proposed by Moe & Di Stefano (2017). These equations result in a quasi-flat initial-period distribution for low-mass primary stars, with a very wide peak between approximately 104 and 106 days, and in a combined distribution of periods and mass ratios, q = Q−1 = M2/M1, which favours small mass ratios, especially in wide orbits. The efficiency of WRLOF decreases with q in the prescription of Abate et al. (2013), while it is higher for relatively long-period systems around ≈104 days. As a result, these two effects compensate one another and the period distribution of CEMP-s stars with model set M13 is very similar to that of our default set M2, although with a slightly smaller proportion of systems with P < 104 days and a decreased overall CEMP fraction.
Our model set M14 has a flat log P–distribution with flog P = 0.15 between 10 and 20 000 days. These assumptions result in a period distribution which resembles the observations more closely, in particular at the long-period end. By construction, only a small fraction of synthetic CEMP-s stars have periods in excess of 20 000 days, as in the sample of Hansen et al. (2016). However, this model also predicts that essentially all CEMP-s stars should have detectable radial-velocity variations when monitored with the same strategy and sensitivity as the study of Hansen et al. (2016), which appears at odds with their finding that four out of 22 observed CEMP-s stars are apparently single. The p-value of 0.11 nevertheless suggests that we cannot reject this model on statistical grounds. We note, however, that the K-S test is relatively insensitive to differences occurring far from the median of the distribution, as is the case here.
4. Discussion
4.1. On the observed binary fraction and orbital periods.
We have assumed that all CEMP-s stars are formed in binary systems, a hypothesis borne out by several theoretical and observational studies (Lucatello et al. 2005; Aoki et al. 2007; Bisterzo et al. 2012; Lugaro et al. 2012; Starkenburg et al. 2014). However, four stars in the sample of Hansen et al. (2016) do not exhibit radial-velocity variations consistent with orbital motion. Based on the sensitivity of their study, the authors exclude as highly unlikely that all four CEMP-s stars are in binary systems observed face-on, and therefore they conclude that these are single stars. However, they did not consider the possibility that these may be binaries with periods much longer than 104 days.
In our simulations we use a Monte Carlo method to account for the likelihood of our synthetic binary systems to be detected with the observing strategy of Hansen et al. (2016). In their study, the precision achieved in the velocity measurements is about 0.1 km s−1. Accordingly, we have assumed a sensitivity to radial-velocity variations of Kmin = 0.1 km s−1, and we find a fraction of undetectable binaries which ranges between 2 and 10% (in model sets M14 and M7, respectively; it is ≈7% in our default set M2). This means that, in a sample of 22 CEMP-s stars, we expect between 0.4 and 2.2 undetected binaries, rather than the four that are observed.
We note that the time span of observations for stars in the Hansen sample is often less than the 3000 days we have assumed for computing the detection probability. For two of the four constant-radial-velocity stars it is indeed much shorter: about 1000 days for HE 0206–1916 and 800 days for HE 1045+0226. It cannot be excluded that evidence for orbital motion would have been detected in these stars if the radial-velocity measurements had lasted for the nominal 3000 days. In addition, for star HE 1045+0226 both the errors and the spread in the observed radial-velocity values are substantially larger than 0.1 km s−1, and an overall downward trend in radial velocities with an amplitude several times 0.1 km s−1 is compatible with the data (Fig. 1 of Hansen et al. 2016). Several other stars in the sample also have radial-velocity measurement errors in excess of 0.1 km s−1. This suggests that both our assumed time span of 3000 days and detection threshold of 0.1 km s−1 are too conservative for the sample as a whole. In fact, if we assume a time-span of radial-velocity monitoring of 1000 days in our simulations, the predicted fractions of undetected binaries approximately double. In our default set M2 we expect about 16% of undetected CEMP-s systems, in rough agreement with the observed sample (see Fig. B.1 in Appendix B). In addition, as we show in Sect. 2.6, if we adopt Kmin = 0.5 km s−1 in our default set M2 about 20% of the CEMP-s stars would not be detected as binaries, approximately as in the observed sample. The same is true for most of our simulations, with the exception of sets M8, M12 and M14, which would require an even higher detection threshold in order to produce approximately 18% of undetected binaries (Kmin = 1.0 km s−1 in set M12, Kmin = 1.5 km s−1 in sets M8 and M14).
Perhaps harder to reconcile with our models than the non-detection of radial-velocity variations in four stars, is the paucity of confirmed binaries with orbital periods between 104 and 105 days. The Hansen sample probably contains one such a very wide binary system, HE 0959–1424, for which it was not possible to determine the orbital solution but which exhibits velocity variations of about 2 km s−1. Its orbital period must be longer than 10 000 days, but is likely less than 105 days, and some of the apparently constant-velocity stars discussed above may also turn out to have periods in this range. We also note, however, that the smallest velocity amplitude measured in a confirmed CEMP-s binary star is K = 1.57 km s−1, which is significantly higher than our adopted threshold, even assuming a generous value of Kmin = 0.5 km s−1. This is hard to reconcile with a continuous distribution of radial-velocity amplitudes down to the detection threshold, as would be expected from our simulation, and suggests that the paucity of CEMP-s binaries with P > 10 000 days is real. An approximate upper limit to the period distribution of the order of 104 days is also suggested by the study of Starkenburg et al. (2014). All of our model sets produce a substantial fraction of detectable binaries with periods larger than 104 days. In a sample of 22 CEMP-s stars, between 5 and 9 such binaries are predicted (with Kmin = 0.1 km s−1). Our only model set that comes close to reproducing the lack of systems in this period range is M8 if we make the additional, extreme assumption that Kmin = 1.5 km s−1, in which case we predict about 2 detectable CEMP-s binaries with period P > 104 days. In all other model sets we cannot reproduce at the same time the proportion of undetectable binaries and the number of long-period detectable binaries, even if we assume a Kmin ≫ 0.1 km s−1.
In the discussion above we have only considered circular orbits. With the Monte Carlo method described in Sect. 2.6, we find that eccentric binaries with orbital periods in the range 5 × 103 ≲ P ≲ 3 × 105 days are less likely to be detected, because the radial-velocity variations are smaller than in the circular case during most of the orbit, except when the system is close to periastron. Assuming Kmin = 0.1 km s−1, the decrease in detection probability is about 5% or less for small eccentricities, e ≤ 0.3, while it can be as high as about 25% for e = 0.7, which corresponds to the highest eccentricity determined in the observed CEMP-s sample. The smaller detection probability of eccentric systems helps to reduce the difference between the observed and predicted numbers of detectable CEMP-s binaries with P > 104 days, but this effect is too small to remove the discrepancy.
One further aspect that needs to be addressed is whether the observed sample of Hansen et al. (2016), which we use to constrain our models, is representative of the overall CEMP-s population. The members of this sample were initially selected for their chemical properties, namely their observed abundances of carbon and barium relative to iron, and subsequently monitored to ascertain whether they belong to binary systems and, eventually, to determine their orbital periods (Hansen et al. 2016). Consequently, in principle there is no obvious observational bias in favour of relatively short orbital periods.
Nevertheless, the fact that most stars in the sample have relatively large carbon enhancements ([C/Fe] > 1.5 in 18 out of 22 stars) may introduce a potential bias. We note that all sample stars are giants that have already undergone first dredge-up, which has mixed and diluted the transferred material throughout the accretor (with the possible exception of HE 1046−1352 which has log10g = 3.5 and is also the star with the highest carbon abundance, [C/Fe] > 3.3). This suggests that they must have accreted substantial amounts of material from their AGB companions and, therefore, that the adopted observed sample may be biased towards systems that experienced highly efficient mass transfer. Consequently wide-period systems, which transferred only a few percent of the mass ejected by the donor, may be underrepresented. A similar selection effect has been pointed out for barium stars, in which higher s-process enrichments are associated with shorter orbital periods (e.g. Boffin & Zacs 1994; Boffin 2015). However, if among the CEMP-s stars simulated in model set M2 we select those that have [C/Fe] > 1.5 and log10g 3.0, only very wide systems at Porb > 105 days are significantly affected. These transfer less than a few 0.01 M⊙, that is just enough to enhance the surface carbon abundance of the accretor up to [C/Fe] ≈ 1. Because these wide systems make up just a few per cent of the total CEMP population in set M2, the final period distributions change only marginally if we exclude them. We conclude that even if there is a bias towards large accreted masses, this does not significantly affect the resulting period distribution.
4.2. Accretion efficiency and angular-momentum loss during wind mass transfer
In the wind mass-transfer process, the amount of mass and angular momentum that are accreted by the companion or lost by the binary system are intricately related. The stronger the wind of the donor interacts with the binary, the higher the accretion rate and angular-momentum loss are expected to be. Many authors have computed hydrodynamical simulations of wind mass transfer in low-mass binary systems with different codes and algorithms, but only a few of these studies have addressed the loss of angular momentum. These simulations produce more or less consistent results concerning the angular momentum lost when similar input physics is adopted (cf. Fig. 11 of Saladino et al. 2018). However, the accretion efficiencies found in hydrodynamical simulations differ significantly, by as much as a factor of ten, depending on physical assumptions such as the acceleration mechanism of the wind, the equation of state used to describe the gas particles, the adopted cooling mechanism, and possibly also the algorithms used to compute the accretion rates (Theuns et al. 1996; Nagae et al. 2004; de Val-Borro et al. 2009; Mohamed 2010; Chen et al. 2017; Liu et al. 2017; Saladino et al. 2018). Because of these discrepancies, and with the aim of investigating multiple combinations of model assumptions, in our work we chose to treat mass accretion and angular-momentum loss as if they were independent processes. To improve on this study it will be necessary to compute these processes self-consistently with a model based on a reliable set of hydrodynamical simulations covering a large parameter space.
We have investigated different models of angular-momentum loss. As demonstrated in Sect. 3.3, most of these models yield periods of CEMP-s binaries that are significantly longer than observed, with the median of the synthetic period distribution typically exceeding the observed value by about a factor of about three. With our model sets M6 and M7, which are based on detailed hydrodynamical calculations, the proportion of synthetic CEMP-s stars between 100 and 2500 days increases compared to the isotropic-wind model, reducing the discrepancy with the observations in this range. However, at longer periods the ejected material only interacts weakly with the binary and the results are the same as with the isotropic-wind model, hence too many wide-orbit CEMP-s systems are formed.
In order to obtain a period distribution of CEMP-s stars that is consistent with the observed population, at least for periods up to about 104 days, it is necessary to assume that much larger amounts of angular momentum are lost with the ejected wind material. This is the case for model sets M8, based on the simulations of Brookshaw & Tavani (1993), and M12, with γ = 6 in Eq. (4), in which binary systems shrink significantly in response to mass loss. However, we emphasize that sets M8 and M12 are not based on realistic physical assumptions. Set M8 is based on ballistic simulations that do not take into account gas pressure and radiative acceleration, which would make the ejected outflow more isotropic, and hence the angular momentum dispersed by wind material is overestimated. Assuming a constant γ in set M12 implies that the specific angular momentum of the ejected material is independent of the orbital period of the systems. In addition, we note that with model sets M8 and M12 the 20% widest CEMP-s systems have periods mostly in the range 15 000–40 000 days, of which the majority should be detectable as binaries (however, see the discussion in Sect. 4.1). In their study of the periods and eccentricities of barium stars, Izzard et al. (2010) show that they reproduce the bulk of the observed distribution by adopting Eq. (4) with γ = 2. With the same assumptions, in our model set M10 we find a cumulative distribution approximately consistent with the observations for periods up to about 104 days. However, at longer periods set M10 predicts only 2% undetected CEMP-s binary systems, and an overall CEMP fraction of about 5%, which is lower than the observed one (see Fig. 10).
Abate et al. (2015a) found that high accretion efficiencies are required to reproduce the surface abundances of their sample of observed CEMP binary stars. A similar conclusion was reached by Abate et al. (2015b), who found that approximately 40% of the analysed CEMP-s stars accreted more than 0.1 M⊙ by wind mass transfer from an AGB companion. In their best-fitting model set B, Abate et al. (2015a) adopted the equation for the BHL wind accretion efficiency proposed by Boffin & Jorissen (1988, Eq. (6)) but they arbitrarily replaced the numerical constant BHL = 1.5 with αBHL = 10. In their model, the high accretion efficiency was combined with strong angular-momentum loss (γ = 2 as in our set M9) which was found to be necessary to reproduce the observed orbital periods. As a test, we computed two simulations adopting the BHL prescription for wind accretion and αBHL = 10, while for the angular-momentum loss either an isotropic wind (set M15) or Eq. (4) with γ = 2 (set M16) are assumed. The results are shown in Fig. 10. The increase in accretion efficiency generated by αBHL = 10 causes a shift in the period distribution of CEMP-s stars towards longer periods than in model sets M4 and M5, which use the BHL model with αBHL = 1.5. This is because in these two sets most systems with periods longer than about 60 000 days do not transfer enough mass to generate CEMP stars, whereas they do if we adopt αBHL = 10. As a result, about 35% of the whole synthetic CEMP-s population come from very wide systems with periods between 60 000 days and a few times 105 days. In model set M16, which has the same assumptions of set B of Abate et al. (2015a), the cumulative distribution we determine is shifted towards periods a factor of two up to ten longer than in our set M2. Overall these results indicate that a simple increase in wind accretion efficiency and specific angular-momentum loss of the ejected material applied to all systems regardless of their separations aggravate the discrepancy between synthetic and observed period distributions.
In our simulations, we implicitly ignore that the material transferred to the secondary star carries angular momentum, which will spin up the accretor. If the angular momentum content is too great, it can prevent the accretion of material (Packet 1981). Matrozis et al. (2017) showed that the transferred material has to dissipate most of its angular momentum for the secondary star to accrete more than a few 0.01 M⊙. Investigating this issue and the constraints it puts on the mass-accretion process is beyond the scope of this paper.
4.3. On the initial orbital-period distribution.
The distribution of initial orbital periods (or separations) and the initial binary fraction are among the largest uncertainties in our simulations. Moe & Di Stefano (2017) have combined and integrated the formidable efforts made by many authors to characterise the orbital-period and mass-ratio distributions of young main-sequence binary systems in the Galactic disk. Adopting their fitting equations to these distributions instead of our default log a-flat initial distribution in our simulations does not significantly change the period distribution of our synthetic CEMP-s stars (see our set M13, Fig. 9).
 |
Fig. 9. As Fig. 5 for different distributions of initial separations and periods. By default ai/R⊙ is in [5, 5 × 106] (solid black line). The dashed line is computed using the initial log P–distribution of Moe & Di Stefano (2017, Eq. (23)). In model set M14 Pi is log-flat between 10 and 20 000 days (dotted line). |
The study of Moe & Di Stefano (2017) does not include a dependence on the metallicity. In particular, little is known about the initial binary properties of the low-metallicity halo population (see e.g. Duchêne & Kraus 2013; and references therein). For example, Rastegaev (2010) and Hettinger et al. (2015) argue that the total binary fraction increases with metallicity. In contrast, Gao et al. (2014, 2017) and Badenes et al. (2018) find an anticorrelation between these two quantities. In addition, Rastegaev (2010) has determined the orbital-period distribution of a sample of about 60 Population-II subdwarf binaries. The result is an asymmetric distribution with a broad peak between periods of 10 and 104 days and a tail up to about 1010 days (see Figs. 8 and 10 of Rastegaev 2010). This distribution is not dissimilar to what we assume in our model M14, although the flog P within the peak of their distribution is smaller, about 0.10. The result of set M14 is a cumulative period distribution of CEMP-s stars that resembles the observed distribution for periods up to about 15 000 days. In addition, with flog P = 0.15 we find a CEMP fraction of 6.5%, similar to that determined from SDSS data (≈6%, Lee et al. 2013). We emphasize that the initial-period distribution in set M14 is adopted for comparison purposes and it is not claimed to be realistic. However, this choice is broadly in agreement with the study of Gao et al. (2014) for F/G/K stars at [Fe/H] < −1.1 in binary systems up to one thousand days, and it is also roughly consistent with the results obtained by Moe & Di Stefano (2017) for relatively massive stars (M1 ≳ 5 M⊙), although these are a marginal fraction of all CEMP-s progenitors in our simulations. Another source of uncertainty is the contribution to the observed period distribution from binary systems with a white dwarf as a companion. The previous evolution of these systems has probably modified their orbit, and consequently their current periods differ from the initial periods at their formation. While in their equations Moe & Di Stefano (2017) take into account this effect, it is not discussed by Rastegaev (2010).
These results are instructive to understand by how much it is necessary to modify the initial period distribution to reproduce the observed CEMP-s period distribution, but we stress that the assumptions adopted in model set M14 are completely arbitrary. In principle, the validity of these assumptions can be tested on a number of different astrophysical phenomena. For example, if the binary fraction per decade of periods, flog P, increases at low metallicity for orbits up to about 104 days, the rate of Type Ia supernovae is expected to increase, because these supernovae progenitors are formed at periods shorter than about 5000 days (e.g. Claeys et al. 2014). A similar argument applies to close symbiotic binaries and blue stragglers, which are expected to be more numerous among metal-poor stars if flog P is weighted towards short orbits.
In conclusion, it is clear that the initial binary population in the Galactic halo needs to be much better characterised in order to put firmer constraints on the physical processes playing a role in the formation of CEMP-s binaries. The final data release of the Gaia mission, in combination with radial-velocity monitoring surveys, will hopefully provide insight into the properties of the binary population in the halo. In particular, binary systems in which both components are low-mass main-sequence stars have likely not evolved much over the ten billion years since their formation, and thus the initial distribution of orbital periods may be inferred from the study of their current orbital properties.
4.4. On the eccentricities of CEMP-s stars.
In our simulations the binary systems have circular orbits, although about half of the observed CEMP-s stars have non-zero eccentricities up to e = 0.67 (Hansen et al. 2016). We performed a number of simulations with the model sets described in Sect. 2 and eight values of the initial eccentricity, ei, uniformly distributed in the range [0, 0.7]. We find that the period distributions computed in Sect. 3 do not vary significantly when non-zero eccentricities are considered. CEMP stars with periods longer than about 2500 days are formed at every eccentricity in our range, hence reproducing the spread of the observations. The effect of tidal friction is increasingly important at shorter periods, because when the primary star ascends the giant branch it fills a significant portion of its Roche lobe. Below P ≈ 1000 days the binary systems experience RLOF, during which the orbit is fully circularised. As a consequence, if tides are as efficient as assumed (Hurley et al. 2002) and in the absence of a physical mechanism that re-enhances the eccentricity, all these short-period synthetic CEMP-s systems are in circular orbits, in contrast with at least four observed CEMP-s stars (two of which are in the sample of Hansen et al. 2016, see Fig. 1).
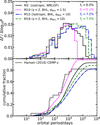 |
Fig. 10. As Fig. 5 for different accretion-efficiency and angular-momentum-loss prescriptions. Model set M2 adopts the WRLOF model of wind accretion and assumes isotropic wind mass loss. Model set M10 (dotted magenta line) is computed with Eq. (4) and γ = 2, and adopts the BHL model with α = 1.5. Model sets M15 and M16 (dot-dashed blue and dashed green lines, respectively) compute wind accretion efficiency with α = 10 within the BHL model. Set M15 assumes isotropic wind mass loss, whereas set M16 uses Eq. (4) with γ = 2. |
A mechanism that counteracts the tidal forces in binary systems with a giant component close to filling its Roche lobe has been invoked to model the eccentricities in a variety of contexts, including post-AGB binary systems and barium stars. The nature of such a mechanism that can enhance the eccentricity is currently unclear. Van Winckel et al. (1995) and Soker (2000) suggested that enhanced mass transfer at periastron may counteract the circularisation of the orbit. Bonačić Marinović et al. (2008) successfully applied a tidally-enhanced model of mass loss from AGB stars to reproduce the eccentricities observed in moderately wide binary systems with a white dwarf and a less evolved companion, such as Sirius. Alternatively, it has been suggested that a fraction of the material expelled by the donor star may escape through the outer Lagrangian points and form a circumbinary disk. The interaction between this disk and the binary may lead to an increase of the system’s eccentricity which depends on properties such as the orbital separation, the mass of the disk, its lifetime, viscosity and density distribution (e.g. Artymowicz & Lubow 1994; Waelkens et al. 1996; Dermine et al. 2013; Vos et al. 2015). Regardless of its nature, a mechanism that enhances the eccentricity of close systems will necessarily affect the final orbital periods. Consequently, any model promising to reconcile the synthetic period distribution of CEMP-s stars with the observations will have to take into account a mechanism to counteract circularisation in short-period binaries.
In our study we focused on binary systems and we did not consider triples. The presence of a third star orbiting a binary system may in some circumstances increase its eccentricity, as described by the Kozai-Lidov mechanism (Kozai 1962; Lidov 1962), opposing the effect of circularisation (see e.g. Perets & Kratter 2012). The observed proportion of triple-to-binary systems varies between approximately 10% and 20% depending on the sample and on the detection techniques, (e.g. Eggleton & Tokovinin 2008; Rastegaev 2010; Tokovinin 2014; Borkovits et al. 2016). Consequently, we could expect that in CEMP-s sample of Hansen et al. (2016) between two and four objects are, or were, in fact triple systems. This might help to explain the presence of some of the eccentric CEMP-s stars with periods shorter than 103 days. For example, in the eccentric system CS22964–161AB (P = 252 days and e = 0.66, from Thompson et al. 2008), which is not included in the survey of Hansen et al. (2016), both components are CEMP-s stars in the early phases of their evolution, and hence have likely been polluted in the past by a third object (see e.g. Thompson et al. 2008; Abate et al. 2015b).
4.5. On the origin of single CEMP-s stars
If the four CEMP-s stars that do not exhibit radial-velocity variations are actually single stars, their formation history has to be understood. Their observed effective temperatures and surface gravities are relatively high (see Table 6 of Hansen et al. 2016; and references therein), which excludes the possibility that they are self-polluted AGB stars. Also, it is very unlikely that they were formed in binary systems that merged after mass transfer, as this would require fine-tuning of the system initial parameters. The initial separation has to be just long enough that the primary reaches the AGB phase, during which some material is transferred onto the companion, before a common-envelope phase shrinks the orbit so much that the system merges within a Hubble time. Furthermore, the merger product would itself end up on the AGB, and the same counter-argument as given above against self-pollution applies. Hence, the most likely hypothesis is that these stars were born with enhanced abundances of carbon and s-elements from an already enriched interstellar medium.
Choplin et al. (2017) present a model in which the winds of rapidly-rotating massive stars (also called “spinstars”) are the cause of this pollution. They were able to reproduce the abundances of most detected elements in the four apparently-single CEMP-s stars with a model of a 25 M⊙ star rotating at 70% of the break-up velocity at [Fe/H] ≈ −1.8 (their Fig. 3). The comparison between the best fits of Choplin et al. (2017) and those of Abate et al. (2015b), who in their model set A used essentially the same input physics as in our model set M2, indicates that for two of these stars (HE 0206–1916 and CS 30301–015) the binary mass-transfer model gives a better fit to the observed abundances. In addition, in one case (star HE 1045+0225) both models fail to reproduce at the same time the abundances of light elements (carbon, sodium, magnesium) and light s-elements (strontium and yttrium), with the spinstar model correctly fitting the s-elements and the binary model better reproducing the light elements.
Star CS 30301–015 is particularly interesting as it has the largest set of measured abundances, including heavy s-elements up to lead, that can put tighter constrains on the nucleosynthesis models. While the analysis of Hansen et al. (2016) shows no radial-velocity variations within 0.3 km s−1 over a 2300-day time span, the combination of relatively low abundances of light s-elements ([ls/Fe] ≈ 0.4), mild enrichment in heavy s-elements([hs/Fe] ≈ 1,thoughwithsomescatter)andstronglead enhancement ([Pb/Fe] = 2, Aoki et al. 2002) cannot be reconciled with the predictions of the spinstar model and is much more consistent with AGB nucleosynthesis. Also, the binary model of Abate et al. (2015b) for this star predicts an orbital period which could be as long as 106 days, which would likely go undetected.
In conclusion, although the spinstar model naturally explains why no orbital motion is detected, binary-star models (Abate et al. 2015b, and our model set M2) generally predict wide orbits for these systems (P > 15 000), which would be difficult to detect. The abundances of more elements are necessary to discriminate between a spinstar or AGB origin of the chemical enrichment in these stars. In particular, rotating massive stars generally yield more oxygen and sodium compared to AGB stars for a given amount of carbon. Also, they produce more light s-elements (e.g. strontium) than heavy s-elements (e.g. barium) and not much lead (Frischknecht et al. 2012; Choplin et al. 2017). By contrast, in AGB stars heavy s-elements and lead are usually more strongly enhanced than light s-elements. When a set of observed abundances of all these elements will be available for these stars, it will be possible to put stronger constraints on their origin.
5. Summary and conclusions
The motivation for this work is that in population-synthesis models of metal-poor binary systems the majority of CEMP-s stars have periods several times longer than in the observed sample of CEMP-s stars compiled by Hansen et al. (2016). This sample is taken as a reference because arguably it is not biased towards a particular period range. In previous studies it has normally been assumed that Roche-lobe overflow is unstable when the donor is an AGB star (except in rare circumstances), that wind ejection occurs in spherical symmetry, and that the initial distribution of orbital separations is flat in the logarithm. This results in about 45% of the synthetic CEMP-s stars having periods exceeding 10 000 days, which is currently the longest period measured for an observed system. If these wide systems are excluded from the synthetic population, the models underestimate the observed CEMP fraction by almost a factor of two.
In this study we consider several modifications of these standard assumptions and investigate their effect on the CEMP period distribution. We show that the stability criterion of Rochelobe overflow plays a role in determining the proportion of CEMP stars that are formed at periods between a few hundred and a few thousand days. However, even if we assume that Roche-lobe overflow from AGB donors is always stable, the consequences for the period distribution of the synthetic CEMP population are small, because only a relatively small fraction of all our simulated CEMP stars experience a phase of Roche-lobe overflow, between about 15% and 30% in the most extreme case, while the remainder form by wind accretion. Hence, to reproduce the observed fraction of CEMP stars, wind mass transfer from AGB donors in binary systems has to be efficient.
A large uncertainty in our study is the original binary fraction per decade of orbital period in the very metal-poor stellar population of the halo. Assuming that it was similar to that observed at higher metallicity in the solar neighbourhood, the constraint placed by the observed period distribution of CEMP-s stars requires that the wind ejected by binary systems has to carry away a large amount of angular momentum, up to about ten times higher than in the simplistic case of isotropic wind ejection. At present, state-of-the-art hydrodynamical simulations do not predict the high angular-momentum loss necessary to reconcile the results of our population-synthesis models with the observations. However, another possibility is that at very low metallicity binary systems formed at periods distributed differently from today. Our simulations show that if binary systems are initially formed in a significantly narrower range of periods, up to around ten thousand days, then the period distribution of observed CEMP-s stars can be reproduced.
The CEMP-s star sample of Hansen et al. (2016) contains four stars that appear to be single, that is, no evidence for binary-induced radial-velocity variations was found. Our simulations show that at least some, and perhaps all, of these could be binaries at periods (much) longer than 10 000 days that are observed at unfavourable orbital phases and inclinations. However, it is hard to reconcile at the same time both the substantial number of apparently single stars and the fact that only one detected binary has a (still unmeasured) period exceeding 10 000 days with any of our simulations.
In conclusion, a combination of significant wind accretion efficiency, higher than the predictions of the canonical Bondi-Hoyle-Lyttleton approximation, strong angular-momentum loss carried away by the wind material that escapes the binary system, and possibly an initial distribution of orbital separations significantly different from that observed in solar-vicinity stars, is required to reproduce the orbital periods of the observed population of CEMP-s stars.
We refer to Sect. 5 of Abate et al. (2013) for a discussion about the consequences of varying Tcond.
These were calculated with a version, adapted for Python, of the procedure ksone presented in “Numerical Recipes” (Press et al. 1989).
Acknowledgments
We thank the anonymous referee for valuable comments that have helped improve our paper. CA is the recipient of an Alexander von Humboldt Fellowship. RJS is the recipient of a Sofja Kovalevskaja Award from the Alexander von Humboldt Foundation.
References
- Abate, C., Pols, O. R., Izzard, R. G., Mohamed, S. S., & de Mink, S. E. 2013, A&A, 552, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C., Pols, O. R., Karakas, A. I., & Izzard, R. G. 2015a, A&A, 576, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C., Pols, O. R., Karakas, A. I., & Izzard, R. G. 2015b, A&A, 581, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abate, C., Pols, O. R., Stancliffe, R. J., et al. 2015c, A&A, 581, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Ryan, S. G., Norris, J. E., et al. 2002, ApJ, 580, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Badenes, C., Mazzola, C., Thompson, T. A., et al. 2018, ApJ, 854, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2012, MNRAS, 422, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Bladh, S., & Höfner, S. 2012, A&A, 546, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bladh, S., Höfner, S., Aringer, B., & Eriksson, K. 2015, A&A, 575, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boffin, H. M. J. 2015, Mass Transfer by Stellar Wind, eds. H. M. J. Boffin, G. Carraro, & G. Beccari (Springer), 153 [Google Scholar]
- Boffin, H. M. J., & Jorissen, A. 1988, A&A, 205, 155 [NASA ADS] [Google Scholar]
- Boffin, H. M. J., & Zacs, L. 1994, A&A, 291, 811 [NASA ADS] [Google Scholar]
- Bonačić Marinović, A. A., Glebbeek, E., & Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Hajdu, T., Sztakovics, J., et al. 2016, MNRAS, 455, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Boyer, M. L., McDonald, I., Srinivasan, S., et al. 2015a, ApJ, 810, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Boyer, M. L., McQuinn, K. B. W., Barmby, P., et al. 2015b, ApJ, 800, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Brookshaw, L., & Tavani, M. 1993, ApJ, 410, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Castro-Carrizo, A., Bujarrabal, V., Castro-Carrizo, A., et al. 2002, A&A, 386, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, X., & Han, Z. 2008, MNRAS, 387, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Z., Frank, A., Blackman, E. G., Nordhaus, J., & Carroll-Nellenback, J. 2017, MNRAS, 468, 4465 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Z., Blackman, E. G., Nordhaus, J., Frank, A., & Carroll-Nellenback, J. 2018, MNRAS, 473, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Choplin, A., Hirschi, R., Meynet, G., & Ekström, S. 2017, A&A, 607, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, J. G., Shectman, S., Thompson, I., et al. 2005, ApJ, 633, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovich, T., Teyssier, D., Justtanont, K., et al. 2015, A&A, 581, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Karovska, M., & Sasselov, D. 2009, ApJ, 700, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Karovska, M., Sasselov, D. D., & Stone, J. M. 2017, MNRAS, 468, 3408 [NASA ADS] [CrossRef] [Google Scholar]
- Dermine, T., Izzard, R. G., Jorissen, A., & Van Winckel, H. 2013, A&A, 551, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Edgar, R. 2004, New Astron. Rev., 48, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., & Tokovinin, A. A. 2008, MNRAS, 389, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Christlieb, N., Norris, J. E., et al. 2006, ApJ, 652, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., & Höfner, S. 2008, A&A, 483, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frischknecht, U., Hirschi, R., & Thielemann, F.-K. 2012, A&A, 538, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gao, S., Liu, C., Zhang, X., et al. 2014, ApJ, 788, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, S., Zhao, H., Yang, H., & Gao, R. 2017, MNRAS, 469, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, H., Hjellming, M. S., Webbink, R. F., Chen, X., & Han, Z. 2010, ApJ, 717, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, H., Webbink, R. F., Chen, X., & Han, Z. 2015, ApJ, 812, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Goldman, S. R., van Loon, J. T., Zijlstra, A. A., et al. 2017, MNRAS, 465, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, T. T., Andersen, J., Nordström, B., et al. 2016, A&A, 588, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hettinger, T., Badenes, C., Strader, J., Bickerton, S. J., & Beers, T. C. 2015, ApJ, 806, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Höfner, S. 2007, in Why Galaxies Care About AGB Stars: Their Importance as Actors and Probes, eds. F. Kerschbaum, C. Charbonnel, & R. F. Wing, ASP Conf. Ser., 378, 145 [NASA ADS] [Google Scholar]
- Höfner, S. 2009, in ASP Conf. Ser., eds. T. Henning, E. Grün, & J. Steinacker, 414, 3 [NASA ADS] [Google Scholar]
- Höfner, S. 2015, in Why Galaxies Care about AGB Stars III: A Closer Look in Space and Time, eds. F. Kerschbaum, R. F. Wing, & J. Hron, ASP, 497, 333 [NASA ADS] [Google Scholar]
- Hoyle, F., & Lyttleton, R. A. 1939, Proceedings of the Cambridge Philosophical Society, 35, 405 [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Tout, C. A., Karakas, A. I., & Pols, O. R. 2004, MNRAS, 350, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Dray, L. M., Karakas, A. I., Lugaro, M., & Tout, C. A. 2006, A&A, 460, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Glebbeek, E., Stancliffe, R. J., & Pols, O. R. 2009, A&A, 508, 1359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Dermine, T., & Church, R. P. 2010, A&A, 523, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzard, R. G., Preece, H., Jofre, P., et al. 2018, MNRAS, 473, 2984 [NASA ADS] [CrossRef] [Google Scholar]
- Jahanara, B., Mitsumoto, M., Oka, K., et al. 2005, A&A, 441, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorissen, A., Van Eck, S., Mayor, M., & Udry, S. 1998, A&A, 332, 877 [NASA ADS] [Google Scholar]
- Jorissen, A., Van Eck, S., Van Winckel, H., et al. 2016, A&A, 586, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karakas, A. I. 2010, MNRAS, 403, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Karovska, M., Hack, W., Raymond, J., & Guinan, E. 1997, ApJ, 482, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Karovska, M., Schlegel, E., Hack, W., Raymond, J. C., & Wood, B. E. 2005, ApJ, 623, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Karovska, M., Gaetz, T. J., Carilli, C. L., et al. 2010, ApJ, 710, L132 [NASA ADS] [CrossRef] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007. A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y. S., Beers, T. C., Masseron, T., et al. 2013, AJ, 146, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z.-W., Stancliffe, R. J., Abate, C., & Matrozis, E. 2017, ApJ, 846, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Tsangarides, S., Beers, T. C., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Beers, T. C., Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Karakas, A. I., Stancliffe, R. J., & Rijs, C. 2012, ApJ, 47, 1998 [Google Scholar]
- Matrozis, E., Abate, C., & Stancliffe, R. J. 2017, A&A, 606, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClure, R. D., & Woodsworth, A. W. 1990, ApJ, 352, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
- Mohamed, S. 2010, PhD Thesis, St Edmund Hall, University of Oxford [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2007, in 15th European Workshop on White Dwarfs, eds. R. Napiwotzki, & M. R. Burleigh, ASP Conf. Ser., 372, 397 [NASA ADS] [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2011, in Why Galaxies Care about AGB Stars II: Shining Examples and Common Inhabitants, eds. F. Kerschbaum, T. Lebzelter, & R. F. Wing, ASP, 445, 355 [NASA ADS] [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2012, Balt. Astron., 21, 88 [Google Scholar]
- Nagae, T., Oka, K., Matsuda, T., et al. 2004, A&A, 419, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowotny, W., Höfner, S., & Aringer, B. 2010, A&A, 514, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Paczyński, B. 1965, Acta Astron., 15, 89 [NASA ADS] [Google Scholar]
- Paczyński, B. 1971, ARA&A, 9, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [Google Scholar]
- Passy, J.-C., De Marco, O., Fryer, C. L., et al. 2012a, ApJ, 744, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Passy, J.-C., Herwig, F., & Paxton, B. 2012b, ApJ, 760, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlovskii, K., & Ivanova, N. 2015, MNRAS, 449, 4415 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B., & Kratter, K. M. 2012, ApJ, 760, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Placco, V. M., Frebel, A., Beers, T. C., & Stancliffe, R. J. 2014, ApJ, 797, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1989, Numerical Recipes in C. The Art of Scientific Computing (Cambridge: University Press) [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rastegaev, D. A. 2010, AJ, 140, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2008, ApJ, 672, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., & Matteucci, F. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saladino, M. I., Pols, O. R., van der Helm, E., Pelupessy, I., & Portegies Zwart, S. 2018, A&A, 618, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soker, N. 2000, A&A, 357, 557 [NASA ADS] [Google Scholar]
- Stancliffe, R. J. 2009, MNRAS, 394, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Stancliffe, R. J., & Glebbeek, E. 2008, MNRAS, 389, 1828 [Google Scholar]
- Stancliffe, R. J., Glebbeek, E., Izzard, R. G., & Pols, O. R. 2007, A&A, 464, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starkenburg, E., Shetrone, M. D., McConnachie, A. W., & Venn, K. A. 2014, MNRAS, 441, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Suda, T., Katsuta, Y., Yamada, S., et al. 2008, PASJ, 60, 1159 [NASA ADS] [Google Scholar]
- Suda, T., Yamada, S., Katsuta, Y., et al. 2011, MNRAS, 412, 843 [NASA ADS] [Google Scholar]
- Theuns, T., & Jorissen, A. 1993, MNRAS, 265, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Theuns, T., Boffin, H. M. J., & Jorissen, A. 1996, MNRAS, 280, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, I. B., Ivans, I. I., Bisterzo, S., et al. 2008, ApJ, 677, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A. 2014, AJ, 147, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Swaelmen, M., Boffin, H. M. J., Jorissen, A., & Van Eck, S. 2017, A&A, 597, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loon, J. T., Cioni, M.-R. L., Zijlstra, A. A., & Loup, C. 2005, A&A, 438, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Winckel, H., Waelkens, C., & Waters, L. B. F. M. 1995, A&A, 293 [Google Scholar]
- Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Vos, J., Østensen, R. H., Marchant, P., & Van Winckel, H. 2015, A&A, 579, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Waelkens, C., Van Winckel, H., Waters, L. B. F. M., & Bakker, E. J. 1996, A&A, 314, L17 [NASA ADS] [Google Scholar]
- Woods, T. E., & Ivanova, N. 2011, ApJ, 739, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Yong, D., Norris, J. E., Bessell, M. S., et al. 2013, ApJ, 762, 27 [CrossRef] [Google Scholar]
Appendix A: Fit to ballistic calculations
Brookshaw & Tavani (1993) compute the average specific angular momentum 〈jw〉 of test particles ejected from the surface of a star and subsequently lost from a binary system, after following their ballistic trajectories in the binary potential. They present their results in terms of a quantity
which is related to our parameter η as hcm = η(1 + Q). However, in their calculations the mass-losing star co-rotates with the orbit, so that hcm includes both orbital and spin angular-momentum loss. Since the binary_c code already accounts for spin angular-momentum loss and spin-orbit coupling explicitly, we should avoid including this effect twice. Thus η should include only the orbital angular-momentum loss. We expect the spin angular momentum loss to contribute a term equal to 〈jrot〉 = ⅔ R2Ωorb for a co-rotating star of radius R, which implies that
Table 13 of Brookshaw & Tavani (1993) presents values of hcm for various mass ratios and Roche-lobe filling factors, Ψ = R/RL, of the mass-losing star. Because in these calculations the particles are ejected at very high velocity, we expect the Jeans approximation to be valid, that is we expect η to be equal to ηiso = (1 + Q)−2 (Eq. (3)). We verified that this is indeed the case when applying Eq. (A.2) to all the values in Table 13.
We thus proceed to use Eq. (A.2) to study the dependence of η on the particle injection velocity υin. We use the results of Table 1, in which isotropic mass loss from the surface of a Roche-lobe filling star is assumed. Applying Eq. (A.2) in this case is not quite correct because it neglects the non-spherical shape of a Roche-lobe filling star, but it is accurate enough for our purposes. Table 1 tabulates hcm as a function of the mass ratio Q and the parameter V = υin/υorb,d, where υorb,d = υorb/(1 + Q) is the orbital velocity of the donor star around the centre of mass and υorb is the relative orbital velocity of the binary. Figure A.1 shows the corresponding η as a function of υin/υorb for several values of Q, together with the fitting formula of Eq. (6). In using the latter we have identified υw with υin. For υin ≳ 3υorb the results of the ballistic calculations reproduce the Jeans mode, ηiso (horizontal parts of the curves) while for υin ≲ υorb the results converge to a constant value of η ≈ 1.7, independent of mass ratio.
 |
Fig. A.1. Results from Table 1 of Brookshaw & Tavani (1993) for several mass ratios Q (coloured squares) as a function of υin/υorb. Solid lines show the fitting formula Eq. (6) for the corresponding mass ratios. |
Appendix B: Reduced time of radial-velocity monitoring
Figure B.1 illustrates how the assumption of two different radial-velocity monitoring times, namely tobs = 3000 and tobs = 1000 days (blue-dashed and red-dotted lines, respectively) modifies the period distribution of the synthetic CEMP-s systems. The period distributions are computed with our default model set M2 and a detection threshold of Kmin = 0.1 km s−1. The period distribution of all our synthetic CEMP-s stars is also shown for comparison (black-dashed line).
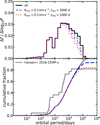 |
Fig. B.1. As Fig. 5 for models with different time-span of the radial-velocity monitoring. The solid black line shows the period distribution of all the CEMP-s stars in our simulation. The dashed blue and dotted red lines are computed with a detection threshold Kmin = 0.1 km s−1 and a time-span of 3000 and 1000 days, respectively. |
All Tables
Input physics adopted in our calculated binary-population models and predicted fraction of CEMP stars.
All Figures
 |
Fig. 1. Period-eccentricity diagram of the binary systems detected by Hansen et al. (2016, blue-filled circles) and of all other known binary CEMP-s stars in the literature (Suda et al. 2008, 2011; Jorissen et al. 2016, black crosses). |
| In the text | |
 |
Fig. 2. Specific angular momentum, (in units of a2Ωorb), as a function of the orbital period of binary systems with fixed primary mass, Mdon = 0.9 M⊙, and mass ratios Q = 1.05, 2 (left and right panels, respectively). The solid, dashed, dot-dashed and dotted lines show, respectively, the profiles of η as computed with Eqs. (2) and (3) with γ = 2, (4) and (5). |
| In the text | |
 |
Fig. 3. Initial period distributions adopted in our models. The vertical axis represents the binary fraction in each period bin, i.e. flog P. The solid black line represents our default initial distribution of separations, which is flat in log10 ai between 5 R⊙ and 5 × 106 R⊙, with flog P = 0.11 over this interval. The dashed brown line shows the prescription of Moe & Di Stefano (2017), adopted in set M13, for a 1.0 M⊙ primary and mass ratio M2,i/M1,i > 0.1. The shape and maximum of the distribution of Moe & Di Stefano (2017) depend on the primary mass and mass ratio. The dotted green line shows a period distribution flat in log10 Pi and with flog P = 0.15 in the period range [10, 2 × 104] days, which we adopt in our model set M14. The integral of each curve represents the total binary fraction over the period interval. |
| In the text | |
 |
Fig. 4. Panel a: period distributions of synthetic CEMP-s stars computed with our model set M2 and with different adopted detection thresholds for radial-velocity variations. The dashed black line shows the period distribution of all the CEMP-s stars in our simulation. The dot-dashed blue and dotted orange lines show the period distributions of the simulated CEMP-s stars with detection thresholds of Kmin = 0.1 and 0.5 km s−1, respectively. Panel b: same as in panel a for synthetic CEMP-s stars that would be detected as singles with the above thresholds. Panel c: the cumulative orbital-period distributions corresponding to the models in panel a are compared with the observed distribution calculated with the data of Hansen et al. (2016, solid grey line). |
| In the text | |
 |
Fig. 5. As Fig. 4 for models with different RLOF stability criteria. Model set M1 adopting the H02 criterion is shown by the dashed green line. Model set M2 (thin, solid black line) uses the CH08 criterion. Model set M3 with Qcrit = 106 (i.e. RLOF from AGB stars is always stable) is indicated by the dotted magenta line. The top panel shows the entire simulated populations, while in the the bottom panel only CEMP-s stars detectable as binary systems are shown (Kmin = 0.1 km s−1 is adopted). |
| In the text | |
 |
Fig. 6. As Fig. 5 for model sets M2 and M5 (dashed blue line) in which the wind accretion efficiency is computed with the WRLOF and BHL prescriptions, respectively. |
| In the text | |
 |
Fig. 7. As Fig. 5 for different for angular-momentum-loss prescriptions. Model set M2 assumes isotropic wind mass loss. Model sets M9, M11, and M12 (dotted red, dot-dashed orange, and dashed violet lines, respectively) are computed with Eq. (4) and γ = 2, 3, 6, respectively. |
| In the text | |
 |
Fig. 8. As Fig. 7 with model sets M6 (dashed line) and M7 (dot-dashed line), in which the angular-momentum loss is computed with Eq. (5) and υw = 15 and 7.5 km s−1, respectively, and set M8 (dotted line), in which Eq. (6) is adopted. |
| In the text | |
 |
Fig. 9. As Fig. 5 for different distributions of initial separations and periods. By default ai/R⊙ is in [5, 5 × 106] (solid black line). The dashed line is computed using the initial log P–distribution of Moe & Di Stefano (2017, Eq. (23)). In model set M14 Pi is log-flat between 10 and 20 000 days (dotted line). |
| In the text | |
 |
Fig. 10. As Fig. 5 for different accretion-efficiency and angular-momentum-loss prescriptions. Model set M2 adopts the WRLOF model of wind accretion and assumes isotropic wind mass loss. Model set M10 (dotted magenta line) is computed with Eq. (4) and γ = 2, and adopts the BHL model with α = 1.5. Model sets M15 and M16 (dot-dashed blue and dashed green lines, respectively) compute wind accretion efficiency with α = 10 within the BHL model. Set M15 assumes isotropic wind mass loss, whereas set M16 uses Eq. (4) with γ = 2. |
| In the text | |
 |
Fig. A.1. Results from Table 1 of Brookshaw & Tavani (1993) for several mass ratios Q (coloured squares) as a function of υin/υorb. Solid lines show the fitting formula Eq. (6) for the corresponding mass ratios. |
| In the text | |
 |
Fig. B.1. As Fig. 5 for models with different time-span of the radial-velocity monitoring. The solid black line shows the period distribution of all the CEMP-s stars in our simulation. The dashed blue and dotted red lines are computed with a detection threshold Kmin = 0.1 km s−1 and a time-span of 3000 and 1000 days, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ {{\beta }_{\text{BHL}}}=\frac{{{\alpha }_{\text{BHL}}}}{2\sqrt{1-{{e}^{2}}}}.{{\left( \frac{G{{M}_{\text{acc}}}}{a\nu _{\text{w}}^{2}} \right)}^{2}}{{\left[ 1+{{(\frac{{{\nu }_{\text{orb}}}}{{{\nu }_{\text{w}}}})}^{2}} \right]}^{-\frac{3}{2}}}, $$](/articles/aa/full_html/2018/12/aa33780-18/aa33780-18-eq1.gif)
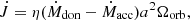
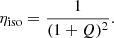
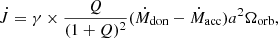
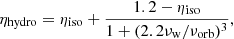
![$$ {{\eta }_{\text{BT93}}}=\text{max}\left\{ {{\eta }_{\text{iso}}},\frac{1.7}{1+{{[(0.6+0.02Q)\cdot {{\nu }_{\text{w}}}/{{\nu }_{\text{orb}}}]}^{6}}} \right\}. $$](/articles/aa/full_html/2018/12/aa33780-18/aa33780-18-eq6.gif)