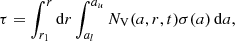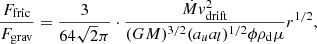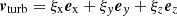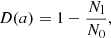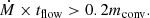| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833353 | |
| Published online | 28 November 2018 | |
Dust cleansing of star-forming gas
II. Did late accretion flows change the chemical composition of the solar atmosphere?
1 Department of Physics and Astronomy, Uppsala University, Sweden
e-mail: bengt.gustafsson@physics.uu.se
2 Nordic Institute for Theoretical Physics (NORDITA), Stockholm, Sweden
Received:
3
May
2018
Accepted:
31
August
2018
Aims. The possibility that the chemical composition of the solar atmosphere has been affected by radiative dust cleansing of late and weak accretion flows by the proto-sun itself is explored.
Methods. Estimates, using semi-analytical methods and numerical simulations of the motion of dust grains in a collapsing non-magnetic and non-rotating gas sphere with a central light source are made in order to model possible dust-cleansing effects.
Results. Our calculations indicate that the amount of cleansed material may well be consistent with the abundance differences observed for the Sun when compared with solar-like stars and with the relations found between these differences and the condensation temperature of the element.
Conclusions. It seems quite possible that the proposed mechanism produced the significant abundance effects observed for the Sun, provided that late and relatively weak accretion did occur. The effects of cleansing may, however, be affected by outflows from the Sun, the existence and dynamics of magnetic fields and of the accretion disk, and the possible presence and location of the early Sun in a rich stellar cluster.
Key words: dust, extinction / stars: abundances / stars: formation / Sun: abundances
© ESO 2018
1. Introduction
The results by Meléndez et al. (2009), showing that the Sun departs from most solar twins in the solar neighbourhood in that the composition of its surface layers is comparatively rich in volatile elements and poor in refractory elements, have led to considerable discussion (for a recent review see Adibekyan et al. 2017). Although the finding, a correlation between the chemical abundances for the Sun relative to the twins with the condensation temperatures of the elements in a gas, has been verified by several independent studies (Ramírez et al. 2009; Gonzalez et al. 2010; Adibekyan et al. 2014; Nissen 2015; Spina et al. 2016), its interpretation is still disputed. The early suggestion by Meléndez et al. (2009) that it could be due to the formation of terrestrial planets in the proto-planetary nebula before the latter was dumped onto the Sun, polluting its convection zone by dust-cleansed gas, requires either an unusually long-lived nebula or a very rapid retraction of the solar convection zone to the surface (cf. Gustafsson et al. 2010). As suggested by Önehag et al. (2011) this early retraction might result from the episodic accretion scenario according to Baraffe & Chabrier (2010), if applied to the Sun but not to the twins. The alternative, that is, that the effect is due to Galactic chemical evolution, and migration of the Sun from other galactic regions than those of the twins, was suggested and partly supported by tendencies found by Adibekyan et al. (2014), Maldonado et al. (2015), Maldonado & Villaver (2016), and Nissen (2015) for some correlation of the abundance effects to depend on stellar ages. Still another possibility was offered by Gustafsson et al. (2010) who proposed that the pre-solar nebula was cleansed early on from dust by the radiation pressure from hot stars in the neighbourhood. This was supported by the results of Önehag et al. (2011, 2014) who carried out detailed analyses of solar-twins and solar analogues in the rich, old cluster M 67, and found the cluster stars to have an abundance profile more similar to that of the Sun than most solar twins in the neighbourhood. However, Gustafsson (2018) recently found that the cleansing mechanism proposed was unlikely to be efficient enough to explain the chemical peculiarities of a relatively massive cluster like M 67. Also, the recent finding of binary stars with one component showing deviating abundances from that of the other, such as 16 Cyg (Tucci Maia et al. 2014; Nissen et al. 2017), XO-2N/XO-2S (Ramírez et al. 2015; Biazzo et al. 2015), WASP 94 A/B (Teske et al. 2016a), HD 133131 A/B (Teske et al. 2016b), HAT-P-4 (Saffe et al. 2017) and the co-moving pair HD 240430/HD 1240429 (Oh et al. 2018), and sometimes with differences correlating with the condensation temperature of the element, suggests that the phenomenon may be local.
The results by Meléndez et al. (2009), showing that the Sun departs from most solar twins in the solar neighbourhood in that the composition of its surface layers is comparatively rich in volatile elements and poor in refractory elements, have led to considerable discussion (for a recent review see Adibekyan et al. 2017). Although the finding, a correlation between the chemical abundances for the Sun relative to the twins with the condensation temperatures of the elements in a gas, has been verified by several independent studies (Ramírez et al. 2009; Gonzalez et al. 2010; Adibekyan et al. 2014; Nissen 2015; Spina et al. 2016), its interpretation is still disputed. The early suggestion by Meléndez et al. (2009) that it could be due to the formation of terrestrial planets in the proto-planetary nebula before the latter was dumped onto the Sun, polluting its convection zone by dust-cleansed gas, requires either an unusually long-lived nebula or a very rapid retraction of the solar convection zone to the surface (cf. Gustafsson et al. 2010). As suggested by Önehag et al. (2011) this early retraction might result from the episodic accretion scenario according to Baraffe & Chabrier (2010), if applied to the Sun but not to the twins. The alternative, that is, that the effect is due to Galactic chemical evolution, and migration of the Sun from other galactic regions than those of the twins, was suggested and partly supported by tendencies found by Adibekyan et al. (2014), Maldonado et al. (2015), Maldonado & Villaver (2016), and Nissen (2015) for some correlation of the abundance effects to depend on stellar ages. Still another possibility was offered by Gustafsson et al. (2010) who proposed that the pre-solar nebula was cleansed early on from dust by the radiation pressure from hot stars in the neighbourhood. This was supported by the results of Önehag et al. (2011, 2014) who carried out detailed analyses of solar-twins and solar analogues in the rich, old cluster M 67, and found the cluster stars to have an abundance profile more similar to that of the Sun than most solar twins in the neighbourhood. However, Gustafsson (2018) recently found that the cleansing mechanism proposed was unlikely to be efficient enough to explain the chemical peculiarities of a relatively massive cluster like M 67. Also, the recent finding of binary stars with one component showing deviating abundances from that of the other, such as 16 Cyg (Tucci Maia et al. 2014; Nissen et al. 2017), XO-2N/XO-2S (Ramírez et al. 2015; Biazzo et al. 2015), WASP 94 A/B (Teske et al. 2016a), HD 133131 A/B (Teske et al. 2016b), HAT-P-4 (Saffe et al. 2017) and the co-moving pair HD 240430/HD 1240429 (Oh et al. 2018), and sometimes with differences correlating with the condensation temperature of the element, suggests that the phenomenon may be local.
An interesting fact, first noted by Gonzalez et al. (2010), is that the meteoritic elemental abundances show a similar tendency with the condensation temperature to the solar photospheric abundances, in the sense that the meteorites tend to have an even lower ratio of refractory elements relative to volatiles, than the photosphere. This also suggests that the phenomenon should at least partially be local.
The issue studied in the present paper is whether radiative cleansing of the matter accreted onto the Sun could be provided by the proto-Sun itself, in its accretion flow. For this mechanism to work, the friction forces between the dust-grains and the gas as well as the gravity forces must be balanced by the radiative forces. Since the friction is dependent on the flow, this mechanism requires constraints on the density of the flow and on its infall velocity in order to work. Other constraints will be important, such as those on the luminosity of the proto-Sun and on the extinction in the cloud around it. We shall use elementary considerations to explore these constraints and shall then apply a somewhat more detailed model to quantify the possibilities of the suggested mechanism to explain the observed abundances in the presence of turbulence in the cloud.
Our model mimics an initially homogeneous cloud of neutral atomic or molecular gas with dust, and with a light source representing the early Sun in its centre. The aim will be to find out of whether or not the radiative pressure from the Sun is able to prevent the dust, and thus the chemical elements in the dust, to fall onto the star.
2. The model and the results
We consider a specific dust grain, assumed to be spherical with radius a and mass m. We set the vector, extending in space from the Sun to the grain, r , with a unit vector er in the direction of r. In interstellar clouds, the mean free path of the molecules is orders of magnitude longer than the size of the dust grains. In this case the equation of motion for a grain with mass m, illuminated by the Sun with luminosity L and mass M, can be written (see Draine 2011a))
The three terms on the right-hand side (RHS) represent the radiative force, the gravity, and the friction force exerted by the gas on the grain, respectively. The electromagnetic radiation is attenuated by extinction, and the grain is located at an optical depth τ from the Sun at time t. The factor qpr is numerical, and is dependent on the grain composition and shape, and on wavelength. For the relevant dust and stellar light discussed here a mean 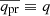 of about 1.5 may be adopted, see, however, Fig. 1 of Ferrara et al. (1991), indicating that a higher value up to q = 2.5 could be appropriate for minor graphite grains. Similarly, if the grains have a composite fluffy character, as suggested by Kimura (2017) on the basis of captured Local Interstellar Cloud grains, an increase of q by up to a factor of two may be adequate for the more massive particles. The speed of light is c and Newton’s constant of gravity is G. The dust grain is retarded by a drag force, described by the last term of the right-hand side of Eq. (1). The number density of atoms or of molecules is n(t), the kinetic temperature is T, and k is Boltzmann’s constant. Following Draine (2011a) we may write
of about 1.5 may be adopted, see, however, Fig. 1 of Ferrara et al. (1991), indicating that a higher value up to q = 2.5 could be appropriate for minor graphite grains. Similarly, if the grains have a composite fluffy character, as suggested by Kimura (2017) on the basis of captured Local Interstellar Cloud grains, an increase of q by up to a factor of two may be adequate for the more massive particles. The speed of light is c and Newton’s constant of gravity is G. The dust grain is retarded by a drag force, described by the last term of the right-hand side of Eq. (1). The number density of atoms or of molecules is n(t), the kinetic temperature is T, and k is Boltzmann’s constant. Following Draine (2011a) we may write
where vdriftev, vg = v − vg is the drift velocity of the grain relative to the gas in the direction ev, vg, with v = dr/dt and vg being the velocities of the grain and the gas, respectively, and mH the mass of the hydrogen atoms or molecules, whatever species is assumed to dominate the gas. In the expression for B(s) in Eq. (2), the last term represents the Coulomb forces, where U is the grain potential, e the electron charge, and ne the electron density in the gas. The potential is determined by the electric charge on the grain. Neglecting photoelectric emission, this charge is set by the requirement that the positive ions captured per time unit be balanced by the number of electron captured. For small degrees of ionization one then finds from Eqs. (9–15) of Spitzer (1978) that eU/kT = −3.76. One may schematically estimate the photoelectic emission (positive) contribution to the potential, as a result of the interstellar ultraviolet (UV) background. Following Spitzer (1978), p. 144–146 and his Eqs. (6–20), setting the sticking probability of electrons striking the grain and the absorption efficiency factor equal to 1, and adopting a value of 0.1 for the photoelectric efficiency of radiation with wavelengths in the interval 91–110 nm, and else much smaller, and assuming the optical depth to be small, we obtain a photoelectric contribution to eU/kT of:
To this we should add a contribution due to the radiation from the early Sun. We take the flux in the relevant UV interval of the present Sun from Lean (1987) to be representative, and then multiply the right-hand side of Eq. (4) by a factor (1 + 2.2 × 1030/r 2) where the distance to the Sun is r in centimetres. For our neutral gas (with degrees of ionization n(e)/n(H)=2.72 × 10−4 at T = 160 K from Table 30.1 in Draine 2011b) we find the Coulomb force term to be relatively small for the local contribution from the electron-ion balance. However, we shall see that the photoelectric charging of the grains has some significance.
We note that the dependence of the drag force on the drift velocity is linear for small speeds – in typical cases with T = 10 K the shift to a mainly quadratic dependence occurs around vdrift ∼ 400 m s−1 which is higher than typical sound speeds in the cool neutral gas but smaller than typical free-fall velocities for gas at distances of several thousand astronomical units (AU) from the Sun.
We assume that the gas velocity is not affected notably by the friction of the grains, and is set by
where the free-fall velocity in the first term is corrected by the fluctuating turbulent velocity of the gas, vturb = vturb(r, t). For the gas density we assume spherical symmetry around the Sun and a time-independent situation, that is,
where β is usually chosen to be 3/2, corresponding to a stationary flow, or alternatively 2, as suggested by Shu (1977), and with the density profile of an isothermal sphere. There is observational support for such power-law density profiles for collapsing proto-stellar clouds and low-mass protostars (e.g. Loren et al. 1983; Jørgensen et al. 2002; Persson et al. 2016), but they are singular at r = 0 and invalid close to the star. We have stopped the integration at r = 100 AU to take the existence of an accretion disk into account. In solving Eq. (1), we alternatively set the initial velocity of the grain to v0 = 0 or 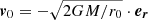 , that is, the free-fall velocity, at t = 0 and r = r0. The factor r0 is set to 1000 AU and alternatively 10 000 AU. The number density of hydrogen atoms/molecules at r0 is calculated to correspond to a given accretion rate Ṁ at r0, calculated with the assumption of the free-fall speed from zero speed at infinity and a stationary flow which leads to
, that is, the free-fall velocity, at t = 0 and r = r0. The factor r0 is set to 1000 AU and alternatively 10 000 AU. The number density of hydrogen atoms/molecules at r0 is calculated to correspond to a given accretion rate Ṁ at r0, calculated with the assumption of the free-fall speed from zero speed at infinity and a stationary flow which leads to
where μ is 1 + (Y + Z)/X with X, Y and Z being the mass fractions of hydrogen, helium, and elements heavier than helium, respectively, in the gas. We end the calculation when the dust grain has reached a certain inner radius r1; here, the neglect of a net angular momentum for the system is certainly inadequate, and the dust should in reality have ended up in an accretion disk. We also stop the integration at a time of 6 Myr. Then, in practice dust grains that have not reached the inner radius are pushed out to relatively large distances from the Sun by the radiative forces and are regarded as lost from the system.
2.1. The non-turbulent case
We shall first assume the turbulence velocities to be zero, that is, vturb is set equal to 0 in Eq. (5). In this case the flows of grains and gas will constantly be directed towards the Sun, and the model will remain spherically symmetric. The equation of motion is simplified to
where ρd is the mass density in the dust grains.
The present discussion is focussed on the conditions in the gas at a considerable distance from the Sun during the last accretion in its formation history, assumed to entail relatively thin gas. Therefore, an approximation made in our estimates below is the assumption of small optical depths; for example, we assume τ = 0 in Eqs. (1) and (8). In a subsection below, we explore the adequacy of this assumption.
Two necessary conditions for the dust to be accelerated outwards are seen directly from Eq. (8). The radiative force has to be greater than the gravity force on the grain, that is, the large parenthesis on the RHS has to be positive, such that
With characteristic numbers for the parameters (L = 0.5 L⊙, q = 1.5, ρd = 1 g cm−3, and M = 1 M⊙) we find amax = 4.5 × 10−5 cm. This constraint implies that, with a dust size distribution N(a)∼a −3.5, as is often assumed following Mathis et al. (1977), see also Casuso & Beckman (2010), and extending from a = 10−7 to 10−4 cm−3, more than half of the total dust mass in the accreting flows may be pushed out by radiation with this choice of parameters.
The second necessary condition for an outward acceleration is that the radiative force in Eq. (8) is stronger than the friction force due to the down-streaming gas. Since 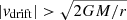 for outgoing grains and neglecting the electric forces, we find from Eqs. (2), (3) and (8)
for outgoing grains and neglecting the electric forces, we find from Eqs. (2), (3) and (8)
With characteristic numbers as above, and with T = 10 K, we find from Eq. (10) a maximum accretion rate of 0.050 M⊙ Myr−1 at r = 104 AU or 0.016 M⊙ Myr−1 at r = 103 AU. For small graphite grains with q ∼ 2.5, maximum accretion rates that are almost double this latter rate may be possible. If we require a significant contribution to the star by dust-rarefied gas with a mass of at least the mass of the present convection zone (or more, since the convection zone during the first millions of years of the Sun should have been significantly more massive) we have to assume that the last percents of the solar mass were accreted slowly, during a time of several hundred thousand years or more in order to satisfy the condition of Eq. (10). We note that such accretion rates are at least two orders of magnitude smaller than those of the zoom-in simulations of forming accretion disks in giant molecular clouds (GMCs) by Kuffmeier et al. (2017), and that the timescale of our slow accretion extends far beyond that of these authors as well as the timescale of Shu (1977).
The relative significance of the radiative pressure and the gravity is not dependent on the distance from the star if the optical depth is small, as is demonstrated by the terms within the parentheses in Eq. (8). The r 1/2 dependence in Eq. (10) implies, however, that the upper limit on Ṁ, set by the requirement that dust grains should be stopped from falling inwards by radiation pressure, becomes tighter as the dust grain is brought closer to the star (e.g. by initial momentum or by turbulence). This means that if moving inwards in a given free-fall flow of gas, the dust grains may finally come to a radius rc where they cannot escape from falling into the accretion disk. For the case with high drift speed, we obtain
With characteristic parameters, as above, and with Ṁ = 0.01 M⊙ Myr−1 and a = 2 × 10−5 cm, we find rc = 1.5 × 103 AU. In practice this means that the dust that separates from the infalling gas will have to decouple from the gas already at distances on the order of 1000 AU from the proto-Sun or further out. It is worth noting that these distances overlap with the location of the Oort cometary cloud. Also, the last factor of the last term in Eq. (11) suggests a possible fractionation of dust of different sizes: with the characteristic parameters chosen above, rc = 480 AU for grains with a = 0.35 × 10−5 cm, while rc = 13 000 AU for a = 3.5 × 10−5 cm.
We have explored the possibilities for dust-grains to exist at various distances from the proto-Sun by setting the LHS equal to zero in Eq. (8) and then solving it for different values of Ṁ, a and r. The results for the non-electric case are displayed as full lines in Fig. 1, where the regions in the diagram below each curve are the “allowed” regions, that is, where dust grains will be pushed out by radiation and not pulled by gravity and friction from the in-falling gas towards the stellar accretion disk. The corresponding curves for the case when electric forces are included (dashed blue lines in Fig. 1) clearly show that the critical gas accretion rates, able to sweep dust grains close to the star, are reduced by almost a factor of two, as compared with the case when coulomb forces are neglected. In particular, the results of considering the photo-electric effects on the grains are noteworthy. The effects are particularly important for the larger grains which contribute significantly to the totally accreted mass of dust.
 |
Fig. 1. The “allowed” parameter space (under each curve) for dust grains with radius a that may exist around a star at a certain distance (indicated in AU at each curve) without being accreted to the star by gravity and friction from the in-falling gas with different accretion rates Ṁ. The full lines correspond to cases with neutral grains while dashed blue curves indicate corresponding cases with electrically charged grains. The approximate upper limit on a, according to Eq. (9), is indicated by a vertical red line, while the approximate upper limit on dM/dt ≡ Ṁ for a distance from the star of 103 AU, according to Eq. (10), is indicated by a horizontal red line. Also shown is the approximate critical radius rc as calculated by Eq. (11) as a dashed red curve. The fair agreement between the approximate (in red) and the more exact (black) curves is due to the fact that the quadratic term in the dependence of the friction force on drift speed, cf. Eq. (2), is indeed dominating, as assumed in the approximations. The reduction of the “allowed” accretion rates for the charged grains relative to the corresponding cases with neutral ones is obvious. |
2.2. The optical depth effects and the friction forces onto the gas
Above, we have assumed that the medium is transparent to the radiation from the star in the centre, thus assuming that the dust grains close to the star do not shadow the grains behind. In order to take such possible shadowing effects into consideration, we shall calculate the optical depth in the stellar envelope. We then disregard the effect of the dust in the accretion disk, which may well be optically thick in certain directions. The optical depth τ in the converging accretion flow, assumed to be spherically symmetric around the star, is
where σ(a), which we here set equal to πa 2, is the absorption cross-section per grain, and NV(a, r, t) is the number of dust grains with radii in the interval (a, a + da) per volume unit at time t. When calculating NV we have solved the equation of motion (Eq. (8)) for a range of different a values from al = 10−7 cm to au = 10−4 cm, distributed in size in proportion to ∼a −3.5 according to Mathis et al. (1977), in a convergent and stationary gas flow in free fall (i.e. applying Eq. (5) with vturb = 0 and with β = 3/2 in Eq. (6)). The gas-to-dust mass ratio was assumed to be 100, however, noting that there may be considerable variations in this ratio in interstellar clouds (see, e.g. Reach et al. 2015). As initial conditions we have alternatively chosen v(r0)=0 and v(r0)=vff(r0), with vff denoting the free-fall velocity with a start at rest in infinity, however with little effects on the end results. Typical values of r0 and r1 were 10 000 and 1000 AU, respectively. The individual grain orbits have been integrated for at least 1 Myr each in order to ascertain that a stationary situation has been achieved.
When calculating τ we have used an iterative procedure, first setting τ(r)=0 when solving Eq. (8), subsequently calculating τ(r) by Eq. (12), feeding the result into Eq. (8), and so on. In these calculations, we have neglected the coulomb forces in B(s). In practice, with the small resulting τ values, we have found that three iterations are enough to ascertain a satisfactory convergence.The resulting optical depths for three different accretion rates are shown in Fig. 2. As is seen, at these rates the depths are relatively small or even negligible.
 |
Fig. 2. Optical depth as a function of distance from the star for three different accretion rates, 1017 g s−1, 3 × 1017 g s−1 and 1018 g s−1, corresponding to 0.0016, 0.0047 and 0.016 M⊙ Myr−1, respectively. |
A basic reason for the small optical depths is the fact that the numerous grains with small radii are already pushed out by the stellar radiation at great distances from the star, where the gas flow has still not become strong and dense enough to pull them inwards by friction. The dominating dust opacity is instead contributed by the more massive grains, in particular those that have a close to amax as estimated in Eq. (9). The close balance between radiative forces and gravity makes them fall slower towards the star than the more heavy ones, which they also outnumber due to the a −3.5 dependence of the initial number density. The situation is illustrated in Fig. 3, where the opacity contribution by grains of different sizes and at different distances from the star is illustrated.
 |
Fig. 3. Contributions to the dust opacity for grains of different radii a, at different distances from the accreting star indicated at each curve in AU. The opacity contribution is given in cm−1, per logarithmic interval in a. The dominating contribution from grains on the order of a = amax in size, cf. Eq. (9), is seen in the inner regions, and is enhanced by the convergence of the flow, while at greater distances from the star the more numerous smaller grains contribute more, as a result of their initial motion inwards due to the starting condition v(rout)=vff. The curves have been smoothed by a filter with a width of 5 × 10−6 cm, to compensate for fluctuations due to the stochastic nature of the method used. |
In addition to neglecting dust opacities in the model calculations, we have neglected the friction forces from the dust onto the gas. Applying Newton’s third law, one easily finds in the high drift-velocity case that the friction force per gas mass, relative to the corresponding gravity force, is
where ϕ is the gas-to-dust mass ratio. By setting in representative numbers one finds that for our models this ratio is on the order of 10−2 or less, which means that the friction forces on the gas can be neglected. It is obvious, however, that for considerably more intensive gas flows, such that Ṁ > 0.1 M⊙ per million years, or high luminosities increasing the radiative forces and thus vdrift, the friction forces might become significant.
2.3. Conclusions from the spherically symmetric model
It is clear from the results presented above that a slow accretion of gas, with an accretion rate on the order of a few percent of a solar mass per million years, should enable the central star to push most of the grains with radii less than about 5 × 10−5 cm, corresponding to roughly half the grain mass, out of the accretion gas flow. A considerably higher accretion rate will both increase the friction forces and the optical depth of the envelope, due to relatively large grains, so much that the smaller grains fall inwards, and the cleansing becomes significantly weaker. Thus, a model with a moderate accretion flow seems viable to explain stellar atmospheres depleted in dust-forming elements for stars with convection zones of a few percent of the stellar mass, provided that such relatively thin convection zones exist at times when this mild accretion is still active. According to standard models of PMS evolution (Montalbán et al. 2008) the convection zone remains massive, with masses greater than about 0.1 M⊙ until about 20 Myr, while typical accretion gas disks only remain for less than 10 Myr (see, however, Pfalzner et al. 2014). Thus, we may have a timescale problem similar to that discussed for the planet-cleansing hypothesis for the abnormal volatiles/refractories ratio of the Sun (Meléndez et al. 2009; Gustafsson et al. 2010). This could possibly be explained as a result of episodic accretion or more long-lived stages of the late accretion disks.
Another possible caveat of the present model is, however, turbulence which was found by Gustafsson (2018) to be a major problem with the alternative hypothesis of massive dust-cleansing by bright stars as an explanation for the Meléndez effect. The effects of turbulence on the present self-cleansing model are discussed below.
2.4. The turbulent case
The origins and the consequences of the motions in giant molecular clouds are still discussed intensively. Observationally, however, it seems clear that turbulence is present in star-forming regions as well as quiet clouds. Solomon et al. (1987) showed that the CO line widths of the GMCs scaled with the square root of their radii R, according to σv ≈ 0.72(R/pc)0.5 km s−1, which seems to hold down to small scales (cf. Bolatto et al. 2008; Rosolowsky et al. 2008; Heyer & Brunt 2004). The ideal value of σv to be chosen for a model of the solar birth cloud is therefore, however, highly uncertain. We therefor treat it as a free parameter here, varying it between 0.1 and 5 km s−1. To handle the turbulence in the accretion flow of the gas in our model in full detail is beyond the scope of the present paper. Instead, we have followed the schematic recipe of Higham (2001), by re-setting the turbulent velocity, vturb, when solving Eq. (1) numerically every time the derivatives are to be calculated for this solution. We have used the MATLAB routine ODE23 for this purpose, which is based on a Runge–Kutta method with variable (and continuously adjusted) step size in time. The step size is typically 30 yr, which is less than one thousandth of the free-fall time from 10 000 AU. We thus set
in Eq. (5), where ξx, y, z are three independent random numbers drawn for each time step from a Gaussian distribution with a dispersion σv.
Another effect of turbulence is a fluctuating gas density. In order to study the effects of such fluctuations, we have run some models with the density perturbations guided by the log-normal distribution found from detailed simulations by Padoan & Nordlund (2002; their Eq. (6)), around values calculated according to Eq. (6), with a characteristic fluctuation time of 104 years.
At the solution of Eq. (1) we have set the optical depth equal to zero, guided by our results in Sect. 2.2. Subsequently, the solution entails solving three coupled second-order non-linear differential equations. For each run, this has been done for 1000 different dust grains of given radii a, initially located at a distance of r0 = 10 000 AU from the star (along the positive z axis). In subsequent runs, a, σv, Ṁ, and the initial condition have been varied, one at a time. For the initial velocity of the dust grain at the starting distance we have alternatively used v(r0) = 0 and 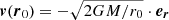 . The integration proceeds for 5 Myr. If the orbit during this time gets closer to the star than 100 AU, we assume the grain to be caught in the accretion disk around the star, and finally fall into the star. Conversely, if it does not get closer to the star during this time we consider it lost. Grains that belong to this class are usually accelerated to very large distances from the star by the radiative pressure. One should note that in these simulations we totally neglect the outflows from the central disk, known observationally to carry away a considerable fraction of the mass; see Alexander et al. (2014) and references therein.
. The integration proceeds for 5 Myr. If the orbit during this time gets closer to the star than 100 AU, we assume the grain to be caught in the accretion disk around the star, and finally fall into the star. Conversely, if it does not get closer to the star during this time we consider it lost. Grains that belong to this class are usually accelerated to very large distances from the star by the radiative pressure. One should note that in these simulations we totally neglect the outflows from the central disk, known observationally to carry away a considerable fraction of the mass; see Alexander et al. (2014) and references therein.
In most of these simulations for the turbulent case we have neglected the effects of coulomb forces on the grains. To check their significance, however, we made a series of simulations, taking the charging of the grains into account. With the parameters of these effects set as described above, they are found to have relatively limited effects on the results, the most important one being that due to the photoelectric charging. This is further illustrated below.
Two typical runs, though limited to 100 grains for each a value and with integration times of only 0.1 Myr for clarity, are illustrated in Figs. 4 and 5. The spread of the orbits into broom-like structures is entirely due to the turbulence; if vturb is set equal to 0 the orbits collapse to a single vertical line. It is obvious from these figures that the choice of initial conditions for the velocity is important for the orbits, although the fraction of grains falling into the star as a function of grain radius is not as dependent on these conditions.
 |
Fig. 4. The orbits of grains over 105 yr, from a point indicated by an “x” in black along the z axis at a distance of 104 AU from the star (which is at the origin of the coordinate system), and with different grain radii a as indicated by the different colours. The dust grains were given an initial velocity identical to the gas free-fall velocity. The turbulent mean speed was set to 0.1 km s−1. We note that the scales of the x and y axes are different from that of the z axis. |
 |
Fig. 5. The orbits of grains over 105 yr, from a point indicated by an “x” in white along the z axis at a distance of 104 AU from the star (which is at the origin of the coordinate system), and with different grain radii a as indicated by the different colours. The initial velocity of the dust grains was set to zero. The turbulent mean speed was set to 0.1 km s−1. We note that the scales of the x and y axes are different from that of the z axis. |
The main results of these numerical experiments are displayed in Fig. 6. Here we have plotted a quantity called “the defect”, D(a), of the run, as a function of a for different choices of the defining parameters. D(a) measures the fraction of grains that leave the proto-solar cloud as a result of the radiative cleansing. It is defined as
where Nl is the number of dust grains lost inside 100 AU, and N0 is the corresponding number lost in a run with identical parameters with the exception that the stellar luminosity L is set equal to zero. In this way, we try to correct for the fact that even at zero luminosity some of the gas may depart at high turbulence speeds from the stellar neighbourhood. It is seen from the figure that the variation of D with a is smoothed when vturb increases, from a very steep change when a passes the limiting value in Eq. (9) for small turbulence, to a less steep variation. We also note that an increased inflow of gas decreases the deficit at a given a, as does a change of the initial condition from v(r0)=0 to setting v(r0) equal to the free fall velocity of the gas flow. Also, the coulomb forces diminish D but not drastically so. None of these effects is unexpected. Obviously, these variations of the deficit with the different parameters are not very dramatic: the conclusions concerning the cleansing effects in our model are clearly relatively robust with regard to its uncertain parameters. This may be seen by calculating the integrated deficit, 𝒟, as
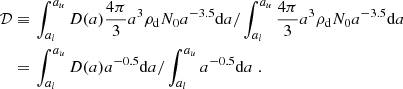 (16)𝒟 measures the fraction of the dust mass that is pushed away from the star instead of falling into it. In Table 1 we present the values of 𝒟 for our different models in Fig. 6, and some other models. The inclusion of electrical forces and in particular the photo-electric charging obviously leads to a moderate decrease of 𝒟. Also, turbulence-generated density variations lead to a not very dramatic shift of D(a) to smaller values (model no. 10 in the table). As seen in the table (model no. 11), an adopted variation of the density as 1/r2, still assuming the inflow gas velocity to be roughly proportional to 1/r
3/2 which means that the gas is piling up in the inner region of the gas envelope, leads only to small effects compared with the standard stationary flow models with ρ ∝ r−3/2. It seems that a rather robust conclusion may be drawn: about half the mass of dust in a late accretion flow towards a solar-type star is cleansed from the flow by the radiative forces of the star itself, as long as the in-falling gas mass rate is not higher than about 0.01 M⊙ Myr−1.
(16)𝒟 measures the fraction of the dust mass that is pushed away from the star instead of falling into it. In Table 1 we present the values of 𝒟 for our different models in Fig. 6, and some other models. The inclusion of electrical forces and in particular the photo-electric charging obviously leads to a moderate decrease of 𝒟. Also, turbulence-generated density variations lead to a not very dramatic shift of D(a) to smaller values (model no. 10 in the table). As seen in the table (model no. 11), an adopted variation of the density as 1/r2, still assuming the inflow gas velocity to be roughly proportional to 1/r
3/2 which means that the gas is piling up in the inner region of the gas envelope, leads only to small effects compared with the standard stationary flow models with ρ ∝ r−3/2. It seems that a rather robust conclusion may be drawn: about half the mass of dust in a late accretion flow towards a solar-type star is cleansed from the flow by the radiative forces of the star itself, as long as the in-falling gas mass rate is not higher than about 0.01 M⊙ Myr−1.
 |
Fig. 6. The defect, D(a), (cf. Eq. (15)) as a function of grain radius a for different values of the turbulence speeds vturb and with initial dust velocities = v0 = 0 and with infall rate of gas Ṁ = 0.002 M⊙ Myr−1 shown in thin lines. Red line: Coulomb forces, excluding photo-electric effect, taken into account with an ionization ratio of n(e)/n(H)=2.72 × 10−4. Thick line: doubled infall rate, vturb = 1 km s−1. Dashed line: initial speed v0= initial free-fall velocity of the gas, vturb = 1 km s−1, Ṁ = 0.002 M⊙ Myr−1. |
Values of the integrated deficit, 𝒟, for runs of models with turbulence.
The present model is unrealistic in several respects. One of the most important simplifications relative to reality is the neglect of magnetic fields. The star-forming clouds and the protostars are known to be magnetic (see e.g. Higuchi et al. 2018; Hull et al. 2018, and references therein), which may have consequences for the dynamics of the in-falling gas. Also, since the grains may be charged, their dynamics may be directly affected by the fields. We have addressed the question of whether the fields threading the gas are swept along by it by estimating the timescale for ambipolar diffusion of the field out of the gas, following Eq. (2.18) of Hennebelle (2012), which shows that the diffusion time varies as n ⋅ ni (L/B)2 where n and ni are the number densities of atoms and of ions, respectively, L is a characteristic length scale and B is the field strength. For our extended and thin flows (L ∼ 1000 AU, n ∼ 0.3 × 103 cm−3 and for characteristic numbers of the ionization fractions in the cold gas and with B set to a few microGauss (Padoan 2018), diffusion timescales are at least one order of magnitude greater than 106 years. Therefore, the magnetic fields are swept along by the in-falling gas. Our estimates of the magnetic-field energy density EB, as compared with the kinetic energy density EK of the gas and its gravitational energy density EG, show that EB ≪ EK ∼ EG, which suggests that the magnetic effects on the gas dynamics are only marginal. As regards the direct effects of the magnetic fields on the dynamics of the grains, they may, however be very considerable. According to Draine (2011a) the dynamics is determined by the dimensionless quantity ω ⋅ τdrag where ω is the gyro-frequency (proportional to the field strength and the charge-to-mass ratio of the grain), and τdrag = (m ⋅ v)/Fdrag is the drag timescale for the grain with a drag force Fdrag, a mass m and a speed v. From Eq. (30) of Draine (2011a), we find with our characteristic numbers that ωτdrag may be typically in the range 1–10, which means that the magnetic fields, if oriented at angles relative to the forces on the grain, may significantly affect its motions. In particular, if the magnetic field is perpendicular to the direction from the grain towards the star, with the radiative force on the grain dominating relative to gravity and the gas drag force, the grain will nevertheless be dragged along in the inflow motion of the gas by the magnetic field. Key factors affecting the degree to which magnetic fields may thus hamper the radiative dust cleansing are therefore (1) the number of magnetic field lines in the outer regions of the gas (at r ∼ 103 AU) in late and thin accretion flows that are close to perpendicular to the flow lines and (2) how stationary such regions are, that are locking the grains to the collapsing gas; that is, if the characteristic time for reorientation of the field in the gas due to turbulence is smaller or greater than the free-fall time of the gas towards the star. The study of such questions requires more detailed numerical MHD simulations.
The effects of angular momentum are also neglected in the present simple model, which may be relevant since much of the dust-gas separation takes place at relatively great distances from the central star. However, closer to the star the orbits of the grains may be quite different due to their intrinsic angular momentum, and the non-radial drag of the rotating gas with the magnetic field. If the magnetic field drags the dust inwards from large distances, the winding-up of the field lines in the accretion disk may finally decelerate dust as it falls inwards, and outflows at angles with the disk field may even accelerate the grains selectively outwards again.
For dust located in the inner part of the disk, the radiative field from the star may be very severely reduced by extinction. In this case, the pressure by infrared radiation from the hot disk may dominate and cause large dust grains to slide above the surface of the disk to larger radii (Vinković 2009) while smaller grains are less affected. As suggested by the referee of the present paper, for grains orbiting the star, the Poynting-Robertson drag will tend to selectively decelerate the smaller grains and make them move inward towards the star. Both these effects may therefore favour larger grains at greater stellar distances as compared with smaller grains, which is contrary to the mechanism discussed in the present paper. As highlighted above, the composition and structure of the grains are also expected to affect the q value in Eq. (8); flows with small graphite grains and relatively large fluffy composites may for that reason also be expected to be more effectively radiatively cleansed.
2.5. Stellar fields
Above, we have studied the case of a single star with a relatively mild flow of gas falling in towards it. The integrations of the dust orbits started at considerable distance (10 000 AU) from the star, and the gas flow was assumed to continue in a stationary way for several million years, which implies that regions far outside this distance from the star may also be involved. In reality, such an isolated situation should be rare: stars are known to be formed in associations or clusters, and the effects of the companion stars should be considered. In the case of the Sun, it is often argued that it had its origin in a relatively dense stellar environment on the basis of the abundances of some daughter elements of radioactive supernova products like 26Al, 41Ca and 60Fe. The situation has been summarised by Adams (2010) who also included various dynamic arguments in his discussion and concluded that the number of members of the solar birth cluster should fall in the range N ∼ 103 − 104, which suggests a cluster radius of about 6 pc (cf. Joshi et al. 2016), and a typical distance to the closest star of about 0.5 pc. We note, however, the recent discussion by Fujimoto et al. (2018) who argue that “normal” chemo-galactic evolution with new generations of stars preferentially forming in patches of the Galaxy that were contaminated by previous generations of stars can account for the observed radioisotopes without invoking a nearby supernova very close to the forming Solar system. Nearby stars and star passages may episodically affect the dynamics of the gas flows towards the accreting star. However, such effects on 𝒟 are probably not very significant, in view of the relatively small effects of the persistent turbulence found above. However, if the neighbouring stars are assumed to actively cleans their envelopes, similarly to and simultaneously with the corresponding self-cleansing of the Sun, we expect flows of radiatively driven grains from those stars towards the Sun. Therefore, a reduction of 𝒟 for the Sun is possible.
We explored the effects of the dust from stellar neighbours by surrounding the star in the centre by a box of d × d × d pc3 in dimension, and then reflected the velocities of the outgoing particles when they hit the walls of the box. In order to avoid biases, we then shifted the starting point of the grain on the box side randomly (a precaution which was found to be of little significance for the result). The reflection was repeated if the grain hit another box surface until the full integration time of 5 Myr had elapsed. As is seen in Table 1, the effects of this closed box around the star are relatively small: the value of 𝒟 is reduced by only one percent, and, in fact, does not significantly depend on the value of d. The reason for the small magnitude of these effects is the symmetry in the forces dominating at a given distance from the star, radiative pressure and gravity, which both scale as 1/r 2, for a dust grain that departs from, or approaches, the star. Only when the grain is much closer (with the mild accretion rates adopted here), does friction introduce an asymmetry, so that the speed of the grain at a given distance from the star becomes different and higher in the approach than in the departure. For radiative cleansing to be significant at all, the accretion rates should not be too high, as is illustrated in Fig. 1, and this requirement prevents the asymmetries from becoming larger.
The conclusion of these schematic experiments is that the effects on dust in a stellar envelope of the emission of dust from solar-type stars in a dense stellar environment should not be very significant in reducing the cleansing net-effects from those of isolated stars. One should note, however, that the radiation from neighbouring stars may be of considerable significance, not by pushing dust grains from their own envelopes towards the Sun but by helping in pushing the dust away from the accreting Sun and thus increasing 𝒟. Nevertheless, effects of the gas flows from stellar winds and expanding H II regions may be equally significant, and in practice reduce the final accretion of dust-poor matter onto the Sun. Obviously, this complex situation requires more detailed modelling, and the results may well turn out to be quite dependent on initial conditions and the geometrical characteristics of the arrangement.
2.6. The inflow: its rate and anisotropy, and the accretion disk
In order for the proposed mechanism to lead to the consequences observed, that is, a depletion of the dust-forming elements in the solar atmosphere of ∼20%, the inflow rate of the gas (assumed here to correspond to the accretion rate via the accretion disk) multiplied by the time tflowwhen the flow is active must match the mass mconv of the stellar convection zone such that
Adopting the mass of the convection zone following Fig. 4 of Baraffe & Chabrier (2010) for a non-accreting 1 M⊙ model, we find typical convective masses of 0.5, 0.2, and 0.05 M⊙ at 10, 20, and 30 Myr, respectively. With those numbers, the condition of Eq. (17) would be fulfilled, even with significantly smaller flow rates Ṁ than 0.02 M⊙ Myr−1, provided that these remain relatively constant during the respective times.
Star-forming gas is far from homogeneous. Instead, these gas clouds show cores, sheets, and filaments. This is clearly displayed in the simulations by Kuffmeier et al. (2017) which demonstrate that stars accrete gas often streaming in filaments that simply fill a part (typically about 10%) of the full space angle as seen from the central region with the protostar and its accretion disk (see their Fig. 7). If such inhomogeneities are also characteristic of the much later accretion stages hypothesised here, the inflow rates in the filaments must be increased correspondingly, relative to those of the isotropic case discussed above. Such an increase is still possible within the conditions set by Eq. (10) and would admit a small optical depth in the filament.
The basic conclusion of the present study is that the early Sun may have radiatively cleansed its outer layers from refractory elements if the accretion rates in late phases were small but significant. An interesting question would then be whether or not an accretion disk should be observable around stars also at these stages, far beyond the generally quoted observed lifetimes of protoplanetary disks of, at the most, 10 Myr (see Mamajek 2009; Williams & Cieza 2011 and references therein, but also Pfalzner et al. 2014 who point out that the lifetimes may be underestimated). Kraus et al. (2014), on the basis of IR observations, find an upper limit of 5% on the fraction of K3.0–K7.9 stars in the Tuc-Hor moving group (with an estimated age of 30–45 Myr) to host significant amounts of warm circumstellar dust. According to Alexander et al. (2014) “a small (but not negligible ⪅10%) sample of older ∼10 − 20 Myr pre-main sequence stars... retain their dust (and gas) signatures”.
The possible existence of disks at small accretion flows is dependent on the outflow rates from the disk region and the replenishment time for the disk. The outflow, whether due to photo-evaporation by EUV, FUV, X-rays, or MHD disk winds (see Alexander et al. 2014 for a discussion on this controversial issue) may be varying from star to star, but is believed to finally disperse the disk and end the accretion. If the renewal time is also short for late stages, for example ∼30 000 yr as found in the simulations by Kuffmeier et al. (2017), the global accretion rates of our model suggest disk masses of approximately 10−4 M⊙ at most, while with the longer dissipation times, measured from the time when accretion stops as estimated by several authors (see Williams & Cieza 2011, for references) we could find disks that are more massive by one order of magnitude. Hartmann et al. (2016; their Fig. 8) plotted observed accretion rates based on spectroscopic observations of the Balmer continuum and emission lines versus estimated age. We note that for stars with ages between 10 and 30 Myr the rates are of the same order of magnitude as those needed for our mechanism to work, although the data have great scatter and probably suffer from severe bias. It may be rewarding to look further for accretion flows and disks around solar-type stars in associations with ages of 20–30 Myr.
3. Conclusions
In spite of the exploratory nature of our study of the possibility of “self-cleansing” of the dusty envelope around the early Sun, we can safely conclude that the proposed mechanism would cleanse the gas of about half its dust mass early on, provided that the incoming gas flow is not much more massive than 0.01 M⊙ Myr−1, and is sufficiently homogeneous, non-magnetic, and non-rotating. In a dense cluster the situation is uncertain, however, and probably dependent on the geometry of the stellar field, the presence of luminous stars, and of outflows and winds, and so on. Also, the presence of outflows from the early Sun itself may affect the situation considerably. Moreover, we have neglected the inner regions of the solar nebula, where the proto-planetary disk certainly might complicate the situation, both dynamically, via the gas flow and the magnetic field and by shielding the outer envelope from stellar radiation in certain directions, as well as by promoting other dust-fractionation processes. In order to clarify the effects of such complications, detailed MHD simulations, partly analogous to those of more massive stars by Wibking et al. (2018) and those allowing for angular momentum, should be performed.
One may question whether the mechanism proposed could be used to explain the findings by several research groups mentioned in the Introduction, that is, of binary stars with significantly different compositions, and cases with significant trends in these differences with condensation temperature of the elements. A natural way of obtaining the observed differences within the framework of our cleansing paradigm would be to invoke a situation in which the two components of the binary had different accretion rates, one with Eq. (10) satisfied and one where the rate was higher, for example, as a result of an inhomogeneous distribution of the inflowing gas. An alternative explanation might be that the two components were in somewhat different evolutionary phases, with convection zones of significantly different depth, when this final accretion occurred, meaning that the accreted dust-cleansed material was mixed with different amounts of stellar material.
The finding by Gonzalez et al. (2010) that CI meteorites show even lower refractory/volatile abundance ratios than the solar photosphere would also be explained by the present mechanism if the radiatively cleansed matter from which the meteorites formed was not enough to replace all the convection zone but was mixed into it.
The seemingly systematic low abundance ratio of refractory elements to volatile elements of the cluster stars in M 67 seems, however, more difficult to relate to the present scenario. One hypothesis might be that the deep gravity well of the cluster retained gas for a long time, which could then slowly accrete onto the stars with self-cleansing in operation. Another possibility is that the radiative pressure from the bright stars in the cluster could drive away the dust grains from the late accretion flows of the less massive stars. In both these scenarios one would expect the ratio of refractories to volatiles in the stellar atmospheres to increase towards the lower end of the main sequence of the cluster, as a result of the deepening of the convection zone with decreasing temperature.
Acknowledgments
Martin Asplund, Alexis Brandeker, Jorges Meléndez, Dhruba Mitra, Poul Erik Nissen, Åke Nordlund, Henk Spruit and an anonymous referee are thanked for many valuable suggestions.
References
- Adams, F. C. 2010, ARA&A, 48, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Adibekyan, V. Z., González Hernández, J. I., Delgado Mena, E., et al. 2014, A&A, 564, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Delgado-Mena, E., Feltzing, S., et al. 2017, Astron. Nachr., 338, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R., Pascucci, I., Andrews, S., Armitage, P., & Cieza, L. 2014, Protostars and Planets VI, 475 [Google Scholar]
- Baraffe, I., & Chabrier, G. 2010, A&A, 521, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biazzo, K., Gratton, R., Desidera, S., et al. 2015, A&A, 583, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Rosolowsky, E., Walter, F., & Blitz, L. 2008, ApJ, 686, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Casuso, E., & Beckman, J. E. 2010, AJ, 139, 1406 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011a, ApJ, 732, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011b, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Ferrara, A., Ferrini, F., Franco, J., & Barsella, B. 1991, ApJ, 381, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, Y., Krumholz, M. R., & Tachibana, S. 2018, MNRAS, 480, 4025 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G., Carlson, M. K., & Tobin, R. W. 2010, MNRAS, 407, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B. 2018, A&A, 616, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Meléndez, J., Asplund, M., & Yong, D. 2010, Ap&SS, 328, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P. 2012, in EAS Pub. Ser., eds. C. Reylé, C. Charbonnel, & M. Schultheis, 57, 91 [CrossRef] [Google Scholar]
- Heyer, M. H., & Brunt, C. M. 2004, ApJ, 615, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Higham, D. 2001, SIAM Rev., 43, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Higuchi, K., Machida, M. N., & Susa, H. 2018, MNRAS, 475, 3331 [NASA ADS] [CrossRef] [Google Scholar]
- Hull, C. L. H., Carrasco-González, C., Williams, P. K. G., et al. 2018, ArXiv e-prints [arXiv:1806.06313] [Google Scholar]
- Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, Y. C., Dambis, A. K., Pandey, A. K., & Joshi, S. 2016, A&A, 593, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kimura, H. 2017, ApJ, 839, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., Shkolnik, E. L., Allers, K. N., & Liu, M. C. 2014, AJ, 147, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Kuffmeier, M., Haugbølle, T., & Nordlund, Å. 2017, ApJ, 846, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Lean, J. 1987, J. Geophys. Res., 92, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Loren, R. B., Sandqvist, A., & Wootten, A. 1983, ApJ, 270, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Maldonado, J., & Villaver, E. 2016, A&A, 588, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2015, A&A, 579, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E. 2009, in AIP Conf. Ser., eds. T. Usuda, M. Tamura, & M. Ishii, 1158, 3 [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., & Scuflaire, R. 2008, Ap&SS, 316, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E., Silva Aguirre, V., Christensen-Dalsgaard, J., et al. 2017, A&A, 608, A112 [Google Scholar]
- Oh, S., Price-Whelan, A. M., Brewer, J. M., et al 2018, ApJ, 854, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Önehag, A., Korn, A., Gustafsson, B., Stempels, E., & Vandenberg, D. A. 2011, A&A, 528, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Önehag, A., Gustafsson, B., & Korn, A. 2014, A&A, 562, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padoan, P. 2018, Contrib. Astron. Observat. Skalnate Pleso, 48, 32 [NASA ADS] [Google Scholar]
- Padoan, P., & Nordlund, Å. 2002, ApJ, 576, 870 [Google Scholar]
- Persson, M. V., Harsono, D., Tobin, J. J., et al. 2016, A&A, 590, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S., Steinhausen, M., & Menten, K. 2014, ApJ, 793, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Khanal, S., Aleo, P., et al. 2015, ApJ, 808, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Reach, W. T., Heiles, C., & Bernard, J.-P. 2015, ApJ, 811, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Kauffmann, J., & Goodman, A. A. 2008, ApJ, 679, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Saffe, C., Jofré, E., Martioli, E., et al. 2017, A&A, 604, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Spina, L., Meléndez, J., & Ramírez, I. 2016, A&A, 585, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. 1978. Physical Processes in the Interstellar Medium (New York: Wiley-Interscience) [Google Scholar]
- Teske, J. K., Khanal, S., & Ramírez, I. 2016a, ApJ, 819, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Teske, J. K., Shectman, S. A., Vogt, S. S., et al. 2016b, AJ, 152, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Tucci Maia, M., Meléndez, J., & Ramírez, I. 2014, ApJ, 790, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Vinković, D. 2009, Nature, 459, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Wibking, B. D., Thompson, T. A., & Krumholz, M. R. 2018, MNRAS, 477, 4665 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. The “allowed” parameter space (under each curve) for dust grains with radius a that may exist around a star at a certain distance (indicated in AU at each curve) without being accreted to the star by gravity and friction from the in-falling gas with different accretion rates Ṁ. The full lines correspond to cases with neutral grains while dashed blue curves indicate corresponding cases with electrically charged grains. The approximate upper limit on a, according to Eq. (9), is indicated by a vertical red line, while the approximate upper limit on dM/dt ≡ Ṁ for a distance from the star of 103 AU, according to Eq. (10), is indicated by a horizontal red line. Also shown is the approximate critical radius rc as calculated by Eq. (11) as a dashed red curve. The fair agreement between the approximate (in red) and the more exact (black) curves is due to the fact that the quadratic term in the dependence of the friction force on drift speed, cf. Eq. (2), is indeed dominating, as assumed in the approximations. The reduction of the “allowed” accretion rates for the charged grains relative to the corresponding cases with neutral ones is obvious. |
| In the text | |
 |
Fig. 2. Optical depth as a function of distance from the star for three different accretion rates, 1017 g s−1, 3 × 1017 g s−1 and 1018 g s−1, corresponding to 0.0016, 0.0047 and 0.016 M⊙ Myr−1, respectively. |
| In the text | |
 |
Fig. 3. Contributions to the dust opacity for grains of different radii a, at different distances from the accreting star indicated at each curve in AU. The opacity contribution is given in cm−1, per logarithmic interval in a. The dominating contribution from grains on the order of a = amax in size, cf. Eq. (9), is seen in the inner regions, and is enhanced by the convergence of the flow, while at greater distances from the star the more numerous smaller grains contribute more, as a result of their initial motion inwards due to the starting condition v(rout)=vff. The curves have been smoothed by a filter with a width of 5 × 10−6 cm, to compensate for fluctuations due to the stochastic nature of the method used. |
| In the text | |
 |
Fig. 4. The orbits of grains over 105 yr, from a point indicated by an “x” in black along the z axis at a distance of 104 AU from the star (which is at the origin of the coordinate system), and with different grain radii a as indicated by the different colours. The dust grains were given an initial velocity identical to the gas free-fall velocity. The turbulent mean speed was set to 0.1 km s−1. We note that the scales of the x and y axes are different from that of the z axis. |
| In the text | |
 |
Fig. 5. The orbits of grains over 105 yr, from a point indicated by an “x” in white along the z axis at a distance of 104 AU from the star (which is at the origin of the coordinate system), and with different grain radii a as indicated by the different colours. The initial velocity of the dust grains was set to zero. The turbulent mean speed was set to 0.1 km s−1. We note that the scales of the x and y axes are different from that of the z axis. |
| In the text | |
 |
Fig. 6. The defect, D(a), (cf. Eq. (15)) as a function of grain radius a for different values of the turbulence speeds vturb and with initial dust velocities = v0 = 0 and with infall rate of gas Ṁ = 0.002 M⊙ Myr−1 shown in thin lines. Red line: Coulomb forces, excluding photo-electric effect, taken into account with an ionization ratio of n(e)/n(H)=2.72 × 10−4. Thick line: doubled infall rate, vturb = 1 km s−1. Dashed line: initial speed v0= initial free-fall velocity of the gas, vturb = 1 km s−1, Ṁ = 0.002 M⊙ Myr−1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{array}{*{20}{l}}{m\cdot\frac{{{{\rm{d}}^2}r({\rm{t}})}}{{{\rm{d}}{t^2}}}}&{ = \left[ {\frac{{L{e^{ - \tau }}\pi {\mkern 1mu} {a^2}{\mkern 1mu} \overline {{q_{{\rm{pr}}}}} }}{{4\pi c}} - G{\mkern 1mu} m{\mkern 1mu} M} \right]\frac{{{e_r}}}{{r{{(t)}^2}}}}\\{}&{ - 2\pi {a^2}{\mkern 1mu} n(t)kT{\mkern 1mu} {e_{v,{v_g}}}B(s).}\end{array}\ $$](/articles/aa/full_html/2018/12/aa33353-18/aa33353-18-eq1.gif)
![$$ \begin{aligned} B(s)\approx \frac{s}{\alpha }[1+(\alpha \cdot s)^2]^{1/2} + \left(\frac{eU}{kT}\right)^2 \mathrm{ln}\Lambda \frac{s}{3\sqrt{\pi }/4 + s^3}, \end{aligned} $$](/articles/aa/full_html/2018/12/aa33353-18/aa33353-18-eq3.gif)
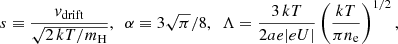
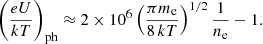
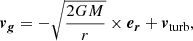
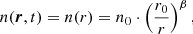
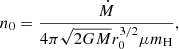
![$$ \begin{aligned} \frac{{\mathrm{d}^{2}} r}{\mathrm{d}t^{2}} =\left[\frac{3}{16 \pi } \frac{ L\mathrm{e}^{-\tau }\,q}{c a {\rho }_{\rm d} }-G\,M\right] \cdot \frac{1}{r^{2}}- \frac{3}{2} \frac{ \,n(t)kT}{a {\rho }_{\rm d} }\cdot B(s) , \end{aligned} $$](/articles/aa/full_html/2018/12/aa33353-18/aa33353-18-eq10.gif)
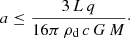
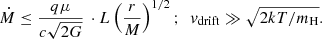
![$$ \begin{aligned} r_{\rm c} =\frac{1}{8\mu ^2} \dot{M}^2 \cdot GM \cdot \left[\frac{Lq}{4c}-\frac{4\pi }{3} G M a\rho _{\rm d}\right]^{-2}. \end{aligned} $$](/articles/aa/full_html/2018/12/aa33353-18/aa33353-18-eq14.gif)