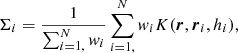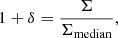| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A186 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832688 | |
| Published online | 14 December 2018 | |
VIS3COS
I. Survey overview and the role of environment and stellar mass on star formation⋆,⋆⋆
1
Instituto de Astrofísica e Ciências do Espaço, Universidade de Lisboa, OAL, Tapada da Ajuda, 1349-018 Lisboa, Portugal
e-mail: aafonso@oal.ul.pt
2
Departamento de Física, Faculdade de Ciências, Universidade de Lisboa, Edifício C8, Campo Grande, 1749-016
Lisboa, Portugal
3
Department of Physics, Lancaster University, Lancaster LA1 4YB UK
4
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
5
Cahill Center for Astrophysics, California Institute of Technology, 1216 East California Boulevard, Pasadena, CA, 91125 USA
6
Centro de Computação Gráfica, CVIG, Campus de Azurém, 4800-058
Guimarães, Portugal
7
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
8
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ UK
9
National Astronomical Observatory of Japan, Osawa 2-21-1, Mitaka, Tokyo, 181-8588 Japan
Received:
23
January
2018
Accepted:
18
May
2018
We present the VIMOS Spectroscopic Survey of a Supercluster in the COSMOS field (VIS3COS) at z ∼ 0.84. We use VIMOS high-resolution spectra (GG475 filter) to spectroscopically select 490 galaxies in and around the superstructure and an additional 481 galaxies in the line of sight. We present the redshift distribution, the catalogue to be made public, and the first results on the properties of individual galaxies and stacked spectra (3500 Å < λ < 4200 Å rest-frame). We probe a wide range of densities and environments (from low-density field to clusters and rich groups). We find a decrease in the median star formation rate from low- to high-density environments in all bins of stellar mass and a sharp rise of the quenched fraction (from ∼10% to ∼40 − 60%) of intermediate-stellar-mass galaxies (10 < log10 (M⋆/M⊙) < 10.75) from filaments to clusters. The quenched fraction for massive galaxies shows little dependence on environment, being constant at ∼30 − 40%. We find a break in the strength of the [O II] emission, with nearly constant line equivalent widths at lower densities (∼ − 11 Å) and then a drop to ∼ − 2.5 Å towards higher densities. The break in the [OII] line strength happens at similar densities (log10(1 + δ) ∼ 0.0 − 0.5) as the observed rise in the quenched fraction. Our results may provide further clues regarding the different environmental processes affecting galaxies with different stellar masses and highlight the advantages of a single dataset in the COSMOS field probing a wide range of stellar masses and environments. We hypothesise that quenching mechanisms are enhanced in high-density regions.
Key words: galaxies: clusters: general / galaxies: evolution / galaxies: high-redshift / large-scale structure of Universe
Based on observations obtained with VIMOS on the ESO/VLT under the programmes 086.A-0895, 088.A-0550, and 090.A-0401.
Full Table B.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/620/A186
© ESO 2018
1. Introduction
In the local Universe, we observe differences in a wide range of galaxy properties (e.g. colours, star formation, morphology) with respect to the environment they reside in (e.g. Oemler 1974; Dressler 1980, 1984). Cluster galaxies are typically red and passive, while in low-density environments the population is dominated by blue star-forming galaxies (e.g. Dressler 1980; Balogh et al. 2004; Kauffmann et al. 2004; Baldry et al. 2006; Bamford et al. 2009). The star formation rate (SFR) and star-forming fraction (fSF) have also been found to correlate strongly with the projected galaxy density (e.g. Lewis et al. 2002; Gómez et al. 2003; Hogg et al. 2004; Best 2004; Kodama et al. 2004; Peng et al. 2010; Darvish et al. 2016; Cohen et al. 2017). Observations also imply that the most massive galaxies assembled their stellar mass more quickly and had their bulk of star formation quenched at z ≳ 1 (e.g. Iovino et al. 2010). While stellar mass and environmental density correlate, it is now possible to disentangle their roles and show that both are relevant for quenching star formation (e.g. Peng et al. 2010; Sobral et al. 2011; Muzzin et al. 2012; Darvish et al. 2016).
Globally, observations show that the SFR density ( ρSFR) peaks at z ∼ 2 − 3 and has been declining ever since (e.g. Lilly et al. 1996; Karim et al. 2011; Burgarella et al. 2013; Sobral et al. 2013; Madau & Dickinson 2014; Khostovan et al. 2015). However, surprisingly, the decline of ρSFR with increasing cosmic time is happening in all environments (e.g. Cooper et al. 2008; Koyama et al. 2013). Recent studies have also shed more light on when the dependency of star-forming galaxies on environment start to become observable (e.g. Scoville et al. 2013; Darvish et al. 2016). However, it is still unclear exactly how the environment affected the evolution of galaxies and how that may have changed across time. In order to properly answer such questions it is mandatory to conduct observational surveys at high redshift (e.g. Tadaki et al. 2012; Koyama et al. 2013; Lemaux et al. 2014; Cucciati et al. 2014; Shimakawa et al. 2018) which can then be used to test theoretical models of galaxy evolution (e.g. Vogelsberger et al. 2014; Genel et al. 2014; Henriques et al. 2015; Schaye et al. 2015; Crain et al. 2015).
There have been a plethora of surveys of clusters and their surroundings at z ≲ 1 (e.g. Treu et al. 2003; Cooper et al. 2008; Poggianti et al. 2009; Lubin et al. 2009; Cucciati et al. 2010a, 2014, 2017; Iovino et al. 2010; Li et al. 2011; Muzzin et al. 2012; Mok et al. 2013; Koyama et al. 2013; Lemaux et al. 2014) with a key focus on the influence of environment on the star formation of galaxies. Emission line surveys of clusters at lower redshifts (z ∼ 0.1 − 0.5) targeting either Hα (e.g. Balogh et al. 2002; Stroe & Sobral 2015; Stroe et al. 2017; Sobral et al. 2016; Rodríguez del Pino et al. 2017) or [OII] (e.g. Nakata et al. 2005) find that star formation is suppressed in cluster environments. This suppression seems to be more effective for early-type galaxies (e.g. Balogh et al. 2002) and to be a slow-acting mechanism that mainly affects the gas component (e.g. Rodríguez del Pino et al. 2017).
By z ∼ 1, some authors have claimed to have found a flattening, or even a definitive reverse, of the relation between the star formation activity and the projected local density, either studying how the average SFRs of galaxies change with local density (Elbaz et al. 2007) or looking at fSF as a function of density (e.g. Ideue et al. 2009; Tran et al. 2010; Santos et al. 2014). These results would be naturally interpreted as a sign of evolution if other studies (e.g. Patel et al. 2009; Sobral et al. 2011; Muzzin et al. 2012; Santos et al. 2013) had not found an opposite result. The differences found between different clusters may be related to their dynamical state, as merging clusters in the low-redshift Universe can also show reverse trends when compared to relaxed clusters at similar epochs (e.g. Stroe et al. 2014, 2015, 2017; Mulroy et al. 2017), but other factors like sample size, active galactic nucleus (AGN) contamination, and environments probed may also play a role (e.g. Darvish et al. 2016). Sobral et al. (2011), probing a wide range of environments and stellar masses, were able to recover and reconcile the previous apparently contradictory results. They attribute the discrepancies to selection effects. If one restricts oneself to similar stellar masses and/or densities, one can find similar trends in different studies. Sobral et al. (2011) also separated the individual roles of mass and environment in galaxy evolution (see also Iovino et al. 2010; Cucciati et al. 2010b; Peng et al. 2010; Li et al. 2011).
Finding the exact mechanisms of galaxy quenching and their physical agents is still one of the unsolved problems in galaxy evolution. Many internal (e.g. stellar and AGN feedback) and external (e.g. galaxy environment) physical drivers are thought to be linked to the quenching process. One might naively expect a continuous decline in the star formation of galaxies from the field to the dense cores of clusters (e.g. due to a lower amount of available gas or faster gas consumption as galaxies move through denser mediums). However, before galaxies undergo a full quenching process in dense regions, they may experience a temporary enhancement in star formation activity (see e.g. Sobral et al. 2011) which may complicate how observations are interpreted (e.g. ram pressure stripping – Gallazzi et al. 2009; Bekki 2009; Owers et al. 2012; Roediger et al. 2014 – and/or tidal interactions – Mihos & Hernquist 1996; Kewley et al. 2006; Ellison et al. 2008).
When looking in more detail at galaxies in the low to intermediate redshift Universe (z ≲ 1), many properties of star-forming galaxies that are directly or indirectly linked to star formation activity (e.g. SFR, sSFR, emission line equivalent widths and the main sequence of star-forming galaxies) seem to be invariant to their environment (but it is still a debated issue, see e.g. Peng et al. 2010; Iovino et al. 2010; Wijesinghe et al. 2012; Muzzin et al. 2012, Koyama et al. 2013, 2014; Hayashi et al. 2014; Darvish et al. 2014, 2015b, 2016). Therefore, the main role of the environment seems to be to set the fraction of quiescent/star-forming galaxies (e.g. Peng et al. 2010; Cucciati et al. 2010b; Sobral et al. 2011; Muzzin et al. 2012; Darvish et al. 2014, 2016) which is likely linked to the reported gas deficit in cluster galaxies (seen in atomic hydrogen, e.g. Giovanelli & Haynes 1985; Cortese et al. 2010; Serra et al. 2012; Brown et al. 2017). But this is not the picture found when looking at molecular hydrogen which is either independent of environment, or depressed or enhanced in high-density regions dependent on the study (e.g. Boselli et al. 2014; Mok et al. 2016; Koyama et al. 2017). Nevertheless, recent studies are finding that not all characteristics of star-forming galaxies are independent of environment. For example, metallicities have been shown to be a function of environment (e.g. Kulas et al. 2013; Shimakawa et al. 2015; Sobral et al. 2015) with studies finding that star-forming galaxies have slightly higher metallicities in high-density environments when compared to lower-density/more typical environments at z ∼ 0.2 − 0.5 (e.g. Sobral et al. 2015; Darvish et al. 2015b). Sobral et al. (2015) study a cluster undergoing a merger and Darvish et al. (2015b) focus on galaxy filaments, which are both regions of enhanced dynamical activity. Denser environments also seem to boost the dust content of star-forming galaxies (e.g. Koyama et al. 2013; Sobral et al. 2016). The higher dust content seen in high-density regions can be a requirement for galaxies to sustain star formation in such environments, by allowing for dense and compact regions to survive environmental stripping.
Issues related to photometric redshift errors and projection effects can limit our understanding of what is occurring in and around clusters. These issues dilute genuine trends and prohibit us from unveiling the role of the environment in sufficient detail to really test our understanding. Surveys such as EDisCS (e.g. White et al. 2005) have aimed to overcome some of these issues by targeting the densest regions at high redshift with extensive spectroscopic observations. These have made significant progress (Poggianti et al. 2006, 2009; Cucciati et al. 2010b, 2017), but either they target deep and small areas or shallow and wide areas. This limits the study on the role of the larger-scale structure and the densest environments simultaneously. A way to make further progress is to conduct a spectroscopic survey (to avoid projection effects and photometric redshift biases and errors) over a superstructure containing the complete range of environments in a sub-deg2 area at high redshift.
In this paper, we present a large spectroscopic follow-up of members of a supercluster in the COSMOS field first detected in X-rays (Finoguenov et al. 2007) and later in Hα (see Fig. 1, Sobral et al. 2011). We organise this paper as follows. Section 2 discusses the sample and presents the observations with VIMOS/VLT and data reduction. Section 3 describes the methods to derive galaxy properties used throughout the paper. In Sects. 4 and 5 we show and discuss the results from both individual and stacked spectral properties. Finally, Sect. 6 presents the conclusions. We use AB magnitudes, a Chabrier (Chabrier 2003) initial mass function (IMF), and assume a ΛCDM cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7. The physical scale at the redshift of the superstructure (z ∼ 0.84) is 7.63 kpc/″.
 |
Fig. 1. Snapshot of the region targeted by our spectroscopic survey. The colour map encodes the information on the galaxy projected surface density at the redshift slice of interest at 0.8 < z < 0.9 estimated from the catalogue made public by Darvish et al. (2017). Each thick white cross represents a targeted galaxy with a measured spectroscopic redshift in the same redshift slice. The white pentagons show a targeted galaxy with measured spectroscopic redshift, outside the defined redshift slice. The blue circles show the targeted galaxies for which we have no measured spectroscopic redshift available. The orange squares show the location of Hα emitters studied by Sobral et al. (2011). The large red circles denote the location of X-ray-detected clusters from Finoguenov et al. (2007) at the same redshifts. The size of the circle shows the clusters’ estimated X-ray radius r500. We see here that we are probing a large range of densities with our survey, in part due to selection effects (e.g. slit placement constraints). |
2. Sample and observations
2.1. The COSMOS superstructure at z ≈ 0.84
By conducting a relatively wide (∼0.8 square degrees) and deep (down to a flux limit of 8 × 10−17 erg s−1 cm−2) Hα survey at z = 0.84 in the COSMOS field, Sobral et al. (2011) found a strikingly large overdensity of Hα emitters within a region that happens to contain three X-ray clusters (first reported in Finoguenov et al. 2007), as shown in Fig. 1. Limited spectroscopic observations from zCOSMOS (Lilly et al. 2007) allowed to securely place the most massive cluster in the region at z = 0.835, but the full structure seemed to span z ≈ 0.82 − 0.85 north to south. The Hα imaging reveals a strong filamentary structure which seems to be connecting at least three cluster regions, but there are other possible groups/smaller clusters within the region (Sobral et al. 2011). Such structures around a massive cluster are similar to those found in other superstructures at z ∼ 0.5 − 0.8 (e.g. Sobral et al. 2011; Darvish et al. 2014, 2015b, Iovino et al. 2016). Given the opportunity to study such a range of environments in a single dataset, we have designed a spectroscopic survey over this full region.
2.2. Target selection
In order to accurately map the three-dimensional (3D) large-scale structure at z = 0.84 and identify the bulk of cluster, group, filament, and field members, we have targeted member candidates (using the VIMOS Mask Preparation Software to maximize the number of targets per mask) down to I = 22.5 (corresponding to stellar masses of ≈1010 M⊙ for older and passive galaxies but much lower for younger galaxies, which have lower M/L ratios – see e.g. Sobral et al. 2011). Our targets are selected by using state-of-the-art photometric redshifts (photo-zs) in COSMOS, using up to 30 narrow, medium, and broad bands (cf. Ilbert et al. 2009). In practice, we use the upper and lower limits of the 99% photo-z confidence interval and select all sources for which such an interval overlaps with 0.8 < z < 0.9 (including sources best-fit by a quasar/AGN template). We reject all sources that are likely to be stars by excluding those sources for which χ2(star)/χ2(galaxy) < 0.2 (cf. Ilbert et al. 2009) or with clear star-like morphologies in high-resolution HST imaging and presenting near-infrared (NIR) vs. optical colours, which clearly classifies them as stars (following e.g. Sobral et al. 2013).
In order to effectively fill the masks, we introduce galaxies down to I = 23.0 and with photo-zs of 0.6 < z < 1.1. We note that we use the 99% photo-z confidence interval instead of the best photo-z to avoid significant bias towards redder and older galaxies (as blue and younger galaxies tend to present the largest scatter in the photometric vs. spectroscopic redshift comparison). We also note that this selection recovers all our blue and star-forming Hα emitters (Sobral et al. 2009, 2011). We can therefore fully map the supercluster without major selection biases. In total, out of our entire parent sample of 1015 primary targets and 2257 secondary targets, we have placed 531 (∼55% of the parent primary) slits on primary targets and 440 (∼19% of the parent secondary) on secondary targets. Due to the six pointings targeting the same area, we are not substantially biased against targets in higher densities (see also Appendix A). Observations are described in Sect. 2.3. We discuss our sample completeness in terms of spectroscopic success and relative to our parent sample in Appendix A and apply corrections whenever completeness effects might bias our results (see example in Sect. 4.2).
2.3. Observations
We have targeted the COSMOS superstructure identified in Sobral et al. (2011) and studied photometrically in Darvish et al. (2014), for example. We have used the High-Resolution Red grism (HR-Red) with VIMOS (Le Fèvre et al. 2003) and the GG475 filter1. Our observations are summarised in Table 2 and probe the rest-frame 3400 − 4600 Å for our main targets (at z ∼ 0.8) with an observed 0.6 Å pixel−1 spatial scale, which at z ∼ 0.8 is ∼0.33 Å pixel−1 rest-frame. This allows for a clear separation of the spectral features and very accurate redshift determinations. Spectra cover a key spectral range at z ≈ 0.84, from [OII] λ3726,λ3729 (partially resolving the doublet, as our resolution is ∼1 Å for z ∼ 0.8 sources) through 4000 Å (allowing us to measure D4000, see Fig. 2) to beyond Hδ at high resolution (allowing us to measure many other absorption lines and obtain their widths).
 |
Fig. 2. Three individual examples of images and spectra obtained with our survey. Each thumbnail (left panel) shows the HST/ACS F814W image of each target from the COSMOS survey (Koekemoer et al. 2007) with the VIMOS slit overlaid (dashed yellow line). To the right of each stamp we show the corresponding 2D (top) and 1D (bottom) spectrum. We use vertical dashed lines to mark the position of some spectral features present in our spectra. |
The observations cover a contiguous overdense region of 21′ × 31′ (9.6 × 14.1 Mpc, see Fig. 1) using 6 VIMOS pointings (chosen to overlap in order to assure both a contiguous coverage and a good target coverage and completeness, particularly for sources located in the densest regions). We have used the VIMOS 1″ width slit with an average of 9″ slit length. Our setup allowed us to offset different observing blocks by ±1.3″ along the slit to guarantee an optimal sky subtraction. Observations were conducted in service mode in April and May 2013 (see Table 1) under clear conditions, a new moon and an average seeing of 0.9″ (ranging from 0.6″ to 0.95″). Our pointings, labelled COSMOS-SS1 through COSMOS-SS6, have a total exposure of 4 h each. Arcs and flats were taken each night. See Table 1 for further details.
Observing log for our observations with VIMOS on the VLT for programmes 086.A-0895, 088.A-0550, and 090.A-0401 (PI: Sobral).
2.4. Data reduction
Data reduction was done using the VIMOS ESO pipeline, version 6.10, through gasgano2. The reduction is performed quadrant by quadrant (VIMOS has 4 different quadrants, labelled Q1–Q4). First, a master bias per night of observations is created by median combining bias frames per quadrant. Appropriate recipes are run in order to create master flats and master arcs for wavelength calibration. The pipeline is used to flag and mask hot pixels and cosmic rays and also to distort correct the observations. We obtain a sky subtracted spectra by estimating the median sky emission in several apertures away from each extracted source. Finally, two-dimensional (2D) spectra are obtained by combining spectra obtained over different observing blocks. The extraction of the one-dimensional (1D) spectra is conducted by collapsing the spectra in wavelength and then extracting along the trace’s FWHM. We obtain our 2D and 1D spectra with a relative flux calibration. We are able to extract 1D spectra for 971 sources, with varying levels of signal-to-noise ratio (S/N). See Fig. 2 for examples of individual 1D and 2D spectra.
2.5. Flux calibration
Due to the wealth of available well-calibrated photometry for all our sources, we use broad- and medium-band data from COSMOS to test and then scale the flux calibration of our spectra. This allows us to obtain more accurate flux calibrations and to slit correct more appropriately than using a single standard star for each quadrant. This also allows us to correct for any misalignment in the slit position relative to each source.
Briefly, we use the I-band-selected photometric catalogue presented by Ilbert et al. (2009) and start by using the I-band magnitudes. We convert I-band magnitudes into flux densities for each of our targets and compare those with the integral of the spectra convolved with the I-band filter. We then scale each spectra by the appropriate flux normalisation such that the integral within the I-band filter equals the flux density derived from photometry. We note that it also allows us to obtain a relatively good slit correction and therefore we do not apply any further slit corrections for our data. For galaxies which are too faint in the I-band, we use the median flux calibration for the pointing and quadrant it was observed in. This flux calibration is done under the assumption that galaxies have a homogeneous colour over their extent.
As a further check, we also use the COSMOS medium-band flux densities (see e.g. Ilbert et al. 2009) and check that our flux calibration is valid for the full range of available medium bands. We find very good agreement at all wavelengths within ±10 − 15% which we interpret as our uncertainty in the flux calibration.
2.6. Redshift measurements
We use the 1D spectra to measure accurate redshifts using SPECPRO (Masters & Capak 2011) and identify the bulk of the superstructure members. Most redshifts are derived from a combination of H + K absorption and other dominant absorption features such as the G-band for passive galaxies, while for star-forming galaxies we can detect [O II] λ3726,λ3729, in addition to absorption features. For a fraction of galaxies, we detect other lines such as Hδ (in either absorption or emission). Redshifts are obtained by visually inspecting all spectra one by one and by searching the features mentioned above. We obtain secure redshifts for 696 sources with high S/N. The redshift distribution for the galaxies in our sample is shown in Fig. 3.
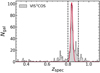 |
Fig. 3. Spectroscopic redshift distribution of the galaxies targeted in our sample as a black histogram. The vertical black dashed lines delimit the redshift selection of the results presented in this paper. The red line shows our Gaussian fit to the distribution without using rejection algorithms, pinpointing z = 0.836 ± 0.008 as the core redshift of the densest structure we find. The peak at slightly higher redshift (z ∼ 0.88) is likely produced by members from the north-western cluster C (see Table 2 and Fig. 1). |
2.7. Final sample
Our final sample is restricted to 0.8 < z < 0.9 to match our primary selection (see Sect. 2.2) and has a total of 490 galaxies spanning a large diversity of environments across several megaparsec that contain three X-ray confirmed galaxy clusters. We are releasing the final catalogue with this paper and we show in Table B.1 the first ten entries.
3. Determination of galaxy properties
3.1. Measurement of [OII] λ3726,λ3729 line
To obtain flux measurements of emission lines from our spectra, we interactively iterate through the entire dataset and zoom to a window of 100 Å around [O II] λ3726,λ3729. We define two regions of ∼15 Å (one blueward, one redward of the line) from which we estimate the median continuum level. Then the local continuum is defined as a straight line that goes through those points. To fit the doublet we use a combination of two Gaussian models through the functional form:
with three free parameters: A1, A2, and σ. The parameters A1 and A2 are the amplitudes of each component, and σ is the width of each Gaussian component. The centre of each component is fixed at λ1 = 3726.08 ± 0.3 Å and λ2 = 3728.88 ± 0.3 Å (we allow for a small shift in the line centre that is of the size of the resolution element of the spectra). To estimate the line properties, we use the information on the error spectra and perturb each flux at all wavelengths considered for the fitting by drawing a random number on the observed value and with a width that is equal to its error. We run this exercise 10 000 times and then estimate the errors on the line fit by taking the 16th and 84th percentile of the distribution in each free parameter.
From now on, we only use individual measurements if the S/N is > 3. We note that in Sect. 3.4 we obtain and measure stacks as a function of environment, allowing us to obtain the median properties of spectral lines for specific subsets of galaxies irrespective of their individual detection. This of course leads to a much higher S/N. We measure the line properties of the stacks with the same procedure described here for individual sources.
3.2. Stellar masses and star formation rates
To estimate the stellar masses and SFRs for the galaxies in our sample, we have performed our own SED fitting using MAGPHYS (da Cunha et al. 2008) and our knowledge of the spectroscopic redshift to better constrain the range of possible models. The models were constructed from the stellar libraries by Bruzual & Charlot (2003) using photometric bands from near-ultraviolet (NUV) to NIR (Galex NUV, Subaru uBVriz, UltraVISTA YJHKs, SPLASH-IRAC 3.6 μm, 4.5 μm, 5.8 μm, 8 μm) taken from the COSMOS2015 photometric catalogue (Laigle et al. 2016) and the dust absorption model by Charlot & Fall (2000). We found COSMOS2015 matches for 466 out of the 490 galaxies that are in our selected redshift range 0.8 < z < 0.9 for which we obtained the physical parameters that we use throughout the paper (stellar mass and SFRs). If not found in the COSMOS2015 catalogue, we do not obtain any estimate for stellar mass and SFRs through SED-fitting, which happens only for 3% of the sample. These missing sources are serendipitous objects which are faint in the I-band and below our completeness limit. We compare our results on stellar mass and SFRs with those provided in the COSMOS2015 catalogue and find a dispersion of ∼0.3 dex for the stellar mass and ∼0.7 dex for the SFRs.
In Fig. 4, we present the stellar masses and SFRs in our sample and show that we are probing galaxies with log10(M⋆/M⊙) ≳ 9 in a wide range of SFRs (−2 ≲ log10(SFR) ≲ 2). We see that our sample includes normal star-forming galaxies as well as galaxies that are found well below the SFR main sequence (see e.g. Noeske et al. 2007; Elbaz et al. 2007; Whitaker et al. 2012), which are characteristic of galaxies in the process of star formation quenching or of those just quenched (e.g. Fumagalli et al. 2014). To select quiescent galaxies within our sample, we impose a specific SFR cut at log10(sSFR) < − 11 (see e.g. Ilbert et al. 2010; Carollo et al. 2013) and find a total of 64 galaxies in these conditions.
 |
Fig. 4. Stellar masses and SFRs derived from SED fitting (see Sect. 3.2) in our spectroscopic sample at 0.8 < z < 0.9. For comparison, we show the derived best-fit relation for star-forming galaxies computed at z = 0.84 using the equation derived by Whitaker et al. (2012) over a large average volume in the COSMOS field. The vertical dotted line shows the completeness limit of our survey. The dotted contours show the COSMOS2015 (Laigle et al. 2016) distribution of galaxies with 0.8 < zphot < 0.9 and iAB < 23 from 10% to 95% of the sample in 5% steps. Empty circles highlight the photometric quiescent sample with log10(sSFR) < − 11. |
We also obtain from MAGPHYS the effective optical depth of the dust in the V-band, τV, which we translate into an average reddening value of E(B − V)=1.086τV/RV (assuming RV = 3.1, see e.g. Draine 2004). We find that our galaxies have an average reddening value of E(B − V)∼0.27 ± 0.02. We report here that above log10(M⋆/M⊙) ≳ 10 there is little dependence of the extinction on stellar mass, with a median reddening value of E(B − V)∼0.32 ± 0.02 (∼0.37 ± 0.02 if we consider star-forming only).
We measure the [OII] line flux by integrating over the best fit model described by Eq. (1), which can be solved analytically as 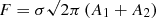 . We correct the measured [OII] luminosity by the SED extinction value. The corrected luminosity is given by
. We correct the measured [OII] luminosity by the SED extinction value. The corrected luminosity is given by
where τ[OII] is the optical depth at λ = 3727 Å derived using the dust model used in MAGPHYS (Charlot & Fall 2000). The effect of extinction on the luminosity of [OII] is displayed in Fig. 5 and it can account for the difference that we find when comparing SED and [OII] SFRs using the calibration derived by Kewley et al. (2004) and applying a conversion factor between Salpeter (1955) and Chabrier (2003) IMFs:
 |
Fig. 5. SFR estimates from SED fitting and from [OII] (derived from Eq. (4) of Kewley et al. 2004) of the galaxies in our spectroscopic sample at 0.8 < z < 0.9. Red circles show the dust uncorrected Hα derived star formation rates for the galaxies in our sample and that were measured by Sobral et al. (2011). The subscript corr denotes the dust-corrected SFRs derived from each estimate using the optical depth derived through SED fitting (see Sect. 3.2). |
We find a spread of 0.64 dex, but on average the derived SFRs are consistent with each other (median difference of 0.07 dex). We also show the SFR as derived from Hα luminosity (Kennicutt 1998) from the HiZELS survey, which was used to first pinpoint the existence of this structure (Sobral et al. 2011).
We stress however that [OII] emission can originate from other sources not related to star formation (e.g. AGN, LINERs) and that it is a poor tracer of SFR for red galaxies (e.g. Yan et al. 2006; Kocevski et al. 2011). This tracer is also dependent on the metallicity of the galaxy (Kewley et al. 2004). Those are the reasons for our choice to do our analysis in terms of star formation in galaxies using the quantity derived from SED fitting instead of relying on [OII] emission as a tracer of SFR.
3.3. Overdensities estimation
The estimate of local overdensity was computed as described by Darvish et al. (2015a, 2017) and is based on the photometric redshift catalogue of the COSMOS survey presented by Ilbert et al. (2013, see also Muzzin et al. 2013; Laigle et al. 2016). The density field was computed over an area of ∼1.8 deg2 using a mass-complete sample with accurate photometric redshifts spanning 0.1 < zphot < 1.2. The surface density field was computed in 2D slices of redshift of widths ±1.5σΔz/(1 + z) (as suggested by Malavasi et al. 2016). To properly account for the uncertainty on the photometric redshift estimate, the full photo-z PDF of each galaxy is taken into account. Then, at each redshift slice, we select all galaxies which fall in that slice and assigned it a weight corresponding to the percentage of the photo-z PDF contained in that slice. We use all galaxies which have weights greater than 10% in the corresponding slice. The surface density assigned to each point in the density field is (based on adaptive kernel smoothing):
where r is a location in the density field, ri is the position of each galaxy, wi is the weight assigned to each galaxy, hi is the kernel width at the position of each galaxy, and K is a 2D Gaussian kernel function.
In these equations, N is the number of galaxies in the slice with weights greater than 10%, ri is the position of the galaxy, rj is the position of all other galaxies in the slice, and hi is the adaptive smoothing parameter for our assumed kernel. The value of 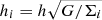 Mpc, where Σi is the initial density estimation at the position of galaxy i using a fixed kernel with a width of 0.5 Mpc, G is the geometric mean of all Σi at each redshift slice, and h is chosen to have a value around the typical size of X-ray clusters (0.5 Mpc, see e.g. Finoguenov et al. 2007). We then evaluate the density field in a 2D grid with a spatial resolution of 50 kpc at each redshift. We define overdensity as:
Mpc, where Σi is the initial density estimation at the position of galaxy i using a fixed kernel with a width of 0.5 Mpc, G is the geometric mean of all Σi at each redshift slice, and h is chosen to have a value around the typical size of X-ray clusters (0.5 Mpc, see e.g. Finoguenov et al. 2007). We then evaluate the density field in a 2D grid with a spatial resolution of 50 kpc at each redshift. We define overdensity as:
with Σ being the projected local density and Σmedian being the median of the density field of the redshift slice the galaxy is in. We choose to use number densities instead of mass density estimates (e.g. Wolf et al. 2009) to avoid introducing any bias due to any underlying relation between stellar mass and density that may exist. For a more detailed description of the method, we refer the reader to Darvish et al. (2014, 2015a).
We have computed the value of the overdensity for each galaxy by interpolating the density field to their angular position and spectroscopic redshift. We show in Fig. 6 the distribution of our galaxies according to their overdensity and labelled by the region they are likely to belong to, as defined by the cosmic web measurements computed by Darvish et al. (2014, 2017). We note that when referring to galaxies within our spectroscopic sample in cluster regions, we are mostly referring to either rich groups or the outskirts of massive clusters as our observational setup does not allow for a good sampling of densely populated regions due to slit collision problems.
 |
Fig. 6. Overdensity distribution for the galaxies in our sample with 0.8 < z < 0.9. We show the different cosmic web environments of galaxies (field, filament, and cluster) according to their classification using the scheme devised by Darvish et al. (2014, 2017). |
We note that there is an overlap between the different labelled regions and the measured local overdensity in Fig. 6. This happens because the region assigned to each galaxy is based on the definition of the strength of the cluster and filament signals, which takes into account the morphology of the density field. That is the reason why a pure density-based definition of the environment of galaxies cannot fully separate them into real physical structures (see e.g. Aragón-Calvo et al. 2010; Darvish et al. 2014). This means for example that we can have dense filaments (as high-density regions with thread-like morphology, likely infall regions of massive clusters) and less dense cluster regions (intermediate density with circular morphology, likely associated with galaxy groups). We refer to Darvish et al. (2014, 2017; see also Aragón-Calvo et al. 2010) for more details.
3.4. Spectral stacks
To increase the S/N on the obtained spectra and investigate details on the spectral properties of galaxies as a function of their stellar mass and local density, we have performed stacking of individual galaxy spectra. Our stacking method can be summarised as a median, interpolated, and normalised spectra. For each set of spectra, we start by shifting the spectrum to its rest-frame wavelengths using the redshift we have measured (see Sect. 2.6). Then we linearly interpolate the spectra onto a common universal grid (3250–4500 Å, Δλ = 0.3 Å pixel−1). We normalise each spectrum to the mean flux measured from 4150–4350 Å. Lastly, we median combine all spectra by taking the median flux at each wavelength. We estimate that our typical errors in the spectroscopic redshift measurements are on the order of ∼0.0005, which translates to an error of ∼1 Å, comparable to our spectral resolution at z ∼ 0.8. Thus, our stacking should not smear the lines enough to affect the measurements on the [O II] λ3726,λ3729 doublet.
4. Results
Throughout this section, our measure of environment is quantified by δ (see Eq. (5)). For a broad comparison between different environments, we defined as lower-density galaxies those residing in log10(1 + δ) < 0.1, and as higher-density galaxies those residing in regions with log10(1 + δ) > 0.4.
4.1. Redshift distribution
From our first redshift measurements, based on two to three lines, and the dispersion of the measurements, we are able to derive the full redshift distribution of our VIMOS sample. We show the results in Fig. 3 which shows a very clear peak at z ≈ 0.84. By fitting a Gaussian to the redshift distribution at z ≈ 0.8 we find that the COSMOS superstructure is well characterised by z = 0.84 ± 0.01 with 367 galaxies fully included within this redshift distribution.
We attempt to estimate the mass of the two clusters for which we have coverage (A and B on Table 2; see also Fig. 1) by computing the radial velocity dispersion, σr, of the spectroscopically confirmed galaxies in our sample. We estimate the size of the cluster by computing the root mean square of the distances, Rrms, to the estimated centre (average position of selected members). We compute the velocity dispersion, σr, using the gapper technique (Beers et al. 1990, see also Balogh et al. 2014). To obtain a final estimate for each cluster, we iterate five times and compute the mean position, Rrms, and σr by selecting at each step galaxies within 2Rrms of the cluster centre and within 2σ of the median cluster redshift. We start our iteration procedure by assuming an initial guess for Rrms = 0.5 Mpc.
We find values of σr = 875 ± 179 km s−1 (43 galaxies) and Rrms = 1.1 Mpc for cluster A and of σr = 598 ± 225 km s−1 (25 galaxies) and Rrms = 1.3 Mpc for cluster B. Assuming a virial state for each cluster, we can estimate their mass as 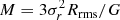 . We find M = 6 ± 3 × 1014 M⊙ and M = 3 ± 2 × 1014 M⊙, respectively. These values are up to an order of magnitude higher than the values reported by Balogh et al. (2014, see Table 2) and this difference is mainly driven by our larger derived values of Rrms. We note here that our measurements are made under the assumption that the clusters are virialized. We hypothesise that when applying a similar criteria for galaxy membership as Balogh et al. (2014), we are likely picking up additional moving substructures (at slightly different redshifts) that are artificially increasing our measured cluster sizes and velocity dispersion. This is supported by the non-Gaussian shape of the velocity distribution histograms of the selected members (see Fig. 7).
. We find M = 6 ± 3 × 1014 M⊙ and M = 3 ± 2 × 1014 M⊙, respectively. These values are up to an order of magnitude higher than the values reported by Balogh et al. (2014, see Table 2) and this difference is mainly driven by our larger derived values of Rrms. We note here that our measurements are made under the assumption that the clusters are virialized. We hypothesise that when applying a similar criteria for galaxy membership as Balogh et al. (2014), we are likely picking up additional moving substructures (at slightly different redshifts) that are artificially increasing our measured cluster sizes and velocity dispersion. This is supported by the non-Gaussian shape of the velocity distribution histograms of the selected members (see Fig. 7).
 |
Fig. 7. The velocity distribution for clusters A (left panel) and B (right panel) of all member galaxies. We note that these structures cannot be described by a single Gaussian shape indicating that these structures are not virialized. |
4.2. SFR dependence on local overdensity
The upper panel of Fig. 8 shows the dependence of SFR on stellar mass and local density. For low-mass galaxies (log10(M⋆/M⊙)≲10) we find the same average SFR in both high- and low-density regions, although there are only very few (∼10) low-mass galaxies in our sample in high-density regions and all of them are star-forming (check completeness in Fig. A.1). At higher stellar masses (log10(M⋆/M⊙) > 10), we find a stronger dependence of SFR on local density. At log10(M⋆/M⊙)∼10.75, the difference is the highest due to a larger fraction of galaxies at these stellar masses being photometrically defined as quiescent in higher-density regions. At the highest stellar masses (log10(M⋆/M⊙)≳11), there are few star-forming galaxies in both higher- and lower-density regions and we see little dependence of the star formation activity in galaxies on the local density in which they reside. We fit a linear model, log10(SFR)=m log10(M)+b, to the stellar mass-SFR relation at log10(M⋆/M⊙) > 10 and find that for lower-density regions the null hypothesis of a flat relation (m = 0) is rejected at ∼3.3σ (m = −0.7 ± 0.22) and for higher-density regions is rejected at ∼3.5σ (m = −0.9 ± 0.25).
 |
Fig. 8. Top panel: SFR (from SED fitting) distribution as a function of stellar mass. Each small circle represents a single galaxy. Large squares show the median value for the population in stellar mass bins. Error bars show the error on the median of each bin. Higher-density regions are coloured in blue while lower- density galaxies are shown in green colours. The empty symbols represent the bins considering star-forming galaxies only, with log10(sSFR) > − 11. The symbols are horizontally shifted for visualisation purposes. The vertical dotted line shows the completeness limit of our survey. Globally, we find that galaxies in higher-density regions have lower SFRs, but only when considering the entire population. When selecting star-forming galaxies, we find no difference between the median SFRs in low- and high-density environments. Bottom panel: dust-corrected [O II] luminosity distribution as a function of stellar mass. We show as small arrows the upper limits on [OII] luminosity for the galaxies for which we have no measure with sufficient S/N. Horizontal lines show three values of SFR = 1, 10, 50 M⊙ yr−1 as derived from Eq. (3). We typically find no differences between low- and high-density regions in terms of the median dust-corrected [OII] luminosity at all stellar masses probed in our sample. |
When looking at the trends, considering star-forming galaxies only (with log10(sSFR) > − 11), the difference between low- and high-density regions vanishes. With a similar linear model as described above, we find m = −0.2 ± 0.23 for low-density regions and m = −0.4 ± 0.20 for higher-density regions. These models are less than 2σ from the null hypothesis. When compared with the full sample, this suggests that the decline in the median SFR of the full sample in dense regions is mainly driven by the higher fraction of quenched galaxies.
We compute the fraction of galaxies that are defined as quenched in our sample (log10(sSFR) < − 11) and show our findings in the Fig. 9. Error bars for the fraction of quiescent galaxies are computed using Poisson statistics 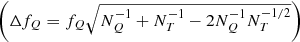 . We inspect the environmental dependence of this fraction on environment for two separate stellar-mass bins. We find that the lower-stellar-mass galaxies (10 < log10(M⋆/M⊙) < 10.75) have a nearly constant quenched fraction at low to intermediate densities. We then find a jump from ∼10% to ∼40 − 60% towards higher-density regions. When considering the higher-stellar-mass bin (log10(M⋆/M⊙) > 10.75), we find no dependence of the quenched fraction on local density, this being nearly constant at ∼30%. We also show the reported values after correcting for our sample completeness and we find qualitatively the same results (see Appendix A for more details on the spectroscopic sample completeness).
. We inspect the environmental dependence of this fraction on environment for two separate stellar-mass bins. We find that the lower-stellar-mass galaxies (10 < log10(M⋆/M⊙) < 10.75) have a nearly constant quenched fraction at low to intermediate densities. We then find a jump from ∼10% to ∼40 − 60% towards higher-density regions. When considering the higher-stellar-mass bin (log10(M⋆/M⊙) > 10.75), we find no dependence of the quenched fraction on local density, this being nearly constant at ∼30%. We also show the reported values after correcting for our sample completeness and we find qualitatively the same results (see Appendix A for more details on the spectroscopic sample completeness).
 |
Fig. 9. The fraction of quenched galaxies within our sample (fQ, with log10(sSFR) < − 11) as a function of local density and in two different bins of stellar mass. Open symbols show the same fraction after correcting for our sample completeness. Error bars are computed using Poisson statistics. We find in both cases that the lower-stellar-mass galaxies show a sharp increase for higher-density environments whereas the highest-stellar-mass galaxies show no environmental dependence of fQ. Shaded regions provide an approximate estimate of the cosmic web environment given the measured overdensity (but see Sect. 3.3 for more details). |
4.3. [OII] luminosity dependence on local overdensity
The lower panel of Fig. 8 shows the resulting distribution of dust-corrected [OII] luminosity for the sample at 0.8 < z < 0.9. The bulk of the population has L[OII] ∼ 1041.5 erg s−1 with the brightest in our sample reaching luminosities of L[OII] ∼ 1043 erg s−1.
When looking at galaxies in high- and low-density environments we find no significant difference in the median (excluding upper limits) dust-corrected [OII] luminosity at all stellar masses probed in our study. If we assume that the luminosity of the [O II] emission doublet is correlated with the galaxy SFR (see e.g. Kennicutt 1998; Kewley et al. 2004; Darvish et al. 2015b), our results on [OII] show that their median luminosity (which traces star formation) is not affected by higher-density environments. This is different from what we show when using SFRs derived from SED fitting. We attribute this discrepancy to the fact that with our observational setup we measure [OII] luminosities more easily for star-forming galaxies than for quiescent galaxies (which are mostly upper limits). The SED fitting results do not suffer from the same problem, meaning that what is likely causing the differences is the quenched fraction as a function of density. Having a higher fraction of quenched galaxies at high densities (see e.g. Fig. 9) will result in a lower median SFR value than what we would get from [OII] luminosities because we miss a fraction of that population (upper limits only in Fig. 8). If one includes the upper limits in the median calculation, we get qualitatively the same trends as we find for SED-derived SFRs.
We note, however, that differences may also arise if the [OII] emission is originating from other sources than star formation (e.g. AGN, LINERs; see e.g. Yan et al. 2006; Kocevski et al. 2011), but we expect this to be a secondary effect due to the lower overall fraction of this type of object (e.g. Pentericci et al. 2013; Ehlert et al. 2014; Oh et al. 2014).
4.4. [OII] properties in stacked spectra
We show in the left panel of Fig. 10 (see also Fig. C.1 for individualized panels) the resulting spectra after stacking all galaxies in bins of stellar mass. We observe a strong decrease in [OII] line strength from low to high stellar masses (a factor of ∼10 in flux from the lowest to the highest stellar-mass bin). We also see the relative strength of the two doublet lines is changing with stellar mass. At lower masses, the [O II]λ3729/[OII]λ3726 ratio is higher and seems to constantly decrease as we move towards higher masses. This ratio is indicative of the electron density in the interstellar medium (e.g. Seaton & Osterbrock 1957; Canto et al. 1980; Pradhan et al. 2006, Darvish et al. 2015b; Sanders et al. 2016; Kaasinen et al. 2017) and will be investigated in a subsequent paper.
 |
Fig. 10. Resulting spectral stacks (normalised by the flux at 4150 Å < λ < 4350 Å) around the [OII] doublet in bins of stellar mass (left panel) and in bins of local density (right panel). This figure shows the comparison between different stacks (for individual inspection, we refer to Fig. C.1). We see a strong dependence of the [OII] strength on the stellar mass with higher-stellar-mass galaxies having weaker [OII] emission, as expected since most quenched galaxies are found at higher stellar masses and should have little to no emission. We also find a dependence of the [OII] strength on the local density with high-density regions having galaxies with weaker [OII] emission, again with massive quiescent galaxies dominating at higher densities being the likely cause of this effect. |
In Fig. 10 (right panel, see also Fig. C.2 for individualized panels), we show our findings of the stacked spectra in bins of local density. In terms of the [OII] emission, we find a decreasing line strength from low- to high-density regions. Interestingly, in the three lowest-density bins the difference in [OII] emission strength is appreciably smaller when compared to the two highest-density bins. This decrease at log10(δ)∼0 − 0.5 hints at a break in star formation around these local overdensity values (see e.g. Darvish et al. 2016).
To quantify the properties of each line, we performed a double Gaussian fitting to [OII] using Eq. (1). Results of the equivalent widths and fluxes of the [OII] doublet are summarised in Table C.1 and Fig. 11. The qualitative remarks we made on the appearance of the spectral stacks are confirmed by our results after fitting each component.
 |
Fig. 11. Line equivalent width for the spectral lines in [OII] as a function of the stellar mass range (left panel) and of the local density range (right panel) for the stacked spectra. We apply no dust correction to the stacked derived values since we assume spatial coincidence between the continuum and line-emitting regions, and they are affected by dust in a similar manner. |
We find a strong decrease in [OII] strength and line equivalent width with stellar mass (see Fig. 11) with a factor of ∼10 between the lowest stellar-mass bin (9.0 < log10(M⋆/M⊙) < 9.4) and the highest stellar-mass bin (log10(M⋆/M⊙) > 10.7) (similar to results by e.g. Darvish et al. 2015b; Khostovan et al. 2016). Performing the same analysis on the stacked spectra per local density bin, the [OII] line strength and equivalent width show a broken relation with a “break” at log10(1 + δ) ∼ 0.0 − 0.5 that translates into a steeper relation at higher densities.
5. Discussion
The survey presented in this paper selects galaxies according to their continuum emission and absorption features down to log10(M⋆/M⊙) ∼ 10 and is able to detect [OII] down to ∼5 × 10−18 erg s−1cm−2. Since our sample is based on accurate measurements of redshifts, it is natural that it only selects galaxies at lower stellar masses if they have clear emission lines characteristic of star-forming galaxies. This means that our results on global trends with stellar mass below our completeness limit is biased against low star formation and passive galaxies (see e.g. Fig. 4). This fact alone is able to explain an apparent lack of trends in star-formation related quantities (SFR and L[OII]) at stellar masses below log10(M⋆/M⊙) = 10, where we see no dependence whatsoever on local overdensity. In summary, our results for the lowest-stellar-mass bins (less than 1010 M⊙) are likely based only on the star-forming population.
One important aspect to consider when looking for environmental effects on galaxy evolution is to attempt to distinguish between stellar-mass-driven and density-driven mechanisms (e.g. Peng et al. 2010; Kovač et al. 2014; Darvish et al. 2016). We attempt to address these issues by computing average quantities in different environments as a function of stellar mass (or at different stellar masses as a function of environment).
Considering our results on galaxies with stellar masses above our completeness limit, we find little influence of environment on galaxy SFRs (from SED fitting) and L[OII]. In higher-density regions, galaxies are typically less star-forming (Fig. 8; except at the highest stellar masses (log10(M⋆/M⊙) > 11) but with comparable [OII] emission. This can easily be explained by the increase of the fraction of quenched galaxies in higher-density regions. These trends support the scenario where environment plays a role in increasing the quiescent fraction of intermediate-stellar-mass galaxies at these redshifts (z ≈ 0.84). This fits well in the scenario where galaxies already have their star formation suppressed due to environmental effects as early as 7 billion years ago. At higher stellar masses, we see no differences in the average SFR and quiescent fractions, hinting that mass quenching should be effective enough to halt star formation even in low-density regions (see e.g. Peng et al. 2010) although it is not clear that environmental and stellar mass quenching are fully separable (see e.g. Lee et al. 2015; Darvish et al. 2016; Kawinwanichakij et al. 2017). This differential effect with stellar mass is a potential indicator that environment acts as a catalyst for star-formation quenching in the sense that we are more likely to see galaxies quench at lower stellar masses if they reside in high-density environments. We stress that for 10 < log10(M⋆/M⊙) < 10.25, we find no differences in the median SFRs between low- and high-density regions; this is likely caused by a lack of quiescent galaxies close to our completeness limit that drives up the median value of the SFR for that bin. Since we see a rise in the quiescent fraction towards high-density regions on the lowest stellar-mass bin that we probe (see Fig. 9 and also Appendix A), it is plausible that this is the reason for the observed results in this stellar-mass bin.
Our findings corroborate those reported by Sobral et al. (2011) which probed the same region using Hα emitters. They are also consistent with others in the literature which already report a decrease in the star-forming fraction with projected galaxy density at similar redshifts (e.g. Patel et al. 2009; Muzzin et al. 2012). We also see similar trends of star formation with environment in lower-redshift surveys (e.g. Balogh et al. 2002; Rodríguez del Pino et al. 2017). This means that environmental effects are shaping the star formation in individual galaxies in a similar manner in the past 6 Gyr. These effects are readily explained by the number of physical mechanisms (e.g. ram pressure stripping, tidal interactions) capable of stripping gas from galaxies and shutting down any new star formation activity. While we note that these can in fact explain the observed trends in SFR with stellar mass and environment, it is beyond the scope of this paper to pinpoint the mechanisms responsible for our observations.
Overall we find that the average SFR is lower in high-density regions, confirming what was reported by Sobral et al. (2011) when studying Hα emitters on the same structure. We report one order of magnitude difference in the average SFR from the lowest- to the highest-density region (∼10 to ∼1 M⊙ yr−1). This trend with environment gives strength to the argument of environmentally driven quenching occurring within our superstructure. These signs of environmental quenching of star formation (also seen in e.g. Patel et al. 2009; Sobral et al. 2011; Muzzin et al. 2012; Santos et al. 2013) are distinct from the structures that show a flat or reverse SFR-density relation (e.g. Elbaz et al. 2007; Ideue et al. 2009; Tran et al. 2010; Santos et al. 2014).
One interesting result is the “break” that we find on the relation between [OII] line equivalent width and local overdensity that occurs at intermediate densities (log10(δ) ∼ 0.0 − 0.5, see Fig. 11 and also e.g. Darvish et al. 2016). We hypothesise that this corresponds to a typical density where environment quenching mechanisms are the most effective. The transition at log10(δ)∼0.0 − 0.5 is consistent with regions of filament-like densities (see transition from filament-dominated to cluster-dominated galaxies in Fig. 6). This result is compatible with intermediate-density regions being the place of enhanced chances for galaxy encounters, promoting galaxy-harassment-related quenching mechanisms (e.g. Moss 2006; Perez et al. 2009; Li et al. 2009; Tonnesen & Cen 2012; Darvish et al. 2014; Malavasi et al. 2017). It might also be caused by strong cluster-cluster interactions that are found to enhance star formation as well (e.g. Stroe et al. 2014, 2015). To further reinforce the existence of such a “break”, we find that the fraction of quenched galaxies at intermediate stellar masses (10 < log10(M⋆/M⊙) < 10.75) increases by a factor of two at the same transition density, being roughly constant below and above. Galaxies at higher stellar masses are likely already quenched due to their own mass (see e.g. Peng et al. 2010) and they are likely not greatly affected by the environment they are in.
6. Conclusions
We have presented in this paper an overview of the VIS3COS survey, which targets a superstructure at z ∼ 0.84 with VIMOS/VLT high-resolution spectra. We report on trends with environment and stellar mass of the SFR and [OII] luminosity. Our main findings are summarised as follows:
-
Above our stellar-mass completeness limit (1010 M⊙), galaxies in higher-density regions have lower SFRs at intermediate masses (10 < log10(M⋆/M⊙) < 10.75). At the highest masses (above 1010.75 M⊙), the star formation activity is similar in low- and high-density environments indicating that mass quenching is probably dominant at high stellar masses.
-
We find that the fraction of quenched galaxies (fQ) increases from ∼10% to ∼40 − 60% with increasing galaxy overdensity, but only for intermediate stellar mass galaxies (10 < log10(M⋆/M⊙) < 10.75). The most massive galaxies in our sample (above 1010.75 M⊙) have a similar value of fQ ∼ 30 − 40% at all densities.
-
We find a break in [OII] strength and equivalent width in the stacked spectra in filament-like regions (log10(δ)∼0.0 − 0.5). We hypothesise that at these densities, quenching mechanisms due to environment play an important role. This is consistent with the increase in the quenched galaxy fraction that we find for intermediate-stellar-mass galaxies.
In summary, the results of this paper shed some light on the properties of galaxies in and around a superstructure on the COSMOS field. In this paper, we have focused on the overall properties of the sample in our survey and the general trends that we find on galaxy properties with respect to environment. More detailed studies focusing on the individual star formation activity of galaxies, galaxy morphology, and electron density estimates will be discussed in forthcoming papers.
This is the same mode used by LEGA-C, see van der Wel et al. (2016) for more details.
Acknowledgments
We thank the anonymous referee for making valuable suggestions, which helped to improve the paper. This work was supported by Fundação para a Ciência e a Tecnologia (FCT) through the research grant UID/FIS/04434/2013. APA, PhD::SPACE fellow, acknowledges support from the FCT through the fellowship PD/BD/52706/2014. DS acknowledges financial support from the Netherlands Organisation for Scientific research (NWO) through a Veni fellowship and from Lancaster University through an Early Career Internal Grant A100679. BD acknowledges financial support from NASA through the Astrophysics Data Analysis Program (ADAP), grant number NNX12AE20G, and the National Science Foundation, grant number 1716907. PNB is grateful for support from STFC via grant ST/M001229/1. This work was made possible by the use of the following PYTHON packages: NumPy & SciPy (Walt et al. 2011; Jones et al. 2001), Matplotlib (Hunter 2007), and Astropy (Astropy Collaboration 2013).
References
- Aragón-Calvo, M. A., van de Weygaert, R., & Jones, B. J. T. 2010, MNRAS, 408, 2163 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldry, I. K., Balogh, M. L., Bower, R. G., et al. 2006, MNRAS, 373, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Couch, W. J., Smail, I., Bower, R. G., & Glazebrook, K. 2002, MNRAS, 335, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M., Eke, V., Miller, C., et al. 2004, MNRAS, 348, 1355 [Google Scholar]
- Balogh, M. L., McGee, S. L., Mok, A., et al. 2014, MNRAS, 443, 2679 [NASA ADS] [CrossRef] [Google Scholar]
- Bamford, S. P., Nichol, R. C., Baldry, I. K., et al. 2009, MNRAS, 393, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K. 2009, MNRAS, 399, 2221 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N. 2004, MNRAS, 351, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Cortese, L., Boquien, M., et al. 2014, A&A, 564, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T., Catinella, B., Cortese, L., et al. 2017, MNRAS, 466, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Burgarella, D., Buat, V., Gruppioni, C., et al. 2013, A&A, 554, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canto, J., Meaburn, J., Theokas, A. C., & Elliott, K. H. 1980, MNRAS, 193, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, C. M., Bschorr, T. J., Renzini, A., et al. 2013, ApJ, 773, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, S. A., Hickox, R. C., Wegner, G. A., Einasto, M., & Vennik, J. 2017, ApJ, 835, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Weiner, B. J., et al. 2008, MNRAS, 383, 1058 [Google Scholar]
- Cortese, L., Davies, J. I., Pohlen, M., et al. 2010, A&A, 518, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crain, R. A., Schaye, J., Bower, R. G., et al. 2015, MNRAS, 450, 1937 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Marinoni, C., Iovino, A., et al. 2010a, A&A, 520, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Iovino, A., Kovač, K., et al. 2010b, A&A, 524, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Zamorani, G., Lemaux, B. C., et al. 2014, A&A, 570, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Davidzon, I., Bolzonella, M., et al. 2017, A&A, 602, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Darvish, B., Sobral, D., Mobasher, B., et al. 2014, ApJ, 796, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Darvish, B., Mobasher, B., Sobral, D., Scoville, N., & Aragon-Calvo, M. 2015a, ApJ, 805, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Darvish, B., Mobasher, B., Sobral, D., et al. 2015b, ApJ, 814, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Darvish, B., Mobasher, B., Sobral, D., et al. 2016, ApJ, 825, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Darvish, B., Mobasher, B., Martin, D. C., et al. 2017, ApJ, 837, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2004, in The Cold Universe, Saas-Fee Advanced Course, 32, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1984, ARA&A, 22, 185 [Google Scholar]
- Ehlert, S., von der Linden, A., Allen, S. W., et al. 2014, MNRAS, 437, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, AJ, 135, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., Guzzo, L., Hasinger, G., et al. 2007, ApJS, 172, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., Labbé, I., Patel, S. G., et al. 2014, ApJ, 796, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Bell, E. F., Wolf, C., et al. 2009, ApJ, 690, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Genel, S., Vogelsberger, M., Springel, V., et al. 2014, MNRAS, 445, 175 [Google Scholar]
- Giovanelli, R., & Haynes, M. P. 1985, ApJ, 292, 404 [CrossRef] [Google Scholar]
- Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, M., Kodama, T., Koyama, Y., et al. 2014, MNRAS, 439, 2571 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2015, MNRAS, 451, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Blanton, M. R., Brinchmann, J., et al. 2004, ApJ, 601, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ideue, Y., Nagao, T., Taniguchi, Y., et al. 2009, ApJ, 700, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iovino, A., Cucciati, O., Scodeggio, M., et al. 2010, A&A, 509, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iovino, A., Petropoulou, V., Scodeggio, M., et al. 2016, A&A, 592, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., & Peterson, P. 2001, SciPy: Open Source Scientific Tools for Python [Google Scholar]
- Kaasinen, M., Bian, F., Groves, B., Kewley, L. J., & Gupta, A. 2017, MNRAS, 465, 3220 [NASA ADS] [CrossRef] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kawinwanichakij, L., Papovich, C., Quadri, R. F., et al. 2017, ApJ, 847, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kewley, L. J., Geller, M. J., & Jansen, R. A. 2004, AJ, 127, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Geller, M. J., & Barton, E. J. 2006, AJ, 131, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Khostovan, A. A., Sobral, D., Mobasher, B., et al. 2015, MNRAS, 452, 3948 [NASA ADS] [CrossRef] [Google Scholar]
- Khostovan, A. A., Sobral, D., Mobasher, B., et al. 2016, MNRAS, 463, 2363 [NASA ADS] [CrossRef] [Google Scholar]
- Kocevski, D. D., Lemaux, B. C., Lubin, L. M., et al. 2011, ApJ, 737, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., Balogh, M. L., Smail, I., Bower, R. G., & Nakata, F. 2004, MNRAS, 354, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Knobel, C., et al. 2014, MNRAS, 438, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, Y., Smail, I., Kurk, J., et al. 2013, MNRAS, 434, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, Y., Kodama, T., Tadaki, K.-I., et al. 2014, ApJ, 789, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, S., Koyama, Y., Yamashita, T., et al. 2017, ApJ, 847, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kulas, K. R., McLean, I. S., Shapley, A. E., et al. 2013, ApJ, 774, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S.-K., Im, M., Kim, J.-W., et al. 2015, ApJ, 810, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., & Mancini, D. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 1670 [CrossRef] [Google Scholar]
- Lemaux, B. C., Cucciati, O., Tasca, L. A. M., et al. 2014, A&A, 572, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, I., Balogh, M., De Propris, R., et al. 2002, MNRAS, 334, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Li, I. H., Yee, H. K. C., & Ellingson, E. 2009, ApJ, 698, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Li, I. H., Glazebrook, K., Gilbank, D., et al. 2011, MNRAS, 411, 1869 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fevre, O., Hammer, F., & Crampton, D. 1996, ApJ, 460, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lubin, L. M., Gal, R. R., Lemaux, B. C., Kocevski, D. D., & Squires, G. K. 2009, AJ, 137, 4867 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Malavasi, N., Pozzetti, L., Cucciati, O., Bardelli, S., & Cimatti, A. 2016, A&A, 585, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malavasi, N., Arnouts, S., Vibert, D., et al. 2017, MNRAS, 465, 3817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masters, D., & Capak, P. 2011, PASP, 123, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Mok, A., Balogh, M. L., McGee, S. L., et al. 2013, MNRAS, 431, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Mok, A., Wilson, C. D., Golding, J., et al. 2016, MNRAS, 456, 4384 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, C. 2006, MNRAS, 373, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Mulroy, S. L., McGee, S. L., Gillman, S., et al. 2017, MNRAS, 472, 3246 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Wilson, G., Yee, H. K. C., et al. 2012, ApJ, 746, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJS, 206, 8 [Google Scholar]
- Nakata, F., Bower, R. G., Balogh, M. L., & Wilman, D. J. 2005, MNRAS, 357, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Oemler, Jr., A. 1974, ApJ, 194, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S., Mulchaey, J. S., Woo, J.-H., et al. 2014, ApJ, 790, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Owers, M. S., Couch, W. J., Nulsen, P. E. J., & Randall, S. W. 2012, ApJ, 750, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, S. G., Holden, B. P., Kelson, D. D., Illingworth, G. D., & Franx, M. 2009, ApJ, 705, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pentericci, L., Castellano, M., Menci, N., et al. 2013, A&A, 552, A111 [Google Scholar]
- Perez, J., Tissera, P., Padilla, N., Alonso, M. S., & Lambas, D. G. 2009, MNRAS, 399, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., von der Linden, A., De Lucia, G., et al. 2006, ApJ, 642, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M., Aragón-Salamanca, A., Zaritsky, D., et al. 2009, ApJ, 693, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Pradhan, A. K., Montenegro, M., Nahar, S. N., & Eissner, W. 2006, MNRAS, 366, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez del Pino, B., Aragón-Salamanca, A., Chies-Santos, A. L., et al. 2017, MNRAS, 467, 4200 [NASA ADS] [Google Scholar]
- Roediger, E., Brüggen, M., Owers, M. S., Ebeling, H., & Sun, M. 2014, MNRAS, 443, L114 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2016, ApJ, 816, 23 [Google Scholar]
- Santos, J. S., Altieri, B., Popesso, P., et al. 2013, MNRAS, 433, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, J. S., Altieri, B., Tanaka, M., et al. 2014, MNRAS, 438, 2565 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Scoville, N., Arnouts, S., Aussel, H., et al. 2013, ApJS, 206, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J., & Osterbrock, D. E. 1957, ApJ, 125, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, P., Oosterloo, T., Morganti, R., et al. 2012, MNRAS, 422, 1835 [NASA ADS] [CrossRef] [Google Scholar]
- Shimakawa, R., Kodama, T., Tadaki, K.-I., et al. 2015, MNRAS, 448, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Shimakawa, R., Kodama, T., Hayashi, M., et al. 2018, MNRAS, 473, 1977 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Geach, J. E., et al. 2009, MNRAS, 398, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Smail, I., et al. 2011, MNRAS, 411, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Smail, I., Best, P. N., et al. 2013, MNRAS, 428, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Stroe, A., Dawson, W. A., et al. 2015, MNRAS, 450, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Stroe, A., Koyama, Y., et al. 2016, MNRAS, 458, 3443 [NASA ADS] [CrossRef] [Google Scholar]
- Stroe, A., & Sobral, D. 2015, MNRAS, 453, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Stroe, A., Sobral, D., Röttgering, H. J. A., & van Weeren, R. J. 2014, MNRAS, 438, 1377 [NASA ADS] [CrossRef] [Google Scholar]
- Stroe, A., Sobral, D., Dawson, W., et al. 2015, MNRAS, 450, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Stroe, A., Sobral, D., Paulino-Afonso, A., et al. 2017, MNRAS, 465, 2916 [NASA ADS] [CrossRef] [Google Scholar]
- Tadaki, K.-I., Kodama, T., Ota, K., et al. 2012, MNRAS, 423, 2617 [CrossRef] [Google Scholar]
- Tonnesen, S., & Cen, R. 2012, MNRAS, 425, 2313 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, K.-V. H., Papovich, C., Saintonge, A., et al. 2010, ApJ, 719, L126 [CrossRef] [Google Scholar]
- Treu, T., Ellis, R. S., Kneib, J.-P., et al. 2003, ApJ, 591, 53 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Noeske, K., Bezanson, R., et al. 2016, ApJS, 223, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, Nature, 509, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Walt, S. V. D., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., & Franx, M. 2012, ApJ, 754, L29 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., Clowe, D. I., Simard, L., et al. 2005, A&A, 444, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijesinghe, D. B., Hopkins, A. M., Brough, S., et al. 2012, MNRAS, 423, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Aragón-Salamanca, A., Balogh, M., et al. 2009, MNRAS, 393, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, R., Newman, J. A., Faber, S. M., et al. 2006, ApJ, 648, 281 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Sample completeness
We estimate the sample completeness of our spectroscopic observations by comparing the number of sources for which we successfully measured a redshift with the number of possible targets in the parent catalogue (given our selection described in Sect. 2.2). We present our results in Fig. A.1. We will discuss the completeness effects in more detail in a forthcoming paper.
 |
Fig. A.1. Spectroscopic sample completeness as a function of stellar mass and local overdensity (top panel) and specific SFR (bottom panel). In each panel, we indicate the completeness for each bin in white numbers (Poisson errors shown in parenthesis). Bins with no targets are shown in white. |
We confirm that we are under-sampling denser regions when compared to the lowest density regions, which is expected given the spatial constraints on the positioning of the slits in the VIMOS masks does not allow to target densely populated areas. In terms of star formation activity, we find that our typical completeness is lower for quiescent galaxies (∼30%) when compared to star-forming ones (∼40%). When taken together, we find that we are most likely missing quiescent galaxies in high-density regions, but that the difference between the two populations is not dramatic in terms of completeness and our derived completeness corrections can tackle this without problems. Therefore we are providing a fair representation of the galaxy population in the regions we are targeting.
Appendix B: Catalogue of superstructure members
We release with this paper the VIS3COS catalogue of all targets in and around the superstructure at z ∼ 1 with spectroscopic redshifts, along with some of their measured properties: SFR, overdensity, stellar mass. We present the first ten entries of the full catalogue in Table B.1.
First 10 galaxies in our sample.
Appendix C: Individual stacks
Since some trends are difficult to see when showing all stacked spectra in a single panel due to line cluttering, here we show all the stacked spectra individually in Figs. C.1 (in bins of stellar mass) and C.2 (in bins of overdensity). All results are also summarised in Table C.1.
Summary of [OII] properties from the stacked spectra.
 |
Fig. C.1. Resulting spectral stacks (solid black line) in bins of stellar mass (high to low stellar mass from top to bottom panels) around the [OII] doublet. We show in green the best fit doublet model with each component shown as blue and red dashed lines. The shaded grey area represents the typical error on the fit of the spectra at each wavelength computed from the 16th and 84th percentiles of 10 000 realizations of perturbing the spectra by its error. In each panel we show the derived ratio between the two doublet components. |
 |
Fig. C.2. Resulting spectral stacks (solid black line) in bins of overdensity (high to low density from top to bottom panels) around the [OII] doublet. We show in green the best fit doublet model with each component shown as blue and red dashed lines. The shaded grey area represents the typical error on the fit of the spectra at each wavelength computed from the 16th and 84th percentiles of 10 000 realizations of perturbing the spectra by its error. In each panel we show the derived ratio between the two doublet components. |
All Tables
Observing log for our observations with VIMOS on the VLT for programmes 086.A-0895, 088.A-0550, and 090.A-0401 (PI: Sobral).
All Figures
 |
Fig. 1. Snapshot of the region targeted by our spectroscopic survey. The colour map encodes the information on the galaxy projected surface density at the redshift slice of interest at 0.8 < z < 0.9 estimated from the catalogue made public by Darvish et al. (2017). Each thick white cross represents a targeted galaxy with a measured spectroscopic redshift in the same redshift slice. The white pentagons show a targeted galaxy with measured spectroscopic redshift, outside the defined redshift slice. The blue circles show the targeted galaxies for which we have no measured spectroscopic redshift available. The orange squares show the location of Hα emitters studied by Sobral et al. (2011). The large red circles denote the location of X-ray-detected clusters from Finoguenov et al. (2007) at the same redshifts. The size of the circle shows the clusters’ estimated X-ray radius r500. We see here that we are probing a large range of densities with our survey, in part due to selection effects (e.g. slit placement constraints). |
| In the text | |
 |
Fig. 2. Three individual examples of images and spectra obtained with our survey. Each thumbnail (left panel) shows the HST/ACS F814W image of each target from the COSMOS survey (Koekemoer et al. 2007) with the VIMOS slit overlaid (dashed yellow line). To the right of each stamp we show the corresponding 2D (top) and 1D (bottom) spectrum. We use vertical dashed lines to mark the position of some spectral features present in our spectra. |
| In the text | |
 |
Fig. 3. Spectroscopic redshift distribution of the galaxies targeted in our sample as a black histogram. The vertical black dashed lines delimit the redshift selection of the results presented in this paper. The red line shows our Gaussian fit to the distribution without using rejection algorithms, pinpointing z = 0.836 ± 0.008 as the core redshift of the densest structure we find. The peak at slightly higher redshift (z ∼ 0.88) is likely produced by members from the north-western cluster C (see Table 2 and Fig. 1). |
| In the text | |
 |
Fig. 4. Stellar masses and SFRs derived from SED fitting (see Sect. 3.2) in our spectroscopic sample at 0.8 < z < 0.9. For comparison, we show the derived best-fit relation for star-forming galaxies computed at z = 0.84 using the equation derived by Whitaker et al. (2012) over a large average volume in the COSMOS field. The vertical dotted line shows the completeness limit of our survey. The dotted contours show the COSMOS2015 (Laigle et al. 2016) distribution of galaxies with 0.8 < zphot < 0.9 and iAB < 23 from 10% to 95% of the sample in 5% steps. Empty circles highlight the photometric quiescent sample with log10(sSFR) < − 11. |
| In the text | |
 |
Fig. 5. SFR estimates from SED fitting and from [OII] (derived from Eq. (4) of Kewley et al. 2004) of the galaxies in our spectroscopic sample at 0.8 < z < 0.9. Red circles show the dust uncorrected Hα derived star formation rates for the galaxies in our sample and that were measured by Sobral et al. (2011). The subscript corr denotes the dust-corrected SFRs derived from each estimate using the optical depth derived through SED fitting (see Sect. 3.2). |
| In the text | |
 |
Fig. 6. Overdensity distribution for the galaxies in our sample with 0.8 < z < 0.9. We show the different cosmic web environments of galaxies (field, filament, and cluster) according to their classification using the scheme devised by Darvish et al. (2014, 2017). |
| In the text | |
 |
Fig. 7. The velocity distribution for clusters A (left panel) and B (right panel) of all member galaxies. We note that these structures cannot be described by a single Gaussian shape indicating that these structures are not virialized. |
| In the text | |
 |
Fig. 8. Top panel: SFR (from SED fitting) distribution as a function of stellar mass. Each small circle represents a single galaxy. Large squares show the median value for the population in stellar mass bins. Error bars show the error on the median of each bin. Higher-density regions are coloured in blue while lower- density galaxies are shown in green colours. The empty symbols represent the bins considering star-forming galaxies only, with log10(sSFR) > − 11. The symbols are horizontally shifted for visualisation purposes. The vertical dotted line shows the completeness limit of our survey. Globally, we find that galaxies in higher-density regions have lower SFRs, but only when considering the entire population. When selecting star-forming galaxies, we find no difference between the median SFRs in low- and high-density environments. Bottom panel: dust-corrected [O II] luminosity distribution as a function of stellar mass. We show as small arrows the upper limits on [OII] luminosity for the galaxies for which we have no measure with sufficient S/N. Horizontal lines show three values of SFR = 1, 10, 50 M⊙ yr−1 as derived from Eq. (3). We typically find no differences between low- and high-density regions in terms of the median dust-corrected [OII] luminosity at all stellar masses probed in our sample. |
| In the text | |
 |
Fig. 9. The fraction of quenched galaxies within our sample (fQ, with log10(sSFR) < − 11) as a function of local density and in two different bins of stellar mass. Open symbols show the same fraction after correcting for our sample completeness. Error bars are computed using Poisson statistics. We find in both cases that the lower-stellar-mass galaxies show a sharp increase for higher-density environments whereas the highest-stellar-mass galaxies show no environmental dependence of fQ. Shaded regions provide an approximate estimate of the cosmic web environment given the measured overdensity (but see Sect. 3.3 for more details). |
| In the text | |
 |
Fig. 10. Resulting spectral stacks (normalised by the flux at 4150 Å < λ < 4350 Å) around the [OII] doublet in bins of stellar mass (left panel) and in bins of local density (right panel). This figure shows the comparison between different stacks (for individual inspection, we refer to Fig. C.1). We see a strong dependence of the [OII] strength on the stellar mass with higher-stellar-mass galaxies having weaker [OII] emission, as expected since most quenched galaxies are found at higher stellar masses and should have little to no emission. We also find a dependence of the [OII] strength on the local density with high-density regions having galaxies with weaker [OII] emission, again with massive quiescent galaxies dominating at higher densities being the likely cause of this effect. |
| In the text | |
 |
Fig. 11. Line equivalent width for the spectral lines in [OII] as a function of the stellar mass range (left panel) and of the local density range (right panel) for the stacked spectra. We apply no dust correction to the stacked derived values since we assume spatial coincidence between the continuum and line-emitting regions, and they are affected by dust in a similar manner. |
| In the text | |
 |
Fig. A.1. Spectroscopic sample completeness as a function of stellar mass and local overdensity (top panel) and specific SFR (bottom panel). In each panel, we indicate the completeness for each bin in white numbers (Poisson errors shown in parenthesis). Bins with no targets are shown in white. |
| In the text | |
 |
Fig. C.1. Resulting spectral stacks (solid black line) in bins of stellar mass (high to low stellar mass from top to bottom panels) around the [OII] doublet. We show in green the best fit doublet model with each component shown as blue and red dashed lines. The shaded grey area represents the typical error on the fit of the spectra at each wavelength computed from the 16th and 84th percentiles of 10 000 realizations of perturbing the spectra by its error. In each panel we show the derived ratio between the two doublet components. |
| In the text | |
 |
Fig. C.2. Resulting spectral stacks (solid black line) in bins of overdensity (high to low density from top to bottom panels) around the [OII] doublet. We show in green the best fit doublet model with each component shown as blue and red dashed lines. The shaded grey area represents the typical error on the fit of the spectra at each wavelength computed from the 16th and 84th percentiles of 10 000 realizations of perturbing the spectra by its error. In each panel we show the derived ratio between the two doublet components. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} {f(\lambda ) = A_1 \exp \left[- \frac{(\lambda - \lambda _1)^2}{2\sigma ^2} \right] + A_2\exp \left[- \frac{(\lambda - \lambda _2 )^2}{2\sigma ^2} \right],} \end{aligned} $$](/articles/aa/full_html/2018/12/aa32688-18/aa32688-18-eq1.gif)
![$$ \begin{aligned} L_\mathrm{[OII],corr} = L_\mathrm{[OII]} /\mathrm{e}^{-\tau _{[\mathrm{O} \mathtt II ]}}, \end{aligned} $$](/articles/aa/full_html/2018/12/aa32688-18/aa32688-18-eq3.gif)
![$$ \begin{aligned} {\mathrm{SFR} = \frac{6.58\times 10^{-42}}{1.7}L_\mathrm{[OII],corr} .} \end{aligned} $$](/articles/aa/full_html/2018/12/aa32688-18/aa32688-18-eq4.gif)