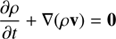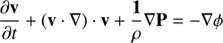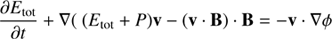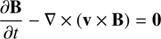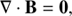| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834153 | |
| Published online | 14 November 2018 | |
Letter to the Editor
Magnetic fields in massive spirals: The role of feedback and initial conditions
1 Foundation for Research and Technology (FORTH), Nikolaou Plastira 100, Vassilika Vouton, 711 10 Heraklion, Crete, Greece
2 Department of Physics and ITCP, University of Crete, 71003 Heraklion, Greece
Received:
29
August
2018
Accepted:
18
October
2018
Context. Magnetic fields play a very important role in the evolution of galaxies through their direct impact on star formation and stellar feedback-induced turbulence. However, their co-evolution with these processes has still not been thoroughly investigated, and the possible effect of the initial conditions is largely unknown.
Aims. This Letter presents the first results from a series of high-resolution numerical models, aimed at deciphering the effect of the initial conditions and of stellar feedback on the evolution of the galactic magnetic field in isolated Milky Way-like galaxies.
Methods. The models start with an ordered magnetic field of varying strength, either poloidal or toroidal, and are evolved with and without supernova feedback. They include a dark matter halo, a stellar and a gaseous disk, as well as the appropriate cooling and heating processes for the interstellar medium.
Results. Independently of the initial conditions, the galaxies develop a turbulent velocity field and a random magnetic field component in under 15 Myr. Supernova feedback is extremely efficient in building a random magnetic field component up to large galactic heights. However, a random magnetic field emerges even in runs without feedback, which points to an inherent instability of the ordered component.
Conclusions. Supernova feedback greatly affects the velocity field of the galaxy up to large galactic heights, and helps restructure the magnetic field up to 10 kpc above the disk, independently of the initial magnetic field morphology. On the other hand, the initial morphology of the magnetic field can accelerate the development of a random component at large heights. These effects have important implications for the study of the magnetic field evolution in galaxy simulations.
Key words: magnetic fields / ISM: magnetic fields / galaxies: magnetic fields
© ESO 2018
1. Introduction
Magnetic fields play a crucial role in all galactic processes: they can affect the evolution of turbulence, the flux of cosmic rays, the formation of the cold molecular gas that is necessary for star formation, and the evolution of feedback regions. In essence, magnetic fields influence all the internal processes that redistribute mass, energy, and momentum in a galaxy.
However, the observational methods available to measure them suffer from inherent uncertainties that prevent us from obtaining the full picture. The little we do know, mainly from Faraday rotation and synchrotron emission measurements, is that the magnetic field in galaxies like our own follows the large-scale spiral pattern, and that it appears to have an important turbulent component (Beck et al. 1996). From the recent full-sky dust polarization studies with Planck, we also know that the magnetic field of the Milky Way is probably in rough equipartition with turbulence (Soler et al. 2013; Planck Collaboration Int. XX 2015). Clearly, the interpretation of these observations requires numerical models targeted at the coevolution of the magnetic field and the galaxy.
So far, the vast majority of galactic evolution models have ignored magnetic fields. However, the increasing realization that galaxy evolution cannot be fully understood without this essential component, together with the necessary computational advances, have led to an increasing number of direct full-galaxy simulations that include magnetization (e.g., Su et al. 2018; Khoperskov & Khrapov 2018; Körtgen et al. 2018). Much of the effort in this field is targeted at the problem of cosmic magnetic field amplification. For instance, Beck et al. (2012) studied the amplification of magnetic fields in galactic halos by indirectly modeling stellar feedback. Pakmor & Springel (2013) simulated weakly magnetized disk galaxies with a moving mesh code, and found that stellar feedback led to a rapid amplification of the magnetic field that brought it in pressure equilibrium with the gas. Rieder & Teyssier (2016, 2017) simulated cosmological dwarf galaxies, showing a significant contribution of feedback-induced turbulence to driving a dynamo, as well as a galactic wind that redistributed the field into the intergalactic medium. Clearly, stellar feedback and magnetic fields largely regulate each other through turbulence. Nonetheless, simulations aiming at long-term evolution studies of the galaxy cannot capture the full dynamical range of turbulence or explore different initial magnetic field configurations.
This Letter presents a series of high-resolution, non-cosmological numerical models, including gas cooling, star formation, and supernova feedback, targeted at exploring the role of the initial magnetic field configuration and of stellar feedback in the evolution of the magnetic field of a massive spiral like the Milky Way. These models can reach the small scales where star formation and feedback act, with enough dynamical range to follow the effects of turbulence on the global magnetic field.
The numerical method is explained in the Sect. 2, the results are presented in Sect. 3, and they are discussed in Sect. 4.
2. Method and setup
2.1. Numerical code
The simulations were performed with the publicly available magnetohydrodynamics (MHD) code RAMSES (Teyssier 2002), which solves the MHD equations on a Cartesian grid and has adaptive mesh refinement (AMR) capabilities.
The equations solved by the code are
where ρ is the gas density, v the velocity, Etot the total energy, P the pressure, B the magnetic field, and ϕ is the gravitational potential. RAMSES uses a constrained transport scheme to evolve the magnetic field, which guarantees ∇ ⋅ B = 0 always (Fromang et al. 2006). This is a significant advantage with respect to codes that have to depend on divergence-cleaning algorithms, known to create spurious effects in studies of turbulent environments (Balsara & Kim 2004).
2.2. Initial setup
The initial conditions were created using the DICE code (Perret et al. 2014; Perret 2016). DICE is a Markov chain Monte Carlo (MCMC) based initial condition generator that ensures the hydrostatic equilibrium of the galaxy. Although DICE already comes with a RAMSES patch, it only allows a toroidal magnetic field configuration. More options for the magnetic field topology were added for the purposes of this work, which are open for download1.
We used a configuration of stellar and dark matter particles, as well as a hydrodynamical fluid, to simulate a Milky Way-like galaxy (total mass Mtot = 2 × 1012 M⊙) at redshift z = 0 with different initial morphologies and strengths of the magnetic field. The virial velocity of the galaxy was 200 km s−1, the mass fraction in stars was about 4.5% (including a stellar bulge with a mass fraction of 0.5%), and the mass fraction in gas was about 1%. The dark matter halo followed a Navarro–Frenk–White (NFW) profile (Navarro et al. 1996), while the gas and stars were initially placed in exponential disks with a scale length of 9 kpc. The galactic disk was perturbed with an m = 2 perturbation, starting at 2 kpc and ending at 12 kpc, which led to the formation of a bar and two spiral arms. The mean gas temperature was set at 104 K and subsonic turbulence, with an rms value of 8 km s−1 introduced throughout the disk. The disk gas had solar metallicity, while the halo gas had 10−4 solar, both constant. Appropriate cooling and heating rates for the interstellar medium were calculated according to Sutherland & Dopita (1993).
Table 1 contains the initial parameters of the different galaxy models. The parameters varied here were the strength and the initial topology of the magnetic field. The simulations started with either a toroidal field (model name ends with T), with a scale height and scale length of 1 kpc, or with a poloidal magnetic field (model name ends with P), with a scale height of 1 kpc and a scale length of 2 kpc. The poloidal magnetic field is model C from Ferrière & Terral (2014). The magnetic field of the disk in runs M_b1_T and M_fb_b1_T was initially just below equipartition with the kinetic energy of the gas in the center and in the interarm regions, and dropped to a factor of 100 below equipartition in the spiral arms. All the other runs start off significantly below equipartition everywhere. In all models, the thermal energy was initially more than 100 times below the total kinetic energy of the gas, but in equipartition with the turbulent kinetic energy. Unfortunately, the limit of initially global energy equipartition has not been explored in this work due to a lack of computational resources.
Summary of the models.
Star formation was simulated in all models by forming sink particles when the density exceeded 1000 cm−3. Models whose name contains “fb” additionally included stellar feedback from supernovae, resulting from previously formed sink particles with a time delay of 3 Myr. Supernovae were implemented by injecting thermal energy into the cells around the sink particle according to the number of supernovae estimated for the predicted size of the formed stellar cluster.
AMR was used here to capture the complex dynamics of the disk. In the box of 60 kpc, we used a coarse resolution of 2563 with four levels of refinement, reaching an effective 10243 in the entire disk, and 20483 in regions with active star formation.
3. Model evolution
Figure 1 shows the morphology of the galaxies and of their global magnetic field after 15 Myr. Independently of the initial conditions, there is a marked difference in the degree of turbulence in the magnetic field between the models with feedback and those without. The models with feedback immediately develop a visible random component up to tens of kiloparsec above the disk, while at the same heights the models without feedback largely retain the initial ordered morphology. This seems to be independent of the initial magnetic field strength.
 |
Fig. 1. Disk density in volume rendering, and the global magnetic field configuration in vectors after 15 Myr of evolution. The box size in this figure is 24 kpc. |
In particular, all models with an initially toroidal magnetic field develop a vertical component, while the two models with an initially poloidal magnetic field develop a horizontal component (panel a of Fig. 2). Interestingly, 22 Myr into the evolution, all models tend to roughly the same component separation: about 10% of the total rms magnetic field is in the vertical component, independently of the initial condition or the presence of feedback.
 |
Fig. 2. Panel a: relative strengths of the total vertical and horizontal rms magnetic fields with time, panel b: kinetic energy power spectra, and panel c: magnetic field power spectra. The black dashed lines in panels b and c show the Kolmogorov ∝k −11/3 dependence. |
The normalized kinetic energy power spectra and volume-weighted magnetic field power spectra are shown in panels b and c of Fig. 2 at 22 Myr for the full simulation box (L = 60 kpc), smoothed at a 5123 resolution. The black and gray curves show the initial toroidal and poloidal magnetic power spectra, respectively, while the dashed black line in both figures shows the Kolmogorov P ∝ k−11/3 dependence.
The kinetic energy power spectra are clearly divided into two families: the models with feedback, showing a Kolmogorov-like dependence on large scales, and the models without feedback, which remain close to the initial conditions on large scales. The fact that supernovae create power so quickly even in the halo implies a rapid communication between distant scales that is due to the very high speed of sound in the halo (cs ≃ 300 km s−1), which permits a disturbance to travel at heights above 8 kpc in 22 Myr. On the other hand, there seems to be no influence of either the strength or the morphology of the initial magnetic field on the kinetic energy power spectra, which is consistent with the fact that the magnetic field stays significantly below equipartition for the entire length of these simulations.
Conversely, the magnetic field power spectra retain a memory of their initial condition after one feedback cycle. Although all models develop a random magnetic field, as evidenced by the flat power spectra on scales smaller than one kiloparsec, those with a poloidal magnetic field remain closer to the initial conditions on large scales, independently of feedback. This is not surprising, since their initial magnetic field has a dominant vertical component, is therefore aligned with the feedback-induced outflow into the halo, and, on these timescales, is only deformed significantly in the disk. As in the kinetic energy power spectra, we observe again a clear separation into models with and without feedback at the largest scales as a result of the rapid communication between scales.
4. Discussion and conclusions
This Letter presented the first results from high-resolution simulations of magnetized massive spirals, exploring the short-term evolution of their velocity and magnetic field under different physical conditions.
The most striking result is that all galaxies, independently of the initial magnetic field morphology, quickly develop a random magnetic field component. A vertical component emerges in runs with an initially purely toroidal field, and a horizontal component in runs with an initially poloidal field. At 22 Myr, all models seem to tend to the same relative rms component separation: about 10% vertical, 90% horizontal. Although supernova feedback is very efficient in accelerating the process of redistributing magnetic energy and randomizing the field up to larger heights (a process reminiscent of the feedback “action at a distance” observed in star formation simulations Offner & Liu 2018), the new components also appear in runs without feedback.
This may be an indication of a Tayler-like instability of the galactic magnetic field, analogous to that of a stellar poloidal or toroidal field (Bonanno et al. 2012; Bonanno & Urpin 2008; Tayler 1973), as a result of the axisymmetric (spiral arms) and turbulent disturbances in the density and velocity field. In this case, the instability seems to be growing much more slowly than the field redistribution due to feedback. Certainly such an investigation is of great interest for a follow-up paper.
Finally, the power spectra of kinetic energy and magnetic field show the following:
-
The velocity field is very rapidly (< 15 Myr) affected by supernova feedback, which builds Kolmogorov-like turbulence up to tens of kiloparsecs above the disk due to the high temperatures of the halo gas.
-
The magnetic field is random at small scales, shaped by the inherent instability of the initial conditions and the feedback, when present. Our magnetic power spectra are very different than those reported, for example, by Rieder & Teyssier (2017), who found a Kolmogorov-like behavior of the magnetic field on small scales in their dynamo studies. It is possible that a longer evolution of the models could create a small-scale turbulent spectrum, but this cannot be deduced from the current state of the models.
Acknowledgments
The author is grateful to Fabio Del Sordo, Kostantinos Tassis, Vassiliki Pavlidou, and to the anonymous referee for useful comments, as well as to Francesca Fragkoudi for advice on using DICE. This research is funded by a Marie Curie Action of the European Union (Grant agreement number 749073). Initial testing of the numerical setup was performed on the HPC resources of CINES, under an allocation led by Patrick Hennebelle.
References
- Balsara, D. S., & Kim, J. 2004, ApJ, 602, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, A. M., Lesch, H., Dolag, K., et al. 2012, MNRAS, 422, 2152 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanno, A., & Urpin, V. 2008, A&A, 477, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanno, A., Brandenburg, A., Del Sordo, F., & Mitra, D. 2012, Phys. Rev. E, 86, 016313 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K., & Terral, P. 2014, A&A, 561, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khoperskov, S. A., & Khrapov, S. S. 2018, A&A, 609, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Körtgen, B., Banerjee, R., Pudritz, R. E., & Schmidt, W. 2018, MNRAS, 479, L40 [NASA ADS] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S. S. R., & Liu, Y. 2018, Nat. Astron., 2 [Google Scholar]
- Pakmor, R., & Springel, V. 2013, MNRAS, 432, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Perret, V. 2016, Astrophysics Source Code Library [record ascl:1607.002] [Google Scholar]
- Perret, V., Renaud, F., Epinat, B., et al. 2014, A&A, 562, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XX 2015, A&A, 576, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieder, M., & Teyssier, R. 2016, MNRAS, 457, 1722 [NASA ADS] [CrossRef] [Google Scholar]
- Rieder, M., & Teyssier, R. 2017, MNRAS, 471, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, J. D., Hennebelle, P., Martin, P. G., et al. 2013, ApJ, 774, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Su, K. Y., Hayward, C. C., Hopkins, P. F., et al. 2018, MNRAS, 473, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Tayler, R. J. 1973, MNRAS, 161, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Disk density in volume rendering, and the global magnetic field configuration in vectors after 15 Myr of evolution. The box size in this figure is 24 kpc. |
| In the text | |
 |
Fig. 2. Panel a: relative strengths of the total vertical and horizontal rms magnetic fields with time, panel b: kinetic energy power spectra, and panel c: magnetic field power spectra. The black dashed lines in panels b and c show the Kolmogorov ∝k −11/3 dependence. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.