| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201833782 | |
| Published online | 19 November 2018 | |
The AMBRE Project: r-process elements in the Milky Way thin and thick discs⋆
1
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482
Potsdam, Germany
2
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, France
e-mail guillaume.guiglion@oca.eu
3
Institut d’Astrophysique de Paris, UMR7095, CNRS, Université P. & M. Curie, 98bis Bd. Arago, 75104
Paris, France
Received:
6
July
2018
Accepted:
6
September
2018
Context. The chemical evolution of neutron capture elements in the Milky Way disc is still a matter of debate. There is a lack of statistically significant catalogues of such element abundances, especially those of the r-process.
Aims. We aim to understand the chemical evolution of r-process elements in Milky Way disc. We focus on three pure r-process elements Eu, Gd, and Dy. We also consider a pure s-process element, Ba, in order to disentangle the different nucleosynthesis processes.
Methods. We take advantage of high-resolution FEROS, HARPS, and UVES spectra from the ESO archive in order to perform a homogeneous analysis on 6500 FGK Milky Way stars. The chemical analysis is performed thanks to the automatic optimization pipeline GAUGUIN. We present abundances of Ba (5057 stars), Eu (6268 stars), Gd (5431 stars), and Dy (5479 stars). Based on the [α/Fe] ratio determined previously by the AMBRE Project, we chemically characterize the thin and the thick discs, and a metal-rich α-rich population.
Results. First, we find that the [Eu/Fe] ratio follows a continuous sequence from the thin disc to the thick disc as a function of the metallicity. Second, in thick disc stars, the [Eu/Ba] ratio is found to be constant, while the [Gd/Ba] and [Dy/Ba] ratios decrease as a function of the metallicity. These observations clearly indicate a different nucleosynthesis history in the thick disc between Eu and Gd–Dy. The [r/Fe] ratio in the thin disc is roughly around +0.1 dex at solar metallicity, which is not the case for Ba. We also find that the α-rich metal-rich stars are also enriched in r-process elements (like thick disc stars), but their [Ba/Fe] is very different from thick disc stars. Finally, we find that the [r/α] ratio tends to decrease with metallicity, indicating that supernovae of different properties probably contribute differently to the synthesis of r-process elements and α-elements.
Conclusions. We provide average abundance trends for [Ba/Fe] and [Eu/Fe] with rather small dispersions, and for the first time for [Gd/Fe] and [Dy/Fe]. This data may help to constrain chemical evolution models of Milky Way r- and s-process elements and the yields of massive stars. We emphasize that including yields of neutron-star or black hole mergers is now crucial if we want to quantitatively compare observations to Galactic chemical evolution models.
Key words: methods: data analysis / stars: abundances / Galaxy: abundances / Galaxy: stellar content
Full Table 3 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/619/A143
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The surface abundances of FGK dwarf stars do not show major changes along their main sequence evolution, reflecting their original pristine chemical composition. The Milky Way stars observable today were created thanks to a gas which had been enriched by several generations of stars, or from the in-fall or accretion of gas in the Galaxy. On the one hand, many comprehensive studies were able to constrain the chemical evolution of and iron peak elements in the Milky Way, thanks to recent massive spectroscopic surveys like RAVE (Steinmetz 2003), APOGEE (Wilson et al. 2010), and Gaia-ESO Survey (Gilmore et al. 2012), but also thanks to more classical studies, for example Adibekyan et al. (2011) and Haywood et al. (2013). On the other hand, less theoretical and observational data are available for elements heavier than Z ~ 35, usually called neutron-capture elements because they are formed by the addition of neutrons in stellar interiors. To create such nuclei, two main processes are known, first through the slow neutron-capture (s-process) or rapid neutron-capture (r-process), depending on whether the neutron-capture is slow or rapid with respect to the timescale of the β decay (Burbidge et al. 1957).
The s-process known to take place in the He-burning core of massive stars and in the convective C-burning shell (Peters 1968; Lamb et al. 1977) is also called the weak s-process. The s-process also happens in the asymptotic giant branch (AGB) of lower mass stars (M < 4 M ⊙) at solar and lower metallicities (Bisterzo et al. 2011), also denoted the main s-process. By ejecting their envelope, AGB stars are thought to be the main contributors for enriching the interstellar medium (ISM) in nuclei with atomic mass number 90 < A < 204. Finally, the last s-process, also called the strong s-process, is responsible for half of the solar 208Pb and takes place in low-metallicity AGB stars (Travaglio et al. 2001). In this study, as detailed later, we focus on barium, which is a heavy s-process element, of the second peak, mostly synthesized via the main s-process.
The rapid neutron capture process takes place on a much shorter timescale with respect to the β decay and when the density of neutrons is high enough. The r-process elements are basically divided into three peaks: A = 80, 130, and 194, depending on the timescale of the neutron flow and the atomic structure (Seeger et al. 1965). At least two production sites involving core-collapse supernovae (CCSN) have been proposed for r-process elements: neutrino induced winds via the so-called weak r-process, but they present limitations in producing nuclei with atomic number A > 100 (Woosley et al. 1994) and magneto-hydrodynamic jet explosions via the so-called main r-process (for A > 130). The main r-process contributes to the ISM enrichment with significant yields of 10−3−10−2 M ⊙ in r-process material for typical initial mass of 13 ≳ M ≳ 25 M ⊙ (Nishimura et al. 2006, 2015) over a typical timescale of few hundred million years. Unfortunately, such yields suffer from larger uncertainty, and are very mass and metallicity dependent. The main r-process is also supposed to occur during the merging of black holes or neutrons stars (NS; Freiburghaus et al. 1999). This has been confirmed observationally by the recent LIGO/Virgo detection of the first gravitational wave signal produced by NS–NS merging (Abbott et al. 2017a,b); however, no robust yields are available for this mechanism.
The chemical evolution of such heavy elements in the Milky Way is still then a matter of debate. Strong efforts on the theoretical side have been made in order to trace the origin of heavy elements in the Galaxy. For example, Travaglio et al. (1999) investigated the evolution of heavy elements from Ba to Eu in the thin disc, thick disc, and halo. Bisterzo et al. (2017) followed the same approach, but focused on the so-called 13C-pocket, a major source of uncertainty in ABG yields. In this study our goal is to understand the chemical evolution of three almost pure r-process elements: europium (Eu), gadolinium (Gd), and dysprosium (Dy). Europium can be considered a pure r-process element because 98% of the solar europium comes from the r-process (Sneden et al. 2008), and gadolinium and dysprosium as well, with 82% and 88% of the solar abundance coming from the r-process. Moreover, a powerful element that can be used to provide more constraints on the chemical evolution of such pure r-process nuclei is barium (Ba). Barium is for the most part an s-process element as 84% of the solar Ba originates from the s-process (Sneden et al. 2008). The [element/Ba] abundance ratios provide a direct way to quantify the relative importance of the r- and s-channels during the evolution of the Galaxy. Eu, Gd, and Dy are basically supposed to be produced via the same channel because of their very similar atomic mass number, and are located between the second and third peaks of the r-process. So we do not expect any major differences in the chemical evolution of these almost pure r-process elements. Because the unclear physical conditions of the astrophysical sites lead to very uncertain r-process predictions, Galactic chemical evolution models of r-process elements are quite challenging. Also, in up-to-date models, for elements heavier than Ba, the solar r-process contribution is directly deduced from the s-fraction of the solar abundances, giving some limitations to the GCE model (Käppeler et al. 2011; Prantzos et al. 2018). Additionally, rotation in massive stars is now known to play a key role in the efficiency of the stellar yields (Chiappini et al. 2006; Prantzos et al. 2018).
Ba and Eu have been observationally studied in the main Milky Way components. For example, Battistini & Bensby (2016) recently studied the temporal evolution of such elements in the thin and the thick discs for 400 stars, while Delgado Mena et al. (2017) presented Ba and Eu abundances for ~600 FGK stars, and also studied the halo.
On the contrary, Gd and Dy have been poorly studied in the the Milky Way disc. Overbeek et al. (2016) measured Gd and Dy for 68 stars in 23 open clusters while Spina et al. (2018) studied the temporal evolution of Gd and Dy for 79 solar twin stars.
We aim here to study homogeneously the evolution of Ba, Eu, Gd, and Dy for a statistically significant sample of stars, covering a large domain of metallicity. To this end we automatically derived a very large set of abundances for these elements, thanks to ESO archive spectra, for a sample of ~6000 stars. This study is placed in the context of the AMBRE Project (de Laverny et al. 2013). In order to put more constraints on the r-process elements origin, we also focus our study on the two main components of the Milky Way: the thin and thick discs.
The paper is organized as follows. In Sect. 2 we present the spectroscopic data used for our analysis, while in Sect. 3 we detail our automatic procedure of abundance determination. In Sect. 4, we validate and present our AMBRE catalogue of Ba, Eu, Gd, and Dy abundances, while in Sect. 5 we define our working stellar sample. The chemical evolution of Ba, Eu, Gd, and Dy in the Milky Way disc is discussed in Sect. 6 in the context of recent chemical evolution models. We conclude this work in Sect. 7.
2. Observational data set from the AMBRE Project
This work is based on ESO archived spectra data from the AMBRE project. We recall that this project is dedicated to the parametrization of the HARPS, FEROS, UVES, and GIRAFFE spectral archives (de Laverny et al. 2013), providing robust automatic determinations of the radial velocity (V rad), effective temperature (T e ff), surface gravity (log(g)), metallicity ([M/H]), and global α enrichment with respect to iron ([α/Fe]) together with their associated errors. The present study focuses on a subsample of the first three spectral sets that have already been parametrized: HARPS (De Pascale et al. 2014), FEROS (Worley et al. 2012), and UVES (Worley et al. 2016).
These analysed subsamples consist of spectra with a good AMBRE quality flag (lower or equal to 1; see e.g. Worley et al. 2012 for details on this label). The typical total errors on T e ff, log(g), and [M/H] are [108 K, 0.16 cm s−2, 0.10 dex] for UVES, [93 K, 0.26 cm s−2, 0.08 dex] for HARPS, and [120 K, 0.20 cm s−2, 0.10 dex] for FEROS. In the following, we also use the AMBRE estimates of the signal-to-noise ratio (S/N) and the FWHM of the cross-correlation function estimated when deriving V rad for a given star (FWHMCCF).
3. Automatic abundance analysis of n-capture elements
The r- and s-abundances of the AMBRE spectra were automatically derived via an optimization method by coupling a pre-computed synthetic spectra grid and the GAUGUIN Gauss–Newton algorithm. This method is presented in detail in Guiglion et al. (2016), but we give here a brief summary of the procedure, focusing mainly on the line-list adopted for the derivation of Ba II, Eu II, Gd II, and Dy II 1.
The main idea was to identify reliable atomic r- and s-process lines common to the FEROS (3500−9200 Å), HARPS (3780−6910 Å), and UVES spectral domains. For UVES, we took advantage of three different set-ups: Red580 (4726−6835 Å), U564 (4583−6686 Å) and U437 (3731−4999 Å). The adopted lines and their spectral synthesis properties are as follows (see also Table 1):
Element, wavelength, log g f, hyperfine structure, and reference for the 15 spectral lines used in this study.
-
Barium suffers from strong hyperfine splitting, and we adopted the lines and the hyperfine and isotopic structure from Rutten (1978) for the lines 5853.69, 6 141.73, 6496.90 Å, including the following isotopes: Ba130, 132, 134, 135, 136, 137, 138. We note that these isotopes are included in the spectral synthesis (with solar isotopic ratios), but we do not derive individual isotopic abundances (because of too low spectral resolution and high enough signal-to-noise ratio).
-
Europium has two main isotopes, Eu151 and Eu153 and suffers from strong hyperfine splitting. We adopted the hyperfine and isotopic structure from the line-list of Lawler et al. (2001) for the four spectral lines considered: 4129.72, 4205.04, 6437.64, and 6645.13 Å.
-
Gadolinium shows weaker lines compared with europium, and uncertain hyperfine splitting data can be found in the literature. We therefore do not take into account such structures. We adopted five lines from the work of Den Hartog et al. (2006): 4085.57, 4191.08, 4316.08, 4483.32, and 4498.28 Å.
-
Weak contribution of the hyperfine splitting is predicted for dysprosium so we do not take it into account in our spectral synthesis. We adopted the atomic data from Wickliffe et al. (2000) for the two lines considered: 4073.12, 4449.70.
We note that all lines are not observed, detected, and unblended in each star.
We then adopted a line-list for the atomic blends from the Vienna Atomic Line Database (VALD3; Kupka et al. 1999, 2000) over the domains covered by the adopted lines for the abundance analysis. Additionally, the line-lists of twelve molecular species were also taken into account: CN (Sneden et al. 2014), TiO (Plez, priv. comm.), C2 (Brooke et al. 2013; Ram et al. 2014), CH (Masseron et al. 2014), ZrO (Plez, priv. comm.), OH and NH (Masseron, priv. comm.), CaH (Plez, priv. comm.), VO (Plez, priv. comm.), FeH (Dulick et al. 2003), MgH (Hinkle et al. 2013), and SiH (Kurucz 1992).
Based on these line lists, a specific synthetic spectra grid was computed using the MARCS model atmosphere (Gustafsson et al. 2008) and the LTE TURBOSPECTRUM code (Plez 2012). Five dimensions were considered for this grid: T eff, log(g), [M/H], [α/Fe], and [X/Fe], where [X/Fe] correspond the r- and s-enhancements. The ranges of the atmospheric parameters are those of the AMBRE grid (de Laverny et al. 2012), 4000 ≤ T eff ≤ 8000 K (in steps of 250 K), +0 ≤ log(g) ≤ +5.5 cm s−2 (in steps of 0.5 cm s−2), −5 ≤ [M/H] +1 dex, whereas the enhancement in r- and s-varies over a range of ±1.2 dex around the metallicity in steps of +0.2 dex (13 different values of [X/Fe]).
For the present grid, a specific microturbulence velocity law (polynomial variation as a function of T eff, log(g), and [Fe/H]) has been adopted for the synthetic spectrum calculation, as was done in our computation of Gaia ESO Survey grids. Moreover, consistent [α/Fe] enrichments for the model atmosphere and the synthetic spectrum calculations were considered.
The micro-turbulence velocity (ξ) was included in the grid computation by varying ξ as a function of T eff, log(g), and [Fe/H] as adopted in the Gaia-ESO Survey (Bergemann et al., in prep.; based on ξ determinations from literature samples). The total number of synthetic spectra is 174 534, computed on a wavelength range of 40 Å, centred on each of the spectral lines presented in Table 1, adopting a sampling of 0.004 Å.
We then interpolate the pre-computed 5D synthetic spectra grid presented above at the atmospheric parameters of the targets (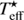 , log(g)⋆, [Fe/H]⋆, and [α/Fe]⋆) derived within the AMBRE Project to prepare a small set of interpolated synthetic spectra for a direct comparison with the observation. The resulting 1D grid in abundance at
, log(g)⋆, [Fe/H]⋆, and [α/Fe]⋆) derived within the AMBRE Project to prepare a small set of interpolated synthetic spectra for a direct comparison with the observation. The resulting 1D grid in abundance at 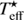 , log(g)⋆, [Fe/H]⋆, and [α/Fe]⋆ varies from −1.2 to +1.2 dex around the metallicity of the star and is composed of 13 model spectra. The resolution of the observed spectra was degraded to 40 000 for UVES and FEROS, while for HARPS, we kept the original spectral resolution of R = 110 000, re-sampling these spectra to a pixel size of 0.05 Å and 0.015 Å, respectively. The same convolution and resampling was performed for the synthetic spectra grid in order to perform the abundance determination by automatically comparing the observed and synthetic spectra. Finally, an automatic adjustment of the continuum and the correction of the radial velocity was performed on the observed spectrum as already described in Guiglion et al. (2016).
, log(g)⋆, [Fe/H]⋆, and [α/Fe]⋆ varies from −1.2 to +1.2 dex around the metallicity of the star and is composed of 13 model spectra. The resolution of the observed spectra was degraded to 40 000 for UVES and FEROS, while for HARPS, we kept the original spectral resolution of R = 110 000, re-sampling these spectra to a pixel size of 0.05 Å and 0.015 Å, respectively. The same convolution and resampling was performed for the synthetic spectra grid in order to perform the abundance determination by automatically comparing the observed and synthetic spectra. Finally, an automatic adjustment of the continuum and the correction of the radial velocity was performed on the observed spectrum as already described in Guiglion et al. (2016).
For a given spectrum, from the 1D grid described above, we compute a quadratic distance between the observed spectrum and each point of the 1D grid. For each spectral line presented in Table 1, we focused on a small wavelength range around the line, basically ±0.2/0.3 Å. The minimum of distance provides a first estimate of the solution, then this first guess is optimized via the Gauss–Newton algorithm GAUGUIN (see Guiglion et al. 2016 for more details). Upper limits are provided when the spectral feature is too weak with respect to the S/N of the spectrum. Finally, we assume for this abundance analysis that all the targets are single stars since binary detection is not a part of the AMBRE parametrization pipeline. However, we point out that most of the spectroscopic binaries present in the original sample should have been rejected when selecting only good parametrized spectra.
3.1. Solar scale and average abundance calculation
No s- and r-process abundances are available for the benchmark stars in the literature. To calibrate our abundances, we searched for solar spectra in the FEROS, HARPS, and UVES samples. We computed an average solar abundance for the available solar spectra (43 for HARPS and FEROS, and 6 for UVES) for each spectral line of Table 1 for each spectrograph. We discarded measurement presenting too low S/N, limits, and too large errors, leading to 22 spectra. Basically, differences (biases) with respect to the solar values (Grevesse et al. 2007) are of the order of 0.15 dex for Ba, 0.10 dex for Eu, and 0.25 dex for Gd and Dy, in absolute value, and vary from one spectrograph to the other. The typical dispersion is quite weak, around 0.12 for Ba corrections and 0.10 dex for Eu, Gd, and Dy corrections. Such biases results from mismatches between solar synthetic and observed spectra due probably to the uncertainties in the adopted line data. We recall that no astrophysical calibration of our line-list has been preformed since we favored our a-posteriory calibration of the abundances. We note that a similar approach has been adopted by the Gaia-ESO Consortium.
Then, for each stellar sample, we computed for each chemical element an average of the available lines (only true measurements, no upper limits) and they have been put on the solar scale thanks to the biases mentioned above.
3.2. Error budget
In order to derive proper uncertainties on the Ba, Eu, Gd, and Dy abundances, we combined two main sources of uncertainty: propagation of the errors of the atmospheric parameters and line-to-line scatter for a given element. We first propagated the errors on the three atmospheric parameters {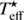 , log(g)⋆, [M/H]⋆} provided by AMBRE and summed them quadratically, leading to a first error term e
[X/Fe]. For a given element with several lines abundance measured, we also computed their standard deviation. This leads to a second error source, denoted σ
[X/Fe]. Quadratically summing e
[X/Fe] and σ
[X/Fe] gives us the final uncertainty, denoted e
tot[X/Fe] (which is probably overestimated). By applying cuts on these errors, in the next section we present our working samples for our science application.
, log(g)⋆, [M/H]⋆} provided by AMBRE and summed them quadratically, leading to a first error term e
[X/Fe]. For a given element with several lines abundance measured, we also computed their standard deviation. This leads to a second error source, denoted σ
[X/Fe]. Quadratically summing e
[X/Fe] and σ
[X/Fe] gives us the final uncertainty, denoted e
tot[X/Fe] (which is probably overestimated). By applying cuts on these errors, in the next section we present our working samples for our science application.
We also estimated the impact of a bad continuum placement. To do so, we modified the continuum of a synthetic solar spectrum of about 3%, thanks to a third-order polynomial function2, around the lines used for the chemical abundance analysis. These tests were done at S/N = 100, for 1000 noisy realizations, at both R = 40 000 (UVES/FEROS like resolution) and R = 100 000 (HARPS-like resolution). The typical errors induced by the bad continuum placement are of the order of 0.04 dex for Ba, 0.08 dex for Eu, and 0.12 dex for Gd and Dy. These tests are very pessimistic because in practice our automatic procedure is able to renormalize to a precision better than 1% of the continuum for S/N > 15. The resulting errors will then be negligible with respect to those due to the atmospheric parameters and line-to-line scatter.
3.3. Repeated observations
As presented in the next section, the FEROS sample is composed of 5981 spectra, including repeated observations. In order to show the robustness of the AMBRE r- and s-process abundances, we present average abundances and typical dispersion for some dwarfs/subgiants with repeated observations (N rep > 10) in Table 2. We first note from this table that the dispersions on the atmospheric parameters are much smaller than the errors on these quantities estimated during the AMBRE parametrization. This confirms that our first error term (e [X/Fe]) is overestimated and it refers mainly to the external error, not to the internal relative error. Then, the typical dispersion of the abundances is around or well below 0.10 dex, for the four elements, even in the metal-poor regime, for example HD 203608. We note that this dispersion can be explained by the fact that for a given star, all the repeats do not have the same atmospheric parameters. In general, Gd and Dy show higher dispersion principally because of weaker spectral features. We observe the same trends for repeated observations in the HARPS sample, and the samples UVES580 and UVES437 for Eu, Gd, and Dy, and in the sample of UVES564 with Ba abundances.
Mean atmospheric parameters, and Ba, Eu, Gd, and Dy abundances for some examples of FEROS stars with repeated observations.
Identifier, atmospheric parameters, S/N, Ba abundance, e tot, number of Ba line used, and spectrograph.
When cross-matching FEROS and HARPS together, 34 subgiants and dwarf stars share spectra with both spectrographs, covering a metallicity range from −0.47 to +0.20 dex. For 19 of them we are able to measure abundances. Basically, for a given star, the dispersion between the repeats is again below 0.1 dex for Eu and Ba abundances, and of the order of 0.10/0.15 dex for Gd and Dy, showing good reliability of the adopted AMBRE atmospheric parameters and abundances derived. For the remaining 15 stars, only upper limits are available, but are fully consistent between FEROS and HARPS spectra for a given star.
4. AMBRE catalogue of Ba and r-process abundances
In this section we present how we combined the three different samples of HARPS, UVES, and FEROS in order to provide a catalogue of Ba and r-process abundances. We also present abundances for 19 identified Gaia benchmark stars in our catalogue. We finally confirm the reliability of our measurements by comparing our abundances with external data sets.
4.1. Combining UVES, FEROS, and HARPS samples
We now have in hand three different samples, HARPS, FEROS, and UVES, containing a few repeated observations.
For FEROS, we performed a cross-match on the spectra coordinates with a radius of 10 arcsec on the sky, leading to a remaining sample composed of 3526 stars. For a given star with several spectra collected with the same spectrograph, we computed averaged atmospheric parameters and averaged chemical abundances, leading to a better precision. For HARPS, we recall that we adopted the sample of 4355 stars from Mikolaitis et al. (2017) based on a search of coordinates and of atmospheric parameter differences, containing then individual stars.
For HARPS and FEROS data, it was easy to combine the two samples because Ba, Eu, Gd, and Dy were measured homogeneously with the same spectral lines. In order to eliminate repeats between the two samples, we made a second cross-match with a radius of 10 arcsec on the sky over the coordinates of the two samples, leading to a remaining sample of 5808 stars (2281 HARPS stars and 3527 FEROS stars). Here again, for a star with several repeats, we computed a mean of its atmospheric parameters and chemical abundances, derived with all the available HARPS and FEROS spectra.
As presented in Table 4, in UVES, Ba was derived thanks to the set-up U564 for 528 spectra, Eu thanks to U437 (1414 spectra) and U580 (3628 spectra), Gd thanks to U437, and Dy thanks to U437 and U580. For each set-up, we searched for repeated observations and we performed a cross-match with a radius of 2 arcsec on the sky, resulting in 258 individual stars in U654, 744 in U437, and 1030 in U580. We note that there are 213 common stars between U437 and U580, showing consistent atmospheric parameters between the two set-ups, with a typical dispersion of 81 K in T eff, 0.21 cm s−2 in log(g) and 0.09 dex in [M/H]. The Eu abundances are also consistent within a 1σ error, beside the fact that different Eu spectral lines are used in each set-up.
Number of stars for each derived abundance (including upper limits) and spectrograph.
As we assume that the stars are slow rotators, and do not include rotation in our procedure based on a synthetic spectra grid, we exclude stars with high FWHM of the cross-correlation function (FWHMCCF) computed during the AMBRE parametrization. The FWHMCCF gives partial information on the rotational velocity. We followed the same criteria as in Guiglion et al. (2016), excluding stars with FWHM CCF > 20 km s−1 for FEROS targets, and FWHM CCF > 15 km s−1 for HARPS and UVES targets. We recall that in their study Guiglion et al. (2016) established these criteria estimating the v sin(i) effect on the lithium abundance measurement, spanning a wide range of line strengths and depths. In our study, we span a wide range of spectral line profiles, from strong lines for Ba and Eu to weak lines for Dy and Gd, allowing us to apply these criteria. These high rotation rate stars are in the minority (around 5%), so the cuts made here do not affect the global statistics that much. We also note that we excluded stars with abundance uncertainty e tot higher than 1 dex, removing then 5% of the sample. Finally, our pipeline did not converge for ~5% of the sample.
Finally, the number of stars per chemical element are presented in Table 4. The mean S/N is 130 for UVES and FEROS, and 50 for HARPS. Our AMBRE Ba and r-process catalogue contains both dwarf and giant stars. It is the first time that such a catalogue has been created, coupling a high statistics, and a wide coverage in atmospheric parameters. The AMBRE catalogue of Ba, Eu, Gd, and Dy abundances is presented in Table 3. In Sect. 5 we build a working subsample from our catalogue.
4.2. Ba, Eu, Gd, and Dy of the Gaia-benchmark stars
In our samples, we identified several Gaia-benchmark stars (Jofré et al. 2014). This identification was performed with the coordinates and TARGNAME identifier, resulting in 19 stars, for which we were able to derive Ba, Eu, Gd, and Dy (including upper limits) using the AMBRE atmospheric parameters. We present our results in Table 5. It is the first time that such a table of s- and r-process abundances in the Gaia-benchmark stars has been published. We note that the uncertainty goes typically from 0.1 to 0.3 dex, but can suffer from larger errors, for example Dy in τ Cet ([Dy/Fe] = +0.22 ± 0.45 dex). The main reason is that for lower metallicity stars, spectral lines start to be too weak to be accurately measured and/or fewer lines are available for the analysis. The same is also true for too hot stars. We finally note that Eu and Gd Arcturus abundances are fully consistent within 1σ with Overbeek et al. (2016). Eu is also in a very good agreement within 1σ with Van der Swaelmen et al. (2013) and Worley et al. (2009).
Ba, Eu, Gd, and Dy abundances and errors for the 19 Gaia benchmarks stars identified in our sample.
4.3. Comparison with literature Eu and Ba abundances
We compare our Eu and Ba abundances with recent studies; not enough data have been published for Gd and Dy. The samples presented above contain 183 HARPS stars in common with Delgado Mena et al. (2017). These 183 stars are subgiant and dwarf stars, covering the domains within 4500 < T eff < 6200 K, 3.7 < log(g) < 4.7 cm s−2 and −0.92 < [M/H] < +0.31 dex. The mean difference and dispersion in the adopted T eff, log(g) and [M/H] between the two groups are about {−24; 42} K, {−0.08; 0.14} cm s−2 and {−0.04; 0.04} dex, respectively. Our samples also contain 48 stars in common with Battistini & Bensby (2016). Also subgiant and dwarfs, these stars cover the atmospheric parameter domains within 5300 < T eff < 6000 K, 3.8 < log(g) < 4.6 cm s−2 and −0.92 < [M/H] < +0.34 dex. The mean difference and dispersion in the adopted T eff, log(g), and [M/H] between their study and our is about {−12; 49} K in T eff, {−0.11; 0.15} cm s−2 in log(g) and {−0.04; 0.05} dex in [M/H].
In Fig. 1, we present comparisons between AMBRE [Ba/H], [Eu/H], and [Eu/Ba] and those reported by Battistini & Bensby (2016) and Delgado Mena et al. (2017). We first see that the [Ba/H] ratio provided by AMBRE is in a very good agreement with both reference samples, showing no biases and weak dispersions (0.06 and 0.07 dex, respectively). We also note that the thin and the thick disc stars show the same trend in these comparisons (see Sect. 5.1 for our definition of the thin/thick disc labelling). Concerning [Eu/H], the comparisons with respect to Battistini & Bensby (2016) also shows very good agreement, with no bias and low dispersion (σ = 0.11 dex). With respect to Delgado Mena et al. (2017), [Eu/H] is in good agreement as well, also with a small dispersion and bias (bias = 0.06 dex and σ = 0.09 dex). The biases and dispersions measured here can originate from differences in the abundance determination method, spectral line selection or normalization procedure. We finally compare the [Eu/Ba] ratios measured in AMBRE with both reference samples. We clearly see that the agreement is very good, in both the thin and the thick discs, a low dispersion being observed (0.10/0.08 dex with respect to the two studies). For all these chemical species, the dispersions between the literature values and our values are always smaller than our reported errors, confirming the good quality of our fully automatic analysis performed for a much larger number of stars.
 |
Fig. 1. Comparison of AMBRE [Ba/H], [Eu/H], and [Eu/Ba] with those from Battistini & Bensby (2016; BB2016, ▵, top row), and Delgado Mena et al. (2017; DM2017, ⋄, bottom row). The thin disc, thick disc, and mrαr stars are shown in blue, red, and green, respectively. |
5. Selecting our working sample
In this section, we explain how we chemically characterized the thin and thick disc stars. We then present our final working subsample for which we selected the best chemical abundances by making proper cuts in the error distributions.
We first note that in this study we only focus on dwarfs and subgiants, selecting stars with log(g) > 3.5 cm s−2. In this way we do not expect large systematics in the abundances due to different spectral diagnostics available for different type of stars. Indeed, the calibration of the abundances was based on the solar abundances. Since barium lines, for example at 6496 Å, can be saturated for cool and metal-rich giants, the abundance determinations could thus suffer from larger errors. In general, cool stars exhibit more blended lines due to the increasing contribution of molecules, so chemical abundance determinations could also be challenging and lead to high systematics, or only upper limits can be measurable. A solution would be to independently calibrate giants with Arcturus r- and s-process individual abundances; however, this is beyond the scope of this paper and we note that most of our sample is dominated by dwarfs.
5.1. Thin to thick disc dichotomy in the solar neighbourhood
The high quality of the statistics and homogeneity of the abundances derived in this paper thanks to the large HARPS, UVES, and FEROS samples allow us to study the evolution of r-process elements in the two main components of the Milky Way disc: the thin disc (characterized by a low-α sequence) and the thick disc (characterized by a higher α sequence). It is the first time that Gd and Dy abundances patterns have been presented in these two Milky Way components. To this end we first needed to define which star belongs to each disc. We took advantage of the [α/Fe] and the metallicity provided by the AMBRE Project. These ratios are commonly used to chemically disentangle the thin and the thick discs (Adibekyan et al. 2011; Recio-Blanco et al. 2014). In this context, we followed the same procedure as in Guiglion et al. (2016), applying the same chemical separation (see their Fig. 10). The main reason is that the sample presented here and the one from Guiglion et al. (2016) are built from similar UVES, HARPS, and FEROS samples. Metal-rich α-rich stars (mrαr) with [M/H] > −0.15 dex and [α/Fe] above the separation are also treated separately because they are too metal-rich compared to the classical definition of the thick disc.
We first selected a high S/N subsample from the 5057 stars of the Ba sample, as seen in Fig. 2. Chemically characterized with [α/Fe] and [M/H], we present the resulting three populations of disc stars: the thin disc, the thick disc, and metal-rich α-rich stars. The abundance pattern presented in Fig. 2 is consistent when using the three other samples of Table 4 (6268, 5431, 5479 stars, respectively) and we adopted the magenta line of Fig. 2 to tag these stars still using the [α/Fe] vs. [M/H] plane.
 |
Fig. 2. [α/Fe] as a function of [M/H] for a subsample of stars with S/N > 30. The full magenta line shows the thin to thick disc separation. The magenta dashed line shows the extrapolated separation for [M/H] > −0.15 dex, while the vertical long-dashed line characterizes halo stars ([M/H] < −1.25 dex). The thin disc stars are colour-coded in blue, while thick disc members are in red. The metal-rich α-rich stars are shown in green, and halo stars in black. |
We flagged stars with [M/H] < −1.50 dex as halo stars. We note that these halo stars present weak spectral lines and larger errors, so we do not expect to include many of them in our final working sample (see Sect. 5.2). Additionally, 95% of halo targets were observed with UVES or FEROS, at R = 40 000, making the detection of such weak lines more difficult. We finally note that our sample contains (labelled) thin disc stars with [M/H] < −0.7 dex characterized by a lower-content with respect to thick disc stars in the same metallicity range. We are conscious that in the metal-poor regime a small contamination by halo stars might exist.
5.2. Selecting the best abundances
In order to understand the evolution of Ba, Eu, Gd, and Dy in the Milky Way discs, we selected the best chemical abundances among the samples presented in Table 4. We note that we were not able to derive Ba, Eu, Gd, and Dy for all of these stars, or in some cases were able to provide only upper limits, which we do not consider here. For a given element, we then removed 16% (for Ba), 26% (for Eu), 35% (for Gd), and 43% (for Dy) of the targets. We also selected abundances derived with at least two detectable spectral lines for a given element.
To better clean our samples, we then took advantage of the error budget. For a given spectrograph and a given element, we carefully visualized the distributions of the error due to the atmospheric parameters, and of the line-to-line scatter. In Fig. 3 we show how we proceeded. For the Ba measurements in the FEROS sample, we cut the tails of the distributions, in this case 0.12 dex for σ [Ba/Fe] and 0.15 for e [Ba/Fe], for the three subpopulations. These cuts are typical for this example, but depends on the elements and the population considered. We repeated this operation for the four elements Ba, Eu, Gd, and Dy, and for the three samples (FEROS, UVES, HARPS). We also recall that the HARPS analysis was performed at R = 110 000, while that of FEROS and UVES was done at R = 40 000. We then applied a different cut in errors for a given sample, HARPS providing generally more accurate abundances.
 |
Fig. 3. For the Ba abundance, line-to-line scatter as a function of the error due to the atmospheric parameters for the FEROS sample. The thin disc (blue dots, 917 stars), thick disc (red dots, 112 stars), and metal-rich α-rich (green dots, 43 stars) samples are shown, with their corresponding normalized distributions. The dashed lines show the adopted cut in errors. |
The final samples are presented in Tables 6 and 7, where the number of stars in each sample is shown and the mean abundance error is provided. We unfortunately have no star belonging to the mrαr population in the UVES sample, nor halo stars with reliable abundances. The typical total errors are 0.1 dex in Ba, 0.15 dex in Eu, and 0.2 dex in Gd and Dy.
Number of selected dwarf stars with available best Ba, Eu, Gd, and Dy abundances for each sample (FEROS, HARPS, UVES) and each population (thin/thick discs, and mrαr).
Mean error (e, due to atmospheric parameter errors), mean line-to-line scatter (σ), and mean total error (defined as 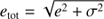 for each dwarf subsample (FEROS, HARPS, UVES) and each population (thin/thick discs, and mrαr).
for each dwarf subsample (FEROS, HARPS, UVES) and each population (thin/thick discs, and mrαr).
We note that our final samples cover the atmospheric parameter domains 5100 < T eff < 6300 K and 3.5 < log(g) < 5.0, which is illustrated in Fig. 4 for the Ba sample. We do not have stars cooler than 5100 K because of large errors, and these stars have been removed when applying cuts of the errors. Finally, we point out that Korotin et al. (2011) reported that Ba abundances can suffer from NLTE effects for hot stars. Our thin disc stars with T eff < 6100 K show on average slightly lower Ba abundances (−0.06 dex) over the whole metallicity range in both thin and thick discs; Ba abundances are fully consistent between hot and cool stars. No such hot stars are present in the mrαr population. We then decide to keep these hot stars with their LTE abundances in the present samples.
 |
Fig. 4. T eff vs. log(g) for the Ba sample. The thin disc (blue, 1476 stars), thick disc (red, 176 stars), and metal-rich α-rich (green, 42 stars) samples are shown. Different symbols are used for HARPS (•), FEROS (□), and UVES (⋄). We note that the coverage on this T eff vs. log(g) plane is similar to the Eu, Gd, and Dy sample, in addition to a different number of stars. |
6. The r-process element evolution in the Milky Way
6.1. Ba and r-process abundances trends with metallicity
We present chemical abundance trends of Ba and r-process in Fig. 5, for the thin disc, thick disc, and the mrαr populations, using the working sample we defined above. We computed average trends (and their associated standard deviations) of Ba, Eu, Gd, and Dy as a function of the metallicity, in the thin and thick discs and for the mrαr population (middle panel). We used a typical metallicity bin of 0.2 dex, and a single bin for stars with [M/H] < −1.0, due to lower statistics. In the same way, we adopted a single bin for the mrαr population. We checked that the trends presented here are robust when changing the metallicity binning, typically by a shift of 0.05 dex. The typical number of stars per bin is 100–200 for the thin disc and 20–30 for the thick disc. We also show histogram distributions. We note that our separation between thin disc, thick disc, and mrαr stars is purely based on the chemistry ([α/Fe] vs. [M/H]), and we cannot exclude any possible contamination between these three populations, especially at high metallicity.
 |
Fig. 5. Left: [Ba/Fe], [Eu/Fe], [Gd/Fe], and [Dy/Fe] ratios in the thin disc (blue), thick disc (red), and in the mrαr population (green). Middle: average abundances binned in metallicity every 0.2 dex. The orange curves show the Galactic chemical evolution models of Prantzos et al. (2018). Right: corresponding normalized distributions. |
The Ba abundance in the thin disc tends to be constant from the metal-poor regime ([M/H] ~ −1 dex) to solar metallicity, and then decreases for super-solar [M/H] revealing a higher rate production of Fe than Ba in the disc at recent epochs. The scatter seems to be the largest around solar [M/H], while this dispersion reduces when going towards metal-poor and metalrich regimes. The bulk of the thin disc shows roughly solar [Ba/Fe] ratios. This trend is consistent with previous [Ba/Fe] patterns from the literature (Battistini & Bensby 2016; Delgado Mena et al. 2017). Our thin disc data also seem to be consistent with the prediction of Bisterzo et al. (2017), in addition to a delay in the maximum [Ba/Fe] ratio. We recall that their Galactic chemical evolution model is based on a three-zone model (thin and thick discs + halo), with two main processes: a primary r-process production in the Galaxy from moderately massive Type II supernovae (8−10 M ⊙, and a second s-process by low- and intermediate-mass AGB stars.
We also note the presence of thin disc stars with peculiar Ba abundances ([Ba/Fe] > 0.5 or [Ba/Fe] < −0.5 dex), especially for [M/H] < −0.2 dex, that could be interpreted as contamination by halo stars (Suda et al. 2011).
The thick disc is characterized by a flat sequence around [Ba/Fe] ~ −0.15 dex, with a quite constant dispersion with [M/H] and then an increase at [M/H] < −0.8 dex, probably caused by a contamination by halo stars. We note that the thick disc clearly presents a smaller Ba abundance with respect to the thin disc, in the same metallicity range, and that both discs show the same dispersion (σ [Ba/Fe] = 0.15 dex). In addition, our thick disc data do not match the [Ba/Fe] model of Bisterzo et al. (2017), predicting an increase in [Ba/Fe] as a function of [M/H]. Delgado Mena et al. (2017) also observed a flat trend in their data, and evoked the fact that a too weak metallicity coverage of their data could create such a mismatch, especially for [M/H] < −0.8 dex. In our data, we cover a wider metallicity range, but the Bisterzo et al. (2017) predictions still do not fit our observations in the thick disc.
The mrαr population Ba abundance seems to be consistent with the thin disc pattern, even though it is a bit more Ba-rich. – The [Eu/Fe] ratio in the thin disc decreases in lower metallicity stars, typically from +0.4/0.5 dex at [M/H] ~ −1.0 dex to [Eu/Fe] = +0.1 dex at [M/H] = 0, and solar value for [M/H] > 0, with a distribution peaking at [Eu/Fe] ~ +0.1 dex. The thick disc Eu abundance also follows a decreasing sequence with increasing metallicity, showing a continuous sequence with the thin disc, peaking at [Eu/Fe] ~ +0.35 dex. On the same metallicity domain ([M/H] < −0.15 dex) the thick disc is more [Eu/Fe]-rich by about [Eu/Fe] = +0.17 dex. These two observations are consistent with Galactic chemical evolution model predictions from Bisterzo et al. (2017). Both thin and thick discs show the same scatter in their [Eu/Fe] pattern (σ [Eu/Fe] = 0.13 dex). We also note that [Eu/Fe] shows a typical [α/Fe] behaviour in both discs, consistent with a lower production of Eu with time while the Fe production increases. We also clearly show that the thick disc is enriched in r-process with respect to the thin disc, when using binned data. The mrαr population [Eu/Fe] ratio seems here to be consistent with the thin disc pattern. We also note here the presence of peculiar stars with [Eu/Fe] > +0.7 dex in the thin disc, also showing high [Gd/Fe] and [Dy/Fe]. These stars, with low-[α/Fe] pattern, were also characterized as thin disc members by Mikolaitis et al. (2017).
-
[Gd/Fe] and [Dy/Fe] show very similar patterns in the three Milky Way disc populations and are almost consistent with the behaviour of [Eu/Fe]. In the thin disc, the [Gd/Fe] and [Dy/Fe] ratios decrease from +0.5/0.6 dex at [M/H] ~ −0.8 dex, to [Eu/Fe] ~ +0.1 dex at [M/H] = 0, and reach −0.2 dex at super-solar [M/H], with their distribution peaking at [Gd/Fe] ~ +0.15 dex. The [Gd/Fe] and [Dy/Fe] histograms both show the same dispersion (σ = 0.17 dex). The thick disc, as for [Eu/Fe], shows a continuous sequence with the thin disc, reaching [Gd/Fe] and [Dy/Fe] ~ 0.7/0.7 dex at [M/H] ~ −1 dex. The thick disc [Gd/Fe] and [Dy/Fe] ratios both peak at ~+0.40 dex, but [Gd/Fe] shows higher dispersion with respect to [Dy/Fe] (σ [Gd/Fe] = 0.20 dex against σ [Dy/Fe] = 0.14 dex). The [Gd/Fe] and [Dy/Fe] ratios are characterized by a steeper decrease as a function of the metallicity in both discs than [Eu/Fe], with a higher dispersion, especially for [Gd/Fe]. Here the [Gd/Fe] and [Dy/Fe] patterns of the mrαr population also seem to be consistent with thin disc patterns. The mrαr population also tends to be slightly more enriched in r-process than the thin disc, and seems to be in the continuity of the thick disc. These stars are then both α-rich and r-rich.
There are no models of Galactic chemical evolution directly comparable to our data, i.e. considering explicitly the cases of the thin and thick discs and including the elements heavier than Fe. This has been done only for elements up to the Fe-peak (e.g. Minchev et al. 2013; Kubryk et al. 2015, see a comparison of the latter with AMBRE data in Mikolaitis et al. 2017). To date the evolution of heavier elements has been studied only with one-zone models (i.e. Travaglio et al. 2004). The most complete model is the one recently published by Prantzos et al. (2018). It includes all elements up to U and their isotopes; a complete set of metallicity-dependent yields of massive, rotating stars from Limongi & Chieffi (2018; including the weak s-process) and of low- and intermediate-mass stars (including the main s-process); as well as a fiducial r-component from massive stars for all isotopes, calibrated to the corresponding yield of 16O. In this way, all heavy elements and isotopes are found to be well coproduced at their corresponding solar values and at the time of the solar system formation, 4.5 Gy ago (see Figs. 10 and 12 in that paper). The local evolution of several elements, i.e. the behaviour of [X/Fe] vs. [Fe/H]) is also found to be well reproduced when compared to observations (their Fig. 16); however, the adopted data sets are not homogenized and no distinction is made between thin and thick discs (neither in the model, nor in the data), making it difficult to draw significant conclusions.
In Fig. 5, we compare our data to the aforementioned results of Prantzos et al. (2018; orange curve). The model curves lie below our data, even for the thin disc. This is obviously because our data display a super-solar [r/Fe] = 0.1−0.15 dex at [Fe/H] = 0, a fact impossible to reproduce by any one-zone model: such models are meant to produce a solar pattern for all elements 4.5 Gy ago. The interpretation of our data requires dedicated multi-zone models, either semi-analytical or fully chemo-dynamical. In particular, the role of neutron-star mergers (NSM) in the production of r-elements should be considered in such models after the recent joint detection of electromagnetic and gravitational signals from the gamma-ray burst GW170817/GRB170817A (Abbott et al. 2017a; Pian et al. 2017, and references therein).
6.2. Ratios of pure r-element to barium
In order to quantify the relative importance of the r- and s-channels during the evolution of the Milky Way, we present in Fig. 6 Eu, Gd, and Dy abundances (pure r-process elements) with respect to Ba (pure s-process) as a function of the metallicity [M/H] for the different disc components. We point out that our statistics becomes lower since we kept only stars with measurement of Ba and one of the r-element.
 |
Fig. 6. [Eu/Ba], [Gd/Ba], and [Dy/Ba] ratios in the thin disc, thick disc, and in the mrαr population (colour-coding as in Fig. 5). We also present average abundances binned in metallicity every 0.2 dex. The thick dotted line shows the pure r-process ratio from the model of Bisterzo et al. (2014) with its 0.1 dex error. The right panel shows normalized distributions. |
In both thin and thick discs, our [Eu/Ba] ratio looks quite constant with [M/H] within the error bars. The thick disc shows a higher [Eu/Ba] ratio ([Eu/Ba] ~ 0.45 dex) than the thin disc ([Eu/Ba] ~ 0.15 dex). The thick disc pattern is consistent with findings of previous studies, for example Battistini & Bensby (2016) and Delgado Mena et al. (2017). However, in Delgado Mena et al. (2017) the thin disc [Eu/Ba] pattern tends to decrease until solar value for [M/H] < 0, and increase for [M/H] > 0 dex, in contradiction with our observations. We note that our statistics is higher by at least a factor of two. On the contrary, we show that the [Gd/Ba] ratio is characterized by a decrease in both discs, about −0.4 dex over 1 dex in [M/H] for the thin discs, and −0.3 dex over 0.7 dex in [M/H] for the thick disc. Similar behaviour is also observed for [Dy/Ba] in addition to a shallower decrease revealing a possible different production history for Eu and Gd–Dy, as confirmed in Fig. 7. We note that [Gd/Ba] and [Dy/Ba] clearly peak at high ratios in the thick disc ([Gd, [Dy/Ba] ~ 0.45 dex) than in the thin disc ([Gd, [Dy/Ba] ~ 0.15 dex).
 |
Fig. 7. As a function of the metallicity: (panel a) Average r-process abundance (defined as the mean of Eu, Gd, and Dy) over Fe; (panel b) [r/Ba]; (panel c) [(Gd + Dy)/Eu]; (panel d) [r/Ba]. Colour-coding as in Fig. 5. |
The mrαr population shows patterns consistent with thin disc chemistry. According to Fig. 5, these stars are α-rich and r-rich (like thick disc stars), but their Ba is very different from thick disc stars. This result raises one more open question on the nucleosynthesis processes history of these two families of elements.
Finally, the [Eu/Ba], [Gd/Ba], and [Dy/Ba] ratios are close to pure r-process in the metal-poor regime, and this is a sign that at the early epoch of our Galaxy, the r-process was the dominant neutron-capture process (Bisterzo et al. 2014). Then, the [r/Ba] ratios decrease when AGB stars start contributing predominantly to the ISM enrichment in s-process elements. As a result, [r/Ba] ratios decrease towards the solar value at solar metallicity. We note that it is the first time that such trends have been presented for Gd and Dy.
6.3. Average r-process abundance trends
In Fig. 7, we finally show the average r-process abundance pattern (defined as the average Eu, Gd, and Dy abundances) in both discs as a function of the metallicity, and confirm some trends already seen in Fig. 6. It corresponds to stars from our working sample with available Ba, Eu, Gd, and Dy, explaining the lower statistics in these plots. First, the [r/Fe] ratio shows a narrow sequence with a small dispersion. It is clear that the thin and the thick discs form a continuous sequence. Moreover, on the one hand the [r/Ba] ratio is globally characterized by a weakly scattered sequence decreasing from the pure r-process abundance of +0.8 dex at [M/H] ~ −0.8 dex to [r/Ba] ~ +0.1 dex at [M/H] = 0 (we already noted that [r/Fe] > 0 in this metallicity regime). On the other hand, the thick disc is roughly constant at [r/Ba] ~ +0.50 dex for [M/H] < −0.2 dex, but then seems to decrease, while the thin disc is rather flat beyond [M/H] > −0.5 dex. We also show that the [(Gd + Dy)/Eu] ratio is not constant as a function of the metallicity, revealing a possible different production history between Eu and Gd–Dy in both discs.
Finally, we took advantage of the [α/Fe] ratio to trace the ratio between r-process and α-elements3. The [r/α] ratio is clearly not constant as a function of the metallicity and tends to decrease by about +0.15 dex from [M/H] ~ −1 dex to [r/α] ~ +0.1 dex at [M/H] = 0. Here again, no clear thin to thick disc separation is visible with [r/α]. Interestingly, α-elements are predominately synthesized in Type II supernovae, while it is known that such core-collapse supernovae are also suitable sites for r-process. The clear slope with [M/H] indicates that supernovae of different properties contribute to the synthesis of r-process elements and α-elements, but with different efficiencies/yields. However, since the recent observational evidence of r-process synthesis via neutron-stars mergers, this trend cannot only be explained by the role of Type II supernovae.
7. Conclusion
In this study, our goal was understanding the evolution of Milky Way disc r-process abundances. We built a homogeneous catalogue of chemical abundances of Ba (pure s-element) and Eu, Gd, and Dy (pure r-elements). In the literature, such a catalogue with high statistics is still lacking. As a result, the chemical evolution of pure r-process elements is still a matter of debate.
We took advantage of the HARPS, FEROS, and UVES ESO archives, coupled with the atmospheric parameters of the AMBRE Project (de Laverny et al. 2012). We performed an automatic derivation of individual chemical abundances and errors of Ba (5057 stars), Eu (6268 stars), Gd (5431 stars), and Dy (5479 stars) thanks to the pipeline GAUGUIN (Guiglion et al. 2016). It is the first time that such a homogeneous data set has been provided, especially for Gd and Dy, and that covers such a wide metallicity range (−1.5 < [M/H] < +0.5 dex). Comparisons of our abundances with previous studies show a very good agreement. We also provided such chemical abundances for 19 Gaia benchmark stars.
From this catalogue, we selected dwarf stars with the most accurate abundances of Ba (1694 stars), Eu (1413 stars), Gd (981 stars), and Dy (1055 stars) and investigated the chemical abundance patterns of these four elements in the Milky Way disc, more precisely focusing on the thin disc, the thick disc, and the metal-rich α-rich population. Identifying such disc stellar populations was done using a chemical separation in the [α/Fe] vs. [M/H] plan. We summarize here our main results:
-
The [Eu/Fe] ratio follows a continuous sequence from the thin disc to the thick disc, with respect to the metallicity.
-
In thick disc stars, the [Eu/Ba] ratio is rather constant, while the [Gd/Ba] and [Dy/Ba] ratios decrease as a function of the metallicity. These observations clearly indicate a different nucleosynthesis history in the thick disc between Eu and Gd–Dy.
-
We find that the mrαr population abundance patterns are consistent with the thin disc chemistry. These stars tend to be both enriched in α- and r-process elements, (like thick disc stars), but their [Ba/Fe] is very different from thick disc stars.
-
We find that the [r/Fe] ratio in the thin disc is roughly around +0.1 dex at solar metallicity, which is not the case for Ba.
-
We also provided average [Ba, Eu, Gd, Dy/Fe] and [Eu, Gd, Dy/Ba] ratios as a function of the metallicity, with associated dispersion. This data is crucial when one wants to constrain Galactic chemical evolution model, more particularly on the stellar yields.
-
We compared our data with the last model of Prantzos et al. (2018) that includes yields of rotating massive stars. In addition to the fact that it is a one-zone model, we find a good quantitative match for [Ba/Fe]. For [Eu, Gd, Dy/Fe] the model underpredicts the observations, being calibrated to obtain [r/Fe] = 0 at [Fe/H] = 0. Taken at face value, the observations imply that the average stellar [r/Fe] of the disc is super-solar at [Fe/H] = 0, suggesting a differential evolution between r-process elements and Fe. This possibility is consistent with our next finding, namely the differential evolution of r- and α-elements that we obtain.
-
We found that the [r/α] ratio tends to decrease with metallicity, clearly indicating that supernovae having different properties contribute to the synthesis of r-process elements and α-elements with different efficiencies/yields. Since the observational evidence of r-process synthesis via neutron-stars mergers, such a trend cannot only be explained by the role of Type II supernovae.
In the context of the Second Gaia Data Release (Gaia Collaboration 2018), this paper will be the object of an extension including individual stellar ages, and a study of the radial and vertical abundance gradients in the Milky Way disc.
Using the [Mg/Fe] ratio from Mikolaitis et al. (2017) provides the same results.
Acknowledgments
We acknowledge financial support form the ANR 14-CE33-014-01. The spectra calculations were performed with the high-performance computing facility MESOCENTRE, hosted by OCA. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. The Authors thank the anonymous referee for the useful comment and suggestions.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, ApJ, 850, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, ApJ, 848, L12 [Google Scholar]
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battistini, C., & Bensby, T. 2016, A&A, 586, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2011, MNRAS, 418, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Travaglio, C., Gallino, R., Wiescher, M., & Käppeler, F. 2014, ApJ, 787, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Bisterzo, S., Travaglio, C., Wiescher, M., Käppeler, F., & Gallino, R. 2017, ApJ, 835, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Brooke, J. S. A., Bernath, P. F., Schmidt, T. W., & Bacskay, G. B. 2013, J. Quant. Spectr. Rad. Transf., 124, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Hirschi, R., Meynet, G., et al. 2006, A&A, 449, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Laverny, P., Recio-Blanco, A., Worley, C. C., & Plez, B. 2012, A&A, 544, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Laverny, P., Recio-Blanco, A., Worley, C. C., et al. 2013, The Messenger, 153, 18 [NASA ADS] [Google Scholar]
- De Pascale, M., Worley, C. C., de Laverny, P., et al. 2014, A&A, 570, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delgado Mena, E., Tsantaki, M., Adibekyan, V. Z., et al. 2017, A&A, 606, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Den Hartog, E. A., Lawler, J. E., Sneden, C., & Cowan, J. J. 2006, ApJS, 167, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Dulick, M., Bauschlicher, Jr., C. W., Burrows, A., et al. 2003, ApJ, 594, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Freiburghaus, C., Rosswog, S., & Thielemann, F.-K. 1999, ApJ, 525, L121 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Guiglion, G., de Laverny, P., Recio-Blanco, A., et al. 2016, A&A, 595, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkle, K. H., Wallace, L., Ram, R. S., et al. 2013, ApJS, 207, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Jofré, P., Heiter, U., Blanco-Cuaresma, S., & Soubiran, C. 2014, Astron. Soc. India Conf. Ser., 11, 159 [Google Scholar]
- Käppeler, F., Gallino, R., Bisterzo, S., & Aoki, W. 2011, Rev. Mod. Phys., 83, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korotin, S., Mishenina, T., Gorbaneva, T., & Soubiran, C. 2011, MNRAS, 415, 2093 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [Google Scholar]
- Kurucz, R. L. 1992, RM&AC, 23 [Google Scholar]
- Lamb, S. A., Howard, W. M., Truran, J. W., & Iben, Jr., I. 1977, ApJ, 217, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Wickliffe, M. E., den Hartog, E. A., & Sneden, C. 2001, ApJ, 563, 1075 [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Masseron, T., Plez, B., Van Eck, S., et al. 2014, A&A, 571, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mikolaitis, Š., de Laverny, P., Recio-Blanco, A., et al. 2017, A&A, 600, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nishimura, S., Kotake, K., Hashimoto, M.-A., et al. 2006, ApJ, 642, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Nishimura, N., Takiwaki, T., & Thielemann, F.-K. 2015, ApJ, 810, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Overbeek, J. C., Friel, E. D., & Jacobson, H. R. 2016, ApJ, 824, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, J. G. 1968, ApJ, 154, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Pian, E., D’Avanzo, P., Benetti, S., et al. 2017, Nature, 551, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
- Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Ram, R. S., Brooke, J. S. A., Bernath, P. F., Sneden, C., & Lucatello, S. 2014, ApJS, 211, 5 [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Kordopatis, G., et al. 2014, A&A, 567, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutten, R. J. 1978, Sol. Phys., 56, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Seeger, P. A., Fowler, W. A., & Clayton, D. D. 1965, ApJS, 11, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Cowan, J. J., & Gallino, R. 2008, ARA&A, 46, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C., Lucatello, S., Ram, R. S., Brooke, J. S. A., & Bernath, P. 2014, ApJS, 214, 26 [Google Scholar]
- Spina, L., Meléndez, J., Karakas, A. I., et al. 2018, MNRAS, 474, 2580 [NASA ADS] [Google Scholar]
- Steinmetz, M. 2003, in Gaia Spectroscopy: Science and Technology, ed. U. Munari, ASP Conf. Ser., 298, 381 [NASA ADS] [Google Scholar]
- Suda, T., Yamada, S., Katsuta, Y., et al. 2011, MNRAS, 412, 843 [NASA ADS] [Google Scholar]
- Travaglio, C., Galli, D., Gallino, R., et al. 1999, ApJ, 521, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Gallino, R., Busso, M., & Gratton, R. 2001, ApJ, 549, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Swaelmen, M., Hill, V., Primas, F., & Cole, A. A. 2013, A&A, 560, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wickliffe, M. E., Lawler, J. E., & Nave, G. 2000, J. Quant. Spectr. Rad. Transf., 66, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, J. C., Hearty, F., & Skrutskie, M. F. 2010, Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 77351C [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Wilson, J. R., Mathews, G. J., Hoffman, R. D., & Meyer, B. S. 1994, ApJ, 433, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Worley, C. C., Cottrell, P. L., Freeman, K. C., & Wylie-de Boer, E. C. 2009, MNRAS, 400, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Worley, C. C., de Laverny, P., Recio-Blanco, A., et al. 2012, A&A, 542, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worley, C. C., de Laverny, P., Recio-Blanco, A., Hill, V., & Bijaoui, A. 2016, A&A, 591, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Element, wavelength, log g f, hyperfine structure, and reference for the 15 spectral lines used in this study.
Mean atmospheric parameters, and Ba, Eu, Gd, and Dy abundances for some examples of FEROS stars with repeated observations.
Identifier, atmospheric parameters, S/N, Ba abundance, e tot, number of Ba line used, and spectrograph.
Number of stars for each derived abundance (including upper limits) and spectrograph.
Ba, Eu, Gd, and Dy abundances and errors for the 19 Gaia benchmarks stars identified in our sample.
Number of selected dwarf stars with available best Ba, Eu, Gd, and Dy abundances for each sample (FEROS, HARPS, UVES) and each population (thin/thick discs, and mrαr).
Mean error (e, due to atmospheric parameter errors), mean line-to-line scatter (σ), and mean total error (defined as 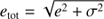 for each dwarf subsample (FEROS, HARPS, UVES) and each population (thin/thick discs, and mrαr).
for each dwarf subsample (FEROS, HARPS, UVES) and each population (thin/thick discs, and mrαr).
All Figures
 |
Fig. 1. Comparison of AMBRE [Ba/H], [Eu/H], and [Eu/Ba] with those from Battistini & Bensby (2016; BB2016, ▵, top row), and Delgado Mena et al. (2017; DM2017, ⋄, bottom row). The thin disc, thick disc, and mrαr stars are shown in blue, red, and green, respectively. |
| In the text | |
 |
Fig. 2. [α/Fe] as a function of [M/H] for a subsample of stars with S/N > 30. The full magenta line shows the thin to thick disc separation. The magenta dashed line shows the extrapolated separation for [M/H] > −0.15 dex, while the vertical long-dashed line characterizes halo stars ([M/H] < −1.25 dex). The thin disc stars are colour-coded in blue, while thick disc members are in red. The metal-rich α-rich stars are shown in green, and halo stars in black. |
| In the text | |
 |
Fig. 3. For the Ba abundance, line-to-line scatter as a function of the error due to the atmospheric parameters for the FEROS sample. The thin disc (blue dots, 917 stars), thick disc (red dots, 112 stars), and metal-rich α-rich (green dots, 43 stars) samples are shown, with their corresponding normalized distributions. The dashed lines show the adopted cut in errors. |
| In the text | |
 |
Fig. 4. T eff vs. log(g) for the Ba sample. The thin disc (blue, 1476 stars), thick disc (red, 176 stars), and metal-rich α-rich (green, 42 stars) samples are shown. Different symbols are used for HARPS (•), FEROS (□), and UVES (⋄). We note that the coverage on this T eff vs. log(g) plane is similar to the Eu, Gd, and Dy sample, in addition to a different number of stars. |
| In the text | |
 |
Fig. 5. Left: [Ba/Fe], [Eu/Fe], [Gd/Fe], and [Dy/Fe] ratios in the thin disc (blue), thick disc (red), and in the mrαr population (green). Middle: average abundances binned in metallicity every 0.2 dex. The orange curves show the Galactic chemical evolution models of Prantzos et al. (2018). Right: corresponding normalized distributions. |
| In the text | |
 |
Fig. 6. [Eu/Ba], [Gd/Ba], and [Dy/Ba] ratios in the thin disc, thick disc, and in the mrαr population (colour-coding as in Fig. 5). We also present average abundances binned in metallicity every 0.2 dex. The thick dotted line shows the pure r-process ratio from the model of Bisterzo et al. (2014) with its 0.1 dex error. The right panel shows normalized distributions. |
| In the text | |
 |
Fig. 7. As a function of the metallicity: (panel a) Average r-process abundance (defined as the mean of Eu, Gd, and Dy) over Fe; (panel b) [r/Ba]; (panel c) [(Gd + Dy)/Eu]; (panel d) [r/Ba]. Colour-coding as in Fig. 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


