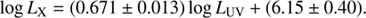| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833631 | |
| Published online | 12 November 2018 | |
The X-ray/UV ratio in active galactic nuclei: dispersion and variability⋆
1
INAF – Istituto di Astrofisica e Planetologia Spaziali (IAPS-INAF), Via del Fosso del Cavaliere 100, 00133 Roma, Italy
e-mail: elia.chiaraluce@iaps.inaf.it
2
Dipartimento di Fisica, Università di Roma Tor Vergata, Via della Ricerca Scientifica 1, 00133 Roma, Italy
3
X-ray Astrophysics Laboratory, NASA Goddard Space Flight Center, Greenbelt, MD, 20771, USA
4
Department of Astronomy, University of Maryland, College Park, MD, 20742, USA
5
Dipartimento di Fisica Ettore Pancini, Università di Napoli Federico II, via Cintia, 80126 Napoli, Italy
6
INFN Unita’di Napoli, via Cintia 9, 80126 Napoli, Italy
7
Agenzia Spaziale Italiana Science Data Center, Via del Politecnico snc, 00133 Roma, Italy
Received:
13
June
2018
Accepted:
20
August
2018
Context. The well established negative correlation between the αOX spectral slope and the optical/ultraviolet (UV) luminosity, a by-product of the relation between X-rays and optical/UV luminosity, is affected by relatively large dispersion. The main contributors to this dispersion can be variability in the X-ray/UV ratio and/or changes in fundamental physical parameters.
Aims. We want to quantify the contribution from variability within single sources (intra-source dispersion) and that from variations of other quantities different from source to source (inter-source dispersion).
Methods. We use archival data from the XMM-Newton Serendipitous Source Catalog (XMMSSC) and from the XMM-OM Serendipitous Ultraviolet Source Survey (XMMOM-SUSS3). We select a sub-sample in order to decrease the dispersion of the relation due to the presence of radio-loud and broad absorption line objects, and that due to absorptions in both X-ray and optical/UV bands. We use the structure function (SF) to estimate the contribution from variability to the dispersion. We analyse the dependence of the residuals of the relation on various physical parameters in order to characterise the inter-source dispersion.
Results. We find a total dispersion of σ ∼ 0.12 and find that intrinsic variability contributes 56% of the variance of the αOX − LUV relation. If we select only sources with a larger number of observational epochs (≥3) the dispersion of the relation decreases by approximately 15%. We find weak but significant dependencies of the residuals of the relation on black-hole mass and on Eddington ratio, which are also confirmed by a multivariate regression analysis of αOX as a function of UV luminosity and black-hole mass and/or Eddington ratio. We find a weak positive correlation of both the αOX index and the residuals of the αOX − LUV relation with inclination indicators, such as the full width at half maximum (Hβ) and the equivalent width (EW)[OIII], suggesting a weak increase of X-ray/UV ratio with the viewing angle. This suggests the development of new viewing angle indicators possibly applicable at higher redshifts. Moreover, our results suggest the possibility of selecting a sample of objects, based on their viewing angle and/or black-hole mass and Eddington ratio, for which the αOX − LUV relation is as tight as possible, in light of the use of the optical/UV – X-ray luminosity relation to build a distance modulus (DM)-z plane and estimate cosmological parameters.
Key words: galaxies: active / quasars: general / X-rays: galaxies
Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/619/A95
© ESO 2018
1. Introduction
The X-ray/UV ratio is a powerful tool which can be used to investigate the distribution of the X-ray and optical/UV properties of active galactic nuclei (AGNs; Lusso & Risaliti 2016; Avni & Tananbaum 1986; Strateva et al. 2005) and their dependence on fundamental quantities like Eddington ratio, black-hole mass, and redshift. The X-ray/ultraviolet (UV) ratio is usually defined in terms of the αOX index as
but it is not rare to find it defined with a minus sign (e.g. Tananbaum et al. 1979; Lusso & Risaliti 2016), and it is usually considered 2 keV for the X-ray frequency and 2500 Å for the Optical/UV frequency (e.g. Vagnetti et al. 2010; Lusso & Risaliti 2016). The αOX index can be thought of as the energy index or slope associated to a power law connecting the X-ray and Optical/UV bands (Tananbaum et al. 1979).
Published studies of the dependence of the X-ray/UV ratio on redshift have found no significant dependence (e.g. Vignali et al. 2003; Strateva et al. 2005; Steffen et al. 2006; Just et al. 2007; Vagnetti et al. 2010, 2013; Dong et al. 2012. This means that energy-generation mechanisms have not changed from early epochs: already at high redshift, AGNs were almost completely built-up systems, notwithstanding short time intervals available for growth (Vignali et al. 2003; Strateva et al. 2005; Just et al. 2007). This picture is consistent with studies finding no significant evolution in AGNs’ continuum shape even at high redshift from radio (Petric et al. 2003), Optical/UV (Pentericci et al. 2003), and X-ray (Page et al. 2005).
The αOX dependence on other parameters is still a matter of debate. Some authors have found a significant correlation with the Eddington ratio L/LEdd (Lusso et al. 2010) while other authors find no significant correlation with L/LEdd (Dong et al. 2012; Vasudevan et al. 2009) and a significant one with MBH (Dong et al. 2012).
The available literature reports a strong, non-linear correlation between the X-ray/UV ratio and the monochromatic UV luminosity at 2500 Å in the form αOX = alog LUV + b, with a in the interval ∼ − 0.2 ÷ −0.1. However, this anti-correlation is the by-product of the well-established positive non-linear correlation between X-ray and optical/UV luminosity 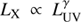 with γ ∼ 0.5 ÷ 0.7 (e.g. Avni & Tananbaum 1986; Vignali et al. 2003; Strateva et al. 2005; Steffen et al. 2006; Just et al. 2007; Gibson et al. 2008; Lusso et al. 2010; Vagnetti et al. 2010, 2013; Lusso & Risaliti 2016). Moreover, Buisson et al. (2017) analysed the variable part of the UV and X-ray emissions for a sample of 21 AGNs, finding that they are also correlated with slopes similar to those found for the average luminosities.
with γ ∼ 0.5 ÷ 0.7 (e.g. Avni & Tananbaum 1986; Vignali et al. 2003; Strateva et al. 2005; Steffen et al. 2006; Just et al. 2007; Gibson et al. 2008; Lusso et al. 2010; Vagnetti et al. 2010, 2013; Lusso & Risaliti 2016). Moreover, Buisson et al. (2017) analysed the variable part of the UV and X-ray emissions for a sample of 21 AGNs, finding that they are also correlated with slopes similar to those found for the average luminosities.
These two relations are symptoms of a tight physical coupling between the two regions responsible for the Optical/UV and X-rays, that is, the accretion disk and X-ray corona, respectively. Indeed, standard accretion disk-corona models postulate an interaction between photons emitted from the accretion disk and a central plasma of relativistic electrons constituting the corona, responsible for the emission of X-rays radiation. Following the standard picture by Haardt & Maraschi (1991); Haardt & Maraschi (1993), the soft thermal photons from the disk, parametrised by L2500 Å, are energised to X-rays by means of inverse Compton scattering on hot (Te ∼ 108 K) corona electrons, resulting in a power-law-like component observed in AGNs’ X-ray spectra, with a cut-off corresponding to electron temperature (e.g. Lusso & Risaliti 2016; Tortosa et al. 2018). In this picture, the study of the αOX − LUV relation, or equivalently of the LX − LUV relation, is of fundamental importance as we still lack a quantitative physical model explaining the existence of this correlation. However, in a recent paper Lusso & Risaliti (2017) advanced a simple, ad-hoc physical model for the accretion disk-corona system, predicting a dependence of the X-ray monochromatic luminosity on the monochromatic UV luminosity and the emission line full-width at half maximum (FWHM) of the form LX ∝ LUV4/7 vFWHM4/7 Their model is based on accretion disk-corona models by Svensson & Zdziarski (1994), in which magnetic loops and reconnection events above a standard Shakura-Sunyaev (Shakura & Sunyaev 1973) accretion disk may be responsible for the emission of X-ray radiation (Lusso & Risaliti 2016).
The αOX − LUV and LX − LUV relations are however characterised by dispersion due to several causes: the radio-loud (RL) and broad absorption line (BAL) nature of some AGN, host galaxy effects, and variability (Lusso & Risaliti 2016) (see Sect. 3 for an extended discussion). Active galactic nuclei are variable in both optical/UV and X-rays bands. In the optical/UV range many authors have confirmed variability (e.g. Cristiani et al. 1996; Giallongo et al. 1991; di Clemente et al. 1996), and the most reliable hypothesis is that of accretion disk instabilities (e.g. Vanden Berk et al. 2004). Variability in the X-ray band has been extensively studied with different methods, such as fractional variability (Almaini et al. 2000; Manners et al. 2002), the power spectral density (Papadakis 2004); ONeill2005; UttleyMcHardy2005; (McHardy et al. 2006; Paolillo et al. 2017), and the SF (Vagnetti et al. 2011, 2016; Middei et al. 2017), and these works indicate that variations occur preferentially on long timescales (e.g. Middei et al. 2017). Variability is a major source of scatter in the above relations, and, once simultaneous observations are selected, its contributions reduce to essentially two factors: an intrinsic variation in the X-ray/UV ratio for single sources and inter-source variations. Previous works have estimated the contribution of the intrinsic variability in X-ray/UV ratio to the total variance of the αOX − LUV relation to be roughly ∼30 ÷ 40% (Vagnetti et al. 2010, 2013), but we still lack a physical explanation for the residual dispersion, and it is with this work that we wish to spread light on this topic.
Recently, the study of the LX − LUV relation has become more and more important as it has been used to build up a Hubble diagram for Quasars (Risaliti & Lusso 2015; Bisogni et al. 2017b). In order to achieve such a goal, the dispersion of the relation must be reduced as much as possible, and Lusso & Risaliti (2016) proved that it is possible to do that by carefully selecting the sample. The use of this relation represents a valid alternative to the supernovae, as it can be used at higher redshifts and provides larger sample sizes for a more statistically robust analysis, but it also has shortcomings, as it relies on the tightness of the relation. For this very reason, a thorough study of the relation and of the physical origin of its dispersion is of fundamental importance, as it will aid in the selection of a sample of objects suited for the construction of a Hubble diagram.
In Sect. 2 we describe the data from which we derived the sample we work with, in Sects. 3 and 4 we describe the data analysis procedure together with results, and in Sect. 5 we discuss the implications of our results in light of present and past works in the literature.
Throughout the paper we use a Λ-CDM cosmological model: H0 = 70 km s−1 Mpc−1, Ωm = 0.3 and Ω Λ = 0.7.
2. The data
The X-ray data used in this work come from the Multi-epoch X-ray Serendipitous AGN Sample (MEXSAS2) catalogue (Serafinelli et al. 2017, Vagnetti et al, in prep.). The MEXSAS2 is a catalogue of 9735 XMM-Newton observations for 3366 unique sources derived from the DR6 of the XMM-Newton Serendipitous Source Catalogue (Rosen et al. 2016) that have been identified with AGNs from SDSS DR7Q (Schneider et al. 2010) and SDSS DR12Q (Pâris et al. 2017) quasar catalogues; MEXSAS2 is an update of the MEXSAS catalogue defined in Vagnetti et al. (2016) and provides black-hole mass, Eddington ratio, and bolometric luminosity by cross-matching with two catalogues of quasar properties published by Shen et al. (2011) and Kozłowski (2017). We caution that the black-hole mass estimates are to be considered with a typical uncertainty of 0.4 dex, and the bolometric luminosities have been derived from bolometric corrections which are only appropriate in a statistical sense, as discussed by Shen et al. (2011).
In order to perform a X-ray/UV ratio variability study, the MEXSAS2 catalogue has been cross-matched with the XMM-SUSS3, the third version of the XMM-OM Serendipitous Ultraviolet Source Survey (Page et al. 2012). This is based on the Optical Monitor (OM) on board the XMM-Newton satellite, an optical/UV telescope with a primary mirror of 30 cm (Mason et al. 2001). The XMMOM-SUSS3 provides fluxes in six filters: UVW2, UVM2, UVW1, U, B, and V, with central wavelengths 1894 Å, 2205 Å, 2675 Å, 3275 Å, 4050 Å and 5235 Å, respectively (see the dedicated page at MSSL1). In the XMM-SUSS3, many sources are observed more than once per filter, and this allows for variability studies to be performed.
The cross-match between the MEXSAS2 catalogue and the XMMOM-SUSS3 has been performed using 1.5 arcsec as matching radius and then comparing the OBS_ID and OBSID flags in 3XMM-DR6 and XMMOM-SUSS3 with the virtual observatory software TOPCAT2 (Taylor 2005): in this way we impose that matched X-ray and UV entries from XMM-Newton and XMMOM-SUSS3 catalogues correspond to the same observation.
The result of the cross match consists of 1857 observations for 944 unique sources, 438 of which are single-epoch; the remaining ones are multi-epoch. We note that, although we started with a multi-epoch catalogue, MEXSAS2, after the cross-match with XMMOM-SUSS3 we ended up with a sample of both single-epoch and multi-epoch sources due to the cross-matching procedure. Indeed, the optical monitor for the optical/UV measurements is co-axial with the Epic Cameras for the X-ray measurements, but the two instruments have different fields of view (FoVs): 17 arcmin2 and 30 arcmin2, respectively. This explains the reduced number of observations and the presence of single-epoch sources in the sample. The XMM-SUSS is available from the XMM-SUSS page3, the XMM-Newton Science Archive4, and the NASA High Energy Astrophysics Science Archive Research Center (HEASARC)5.
In order to calculate the X-ray/UV ratio we need to determine the X-ray and UV rest-frame luminosities. It is customary to choose the 2 keV and 2500 Å luminosities as representatives of the two quantities.
Considering UV measurements, for each object we can have one or more estimate of fluxes from one up to six OM filters. Considering a single object and a single observation, we can calculate the rest-frame monochromatic UV luminosity corresponding to each of the OM filters:
where DL is the luminosity distance of the source at redshift z, and Fν(νobs) is the observed flux in one of the six OM filters. In this way it is possible to build individual spectral energy distributions (SEDs) in the UV for the objects in the sample.
In Fig. 1 we show average SEDs: for each frequency we consider the average Lν(νem) over all observations.
 |
Fig. 1. SEDs averaged in time for the multi-epoch objects in the parent sample: for each frequency we consider the average of the quantities Lν(νem). The red dashed line is the average SED by Richards et al. (2006) for type-1 objects in the SDSS. The vertical line is at log νe = 15.08, corresponding to 2500 Å. |
The rest frame monochromatic UV luminosity L2500 Å is derived with the procedure adopted by Vagnetti et al. (2010), which can be summarised in the following way: (i) In cases where the available Lν(νem) estimates from the OM filters cover only frequencies higher or lower than 2500 Å (log ν2500 Å = 15.08, the vertical dashed line in Fig. 1) the L2500 Å is calculated through curvilinear extrapolation, following the behaviour of the average UV SED by Richards et al. (2006), computed for type-1 objects in the SDSS, shifted vertically to match the luminosity of the frequency of the nearest point. (ii) If the SED extends across log ν2500 Å = 15.08, the L2500 Å is calculated as linear interpolation of two nearest SED points. (iii) If Lν(νobs) is measured at only one frequency, L2500 Å is calculated as in (i). We note that there are some cases of anomalous and steep SEDs at high luminosities and frequency, possibly affected by intergalactic HI absorption, which is subsequently removed according to the discussion in Sect. 3.1, and at low luminosities and frequencies, where the contribution of the host galaxy can be important. In both cases, we assume that the intrinsic SED is similar to the average SED of quasars according to Richards et al. (2006) and our extrapolation is performed from a frequency which is relatively close to 2500 Å.
The UV data were then corrected for extinction following Lusso & Risaliti (2016). The galactic extinction is estimated from Schlegel et al. (1998) for each object6 while the normalised selective extinction were estimated for each filter as linear interpolation of mean extinction curve by Prevot et al. (1984).
The sample described so far is referred to as the “parent” sample, and Fig. 2 shows the distribution of the parent sample in the z-LUV plane.
 |
Fig. 2. Distribution of the parent sample in the LUV-z plane. Straight lines are lines of constant UV flux. Black circles represent objects in common with Vagnetti et al. (2010), empty circles are objects present only in this work. The straight lines are constant UV flux lines. The histogram on top shows the distribution of objects in the parent sample with respect to UV luminosity; the histogram on the right shows the redshift distribution of objects in the parent sample. The histogram inside the plot area (lower-right) shows the distribution of objects in the parent sample with respect to UV flux. |
To calculate the rest-frame monochromatic 2 keV luminosity, we started from fluxes in the XMM-SSC DR6 energy bands: EP_2, EP_3, EP_4 and EP_5, in the intervals 0.5 − 1.0 keV; 1.0 − 2.0 keV; 2.0 − 4.5 keV and 4.5 − 12.0 keV, respectively. We calculated the 2 keV luminosity performing the procedure adopted by Lusso & Risaliti (2016). We combined band 2 and 3 to form a “soft” band by simply summing fluxes in two bands, with uncertainty summed in quadrature; the same has been done to form a “hard” band from bands 4 and 5. The resulting bands are therefore in the intervals 0.5 − 2.0 keV (soft band) and 2.0 − 12.0 keV (hard band):
In each band, we have first assumed a power-law with a typical photon index Γ0 = 1.7, and then we have calculated the rest frame monochromatic luminosity at the frequency corresponding to the geometric mean of the band: Lν(1 keV) and Lν(5 keV) for the Soft and Hard bands, respectively.
Once Lν(1 keV) and Lν(5 keV) were calculated, they were used to derive an estimate of the photon index Γ by assuming a power-law connecting the two bands:
This Γ was then used to determine the rest-frame monochromatic 2 keV luminosity.
3. The αOX − LUV relation and its dispersion
The αOX − LUV relation and the LX − LUV relation are characterised by relatively large dispersions, of roughly 0.13 − 0.15 dex (e.g. Strateva et al. 2005; Just et al. 2007; Gibson et al. 2008) and 0.35 − 0.4 dex (Lusso & Risaliti 2016), respectively. The main factors contributing to the dispersion concern the nature of the objects, the emission properties, the host galaxies effects and the use of simultaneous X-ray and UV data (Lusso & Risaliti 2016).
Indeed, radio-loud objects would lie far above the average relation, because of their enhanced X-ray emission associated with jets (Worrall et al. 1987), resulting in higher X-ray/UV ratios at fixed UV luminosity. It is important to exclude them as their X-ray emission is not only the nuclear component.
Broad-absorption-line quasars would contribute in the opposite sense to the dispersion, as they have lower X-ray/UV ratio at fixed UV luminosity. Although they are believed to be characterised by the same underlying continua, absorption is believed to make them X-ray weak (Vignali et al. 2003; Gallagher et al. 2001, 2002; Green et al. 2001), and this property is not dependent on redshift (Brandt et al. 2000, 2001; Vignali et al. 2001; Gallagher et al. 2002).
Intrinsic X-ray weakness can contribute to the dispersion, as there is evidence for a significant population of soft-X-ray-weak (SFX) objects (Laor et al. 1997; Yuan et al. 1998) which may be caused by absorption, unusual SEDs, and/or optical/X-ray variability (Brandt et al. 2000).
Host galaxy starlight effect can be taken into account (e.g. Lusso et al. 2010; Vagnetti et al. 2013; Lusso & Risaliti 2016). Vagnetti et al. (2013) follow the same approach as Lusso et al. (2010). The optical spectrum is modelled as a combination of host galaxy + AGN contribution: Lν = A[fAFR(ν)+fG(ν/ν*)−3] where FR is the mean SED by Richards et al. (2006), ν* is the frequency corresponding to 2500 Å, and fA, G represent the fractional contribution of the AGN and the galaxy, respectively, at 2500 Å. The normalising constant A is determined in a self-consistent way.
The slope of the αOX − LUV relation corrected for the host galaxy contribution should be steeper than the uncorrected one (Wilkes et al. 1994), although this effect should be more important for samples with a relevant number of low-luminosity objects (Vagnetti et al. 2013).
Variability can be an important factor contributing to the αOX − LUV relation dispersion. Variability in the αOX index can be artificial variability, due to the non-simultaneity of UV and X-ray data, or an intrinsic variability, due to a true variability in the X-ray/UV ratio. It is possible to eliminate artificial variability by using simultaneous UV and X-ray data (Vagnetti et al. 2010; Vagnetti et al. 2013; Lusso & Risaliti 2016), in order to directly investigate true variability in the X-ray/UV ratio. However Vagnetti et al. (2010), using simultaneous data, have found that the dispersion of the relation is not significantly different from that derived by other authors (Strateva et al. 2005; Just et al. 2007; Gibson et al. 2008) using non-simultaneous data, and this result has been confirmed by Lusso & Risaliti (2016).
Although our UV and X-ray measurements are simultaneous, the emission processes in these two bands occur in different regions, so we should also take into account the propagation times. However the X-ray-UV lags are estimated to within a few days (e.g. Marshall et al. 2008; Arévalo et al. 2009), which will be neglected compared to the year-long timescales of our αOX variations; see Sect. 3.2.
The observed dispersion may be due to two factors: an intra-source dispersion and an inter-source one, the former being due to intrinsic variation of the X-ray/UV ratio for individual sources, the latter being due to differences in the X-ray/UV ratio among different sources.
Considering the variability, which accounts for the intra-source dispersion, we can have two scenarios. The first one refers to variability occurring on short timescales, of days and weeks, because of variations in the X-ray flux irradiating the part of the disk responsible for the optical/UV emission (hence X-ray driven variations). The second one refers to perturbations in the outer accretion disk, which propagate inwards, modulating the X-ray emission through variations in the optical/UV photons field on long timescales of months and years (hence optically driven variations; Lyubarskii 1997; Czerny 2004; Arévalo & Uttley 2006; Papadakis et al. 2008; McHardy 2010; Vagnetti et al. 2010, 2013). Vagnetti et al. (20102013) found an increasing SF(αOX) as a function of the time-lag, with variations occurring preferentially on long timescales, suggesting optically driven variations.
3.1. The reference sample
As outlined by Lusso & Risaliti (2016), it is possible to decrease the dispersion of the LX − LUV relation, and, in turn, that of the αOX − LUV relation, by carefully selecting the sample to work with. In Lusso & Risaliti (2016), this has been done in order to build a Hubble diagram for Quasars. Indeed, they use the LX − LUV to build a z−DM diagram (DM – distance modulus) for quasars, analogous to that of supernovae, to estimate cosmological parameters associated to ΛCDM cosmological models, but in order to get competitive results it is necessary to decrease the dispersion of the LX − LUV relation by as much as possible. The αOX − LUV relation is not used here for cosmological applications; nevertheless we perform variability studies with a sample selected with the same criteria as those used by Lusso & Risaliti (2016) and compare our results with theirs.
As mentioned before, radio-loud and BAL sources would increase the dispersion of the αOX − LUV relation, lying far away from the average relation. In order to identify radio-loud sources, we computed the radio-loudness parameter (Kellermann et al. 1989):
An object is identified as radio-loud if R* > 10; otherwise it is classified as radio-quiet. Indeed, objects from SDSS-DR7 were already provided with the radio-loudness parameter, while for objects from SDSS-DR12 we calculated the radio flux density at 5 GHz starting from radio flux density at 1.4 GHz adopting a radio spectral index of α = −0.8 (e.g. Gibson et al. 2008). Both catalogues by Shen et al. (2011) and Kozłowski (2017) flagged BAL sources, so we used their classification. However, the BAL nature is not always obvious, as BALs can appear and or disappear on timescales of months or years, making them difficult to identify (De Cicco et al. 2018)
We have also taken into account the intergalactic HI absorption, which would result in a suppression of the source flux at wavelengths smaller than the Lyα wavelength of 1216 Å, leading to a underestimation of the UV luminosity. We essentially select only those objects whose SEDs are such that the nearest SED point to log νem = 15.08 (corresponding to 2500 Å) is at a frequency smaller than that corresponding to 1216 Å: we exclude those objects for which the effect of intergalactic HI absorption should be significant. We then considered only non-absorbed sources and only those for which there exist reasonable estimates of the photon index, with the conditions 1.6 ≤ ΓC ≤ 2.8 and ΓC/δΓC > 1.5.
The reference sample is therefore defined by the following set of conditions.
-
No radio-loud and no BAL sources;
-
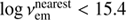 ;
; -
1.6 ≤ ΓC ≤ 2.8 & ΓC/δΓC > 1.5;
Summary of properties for both the Parent and Reference samples.
The data of the Reference sample are reported in Table 2 (available at the CDS) where the columns are: (1) identification number of the source in the MEXSAS2 catalogue; (2) SDSS name; (3) and (4) coordinates of the SDSS identification; (5) redshift; Col. (6) black-hole mass; (7) bolometric luminosity; (8) Eddington ratio; (9) number of observations; (10) time of observation (MJD); (11) and (12) log of the monochromatic luminosity at 2500 Å and its uncertainty; (13) and (14) log of the monochromatic luminosity at 2 keV and its uncertainty; and (15) and (16) the αOX index and its uncertainty.
With the sample described above we studied the αOX − LUV relation. In Fig. 3 we show the distribution of objects belonging to the reference sample in the αOX − LUV plane. Open circles are objects in common with Vagnetti et al. (2010); black points represent objects belonging to the reference sample; open circles with black point inside represent objects in the reference sample which are in common with Vagnetti et al. (2010). Figure 3 also shows the linear least-squares fit to the data for the 636 objects of the reference sample. In order to perform the linear fit, for a single-epoch object we considered the only available estimates of αOX and LUV, and for a multi-epoch object we considered average values of the two quantities over the different epochs. The result of the fit is
 |
Fig. 3. αOX as a function of the UV luminosity for the objects in the reference sample (black points) and for comparison empty circles represent objects from Vagnetti et al. (2010); empty circles with a black point inside represent objects belonging to both groups. The straight line is the linear least squares fit to the data considering only the reference sample. Average uncertainties on the two quantities are shown with a representative point with error bars. |
with a correlation coefficient r = −0.69 and a probability P(> r)=2.7 × 10−90 for the null hypothesis that αOX and LUV are uncorrelated.
Figure 4 shows a histogram of the distribution of the residuals of the αOX − LUV relation:
 |
Fig. 4. Histogram showing the distribution of the residuals of the αOX − LUV relation for the objects in the reference sample, characterised by a standard deviation of σ = 0.12. |
characterised by a standard deviation of σ = 0.12.
For comparison, we also studied the αOX − LUV relation for the parent sample, adopting the same procedure used for the reference sample, and we found αOX = ( − 0.165 ± 0.006)log LUV + (3.45 ± 0.19), with a dispersion of σ ∼ 0.14. This means that the adopted strategy of selecting the sample according to the constraints described above actually translates into a decrease in the dispersion of the relation.
The value of ∼0.12 is consistent with previous works (Strateva et al. 2005; Just et al. 2007; Gibson et al. 2008; Vagnetti et al. 2010). Our slope, Eq. (5), is consistent with Vagnetti et al. (2010), who obtained a correlation of αOX = ( − 0.166 ± 0.012)log LUV + (3.489 ± 0.377), but is not consistent with Gibson et al. (2008), who found αOX = ( − 0.217 ± 0.036)log LUV + (5.075 ± 1.118), or with Grupe et al. (2010), who found αOX = ( − 0.114 ± 0.014)log LUV + (1.177 ± 0.305). However, as already pointed out by Vagnetti et al. (2010), this may be due to the fact that they deal with samples of limited intervals of UV luminosity and/or redshift, and there is evidence of a dependence of the slope of the relation on these quantities (see detailed discussion in Sect. 3.3).
Figure 5 shows the tracks of individual objects of the reference sample in the αOX − LUV plane, clearly indicating the effect of variability on the dispersion of the observed relation.
 |
Fig. 5. αOX index as a function of the UV luminosity for the objects in the reference sample in which tracks of multi-epoch objects in this plane are shown. The straight line is the linear least-squares Eq. (5) to the data of the reference sample. |
In light of trends in Fig. 5, a possible way of reducing the dispersion of the relation would be to remove sources observed only a few times (e.g. one or two epochs). Indeed, the estimates of the average values of αOX (and also UV luminosity) are more robust when considering a larger number of epochs. Excluding single-epoch objects, and therefore considering only the 273 multi-epoch objects, we find αOX = ( − 0.15 ± 0.01) log LUV + (3.0 ± 0.03), with r = 0.71, P(> r) ∼ 2 × 10−43 and a dispersion σ ∼ 0.11. If we consider now 92 objects with three or more observations (see Table 1), we find αOX = ( − 0.14 ± 0.02) log LUV + (2.7 ± 0.5), with r = 0.68, P(> r) ∼ 1 × 10−13 and σ ∼ 0.10.
3.2. Multi-epoch data: the structure function
The structure function (SF) has been extensively used in the literature to perform ensemble variability studies both in the optical/UV band (e.g. Trevese et al. 1994; Cristiani et al. 1996; Wilhite et al. 2008; Bauer et al. 2009; MacLeod et al. 2012) and in the X-ray band (e.g. Vagnetti et al. 2011, 2016; Middei et al. 2017) considering fluxes and magnitudes. The SF gives a measure of variability as a function of time-lag τ between two observations. It can be used in principle to study the variability of any quantity, and has been defined in different ways in the literature (Simonetti et al. 1985; di Clemente et al. 1996). In this work we adopt the definition by Simonetti et al. (1985), which in the case of the αOX can be rewritten as
where 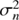 is the contribution of the photometric noise to the observed variability:
is the contribution of the photometric noise to the observed variability:
with δαOX being the uncertainty associated with αOX. The plane is divided into bins of time-lag (in log units), and in each bin the ensemble average value of the square of the difference αOX(t + τ)−αOX(t) is computed, considering all the pairs of observations for each object lying in the relevant bin of time-lag τ. The time-lag value representative of the bin is calculated weighting for the distribution of points within the bin.
The structure function can be used to put constraints on the contribution of variability to the total dispersion of the αOX − LUV relation. Indeed, following (Vagnetti et al. 2010, 2013), it is possible to write the total variance of the αOX − LUV relation as the sum of two contributions (see Sect. 3):
From the SF value at long time-lags we can estimate the fractional contribution of the intra-source dispersion σ2intra − source/σ2, that is, the contribution of the true variation in the X-ray/UV ratio to the dispersion of the αOX − LUV relation. Previous works found it to be ∼30% (Vagnetti et al. 2010) and ∼40% (Vagnetti et al. 2013).
Figure 6 shows the structure function of the αOX as a function of the time-lag for the objects in the reference sample. The error bars shown in Fig. 6 are not measurement errors but they concern the statistical dispersion of the data in the bins. Indeed, estimating the uncertainties from the observed scatter is the only viable approach for sparsely sampled light curves characterised by a red-noise behaviour. In fact, as shown by, for example Allevato et al. (2013), both the photometric errors and the formal uncertainties severely underestimate the scatter intrinsic to any stochastic process.
 |
Fig. 6. Structure function SF(τ) of the αOX index as a function of the time-lag τ for the multi-epoch objects in the reference sample. The dotted line is the noise level; the dashed line is the “uncorrected” structure function (i.e. without noise subtraction); the red line is the “corrected” SF, where red points are representative values of bins; the blue straight line is a weighted least-squares fit to the “corrected” SF. Error bars represent the 1-σ dispersion of the distribution of points in each bin. |
A weak increase of the SF with time-lag can be seen. Figure 6 also shows a weighted least-squares fit to the data of the form logSF(τ) = alog τ + b, in which the weight is the number of points in the bin. The result of the fit is a = 0.09 ± 0.03 and b = −1.32 ± 0.07. These parameters have been used to estimate the SF value at long time-lags,
where τlongest is the time-lag value associated to the last bin (∼2000 days).
The SF value at the longest time-lag is ∼0.09. This can be used to constrain the contribution of the intra-source dispersion to the total variance of the relation
This contribution is higher than that found by Vagnetti et al. (2010); this may be due to the longer time-lags sampled in this work (∼2000 days), considering that variability of αOX increases with time-lag, as shown in Fig. 6 and Eq. (10). Indeed, if we evaluate our SF at the time-lag of ∼300 days as Vagnetti et al. (2010), the relative contribution of variability is 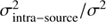 ∼ 44%.
∼ 44%.
3.3. Dependence on LUV and z
We studied the dependence of the αOX index on the redshift for the reference sample, and we found that the two quantities are negatively correlated: αOX = ( − 0.104 ± 0.008)z + ( − 0.009 ± 0.010), with a correlation coefficient r = −0.45 and a probability P(> r)∼8 × 10−3 for the null hypothesis that αOX and z are uncorrelated. However, as already suggested by Vagnetti et al. (2010), this positive correlation between αOX and z may be a by-product of the positive correlation between LUV and z. In order to check this possibility, we performed a partial-correlation analysis for the reference sample and found a partial correlation coefficient of αOX with the UV luminosity, taking into account the dependence on redshift, 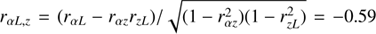 , with P(> r)∼9.5 × 10−50. Similarly, the partial correlation coefficient of αOX with the redshift accounting for the dependence on the UV luminosity is
, with P(> r)∼9.5 × 10−50. Similarly, the partial correlation coefficient of αOX with the redshift accounting for the dependence on the UV luminosity is 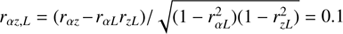 , with P(> r)=0.012. This result is not as strong as that derived by Vagnetti et al. (2010), so we cannot rule out the possibility of a weak dependence on redshift, even when taking into account the effect of luminosity. The difference with respect to Vagnetti et al. (2010) may be due to our larger sample. Indeed, referring to Fig. 2, we added objects in the low-z/low-UV luminosity part of the z − LUV plane, so we may not have added objects uniformly, resulting in a weak redshift dependence. In order to further investigate this possibility, we performed a partial-correlation analysis focusing only on those sources belonging to both Vagnetti et al. (2010) and the reference sample (circles with black dots in, Fig. 3), and we found a partial correlation coefficient of rα z, L = −0.09 with P(> r)=0.42, similar to Vagnetti et al. (2010). This suggests that the result obtained with the reference sample is likely the result of the addition of low-z/low-UV luminosity sources.
, with P(> r)=0.012. This result is not as strong as that derived by Vagnetti et al. (2010), so we cannot rule out the possibility of a weak dependence on redshift, even when taking into account the effect of luminosity. The difference with respect to Vagnetti et al. (2010) may be due to our larger sample. Indeed, referring to Fig. 2, we added objects in the low-z/low-UV luminosity part of the z − LUV plane, so we may not have added objects uniformly, resulting in a weak redshift dependence. In order to further investigate this possibility, we performed a partial-correlation analysis focusing only on those sources belonging to both Vagnetti et al. (2010) and the reference sample (circles with black dots in, Fig. 3), and we found a partial correlation coefficient of rα z, L = −0.09 with P(> r)=0.42, similar to Vagnetti et al. (2010). This suggests that the result obtained with the reference sample is likely the result of the addition of low-z/low-UV luminosity sources.
Subsequently, we divided the sample into two subsamples in redshift and UV luminosity considering the median values z = 1.28 and log LUV = 30.26, respectively: they guarantee an approximately equal number of sources in both subsamples. We found αOX = ( − 0.214 ± 0.014) log LUV + (4.96 ± 0.43) for z > 1.28 sources, with slope in agreement with the high-z sample of Gibson et al. (2008), and αOX = ( − 0.150 ± 0.011)log LUV + (3.01 ± 0.32) for z < 1.28 sources. Considering the UV luminosities, we found slopes of ( − 0.195 ± 0.014) for the log LUV > 30.26 sample and ( − 0.131 ± 0.014) for log LUV < 30.26, in agreement with Vagnetti et al. (2010), and similar results derived by Steffen et al. (2006).
We also studied the dependence of the residuals of the αOX − LUV relation with redshift, and we see that there is a weak and non-significant dependence (Fig. 7):
 |
Fig. 7. Residuals of the αOX − LUV relation as a function of redshift for the objects in the reference sample. The straight line is the linear least squares fit to the data. |
with a correlation coefficient of r = 0.07 and P(> r)∼0.08.
Previous works have established that there is essentially no redshift dependence of the relation (Just et al. 2007; Vagnetti et al. 2010, 2013); however in light of our results we cannot rule out a residual dependence on redshift. For the future, larger samples with a wider coverage of the LUV − z plane would allow for more robust results to be obtained.
Considering the work done by Lusso & Risaliti (2016, 2017), below, we compare our results obtained when studying the LX − LUV relation with theirs (see Sect. 4).
3.4. The dependence on MBH, L/LEdd, viewing angle, and the origin of inter-source dispersion
As already pointed out, our purpose is to further investigate the αOX − LUV relation, and most importantly to understand the physical origin of the residual dispersion, that is, the inter-source dispersion. Indeed, we have found through variability studies performed via structure function that an intrinsic variation in the X-ray/UV ratio can account for 56% of the total variance of the relation. In order to investigate the origin of the residual dispersion, we studied the dependence of αOX and the residuals of the αOX − LUV relation on fundamental quantities such as BH mass and Eddington ratio and we also investigated the role of viewing angle.
Figure 8 shows the dependence of the αOX index as a function of the BH mass:
 |
Fig. 8. αOX index as a function of black-hole mass for the objects in the reference sample. The straight line is the linear least squares fit to the data. |
with a correlation coefficient r = −0.33, the probability for the null hypothesis is P(> r)∼10−17. This result is in agreement with Dong et al. (2012) and can easily be understood considering a standard α-disk accretion disk (Shakura & Sunyaev 1973): for a fixed bolometric luminosity, a decrease in BH mass results in fainter disk emission in the UV, and therefore higher αOX values.
Figure 9 shows the dependence of αOX as a function of Eddington ratio:
 |
Fig. 9. Bottom panel: αOX index as a function of Eddington ratio for the objects in the reference sample. The straight line is the linear least squares fit to the data. Empty circles represent low-MBH objects, filled circles represent high-MBH objects, where the dividing value is the median BH mass of the reference sample log MBH = 8.7. Top panel: distribution of Eddington ratios for the objects in our reference sample. |
with a correlation coefficient r = −0.45, P(> r)∼10−32. From Fig. 9 we can see that, for a fixed Eddington ratio, objects with higher BH mass have lower X-ray/UV ratios, in agreement with Dong et al. (2012) and with Fig. 8. However, the weak anti-correlation we found between αOX and Eddington ratio is not in agreement with the positive one obtained by Dong et al. (2012), and this is also reflected in the trend whereby, for a fixed BH mass, objects with higher Eddington ratios have on average lower X-ray/UV ratios. This discrepancy may be due to the distribution of Eddington ratios in our sample, with objects being mainly concentrated in a narrow interval −1 ≤ log L/LEdd ≤ −0.5 (see Fig. 9). A more homogeneous distribution of Eddington ratios, with more objects populating the high-L/LEdd and low-L/LEdd tails would permit a more robust study of the αOX dependence on this parameter.
The dependence of the αOX on the BH mass could simply be a different representation of the dependence on LUV, given the correlation between the BH mass and UV luminosity in accretion disk models. Therefore, in order to understand the physical origin of the dispersion of the relation, we investigated the dependence of the residuals of the αOX − LUV relation on fundamental quantities. In particular, we studied the dependence of the residuals ΔαOX(LUV)=αOX − αOX(LUV) as a function of BH mass and Eddington ratios, and we find weak but significant trends, as follows:
with r = 0.19, P(> r)∼4 × 10−6, and
with r = −0.21, P(> r)∼10−7.
Another way to describe the same dependencies is to consider αOX as being dependent on both UV luminosity and the black-hole mass or the Eddington ratio. We have used the macro LINFIT of the package SM7 which performs a multivariate linear least-squares fit, and we have found αOX = ( − 0.23 ± 0.01) log LUV + (0.10 ± 0.01)log MBH + (4.44 ± 0.24) with σ=0.11. Considering the Eddington ratio, we have found αOX = ( − 0.15 ± 0.01) log LUV + ( − 0.07 ± 0.01)log L/LEdd + (2.85 ± 0.25) with σ=0.115. As a cross validation, we have performed the same analysis with Python package SCIKIT-LEARN (Pedregosa et al. 2011) and the SCIPY (Jones et al. 2001) package OPTIMIZE, finding consistent values. These results are in agreement with the trends indicated by Eqs. (15) and (16).
These dependencies, although not strong, might be part of the contribution to the inter-source dispersion.
Another possible contribution to the dispersion might come from a spread in corona properties among different sources, as suggested by Dong et al. (2012).
At the beginning of this section we suggested that one contribution to the dispersion may come from the inclination angle, however the problem of finding reliable inclination indicators in AGNs is a hot topic (e.g. Marin 2016). The role of the inclination angle has been discussed by Marziani et al. (2018, 2001) in light of the Eigenvector 1 (EV1) plane by Boroson & Green (1992). We refer to Fig. 2 of Marziani et al. (2018; but see also Fig. 1 in Shen & Ho 2014) which shows the optical plane of the EV1: FWHM(Hβ)−RFeII, where RFeII is the ratio of FeII within 4434 ÷ 4684 Å to broad Hβ EW, RFeII = EW(FeII)/EW(Hβ). Following this idea, we made an attempt to built these two quantities for the sample used in this work. Unfortunately, it was only possible to compute the quantities FWHM(Hβ), EW(FeII) and EW(Hβ) for 50 objects in this sample: they are available only for redshift z ≤ 0.9, and are only present in the catalogue by Shen et al. (2011), not in the one by Kozłowski (2017). However, according to Shen & Ho (2014), the dispersion in the FWHM(Hβ) is mainly attributed to an inclination effect, which makes this parameter a reliable inclination indicator. We therefore correlated the αOX with the FWHM(Hβ) for the 54 objects in the Reference sample which were provided with estimates of the FWHM(Hβ). We obtained:
with a correlation coefficient of r = 0.26 and P(> r)=0.06.
This positive correlation is in agreement with the scenario depicted by You et al. (2012). These latter authors built up a general-relativistic (GR) model for an accretion disk + corona model surrounding a Kerr black-hole, in which the inclination angle plays a crucial role: the emission from the corona can be approximated to be isotropic while the emission from the accretion disk is directional, resulting in an increase of the X-ray/UV ratio with viewing angle.
However, our aim is to investigate the contribution of fundamental physical quantities to the dispersion of the αOX − LUV relation. For this reason, we have studied the dependence of the residuals of the above relation as a function of the FWHM(Hβ) (see Fig. 10):
 |
Fig. 10. Residuals of the αOX − LUV relation as a function of the FWHM(Hβ) for the objects belonging to the reference sample and for which estimates of the FWHM(Hβ) are available. |
with a correlation coefficient of r = 0.27 and P(> r)=0.048.
We note that the EW[OIII] has also been identified as an orientation indicator (Risaliti et al. 2011; Bisogni et al. 2017a). We have therefore correlated our data with this parameter for the Reference sample, finding significant correlations as follows:
with r = 0.5 and P(> r)∼2 × 10−4, and
with r = 0.4 and P(> r)∼5 × 10−3, in agreement with the trend found for the case of the FWHM(Hβ).
Our results, although not statistically robust, indicate a possible interesting trend, and for the future, a sample for which estimates of the three quantities are available for a larger number of objects might allow a quantitative study of the impact of inclination on the dispersion of the αOX − LUV relation. Indeed, such a sample might allow a division of the sample with respect to viewing angle and the selection of sources expected to contribute less to the dispersion of the relation based on their inclination angle.
4. The LX−LUV relation and its use in cosmology
We mention above that the αOX − LUV relation is a byproduct of the well-established positive correlation between LX and LUV luminosity. This relation has been studied thoroughly by Lusso and Risaliti in a series of papers as they use it to build a Hubble diagram for quasars (Risaliti & Lusso 2015; Lusso & Risaliti 2016, 2017; Bisogni et al. 2017b). Indeed, Risaliti & Lusso (2015) considered objects from SDSS cross-matched with samples with X-ray measurements from the literature and used the non-linear relation between X-ray and UV luminosity to build a DM-z plane and estimate cosmological parameters Ωm and Ω Λ. In a more recent paper, Bisogni et al. (2017b) built the same diagram for a sample of 8000 objects obtained by cross-matching catalogues by Shen et al. (2011) and Pâris et al. (2017) with 3XMM-DR5 (Rosen et al. 2016), and in both works they found values for the parameters in agreement with those derived from the well-known Hubble diagram built from supernovae.
This method represents a valid alternative to the supernovae diagram, and has several advantages with respect to the latter: it can be used at higher redshifts (up to ∼5) and can be used in a more statistically robust analysis. However, the use of the LX − LUV relation to build a Hubble diagram for quasars relies on the tightness of the relation, and so the DM-z diagram created will be characterised by a larger dispersion with respect to supernovae. Nevertheless, Lusso & Risaliti (2016) proved that by carefully selecting the sample it is possible to decrease the dispersion of the relation and thus legitimise the use of this relation for cosmological purposes. In our work, we applied constraints to our initial sample in order to decrease the dispersion of the relation as much as possible and we further analysed the data to understand the physical origin of the residual dispersion of the relation. Indeed, it is clear that a thorough study on the dispersion and its origin is of vital importance for the use of the relation in cosmology in the sense described above.
With the reference sample described above we studied the relation between X-ray and UV luminosity. However, while in the case of the αOX − LUV relation the αOX index is assumed to be the dependent variable, the LUV being the independent one, a linear least-squares fit turns out to be a good fit. When considering the LX − LUV relation it is not possible to consider LX as the dependent variable and LUV the independent one (or vice versa), because we still lack a full understanding of the relation between the two regions responsible for the emission and because the relation is affected by large dispersion. Other methods must therefore be employed (Lusso & Risaliti 2016; Tang et al. 2007). We used the orthogonal distance regression (ODR) fitting8. The ODR fitting method treats X and Y variables symmetrically and minimises both the sum of the squares of the X and Y residuals, taking into account uncertainties in both variables. The result of the ODR fitting to the data is
Our slope is comparable with that derived by Lusso & Risaliti (2016), 0.634 ± 0.013, although our dispersion of σ ∼ 0.31 is higher than that derived by those authors due to some differences in the analyses. Indeed, Lusso & Risaliti (2016) use non-simultaneous UV and X-ray measurements. On the one hand, this has the advantage of better photometry, both in the X-rays (using the longest exposures) and in the UV (using the SDSS photometry which takes into account emission lines). On the other hand, our simultaneous analysis is capable of a better treatment of variability via the appropriate use of the SF. In fact, we find a larger contribution of variability, which translates to a residual dispersion (inter-source dispersion) which is similar to that of Lusso & Risaliti (2016).
We notice that the dispersion can be further reduced by selecting only those sources with a large number of observational epochs, as discussed at the end of Sect. 3.1. For the future, a more precise determination of Eqs. (5) and (21) might be achieved, adopting samples containing only objects with a large number of epochs.
5. Discussion and conclusions
The purpose of our work is to estimate the contribution of intrinsic variation of the X-ray/UV ratio to the dispersion of the αOX − LUV relation, and in particular to understand the origin of the residual dispersion of the relation with simultaneous X-ray and UV observations coming from the MEXSAS2 catalogue and the XMM-SUSS3, respectively. Indeed, once simultaneous X-ray and UV observations are used, the dispersion of the αOX − LUV relation is given by two contributions: an intra-source dispersion, due to intrinsic variations in the X-ray/UV ratio in single sources, and an inter-source dispersion, which may be due to fundamental quantities like BH mass, Eddington ratio, and/or viewing angle.
Starting from the parent sample, which is the result of the cross-match between the MEXSAS2 and the XMM-SUSS3 catalogues, we applied stringent constraints in order to decrease the dispersion of the relation as much as possible, following the strategy adopted by Lusso & Risaliti (2016). We considered only non-BAL and non-RL objects, as they would increase the dispersion, and we took into account the effects of intergalactic HI absorption and extinction, and considered only non-absorbed (in X-rays) sources with reliable photon-index estimates.
We have shown that by carefully selecting the sample with the constraints described above, it is possible to decrease the dispersion of the αOX − LUV relation, in agreement with Lusso & Risaliti (2016). We confirm the negative correlation between the two quantities, with a slope of −0.159 ± 0.007, comparable to slopes obtained by other authors (e.g. Just et al. 2007; Lusso et al. 2010; Vagnetti et al. 2010), and we obtained a dispersion of ∼0.12, consistent with Vagnetti et al. (2010).
Moreover, we performed an ensemble variability analysis of the αOX index by means of the SF. Indeed, the variance of the αOX − LUV relation can be written as the sum of two contributions, an intra-source and an inter-source dispersion, and from the SF value at long time-lags we estimated that true variability in the X-ray/UV ratio contributes 56% of the total variance of the relation (intra-source dispersion).
Lusso & Risaliti (2016) found a residual dispersion of σ ∼ 0.19 for the LX − LUV relation, that is, dispersion which is not explained by true variability in the X-ray/UV ratio. Our result means that the dispersion which cannot be explained with true variability in the X-ray/UV ratio is approximately 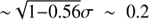 (see Eq. (11)), similar to that derived by Lusso & Risaliti (2016).
(see Eq. (11)), similar to that derived by Lusso & Risaliti (2016).
In an attempt to decrease the dispersion of the relation, we removed sources with only one or two observations, finding that it can decrease by approximately 15%.
The residual dispersion in the relation may be due to other physical quantities, like black-hole mass, Eddington ratio, and inclination angle.
We first studied the dependence of the relation on redshift and optical/UV luminosity. We performed a partial correlation analysis for the αOX − LUV relation taking into account the effect of redshift, and for the αOX − z relation taking into account the effect of UV luminosity. We found rα z, L = 0.1 with P(> r)=0.012: our result is not as statistically robust as that of previous works (e.g. Just et al. 2007; Vagnetti et al. 2010, 2013), and therefore we cannot rule out a residual dependence on redshift. For the future, larger samples with wider and more uniform covering of the LUV − z plane will allow to obtain more robust results in this sense.
Secondly, we studied the dependence of the residuals of the αOX − LUV relation on black-hole mass and Eddington ratio, and of the αOX index on these quantities. We have found weak but significant trends indicating an increase of the residuals of the relation with black-hole mass and a decrease with Eddington ratio. However, the dependence on these quantities may be masked by the dependence on UV luminosity. To test this issue, we performed a multivariate regression analysis considering αOX as a function of UV luminosity and black-hole mass or Eddington ratio. The results we have found are in agreement with the trends in the residuals.
We also studied the dependence of the αOX index and the residuals of the αOX − LUV relation on the inclination angle, and we considered the FWHM(Hβ) as an indicator, following Marziani et al. (2001, 2018) and Shen & Ho (2014). We have found that the residuals of the relation and the αOX index are positively correlated with FWHM(Hβ), with slopes of 0.13 ± 0.06 and 0.18 ± 0.09, respectively. The latter result is in agreement with the scenario depicted by You et al. (2012), according to which, in a GR model of an accretion disk + corona around a Kerr black-hole, objects with higher inclination angles are characterised by higher αOX values. We have performed the same analysis considering another inclination indicator, the EW[OIII], and have found similar results. However, due to the small size of our sample when considering the two quantities, these results are not statistically robust. Nevertheless, they represent a starting point for possible future studies. Indeed, a sample for which estimates of the FWHM(Hβ) (as well as EW[OIII]) are available for a larger number of objects, uniformly distributed in inclination angle, would allow more robust studies. In particular, in light of the use of the LX − LUV relation in cosmology, it would allow the possibility to divide the sample into intervals of inclination and select only those objects characterised by low values of the residuals, in order to decrease the dispersion of the relation.
Acknowledgments
We are grateful to the referee whose comments improved the quality of this work. E.C. acknowledges the National Institute of Astrophysics (INAF) and the University of Rome – Tor Vergata for the PhD scholarships in the XXXIII PhD cycle. F.T. acknowledges support by the Programma per Giovani Ricercatori – anno 2014 Rita Levi Montalcini. F.V. and M.P. acknowledge support from the project Quasars at high redshift: physics and Cosmology financed by the ASI/INAF agreement 2017-14-H.0. This research has made use of data obtained from the 3XMM-Newton serendipitous source catalogue compiled by the 10 institutes of the XMM-Newton Survey Science Centre selected by ESA. This research has made use of the XMM-OM Serendipitous Ultra-violet Source Survey, which has been created at the University College Londons (UCLs) Mullard Space Science Laboratory (MSSL) on behalf of ESA and is a partner resource to the 3XMM serendipitous X-ray source catalogue.
References
- Allevato, V., Paolillo, M., Papadakis, I., & Pinto, C. 2013, ApJ, 771, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Almaini, O., Lawrence, A., Shanks, T., et al. 2000, MNRAS, 315, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Arévalo, P., & Uttley, P. 2006, MNRAS, 367, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Arévalo, P., Uttley, P., Lira, P., et al. 2009, MNRAS, 397, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Avni, Y., & Tananbaum, H. 1986, ApJ, 305, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, A., Baltay, C., Coppi, P., et al. 2009, ApJ, 696, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Bisogni, S., Marconi, A., & Risaliti, G. 2017a, MNRAS, 464, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Bisogni, S., Risaliti, G., & Lusso, E. 2017b, Front. Astron. Space Sci., 4, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Laor, A., & Wills, B. J. 2000, ApJ, 528, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., Guainazzi, M., Kaspi, S., et al. 2001, AJ, 121, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Buisson, D. J. K., Lohfink, A. M., Alston, W. N., & Fabian, A. C. 2017, MNRAS, 464, 3194 [NASA ADS] [CrossRef] [Google Scholar]
- Cristiani, S., Trentini, S., La Franca, F., et al. 1996, A&A, 306, 395 [NASA ADS] [Google Scholar]
- Czerny, B. 2004, ArXiv e-prints [arXiv:astro-ph/0409254] [Google Scholar]
- De Cicco, D., Brandt, W. N., Grier, C. J., et al. 2018, A&A, 616, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- di Clemente, A., Giallongo, E., Natali, G., Trevese, D., & Vagnetti, F. 1996, ApJ, 463, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, R., Greene, J. E., & Ho, L. C. 2012, ApJ, 761, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, S. C., Brandt, W. N., Laor, A., et al. 2001, ApJ, 546, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, S. C., Brandt, W. N., Chartas, G., & Garmire, G. P. 2002, ApJ, 567, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Giallongo, E., Trevese, D., & Vagnetti, F. 1991, ApJ, 377, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, R. R., Brandt, W. N., & Schneider, D. P. 2008, ApJ, 685, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Green, P. J., Aldcroft, T. L., Mathur, S., Wilkes, B. J., & Elvis, M. 2001, ApJ, 558, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K. M., & Page, K. L. 2010, VizieR Online Data Catalog, II/18, [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jones, E., Oliphant, T., & Peterson, P. 2001, SciPy: Open Source Scientific Tools for Python, [Google Scholar]
- Just, D. W., Brandt, W. N., Shemmer, O., et al. 2007, ApJ, 665, 1004 [Google Scholar]
- Kellermann, K. I., Sramek, R., Schmidt, M., Shaffer, D. B., & Green, R. 1989, AJ, 98, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kozłowski, S. 2017, ApJS, 228, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., Fiore, F., Elvis, M., Wilkes, B. J., & McDowell, J. C. 1997, ApJ, 477, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., & Risaliti, G. 2016, ApJ, 819, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., & Risaliti, G. 2017, A&A, 602, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lusso, E., Comastri, A., Vignali, C., et al. 2010, A&A, 512, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyubarskii, Y. E. 1997, MNRAS, 292, 679 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, C. L., Ivezić, Ž., Sesar, B., et al. 2012, ApJ, 753, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Manners, J., Almaini, O., & Lawrence, A. 2002, MNRAS, 330, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F. 2016, MNRAS, 460, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, K., Ryle, W. T., & Miller, H. R. 2008, ApJ, 677, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2001, ApJ, 558, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Dultzin, D., Sulentic, J. W., et al. 2018, Front. Astron. Space Sci., 5, 6 [CrossRef] [Google Scholar]
- Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McHardy, I. 2010, Lect. Notes Phys., 794, 203 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Koerding, E., Knigge, C., Uttley, P., & Fender, R. P. 2006, Nature, 444, 730 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Middei, R., Vagnetti, F., Bianchi, S., et al. 2017, A&A, 599, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Neill, P. M., Nandra, K., Papadakis, I. E., & Turner, T. J. 2005, MNRAS, 358, 1405 [NASA ADS] [CrossRef] [Google Scholar]
- Page, K. L., Reeves, J. N., O’Brien, P. T., & Turner, M. J. L. 2005, MNRAS, 364, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Page, M. J., Brindle, C., Talavera, A., et al. 2012, MNRAS, 426, 903 [Google Scholar]
- Paolillo, M., Papadakis, I., Brandt, W. N., et al. 2017, MNRAS, 471, 4398 [NASA ADS] [CrossRef] [Google Scholar]
- Papadakis, I. E. 2004, MNRAS, 348, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Papadakis, I. E., Chatzopoulos, E., Athanasiadis, D., Markowitz, A., & Georgantopoulos, I. 2008, A&A, 487, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Ross, N. P., et al. 2017, A&A, 597, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Pentericci, L., Rix, H.-W., Prada, F., et al. 2003, A&A, 410, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petric, A. O., Carilli, C. L., Bertoldi, F., et al. 2003, AJ, 126, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Prevot, M. L., Lequeux, J., Prevot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., & Lusso, E. 2015, ApJ, 815, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Salvati, M., & Marconi, A. 2011, MNRAS, 411, 2223 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, S. R., Webb, N. A., Watson, M. G., et al. 2016, VizieR Online Data Catalog: IX/050, [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Serafinelli, R., Vagnetti, F., Chiaraluce, E., & Middei, R. 2017, Front. Astron. Space Sci., 4, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Simonetti, J. H., Cordes, J. M., & Heeschen, D. S. 1985, ApJ, 296, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I. V., Brandt, W. N., Schneider, D. P., Vanden Berk, D. G., & Vignali, C. 2005, AJ, 130, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, R., & Zdziarski, A. A. 1994, ApJ, 436, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Tananbaum, H., Avni, Y., Branduardi, G., et al. 1979, ApJ, 234, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, S. M., Zhang, S. N., & Hopkins, P. F. 2007, MNRAS, 377, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Tortosa, A., Bianchi, S., Marinucci, A., et al. 2018, MNRAS, 473, 3104 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Trevese, D., Kron, R. G., Majewski, S. R., Bershady, M. A., & Koo, D. C. 1994, ApJ, 433, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., & McHardy, I. M. 2005, MNRAS, 363, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Vagnetti, F., Turriziani, S., Trevese, D., & Antonucci, M. 2010, A&A, 519, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vagnetti, F., Turriziani, S., & Trevese, D. 2011, A&A, 536, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vagnetti, F., Antonucci, M., & Trevese, D. 2013, A&A, 550, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vagnetti, F., Middei, R., Antonucci, M., Paolillo, M., & Serafinelli, R. 2016, A&A, 593, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanden Berk, D. E., Wilhite, B. C., Kron, R. G., et al. 2004, ApJ, 601, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Mushotzky, R. F., Winter, L. M., & Fabian, A. C. 2009, MNRAS, 399, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., Fan, X., et al. 2001, AJ, 122, 2143 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Brandt, W. N., & Schneider, D. P. 2003, AJ, 125, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhite, B. C., Brunner, R. J., Grier, C. J., Schneider, D. P., vanden Berk, D. E. 2008, MNRAS, 383, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J., Tananbaum, H., Worrall, D. M., et al. 1994, ApJS, 92, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Worrall, D. M., Tananbaum, H., Giommi, P., & Zamorani, G. 1987, ApJ, 313, 596 [NASA ADS] [CrossRef] [Google Scholar]
- You, B., Cao, X., & Yuan, Y.-F. 2012, ApJ, 761, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Siebert, J., & Brinkmann, W. 1998, A&A, 334, 498 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. SEDs averaged in time for the multi-epoch objects in the parent sample: for each frequency we consider the average of the quantities Lν(νem). The red dashed line is the average SED by Richards et al. (2006) for type-1 objects in the SDSS. The vertical line is at log νe = 15.08, corresponding to 2500 Å. |
| In the text | |
 |
Fig. 2. Distribution of the parent sample in the LUV-z plane. Straight lines are lines of constant UV flux. Black circles represent objects in common with Vagnetti et al. (2010), empty circles are objects present only in this work. The straight lines are constant UV flux lines. The histogram on top shows the distribution of objects in the parent sample with respect to UV luminosity; the histogram on the right shows the redshift distribution of objects in the parent sample. The histogram inside the plot area (lower-right) shows the distribution of objects in the parent sample with respect to UV flux. |
| In the text | |
 |
Fig. 3. αOX as a function of the UV luminosity for the objects in the reference sample (black points) and for comparison empty circles represent objects from Vagnetti et al. (2010); empty circles with a black point inside represent objects belonging to both groups. The straight line is the linear least squares fit to the data considering only the reference sample. Average uncertainties on the two quantities are shown with a representative point with error bars. |
| In the text | |
 |
Fig. 4. Histogram showing the distribution of the residuals of the αOX − LUV relation for the objects in the reference sample, characterised by a standard deviation of σ = 0.12. |
| In the text | |
 |
Fig. 5. αOX index as a function of the UV luminosity for the objects in the reference sample in which tracks of multi-epoch objects in this plane are shown. The straight line is the linear least-squares Eq. (5) to the data of the reference sample. |
| In the text | |
 |
Fig. 6. Structure function SF(τ) of the αOX index as a function of the time-lag τ for the multi-epoch objects in the reference sample. The dotted line is the noise level; the dashed line is the “uncorrected” structure function (i.e. without noise subtraction); the red line is the “corrected” SF, where red points are representative values of bins; the blue straight line is a weighted least-squares fit to the “corrected” SF. Error bars represent the 1-σ dispersion of the distribution of points in each bin. |
| In the text | |
 |
Fig. 7. Residuals of the αOX − LUV relation as a function of redshift for the objects in the reference sample. The straight line is the linear least squares fit to the data. |
| In the text | |
 |
Fig. 8. αOX index as a function of black-hole mass for the objects in the reference sample. The straight line is the linear least squares fit to the data. |
| In the text | |
 |
Fig. 9. Bottom panel: αOX index as a function of Eddington ratio for the objects in the reference sample. The straight line is the linear least squares fit to the data. Empty circles represent low-MBH objects, filled circles represent high-MBH objects, where the dividing value is the median BH mass of the reference sample log MBH = 8.7. Top panel: distribution of Eddington ratios for the objects in our reference sample. |
| In the text | |
 |
Fig. 10. Residuals of the αOX − LUV relation as a function of the FWHM(Hβ) for the objects belonging to the reference sample and for which estimates of the FWHM(Hβ) are available. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



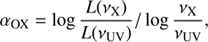
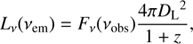
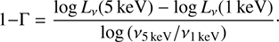
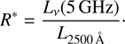
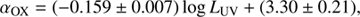
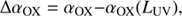
![$$ \begin{aligned} \mathrm{SF}(\tau )=\sqrt{{\langle }[{\alpha _{\rm OX}}(t+\tau )-{\alpha _{\rm OX}}(t)]^2{\rangle }-\sigma _n^2} , \end{aligned} $$](/articles/aa/full_html/2018/11/aa33631-18/aa33631-18-eq9.gif)
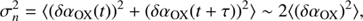
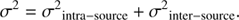
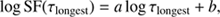
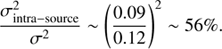
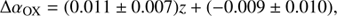
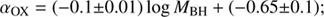
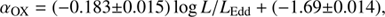
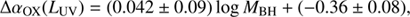
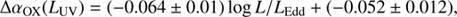
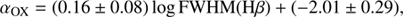
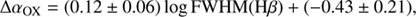
![$$ \begin{aligned} {\alpha _{\rm OX}=(0.17\pm 0.04)\log {EW[O_{\rm III}]}+(-1.65\pm 0.05)}, \end{aligned} $$](/articles/aa/full_html/2018/11/aa33631-18/aa33631-18-eq25.gif)
![$$ \begin{aligned} {\Delta \alpha _{\rm OX}(L_{\rm UV})=(0.10\pm 0.03)\log {EW[O_{III}]}+(0.12\pm 0.04)}, \end{aligned} $$](/articles/aa/full_html/2018/11/aa33631-18/aa33631-18-eq26.gif)