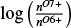EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 619 (November 2018) A&A, 619 (2018) A79 Full HTML
Open Access
Issue
A&A
Volume 619, November 2018
Article Number A79
Number of page(s) 8
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201833454
Published online 09 November 2018

© ESO 2018

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

The solar elemental composition has been under investigation for several decades (Feldman 1992; Schmelz et al. 2012; Meyer 1985). The photospheric elemental composition is typically assumed to be constant with the solar activity cycle and is used as the reference for the elemental composition observed in active regions (Baker et al. 2015), in coronal loops (Del Zanna & Mason 2003), and in the solar wind (Feldman 1992; Schmelz et al. 2012; Meyer 1985). It is well known that some elements are depleted or enriched in the solar wind compared to the photosphere. Since elements with similar first ionization potentials (FIPs) show a similar elemental composition in the solar wind relative to the photosphere, this is called the “FIP effect” and the underlying mechanism behind this effect separates ions from neutrals, and is thus assumed to act preferentially on ions rather than on neutral atoms. It is still unknown whether low FIP elements are enhanced in the solar wind compared to the photosphere or whether instead high FIP elements are depleted. Both interpretations are consistent with the observations.

Several theoretical approaches have been explored in modeling the FIP effect, including quasi-thermal processes of inefficient Coulomb drag/gravitational settling/diffusion (von Steiger & Geiss 1989; Marsch et al. 1995; Bochsler et al. 2000; Pucci et al. 2010; Peter 1996, 1998), heating by coronal ion cyclotron waves (Schwadron 1999), chromospheric reconnection (Arge & Mullan 1998), electric currents (Feldman & Widing 2003), and most recently and most promisingly, the ponderomotive force arising as Alfvén waves propagate through or reflect from the chromosphere (Doschek et al. 2015; Laming 2012, 2015, 2017; Dahlburg et al. 2016).

The FIP effect is more pronounced in the slow solar wind than in the fast coronal hole wind (Feldman 1992; Schmelz et al. 2012; Meyer 1985). Since they have similar FIPs, Mg (with a FIP of 7:646 eV), Si (with a FIP of 8:151 eV), and Fe (with a FIP of 7:870 eV; values taken from Benenson et al. 2006) are typically assumed to express the same FIP effect in the slow solar wind and in the coronal hole wind. This is consistent with long-term averages of the respective elemental abundances (Schmelz et al. 2012) and the dominant models of the FIP effect (Laming 2015). However, as discussed in detail in Laming et al. (2017), the FIP effect is not the only cause of fractionation in the solar wind. Pilleri et al. (2015) have already observed considerable fractionation between low FIP elements.

As visible in Fig. 1 of Schmelz et al. (2012) and discussed in detail in Reames (2018), another interesting fractionation case is S (with a FIP of 10.36 eV), which fractionates as a high FIP element in the closed loop solar corona, but is observed with a higher FIP ratio in the solar wind.

One of the main science goals of the upcoming Solar Orbiter mission (Müller et al. 2013) is to identify the source regions of the slow solar wind. In tune with the general scheme of Solar Orbiter to heavily exploit combined observations of its instruments, a coordinated observation of the elemental abundance by the SPectral Imaging of the Coronal Environment (SPICE) and the Heavy Ion Sensor (HIS) is intended as the main tool for investigating potential slow solar wind source regions. Both instruments can determine the strength of the FIP effect for several elements, and coordinated observations of the same plasma packages are planned. However, this relies on the assumption that in particular the low FIP elements Mg, Si, and Fe show highly correlated behavior even on short timescales. Here, we utilize the available observations of the Solar Wind Ion Composition Spectrometer (SWICS) on the Advanced Composition Explorer (ACE) to scrutinize this assumption and investigate the differences in the behavior of these low FIP elements.

thumbnail Fig. 1.

FIP ratios per year from 2001 to 2010. The columns show the FIP ratios for Fe, Mg, and Si. Each row corresponds to the same year. In each panel, a 2D histogram of all 12 min observations of FIP ratios vs the from the respective year are shown. Each vertical slice is normalized to its maximum. The number of contained data points is given in the inset of each panel. The dashed horizontal line indicates a FIP ratio of one. The gray solid line marks the median of the FIP ratio in each respective O charge state ratio bin.

thumbnail Fig. 2.

Median FIP ratios per year from 2001 to 2010 for Fe, Mg, and Si. The median is given only if at least 100 samples were observed in the respective bin. The colored shading indicates the 15.9th and 81.1th percentile for each year. In the lower panels the number of samples per O charge state bin and year are shown for Fe, Mg, and Si.

thumbnail Fig. 3.

Relative densities for pairs of low FIP elements. The columns correspond to the density ratios Mg/Fe, Si/Fe, and Mg/Si. As in Fig. 1, each panel shows a 2D histogram of 12 min observations for one year normalized for each O charge state ratio bin. The insets again specify the number of data points contained in each panel. Gray shading indicates bins with significantly different mean densities and the cross-hatching marks bins where the standard deviation of the two distributions are significantly different. The dashed horizontal line marks an abundance ratio of one.

thumbnail Fig. 4.

FIP ratios per solar wind type in a similar format to that in Fig. 1 accumulated for the years 2001–2006. Each row shows a different solar wind type (based on Xu & Borovsky 2015), from top to bottom: all non-ICME solar wind, coronal hole wind, all slow solar wind, sector reversal plasma, and helmet streamer plasma.

thumbnail Fig. 5.

FIP ratios per solar wind type in the same format as in Fig. 4 accumulated for the years 2007–2010.

2. Data selection

We are interested in the elemental composition of low FIP elements in the solar wind and apply our analysis to ten years of data from the Solar Wind Ion Composition spectrometer (SWICS; Gloeckler et al. 2003) on the Advanced Composition Explorer (ACE). The solar wind proton plasma parameters are taken from the Solar Wind Electron, Proton, and Alpha Monitor (ACE/SWEPAM; McComas et al. 1998) and magnetic field observations from the magnetometer ACE/MAG (Smith et al. 1998).

The ionic composition is derived from the SWICS Pulse Height Analysis (PHA) words as described in Berger (2008). We use the native 12 min time resolution of ACE/SWICS which results in at most 43 800 data points in non-leap years and 43 920 in leap years.

The elemental abundance of O, Mg, Si, and Fe is taken as the sum of the respective most prominent charge states, namely O6+, O7+, Mg7+, Mg8+, Mg9+, Mg10+, Mg11+, Mg12+, Si7+, Si8+, Si9+, Si10+, Si11+, Si12+, Fe7+, Fe8+, Fe9+, Fe10+, Fe11+, Fe12+, Fe13+, Fe14+, Fe15+, and Fe16+. Furthermore, to reduce statistical noise we require for each element a minimum of ten counts distributed over all respective ions. All data points that violate this condition are disregarded. However, since this induces a bias against very thin solar wind conditions, we also verified that the qualitative effect discussed in this paper remains if data points with fewer counts per element are included as well. We refer to the ratio of the abundance of an element X with density nX relative to O in the solar wind 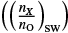divided by the respective photospheric ratio 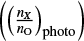taken from Grevesse & Sauval (1998) as the X FIP ratio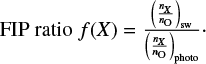

To characterize the solar wind type, we employ the four-type solar wind categorization scheme from Xu & Borovsky (2015). This heuristic scheme distinguishes between coronal hole wind, two types of slow solar wind, sector-reversal plasma and helmet streamer plasma, and ejecta plasma. This solar wind categorization scheme does not rely on the charge state composition, but only on (proton) plasma properties of the solar wind. To exclude interplanetary coronal mass ejections (ICMEs) we use two ICME lists, the Jian et al. (2006, 2011) list and the Richardson & Cane (2010) list, instead of the ejecta category. We exclude all time intervals from the data set that are considered as belonging to an ICME in either of the lists. Nevertheless, unidentified ICMEs are probably still included in the data set. We refer to the union of the two slow solar wind types as “all slow” solar wind. We repeated our analysis based on the composition based solar wind categorization from Zhao & Fisk (2010), and observed the same qualitative behavior.

3. Fractionation of low FIP elements

For Ne, a dependence of the elemental abundance on the solar cycle has been observed (von Steiger & Zurbuchen 2015). Under the assumption that Ne does not behave in a fundamentally different way from other elements in the Sun and the solar wind, this motivates us to independently analyze the FIP effect for Mg, Si, and Fe for each year.

Figure 1 provides yearly overviews of the observed FIP ratios of Mg, Si, and Fe from 2001 to 2010 to the logarithm of the respectively observed O7+/O6+ charge state ratio (we refer to this as the O charge state ratio only in the following). In the context of the Genesis mission, Pilleri et al. (2015) carried out a similar study and observed a decrease in the Fe and Mg FIP ratio with increasing solar wind speeds. Since the O charge state ratio is likely to be better suited to sort by solar wind type than the solar wind speed (Zhao & Fisk 2010), we instead use the O charge state ratio as reference.

Although all three elements show in all years a wide spread in the observed FIP ratios, the most frequently occurring FIP ratios range between 1 and 4. For Mg and Si, each year shows a similar pattern: with increasing O charge state ratio, the FIP ratio increases as well. This is consistent with the observations that the slow solar wind shows a stronger FIP effect than the coronal hole wind (as summarized in Schmelz et al. 2012 and Pilleri et al. 2015 with 2–4 for low FIP elements in slow solar wind and 1–2 for coronal hole wind). For Fe, however, the trend is different, in particular, during the solar activity maximum (for example in 2004) than during the solar activity minimum (for example in 2009). In 2009, the Fe FIP ratio shows no trend (or only a weak one) with increasing O charge state ratio. In 2004, the Fe FIP ratio exhibits a broad peak around 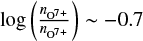. Also, the Fe FIP ratio distribution in most O charge state bins appears broader than for Mg and Si. When using the solar wind speed as a reference value, as in Pilleri et al. (2015), both the Mg and Fe FIP ratio continue to decrease with increasing solar wind speed.

Figure 1 further illustrates that the O charge state ratio changes over the solar cycle. During the solar activity maximum, higher values of the O charge state ratio are reached, while during solar minimum lower O charge state ratio values are observed. Thus, the part of the regime of the O charge state range which exhibits a broad peak in the Fe FIP ratio from 2001 to 2006, is only infrequently observed in the following years. Thus, from this figure it cannot be excluded that the Fe FIP effect always shows the same qualitative behavior in all years, but this is not visible in 2007–2010 because of insufficient statistics for this very slow solar wind. Although most ICMEs are filtered out from the data set, any ICME list can be expected to be incomplete. Since ICMEs are typically also associated with high charge states and are more frequent during the solar activity maximum, undetected ICMEs probably contribute to the broad peak in the Fe FIP ratio. Also, as discussed in, for example, Klecker et al. (2009), the density of high Fe charge states (with charges > 13) is significantly enhanced during ICMEs. However, since during normal solar wind conditions their contribution to the elemental density can be neglected, these high Fe charge states mainly contribute to the Fe elemental abundance for very high O charge state ratios, that is 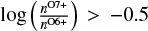. Thus, for corresponding slow solar wind with 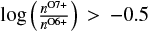, Fig. 1 is probably not representative. It is interesting to note that typically ICMEs are also associated with very high FIP ratios, whereas here the Fe FIP ratio is lower than expected for high O charge state ratios. Furthermore, for Mg and Si, the same high O charge state ratios are shown in 2001–2006 as for Fe, but the FIP ratios of Mg and Si nevertheless continue to increase with increasing O charge state ratio. For each O charge state ratio bin, the distribution of FIP ratios of Mg, Si, and Fe are asymmetric. Therefore, the median per O charge state ratio bin, which is indicated with solid gray lines in Fig. 1, is not a good proxy for the most frequently observated FIP ratios, but instead always overestimate them.

In the upper panels in Fig. 2, the yearly median of the FIP ratio for Mg, Si, and Fe is shown. In the lower panels, the number of samples per bin are given for each year. For all three low FIP elements, the median FIP ratio is lower in the years 2001–2006 and higher in the years 2007–2010. This indicates a solar cycle dependence of the FIP effect for all three elements. However, this effect is small compared to the variability of the observations as indicated by the percentiles in Fig. 2. Unlike the most frequently observed Fe FIP ratios, the median of the Fe FIP ratios behaves more like the respective yearly medians of the Mg and Si FIP ratios. Nevertheless, the slope of the median Fe FIP ratio for high O charge ratios is smaller during the solar activity maximum than during the solar activity minimum. This is not the case for the year 2003, probably because of the unusually high fraction of coronal hole wind during this year (see, e.g., Fig. 2 in Pilleri et al. 2015).

Figure 3 compares the FIP ratios of each pair of low FIP elements (Mg versus Fe, Si versus Fe, and Mg versus Si) for each year. With the help of statistical tests, for each O charge state ratio bin we investigated whether the distributions of FIP ratios of each pair of low FIP elements are likely to follow the same or different distributions. The shaded/hatched areas mark significant differences between the two respective mean values (gray shading, p < 0.05 according to the Kolmogorov–Smirnoff test; Kolmogorov 1933; Smirnov 1948) and empirical standard deviations (cross-hatching, p < 0.05 based on Levene’s test; Olkin 1960). Both statistical tests are suitable for non-normal distributions and were only applied if a minimum of 100 samples were observed per O charge state ratio bin. Both the mean and the standard deviation of Mg and Si are significantly different for all years and over almost the complete range of O charge state ratios. The distributions of Si and Fe are significantly different as well for intermediate O charge state ratio in all years, but show more similarities both for low and high O charge state ratios. For Fe and Mg, the mean of the respective distribution is also significantly different for most O charge state ratio bins, but for most years the empirical standard deviations of the respective distributions are comparable for intermediate and low O charge state ratios (which correspond mainly to the coronal hole wind). Except for 2002, for high O charge state ratios (which correspond mainly to the slow solar wind), and thus for the regime that exhibits the unexpected behavior in the Fe FIP ratio, both mean and empirical standard deviation of Fe and Mg differ significantly. It is also notable that the bulk of the ratio distributions is not at one (except for high O charge state ratio bins in the cases of Mg and Fe). In any O charge state ratio bin, there is on average less Si observed than Fe, and for most O charge state ratio bins} more Mg than Fe. This is consistent with the observations in Reames (2018) who observed higher Mg than Fe abundances for co-rotating interaction regions, the inter stream solar wind, and the coronal hole wind. However, Pilleri et al. (2015) instead found higher abundances for Fe than for Mg. We suspect that the difference arises from a respective omission or inclusion of Ca ions in the fitting process. Including Ca probably leads to some counts that were caused by Fe ions to be incorrectly assigned to Ca which leads to an underestimated Fe abundance. Excluding Ca from the fitting process correspondingly probably leads to incorrectly assigning counts caused by Ca ions to Fe which leads to an overestimation of Fe. One or both effects can result in the different observed relative abundances. However, in all cases these differences of the mean FIP ratio are within the respective error bars.

Although the distribution of the Mg and Si FIP ratios in Fig. 1 appear similar, Fig. 3 shows that for most O charge state ratio bins, the respective distributions of Mg and Si have significantly different means and standard deviations.

To ensure that the effect discussed here is not simply caused by different mixtures of different solar wind types in each year, in the following we sort the observations by solar wind type. Figures 4 and 5 show only solar wind from 2001–2006 and 2007–2010, respectively, but the observations are also separated by solar wind type according to the Xu & Borovsky (2015) scheme. During 2001–2006 for the coronal hole wind, all three elements show the same qualitative increase in the FIP ratio with increasing O charge state ratio; however, the FIP effect is most pronounced for Mg and weakest for Si. Even for the coronal hole wind, the Fe FIP ratio distribution appears broader than for Mg and Si during this time period. For the slow solar wind, in particular for helmet streamer plasma, Fe shows a qualitatively different behavior from that of Mg and Si with increasing O charge state ratio during 2001–2006. For Fe, sector reversal plasma exhibits a particularly broad FIP ratio distribution and no clear dependence of the FIP effect on the O charge state ratio. During 2007–2010, the distribution of the observed Fe FIP ratios is also broader than for Mg and Si, but for each solar wind type the qualitative behavior is more similar.

4. Discussion and conclusion

The observations reveal that the long-term behavior of the elemental composition is qualitatively different for Fe and for Mg and Si. While for Mg and Si the FIP ratio always increases with increasing O charge state ratio in all considered years and for all solar wind types, this is not the case for Fe. For Fe, the FIP ratio reaches a plateau or broad peak for logarithms of the O charge state ratio between 0.1 and 1 during the years 2001–2006. As also supported by Figs. 4 and 5, the differences are most pronounced for slow solar wind. That the Fe FIP ratio behaves differently from Mg and Si mainly in the slow solar wind during the declining phase of the solar activity maximum can indicate that a different fractionation or release mechanism is dominant during this period than during the solar activity minimum.

In addition, the Fe FIP distribution per O charge state ratio bin is typically broader than the respective distributions for Mg and Si. Based on the available models of the FIP effect, such a qualitative difference between the FIP ratios of low FIP elements is not expected. Thus, we believe that a full explanation of the observations discussed here requires refinement and improvement of the available models of the FIP effect.

The observations presented here clearly indicate that the assumption that all low FIP elements show a highly correlated FIP effect is not always valid, and thus that ne or more other fractionation mechanisms play an important role.

Acknowledgments

Part of this work was supported by the Deutsche Forschungsgemeinschaft (DFG) project number Wi-2139/11-1. We thank the referee, Martin Laming, for his insightful, helpful, and detailed remarks. We also thank the science teams of ACE/SWEPAM, ACE/MAG, as well as ACE/SWICS for providing the respective level 2 and level 1 data products.

References

  1. Arge, C., & Mullan, D. 1998, Sol. Phys., 182, 293 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baker, D., Brooks, D., Démoulin, P., et al. 2015, ApJ, 802, 104 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benenson, W., Harris, J. W., Stöcker, H., Lutz, H., et al. 2006, Handbook of Physics (Berlin: Springer) [Google Scholar]
  4. Berger, L. 2008, PhD Thesis, Christian Albrechts Universität, Kiel, Ukraine [Google Scholar]
  5. Bochsler, P., Ipavich, F. M., Paquette, J. A., Weygand, J. M., & Wurz, P. 2000, J. Geophys. Res., 105, 12 [CrossRef] [Google Scholar]
  6. Dahlburg, R. B., Laming, J. M., Taylor, B., & Obenschain, K. 2016, ApJ, 831, 160 [NASA ADS] [CrossRef] [Google Scholar]
  7. Del Zanna, G., & Mason, H. 2003, A&A, 406, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Doschek, G., Warren, H., & Feldman, U. 2015, ApJ, 808, L7 [NASA ADS] [CrossRef] [Google Scholar]
  9. Feldman, U. 1992, Phys. Scr., 46, 202 [CrossRef] [Google Scholar]
  10. Feldman, U., & Widing, K. G. 2003, Space Sci. Rev., 107, 665 [NASA ADS] [CrossRef] [Google Scholar]
  11. Gloeckler, G., Cain, J., Ipavich, F., et al. 2006, in The Advanced Composition Explorer Mission (Berlin: Springer), 497 [Google Scholar]
  12. Grevesse, N., & Sauval, A. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
  13. Jian, L., Russell, C., Luhmann, J., & Skoug, R. 2006, Sol. Phys., 239, 393 [NASA ADS] [CrossRef] [Google Scholar]
  14. Jian, L., Russell, C., & Luhmann, J. 2011, Sol. Phys., 274, 321 [NASA ADS] [CrossRef] [Google Scholar]
  15. Klecker, B., Möbius, E., Popecki, M., et al. 2009, in Proc. 31st Int. Cosmic Ray Conf., 3104 [Google Scholar]
  16. Kolmogorov, A. 1933, Inst. Ital. Attuari Giorn., 4, 83 [Google Scholar]
  17. Laming, J. M. 2012, ApJ, 744, 115 [NASA ADS] [CrossRef] [Google Scholar]
  18. Laming, J. M. 2015, Liv. Rev. Sol. Phys., 12, 1 [NASA ADS] [CrossRef] [Google Scholar]
  19. Laming, J. M. 2017, ApJ, 844, 153 [NASA ADS] [CrossRef] [Google Scholar]
  20. Laming, J. M., Heber, V. S., Burnett, D. S., et al. 2017, ApJ, 851, L12 [NASA ADS] [CrossRef] [Google Scholar]
  21. Marsch, E., von Steiger, R., & Bochsler, P. 1995, A&A, 301, 261 [NASA ADS] [Google Scholar]
  22. McComas, D., Bame, S., Barker, P., et al. 1998, in The Advanced Composition Explorer Mission (Berlin: Springer), 563 [CrossRef] [Google Scholar]
  23. Meyer, J.-P. 1985, ApJS, 57, 173 [NASA ADS] [CrossRef] [Google Scholar]
  24. Müller, D., Marsden, R. G., Cyr, O. S., & Gilbert, H. R. 2013, Sol. Phys., 285, 25 [NASA ADS] [CrossRef] [Google Scholar]
  25. Olkin, I. 1960, in Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling (Palo Alto, CA: Stanford University Press) [Google Scholar]
  26. Peter, H. 1996, A&A, 312, L37 [NASA ADS] [Google Scholar]
  27. Peter, H. 1998, A&A, 335, 691 [NASA ADS] [Google Scholar]
  28. Pilleri, P., Reisenfeld, D. B., Zurbuchen, T., et al. 2015, ApJ, 812, 1 [NASA ADS] [CrossRef] [Google Scholar]
  29. Pucci, S., Lie-Svendsen, Ø., & Esser, R. 2010, ApJ, 709, 993 [NASA ADS] [CrossRef] [Google Scholar]
  30. Reames, D. V. 2018, Sol. Phys., 293, 47 [NASA ADS] [CrossRef] [Google Scholar]
  31. Richardson, I., & Cane, H. 2010, Sol. Phys., 264, 189 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schmelz, J. T., Reames, D. V., von Steiger, R., & Basu, S. 2012, ApJ, 755, 33 [NASA ADS] [CrossRef] [Google Scholar]
  33. Schwadron, N. 1999, ApJ, 521, 868 [NASA ADS] [CrossRef] [Google Scholar]
  34. Smirnov, N. 1948, Ann. Math. Stat., 19, 279 [CrossRef] [Google Scholar]
  35. Smith, C. W., L’Heureux, J., Ness, N. F., et al. 1998, in The Advanced Composition Explorer Mission (Berlin: Springer), 613 [CrossRef] [Google Scholar]
  36. von Steiger, R., & Geiss, J. 1989, A&A, 225, 222 [NASA ADS] [Google Scholar]
  37. von Steiger, R., & Zurbuchen, T. 2015, ApJ, 816, 13 [Google Scholar]
  38. Xu, F., & Borovsky, J. E. 2015, J. Geophys. Res.: Space Phys., 120, 70 [NASA ADS] [CrossRef] [Google Scholar]
  39. Zhao, L., & Fisk, L. 2010, in SOHO-23: Understanding a Peculiar Solar Minimum, 428, 229 [NASA ADS] [Google Scholar]

All Figures

thumbnail Fig. 1.

FIP ratios per year from 2001 to 2010. The columns show the FIP ratios for Fe, Mg, and Si. Each row corresponds to the same year. In each panel, a 2D histogram of all 12 min observations of FIP ratios vs the from the respective year are shown. Each vertical slice is normalized to its maximum. The number of contained data points is given in the inset of each panel. The dashed horizontal line indicates a FIP ratio of one. The gray solid line marks the median of the FIP ratio in each respective O charge state ratio bin.
In the text
thumbnail Fig. 2.

Median FIP ratios per year from 2001 to 2010 for Fe, Mg, and Si. The median is given only if at least 100 samples were observed in the respective bin. The colored shading indicates the 15.9th and 81.1th percentile for each year. In the lower panels the number of samples per O charge state bin and year are shown for Fe, Mg, and Si.
In the text
thumbnail Fig. 3.

Relative densities for pairs of low FIP elements. The columns correspond to the density ratios Mg/Fe, Si/Fe, and Mg/Si. As in Fig. 1, each panel shows a 2D histogram of 12 min observations for one year normalized for each O charge state ratio bin. The insets again specify the number of data points contained in each panel. Gray shading indicates bins with significantly different mean densities and the cross-hatching marks bins where the standard deviation of the two distributions are significantly different. The dashed horizontal line marks an abundance ratio of one.
In the text
thumbnail Fig. 4.

FIP ratios per solar wind type in a similar format to that in Fig. 1 accumulated for the years 2001–2006. Each row shows a different solar wind type (based on Xu & Borovsky 2015), from top to bottom: all non-ICME solar wind, coronal hole wind, all slow solar wind, sector reversal plasma, and helmet streamer plasma.
In the text
thumbnail Fig. 5.

FIP ratios per solar wind type in the same format as in Fig. 4 accumulated for the years 2007–2010.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.