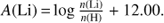EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 618 (October 2018) A&A, 618 (2018) A134 Full HTML
Free Access
Issue
A&A
Volume 618, October 2018
Article Number A134
Number of page(s) 10
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201833457
Published online 23 October 2018

© ESO 2018

1. Introduction

The emergent and generally accepted picture of stellar populations in globular clusters (GCs) is that these stellar systems host various (chemically distinct) stellar populations. In the majority of the cases, the stars of a GC share the same abundances of most of the elements, in particular Fe and iron-peak elements (see e.g. Carretta et al. 2009c; Willman & Strader 2012). This demonstrate that these systems are not able to retain the ejecta of the supernovae. On the other hand, light elements (C, N, O, Na, Mg, and Al) exhibit large star-to-star variations and often coherent patterns, i.e. C–N, Na–O, and Mg-Al anti-correlations (see e.g. Smith & Norris 1982; Kraft et al. 1992; Carretta et al. 2009a, b; Gratton et al. 2012; Meszaros et al. 2015; Pancino et al. 2017; Bastian & Lardo 2018). These chemical patterns are usually interpreted as the signature of internal pollution by low-energy ejecta of stars where high-temperature proton-capture cycles (CNO, NeNa, and MgAl cycles) have occurred. The so-called first population (1P) of the cluster is composed by stars with the same chemical composition of the original cloud from which the cluster formed. Instead, the subsequent second populations (2P) stars show variations of the light element abundances and they are expected to form from the pristine gas diluted with the ejecta of the polluter stars. A complete and quantitatively successful model for this self-enrichment process is still lacking because there is still debate about several details of the model (see e.g. Renzini et al. 2015; Bastian & Lardo 2015), for instance the identification of the main polluter stars. The most favorite candidate polluter stars are asymptotic giant branch (AGB) stars with masses of 4–8 M⊙ (Ventura et al. 2001; D’Ercole et al. 2008, 2010) and fast rotating massive stars (Meynet et al. 2006; Prantzos & Charbonnel 2006; Decressin et al. 2007).

The abundance of lithium, A(Li)1, in GC stars is a valuable diagnostic to understand this self-enrichment process, which poses challenges to the current theoretical models for the formation/evolution of GCs. Lithium is one of the few elements created during the Big Bang nucleosynthesis, together with H and He. In the subsequent evolution of the stars, Li is destroyed in the stellar interiors owing to proton capture reactions occurring at ∼2.5 × 106 K. However, Li should be preserved in the stellar envelopes of unevolved stars or partially diluted in the photospheres of stars that have undergone processes of mixing. The main mixing episodes are the first dredge-up (FDU) after the completion of the main sequence stage, and the extra-mixing episode occurring at the luminosity level of the red giant branch (RGB) bump. Because the proton-capture reactions responsible for the chemical anomalies observed in GC stars occurred at temperatures significantly higher (>107 K) than that of the Li burning (∼106 K), the enriched material from which the 2P stars formed should be Li free. Therefore, a Li–Na anti-correlation and a Li–O correlation are expected within the individual clusters.

Abundances of Li in GCs have been obtained from dwarf and lower RGB (LRGB) stars. The latter are stars located between the FDU and RGB bump. Even if measures of A(Li) are limited to a few GCs, the emerging scenario turns out to be complex and some GCs show evidence of star-to-star scatter in A(Li), such as in the cases of NGC 6397 (Lind et al. 2009; Gonzalez Hernandez et al. 2009), NGC 6752 (Pasquini et al. 2005; Shen et al. 2010), M4 (Monaco et al. 2012), NGC 2808 (D’Orazi et al. 2015), and 47 Tucanae (D’Orazi et al. 2010; Dobrovolskas et al. 2014). Other clusters (M92, NGC 362, NGC 1904, NGC5904, and NGC 6218; Bonifacio 2002; D’Orazi et al. 2014, 2015) show a remarkably homogeneous Li abundance. Up to now the only clusters that exhibit undeniable evidence of correlations between Li and light elements are NGC 6752, which shows both a Li–O correlation (Shen et al. 2010) and a Li–Na anti-correlation (Pasquini et al. 2005); NGC 6397, where three Li-poor, Na-rich dwarf stars have been found (Lind et al. 2009); and NGC 2808, where some Al-rich RGB stars have A(Li) lower than that in other stars with similar Al content (D’Orazi et al. 2015). In M4 a hint of Li–Na anti-correlation is found (Monaco et al. 2012) and has a larger A(Li) scatter among 2P stars with respect to 1P stars but no evidence of Li–O correlation (Mucciarelli et al. 2011). 47 Tucanae shows the opposite situation; there is a statistically significant Li–O correlation, but no clear evidence of a Li–Na anti-correlation (Dobrovolskas et al. 2014).

In this paper we investigate the Li content in the stellar system Omega Centauri (NGC 5139) using LRGB stars and we aim to highlight possible correlations with abundances of light elements involved in the chemical anomalies. Traditionally classified as a GC, Omega Centauri exhibits (at variance with the other globulars) a wide iron distribution (Johnson et al. 2008, 2009; Johnson & Pilachowski 2010; Villanova et al. 2014; Pancino et al. 2011a; Marino et al. 2011) and a variety of discrete sub-sequences in its colour-magnitude diagram (CMD, Lee et al. 1999; Pancino et al. 2000; Ferraro et al. 2004; Bedin et al. 2004; Sollima et al. 2005a, 2007; Milone et al. 2008), suggesting that this system has been able to retain the ejecta of the supernovae, experiencing a chemical enrichment history more complex than that of a normal GC. According to this evidence, Omega Centauri is usually interpreted as the remnant of a disrupted dwarf spheroidal galaxy (Bekki & Freeman 2003). On the other hand, its dominant (metal-poor) population shows a clear Na–O anti-correlation (Johnson & Pilachowski 2010; Marino et al. 2011), demonstrating that the same self-enrichment process observed in mono-metallic GCs also occurred in this stellar system.

The only determination of A(Li) in Omega Centauri stars has been presented by Monaco et al. (2010) who analysed a sample of 91 dwarf stars in the iron range [Fe/H] = –2.0/–1.4 dex, finding an average lithium A(Li) = 2.19 dex (σ = 0.14 dex). This abundance is compatible with the values usually measured among the Galactic dwarf stars. Measures for light element abundances are not available for this sample of dwarf stars. Because of the faintness of the dwarf stars in Omega Centauri (V > 18), large samples of high quality spectra can only be obtained with a huge amount of telescope time. The observation of LRGB stars (instead of dwarf stars) allows us to study the lithium content in Omega Centauri using a large sample of high signal-to-noise (S/N), high-resolution spectra, coupling these abundances with those of the light elements to study the lithium content in 1P and 2P stars.

2. Observations and membership

The observations have been collected under the ESO programme 096.D-0728 (PI: Mucciarelli) using the multi-object spectrograph FLAMES (Pasquini et al. 2000) at the Very Large Telescope. The GIRAFFE+UVES combined mode was used, allowing the simultaneous allocation of 132 mid-resolution GIRAFFE fibres and 8 high-resolution UVES (Dekker et al. 2000) fibres.

All the stars were observed with three FLAMES-GIRAFFE set-ups, namely HR12 (Δλ = 5821−6146 Å, R ∼ 20 000), HR13 (Δλ = 6120−6405 Å, R ∼ 26 000), and HR15N (Δλ = 6470−6790 Å, R ∼ 19 000), allowing the measure of several Fe spectral lines, as well as the Li line at 6708 Å, the Na D doublet at 5890–5896 Å, and the Al I doublet at 6696–6698 Å. Two observations of 1350 s each have been secured for HR12: four exposures of 1800 s each for HR12 and six exposures of 2700 s each for HR15N. Two target configurations have been taken, observing a total of 211 stars.

The targets were selected from the Bellini et al. (2009) BVRI WFI2.2 m photometric catalogue; stars ∼0.6 mag fainter than the mean locus of the RGB bump were picked. These stars are hence located after the completion of the FDU and before the onset of the extra mixing usually observed after the RGB bump. Figure 1 shows the positions of the observed targets (red circles), together with the mean locus of the RGB bump (red thick line). Only stars without close companions of comparable or brighter luminosity were selected to avoid stellar contamination within the fibres.

thumbnail Fig. 1.

Colour-magnitude diagram of Omega Centauri (Bellini et al. 2009, stars selected within 750 arcsec from the cluster centre). The position of the spectroscopic targets (red circles) and the mean locus (red line) of the RGB bump of the various stellar populations of Omega Centauri are shown.

The paper is structured as follows: Sect. 2 describes the observations and selection of the member stars of Omega Centauri; Sect. 3 describes the adopted procedure for the chemical analysis; and the results are presented in Sects. 4–6 and discussed in Sect. 7.

All the spectra were reduced with the standard ESO GIRAFFE pipeline2, including bias-subtraction, flat-fielding, wavelength calibration with a reference Th-Ar lamp, and extraction of the one-dimensional spectra.

Radial velocities (RVs) were measured for each individual spectrum from the position of several metallic lines using the code DAOSPEC (Stetson & Pancino 2008). After the correction for the corresponding heliocentric velocity, the spectra of each star were coadded together and used for the chemical analysis. Typical S/N per pixel are 70–100 for HR12, 120–150 for HR13, and 180–230 for HR15N.

We excluded from the following chemical analysis six stars with RV not compatible with that of Omega Centauri and four stars with RV dispersion larger than 1.7 km s−1 (while all the other targets have RV dispersions significantly smaller than 1kms−1) and considered as candidate binary stars. Finally, we derived chemical abundances for a total of 201 member stars of Omega Centauri. All the main information (coordinates, magnitudes, and RVs) of the member stars are listed in Table 1.

Table 1.

Main information on the member LRGB targets of Omega Centauri.

3. Chemical analysis

Effective temperatures (Teff) and surface gravities (log ɡ) were derived from the photometric information. The values Teff were obtained by averaging Teff derived from (B − V)0, (V − I)0 and (V − Ks)0 from the Alonso et al. (1999) transformations. The B, V, and I magnitudes are from Bellini et al. (2009), Ks magnitude from 2MASS database (Skrutskie et al. 2006). Because the Alonso et al. (1999) calibration adopted the Johnson I-filter, the Cousin I-band magnitudes by Bellini et al. (2009) were transformed to the Johnson photometric system adopting the transformation provided by Bessell (1979). The Ks 2MASS magnitudes were transformed to the Telescopio Carlos Sanchez photometric system (used by Alonso et al. 1999) by means of the relations by Carpenter (2001) and Alonso et al. (1998).

The dereddened colours were obtained by adopting the extinction coefficients from McCall (2004) and the colour excess quoted in the Harris (1996) catalogue (E(B − V) = 0.12 mag). We note that Omega Centauri is not significantly affected by differential reddening (Bellini et al. 2009) and this effect was neglected in the atmospheric parameters determination,

2MASS Ks magnitudes are available for 143 stars and, for these, we averaged the three Teff values. For 54 stars we used only Teff derived from (B − V)0 and (V − I)0, and for 4 stars (for which I and Ks magnitudes are not available) Teff from (B − V)0 were adopted. We checked that no significant offset exists among the different Teff scales: the average differences between the Teff scales are 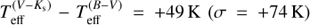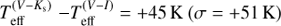Teff(V−Ks)−Teff(B−V)=+49K(σ=+74K)$T_{{\rm{eff}}}^{(V - {K_{\rm{s}}})} - T_{{\rm{eff}}}^{(B - V)} = + 49{\rm{K}}(\sigma = + 74{\mkern 1mu} {\rm{K}})$, Teff(V−Ks)−Teff(V−I)=+45K(σ=+51K)$T_{{\rm{eff}}}^{(V - {K_{\rm{s}}})} - T_{{\rm{eff}}}^{(V - I)} = + 45{\mkern 1mu} {\rm{K}}(\sigma = + 51{\mkern 1mu} {\rm{K}})$, and Teff(B−V)−Teff(V−I)=−30K(σ=+61K)$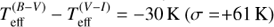T_{{\rm{eff}}}^{(B - V)} - T_{{\rm{eff}}}^{(V - I)} = - 30{\mkern 1mu} {\rm{K}}(\sigma = + 61{\rm{K}})$.

Gravities were derived through the Stefan–Boltzmann relation, adopting the photometric Teff described above, a true distance modulus of (m − M)0 = 13.70 mag (Bellazzini et al. 2004), the bolometric corrections calculated according to Alonso et al. (1999), while the evolutive mass was estimated according to a grid of theoretical isochrones of different metallicities from the BaSTI database (Pietrinferni et al. 2006). Microturbulent velocities (vt) were derived spectroscopically by erasing any trend between the line strength and iron abundance using ∼35–40 Fe I lines.

Chemical abundances for Fe and Al were derived with the code GALA (Mucciarelli et al. 2013)3 by comparing the theoretical and measured equivalent widths (EWs) of unblended metallic lines. The adopted model atmospheres were calculated with the last version of the code ATLAS94 (see Sbordone et al. 2004; Kurucz 2005). We measured the EWs with the code DAOSPEC (Stetson & Pancino 2008) managed through the wrapper 4DAO (Mucciarelli 2013)5. For some stars, Al lines are too weak to be measured and we computed upper limits adopting as EW three times the uncertainty calculated according to the Cayrel (1988) formula.

We derived abundances for Li and Na through a χ2 minimization, performed with our own code SALVADOR, between the observed and synthetic spectra. The synthetic spectra were computed with the code SYNTHE (Sbordone et al. 2004; Kurucz 2005), including all the atomic and molecular transitions from the Kurucz/Castelli linelist. We derived the Li abundances from the Li resonance doublet at ∼6708 Å, including the corrections for non-local thermodynamical equilibrium from Lind et al. (2008). Lithium abundances were derived for 168 targets, while for 33 stars the Li line is too weak and only upper limits are provided. Na abundances from the Na D doublet at 5890–5896 Å were corrected for departures from local thermodynamical equilibrium adopting the corrections computed by Lind et al. (2011).

We calculated abundance uncertainties by adding in quadrature the errors arising from the measurement procedure (EW or spectral fitting) and those arising from the adopted atmospheric parameters; uncertainties in Teff and log ɡ were added directly because the two parameters are correlated. For Fe and Al, we consider as internal error the dispersion normalized to the root mean square of the number of used lines. For Li and Na abundances, derived from spectral synthesis, we estimated the uncertainties in the fitting procedure resorting to Monte Carlo simulations. For each star, a sample of 300 noisy spectra was created, injecting Poissonian noise in the best-fit synthetic spectrum (rebinning to the FLAMES-GIRAFFE pixel size). Each sample of spectra was analysed with the same procedure adopted for the real spectra. The dispersion of the derived abundance distribution was assumed as 1σ uncertainty in the abundance. Uncertainties due to the atmospheric parameters were derived by repeating the analysis varying each time one only parameter by the corresponding uncertainty (σTeff = ±50 K, σvt = ±0.1km s−1, σlogɡ = ±0.1).

Typical formal uncertainties in A(Li) are of the order of 0.05– 0.07 dex because the uncertainty in Teff is the dominant source of error for these abundances, while the error due to the fitting procedure is smaller than 0.03 dex because of the high S/N of the spectra. Atmospheric parameters, abundance ratios, and their uncertainties for all the member stars are listed in Table 2.

Table 2.

Atmospheric parameters and abundance ratios (and corresponding uncertainties) for the member LRGB stars in Omega Centauri.

4. [Fe/H] distribution

Figure 2 shows the [Fe/H] distribution of the entire sample (upper panel) as a generalized histogram, i.e. a representation that removes the effects due to the choice of the starting point and bin size by taking the uncertainties in each individual value into account (see Laird et al. 1988).

thumbnail Fig. 2.

Generalized histograms for the LRGB stars of Omega Centauri discussed in this study (upper panel) and for the bright RGB stars discussed by Johnson & Pilachowski (2010), shifted by –0.08 dex to match the main peaks of the two distributions.

The iron distribution ranges from –2.06 dex to – 0.76 dex with a main peak at [Fe/H] ∼ –1.85 dex, a clear second peak at [Fe/H] ∼ –1.55 dex, a long metal-rich tail with a clump of stars at [Fe/H] ∼ – 0.9 dex, and a possible small peak at [Fe/H] ∼ –1.3 dex. This distribution is qualitatively similar to those previously discussed in other studies (Johnson et al. 2008, 2009; Johnson & Pilachowski 2010; Marino et al. 2011). The lower panel of Fig. 2 shows the [Fe/H] distribution by Johnson & Pilachowski (2010) that presented the largest (855 stars) dataset of abundances for RGB stars of Omega Centauri. We note that the main peak of our distribution is slightly more metal poor than that by Johnson & Pilachowski (2010). We estimate a difference of –0.08 dex between the median values of the metal-poor components of the two distributions. In Fig. 2 the [Fe/H] distribution by Johnson & Pilachowski (2010) has been shifted by –0.08 dex to match the main peaks of the two distributions. Because there are no stars in common with this study (that is focussed on RGB stars brighter than the RGB bump), we cannot directly investigate the origin of this small difference. However, we noted that the V-band magnitudes used by Johnson & Pilachowski (2010) are brighter than those of Bellini et al. (2009) by about 0.1 mag (while the Ks-band magnitudes are the same), leading to slightly hotter Teff with respect to our values. Despite this small offset, the two distributions are very similar. Following the scheme used by Johnson & Pilachowski (2010) to describe their [Fe/H] distribution, we adopted the nomenclature proposed by Sollima et al. (2005a) to associate the individual RGBs observed in the CMD of Omega Centauri with the components of its iron distribution. The main peak in our [Fe/H] distribution can be associated with the RGB-MP (the main giant branch observed in the CMD of Omega Centauri), the second peak to the RGB-Int1, while the most metal-rich peak to the anomalous RGB. Sollima et al. (2005a) identified two other RGBs with metallicites intermediate between those of RGB-Int1 and the anomalous RGB. Johnson & Pilachowski (2010) identified the stars in the range [Fe/H] ∼ –1.4/–1.0 dex in their [Fe/H] distribution as belonging to the RGB-Int2 and RGB-Int3. In our distribution this [Fe/H] range is less populated with respect to the Johnson & Pilachowski (2010) distribution, probably because of a poor sampling of the reddest stars; our targets are confined to a narrow strip on the CMD (see Fig. 1).

5. Lithium in Omega Centauri

We discuss the A(Li) distribution in 199 LRGB stars of Omega Centauri, excluding two targets that reveal a high Li content and that will be discussed in a forthcoming paper.

The upper panel of Fig. 3 shows the behaviour of A(Li) as a function of [Fe/H] for the true measures (166 stars, gray circles) and the upper limits (33 stars, red arrows). Considering only the true measures, the A(Li) distribution ranges from 0.47 to 1.19 dex. The A(Li) distribution clearly peaks at A(Li) ∼ 1 dex but with the presence of a significant percentage of stars with A(Li) < 0.8 dex. Stars with A(Li) ∼ 1 dex are found only at [Fe/H] < –1.3 dex, while Li-poor stars are found at all the metallicities. In particular, the A(Li) distribution for stars with [Fe/H] < –1.6 dex (corresponding to the main population of Omega Centauri, RGB-MP) is dominated by stars with A(Li) ∼ 1 dex. In the [Fe/H] range between –1.6 and –1.3 dex (likely connected to RGB-Int1) the distribution is dominated by stars with A(Li) < 0.8 dex, while the component at A(Li) ∼ 1dex decreases in number. For [Fe/H] > –1.3 dex the component with A(Li) ∼ 1 dex totally disappears and all stars have A(Li) lower than ∼0.6–0.7 dex.

thumbnail Fig. 3.

Upper panel: behaviour of A(Li) as a function of [Fe/H]. The gray points indicate the true measures; red arrows indicate the upper limits. The blue line shows the theoretical behaviour of A(Li) as a function of [Fe/H] in LRGB stars starting from the same initial A(Li). Lower panel: behaviour of the fraction of number of stars with A(Li) > 0.8 and with A(Li) < 0.8 as a function of [Fe/H] computed for four metallicity bins. Vertical error bars represent the uncertainties in the number ratio, the horizontal error bars denote the corresponding metallicity range.

The lower panel of Fig. 3 shows the run of the ratio of the number of Li-rich to Li-poor stars (defined assuming A(Li) = 0.8 dex as threshold) as a function of the iron abundance. The data were grouped into four metallicity bins, chosen according to the metallicity distribution (Fig. 2) centred at [Fe/H] = –1.85, –1.55, –1.30, and –0.9 dex, and with width of 0.45, 0.20, 0.34, and 0.3 dex. The stars with [Fe/H] < –1.65 dex show a constant number ratio that drops at higher metallicity, reaching 0 for the most metal-rich stars where all the stars have A(Li) < 0.8.

In order to assess whether the lack of Li-rich stars in the metal-rich regime is real or due to small number statistics, we performed a Monte Carlo simulation from a A(Li) distribution resembling that observed for stars with [Fe/H] < –1.6 dex. We extracted from this distribution 10 000 samples of 40 stars and 10 000 samples of 15 stars, corresponding to the number of stars observed in the third and forth metallicity bin, respectively. We found that the probability to observe a NLi−rich/NLi−poor number ratio smaller than 0.5 is 0 and less than 0.03% for the two samples, ruling out that the observed lack of stars with A(Li) ∼ 1dex is due to the small number of stars. Also, we checked that different choices for the metallicity bins do not change this conclusion. Hence, the difference between the A(Li) distributions of metal-poor and metal-rich stars is real.

The peak of the number distribution of A(Li) for the metalpoor stars well agrees with the A(Li) abundances previously measured in Population II LRGB stars, i.e. in Milky Way field stars (Mucciarelli et al. 2012), Galactic GCs (Lind et al. 2009; Mucciarelli et al. 2011; D’Orazi et al. 2014, 2015) and the extragalactic GC M54 (Mucciarelli et al. 2014). This finding confirms the previous result (based on dwarf stars) by Monaco et al. (2010) that Omega Centauri formed with the same lithium content of other Population II stars, formed in the Milky Way. Considering only the stars with [Fe/H] < –1.3 dex, the main peak of the A(Li) number distribution (A(Li) > 0.8 dex) includes about 60% of the stars. This fraction well matches the fraction of the true measures of A(Li) among dwarf stars of Omega Centauri analysed by Monaco et al. (2010) in a similar range of metallicity ([Fe/H] < –1.4 dex).

The most interesting feature in this A(Li) distribution is the lack of stars with A(Li) ∼ 1 dex at metallicities higher than [Fe/H] ∼ –1.3 dex. The blue line shown in Fig. 3 is the expected run of A(Li) with [Fe/H] in LRGB stars assuming that they are all born with the same initial A(Li), according to models from Mucciarelli et al. (2012) and assuming an age of 12.5 Gyr. In particular, we assumed an initial value able to match the observed A(Li) of the peak of the number distribution of the metal-poor component; however the shape of the curve is independent of the assumed value for the initial A(Li). The model predicts that A(Li) in LRGB stars mildly decreases over a large range of [Fe/H] and should only rapidly drop because of the deeper convective envelope of such metal-rich stars for [Fe/H] > –0.9 dex. If we assume that all the stars in Omega Centauri formed with the same initial Li content, a clear drop of the Li abundance is expected at [Fe/H] > –0.9/–0.8 dex. Instead, the stars of Omega Centauri with [Fe/H] > –1.3 dex are systematically depleted in lithium. We recall that LRGB stars of GCs with [Fe/H] ∼ –1.1/–1.2 dex (see e.g. M4, Mucciarelli et al. 2011; Monaco et al. 2012 and NGC 2808, D’Orazi et al. 2015) have A(Li) compatible with that measured in metal-poor clusters.

We investigated whether other parameters can affect the behaviour of A(Li) in these stars, in particular the helium mass fraction Y and stellar age. Several photometric observations (such as the extended blue horizontal branch and splitting of the main sequence) reveal a large spread in the initial He content of Omega Centauri stars. In particular, the most metalrich populations were suggested to have a helium mass fraction up to Y ∼ 0.35 (Norris 2004; Piotto et al. 2005; Sollima et al. 2005b; Renzini 2008). We checked that for metallicity [M/H] = –1.01 dex, an increase of Y from 0.24 up to 0.35 changes the value of A(Li) in LRGB stars by only 0.03 dex.

The precise age spread in Omega Centauri is still debated and the metal-rich populations are proposed to be coeval to the main population or significantly younger by some Gyr (see e.g. Ferraro et al. 2004; Freyhammer et al. 2005; Villanova et al. 2014; Tailo et al. 2016). However, a decrease of the age from 12.5 Gyr to 8.5 Gyr (both adopting Y = 0.25 and Y = 0.35) leads to a decrease of A(Li) by ∼0.05–0.06 dex with respect to the value calculated for 12.5 Gyr and Y = 0.25. Therefore, an increase of the He content and/or a decrease of the age cannot explain the drop of A(Li) observed for [Fe/H] > –1.3 dex.

Finally, we note that the model predictions for the surface A(Li) of the observed RGB stars (blue line in Fig. 3) include potential surface Li depletion during the MS due to burning at the bottom of the convective envelopes.

6. Li–Na anti-correlation

The comparison between Li and Na abundances provides important clues to understand the nature of the Li-poor stars observed at all the metallicities in Omega Centauri. This stellar system has a wide range of [Na/Fe] from [Na/Fe] ∼ –0.5 dex to ∼+0.6 dex. We note that our [Na/Fe] distribution is shifted towards lower values with respect to those measured by Johnson & Pilachowski (2010) and Marino et al. (2011) because these two works do not take into account departures from the local thermodynamical equilibrium (the corrections for the Na abundances are usually negative). Figures 4 and 5 show the run of [Na/Fe] and [Al/Fe] as a function of A(Li), respectively. The red arrows represent the upper limits for Li and the blue arrows indicate the upper limits for [Al/Fe]. In both plots a clear anti-correlation is found; the stars with the higher A(Li) cover a large range of [Na/Fe] and [Al/Fe], while the stars with A(Li) lower than ∼0.8 dex have systematically higher [Na/Fe] and [Al/Fe] abundances. Direct evidence of this behaviour is shown in Fig. 6, where the spectra of two stars stars with similar atmospheric parameters and metallicity are compared (namely #206770 and #213229, red and black curves, respectively). As clearly visible, the spectrum of #213229 shows Al and Na lines stronger than those of #206770 (where the Al lines are totally lacking), but also an undetectable Li line, clearly visible in the other spectrum.

thumbnail Fig. 4.

Behaviour of [Na/Fe] as a function of A(Li) for the entire spectroscopic sample studied in this work (gray circles). Red arrows indicate the upper limits for A(Li).

thumbnail Fig. 5.

Behaviour of [Al/Fe] as a function of A(Li) for the entire spectroscopic sample studied in this work (gray circles). Red arrows indicate the upper limits for A(Li), blue arrows show the upper limits for Al.

thumbnail Fig. 6.

Comparison between two stars of Omega Centauri, namely #206770 and #213229 (red and black curves respectively). Showing these two stars have similar atmospheric parameters and metallicity but different depths for Li, Na, and Al lines. The two strong lines at ∼5891 Å visible in the lower panel and shifted each other are Na interstellar lines.

The Li–Na anti-correlation is visible only in the metal-poor stars because the presence of a significant star-to-star A(Li) scatter is restricted to [Fe/H] < –1.3 dex (see Fig. 3). In particular, the stars with low A(Li) are all significantly enriched in Na, even if other stars with similar high Na have normal A(Li). Figure 7 shows the behaviour of [Na/Fe] as a function of [Fe/H] for our sample (a similar run has also been found by Johnson & Pilachowski 2010; Marino et al. 2011). [Na/Fe] increases with the iron content and the higher Na abundances are measured in the most metal-rich stars. Hence, stars with [Fe/H] > –1.3 dex are all depleted in Li but enriched in Na.

thumbnail Fig. 7.

Behaviour of [Na/Fe] as a function of [Fe/H].

We compare the Li–Na distribution of Omega Centauri with those measured in mono-metallic GCs, namely NGC 6397, NGC 6752, M4, and 47 Tucanae. The distributions of Li–Na of these clusters are shown in Fig. 8 in comparison with that of the LRGB stars in Omega Centauri: light gray points and arrows show the entire sample of target stars studied, while dark gray points and arrows show the target stars of Omega Centauri selected with metallicities close to those of the comparison GCs included in each panel. Because the Li abundances in these GCs are measured in dwarf stars we shifted these abundances in order to match the median A(Li) of each cluster with the peak of the A(Li) distribution of Omega Centauri, which is lower owing to the effect of the FDU.

In NGC 6397 (blue circles in Fig. 8) most of the 100 dwarf stars studied by Lind et al. (2009) have a similar A(Li) but over a large range of Na (hence corresponding to 1P and 2P stars). Among these 100 targets, three stars have A(Li) lower than the other stars by ∼0.4–0.5 dex and they have the highest values of [Na/Fe] of the sample.

NGC 6752 (green circles) shows a clear Li–Na anti-correlation (Pasquini et al. 2005) where the most Li-poor stars have A(Li) lower by ∼0.4 dex with respect to the most Li-rich stars. At variance with NGC 6397 (and also Omega Centauri) where most of the stars exhibit a large Na spread but similar A(Li), in NGC 6752 the Na and Li abundances in the studied stars follow a linear behaviour. Even if the sample discussed by Pasquini et al. (2005) includes only 9 dwarf stars, its large spread in A(Li) has been confirmed by Shen et al. (2010) with a sample of 112 dwarf stars (and where a Li–O correlation has been detected).

thumbnail Fig. 8.

Comparison between the [Na/Fe]–A(Li) distribution of the stars in Omega Centauri (gray points and arrows) and the abundances measured in dwarf stars of some mono-metallic GCs from the literature, namely NGC 6397 (blue circles; Lind et al. 2009), NGC 6752 (green circles; Pasquini et al. 2005), M4 (red triangles; Monaco et al. 2012) and 47 Tucanae (cyan squares; Dobrovolskas et al. 2014). Light gray points and arrows indicate the entire sample of stars in Omega Centauri studied; dark gray points and arrows represent the target stars selected with a metallicity similar to that of the reference Galactic GC shown in each panel.

Monaco et al. (2012) present Na and Li abundances in 70 dwarf stars in M4 (red triangles in Fig. 8), excluding one Lirich star. The Na–Li distribution in M4 is similar to that of NGC 6397, with most of the stars with similar Li content and different [Na/Fe] but a larger star-to-star scatter in A(Li) among the 2P stars. We note that the most Li-poor star in this sample has a A(Li) lower by ∼0.3 dex than the median A(Li) value and it is among the most Na-rich stars.

47Tucanae (cyan squares in Fig. 8) exhibits a large star-to-star scatter in its Li content. D’Orazi et al. (2010) and Dobrovolskas et al. (2014) from the analysis of 110 dwarf stars in this cluster do not find clear evidence of Li–Na anti-correlation, while a hint of Li–O correlation is detected.

Other GCs have been investigated by D’Orazi et al. (2014, 2015), who discuss the behaviour of A(Li) in LRGB stars as a function of Al abundance. In most of these GCs (namely NGC 362, NGC 1904, NGC 5904, and NGC 6218) all the stars have the same A(Li) regardless of the Al abundance. On the other hand, in NGC 2808 some Al-rich LRGB stars have A(Li) lower by ∼0.3 dex than that in other stars with similar Al content.

7. Summary and conclusions

We derived surface lithium abundances for 199 LRGB stars members of the stellar system Omega Centauri and distributed over its entire metallicity range. The main results are as follows:

  • The A(Li) number distribution of LRGB stars in Omega Centauri is peaked at A(Li) ∼ 1 dex. This value is compatible with the abundances measured in LRGB stars belonging to other GCs and in metal poor field stars and this abundance can be considered as the normal A(Li) in Population II LRGB stars. Additionally, the A(Li) distribution of Omega Centauri shows also a prominent Li-poor tail (A(Li) ≲ 0.8 dex).

  • The stars with normal A(Li) are found at [Fe/H] < –1.3 dex, while the Li-poor stars are found at all the metallicities. All the stars with [Fe/H] > –1.3 dex exhibit low A(Li) values.

  • A clear Li–Na anti-correlation is found. The stars with normal A(Li) cover a large range of [Na/Fe]; A(Li) ≲ 0.8 dex are characterized by enhanced values of [Na/Fe]. Similarly, a Li-Al anti-correlation is detected.

The A(Li) distribution in Omega Centauri is more complex than those observed in mono-metallic GCs, reflecting the peculiar (and not yet totally understood) chemical evolution of this system. We can draw a qualitative scheme to describe this distribution, classifying the stars according to their, Li, Na, and Fe abundances. In particular, we used [Na/Fe] to discriminate between 1P (low [Na/Fe]) and 2P (high [Na/Fe]) stars. We identify four main groups of stars, sketched in Fig. 9:

  1. 1P stars ([Fe/H] < –1.3 dex), with low [Na/Fe] and normal Li.

  2. 2P stars ([Fe/H] < –1.3 dex) enriched in [Na/Fe] and with the same (normal) A(Li) measured in 1P stars; hereafter we refer to these stars as 2P-Li-normal.

  3. 2P stars ([Fe/H] < –1.3 dex) enriched in [Na/Fe] similar to the 2P-Li-normal stars, but depleted Li (A(Li) ≲ 0.8 dex) and referred to in this work as 2P-Li-depleted.

  4. Stars with [Fe/H] > –1.3 dex (labelled as MR-Li-depleted) that have A(Li) ≲ 0.6 dex and high [Na/Fe] abundances. In particular, the [Na/Fe] abundance of these stars is slightly higher than that of 2P stars because the [Na/Fe] increases with the metallicity (see Fig. 7 and also Johnson & Pilachowski 2010; Marino et al. 2011).

thumbnail Fig. 9.

Same as Fig. 4 but with superimposed the mean loci for the proposed classification of the Omega Centauri’s stars according to their Li and Na abundances.

The classification proposed in Fig. 9 only provides a simple guideline to highlight the complexity of the Li–Na distribution in this system, and the main features to be explained by models for the formation of Omega Centauri. It does not imply a specific formation timeline.

The overall picture is that mono-metallic GCs (see Fig. 8) show, to a lesser extent, the same sub-populations identified in the metal-poor stars of Omega Centauri. These clusters are dominated by 1P and 2P-Li-normal stars, with the presence of a minor component of Na-rich, Li-poor stars (even if the identification of a clear boundary between 2P-Li-normal and 2P-Li-depleted populations is not trivial). On the other hand, the fraction of 2P-Li-depleted stars observed in Omega Centauri (∼30%) turns out to be exceptional with respect to the other GCs, where the fraction of these stars is about 3–5%.

Within the canonical views of the formation of multiple populations, 1P stars would correspond to the first stellar generation and we can consider their surface A(Li) as a good tracer of the initial lithium content of the stellar system (after the effect of the FDU is taken into account). The high [Na/Fe] measured in the other (2P) stars indicates that these stars formed from a gas enriched by the products of proton-capture cycles (occurring at temperatures higher than that of Li burning). The timeline of the formation of the 2P stars (both with normal and depleted Li content) in Omega Centauri depends on the chemical evolution of the system and the role played by the different polluter stars. The 2P-Li-depleted stars may have formed from a Li-poor or Li-free gas (diluted with pristine gas) coming from fast-rotating massive stars that are not able to produce fresh Li (Decressin et al. 2007). On the other hand, the high A(Li) measured among the 2P-Li-normal stars suggests a production of new Li. Massive AGB stars are potentially able to produce Li through the Cameron-Fowler mechanism and they may explain the Li abundance in most of the Na-rich stars.

However, theoretical models for A(Li) in GCs based on AGB stars as main polluters depend on several parameters, in particular the yields of the AGB models and the lithium abundance of the pristine material; the production of Li in AGB stars is sensitive to the stellar mass (see D’Antona et al. 2012, for a discussion on these assumptions). D’Antona et al. (2012) discussed for M4 the case of polluters ejecta that are Li free (a case similar to that of fast-rotating massive stars) and diluted with pristine gas, finding only a mildly lower (by about 0.1 dex) A(Li) in 2P stars with respect to 1P stars. Hence, high A(Li) in Na-rich stars could also be explained with polluter stars not able to produce fresh Li, depending on the details of the dilution process. The need for some fine-tuning to reproduce the uniform Li content observed in stars with a large spread in Na abundance, as well as uncertainties in the theoretical mass-loss rates and Li yields, reduces the predictive power of these models.

Another peculiarity of Omega Centauri is the low Li abundance in its metal-rich stars. The stars with [Fe/H] > –1.3 dex exhibit an unexpected depletion of A(Li) that is not observed in GCs with comparable metallicities (i.e. M4 and NGC 2808), which show in most of their (dwarf or LRGB) stars A(Li) similar to that measured in metal-poor clusters. We demonstrated that the effect of high metallicity, high He content, and/or young age (that could characterize the high-metallicity stars in Omega Centauri) cannot explain the observed values, under the assumption that all the stars of Omega Centauri formed with the same initial A(Li). Hence, we conclude that the MR-Li-depleted stars formed from a gas already depleted in A(Li) (similar to the 2P-Li-depleted stars) and the observed Li depletion is not an effect of the FDU. According to this finding, we should observe in the metal-rich main sequence stars of Omega Centauri a surface A(Li) smaller than the typical value of the Spite Plateau. The observation of these stars is very challenging owing to their faintness. Monaco et al. (2010) and Pancino et al. (2011b) provided upper limits for A(Li) in 18 stars belonging to the metal-rich subgiant branch of Omega Centauri. Unfortunately, the upper limits for the initial Li content of these stars do not provide conclusive answers.

An additional hurdle with respect to mono-metallic GCs is the possible age spread of the stellar populations of Omega Centauri. There is no general consensus about the relative ages of the different stellar components of the system, in particular between the main (metal-poor) population and the most metal-rich population, which could be virtually coeval (see e.g. Tailo et al. 2016) or several Gyr younger (see e.g. Villanova et al. 2014). If the metallicity enrichment of Omega Centauri took place on short timescales, and in particular if the metal-rich stars are coeval or only slightly younger than the other populations, the most metal-rich stars have formed before other sources of Li production occur, such as novae and cosmic rays spallation (see e.g. Romano et al. 1999).

Detailed theoretical models for the Li–Na behaviour in Omega Centauri are not available so far. In particular, future theoretical models for Omega Centauri need to simultaneously explain: (i) the existence of stars with similar A(Li) but different [Na/Fe] (1P and 2P-Li-normal); (ii) the existence of stars with similar [Na/Fe] but different A(Li) (2P-LiR and 2P-Li-depleted); and (iii) the MR-Li-depleted component with the lowest A(Li) and the highest [Na/Fe]. The discussed set of abundances will be crucial to put new constraints on the chemical enrichment history of this stellar system.

1

A(Li)=logn(Li)n(H)+12.00.$$A({\rm{Li}}) = \log {{n({\rm{Li}})} \over {n({\rm{H}})}} + 12.00.$$

Acknowledgments

The authors thank the anonymous referee for his/her useful comments and suggestions. SV gratefully acknowledges the support provided by Fondecyt reg. n. 1170518. LM acknowledges the support from “Proyecto interno” of the Universidad Andres Bello. AM warmly thanks Federico Montaguti and Olma for their essential support during the last year.

References

  1. Alonso, A., Arribas, S., & Martinez-Roger, C. 1998, A&AS, 131, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bastian, N., & Lardo, C. 2015, MNRAS, 453, 357 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bastian, N., & Lardo, C. 2018, ARA&A, 56, 83 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bekki, K., & Freeman, K. C. 2003, MNRAS, 346, L11 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bellazzini, M., Ferraro, F. R., Sollima, A., Pancino, E., & Origlia, L. 2004, A&A, 424, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bellini, A., Piott, G., Bedin, L. R., et al. 2009, A&A, 493, 958 [Google Scholar]
  9. Bessell, M. S. 1979, PASP, 91, 589 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bonifacio, P. 2002, A&A, 390, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cayrel, R. 1988, in The Impact of Very High S/N Spectroscopy on Stellar Physics, eds. G. Cayrel de Strobel, & M. Spite, IAU Symp., 132, 345 [NASA ADS] [CrossRef] [Google Scholar]
  12. Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
  13. Carretta, E., Bragaglia, A., Gratton, R., et al. 2009a, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009b, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. D’Antona, F., D’Ercole, A., Carini, R., Vesperini, E., & Ventura, P. 2012, MNRAS, 426, 1710 [NASA ADS] [CrossRef] [Google Scholar]
  17. Decressin, T., Charbonnel, C., & Meynet, G. 2007, A&A, 475, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, SPIE, 4008, 534 [Google Scholar]
  19. D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
  20. D’Ercole, A., D’Antona, F., Ventura, P., Vesperini, E., & McMillan, S. L. W. 2010, MNRAS, 407, 854 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  21. Dobrovolskas, V., Kučinskas, A., Bonifacio, P., et al. 2014, A&A, 565, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. D’Orazi, V., Lucatello, S., Gratton, R., et al. 2010, ApJ, 713, L1 [NASA ADS] [CrossRef] [Google Scholar]
  23. D’Orazi, V., Angelou, G. C., Gratton, R. G., et al. 2014, ApJ, 791, 39 [NASA ADS] [CrossRef] [Google Scholar]
  24. D’Orazi, V., Gratton, R. G., Angelou, G. C., et al. 2015, MNRAS, 449, 4038 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ferraro, F. R., Sollima, A., Pancino, E., et al. 2004, ApJ, 603, L81 [NASA ADS] [CrossRef] [Google Scholar]
  26. Freyhammer, L. M., Monelli, M., Bono, G., et al. 2005, ApJ, 623, 860 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gonzalez Hernandez, J. I., Bonifacio, P., Caffau, E., et al. 2009, A&A, 505, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
  29. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  30. Johnson, C. O., Pilachowski, C. A., Simmerer, J., & Schwenk, D. 2008, ApJ, 681, 1505 [NASA ADS] [CrossRef] [Google Scholar]
  31. Johnson, C. O., Pilachowski, C. A., Michael, R. R., & Fulbright, J. P. 2009, ApJ, 698, 2048 [NASA ADS] [CrossRef] [Google Scholar]
  32. Johnson, C. I., & Pilachowski, C. A. 2010, ApJ, 722, 1373 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kraft, R. P., Sneden, C., Langer, G. E., & Prosser, C. F. 1992, AJ, 104, 645 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 14 [Google Scholar]
  35. Laird, J. B., Rupen, M. P., Carney, B. W., & Latham, D. W. 1988, AJ, 96, 1908 [NASA ADS] [CrossRef] [Google Scholar]
  36. Lee, Y.-W., Joo, J.-M., Sohn, Y.-J., et al. 1999, Nature, 402, 55 [NASA ADS] [CrossRef] [Google Scholar]
  37. Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2008, A&A, 528, 103 [Google Scholar]
  38. Lind, K., Primas, F., Charbonnel, C., Grundahl, F., & Asplund, M. 2009, A&A, 503, 545 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  39. Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Marino, A. F., Milone, A. P., Piotto, G., et al. 2011, ApJ, 731, 64 [NASA ADS] [CrossRef] [Google Scholar]
  41. McCall, M. L. 2004, AJ, 128, 2144 [NASA ADS] [CrossRef] [Google Scholar]
  42. Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Meszaros, S., Martell, S. L., Shetrone, M., et al. 2015, AJ, 149, 153 [NASA ADS] [CrossRef] [Google Scholar]
  44. Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] [Google Scholar]
  45. Monaco, L., Bonifacio, P., Sbordone, L., Villanova, S., & Pancino, E. 2010, A&A, 519, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Monaco, L., Villanova, S., Bonifacio, P., et al. 2012, A&A, 539, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Mucciarelli, A. 2013, ArXiv e-prints [arXiv:1311.1403] [Google Scholar]
  48. Mucciarelli, A., Salaris, M., Lovisi, L., et al. 2011, MNRAS, 412, 81 [NASA ADS] [CrossRef] [Google Scholar]
  49. Mucciarelli, A., Salaris, M., & Bonifacio, P. 2012, MNRAS, 419, 2195 [NASA ADS] [CrossRef] [Google Scholar]
  50. Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
  51. Mucciarelli, A., Salaris, M., Bonifacio, P., Monaco, L., & Villanova, S. 2014, MNRAS, 444, 1812 [NASA ADS] [CrossRef] [Google Scholar]
  52. Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]
  53. Pancino, E., Ferraro, F. R., Bellazzini, M., Piotto, G., & Zoccali, M. 2000, ApJ, 534, L83 [NASA ADS] [CrossRef] [Google Scholar]
  54. Pancino, E., Mucciarelli, A., Sbordone, L., et al. 2011a, A&A, 527, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Pancino, E., Mucciarelli, A., Bonifacio, P., Monaco, L., & Sbordone, L. 2011b, A&A, 534, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Pancino, E., Romano, D., Tang, B., et al. 2017, A&A, 601, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Pasquini, L., Avila, G., Allaert, E., et al. 2000, SPIE, 4008, 129 [Google Scholar]
  58. Pasquini, L., Bonifacio, P., Molaro, P., et al. 2005, A&A, 441, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
  60. Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]
  61. Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Renzini, A. 2008, MNRAS, 391, 354 [NASA ADS] [CrossRef] [Google Scholar]
  63. Renzini, A., D’Antona, F., Cassisi, S., et al. 2015, MNRAS, 454, 4197 [NASA ADS] [CrossRef] [Google Scholar]
  64. Romano, D., Matteuci, F., Molaro, P., & Bonifacio, P. 1999, A&A, 352, 117 [NASA ADS] [Google Scholar]
  65. Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, MSAIS, 5, 93 [Google Scholar]
  66. Shen, Z.-X., Bonifacio, P., Pasquini, L., & Zaggia, S. 2010, A&A, 524, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  68. Smith, G. H., & Norris, J. 1982, ApJ, 254, 149 [NASA ADS] [CrossRef] [Google Scholar]
  69. Sollima, A., Ferraro, F. R., Pancino, E., & Bellazzini, M. 2005a, MNRAS, 357, 265 [NASA ADS] [CrossRef] [Google Scholar]
  70. Sollima, A., Pancino, E., Ferraro, F. R., et al. 2005b, ApJ, 634, 332 [NASA ADS] [CrossRef] [Google Scholar]
  71. Sollima, A., Ferraro, F. R., Bellazzini, M., et al. 2007, ApJ, 654, 915 [NASA ADS] [CrossRef] [Google Scholar]
  72. Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
  73. Tailo, M., Di Criscienzo, M., D’Antona, F., Caloi, V., & Ventura, P. 2016, MNRAS, 457, 4525 [NASA ADS] [CrossRef] [Google Scholar]
  74. Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. G. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
  75. Villanova, S., Geisler, D., Gratton, R. G., & Cassisi, S. 2014, ApJ, 791, 107 [NASA ADS] [CrossRef] [Google Scholar]
  76. Willman, B., & Strader, J. 2012, AJ, 144, 76 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Main information on the member LRGB targets of Omega Centauri.

In the text
Table 2.

Atmospheric parameters and abundance ratios (and corresponding uncertainties) for the member LRGB stars in Omega Centauri.

In the text

All Figures

thumbnail Fig. 1.

Colour-magnitude diagram of Omega Centauri (Bellini et al. 2009, stars selected within 750 arcsec from the cluster centre). The position of the spectroscopic targets (red circles) and the mean locus (red line) of the RGB bump of the various stellar populations of Omega Centauri are shown.

The paper is structured as follows: Sect. 2 describes the observations and selection of the member stars of Omega Centauri; Sect. 3 describes the adopted procedure for the chemical analysis; and the results are presented in Sects. 4–6 and discussed in Sect. 7.
In the text
thumbnail Fig. 2.

Generalized histograms for the LRGB stars of Omega Centauri discussed in this study (upper panel) and for the bright RGB stars discussed by Johnson & Pilachowski (2010), shifted by –0.08 dex to match the main peaks of the two distributions.
In the text
thumbnail Fig. 3.

Upper panel: behaviour of A(Li) as a function of [Fe/H]. The gray points indicate the true measures; red arrows indicate the upper limits. The blue line shows the theoretical behaviour of A(Li) as a function of [Fe/H] in LRGB stars starting from the same initial A(Li). Lower panel: behaviour of the fraction of number of stars with A(Li) > 0.8 and with A(Li) < 0.8 as a function of [Fe/H] computed for four metallicity bins. Vertical error bars represent the uncertainties in the number ratio, the horizontal error bars denote the corresponding metallicity range.
In the text
thumbnail Fig. 4.

Behaviour of [Na/Fe] as a function of A(Li) for the entire spectroscopic sample studied in this work (gray circles). Red arrows indicate the upper limits for A(Li).
In the text
thumbnail Fig. 5.

Behaviour of [Al/Fe] as a function of A(Li) for the entire spectroscopic sample studied in this work (gray circles). Red arrows indicate the upper limits for A(Li), blue arrows show the upper limits for Al.
In the text
thumbnail Fig. 6.

Comparison between two stars of Omega Centauri, namely #206770 and #213229 (red and black curves respectively). Showing these two stars have similar atmospheric parameters and metallicity but different depths for Li, Na, and Al lines. The two strong lines at ∼5891 Å visible in the lower panel and shifted each other are Na interstellar lines.
In the text
thumbnail Fig. 7.

Behaviour of [Na/Fe] as a function of [Fe/H].
In the text
thumbnail Fig. 8.

Comparison between the [Na/Fe]–A(Li) distribution of the stars in Omega Centauri (gray points and arrows) and the abundances measured in dwarf stars of some mono-metallic GCs from the literature, namely NGC 6397 (blue circles; Lind et al. 2009), NGC 6752 (green circles; Pasquini et al. 2005), M4 (red triangles; Monaco et al. 2012) and 47 Tucanae (cyan squares; Dobrovolskas et al. 2014). Light gray points and arrows indicate the entire sample of stars in Omega Centauri studied; dark gray points and arrows represent the target stars selected with a metallicity similar to that of the reference Galactic GC shown in each panel.
In the text
thumbnail Fig. 9.

Same as Fig. 4 but with superimposed the mean loci for the proposed classification of the Omega Centauri’s stars according to their Li and Na abundances.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.