| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201832937 | |
| Published online | 12 October 2018 | |
Horizontal photospheric flows trigger a filament eruption⋆
1
Institut de Recherche en Astrophysique et Planétologie, Université de Toulouse, CNRS, UPS, CNES 14 Avenue Édouard Belin, 31400 Toulouse, France
e-mail: thierry.roudier@irap.omp.eu
2
Observatoire de Paris, LESIA, 5 Place Jules Janssen, 92195 Meudon, France
3
PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, France
4
Pushkov Institute of Terrestrial Magnetism, Ionosphere and Radio Wave Propagation of the Russian Academy of Sciences (IZMIRAN), Troitsk, Moscow, 108840
Russia
5
Department of Physics, DSB Campus, Kumaun University, Nainital, 263 001
India
Received:
2
March
2018
Accepted:
9
July
2018
Context. A large filament composed principally of two sections erupted sequentially in the southern hemisphere on January 26, 2016. The central, thick part of the northern section was first lifted up and lead to the eruption of the full filament. This event was observed in Hα with the Global Oscillation Network Group (GONG) and Christian Latouche IMageur Solaire (CLIMSO), and in ultraviolet (UV) with the Atmospheric Imaging Assembly (AIA) imager on board the Solar Dynamic Observatory (SDO).
Aims. The aim of the paper is to relate the photospheric motions below the filament and its environment to the eruption of the filament.
Methods. An analysis of the photospheric motions using Solar Dynamic Observatory Helioseismic and Magnetic Imager (SDO/HMI) continuum images with the new version of the coherent structure tracking (CST) algorithm developed to track granules, as well as large-scale photospheric flows, has been performed. Following velocity vectors, corks migrate towards converging areas.
Results. The supergranule pattern is clearly visible outside the filament channel but difficult to detect inside because the modulus of the vector velocity is reduced in the filament channel, mainly in the magnetized areas. The horizontal photospheric flows are strong on the west side of the filament channel and oriented towards the filament. The ends of the filament sections are found in areas of concentration of corks. Whirled flows are found locally around the feet.
Conclusions. The strong horizontal flows with an opposite direction to the differential rotation create strong shear and convergence along the magnetic polarity inversion line (PIL) in the filament channel. The filament has been destabilized by the converging flows, which initiate an ascent of the middle section of the filament until the filament reaches the critical height of the torus instability inducing, consequently, the eruption. The n decay index indicated an altitude of 60 Mm for the critical height. It is conjectured that the convergence along the PIL is due to the large-scale size cells of convection that transport the magnetic field to their borders.
Key words: Sun: filaments / prominences / Sun: photosphere
The movies associated to Figs. 1, 2, 4 and 5 are available at https://www.aanda.org.
© ESO 2018
1. Introduction
The physical conditions leading to filament eruptions and coronal mass ejections (CMEs) have been recently reviewed by Schmieder et al. (2013). They are based on the existence of flux ropes in the corona submitted to increasing electric currents. The decrease of the magnetic tension that restrains the flux rope favors its eruption. Twist motions, shears, and canceling flux are observed or involved in the magnetohydrodynamics MHD models as producing instabilities of the filament flux rope. Commonly it is found that eruptions are due to converging flows and canceling polarities along the polarity inversion lines (PIL). A filament consists of a magnetic structure aligned along the PIL with untwisted magnetic field lines anchored at both ends in opposite magnetic photospheric polarities of the network as linear force-free field extrapolations suggest (Aulanier & Démoulin 1998; Aulanier & Schmieder 2002). The cool filament material is suspended in the dips. Along an Hα filament or prominence, footpoints or legs are observed with an equidistant distance of about 30 Mm, which we also call barbs when observed on the disk. A filament barb is directly related to a parasitic polarity close to the PIL (Aulanier & Démoulin 1998; Martin et al. 1994). If the parasitic polarity is canceled by merging with opposite sign polarities, the barb disappears and the filament is no longer anchored in place. Material may be falling along the field lines, which transforms the dips to loops as was suggested in an MHD simulation (Schmieder et al. 2006). This explains the counter streaming often observed in rising filaments before eruptions (Zirker et al. 1998; Schmieder et al. 2008).
In MHD models, it is shown that canceling flux, twist, or rotation of sunspots induce a strong shear along the PIL. Progressively a flux rope is formed by reconnection of low magnetic field lines in a region of convergence (van Ballegooijen & Martens 1989; Aulanier et al. 2010). The reconnection is driven by the diffusion of the photospheric magnetic field. It allows the flux rope to rise progressively in the upper atmosphere. When the flux rope reaches a critical height, a torus-type instability starts accelerating the rise of the flux rope and leading to eruption (van Tend & Kuperus 1978; Kliem & Török 2006). The critical altitude is estimated by the computation of the decay index (n = −dlnB/dlnz), which represents the decay of the background magnetic field in the vertical direction. The critical height is defined as the height where the decay index reaches a critical value slightly dependent on the model of the flux rope used. For a thin straight current channel the critical value of the decay index is equal to unit (van Tend & Kuperus 1978; Filippov & Den 2001).
Török & Kliem (2007) found that for a thin circular current channel a torus instability of the flux rope is initiated when n is larger than 1.5. From an observational point of view, Filippov & Den (2001) and Filippov & Zagnetko (2008) performed a statistical study of quiescent prominences and concluded that prominences were more prone to erupt when they approach a height where the decay index of the external field was close to 1. Zuccarello et al. (2016) computed the decay index for different MHD configuration models and derived a possible range for the critical decay index between 1.3 and 1.5 when the apex of the flux rope is considered, otherwise it can be lower. The difference referred to in these works between the values of the critical index 1 and 1.4 can be considered unimportant, while the decay index in regions with filaments changes from ≪ 1 to 3. The exact value of the critical decay index depends on the shape of the flux-rope axis and the properties of the flux-rope cross-section as was shown by Démoulin & Aulanier (2010). In the model simulations of Zuccarello et al. (2016), the axis of the flux rope is more curved, which is more appropriate for three-dimensional (3D) modeling. However, even in this model the topmost part of the distribution of magnetic dips, where filament material sits, is located at n = 1.1 when the instability starts. Since in the works of Filippov and colleagues the relationship between decay indexes and filament top heights was studied, there is no discrepancy with the results of Zuccarello et al. (2016).
Surface motion on long-term as well on short-term scales is important for the formation and the stability of filaments. Photospheric motions are due to the coupling of the convection with the diffusion of the magnetic field at the solar surface. It is important to be able to quantify the horizontal flows in the photosphere and follow their evolution.
A few analyses of surface motions have been done with high cadence and high spatial resolution. Mainly the local correlation tracking (LCT) method is applied to magnetic field polarities in order to explain eruptions or flares with Michelson Doppler Imager (MDI) data, with a spatial resolution of 1.96 arcsec, and only recently with Helioseismic and Magnetic Imager (HMI) data, with a resolution of 0.5 arcsec (Ahn et al. 2010; Zhou et al. 2006; Green et al. 2011; Liu et al. 2012). The techniques of correlation tracking (LCT; November & Simon 1988; Chae & Sakurai 2008) have been developed in two ways: either by tracing the surface flows with the differential affine velocity estimator for vector magnetograms (DAVE4VM; Schuck 2008) or by tracking coherent structures (CST) on various scales (spatial and temporal; Roudier et al. 2012).
Roudier et al. (2008) studied the flow pattern in a filament channel in a bipolar region using LCT, from MDI magnetograms and Dopplergrams supergranular flow pattern. It was found that the flow field changes significantly during the eruption phase, measuring an increase of the shear below the point where the eruption starts and a decrease after it (Roudier et al. 2008). They found a pattern in the large scale horizontal flows at the solar surface that interacts with the differential rotation. The local photospheric flows were also measured with a higher spatial resolution (0.5 arcsec) in the filament channel during its eruption phase using Transition Region and Coronal Explorer (TRACE) 1600 Å to show the coupling between convection and magnetic field (Rondi et al. 2007). Apparently along the PIL both parasitic and normal polarities were continuously swept by the diverging supergranular flow and canceled, which leads to the filament eruption. Schmieder et al. (2014) computed the proper horizontal flows in a filament channel using the CST method and conjectured that the shear flows were responsible for the counterstreaming along the filament axis and finally for the eruption. Flux cancellation and magnetic shear were already proposed to play a major role in the filament eruption based on observations (Martin 1986; Martin 1998; Litvinenko & Martin 1999; Hermans & Martin 1986) and models (Priest 1987; van Ballegooijen & Martens 1989; Priest et al. 1994). Still now, similar measurements are done using magnetograms showing the disappearance on a single bipole by flux cancellation as responsible for a filament eruption (Wang & Muglach 2013; Yardley et al. 2016). The action of large-scale flows on the filament (formation and eruption) has not yet been quantified. In the present study, we take advantage of the CST method applied to the full Sun data (SDO/HMI) to get flow fields over the whole of the Sun’s surface at high and low spatial and temporal resolutions. In particular the CST method allows us to get large-scale flows such as solar differential rotation, meridian circulation, and supergranulation flows (Chian et al. 2014; Roudier et al. 2018). Previous works use LCT and many other methods for detecting approaching bipoles (see the benchmark paper of Welsch et al. 2007), but no detection of large-scale inflow or shear has been done. Therefore, the measurement of large-scale flow such as differential rotation or supergranular flow is fundamental with regards to this question of filament eruption.
We propose in this paper to correlate the horizontal photospheric flows, the Hα (see Movie 1), and the UV dynamics (see Movies 2 and 3) of the filament before its eruption. In Sect. 2 we describe the observations of the filament and its dynamics observed with space- and ground-based instruments. We pay particular attention to the ends or anchorages of the filament in the network and the progressive lift up of the main body of the filament until it reaches the critical height for developing the torus instability. In Sect. 3 the new CST method that allows us to compute the horizontal photospheric flows in the filament channel and its environment is described. The results are presented in Sect. 4 and discussed in the conclusion from the perspective of the coupling between magnetic field and convection (Sect. 5).
 |
Fig. 1. Huge filament starting to lift up observed on January 26, 2016 at 16:30 UT with SDO/AIA (before the eruption; left panel): combined image of three filters (211 Å, 193 Å, 171 Å; right panel) HMI longitudinal magnetogram showing the magnetic channel of the filament. A, B, C, D are the places in the network where the magnetic field lines supporting the filament are anchored. The filament consists of two sections or two filaments (filament one: AB and filament two: CD). The temporal evolution of the left panel showing the huge filament eruption is available as a movie online. |
 |
Fig. 2. Filament eruption is related to two CMEs observed by the Large Angle and Spectrometric Coronagraph Experiment (LASCO/SOHO) coronagraph. The temporal evolution is available as a movie online. |
2. Eruption of the filament
2.1. Overview
A long filament elongated over more than one solar radius (500 arcsec, between latitude −10° and −4°) was located in the southern part of the NOAA AR12486 active region. This filament has three different sections: a narrow filament inside the active region between strong polarities on both sides of the PIL, a very wide part in the middle (300 Mm), and again relatively narrow patches in the east. In fact the two first sections belong to one filament (Filament one) and the third section to a second filament (Filament two). These filaments have been observed in multi-wavelengths by the Atmospheric Imaging Assembly (AIA, Lemen et al. 2012) aboard the SDO satellite (SDO, Pesnell et al. 2012). The spatial resolution of AIA is 0.6 arcsec per pixel, and the cadence 12 s. From the ground the filament was followed by GONG with a cadence of one minute and a pixel of 1 arcsec, and by CLIMSO with a cadence of 1 minute and a pixel of 1.2 arcsec (see Movie 1). In addition, the magnetic field and the continuum were continuously observed with the HMI, (Scherrer et al. 2012; Schou et al. 2012). The evolution and the eruption of this long filament have been reported by Zheng et al. (2017) and Luna et al. (2017). On January 26 around 17:00 UT, the middle part of the filament started to rise (Fig. 1). Long loops in Filament one with untwisted threads representing magnetic field lines are observed in AIA 211, 171, 193 Å. These loops are anchored in positive magnetic polarities of plage regions that we designate as “A” in the top right of the Fig. 1. The second end is located in negative magnetic polarities that we called “B”, far away from the PIL.
The southern patched section of the filament (Filament two) appears to be anchored below the central thick part of the filament in C and its other end, D, is in the far east. The section AB (Filament one) is lifted up and it erupted at 17:13 UT with untwisted loops leading to the eruption of Filament two as well (Fig. 1, left panel). Material returned and fell in the eastern part of the filament. The loops anchored in B slipped along the magnetic field area towards the south-east during the eruption allowing the two filaments to merge (see Movies 2 and 3 attached to Fig. 1). The material went back and forth exhibiting an oscillation motion for several hours with a period of 60 min (Luna et al. 2017). The magnetic structure of this filament has been modeled using the flux inserting method and the above description of the different anchorages of each filament end is confirmed (see the Fig. 16 in Luna et al. (2017). A flare is observed around 1700 UT close to the filament eruption (Luna et al. 2017). This eruption is related to the two Coronal Mass Ejections (CMEs) observed by the Large Angle and Spectrometric Coronagraph Experiment (LASCO) coronagraph (see Fig. 2 and Movie 4).
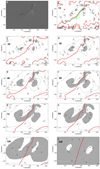 |
Fig. 3. Panel a: HMI magnetogram of the selected area taken on January 26, 2016 at 16:30 UT. Panels b–j: distribution of the decay index n of the potential magnetic field at different heights above the area shown in first figure (panel a). Areas where n > 1 are tinted with gray, while regions with n < 1 are white. Red lines indicate the position of the polarity inversion lines (PIL). The green contour shows the position of the filament taken from the co-aligned BBSO Hα filtergram. The torus instability in the zone of the PIL occurs for decay-index values n > 1. |
 |
Fig. 4. Prominence and polarity inversion lines. Top left panel: BBSO Hα filtergram, bottom left panel: AIA 193 Å image of the prominence. The field of view is the same as in Fig. 3a. Right panels: corresponding images with polarity inversion lines (PIL) at different heights (12 Mm–84 Mm) overplotted. The temporal evolution of the filament eruption as seen in the (extreme) UV by AIA in 1600 Å, 304 Å, 171 Å, and 131 Å is available as a movie online. |
 |
Fig. 5. Top row left: Hα filament at 16:42 UT. The yellow crosses define the polarity inversion line (PIL); the temporal evolution is available online Movie 1. Top right: HMI magnetogram (averaged over 24 h). Middle row left: vr radial velocity (averaged over 24 h), white and dark indicating outgoing (positive) and ingoing (negative) radial velocity respectively, with the amplitude between 0.15 and −0.2 km s−1. Middle row right: vh horizontal velocity (averaged over 24 h). Bottom row left: divergence (averaged over 24 h) with a mean value of (3.6 × 10−4s−1) for positive divergence (white). Bottom row right: vorticity (averaged over 24 h), with a mean value of (3.35 × 10−4s−1), for positive vorticity (white). We note that the divergence is reduced in the filament channel around the PIL between A, B, and C (gray areas) and is nearly co-spatial with black areas in the vh modulus panel. In this map, we see the supergranular pattern except in the regions of black areas, which correspond to strong magnetic field regions. For the four bottom panels, the granules were followed during 24 h to increase the contrast. The temporal evolution of the filament in α is available as a movie online. The movie shows the full disk, and the data in the movie before 16:00 UT are from CLIMSO and after 16:00 UT from GONG. CLIMSO and GONG data are centered and resized to the same solar diameter. The images in the movie are de-rotated from the solar differential rotation, allowing us to follow the filament evolution at the same location. |
2.2. Torus instability
The traditional (logical) cause of the eruption of this filament is a torus instability or a critical loss of equilibrium (nearly the same). The catastrophic loss of equilibrium and the torus instability are different formulations of the onset of solar eruptions. However, Démoulin & Aulanier (2010) and Kliem et al. (2014) showed their equivalency. They are based on the same force balance for equilibrium and produce an onset of eruption at the same point. This is consistent with the estimations of the filament height and the decay-index distribution as we show in the following.
The decay index characterizes the scale of the magnetic field. It is low in the eastern part of our filament region because the photospheric fields are more or less evenly spread over large areas. In the western part, there are strong compact sources of the field. They create a smaller scale field in the corona that cannot be shaded by weaker larger scale fields. Cold plasma falls along both legs of an erupting prominence. It is observed in many events. The falling dark features are observed in the eastern leg of the prominence too. When some parts of the erupting loop become nearly vertical, there is competition between the motion of the rising loop and falling back along the vertical flux tubes.
The distribution of the decay index shows that the instability zone (n > 1) appears at the position of the filament above 60 Mm (Fig. 3). The instability zone spreads from the north-western side of the polarity inversion line (PIL) to the south-eastern side. We might expect that the north-western side of the filament is able to begin erupting first. However, this part of the filament is narrow and presumably low. The left panels of Fig. 4 show PILs at different heights superposed on filtergrams containing the filament (the projection of the magnetic neutral surface on the filtergrams). The narrow north-western section of the filament is very close to low PILs (12–24 Mm). The opposite end of the filament is also rather narrow and low, while the middle section is widest and touches the PIL at the level of about 60 Mm. This is the height where we expect the instability of the flux rope, which started just before 17:00 UT. A day before, the filament was less wide in the middle section and less high. This is in agreement with the observations showing that the middle part of the filament started to rise first.
However, a question concerning the cause of the eruption is still open: How does the system come to the instability threshold? It is commonly explained by photospheric changes: horizontal motions, vertical motions (magnetic flux emergence and submergence; Schmieder et al. 2013), canceling flux (Martin et al. 1985), or magnetic flux tube interactions (Schmieder et al. 2004; Joshi et al. 2016). Therefore we need to quantify the photospheric motions by analyzing the photospheric flows in the filament channel and its environment. For that we used the CST method.
 |
Fig. 6. Flows (computed between 09 and 16 UT) below the filament with three different spatial resolutions: over an Hα image (16:42 UT) (left panels), over a divergence map (right panels). From top to bottom the spatial window used is 22 000 km, 44 000 km, and 66 000 km, respectively. The granules have been followed during seven hours. The velocity is ±0.400, 0.250 km s−1, and 0.180 km s−1 for the smaller to the largest windows. A, B, and C are the ends of the filament (see Fig. 1). The amplitudes of the velocity are reduced in the filament channel and are large on the west side of the filament. We see three lanes of strong flows from the west. The filament in Hα is indicated by pink contours in the right panels. |
3. Photospheric horizontal motions and structures
3.1. CST method
The representative description of solar plasma evolution is obtained by using the Coherent Structure Tracking (CST; Rieutord et al. 2007; Roudier et al. 2012) code to follow the proper motions of solar granules in full-disk SDO/HMI data. The CST allows us to obtain flow field from covering the spatial scales from 2.5 Mm up to nearly 85% of the solar radius. CST is a granule tracking technique that produces estimates of the field direction and amplitude (Rieutord et al. 2007). In CST, the code identifies individual features (granules) and tracks these individual features coherently throughout the image sequence. The resulting velocity field is thus discontinuous and the differentiable extension is estimated based on multi-resolution analysis. HMI provides uninterrupted observations of the full disk of the Sun. This gives a unique opportunity to map surface flows on various spatial and temporal scales. We selected the HMI continuum intensity data on 26 January 2016. In order to be suitable for the CST application, the data series of the HMI intensitygrams must first be prepared. All frames of the sequence are aligned such that the center of the solar disk lies exactly on the same pixel in charge-coupled device (CCD) coordinates, and the radius of the solar disk is exactly the same for all the frames. The reference values for the position of the disk center and the radius are obtained from the first image (obtained on 26 January 2016 at 00:00:45 UT). The original intensity and Doppler images are de-rotated by removing the differential rotation determined from 24 h of Doppler data on 26 January 2016 (see next section).
3.2. Differential rotation
It is well known that the profile
of the differential rotation of the Sun differs by method, data set, and time. However, there have been rotational
profiles published in the literature that are considered a reference. A class of the reference profiles was obtained by a spectroscopic method (Paternò 2010), where historically the profile of, for example, Howard & Harvey (1970) is often used.
Following the spectroscopic technique, we obtained our reference solar differential rotation profile from the corrected sequence of Dopplergrams described above. That rotational profile is computed through the relation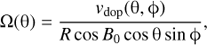 (1)
(1)
where θ and ϕ are the latitude and longitude respectively, and R the solar radius expressed in km. The profile inferred from an average 24 h of observation is fitted by the polynomial in sin(θ), in microrad s−1, by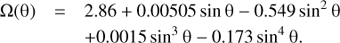 (2)
(2)
The fit was performed in longitudes ±80° and the corresponding equatorial rotation velocity is 1.990 ± 0.002 km s−1.
3.3. Horizontal velocity
Then we perform the granulation tracking using the CST code (Roudier et al. 2012) to reconstruct the projection of the photospheric velocity field (vx,vy) in the plane of the sky (CCD plane; Rincon et al. 2017). The application of CST to the data series of the prepared HMI intensitygrams leads to a sequence of horizontal velocity field maps in the projection to a sky plane with a temporal resolution of 30 min and a spatial resolution of 2.5 Mm (3ʺ̣5), which is the full-disk velocity map with a size of 586 × 586 pixel2. We further removed the (x, y) velocity signal associated with the motions of the SDO satellite and Earth’s orbital displacements from the CST velocity maps following the procedure described by Rincon et al. (2017).
3.4. Dopplergrams
The dopplergrams provide a key piece of information to reconstruct the full vector field. The HMI convention is that the line-of-sight (l.o.s.) velocity signal vz is taken to be positive when the flow is away from the observer, so that the out-of-plane toward the observer is vdop = −vz. (see Fig. 10 in Roudier et al. 2013). The processing steps of the Dopplergrams were to remove Doppler shift associated with the proper motion of satellite and Earth displacement from the raw Doppler signal (see Rincon et al. 2017). Then in the Doppler data we corrected a polynomial radial limbshift function adjusted from ring averages of two hours of data. Since the 586 × 586 pixel2 velocity maps obtained from the CST are limited to an effective resolution of 2.5 Mm, we then down-sampled the 4096 × 4096 pixel2 Dopplergrams to the size of CST maps. The down-sampled Doppler images were finally averaged over 30 min to match the temporal sampling of the CST-derived flow maps.
3.5. Velocity vector
The horizontal flow (vx,vy) measured in the plane-of-the-sky coordinates by the CST code together with vdop obtained from corresponding Dopplergrams may be transformed to spherical velocity components (vr, vϕ, vθ). For a detailed description of the transformation, we refer to Roudier et al. (2013), namely to Chap. 5 and Fig. 10. The vϕ (longitudinal velocity) and vθ (latitudinal velocity) are used in the following as the components of the horizontal velocity vector (vh) in the different plots.
4. Results
4.1. Modulus of the horizontal flow velocity and divergence
Using the HMI continuum, we applied the CST method to follow the granules over seven to 24 h with different spatial windows. We computed the modulus of vϕ and vθ, always positive, to see the global surface motions: 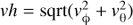 .
.
The vector amplitude depends on the spatial window that we choose and the time that we use for following the granules. The divergence and the vorticity of the velocity are computed for two different times of integration before the eruption (seven and 24 h). Long integration increases the contrast of the images. Figure 5 shows, in the middle the panels, the radial velocities vr and the modulus of the velocities (vh), and in the bottom panels the divergence (div(vϕ, vθ)) and the vorticity (vort(vϕ, vθ)) after following the granules during 24 h. We see in the divergence map some areas of gray uniform color among the small bubbles that represent the supergranules. The low divergence areas correspond to regions where the modulus of the vh velocity is reduced (dark areas in the vh velocity map). They are co-spatial with the magnetized areas of the network (top right panel). These dark areas of reduced vh are located in the large filament channel including the ends of the filament in A, B, and C. The vorticity field does not appear affected by the magnetized areas (Fig. 5, bottom right). The radial velocities, perpendicular to the solar surface, are found to be negative (downflow motions) where the magnetic field is present around the PIL (Fig. 5, middle right).
Figure 6 presents the map of the vector velocity: (right panels) overlying the divergence map and (left panels) overlying an Hα image for three different windows (from top to bottom: 22 000 km, 44 000 km, 66 000 km). The integration time is seven hours. We note three horizontal lines of higher velocities, which cross the filament channel when we use the largest window. However, we see that the velocities are always reduced in the filament channel and also in the divergence compared to both side areas of the filament channel. This behavior does not depend on the size of the chosen windows. Figure 7 presents the concentration of the corks (white lanes) after launching them uniformly seven hours before. Corks are diffused over the solar surface by the horizontal flows. They are concentrated over the network where the ends of the filament are anchored. Convergence lanes are in the vicinity of points A, B, and C (Fig. 7). The vh velocity modulus is found up to 0.400 km s−1, 0.250 km s−1 for narrow and middle size windows compared with 0.180 km s−1 for the largest windows. We measure downflows along the PIL (vr) around 0.100–0.200 km s−1) indicating that the magnetic field is well anchored in the deeper layers and probably stable.
 |
Fig. 7. Corks distribution after seven hours tracking (from 09 to 16 UT), visible as white lanes overlaid over the magnetic field (17:00 UT). B is in the middle of the field of view and corresponds to negative polarity (black), A is in the upper right corner in the positive polarity (white). C is in the white polarity. The filament in Hα is indicated by red contours. |
 |
Fig. 8. Horizontal velocities (computed between 09 and 16 UT) over an Hα image (16:42 UT). Yellow contours indicate the supergranules. The black arrows indicate flows going through the filament channel from the north towards the south in the eastern part or from west to east in the northern part, perpendicular to the filament axis. The red arrows indicate flows perpendicular to the filament with some whirls. The large west-east flows on the western side of the filament are stopped at the western edge of the filament channel. |
 |
Fig. 9. Horizontal flows (spherical velocity components (vϕ, vθ) computed between 9 and 16 UT including the differential rotation under the filament observed at 16:42 UT. The main flow is the solar rotation vector from right to left disrupted by other surface flows (mainly supergranules). The velocity is reduced on the western part of the filament compared to the eastern part. It indicates the presence of convergence along the filament PIL. |
4.2. Local horizontal flows
In Fig. 8 we have drawn the contours of a few supergranules and emphasized the large flows by arrows over the horizontal velocity flows obtained with a window of 44 000 km presented already in Fig. 6. The supergranular pattern is well observed in and outside the filament channel with no real changes of size. The black arrows represent flows that cross the filament channel. The red arrows represent the flows that are stopped at the border of the filament channel.
The velocity vector maps show large flows on the west side (right side) of the filament channel. They are stopped close to the channel and turned to the north (near points A, B, and C). Below the large extension of the filament, where the end of the south section of Filament two (point C) is anchored, high speed flows from a SW to NE direction meet with other flows coming from the NE. These flows stop in C. We could guess that they initiate vertical motions and could be the trigger for the rise of the filament that allows the filament to reach the altitude where the torus instability can operate. In the eastern part of the filament, the flow runs from north to south, crossing the filament channel. In B region, which corresponds to a strong network magnetic field, large flows converge in the region and push the magnetic field lines, which are sliding along the magnetized region. During the eruption (see Movie 2 of Fig. 1, left panel) Whirled flows are found locally around A, B, and C.
4.3. Differential rotation and shear flow
The velocity in the preceding sections has been measured on de-rotated data. In order to take into account the large flow undergone by the filament feet, we now add the solar differential rotation that was measured on the Doppler data (see Sect. 3.2). Figure 9 presents the horizontal flows (spherical velocity components (vϕ, vθ)) including the differential rotation. That plot shows the full motions on the solar surface, which are a combination of the solar rotation and other larger flows provided by the conjugation of all the supergranular flows. Stronger velocity amplitude is found close to the equator with a decrease at higher latitude. It shows strong flows from west to east reducing the differential rotation velocity in the central part of the filament (B and C) where the anchorages of the field lines of the flux rope are sustaining the filament. At point A, the velocity, mainly due to solar rotation, is found to be 1.82 km s−1. At point C, the velocity is measured at 1.53 km s−1 while at this latitude (31° south) that day, the average velocity is 1.63 km s−1. This difference increases the shearing experienced by the filament between points A and C. We also note, below point C at longitude 8° and latitude −37°, some larger velocities (1.48 km s−1), while solar rotation at that latitude is 1.35 km s−1. These velocities are located between Filament one and Filament two and are probably involved in the filament eruption. The PIL corresponding to the filament in the photosphere is submitted to strong convergence flows creating a strong shear flow.
5. Conclusion
We analyzed the dynamics of the photosphere below a long filament during 24 h on January 26, 2016 before its eruption. Counterstreamings along the filament before its eruption are observed in Hα, as well as moving brightenings in 304 Å along its spine during all this time period. The main results of the Coherent Structure Tracking (CST) analysis concerning the flows in the photosphere are the following:
-
Supergranules with diverging flow pattern have a similar size in and outside the filament channel but have a lower amplitude in the magnetized areas. In the same way, the modulus of the horizontal velocity is reduced in the filament channel, particularly in the magnetized region where the field lines of the flux rope of the filament are anchored (A, B, C).
-
The ends of the two filament sections (A, B, C) are between supergranules in regions of convergent flows nearly perpendicular to the axis of the filament.
-
Whirled flows are found locally around points A, B, and C.
-
Corks meet in magnetized areas (convergence areas) and consequently are associated to the filament ends.
-
Large zones of flows lie at the western border of the filament channel according to the analysis of large-scale coherent structures.
-
Strong flows from west to east reduce the differential rotation velocity in the central part of the filament where the anchorage of the field lines are in B and C. That difference in flows creates a stronger shear flow experienced by the filament feets.
Movies
Movie of Fig. 1 Access here
Movie of Fig. 2 Access here
Movie of Fig. 4 Access here
Movie of Fig. 5 Access here
Acknowledgments
The SDO data are courtesy of NASA and the SDO/HMI, SDO/AIA, and SOHO science team. The CLIMSO instrument and its operation are funded respectively by the Fiducial company and by French government funds through University Paul Sabatier and Centre National de la Recherche Scientifique (CNRS). This work utilizes data obtained by the Global Oscillation Network Group (GONG) program, managed by the National Solar Observatory, which is operated by AURA, Inc. under a cooperative agreement with the National Science Foundation. The data were acquired by instruments operated by the Big Bear Solar Observatory, High Altitude Observatory, Learmonth Solar Observatory, Udaipur Solar Observatory, Instituto de Astrofísica de Canarias, and Cerro Tololo Interamerican Observatory. This work was granted access to the HPC resources of CALMIP under the allocation 2011-[P1115]. This work was supported by the CNRS Programme National Soleil Terre. This work was inspired during discussions in the ISSI workshops organized by Nicolas Labrosse in Berne on Solving the prominence paradox. RC acknowledges the support from SERB/DST, New Delhi, Govt. of India project no. SERB/F/7455/2017-17. We thank the anonymous referee for his/her careful reading of our manuscript and his/her many insightful comments and suggestions.
References
- Ahn, K., Chae, J., Cao, W., & Goode, P. R. 2010, ApJ, 721, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Aulanier, G., & Démoulin, P. 1998, A&A, 329, 1125 [Google Scholar]
- Aulanier, G., & Schmieder, B. 2002, A&A, 386, 1106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aulanier, G., Török, T., Démoulin, P., & DeLuca, E. E. 2010, ApJ, 708, 314 [Google Scholar]
- Chae, J., & Sakurai, T. 2008, ApJ, 689, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Chian, A. C.-L., Rempel, E. L., Aulanier, G., et al. 2014, ApJ, 786, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., & Aulanier, G. 2010, ApJ, 718, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Filippov, B. P., & Den, O. G. 2001, J. Geophys. Res., 106, 25177 [NASA ADS] [CrossRef] [Google Scholar]
- Filippov, B., & Zagnetko, A. 2008, J. Atmos. Sol. Terr. Phys., 70, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., Kliem, B., & Wallace, A. J. 2011, A&A, 526, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hermans, L. M., & Martin, S. F. 1986, in NASA Conf. Pub., ed. A. I. Poland, 2442 [Google Scholar]
- Howard, R., & Harvey, J. 1970, Sol. Phys., 12, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, N. C., Filippov, B., Schmieder, B., et al. 2016, ApJ, 825, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Kliem, B., & Török, T. 2006, Phys. Rev. Lett., 96, 255002 [Google Scholar]
- Kliem, B., Lin, J., Forbes, T. G., Priest, E. R., & Török, T. 2014, ApJ, 789, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Litvinenko, Y. E., & Martin, S. F. 1999, Sol. Phys., 190, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Berger, T. E., & Low, B. C. 2012, ApJ, 745, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Su, Y., Schmieder, B., Chandra, R., & Kucera, T. A. 2017, ApJ, 850, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F. 1986, in NASA Conf. Pub., ed. A. I. Poland, 2442 [Google Scholar]
- Martin, S. F. 1998, ASP Conf. Ser., 150, 419 [Google Scholar]
- Martin, S. F., Livi, S. H. B., & Wang, J. 1985, Aust. J. Phys., 38, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, S. F., Bilimoria, R., & Tracadas, P. W. 1994, in Solar Surface Magnetism, eds. R. J. Rutten, & C. J. Schrijver, 303 [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Paternò, L. 2010, Ap&SS, 328, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Priest, E. R. 1987, in The Role of Fine-Scale Magnetic Fields on the Structure of the Solar Atmosphere, eds. E. H. Schröter, M. Vázquez, & A. A. Wyller, 297 [Google Scholar]
- Priest, E. R., Parnell, C. E., & Martin, S. F. 1994, ApJ, 427, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., Roudier, T., Roques, S., & Ducottet, C. 2007, A&A, 471, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rincon, F., Roudier, T., Schekochihin, A. A., & Rieutord, M. 2017, A&A, 599, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rondi, S., Roudier, T., Molodij, G., et al. 2007, A&A, 467, 1289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Švanda, M., Meunier, N., et al. 2008, A&A, 480, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Malherbe, J. M., et al. 2012, A&A, 540, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Prat, V., et al. 2013, A&A, 552, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Švanda, M., Ballot, J., Malherbe, J. M., & Rieutord, M. 2018, A&A, 611, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schmieder, B., Mein, N., Deng, Y., et al. 2004, Sol. Phys., 223, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Aulanier, G., Mein, P., & López Ariste, A. 2006, Sol. Phys., 238, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Bommier, V., Kitai, R., et al. 2008, Sol. Phys., 247, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Démoulin, P., & Aulanier, G. 2013, Adv. Space Res., 51, 1967 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Roudier, T., Mein, N., et al. 2014, A&A, 564, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schuck, P. W. 2008, ApJ, 683, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Török, T., & Kliem, B. 2007, Astron. Nachr., 328, 743 [NASA ADS] [CrossRef] [Google Scholar]
- van Ballegooijen, A. A., & Martens, P. C. H. 1989, ApJ, 343, 971 [Google Scholar]
- van Tend, W., & Kuperus, M. 1978, Sol. Phys., 59, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., & Muglach, K. 2013, ApJ, 763, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Welsch, B. T., Abbett, W. P., De Rosa, M. L., et al. 2007, ApJ, 670, 1434 [NASA ADS] [CrossRef] [Google Scholar]
- Yardley, S. L., Green, L. M., Williams, D. R., et al. 2016, ApJ, 827, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, R., Zhang, Q., Chen, Y., et al. 2017, ApJ, 836, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, G., Wang, Y., & Wang, J. 2006, Adv. Space Res., 38, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Zirker, J. B., Engvold, O., & Martin, S. F. 1998, Nature, 396, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Zuccarello, F. P., Aulanier, G., & Gilchrist, S. A. 2016, ApJ, 821, L23 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Huge filament starting to lift up observed on January 26, 2016 at 16:30 UT with SDO/AIA (before the eruption; left panel): combined image of three filters (211 Å, 193 Å, 171 Å; right panel) HMI longitudinal magnetogram showing the magnetic channel of the filament. A, B, C, D are the places in the network where the magnetic field lines supporting the filament are anchored. The filament consists of two sections or two filaments (filament one: AB and filament two: CD). The temporal evolution of the left panel showing the huge filament eruption is available as a movie online. |
| In the text | |
 |
Fig. 2. Filament eruption is related to two CMEs observed by the Large Angle and Spectrometric Coronagraph Experiment (LASCO/SOHO) coronagraph. The temporal evolution is available as a movie online. |
| In the text | |
 |
Fig. 3. Panel a: HMI magnetogram of the selected area taken on January 26, 2016 at 16:30 UT. Panels b–j: distribution of the decay index n of the potential magnetic field at different heights above the area shown in first figure (panel a). Areas where n > 1 are tinted with gray, while regions with n < 1 are white. Red lines indicate the position of the polarity inversion lines (PIL). The green contour shows the position of the filament taken from the co-aligned BBSO Hα filtergram. The torus instability in the zone of the PIL occurs for decay-index values n > 1. |
| In the text | |
 |
Fig. 4. Prominence and polarity inversion lines. Top left panel: BBSO Hα filtergram, bottom left panel: AIA 193 Å image of the prominence. The field of view is the same as in Fig. 3a. Right panels: corresponding images with polarity inversion lines (PIL) at different heights (12 Mm–84 Mm) overplotted. The temporal evolution of the filament eruption as seen in the (extreme) UV by AIA in 1600 Å, 304 Å, 171 Å, and 131 Å is available as a movie online. |
| In the text | |
 |
Fig. 5. Top row left: Hα filament at 16:42 UT. The yellow crosses define the polarity inversion line (PIL); the temporal evolution is available online Movie 1. Top right: HMI magnetogram (averaged over 24 h). Middle row left: vr radial velocity (averaged over 24 h), white and dark indicating outgoing (positive) and ingoing (negative) radial velocity respectively, with the amplitude between 0.15 and −0.2 km s−1. Middle row right: vh horizontal velocity (averaged over 24 h). Bottom row left: divergence (averaged over 24 h) with a mean value of (3.6 × 10−4s−1) for positive divergence (white). Bottom row right: vorticity (averaged over 24 h), with a mean value of (3.35 × 10−4s−1), for positive vorticity (white). We note that the divergence is reduced in the filament channel around the PIL between A, B, and C (gray areas) and is nearly co-spatial with black areas in the vh modulus panel. In this map, we see the supergranular pattern except in the regions of black areas, which correspond to strong magnetic field regions. For the four bottom panels, the granules were followed during 24 h to increase the contrast. The temporal evolution of the filament in α is available as a movie online. The movie shows the full disk, and the data in the movie before 16:00 UT are from CLIMSO and after 16:00 UT from GONG. CLIMSO and GONG data are centered and resized to the same solar diameter. The images in the movie are de-rotated from the solar differential rotation, allowing us to follow the filament evolution at the same location. |
| In the text | |
 |
Fig. 6. Flows (computed between 09 and 16 UT) below the filament with three different spatial resolutions: over an Hα image (16:42 UT) (left panels), over a divergence map (right panels). From top to bottom the spatial window used is 22 000 km, 44 000 km, and 66 000 km, respectively. The granules have been followed during seven hours. The velocity is ±0.400, 0.250 km s−1, and 0.180 km s−1 for the smaller to the largest windows. A, B, and C are the ends of the filament (see Fig. 1). The amplitudes of the velocity are reduced in the filament channel and are large on the west side of the filament. We see three lanes of strong flows from the west. The filament in Hα is indicated by pink contours in the right panels. |
| In the text | |
 |
Fig. 7. Corks distribution after seven hours tracking (from 09 to 16 UT), visible as white lanes overlaid over the magnetic field (17:00 UT). B is in the middle of the field of view and corresponds to negative polarity (black), A is in the upper right corner in the positive polarity (white). C is in the white polarity. The filament in Hα is indicated by red contours. |
| In the text | |
 |
Fig. 8. Horizontal velocities (computed between 09 and 16 UT) over an Hα image (16:42 UT). Yellow contours indicate the supergranules. The black arrows indicate flows going through the filament channel from the north towards the south in the eastern part or from west to east in the northern part, perpendicular to the filament axis. The red arrows indicate flows perpendicular to the filament with some whirls. The large west-east flows on the western side of the filament are stopped at the western edge of the filament channel. |
| In the text | |
 |
Fig. 9. Horizontal flows (spherical velocity components (vϕ, vθ) computed between 9 and 16 UT including the differential rotation under the filament observed at 16:42 UT. The main flow is the solar rotation vector from right to left disrupted by other surface flows (mainly supergranules). The velocity is reduced on the western part of the filament compared to the eastern part. It indicates the presence of convergence along the filament PIL. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


