| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201832890 | |
| Published online | 19 October 2018 | |
Optical polarisation variability of radio-loud narrow-line Seyfert 1 galaxies⋆
Search for long rotations of the polarisation plane
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: eangelakis@mpifr-bonn.mpg.de
2
Owens Valley Radio Observatory, California Institute of Technology, Pasadena, CA 91125, USA
3
Department of Physics and Institute of Theoretical & Computational Physics, University of Crete, 710 03 Heraklion, Greece
4
Center for Research and Exploration in Space Science, NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
5
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
6
Department of Physics, School of Science, Tokyo Institute of Technology, 2-12-1 Ohokayama, Meguro, Tokyo 152-8551, Japan
7
Istituto di Astrofisica e Planetologia Spaziali Via Fosso del Cavaliere 100, 00133 Rome, Italy
Received:
23
February
2018
Accepted:
5
July
2018
Context. Narrow-line Seyfert 1 galaxies (NLSy1s) constitute the active galactic nuclei subclass associated with systematically lower black hole masses. A few radio-loud NLSy1s have been detected in MeV-GeV energy bands by Fermi, and evidence that blazar-like jets are operating also in radio-loud NLSy1s, has been accumulated.
Aims. We wish to quantify the temporal behaviour of the optical polarisation, fraction, and angle for a selected sample of radio-loud NLSy1s. We also search for rotations of the polarisation plane similar to those commonly observed in blazars.
Methods. We have conducted R-band optical linear polarisation monitoring of a sample of ten radio-loud NLSy1 galaxies; five of them have previously been detected by Fermi. The dataset obtained with our pivoting instrument, the RoboPol polarimeter of the Skinakas observatory, has been complemented with observations from the KANATA, Perkins, and Steward observatories. When evidence for long rotations of the polarisation plane was found (at least three consecutive measurements covering at least 90°), we carried out numerical simulations to assess the probability that they are caused by intrinsically evolving electric vector position angles (EVPAs) instead of observational noise.
Results. Even our moderately sampled sources show clear indications of variability in both polarisation fraction and angle. For the four best-sampled objects in our sample we find multiple periods of significant polarisation angle variability. Several of these events qualify as long rotations. In the two best-sampled cases, namely J1505+0326 and J0324+3410, we find indications for three long rotations of the polarisation angle. We show that although noise can induce the observed behaviour, it is much more likely that the apparent rotation is indeed caused by intrinsic evolution of the EVPA. To our knowledge, this is the very first detection of such events in this class of sources. In the largest dataset (J0324+3410), we find that the EVPA concentrates around a direction that is at 49.3° to the 15 GHz radio jet, implying a projected magnetic field at an angle of 40.7° to that axis.
Conclusions. We assess the probability that pure measurement uncertainties are the reason behind the observed long rotations of the polarisation plane. We conclude that although this is not improbable, it is much more likely that intrinsic rotations are responsible for the observed phenomenology. We conclude, however, that much better sampled and larger datasets of larger source samples are necessary to constrain the physical mechanism(s) that generate long EVPA rotations in NLSy1s.
Key words: galaxies: active / galaxies: Seyfert / polarization / techniques: polarimetric / methods: numerical / methods: statistical
Table 2 and the polarisation curves shown in figures 1, 8, 12, 14 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/618/A92
© ESO 2018
1. Introduction
The term narrow-line Seyfert 1 galaxies (hereafter NLSy1s) signifies the subset of active galactic nuclei whose broad Balmer emission line has a width of FWHM(Hβ) ≲ 2000 km s−1, and which have weak forbidden lines with [O III]λ5007/Hβ < 3 (Osterbrock & Pogge 1985; Goodrich 1989; Zhou et al. 2006). They are thus associated with black hole masses in the range 106 – 108 M⊙ (e.g. Xu et al. 2012; Foschini et al. 2015), which is lower than those of powerful radio galaxies, which typically exceed 108 M⊙. Assuming these estimates to be free of biases (for claims of the opposite, see Marconi et al. 2008; Baldi et al. 2016), the detection of jet GeV emission (Abdo et al. 2009a,b; D’Ammando et al. 2012, 2015) and jet radio emission (e.g. Foschini et al. 2012; Angelakis et al. 2015; Lähteenmäki et al. 2017) from radio-loud (RL)1 NLSy1s challenges the current understanding of relativistic jet formation, in which powerful relativistic jets are preferentially found in elliptical galaxies with nuclear black hole masses beyond 108 M⊙ (for a review of the main arguments, see e.g. D’Ammando et al. 2017).
Angelakis et al. (2015) presented a comprehensive study of the radio emission of the four RL NLSy1s detected by Fermi. The dataset covered the band from 2.64 GHz to 142.33 GHz at ten frequencies and with a cadence of less than 30 days (for three of the four sources). Despite the generally lower fluxes, all sources showed the typical characteristics seen in blazars: intense variability accompanied by dramatic spectral evolution, which is indicative of shocks operating in a plasma outflow. We computed limiting values of the brightness temperature and inferred rather moderate Doppler factors, implying the presence of mildly relativistic jets. The computed jet powers appeared comparable to the least energetic blazars, the BL Lac objects. In conclusion, the sources showed all the typical characteristics of blazars, only scaled to lower intensities. Fuhrmann et al. (2016) focused on the dynamics of the 15 GHz jet of 1H 0323+342. Our analysis revealed superluminal components that are indicative of a relativistic jet, from which we inferred a viewing angle smaller than 9°, which confirmed the “aligned jet” scenario.
We currently focus on the optical polarisation of RL NLSy1s. Eggen (2012) and Eggen et al. (2013), among the first studies on the subject, reported that PMNJ0948+0022 showed significant and variable polarisation in optical bands. The same source was observed by Itoh et al. (2013), who found minute timescale optical polarisation variability. During this “pulse”, the polarisation exceeded 30%, while interestingly, the polarisation angle, that is, the electric vector position angle (EVPA), appeared to be unchanged. The authors interpreted their findings as evidence of synchrotron emission radiated from a compact region of highly ordered magnetic field. In the case of J0849+5108, on the other hand, Maune et al. (2014) observed rapid intra-night variability in polarisation degree and angle during a major broadband outburst event that lasted for roughly five days. More recently, Itoh et al. (2014) studied 1H 0323+342. They reported that the EVPA remained roughly parallel to the jet orientation, implying a magnetic field transverse to the jet axis.
Long rotations of the optical polarisation plane have been found in blazars (e.g. Kikuchi et al. 1988; Marscher et al. 2008, 2010; Abdo et al. 2010; Blinov et al. 2016a). Models that have been put forth to interpret the observations include physical rotation of emission elements on a helical trajectory (Marscher et al. 2008), propagation in large-scale bent jet (Abdo et al. 2010), turbulent plasma processes resulting in random walks (Marscher 2014), or light travel-time effects within an axisymmetric emission region (Zhang et al. 2015). Interestingly, it has been argued that these physical processes are likely associated with increased episodic gamma-ray activity (Blinov et al. 2018).
Beyond the potential of using polarisation monitoring to probe the physical processes at the emission site, the variability of the EVPA in particular can further our understanding of the conditions present during the high-energy jet emission production. In this context, we wish to (a) quantify the variability of the R-band optical polarisation fraction and angle for a selected sample of RL NLSy1 galaxies, (b) examine whether long rotations of the polarisation plane occur in RL NLSy1s, (c) parametrise these rotations and examine their association with the high-energy activity, and (d) ultimately understand the physical mechanisms producing them.
Here we present a study of a sample of ten RL NLSy1s; five of them have been detected by Fermi (cf. Sect. 2 and Table 1). When the datasets allowed, we studied the variability of both polarisation parameters and searched for EVPA rotation candidates. For the two best-sampled cases, we assesed the probability of these events being driven by intrinsic EVPA variability rather than observational noise. This distinction was accomplished by conducting exhaustive simulations. In the following, we emphasise both our findings and the method for assessing the probability itself. In these two cases we indeed find evidence that the rotations are intrinsic to each source. This is the first time that such events are reported for RL NLSy1s.
List of sources in our sample and their relevant parameters.
2. Source sample and dataset
The selection of our sample has been based mostly on the radio loudness and observability of the sources from the Skinakas telescope (i.e. optical magnitude and position). It includes five of the eight sources that have been reported to radiate significant emission in the MeV-GeV energy range (Abdo et al. 2009a,b; D’Ammando et al. 2012, 2015; Yao et al. 2015; Liao et al. 2015). It also includes another five RL sources, which together with the first five, make up a total of ten targets. All the sources with at least one data point from our monitoring are listed in Table 2. Median values and ranges of the polarisation parameters for all the sources discussed here are shown in Table 3.
Integrated polarisation characteristics.
2.1. RoboPol dataset
The RoboPol2 dataset is the basis for this study. The instrument is mounted on the 1.3m telescope of the Skinakas observatory (Papamastorakis 2007) and has been monitoring our sample in the R band. All the details of the measurement techniques and the instrument characteristics are discussed in King et al. (2014) and Angelakis et al. (2016), where post-measurement quality criteria are discussed in depth.
2.2. KANATA dataset
The KANATA observations were conducted with the 1.5m telescope of Higashi-Hiroshima Observatory. The polarimetry was performed with the HOWPol polarimeter (Kawabata et al. 2008). The observing cycle includes successive exposures at four position angles of a half-wave plate at 0, 45, 22.5, and 67.5°. The instrumental polarisation (peaking at ∼4%) was modelled and removed before further analysis. The residual uncertainties are estimated from large numbers of unpolarised standard stars and are smaller than 0.5%.
2.3. Perkins dataset
The Perkins dataset was obtained with a Johnson R filter using the PRISM instrument on the 1.8 m Perkins Telescope of the Lowell Observatory, which also includes a rotating half-wave plate polarimeter. The observing cycle included exposures with the half-wave plate at 0, 45, 90, and 135°. The averages of two to four such cycles were used as the final measurement. Instrumental offsets of the EVPA and percent polarisation (usually less than 1%) were determined by observing in-field polarised and unpolarised standard stars (Schmidt et al. 1992).
2.4. Steward Observatory dataset
The Steward Observatory data have also been obtained at R band, and they have been retrieved from the online archive3. The data acquisition and reduction is described in Smith et al. (2009).
3. Rice bias treatment
The functional dependence of the polarisation fraction p̂ on the normalised Stokes parameters q and u introduces a bias in its determination from repeated observations in the presence of noise. The effect becomes particularly important at low signal-to-noise ratios (S/Ns). Here we study the temporal behaviour of the EVPA from observations of already moderate sampling. To avoid unnecessary data loss that could be imposed by using only high-significance data, we used all available observations after we corrected for the Rice bias.
We assumed a fixed polarisation vector with real amplitude p0 at an angle of χ0, observed in the presence of experimental noise. Unless the S/N is high, none of the observed polarisation parameters p and χ determined from repeated observations will follow a normal distribution, even though χ will populate a distribution symmetric around χ0.
Gaussian noise causes q and u to be normally distributed about their true values q0 and u0, respectively, and with equal uncertainties σq = σu = σq0 = σu0, which are also equal to the uncertainties in p, σp. However, the probability of measuring polarisation in the range [p, p + dp] independent of polarisation angle (integrating over all angles), as was first demonstrated by Serkowski (1958), is given by the Rice distribution (Rice 1945),![$$ F(p\mid p_0 ){\rm d}p{\mkern 1mu} = {\mkern 1mu} {p \over {\sigma _p }}\exp \left[ { - {{p^2 {\mkern 1mu} + {\mkern 1mu} p_0^2 } \over {2\sigma _p^2 }}} \right]I_0 \left( {{{pp_0 } \over {\sigma _p^2 }}} \right){{{\rm d}p} \over {\sigma _p }}, $$](/articles/aa/full_html/2018/10/aa32890-18/aa32890-18-eq1.gif) (1)with I0 the zeroth-order modified Bessel function. The asymmetry of Eq. (1) with respect to p and p0 is the cause for the observed polarisation bias especially at low S/Ns. At high S/Ns, the Rice distribution tends to a normal distribution with a mean around the true value of polarisation p0 and a spread σp. Vinokur (1965), Simmons & Stewart (1985) and Naghizadeh-Khouei & Clarke (1993) have investigated the distributions of the observed amplitudes and the angles from repeated observation and thorough descriptions of the problem can be found in Wardle & Kronberg (1974), Vaillancourt (2006) and Clarke (2010).
(1)with I0 the zeroth-order modified Bessel function. The asymmetry of Eq. (1) with respect to p and p0 is the cause for the observed polarisation bias especially at low S/Ns. At high S/Ns, the Rice distribution tends to a normal distribution with a mean around the true value of polarisation p0 and a spread σp. Vinokur (1965), Simmons & Stewart (1985) and Naghizadeh-Khouei & Clarke (1993) have investigated the distributions of the observed amplitudes and the angles from repeated observation and thorough descriptions of the problem can be found in Wardle & Kronberg (1974), Vaillancourt (2006) and Clarke (2010).
We adopted the same approach as in Pavlidou et al. (2014) to determine the polarisation amplitude. As a best-guess of p0, we took the approximation of the maximum-likelihood estimator p̂ given by Vaillancourt (2006):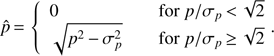 (2)The uncertainty in the debiased polarisation fraction is set to that of the observed p, σp as long as it is bounded at zero.
(2)The uncertainty in the debiased polarisation fraction is set to that of the observed p, σp as long as it is bounded at zero.
Because we are interested in the occurrence of long rotations of the polarisation plane, it is particularly important to assess the uncertainty in the polarisation angle even in cases of low S/N. To do this, we adopted the approach presented by Naghizadeh-Khouei & Clarke (1993). We solved their Eq. (4) for σθ with the S/N of the debiased value (p̂/σp). σθ was then taken as the uncertainty in the angle σχ.
4. Long rotations of the polarisation plane
In Sect. 3 we discussed the treatment of the polarisation fraction. Here we clarify the conventions and terminology used for the EVPA.
The EVPAs were initially computed from the observed q and u as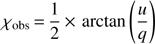 (3)and hence carry the inherent “n × π” ambiguity. For each (q, u) pair, we chose the solution of Eq. (3) for which the difference from the previous data point is smaller than 90°.
(3)and hence carry the inherent “n × π” ambiguity. For each (q, u) pair, we chose the solution of Eq. (3) for which the difference from the previous data point is smaller than 90°.
The resulting data points were then termed “adjusted” and are the values we use in the following discussion. Thus, the adjustment is made under the assumption of minimum variability between adjacent data points.
Phases of significant EVPA variability are defined as sequences of data points over which the adjusted polarisation angle χ changes significantly between consecutive observations 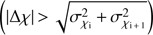 . Such periods are marked in the plots of Fig. 1 by dotted coloured lines. Lines of the same colour connect data points that show an overall trend in the same direction. Over such periods, insignificant changes in the opposite direction are allowed. This approach is described in detail in Kiehlmann et al. (2016). We defined such periods as long EVPA rotations (i.e. long rotations of the polarisation plane), when they
. Such periods are marked in the plots of Fig. 1 by dotted coloured lines. Lines of the same colour connect data points that show an overall trend in the same direction. Over such periods, insignificant changes in the opposite direction are allowed. This approach is described in detail in Kiehlmann et al. (2016). We defined such periods as long EVPA rotations (i.e. long rotations of the polarisation plane), when they
-
consisted of at least three data points, and
-
exceeded 90°.
Such periods are marked with solid coloured lines. A rotation was terminated when significant variability showed a change in sign.
 |
Fig. 1. J1505+0326: Debiased polarisation fraction p and adjusted EVPA (χ) as a function of time. The coloured lines mark periods of significant monotonous (within the uncertainties) EVPA evolution. Solid lines mark periods of long rotations (i.e. at least three sequential data points and an angle larger than 90°). Blue and orange connecting lines are used alternately for clarity. |
5. Analysis of the polarisation fraction and angle variability
Here, we study the temporal behaviour of the optical polarisation (fraction and angle) for sources whose datasets are large enough. We list all the RoboPol measurements of the remaining sources in Table 2. Median values and ranges of the polarisation parameters for all the sources discussed here are shown in Table 3.
5.1. J1505+0326
We start with the source J1505+0326 because (a) it shows clearly discernible events that facilitate implementing our approach, and (b) because our analysis shows that it is the best candidate to have undergone an intrinsic long rotation of the polarisation plane.
Figure 1 presents the RoboPol and Perkins observations of the optical linear polarisation parameters p̂ and χ.
The coloured lines there (dotted or solid) mark five periods of significant, continuous EVPA variability that we have detected. The absolute rotation angles of those events in order of occurrence are 77.9, 85.7, 82.2, 309.5, and 145.1°.
The first three events consist of only two consecutive data points (dotted lines). The last two, however, consist of at least three sequential data points and exceed the limit of 90°; they thus qualify as long-rotation candidates (solid lines).
The polarisation fraction spreads around a median of around 0.04 with a standard deviation ∼0.03 (Table 3). Figure 2 shows its cumulative distribution function for all the measurements (dotted black line), during phases of rotation (solid blue line), and during non-rotating phases (dashed blue line). The median, p̂, of the non-rotating phases alone is 0.022, while that over rotating phases is 0.043. Despite the difference, a two-sample Kolmogorov-Smirnov (KS) test, however, gave no indication for different parent populations, which in turn prohibits any conclusion about the behaviour of the polarisation during the rotations.
 |
Fig. 2. J1505+0326: Distribution of the debiased polarisation fraction p. The dot-dashed vertical line marks the median of the distribution. The blue dashed line shows the distribution of p̂ during the non-rotating phases and the solid line shows this during the rotating phases. The black dotted line corresponds to all the measurements. |
In the following we focus on the largest long rotation and asses the probability that it is driven by an intrinsically rotating polarisation plane.
5.1.1. J1505+0326: Long rotation
Figure 3 zooms in on the largest of the potential rotations (MJD 56790–56880). Its change in angle Δχ is –309.5°, and it lasts for approximately 83 days, yielding a mean rotation rate of –3.7 deg d−1. However, the combination of sparse sampling and large uncertainties in the angle makes the estimate of the direction of a rotation highly uncertain, which in turn makes the detection of the rotation itself uncertain.
 |
Fig. 3. J1505+0326: Apparent long rotation. With the exception of the left-most point, each angle measurement (solid symbols) is paired with its 180° conjugate (empty symbols). The upper values note EVPA differences (Δχ) and the lower values their uncertainties (σΔχ). Red marks highlight points in which the uncertainty (σΔχ in Δχ is so large that both solutions of Eq. (3), χ and χ + π, could be valid, making the direction of the rotation uncertain. |
As we discussed in Sect. 4, for each pair (q, u), we chose the solution of Eq. (3) for which the absolute difference, |Δχ|, from the previous angle is less than 90°. This condition controls the direction of the EVPA evolution. However, the uncertainty associated with each angle computation must also be accounted for when this condition is checked. If the sum of the absolute difference |Δχ| between two consecutive data points and the uncertainty in that difference σΔχ exceeds 90°, that is, 90° ≤ |Δχ| + σΔχ, the direction of the rotation becomes uncertain because both solutions of Eq. (3), χ and χ + π could be valid4.
With the exception of the earliest measurement (left-most point), each angle measurement (solid symbols) in Fig. 3 is paired with its 180° conjugate (empty symbols).
The critical steps with 90° ≤ |Δχ| + σΔχ are shown in red. Clearly, their number prevents us from reliably telling the direction that the EVPA follows, making the detection of the rotation uncertain.
The uncertainty in the detected rotation can also be shown by examining the effect of the uncertainties in q and u on the rotation angle. For simplicity, we assumed that the measured q and u are the means of the Gaussian distributed fractional Stokes parameters which is equivalent to saying that they describe the “real” intrinsic behaviour of the source.
We then added Gaussian noise based on their uncertainties, recalculated the EVPA curve, and compared its parameters with those of the observed one.
In Fig. 4 we show the distribution of rotation angles, Δχ, for a total of 104 simulated light curves. On the basis of our assumptions, the probability of detecting a rotation with an absolute angle |Δχ| within 1σ of the observed value is approximately 0.22. For larger rotations (|Δχ| ≥ 309.5°) the probability is around 0.081.
 |
Fig. 4. J1505+0326: Distribution of Δχ in simulated EVPA curves. The grey areas mark the 1, 2, and 3σ intervals, while the dashed line is the observed rotation of 309.5°. The most probable value (peak of the solid distribution) is at about −140 deg. |
From this we conclude that we cannot be confident about the intrinsic evolution of the EVPA. Even if we knew the intrinsic variability, the limited sampling and the measurement uncertainties would allow a vast range of possible EVPA curves that would result in varying changes of the EVPA (i.e. Δχ).
Subsequently, the previous test can determine the most likely observation, but it cannot tell us anything about the intrinsic variability. For example, although the bin with the highest probability appears at about –140°, this does not imply that the intrinsic EVPA rotation covers, most probably, 140°.
Finally, the data points in Fig. 3 could be aligned with roughly the same rotation rate if 180-degree shifts were chosen accordingly instead of obeying the convention of smallest change between consecutive measurements. This would result in a rotation 360° larger than shown in Fig. 3.
Clearly, the measurement of an intrinsic rotation is limited by the sparse sampling and the 180° ambiguity. In order to assess the reliability of the observed event, we took two steps.
-
We first estimated the probability that the measurement uncertainties induce a fake rotation in the absence of a real one, and
-
We then estimated the likelihood of an intrinsic rotation given the observed data.
The following simulations used exactly the same time sampling as the data and thus are affected by the 180-degree ambiguity in the same way.
5.1.2. Is the observed rotation an artefact of noise?
Here we assess the probability of the observational noise inducing the apparent rotation in the absence of an intrinsic rotation; that is, assuming dχintr/dt = 0 deg d–1.
For simplicity, we set q to the mean polarisation fraction in our simulations during the observed rotation 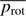 and u to zero, which results in χ = 0°. Subsequently, we added Gaussian noise 𝒩 to these values according to the estimated uncertainties:
and u to zero, which results in χ = 0°. Subsequently, we added Gaussian noise 𝒩 to these values according to the estimated uncertainties: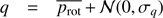 (4)
(4)
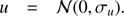 (5)N(0, σ) denotes that the noise is centred at 0. We ran 104 simulations. For each run the same algorithm as used for the observed data was used to identify full rotations. We define as “full rotation” in our simulations a rotation that consists of as many data points as the observed long rotations. The probability of finding a full rotation is
(5)N(0, σ) denotes that the noise is centred at 0. We ran 104 simulations. For each run the same algorithm as used for the observed data was used to identify full rotations. We define as “full rotation” in our simulations a rotation that consists of as many data points as the observed long rotations. The probability of finding a full rotation is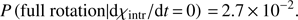 (6)We also find that
(6)We also find that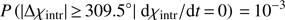 (7)and
(7)and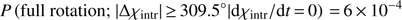 (8)In Fig. 5 we show the results of the simulations.
(8)In Fig. 5 we show the results of the simulations.
 |
Fig. 5. J1505+0326: Distribution of Δχ in the simulated EVPA curves where we assume the absence of intrinsic variability and the operation solely of noise. The dashed line is the observed rotation angle of 309.5°. |
This exercise shows that although it is not impossible that the observed event is merely an artefact of noise, it is fairly improbable. Thus, there must be intrinsic variability even if we cannot be sure of its exact nature.
5.1.3. Most probable parameters of the intrinsic event
Having shown that intrinsic variability seems much more likely to be driving the observed EVPA behaviour, we wish to estimate the most probable parameters of the potential intrinsic rotation.
Our analysis relies on the assumption of a constant intrinsic rotation rate dχintr/dt as well as a constant polarisation fraction(during the rotation). The rotation is simulated in q–u space by adding Gaussian noise to q and u.
We tested a range of rotation rates dχintr/dt = {–12., –11.5, …, +0.5} in units of deg d–1. For each rate we ran 25 × 103 simulations and computed the probability of
-
observing a full rotation, that is, over the entire period we simulated (i.e. including all data points); this is shown with blue squares in Fig. 6;

Fig. 6. J1505+0326: Probability distributions assuming an intrinsic EVPA rotation with a constant rate.
-
observing a full rotation in the same direction as in the data (in this case, negative derivative in EVPA); this is shown with red circles in Fig. 6;
-
observing a full rotation over an angle at least as large (in absolute terms) as the observed one (|Δχsim| ≥ |Δχobs| i.e. Δχsim ≤ Δχobs); this is shown with green triangles in Fig. 6;
-
observing a full rotation with an angle within the 1σ range of the rotation angle observed in the data (Δχobs – σΔχ,obs ≤ Δχsim ≤ Δχobs + σΔχ,obs); this is shown with orange diamonds in Fig. 6.
Figure 6 shows the resulting probability distributions. For a full rotation over angles at least as large as the observed one, the most likely intrinsic rotation rate is –8.9 ± 0.1 degd–1 with a corresponding probability of 0.11 (green diamonds). The second most probable rate is –3.9 ± 0.1 deg d–1 with a probability of 0.068. For a full rotation over an angle within 1σ of the observed one (orange diamonds), the most probable intrinsic rotation rate is found to be –3.1 ± 0.1 degd–1 with a probability of 0.129, while the second most likely one is –8.3 ± 0.1 deg d–1 with a probability of 0.119.
In Fig. 7 we show the distribution of rotation angle at the most likely intrinsic rotation rates based on the 1σ criterion (upper panel) and on the basis of the extreme-span criterion (lower panel, case 3 of Sect. 5.1.3). The observed rotation angle (dashed vertical line) is consistent with an intrinsically constant rotation.
 |
Fig. 7. J1505+0326: Distribution of rotation angles at the most likely intrinsic rotation rates based on the 1σ (upper panel) and the extreme-span criterion (lower panel, case 3 of Sect. 5.1.3). The dashed line marks the observed value, and the grey area shows the 1σ uncertainty. |
Considering all this and the conclusions of Sect. 5.1.2, we realise that it is much more likely that an intrinsic EVPA rotation (with the addition of pseudo-variability introduced by the uncertainties) is causing the observed event. Assuming a constant rotation rate also shows that the observed rotation is more likely the result of an intrinsic event than that of pure noise.
5.2. J0324+3410
In Fig. 8 we show the debiased polarisation fraction p̂ and angle χ as a function of time. The dataset includes RoboPol, KANATA, Perkins, and Steward observatory measurements. Both χ and p show significant variability.
 |
Fig. 8. J0324+3410: Polarisation variability curve. Upper panel: Debiased polarisation fraction over time. Lower panel: EVPA over time. The coloured lines mark periods of monotonous (within the uncertainties) EVPA evolution. |
The polarisation fraction p̂ spreads around a median of 0.012 with a standard deviation of 0.016 (see Fig. 9 and Table 3). The distribution of the EVPA confined in the [–90°, 90°] range is shown in Fig. 10. It is distributed rather narrowly around a median of –6.7° (with a standard deviation of 40.2°). This preferred direction is at an angle of 49.3° with the 15 GHz radio jet axis, which is found to be remarkably stable at a position angle of 124° (Fuhrmann et al. 2016).
 |
Fig. 9. J0324+3410: Distribution of the debiased polarisation fraction p. The dot-dashed vertical line marks the median of the distribution. The blue dashed line shows the distribution of p̂ during the non-rotating phases, and the solid line the distribution during the rotating phases. The black dotted line corresponds to all the measurements. |
 |
Fig. 10. J0324+3410: Distribution of the observed polarisation angles in the range [–90°, 90°]. |
In total, we detected 28 apparent rotations of the polarisation plane with rotation angle Δχ, ranging from approximately 19° to 402° (Fig. 11). Ten of these qualify as long rotations as they include at least three measurements and exceed 90°. In Fig. 9 we show the distribution of p̂ during phases of rotation and of non-rotation separately. In the former case, the median p̂ is 0.014 and in the latter, it is only 0.007. This indication that the polarisation fraction centres around different values in these two phases is not supported by a two-sample KS test.
 |
Fig. 11. J0324+3410: Distribution of rotation angles Δχ for all the apparent rotations. |
As in the case of 1505+0326, in the following we concentrate on the rotation candidates. Figure 12 focuses on the area where the two main potential rotations occur. The largest occurs at around MJD 56640.5–56672.4 over 402 ± 87°, corresponding to a mean rate of approximately 13 deg d–1. The second largest event occurs around MJD 56595.6–56633.5 with an angle of 349 ± 66° and a mean rate of 9 deg d–1.
 |
Fig. 12. J0324+3410: Zoom on the region of the largest potential rotations. |
5.1.1. Largest potential rotation
Figure 13 (upper panel) demonstrates the uncertainty associated with the evolution of the measured EVPA. All steps are critical, and we cannot be certain of the direction the EVPA intrinsically takes at any point in its evolution. All this makes the very detection of the rotation uncertain.
 |
Fig. 13. J0324+3410: Two main potential EVPA rotations: the largest (upper panel) and the second largest potential (lower panel). The uncertainty in the observed events caused by sparse sampling and large measurement uncertainties becomes apparent. |
Following the approach presented in Sect. 5.1.2, we examined whether the uncertainties in q and u alone can cause the observed rotation in the absence of an intrinsic rotation. We assumed again that the measured q and u are correct estimates of the means of the Gaussian-distributed Stokes parameters. After running 104 simulations, we find that the probability of finding one full rotation (passing over all points) is ∼2 × 10–2 (Eq. (6)), while that of finding a full rotation with absolute angle larger than observed is only 8 × 10–4 (Eq. (8)). Hence, although it is not impossible that the observed event is an artefact of noise while the EVPA remains intrinsically unchanged, it is rather unlikely. The associated probability is only ∼10–3. It is then possible that the EVPA indeed undergoes an intrinsic variability event.
To estimate the most probable parameters of the intrinsic EVPA variability, we assumed (as in Sect. 5.1.3) a constant intrinsic EVPA rotation rate and constancy of the polarisation fraction during the intrinsic rotation.
After 2.5 × 104 iterations, we find that the most likely intrinsic rotation rate for a full rotation with an angle at least as large as the observed one is 19 ± 0.5 deg d–1 (the probability is about 10–2). The most probable rotation rate for a full rotation with an angle within 1σ of the observed one is 10 ± 0.25 deg d–1 (the probability is about 0.033).
These probabilities are indeed low, but they are higher than those for the pure-noise scenario, indicating that intrinsic variability is more likely. Nevertheless, the low probability indicates that the simple assumption of a constant rotation rate is not likely in any case.
5.2.2. Second largest potential rotation
In the lower panel of Fig. 13 we show the second largest potential rotation. The probability that this event is the mere result of noise is as low as ∼10–3.
We repeated the analysis we presented earlier. After 2.5 × 104 simulated EVPA curves, we find that for a full rotation with an angle at least as large as the observed one, the most probable intrinsic rate is 10 ± 0.25 deg d–1 (P = 0.01). For a full rotation over an angle within 1σ of the observed one, the most probable rate is 9.5 ± 0.25 deg d–1 (P = 0.008).
These probabilities are low and comparable to those of the noise artefact hypothesis. An intrinsic rotation of constant rate is only marginally more likely than noise. A realistic scenario would be that the observed behaviour results from thecombination of intrinsic variability and observational noise. The noise, however, makes the observed rotation angle an inadequate indicator of the intrinsic behaviour. Hence, although there may be intrinsic variability, we cannot recover it due to the noisy data.
5.3. J0849+5108 and J0948+0022: Polarisation variability
In Fig. 14 we show the χ and p̂ datasets for J0849+5108 (upper panel) and J0948+0022 (lower panel) as a function of time. As shown in Fig. 14 and summarised in Table 3, the limited dataset does not allow sound quantification of the variability characteristics for either of the polarisation parameters. Intense variability is, nevertheless, clearly visible for both p̂ and χ.
 |
Fig. 14. Polarisation fraction and EVPA as a function of time for J0849+5108 (upper panel) and J0948+0022 (lower panel). The coloured lines mark periods of significant, monotonous (within the uncertainties) EVPA evolution. Dotted lines mark periods of significant evolution, while solid lines show periods of long rotations. |
For J0849+5108 the median 〈p̂〉 is around 0.1 with a standard deviation 0.078. Concerning the angle, the available dataset revealed a total of nine rotations, none of which exceeded 90°. Clearly, despite the clear signs of variability, the data sparseness prevents any understanding of the intrinsic nature of the variability.
In the case of J0948+0022, the slightly richer dataset (KANATA, Perkins, RoboPol, and Steward) reveals the occurrence of 11 rotations, 2 of which over angles beyond 90°. For the largest rotation, the EVPA changed by 268° (Fig. 15). Although this EVPA curve is fairly reliable, the steps χi – χi+1 between adjacent data points are very large and close to 90°, making this curve unsuitable for further analysis. Subsequently, nothing can be said as to whether the source underwent intrinsic EVPA rotations or not. For both sources, better sampled datasets are necessary. As in previous sections, in Fig. 16 we show the cumulative distribution function of p̂ separately for all measurements and for phases with rotation candidates. The median 〈p̂〉 is around 024 with a spread of 0.028. During phases of rotation, the median is 0.028, and over non-rotating phases, it drops to 0.016. As in previous cases, however, a two-sample KS test did not support the hypothesis of a different behaviour in the two activity states.
 |
Fig. 15. J0948+0022: Main potential EVPA rotation. The uncertainty in the observed events caused by sparse sampling and large uncertainties is obvious. |
 |
Fig. 16. J0948+0022: Distribution of the debiased polarisation fraction p̂. The dot-dashed vertical line marks the median of the distribution. The blue dashed line shows the distribution of p̂ during the non-rotating phases, and the solid line shows this during the rotating phases. The black dotted line corresponds to all the measurements. |
6. Discussion
As a result of the scarcity of high-cadence datasets, the current understanding of the optical polarisation variability of RL NLSy1s is incomplete and has been gained through selected case studies rather than a systematic population study. PMN J0948+0022, for example, was found to have variable optical polarisation (degree and angle, Eggen 2012; Eggen et al. 2013) even on minute timescales (Itoh et al. 2013). Itoh and collaborators reported that the polarisation briefly exceeded 30%, while the EVPA remained unchanged. Maune et al. (2014) reported that J0849+5108 also showed rapid intra-night variability both in degree of polarisation and angle. 1H 0323+342 was found by Itoh et al. (2014) to possess an EVPA that remained constantly parallel to the jet orientation. All these findings indicate how unknown the optical polarisation from such systems and its temporal behaviour remains. Our study attempts to overcome this barrier by examining a larger sample that would potentially allow us to extract general conclusions and further compare them with blazars. Larger systematic studies are, however, needed to further clarify (a) the confirmation of EVPA rotation events in RL NLSy1s and later a comparison of their parameters to those in blazars, (b) the behaviour of the polarisation degree during rotations of the EVPA (Blinov et al. 2016b), and (c) the association of rotation events with the GeV energy band activity (Blinov et al. 2018). Below we discuss some of the understanding we have gained with this work, which seems to indicate similarities to the behaviour seen in blazars.
The polarisation variability. As we have shown, the optical polarisation parameters of RL NLSy1 galaxies show clear signs of variability. Both the polarisation fraction p̂ and angle χ show phenomenologies similar to those seen in blazars, indicating similar processes in the two classes. It would be premature to conclude that the observed variability of RL NLSY1s implies turbulent processes until datasets with much higher cadence of a much larger sample of sources have been considered. The “blazars-like” character of these sources is established anew, however, and it is important for future studies to focus on examining the fundamental differences and similarities between the two classes.
The polarisation angle variability. The very detection of significant variability of the EVPA represents a particularly important finding. Earlier studies have indicated that in selected cases, the polarisation angle remained stable even during phases of intense polarisation fraction variability. This stability was interpreted as an indication for a high degree of magnetic field organisation in the regions where the radiation is produced. Our analysis establishes that the variability of the polarisation angle is common in all our sources with at least moderate sampling.
Preferred orientation of the polarisation plane. In the one case with a sufficiently large dataset (namely J0324+3410), we examined the distribution of the polarisation plane orientations. This was done by confining the polarisation orientations within the range [–90°, 90°]. The EVPA of this source is not oriented randomly. It instead shows a concentration (with some breadth) around a preferred direction of –6.7°. This orientation is at 49.3° to the position angle of the 15 GHz radio jet. The behaviour of preferential orientation of the EVPA resembles the high synchrotron peak frequency sources discussed by Angelakis et al. (2016, 2017).
Under the assumption that the optical emission is thin, this configuration implies a projected net magnetic field that is oriented at 40.7° to the radio jet5. This misalignment could be an indication of a combination of poloidal and toroidal field components. A more systematic approach, of course, would require the careful consideration of projection effects, the location and size of the emission region (potentially very different for the optical and radio emission), and the effects of relativistic aberration (Lyutikov et al. 2005). The variability accompanying the preferential orientation, on the other hand, could be understood in terms of an additional turbulent magnetic field component (e.g. Marscher 2014), a regular modulation of the emission region location (e.g. Marscher et al. 2008), and relativistic delays and projection effects (Zhang et al. 2014). Such configurations are not un-realistic. It should be noted, however, that the optical emission likely originates from a more compact region much closer to the jet base when interpreting these observations.
The detection of long polarisation plane rotations. In the general framework of polarisation variability, we have searched for long rotations of the polarisation plane and assessed the probability of such events being driven by intrinsic rotations of the polarisation plane. As we have shown, the events detected (even for the best sampled EVPA curves) have to be viewed with caution. The probability that they are the mere result of noise is not null. Our analysis clearly shows, however, that the probability of an intrinsic event driving the apparent behaviour is significantly higher, especially in the case of J1505+0326. We emphasise the importance of this analysis for the assessment of these probabilities, which we consider a part of our work equally as important as the detection of the rotation events themselves. Denser datasets of larger samples are necessary to prove that the occurrence of such events is a general characteristic of RL NLSy1s.
The fractional polarisation during rotations. As suggested by Blinov et al. (2016b), EVPA rotations in blazars seem to be associated with lower fractional polarisation in a statistical sense. This is a rather mild effect, but it may provide a diagnostic for the rotation mechanisms (Kiehlmann et al. 2017). Although our dataset is insufficient to test this, for the two largest datasets (J0324+3410 and J1505+0326), the polarisation tends to be marginally higher during the rotation phases. A two-sample KS tests did not provide any evidence that the distributions of p in the two activity phases are really different, however. This ambiguity will be studied in a future publication.
Physical interpretation. Clearly, the current dataset cannot shed light on the physical interpretation of the observed variability. We cannot tell whether it is the physical rotation of the emission element on a helical trajectory, the macroscopic properties of the jet, turbulent processes resulting in random walks, light travel-time effects, or any other process that causes EVPA rotations. Much longer and better sampled light curves of larger samples are necessary to prove that the apparent EVPA rotation is caused by intrinsic variability. Furthermore, studying whether EVPA variability is correlated with gamma-ray flaring might also provide insights into the physical processes driving these rotations. Blinov et al. (2018) reported that no EVPA rotations have been detected in blazars that are not associated with some activity in the Fermi energy bands. This is of fundamental importance to understanding the mechanism behind the long rotations of the polarisation plane. Investigating whether this is true for RL NLSy1s would be a natural next step.
7. Conclusions
We have conducted optical polarisation monitoring of a sample of ten RL NLSy1 galaxies, five of which have been found to radiate significant MeV-GeV emission. Our main goal was to quantify the variability of the two polarisation parameters, the debiased fraction p̂ and angle χ We further examined whether long rotations of the EVPA (similar to those found in blazars), are present. Our main conclusions are listed below.
-
All cases with adequately large datasets for both p̂ and χ show significant variability.
-
For the four GeV emitting sources in our sample that also had dense and long enough datasets, we find significant variability in the EVPA. For the remaining sources, either the sparseness of the datasets or the noise do not allow such studies.
-
In the case J0324+3410, we find that the EVPA spreads around a preferred orientation that is at an angle of 49.3° to the 15 GHz radio jet. Hence the projected magnetic field is at an angle of 40.7 to the jet axis.
-
In two of those cases, namely J1505+0326 and J0324+3410, we have found evidence for the presence of intrinsic EVPA rotations. Careful numerical simulations have been conducted to assess the probability that these events are driven by intrinsic variability.
-
For the three largest apparent rotations, we have assessed the likeliness that the observed rotations are the result of pure observational noise in the absence of an intrinsic event. We showed that although measurement uncertainties may indeed induce such behaviours, it is rather unlikely. It appears much more likely that the observed variability is indeed driven by intrinsic rotation at a constant rate.
-
For the two main candidate events, we estimated the most probable parameters for the intrinsic rotation on the basis of the constant rate assumption. We conclude that a linear trend of the intrinsic rotation is more likely than a non-varying EVPA. Most likely, however, a more complex situation appears more realistic. Relaxing this condition would make the probability of an intrinsic event causing the observed rotation even higher.
-
For the best-sampled cases, we examined the behaviour of the polarisation fraction during rotation and non-rotation periods. A two-sample KS tests indicates no significant difference between them.
-
Our analyses show that more observations are clearly needed for further concluding on all the topics discussed here. Although there is evidence for long rotations of the optical polarisation plane, higher cadence data of larger samples are needed.
The radio loudness R is defined as the ratio of the 6 cm flux to the optical flux at 4400 Å (Kellermann et al. 1989).
Acknowledgments
The authors wish to thank the anonymous referee for the very careful examination of the manuscript and the constructive comments, S. Komossa for selecting the non-Fermi-detected RL NLSy1s of our sample based on the criteria given in Table 1, the internal MPIfR referee N. MacDonald for the careful multiple reading of the manuscript and the detailed comments, V. Karamanavis for the project planing, discussions, and comments on the manuscript, and V. Pavlidou for the discussions and comments as well as the support to the Skinakas observing proposal, and Dr. J. Maune for acquisition of a large portion of the Perkins data. The RoboPol project is a collaboration between Caltech in the USA, MPIfR in Germany, the Toruń Centre for Astronomy in Poland, the University of Crete/FORTH in Greece, and IUCAA in India. Data acquired with the Perkins telescope was funded by the PEGA RPE grant at Georgia State University. Data from the Steward Observatory spectropolarimetric monitoring project were used. This program is supported by Fermi Guest Investigator grants NNX08AW56G, NNX09AU10G, NNX12AO93G, and NNX15AU81G.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 699, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 707, L142 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, Nature, 463, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Angelakis, E., Fuhrmann, L., Marchili, N., et al. 2015, A&A, 575, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Angelakis, E., Hovatta, T., Blinov, D., et al. 2016, MNRAS, 463, 3365 [NASA ADS] [CrossRef] [Google Scholar]
- Angelakis, E., Blinov, D., Bottcher, M., et al. 2017, ArXiv e-prints [arXiv:1711.4824] [Google Scholar]
- Baldi, R. D., Capetti, A., Robinson, A., Laor, A., &Behar, E. 2016, MNRAS, 458, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Blinov, D., Pavlidou, V., Papadakis, I., et al. 2016a, MNRAS, 462, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Blinov, D., Pavlidou, V., Papadakis, I. E., et al. 2016b, MNRAS, 457, 2252 [NASA ADS] [CrossRef] [Google Scholar]
- Blinov, D., Pavlidou, V., Papadakis, I., et al. 2018, MNRAS, 474, 1296 [NASA ADS] [CrossRef] [Google Scholar]
- Calderone, G., Ghisellini, G., Colpi, M., &Dotti, M. 2013, MNRAS, 431, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, D. 2010, Stellar Polarimetry [Google Scholar]
- D’Ammando, F., Orienti, M., Finke, J., et al. 2012, MNRAS, 426, 317 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ammando, F., Orienti, M., Larsson, J., &Giroletti, M. 2015, MNRAS, 452, 520 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ammando, F., Acosta-Pulido, J. A., Capetti, A., et al. 2017, MNRAS, 469, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Doi, A., Oyama, T., Kono, Y., et al. 2016, PASJ, 68, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Eggen, J. R. 2012, in Am. Astron. Soc. Meet. Abstr., 219, 243.29 [NASA ADS] [Google Scholar]
- Eggen, J. R., Miller, H. R., &Maune, J. D. 2013, ApJ, 773, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L. 2011, in Narrow-Line Seyfert 1 Galaxies and their Place in the Universe [Google Scholar]
- Foschini, L., Angelakis, E., Fuhrmann, L., et al. 2012, A&A, 548, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foschini, L., Berton, M., Caccianiga, A., et al. 2015, A&A, 575, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, L., Karamanavis, V., Komossa, S., et al. 2016, Res. Astron.Astrophys., 16, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Goodrich, R. W. 1989, ApJ, 342, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, P. C., &Wild, V. 2010, MNRAS, 405, 2302 [NASA ADS] [Google Scholar]
- Itoh, R., Tanaka, Y. T., Fukazawa, Y., et al. 2013, ApJ, 775, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, R., Tanaka, Y. T., Akitaya, H., et al. 2014, PASJ, 66, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Kawabata, K. S., Nagae, O., Chiyonobu, S., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 70144L [CrossRef] [Google Scholar]
- Kellermann, K. I., Sramek, R., Schmidt, M., Shaffer, D. B., &Green, R. 1989, AJ, 98, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kiehlmann, S., Savolainen, T., Jorstad, S. G., et al. 2016, A&A, 592, C1 [CrossRef] [EDP Sciences] [Google Scholar]
- Kiehlmann, S., Blinov, D., Pearson, T. J., &Liodakis, I. 2017, MNRAS, 472, 3589 [NASA ADS] [CrossRef] [Google Scholar]
- Kikuchi, S., Mikami, Y., Inoue, M., Tabara, H., &Kato, T. 1988, A&A, 190, L8 [NASA ADS] [Google Scholar]
- King, O. G., Blinov, D., Ramaprakash, A. N., et al. 2014, MNRAS, 442, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Voges, W., Adorf, H.-M., et al. 2006a, ApJ, 639, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Voges, W., Xu, D., et al. 2006b, AJ, 132, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Xu, D., &Zensus, J. A. 2016, in Star Clusters and Black Holes in Galaxies across Cosmic Time, eds. Y. Meiron, S. Li, F.-K. Liu, &R. Spurzem, IAU Symp., 312, 63 [NASA ADS] [Google Scholar]
- Kynoch, D., Landt, H., Ward, M. J., et al. 2018, MNRAS, 475, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Lähteenmäki, A., Järvelä, E., Hovatta, T., et al. 2017, A&A, 603, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landt, H., Ward, M. J., Baloković, M., et al. 2017, MNRAS, 464, 2565 [NASA ADS] [CrossRef] [Google Scholar]
- Liao, N.-H., Liang, Y.-F., Weng, S.-S., Gu, M.-F., &Fan, Y.-Z. 2015, ArXiv e-prints [1510.05584] [Google Scholar]
- Lyutikov, M., Pariev, V. I., &Gabuzda, D. C. 2005, MNRAS, 360, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Axon, D. J., Maiolino, R., et al. 2008, ApJ, 678, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Larionov, V. M., et al. 2010, ApJ, 710, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Maune, J. D., Eggen, J. R., Miller, H. R., et al. 2014, ApJ, 794, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Naghizadeh-Khouei, J., &Clarke, D. 1993, A&A, 274, 968 [NASA ADS] [Google Scholar]
- Oh, K., Yi, S. K., Schawinski, K., et al. 2015, ApJS, 219, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., &Pogge, R. 1985, ApJ, 297, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S., &Stalin, C. S. 2016, ApJ, 820, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S., Rajput, B., Stalin, C. S., &Pandey, S. B. 2016, ApJ, 819, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Papamastorakis, Y. 2007, Ipparchos, 2, 14 [Google Scholar]
- Pavlidou, V., Angelakis, E., Myserlis, I., et al. 2014, MNRAS, 442, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, S. O. 1945, Bell Systems Tech. J., 24, 46 [CrossRef] [Google Scholar]
- Schmidt, G. D., Elston, R., &Lupie, O. L. 1992, AJ, 104, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Serkowski, K. 1958, Acta Astron., 8, 135 [NASA ADS] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Simmons, J. F. L., &Stewart, B. G. 1985, A&A, 142, 100 [NASA ADS] [Google Scholar]
- Smith, P. S., Montiel, E., Rightley, S., et al. 2009, Fermi Symposium, eConf Proceedings C091122, [arXiv:0912.3621] [Google Scholar]
- Vaillancourt, J. E. 2006, PASP, 118, 1340 [Google Scholar]
- Vinokur, M. 1965, Ann. Astrophys., 28, 412 [NASA ADS] [Google Scholar]
- Wang, F., Du, P., Hu, C., et al. 2016, ApJ, 824, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, J. F. C., &Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, D., Komossa, S., Zhou, H., et al. 2012, AJ, 143, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, S., Yuan, W., Zhou, H., et al. 2015, MNRAS, 454, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Zhou, H. Y., Komossa, S., et al. 2008, ApJ, 685, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Liu, B. F., Zhou, H., &Wang, T. G. 2010, ApJ, 723, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H., Chen, X., &Böttcher, M. 2014, ApJ, 789, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H., Chen, X., Böttcher, M., Guo, F., &Li, H. 2015, ApJ, 804, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H.-Y., Wang, T.-G., Dong, X.-B., Zhou, Y.-Y., &Li, C. 2003, ApJ, 584, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H.-Y., Wang, T.-G., Dong, X.-B., Li, C., &Zhang, X.-G. 2005, Chin. J.Astron. Astrophys., 5, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H., Wang, T., Yuan, W., et al. 2006, ApJS, 166, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H., Wang, T., Yuan, W., et al. 2007, ApJ, 658, L13 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. J1505+0326: Debiased polarisation fraction p and adjusted EVPA (χ) as a function of time. The coloured lines mark periods of significant monotonous (within the uncertainties) EVPA evolution. Solid lines mark periods of long rotations (i.e. at least three sequential data points and an angle larger than 90°). Blue and orange connecting lines are used alternately for clarity. |
| In the text | |
 |
Fig. 2. J1505+0326: Distribution of the debiased polarisation fraction p. The dot-dashed vertical line marks the median of the distribution. The blue dashed line shows the distribution of p̂ during the non-rotating phases and the solid line shows this during the rotating phases. The black dotted line corresponds to all the measurements. |
| In the text | |
 |
Fig. 3. J1505+0326: Apparent long rotation. With the exception of the left-most point, each angle measurement (solid symbols) is paired with its 180° conjugate (empty symbols). The upper values note EVPA differences (Δχ) and the lower values their uncertainties (σΔχ). Red marks highlight points in which the uncertainty (σΔχ in Δχ is so large that both solutions of Eq. (3), χ and χ + π, could be valid, making the direction of the rotation uncertain. |
| In the text | |
 |
Fig. 4. J1505+0326: Distribution of Δχ in simulated EVPA curves. The grey areas mark the 1, 2, and 3σ intervals, while the dashed line is the observed rotation of 309.5°. The most probable value (peak of the solid distribution) is at about −140 deg. |
| In the text | |
 |
Fig. 5. J1505+0326: Distribution of Δχ in the simulated EVPA curves where we assume the absence of intrinsic variability and the operation solely of noise. The dashed line is the observed rotation angle of 309.5°. |
| In the text | |
 |
Fig. 6. J1505+0326: Probability distributions assuming an intrinsic EVPA rotation with a constant rate. |
| In the text | |
 |
Fig. 7. J1505+0326: Distribution of rotation angles at the most likely intrinsic rotation rates based on the 1σ (upper panel) and the extreme-span criterion (lower panel, case 3 of Sect. 5.1.3). The dashed line marks the observed value, and the grey area shows the 1σ uncertainty. |
| In the text | |
 |
Fig. 8. J0324+3410: Polarisation variability curve. Upper panel: Debiased polarisation fraction over time. Lower panel: EVPA over time. The coloured lines mark periods of monotonous (within the uncertainties) EVPA evolution. |
| In the text | |
 |
Fig. 9. J0324+3410: Distribution of the debiased polarisation fraction p. The dot-dashed vertical line marks the median of the distribution. The blue dashed line shows the distribution of p̂ during the non-rotating phases, and the solid line the distribution during the rotating phases. The black dotted line corresponds to all the measurements. |
| In the text | |
 |
Fig. 10. J0324+3410: Distribution of the observed polarisation angles in the range [–90°, 90°]. |
| In the text | |
 |
Fig. 11. J0324+3410: Distribution of rotation angles Δχ for all the apparent rotations. |
| In the text | |
 |
Fig. 12. J0324+3410: Zoom on the region of the largest potential rotations. |
| In the text | |
 |
Fig. 13. J0324+3410: Two main potential EVPA rotations: the largest (upper panel) and the second largest potential (lower panel). The uncertainty in the observed events caused by sparse sampling and large measurement uncertainties becomes apparent. |
| In the text | |
 |
Fig. 14. Polarisation fraction and EVPA as a function of time for J0849+5108 (upper panel) and J0948+0022 (lower panel). The coloured lines mark periods of significant, monotonous (within the uncertainties) EVPA evolution. Dotted lines mark periods of significant evolution, while solid lines show periods of long rotations. |
| In the text | |
 |
Fig. 15. J0948+0022: Main potential EVPA rotation. The uncertainty in the observed events caused by sparse sampling and large uncertainties is obvious. |
| In the text | |
 |
Fig. 16. J0948+0022: Distribution of the debiased polarisation fraction p̂. The dot-dashed vertical line marks the median of the distribution. The blue dashed line shows the distribution of p̂ during the non-rotating phases, and the solid line shows this during the rotating phases. The black dotted line corresponds to all the measurements. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


