| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A172 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832625 | |
| Published online | 26 October 2018 | |
Fossil group origins
IX. Probing the formation of fossil galaxy groups with stellar population gradients of their central galaxies⋆,⋆⋆
1 Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, vicolo dell’Osservatorio 3, 35122 Padova, Italy
e-mail: enricomaria.corsini@unipd.it
2 INAF–Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 2, 35122 Padova, Italy
3 Instituto de Astronomía y Ciencias Planetarias, Universidad de Atacama, Copayapu 485, Copiapó, Chile
4 Dipartimento di Fisica–Sezione Astronomia, Università di Trieste, via Tiepolo 11, 34143 Trieste, Italy
5 INAF–Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
6 Institut de Recherche sur les Lois Fondamentales de l’Univers, Commissariat à l’Énergie Atomique, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
7 Instituto de Astrofísica de Canarias, calle Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
8 Departamento de Astrofísica, Universidad de La Laguna, Avenida Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Tenerife, Spain
9 Astronomy Department, University of Wisconsin, 475 Charter St., Madison, WI 53706, USA
10 Center for Computational Astrophysics, Flatiron Institute, 162 Fifth Avenue, New York, NY 10010, USA
11 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
Received:
12
January
2018
Accepted:
10
August
2018
Context. Fossil groups (FGs) are galaxy aggregates with an extended and luminous X-ray halo, which are dominated by a very massive early-type galaxy and lack of L∗ objects. FGs are indeed characterized by a large magnitude gap between their central and surrounding galaxies. This is explained by either speculating that FGs are failed groups that formed without bright satellite galaxies and did not suffer any major merger, or by suggesting that FGs are very old systems that had enough time to exhaust their bright satellite galaxies through multiple major mergers.
Aims. Since major mergers leave signatures in the stellar populations of the resulting galaxy, we study the stellar population parameters of the brightest central galaxies (BCGs) of FGs as a benchmark against which the formation and evolution scenarios of FGs can be compared.
Methods. We present long-slit spectroscopic observations along the major, minor, and diagonal axes of NGC 6482 and NGC 7556, which are the BCGs of two nearby FGs. The measurements include spatially resolved stellar kinematics and radial profiles of line-strength indices, which we converted into stellar population parameters using single stellar-population models.
Results. NGC 6482 and NGC 7556 are very massive (M∗ ≃ 1011.5 M⊙) and large (D25 ≃ 50 kpc) galaxies. They host a centrally concentrated stellar population, which is significantly younger and more metal rich than the rest of the galaxy. The age gradients of both galaxies are somewhat larger than those of the other FG BCGs studied so far, whereas their metallicity gradients are similarly negative and shallow. Moreover, they have negligible gradients of α-element abundance ratio.
Conclusions. The measured metallicity gradients are less steep than those predicted for massive galaxies that formed monolithically and evolved without experiencing any major merger. We conclude that the observed FGs formed through major mergers rather than being failed groups that lacked bright satellite galaxies from the beginning.
Key words: galaxies: elliptical and lenticular, cD / galaxies: formation / galaxies: individual: NGC 6482 / galaxies: individual: NGC 7556 / galaxies: kinematics and dynamics / galaxies: stellar content
Based on observations made with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias (IAC).
Full Tables A.1–A.3 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/618/A172
© ESO 2018
1. Introduction
Fossil groups (FGs) were first proposed by Ponman et al. (1994), when they found that the apparently isolated galaxy RX J1340.6+4018 was surrounded by an X-ray halo typical of a galaxy group. They suggested that this was a fossil relic of an old galaxy group that had enough time to merge all its bright satellite galaxies into the central one. In this scenario, FGs formed at high redshift (z > 1), with few subsequent accretions (D’Onghia et al. 2005). If these systems really exist today, they can offer a unique opportunity to directly study the formation processes that occurred several gigayears ago, thus shedding light on the assembly of massive halos in the early universe.
FGs are defined, from an observational point of view, as groups or clusters of galaxies dominated by a large early-type galaxy (ETG), in which the second-ranked member within half the virial radius is at least two magnitudes fainter in the r-band (Δm12 > 2, Jones et al. 2003). Moreover, an extended X-ray halo of at least LX > 1042 h50 erg s−1 must be detected in order to avoid the classification of large isolated galaxies as FGs. The lack of L∗ galaxies is thought to be the result of the cannibalism of the central galaxy. In fact, dynamical friction is the process responsible for the merging of galaxies and it is more effective when massive galaxies are involved. Furthermore, the relaxed dynamical status of RX J1340.6+4018 was considered an indicator of the old age of the system. The observational definition was slightly modified by Dariush et al. (2010), who proposed to use the gap in magnitude between the first and the fourth brightest galaxies (Δm14) as a reference. In particular, they suggested that Δm14 > 2.5 within half the virial radius was a more stable identification criterion than the Δm12 > 2 criterion proposed by Jones et al. (2003).
Several samples of FGs selected using the Δm12 or Δm14 criteria have been presented in the last decade thanks to the availability of new surveys (Khosroshahi et al. 2007; Santos et al. 2007; Voevodkin et al. 2010; Proctor et al. 2011; Harrison et al. 2012). As the number of FGs increased, their observational properties became clearer. In particular, many studies focused on the properties of the hot intracluster component (Khosroshahi et al. 2007, 2014; Proctor et al. 2011; Harrison et al. 2012; Girardi et al. 2014; Kundert et al. 2015) or on the properties of the satellite galaxy population (Khosroshahi et al. 2006, 2014; Mendes de Oliveira et al. 2006; Aguerri et al. 2011, 2018; Adami et al. 2012; Lieder et al. 2013; Zarattini et al. 2014, 2015, 2016).
At the same time, numerical simulations show that the magnitude gap alone is not a good indicator of the dynamical stage of a group or cluster (D’Onghia & Lake 2004; D’Onghia et al. 2005). von Benda-Beckmann et al. (2008) suggested that the fossil status is just a stage in the evolution of a system. This result has been recently confirmed by Kundert et al. (2017), who showed how the fossil status changes every 2−3 Gyr. Moreover, there are hints that FGs suffered the last major mergers more recently than non-FGs (Díaz-Giménez et al. 2008; Kundert et al. 2017). On the other hand, Gozaliasl et al. (2014) pointed out that there is a difference in the evolution of the faint end of the luminosity function (LF) in FGs and non-FGs. In particular, the faint end of the LF of FGs suffered no evolution after z ∼ 1, whereas non-FGs went through an intense evolution, as also confirmed by Kundert et al. (2017). They found that the main difference between FGs and non-FGs is the halo accretion history in the last few gigayears.
The formation and evolution of the brightest cluster galaxies (BCGs) has also been a main topic in the study of FGs. Indeed, BCGs are a fundamental component of a galaxy group or cluster. They are often located close to the X-ray center of the cluster (Jones & Forman 1984; Lin & Mohr 2004; Lauer et al. 2014), and they can be as luminous as 10L∗, where L∗ is the characteristic luminosity of the cluster LF (e.g., Schombert 1986. Their growth is expected to be driven by wet mergers if they formed at high redshift, whereas their formation at lower redshifts could be driven by dry mergers. This should leave an imprint on the stellar populations of BCGs, in particular in those residing in old and relaxed FGs. Indeed, Khosroshahi et al. (2006) found differences in the isophotal shapes of BCGs in FGs compatible with a formation at high redshift and via wet mergers. They found that the isophotes were more disky in FGs than in non-FGs. Although Méndez-Abreu et al. (2012) did not confirm such a difference, they demonstrated using the scaling relations of the BCGs that they assembled part of their mass at high redshift and via wet mergers. At the same time, they suggested that the majority of the mass was assembled at lower redshift via dry mergers. As a consequence, the hints about the relative importance of the different kinds of mergers in shaping FG BCGs appear to be quite controversial. However, the BCGs in FGs are amongst the most massive and luminous galaxies observed in the universe (Méndez-Abreu et al. 2012; Kundert et al. 2017) and this means that the merging process in FGs had to be particularly efficient.
The stellar populations of the BCGs could help in shedding light on the possible differences in the formation processes of FGs and non-FGs. La Barbera et al. (2009) found a striking similarity between the stellar population properties of FG BCGs and bright field galaxies indicating that they had similar star formation histories. This observational result is in agreement with subsequent findings obtained by Cui et al. (2011) from cosmological simulations and galaxy formation models. They showed that FG BCGs have similar properties to those in non-FGs in terms of age, metallicity, color, concentration, and total mass-to-light ratio. Results along these lines were also reported for compact (Proctor et al. 2004; Mendes de Oliveira et al. 2005) and large-gap groups (Trevisan et al. 2017), which are somehow related to FGs. According to Proctor et al. (2004) and Mendes de Oliveira et al. (2005), the majority of galaxies in compact groups, which are possible progenitors of FGs, are older than those in the field but have similar metallicities and α-element abundance ratios. However, the connection between compact groups and FGs is not straightforward because they usually follow different evolutionary tracks, as recently investigated by Farhang et al. (2017) with semi-analytic models of galaxy formation. Trevisan et al. (2017) compared the stellar populations of the first and second brightest group galaxies as a function of their magnitude gap using a complete sample of groups. The magnitude gap does not correlate with the age, metallicity, α-element abundance ratio, and star formation history. Although many large-gap groups with Δm12 > 2 are expected to be FGs, their true link has not yet been addressed.
All the previous studies investigated the integrated stellar population properties of BCGs in FGs, except for Eigenthaler & Zeilinger (2013) and Proctor et al. (2014). Eigenthaler & Zeilinger (2013) analyzed spatially resolved stellar populations in a sample of six BCGs in FGs: they concluded that FGs formed via the merging of the L∗ galaxies with the central one, excluding the monolithic collapse in which the magnitude gap would not be produced by evolutionary effect but would have been in place a priori. Proctor et al. (2014) performed a similar analysis on a sample of two FGs finding that, despite remarkable similarities in their morphology, photometric properties, and kinematics, the stellar populations of the two galaxies were clearly different. One shows a strong gradient all the way to the center, with signs of a burst of stellar formation located in the center of the galaxy and superimposed onto an old and extended population. On the contrary, the second galaxy of their sample showed a flat core-like structure in the metallicity gradient, but no age gradient.
This paper is part of the Fossil Group Origins (FOGO) project (Aguerri et al. 2011), whose aim was to study a large sample of FG candidates, spanning wide ranges in mass and redshift by using multi-wavelength observations. To date, the collaboration has published results on the properties of the BCGs (Méndez-Abreu et al. 2012; Zarattini et al. 2014), on their dark matter halos (Girardi et al. 2014; Kundert et al. 2015), on the galaxy population (Zarattini et al. 2015, 2016; Aguerri et al. 2018), and on the comparison between observations and current cosmological simulations (Kundert et al. 2017). Here, we focus our attention on the stellar populations of two BCGs in FGs, namely NGC 6482 and NGC 7556. They are interesting because there are only a few nearby FG BCGs that are sufficiently bright at radii larger than the effective radius to obtain in a reasonable amount of time the high signal-to-noise ratio spectra needed for measuring their stellar population gradients. We aim at increasing the number of FG BCGs for which age, metallicity, and α-element abundance ratio are known at the same level of detail as those of BCGs in non-FGs (e.g., Mehlert et al. 2003; Brough et al. 2007; Loubser & Sánchez-Blázquez 2012). A reliable comparison between the stellar populations of FG and non-FG BCGs is highly desirable, but not yet possible given the current small number statistics of FG BCGs.
The paper is organized as follows. We present the target galaxies in Sect. 2, and we describe the analysis of their photometric and spectroscopic data in Sects. 3 and 4, respectively. We derive the stellar population properties in Sect. 5. We discuss the results in Sect. 6 and give our conclusions in Sect. 7. We adopt H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7 as cosmological parameters all throughout the paper.
2. Sample selection
The selected galaxies, whose main properties are listed in Table 1, are the BCGs of two nearby FGs with X-ray observations.
Properties of the sample galaxies.
NGC 6482 is the BCG of MCXC J1751.7+2304, which is the closest known FG at z = 0.013. It is a non-cool core system with an X-ray luminosity LX = 1.0 × 1042 erg s−1, a virial mass M200 = 4.0 × 1012 M⊙, and a virial radius R200 = 310 kpc (Khosroshahi et al. 2004). The magnitude gap between the two brightest member galaxies is Δm12 = 2.19 ± 0.04 mag (Lieder et al. 2013).
NGC 7556 is the dominant galaxy of RXC J2315.7−0222 at a redshift of z = 0.025. This system is characterized by a cool core and it has an X-ray luminosity LX = 2.1 × 1043 erg s−1, a mass M500 = 5.4 × 1013 M⊙, and a radius R500 = 569 kpc (Démoclès et al. 2010). We derived its virial mass M200 = 7.4 × 1013 M⊙ and virial radius R200 = 859 kpc. RXC J2315.7−0222 is actually a bona fide FG, since its magnitude gap is Δm12 = 1.88±0.03 mag (Démoclès et al. 2010). Nevertheless, we decided to analyze it due to the paucity of nearby FGs.
3. Broad-band photometry
We need the effective radius of NGC 6482 and NGC 7556 to derive the central values and radial gradients of their stellar population parameters.
For NGC 6482 we adopted the structural parameters obtained by Lieder et al. (2013). They performed a deep R-band imaging of NGC 6482 with the Suprime camera mounted at the 8.2 m Subaru telescope and modeled the surface brightness distribution of the galaxy with a Sérsic law (see Eq. (1)). The parameters are reported in Table 2.
Structural parameters of the sample galaxies.
For NGC 7556 we retrieved the flux-calibrated r-band image available in the Data Release 12 of the Sloan Digital Sky Survey (SDSS-DR12, Alam et al. 2015) and analyzed it to obtain the structural parameters of the galaxy.
3.1. Image reduction
We measured the sky level to be subtracted from the SDSS r-band image of NGC 7556 following the procedure proposed by Pohlen & Trujillo (2006), as done in Morelli et al. (2016). We masked the stars, galaxies, and spurious sources in the neighborhood of the galaxy and measured its surface brightness radial profile with the ELLIPSE task in IRAF1. First, we fitted the galaxy isophotes with ellipses having the center, ellipticity, and position angle free to vary. Then, we repeated the isophotal fit, fixing the center we previously obtained for the inner ellipses and the ellipticity and position angle of the outer ones. We calculated the sky level by averaging the surface brightness measured at large radii where there is no light contribution from the galaxy. We used the IRAF task IMEXAMINE to measure the standard deviation of the background in the sky-subtracted images and to fit the stars of the field of view with a circular Moffat profile (Moffat 1969), which we adopted to model the point spread function (PSF). Finally, we trimmed the sky-subtracted image to reduce the computing time required to perform a reliable photometric decomposition and we ran ELLIPSE on the trimmed images to derive the radial profiles of surface brightness, ellipticity, and position angle to be used for the photometric decomposition. They are given in Table A.1.
3.2. Photometric decomposition
We performed the photometric decomposition of the sky-subtracted image of NGC 7556 by using the Galaxy Surface Photometry 2-Dimensional Decomposition algorithm (GASP2D, Méndez-Abreu et al. 2008, 2014).
GASP2D assumes that the observed surface brightness in each image pixel is expressed as the sum of analytical functions describing the light contribution of the structural components of the galaxy. Although classified as an early S0 galaxy (de Vaucouleurs et al. 1991), NGC 7556 shows a bright spheroidal component surrounded by a faint extended envelope rather than a disk. This envelope contributes a light excess at large radii over the de Vaucouleurs profile (de Vaucouleurs 1948) fitted to the surface brightness in the inner parts of the galaxy. Such an excess is typical for central dominant galaxies (cDs) in clusters (Schombert 1987). Therefore, we modeled the surface brightness of the spheroidal body of the galaxy with a Sérsic law (Sérsic 1968) and the surface brightness of the stellar envelope with an exponential law (Freeman 1970). Adopting a single Sérsic law did not provide a reliable fit of the galaxy surface brightness at all radii (see also Ascaso et al. 2011, and references therein).
For the spheroidal component, the surface brightness profile is
where re, Ie, and n are the effective radius, effective surface brightness, and shape parameter of the surface brightness profile, respectively, while bn = 0.868n − 0.142 (Caon et al. 1993) is a normalization coefficient. For the luminous envelope, the surface brightness profile is
where I0 and h are the central surface brightness and scalelength of the surface brightness profile, respectively. We assumed the isophotes of both the spheroid and envelope to be elliptical, centered onto the galaxy center, and with constant position angle PAsph and PAenv, and constant axial ratio qsph and qenv, respectively. We did not consider other components such as rings.
We obtained the best-fitting values of the structural parameters of the spheroid and envelope by weighting the surface brightness of the image pixels according to the variance of the total observed photon counts due to the contribution of both galaxy and sky. Moreover, GASP2D accounts for photon noise, charge-coupled device (CCD) gain and read-out noise, and image PSF. We show the photometric decomposition of NGC 7556 in Fig. 1 and give its structural parameters in Table 2. The surface brightness contribution of the spheroidal component is equal to the contribution from the surrounding luminous envelope at rse = 14.2 arcsec.
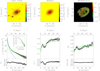 |
Fig. 1. Two-dimensional photometric decomposition of the r-band image of the NGC 7556. The upper panels (from left to right) show the map of the observed, modeled, and residual (observed−modeled) surface brightness distributions. The field of view is oriented with North up and East left. The black areas in the residual image correspond to pixels excluded from the fit. The lower panels (from left to right) show the ellipse-averaged radial profile of surface brightness, position angle, and ellipticity measured in the observed (black dots with gray error bars) and seeing-convolved modeled image (green solid line) and their corresponding difference. The intrinsic surface-brightness radial profiles of the best-fitting spheroid (blue dashed line) and halo (red dotted line) components are also shown in both linear and logarithmic scale for the distance to the center of the galaxy. |
We derived the errors on the structural parameters from Méndez-Abreu et al. (2017). They built a large set of images of mock galaxies of different morphological types and analyzed them as if they were real using GASP2D. We considered their results for the magnitude bin 12 < mr < 13 mag since NGC 7556 has mr = 12.32 (Alam et al. 2015). For Ie, re, n, I0, and h we adopted the mean and standard deviation of the relative errors of the mock galaxies as the systematic and statistical errors of the observed galaxies, respectively. For qsph, qenv, and PAsph, PAenv we adopted the mean and standard deviation of the absolute errors of the mock galaxies as the systematic and statistical errors σsyst and σstat of the observed galaxies, respectively. We computed the errors as 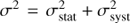 , with the systematic errors negligible compared to the statistical ones.
, with the systematic errors negligible compared to the statistical ones.
4. Long-slit spectroscopy
We measured the stellar and ionized-gas kinematics and line-strength indices of NGC 6482 and NGC 7556 from the long-slit spectra we obtained at the 10.4 m Gran Telescopio Canarias (GTC) telescope in La Palma (Spain).
4.1. Observations and spectra reduction
We carried out the spectroscopic observations at GTC in service mode between April and August 2013. The Optical System for Imaging and low-intermediate-Resolution Integrated Spectroscopy imager and spectrograph (OSIRIS, Cabrera-Lavers 2014) was used in combination with the R2500V grism and the 1.0 arcsec × 7.4 arcmin slit. The detector was a mosaic of two Marconi CCD42-82 chips with a gain and readout noise of 1.18 e− ADU−1 and 3.5 e− rms, respectively. The CCDs have 2048 × 2048 pixels of 15 × 15 μm2 and are separated by a gap of 37 pixels giving a field of view of 7.0 × 7.0 arcmin2 with a spatial scale of 0.127 arcsec pixel−1. We adopted an on-chip binning of 2 × 2 pixels to cover the wavelength range from about 4500 to about 6000 Å with a reciprocal dispersion of 1.60 Å pixel−1 and a spatial scale of 0.254 arcsec pixel−1. We derived the instrumental resolution by measuring the full width at half maximum (FWHM) of 12 unblended emission lines of a comparison arc-lamp spectrum after wavelength calibration. The mean FWHM of the arc-lamp lines from different observing nights was 2.62 ± 0.01 Å, corresponding to σinst = 64 km s−1 at 5185 Å.
We obtained the spectra along the major, minor, and a diagonal axis of both galaxies by centering the slit on their nucleus. We also observed several spectrophotometric standard stars to calibrate the flux of the galaxy spectra before measuring the line-strength indices. We took spectra of the comparison arc lamp during each observing night to perform the wavelength calibration. The seeing FWHM during the observations was computed by fitting a circular Gaussian to the guide star. It ranged between 0.5 and 1.2 arcsec with a median value of 1.0 arcsec. We give the integration times of the single exposures, total integration times for each observed axis, and slit position angle of the galaxy spectra in Table 3.
Log of the spectroscopic observations of the sample galaxies.
We reduced the spectra using standard tasks in IRAF, as done in Corsini et al. (2017). The reduction steps included the subtraction of bias, correction for internal and sky flat-field, trimming of the spectra, identification and removal of bad pixels and cosmic rays, correction for CCD misalignment, subtraction of the sky contribution, and wavelength and flux calibration. Finally, we aligned and coadded the spectra obtained for the same galaxy along the same axis using as reference the center of the galaxy light profile extracted along the spatial direction.
4.2. Stellar kinematics
We measured the stellar kinematics of both the galaxies with the Penalized Pixel Fitting (PPXF, Cappellari & Emsellem 2004) algorithm, which we adapted to deal with the OSIRIS spectra.
We rebinned each summed galaxy spectrum along the dispersion direction to a logarithmic scale. Then, we averaged the rebinned spectrum along the spatial direction to obtain a signalto-noise ratio S/N ≥ 70 per resolution element. The resulting spectra are characterized by a maximum S/N = 327 per resolution element in the innermost radial bin along the major axis of NGC 6482 and a minimum S/N = 72 per resolution element in the outermost radial bins along the major axis of NGC 7556. In Fig. 2 we show, as an example, the central rest-frame spectra extracted along the major axis of NGC 6482 and NGC 7556. For each radial bin, we convolved a linear combination of stellar spectra from the Medium Resolution Isaac Newton Telescope Library of Empirical Spectra (MILES, Sánchez-Blázquez et al. 2006a; Falcón-Barroso et al. 2011) with a line-of-sight velocity distribution (LOSVD) modeled as a truncated Gauss–Hermite series (Gerhard 1993; van der Marel & Franx 1993)
 |
Fig. 2. Central rest-frame spectra extracted along the major axis of NGC 6482 (top panel) and NGC 7556 (bottom panel). Relative fluxes have false zero points for viewing convenience. In each panel the best-fitting model (red line) is the sum of the spectra of the ionized-gas (blue line) and stellar component (green line). The latter is obtained convolving the synthetic templates with the best-fitting LOSVD and multiplying them by the best-fitting Legendre polynomials. The residuals (gray dots) are obtained by subtracting the model from the spectrum. The vertical lines mark the wavelength ranges excluded from the fit. |
where w = (νlos − ν)/σ to fit the galaxy spectrum by a χ2 minimization in pixel space. To this aim, we degraded the spectral resolution of the stellar spectra (FWHM = 2.54 Å, Beifiori et al. 2011) by convolving them with a Gaussian function in order to match the spectral resolution of the galaxy spectra. After rebinning the stellar spectra to a logarithmic scale along the dispersion direction, we de-reshifted them to rest frame and cropped their wavelength range to match the redshifted frame of the galaxy spectra. Moreover, we added a low-order multiplicative Legendre polynomial to correct for reddening and large-scale residuals of flat-fielding. We excluded from the fitting procedure the wavelength ranges with a spurious signal coming from the imperfect subtraction of cosmic rays and bright sky emission lines.
In this way, we determined the value of the mean velocity ν, velocity dispersion σ, and the third- and fourth-order LOSVD moments h3 and h4 of the stellar component along the different observed axes of both galaxies. We assumed the statistical errors on the stellar kinematic parameters to be the formal errors of the pPXF best fit after rescaling the minimum χ2 to achieve 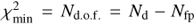 , with Nd.o.f., Nd, and Nfp the number of the degrees of freedom, data points, and fitting parameters, respectively (Press et al. 1992). We report the measured stellar kinematics of both galaxies in Table A.2.
, with Nd.o.f., Nd, and Nfp the number of the degrees of freedom, data points, and fitting parameters, respectively (Press et al. 1992). We report the measured stellar kinematics of both galaxies in Table A.2.
We fitted the emission lines present in the galaxy spectra with Gaussian functions using the Gas and Absorption Line Fitting (GANDALF, Sarzi et al. 2006) algorithm. The [O III]λλ4959, 5007 and [N I]λλ5198, 5200 emission doublets were nearly detected in the spectra of NGC 6482. Indeed, they have S/rN ≳ 3, where we estimated the residual noise rN as the standard deviation of the difference between the galaxy and best-fitting stellar spectrum. No emission line was detected in NGC 7556 (Fig. 2).
We show the folded kinematic profiles of NGC 6482 and NGC 7556 in Figs. B.1 and B.2. We plot the stellar velocities with respect to the galaxy center after subtracting the systemic velocity and without correcting for galaxy inclination, while the velocity dispersions are corrected for instrumental FWHM. There is a good agreement between the radial profiles of the kinematic parameters measured on either side of each axis and between the different axes of each galaxy.
Along the major axis, NGC 6482 is slowly rotating for r ≲ 3 arcsec, where the velocity linearly increases to ν ≃ 20 km s−1. Outwards, the velocity sharply rises to a maximum of ν ≃ 110 km s−1 at r ≃ 10 arcsec and then it stays constant out to the last measured radius. A velocity of ν ≃ 20 km s−1 is observed along the diagonal axis for 3 ≲ r ≲ 18 arcsec, while no rotation is measured along the minor axis. The velocity dispersion profile is almost flat at σ ≃ 320 km s−1 within the innermost 3 arcsec and it mildly declines to σ ≃ 250 km s−1 at larger radii. Constant h3 ≃ 0 and h4 ≃ 0.05 are measured. The measured kinematics is in agreement with the integral-field spectroscopic data by Raskutti et al. (2014), who investigated the kinematic properties of the stellar halos of a sample of massive ETGs (Greene et al. 2013).
NGC 7556 displays a velocity ν ≲ 20 km s−1 for r ≳ 5 arcsec along all the observed axes. No rotation is measured for r > rse confirming that the stellar envelope is not a rotating disk. The velocity dispersion drops from a central value of σ ≃ 270 km s−1 to about 250 km s−1 at r ≃ 2 arcsec and it remains nearly constant further out. The Gauss–Hermite coefficients are characterized by a flat radial profile of h3 ≃ 0 and a profile of h4 rising from about 0.05 to 0.1 within 2 arcsec and flattening outwards. The measured kinematics is consistent with that obtained with integral-field spectroscopy by Veale et al. (2017) for the MASSIVE Survey, which targets the most massive ETGs in the local universe (Ma et al. 2014).
4.3. Line-strength indices
We measured the Mg, Fe, and Hβ line-strength indices of the Lick/Cassegrain Image Dissector Scanner Spectrograph (Lick/IDS) system (Worthey et al. 1994) from the galaxy spectra rebinned in the dispersion and radial directions. Then, we computed the average iron index 〈Fe〉 = (Fe5270 + Fe5335)/2 (Gorgas et al. 1990) and the combined magnesium-iron index ![$${\left[ {{\rm{MgFe}}} \right]^\prime } = \sqrt {{\rm{Mg}}b\left( {{\rm{0}}.{\rm{72}} \times {\rm{F}}{{\rm{e}}_{{\rm{5270}}}}{\rm{ + 0}}.{\rm{28}} \times {\rm{F}}{{\rm{e}}_{{\rm{5335}}}}} \right)} $$](/articles/aa/full_html/2018/10/aa32625-18/aa32625-18-eq8.gif) (Thomas et al. 2003). We took into account the difference between our and Lick/IDS spectral resolutions by degrading our spectra to match the Lick/IDS resolution (FWHM = 8.6Å, Worthey & Ottaviani 1997) before measuring the line-strength indices. The offsets between our line-strength measurements and Lick/IDS line-strength values were smaller than the mean error of the differences and therefore we did not apply any offset correction to our line-strength measurements. We also corrected the line-strength indices for broadening due to the galaxy velocity dispersion as in Trager et al. (1998). The same method was adopted by Eigenthaler & Zeilinger (2013) to correct the line-strength indices of their FG BCGs.
(Thomas et al. 2003). We took into account the difference between our and Lick/IDS spectral resolutions by degrading our spectra to match the Lick/IDS resolution (FWHM = 8.6Å, Worthey & Ottaviani 1997) before measuring the line-strength indices. The offsets between our line-strength measurements and Lick/IDS line-strength values were smaller than the mean error of the differences and therefore we did not apply any offset correction to our line-strength measurements. We also corrected the line-strength indices for broadening due to the galaxy velocity dispersion as in Trager et al. (1998). The same method was adopted by Eigenthaler & Zeilinger (2013) to correct the line-strength indices of their FG BCGs.
We derived the errors on the line-strength indices by means of Monte Carlo simulations, as done in Morelli et al. (2015). At each radius, we generated a set of simulated galaxy spectra by adding photon, readout, and sky noise to the best-fitting stellar spectrum obtained from the kinematic analysis. We measured the line-strength indices in the simulated spectra as if they were real. We used the mean and standard deviation of the line-strength indices in the simulated spectra to estimate the systematic σsyst and statistical σstat errors of the measured indices, respectively. We computed the errors as 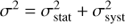 .
.
We list the measured values of Hβ, Mg2, Mgb, Fe5270, and Fe5335 in Table A.3 and plot the folded radial profiles of Hβ, Mgb, [MgFe]′, and 〈Fe〉 in Figs. B.1 and B.2. For NGC 6482, there are significant differences in Hβ and Mgb (and consequently on [MgFe]′) on the two galaxy sides only within the inner 3 arcsec of the major and minor axes. For NGC 7556 there is a good agreement between the radial profiles of the measured line-strength indices on either side of each axis. The central values of the line-strength indices measured on the different axes are consistent with each other for both galaxies.
All the radial profiles of the line-strength indices of NGC 6482 show a central maximum followed by a mild decline to the outermost measured radius with a gradient change observed at r ≃ 3 arcsec. We find that Hβ decreases from about 1.8 to 1.5 Å, [MgFe]′ from about 4.3 to 3.0 Å, 〈Fe〉 from about 3.2 to 2.7 Å, Mgb from about 5.7 to 4.0 Å, and Mg2 from about 0.35 to 0.20 mag. All the line-strength indices we measured are consistent with those obtained by Trager et al. (1998) with an aperture of 1.4 × 4.0 arcsec2, except for Hβ. This discrepancy is due to the different correction adopted to deal with the contamination of the Hβ emission line, which fills in the absorption line and lowers its actual equivalent width. We measured the Hβ index on the best-fitting stellar spectrum obtained from the kinematic analysis.
In NGC 7556, the Hβ index is almost constant at all radii, contrary to the other line-strength indices. They are characterized by decreasing radial profiles, which become flat along the minor and diagonal axes for r ≳ 5 arcsec. The measurement for Hβ is Hβ ≃ 1.7 Å, whereas [MgFe]′ decreases from about 4.0 to 3.0 Å, 〈Fe〉 from about 3.0 to 2.8 Å, Mgb from about 5.2 to 4.0 Å, and Mg2 from about 0.33 to 0.25 mag. The central value of Mg2 is in agreement with that reported by Wegner et al. (2003) for a circularized aperture of 0.9 arcsec at the adopted distance.
5. Properties of the stellar populations
We obtained the stellar population properties of NGC 6482 and NGC 7556 by comparing the measurements of the line-strength indices with the model predictions by Thomas et al. (2003) for the single stellar population as a function of age, metallicity, and α/Fe enhancement following Morelli et al. (2008, 2012, 2015). The central values of velocity dispersion σ0 and line-strength indices Mgb, Hβ, 〈Fe〉, and [MgFe]′ of both galaxies were derived from the radial profiles along the major, diagonal, and minor axes. The data points inside an aperture of radius 0.1re were averaged adopting a relative weight proportional to their S/N. This is re = 4.4 and 4.6 kpc for NGC 6482 and NGC 7556, respectively. We found that the central regions of NGC 6482 (σ0 = 323 ± 3kms−1) are made by relatively young stars (Age0 = 3.3 ± 0.4 Gyr) with high metallicity ([Z/H]0 > 0.67 dex) and supersolar α/Fe enhancement ([α/Fe]0 = 0.38 ± 0.03 dex). This result holds also when the central population properties are independently derived along the three available axes, but it is different from Sánchez-Blázquez et al. (2006b) who pointed out the presence of older (Age0 = 11 ± 1 Gyr) and less metal rich ([Z/H]0 = 0.11 ± 0.03 dex) stars using spectral synthesis models. As a consequence, their gradients of age and metallicity are much flatter than ours (Sánchez-Blázquez et al. 2006c). This difference in the population properties obtained for NGC 6482 could be due to the fact that Sánchez-Blázquez et al. (2006b) derived the equivalent width of the Hβ emission line from that of [O III]λ5007 to correct the Hβ line-strength index for the effect of emission. They adopted the ratio EW(Hβem)/EW([O III]λ5007) = 0.7 by González (1993). However, there is evidence that this correction is uncertain for individual galaxies (Mehlert et al. 2000) although it is good in a statistical sense (Trager et al. 2000). The central stellar population of NGC 7556 (σ0 = 265 ± 3kms−1) is older (Age0 = 7 ± 1 Gyr), less metal rich ([Z/H]0 = 0.46 ± 0.03 dex), and with lower α/Fe enhancement ([α/Fe]0 = 0.28 ± 0.02 dex) than NGC 6482.
For comparison, Khosroshahi & Nolan (2013) reported a few other cases of FG BCGs hosting a secondary stellar component. It is on average less old (〈Ages〉 ⋍ 10 Gyr) and metal rich (〈[Z/H]s〉 ⋍ 0.3 dex) than the galaxy main component (〈Agem〉 ⋍ 14 Gyr, ≃ [Z/H]m〉 ⋍ 1.7 dex). These secondary components are in any case much older and more metal rich than that we found in NGC 6482.
The radial trends of the line-strength indices Mgb,Hβ, 〈Fe〉, and [MgFe]′ were derived along all the observed axes and are shown in Fig. 3 for NGC 6482 and in Fig. 4 for NGC 7556. We averaged the data points along the major axis adopting a relative weight proportional to their S/N within 0.1re < r ≤ 0.5re, 0.5re < r ≤ re, and r > re, respectively. We defined the corresponding radial ranges along the diagonal and minor axes by taking into account the misalignment with respect to the major axis and axial ratio of the spheroidal component in order to map the same galaxy regions along the different directions. We did not find any significant difference in the properties of stellar populations measured along the different axes of both NGC 6482 and NGC 7556, because the averaged line-strength indices measured on the different axes at the same radius are nearly consistent within the errors. As soon as the radius increases, the age and metallicity of NGC 6482 steadily increases to Age ≃ 15 Gyr and decreases to [Z/H] ≃ 0dex, respectively while the α/Fe enhancement is constant. Also the stellar population of NGC 7556 is much older (Age ≃ 15 Gyr) at larger radii with respect to the center, but it is characterized by a subsolar metallicity ([Z/H] ≃ −0.1 dex) and lower α/Fe enhancement ([α/Fe] ≃ 0.2 dex).
 |
Fig. 3. Averaged values of the Hβ and [MgFe]′ (left panel) and 〈Fe〉 and Mgb line-strength indices (right panel) measured inside an aperture of radius r = 0.1re (black circles) of NGC 6482. The averaged line-strength indices measured for 0.1re < r ≤ 0.5re, 0.5re < r ≤ re, and r > re are plotted with circles of different color tone (from darker to lighter), respectively. Blue, green, and red circles correspond to data obtained along the major, diagonal, and minor axes, respectively. The gray lines indicate the models by Thomas et al. (2003). In the left panel, the age-metallicity grids are plotted with two different α/Fe enhancements: [α/Fe] = 0 dex (continuous lines) and [α/Fe] = 0.5 dex (dash-dotted lines). In the right panel, the [α/Fe]-metallicity grids are plotted with two different ages: 2 Gyr (continuous lines) and 8 Gyr (dash-dotted lines). |
 |
Fig. 4. Same as in Fig. 3 but for NGC 7556. |
To quantify the gradients of age, metallicity, and α/Fe enhancement along the observed axes of NGC 6482 and NGC 7556, we analyzed the stellar population parameters obtained from the single stellar population fit of the line-strength indices Hβ, Mgb, 〈Fe〉, and [MgFe]′. Following Mehlert et al. (2003), we assumed a power-law radial profile for Hβ, Mgb, and 〈Fe〉 and calculated their best-fitting values at 0.1re and re (Fig. B.3). From the best-fitting values of Mgb and 〈Fe〉, we derived the values of [MgFe]′ at 0.1re and re. Then, we converted the values of the line-strength indices into the stellar population parameters at 0.1re and re using the model predictions by Thomas et al. (2003). Finally, we obtained the gradient of the age, metallicity, and α/Fe enhancement as the difference between their values at re and 0.1re. This is
where ![$${\rm{Ag}}{{\rm{e}}_{0.1{r_e}}},{\left[ {{\rm{Z/H}}} \right]_{0.1{r_e}}}$$](/articles/aa/full_html/2018/10/aa32625-18/aa32625-18-eq11.gif) , and
, and ![$${\left[ {\alpha /{\rm{Fe}}} \right]_{0.1{r_e}}}$$](/articles/aa/full_html/2018/10/aa32625-18/aa32625-18-eq12.gif) are the parameters calculated at 0.1re and Agee, [Z/H]e, and [α/Fe]e are at re. These gradients match those commonly derived by assuming power-law radial profiles for the stellar population parameters, which are fitted with the linear relations
are the parameters calculated at 0.1re and Agee, [Z/H]e, and [α/Fe]e are at re. These gradients match those commonly derived by assuming power-law radial profiles for the stellar population parameters, which are fitted with the linear relations
Our approach makes the measured gradients less sensitive to variations of the line-strength indices and, as a consequence, of the stellar population parameters over small radial scales. We derived the stellar population gradients separately for each axis by taking into account the misalignment with respect to the major axis and axial ratio of the spheroidal component to cover the same galaxy regions. The uncertainties on the gradients were calculated using Monte Carlo simulations taking into account the errors on the available data, as done in Morelli et al. (2012). We report the gradients of age, metallicity, and α/Fe enhancement together with the age difference within re in Table 4.
Stellar population gradients in the sample galaxies.
The gradients measured on the different axes for the same galaxy are consistent with each other within errors. This is also true for the age difference measured within re along the minor axis of both galaxies, which at face value seem to be smaller than the corresponding values measured along the major and diagonal axes. This findings confirm the trends we observed for the line-strength indices and exclude the presence of non-virialized stellar substructures possibly due to recent merging events. It was not possible to completely remove the contribution from the stellar envelope surrounding the spheroidal component of NGC 7556. However, by limiting the analysis to re we ensured a low contamination of the stellar population of the envelope that dominates the galaxy light for r ≥ rse > re. The envelope contributes from 0.4% to 34% of the total surface brightness moving from the center to re.
6. Results and discussion
We used the spatially resolved parameters of the stellar populations of two FG BCGs, NGC 6482 and NGC 7556, as a benchmark against which the formation and evolution scenarios of FGs can be tested. We compared the central values and radial gradients of age and metallicity of these two galaxies with those of other FG BCGs and normal ETGs to understand whether they had similar assembly histories.
Figure 5 displays the central metallicity and central age of NGC 6482 and NGC 7556 against their central velocity dispersions in comparison with the stellar population properties of the FG BCGs studied by Eigenthaler & Zeilinger (2013) and Proctor et al. (2014) and the ETGs from Koleva et al. (2011). To this aim, we converted our estimates of [Z/H] and [α/Fe] into [Fe/H] values with [Fe/H] = [Z/H] − 0.94[α/Fe] following Thomas et al. (2003). The central velocity dispersions of both NGC 6482 and NGC 7556 are in the same range of more massive ETGs and FG BCGs. The stellar populations in the central regions of the two galaxies are younger and more metal rich than those of the FG BCGs studied so far. The intermediate age of the central stellar population of NGC 6482 is more typical for dwarf rather than massive ETGs. The center of NGC 7556 is slightly younger than BCGs in FGs, but its age falls within the range observed for the other ETGs and its metallicity is consistent with the less massive ones. The central metallicities and central ages plotted in Fig. 5 are obtained with different methods using different stellar population models in some cases. Eigenthaler & Zeilinger (2013) and Proctor et al. (2014) explored the issue of the systematic differences by measuring the stellar population parameters derived from line-strength indices and full spectral fitting. They found a fair agreement in most of their FG BCGs. Unfortunately, Eigenthaler & Zeilinger (2013) and Proctor et al. (2014) do not provide their line-strength indices and a direct comparison with ours is not possible.
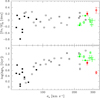 |
Fig. 5. Central metallicity (top panel) and central age (bottom panel)as a function of the central velocity dispersion for NGC 6482 (red open diamond) and NGC 7556 (red filled diamond), the FG BCGs from Eigenthaler & Zeilinger 2013, green open circles) and Proctor et al. 2014, green filled circles), and the early-type normal (open squares) and dwarf (filled squares) galaxies with σ > 50 km s−1 from Koleva et al. (2011). |
The age and metallicity gradients of FG BCGs are compared to those of ETGs as a function of their central values of velocity dispersion, age, and metallicity in Fig. 6. The metallicity gradients of both NGC 6482 (∇[Fe/H] = −0.32 ± 0.06 dex decade−1) and NGC 7556 (∇[Fe/H] = −0.25 ± 0.06 dex decade−1) are within the range observed for ETGs and FG BCGs. The age gradient of NGC 6482 (∇ log (Age) = 0.25 ± 0.06 dex decade−1) is remarkably larger than that of FG BCGs, while that of NGC 7556 (∇ log (Age) = 0.13±0.05 dex decade−1) is marginally consistent with them. Both values fall within the range of age gradients found for ETGs.
 |
Fig. 6. Gradients of metallicity and age as a function of the central velocity dispersion (top panels) and central age (middle panels) and central metallicity (bottom panels) of the galaxies plotted in Fig. 5. |
This trend is even clearer in Fig. 7, which shows that FG BCGs have the same metallicity and age gradients as the bulk of ETGs when our galaxies are considered together with those of Eigenthaler & Zeilinger (2013) and Proctor et al. (2014). The FG BCGs are very massive, in fact the weighted mean of their central velocity dispersion is 〈σ0〉 = 271 ± 1 kms−1. Their gradients of metallicity and age span over the ranges −0.1 ≲ ∇[Fe/H] ≲ 0.3 dex decade−1 and −0.4 ≲ ∇log(Age) ≲ 0.0 dex decade−1, respectively. Their weighted means are 〈∇[Fe/H]〉 = −0.16 ± 0.01 dex decade−1 and 〈∇log(Age)〉 = 0.01 ± 0.01 dex decade−1. The mean value of the metallicity gradient is driven by NGC 1132 (∇[Fe/H] = −0.14 ± 0.02 dex decade−1) and RX J0844.9+4258 (∇[Fe/H] = −0.12 ± 0.02 dex decade−1). By excluding these two galaxies, it is 〈∇[Fe/H]〉 = −0.26 ± 0.03 dex decade−1. We also find 〈∇[Z/H]〉 = −0.32 ± 0.03 dex decade−1 for the FG BCGs for which ∇[Z/H] is available.
 |
Fig. 7. Gradient of metallicity as a function of the gradient of age of the galaxies plotted in Fig. 5. |
Two competing scenarios have been proposed for the formation of FGs in order to explain the large magnitude gap between the BCGs and their surrounding galaxies. It has been suggested that FGs are either failed groups, which formed monolithically from the dissipative collapse of a pristine gas cloud without bright satellite galaxies and did not suffer any major merger, or very old systems that assembled hierarchically and had enough time to exhaust their bright satellite galaxies through multiple major mergers.
The monolithic formation of ETGs through a pure dissipational collapse results in steep metallicity gradients (∇[Z/H] = −0.5 dex decade−1, Carlberg 1984), since the gas is continuously enriched by metals ejected from the stars formed as the gas falls toward the galaxy center. These early findings were confirmed by Pipino et al. (2008, 2010) by taking into account the gas outflows triggered by supernova activity and star formation efficiency in quasi-monolithic collapse models for galaxy formation. Indeed, Pipino et al. (2010) found metallicity gradients as large as ∇[Z/H] = −0.5 dex decade−1 for a few very massive ETGs with σ0 ≃ 250 km s−1 and M∗ ≃ 1011.4 M⊙, which are actually in the same mass range as FG BCGs. On the other hand, Kobayashi (2004) investigated a further adaptation of monolithic collapse and predicted steep metallicity gradients (∇[Z/H] = −0.46 dex decade−1) also for galaxies assembled from the early merging (at z ≳ 3) of many small and gas-rich galaxies (with M∗ ≃ 109 M⊙ and Mgas ≥ M∗). Present-day galaxies resulting from this pseudo-monolithic process can be hardly distinguished from those formed from monolithic collapse. The pure monolithic collapse and its variants also predict a correlation between the galaxy mass and metallicity gradient since a deeper potential retains more metals. On the contrary, late major mergers (at z ≲ 3) are found to dilute the metallicity gradients (Kobayashi 2004; Di Matteo et al. 2009).
The shallower metallicity gradient measured in FG BCGs with respect to that predicted from pure monolithic (Carlberg 1984), extreme quasi-monolithic (Pipino et al. 2008), and pseudo-monolithic (Kobayashi 2004) collapse scenarios suggests that major mergers played a role in the formation of these very massive galaxies. Therefore, as alternative routes to form FG BCGs, we considered the quasi-monolithic collapse in combination with dry major mergers (Di Matteo et al. 2009) and the early assembly of either many small galaxies (as in the pseudo-monolithic collapse scenario) or a few large galaxies (with M∗ ≃ 1010 M⊙ and Mgas ≤ 0.7M∗) followed at z ≲ 3 by one or more wet major mergers (Kobayashi 2004).
Quasi-monolithic collapse predicts steeper metallicity gradients for more massive galaxies, as well as a larger spread of the metallicity gradients for more massive galaxies (−0.5 ≲ ∇[Z/H] ≲ 0 dex decade−1 for M∗ ≈ 1011 M⊙) with respect to the less massive ones (−0.4 ≲ ∇[Z/H] ≲ −0.2 dex decade−1 for M∗ ≈ 1010 M⊙, Pipino et al. 2010). On the contrary, we found the same scatter of ∇[Fe/H] for FG BCGs and less massive ETGs and a remarkably small spread of ∇[Z/H] for the FG BCGs for which this value is available. If FG BCGs did not suffer any major merger, then having the same metallicity gradients means that all of them formed in a very similar way. The large variance of ∇[Z/H] predicted by Pipino et al. (2010) should be observed for more massive galaxies also when dry major mergers are considered. Indeed, they may or may not flatten the metallicity gradient in the remnant depending on the shape of the metallicity profiles of the progenitors (Di Matteo et al. 2009). Therefore, observing similar metallicity gradients in the case of dry major mergers implies that all FG BCGs had the same merging history. In summary, building FG BCGs through quasi-monolithic collapse requires a significant fine-tuning of their evolution history. In addition, no correlation between mass and metallicity gradient is observed when FG BCGs are compared to giant and dwarf ETGs, favoring early hierarchical assembly followed by wet major mergers as the formation scenario for FG BCGs. It is worth noting that for massive galaxies the effects of cold gas accretion in the galactic cores at high redshift mimic a monolithic collapse (e.g., Kereš et al. 2009; Birnboim & Dekel 2011; Davé et al. 2011).
The numerical experiments of galaxy merging by Kobayashi (2004) show that wet major mergers flatten the metallicity gradient of the remnant in a way that depends on the gas fraction and stellar mass ratio of the progenitors. They found a typical value of ∇[Z/H] = −0.22 dex decade−1, which is close to what we measured for FG BCGs. We can conclude that FGs are not failed groups because their BCGs assembled from the merging of large galaxies. This supports the recent results of Kundert et al. (2017), who have investigated FGs in the Illustris cosmological hydrodynamical simulation (Vogelsberger et al. 2014). FGs assembled most of their mass through mergers before z ∼ 0.4, with massive galaxies accreted during this period having enough time to merge with the BCG by today. According to Kundert et al. (2017), the lack of recent group accretion has prevented the refilling of the bright satellite population and allowed for a large magnitude gap to develop within the past few Gyr.
NGC 6482 is the dominant galaxy of a non-cool core FG (Khosroshahi et al. 2004), while the galaxy cluster of NGC 7556 hosts a cool core (Démoclès et al. 2010). In the past, this feature was interpreted as due to the different merging history of non-cool and cool core clusters. According to hydrodynamical simulations (McCarthy et al. 2002; Burns et al. 2008), most cool core systems accreted their mass slowly over time, with major mergers enhancing the central cool core. On the other hand, non-cool core systems only experienced major mergers early in their evolution, which destroyed the embryonic cool core and produced conditions that prevented its re-formation. In this picture, non-cool core FGs are the real relics of early structure formation. However, this scenario can be hardly reconciled with the presence of relatively young and metal-rich stars in the inner regions of NGC 6482. They are the signature of a recent merging event which occurred about 3 Gyr ago, when the induced star formation of reprocessed gas (i.e., with high metallicity) of external origin rejuvenated the central stellar population and further increased its metallicity. More recent cosmological hydrodynamic simulations show that the effects of stellar and active galactic nucleus feedback (Rasia et al. 2015) and angular momentum of the merger event (Hahn et al. 2017) are key to explain the diversity of non-cool and cool core clusters. Simulated cool core clusters have metallicity profiles that are steeper than those of non-cool core clusters and mergers with low angular momentum dissolve cool cores, whereas this is not the case for high angular momentum mergers. This gives further support to the importance of mergers in building FG BCGs and to the investigation of their stellar population properties over a much larger radial range.
7. Conclusions
We presented long-slit spectroscopic observations along the major, minor, and diagonal axes of NGC 6482 and NGC 7556, which are the BCGs of two nearby FGs. The measurements included spatially resolved stellar kinematics and radial profiles of line-strength indices, which we converted into age, metallicity, and α-element abundance ratio of the stellar populations using the single stellar-population models by Thomas et al. (2003).
Both NGC 6482 and NGC 7556 are very massive (M∗ ≃ 1011.5 M⊙) and large (D25 ≃ 50 kpc) elliptical galaxies. In spite of being classified as an early S0 galaxy (de Vaucouleurs et al. 1991), we found that NGC 7556 is embedded in a faint and nonrotating spheroidal envelope rather than in a disk. From the analysis of the spatially resolved properties of the stellar populations, we argue that NGC 6482 hosts a central and relatively recent burst of star formation superimposed onto an old stellar body. NGC 7556 displays a centrally-concentrated stellar population of intermediate age, which is significantly younger and more metal rich than the rest of the galaxy. We did not come across any remarkable difference in the properties of stellar populations measured along the different axes of NGC 6482 and NGC 7556. This excludes the presence of non-virialized stellar substructures in the observed radial range, possibly due to recent merging events. The age gradients of both galaxies are somewhat larger than those of the other FG BCGs with stellar population parameters measured at different radii (Eigenthaler & Zeilinger 2013; Proctor et al. 2014), whereas their metallicity gradients are similarly negative and shallow. Moreover, both galaxies have negligible gradients of α-element abundance ratio at supersolar value.
The metallicity gradients of all the FG BCGs studied so far are less steep than those predicted for massive galaxies that formed monolithically and evolved without experiencing any major merger. This result holds for different models of galaxy formation based on the dissipative collapse of pristine gas clouds (Carlberg 1984; Kobayashi 2004; Pipino et al. 2010). In addition, we do not observe a correlation between metallicity gradient and mass and an increase of the scatter of the metallicity gradients with mass, when FG BCGs are compared to giant and dwarf ETGs from Koleva et al. (2011). FG BCGs have the same metallicity and age gradients of the bulk of ETGs confirming early results by La Barbera et al. (2009). They found no difference between the integrated stellar population properties of FG BCGs and bright field ellipticals and concluded that the FGs might not be a distinct family of true fossil systems, but rather the final stage of mass assembly. All these findings favor a formation scenario of FG BCGs from wet major mergers following an early hierarchical assembly, as investigated by Kobayashi (2004) with numerical simulations of galaxy merging. They reported a typical value of the metallicity gradient for major merger galaxies, which is close to what we measure for FG BCGs. Therefore, we conclude that the observed BCGs assembled through major mergers and their FGs are not failed galaxy groups that lacked bright satellite galaxies from the beginning. This is in agreement with the recent findings by Kundert et al. (2017) based on cosmological hydrodynamic simulations. They showed that the origin of the magnitude gap and BCGs of FGs depends on the recent accretion history of the groups and that selecting galaxy groups by their magnitude gap does not guarantee obtaining either early-formed galaxy systems or undisturbed central galaxies.
Acknowledgments
We are indebted to the anonymous referee for a constructive report that helped us to improve the manuscript. E.M.C., L.M., and L.C. acknowledge financial support from Padua University through grants DOR1699945/16, DOR1715817/17, DOR1885254/18, and BIRD164402/16. L.C. is also grateful to the Instituto de Astrofìsica de Canarias for hospitality while this paper was in progress. J.A.L.A. and J.M.A. thank the support from the Spanish Ministerio de Economia y Competitividad (MINECO) through the grants AYA2013-43188-P and AYA2017-83204-P. S.Z. and M.G. acknowledge financial support from the University of Trieste through the program “Finanziamento di Ateneo per progetti di ricerca scientifica (FRA2015)”. S.Z. is also supported by the grant PRIN-INAF2014-1.05.01.94.02. E.D. gratefully acknowledges the hospitality of the Center for Computational Astrophysics at the Flatiron Institute during the completion of this work. Part of the data used in this research were acquired through the SDSS Archive (http://www.sdss.org/). This research also made use of the HyperLeda Database (http://leda.univ-lyon1.fr/) and NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration (http://ned.ipac.caltech.edu/).
References
- Adami, C., Jouvel, S., Guennou, L., et al. 2012, A&A, 540, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguerri, J. A. L., Girardi, M., Boschin, W., et al. 2011, A&A, 527, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguerri, J. A. L., Longobardi, A., Zarattini, S., et al. 2018, A&A, 609, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Ascaso, B., Aguerri, J. A. L., Varela, J., et al. 2011, ApJ, 726, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Beifiori, A., Maraston, C., Thomas, D., & Johansson, J. 2011, A&A, 531, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Birnboim, Y., & Dekel, A. 2011, MNRAS, 415, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Brough, S., Proctor, R., Forbes, D. A., et al. 2007, MNRAS, 378, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. O., Hallman, E. J., Gantner, B., Motl, P. M., & Norman, M. L. 2008, ApJ, 675, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera-Lavers, A. 2014, OSIRIS User Manual v. 3.1, GTC Internal Report (La Palma: Grantecan S.A.) [Google Scholar]
- Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G. 1984, ApJ, 286, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., Melchior, A.-L., & Zolotukhin, I. Y. 2010, MNRAS, 405, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Corsini, E. M., Wegner, G. A., Thomas, J., Saglia, R. P., & Bender, R. 2017, MNRAS, 466, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, W., Springel, V., Yang, X., De Lucia, G., & Borgani, S. 2011, MNRAS, 416, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A. A., Raychaudhury, S., Ponman, T. J., et al. 2010, MNRAS, 405, 1873 [NASA ADS] [Google Scholar]
- Davé, R., Oppenheimer, B. D., & Finlator, K. 2011, MNRAS, 415, 11 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1948, Ann. Astrophys., 11, 247 [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (Berlin: Springer) [Google Scholar]
- Démoclès, J., Pratt, G. W., Pierini, D., et al. 2010, A&A, 517, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Pipino, A., Lehnert, M. D., Combes, F., & Semelin, B. 2009, A&A, 499, 427 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Giménez, E., Muriel, H. & Mendes de Oliveira, C. 2008, A&A, 490, 965 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Onghia, E., & Lake, G. 2004, ApJ, 612, 628 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Sommer-Larsen, J., Romeo, A. D., et al. 2005, ApJ, 630, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Eigenthaler, P., & Zeilinger, W. W. 2013, A&A, 553, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farhang, A., Khosroshahi, H. G., Mamon, G. A., Dariush, A. A., & Raouf, M. 2017, ApJ, 840, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O. E. 1993, MNRAS, 265, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Aguerri, J. A. L., De Grandi, S., et al. 2014, A&A, 565, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González, J. J. 1993, PhD Thesis, University of California, Santa Cruz [Google Scholar]
- Gorgas, J., Efstathiou, G., & Aragón-Salamanca, A. 1990, MNRAS, 245, 217 [NASA ADS] [Google Scholar]
- Gozaliasl, G., Khosroshahi, H. G., Dariush, A. A., et al. 2014, A&A, 571, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greene, J. E., Murphy, J. D., Graves, G. J., et al. 2013, ApJ, 776, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, O., Martizzi, D., Wu, H.-Y., et al. 2017, MNRAS, 470, 166 [NASA ADS] [Google Scholar]
- Harrison, C. D., Miller, C. J., Richards, J. W., et al. 2012, ApJ, 752, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., et al. 2000, AJ, 119, 2498 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C., & Forman, W. 1984, ApJ, 276, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, L. R., Ponman, T. J., Horton, A., et al. 2003, MNRAS, 343, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Fardal, M., Davé, R., & Weinberg, D. H. 2009, MNRAS, 395, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., & Nolan, L. A. 2013, Iran. J. Astron. Astrophys., 1, 65 [Google Scholar]
- Khosroshahi, H. G., Jones, L. R., & Ponman, T. J. 2004, MNRAS, 349, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Ponman, T. J., & Jones, L. R. 2006, MNRAS, 372, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Ponman, T. J., & Jones, L. R. 2007, MNRAS, 377, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Gozaliasl, G., Rasmussen, J., et al. 2014, MNRAS, 443, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C. 2004, MNRAS, 347, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Prugniel, P., De Rijcke, S., & Zeilinger, W. W. 2011, MNRAS, 417, 1643 [NASA ADS] [CrossRef] [Google Scholar]
- Kundert, A., Gastaldello, F., D’Onghia, E., et al. 2015, MNRAS, 454, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kundert, A., D’Onghia, E., & Aguerri, J. A. L. 2017, ApJ, 845, 45 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., de Carvalho, R. R., de la Rosa, I. G., et al. 2009, AJ, 137, 3942 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Postman, M., Strauss, M. A., Graves, G. J., & Chisari, N. E. 2014, ApJ, 797, 82 [Google Scholar]
- Lieder, S., Mieske, S., Sánchez-Janssen, R., et al. 2013, A&A, 559, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Y.-T., & Mohr, J. J. 2004, ApJ, 617, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Loubser, S. I., & Sánchez-Blázquez, P. 2012, MNRAS, 425, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C.-P., Greene, J. E., McConnell, N., et al. 2014, ApJ, 795, 158 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Babul, A., & Balogh, M. L. 2002, ApJ, 573, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Mehlert, D., Saglia, R. P., Bender, R., & Wegner, G. 2000, A&AS, 141, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mehlert, D., Thomas, D., Saglia, R. P., Bender, R., & Wegner, G. 2003, A&A, 407, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendes de Oliveira, C., Coelho, P., González, J. J. & Barbuy, B. 2005, AJ, 130, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Mendes de Oliveira, C. L., Cypriano, E. S. & Sodré, L., Jr., 2006, AJ, 131, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Corsini, E. M., & Simonneau, E. 2008, A&A, 478, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Barrena, R., et al. 2012, A&A, 537, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez-Abreu, J., Debattista, V. P., Corsini, E. M., & Aguerri, J. A. L. 2014, A&A, 572, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez-Abreu, J., Ruiz-Lara, T., Sánchez-Menguiano, L., et al. 2017, A&A, 598, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Morelli, L., Pompei, E., Pizzella, A., et al. 2008, MNRAS, 389, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Morelli, L., Corsini, E. M., Pizzella, A., et al. 2012, MNRAS, 423, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Morelli, L., Corsini, E. M., Pizzella, A., et al. 2015, MNRAS, 452, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Morelli, L., Parmiggiani, M., Corsini, E. M., et al. 2016, MNRAS, 463, 4396 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., D’Ercole, A., & Matteucci, F. 2008, A&A, 484, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pipino, A., D’Ercole, A., Chiappini, C., & Matteucci, F. 2010, MNRAS, 407, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Pohlen, M., & Trujillo, I. 2006, A&A, 454, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponman, T. J., Allan, D. J., Jones, L. R., et al. 1994, Nature, 369, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Proctor, R. N., Forbes, D. A., Hau, G. K. T., et al. 2004, MNRAS, 349, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- Proctor, R. N., de Oliveira, C. M., Dupke, R., et al. 2011, MNRAS, 418, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Proctor, R. N., Mendes de Oliveira, C. & Eigenthaler, P. 2014, MNRAS, 439, 2281 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Borgani, S., Murante, G., et al. 2015, ApJ, 813, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Raskutti, S., Greene, J. E., & Murphy, J. D. 2014, ApJ, 786, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006a, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Gorgas, J., Cardiel, N., & González, J. J. 2006b, A&A, 457, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Gorgas, J., & Cardiel, N. 2006c, A&A, 457, 823 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, W. A., Mendes de Oliveira, C. & Sodré, L., Jr., 2007, AJ, 134, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Falcón-Barroso, J., Davies, R. L., et al. 2006, MNRAS, 366, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de Galaxias Australes (Córdoba: Observatorio Astronómico de Córdoba) [Google Scholar]
- Schombert, J. M. 1986, ApJS, 60, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J. M. 1987, ApJS, 64, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., & Bender, R. 2003, MNRAS, 339, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Worthey, G., Faber, S. M., Burstein, D., & González, J. J. 1998, ApJS, 116, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 119, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Trevisan, M., Mamon, G. A., & Khosroshahi, H. G. 2017, MNRAS, 464, 4593 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., & Franx, M. 1993, ApJ, 407, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Veale, M., Ma, C.-P., Thomas, J., et al. 2017, MNRAS, 464, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Voevodkin, A., Borozdin, K., Heitmann, K., et al. 2010, ApJ, 708, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, MNRAS, 444, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- von Benda-Beckmann, A. M., D’Onghia, E., Gottlöber, S., et al. 2008, MNRAS, 386, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., Gonzalez, J. J., & Burstein, D. 1994, ApJS, 94, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Wegner, G., Bernardi, M., Willmer, C. N. A., et al. 2003, AJ, 126, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., & Ottaviani, D. L. 1997, ApJS, 111, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Zarattini, S., Barrena, R., Girardi, M., et al. 2014, A&A, 565, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zarattini, S., Aguerri, J. A. L., Sánchez-Janssen, R., et al. 2015, A&A, 581, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zarattini, S., Girardi, M., Aguerri, J. A. L., et al. 2016, A&A, 586, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Data tables
Isophotal parameters of NGC 7556.
Stellar kinematics of NGC 6482 and NGC 7556.
Line-strength indices of NGC 6482 and NGC 7556.
Appendix B: Additional figures
 |
Fig. B.1. Stellar kinematics and line-strength indices measured along the major (top panels), diagonal (middle panels) and minor axis (bottom panels) of NGC 6482. For each axis, the curves are folded around the nucleus. Blue asterisks and red circles refer to data measured along the approaching and residing sides of the galaxy, respectively. The left panels (from top to bottom) show the radial profiles of the mean velocity (ν) after the subtraction of the systemic velocity, velocity dispersion (σ), third- and fourth-order coefficients of the Gauss–Hermite decomposition of the LOSVD (h3 and h4). The right panels (from top to bottom) show the radial profiles of the line-strength indices Hβ, [MgFe]′, 〈Fe〉, Mgb, and Mg2. The vertical dotted line corresponds to the effective radius re of the spheroidal component. The name of the galaxy and orientation of the slit are given for each data set. |
 |
Fig. B.3. Gradients of the line-strength indices Hβ, 〈Fe〉, and Mgb measured along the major (top panels), diagonal (middle panels), and minor axis (bottom panels) of NGC 6482 (left panels) and NGC 7556 (right panels). For each axis, the curves are folded around the nucleus. Blue asterisks and red circles refer to data measured along the approaching and residing sides of the galaxy, respectively. The solid line corresponds to the best-fitting power law to the available data, while the vertical dotted lines mark the radial range between 0.1re and re of the spheroidal component. The name of the galaxy and orientation of the slit are given for each data set. |
All Tables
All Figures
 |
Fig. 1. Two-dimensional photometric decomposition of the r-band image of the NGC 7556. The upper panels (from left to right) show the map of the observed, modeled, and residual (observed−modeled) surface brightness distributions. The field of view is oriented with North up and East left. The black areas in the residual image correspond to pixels excluded from the fit. The lower panels (from left to right) show the ellipse-averaged radial profile of surface brightness, position angle, and ellipticity measured in the observed (black dots with gray error bars) and seeing-convolved modeled image (green solid line) and their corresponding difference. The intrinsic surface-brightness radial profiles of the best-fitting spheroid (blue dashed line) and halo (red dotted line) components are also shown in both linear and logarithmic scale for the distance to the center of the galaxy. |
| In the text | |
 |
Fig. 2. Central rest-frame spectra extracted along the major axis of NGC 6482 (top panel) and NGC 7556 (bottom panel). Relative fluxes have false zero points for viewing convenience. In each panel the best-fitting model (red line) is the sum of the spectra of the ionized-gas (blue line) and stellar component (green line). The latter is obtained convolving the synthetic templates with the best-fitting LOSVD and multiplying them by the best-fitting Legendre polynomials. The residuals (gray dots) are obtained by subtracting the model from the spectrum. The vertical lines mark the wavelength ranges excluded from the fit. |
| In the text | |
 |
Fig. 3. Averaged values of the Hβ and [MgFe]′ (left panel) and 〈Fe〉 and Mgb line-strength indices (right panel) measured inside an aperture of radius r = 0.1re (black circles) of NGC 6482. The averaged line-strength indices measured for 0.1re < r ≤ 0.5re, 0.5re < r ≤ re, and r > re are plotted with circles of different color tone (from darker to lighter), respectively. Blue, green, and red circles correspond to data obtained along the major, diagonal, and minor axes, respectively. The gray lines indicate the models by Thomas et al. (2003). In the left panel, the age-metallicity grids are plotted with two different α/Fe enhancements: [α/Fe] = 0 dex (continuous lines) and [α/Fe] = 0.5 dex (dash-dotted lines). In the right panel, the [α/Fe]-metallicity grids are plotted with two different ages: 2 Gyr (continuous lines) and 8 Gyr (dash-dotted lines). |
| In the text | |
 |
Fig. 4. Same as in Fig. 3 but for NGC 7556. |
| In the text | |
 |
Fig. 5. Central metallicity (top panel) and central age (bottom panel)as a function of the central velocity dispersion for NGC 6482 (red open diamond) and NGC 7556 (red filled diamond), the FG BCGs from Eigenthaler & Zeilinger 2013, green open circles) and Proctor et al. 2014, green filled circles), and the early-type normal (open squares) and dwarf (filled squares) galaxies with σ > 50 km s−1 from Koleva et al. (2011). |
| In the text | |
 |
Fig. 6. Gradients of metallicity and age as a function of the central velocity dispersion (top panels) and central age (middle panels) and central metallicity (bottom panels) of the galaxies plotted in Fig. 5. |
| In the text | |
 |
Fig. 7. Gradient of metallicity as a function of the gradient of age of the galaxies plotted in Fig. 5. |
| In the text | |
 |
Fig. B.1. Stellar kinematics and line-strength indices measured along the major (top panels), diagonal (middle panels) and minor axis (bottom panels) of NGC 6482. For each axis, the curves are folded around the nucleus. Blue asterisks and red circles refer to data measured along the approaching and residing sides of the galaxy, respectively. The left panels (from top to bottom) show the radial profiles of the mean velocity (ν) after the subtraction of the systemic velocity, velocity dispersion (σ), third- and fourth-order coefficients of the Gauss–Hermite decomposition of the LOSVD (h3 and h4). The right panels (from top to bottom) show the radial profiles of the line-strength indices Hβ, [MgFe]′, 〈Fe〉, Mgb, and Mg2. The vertical dotted line corresponds to the effective radius re of the spheroidal component. The name of the galaxy and orientation of the slit are given for each data set. |
| In the text | |
 |
Fig. B.2. Same as in Fig. B.1 but for NGC 7556. |
| In the text | |
 |
Fig. B.3. Gradients of the line-strength indices Hβ, 〈Fe〉, and Mgb measured along the major (top panels), diagonal (middle panels), and minor axis (bottom panels) of NGC 6482 (left panels) and NGC 7556 (right panels). For each axis, the curves are folded around the nucleus. Blue asterisks and red circles refer to data measured along the approaching and residing sides of the galaxy, respectively. The solid line corresponds to the best-fitting power law to the available data, while the vertical dotted lines mark the radial range between 0.1re and re of the spheroidal component. The name of the galaxy and orientation of the slit are given for each data set. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$${I_{{\rm{sph}}}}\left( r \right) = {I_{\rm{e}}}{10^{ - {b_n}\left[ {{{\left( {r/{r_{\rm{e}}}} \right)}^{1/n}} - 1} \right]}},$$](/articles/aa/full_html/2018/10/aa32625-18/aa32625-18-eq3.gif)
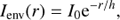
![$$L\left( {{\nu _{{\rm{los}}}}} \right) = {{{{\rm{e}}^{ - {1 \over 2}{w^2}}}} \over {\sqrt {2\pi } }}\left[ {1 + {{{h_3}} \over {\sqrt 3 }}\left( {2{w^3} - 3w} \right) + {{{h_4}} \over {\sqrt 6 }}\left( {2{w^4} - 6{w^2} + {3 \over 2}} \right)} \right],$$](/articles/aa/full_html/2018/10/aa32625-18/aa32625-18-eq6.gif)
![$$\matrix{ {\nabla {\rm{ log}}\left( {{\rm{Age}}} \right)} \hfill & = \hfill & {\left[ {{\rm{log}}\left( {{\rm{Ag}}{{\rm{e}}_{0.9{r_e}}}} \right) - {\rm{log}}\left( {{\rm{Ag}}{{\rm{e}}_{\rm{e}}}} \right)} \right]{\rm{/log}}\left( {0.1{r_e}/{r_e}} \right)} \hfill \cr {} \hfill & = \hfill & {{\rm{log}}\left( {{\rm{Ag}}{{\rm{e}}_{\rm{e}}}} \right) - {\rm{log}}\left( {{\rm{Ag}}{{\rm{e}}_{0.1{r_e}}}} \right),} \hfill \cr {\nabla \left[ {{\rm{Z/H}}} \right]} \hfill & = \hfill & {{\rm{ }}\left[ {{\rm{log}}\left( {{{\left[ {{\rm{Z/H}}} \right]}_{0.1{r_e}}}} \right) - {\rm{log}}\left( {{{\left[ {{\rm{Z/H}}} \right]}_{0.1{r_e}}}} \right)} \right]{\rm{/log}}\left( {{\rm{0}}{\rm{.1}}{r_e}{\rm{/}}{r_e}} \right)} \hfill \cr {} \hfill & = \hfill & {{\rm{log}}\left( {{{\left[ {{\rm{Z/H}}} \right]}_e}} \right) - {\rm{log}}\left( {{{\left[ {{\rm{Z/H}}} \right]}_{0.1{r_e}}}} \right),} \hfill \cr {\nabla \left[ {\alpha /{\rm{Fe}}} \right]} \hfill & = \hfill & {\left[ {{\rm{log}}\left( {{{\left[ {\alpha /{\rm{Fe}}} \right]}_{0.1{r_e}}}} \right) - {\rm{log}}\left( {{{\left[ {\alpha /{\rm{Fe}}} \right]}_e}} \right)} \right]/{\rm{log}}\left( {0.1{r_e}/{r_e}} \right)} \hfill \cr {} \hfill & = \hfill & {{\rm{log}}\left( {{{\left[ {\alpha /{\rm{Fe}}} \right]}_e}} \right) - {\rm{log}}\left( {{{\left[ {\alpha /{\rm{Fe}}} \right]}_{0.1{r_e}}}} \right),} \hfill \cr } $$](/articles/aa/full_html/2018/10/aa32625-18/aa32625-18-eq10.gif)
![$$\matrix{ {{\rm{log}}\left( {{\rm{Age}}\left( {r/{r_{\rm{e}}}} \right)} \right)} \hfill & = \hfill & {{\rm{log}}\left( {{\rm{Ag}}{{\rm{e}}_{\rm{e}}}} \right) + \nabla {\rm{log}}\left( {{\rm{Age}}} \right){\rm{log}}\left( {r/{r_{\rm{e}}}} \right),} \hfill \cr {\left[ {{\rm{Z/H}}} \right]\left( {r/{r_{\rm{e}}}} \right)} \hfill & = \hfill & {{{\left[ {{\rm{Z/H}}} \right]}_{\rm{e}}} + \nabla \left[ {{\rm{Z/H}}} \right]{\rm{log}}\left( {r/{r_{\rm{e}}}} \right)} \hfill \cr {\left[ {\alpha /{\rm{Fe}}} \right]\left( {r/{r_{\rm{e}}}} \right)} \hfill & = \hfill & {{{\left[ {\alpha /{\rm{Fe}}} \right]}_{\rm{e}}} + \nabla \left[ {\alpha /{\rm{Fe}}} \right]{\rm{log}}\left( {r/{r_{\rm{e}}}} \right)} \hfill \cr } $$](/articles/aa/full_html/2018/10/aa32625-18/aa32625-18-eq13.gif)