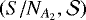| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 16 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201833153 | |
| Published online | 13 September 2018 | |
Detecting the Yarkovsky effect among near-Earth asteroids from astrometric data
1
Dipartimento di Matematica, Università di Pisa,
Largo Bruno Pontecorvo 5,
Pisa,
Italy
e-mail: delvigna@mail.dm.unipi.it
2
Space Dynamics Services s.r.l.,
via Mario Giuntini,
Navacchio di Cascina,
Pisa,
Italy
3
ESA SSA-NEO Coordination Centre,
Largo Galileo Galilei, 1
00044
Frascati (RM),
Italy
4
IMCCE, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06,
Univ. Lille, 77 av. Denfert-Rochereau,
75014
Paris,
France
5
Jet Propulsion Laboratory/California Institute of Technology,
4800 Oak Grove Drive,
Pasadena,
91109 CA,
USA
6
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Boulevard de l’Observatoire,
Nice,
France
Received:
4
April
2018
Accepted:
16
May
2018
We present an updated set of near-Earth asteroids with a Yarkovsky-related semimajor axis drift detected from the orbital fit to the astrometry. We find 87 reliable detections after filtering for the signal-to-noise ratio of the Yarkovsky drift estimate and making sure the estimate is compatible with the physical properties of the analysed object. Furthermore, we find a list of 24 marginally significant detections for which future astrometry could result in a Yarkovsky detection. A further outcome of the filtering procedure is a list of detections that we consider spurious because they are either unrealistic or not explicable by the Yarkovsky effect. Among the smallest asteroids of our sample, we determined four detections of solar radiation pressure in addition to the Yarkovsky effect. As the data volume increases in the near future, our goal is to develop methods to generate very long lists of asteroids that have a Yarkovsky effect that is reliably detected and have limited amounts of case by case specific adjustments. Furthermore, we discuss the improvements this work could bring to impact monitoring. In particular, we exhibit two asteroids for which the adoption of a non-gravitational model is needed to make reliable impact predictions.
Key words: minor planets, asteroids: general / astrometry / celestial mechanics
© ESO 2018
1 Introduction
Several complex phenomena cause asteroid orbital evolution to be a difficult problem. By definition, near-Earth asteroids (NEAs) experience close approaches with terrestrial planets, which are the main source of chaos in their orbital evolution. Small perturbations, such as non-gravitational perturbations, can significantly affect a NEA trajectory because of this chaoticity.
The Yarkovsky effect is due to the recoil force undergone by a rotating body as a consequence of its anisotropic thermal emission (Vokrouhlický et al. 2000, 2015a). The main manifestation of the Yarkovsky effect is a secular semimajor axis drift da∕dt, which leads to a mean anomaly run-off that grows quadratically with time. Typical values of this perturbation for sub-kilometre NEAs are da∕dt ≃ 10−4–10−3 au My−1. Because of its small size, the Yarkovsky effect can only be detected for asteroids with a well-constrained orbit.
The Yarkovsky effect is a non-gravitational perturbation that is generally split into a seasonal and a diurnal component. The seasonal component arises from the temperature variations that the heliocentric asteroid experiences as a consequence of its orbital motion. An explicit computation of the corresponding acceleration is not easy, even for a spherical body, and becomes very difficult for complex shaped bodies. On the other hand, the diurnal component is due to the lag between the absorption of the radiation coming from the Sun and the corresponding re-emission in the thermal wavelength. The surface of a rotating body illuminated by the Sun is warmed by solar radiation during the day and cools at night. It is worth noticing that the diurnal and seasonal components have different consequences on the secular semimajor axis drift. In particular, the diurnal effect produces a positive drift for prograde rotators and a negative drift for retrograde rotators, whereas the seasonal secular drift is always negative. The magnitude of the diurnal effect is generally larger than that of the seasonal effect (Vokrouhlický et al. 2000).
The Yarkovsky effect is key to understanding several aspects of asteroids dynamics:
1. Non-gravitational forces can be relevant for a reliable impact risk assessment when in the presence of deep planetary encounters or when having a long time horizon for the potential impact search (Farnocchia et al. 2015b). As a matter of fact, both of these factors call for a greater consideration of the sources of orbit propagation uncertainty, such as non-gravitational perturbations. Currently, there are four known cases that required the inclusion of the Yarkovsky effect in term of hazard assessment: (101955) Bennu (Milani et al. 2009; Chesley et al. 2014), (99942) Apophis (Chesley 2006; Giorgini et al. 2008; Farnocchia et al. 2013a; Vokrouhlický et al. 2015b), (29075) 1950 DA (Giorgini et al. 2002; Farnocchia & Chesley 2014), and (410777) 2009 FD (Spoto et al. 2014).
2. The semimajor axis drift produced by the Yarkovsky effect has sculpted the main belt for millions of years (Vokrouhlický et al. 2006). The Yarkovsky effect is crucial to understanding the ageing process of asteroid families and the transport mechanism from the main belt to the inner solar system (Vokrouhlický et al. 2000). The Yarkovsky effect has still not been measured in the main belt, thus Spoto et al. (2015) used a calibration based on asteroid (101955) Bennu to compute the ages of more than 50 families in the main belt. The improvement in the detection of the Yarkovsky drift for NEAs represents a new step forward in creating a reliable chronology of the asteroid belt.
3. Yarkovsky detections provide constraints on asteroid physical properties. Two remarkable efforts in estimating the bulk density from the Yarkovsky drift have already been carried out for two potentially hazardous asteroids: (101955) Bennu (Chesley et al. 2014) and (29075) 1950 DA (Rozitis et al. 2014). Furthermore, the dependence of the Yarkosvky effect on the obliquity can be useful to model the spin axis obliquity distribution of NEAs (Tardioli et al. 2017).
There have been several efforts to model and determine the Yarkovsky effect on the NEA population. The first detection of the Yarkovsky effect was predicted for the asteroid (6489) Golevka in Vokrouhlický et al. (2000) and achieved in 2003 thanks to radar ranging of this object (Chesley et al. 2003). Later, the Yarkovsky effect played a fundamental role in the attribution of four 1953 precovery observations to the asteroid (152563) 1992 BF (Vokrouhlický et al. 2008). Moreover, Chesley et al. (2014) detected the Yarkovsky effect acting on (101955) Bennu from astrometric observations and high-quality radar measurements over three apparitions. Currently, asteroid Bennu has the best determined value for the Yarkovsky acceleration, which also led to an estimation of its bulk density (Chesley et al. 2014). In general, Nugent et al. (2012) provided a list of 13 Yarkovsky detections with S∕N > 3 and later work increased this number to 21 (Farnocchia et al. 2013b). The most recent census is from Chesley et al. (2016), which identified 42NEAs with valid Yarkovsky detections. Both Farnocchia et al. (2013b) and Chesley et al. (2016) flag spurious cases based on whether the detected drift is compatible with the physical properties of the corresponding object and the Yarkovsky mechanism. Since the number of significant Yarkovsky detections in the NEA population is steadily increasing, we decided to update the list.
2 Method
2.1 Force model
Usually, there is not enough information on the physical model of an asteroid to directly compute the Yarkovsky acceleration through a thermophysical model. Instead, evidence of the Yarkovsky-related drift may be detectable from the observational dataset via orbit determination. Indeed, a gravity-only model may not provide a satisfactory fit to the available data. A Yarkovsky detection is more likely when a very accurate astrometric dataset is available, especially in case of radar measurements at multiple apparitions or when the observational arc is long, thus allowing the orbital drift to become detectable. In such cases, a force model that also includes the Yarkovsky acceleration could result in a better fit to the observations.
We modelled the Yarkovsky perturbation with a formulation that depends on a single dynamical parameter, to be determined in the orbital fit together with the orbital elements. Since the secular perturbation caused by the Yarkovsky effect is a semimajor axis drift, we used a transverse acceleration
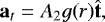 (1)
(1)
as in Marsden et al. (1973) and Farnocchia et al. (2013b). In Eq. (1), A2 is a free parameter and g(r) is a suitable function of the heliocentric distance of the asteroid. In particular we assumed a power law
![\[ g(r) = \left(\frac{r_0}{r}\right)^d, \]](/articles/aa/full_html/2018/09/aa33153-18/aa33153-18-eq2.png)
where r0 = 1 au is used as normalization factor. The exponent d depends on the asteroid and is related to the thermophysical properties of the asteroid. Farnocchia et al. (2013b) showed that the value of d is always between 0.5 and 3.5. They used d =2 for all asteroids because no thermophysical data are available. In our analysis we adopted the same values for d, apart from (101955) Bennu for which the value d = 2.25 is assumed (Chesley et al. 2014).
Typical values of the Yarkovsky acceleration for a sub-kilometre NEA are 10−15–10−13 au d−2. As a consequence, to reliably estimate the Yarkovsky effect, the right-hand side of the equations of motion has to include all the accelerations down to the same order of magnitude. Our force model includes the gravitational accelerations of the Sun, the eight planets, and the Moon based on the Jet Propulsion Lab (JPL) planetary ephemerides DE431 (Folkner et al. 2014). To ensure a more complete force model, we also included the contributions coming from 16 massive main belt bodies and Pluto. All the gravitational masses we used are listed in Table 1. Since we compared our results with those obtained by JPL, we point out that the JPL team used the 16 most massive main belt asteroids as estimated by Folkner et al. (2014), which produces a slight difference, both in the list and masses.
The relativity model includes the relativistic contribution of the Sun, the planets and the Moon. In particular, we used the Einstein–Infeld–Hoffman equations, namely, the equations of the approximate dynamics ofa system of point-like masses due to their mutual gravitational interactions, in a first order post-Newtonian expansion, as described in Einstein et al. (1938), Will (1993), and Moyer (2003).
Perturbing bodies included in the dynamical model in addition to the Sun, the planets, and the Moon.
2.2 Statistical treatment of the astrometry
The statistical treatment of the astrometry is key to a reliable orbit determination. The differential corrections procedure provides the nominal orbit of the asteroid and its uncertainty (Milani & Gronchi 2010, Chap. 5), which strongly depend upon the observationsaccuracy and error modelling. For the computations carried out for this paper, we used the debiasing and weighting scheme provided in Farnocchia et al. (2015a). The JPL team uses the more recent Vereš et al. (2017) weighting scheme.
The astrometric data usually can contain outliers that can affect the solution of the orbit determination. To remove erroneous observations from the fit, we applied the outlier rejection procedure described in Carpino et al. (2003).
In addition to our default data treatment, we applied ad hoc modifications for the following cases:
(152563) 1992 BF. The four 1953 precovery observations of this NEA have been carefully re-measured in Vokrouhlický et al. (2008). We adopt the given positions and standard deviations, the latter being 0.5 arcsec in right ascension and 1 arcsec in declination.
2009 BD. This object is one of the smallest NEAs currently known (Mommert et al. 2014b) and thus solar radiation pressure (SRP) affects its orbit. A direct detection of the area-to-mass ratio is contained in Micheli et al. (2012), which provided high-qualityastrometry from Mauna Kea and replaced all the observations from the Tzec Maun Observatory (H10) with a single position. For these observations we set data weights based on the uncertainties provided by Micheli et al. (2012) and we included both the Yarkovsky effect and SRP in the orbital fit (see Sect. 6).
2011 MD. As 2009 BD, this asteroid is very small and is among those for which we determined both the Yarkovsky effect and SRP. 2011 MD has been observed during the 2011 very close approach with the Earth. Despite the short arc of three months, a very large number of optical observations of 2011 MD were collected, precisely 1555. Following the strategy presented in Mommert et al. (2014a), we relaxed the weights for the observations collected during the close approach1 and we added the Spitzer detection (on February 11, 2014), which extends the observation arc by almost three years.
2015 TC25. Asteroid 2015 TC25 was discovered by the Catalina Sky Survey in October 2015, just two days before an Earth flyby at 0.3 lunar distances. It is one of the smallest asteroids ever discovered, about 2 m in diameter (Reddy et al. 2016), and the 2017 astrometry permits us to achieve an estimate of SRP. We are aware that for 2015 TC25 the JPL team carried out a specific study (Farnocchia et al. 2017), which adopted ad hoc weights based on observer-provided uncertainty estimates. To handle this case, we used the same data treatment as JPL.
We note that it is desirable to keep the number of “manual” interventions on the observational data as small as possible. Indeed we are trying to figure out how to automatize the determination of the set of NEAs with significant and reliable Yarkovsky effect. Anyway, in some cases a manual intervention is needed to properly handle observational issues, for example too many close observations taken during a very close approach and affected by timing errors or remeasurement of old observations.
2.3 Starting sample of NEAs
As first sample of asteroids, we started selecting those objects in NEODyS2 that have a formal uncertainty on the semimajor axis σ(a) < 3 × 10−9 au. The choice of the threshold for σ(a) comes from an order of magnitude estimate: for an asteroid with diameter 1 km the Yarkovsky drift is about 3 × 10−10 au y−1, thus it causes a variation of 3 × 10−9 au in ten years. The value of σ(a) has to be computed at the mean epoch of the observations, since it is the best choice for the orbital fit quality. Moreover, this uncertainty threshold corresponds to a gravity-only fit. After the Yarkovsky coefficient is estimated, the uncertainty of the semimajor axis sharply increases because of the strong correlation between A2 and the semimajor axis.
The list of asteroids satisfying this criterion contained 519 objects (as of February 2018). As a second step, we extracted from the JPL database a set of 89 asteroids having A2 determined3. Among these, only 16 were not contained in our first list, thus we added them. Furthermore, we considered all the reliable detections from Farnocchia et al. (2013b) and it turned out that only 3 asteroids did not belong to any of the previous lists, thus we added these to our sample as well.
Summarizing, we started with a sample of 519 + 16 + 3 = 538 objects. For each one of these objects we performed an orbital fit for the initial conditions together with the Yarkovsky parameter A2, without any a prioriconstraint. For a few of these objects we also estimated SRP. As a result of the fit, we derived the signal-to-noise ratio 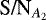 of the A2 parameter, obtaining 101 detections with
of the A2 parameter, obtaining 101 detections with 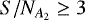 and 437 with
and 437 with 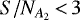 , most of which showing a negligible S/N.
, most of which showing a negligible S/N.
2.4 Yarkovsky expected value
By means oforbit determination, we determined a transverse acceleration directly from the astrometry. However, to claim that the measured acceleration is caused by the Yarkovsky effect we needed to make sure that its magnitude is compatible with the physical properties of the object and the Yarkovsky mechanism. Therefore, we provide an expected value of the Yarkovsky-related orbital drift.
In Farnocchia et al. (2013b), an expected value for A2 is computed by exploiting the diameter of the asteroid and scaling from the corresponding value of (101955) Bennu, the best determined and reliable Yarkovsky detection. In this paper, we make use of the Yarkovsky calibration as in Spoto et al. (2015) as follows:
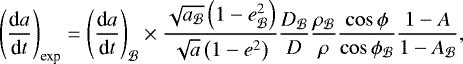 (2)
(2)
where D is the diameter of the asteroid, ρ is the density, ϕ is the obliquity (angle between the spin axis and the normal to the orbit plane), and A is the Bond albedo. We computed the latter from the geometric albedo pv, using 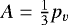 (Muinonen et al. 2010). The symbols with a “
(Muinonen et al. 2010). The symbols with a “ ” refer to asteroid (101955) Bennu, and the assumed values are listed in Table 2 with their references.
” refer to asteroid (101955) Bennu, and the assumed values are listed in Table 2 with their references.
For the diameter D we used the known physical value when available. When the shape of the asteroid is not simple enough to be approximated by an ellipsoidal model, we used the dynamically equivalent equal volume ellipsoid dimensions to compute the equivalent diameter. In particular, this effort has been carried out for three asteroids, namely (4179) Toutatis (Hudson et al. 2003), (162421) 2000 ET70 (Naidu et al. 2013), and (275677) 2000 RS11 (Brauer et al. 2015). Otherwise, when no physical information are available, we estimated the diameter from the absolute magnitude H following the relation (Pravec & Harris 2007)
![\[ D = 1329\text{ km} \times 10^{-H/5} \times \frac{1}{\sqrt{p_v}}, \]](/articles/aa/full_html/2018/09/aa33153-18/aa33153-18-eq9.png)
where the geometric albedo pv is assumed to be pv = 0.154 if unknown.
As shown in Eq. (2), the density is required to estimate the strength of the Yarkovsky effect for asteroids with small diameters. Carry (2012) reported a large number of asteroid densities that we used as starting point. However, in general, density estimates are more reliable and accurate for massive bodies and there is a trend of a decreasing density with diameter because of the increasing macroporosity4 resulting from the cascade of collisions suffered by the body (Carry 2012; Scheeres et al. 2015). We thus extrapolated the density of small asteroids from the density of large asteroids belonging to the same taxonomic class by increasing their macroporosity to that of Bennu (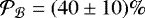 , from Chesley et al. 2014). Such macroporosity is typical for (sub-)kilometre-sized asteroids, as illustrated by (25143) Itokawa, visited by the JAXA Hayabusa mission (Fujiwara et al. 2006). This is a modified version of the approach given in Spoto et al. (2015), still using Bennu for the scaling since it has the best estimated Yarkovsky acceleration and a comprehensive physical characterization5. Thus, the scaled density is given by
, from Chesley et al. 2014). Such macroporosity is typical for (sub-)kilometre-sized asteroids, as illustrated by (25143) Itokawa, visited by the JAXA Hayabusa mission (Fujiwara et al. 2006). This is a modified version of the approach given in Spoto et al. (2015), still using Bennu for the scaling since it has the best estimated Yarkovsky acceleration and a comprehensive physical characterization5. Thus, the scaled density is given by
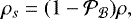 (3)
(3)
where the density scaling factor is 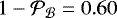 and ρ is the known density of the large asteroid. Equation (3) follows from the above assumptions and from the definition of macroporosity. We selected the large asteroids (4) Vesta, (10) Hygiea, (15) Eunomia, and (216) Kleopatra as representative of the taxonomic classes V, C, S, Xe, respectively. The density of the representative asteroids and their scaled values are listed in Table 3.
and ρ is the known density of the large asteroid. Equation (3) follows from the above assumptions and from the definition of macroporosity. We selected the large asteroids (4) Vesta, (10) Hygiea, (15) Eunomia, and (216) Kleopatra as representative of the taxonomic classes V, C, S, Xe, respectively. The density of the representative asteroids and their scaled values are listed in Table 3.
We used three sources of asteroid physical information: the database of physical properties of NEAs provided by E.A.R.N., the JPL Small-Body Database, and the data provided by the WISE mission, such as diameters and albedos (Mainzer et al. 2011). It is important to point out that we have no physical information concerning the large majority of the objects discussed in this paper. For instance, for the 44% of our detections with 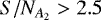 we have no physical data, for 62% we have no measured albedo values, and less than half of our detections can be assigned to a taxonomic class.
we have no physical data, for 62% we have no measured albedo values, and less than half of our detections can be assigned to a taxonomic class.
Representative asteroids for some taxonomic classes.
2.5 Filtering criterion
We used theYarkovsky-related expected value as a filtering criterion to understand whether the estimated orbital drift d a∕d t is physically consistent with the Yarkovsky effect. If the estimated da∕dt is significantly larger than the maximum absolute expected value (assuming cos ϕ= ±1), the result is inconsistent with the Yarkovsky mechanism. We computed the indicator parameter
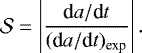 (4)
(4)
Since most times there is very little to no physical information, we needed some margin on the upper threshold for 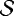 , which therefore should be larger than 1. We filtered out the candidate detections with
, which therefore should be larger than 1. We filtered out the candidate detections with 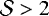 . The current maximum value allowed for
. The current maximum value allowed for 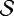 is empirical, but it could be refined. In particular, this upper threshold can be lowered when better data are available. Improving the computation of the expected value – thus decreasing the uncertainty of the indicator parameter
is empirical, but it could be refined. In particular, this upper threshold can be lowered when better data are available. Improving the computation of the expected value – thus decreasing the uncertainty of the indicator parameter 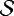 – requires at least a reliable taxonomic type (for the scaling needed for the density) and better diameters. Values of
– requires at least a reliable taxonomic type (for the scaling needed for the density) and better diameters. Values of 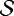 greater than the maximum threshold indicate questionable results. These spurious detections should be investigated to find possible causes and solutions. In general, either the
greater than the maximum threshold indicate questionable results. These spurious detections should be investigated to find possible causes and solutions. In general, either the 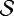 value is too high to be compatible with an acceptable detection or it is barely above the maximum threshold, in such a way that additional information would clarify the situation and allow us to decide whether the detection is accepted or refused. For further details, see Sect. 4.
value is too high to be compatible with an acceptable detection or it is barely above the maximum threshold, in such a way that additional information would clarify the situation and allow us to decide whether the detection is accepted or refused. For further details, see Sect. 4.
We point out that values 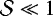 are permitted. Indeed, Eq. (2) employed asteroid size and bulk density, thus
are permitted. Indeed, Eq. (2) employed asteroid size and bulk density, thus 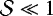 means that the orbital drift is significantly lower than the maximum expected value. Several phenomena can lower the Yarkovsky effect: obliquity ϕ ≃ 90°, very large or very small thermal inertia, larger density than expected, or small rotation angular velocity. For instance, asteroid (85774) 1998 UT18 has a rotation period of about 34 h, and indeed the indicator
means that the orbital drift is significantly lower than the maximum expected value. Several phenomena can lower the Yarkovsky effect: obliquity ϕ ≃ 90°, very large or very small thermal inertia, larger density than expected, or small rotation angular velocity. For instance, asteroid (85774) 1998 UT18 has a rotation period of about 34 h, and indeed the indicator 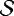 is low (≃0.3, cf. Table A.1). Detections of this kind are significant detections of a weak Yarkovsky drift. A second class of weak Yarkovsky drifts can be defined. These are non-detections, that is
is low (≃0.3, cf. Table A.1). Detections of this kind are significant detections of a weak Yarkovsky drift. A second class of weak Yarkovsky drifts can be defined. These are non-detections, that is 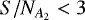 , but the asteroid has physical properties that would permit a significant detection if the Yarkovsky effect were maximized. Chesley et al. (2016) referred to these detections as weak detections. Despite the low S/N, the result of the A2 estimation can provide useful constraints on the physical properties of the asteroid.
, but the asteroid has physical properties that would permit a significant detection if the Yarkovsky effect were maximized. Chesley et al. (2016) referred to these detections as weak detections. Despite the low S/N, the result of the A2 estimation can provide useful constraints on the physical properties of the asteroid.
By combining the value of the 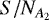 coming from the orbital fit with the value of the filtering parameter
coming from the orbital fit with the value of the filtering parameter 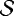 , we divided our detections in three categories as follows:
, we divided our detections in three categories as follows:
-
the detections satisfying both
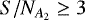 and
and 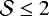 are considered accepted;
are considered accepted; -
the category called marginal significance includes the asteroids for which
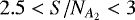 and
and 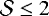 , plus (410777) 2009 FD and (99942) Apophis, both remarkable for their impact monitoring;
, plus (410777) 2009 FD and (99942) Apophis, both remarkable for their impact monitoring; -
the detections with
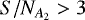 and
and 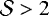 are rejected because they have a value that is too high for the indicator parameter
are rejected because they have a value that is too high for the indicator parameter 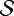 , suggesting that the detected A2
signal isunrealistic or not explicable with the Yarkovsky effect (see 2003 RM in Chesley et al. (2016), or (4015) Wilson-Harrington in Sect. 4).
, suggesting that the detected A2
signal isunrealistic or not explicable with the Yarkovsky effect (see 2003 RM in Chesley et al. (2016), or (4015) Wilson-Harrington in Sect. 4).
The results only include detections, that is we do not list the asteroids for which we did not find a significant Yarkovsky signal from the observational dataset (85% of the initial sample). Figure 1 provides an overall view of our classification. In particular, we consider the plane 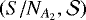 and we indicate the detections of each class (but the rejected) with a different colour as follows: the accepted detections are indicated with a green dot; the marginal significance detections are represented with a blue dot, except for (410777) 2009 FD and (99942) Apophis, which are indicated with a blue asterisk (special cases); the rejected detections are indicated with a red cross.
and we indicate the detections of each class (but the rejected) with a different colour as follows: the accepted detections are indicated with a green dot; the marginal significance detections are represented with a blue dot, except for (410777) 2009 FD and (99942) Apophis, which are indicated with a blue asterisk (special cases); the rejected detections are indicated with a red cross.
 |
Fig. 1 Graphical representation of the partition of the detections set into classes on the plane
|
3 Accepted and significant results
As explained in Sect. 2.3, we started from the initial sample of NEAs and we performed an orbital fit including the Yarkovsky parameter A2. Then we applied the filtering procedure and obtained 87 detections, which are listed in Table A.1 and Table A.2. For each asteroid, we report the value of the absolute magnitude H, the A2 parameter along with its uncertainty, the S/N of A2, the value of the semimajor axis drift da∕dt, the indicator parameter 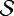 , and the available physical data such as the geometric albedo pv, the diameter D, density ρ, and taxonomic class. As explained in Sect. 2.4, when no information on the diameter is available, we infer a diameter from the absolute magnitude. We denote these cases with an asterisk (*) in the diameter column. When the albedo is not directly measured but the taxonomic class is known, we assign the albedo according to Binzel et al. (2002) and denote the albedo value with a dagger (†). When the albedo is not known we assume pv = 0.154, and indicate thisvalue with a “d”. We note that 0.154 is a mean value, which has a low probability of being accurate because of the bimodality of the albedo distribution of NEAs. Most asteroids are either significantly brighter or significantly darker. Thus, when a diameter D is derived from the absolute magnitude and this default albedo, its relative uncertainty is larger, and in turn the value of
, and the available physical data such as the geometric albedo pv, the diameter D, density ρ, and taxonomic class. As explained in Sect. 2.4, when no information on the diameter is available, we infer a diameter from the absolute magnitude. We denote these cases with an asterisk (*) in the diameter column. When the albedo is not directly measured but the taxonomic class is known, we assign the albedo according to Binzel et al. (2002) and denote the albedo value with a dagger (†). When the albedo is not known we assume pv = 0.154, and indicate thisvalue with a “d”. We note that 0.154 is a mean value, which has a low probability of being accurate because of the bimodality of the albedo distribution of NEAs. Most asteroids are either significantly brighter or significantly darker. Thus, when a diameter D is derived from the absolute magnitude and this default albedo, its relative uncertainty is larger, and in turn the value of 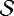 (containing the factor 1∕D) is uncertain.
(containing the factor 1∕D) is uncertain.
Some of the asteroids included in Tables A.1 and A.2 deserve dedicated comments.
(1566) Icarus. It is known that the 1968 observations of (1566) Icarus are affected by large timing errors. A possible solution to this problem is to include timing errors in the observations uncertainty possibly even removing the systematic timing errors. A possible alternative is to properly treat the correlation between the right ascension and declination. This operation will be made easier after the adoption of the new Astrometric Data Exchange Standard (ADES6). For now, it is possible to adapt the weighting scheme to underweight the observations during the 1968 close approach. The JPL team took this approach, but the Pisa team did not. By comparing the result of the two groups and also that of Greenberg et al. (2017), we can claim that the detection of the Yarkovsky effect is confirmed, even if there is a significant difference between the standard deviations (see Sect. 7), which is explained by the different weighting scheme.
(3908) Nyx. Asteroid (3908) Nyx is classified as V type, but it has many properties that are inconsistent with (4) Vesta. Thus, the density scaling is not performed using the density of Vesta as for the other V-type asteroids. Asteroid (5381) Sekhmet is a V-type with a diameter that is comparable to that of Nyx. The density of Sekhmet is (1.30 ± 0.65) g cm−3 (Carry 2012), compatible with the estimate in Farnocchia et al. (2014) and we also assume this value for Nyx.
(4179) Toutatis This asteroid shows a significant Yarkovsky detection with 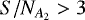 and
and 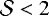 and is therefore included in the list of accepted detections. However, we point out that this detection is subject to substantial uncertainties beyond the formal uncertainties resulting from the fit to the optical and radar astrometry. The large aphelion of the orbit of Toutatis and the small magnitude of the Yarkovsky perturbation make the A2 estimate sensitive to the set of main belt perturbers included in the force model and the uncertainty in their masses.
and is therefore included in the list of accepted detections. However, we point out that this detection is subject to substantial uncertainties beyond the formal uncertainties resulting from the fit to the optical and radar astrometry. The large aphelion of the orbit of Toutatis and the small magnitude of the Yarkovsky perturbation make the A2 estimate sensitive to the set of main belt perturbers included in the force model and the uncertainty in their masses.
4 Rejected results
In this section we consider the significant detections that we rated as spurious, i.e. for which we obtained a Yarkovsky detection greater than reasonably expected from the Yarkovsky effect. Despite the S/N being less than 3, we also add(4015) Wilson-Harrington to this category as a special case, as explained below.
There are several reasons for refusing a detection. First, dynamical model problems can occur in a few cases, such as (4015) Wilson-Harrington. Second, the results are sometimes strongly dependent on few observations, typically old isolated observationsthat are separated by a long time interval from the bulk of the dataset. In these cases we usually reject the detection unless the precovery has been carefully remeasured, as for (152563) 1992 BF. Third, there are solutions with Yarkovsky that are affected by observational data of questionable reliability. The list of all the rejected detections contains 14 cases; see Table A.3. Below we provide dedicated comments for each rejected detection.
(4015) Wilson-Harrington. This asteroid was initially discovered in 1949 as a comet at the Palomar Sky Survey. It was named 107P/Wilson-Harrington, but then it was lost. Thirty years later the asteroid 1979 VA was discovered and, after the 1988 apparition, it was numbered as (4015) 1979 VA. On August 13, 1992, the IAU circular 5585 (Bowell et al. 1992) reported that the asteroid (4015) 1979 VA and the comet 107P/Wilson-Harrington were indeed the same object. Furthermore, no cometary activity was noted during the well-observed 1979–80 apparition, confirming that it is actually an extinct comet. The detection of the Yarkovsky parameter is indeed significant, but the 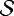 value indicates a value of the non-gravitational acceleration that is larger than that expected from the Yarkovsky effect. Since the observed arc contains the time span of cometary activity, the most likely interpretation is that the large detected transverse acceleration is caused by the out-gassing rather than the Yarkovsky effect. Furthermore, a dynamical model assuming a constant value for A2, as this is the model we employed, is not sufficiently representative of the real orbital dynamics, given that the cometary activity has ceased. Thus in this case we consider that a non-gravitational effect has been detected, but not Yarkovsky.
value indicates a value of the non-gravitational acceleration that is larger than that expected from the Yarkovsky effect. Since the observed arc contains the time span of cometary activity, the most likely interpretation is that the large detected transverse acceleration is caused by the out-gassing rather than the Yarkovsky effect. Furthermore, a dynamical model assuming a constant value for A2, as this is the model we employed, is not sufficiently representative of the real orbital dynamics, given that the cometary activity has ceased. Thus in this case we consider that a non-gravitational effect has been detected, but not Yarkovsky.
In some cases, spurious detections are due to poor optical astrometry, often affecting isolated old observations. In this case we rejected the detection and a remeasurement of these old observations would be desirable to clarify the situation: the Yarkovsky signal could significantly either increase or disappear. This is the case for the asteroids listed below.
(260141) 2004 QT24. The detected signal is strongly dependent on four observations in 1993 and 1998 from Siding Spring Observatory DSS.
(350751) 2002 AW. This asteroid has two isolated observations in 1991 from Palomar Mountain-DSS.
(39565) 1992 SL. This asteroid has one isolated observation in 1950 from Palomar Mountain.
(4486) Mithra. This asteroid has a signal that is strongly dependent on a single isolated observation in 1974 from Crimea-Nauchnij (MPC code 095).
(474158) 1999 FA. This object has one isolated observation in 1978, from Siding Spring Observatory. In agreement with Farnocchia et al. (2013b), we consider that the 1978 observation would need to be remeasured before accepting the Yarkovsky detection for (474158) 1999 FA.
(162421) 2000 ET70. This asteroid has two isolated observations in 1977 from European Southern Observatory, La Silla DSS.
There are detections that have to be rated as spurious because 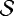 indicates a Yarkovsky drift that is way larger than expected even though the S/N of the A2 parameter is greater than 3. This holds for 2010 KP10, (308635) 2005 YU55, (139359) 2001 ME1, (142561) 2002 TX68, and (192563) 1998 WZ6. To confirm the reliability of our filtering criterion, we carefully checked each of these spurious detections. They show problematic astrometry, which resulted in a incorrect determination of the Yarkovsky effect.
indicates a Yarkovsky drift that is way larger than expected even though the S/N of the A2 parameter is greater than 3. This holds for 2010 KP10, (308635) 2005 YU55, (139359) 2001 ME1, (142561) 2002 TX68, and (192563) 1998 WZ6. To confirm the reliability of our filtering criterion, we carefully checked each of these spurious detections. They show problematic astrometry, which resulted in a incorrect determination of the Yarkovsky effect.
A separate comment holds for (175706) 1996 FG3, since it is a binary asteroid (Scheirich et al. 2015). The signal found for the Yarkovsky detection is likely due to the astrometric data treatment, as confirmed by the fact that it disappears when the weighting scheme proposed in Vereš et al. (2017) is applied. Once we have a Yarkovsky detection for this object it will be possible to compare with the Yarkovsky theory for binary asteroids as described by Vokrouhlický et al. (2005).
A remarkable case is (433) Eros. This asteroid shows a significant value for the Yarkovsky effect, but a very high value for the indicator parameter. Moreover, the obliquity of Eros is known to be ≃ 89° (Yeomans et al. 2000), therefore we would expect a value for 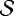 much less than 1. Thus, this detection is spurious, likely caused by historical data dating back to 1893 for which it is challenging to come up with a reliable statistical treatment.
much less than 1. Thus, this detection is spurious, likely caused by historical data dating back to 1893 for which it is challenging to come up with a reliable statistical treatment.
5 Marginal significance
We now consider the marginal significance class, containing the detections for which 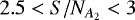 and
and 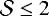 . These detections are physically meaningful since they satisfy the filtering on
. These detections are physically meaningful since they satisfy the filtering on 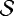 , but the signal to noise for the A2 parameter as determined from the observations is not enough for a reliable detection. In addition, as mentioned before, we include two special casesin this category, namely (410777) 2009 FD and (99942) Apophis. These two objects show acceptable values of the indicator
, but the signal to noise for the A2 parameter as determined from the observations is not enough for a reliable detection. In addition, as mentioned before, we include two special casesin this category, namely (410777) 2009 FD and (99942) Apophis. These two objects show acceptable values of the indicator 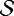 but the S/N of the A2 parameter isvery low (cf. Table A.4). Nevertheless, we decided to keep these objects because the Yarkovsky drift plays a fundamental role for its impact predictions (see the introduction). In this way we grouped 24 detections in this class, which are listed in Table A.4.
but the S/N of the A2 parameter isvery low (cf. Table A.4). Nevertheless, we decided to keep these objects because the Yarkovsky drift plays a fundamental role for its impact predictions (see the introduction). In this way we grouped 24 detections in this class, which are listed in Table A.4.
(99942) Apophis. Similar to Toutatis, Apophis also has a complex rotation, as shown in Pravec et al. (2014); Vokrouhlický et al. (2015b). However, the Yarkovsky effect is not significantly weakened by the tumbling state. Vokrouhlický et al. (2015b) used the available rotation state, shape, size, and thermophysical model of Apophis to predict the Yarkovsky semimajor axis drift. The drift obtained by fitting the astrometric data is compatible with the model prediction. We obtained d a∕dt = (−24.50 ± 13.58) × 10−4 au Myr−1 for the fitted value, which is completely consistent with Vokrouhlický et al. (2015b). There is no question that the Yarkovsky effect has to be taken into account for Apophis to predict future motion, especially for impact hazard assessment (Chesley 2006; Giorgini et al. 2008; Farnocchia et al. 2013a).
(410777) 2009 FD. The Yarkovsky effect found is below the significance level, and nevertheless it has to be taken into account for long-term impact monitoring purposes (Spoto et al. 2014).
Maintaining a list of marginal significance detections is useful because they are candidates for future detections as observational data improves and increases.
6 Direct radiation pressure detection
Solar radiation pressure is a more complicated perturbation to detect. So far, SRP has only been detected for very small objects (H > 27) that experienced Earth encounters. Thus we started selecting the smallest asteroids of the initial sample (more precisely, those with H > 24) since the effect becomes larger for smaller size objects and we tried to detect SRP along with the Yarkovsky parameter.
The acceleration caused by SRP is radial and can be modelled with a single parameter A1,
![\[ \mathbf{a}_r = A_1g(r)\hat{\mathbf{r}}. \]](/articles/aa/full_html/2018/09/aa33153-18/aa33153-18-eq46.png)
In this equation, A1 is a free parameter, and g(r) = 1∕r2, where r is the heliocentric distance in astronomical units. Physically, the value of A1 depends mostly on the area-to-mass ratio 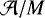 . The relationbetween these parameters is the following:
. The relationbetween these parameters is the following:
![\[ A_1 = \frac{\mathrm\Phi_{\odot}}{c}\times C_R \times\mathcal{A}/M, \]](/articles/aa/full_html/2018/09/aa33153-18/aa33153-18-eq48.png)
where c is the speed of light, Φ⊙ is the solar radiation energy flux at 1 au whose value is Φ⊙ ≃ 1.361 kW m−2, and CR is a coefficient (on the order of 1) depending upon the shape and optical properties of the surface.
The starting sample of asteroids for which we attempted an 8-dimensional fit contained ten objects. We found four accepted detections, i.e. 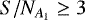 , which are listed in Table A.5. For three asteroids of this category, namely, 2011 MD, 2012 LA, and 2015 TC25, the Yarkovsky detection is not significant and thus the
, which are listed in Table A.5. For three asteroids of this category, namely, 2011 MD, 2012 LA, and 2015 TC25, the Yarkovsky detection is not significant and thus the 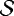 value, although above the threshold in one case, does not provide any information. Concerning the area-to-mass ratio, we would compare the value of
value, although above the threshold in one case, does not provide any information. Concerning the area-to-mass ratio, we would compare the value of 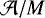 with an expected value, as we do with the secular semimajor axis drift da∕dt, but this is not possible for now since the diameter is very uncertain and the other physical properties are currently unknown. Other fitted values of the area-to-mass ratio have already been determined for 2009 BD (Micheli et al. 2012), 2012 LA (Micheli et al. 2013), and 2011 MD (Micheli et al. 2014), although without including the Yarkovsky effect in the dynamical model. Asteroid 2006 RH120 is listed separately from the others since we consider it spurious, as we explain in what follows.
with an expected value, as we do with the secular semimajor axis drift da∕dt, but this is not possible for now since the diameter is very uncertain and the other physical properties are currently unknown. Other fitted values of the area-to-mass ratio have already been determined for 2009 BD (Micheli et al. 2012), 2012 LA (Micheli et al. 2013), and 2011 MD (Micheli et al. 2014), although without including the Yarkovsky effect in the dynamical model. Asteroid 2006 RH120 is listed separately from the others since we consider it spurious, as we explain in what follows.
2006 RH120. This strange detection has already been discussed in Chesley et al. (2016). Our results are very compatible with those of that paper and we agree with the motivations provided to reject this detection. The most likely explanation for the high transverse acceleration can be the presence of some non-conservative force, for example mass shedding, outgassing, or micrometeorite flux, which can become as relevant as the Yarkovsky effect for objects of this size. The area-to-mass ratio, which results in a significant detection, is not compatible with the hypothesis that 2006 RH120 is an artificial object.
7 Comparison with JPL results
As we already mentioned, the JPL database is regularly updated with the asteroids for which the orbital fit shows evidence of the Yarkovsky effect. The SRP is also regularly updated as well when appropriate. The results produced by two independent software areexpected to be different, but compatible. In order to compare them we compute the relative errors
![\[ \varepsilon_r(A_2)= \frac{|A_2-A_2^{\textsc{jpl}}|}{\sigma_{A_2}} \quad\text{and}\quad \varepsilon_r^{\textsc{jpl}}(A_2) =\frac{|A_2-A_2^{\textsc{jpl}}|}{\sigma_{A_2, \textsc{jpl}}}, \]](/articles/aa/full_html/2018/09/aa33153-18/aa33153-18-eq52.png)
where the superscript “JPL” refers to the JPL solution. To quantify the difference between the results presented in this paper and the JPL values, we use the quantity
![\[ \chi_{A_2} = \frac{|A_2-A_2^{\textsc{jpl}}|}{\sqrt{\sigma_{A_2}^2+\sigma_{A_2, \textsc{jpl}}^2}}, \]](/articles/aa/full_html/2018/09/aa33153-18/aa33153-18-eq53.png)
from (Milani & Gronchi 2010, Sect. 7.2). We consider compatible two solutions for which 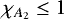 .
.
Starting from the list of our accepted detections, we compared the results every time an asteroid is included in the JPL database of Yarkovsky effect detections. The results of the comparison are contained in Tables A.6 and A.7. Just for five asteroids in this list both the relative errors are greater than 1, even though never above 2.5. Using the metric given by 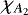 , we identify just 3 asteroids (marked with a star in Tables A.6 and A.7) whose detections are not fully compatible with respect to our criteria. Anyway, a
, we identify just 3 asteroids (marked with a star in Tables A.6 and A.7) whose detections are not fully compatible with respect to our criteria. Anyway, a 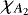 moderately above 1 for 3 cases out of 92 being compared shows a strong agreement between our results and the results from JPL.
moderately above 1 for 3 cases out of 92 being compared shows a strong agreement between our results and the results from JPL.
We note that this result is not a null test, that is the expected value of the difference in the estimated values of A2 is not zero. This because the two computations have used two different astrometric error models, that is Farnocchia et al. (2015a) at NEODyS and Vereš et al. (2017) at JPL. The comparative results described in the last three columns indicate an exceptionally good agreement. This agreement may be interpreted as a validation of the procedures used both at NEODyS and at JPL, both to compute the Yarkovsky effect constants and to select the cases in which the results are reliable.
The comparison was also performed for the shorter list of objects for which we have both A2 and A1, that is both Yarkovsky effect and direct radiation pressure were included in the dynamical model. Table A.8 contains theS/Ns for both parameters in both solutions and all the metrics for the discrepancies. Apart from the results for 2006 RH120, which are rated as spurious, the accepted results are fully consistent.
8 Impactmonitoring with non-gravitational parameters
A force model including non-gravitational forces is sometimes needed to make reliable impact predictions, especially if we want to extend the hazard analysis time span to longer intervals with respect to one century (the default time span adopted by the current impact monitoring systems). More precisely, the non-gravitational model also plays a fundamental role in the Line Of Variations (LOV) computation and propagation (Milani et al. 2000, 2005a,b). If an asteroid with a very well-constrained orbit experiences a very deep close approach, the post-encounter situation is equal to that of a poorly determined orbit; the difference is that the large uncertainty of the asteroid state is due to the divergence of nearby orbits caused by the encounter and not to the poor constraints of the initial conditions. In this case, the initial confidence region is very small, thus the use of the linear approximation of the LOV is allowed. In case such an encounter occurs the linear LOV direction is derived by analysing that encounter and mapping back the corresponding LOV trace on the target plane (TP; Valsecchi et al. 2003) to the space of initial conditions. This method has been used in Spoto et al. (2014) to properly assess the impact risk of (410777) 2009 FD, exploiting its 2185 scattering encounter with the Earth. The same formalism can be used even when we are not in the presence of a scattering encounter, but the close encounter isso deep that the LOV turns out to be very stretched at the next encounter, as in the cases analysed below.
So far, just four asteroids required such special treatment for a proper impact risk assessment, namely (101955) Bennu, (99942) Apophis, (29075) 1950 DA, and (410777) 2009 FD, but this list is expected to grow as a consequence of the work presented inthis paper. Below we show two examples of asteroids for which we found virtual impactors using a non-gravitational model and that have no possible impacts with a purely gravitational model. We are aware that such a work could be performed on many asteroids with accepted Yarkovsky detections, but this is beyond the scope of this paper.
2001 BB16. Currently, this asteroid has a low Minimum Orbit Intersection Distance (MOID) value, ≃ 0.0043 au, but no chance of impacting the Earth in the next century. 2001 BB16 has a deep close approach with the Earth in 2082, which causes an increase of the stretching of two orders of magnitude with respect to the next 2086 encounter, whereas the stretching value remains essentially constant until the 2082 close approach. We used this close approach to derive the LOV direction and we performed the impact monitoring through 2200 employing a non-gravitational model including the Yarkovsky effect. The results are shown in Table 4. In particular we found two VIs at the very end of the 22nd century, which we would not find with a gravity-only model.
2011 MD. This is a very small asteroid, about 6 m in diameter, as determined in Mommert et al. (2014a). In this case as well, the MOID value is very low, ≃ 0.00036 au and it has no virtual impactor in the next century. In 2049, this asteroid will experience two very close approaches with the Earth, causing an increase of two orders of magnitude in the stretching between these encounters and the following approach in 2067. We used thefirst 2049 close approach (the deepest of the two) to compute the LOV direction in the space of initial conditions. We thus performed the impact monitoring using a dynamical model including both the Yarkovsky effect and SRP. The results are shown in Table 5. When we only include SRP, the orbit uncertainty shrinks and thus the number of VIs is much lower than before (see Table 6). Both Tables 5 and 6 list the virtual impactors with IP ≥ 10−7, since this threshold is the completeness limit used for the LOV sampling (Del Vigna et al. 2018).
It is worth noting that this asteroid is so small that it would not reach the Earth in case of a real impact because it would be burnt in theatmosphere. This case is studied to show that, in some cases, a non-gravitational model is needed to make reliable impact predictions and also that different models of non-gravitational perturbations can give very different results.
Impact monitoring of asteroid 2001 BB16 with a non-gravitational model that includes the Yarkovsky effect.
Impact monitoring of asteroid 2011 MD with a non-gravitational model that includes both the Yarkovsky effect and SRP.
Impact monitoring of asteroid 2011 MD with a non-gravitational model including SRP only.
9 Conclusions and future work
In this paper, we significantly increased the knowledge of non-gravitational perturbations on NEAs based on actual measurements rather than on modelling. The number of significant and reliable Yarkovsky detections in the NEA catalogue is expected to grow continuously. In fact, the data volume of future surveys, the increased astrometric accuracy for optical observations, more accurate star catalogue debiasing techniques, and expanded efforts in radar astrometry provide ever better constraints to measure this small effect. We identified 87 NEAs with significant and reliable Yarkovsky detections, thus doubling the list provided in Chesley et al. (2016). For few exceedingly small asteroids, we attempted to directly detect SRP together with the Yarkovsky-related acceleration. For such cases, SRP is needed to obtain a more satisfactory orbital fit.
There are several research centres handling the computation of asteroid orbits as an industrial production. These centres are recomputing either all the orbits of more than 500 000 numbered asteroids every time a change in the error model occurs or a large portion of these orbits just to take into account new observations and new asteroid discoveries7. There are important scientific goals such as asteroid families and impact monitoring that can only be achieved by maintaining and constantly updating such large lists of orbits.
We dedicated a significant effort to clarifying a number of marginal and/or spurious cases, not only to recover a few dubious cases but also to refine the methodology and therefore be ready for the future increase of significant detections. Indeed, the problem to be faced in the near future is not another increase by a factor two, rather an increase by orders of magnitude. The second Gaiadata release (April 2018) will contain about 1.7 billion of sources that are brighter than magnitude 21 and ≃ 14 000 asteroids with astrometry reaching the sub-milliarcsec accuracy in an optimal range of magnitude G ≃ 12−17 (Gaia Collaboration 2018a,b). The stellar catalogue produced by Gaia will represent the starting point for a new debiasing and weighting scheme. Moreover, the combination of Gaia asteroid observations with the already available observations will produce a sharp increase in the number of objects for which the Yarkovsky effect will be detectable. Thus, the challenge in papers like this is not to establish a new record list of Yarkovsky and/or radiation pressure detections, but rather to develop an automated calculation of orbits with estimated non-gravitational parameters.
The computations of orbits with non-gravitational effects is still very far from an automated process. To avoid spurious detections, we used the most recent error models for the observations and a filtering criterion based on an estimate of the Yarkovsky effect based upon a physical model of the asteroid. Unfortunately, both of these tools are still incomplete. The error models suffer from the continued unavailability of metadata, such as the signal-to-noise of individual observations, with the result that observations with different quality are bundled together and the statistical analysis of the residuals does not yet allow a correct derivation of uncertainty of the measurement error. The physical models of asteroids, which are needed to estimate the expected Yarkovsky effect, are very rough approximations when the main physical data are not available, as is the case for the majority of the asteroids in our tables. Moreover, such small perturbations can be sensitive to old isolated and possibly bad astrometric positions.
In conclusion, we made a step in the right direction by developing and testing the use of different error models and by using the difference in the results as an estimate of the sensitivity of the results on the error model. We developed and tested the use of a filter for spurious cases, which is based on an estimate of the expected Yarkovsky effect, which is roughly the same as the Yarkovsky calibration used to compute the age of asteroid families (Milani et al. 2014; Spoto et al. 2015). Both tools improved our capability to obtain a list of reliable Yarkovsky detections and a much shorter list of radiation pressure detections for natural bodies.
Acknowledgements
We thank the referee Dr. David Vokrouhlicky for his useful comments that have improved the quality of the paper. A. D.V. and L.F. acknowledge support by the company SpaceDyS. D.F. conducted this research at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA. This research was conducted under European Space Agency contract No. 4000113555/15/DMRP “P2-NEO-II Improved NEO Data Processing Capabilities”.
Appendix A Additional tables
Yarkovsky detections with 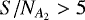 and with
and with 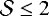 .
.
Yarkovsky detections with 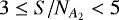 and with
and with 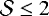 .
.
Rejected Yarkovsky detections.
Marginal significance detections, which means 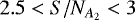 and
and 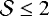 .
.
Detections including both the Yarkovsky effect and SRP, which is the set of asteroids for which the parameter A1 was reliably determined with a 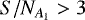 .
.
Comparison between the accepted results of this paper (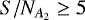 ) and the JPL values.
) and the JPL values.
Comparison between the accepted results of this paper (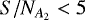 ) and the JPL results.
) and the JPL results.
Results of the comparison between the estimated values of A2 and A1, as contained in this paper and the JPL database.
References
- Baer, J., Chesley, S. R., & Matson, R. D. 2011, AJ, 141, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Binzel, R. P., Lupishko, D., di Martino, M., Whiteley, R. J., & Hahn, G. J. 2002, Physical Properties of Near-Earth Objects (Tucson, AZ: University of Arizona Press), 255 [Google Scholar]
- Bowell, E., West, R. M., Heyer, H.-H., et al. 1992, IAU Circ., 5585 [Google Scholar]
- Brauer, K., Busch, M. W., Benner, L. A. M., et al. 2015, in AAS/Division for Planetary Sciences Meeting Abstracts, 47 [Google Scholar]
- Carpino, M., Milani, A., & Chesley, S. R. 2003, Icarus, 166, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Carry, B. 2012, Planet. Space Sci., 73, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R. 2006, in Asteroids, Comets, Meteors, eds. L. Daniela, M. Sylvio Ferraz, & F. J. Angel, IAU Symp., 229 215 [NASA ADS] [Google Scholar]
- Chesley, S. R., Ostro, S. J., Vokrouhlický, D., et al. 2003, Science, 302, 1739 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R., Farnocchia, D., Nolan, M. C., et al. 2014, Icarus, 235, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R., Farnocchia, D., Pravec, P., & Vokrouhlický, D. 2016, in Asteroids: New Observations, New Models, eds. S. R. Chesley, A. Morbidelli, R. Jedicke, & D. Farnocchia, IAU Symp., 318, 250 [NASA ADS] [Google Scholar]
- Clark, B. E., Binzel, R. P., Howell, E. S., et al. 2011, Icarus, 216, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Del Vigna, A., Milani, A., Spoto, F., Chessa, A., & Valsecchi, G. B. 2018, Icarus, submitted [Google Scholar]
- Einstein, A., Infeld, L., & Hoffmann, B. 1938, Ann. Math., 39, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Emery, J. P., Fernández, Y. R., Kelley, M. S. P., et al. 2014, Icarus, 234, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., & Chesley, S. R. 2014, Icarus, 229, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Chodas, P. W., et al. 2013a, Icarus, 224, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Vokrouhlický, D., et al. 2013b, Icarus, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Tholen, D. J., & Micheli, M. 2014, Celest. Mech. Dyn. Astron., 119, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Chamberlin, A. B., & Tholen, D. J. 2015a, Icarus, 245, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Milani, A., Gronchi, G. F., & Chodas, P. W. 2015b, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson, AZ: University of Arizona Press), 815 [Google Scholar]
- Farnocchia, D., Tholen, D. J., Micheli, M., et al. 2017, in AAS/Division for Planetary Sciences Meeting Abstracts, 49, 100.09 [NASA ADS] [Google Scholar]
- Folkner, W. M., Williams, J. G., Boggs, D. H., Park, R. S., & Kuchynka, P. 2014, Interplanetary Network Progress Report, 196, 1 [Google Scholar]
- Fujiwara, A., Kawaguchi, J., Yeomans, D. K., et al. 2006, Science, 312, 1330 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., Vallenari, A et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Spoto, F., Tanga, P et al.) 2018b, A&A, 616, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giorgini, J. D., Ostro, S. J., Benner, L. A. M., et al. 2002, in Bulletin of the American Astronomical Society, Vol. 34, AAS/Division of Dynamical Astronomy Meeting #33, 934 [NASA ADS] [Google Scholar]
- Giorgini, J. D., Benner, L. A. M., Ostro, S. J., Nolan, M. C., & Busch, M. W. 2008, Icarus, 193, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, A. H., Margot, J.-L., Verma, A. K., et al. 2017, AJ, 153, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, R. S., Ostro, S. J., & Scheeres, D. J. 2003, Icarus, 161, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Konopliv, A. S., Asmar, S. W., Folkner, W. M., et al. 2011, Icarus, 211, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Mainzer, A., Grav, T., Bauer, J., et al. 2011, ApJ, 743, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, Astron. J., 78, 211 [Google Scholar]
- Micheli, M., Tholen, D. J., & Elliott, G. T. 2012, New A, 17, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Micheli, M., Tholen, D. J., & Elliott, G. T. 2013, Icarus, 226, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Micheli, M., Tholen, D. J., & Elliott, G. T. 2014, ApJ, 788, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., & Gronchi, G. F. 2010, Theory of Orbit Determination (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Milani, A., Chesley, S. R., & Valsecchi, G. B. 2000, Planet. Space Sci., 48, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Sansaturio, M., Tommei, G., Arratia, O., & Chesley, S. R. 2005a, A&A, 431, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milani, A., Chesley, S. R., Sansaturio, M. E., Tommei, G., & Valsecchi, G. B. 2005b, Icarus, 173, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Chesley, S. R., Sansaturio, M. E., et al. 2009, Icarus, 203, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Cellino, A., Knežević, Z., et al. 2014, Icarus, 239, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Mommert, M., Farnocchia, D., Hora, J. L., et al. 2014a, ApJ, 789, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Mommert, M., Hora, J. L., Farnocchia, D., et al. 2014b, ApJ, 786, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Moyer, T. 2003, in Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation, Deep-Space Communications and Navigation Series (Hoboken: Wiley-) [CrossRef] [Google Scholar]
- Muinonen, K., Belskaya, I. N., Cellino, A., et al. 2010, Icarus, 209, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, S. P., Margot, J.-L., Busch, M. W., et al. 2013, Icarus, 226, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Nolan, M. C., Magri, C., Howell, E. S., et al. 2013, Icarus, 226, 629 [Google Scholar]
- Nugent, C. R., Margot, J. L., Chesley, S. R., & Vokrouhlický, D. 2012, AJ, 144, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., & Harris, A. W. 2007, Icarus, 190, 250 [CrossRef] [Google Scholar]
- Pravec, P., Scheirich, P., Ďurech, J., et al. 2014, Icarus, 233, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, V., Sanchez, J. A., Bottke, W. F., et al. 2016, AJ, 152, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Rozitis, B., Maclennan, E., & Emery, J. P. 2014, Nature, 512, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Scheeres, D. J., Britt, D., Carry, B., & Holsapple, K. A. 2015, Asteroid Interiors and Morphology, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press) 745 [Google Scholar]
- Scheirich, P., Pravec, P., Jacobson, S. A., et al. 2015, Icarus, 245, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Spoto, F., Milani, A., Farnocchia, D., et al. 2014, A&A 572 [Google Scholar]
- Spoto, F., Milani, A., & Knežević, Z. 2015, Icarus, 257, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Standish, E. M., & Hellings, R. W. 1989, Icarus, 80, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Tardioli, C., Farnocchia, D., Rozitis, B., et al. 2017, A&A, 608, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valsecchi, G. B., Milani, A., Gronchi, G. F., & Chesley, S. R. 2003, A&A, 408, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Milani, A., & Chesley, S. R. 2000, Icarus, 148, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Čapek, D., Chesley, S. R., & Ostro, S. J. 2005, Icarus, 179, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Brož, M., Bottke, W. F., Nesvorný, D., & Morbidelli, A. 2006, Icarus, 182, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Chesley, S. R., & Matson, R. D. 2008, Astron. J., 135, 2336 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015a, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 509 [Google Scholar]
- Vokrouhlický, D., Farnocchia, D., Čapek, D., et al. 2015b, Icarus, 252, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Vereš, P., Farnocchia, D., Chesley, S. R., & Chamberlin, A. B. 2017, Icarus, 296, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Will, C. M. 1993, Theory and Experiment in Gravitational Physics (Cambridge, UK: Cambridge University Press), 396 [Google Scholar]
- Yeomans, D. K., Antreasian, P. G., Barriot, J.-P., et al. 2000, Science, 289, 2085 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
The NEODyS database is available at http://newton.dm.unipi.it.
The JPL Small-Body Database is available at http://ssd.jpl.nasa.gov/sbdb.cgi.
Previously Spoto et al. (2015) used the known density of (704) Interamnia, considered to be a large asteroid with similar composition to Bennu, to estimate porosity of the latter. Recently, the composition of (101955) Bennu was modelled by Clark et al. (2011) based on spectral observations, and it has been found to be closer to other large asteroids, such as (24) Themis and (2) Pallas.
All Tables
Perturbing bodies included in the dynamical model in addition to the Sun, the planets, and the Moon.
Impact monitoring of asteroid 2001 BB16 with a non-gravitational model that includes the Yarkovsky effect.
Impact monitoring of asteroid 2011 MD with a non-gravitational model that includes both the Yarkovsky effect and SRP.
Impact monitoring of asteroid 2011 MD with a non-gravitational model including SRP only.
Detections including both the Yarkovsky effect and SRP, which is the set of asteroids for which the parameter A1 was reliably determined with a 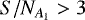 .
.
Results of the comparison between the estimated values of A2 and A1, as contained in this paper and the JPL database.
All Figures
 |
Fig. 1 Graphical representation of the partition of the detections set into classes on the plane
|
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.