| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201832944 | |
| Published online | 10 August 2018 | |
Comparison of the power-2 limb-darkening law from the STAGGER-grid to Kepler light curves of transiting exoplanets★
Astrophysics Group, Keele University,
Keele,
Staffordshire,
ST5 5BG, UK
e-mail: p.maxted@keele.ac.uk
Received:
2
March
2018
Accepted:
21
April
2018
Context. Inaccurate limb-darkening models can be a significant source of error in the analysis of the light curves for transiting exoplanet and eclipsing binary star systems, particularly for high-precision light curves at optical wavelengths. The power-2 limb-darkening law, Iλ(µ) = 1 − c(1−µα), has recently been proposed as a good compromise between complexity and precision in the treatment of limb-darkening.
Aims. My aim is to develop a practical implementation of the power-2 limb-darkening law and to quantify the accuracy of this implementation.
Methods. I have used synthetic spectra based on the 3D stellar atmosphere models from the STAGGER-grid to compute the limb-darkening for several passbands (UBVRI, CHEOPS, TESS, Kepler, etc.). The parameters of the power-2 limb-darkening laws are optimized using a least-squares fit to a simulated light curve computed directly from the tabulated Iλ(μ) values. I use the transformed parameters h1 = 1 − c(1 − 2−α) and h2 = c2−α to directly compare these optimized limb-darkening parameters to the limb darkening measured from Kepler light curves of 16 transiting exoplanet systems.
Results. The posterior probability distributions (PPDs) of the transformed parameters h1 and h2 resulting from the light curve analysis are found to be much less strongly correlated than the PPDs for c and α. The agreement between the computed and observed values of (h1, h2) is generally very good but there are significant differences between the observed and computed values for Kepler-17, the only star in the sample that shows significant variability between the eclipses due to magnetic activity (star spots).
Conclusions. The tabulation of h1 and h2 provided here can be used to accurately model the light curves of transiting exoplanets. I also provide estimates of the priors that should be applied to transformed parameters h1 and h2 based on my analysis of the Kepler light curves of 16 stars with transiting exoplanets.
Key words: techniques: photometric / binaries: eclipsing / stars: fundamental parameters
Tables 1 and 2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/616/A39
© ESO 2018
1 Introduction
The specific intensity emitted from a stellar photosphere depends on both wavelength and viewing angle. For a source function that varies linearly with optical depth the specific intensity can be described by a linear limb darkening law, ![$I_{\lambda}(\mu) = I_{\lambda}(1)\left[1 - u(1-\mu)\right]$](/articles/aa/full_html/2018/08/aa32944-18/aa32944-18-eq3.png) , where μ = cos(θ) is the cosine of the angle between the line of sight and the surface normal vector, and the wavelength dependence is implicit in the linear limb-darkening coefficient, u (Schwarzschild 1906). In general, limb-darkening is more pronounced at shorter wavelengths, becoming almost negligible at infrared wavelengths. At optical wavelengths the best-fit linear limb-darkening coefficient computed from stellar atmosphere models are u ≈ 0.3 for hot stars (effective temperature Teff≳15 000 K) and then increases with decreasing Teff from this value to u ≈ 0.9 for stars with Teff ≈ 3500 K (e.g., Claret 2004). Realistic stellar model atmospheres show that the actual limb darkening of solar-type stars varies by 10% or more around the best-fit linear limb-darkening law (e.g., Howarth 2011).
, where μ = cos(θ) is the cosine of the angle between the line of sight and the surface normal vector, and the wavelength dependence is implicit in the linear limb-darkening coefficient, u (Schwarzschild 1906). In general, limb-darkening is more pronounced at shorter wavelengths, becoming almost negligible at infrared wavelengths. At optical wavelengths the best-fit linear limb-darkening coefficient computed from stellar atmosphere models are u ≈ 0.3 for hot stars (effective temperature Teff≳15 000 K) and then increases with decreasing Teff from this value to u ≈ 0.9 for stars with Teff ≈ 3500 K (e.g., Claret 2004). Realistic stellar model atmospheres show that the actual limb darkening of solar-type stars varies by 10% or more around the best-fit linear limb-darkening law (e.g., Howarth 2011).
The advent of very high-precision photometry for transiting exoplanet systems has led to extensive discussion in the literature of the systematic errors in the parameters for these exoplanet systems that result from inaccuracies and uncertainties in the treatment of limb darkening, e.g., Espinoza & Jordán (2016), Müller et al. (2013), Howarth (2011), Sing et al. (2008), Morello et al. (2017), Neilson et al. (2017), Kipping (2013), etc. One well-established result from such studies is that using a linear limb darkening law can lead to significant bias in the parameters derived from the analysis of high-quality photometry. For example, Espinoza & Jordán (2016) found systematic errors in the radius estimates for small planets as large as 3% as a result of using linear limb-darkening coefficients. There are several alternative ways to parametrize limb-darkening. Among the alternative two-parameter laws, the most commonly used in exoplanet studies is the quadratic limb-darkening law (Kopal 1950):
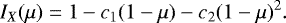
This limb-darkening law has the advantage of being relatively simple and well-understood in terms of the correlations between the coefficients (Pál 2008; Kipping & Bakos 2011; Howarth 2011) and how to sample the parameter space to achieve a non-informative prior (Kipping 2013) but it fails to match optical high-precision light curves of transiting exoplanet systems (Knutson et al. 2007).
The Claret 4-parameter limb-darkening law (Claret 2000) is often used in exoplanet studies. As the name suggests, this limb-darkening law uses four coefficients to capture the detailed shape of the limb-darkening profile IX (μ) for a given bandpass X using the following equation:
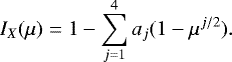
Including the coefficients of this limb-darkening law in a least-squares fit to observed transit light curves is impractical because they are found to be strongly correlated with each other and degenerate with other parameters of the fit. Instead, it is common practice to use interpolation within a grid of tabulated coefficients (e.g., Claret et al. 2013) to select the values of a1, …, a4. These coefficients may be fixed or the effective temperature used for the interpolation, Teff,ld, can be included as a free parameter in the fit (e.g., Maxted et al. 2016).
Among the limb-darkening laws with 2 coefficients, the power-2 limb-darkening law (Hestroffer 1997) has been recommended by Morello et al. (2017) as they find that it outperforms other two-coefficient laws adopted in the exoplanet literature in most cases, particularly for cool stars. The form of this limb-darkening law is
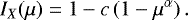
Using an exponent of μ rather than a coefficient of some function of μ enables this two-parameter law to match accurately the shape of the limb darkening profile towards the limb of the star using only one extra parameter cf. a linear limb-darkening law. There has been very little discussion in the literature of the power-2 limb-darkening law applied to exoplanet transit studies and so its properties and the practicalities of using this law to determine exoplanet properties are not yet well understood. Here I describe a practical implementation of the power-2 limb-darkening law, including a tabulation of the parameters for various passbands and instruments, and present an analysis of the Kepler light curves for 16 transiting exoplanet systems that has been used quantify the accuracy of these parameters.
2 Analysis
The following section describes the calculation of the limb-darkening profiles, IX (μ), for various passbands and how the parameters of a power-2 limb-darkening law based on these profiles can be optimized for the analysis of the light curve for a given exoplanet system or binary star. I then compare these optimized power-2 limb-darkening law parameters to observed values for transiting planet host stars derived from the analysis of their Kepler light curves. This comparison shows a very good level of agreement between theory and observationsso I then proceed to provide a tabulation of power-2 limb-darkening law parameters that can be used to model the light curves of exoplanet systems and binary stars together with some recommendations for their use.
2.1 Calculation of the limb-darkening profiles
I have calculated the variation of specific intensity with viewing angle integrated over various passbands, i.e., the limb-darkening profile, IX (μ), where the subscript X denotes the passband. For the specific intensity as a function of wavelength and viewing angle, Iλ (μ), I have used the synthetic 3D LTE spectra from the STAGGER-grid calculated by Magic et al. (2015). This grid of models spans a range of effective temperature, surface gravity and metallicity that covers the majority of known exoplanet host stars. There are small but, for high-precision work, significant differences between the limb darkening predictions from 3D model atmospheres compared to 1D model atmospheres (Magic et al. 2015). 3D model atmospheres provide a more realistic description of the convective motions at different heights in cool star atmospheres than the simplified mixing-length approach adopted in 1D stellar model atmospheres. This is essential for accurate prediction of the limb darkening, which is determined mainly by the temperature gradient. The limb darkening predictions from 3D model atmospheres are a good match to the observed limb darkening profiles of the Sun (Pereira et al. 2013), α Cen A and B (Bigot et al. 2006) and HD 209458 (Hayek et al. 2012). In all three cases, the 3D model atmospheres provide a better match to the observations than 1D model atmospheres. The 3D radiative hydrodynamic atmosphere models from which the spectra used here are calculated are described in more detail by Chiavassa et al. (2018). The grid of stellar atmosphere models covers the effective temperature range Teff ≈ 4000–7000 K in steps of approximately 500 K, the surface gravity range log g = 1.5–5.0 in steps of 0.5 dex, and metallicity values of [Fe/H] = −2.0, − 1.0, − 0.5, 0.0, and + 0.5. The coverage within these ranges is not uniform – the complete set of available models is shown in Fig. 1. The effective temperatureassigned to each model using the Stefan–Boltzmann law applied to the computed emergent spectrum is taken from Table B0 of Chiavassa et al. (2018). The spectra computed from the STAGGER-grid model atmospheres are provided at 11 values of μ from 0 to 1 for [Fe/H] = −2, −1 and 0, and at 10 values of μ from 0.01 to 1 for the models at [Fe/H] = ±0.5. The computed spectra for μ = 0 have very low flux levels compared to the other spectra so for [Fe/H] = ±0.5 I assume IX(0) = 0. The spectra are sampled with variable wavelength step Δλ such that λ∕Δλ = 20 000.
The limb-darkening profile, IX(μ), has been calculated for the following instruments and passbands: CHEOPS (Cessa et al. 2017); Kepler (Borucki et al. 2010); TESS (Ricker et al. 2015); Gaia (Gaia Collaboration 2016); Johnson/Bessell UBVRI (Bessell 1990); Sloan SDSS ugriz (Doi et al. 2010); MOST (Walker et al. 2003); CoRoT (Auvergne et al. 2009).
The spectra at [Fe/H] = ±0.5 only cover the wavelength range up to 1 μm. The bandpasses for the CHEOPS and TESS instruments extend a small way beyond this limit. This was handled by calculating a linear fit to the log of the model flux, logfλ over the region 0.8–1 μm, and then extrapolating this linear fit up to 1.15 μm. Comparing this linear extrapolation to the computed flux at other values of [Fe/H] shows that it provides a very good match to the actual flux distribution in this region, on average. In addition, the fraction of the stellar flux emitted in this extrapolated wavelength region for the CHEOPS and TESS bandpasses is ≲1% so this extrapolation will introduce negli- gible systematic error in the computed values of IX(μ).
The nature of the detector used in the instrument must be accounted for in the calculation of the limb-darkening profile (Bessell et al. 1998). Charge-coupled devices (CCDs) count photons, they do not measure energy, so for the accurate computation of IX (μ) over a passband with response function RX(λ) for an instrument with a CCD detector, the specfic intensity must be converted from energy flux to photon number flux, i.e.,
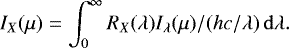
This has little effect for narrow passbands but can be a noticable effect for the broad-band photometers often used for planetary transit surveys such as Kepler and CHEOPS.
The irregular spacing of Teff values within the model grid and their relatively large spacing of about 500 K can be difficult to deal with when interpolating within the grid of IX (μ) values. To remedy this problem I have used interpolation of IX(μ) as a function Teff at each value of logg, [Fe/H] and μ to create a tabulation of IX(μ) on a regular grid of Teff with a grid spacing of 250 K. This requires a small degree of extrapolation at the edge of the model grid so I used quadratic spline interpolation to ensure that this extrapolation is stable. In a few cases, there are only two values of Teff for a given pair of log g and [Fe/H] values, in which case I use a linear fit to IX(μ) points for the interpolation and extrapolation. The model spectra for log g = 4.44 and (log g, [Fe/H]) = (3.0, −2) are only available for one value of Teff so there are no corresponding entries for these logg and [Fe/H] values in the tabulations provided here. A complete tabulation of IX (μ) for each passband is provided at the CDS, an excerpt from this table is shown in Table 1.
The limb-darkening profiles for Teff ≈ 5777 K are not included in tabulation of IX(μ), so interpolating in this table to match these profiles is a good test of the tabulated values and the interpolation scheme used. In Fig. 2 we compare the directly computed values of IX (μ) for Teff ≈ 5777 K and log g = 4.44 to the interpolated values using linear barycentric interpolation1. The rms residual between the computed and interpolated values is 0.5% or less over the μ range 0.01–1.0 for these data. Also shown in Fig. 2 are the corresponding power-2 limb-darkening laws where the parameters have been optimized as described in Sect. 2.5.
 |
Fig. 1 Grid of STAGGER-grid atmosphere models used to calculate the limb-darkening profiles of cool stars in this study. Note that the points are offset vertically according to [Fe/H] at each value of log g so that they can be distinguished, but no horizontal offset has been applied, i.e., the plotted positions give the actual value of Teff for each model. Small crosses show the regular grid of Teff values that have been used for the tabulations provided here. |
 |
Fig. 2 Comparison of directly calculated (points) and interpolated (dotted lines) limb-darkening profiles for the CHEOPS bandpass at Teff ≈ 5777 K, log g = 4.44 and for [Fe/H] = −2, −1, −0.5, 0, +0.5. The corresponding power-2 limb-darkening laws optimized to fit the light curve for a typical Jupiter-like transiting exoplanet are also shown (dotted lines). Note that the profiles are offset vertically according to [Fe/H]. The lower panel is plotted as a function of the distancefrom the centre of the stellar disc in units of the stellar radius. |
2.2 Kepler light curves
To test the accuracy of the power-2 limb-darkening profiles calculated from the STAGGER-grid I have compared model light curves generated from these data to high-precision light curves for transiting exoplanet systems observed with Kepler. Transiting exoplanet systems with deep eclipses observed at high signal-to-noise with Kepler were selected from the list of 38 systems studied by Müller et al. (2013). I excluded stars for which there is no published estimate of Teff, log g and [Fe/H] based on high-resolution spectroscopy and also systems with stellar companions or eccentric orbits. There are also a few stars that had to be excluded from this study because they are too hot or too cool, i.e., the observed values of Teff, log g and [Fe/H] for these stars lie outside the grid of limb-darkening profiles from the STAGGER-grid.
Short cadence (SC) light curves from Data Release 25 (DR25; Thompson et al. 2016) for the remaining 16 systems were downloaded from the the Mikulski Archive for Space Telescopes2 (MAST). DR25 is the final data release from the Kepler mission and contains all the observation obtained during the original Kepler mission divided in to 18 “quarters” (Q0 to Q17) with a typical duration of about 90 days each. I used the observations provided in the column PDCSAP_FLUX and their associated errors for this analysis. Observations with a non-zero value of the SAP_QUALITY quality flag were excluded from further processing. I also excluded outliers that deviated by more than 4 standard deviations from a running median filter. Trends in the data due to instrumental and stellar noise sources were modelled using a Gaussian process (GP) fitted to the data between the transits. I used the CELERITE package (Foreman-Mackey et al. 2017) to model these data using the following kernel with the default value of ϵ = 0.01 to approximate the Matérn–3/2 covariance function:
![\begin{align*} k(\tau) = \sigma^2\,\left[ \left(1+1/\epsilon\right)\,e^{-(1-\epsilon)\sqrt{3}\,\tau/\rho} \left(1-1/\epsilon\right)\,e^{-(1+\epsilon)\sqrt{3}\,\tau/\rho} \right]. \nonumber \end{align*}](/articles/aa/full_html/2018/08/aa32944-18/aa32944-18-eq8.png)
Here, τ is the time difference between two observations and ρ is a parameter that controls the timescale over which observational errors are correlated. Evaluating the GP at all data points was slow, so instead it was evaluated at 1000 points evenly distributed in time across each quarter of the Kepler data and then spline interpolation was used to evaulate the trend for all the observations in each quarter, including those obtained during a transit. The data were divided by the trend and saved with their time of observation and errors for further analysis.
Specific intensity as function of the cosine of the viewing angle integrated over various bandpbasses, IX (μ).
2.3 Light curve analysis
I used version 1.8.0 of the ellc light curve model (Maxted 2016) to determine the geometry and limb-darkening parameters for each of these 16 transiting exoplanet systems. The free parameters in the model for each system were the radius of the host star in units of the semi-major axis, R⋆ ∕a, the ratio of the radii, k = Rpl∕R⋆, where Rpl is the radius of the companion; the impact parameter, b = acos(i)∕R⋆, where i is the orbital inclination; the time of primary eclipse, T0; the orbital period, P; and the power-2 limb-darkening parameters, c and α. For systems where contamination of the photometric aperture is noted in the MAST archive data I also include a “third-light” parameter, ℓ3, as a free parameter in the fit with a prior set by the mean and standard deviation of the contamination values given for each Kepler quarter. These contamination values are all very small (≲1%), so they have little influence on the analysis.
I assume that the star in these exoplanet systems is spherical and use a polytrope with index n =1.5 to calculate the dimensions of the ellipsoid used to approximate the shape of the planet. The flux contribution in the Kepler bandpass from the planet is assumed to be negligible for these systems. There is little or no information about the geometry of these systems in the observations between the eclipses so this analysis uses only observations obtained during transit plus an additional 25% of the transit width before and after start and end of the transit. Circular orbits have been assumed for all systems.
Some of the targets studied here show quasi-periodic variability due to magnetic activity (star spots). It is notoriously difficult to include star spots in the model for a transiting planet system because the number of free parameters required is large and the constraints on these parameters from the light curve are generally weak and highly degenerate. I did not attempt to model star spots for any of the systems here. Instead, I simply divide-out the trend established from the Gaussian process fit to the out-of-eclipse data. The effect of this approach on the results will be discussed below.
I used EMCEE (Foreman-Mackey et al. 2013), a PYTHON implementation of an affine invariant Markov chain Monte Carlo (MCMC) ensemble sampler, to calculate the posterior probability distribution (PPD) of the model parameters. An ensemble with 72 or (for cases where ℓ3 was a free parameter) 80 samples per chain step (“walkers”) was initialized using 512 “burn-in” chain steps. The PPD was then calculated using 256 chain steps starting with the last ensemble from the burn-in phase. The convergence of the chain was judged by visual inspection of the parameters and the likelihood as a function of step number. In cases where it was suspected that the chain had not sampled the posterior probability distribution accurately, a new Markov Chain was calculated starting from the best-fit parameters in the previous chain. This initial optimization of the parameters was done using the “grid_1 = very_sparse” option in ellc to specify the minimum number of grid points for the numerical integration of the flux from the host star. This has the advantage of reducing the computation time but introduces a bias of approximately 50 ppm in the simulated eclipse depth. This bias is significant for the analysis of the very high-precision light curves being used in this study so the results below were calculated using a second Markov chain with 256 chain steps following a burn-in phase of 128 steps using the option “grid_1 = default”. The second chain was initialised using the best fit parameters found from the first Markov chain. In practice, this made a neglible difference to the result presented below for h1 and h2 but there are very small but significant differences to the parameters R⋆∕a, k and b for some stars.
The standard error for observation i was assumed to be  where σi is the standard error derived from the value PDCSAP_FLUX_ERR in the MAST archive file and σext is a constant that is optimized by including the relevant term in the calculation of the likelihood for each trial set of parameters. For most of the light curves studied here, we find σext ≈ 20 ppm. If the out-of-eclipse level is included as a free parameter, it is found to be always very close to the value 1 with a very small error and is not correlated with the other parameters so it was fixed to this value for the analysis presented here.
where σi is the standard error derived from the value PDCSAP_FLUX_ERR in the MAST archive file and σext is a constant that is optimized by including the relevant term in the calculation of the likelihood for each trial set of parameters. For most of the light curves studied here, we find σext ≈ 20 ppm. If the out-of-eclipse level is included as a free parameter, it is found to be always very close to the value 1 with a very small error and is not correlated with the other parameters so it was fixed to this value for the analysis presented here.
A summary of the results from this analysis are given in Table A.1. The best fit found for each light curve is shown in Fig. A.1. The values of T0 and P are not quoted here because the long cadence (LC) data from Kepler and other times of mid-eclipse reported in the literature are not included in the analysis and so these estimates are not optimal. We also do not quote directly the values of c and α determined from these fits for the reasons described in the following section.
2.4 Comparison of observations and theory
The joint PPDs for c and α calculated using EMCEE from the Kepler light curves are shown in Fig. A.2. It can be seen that these parameters are strongly correlated, i.e., neither parameter is determined very accurately, but the shape of the transit light curve does impose a strong constraint on the relationship between these two parameters. This makes it awkward to compare the computed values of these parameters directly to the observed values because the two observed values may agree within their error bars with the computed values while being inconsistent with the constraints on the relationship between them imposed by the light curve.
Instead of c and α, I use the parameters
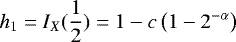 (1)
(1)
to compare the computed and observed limb-darkening profiles. The value of h1 measures the bandpass-integrated specific intensity relative to the centre of the disc, IX, in the region on the stellar disc at a distance 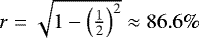 towards the limb. Similarly, h2 measures the drop in IX between the same radius and the limb. These definitions impose the constraints h1 < 1 and h1 + h2 ≤ 1 that are required so that the flux is positive at all points on the stellar disc. The inverse relations, provided here for convenience, are
towards the limb. Similarly, h2 measures the drop in IX between the same radius and the limb. These definitions impose the constraints h1 < 1 and h1 + h2 ≤ 1 that are required so that the flux is positive at all points on the stellar disc. The inverse relations, provided here for convenience, are
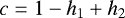 (3)
(3)
The values of h1 and h2 derived from the analysis of the Kepler light curves are given in Table A.1. Also given in this table are the optimized values of h1 and h2 computed from the STAGGER-grid, as described below.
2.5 Optimized power-2 limb-darkening law parameters
Howarth (2011) has outlined a simple and elegant method to achieve a “like-for-like” comparison between observed and theoretical limb-darkening profiles for transiting exoplanet systems. The essence of the method is to simulate light curves using the limb-darkening profile and then to find the parameters of the limb-darkening law that provide the best least-squares fit to this simulated light curve. These optimized limb-darkening parameters can then be compared directly to the values obtained by fitting the light curves of transiting exoplanet systems.
I used version 1.8.0 of the ellc light curve model to simulate light curves of transiting exoplanet systems using the limb-darkening profile data for the Kepler bandpass described in Sect. 2.1. After some experimentation I found that a simulated light curve with 32 points uniformly distributed from mid-transit to the end of the transit is sufficient to calculate h1 and h2 to a precision much better than the observed accuracy of these parameters. Similarly, the grid size option “very_sparse” is sufficient to precisely calculate the h1 and h2 for the transiting exoplanet systems studied here, although for the direct comparison with the values of h1 and h2 from the Kepler light curves in Table A.1 we used the “default” grid size option in order to minimize the numerical noise in these results. The optimization of the limb-darkening parameters uses spheres to model both the star and the planet and a tabulation of the limb-darkening profile interpolated using a monotonic piecewise cubic Hermite interpolating polynomial3 onto a regular grid of 51 μ values. The light curve is independent of the assumed value for R⋆∕a = 0.1 with these assumptions. The values of b = acosi∕R⋆ and k = Rpl∕R⋆ used for each system were taken from Table A.1. These calculations were done using the PYTHON module pycheops4 that is currently under development in support of the ESA CHEOPS mission.
The values of h1 and h2 each define a relation between c and α, as follows:
![\begin{align}& c = h_2 2^{\alpha} , \\[5pt] & c = (1-h_1)/(1-2^{-\alpha}). \end{align}](/articles/aa/full_html/2018/08/aa32944-18/aa32944-18-eq15.png)
These relations are shown in Fig. A.2 for the values of h1,comp and h2,comp optimized as described above using limb-darkening profiles interpolated from Table 1. Unless otherwise stated, the values of Teff, log g and [Fe/H] in this table used to compute h1,comp and h2,comp were taken from TEPCat5 (Southworth 2011) using values published up to 2018 Feb 25. The standard errors on h1,comp and h2,comp due to the uncertainties in the observed values of Teff, log g and [Fe/H] were calculated using a Monte Carlo method, i.e., we generated a small sample of h1,comp and h2,comp values using values of Teff, log g and [Fe/H] randomly selected from Gaussian distributions with mean and standard deviation set from the observed values with their quoted standard errors, then took the standard deviations of these samples as the standard errors for h1,comp and h2,comp.
Figure 3 shows the how the parameters h1 and h2 vary as a function of impact parameter, b, for three different test cases. The first case is similar to the exoplanet systems studied above but assuming that the observations have been done with CHEOPS rather than Kepler. The second case simulates an eclipsing binary containing two similar cool dwarf stars observed with TESS. The third case is a “worst-case scenario” of an eclipse of a metal-poor red giant observed in the Sloan u′ passband. The vertical scale in these diagrams is set by the median standard errors on h1,obs and h2,obs from Table A.1 (± 0.003 and ± 0.046, respectively). For the first two cases, the variation of h1 and h2 is always much less than the typical uncertainty on these values that can be achieved with the best data currently available. The variations in h1 and h2 are also less than ± 0.003 and ± 0.046 for b≲0.9 in the worst-case scenario. For the first case we also simulated the case k = 0.9. In this case, h1 and h2 are also seen to have negligible dependence on k.
The optimized parameters of a power-2 limb-darkening law for all passbands are given in Table 2 for all values of Teff, log g and [Fe/H] in our re-sampled model grid. The optimization has only been done for the case b = 0 and k = 0.1 since, in general, the parameters h1 and h2 show very little dependence on these parameters. The calculation was done using the grid size option “default” in ELLC to simulate 32 points evenly distributed through one half of a symmetrical transit light curve, as described above.
 |
Fig. 3 Optimized and transformed power-2 limb-darkening law parameters, h1 and h2 as a functionof impact parameter, b. The values of Teff, [Fe/H], logg and radius ratio, k, and the bandpass used for the simulation are noted in the title to each pair of panels. Note that the vertical scale on each axis is set by the median standard errors on h1,obs and h2,obs from Table A.1 (± 0.003 and ± 0.046, respectively). Also shown for the CHEOPS passband are the results for k = 0.9 (dashed line). The small spikes seen on the curves for the u′ passband are the result of numerical noise in the light curves at the few ppm level. |
Optimized power-2 limb-darkening law parameters, c and α, and the corresponding transformed parameters, h1 and h2.
3 Discussion
The differences Δh1 = h1,obs − h1comp and Δh2 = h2,obs − h2comp between the observed and computed values of h1 and h2 are shown as a function of effective temperature, Teff, in Fig. 4. Kepler-17 is a clear outlier in these plots. This is very likely to be a consequence of the magnetic activity that is obvious in the light curve of this star. The root mean square of this variation is about 0.8% on average in the Kepler SC light curves of Kepler-17, which is an order of magnitude larger than the next most variable star and approximately 60 times larger than the median value of this statistic for the other 15 stars in this sample. For this reason, we ignore Kepler-17 in the following discussion of the random and systematic errors in Δh1 and Δh2.
The square root of the mean residuals excluding Kepler-17 are 0.012 for h1 and 0.055 for h2. The mean value of the residuals are ⟨Δh1⟩ = 0.010 ± 0.002 and ⟨Δh2⟩ = −0.042 ± 0.010, where the uncertainty quoted here is the standard error on the mean. If we assume that there is some additional error σ1 in either the computed or observed values of h1, and similarly for h2, then we findthat σ1 = 0.011 and σ2 = 0.045 are required to achieve χ2 = Ndf for the null hypothesis Δh1 = Δh2 = 0, where Ndf = 15 is the number of degrees of freedom, which is equal to the number of observations here since there are no free parameters in this model.
The origin of this small additional uncertainty in h1, and h2 will be discussed below, but it should be stated immediately that these statistics represent a remarkably good level of agreement between the state-of-the-art in stellar atmospheric models and the best available observational data for planet host stars. They also demonstrate that the power-2 limb-darkening law does indeed represent a very good approximation to both the observed and theoretical limb-darkening profiles of cool stars. It also has the advantage of being a simple function of two parameters, and the transformed parameters h1 and h2 provide a way to represent this limb-darkening law that allows for direct comparison between theory and observations. These transformed parameters have the useful feature that they are not strongly correlated when used as free parameters for the least-squares fit to the light curves of transiting exoplanet systems.
In general, there remains a weak correlation between h1 and h2 in the PPDs shown in Fig. A.2. It is possible to reduce or remove this correlation by adjusting the choice of a reference value of μref in the definition of the parameters 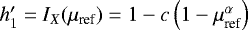 and
and 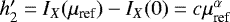 . We have not made this adjustment here because the aim is to compare the values of h1 and h2 for different stars. It is not straightforward to compare the values of
. We have not made this adjustment here because the aim is to compare the values of h1 and h2 for different stars. It is not straightforward to compare the values of 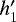 and
and 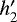 across a sample of stars because these values will depend on the different values of μref used for each transiting exoplanet as well as the properties of the star itself.
across a sample of stars because these values will depend on the different values of μref used for each transiting exoplanet as well as the properties of the star itself.
Kepler-17 is a clear outlier in terms of its variability between the transits and also an outlier in Fig. 4. A likely reason for this disagreement can be seen from careful inspection of the residuals from the light curve fit in Fig. A.1. There is clear excess noise during the transit that is not seen before or after the transit. This excess noise is due to the planet transiting magnetically active regions on the star (star spots and faculae). This strongly suggests that the reason for the offset between the observed and computed values of h1 and h2 is due to the relatively high level of magnetic activity in this star. It is also noticable that the small but significant mean offset between the observed and computed values of h1 and h2 for the other 15 stars in the sample are both in the same sense as for Kepler-17, i.e., Δh1 is positive and Δh2 is negative. This suggests that part of the reason for this offset may be weak magnetic activity in these solar-type stars that is not included in the stellar atmosphere models used here.
Figure 5 shows the effect on a typical light curve of perturbing h1 by σ1 and similarly for h2 and σ2. It can be seen that h1 influences the overall shape and depth of the transit, whereas the influence of h2 is mostly confined to the ingress and egress phases, as might be expected given that it is defined as the change in specific intensity due to limb darkening near the limb of the stars (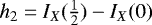 ). It should be emphasized that changes in the transit depth and shape due to the uncertainties in h1 and h2 are very small (≲50 ppm) and so will only be noticable in light curves of the very highest quality for bright systems with deep eclipses. Indeed, it may be that some of the offset between the observed and computed values of h1 and h2 is due to small systematic errors in the photometry. In general, the current level of uncertainty in the computed values of h1 and h2 will have a negligible impact on the analysis of most light curves at optical wavelengths for many transiting exoplanets. Figure 5 also demonstrates that using a sphere to optimize of the power-2 limb-darkening law coefficients instead of an ellipsoid will have a negligible effect.
). It should be emphasized that changes in the transit depth and shape due to the uncertainties in h1 and h2 are very small (≲50 ppm) and so will only be noticable in light curves of the very highest quality for bright systems with deep eclipses. Indeed, it may be that some of the offset between the observed and computed values of h1 and h2 is due to small systematic errors in the photometry. In general, the current level of uncertainty in the computed values of h1 and h2 will have a negligible impact on the analysis of most light curves at optical wavelengths for many transiting exoplanets. Figure 5 also demonstrates that using a sphere to optimize of the power-2 limb-darkening law coefficients instead of an ellipsoid will have a negligible effect.
The analysis above supports the conclusion of Morello et al. (2017) that the power-2 limb-darkening law is to be recommended for the analysis of transiting exoplanet light curves. The atmospheric parameters (Tref, log g and [Fe/H]) for many planet host stars are covered by the grid of parameters for the power-2 limb-darkening law provided in Table 2. The power-2 limb-darkening law has been implemented in the light curve model ELLC and can also be used with other light curve models, e.g., batman (Kreidberg 2015). It is quite straightforward to implement this simple law in other light curve models. There does not appear to be any reason why the power-2 limb-darkening law cannot also be used to model eclipsing binary stars, and the results in Fig. 4 suggest that the convenient properties of the transformed parameters h1 and h2 apply equally to these systems as for transiting exoplanet systems.
The transformed parameters h1 and h2 also make it straightforward to calculate a Bayesian prior that accounts for the uncertainties in the model coefficients when calculating the likelihood during the analysis of light curves using methods such as EMCEE or other Markov chain methods. For passbands similar to Kepler, e.g., CHEOPS, CoRoT and Gaia, the results from the analysis above can be used directly. For stars that do not show strong magnetic activity, it can be assumed that h1 is accurate to ± σ1 = ±0.011 and h2 is accurate to ± σ2 = ±0.045. The Bayesian prior can then be calculated using a Gaussian centred on the values of h1 and h2 interpolated from Table 2 with standard deviations 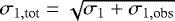 , where σ1,obs is the standard error on h1 due to the uncertainties in the observed values of Teff, log g and [Fe/H], and similarly for σ2,obs. The values of σ1,obs and σ2,obs can be calculated using a Monte Carlo method, as described in Sect. 2.5.
, where σ1,obs is the standard error on h1 due to the uncertainties in the observed values of Teff, log g and [Fe/H], and similarly for σ2,obs. The values of σ1,obs and σ2,obs can be calculated using a Monte Carlo method, as described in Sect. 2.5.
Limb darkening becomes less important at longer wavelengths so the same assumptions can also be made for redder passbands such as TESS, Johnson I band and Sloan z′ band. This assumptions may be a little pessimistic, but this is a sensible approach to take until the cause of the uncertainties in h1 and h2 are better understood. For bandpasses such as Johnson B band that cover shorter wavelengths where limb darkening is a stronger effect I would recommend increasing the assumed values of σ1 and σ2 by a factor of 2 or 3, perhaps even more for the Johnson U band and Sloan u′ band where the effect of uncertainties in the atomic data for the large number of atomic lines in these strongly line-blanketed regions may be much worse.
The analysis above only quantifies the uncertainties in the model coefficients for dwarf stars with [Fe/H] ≳0 showing weak magnetic activity. It is likely that the model uncertainties are larger for stars that are magnetically active and may well be biased in the sense that h1 is too low and h2 is too high. However, this conclusion is only based on one magnetically active star in the sample studied so far so it needs further investigation. Similarly, there is currently very little information available to quantify the uncertainties in the power-2 limb-darkening law coefficients for metal poor stars or giant stars.
 |
Fig. 4 Difference between the observed and computed values of h1 and h2. Data for Kepler-17 are plotted using an open symbol. The vertical error bars are calculated from the square root of the sum of the variances of the observed and calculated values. |
 |
Fig. 5 A simulated light curve for the following parameters: R⋆/a = 0.2, k = 0.1, b = 0.4, q = 0.0008, h1 = 0.75 ± 0.01, h2 = 0.45 ± 0.05. The upper plot shows the light curve for the nominal values of h1 and h2 and (indistinguishable at this scale) the light curves for both h1 and h2 perturbed upwards by one standard deviation. The lower plot shows the change in flux due to a change by +1 standard deviation in h1 (dashed line) and h2 (dotted line). Also shown in the lower panel is the effect of using a sphere to model the shape of the transiting planet instead of a polytrope (dot-dashed line). Note that in the latter case the radius of the sphere has been reduced by 0.5% cf. the volume-average radius of the ellipsoid used to model the planet as a polytrope. This correction is required so that the eclipse depth for the spherical planet case matches the eclipse depth for the ellipsoidal planet model. |
4 Conclusions
The power-2 limb-darkening law can be recommended for the analysis of light curves for transiting exoplanet systems and binary stars for stars with Teff, log g and [Fe/H] within the model grid range studied here. Tabulations of the parameters of the power-2 limb-darkening law have been provided and tested against very high-quality observations of transiting exoplanet systems obtained with Kepler. These observations have been used to quantify the uncertainties in the parameters h1 and h2 for dwarf stars with [Fe/H] ≳0 showing weak magnetic activity. There may be a small bias in the computed values of h1 and h2 compared to the best-fit values for magneticically active stars, but this needs further investigation. Further work is also needed to quantify the uncertainties in h1 and h2 for metal poor stars and red giants.
Acknowledgements
This paper includes data collected by the K2 mission. Funding for the K2 mission is provided by the NASA Science Mission directorate. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. PM would like to thank Andrea Chiavassa and Martin Asplund for providing additional limb-darkening data calculated from the STAGGER-grid. PM gratefully acknowledges support provided by the UK Science and Technology Facilities Council through grant number ST/M001040/1.
Appendix A Light curve analysis – results
The results for the fits to the light curves of 16 transiting exoplanet systems are shown in this appendix.
Results for ellc light curve model fits to Kepler light curves of transiting exoplanet systems.
 |
Fig. A.1 Kepler light curves of transiting exoplanet and binary star systems. Observations are plotted using small points and the best-fit light curve model is shown as a line. The name of each star is noted in the title to each panel together with the impact parameter b = a cosi∕R⋆ and the ratioof the radii k = Rpl∕R⋆. |
 |
Fig. A.2 Posterior probability distributions for the limb-darkening parameters from the analysis of the Kepler light curves. The PPDs are shown as gray-scale density plots. The median values and standard deviations for each parameter are shown as an error bar. The vertical and horizontal lines in the left-hand panel for each star show the ± 1-σ limits on the computed values of c and α. The corresponding ± 1-σ limits on h1 and h2 are shown as curved lines in the same panel and as vertical and horizontal lines in the right-hand panel. |
References
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Bigot, L., Kervella, P., Thévenin, F., & Ségransan, D. 2006, A&A, 446, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cessa, V., Beck, T., Benz, W., et al. 2017, SPIE Conf. Ser., 10563, 105631L [Google Scholar]
- Chiavassa, A., Casagrande, L., Collet, R., et al. 2018, A&A, 611, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2013, A&A, 552, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Doi, M., Tanaka, M., Fukugita, M., et al. 2010, AJ, 139, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, N., & Jordán, A. 2016, MNRAS, 457, 3573 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Agol, E., Ambikasaran, S., & Angus, R. 2017, AJ, 154, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayek, W., Sing, D., Pont, F., & Asplund, M. 2012, A&A, 539, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hébrard, G., Santerne, A., Montagnier, G., et al. 2014, A&A, 572, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hestroffer, D. 1997, A&A, 327, 199 [NASA ADS] [Google Scholar]
- Howarth, I. D. 2011, MNRAS, 418, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 435, 2152 [Google Scholar]
- Kipping, D., & Bakos, G. 2011, ApJ, 730, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Noyes, R. W., Brown, T. M., & Gilliland, R. L. 2007, ApJ, 655, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Kopal, Z. 1950, Harvard College Observatory Circular, 454, 1 [Google Scholar]
- Kreidberg, L. 2015, PASP, 127, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- Magic, Z., Chiavassa, A., Collet, R., & Asplund, M. 2015, A&A, 573, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maxted, P. F. L. 2016, A&A, 591, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Collier Cameron, A., et al. 2016, A&A, 591, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morello, G., Tsiaras, A., Howarth, I. D., & Homeier, D. 2017, AJ, 154, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. M., Huber, K. F., Czesla, S., Wolter, U., & Schmitt, J. H. M. M. 2013, A&A, 560, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neilson, H. R., McNeil, J. T., Ignace, R., & Lester, J. B. 2017, ApJ, 845, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A. 2008, MNRAS, 390, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A., Díaz, R. F., Moutou, C., et al. 2012, A&A, 545, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarzschild,K. 1906, Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, 43 [Google Scholar]
- Sing, D. K., Vidal-Madjar, A., Désert, J.-M., Lecavelier des Etangs, A., & Ballester, G. 2008, ApJ, 686, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, S. E., Fraquelli, D., Van Cleve, J. E., & Caldwell, D. A. 2016, Kepler Archive Manual, Tech. Rep., Space Telescope Science Institute [Google Scholar]
- Walker, G., Matthews, J., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Specific intensity as function of the cosine of the viewing angle integrated over various bandpbasses, IX (μ).
Optimized power-2 limb-darkening law parameters, c and α, and the corresponding transformed parameters, h1 and h2.
Results for ellc light curve model fits to Kepler light curves of transiting exoplanet systems.
All Figures
 |
Fig. 1 Grid of STAGGER-grid atmosphere models used to calculate the limb-darkening profiles of cool stars in this study. Note that the points are offset vertically according to [Fe/H] at each value of log g so that they can be distinguished, but no horizontal offset has been applied, i.e., the plotted positions give the actual value of Teff for each model. Small crosses show the regular grid of Teff values that have been used for the tabulations provided here. |
| In the text | |
 |
Fig. 2 Comparison of directly calculated (points) and interpolated (dotted lines) limb-darkening profiles for the CHEOPS bandpass at Teff ≈ 5777 K, log g = 4.44 and for [Fe/H] = −2, −1, −0.5, 0, +0.5. The corresponding power-2 limb-darkening laws optimized to fit the light curve for a typical Jupiter-like transiting exoplanet are also shown (dotted lines). Note that the profiles are offset vertically according to [Fe/H]. The lower panel is plotted as a function of the distancefrom the centre of the stellar disc in units of the stellar radius. |
| In the text | |
 |
Fig. 3 Optimized and transformed power-2 limb-darkening law parameters, h1 and h2 as a functionof impact parameter, b. The values of Teff, [Fe/H], logg and radius ratio, k, and the bandpass used for the simulation are noted in the title to each pair of panels. Note that the vertical scale on each axis is set by the median standard errors on h1,obs and h2,obs from Table A.1 (± 0.003 and ± 0.046, respectively). Also shown for the CHEOPS passband are the results for k = 0.9 (dashed line). The small spikes seen on the curves for the u′ passband are the result of numerical noise in the light curves at the few ppm level. |
| In the text | |
 |
Fig. 4 Difference between the observed and computed values of h1 and h2. Data for Kepler-17 are plotted using an open symbol. The vertical error bars are calculated from the square root of the sum of the variances of the observed and calculated values. |
| In the text | |
 |
Fig. 5 A simulated light curve for the following parameters: R⋆/a = 0.2, k = 0.1, b = 0.4, q = 0.0008, h1 = 0.75 ± 0.01, h2 = 0.45 ± 0.05. The upper plot shows the light curve for the nominal values of h1 and h2 and (indistinguishable at this scale) the light curves for both h1 and h2 perturbed upwards by one standard deviation. The lower plot shows the change in flux due to a change by +1 standard deviation in h1 (dashed line) and h2 (dotted line). Also shown in the lower panel is the effect of using a sphere to model the shape of the transiting planet instead of a polytrope (dot-dashed line). Note that in the latter case the radius of the sphere has been reduced by 0.5% cf. the volume-average radius of the ellipsoid used to model the planet as a polytrope. This correction is required so that the eclipse depth for the spherical planet case matches the eclipse depth for the ellipsoidal planet model. |
| In the text | |
 |
Fig. A.1 Kepler light curves of transiting exoplanet and binary star systems. Observations are plotted using small points and the best-fit light curve model is shown as a line. The name of each star is noted in the title to each panel together with the impact parameter b = a cosi∕R⋆ and the ratioof the radii k = Rpl∕R⋆. |
| In the text | |
 |
Fig. A.2 Posterior probability distributions for the limb-darkening parameters from the analysis of the Kepler light curves. The PPDs are shown as gray-scale density plots. The median values and standard deviations for each parameter are shown as an error bar. The vertical and horizontal lines in the left-hand panel for each star show the ± 1-σ limits on the computed values of c and α. The corresponding ± 1-σ limits on h1 and h2 are shown as curved lines in the same panel and as vertical and horizontal lines in the right-hand panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



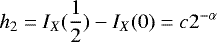
![\begin{equation*} \alpha = \log_2 \left([1 - h_1 + h_2]/h_2\right) = \log_2(c/h_2). \end{equation*}](/articles/aa/full_html/2018/08/aa32944-18/aa32944-18-eq14.png)