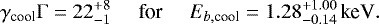| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A170 | |
| Number of page(s) | 32 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201732322 | |
| Published online | 31 August 2018 | |
X-ray absorption towards high-redshift sources: probing the intergalactic medium with blazars
1
Department of Physics G. Occhialini, University of Milano-Bicocca,
Piazza della Scienza 3,
20126
Milano, Italy
e-mail: arcodia@mpe.mpg.de
2
INAF-Osservatorio Astronomico di Brera,
Via Bianchi 46,
23807
Merate (LC), Italy
3
Max-Planck-Institut für extraterrestrische Physik (MPE),
Giessenbachstrasse 1,
85748 Garching bei München, Germany
4
INAF,
IASF Milano,
Via E. Bassini 15,
20133
Milano, Italy
Received:
20
November
2017
Accepted:
9
April
2018
The role played by the intergalactic medium (IGM) in the X-ray absorption towards high-redshift sources has recently drawn more attention in spectral analysis studies. Here, we study the X-ray absorption towards 15 flat-spectrum radio quasars at z > 2, relying on high counting statistic (≳10 000 photons) provided by XMM-Newton, with additional NuSTAR (and simultaneous Swift-XRT) observations when available. Blazars can be confidently considered to have negligible X-ray absorption along the line of sight within the host galaxy, likely swept by the kpc-scale relativistic jet. This makes our sources ideal for testing the absorption component along the IGM. Our new approach is to revisit the origin of the soft X-ray spectral hardening observed in high-z blazars in terms of X-ray absorption occurring along the IGM, with the help of a low-z sample used as comparison. We have verified that the presence of absorption in excess of the Galactic value is the preferred explanation to explain the observed hardening, while intrinsic energy breaks, predicted by blazars’ emission models, can easily occur out of the observing energy band in most sources. First, we performed an indirect analysis comparing the inferred amount of absorption in excess of the Galactic value with a simulated IGM absorption contribution, that increases with redshift and includes both a minimum component from diffuse IGM metals, and the additional contribution of discrete denser intervening regions. Then, we directly investigated the warm-hot IGM with a spectral model on the best candidates of our sample, obtaining an average IGM density of n0 = 1.01−0.72+0.53 × 10−7 cm−3 and temperature of log(T/K) = 6.45−2.12+0.51. A more dedicated study is currently beyond our reach, but our results can be used as a stepping stone for future more accurate analysis, involving Athena.
Key words: X-rays: general / quasars: general / intergalactic medium / galaxies: active / galaxies: high-redshift / galaxies: jets
© ESO 2018
1 Introduction
X-ray spectral analysis involving extragalactic sources is currently not able to detect simple absorption spectral features (lines, edges…), hence typically only the total amount of absorbing matter (in NH, cm−2) can be inferred. Of this, X-ray absorption occurring within our Galaxy usually accounts for a known fraction (e.g., Dickey & Lockman 1990; Kalberla et al. 2005; Willingale et al. 2013). An absorption component in addition to the Galactic value (hereafter simply called “excess absorption”), if needed, was often uniquely attributed to the galaxy hosting the X-ray source, while the absorption produced by intergalactic intervening matter (IGM) was rarely included. As a matter of fact, most of the cosmic matter resides among galaxies within the IGM (see McQuinn 2016, for an extensive and recent review). Here, we are interested in the low-redshift IGM (z ≤ 2), focusing on the missing “metal fog” that is predicted to lie in a hot phase at ~(105−107) K, composing the so-called warm-hot IGM (WHIM; see Cen & Ostriker 1999, 2006; Davé et al. 2001; Bregman 2007; Shull et al. 2012, and references therein). Hence, when fitting a low-energy X-ray spectrum requires excess absorption, both the host and the IGM component should be considered. Besides, while the former varies among different types of sources and should be physically motivated depending on their environment, an IGM absorption component is unaffected by the type of source emitting behind.
A soft X-ray spectral hardening has been typically observed towards distant sources, such as high-z active galactic nuclei (AGN; Padovani et al. 2017, for a recent review) and gamma-ray bursts (GRBs; Schady 2017, for a recent review). In principle, it is unclear whether the observed spectrum is congruent to the emitted one or some excess absorption is occurring. In GRBs the observed X-ray hardening was promptly attributed to excess absorption intrinsic to the host (e.g., Owens et al. 1998; Galama & Wijers 2001; Stratta et al. 2004; de Luca et al. 2005; Campana et al. 2006, 2010, 2012; Arcodia et al. 2016), since their environment is known to be dense (Fruchter et al. 2006; Woosley & Bloom 2006). By contrast, in distant quasars also different origins, for example spectral breaks intrinsic to the emission, were considered as alternative to the excess absorption scenario (see Elvis et al. 1994a; Cappi et al. 1997; Fiore et al. 1998; Reeves & Turner 2000; Fabian et al. 2001a,b; Worsley et al. 2004a,b; Page et al. 2005; Yuan et al. 2006; Grupe et al. 2006; Sambruna et al. 2007; Saez et al. 2011). Explaining the observed hardening with excess absorption uniquely attributed to the host galaxy resulted in an increasing trend of the intrinsic column densities (hereafter NH (z), with z = zsource) with redshift. For all extragalactic sources, this so-called NH(z)−z relation typically showed at low-z both non- and highly-absorbed sources (from columns slightly above the Galactic value to NH (z) ≥ 1023 cm−2), while at high-z, surprisingly, only heavily-absorbed sources were observed. Apparently, this is against the idea of an environment less polluted by metals within galaxies of the younger Universe. This contrast can be resolved interpreting the excess absorption values in the NH(z)−z relation not only as intrinsic to the source, but also due to intervening IGM matter.
The idea of an IGM absorbing component common to all sources emerged through the years, first as a simple suggestive hypothesis (e.g., see Fabian et al. 2001a). A more quantitative approach was adopted only recently in a series of papers, in which both a diffuse IGM and additional discrete intervening systems were considered towards quasars and GRBs (Behar et al. 2011; Campana et al. 2012; Starling et al. 2013; Eitan & Behar 2013). This scenario was later confirmed with dedicated cosmological simulations by Campana et al. (2015), who matched the observed NH (z)−z relation with a simulated absorption contribution occurring along the IGM, that obviously increases with redshift. This would explain the lack of unabsorbed high-z sources without invoking complicated scenarios occurring within distant host galaxies.
Here, we report a study of X-ray absorption towards high-redshift blazars (Madejski & Sikora 2016; Foschini 2017, for recent reviews). They consist in jetted-AGN in which the relativistic jet is pointing towards us. Then, it is reasonable to assume that any host absorber was likely swept by the kpc-scale jet. This assumption makes blazars, in principle, the ideal sources to test the IGM absorption scenario. Their spectral energy distribution (SED) is characterised by two broad humps (in νFν), tracing the beamed emission of the relativistic jet, that dominates over the typical AGN emission at almost all frequencies. The two humps are thought to be related to synchrotron and inverse Compton (IC) processes, at low and high frequencies, respectively.The photons emitted by the former mechanisms can be used as seed by the latter via synchrotron self-Compton (SSC), but in most powerful blazars electrons responsible for the IC emission are thought to interact with photons external to the jet (External Compton, EC), the most accredited being produced by the broad line region (BLR) or by the dusty torus (Ghisellini et al. 2010, and references therein). These most powerful blazars, called flat-spectrum radio quasars (FSRQs), are of interest in this work, the other sub-class being BL Lacertae objects (BL Lacs; Urry & Padovani 1995; Ghisellini et al. 2011).
Most of the objects analysed in this work were already studied in the last two decades (e.g., Elvis et al. 1994a,b; Cappi et al. 1997; Reeves et al. 1997, 2001; Fiore et al. 1998; Reeves & Turner 2000; Yuan et al. 2000, 2005, 2006; Tavecchio et al. 2000, 2007; Fabian et al. 2001a,b; Worsley et al. 2004a,b, 2006; Page et al. 2005; Grupe et al. 2004, 2006; Sambruna et al. 2007; Eitan & Behar 2013; Tagliaferri et al. 2015; Paliya 2015, 2016; Sbarrato et al. 2016). In these works, if the observed soft X-ray spectral hardening was attributed to excess absorption, only an absorber intrinsic to the host galaxy or few discrete intervening absorbers, namely Damped or sub-Damped Lyman-α absorbers (DLAs or subDLAs; Wolfe et al. 1986, 2005), were investigated. Nonetheless, in blazars the former contribution is negligible and typically in contrast with the optical-UV observations, and the latter is insufficient (e.g., see the discussions in Elvis et al. 1994a; Cappi et al. 1997; Fabian et al. 2001a,b; Worsley et al. 2004a,b; Page et al. 2005). Hence, an alternative explanation involving intrinsic energy breaks started to be preferred to account for the observed hardening in blazars’ X-ray spectra (e.g., Tavecchio et al. 2007).
Our new approach is to consider the observed X-ray spectrum of distant blazars to be absorbed, in excess of the Galactic component, uniquely by the WHIM plus additional intervening systems along the IGM line of sight, if known. Intrinsic spectral breaks, predicted by blazars’ emission models (see, e.g., Sikora et al. 1994, 1997, 2009; Tavecchio et al. 2007; Tavecchio & Ghisellini 2008; Ghisellini & Tavecchio 2009, 2015, and references therein), are also considered, although they can easily occur out of the observing band.
In Sect. 2 we outline the criteria with which we built our samples. In Sect. 3 (and Appendix B) we report the details of the filtering and processing of our sources. In Sect. 4 we check for possible flux variations in the processed observations. In Sect. 5 we describe the models adopted and our fitting methods, along with spectral results. In Sect. 6, we discuss how our results fit in the NH (z)−z relation along with the current literature, testing the IGM absorption contribution in an indirect way. Then, we also directly tested the WHIM absorption component with a spectral model. The coexistence between the IGM excess absorption scenario and blazars’ emission models is investigated in details in Appendix D. Conclusions are drawn is Sect. 7.
2 Samples
The IGM absorption contribution is thought to become dominant at z ≳ 2 (Starling et al. 2013; Campana et al. 2015), thus our first criterion was to select z ≥ 2 blazars. Moreover, high signal-to-noise X-ray spectra are necessary to properly assess the presence of a curved spectrum indistant extragalactic sources with a fine-tuned analysis. This purpose could be fulfilled with the XMM-Newton satellite (Jansen et al. 2001). The second criterion was then to include in the analysis all blazars for which the three EPIC cameras (Strüder et al. 2001; Turner et al. 2001) jointly recorded more than ~ 10 000 photons1.
We used several published catalogues of blazars and other publications to build up our samples. We first obtained a list of z ≥ 2 blazars cross-checking the BAT70 catalogue (Baumgartner et al. 2013) and the “List of LAT AGN” catalogue2. The latter consists in a list of all the AGN published by both the LAT team in several catalogues, namely 1LAC (Abdo et al. 2010), 2LAC (Ackermann et al. 2011), 3LAC (Ackermann et al. 2015), 1FHL (Ackermann et al. 2013), 2FHL (Ackermann et al. 2016), ATels3 and papers from scientists external to the LAT collaboration. In addition, we cross-checked this provisional list with the sample of X-ray selected quasars of Eitan & Behar (2013).
Startingfrom this huge parent sample, we selected all blazars with at least an XMM-Newton observation and then discarded all faint objects. In order to securely classify the remaining sources as FSRQs, we relied on several blazar catalogues, SIMBAD and other works available in the literature. We also analysed their SED with the ASDC “SED Builder”4.
We call “Silver Sample” the final catalogue containing 15 XMM-Newton FSRQs selected according to the above criteria, ranging from redshift 2.07 to 4.72 (see Table 1). Among them, we searched for NuSTAR (Harrison et al. 2013) and simultaneous Swift-XRT (Burrows et al. 2005)observations, when possible, with the aim to provide a superior broadband analysis of blazars’ X-ray spectral curvature. They were available for six objects of the Silver sample, highlighted in bold in Table 1, that form the “Golden Sample”.
We alsobuilt a low-redshift sample to perform useful comparisons. We restricted the selection to sources in which a significant amount of excess IGM absorption is not expected, thus we opted for the 0− 0.5 redshift range. We selected low-redshift blazars following the same criteria and methods outlined for the high-z Silver Sample, drawing a list of candidates from the same catalogues, mostly from the “List of LAT AGN”. Being interested in comparing the same region of the SED, short of the redshift scaling, we looked for FSRQs but considered also low-energy peaked BL Lac objects (LBLs), that show a low synchrotron peak frequency (< 1014 Hz). After discarding the faint objects and all the unsuited BL Lacs, we ended up with five FSRQs, one NLS1 and two LBLs (see Table 2). In particular, blazar PKS 0521–365 was classified as a misaligned blazar (D’Ammando et al. 2015), although itsSED resembles the characteristics of a typical FSRQ (Ghisellini et al. 2011). PKS 2004–447, the γ-ray emitting NLS1, was included since these sources are thought to be FSRQs at an early stage of their evolution or rejuvenated by a recent merger (see Foschini 2017, for a recent review). Their X-ray emission is thought to be similar and this was confirmed for the specific case of PKS 2004–447 (Paliya et al. 2013; Kreikenbohm et al. 2016).
In Fig. 1, the position in the sky of both high- and low-z blazars is shown superimposed to the Leiden Argentine Bonn (LAB) absorption map (Kalberla et al. 2005), that represents Galactic column densities yielded by the HI integrated emission.
List of z > 2 XMM-Newton FSRQs of the “Silver Sample”.
List of low-redshift XMM-Newton blazars.
 |
Fig. 1 Distribution of blazars in the sky in Galactic coordinates (Aitoff projection), superimposed to the LAB absorption map, representing the distribution of Galactic column densities (see Kalberla et al. 2005, for further details). Black stars represent the high-z Silver sample. As black diamonds, blazars of the low-z sample. |
3 Observations
Here we report the tools used for the processing, screening and analysis of XMM-Newton data, along with the procedure adopted for NuSTAR and Swift-XRT data. Details on the processed observation(s) for each of ours high-z blazars are provided in Appendix B.
3.1 XMM-Newton
For the processing, screening, and analysis of the data from the EPIC MOS1, MOS2 (Turner et al. 2001) and pn (Strüder et al. 2001) cameras, standard tools have been used (XMM SAS v. 15.0.0 and HEAsoft v. 6.20). Observationdata files (ODFs) were downloaded and regularly processed according to the SAS Data Analysis Threads5. The event file of each observation was filtered from flaring particle background (FPB): a good time interval (GTI) was created accepting only times when the background count rate of single pixel events (“PATTERN==0”) with high energies (≥ 10 keV for EPIC-MOS and 10−12 keV for EPIC-pn) was less than a chosen threshold (e.g., the default choice is < 0.35 c s−1 for MOS1 and MOS2, < 0.4 c s−1 for pn).
The source spectrum was first extracted from a circular region. Background was extracted from a nearby region with the same radius for EPIC-MOS cameras, whilst for EPIC-pn it was extracted from a region at the same distance to the readout node (RAWY position) as the source region6. When extracting the source and background EPIC-pn spectrum with the SAS evselect task, the strings “FLAG==0” and “PATTERN<=4” (i.e., up to double-pixel events) were included in the selection expression, while for EPIC-MOS we included the string “PATTERN<=12” (i.e., up to quadruple-pixel events). The “FLAG==0” string omits parts of the detector area like border pixels or columns with higher offset.
Any possible pile-up effect on each spectrum was then checked with the SAS task epatplot. The plot allows us to compare the observed versus the expected pattern distribution within a source extraction region. If both agree, pile-up is not considered to be present for the observation. In some cases, also the (more approximate) tool WebPIMMS was used for consistency. In some sources (see Appendix B) pile-up was present and the circular source region was corrected excising a core with increasing radius up to the best agreement between the expected and observed pattern distribution in the epatplot.
For all sources, XMM-Newton spectra were rebinned, so that each energy bin contained a minimum of 20 counts. Moreover, the SAS task oversample=3 was adopted to ensure that no group was narrower than 1/3 of the FWHM resolution7.
3.2 NuSTAR
Throughout this work, the NuSTAR Focal Plane Module A (FPMA) and B (FPMB) data were processed with NuSTARDAS v1.7.1, jointly developed by the ASI Science Data Center (ASDC, Italy) and the California Institute of Technology (Caltech, USA). Event files were calibrated and cleaned using the nupipeline task (v0.4.6). After the selection of the source (and background) region, spectra were obtained with the nuproducts task (v0.3.0), in the energy range 3− 79 keV. Since NuSTAR has a triggered readout, it does not suffer from pile-up effects (Harrison et al. 2013). Throughout this work every NuSTAR spectrum was binned to ensure a minimum of 20 counts per bin.
3.3 Swift-XRT
We processed Swift-XRT data through the UK Swift Science Data Centre (UKSSDC) XRT tool8, designed to build XRT products (Evans et al. 2009). Spectra were all extracted in Photon Counting mode and the analysis was carried out in the 0.3−10 keV energy range. Spectra were then rebinned with a minimum of 20 counts, through the group min 20 command within the grppha tool.
4 Variability analysis
Due to the spectral variability commonly observed in blazars (e.g., Marscher & Gear 1985; Wagner & Witzel 1995; Ulrich et al. 1997)we checked for possible flux variations extracting X-ray light curves for every processed XMM-Newton observation. Source and background regions were the same selected for the extraction of the spectra (see Appendix B).
After the extraction, light curves were corrected for various effects (vignetting, bad pixels, PSF variation, and quantum efficiency, dead time and GTIs) at once with the task epiclccorr. A time bin-size of 500 s was adopted. The exposure time of the observations set the x-axis, the holes in the data representing the time-regions filtered from FPB. No significant flux variations were observed within the single observation of any source, hence spectral results (see Sect. 5) are to be considered free from intra-observation variability.
5 Spectral analysis
5.1 Rationale
XMM-Newton data of the three EPIC cameras were jointly fitted (in the 0.2− 10 keV energy range for the EPIC-pn detector and 0.3−10 keV for EPIC-MOS) in Silver sample’s blazars, with a floating constant representing the cross-normalization parameter among the different cameras, fixed at 1 for EPIC-pn (see Madsen et al. 2017). If several observations were present, the different states of the source were fitted with untied parameters (i.e., photon indexes, normalizations, curvature terms were left free to vary among the different observations). X-ray absorption terms were always tied together.
In case of additional NuSTAR observations of the source, a broadband 0.2− 79 keV fit was performed. Due to the high variability typically observed in blazars, non-simultaneous XMM-Newton, and NuSTAR observations are expected to describe different states of the object, thus we used varying photon indexes, normalizations, curvature terms, and spectral breaks. In Golden sample’s blazars the simultaneous Swift-XRT and NuSTAR observations were then fitted keeping the same source parameters, jointly with XMM-Newton data fitted using different parameters. The absorption column densities were held fixed between XMM-Newton and Swift-XRT+NuSTAR. Similarly to the adopted procedure for the EPIC cameras, inter-calibration constants were left free to vary for FPMB and Swift-XRT with respect to FPMA, fixed at 1 (see Madsen et al. 2017).
No significant background contaminations were found in our data, as the observed background-to-source ratio was typically around or below 1%. Even in QSO B1026-084, the source with the lowest number of photons (~ 10 000), the ratio reached ~10% only above ~8 keV, and for EPIC-MOS cameras only. Moreover, the impact of the current relative uncertainties on the XMM-Newton effective area calibration on our fitted parameters was minimal. We acknowledge the use of the CORRAREA correction9 for this verification.
One or more DLA or sub-DLA systems were detected in the literature towards QSO B0237–2322, QSO B0537–287, QSO B0438–43, QSO B1026–084, and PKS 2126–158 (Péroux et al. 2001; Ellison et al. 2001; Fathivavsari et al. 2013; Quiret et al. 2016; Lehner et al. 2016). The systems were included in the analysis and are shown in Table 3. In any case their contribution to the overall curvature is minor.
List of DLA candidates from the literature (see text) included in the spectral analysis.
5.2 Simple power-law fits
Blazars’ emission can be approximated by simple power-laws in limited energy ranges, e.g., within the rise (in νFν) of the IC hump. This is the SED region that we likely observed in z > 2 FSRQs. Then, we first modelled the observed spectra using a power-law continuum with fixed Galactic column density (Willingale et al. 2013). This “null” model, hereafter PL, is described by:
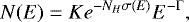 (1)
(1)
in which the photon flux N(E) [photons s−1 cm−2 keV−1] is modelled with a power-law with photon index Γ (powerlaw within XSPEC) and an exponential cut-off caused by a column density of absorbing matter (in unity of 1022 atoms cm−2) interacting with an energy-dependent cross-section σ(E). K is the normalization at 1 keV. This Tuebingen-Boulder ISM absorption model (tbabs within XSPEC) is actually the improved version tbnew10, automatically included within XSPEC 12.9.1. Cross sections from Verner et al. (1996) and abundances from Wilms et al. (2000) are used.
PL fit results of XMM-Newton data are shown in Table A.1 for each source. Related data-model ratios are reported in Fig. 2. They both suggest that a significant additional curvature is required in almost all objects, except for QSO B0014+810, PKS 2149–306 and QSO B0237–2322. The aggregate reduced chi-square is 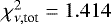 (10 675/7552), suggesting that a more complex modelling overall is needed.
(10 675/7552), suggesting that a more complex modelling overall is needed.
Adding NuSTAR (with simultaneous Swift-XRT) data to the analysis allowed us to extend the observing bandwidth up to 79 keV in the six blazars belonging to the Golden sample. The results are reported in Table A.1 for the single source. The total reduced chi-square for the PL model is 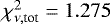 (12 150/9529) and confirms that some additional curvature is suggested, to a greater or lesser extent, in all the high-z blazars.
(12 150/9529) and confirms that some additional curvature is suggested, to a greater or lesser extent, in all the high-z blazars.
 |
Fig. 2 Data-model ratio of a simple PL model for XMM-Newton observations of Silver-sample blazars. EPIC-pn, MOS1, and MOS2 data are displayed for each observation in different colours, with pn data extending down to 0.2 keV. |
5.3 Intrinsic curvature fits
The curvature in addition to the PL model could be due to spectral breaks intrinsic to the emission. Such features are predicted by blazars’ emission models (e.g., Tavecchio et al. 2007; Sikora et al. 2009; Ghisellini & Tavecchio 2009, 2015) and details will be discussed in Appendix D.
The power-law continuum can be improved with a broken power-law (BKN) or with a log-parabola (LGP), still with a fixed Galactic absorption value. The broken power-law model (bknpower within XSPEC) simply consists in two different power-laws separated by a break at Eb (in keV):
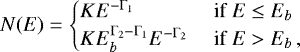 (2)
(2)
where Γ1 and Γ2 are the low- and high-energy photon index, respectively.
The log-parabolic model (Massaro et al. 2004, 2006, logpar within XSPEC) is given by the following equation:
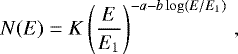 (3)
(3)
where E1 is the fixed pivot energy (typically 1 keV in soft X-ray fits), a is the slope at E1 and b the curvature term. In both BKN and LGP models, the photon flux is absorbed by a Galactic column density represented by the same exponential cut-off of the PL equation.
Results obtained with both models are shown in Table A.1 for each source, along with the F-test (Protassov et al. 2002) p-value computed with respect to the null PL model, that represents a clear improvement in most cases. In order to compare the overall improvement, we then calculated the total reduced chi-square for both BKN and LGP model, obtaining 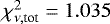 (
(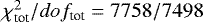 ) and 1.094 (8228/7521), respectively. The F-test yielded a telling p-value < 10−200 in both cases. When broadband data are fitted for Golden sample’s sources, the narrowband conclusions are confirmed (see Table A.1 for individual results). The overall reduced chi-squares are 1.027 (9728/9473) and 1.043 (9899/9491), for BKN and LGP model, respectively. The related F-test p-values are again <10−200.
) and 1.094 (8228/7521), respectively. The F-test yielded a telling p-value < 10−200 in both cases. When broadband data are fitted for Golden sample’s sources, the narrowband conclusions are confirmed (see Table A.1 for individual results). The overall reduced chi-squares are 1.027 (9728/9473) and 1.043 (9899/9491), for BKN and LGP model, respectively. The related F-test p-values are again <10−200.
5.4 Excess absorption fits
The PL model can also be improved adding absorption in excess of the Galactic value, to account for the additional curvature required. We already stressed the concept that in blazars any excess absorber should be considered intervening, since no intrinsic absorption likely occurs due to the presence of a relativistic jet sweeping the local environment up to kpc-scales. However, using a cold absorber intrinsic to the host galaxy (ztbabs within XSPEC) is the easiest and fastest way to investigate the presence of additional absorbers in excess of the Galactic value.
Individual fit results for all blazars of the Silver sample are reported in Table A.1. In general, excess absorption always improved the simple PL fit. The majority of sources yielded a detection of a significant column density, while un upper limit was obtained for QSO B0014+810, QSO B0537–286, PBC J1656.2–3303, QSO J0555+3948, PKS 2149–306, QSO B0237–2322. The total reduced chi-square is 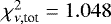 (7880/7520), the F-test p-value with respect to the PL model is <10−200.
(7880/7520), the F-test p-value with respect to the PL model is <10−200.
When NuSTAR (with simultaneous Swift-XRT) data are added to the analysis, the fitted column densities are fully consistent, within the errors, with the results of the “narrow-band” XMM-Newton fits. The overall reduced chi-square is 1.081 (10 265/9497), yielding a p-value of < 10−200.
We note that in this model (PL+EX), the Galactic value was left free to vary between ± 15% boundaries of the tabulated value (see Sect. 5.7 for a motivation). However, this choice did not favour the detection of excess absorption within spectral fits, since the Galactic value was fitted towards the lower boundary allowed by the ± 15% errors only in five blazars out of 15. On the contrary, in eight sources it was fitted towards the upper boundary, thus disfavouring any extra-absorber.
5.5 Intrinsic curvature + excess absorption fits
Poor PL fitswere adequately improved with both excess absorption or an intrinsic spectral break. We can not discern which model among BKN, LGP, and PL+EX is better using the F-test, nor looking at the residuals, as these models are nearly statistically undistinguishable for the single source. A more complex modelling could be hardly introduced by these arguments. Nonetheless, we fitted XMM-Newton spectra with both models simultaneously, assuming a priori that radiation coming from every z > 2 source couldbe partly absorbed along the IGM and that, in addition, for some of the sources an intrinsic energy break could have occurred within the observed energy band. Then, a posteriori we verified the inclusion of this model in the analysis with more thorough statistical tools and arguments (see Sect. 5.6).
This LGP+EX model includes ztbabs and logpar (the LGP was chosen as reference for modelling a curved continuum, see Sects. 5.6 and 5.7). We note that also in the LGP+EX fits the Galactic value was left free to vary between ± 15% boundaries. Results are reported in Table A.1, along with the F-test p-value computed with respect to the PL+EX model, for each individual source. The total reduced chi-square for the LGP+EX model, namely 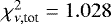 (7705/7495), is a clear improvement of the PL+EX model (F-test p-value ~ 10−23), but also of the LGP (p-value ~ 10−87).
(7705/7495), is a clear improvement of the PL+EX model (F-test p-value ~ 10−23), but also of the LGP (p-value ~ 10−87).
Moreover, despite the presence of some degeneracies, we were able to draw general conclusions. The excess absorption component was always fitted, with column density values compatibles with the PL+EX scenario, while continuum curvature terms were consistent with a power-law in 11 out of 15 blazars. Only in few cases both terms appeared to be required by the data, e.g., in QSO B0537–286, RBS 315, QSO J0555+3948, and 4C 71.07. These sources were fundamental, since they proved that when excess absorption is present and some intrinsic curvature is within the observed band, they both can be fitted.
Also when NuSTAR (with simultaneous Swift-XRT) data were added to the analysis in the six blazars of the Golden sample, they were, as a general rule, better modelled with a LGP+EX (see Table A.1 for individual results). Exceptions were 7C 1428+4218 and QSO B0014+810, in which a curved continuum was not statistically required. The overall chi square is 1.018 (9654/9480), with p-values of ~ 10−44 and ~ 10−113 with respect to LGP and PL+EX models, respectively.
5.6 Best-fit model
Using the F-test, we were only able to tell that every suggested alternative model (namely BKN, LGP, PL+EX, and LGP+EX) was a clear refinement with respect to a simple PL model, with no information on the relative quality between these models. We now want to infer the overall best-fit model, balancing the quality of the fit (given by the chi-square statistic) with the complexity of the model (the number of parameters involved), taking always into account the physics behind it.
The ideal statistics for this purpose is represented by the Akaike information criterion (AIC; Akaike 1974), since it can be used to compare non-nested models as well. The AIC has been widely applied to astrophysical problems (e.g., Liddle 2004, 2007; Tan & Biswas 2012), defined as:
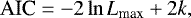 (4)
(4)
where Lmax is the maximum likelihood that can be achieved by the model and k is the number of parameters of the model. The second term is a penalty for models that yield better fits but with many more parameters. With the assumption of Gaussian-distributed errors, the equation further reduces to:
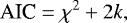 (5)
(5)
where χ2 is yielded by the spectral fits for each model. Hence, the model with the smallest AIC value is determined to be the “best”, although a confidence level needs to be associated for distinguishing the best among several models. Given two models A and B, A is ranked to be better than B if
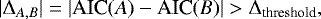 (6)
(6)
where Δthreshold is conventionally 5(10) for a “strong” (“decisive”) evidence against the model with higher criterion value (see Liddle 2007, and references therein).
We computed the AIC for XMM-Newton results of each Silver-sample blazar (see Table 4), confirming the ambiguity outlined in the previous sections, as well as in other works. For almost each individual source, the model with the lowest AIC (among BKN, LGP, PL+EX, and LGP+EX) had at least another model within a Δthreshold = 10. In Table 4 we highlighted in bold the lowest AIC and in italics any additional model within a Δthreshold = 10. This states that as long as the single source is analysed, the suggested models are mostly statistically undistinguishable.
Then, we computed the total AIC value for each model, inserting in Eq. (5) the total chi-square values and the sum of the parameters. The values correspond to a  , 8228, 7880, 7705 with 141, 118, 119, and 144 parameters involved, for BKN, LGP, PL+EX, and LGP+EX, respectively. The total AIC is reported in the last row of Table 4. Results indicate that on the strength of an overall analysis on the whole sample, the best-fit model is indeed LGP+EX. Hence, the coexistence of excess absorption and intrinsic curvature is the preferred explanation for high-z blazars, from physical and statistical motivations.
, 8228, 7880, 7705 with 141, 118, 119, and 144 parameters involved, for BKN, LGP, PL+EX, and LGP+EX, respectively. The total AIC is reported in the last row of Table 4. Results indicate that on the strength of an overall analysis on the whole sample, the best-fit model is indeed LGP+EX. Hence, the coexistence of excess absorption and intrinsic curvature is the preferred explanation for high-z blazars, from physical and statistical motivations.
We would like to highlight that the LGP+EX model is basically equivalent to the PL+EX model for 11 sources, in which the fitted curvature term was consistent with zero (see Sect. 5.5). Hence, the better AIC value of LGP+EX isprobably driven by the good description of the PL+EX for these 11 sources, with the additional optimal description of LGP+EX for the remaining 4, namely QSO B0537–286, RBS 315, QSO J0555+3948, and 4C 71.07.
Among the intrinsic curvature models, a BKN seems to be significantly preferred with respect to a LGP. This is clear in Table 4, but it was also evident in Sect. 5.3 looking at the 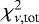 values. However, note that several BKN fits yielded excellent results with unlikely parameters, e.g. low-energy photon indexes consistent with zero or negative values, and energy-breaks close to one of the XMM-Newton energy-band limit (see Table A.1). In blazars QSO B0014+810, PKS 2149–306, and QSO B0237–2322 these non-physical parameters were consistent with having good results also in the simple PL fits, but in other objects (e.g., 7C 1428+4218, QSO J0525–3343, QSO B0438–43, and QSO J2354–1513) some additional curvature was indeed required by the data, hence physical BKN parameters were expected.
values. However, note that several BKN fits yielded excellent results with unlikely parameters, e.g. low-energy photon indexes consistent with zero or negative values, and energy-breaks close to one of the XMM-Newton energy-band limit (see Table A.1). In blazars QSO B0014+810, PKS 2149–306, and QSO B0237–2322 these non-physical parameters were consistent with having good results also in the simple PL fits, but in other objects (e.g., 7C 1428+4218, QSO J0525–3343, QSO B0438–43, and QSO J2354–1513) some additional curvature was indeed required by the data, hence physical BKN parameters were expected.
We suggest that in the scenario (strengthened by the AIC overall results) in which both excess absorption and intrinsic curvature are present, when the analysis is limited to the sole intrinsic curvature term (i.e., with a BKN or LGP model) it could be possible that BKN sharp-break parameters yield very good results favoured by absorption features (e.g., edges). On the other hand, a LGP would yield worse results, since it simply discerns a curved from a non-curved continuum. An existing excess absorption feature would be likely better mimicked by the BKN model, rather than a LGP. To better understand this ambiguity, we used the low-z blazar sample as comparison for determining the reference model for a curved continuum, as in close objects even the excess absorption along the IGM would be negligible. It turned out that at low-z better fits were obtained with a LGP rather than a BKN (see Sect. 5.7 for details).
5.7 The low-z sample
We analysed XMM-Newton spectra of six FSRQs and two LBLs below z = 0.5 (see Sect. 2) and individual results are reported in Table A.2. Overall, the simple PL model resulted in a poor 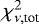 of 1.39 (with 5748 dof). Intrinsic curvature models improved the fits, yielding
of 1.39 (with 5748 dof). Intrinsic curvature models improved the fits, yielding 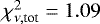 (5501/5037) and 1.11 (5549/5024) for the LGP and BKN models, that correspond to F-test p-values of ~ 10−124 and ~ 10−115, respectively. The two
(5501/5037) and 1.11 (5549/5024) for the LGP and BKN models, that correspond to F-test p-values of ~ 10−124 and ~ 10−115, respectively. The two 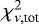 are similar, hence we computed the total AIC value (from Eq. (5)). In low-z blazars, in which even the IGM absorption contribution is not expected due to their proximity, the AIC statistics would allow us to assess the preferred model for a curved continuum. The total number of parameters is 66 and 79 for LGP and BKN, that yield AIC = 5633 and 5707, respectively. The Δthreshold is significantly greater than 10, indicating a “decisive” evidence in favour of LGP against the BKN model. Hence, on the strength of an overall analysis, a LGP is the reference for a curved continuum. Then, we also performed LGP+EX fits to provide upper limits for the NH(z)−z relation.
are similar, hence we computed the total AIC value (from Eq. (5)). In low-z blazars, in which even the IGM absorption contribution is not expected due to their proximity, the AIC statistics would allow us to assess the preferred model for a curved continuum. The total number of parameters is 66 and 79 for LGP and BKN, that yield AIC = 5633 and 5707, respectively. The Δthreshold is significantly greater than 10, indicating a “decisive” evidence in favour of LGP against the BKN model. Hence, on the strength of an overall analysis, a LGP is the reference for a curved continuum. Then, we also performed LGP+EX fits to provide upper limits for the NH(z)−z relation.
All spectra showed a concave curvature (see Table A.2). This can be explained by the appearance of the SSC component. We note that, while at high redshift we were selecting the most powerful sources, that show an almost “naked” EC component (namely without the SSC contribution or the X-ray corona component), at low redshift also weaker blazars could be easily observed. Two low-z FSRQs, namely TXS 2331+073 and 4C 31.63, were analysed with the Very Long Baseline Array (VLBA) during the MOJAVE program11. Relatively low apparent velocities (βapp) were reported, upto 5.35 ± 0.74 (Lister et al. 2013)and up to 8.3 ± 0.1 (Homan et al. 2015) for TXS 2331+073 and 4C 31.63, respectively. This indicates a moderate beaming, and since the EC component is more dependent than SSC from the beaming factor, we expected that in these sources the SSC could contribute. A concave spectrum in low-z blazars can be also produced by the upturn from the steep high-energy tail of the synchrotron emission and the flatter low-energy rise of the IC hump (see e.g., Gaur et al. 2018).
5.7.1 Comparison with high-z results
In Sect. 5.6 we obtained with an AIC test that the best-fit model for our high-z FSRQs is the LGP+EX. Here, benefiting from the low-z sample, we further disfavour the pure BKN scenario, in which no excess absorption is required. Intrinsic spectral breaks predicted by blazars’ models are convex (see Appendix D for details). If the spectral hardening observed in high-z blazars is uniquely attributed to energy breaks intrinsic to the emission, their absence within the observing band in the low-z sample (we even reached 79 keV with NuSTAR in PKS 2004–447) is striking. In fact, any spectral break observed around 1− 2 keV at z = 3 could be, in principle, observed around 4−8 keV in the same sources at low-z. Furthermore, the SSC component cannot be invoked for covering the putative breaks at 4− 8 keV, since in our low-z FSRQs it appears below ~ 3 keV (the fitted breaks are concave and within ~1−3 keV, see Table A.2). On the other hand, low-z blazars are consistent with the excess absorption scenario, since they show only a marginal IGM excess absorption contribution, in agreement with their proximity (see Sect. 6).
5.7.2 Errors on the Galactic value
Here, we also investigate with low-z blazars the accuracy of the tabulated Galactic column densities. An error should always be added, given the many uncertainties in the determination of Galactic column densities from radio surveys12, plus the averaging over a conical region, e.g., with a 1-deg radius (Kalberla et al. 2005), around the input position of the source. Hence, an error should be always expected, also in values provided by Willingale et al. (2013), that basically added the molecular hydrogen contribution to the LAB absorption map (Kalberla et al. 2005).
We first explored the literature and found that it is quite common to add an arbitrary error to the Galactic value (Elvis et al. 1986, 1989). The issue was to adopt a boundary without biasing our analysis, as a wide range of values have been adopted through the years, e.g., a ± 20% (Watson et al. 2007; Campana et al. 2016)or even a ± 30% (Cappi et al. 1997).
We opted for a ± 15% error on our Galactic values, to be verified a posteriori with our low-z blazars. Without excess absorption in play, the fitted Galactic values, 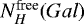 , should havesettled nearby the tabulated value provided by Willingale et al. (2013),
, should havesettled nearby the tabulated value provided by Willingale et al. (2013), 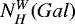 . The fitted Galactic values, along with their errors, were compared to tabulated values and then to their ± 15% boundaries (see Fig. 3). The result confirmed our choice, since the new fitted values were not always compatible with Willingale’s values (vertical dashed line in Fig. 3), but they were indeed consistent within the errors with its ± 15% boundaries (yellow region in Fig. 3). We note also that a ± 15% boundary is among the lowest adopted by the literature.
. The fitted Galactic values, along with their errors, were compared to tabulated values and then to their ± 15% boundaries (see Fig. 3). The result confirmed our choice, since the new fitted values were not always compatible with Willingale’s values (vertical dashed line in Fig. 3), but they were indeed consistent within the errors with its ± 15% boundaries (yellow region in Fig. 3). We note also that a ± 15% boundary is among the lowest adopted by the literature.
 |
Fig. 3 Difference between the fitted Galactic column densities, |
6 Discussion
In Sect. 5 we obtained for high-z blazars that the best-fit model is LGP+EX. An excess absorption component, modelled as intrinsic for simplicity, was always fitted, and this component in blazars should be attributed to the IGM. Here, we first test the role of IGM X-ray absorption indirectly with the NH(z)−z relation (Sect. 6.1), then directly with a spectral model for a WHIM (Sect. 6.2). In a few sources, there was evidence of a spectral break within the observed band, in addition to the fitted excess absorption. The coexistence between the excess absorption and the presence/absence of intrinsic spectral breaks will be thoroughly treated for each source in Appendix D.
6.1 The NH(z)–z relation
At the beginning of this paper we introduced the NH(z)−z relation, only apparently describing the increase of intrinsic absorption with redshift, since the IGM absorption component was neglected. Even considering the existence of the IGM contribution, a definitive direct detection is probably beyond the reach of current instruments (e.g., Nicastro et al. 2016, 2017), thus it is not possible to “subtract” its cumulative effect from the single source, along with the Galactic component, to produce a real NH (zsource)−z relation. Campana et al. (2015) indirectly included the IGM absorption component from a cosmological simulation (in which they pierced through a number of line of sights), matching it to the observed NH (z)−z relation. This was achieved by attributing, for each redshift bin, the IGM absorption to a host galaxy at a given redshift, erroneously on purpose. This produced the curves and coloured areas (see Fig. 2 of Campana et al. 2015), that we used in our paper. In particular, among their 100 simulated LOS, the median of the absorbed LOS distribution (solid line in Fig. 4, along with its corresponding 1- and 2-sigma envelopes in brown and green, respectively) is dominated by two or more intervening over-densities (with density contrast13 Δ > 300 and temperature T > 106 K) that can be associated to, e.g., circumgalactic gas within small galaxy groups. The true IGM, namely the diffuse “metal fog” that is thought to compose the WHIM, produces a minimum absorbing contribution, here represented in Fig. 4 by the lower 2-sigma curve of the median LOS. This simulated least absorbed LOS is free from any absorber with Δ > 100 and it is relative to hot 105−7 K regions far from being collapsed.
We explored the NH(z)−z relation with our results for low- and high-z blazars, reported in Table 5 and shown in Fig. 4. The column densities obtained from our analysis seem to follow the increasing trend with redshift, consistently with the IGM curves simulated by Campana et al. (2015). Only PKS 0528+134 (z = 2.07) showed a moderately high column density above the 2-sigma upper boundary of the IGM mean contribution (the upper green region in Fig. 4). This outlier could be explained with a particularly absorbed LOS, starting with its high Galactic column density (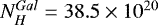 cm−2), due to its low Galactic latitude and to the intervening outer edge of the molecular cloud Barnard 30 in the λ Orion ring of clouds (Liszt & Wilson 1993; Hogerheijde et al. 1995). Consequently, the tabulated value (Willingale et al. 2013), even if it includes the contribution from molecular hydrogen, could be underestimating the amount of absorbing matter within our Galaxy. As a matter of fact, in the PL+EX fit the fitted Galactic value, free to vary between ± 15% uncertainties, was a lower limit, hinting a preference for Galactic columns close to the upper boundary (see Table A.1). Besides, this source would also be compatible with the 3-sigma superior limit of the mean envelope, thus we considered it consistent with our proposed scenario.
cm−2), due to its low Galactic latitude and to the intervening outer edge of the molecular cloud Barnard 30 in the λ Orion ring of clouds (Liszt & Wilson 1993; Hogerheijde et al. 1995). Consequently, the tabulated value (Willingale et al. 2013), even if it includes the contribution from molecular hydrogen, could be underestimating the amount of absorbing matter within our Galaxy. As a matter of fact, in the PL+EX fit the fitted Galactic value, free to vary between ± 15% uncertainties, was a lower limit, hinting a preference for Galactic columns close to the upper boundary (see Table A.1). Besides, this source would also be compatible with the 3-sigma superior limit of the mean envelope, thus we considered it consistent with our proposed scenario.
Two outliers, namely 4C 71.07 (z = 2.172) and PKS 2149–306 (z = 2.345), happened tobe below the 2σ lower simulated curve, that represent the minimum absorption contribution due to a diffuse WHIM. In our work we used higher Galactic values (Willingale et al. 2013) with respect to the earlier literature (Ferrero & Brinkmann 2003; Page et al. 2005; Foschini et al. 2006; Eitan & Behar 2013). However, these sources were already known for their low excess absorption column densities obtained with XMM-Newton data. In fact, even using the LAB Galactic value (Kalberla et al. 2005) for the two outliers did not solve the issue, yielding excess column density upper limits of < 0.09 and < 0.07 × 1022 cm−2, respectively.These two outliers should not be taken as a confutation of the excess absorption scenario emerged through the years for all extragalactic sources, although they cannot be ignored. They could be used as a “worst case” to re-build the lower envelope. However, this should not imply a dramatical change in the simulated characteristics of the IGM, since lowering the metallicity by less than a factor two would be probably enough.
 |
Fig. 4 Distribution of NH(z) with redshift for blazars from this work. Blue objects belong to the Silver sample, while in cyan low-z data are shown. Error bars were computed within XSPEC at 90% confidence level (Δχ2 = 2.71), as were the upper limits (denoted with arrows). All curves and coloured areas were obtained from Campana et al. (2015): the solid line, along with its corresponding 1- and 2-sigma envelopes in brown and green, respectively, is the median of the absorbed LOS distribution, representing the mean absorption contribution from both a diffuse WHIM and additional intervening over-densities. We take the 2-sigma lower envelope as the minimum contribution from a diffuse WHIM alone. |
6.1.1 The role of the instrument’s limits
Typical fair objections can be arisen, e.g., it could be argued whether this observed increasing NH (z)−z relation is real. The validity of the increasing trend was already verified, also with statistical tests (e.g., Campana et al. 2012; Starling et al. 2013; Eitan & Behar 2013; Arcodia et al. 2016). Moreover, high-z column densities only increase as more realistic, lower metallicity values14 are used, thus the trend would be enhanced.
It could be also questioned the physical origin of the increasing trend. The lack of unabsorbed sources at high-redshift would be then only due to the incapability of measuring relatively low column densities towards distant sources. In principle, the minimum NH that can be detected is expected to increase with redshift, as more of the absorbed sub-keV energies are shifted below the observed band. There are indeed instrumental limits, but they influence regions in the NH (z)−z plot way below the observed impressive high-z column densities (e.g., Starling et al. 2013). This gap between the instrument’s limits and the observed column densities is considered significant for validating the physical origin of the increasing NH (z)−z trend. Nonetheless, the presence of instrumental limits provides a fair argument against our conclusions and it should be verified also for our sources.
The instrumental incapability of detecting an (existing) high-z excess column density can be enhanced, e.g., by a high Galactic absorption value and by a low photon statistic. In principle, the role of latter could be confidently excluded, since we analysed sources with more than ~ 10 000 photons. Then, our aim was to compute for each blazar what we called its “last-detection limit”, namely the excess absorption column density value below which only upper limits can be fitted, due to instrumental limits. This purpose wasfulfilled with the fake task within XSPEC, simulating for each blazar the spectrum that would have been extracted by XMM-Newton, given its response and the observation(s) exposure time and its absorbing  with ± 15% boundaries15. The input values for the simulations were obtained from our spectral fits (Table A.1) with the PL+EX scenario. Each simulated spectrum was then fitted with a PL+EX model to compute the errors of the fitted excess column density. Different spectra were simulated for each source, using decreasing arbitrary excess column densities in input, down to the value that yielded an upper limit in the subsequent spectral fit. All three cameras were used to compute the final last-detection limit.
with ± 15% boundaries15. The input values for the simulations were obtained from our spectral fits (Table A.1) with the PL+EX scenario. Each simulated spectrum was then fitted with a PL+EX model to compute the errors of the fitted excess column density. Different spectra were simulated for each source, using decreasing arbitrary excess column densities in input, down to the value that yielded an upper limit in the subsequent spectral fit. All three cameras were used to compute the final last-detection limit.
The left panels of Fig. 5 show the NH(z)−z relation, along with the last-detection limit of each blazar, that was extrapolated with the scaling relation 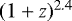 (see Campana et al. 2014). These curves provided an overall sensitivity range for the detection of excess column densities for our sources. In our sample, no selection criteria on Galactic column density values were included, leading to
(see Campana et al. 2014). These curves provided an overall sensitivity range for the detection of excess column densities for our sources. In our sample, no selection criteria on Galactic column density values were included, leading to 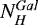 ranging from 1.22 to 42.5 × 1020 cm−2. Excluding sources with a Galactic column density greater than 1021 cm−2, the instrument reaches sensitivity for excess column detections well below the simulated lower IGM absorption contribution (see the bottom left panel). In the right panels of Fig. 5 last-detection limits are shown for each source with a red horizontal dash, along with the underlying “upper-limit” area in grey. Again, the bottom panel was obtained excluding any blazar with a Galactic column density greater than 1021 cm−2.
ranging from 1.22 to 42.5 × 1020 cm−2. Excluding sources with a Galactic column density greater than 1021 cm−2, the instrument reaches sensitivity for excess column detections well below the simulated lower IGM absorption contribution (see the bottom left panel). In the right panels of Fig. 5 last-detection limits are shown for each source with a red horizontal dash, along with the underlying “upper-limit” area in grey. Again, the bottom panel was obtained excluding any blazar with a Galactic column density greater than 1021 cm−2.
Both left and right panels lead to the same conclusion. It is true that any instrument has its limits in detecting low column densities at high-z and we were not incredibly sensitive to very low column densities per se. Nonetheless, we were sensitive enough to conclude that our high-z column densities are high for physical reasons, since our fitted values are significantly above the minimum values reachable by XMM-Newton for each source (red dashes in Fig. 5). If the increasing trend was only produced by the instrument’s limits, we would have expected upper limits consistent with the upper edge of the grey area and not, as we observed at high-z, clear detections above it. This is more evident in bottom panels of Fig. 5, where only blazars with Galactic column densities below 1021 cm−2 were considered (actually, it is below 6.15 × 1020 cm−2). Hence, selecting sources with a relatively low Galactic absorption component is extremely important to reach sufficient sensitivity to probe thediffuse IGM. Moreover, longer exposures with current instruments, e.g., XMM-Newton, should be adopted to provide even lower last-detection limits.
 |
Fig. 5 NH(z)−z relation, see Fig. 4 for the general description. Left panels: the solid grey curves represent the extrapolation of the last-detection limit of each blazar, providing an overall sensitivity range of the instrument for excess absorption detections. Right panels: the same last-detection limits are shown for each blazar with red horizontal dashes. The underlying grey area is the “upper-limit” region for each blazar. Observing a blazar with a specific XMM-Newton response, exposure time, absorbed by its |
6.1.2 Comparison with previous works
Our results are generally in accordance with the literature involving the same sources and instruments (e.g., Reeves et al. 2001; Ferrero & Brinkmann 2003; Worsley et al. 2004a,b; Brocksopp et al. 2004; Page et al. 2005; Piconcelli & Guainazzi 2005; Yuan et al. 2005; Grupe et al. 2006; Foschini et al. 2006; Tavecchio et al. 2007; Bottacini et al. 2010; Eitan & Behar 2013; Tagliaferri et al. 2015; Paliya 2015; D’Ammando & Orienti 2016; Paliya et al. 2016; Sbarrato et al. 2016), of course taking into account the possible differences (e.g., the Galactic absorption model).
It is worth discussing that Paliya et al. (2016) obtained a large disagreement between column densities measured from XMM-Newton spectra and from broadband Swift-XRT+NuSTAR spectra, the latter several times larger (up to an order of magnitude). From this, they concluded that spectral curvature in high-z blazars is not caused by excess absorption, but it is due to spectral breaks intrinsic to the blazar’s emission, better investigated with a broadband analysis. Actually, our broadband fits, in which excess absorption was also constrained by XMM-Newton, yielded column densities compatible with the narrowband fits (see Table A.1). Hence, while a broadband spectrum does provide an extensive view on the curved spectral continuum, their claim is possibly driven by a misleading comparison between XMM-Newton’s and Swift-XRT’s performances. The former, with its larger effective area, allows us to assess the soft X-ray properties better than the latter can do. As a matter of fact, removing XMM-Newton from our broadband analysis, Swift-XRT+NuSTAR data alone did yield higher intrinsic column densities, e.g., 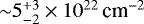 in QSO B0014+810 or
in QSO B0014+810 or 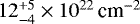 in PBC J1656.2–3303. Moreover, fitting only Swift-XRT data of QSO B0014+810 with a PL+EX model yielded a column density upper limit (NH(z) < 3.81 × 1022 cm−2) around half order of magnitude higher than the XMM-Newton results (NH(z) < 0.84 × 1022 cm−2). We attribute the difference in the fitted column densities to Swift-XRT’s lower photon counts (e.g., ~ 500−600 for the two observations of QSO B0014+810) compared to the larger statistic provided by XMM-Newton. The same conclusion is valid for the discrepancies obtained in 7C 1428+4218, RBS 315, and PBC J1656.2–3303.
in PBC J1656.2–3303. Moreover, fitting only Swift-XRT data of QSO B0014+810 with a PL+EX model yielded a column density upper limit (NH(z) < 3.81 × 1022 cm−2) around half order of magnitude higher than the XMM-Newton results (NH(z) < 0.84 × 1022 cm−2). We attribute the difference in the fitted column densities to Swift-XRT’s lower photon counts (e.g., ~ 500−600 for the two observations of QSO B0014+810) compared to the larger statistic provided by XMM-Newton. The same conclusion is valid for the discrepancies obtained in 7C 1428+4218, RBS 315, and PBC J1656.2–3303.
The most complete window on the X-ray spectra would be provided by simultaneous XMM-Newton and NuSTAR observations. In the absence of this possibility, XMM-Newton should be added anyway to Swift-XRT+NuSTAR data in a broadband analysis (see Sect. 5).
Then, we compared our results with other extragalactic sources from the literature. GRBs typically show a large scatter in NH (z), particularly at low z, due to their known prominent intrinsic absorption component, although a lower contribution, increasing with z and enclosing allsources, is evident and was attributed to the diffuse IGM (see Campana et al. 2010, 2012, 2015; Behar et al. 2011; Starling et al. 2013; Arcodia et al. 2016). In the left panel of Fig. 6, we show intrinsic column densities from this work, along with GRB data from Arcodia et al. (2016). Both types of sources seem to agree with the simulated IGM absorption contributions, reported from Campana et al. (2015). In particular, GRBs are distributed upwards from the simulated areas, in agreement with having both intervening and intrinsic absorption contributions, while blazars clearly follow specifically the coloured areas representing the IGM contribution, in accordance with the idea of a missing absorption component within the host galaxy.
The NH(z)−z relation was previously studied also in quasars, although mostly focused on the greater amount of X-ray absorption detected in radio-loud16 (RLQs) rather than in radio-quiet quasars (RQQs), perhaps suggesting that it was due to the presence of the relativistic jet (see discussions in, e.g., Elvis et al. 1994a; Cappi et al. 1997; Fiore et al. 1998; Reeves & Turner 2000; Page et al. 2005; Eitan & Behar 2013, and references therein). Nonetheless, at the time there was no clear distinction between blazars and other jetted AGN, in which the relativistic jet is pointing at wider angles (θview ≳ 1∕Γ, where Γ is the bulk Lorentz factor of the jet emitting region) with respect to the LOS. In the former the SED is dominated by the beamed non-thermal emission of the jet, while the latter shows, for increasingly wide angles, an X-ray spectrum always more similar to non-jetted AGN (see Fig. 3 in Dermer 1995; Sbarrato et al. 2015). Moreover, in these works RLQs (in the way they interpreted it, e.g., jetted AGN regardless of the jet direction) typically had better statistics with respect to RQQs and/or were observed up to larger distances. The reason is that most of their RLQs were later identified as blazars and then benefited of the relativistic beaming. On the contrary, RQQ-samples of these earlier works consisted mainly in lower-redshift sources (e.g., 12 RQQs out of 286 at z > 2.2 in Fiore et al. 1998; Eitan & Behar 2013), for which negligible IGM excess absorption is expected, and/or in quasars with lower counts statistic (e.g., Page et al. 2005), for which a column density detection cannot be clearly established. Hence, the lack, in the above-mentioned works, of clear detections of excess column densities in RQQs, with respect to the corresponding RLQ-samples, is perfectly understandable.
Here we promoted a different point of view, attributing the observed hardening to absorption in excess of the Galactic value, occurring along the IGM. This would solve the paradox of the incomparably lower amount of intrinsic absorption detected in the optical/UV compared to X-ray analysis (e.g., see the discussions in Elvis et al. 1994a; Cappi et al. 1997; Fabian et al. 2001b; Worsley et al. 2004a,b; Page et al. 2005), that through the years led to preferring the intrinsic spectral breaks scenario. Nonetheless, our suggested scenario needed to be tested with quasars of the previous works, obtained by selecting only sources observed with XMM-Newton17 and excluding sources below z = 0.1 (the first redshift bin of the simulated IGM). References for intrinsic column density values are reported in the description of Fig. 6. If the same object was studied in different works, we favoured the literature in which the analysis was performed with all EPIC cameras. We excluded quasars when clear evidence of lensing was found in the literature. We only reported from Corral et al. (2011) quasars with a detection in NH(z) and with a power-law as best-fit model (see Campana et al. 2015, for a complete comparison between all their results and the simulated IGM).
The right panel of Fig. 6 shows the NH(z)−z plot filled with our low- and high-z blazars (blue stars) and with AGN from the literature, divided between blazars (stars) and non-blazars (squares). The latter are observed also above the simulated IGM curves, as for some generic AGN an intrinsic absorption component is expected (e.g., Ricci et al. 2017), while the former are again consistent with having only the IGM absorption component. Few outliers, some of which were reprocessed, are discussed in Appendix C.
 |
Fig. 6 See Fig. 4 for a general description of the plot. Left panel: additional GRB data from Arcodia et al. (2016) are plotted. Right panel: the distribution of NH (z) with redshift for blazars from this work (blue stars) and for quasars from the literature (black symbols are related to Page et al. 2005; magenta to Nanni et al. 2017; grey to Eitan & Behar 2013; dark green and orange to Shemmer et al. 2006 and Shemmer et al. 2008, respectively; red to Saez et al. 2011; cyan to Yuan et al. 2006; purple to Grupe et al. 2006; lime to Shemmer et al. 2005; dark red to Campana et al. 2015; brown to Ricci et al. 2017; dark orange to Corral et al. 2011). Squares stand for generic non-blazars AGN, while stars for blazars. Error bars were computed within XSPEC at 90% confidence level (Δχ2 = 2.71), as were the upper limits (denoted with arrows below the related symbol). |
6.2 The warm-hot IGM absorption contribution
Within XSPEC, it is possible to directly model the IGM absorption component with igmabs18. This model computes the X-ray absorption expected from a WHIM with a uniform medium (expressed in hydrogen density n0, at solar metallicity), constant temperature T and ionisation state ξ. Other parameters involved are the redshift of the source and the photon index of the photo-ionising spectrum, typically estimated with the measured cosmic X-ray background (CXRB). If all the main parameters of the WHIM, such as T, ξ, and n0, are left free to vary some degeneracy is expected (see Starling et al. 2013). Some constraints can be adopted, e.g., n0 can be fixed to 1.7 × 10−7 cm−3 (Behar et al. 2011, and references therein), or the temperature can be constrained to be 106 K (Starling et al. 2013; Campana et al. 2015). We chose to tie the ionization parameter to n0, leaving the latter and T as the only free parameters of the igmabs model. The ionization parameter of the IGM is given by:
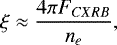 (7)
(7)
where the electron density ne is ~ 1.2n0 and FCXRB = 2.9 × 10−7 erg cm−2 s−1 sr−1 (De Luca & Molendi 2004; Starling et al. 2013; Campana et al. 2015). Hence, we constrained log ξ = 1.48 − log(n0) throughout all the igmabs fits.
According to Fig. 4, only a few sources showed an intrinsic column density compatible with the lower IGM absorption curve, proper of a diffuse WHIM, namely 4C 71.07, QSO B0237–2322, PKS 2149–306, PBC J1656.2–3303, and QSO B0014+810. Nonetheless, spectral fits performed with 0.2−10 keV XMM-Newton spectra were incapable to constrain both n0 and T. However, using also Swift-XRT+NuSTAR, together with XMM-Newton, the fits started to be sensitive to those parameters. Luckily, among the five blazars compatible with the lower envelope, four had broadband data available (QSO B0237–2322 is the only source cut out).
We then performed 0.2−79 keV spectral fits for individual sources, as described in Sect. 5, but fixing the Galactic absorption19 and modelling the excess absorption with a WHIM component. The continuum of the sources in the broadband LGP+igmabs fit was constrained with the results of the LGP+EX model. Hence, XMM-Newton continua of QSO B0014+810, PKS 2149–306 and PBC J1656.2–3303 were constrained to a simple power-law, while for 4C 71.07 a fixed curvature of 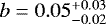 was assumed. In addition, Swift-XRT+NuSTAR continua were left free to vary with LGP parameters except for QSO B0014+810, in which a power-law continuum was used. This is a reasonable approximation, arisen to obviate experimental and computational limits of the model, that allowed us to better constrain the fitted parameters. A more rigorous fit with free continuum parameters would probably lead to upper limit measures for the WHIM characteristics. Results are shown in Table 6 and they are quite consistent with each other, due to the huge errors. The remaining parameters were fully compatibles, within the errors, with the values obtained in the LGP+EX scenario and were not reported.
was assumed. In addition, Swift-XRT+NuSTAR continua were left free to vary with LGP parameters except for QSO B0014+810, in which a power-law continuum was used. This is a reasonable approximation, arisen to obviate experimental and computational limits of the model, that allowed us to better constrain the fitted parameters. A more rigorous fit with free continuum parameters would probably lead to upper limit measures for the WHIM characteristics. Results are shown in Table 6 and they are quite consistent with each other, due to the huge errors. The remaining parameters were fully compatibles, within the errors, with the values obtained in the LGP+EX scenario and were not reported.
We thenperformed a joint fit with all four sources to obtain an overall measurement of the WHIM characteristics. The IGM absorption parameters (namely n0, T, and ξ) were tied together among all the different observations. Results are displayed in Table 6 and the related contour plot is reported in Fig. 7. The overall fitted values are consistent with the expected properties of the WHIM, namely an average hydrogen density ≈10−7 cm−3 and a temperature≈106 K (e.g., Cen & Ostriker 2006; Bregman 2007; Starling et al. 2013; Campana et al. 2015, and references therein).
Furthermore, the hydrogen density obtained within XSPEC spectral fits is expressed using solar abundances and metallicity. Hence, if the estimate n0 = 1.7 × 10−7 cm−3 (Behar et al. 2011, and references therein) is to be trusted, we can infer the metallicity of the WHIM comparing it with our fitted value of n0. The inferredmetallicity is:
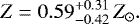 (8)
(8)
This should be only considered as an important consistency check. What is more, we provided suitable candidates for deeper exposures with current instruments. Among the four sources used for this analysis, 4C 71.07 and PKS 2149–306 are the best candidates, given the higher Galactic column densities of the other two sources. The deleterious effect of such high Galactic values was shown in Fig. 5. A long simultaneous XMM-Newton+NuSTAR should provide more stringent limits.
Moreover, our work stands as a valid supporting alternative to methods involving direct detections of (extremely weak) absorption signals from the WHIM towards distant sources (e.g., Nicastro et al. 2013; Ren et al. 2014, and references therein), in which, however, definitive detections can not be easily obtained with current instruments, yet (see Nicastro et al. 2016, 2017, and references therein).
Fit results with igmabs.
 |
Fig. 7 Results of the joint igmabs fit with QSO B0014+810, PBC J1656.2–3303, PKS 2149–306, and 4C 71.07 fitted together. Confidence contours are shown for the hydrogen density n0 (x-axis) and the temperature (y-axis) of the IGM. We display 68, 95, and 99 percent contours in red, green, and blue, respectively. |
7 Conclusions
The role played by the IGM in X-ray absorption, obviously increasing with redshift and likely dominating above z ~ 2, was first inferred empirically (see Behar et al. 2011; Campana et al. 2012; Starling et al. 2013; Eitan & Behar 2013; Arcodia et al. 2016, and references therein) and then confirmed through dedicated cosmological simulations (Campana et al. 2015). We tested it studying a sample of high-redshift blazars. Since blazars are characterised by a kpc-scale relativistic jet pointing towards us, the host X-ray absorption component along the LOS have been likely swept. Hence, detecting the signature of X-ray absorption in excess to the Galactic value in the X-ray spectra of distant blazars provided strong insights in favour of the IGM absorption scenario.
Our sample of blazars consisted in 15 sources selected above z = 2 and observed by XMM-Newton with at least ~10 000 photons detected (by all the three EPIC cameras combined). Moreover, six of these blazars boasted additional NuSTAR (and simultaneous Swift-XRT) observations, thus providing a large broadband spectrum that allowed a more detailed analysis. In all sources an additional curvature term was required by data, in excess to a Galactic absorption component. It was first characterised in terms of either an intrinsic extra-absorber (the easiest way to assess the presence of excess absorption) or an intrinsic spectral break. Both alternatives separately improved the fits, although often yielding statistically undistinguishable results for the single source. Then, for the first time we included both terms and this description was assessed to be the best-fit model. In particular, we obtained that excess absorption was fitted in all sources, while the continuum curvature terms were consistent with a power-law in 11 sources out of 15.
Hence, thanks to an overall sample analysis, with the additional help of a low-redshift sample used for comparisons, we were able to conclude that excess absorption is preferred to explain the observed soft X-ray spectral hardening. The intrinsic excess column densities obtained were compatible with the NH (z)−z relation and the simulated IGM absorption contributions (Campana et al. 2015), along with the other extragalactic sources. Only a couple of outliers lied below the simulated envelopes and should perhaps be considered for a slight re-adaptation of the IGM characteristics.
In addition, we performed spectral fits directly modelling a WHIM contribution, finding agreement with its expected characteristics (e.g., Bregman 2007). A joint fit with four sources (consistent with the IGM lowest absorption contribution) yielded a WHIM with average density 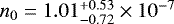 cm−3 (at solar metallicity) and temperature
cm−3 (at solar metallicity) and temperature 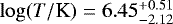 . In deriving these parameters some of the continua in the spectral models were constrained to power-laws, so that a more flexible spectral analysis would probably yield upper limit measures for the WHIM characteristics. Then, the fitted hydrogen density value corresponds to an ionisation parameter of log ξ = 1.47 ± 0.27, if a constant CXRB flux is used (from De Luca & Molendi 2004), and to an IGM metallicity of
. In deriving these parameters some of the continua in the spectral models were constrained to power-laws, so that a more flexible spectral analysis would probably yield upper limit measures for the WHIM characteristics. Then, the fitted hydrogen density value corresponds to an ionisation parameter of log ξ = 1.47 ± 0.27, if a constant CXRB flux is used (from De Luca & Molendi 2004), and to an IGM metallicity of 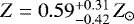 , if an hydrogen density of 1.7 × 10−7 cm−3 is assumed (from Behar et al. 2011, and references therein). This is an important consistency check for our scenario.
, if an hydrogen density of 1.7 × 10−7 cm−3 is assumed (from Behar et al. 2011, and references therein). This is an important consistency check for our scenario.
Furthermore, by attributing the X-ray spectral hardening in high-z blazars uniquely to excess absorption along the IGM in 11 sources, we were necessarily suggesting that intrinsic spectral breaks, predicted by emission models, were “missed” within the observed band. We thoroughly checked for each source that the observed parameters, for example photon indexes, were consistent with such an explanation. We proved that, in principle, our proposed scenario is valid and does not contradict blazars’ emission models, short of a condition on the product γcoolΓ (or γminΓ).
Future prospects are aimed to obtain deeper exposures with current instruments of the best candidates, namely sources with a low Galactic column and compatible with the IGM absorbing envelope (e.g., the two outliers 4C 71.07 and PKS 2149–306). Simultaneous XMM-Newton+NuSTAR observations are suggested for a thorough and reliable spectral analysis. Looking beyond, our work can be used as a stepping stone for more meticulous studies involving Athena (Nandra et al. 2013).
Acknowledgements
We thank Fabrizio Tavecchio for useful discussions and Tullia Sbarrato for her precious help in building the samples.We thank the anonymous referees for helpful comments. This work made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory and funded by the National Aeronautics and Space Administration. This work made use of data supplied by the UK Swift Science Data Centre at the University of Leicester. Additionally, we acknowledge the use of the matplotlib package (Hunter 2007).
Note added in proof. After the article was accepted, Nicastro et al. (2018) reported the detection of two highly ionized intervening absorbers in their extremely high signal-to-noise spectrum of the low-z blazar 1ES 1553+113. The detection was highly significant and was associated with the WHIM, possibly solving a long-standing quest for the missing baryons. This discovery strengthens the conclusions of our work and proves our method to be a valuable alternative to probe the intergalactic medium.
Appendix A Additional tables
Spectral fit results.
XMM-Newton spectral fits for six FSRQ-type blazars and two LBLs of the low-redshift sample, performed in the 0.2− 10 keV energy range for the pn detector and 0.3−10 keV for MOS detectors.
Appendix B Individual sources processing
B.1 7C 1428+4218 (z = 4.715)
XMM-Newton observed 7C 1428+4218 three times: on 2002 December 9 (ObsID 0111260101) for a total exposure time of 18.9 ks; on 2003 January 17 (ObsID 0111260701) for a total exposure time of 14.6 ks; on 2005 June 5 (ObsID 0212480701) for a total exposure time of 19.7 ks. All three observations were performed with thin filter and Full Frame mode for all the EPIC cameras.
The first observation was discarded after being processed due to low photon counts (≈ 3000), compared tothe others. The second observation, hereafter Obs2003, was regularly processed, selecting the default limit rate choice (< 0.35 c s−1 for MOS1 and MOS2, < 0.4 c s−1 for pn) for FPB filtering. The source spectrum was extracted from a circular region with a radius of 38″ for all the threeEPIC cameras (paying particular attention in avoiding the faint X-ray source 2XMM J143020.9+420529, located ~ 62″ away). The background was derived from a circular source-free region with the same radius (54″ only for MOS2) near the selected source (this is valid throughout this section, unless otherwise stated). Using the epatplot task, we observed no pile-up for this observation. Also, according to WebPIMMS, the expected pile-up fraction was 0.6% for EPIC-MOS cameras, 0.7% for EPIC-pn (values under 5% are typically fine). At the end of the processing for Obs2003, the result was a series of spectra with a count rate of 0.57 c s−1 in 11.5 ks, 0.15 c s−1 in 14.2 ks, and 0.16 c s−1 in 14.2 ks for EPIC-pn, MOS1 and MOS2 respectively. They provide a total number of ~ 11 000 photons.
The same procedure was adopted for the third observation (hereafter Obs2005), with only a few slightly different choices. First of all, the EPIC-pn event list was filtered from FPB below < 0.5 c s−1. The source and background regions were selected similarly to Obs2003 (38″ circle for MOS2 and pn, 36″ for MOS1). No pile-up is apparent for this observation as well. The result is a series of spectra with a count rate of 0.52 c s−1 in 11.7 ks, 0.14 c s−1 in 17.4 ks, and 0.14 c s−1 in 17.3 ks for EPIC-pn, MOS1 and MOS2 respectively. They provide a total number of ~ 11 000 photons, as much as in Obs2003.
7C 1428+4218 has been observed by NuSTAR on 2014 July 14 (ObsID 60001103002) for a total exposure of 49.2 ks. The source spectrum has been extracted for FPMA (FPMB) from a circular region with a radius of ~ 32″ (~ 31″). At the end of the processing, FPMA and FPMB spectra provided a count rate of 0.023 c s−1 in 49.2 ks and 0.022 c s−1 in 48.9 ks, respectively and a total number of ~2200 photons.
Swift-XRT observed the source on 2014 July 13 (ObsID 00080752002) for a total exposure of 7.5 ks. The resulting spectrum showed a count rate of 0.033 c s−1 in 7.4 ks, providing ~250 photons.
In Table B.1 we report a summary of exposure times and photon counts for each observation of every source.
Summary for individual sources processing.
B.2 QSO J0525-3343 (z = 4.413)
XMM-Newton observed QSO J0525-3343 eight times: first, on 2001 February 11 and on 2001 September 15; then, a series of six more was made between 2003 February 14 and 2003 August 8. All observations were performed with thin filter and Full Frame imaging mode for all the EPIC cameras.
Following Worsley et al. (2004b), we discarded the first observation because badly affected by background flaring. The second (ObsID 0050150301, Rev. 324; hereafter Obs324) was processed and analysed. Then, three of the remaining observations (Rev. 593, 598, and 603) were discarded, before processing, since their expected photon counts (see Worsley et al. 2004b, Table 1) were deemed to be non influential on the total amount of photons expected from the combined analysis. In addition, another observation was discarded after being processed for the same reason (Rev. 671). Three observations remained: Obs324, for a total exposure time of 28.4 ks; Obs583 (ID 0149500601, Rev. 583) and Obs588 (ID 0149500701, Rev. 588), both for a total exposure time of 12.2 ks.
For each observation, the event file was filtered from FPB: for Obs324 below < 0.45 c s−1 for MOS1 and MOS2, < 0.5 c s−1 for pn; Obs583 and 588 were filtered with the default limit rate choice. For all the three EPIC cameras of Obs324, the source spectrum was extracted from a circular region with a radius of 42″. Regarding Obs583, the radius of the source and background region was 42″ for the MOS cameras, 38″ for the pn. In Obs588, circular regions with radius 34″ (MOS1) and36″ (MOS2, pn) were chosen. No pile-up effect was observed for any observation of QSO J0525–3343.
At the end of the processing for Obs324, the result was three spectra with a total number of ~ 12 000 photons. Obs583 and 588 consist in a total number of ~6500 photons each.
B.3 QSO B1026-084 (z = 4.276)
XMM-Newton observed QSO B1026–084 twice: on 2002 May 15 (ObsID 0093160701) for a total exposure time of 7.9 ks and on 2003 June 13 (ObsID 0153290101) for a total exposure time of 43.4 ks. Both observations were performed with thin filter and Full Frame mode for all the EPIC cameras.
Only the second (longer) observation was processed. The event file was filtered from FPB selecting the default limit rate choice. The source spectrum was extracted from a circular region with a radius of 36″ for the EPIC-MOS cameras. Circular regions with a radius of 34″ were taken for the EPIC-pn camera, paying particular attention in avoiding the couple of unidentified faint X-ray sources located few arc-seconds away. No pile-up effect was apparent for this blazar.
The result was a series of spectra with a count rate of 0.31 c s−1 in 15.6 ks, 0.09 c s−1 in 21.5 ks, and 0.09 c s−1 in 22.1 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 9000 photons. It is slightly below the threshold of our selection criterion, but it was included in the analysis.
B.4 QSO B0014+810 (z = 3.366)
XMM-Newton observed QSO B0014+810 on 2001 August 23 (ObsID 0112620201) for a total exposure time of 42.9 ks. The observation was performed with medium filter and Full Frame mode for all the EPIC cameras.
The event file was filtered from FPB selecting the default limit rate choice. The source spectrum was extracted from a circular region with a radius of 42″ for the MOS cameras, 35″ for the EPIC-pn. No pile-up was observed for this blazar. Also, the tool WebPIMMS yielded an expected pile-up fraction of 1.3% for EPIC-MOS cameras, 1.1% for EPIC-pn. The result was a series of spectra with a count rate of 0.96 c s−1 in 13.4 ks, 0.31 c s−1 in 19.8 ks, and 0.31 c s−1 in 20.4 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~25 000 photons.
QSO B0014+081 has been observed three times by NuSTAR: on 2014 December 21 (ObsID 60001098002, hereafter Obs2014) for a total exposure of 31.0 ks; on 2015 January 23 (ObsID 60001098004, hereafter Obs2015) for a total exposure of 36.4 ks; the most recent and shortest observation (ObsID 90201019002, 2016 April 12) was not processed.
In Obs2014 (Obs2015), the source spectrum has been extracted for both FPMA and FPMB from a circular region with a radius of ~ 42″ (~ 41″). In Obs2014 (Obs2015), FPMA and FPMB spectra have a count rate of 0.08 c s−1 in 31.0 ks (0.07 in 36.1) and 0.07 c s−1 in 31.0 ks (0.07 in 36.3), respectively, providing a total number of ~ 4700 (5000) photons.
Swift-XRT performed two observations of blazar QSO B0014+810, simultaneously with NuSTAR, on 2014 December 21 (ObsID 00080003001), and on 2015 January 23 (ObsID 00080003002). The resulting spectrum for Obs2014 (Obs2015) showed a count rate of 0.09 c s−1 in 6.5 ks (0.07 in 6.6), providing ~590 (460) photons.
B.5 PKS 2126-158 (z = 3.268)
XMM-Newton observed PKS 2126–158 on 2001 May 1 (ObsID 0103060101) for a total exposure time of 23.4 ks. The observation was performed with medium filter and Full Frame mode for the EPIC-MOS cameras, with the same filter but in Extended Full Frame mode for the EPIC-pn.
The event file of the EPIC-pn has been filtered from FPB selecting the default limit rate choice, while for the EPIC-MOS cameras the event file has been filtered below < 0.18 c s−1. The source spectrum was first extracted from a circular region with a radius of 40″ for the MOS cameras, 36″ for the EPIC-pn. However, a possible pile-up contamination was found using the SAS task epatplot, as the expected pattern distributions seemed to be discrepant from the observed ones. A more conservative annular region was then opted for all the EPIC cameras. We excised a 5″ core from the MOS1 circular source region, obtaining a better fit with epatplot. The same internal radius was then adopted for the EPIC-MOS2 annular region. We then excised the core from the EPIC-pn source region up to 12″ before finding an adequate result with epatplot. A greater excision was expected because EPIC-pn operated in Extended Full Frame mode, for which the image collection time is longer than in the normal Full Frame mode. Thus, pile-up becomes non negligible at a lower count rate. No pile-up effects were observed for this blazar after the selection of annular regions. Also the tool WebPIMMS was used for consistency, confirming the result: the expected pile-up fraction is 2.5% for EPIC-MOS cameras, 3.9% for EPIC-pn.
At the end of the processing, the result was a series of spectra with a count rate of 0.78 c s−1 in 13.1 ks,0.55 c s−1 in 19.9 ks, and 0.56 c s−1 in 19.9 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 32 000 photons.
B.6 QSO B0537-286 (z = 3.104)
XMM-Newton observed QSO B0537–286 first on 2000 March 19 (ObsID 0114090101, hereafter Obs00) for a total exposure time of 53.0 ks. The observation was separated in two consecutive exposures for each EPIC camera. The first exposure was performed with medium filter and Full Frame mode for MOS1 and pn, in Large Window mode for MOS2. During the second exposure, MOS1 operated in Large Window mode, whilst MOS2 and pn in Full Frame mode.
For each exposure, the event file has been filtered from FPB selecting the default limit rate choice. For each EPIC camera, the two consecutive exposures were then merged through the XMM SAS task merge.
XMM-Newton observed QSO B0537–286 a second time on 2005 March 20 (ObsID 0206350101, hereafter Obs05) for a total exposure time of 81.9 ks. This observation was performed with thin filter and all the EPIC cameras operated in Full Frame mode. The event file of the EPIC-pn was filtered from FPB below < 0.35 c s−1, while the EPIC-MOS cameras were filtered below < 0.15 c s−1.
The source spectrum of Obs00 was extracted from a circular region with a radius of 38″ for the MOS cameras, 33″ for the EPIC-pn. We note that the two EPIC-MOS cameras operated alternatively in Large Window and Full frame mode in the two consecutive exposures. Thus, the outer regions of the merged central chip have lower background. We then selected the background region from an external chip. The same radii were adopted for Obs05, in which QSO B0537–286 was detected at a moderately large off-axis angle. We note that no pile-up contamination was apparent in both observations.
At the end of the processing, the result for Obs00 (Obs05) was a series of spectra with a count rate of 0.81 (0.76) c s−1 in 32.2 (13.5) ks, 0.25 (0.23) c s−1 in 38.1 (23.4) ks, and 0.25 (0.23) c s−1 in 38.4 (19.1) ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 45 000 (20 000) photons.
B.7 QSO B0438-43 (z = 2.852)
XMM.Newton observed QSO B0438–43 on 2002 April 6 (ObsID 0104860201) for a total exposure time of 12.9 ks. The observation was performed with thin filter and Full Frame mode for all the EPIC cameras.
The event file was filtered from FPB selecting the default limit rate choices. The source spectrum was extracted from a circular region with a radius of 46″ for the MOS cameras, 35″ for the EPIC-pn. The result was a series of spectra with a count rate of 0.89 c s−1 in 8.8 ks, 0.27 c s−1 in 12.2 ks, and 0.28 c s−1 in 12.2 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 14 500 photons.
B.8 RBS 315 (z = 2.69)
XMM-Newton observed RBS 315 three times: the first on 2003 July 25 (ObsID 0150180101, hereafter Obs2003) for a total exposure time of 22.2 ks; then twice (2-days apart) on 2013, on January 13 (ObsID 0690900101, hereafter Obs2013a) and on January 15 (ObsID 0690900201, hereafter Obs2013b), for a total exposure time of 108.0 and 96.7 ks, respectively. All the observations were performed with thin filter and Full Frame mode for all the EPIC cameras.
The event files of Obs2003 have been filtered from FPB selecting the default limit rate choice. Obs2013a was quite affected by FPB, particularly at the beginning and at the end of the exposure. In the EPIC-MOS event files the background rate was lower than the default selection, hence we filtered below 0.15 and 0.2 c s−1 for MOS1 and 2, respectively. Moreover, we excluded any t < 4.74516E08 s (the first ~ 17 ks of the exposure) from the Good Time Intervals (GTI) for both MOS cameras. The EPIC-pn event list was filtered with the default limit rate choice and in addition any t ≥ 4.74588E08 s was excluded. Obs2013b was comparably affected by FPB and the event lists were filtered with a similar modus operandi: all the EPIC event files were filtered with the same rate thresholds of Obs2013a; any t > 4.7475E08 s was excluded from all the EPIC event files, whilst EPIC-pn was additionally shortened excising any t < 4.74718E08 s.
In all the observations, the source spectrum was first extracted from circular regions. However, some pile-up contamination was found using the SAS task epatplot, as the expected pattern distributions seemed to be discrepant from the observed ones. A more conservative annular region was then opted for all the EPIC cameras. In Obs2003, we excised a 10″ core from all the source regions, obtaining a better fit with epatplot. The selected external radius is 44″ for MOS cameras, and 37″ for EPIC-pn. Same for Obs2013a [Obs2013b], selecting annuli with Ri, Re = (10″, 40″) [(13″, 44″)] for MOS1/2 and annuli with Ri, Re = (10″, 36″) [(13″, 38″)] for pn. In all observations, the background was extracted from a circular (source-free) region with radius equal to Re, for each EPIC camera. No pile-up was apparent for this blazar after the selction of annular regions. Also the tool WebPIMMS was used for consistency, confirming the result: the expected pile-up fraction in Obs2013a (the one with the highest count rate) is 1.9% for all EPIC cameras. For Obs2003 and Obs2013b, with a lower count rate, the pile-up fraction is expected to be even smaller.
At the end of the processing, Obs2003 consists in a series of spectra with a count rate of 1.24 c s−1 in 18.2 ks, 0.42 c s−1 in 21.6 ks, and 0.41 c s−1 in 21.7 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 40 500 photons. In Obs2013a (Obs2013b), count rates of 1.32 in 40.4 ks (0.93 in 28.4 ks), 0.43 in 54.7 ks (0.31 in 66.8 ks) and 0.43 in 56.6 ks (0.32 in 67.6 ks) for pn, MOS1 and MOS2 respectively, provide a total number of ~ 101 000 (~ 69 000) photons.
RBS 315 was observed twice by NuSTAR: on 2014 December 24 (ObsID 60001101002, hereafter Obs2014) for a total exposure of 37.4 ks and on 2015 January 18 (ObsID 60001101004, hereafter Obs2015) for a total exposure of 31.9 ks. In both observations the source spectrum was extracted for both FPMA and FPMB from a circular region with a radius of ~ 70″. At the end of the processing for Obs2014 (Obs2015), FPMA and FPMB spectra showed a count rate of 0.38 c s−1 in 31.5 ks (0.26 in 37.4) and 0.35 c s−1 in 31.7 ks (0.24 in 37.4), respectively. They provide a total number of ~ 23 000 (19 000) photons.
Swift-XRT performed two observations of blazar RBS 315, simultaneously with NuSTAR, on 2014 December 24 (ObsID 00080243001), and on 2015 January 18 (ObsID 00080243002). The resulting spectrum for Obs2014 (Obs2015) showed a count rate of 0.21 c s−1 in 4.9 ks (0.15 in 5.1), providing ~1000 (800) photons.
B.9 QSO J2354–1513 (z = 2.675)
XMM-Newton observed QSO J2354–1513 on 2004 December 5 (ObsID 0203240201) for a total exposure time of 86.9 ks. The observation was performed with thin filter and Full Frame mode for all the EPIC cameras.
The event file was filtered from FPB below < 0.4 c s−1 for MOS1 and MOS2, < 0.7 c s−1 for pn. Moreover, a time-threshold was added to the MOS2 event file and we excluded any exposure time after 2.18641E08 s. The source spectrum was extracted from a circular region with a radius of 38″ for the MOS cameras, 30″ for the EPIC-pn. At the end of the processing, the result was a series of spectra with a count rate of 0.32 c s−1 in 33.2 ks, 0.09 c s−1 in 49.7 ks, and 0.09 c s−1 in 31.5 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 18 000 photons.
B.10 PBC 1656.2–3303 (z = 2.4)
XMM-Newton observed PBC 1656.2–3303 on 2009 September 11 (ObsID 0601741401) for a total exposure time of 22.6 ks. The observation was performed with medium filter and Full Frame mode for all the EPIC cameras.
The event file was filtered from FPB below the default limit-rate for MOS1 and MOS2, < 0.55 c s−1 for pn. Thesource spectrum was extracted from a circular region with a radius of 50″ for the MOS cameras, 43″ for the EPIC-pn. No pile-up contamination was noted for this blazar. At the end of the processing, the result was a series of spectra with a count rate of 0.98 c s−1 in 17.9 ks and 0.34 c s−1 in 22.0 ks for EPIC-pn and EPIC-MOS cameras, respectively. They provide a total number of ~ 32 500 photons.
PBC 1656.2–3303 was observed by NuSTAR on 2015 September 27 (ObsID 60160657002) for a total exposure of 21.1 ks. The source spectrum was extracted from a circular region with a radius of ~ 63″ (~ 60″) for FPMA (FPMB). At the end of the processing, FPMA and FPMB spectra showed a count rate of 0.14 c s−1 in 20.5 ks and 0.13 c s−1 in 20.8 ks, respectively. They provide a total number of ~5600 photons.
Swift-XRT observed PBC 1656.2–3303, simultaneously with NuSTAR, on 2015 September 27 (ObsID 00081202001). The processed spectrum showed a count rate of 0.09 c s−1 in 6.9 ks, providing ~620 photons.
B.11 QSO J0555+3948 (z = 2.363)
XMM-Newton observed QSO J0555+3948 on 2005 April 1 (ObsID 0300630101) for a total exposure time of 31.2 ks. The observation was performed with medium filter and Full Frame mode for all the EPIC cameras.
The event file was filtered from FPB below the default limit rate for MOS1 and MOS2, < 0.5 c s−1 for pn. Thesource spectrum was extracted from a circular region with a radius of 45″ for the MOS cameras, 40″ for the EPIC-pn. No pile-up was observed in this processing analysis for QSO J0555+3948. The result was a series of spectra with a count rate of 0.40 c s−1 in 12.4 ks,0.13 c s−1 in 19.3 ks and 0.14 c s−1 in 19.0 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 10 100 photons.
B.12 PKS 2149–306 (z = 2.345)
XMM-Newton observed PKS 2149–306 on 2001 May 1 (ObsID 0103060401) for a total exposure time of 24.9 ks. The observation was performed with medium filter for all the EPIC cameras and the EPIC-MOS operated in Full Frame mode, while EPIC-pn in Large Window mode. The event file was filtered from FPB selecting the default limit rate choice. The source spectrum was extracted from a circular region with a radius of 46″ for MOS1, 42″ for MOS2 and 38″ for the EPIC-pn (paying particular attention in avoiding the near faint X-ray source, likely 2XMM J215159.2–302735 located ≳ 50″ away). No pile-up contamination was apparent in this analysis and WebPIMMS yielded an expected pile-up fraction of 2.9% for MOS cameras, 1.8% for pn. At the end of the processing, XMM-Newton spectra showed a count rate of 2.06 c s−1 in 19.6 ks, 0.60 c s−1 in 23.9 ks, and 0.59 c s−1 in 23.9 ks for pn, MOS1 and MOS2 respectively. They provide a total number of ~69 000 photons.
PKS 2149–306 was observed twice by NuSTAR: on 2013 December 17 (ObsID 60001099002, hereafter Obs2013) for a total exposure of 38.5 ks and on 2014 April 18 (ObsID 60001099004, hereafter Obs2014) for a total exposure of 44.2 ks. In both observations, the source spectrum was extracted for FPMA (FPMB) from a circular region with a radius of ~ 83″ (~ 76″). FPMA and FPMB spectra yielded a count rate of 0.78 c s−1 in 38.4 ks (0.67 in 44.0) and 0.78 c s−1 in 38.3 ks (0.58 in 43.9), respectively, providing a total number of ~ 60 000 (54 900) photons.
Swift-XRT performed two observations of blazar PKS 2149–306, simultaneously with NuSTAR, on 2013 December 16 (ObsID 00031404013), and on 2014 April 18 (ObsID 00031404015). The processed Obs2013 (Obs2014) resulted in a count rate of 0.36 c s−1 in 7.1 ks (0.33 in 6.4), providing ~2600 (2100) photons.
B.13 QSO B0237–2322 (z = 2.225)
XMM-Newton observed QSO B0237–2322 on 2006 January 20 (ObsID 0300630301) for a total exposure time of 26.9 ks. The observation was performed with thin filter and Full Frame mode for all the EPIC cameras.
The event file was filtered from FPB below < 0.2 c s−1 for the two EPIC-MOS cameras and < 0.45 c s−1 for EPIC-pn. In the latter case, we also opted for a time selection excluding the exposure up to t = 2.54094E08 s (corresponding roughly to the first 10 ks of the observation). The source spectrum was extracted from a circular region with a radius of 40″ for MOS1, 36″ for MOS2 and 30″ for the EPIC-pn (paying particular attention in avoiding the unidentified faint X-ray source located ≈ 60″ away). No pile-up contaminated this XMM-Newton observation, according to our analysis with epatplot. The result was a series of spectra with a count rate of 0.89 c s−1 in 9.7 ks, 0.24 c s−1 in 19.1 ks, and 0.24 c s−1 in 17.6 ks for pn, MOS1 and MOS2 respectively, with a total number of ~ 17 400 photons.
B.14 4C 71.07 (z = 2.172)
XMM-Newton observed 4C 71.07 on 2001 April 13 (ObsID 0112620101) for a total exposure time of 36.7 ks. The observation was performed with medium filter and Large Window mode for the EPIC-MOS cameras, with the same filter but in Full Frame mode for the EPIC-pn.
The event file of the EPIC-MOS cameras was filtered from FPB below < 0.4 c s−1, below < 0.8 c s−1 for EPIC-pn. In the latter case, we also excluded any exposure time prior to t = 1.03494E08 s (roughly the first 7 ks of the observation). The source spectrum was first extracted from a circular region with a radius of 55″ for the MOS cameras, 41″ for the EPIC-pn. Since the MOS cameras operated in Large Window mode, the background region was selected on an outer chip. However, some pile-up contamination was found using the SAS task epatplot. A more conservative annular region was then opted for all the EPIC cameras excising a 12″ core. At the end of the processing, count rates of 3.65 c s−1 in 22.3 ks, 1.22 c s−1 in 28.0 ks, and 1.18 c s−1 in 28.0 ks were obtained for pn, MOS1 and MOS2 respectively. They provide a total number of ~ 149 000 photons.
4C 71.07 was observed twice by NuSTAR: on 2013 December 15 (ObsID 60002045002, hereafter Obs2013) for a total exposure of 30.0 ks and on 2014 January 18 (ObsID 60002045004, hereafter Obs2014) for a total exposure of 36.4 ks. In Obs2013 (Obs2014), the source spectrum has been extracted for both FPMs from a circular region with a radius of ~ 65″ (~ 69″). In Obs2013 (Obs2014), FPMA and FPMB spectra resulted in a count rate of 0.37 c s−1 in 29.6 ks (0.68 in 36.2) and 0.40 c s−1 in 29.6 ks (0.64 in 36.2), respectively, with a total number of ~ 23 000 (48 000) photons.
Swift-XRT performed two observations of blazar 4C 71.07, simultaneously with NuSTAR, on 2013 December 16 (ObsID 00080399001), and on 2014 January 18 (ObsID 00080399002). The processed spectrum for Obs2013 (Obs2014) showed a count rate of 0.29 c s−1 in 5.0 ks (0.33 in 4.7), providing ~1450 (1550) photons.
B.15 PKS 0528+134 (z = 2.07)
XMM-Newton observed PKS 0528+134 four times within six days on 2009. The first 30.2 ks observation (ObsID 0600121401) was performed on September 8, followed by a 29.2 ks observation (ObsID 0600121501, hereafter Obs501) on September 10, a 27.6 ks observation (ObsID 0600121601, hereafter Obs601) on September 11 and a 39.3 ks observation (ObsID 0600121701, hereafter Obs701) on September 14. All observations were performed with thin filter and Full Frame imaging mode for all the EPIC cameras, except the EPIC-pn exposure of Obs501 performed in Small Window mode.
Obs401 was heavily affected by background flaring. The EPIC-pn event file was shortened up to a ~ 6 ks residual duration and the processed observation, that has the highest count rate among the EPIC cameras, would have provided just ≈ 1500 photons. This observation was then discarded. In Obs501 the EPIC-pn exposure (performed in Small Window mode) was conservatively discarded after processing due to heavy background contamination resulting in a low number of photons and in an ambiguous pile-up epatplot check. For the remaining observations (Obs601 and 701) all EPIC exposures were processed and analysed. For each observation, the event file of the MOS cameras was filtered from FPB below the default limit choice, while the EPIC-pn event file was filtered below 0.6 c s−1 (0.55) for Obs601 (Obs701). In addition to the rate threshold, the MOS cameras in Obs701 were filtered excluding all the exposure time above t = 3.693E08 s. For Obs501, the source spectrum was extracted from a circular region with a radius of 42″ for MOS1 and 40″ for MOS2, while for Obs601 a 45″- and 30″-radius was opted for the source region of the MOS cameras and pn, respectively. In Obs701, 38″, 36″, and 38″ for MOS1, MOS2, and pn, respectively.
No pile-up contamination was observed in any observation of this blazar. At the end of the processing a total number of ~ 3900, ~ 9900 and ~ 4000 photons was provided by Obs501, Obs601, and 701, respectively.
Appendix C Comparison with previous works: outliers of the NH(z)–z relation
The NH(z)−z relation is confirmed by data of the literature (see Sect. 6.1). Only one object showed an incompatibly low column density, that is 4C 06.41 (z = 1.27), for which Eitan & Behar (2013) reported from EPIC-pn data an intrinsic column density upper limit of NH(z) < 0.5 × 1020 cm−2. We reprocessed the XMM-Newton observation (ObsID 0151390101) for all EPIC cameras, following the standard procedures explained in Sect. 3. Fitting the X-ray spectrum with a PL model yielded a reduced chi-square of 1.17 (with 394 dof). Adding an excess absorption component did not improve the fit (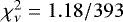 ) and an even lower column density was obtained (NH(z) < 0.2 × 1020 cm−2). Nonetheless, the data-model ratio showed some residual curvature in the data, thus we switched to a LGP continuum. The fit was significantly improved to a reduced chi-square of
) and an even lower column density was obtained (NH(z) < 0.2 × 1020 cm−2). Nonetheless, the data-model ratio showed some residual curvature in the data, thus we switched to a LGP continuum. The fit was significantly improved to a reduced chi-square of 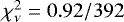 (F-test p-value of ~ 10−23), with an excess column density upper limit of NH(z) < 0.5 × 1021 cm−2 and a non-zero curvature term. This column density is perfectly consistent with our proposed scenario.
(F-test p-value of ~ 10−23), with an excess column density upper limit of NH(z) < 0.5 × 1021 cm−2 and a non-zero curvature term. This column density is perfectly consistent with our proposed scenario.
Furthermore, different Galactic absorption models were used in the literature. However, in 4C 71.07 (PKS 2149–306) the upper limit changed from <0.09 × 1022 cm−2 (<0.07) to < 0.06 × 1022 cm−2 (0.06) when the Galactic model was switched from LAB to Willingale’s (see also Arcodia et al. 2016). Hence, even in the most critical case, we can confidently take 4C 71.07 and PKS 2149–306 as the lowest absorbed extragalactic objects.
In addition, a few objects apparently yielded a column density detection above the 2-sigma upper boundary of the mean IGM absorption contribution. As a matter of fact, non-blazar quasars are allowed to be observed above the simulated IGM curves, since some intrinsic absorption could be present and it is typically observed (e.g., Ricci et al. 2017). In blazars, the lack of an intrinsic component invokes full consistency with the simulated mean IGM curve and its 1 and 2-sigma boundaries, although it is also true that, by definition, a few objects are allowed to lie outside of the coloured areas. One outlier, PKS 0528+134, is ours and was already discussed. Three other blazars from the literature showed a relatively high detection of NH(z), namely QSO B0235+1624 (z = 0.94), PKS 0838+133 (z = 0.68), and QSO B0607+710 (z = 0.27).
In QSO B0235+1624, an excess column density of NH(z) = (0.60 ± 0.03) × 1022 cm−2 was obtained with EPIC-pn data by Eitan & Behar (2013) using a Galactic column density of 7.7 × 1020 cm−2 (Kalberla et al. 2005). Nonetheless, switching to the Willingale’s Galactic model yields a greater value, namely 10.9 × 1020 cm−2. This is a moderately high increase of a factor ~42%, hence it could contribute to the excessively high intrinsic column density fitted by Eitan & Behar (2013). We reprocessed the four archival XMM-Newton observations of the source (i.e., ObsIDs 0110990101, 0206740101, 0206740501, and 0206740701). A PL model yielded a poor fit, with reduced chi-square of 6.73 (387 dof), 2.39 (332 dof), 1.55 (248 dof), and 1.51 (197 dof), for the four ObsIDs as ordered above, respectively. Adding excess absorption, the fit was significantly improved for all the four observations, although in Obs. 0110990101 a curved (concave) continuum was required. We then fitted all the observations simultaneously with a LGP+EX tying the excess absorption, while the source parameters were left free to vary in order to model the different states of blazar QSO B0235+1624 (see Raiteri et al. 2006). The fit yielded a good result (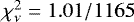 ), with an absorbing excess column density of
), with an absorbing excess column density of 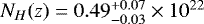 cm−2. This blazar was confirmed to be slightly above the upper 2-sigma mean envelope, although to a lesser extent and still compatibly with a 3-sigma envelope. Its line of sight could be considered particularly absorbed (e.g., a DLA with logNHI = 21.79 ± 0.09, Junkkarinen et al. 2004; Kanekar et al. 2014). Moreover, its Galactic column density is relatively high and the fitted value was a lower limit (> 10.5 × 1020 cm−2), perhaps implying that some more Galactic matter is required to better fit the data.
cm−2. This blazar was confirmed to be slightly above the upper 2-sigma mean envelope, although to a lesser extent and still compatibly with a 3-sigma envelope. Its line of sight could be considered particularly absorbed (e.g., a DLA with logNHI = 21.79 ± 0.09, Junkkarinen et al. 2004; Kanekar et al. 2014). Moreover, its Galactic column density is relatively high and the fitted value was a lower limit (> 10.5 × 1020 cm−2), perhaps implying that some more Galactic matter is required to better fit the data.
In PKS 0838+133 and QSO B0607+710, the detection is really close to the 2-sigma superior limit of the mean envelope. Thus, this source would probably become consistent with our envelopes just including the Galactic molecular hydrogen in the X-ray spectral analysis.
Appendix D Intrinsic spectral breaks
Several parameters are needed to shape intrinsic spectral breaks, such as the bulk Lorentz factor of the relativistic jet, the minimum energy of the electrons distribution or, in general, its shape and its cooling efficiency, the peak frequency of the photons distribution and the redshift of the source. The large number of parameters introduces some degeneracy among them, and if on the one hand it is possible to model any break in the X-ray band, on the other hand these breaks can easily occur out of the observing band. In this scenario the hardening would be attributed to excess absorption along the IGM.
The physics of the jet emission is complex (see e.g., Sikora et al. 1994, 1997, 2009; Tavecchio & Ghisellini 2008; Ghisellini & Tavecchio 2009, 2015, and references therein). We here briefly report the concepts essential for our discussion. The electrons injection function in the emitting region (supposed spherical with radius R) is a smoothly joining broken power-law:
![\begin{equation*}Q(\gamma)=Q_0\frac{\left(\gamma/\gamma_b\right)^{-s_1}}{1+\left(\gamma/\gamma_b\right)^{-s_1+s_2}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,[\text{s}^{-1}\,\text{cm}^{-3}]\,{,} \end{equation*}](/articles/aa/full_html/2018/08/aa32322-17/aa32322-17-eq38.png) (D.1)
(D.1)
and it is assumed constant in time within ~R∕c (e.g., Ghisellini & Tavecchio 2009). This is the time when the electrons energy distribution N(γ) is computed:
![\begin{equation*}N(\gamma)=\frac{\int_{\gamma}^{\gamma_{\textrm{max}}}\left[Q(\gamma)+P(\gamma)\right]\textrm{d}\gamma}{\dot{\gamma}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,[\text{cm}^{-3}]. \end{equation*}](/articles/aa/full_html/2018/08/aa32322-17/aa32322-17-eq39.png) (D.2)
(D.2)
This holds above a particular energy, named γcool, while below it is proportional to the underlying Q(γ). P(γ) is the term representing the electron–positron pairs produced in photon-photon collisions, here neglected for simplicity.
For our purposes, it is sufficient to say that energy breaks in the emission spectrum are linked to the shape of the electrons energy distribution, hence to breaks between different slopes (refer to e.g., Ghisellini & Tavecchio (2015) for a detailed explanation). However, this is valid provided that the photons spectrum can be approximated by a peaked distribution. In the BLR (torus) case, it is considered to be peaked at νext, equal to 2.46 × 1015 Hz (7.7 × 1013 Hz) and it is typically approximated by a black-body (Tavecchio & Ghisellini 2008).
Breaks in the electrons distribution can be due to incomplete cooling and/or to photon starving. A break due to incomplete cooling arises if electrons efficiently cool down to a γcool (with N(γ) ∝ γ−2), while below this energy electrons reflect the underlying (harder) injection function (see Fig. D.1). This break reverberates in the emission spectrum20:
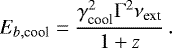 (D.3)
(D.3)
In addition, there could be an energy break due to photon starving, as electrons with the minimum energy will scatter the photon distribution mostly at an energy:
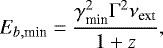 (D.4)
(D.4)
related to the peak of the black-body that approximates the photons energy distribution. Below this energy, since γmin is the minimum electron energy and below νext there is a lack of photons, the spectrum becomes harder.
The absence of a break within the observing band can be explained if the expected breaks occur below the observing band, that is if Eb ≲ 0.3 keV. We take this values to be conservative, even if a break at 0.4−0.6 keV would be likely missed within the absorption features. Alternatively, a break can be shifted above the observing band, taking as a limit Eb ≳ 8−10 keV for emphXMM-Newton. Where a break is expected to be shifted depends on a match between observed photon indexes and slopes predicted by emission models.
The BKN+EX scenario was explored for each blazar, since photon indexes are necessary to test our hypothesis, although it confirmed what emerged from the LGP+EX scenario. Only in four sources out of 15 (namely QSO B0537–286, RBS 315, QSO J0555+3948, and 4C 71.07) both absorption and intrinsic curvature terms coexisted. From the lack or presence of energy breaks in the spectrum (in addition to the excess absorption component) we obtained limits on 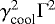 . When available, bulk Lorentz factors where obtained from the βapp values of theliterature. Formally βapp ≲Γ, although we assumed θv ~ 1∕Γ and βapp ~Γ, unless otherwise stated.
. When available, bulk Lorentz factors where obtained from the βapp values of theliterature. Formally βapp ≲Γ, although we assumed θv ~ 1∕Γ and βapp ~Γ, unless otherwise stated.
We proved that emission models hold, short of a condition on the product 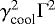 , varying from source to source, even from different observations of the same object. In general, since in the torus case the typical frequency is a factor ~ 10−2 with respect to the BLR case, the torus likely represents a safer explanation if breaks are shifted below the observing band, since it requires loose conditions on
, varying from source to source, even from different observations of the same object. In general, since in the torus case the typical frequency is a factor ~ 10−2 with respect to the BLR case, the torus likely represents a safer explanation if breaks are shifted below the observing band, since it requires loose conditions on 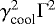 . Nonetheless, beware that γcool would be probably significantly different between the two scenarios, since the jet conditions change. Future VLBA/VLBI studies will be able to provide more accurate bulk Lorentz factors and this will possibly rule out one of the emission models for some specific sources, or our explanation.
. Nonetheless, beware that γcool would be probably significantly different between the two scenarios, since the jet conditions change. Future VLBA/VLBI studies will be able to provide more accurate bulk Lorentz factors and this will possibly rule out one of the emission models for some specific sources, or our explanation.
Furthermore, this scenario is consistent with the absence of intrinsic breaks in our low-z FSRQs. For most high-z blazars, we proved that intrinsic breaks can easily occur below ~0.3 keV. For a high-z source at z ~ 2 (z ~ 5) this is equivalent in shifting the break below ~0.9 keV (~ 1.8 keV) in a local FSRQ, where they could be in principle observed. Nonetheless, all low-z blazars show concave spectra, in accord with the presence of a SSC component (or of the upturn from synchrotron to IC emission, see Sect. 5.7) at low energies, observed up to 1− 3 keV. Hence, any spectral break around 0.3−1.8 keV would be covered. This is in agreement with observing high-energy Γ compatibles with, or softer than, 1.5 in our low-z blazars (see Table A.2), indicating that we are indeed observing the emission above the covered break.
D.1 7C 1428+4218 (z = 4.715)
Blazar 7C 1428+4218 was consistent with a PL+EX model, thus the absence of a break in the broadband 0.2−79 keV has to be explained.
Fitted photon indexes are:
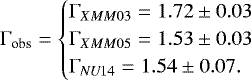 (D.5)
(D.5)
XMM05 and NU14 show consistency with a complete cooling and a N(γ) ∝ γ−2 from γcool up to γb. This corresponds to F(ν) ∝ ν−0.5, hence to photon indexes ~1.5. XMM03 is apparently in disagreement, but it can be explained with an expedient. In particular, a varying electrons injection among different observations may have played the required role. In XMM03 a Γ > 1.5 requires the electrons to be injected down to a γb ≈ γcool ~ γmin. In this case the observed index would be related to the slope above the break in the electrons distribution. Figure D.1 (top panel) show this case with simplicity. Being s2 the slope of Q(γ) above γb, the slope of N(γ) is n2 = s2 + 1. This slope should be > 2 to be steeper than the typical cooling slope, but also <3 to produce the high-energy peak of the IC hump (in νFν). This states that the above-mentioned explanation holds as long as photon indexes between 1.5−2 are observed. InXMM03, this requirement is fulfilled.
 |
Fig. D.1 Slopes of N(γ) related to the underlying Q(γ). The scenario in the top panel is suggested for all blazars in which the observed photon index is significantly greater than ~ 1.5. It represents a N(γ) in which electrons are injected down to a γb close to the minimum energy, so that we would be observing the emission related to the N(γ) ∝ γ−(s2+1) region. The bottom panel is suggested to explain all blazars in which the observed photon index is significantly smaller than ~ 1.5, being related to N(γ) ∝ γ−s1, plus a possible additional hardening due to photon starving. Then, depending on γmin and γcool (multiplied by Γ), spectral breaks can be detected or not within the observing band. |
The fitted photon indexes are compatible with an energy break occurring below the observing band. Hence, from Eb≲ 0.3 keV we inferred that:
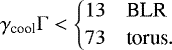 (D.6)
(D.6)
Veres et al. (2010) studied jet properties of 7C 1428+4218 from the brightness temperature measured with VLBI. The authors actually inferred δ and provided Γ assuming a viewing angle of ~3deg, reported from a SED fit performed by Celotti et al. (2007). We decided to neglect this fitted viewing angle and to approximate δ ~Γ, varying in the range 8.6−12.0. According to our inferred limits, the BLR emission model holds provided that γcool ~ γmin ~ 1, but the torus is probably a safer bet, since it allows a considerable margin in the estimate of the product γcoolΓ. Hence, unless otherwise stated, throughout this section we will focus on the compatibility of our proposed scenario with the BLR emission model.
D.2 QSO J0525–3343 (z = 4.413)
The reference model for QSO J0525–3343 is PL+EX. No spectral break is then required within the observed XMM-Newton band.
Fitted photon indexes are:
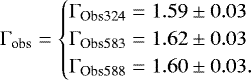 (D.7)
(D.7)
They are all compatibles, within the errors, and slightly higher than the expected photon index in case of a complete cooling. N(γ) is then required to be similar to the scenario outlined for blazar 7C 1428+4218 (see Fig. D.1), namely the electrons have to be injected down to a γb close to γcool and to the minimum of the distribution. We inferred:
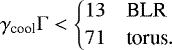 (D.8)
(D.8)
Future VLBI studies involving QSO J0525–3343 will help to validate or exclude the BLR emission model.
D.3 QSO B1026-084 (z = 4.276)
The XMM-Newton X-ray spectrum of blazar QSO B1026-084 is consistent with a PL+EX.
The fitted photon index is Γ = 1.46 ± 0.04, hence it is compatible, within the errors, with the slope expected for a complete cooling of the emitting electrons, that is ~ 1.5. Consequently, the energy break due to incomplete cooling occurred below the observing band if:
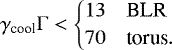 (D.9)
(D.9)
No bulk Lorentz factor is available in the literature.
D.4 QSO B0014+810 (z = 3.366)
The broadband 0.3−79 keV X-ray spectrum of QSO B0014+810 is, similarly to 7C 1428+4218, consistent with a PL+EX model. The fitted photon indexes are:
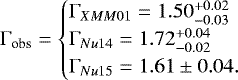 (D.10)
(D.10)
In XMM-Newton the photon index is compatible with a complete cooling of the electrons population, whilst the two Swift-XRT+NuSTAR observations show instead steeper photon indexes. They can be easily explained with a scenario analogous to 7C 1428+4218, in which the electrons have to be injected down to a γb close to the minimum of the electrons energy distribution (see Fig. D.1). All observations suggest that energy breaks occurred below the observing band, thus we can provide upper limits on the product γcoolΓ from Eq. (D.3):
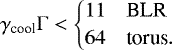 (D.11)
(D.11)
Apparent velocities were obtained for several jet components of blazar QSO B0014+810 by Britzen et al. (2008). Approximating Γ ~ βapp and conservatively taking the jet component with the higher apparent velocity, namely βapp ~ 12.0 ± 1.9, the BLR model seems to be barely validated, even with γcool ~ 1. The torus case is likely to be a safer bet for QSO B0014+810.
D.5 PKS 2126–158 (z = 3.268)
The reference model for the XMM-Newton spectrum of blazar PKS 2126–158 is a PL+EX scenario.
The fitted photon index is Γ = 1.45 ± 0.02. Although it is not precisely compatible with the ~1.5 index expected for a complete cooling of the electron, it is reasonably close to it. Then, blazars’ emission models hold, provided that energy breaks occurred below the observing band. Thus, the product γcoolΓ should be smaller than 11 and 63, for the BLR and torus case, respectively.
No bulkLorentz factor was available in the literature.
D.6 QSO B0537-286 (z = 3.104)
The two XMM-Newton observations showed different continua, but were fitted with a common excess column density. The spectrum in Obs00 is concave, while Obs05 is consistent with a power-law continuum. Nonetheless, both observations show a rather hard photon index of Γ ~ 1.18 (Γhigh for Obs00). A similar case was reported in Ajello et al. (2016) and also the herewith proposed explanation is similar. The hard photon index can be explained with a moderate value of γcool, that would shift the energy break above the observed XMM-Newton band. This break can be due to inefficient cooling alone, in which case the observed slope in F(ν) should be related to the underlying electrons distribution, that goes as s1. Alternatively, the break can be due to a combined effect of inefficient cooling plus photon-starving, in which case an even harder photon index is expected. See Fig. D.1 for more details on the behaviour of Q(γ) and N(γ) in a similar case.
The concave continuum in Obs00 can be explained invoking an underlying component in the SED (νFν), seen thanks to the very hard X-ray spectrum. The presence of this underlying component in one of the two XMM-Newton observations could be due to a different state of the source, for instance see Fig. 4 of Bottacini et al. (2010). In any case, both observations are consistent with an energy break occurring above the observing band, thus we can provide lower limits on the product γcoolΓ imposing the break to be above 8−10 keV:
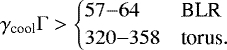 (D.12)
(D.12)
Hence, for QSO B0537-286 the BLR case represents the safer bet, provided γcool ~a few.
D.7 QSO B0438–43 (z = 2.852)
The XMM-Newton spectrum of blazar QSO B0438–43 is consistent with a PL+EX.
The fitted photon index is Γ = 1.71 ± 0.03. It is steeper than the ~1.5 index expected for a complete cooling of the electrons, hence the explanation is analogous to blazar 7C 1428+4218 (see Fig. D.1). Energy breaks may occur below the observing band, provided that the product γcoolΓ is smaller than 11 and 60, for the BLR and torus case, respectively.
No bulk Lorentz factor was available in the literature.
D.8 RBS 315(z = 2.69)
The reference model for both the 0.2−10 keV and the 0.2−79 keV spectrum ofblazar RBS 315 is provided by the LGP+EX scenario. Hence, we performed also the 0.2−79 keV fit with the BKN+EX model, in order to provide photon indexes and to distinguish the energy breaks involved. In Table D.1 results are shown for the three XMM-Newton archive observations and the two Swift-XRT+NuSTAR spectra, respectively. The Galactic value was left free to vary between the ± 15% boundaries of the tabulated value (Willingale et al. 2013). The fitted lower limit (> 17.6 × 1020 cm−2) has also the upper + 15% bound at 18.7 × 1020 cm−2. An excess column density of 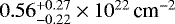 was fitted, compatible, within the errors, with LGP+EX results.
was fitted, compatible, within the errors, with LGP+EX results.
Broadband 0.2−79 keV spectral fit for blazar RBS 315, using the BKN+EX model.
XMM-Newton Obs2003 shows a hard spectrum down to a spectral break at ~ 1.4 keV, below whichit becomes even harder. An excess column density was already considered in the BKN+EX fit, but it was not enough. The observed hardening has to be modelled with an additional spectral break, produced by the minimum Lorentz factor of the electrons energy distribution (see Eq. (D.4)). Moreover, the energy break for an incomplete cooling has to occur above the observed XMM-Newton band, because the high-energy photon index is hard (Γ ~ 1.25). The explanation is similar to blazar QSO B0537–286, with the addition, within the observing band, of a break due to photon starving that hardens even more (Γ ~ 1.05) the soft X-ray spectrum below Eb,min. In Fig. D.1 (bottom panel) we display N(γ) with the underlying injection function required to produce the observed X-ray spectrum in Obs2003. The conditions of the BLR emission model are:
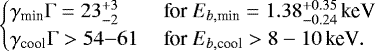 (D.13)
(D.13)
that can be adapted to the torus case simply changing the external frequency at which the seed photons distribution peaks.
XMM-Newton Obs2013a and b can be treated similarly. They both show an energy break at ~ 1.3 keV, above which the photon index is slightly harder than 1.5, but can be easily considered consistent with a complete cooling scenario. Referring to Fig. D.1, this ~ 1.5 slope would be related to the N(γ) ∝ γ−2 region, while below the break the hardening can be adequately accounted for with the slope of the underlying injection function. Hence, γmin can be considered ~1. A constraint on γcoolΓ can be obtained for Obs2013a:
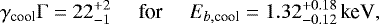 (D.14)
(D.14)
Swift-XRT+NuSTAR data show a break around 5 and 6 keV, in Obs2014 and 2015 respectively.Below the break, they both show a hard photon index, while above they are softer than ~ 1.5 (see Table D.1). We already highlighted for blazar 7C 1428+4218 that a soft high-energy photon index can be explained with a particular injection function. Comparing to Fig. D.1, this would be obtained with γcool ~ γb ~a few:
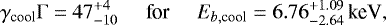 (D.16)
(D.16)
for Obs2014, while for Obs2015:
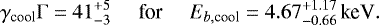 (D.17)
(D.17)
No bulk Lorentz factor was found in the literature for RBS 315.
D.9 QSO J2354-1513 (z = 2.675)
The XMM-Newton spectrum of blazar QSO J2354–1513 was adequately fitted with a PL+EX.
The fitted photon index is 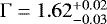 . It is slightly steeper than the 1.5 index expected for a complete cooling of the electrons, hence the explanation is analogous to blazar 7C 1428+4218 (see Fig. D.1). Being the XMM-Newton spectrum consistent with a power-law continuum, the product γcoolΓ is required to be smaller than 11 and 59, for the BLR and torus case, respectively. No bulk Lorentz factor was available in the literature.
. It is slightly steeper than the 1.5 index expected for a complete cooling of the electrons, hence the explanation is analogous to blazar 7C 1428+4218 (see Fig. D.1). Being the XMM-Newton spectrum consistent with a power-law continuum, the product γcoolΓ is required to be smaller than 11 and 59, for the BLR and torus case, respectively. No bulk Lorentz factor was available in the literature.
D.10 PBC J1656.2-3303 (z = 2.4)
The XMM-Newton observation of blazar PBC J1656.2–3303 showed a simple power-law continuum, with a soft X-ray hardening adequately explained by an excess column density. The observed photon index is extremely hard, being Γ = 1.21 ± 0.02. This spectrum can be explained similarly to QSO B0537–286. A moderate value of γcool would shift the energy break due to incomplete cooling above the observed XMM-Newton band. Thus:
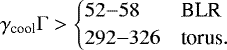 (D.18)
(D.18)
No bulk Lorentz factor was obtained in the literature for blazar PBC J1656.2–3303.
In the broadband 0.2−79 keV fit Swift-XRT+NuSTAR data showed some additional curvature in the LGP+EX model, along with a column density in excess of the Galacticvalue. We then fitted the broadband spectrum with a BKN+EX model, although XMM-Newton data were constrained to a power-law continuum. We obtained:
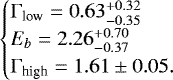 (D.19)
(D.19)
The high-energy photon index is softer than 1.5, while the low-energy slope is extremely hard, to the point of requiring both an incomplete cooling and photon starving. Hence, the fitted energy break should be produced by γmin ~ γcool ~ γb ~a few (re-adapt Fig. D.1 to picture this scenario):
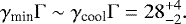 (D.20)
(D.20)
D.11 QSO J0555+3948 (z = 2.363)
QSO J0555+3948 is one of the four sources in which a curvature term was fitted in the LGP+EX scenario, in addition to an excess column density. The BKN+EX fit was performed to obtain a value of the energy break and the related photon indexes, obtaining:
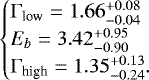 (D.21)
(D.21)
The XMM-Newton spectrum is concave, although the explanation seems to be totally different with respect to Obs00 of blazar QSO B0537–286, in which the break was from a very hard to a hard spectrum. In QSO J0555+3948 the low-energy index is soft, while the high-energy slope is slightly harder than 1.5. This concavity can be easily explained with a SSC component, provided the bulk Lorentz factor is low, otherwise a high-z FSRQ would typically show a naked IC component. The source shows Γ = 1.6 ± 0.1 (Homan et al. 2015), thus the SSC scenario is a favourable explanation.
Still, the high-energy photon index has to be accounted for. In principle, it should be considered as a harder-than-1.5 case, hence it would require the energy break due to γcool to be shifted above the observed XMM-Newton band. Nonetheless, we mentioned that the bulk Lorentz factor is low, then this would imply a γcool ≈ 30 (following the usual upper/lower limits computation). However, note that an intervening SSC component would likely produce a smooth transition and the fitted high-energy photon index is compatible, within the errors, with a Γ = 1.48 slope. Thus, we do not deem necessary for this source to invoke a shift of the energy break due to incomplete cooling. The SSC component is likely covering any intrinsic spectral break.
D.12 PKS 2149-306 (z = 2.345)
The XMM-Newton X-ray spectrum of blazar PKS 2149–306 is consistent with a PL with marginal excess absorption.
The fitted photon index is Γ = 1.46 ± 0.01, hence it can be considered consistent with a complete cooling of the emitting electrons. Consequently, the BLR scenario holds if the energy break due to incomplete cooling occurred below the observing band, thus if:
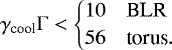 (D.22)
(D.22)
In the broadband fit Swift-XRT+NuSTAR data required, instead, some additional curvature in the LGP+EX model. We then tested the BKN+EX model, with XMM-Newton data constrained to a power-law continuum, obtaining:
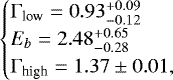 (D.23)
(D.23)
for Obs2013. In the same fit, Obs2014 was fitted by:
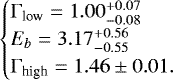 (D.24)
(D.24)
In Obs2013 the high-energy photon index is harder than 1.5, while the lower-energy slope is extremely hard. Hence this observation can be explained with the observed break being produced by the γmin of the electrons energy distribution, while the hard photon index above the break can be accounted for if the break due to incomplete cooling is shifted above the observing band. Thus, from this observation we inferred the following conditions:
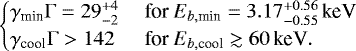 (D.25)
(D.25)
The second condition is quite severe for the BLR model and the torus case would provide an ever higher limit21. No bulk Lorentz factor is available in the literature for PKS 2149–306, hence the disproof for the proposed scenario is up to future VLBI observations. However, note that in this fit the break was uniquely fitted by Swift-XRT (being below 3 keV) and we already stressed that it probably yield unreliable results compared to XMM-Newton (see the discussion in Sect. 6.1.2). Hence, whenever a break below 3 keV is fitted with Swift-XRT+NuSTAR data, results are to be taken with caution.
In Obs2014 the situation is similar, except that the high-energy photon index is consistent with a complete cooling scenario, thus the only condition that has to be respected is on the observed energy break. Given the extremely hard low-energy photon index, this break should be due to both an incomplete cooling and photon starving, thus γminΓ ~ γcoolΓ = 33 ± 3.
D.13 QSO B0237-2322 (z = 2.225)
The XMM-Newton spectrum of blazar QSO B0237–2322 is consistent with a PL with a marginal excess absorption component.
The fitted photon index is Γ = 1.73 ± 0.03. It is steeper than the ~1.5 index expected for a complete cooling of the electrons, hence the explanation is similar, for instance, to blazar 7C 1428+4218 (see Fig. D.1). Hence, the product γcoolΓ is expected to be smaller than 10 and 55, for the BLR and torus case, respectively. No bulk Lorentz factor was available in the literature.
D.14 4C 71.07(z = 2.172)
In blazar 4C71.07, both the 0.2−10 keV and the 0.2−79 keV spectrum were better fitted with a LGP+EX model, with marginal evidence of an excess column density. Hence, we performed also a broadband fit with the BKN+EX model, in order to provide photon indexes and energy break values. In Table D.2 we show the results for the XMM-Newton observation (first row) and the two Swift-XRT+NuSTAR spectra (second and third row). The Galactic value was left free to vary between the ± 15% boundaries of the tabulated value (Willingale et al. 2013). The fitted lower limit (> 2.85 × 1020 cm−2) has also the upper + 15% bound at 3.63 × 1020 cm−2. A marginal excess column was fitted (< 0.07 × 1022 cm−2), compatibly with the LGP+EX case.
Broadband 0.2−79 keV spectral fit for blazar 4C 71.07, using the BKN+EX model.
The XMM-Newton observation shows a hard spectrum with a mild break (the two photon indexes are slightly non-compatibles) at ~ 1.6 keV, that can be then attributed to the minimum Lorentz factor of the electrons energy distribution (Eq. (D.4)), provided that the following condition is satisfied:
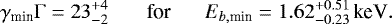 (D.26)
(D.26)
A series of bulk Lorentz factors was obtained for different emitting regions of 4C 71.07 (Homan et al. 2015), ranging from 13 ± 1 to 20 ± 1. This is consistent with the averaged value of Γ = 17.0 ± 2.2 reported by Jorstad et al. (2017). Hence, the above condition is fulfilled with a minimum energy of the electrons distribution of ~ 1−2.
Moreover, given the harder-than-1.5 spectrum observed, the energy break for an incomplete cooling has to be shifted above ~ 8−10 keV, thus providing the condition:
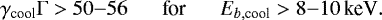 (D.27)
(D.27)
With the constraints on Γ provided by Homan et al. (2015), a γcool ~ 3−4 is required by XMM-Newton data.
The two Swift-XRT+NuSTAR observations were fitted with an energy break around 2 and 4 keV, in Obs2013 and 2014 respectively. Below the break, a hard photon index is observed, while above it is steeper than ~ 1.5. This results can be adequately explained with γcool ~ γb constrained by the observed breaks:
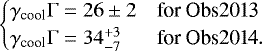 (D.28)
(D.28)
Furthermore, given the bulk Lorentz factors reported in the literature, the BLR emission model can be considered consistent provided γcool ~ 1−2. In case the additionof photon starving is required by the hard low-energy photon indexes, the same condition would be extended also to γmin.
D.15 PKS 0528+134 (z = 2.07)
The reference model for PKS 0528+134 is a simple PL+EX. No spectral break is then observed within the XMM-Newton band. The fitted photon indexes are:
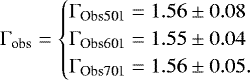 (D.29)
(D.29)
They are all compatibles, within the errors, and consistent with a complete cooling. Hence, we can provide a condition on γmin ~ γcool, that are required to be shifted below the XMM-Newton band:
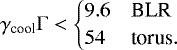 (D.30)
(D.30)
Homan et al. (2015) reported two measures of Γ, namely 9.4 ± 0.5 and 17.3 ± 0.5, and Jorstad et al. (2017) recently reported a compatible averaged Γ = 12.6 ± 3.1. Hence, the torus case has to be considered a safer bet for PKS 0528+134.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 715, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011, ApJ, 743, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, ApJS, 209, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2015, ApJ, 810, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2016, ApJS, 222, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Ghisellini, G., Paliya, V. S., et al. 2016, ApJ, 826, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Akaike, H. 1974, IEEE Trans. Autom. Control, 19, 716 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Arcodia, R., Campana, S., & Salvaterra, R. 2016, A&A, 590, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJS, 207, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Behar, E., Dado, S., Dar, A., & Laor, A. 2011, ApJ, 734, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Bottacini, E., Ajello, M., Greiner, J., et al. 2010, A&A, 509, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bregman, J. N. 2007, ARA&A, 45, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Britzen, S., Vermeulen, R. C., Campbell, R. M., et al. 2008, A&A, 484, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brocksopp, C., Puchnarewicz, E. M., Mason, K. O., Córdova, F. A., & Priedhorsky, W. C. 2004, MNRAS, 349, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Romano, P., Covino, S., et al. 2006, A&A, 449, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campana, S., Thöne, C. C., de Ugarte Postigo, A., et al. 2010, MNRAS, 402, 2429 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Salvaterra, R., Melandri, A., et al. 2012, MNRAS, 421, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Bernardini, M. G., Braito, V., et al. 2014, MNRAS, 441, 3634 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Salvaterra, R., Ferrara, A., & Pallottini, A. 2015, A&A, 575, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campana, S., Braito, V., D’Avanzo, P., et al. 2016, A&A, 592, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cappi, M., Matsuoka, M., Comastri, A., et al. 1997, ApJ, 478, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., Ghisellini, G., & Fabian, A. C. 2007, MNRAS, 375, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., & Ostriker, J. P. 2006, ApJ, 650, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Corral, A., Della Ceca, R., Caccianiga, A., et al. 2011, A&A, 530, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Agostini, G. 2003, Bayesian Reasoning in Data Analysis: A Critical Introduction (Singapore: World Scientific) [CrossRef] [Google Scholar]
- D’Ammando, F., & Orienti, M. 2016, MNRAS, 455, 1881 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ammando, F., Orienti, M., Tavecchio, F., et al. 2015, MNRAS, 450, 3975 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Cen, R., Ostriker, J. P., et al. 2001, ApJ, 552, 473 [NASA ADS] [CrossRef] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Luca, A., Melandri, A., Caraveo, P. A., et al. 2005, A&A, 440, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dermer, C. D. 1995, ApJ, 446, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eitan, A., & Behar, E. 2013, ApJ, 774, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Yan, L., Hook, I. M., et al. 2001, A&A, 379, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elvis, M., Green, R. F., Bechtold, J., et al. 1986, ApJ, 310, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Wilkes, B. J., & Lockman, F. J. 1989, AJ, 97, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Fiore, F., Wilkes, B., McDowell, J., & Bechtold, J. 1994a, ApJ, 422, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Matsuoka, M., Siemiginowska, A., et al. 1994b, ApJ, 436, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Celotti, A., Iwasawa, K., & Ghisellini, G. 2001a, MNRAS, 324, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Celotti, A., Iwasawa, K., et al. 2001b, MNRAS, 323, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Fathivavsari, H., Petitjean, P., Ledoux, C., et al. 2013, MNRAS, 435, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrero, E., & Brinkmann, W. 2003, A&A, 402, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Elvis, M., Giommi, P., & Padovani, P. 1998, ApJ, 492, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L. 2017, Frontiers Astron. Space Sci., 4, 6 [Google Scholar]
- Foschini, L., Ghisellini, G., Raiteri, C. M., et al. 2006, A&A, 453, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fruchter, A. S., Levan, A. J., Strolger, L., et al. 2006, Nature, 441, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Galama, T. J., & Wijers, R. A. M. J. 2001, ApJ, 549, L209 [NASA ADS] [CrossRef] [Google Scholar]
- Gaur, H., Mohan, P., Wierzcholska, A., & Gu, M. 2018, MNRAS, 473, 3638 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2009, MNRAS, 397, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2015, MNRAS, 448, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2010, MNRAS, 402, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., & Ghirlanda, G. 2011, MNRAS, 414, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Mathur, S., Wilkes, B., & Elvis, M. 2004, AJ, 127, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Mathur, S., Wilkes, B., & Osmer, P. 2006, AJ, 131, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., de Geus, E. J., Spaans, M., van Langevelde, H. J., & van Dishoeck E. F. 1995, ApJ, 441, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Lister, M. L., Kovalev, Y. Y., et al. 2015, ApJ, 798, 134 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Morozova, D. A., et al. 2017, ApJ, 846, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Junkkarinen, V. T., Cohen, R. D., Beaver, E. A., et al. 2004, ApJ, 614, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanekar, N., Prochaska, J. X., Smette, A., et al. 2014, MNRAS, 438, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Kreikenbohm, A., Schulz, R., Kadler, M., et al. 2016, A&A, 585, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehner, N., O’Meara, J. M., Howk, J. C., Prochaska, J. X., & Fumagalli, M. 2016, ApJ, 833, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Liddle, A. R. 2004, MNRAS, 351, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Liddle, A. R. 2007, MNRAS, 377, L74 [NASA ADS] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2013, AJ, 146, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H. S., & Wilson, R. W. 1993, ApJ, 403, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Madejski, G. & Sikora, M. 2016, ARA&A, 54, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K. K., Beardmore, A. P., Forster, K., et al. 2017, AJ, 153, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., & Nesci, R. 2004, A&A, 413, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Tramacere, A., Perri, M., Giommi, P., & Tosti, G. 2006, A&A, 448, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McQuinn, M. 2016, ARA&A, 54, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Nanni, R., Vignali, C., Gilli, R., Moretti, A., & Brandt, W. N. 2017, A&A, 603, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nicastro, F., Elvis, M., Krongold, Y., et al. 2013, ApJ, 769, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, F., Senatore, F., Gupta, A., et al. 2016, MNRAS, 458, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, F., Krongold, Y., Mathur, S., & Elvis, M. 2017, Astron. Nachr., 338, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Nicastro, F., Kaastra, J., Krongold, Y., et al. 2018, Nature 558, 406 [Google Scholar]
- Owens, A., Guainazzi, M., Oosterbroek, T., et al. 1998, A&A, 339, L37 [NASA ADS] [Google Scholar]
- Padovani, P. 2016, A&ARv, 24, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P. 2017, Nat. Astron., 1, 0194 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Alexander, D. M., Assef, R. J., et al. 2017, A&ARv, 25, 2 [Google Scholar]
- Page, K. L., Reeves, J. N., O’Brien, P. T., & Turner, M. J. L. 2005, MNRAS, 364, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S. 2015, ApJ, 804, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S., Stalin, C. S., Shukla, A., & Sahayanathan, S. 2013, ApJ, 768, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S., Parker, M. L., Fabian, A. C., & Stalin, C. S. 2016, ApJ, 825, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Storrie-Lombardi, L. J., McMahon, R. G., Irwin, M., & Hook, I. M. 2001, AJ, 121, 1799 [NASA ADS] [CrossRef] [Google Scholar]
- Piconcelli, E., & Guainazzi, M. 2005, A&A, 442, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Quiret, S., Péroux, C., Zafar, T., et al. 2016, MNRAS, 458, 4074 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Kadler, M., et al. 2006, A&A, 452, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reeves, J. N., & Turner, M. J. L. 2000, MNRAS, 316, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Turner, M. J. L., Ohashi, T., & Kii, T. 1997, MNRAS, 292, 468 [NASA ADS] [Google Scholar]
- Reeves, J. N., Turner, M. J. L., Bennie, P. J., et al. 2001, A&A, 365, L116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ren, B., Fang,T., & Buote, D. A. 2014, ApJ, 782, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Saez, C., Brandt, W. N., Shemmer, O., et al. 2011, ApJ, 738, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Tavecchio, F., Ghisellini, G., et al. 2007, ApJ, 669, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Tagliaferri, G., et al. 2015, MNRAS, 446, 2483 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Tagliaferri, G., et al. 2016, MNRAS, 462, 1542 [NASA ADS] [CrossRef] [Google Scholar]
- Schady, P. 2017, Royal Soc. Open Sci., 4, 170304 [Google Scholar]
- Shemmer, O., Brandt, W. N., Vignali, C., et al. 2005, ApJ, 630, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2006, ApJ, 646, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2008, ApJ, 682, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., Smith, B. D., & Danforth, C. W. 2012, ApJ, 759, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Madejski, G., Moderski, R., & Poutanen, J. 1997, ApJ, 484, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Stawarz, Ł., Moderski, R., Nalewajko, K., & Madejski, G. M. 2009, ApJ, 704, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Starling, R. L. C., Willingale, R., Tanvir, N. R., et al. 2013, MNRAS, 431, 3159 [NASA ADS] [CrossRef] [Google Scholar]
- Stratta, G., Fiore, F., Antonelli, L. A., Piro, L., & De Pasquale M. 2004, ApJ, 608, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tagliaferri, G., Ghisellini, G., Perri, M., et al. 2015, ApJ, 807, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, M. Y. J., & Biswas, R. 2012, MNRAS, 419, 3292 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2008, MNRAS, 386, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Maraschi, L., Ghisellini, G., et al. 2000, ApJ, 543, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Maraschi, L., Ghisellini, G., et al. 2007, ApJ, 665, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ulrich, M.-H., Maraschi, L., & Urry, C. M. 1997, ARA&A, 35, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Veres, P., Frey, S., Paragi, Z., & Gurvits, L. I. 2010, A&A, 521, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, D., Hjorth, J., Fynbo, J. P. U., et al. 2007, ApJ, 660, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Brinkman, B., Canizares, C., et al. 2002, PASP, 114, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Turnshek, D. A., Smith, H. E., & Cohen, R. D. 1986, ApJS, 61, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2005, ARA&A, 43, 861 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Woosley, S., & Bloom, J. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Celotti, A., & Iwasawa, K. 2004a, MNRAS, 350, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Turner, A. K., Celotti, A., & Iwasawa, K. 2004b, MNRAS, 350, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Pooley, G. G., & Chandler, C. J. 2006, MNRAS, 368, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Matsuoka, M., Wang, T., et al. 2000, ApJ, 545, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Fabian, A. C., Celotti, A., McMahon, R. G., & Matsuoka, M. 2005, MNRAS, 358, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, W., Fabian, A. C., Worsley, M. A., & McMahon, R. G. 2006, MNRAS, 368, 985 [NASA ADS] [CrossRef] [Google Scholar]
For further details, see XMM-SOC-CAL-TN-0018.
See the specgroup documentation.
That is, due to scale, stray radiation, noise, baseline errors, RFIs, etc., see https://www.astro.uni-bonn.de/hisurvey/ AllSky_profiles/index.php.
The distinction between radio-quiet and radio-loud AGN may be obsolete (see the discussion in Padovani 2016, 2017).
Only a few sources from Nanni et al. (2017) were analysed with Chandra (Weisskopf et al. 2002).
In the frame comoving with the emitting blob, all seed photons are observed as coming frontally (if the blob is located inside the BLR or the torus) within a ~ 1Γ cone. The radiation is then seen boosted by the relativistic Doppler factor δ, that ranges between 2Γ, for axis-photons at θ = 0, and Γ, for edge-photons at θ ~ 1Γ. For several reasons, equally acceptable, a factor Γ, 1.5Γ, or 2Γ has been used in the literature (see, e.g., Tavecchio et al. 2007; Tavecchio & Ghisellini 2008; Ghisellini & Tavecchio 2009, 2015). We adopted a factor Γ νext because we aimed to provide an upper limit to the product γcoolΓ in most cases. The scattered photons are then seen Doppler boosted by δ by the external observer (us). Throughout this section we make the general assumption that δ ~ Γ, thus that the viewing angle of the observer is ~1Γ.
All Tables
List of DLA candidates from the literature (see text) included in the spectral analysis.
XMM-Newton spectral fits for six FSRQ-type blazars and two LBLs of the low-redshift sample, performed in the 0.2− 10 keV energy range for the pn detector and 0.3−10 keV for MOS detectors.
All Figures
 |
Fig. 1 Distribution of blazars in the sky in Galactic coordinates (Aitoff projection), superimposed to the LAB absorption map, representing the distribution of Galactic column densities (see Kalberla et al. 2005, for further details). Black stars represent the high-z Silver sample. As black diamonds, blazars of the low-z sample. |
| In the text | |
 |
Fig. 2 Data-model ratio of a simple PL model for XMM-Newton observations of Silver-sample blazars. EPIC-pn, MOS1, and MOS2 data are displayed for each observation in different colours, with pn data extending down to 0.2 keV. |
| In the text | |
 |
Fig. 3 Difference between the fitted Galactic column densities, |
| In the text | |
 |
Fig. 4 Distribution of NH(z) with redshift for blazars from this work. Blue objects belong to the Silver sample, while in cyan low-z data are shown. Error bars were computed within XSPEC at 90% confidence level (Δχ2 = 2.71), as were the upper limits (denoted with arrows). All curves and coloured areas were obtained from Campana et al. (2015): the solid line, along with its corresponding 1- and 2-sigma envelopes in brown and green, respectively, is the median of the absorbed LOS distribution, representing the mean absorption contribution from both a diffuse WHIM and additional intervening over-densities. We take the 2-sigma lower envelope as the minimum contribution from a diffuse WHIM alone. |
| In the text | |
 |
Fig. 5 NH(z)−z relation, see Fig. 4 for the general description. Left panels: the solid grey curves represent the extrapolation of the last-detection limit of each blazar, providing an overall sensitivity range of the instrument for excess absorption detections. Right panels: the same last-detection limits are shown for each blazar with red horizontal dashes. The underlying grey area is the “upper-limit” region for each blazar. Observing a blazar with a specific XMM-Newton response, exposure time, absorbed by its |
| In the text | |
 |
Fig. 6 See Fig. 4 for a general description of the plot. Left panel: additional GRB data from Arcodia et al. (2016) are plotted. Right panel: the distribution of NH (z) with redshift for blazars from this work (blue stars) and for quasars from the literature (black symbols are related to Page et al. 2005; magenta to Nanni et al. 2017; grey to Eitan & Behar 2013; dark green and orange to Shemmer et al. 2006 and Shemmer et al. 2008, respectively; red to Saez et al. 2011; cyan to Yuan et al. 2006; purple to Grupe et al. 2006; lime to Shemmer et al. 2005; dark red to Campana et al. 2015; brown to Ricci et al. 2017; dark orange to Corral et al. 2011). Squares stand for generic non-blazars AGN, while stars for blazars. Error bars were computed within XSPEC at 90% confidence level (Δχ2 = 2.71), as were the upper limits (denoted with arrows below the related symbol). |
| In the text | |
 |
Fig. 7 Results of the joint igmabs fit with QSO B0014+810, PBC J1656.2–3303, PKS 2149–306, and 4C 71.07 fitted together. Confidence contours are shown for the hydrogen density n0 (x-axis) and the temperature (y-axis) of the IGM. We display 68, 95, and 99 percent contours in red, green, and blue, respectively. |
| In the text | |
 |
Fig. D.1 Slopes of N(γ) related to the underlying Q(γ). The scenario in the top panel is suggested for all blazars in which the observed photon index is significantly greater than ~ 1.5. It represents a N(γ) in which electrons are injected down to a γb close to the minimum energy, so that we would be observing the emission related to the N(γ) ∝ γ−(s2+1) region. The bottom panel is suggested to explain all blazars in which the observed photon index is significantly smaller than ~ 1.5, being related to N(γ) ∝ γ−s1, plus a possible additional hardening due to photon starving. Then, depending on γmin and γcool (multiplied by Γ), spectral breaks can be detected or not within the observing band. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.