| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 5 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201832752 | |
| Published online | 24 July 2018 | |
J1342+0928 supports the timeline in the Rh = ct cosmology
Department of Physics, The Applied Math Program, and Department of Astronomy, The University of Arizona,
AZ 85721, USA
e-mail: fmelia@email.arizona.edu
Received:
1
February
2018
Accepted:
17
April
2018
Aims. The discovery of quasar J1342+0928 (z = 7.54) reinforces the time compression problem associated with the premature formation of structure in Λ cold dark matter (ΛCDM). Adopting the Planck parameters, we see this quasar barely 690 Myr after the big bang, no more than several hundred Myr after the transition from Pop III to Pop II star formation. Yet conventional astrophysics would tell us that a 10 M⊙ seed, created by a Pop II/III supernova, should have taken at least 820 Myr to grow via Eddington-limited accretion. This failure by ΛCDM constitutes one of its most serious challenges, requiring exotic “fixes”, such as anomalously high accretion rates, or the creation of enormously massive (~ 105 M⊙) seeds, neither of which is ever seen in the local Universe, or anywhere else for that matter. Indeed, to emphasize this point, J1342+0928 is seen to be accreting at about the Eddington rate, negating any attempt at explaining its unusually high mass due to such exotic means. In this paper, we aim to demonstrate that the discovery of this quasar instead strongly confirms the cosmological timeline predicted by the Rh = ct Universe.
Methods. We assume conventional Eddington-limited accretion and the time versus redshift relation in this model to calculate when a seed needed to start growing as a function of its mass in order to reach the observed mass of J1342+0928 at z = 7.54.
Results. Contrary to the tension created in the standard model by the appearance of this massive quasar so early in its history, we find that in the Rh = ct cosmology, a 10 M⊙ seed at z ~ 15 (the start of the Epoch of Reionization at t ~ 878 Myr) would have easily grown into an 8 × 108 M⊙ black hole at z = 7.54 (t ~ 1.65 Gyr) via conventional Eddington-limited accretion.
Key words: cosmology: theory / cosmology: observations / early Universe / galaxies: active / quasars: supermassive black holes
© ESO 2018
1 Introduction
The recent discovery of ULAS J134208.10+092838.61 (henceforth J1342+0928; Bañados et al. 2018), an ultraluminous quasar at redshift z = 7.54, emphasizes more than ever the time compression problem in the early Λ cold dark matter (ΛCDM) Universe. Weighing in at a mass of 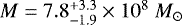 , this supermassive black hole should have taken over 820 Myr to grow via standard Eddington-limited accretion. Yet we see it barely several hundred Myr after Pop II and III supernovae could have created the ~ 5–25 M⊙ seeds to initiate the black-hole growth. Worse, this timeline would suggest that J1342+0928 started growing ~ 130 Myr before the big bang, which is completely unrealistic (Melia 2013a, 2015). And what is particularly challenging to the concordance model is that J1342+0928 is seen to be accreting at
, this supermassive black hole should have taken over 820 Myr to grow via standard Eddington-limited accretion. Yet we see it barely several hundred Myr after Pop II and III supernovae could have created the ~ 5–25 M⊙ seeds to initiate the black-hole growth. Worse, this timeline would suggest that J1342+0928 started growing ~ 130 Myr before the big bang, which is completely unrealistic (Melia 2013a, 2015). And what is particularly challenging to the concordance model is that J1342+0928 is seen to be accreting at 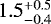 times the Eddington rate, arguing against any attempt to mitigate the compression problem by invoking exotic, greatly super-Eddington growth (Volonteri & Rees 2005; Pacucci et al. 2015; Inayoshi et al. 2016).
times the Eddington rate, arguing against any attempt to mitigate the compression problem by invoking exotic, greatly super-Eddington growth (Volonteri & Rees 2005; Pacucci et al. 2015; Inayoshi et al. 2016).
This discovery follows on the heels of another problematic source, SDSS J010013.02+280225.8, an ultraluminous quasar at z = 6.30 (Wu et al. 2015), and about 50 others uncovered at redshifts z > 6 (Fan et al. 2003; Jiang et al. 2007, 2008; Willott et al. 2007, 2010a,b; Mortlock et al. 2011; Venemans et al. 2013; Bañados et al. 2014), all of which contain a black hole with mass ~ 109 M⊙, and all of which are difficult to accommodate within the standard model’s predicted timeline. Attempts to resolve the mystery of how such large aggregates of matter could have assembled so quickly in Λ CDM have generally fallen into two categories of exotic mechanisms: either an anomalously high accretion rate (Volonteri & Rees 2005; Pacucci et al. 2015; Inayoshi et al. 2016), and/or the creation of enormously massive seeds (Yoshida et al. 2004; Latif et al. 2013; Alexander & Natarajan 2014). But neither of these is entirely satisfying because no compelling evidence in support of such extreme conditions has yet been found. Note, for example, that J1342+0928 itself is accreting right at the Eddington rate. And for other high-z supermassive black holes with a reasonably estimated mass, the inferred luminosity has thus far been at, or close to, the Eddington value (see, e.g., Fig. 5 in Willott et al. 2010a).
The formation of massive seeds, which in this context implies the birth of black holes with a mass ~ 105 M⊙, is even more difficult to confirm observationally. Such events would presumably last too short a time to offer any meaningful probability of being seen directly. The best hope would be to find such objects, known as “intermediate-mass” black holes, after they have formed sufficiently nearby for us to be able to detect their relatively feeble emission. But even here the evidence is sparse and inconclusive. A handful of low-luminosity active galactic nuclei may be such candidates. For example, NGC 4395 at 4 Mpc appears to harbor a ~ 3.6 × 105 M⊙ black hole in its center (Peterson et al. 2005). Some ultra-luminous X-ray sources (ULXs) in nearby galaxies may be intermediate-mass black holes with a mass up to ~ 1000 M⊙ (Maccarone et al. 2007), but even these masses are well below what is required. Some intermediate-mass black holes may have been seen inglobular clusters, e.g., M31 G1, based on the stellar velocities measured near their center, but none has yet stood up to follow-up scrutiny (see, e.g., Baumgardt et al. 2003). Most recently, we have witnessed the LIGO discovery of ~ 30–50 M⊙ black holes via the gravitational waves they emit as they spiral towards an eventual merger in binaries (Abbott et al. 2017). This opens up the possibility of eventually discovering even more massive objects during similar merger events, but none have been seen thus far. It is safe to conclude that massive seeds may be contemplated theoretically, but no compelling evidence has yet been found to confirm their existence beyond a possible handful designated as dwarf active galactic nuclei. The ambiguity with the latter is, of course, that these objects may have simply grown to their observed intermediate mass via steady accretion rather than having appeared via some catastrophic event.
The purpose of this paper is to demonstrate that such mysterious, unseen processes are not needed to explain the formation of these supermassive black holes, arguing that the anomaly is not with the astrophysics, but with the cosmology itself. As we shall see, the timeline implied by J1342+0928 may be a significant problem for Λ CDM, but not at all for the Rh = ct Universe (Melia 2007; Melia et al. 2012), a Friedmann–Robertson–Walker (FRW) cosmology with zero active mass (Melia 2016, 2017a). In this cosmology, a ~ 10 M⊙ seed created at z ~ 15–16, i.e., the beginning of the Epoch of Reionization (EoR), would have grown via conventional Eddington-limited accretion to a mass of ~ 8 × 108 M⊙ at z = 7.54, exactly matching the observed properties of J1342+0928.
2 The Early Universe
In the context of ΛCDM, with Planck parameters Ωm = 0.307, k = 0, wΛ = −1 and Hubble constant H0 = 67.7 km s−1 Mpc−1 (Planck Collaboration XIII 2016), the Universe is believed to have become transparent at tΛCDM ~ 0.4 Myr, initiating the so-called Dark Ages that lasted until the first (Pop III) stars formed several hundred Myr later. Reionization presumably started when these objects – and subsequently the black holes they spawned – started emitting UV radiation, a process that apparently lasted from z ~ 15 to z ~ 6 (Jiang et al 2006; Zaroubi et al. 2012). The EoR in the standard model therefore stretched over a cosmic time tΛCDM ~ 400–900 Myr. By comparison, the redshift-time relation in Rh = ct is given by the relation
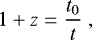 (1)
(1)
where 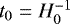 is the age of the Universe today, in terms of the Hubble constant H0. This equation is straightforward to derive, noting that 1 + z = a(t0)∕a(t) in terms of the expansion factor a(t) (e.g., Weinberg 1972), while a(t) = t∕t0 in the Rh = ct Universe (Melia et al. 2012). Thus, if we simply adopt the same Planck measured value H0 = 67.7 km s−1 Mpc−1, the Dark Ages in this cosmology ended at tRh=ct ~ 878 Myr, while the EoR extended from tRh=ct ~ 878 Myr to ~ 2 Gyr (see Fig. 1). Note that the redshift range over which reionization took place is inferred from observations, and is therefore independent of the cosmology. But each model predicts its own unique mapping of redshift to age. Thus, although the EoR lasted from z ~ 15 to z ~ 6 in both cosmologies, the starting and ending times are different. With a redshift z = 7.54, J1342+0928 is being viewed at cosmic time tRh=ct ~ 1.65 Gyr in the Rh = ct Universe, approximately 772 Myr after the onset of the EoR, when the ramp-up in stellar formation and supernova activity is believed to have occurred.
is the age of the Universe today, in terms of the Hubble constant H0. This equation is straightforward to derive, noting that 1 + z = a(t0)∕a(t) in terms of the expansion factor a(t) (e.g., Weinberg 1972), while a(t) = t∕t0 in the Rh = ct Universe (Melia et al. 2012). Thus, if we simply adopt the same Planck measured value H0 = 67.7 km s−1 Mpc−1, the Dark Ages in this cosmology ended at tRh=ct ~ 878 Myr, while the EoR extended from tRh=ct ~ 878 Myr to ~ 2 Gyr (see Fig. 1). Note that the redshift range over which reionization took place is inferred from observations, and is therefore independent of the cosmology. But each model predicts its own unique mapping of redshift to age. Thus, although the EoR lasted from z ~ 15 to z ~ 6 in both cosmologies, the starting and ending times are different. With a redshift z = 7.54, J1342+0928 is being viewed at cosmic time tRh=ct ~ 1.65 Gyr in the Rh = ct Universe, approximately 772 Myr after the onset of the EoR, when the ramp-up in stellar formation and supernova activity is believed to have occurred.
Though not yet fully confirmed, this temporal sequence of events and epochs in the early Universe is suggested by many detailed simulations carried out in recent years (Barkana & Loeb 2001; Miralda-Escudé 2003; Bromm & Larson 2004; Ciardi & Ferrara 2005; Glover 2005; Greif et al. 2007, 2012; Wise & Abel 2008; Salvaterra et al. 2011; Jaacks et al. 2012; see also the recent reviews by Bromm et al. 2009 and Yoshida et al. 2012). In this scenario, Pop III stars started forming by z ~ 20 at the core of mini halos with mass ~ 106 M⊙ (Haiman et al. 1996; Tegmark et al. 1997; Abel et al. 2002; Bromm et al. 2002). In Planck Λ CDM, this redshift corresponds to a cosmic time tΛCDM ~ 200 Myr. By comparison, Pop III stars in Rh = ct would have started forming by z ~ 70.
This delay of ~ 200 Myr between the big bang and the appearance of the first stars is difficult to circumvent due to the inefficient cooling of the primordial gas. There was another delay of at least ~ 100 Myr (Yoshida et al. 2004; Johnson et al. 2007) before Pop II stars could form, while the hot gas expelled by the Pop III stars cooled and re-collapsed. Thus, black-hole seeds created during supernova explosions of evolved Pop II and III stars would have started their growth more than ~ 300 Myr after the big bang, which would not have afforded them anywhere near enough time to reach ~ 109 M⊙ status by z ~ 7 in standard cosmology. Of course, this is the primary reason proponents of the massive seed scenario require exotic mechanisms to create ~ 105 M⊙ black holes by other means (Yoshida et al. 2004; Latif et al. 2013; Alexander & Natarajan 2014).
In conventional astrophysics, the subsequent growth of black-hole seeds (massive or otherwise) would have been constrained by the maximum luminosity attainable with the outward radiation pressure acting on ionized matter under the influence of gravity. In hydrogen-rich plasma, this limiting power is known as the Eddington limit LEdd ≈ 1.3 × 1038(M∕M⊙) ergs s−1. One also needs to know the efficiency ϵ for converting rest-mass energy into radiation in order to estimate the accretion rate Ṁ, in which case one then assumes that Ṁ = Lbol∕ϵc2, where Lbol is the bolometric luminosity. To allow for all possible variations of basic accretion-disk theory, one typically adopts a fiducial value ϵ = 0.1 for this quantity (see, e.g., Melia 2009). Therefore, with Eddington-limited accretion, one may combine the expressions for Lbol = LEdd and Ṁ, i.e.,
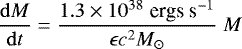 (2)
(2)
(Salpeter 1964; see also Melia 2013a), whose straightforward solution is the so-called Salpeter relation,
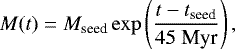 (3)
(3)
where Mseed (~ 5–25 M⊙) is the seed mass produced at time tseed. According to this expression, it would have taken J1342+0928 approximately 820 Myr to grow from an initial black-hole seed of 10 M⊙.
In principle, this growth time could have been shortened by mergers in the early Universe (Tanaka & Haiman 2009; Lippai et al. 2009; Hirschmann et al. 2010). But according to the simulations, there are restrictions on how this mechanism could have worked that mitigate its likelihood of success. On the plus side, detailed merger simulations show that the black-hole population always converges towards a Gaussian distribution, regardless of the initial seed profile. There is therefore some flexibility in the modeling. To comply with all of the available data, however, ~ 100 M⊙ seeds would have had to start forming by z ~ 40 (e.g., Tanaka & Haiman 2009). This is well before the EoR (which apparently started at z ~ 15). In addition, this creation of seeds could not have continued after z ~ 20–30. The simulations show that if they did form past this redshift, then there would have been an overproduction of the mass density in lower-mass (a few × 105 M⊙ to a few × 107 M⊙) black holes, compared to what is actually seen (see, e.g., Figs. 5 and 6 in Tanaka & Haiman 2009). In fact, without thiscutoff, the lower mass black holes would have been overproduced by a factor of as much as 100 to 1000.
So the argument that mergers in the early (Λ CDM) Universe might have played a critical role in forming the supermassive black holes at high-z does not sit comfortably with our current interpretation of Pop III star-formation. Our understanding of why the EoR occurred at t ~ 400 Myr is based on our estimate of the cooling time required to form this first generation of stars, which corresponded to a redshift (i.e., ~ 15) much smaller than ~ 40. And it would be difficult to understand why these stars stopped forming below z ~ 20–30, before the EoR even started. The implication is that some mechanism other than Pop III supernovae would have been responsible for creating these massive seeds well before the EoR, yet this would require new, unknown physics and, even more importantly, there is currently no observational evidence for such events occurring prior to z ~ 15.
The viability of this scenario has been further mitigated by recent arguments showing that the halo abundance was at least an order of magnitude smaller than previously thought. Johnson et al. (2013) have recently carried out large (4 Mpc3) high-resolution simulations of the formation of halos – and Pop III stars within them – in the early Universe, self-consistently modeling the subsequent metal enrichment and the stellar radiation produced by the next generation of stars (i.e., Pop II). It turns out that Pop III and II stars formed and evolved co-evally down to a redshift z ~ 6. These simulations showed that the enhanced metal enrichment and the feedback radiation – which would have included molecule-dissociating Lyman–Werner photons responsible for the destruction of the coolants H2 and HD required for the condensation of matter in the early Universe – would have significantly changed the rate at which halos and Pop III stars formed.
Specifically, Johnson et al. (2013) found that the Lyman–Werner radiation produced both near the halos and over cosmological distances would have effectively reduced the halo and Pop III star formation rate at z ≳ 10 by as much as an order of magnitude compared to previous simulations in which this radiation was ignored, to a rate per comoving volume of ~ 10−4 M⊙ yr−1 Mpc−3. Ironically, these same effects would have actually resulted in a higher stellar mass per unit volume by z ~ 6 because, though they negatively impacted the rate of halo and Pop III star formation, they extended the time over which Pop III and Pop II formed and evolved co-evally. In fact, the Pop III star formation rate at z ~ 6 is found to be ~ 10−5 M⊙ yr−1 Mpc−3, just an order of magnitude lower than its peak at z ~ 10. But insofar as the production of halos for mergers in the early Universe is concerned, this net shift in the time when they would have formed reduces the volume density of Pop III supernovae – and therefore the density of black-hole seeds – at a time (corresponding to z ≳ 10) when the frequency ofcollisions and mergers among these objects would have mattered most to rapidly grow the black-hole mass to allow J1342+0928 to appear atz = 7.54.
The bottom line is that any attempt at explaining the mysterious appearance of billion-solar mass black holes at z ~ 7 in the context of Λ CDM faces a very daunting task that is unlikely to get easier as more of these objects are found at progressively higher redshifts.
3 J1342+0928 in Rh = ct
Over the past decade, the predictions of Rh = ct have been compared with those of ΛCDM using over 20 different kinds of data, from low to high redshifts, and a wide assortment of observational signatures, including the redshift-time relation, the redshift dependence of the Hubble constant H(z), and various distance measures, such as the luminosity and angular-diameter distances. A summary of these comparative studies and their outcomes appears in Table 1 of Melia (2017b). In each and every comparison, Rh = ct has been favoured by the data over ΛCDM. In other words, there is now compelling evidence to suggest that a resolution of the time-compression problem associated with the premature appearance of massive quasars at z ~ 6–7 may be found in the cosmology itself, rather than unseen, exotic “fixes” to the formation and growth of supermassive black holes.
In Fig. 1, we show the seed mass required in Rh = ct versus the time tseed (and corresponding redshift) at which it was produced in order to account for the appearance of J1342+0928 at z = 7.54 (solid black curve). This plot also shows the 1σ (dark) and 2σ (light) confidence regions, estimated via error propagation from the uncertainty in the measurement of the mass M. In other words, the 1σ confidence region corresponds to the mass range (5.9–11.1) × 108 M⊙. For comparison, we also see in this figure the demarcation between the Dark Ages (at z ≳ 15) and the ensuing EoR (6 ≲ z ≲ 15). One cannot avoid emphasizingthe fact that the ~ 820 Myr required for J1342+0928 to grow via Eddington-limited accretion from its initial supernova produced 10 M⊙ seed at z≲ 16 to its observed 7.8 × 108 M⊙ mass at z = 7.54 coincides very nicely with two critically important observations: (1) the redshift range of the EoR, which was apparently sustained by UV photons emitted by Pop II and III stars, and the quasars they subsequently spawned; and (2) the approximately Eddington-limited luminosity observed from J1342+0928 at z = 7.54.
 |
Fig. 1 Seed mass of J1342+0928 versus redshift at the time it was formed (solid black curve), assuming this quasar reached its mass |
4 Discussion and Conclusions
All the estimates we have made in this paper are based on the assumption that high-z quasars accreted steadily at the Eddington rate. We do not know their duty cycle, however, so their average growth rate could have been less than Eddington. But this just makes the situation worse for the standard model because the implied efficiency ϵ in Eq. (2) would then be larger in order to achieve the observed final high masses. And since the characteristic (Salpeter 1964) time (τSal ~ 45 Myr) scales linearly with ϵ, a bigger efficiency would imply a longer characteristic time (i.e., τSal ~ 45[ϵ∕0.1] Myr) in the exponential of Eq. (3). In other words, a greater efficiency would imply that the same amount of light could be produced with a lower mass accretion rate, which would have delayed the growth and therefore worsenend the time compression problem. In fact, several observations suggest that, when they turned on, high-z quasars must have accreted at close to Eddington. For example, Shankar et al. (2009) have argued that only a few 1010 M⊙ black holes have been seen in the local Universe, in spite of peak quasar activity at 1 ≲ z ≲ 3 (McConnell et al. 2012). Yet quasar masses at z > 3 would have had to exceed 1010 M⊙ for us to detect their fluxes at Earth if they were sub-Eddington.
On the flip side, one can see from Eq. (3) that J1342+0928 could have grown to its observed mass in only ~ 270 Myr if it had been accreting steadily throughout its growth at 3 times the Eddington rate. This would accommodate the timeline in Λ CDM, starting with the creation of a 10 M⊙ seed at z ~ 15 growing to 7.8 × 108 M⊙ by z = 7.54. A similar solution would work for all the other high-z supermassive black holes as well. But we should then be able to detect at least some super-Eddington quasars at z ≳ 6. Unfortunately, all the current observations rule out such sources (Willott et al. 2010b; Mortlock et al. 2011; De Rosa et al. 2011). All the measured accretion rates are at, or below, the standard Eddington value, with a clear trend towards even lower rates towards smaller redshifts.
In this paper, we have highlighted the time compression problem associated with the early appearance of J1342+0928 and other supermassive black holes at z> 6. But today the reality is that the timeline predicted by ΛCDM is in conflict with several kinds of observation, not just the high-z quasars. The fact that galaxies started forming at z ~ 10–12 is just as difficult to understand (Melia 2014). For example, with a photometric redshift of z ≈ 10.7, MACS0647-JD is the most distant galaxy known reliably to date (Coe et al. 2013). Its mass is estimated from the typical star-formation rate measured at lower redshifts and from the inference that the average stellar mass (~ 109 M⊙) of galaxies at z ~ 7–8 grew to ~ 1010 M⊙ by z ~ 2 (Gonzalez et al. 2010). This trend suggests that galaxies at z ~ 11, including MACS0647-JD, have an average stellar mass ≲109 M⊙. The problem in ΛCDM is that this redshift corresponds to a cosmic time t ~ 427 Myr, implying that about a billion solar masses had to assemble inside a galaxy at this redshift in only ~ 130 Myr following the transition from Pop III to Pop II star formation, which is difficult to understand theoretically. Whereas exotic mechanisms for the formation and growth of black holes may still be considered, there are no such unconventional mechanisms possible for creating galaxies.
A diverse set of simulations carried out by independent workers essentially confirm each other’s conclusions because, in the end, they incorporate the same basic physics. Take the calculations by Salvaterra et al. (2013) as an illustrative example that captures the key results. According to their calculations, the ratio between the mass doubling time tdb and the cosmic time in these early galaxies is universally equal to ~ 0.1–0.3, more or less independently of redshift. This result appears to be consistent with ~ 106–108 M⊙ galaxies observed at z ~ 6–10, particularly their measured specific star-formation rate of ~ 3–10 M⊙ Gyr−1. One can easily show (see, e.g., Melia 2014) that a ratio tdb ∕t ~ 0.1–0.3 is sufficient to form such galaxies starting with a condensation of ~ 104 M⊙ at t ~ 230 Myr, roughly where one would expect the transition from Population III to Population II stars to occur. So there is no problem forming 108 M⊙ galaxies by z = 6. By the same token, a ~ 109 M⊙ galaxy at z = 10.7 (i.e., t ≈ 490 Myr in Λ CDM) would have needed to start growing at t ~ 82 Myr, well before even Pop III stars could have emerged and exploded, producing the necessary conditions to begin the subsequent growth of galactic structure. This is inconsistent with what is thought to have occurred prior to the end of the dark ages at t ~ 400 Myr.
The time compression problem with J1342+0928 in the standard model therefore has much in common with other evidence suggesting that the timeline prior to z ~ 6 is too short in ΛCDM. Taken together, all of the evidence thus far suggests that the growth of J1342+0928 is best understood in the context of Rh = ct. As we have seen, its birth, growth and evolution are fully consistent with the principal timescales associated with Pop II and III star formation, and the subsequent EoR. This result has significant implications because it relies on the time-redshift relation, rather than integrated distances, during that crucial early period (t ≲ 1–2 Gyr) of expansion when cosmologies differ significantly in their respective predictions. Ultimately, if Rh = ct survives as the correct cosmology, it would obviate the need for inflation, a considerable shift in the current paradigm (Melia 2013b).
Acknowledgements
I am very grateful to the anonymous referee for his/her helpful comments and suggestions that have led to a significant improvement in the presentation of this manuscript. I am also grateful to Amherst College for its support through a John Woodruff Simpson Lectureship, and to Purple Mountain Observatory in Nanjing, China, for its hospitality while part of this work was being carried out.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, PRL, 119, 141101 [CrossRef] [PubMed] [Google Scholar]
- Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Alexander, T., & Natarajan, P. 2014, Science, 345, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Bañados, E., Venemans, B. P., Morganson, E., et al. 2014, AJ, 148, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018, Nature, 553, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Barkana, R., & Loeb, A. 2001, PRep, 349, 125 [Google Scholar]
- Baumgardt, H. et al. 2003, ApJ, 589, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Bromm, V., Yoshida, N., Hernquist, L., & McKee, C. F. 2009, Nature, 459, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ciardi, B., & Ferrara, A. 2005, SpSRev, 116, 625 [Google Scholar]
- Coe, D., Zitrin, A., Carrasco, M., et al. 2013, ApJ, 762, 32 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, G., Decarli, R., Walter, F., et al. 2011, AJ, 739, 56 [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Schneider, D. P., et al. 2003, AJ, 125, 1649 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. 2005, Space Sci. Rev., 117, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, V., Labbé, I., Bouwens, R. J., et al. 2010, ApJ, 713, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Greif, T. H., Johnson, J. L., Bromm, V., & Klessen, R. S. 2007, ApJ, 670, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Greif, T. H., Bromm, V., Clark, P. C., et al. 2012, MNRAS, 424, 399 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Haiman, Z., Thoul, A. A., & Loeb, A. 1996, ApJ, 464, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Khochfar, S., Burkert, A., et al. 2010, MNRAS, 407, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Inayoshi, K., Haiman, Z., & Ostriker, J. P. 2016, MNRAS, 459, 3738 [CrossRef] [Google Scholar]
- Jaacks, J., Nagamine, K., & Choi, J.-H. 2012, MNRAS, 427, 403 [CrossRef] [Google Scholar]
- Jiang, L., Fan, X., Hines, D. C., et al. 2006, AJ, 132, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Fan, X., Vestergaard, M., et al. 2007, AJ, 134, 1150 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Fan, X., Annis, J., et al. 2008, AJ, 135, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L., Greif, T. H., & Bromm, V. 2007, ApJ, 665, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L., Dalla, V. C., & Khochfar, S., et al. 2013, MNRAS, 428, 1857 [NASA ADS] [CrossRef] [Google Scholar]
- Latif, M. A., Schleicher, D. R. G., Shmidt, W., & Niemeyer, J. 2013, MNRAS, 433, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Lippai, Z., Frei, Z., & Haiman, Z. 2009, ApJ, 701, 360 [CrossRef] [Google Scholar]
- Maccarone, T. J., Kundu, A., Zepf, S. E., & Rhode, K. L. 2007, Nature, 445, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McConnell, N. J., Ma, C.-P., Murphy, J. D., et al. 2012, ApJ, 756, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F. 2007, MNRAS, 382, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F. 2009, High-Energy Astrophysics, (New York: Princeton University Press) [Google Scholar]
- Melia, F. 2013a, ApJ, 764, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F. 2013b, A&A, 553, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melia, F. 2014, AJ, 147, 120 [CrossRef] [Google Scholar]
- Melia, F. 2016, Front. Phys., 11, 119801 [CrossRef] [Google Scholar]
- Melia, F. 2017a, Front. Phys., 12, 129802 [CrossRef] [Google Scholar]
- Melia, F. 2017b, MNRAS, 464, 1966 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F., & Shevchuk, A. S. H. 2012, MNRAS, 419, 2579 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F., & McClintock, T. M. 2015, Proc. R. Soc. A, 471, 20150449 [CrossRef] [Google Scholar]
- Miralda-Escudé, J. 2003, Science, 300, 1904 [NASA ADS] [CrossRef] [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pacucci, F., Volonteri, M., & Ferrara, A. 2015, MNRAS, 452, 1922 [CrossRef] [Google Scholar]
- Peterson, B., Bentz, M. C., Desroches, L. B., et al. 2005, ApJ, 632, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1964, ApJ, 140, 796 [CrossRef] [Google Scholar]
- Salvaterra, F., Ferrara, A., & Dayal, P. 2011, MNRAS, 414, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Salvaterra, R., Maio, U., Ciardi, B., & Campisi, M. A. 2013, MNRAS, 429, 4718 [Google Scholar]
- Shankar, F., Weinberg, D. H., & Miralda Escudé, J. 2009, ApJ, 690, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, T., & Haiman, Z. 2009, ApJ, 696, 1798 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Silk, J., Rees, M. J., et al. 1997, ApJ, 474, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Venemans, E. P., Findlay, J. R., Sutherland, W. J., et al. 2013, ApJ, 779, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., & Rees, M. J. 2005, ApJ, 633, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 1972, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (New York: John Wiley & Sons, Inc.) [Google Scholar]
- Willott, C. J., Delorme, P., Omont, A., et al. 2007, AJ, 134, 2435 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Delorme, P., Reylé, C., et al. 2010a, AJ, 139, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Willott, C. J., Albert, L., Arzoumanian, D., et al. 2010b, AJ, 140, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., & Abel, T. 2008, ApJ, 685, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X.-B., Wang, F., Fan, X., et al. 2015, Nature, 518, 512 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yoo, J., & Miralda-Escudé, J. 2004, ApJL, 614, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, N., Bromm, V., & Hernquist, L. 2004, ApJ, 605, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida,N., Hosokawa, T., & Omukai, K. 2012, Prog. Theor. Exp. Phys., 01A305 [Google Scholar]
- Zaroubi, S. 2012, in The First Galaxies Theoretical Predictions and Observational Clues, eds. T. Wiklind, B. Mobasher, and V. Bromm (Berlin: Springer) [Google Scholar]
All Figures
 |
Fig. 1 Seed mass of J1342+0928 versus redshift at the time it was formed (solid black curve), assuming this quasar reached its mass |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.