| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201832675 | |
| Published online | 22 June 2018 | |
Modelling the early time behaviour of type Ia supernovae: effects of the 56Ni distribution
1
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast,
Belfast
BT7 1NN, UK
e-mail: mmagee37@qub.ac.uk
2
Tuorla Observatory, Department of Physics and Astronomy, University of Turku,
Väisäläntie 20,
21500
Piikkiö, Finland
3
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching bei München, Germany
Received:
19
January
2018
Accepted:
9
March
2018
Recent studies have demonstrated the diversity in type Ia supernovae (SNe Ia) at early times and highlighted a need for a better understanding of the explosion physics as manifested by observations soon after explosion. To this end, we present a Monte Carlo code designed to model the light curves of radioactively driven, hydrogen-free transients from explosion to approximately maximum light. In this initial study, we have used a parametrised description of the ejecta in SNe Ia, and performed a parameter study of the effects of the 56Ni distribution on the observed colours and light curves for a fixed 56Ni mass of 0.6 M⊙. For a given density profile, we find that models with 56Ni extending throughout the entirety of the ejecta are typically brighter and bluer shortly after explosion. Additionally, the shape of the density profile itself also plays an important role in determining the shape, rise time, and colours of observed light curves. We find that the multi-band light curves of at least one SNe Ia (SN 2009ig) are inconsistent with less extended 56Ni distributions, but show good agreement with models that incorporate 56Ni throughout the entire ejecta. We further demonstrate that comparisons with full UV OIR colour light curves are powerful tools in discriminating various 56Ni distributions, and hence explosion models.
Key words: supernovae: general / radiative transfer / methods: numerical
© ESO 2018
1 Introduction
Modern optical transient surveys have led to a wealth of supernova (SN) discoveries at increasingly early times. As the number of type Ia supernovae (SNe) discoveries grows, their diversity becomes ever more apparent – despite being once thought of as a relatively homogeneous group. Particular attention has been paid to epochs shortly after explosion, as they probe the outermost layers of the ejecta and provide information on the progenitor not available at later epochs (e.g. Arnett 1982; Riess et al. 1999b; Nugent et al. 2011).
A sample of 18 low redshift SNe Ia considered by Firth et al. (2015) showed significant variation in the rise time to maximum light, ranging from ~16 to 25 days, and some SNe rising more sharply than others. Based on the work of Piro & Nakar (2013, 2014), this variation was interpreted as being due to differences in the distribution of 56Ni within the SN ejecta. Piro & Nakar (2013) show how shallow 56Ni distributions (i.e. closer to the ejecta surface) lead to shallower rises, and Piro & Nakar (2014) apply this study to observations of three SNe Ia shortly after explosion. There is also clear diversity in the observed colours of SNe Ia before and around maximum light (Maeda et al. 2011; Cartier et al. 2011). Recent multi-dimensional explosion simulations have argued that SNe Ia may be highly asymmetric (e.g. Livne et al. 2005; Kuhlen et al. 2006; Kasen et al. 2009). Based on observations of velocity shifts in late-phase nebular spectra, Maeda et al. (2010a,b) also argued that SNe Ia may result from asymmetric explosions. The colour differences of Maeda et al. (2011) were found to be correlated with these velocity shifts, therefore Maeda et al. (2011) and Cartier et al. (2011) interpret the observed diversity as resulting from asymmetric explosions. Although some degree of asymmetry has been argued in SNe Ia explosions, the effect of different 56Ni distributions on the rise time, and in particular colours, has not been fully quantified for even the spherically symmetric case. The purpose of this work is to develop and exploit light curve models that can address this topic and provide physical links between model parameters and observations of SNe Ia.
Analytical work by Arnett (1982) modelled the early light curves of SNe with a constant, grey opacity. Subsequent numerical work extended this to variable, grey opacities (Cappellaro et al. 1997; Bersten et al. 2011; Morozova et al. 2015). Further advancements came from incorporating realistic treatments of the plasma state and physics (making as few assumptions as possible), multi-dimensionality, and non-grey opacities (Höflich 1995, 2003; Blinnikov et al. 1998, 2006; Kasen et al. 2006; Kromer & Sim 2009; Hillier & Dessart 2012; van Rossum 2012). We aim to bridge the gap between these simple and detailed approaches. We present a Monte Carlo radiative transfer code, TURTLS1, that combines these advantages: it is fast and flexible, like the fixed and grey opacity models, but also implements realistic descriptions of the most important physical processes at the epochs of interest. By including realistic time and frequency dependent opacities, our approach allows us to compute band-limited light curves for any UV OIR filter. This substantially increases the utility of our calculations for direct interpretation of data compared to simpler treatments. The flexibility afforded by our approach coupled with the relatively short (~dozens of CPU hours) run times facilitates a systematic exploration of the parameter space. It can therefore be used to explore the early light curves and colours of radioactively driven SNe.
In Sect. 2 we describe our code. Section 3 presents the results of convergence studies and tests of our sensitivity to various approximations made, while Sect. 4 presents a comparison to existing codes in the literature for the well-studied W7 (Nomoto et al. 1984) explosion model. Section 5 presents a set of models for which light curves are simulated, as discussed in Sect. 6. We focus on the effects of the 56Ni distribution, followed by the density profile. In Sect. 7 we demonstrate the importance of a non-grey opacity in determining the light curves. We test the importance of the amount of surface 56Ni in Sect. 8 and quantify the rising phase in Sect. 9. Section 10 provides a comparison between ourmodels and observations of a SNe Ia. Finally, we present our conclusions in Sect. 11.
2 Monte Carlo method
2.1 General overview
Our Monte Carlo light curve code follows the indivisible energy-packet scheme outlined by Lucy (2005) and previous studies (Abbott & Lucy 1985; Lucy & Abbott 1993; Mazzali & Lucy 1993; Lucy 2002, 2003), applied in one dimension. Throughout the following, we adopt the naming convention of Lucy (2005); γ-packets represent bundles of γ-ray photons; radiation-packets (r-packets) represent bundles of UV OIR photons; z, z1, z2, etc. are independent, random numbers.
Packets represent discrete monochromatic bundles of photons. They are injected into the model region and their propagation followed, during which they may undergo electron scattering or absorption and re-emission by the ions and atoms in the ejecta. The number of photons and frequencies represented by a packet may change during the simulation; however, energy is always conserved in the fluid frame, and packets are neither created nor destroyed during interactions with the ejecta. Radiative equilibrium and conservation of the total energy are therefore enforced throughout the simulation. Observed light curves are created by binning emerging packets in frequency and time.
Throughout our simulations, packet properties such as propagation direction, energy, etc. are followed in the observer frame, and transformed to and from the fluid frame when appropriate, through a first-order Doppler correction.
2.2 Model set-up
In our implementation, the form of the SN ejecta is entirely free, and is assumed to be spherically symmetric. The ejecta is defined by a series of zones, each having the following properties upon input: inner and outer velocity boundaries; density at some reference time, t0; 56Ni mass fraction and composition at t0.
The temperature of each zone at the start of the simulation, ts, is determined by the local heating that has occurred due to the decay of 56Ni since the explosion. Following Lucy (2005), we determine the radiation energy density in each zone as:
![\begin{equation*} U_{\rm{R}} = \left(\frac{t_{\rm{Ni}}}{t_{\rm{s}}} - \left[\left( 1 + \frac{t_{\rm{Ni}}}{t_{\rm{s}}}\right) \exp\left(\frac{-t_{\rm{s}}}{t_{\rm{Ni}}}\right) \right] \right) \frac{\chi~\rho~E_{\rm{{Ni}}}}{m_{\rm{Ni}}}, \end{equation*}](/articles/aa/full_html/2018/06/aa32675-18/aa32675-18-eq1.png) (1)
(1)
where tNi is the decay time of 56Ni (8.8 days), χ is the initial mass fraction of 56Ni in that zone, ρ is the density of that zone at ts, ENi is the energy emitted by the decayof a 56Ni atom (1.728 MeV), and mNi is the mass of a 56Ni atom (9.3 × 10−26 kg). The mean intensity of the radiation field in each zone is given by:
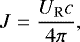 (2)
(2)
and the radiation temperature of each zone by:
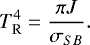 (3)
(3)
For zones without 56Ni at the start of the simulation, we set an initial temperature of 1000 K. We treated 1000 K as a minimum temperature in each zone throughout the entire simulation. We tested other values for a minimum temperature (up to 5000 K) but found that this did not have a noticeable effect on the resultant light curves. For the epochs considered in this work, we do not expect the outer temperature to be significantly lower.
2.3 Packet initialisation
With the model region constructed, packets must be initialised with the following properties: time of injection, position, direction of propagation, and energy. Following the 56Ni decay chain, 56Ni → 56Co → 56Fe, γ-packets are injected and randomly assigned an emitting species (proportional to their probabilities) of either a 56Ni or 56Co nucleus. The 56Ni decay chain is assumed to be the dominant form of energy production. Other decay chains are therefore not implemented currently, but could be included in future work. The injection time for 56Ni decays is given by tγ = – ln z × tNi. For 56Co decays, the time of injection is given by tγ = – lnz1 × tNi – ln z2 × tCo, where tCo is the decay time of 56Co. Following from Lucy (2005), γ-packets injected before the start time of the simulation are converted to r-packets, and given an injection time equal to this start time. Work done by packets on the ejecta during this time is also accounted for.
The radial position of the packet at the injection time is determined by sampling the 56Ni distribution within the SN ejecta. The distribution of propagation directions within the fluid frame is assumed to be isotropic. Each packet is assigned a random propagation direction, μf = 2z − 1, which is then transformed into the observer frame following Castor (1972). The energy of each packet is given by discretising the total energy emitted by the SN in the fluid frame among all packets.
Packets that have converted from γ- to r-packets by the start of the simulation also require an initial frequency. The fluid frame frequency is selected by sampling the Planck function at the temperature appropriate for that packet’s zone, following from Carter & Cashwell (1975) and Bjorkman & Wood (2001).
2.4 Packet propagation
With all packets initialised, the simulation can begin. The simulation operates by propagating packets in logarithmically spaced time intervals between chosen start, ts, and end, te, times.
Once a packet has been injected we simulate its random walk by calculating four time intervals: time for the packet to redshift into the next frequency bin (tf), time for the packet to reach a zone boundary (tb), time for the packet to reach an interaction point (ti), and time until the end of the current time step (tnts). We propagate each packet until it reaches the first of these four events to occur and perform the event. New time intervals are then calculated and the procedure repeated, if necessary. This is performed for all packets in all time steps until the chosen end of the simulation is reached.
In the following, we describe each interval in more detail. We begin by describing numerical events in Sect. 2.4.1, followed by physical events in Sect. 2.4.2.
2.4.1 Numerical events
As packets propagate, their fluid frame frequency is constantly redshifted. If the time to the next frequency bin is shortest, the packet is propagated to this point, the fluid frame frequency updated, and new time intervals calculated.
The trajectory of the packet is followed from its current position until it intersects either the inner or outer boundary of the zone – depending on the direction of travel. If the time to a boundary is shortest, the packet is propagated to the appropriate boundary and new time intervals are calculated. If a packet is propagated to the outer boundary of the final zone, it has escaped the simulation. See Sect. 2.6 for further details.
If the beginning of the next time step is the next event to occur, the packet is propagated along its current trajectory until the end of the current time step. Once the next time step has begun, the process of calculating new time intervals begins again.
2.4.2 Physical events
The final interval calculated is the time until a packet reaches a randomly selected optical depth, given by:
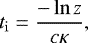 (4)
(4)
where ρ is the density of the packet’s zone, and κ is the opacity.
For γ-packets, we used a fixed grey opacity of κ∕ρ = 0.03 cm2 g−1 (Ambwani & Sutherland 1988). Despite this approximation, our code is able to reproduce the γ-ray deposition obtained using the more sophisticated treatment of Lucy (2005; see Sect. 4.1, Fig. 1). For a γ-packet experiencing its first interaction, it is immediately destroyed and re-emitted as an r-packet.
For r-packets, we used TARDIS (Kerzendorf & Sim 2014) to calculate Thomson scattering opacities and expansion opacities (Eastman & Pinto 1993). We assumed LTE when determining the ionisation and excitation levels. At the end of each time step, the zone densities and temperatures, and time since explosion are input into TARDIS to calculate the opacities. We also took into account the change in composition that results from the decay of 56Ni → 56Co → 56Fe.
The use of expansion opacities represents a significant simplification in the treatment of photon-matter interactions. As our atomic dataset includes 4.5 × 105 lines, treating each line individually would be computationally prohibitive. In the expansion opacity formalism, lines are combined into opacity bins in discrete frequency intervals. The expansion opacity in the frequency interval ν + Δν is therefore the contribution from all lines within the given interval, and calculated as:
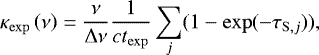 (5)
(5)
where texp is the time since explosion, and τS,j is the Sobolev optical depth for the line j, given by:
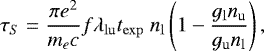 (6)
(6)
where f is the absorption oscillator strength of the transition, as in Kerzendorf & Sim (2014).
If an interaction is the next event, the packet is propagated to the interaction point and a new fluid frame direction randomly selected. Energy is always conserved in the fluid frame during interactions. The form of interaction (electron-scattering or absorption) is chosen randomly at the point of interaction, in proportion to their probabilities. If a packet is electron-scattered, we also conserve frequency in the fluid frame.
For packets that experience absorption, we use the two-level atom approach (TLA) outlined by Kasen et al. (2006), which greatly reduces the computational demands of the simulation. In real systems, when an atom absorbs a photon through a line transition, there may be multiple transitions through which that photon could be re-emitted. In the TLA approach, once packets are absorbed, they are immediately re-emitted with either the same frequency or a new frequency chosen by randomly sampling the local thermal emissivity, S(νi), given by:
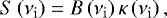 (7)
(7)
where 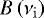 is the Planck function, and
is the Planck function, and 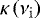 is the expansion opacity. The probability of redistribution, as opposed to coherent line scattering, is given by the redistribution parameter, ϵ. In principle, ϵ is unique for each line, however, Kasen et al. (2006) show that a single value close to unity for all lines is sufficient to reproduce a more detailed treatment of fluorescence. Throughout our simulations, we fix ϵ = 0.9. Varying ϵ is discussed in Sect. 3.5. Once a packet has finished the interaction process, new time intervals are calculated.
is the expansion opacity. The probability of redistribution, as opposed to coherent line scattering, is given by the redistribution parameter, ϵ. In principle, ϵ is unique for each line, however, Kasen et al. (2006) show that a single value close to unity for all lines is sufficient to reproduce a more detailed treatment of fluorescence. Throughout our simulations, we fix ϵ = 0.9. Varying ϵ is discussed in Sect. 3.5. Once a packet has finished the interaction process, new time intervals are calculated.
2.5 Updates to the plasma state
Once all packets have propagated through the current time step, the density, temperature, and source function for each zone are updated. Following from Mazzali & Lucy (1993) and Long & Knigge (2002), we use a Monte Carlo estimator to determine the mean intensity in each zone, given by:
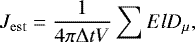 (8)
(8)
where Δt is the time step duration, V is the volume of the zone, E is the energy of the packet, and l is the distance travelled by the packet during the current time step. The summation is performed over all packets that have travelled inside the zone during the current time step. We then calculate new temperatures using Eq. (3), new opacities using TARDIS, and update the source function (Eq. (7)) in each zone.
2.6 Constructing light curves
As packets escape the outer grid zone with an escape time tn, they are perceived by a distant observer to have been emitted at an observed time τn = tn − μRmax/c (Lucy 2005). R-packets that have escaped the model domain are binned in observed time and frequency. Frequency bins are then convolved with the desired set of filter functions to construct the model light curves.
3 Convergence and sensitivity tests
In this section, we describe the tests conducted to assess the robustness of our results. All calculations described in this section use the density and composition from the W7 explosion model (Nomoto et al. 1984).
3.1 Number of packets
As discussed in Sect. 2.5, we use a Monte Carlo estimator to determine the temperature of each zone. Therefore, the number of packets will affect not only the noise present in the light curve but also the opacities used in the simulation. We find that, even with a relatively small number of packets (105), noise in the temperature profile does not have a noticeable effect on the light curves beginning ~3 days post-explosion.
The effect of a small number of packets is most pronounced at early times (≲ 2.5 days post explosion) for models that do not have 56Ni extending to the surface of the ejecta. In these models, the diffusion of packets into the outer regions of the ejecta can cause relatively large fluctuations in the temperature across zones, as individual zones may contain only a handful of packets. Nevertheless, sufficiently good statistics can be achieved by selecting an appropriate time span for the simulation.
3.2 Number of time steps
After each time step, the plasma state is updated with new temperatures and source functions in each zone, and new opacities are calculated. The number of time steps may affect the light curve if they are too few to accurately represent the smooth evolution of the SN ejecta. We test models with 50, 100, 250, and 500 time steps logarithmically spaced between 1.5 and 30 days post explosion. We found that even with a relatively small number of steps, light curves showed little variation. Typically the largest difference between these light curves is ≲0.05 mag for models with more than 100 time steps. We use 250 time steps, as a compromise between accurately capturing the light curve evolution and the computational requirement.
3.3 Number of frequency bins
The use of expansion opacities requires that lines are collected into discrete frequency bins. We calculate models for 1000, 5000, and 10 000 bins ranging from 1014 to 1016 Hz, and find that increasing the number of frequency bins beyond 1000 has a negligible effect on the resultant light curves (≲ 0.05 mag).
3.4 Atomic dataset
Our atomic dataset comprises lines drawn from Kurucz & Bell (1995), with a cut in log (gf) applied to limit the number of weak lines included, and hence the computational time requirement, as in Kromer & Sim (2009). We find that a cut of log(gf) ≥−2 typically produces brighter light curves, particularly in bluer bands. It is unsurprising that a smaller atomic data set would result in brighter early light curves, given that a reduction in the number of lines will result in a reduced opacity. That the effect is most prominent at short wavelengths highlights the importance of the weaker lines due to iron group elements. The difference between −3 and −5 cuts is far less pronounced but follows the same trend. Including even weaker lines (log (gf) ≥−20) does not alter the model light curves (Kromer & Sim 2009). We therefore use the log (gf) ≥−5 atomic data set.
Kromer & Sim (2009) also performed tests with atomic data sets that include many more weak lines due to singly- and doubly ionised Fe, Co, and Ni. These transitions primarily occur at red and NIR wavelengths. Kromer & Sim (2009) showed that including these lines can produce a noticeable deviation in the NIR bands (particularly J, H, and K) but has little effect on the optical light curves.
As shown by Dessart et al. (2014), forbidden line transitions play an important role in cooling from ~30 days post explosion. We note that the atomic dataset used in our simulations includes only permitted line transitions, and therefore do not extend our simulations beyond approximately maximum light.
3.5 Fluorescence parameter
We use the two-level atom approach – defined through the use of the redistribution parameter, ϵ – to approximate fluorescence (Kasen et al. 2006). The probability that packets will be re-emitted with frequencies sampled from the source function is given by ϵ.
As ϵ values close to unity have been shown to broadly reproduce the effects of a full fluorescence treatment (Kasen et al. 2006), we adopted ϵ = 0.9 throughout our simulations. Figure 2 shows the redistribution of packet wavelengths for three models (ϵ = 0.1, 0.5, and 0.9), following the last interaction experienced by each packet, and demonstrates how models with a low ϵ value (0.1) do not redistribute as effectively following interactions.
 |
Fig. 1 Bolometric light curve and γ-ray deposition curve for the model presented by Lucy (2005) compared to a calculation performed in this work. Our code reproduces the results of Lucy (2005). |
 |
Fig. 2 Wavelength at which packets are absorbed and re-emitted following their last interaction, and before exiting the simulation. Three values of the redistribution parameter are shown from left to right: scattering dominated (ϵ = 0.1), equal probability for scattering and redistribution (ϵ = 0.5), and redistribution dominated (ϵ = 0.9). |
4 Code verification
In this section, we test whether our code is consistent with other radiative transfer codes. We first compared our code using models calculated with a grey opacity (Sect. 4.1), followed by models calculated with a non-grey opacity (Sect. 4.2).
4.1 Greyopacity
We compare the simple, grey opacity (κ∕ρ = 0.1 cm2 g−1) model presented by Lucy (2005) to a calculation performed using our code that also incorporates a fixed, grey opacity. This model has a uniform density structure, with an ejecta mass of 1.39 M⊙, a 56Ni mass of 0.625 M⊙, and a maximum velocity of 104 km s−1. The mass fraction of 56Ni at the centre of theejecta (M(r) < 0.5 M⊙) is equal to one, and drops linearly to zero at M(r) = 0.75 M⊙.
We used a grey opacity for γ-ray transport (0.03 cm2 g−1; Ambwani & Sutherland 1988), while Lucy (2005) perform a more complete treatment, including non-grey opacities and Compton scattering. Figure 1 shows, however, that our code is able to reproduce the results of Lucy (2005), including the γ-ray deposition. This suggests that our simplified approach to γ-ray transport does not have a significant effect on our model light curves.
4.2 Non-grey opacity
We compareto other non-grey radiative transfer codes using the well studied W7 explosion model (Nomoto et al. 1984). We use 1 × 107 packets, 1000 frequency bins, 250 time steps, and begin the simulation 1.5 days after explosion.
ARTIS (Kromer & Sim 2009) is a 3D Monte Carlo radiative transfer code for calculating time-dependent supernova spectra. An important difference between our code and ARTIS is that ARTIS does not use the expansion opacity approximation, but treats each line individually. This is a significant improvement over our code; however, ARTIS also requires orders of magnitude greater computational time (~100 vs. ~5000 CPU hours for the models presented here). Figure 3 presents ARTIS light curves calculated using an LTE approximation with a standard atomic data set (4.1 × 105 lines), and a more detailed ionisation treatment with a larger atomic data set (8.2 × 106 lines). This larger atomic data set includes more transitions for singly and doubly ionised Fe, Co, and Ni. See Kromer & Sim (2009) for further details.
Figure 3 demonstrates that the expansion opacity approximation is able to reproduce the full line treatment implemented in ARTIS. In particular, our model W7 light curves more closely match those of the LTE ARTIS model – this is unsurprising given the LTE assumptions used in calculating our opacities.
Figure 3 also shows early-phase light curves calculated by Noebauer et al. (2017) using STELLA (Blinnikov et al. 1998, 2006), a one-dimensional radiation hydrodynamics code. Similar to our code, LTE is assumed in determining the ionisation and excitation levels in STELLA. STELLA also makes use of a slightly smaller atomic data set, ~ 1.6 × 105 lines, and the expansion opacity approximation. Light curves produced by STELLA also show good agreement with those produced by our code, and ARTIS.
 |
Fig. 3 Comparison of bolometric and UBV RI light curves for the W7 explosion model generated by different light curve codes. ARTIS and STELLA light curves are from by Kromer & Sim (2009) and Noebauer et al. (2017), respectively. |
5 Construction of model density and composition profiles
Having described the operation of our code and demonstrated that it produces results similar to other codes in the literature (see Sect. 4), we apply it to test the effects of varying the 56Ni distribution.We describe the set-up of the models presented in this work, while Sect. 6 presents the light curves.
Our code requires the density and composition of the SN ejecta as input, both of which are freely defined by the user. Following Botyánszki & Kasen (2017), we parametrise the density profile of the ejecta as a broken power law. This produces anejecta with a shallow inner region, and a more steeply declining outer region. The density at velocity v is given as:
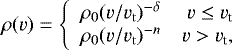 (9)
(9)
where vt gives the velocity boundary between the two regions, δ gives the slope of the inner region, n gives the slope of the outer region, and the reference density, ρ0, is given by:
![\begin{equation*} \rho_0 = \frac{{M}_{\rm{ej}}}{4 \pi (v_{\rm{t}} t_{exp})^3} \left[\frac{1}{3 - \delta} + \frac{1}{n - 3}\right]^{-1}, \end{equation*}](/articles/aa/full_html/2018/06/aa32675-18/aa32675-18-eq12.png) (10)
(10)
where δ < 3, n >3, Mej is the ejecta mass, and texp is the time since explosion (Botyánszki & Kasen 2017). In order to test only the effects of the 56Ni distribution, we fix the mass and maximum velocity of the ejecta to be 1.4 M⊙ and 30 000 km s−1, respectively, for all density profiles discussed in this section. Parameters of the models used in this study are given in Table 1. These density profiles were constructed such that they broadly span the range predicted by various explosion models, such as pure deflagrations (Nomoto et al. 1984; Fink et al. 2014), deflagration-to-detonation transitions (Seitenzahl et al. 2013), and the violent merger of two WDs (Pakmor et al. 2012).
We haveconstructed 56Ni distributions such that 56Ni is concentrated towards the inner ejecta, and extends outwards to varying degrees – approximately following predictions by explosion models for SNe Ia. As a simple functional form, we adopt:
![\begin{equation*} ^{56}\textrm{Ni}(m) = \frac{1}{\exp(s[m - {{M}}_{\rm{Ni}}]/M_{\odot}) + 1}, \end{equation*}](/articles/aa/full_html/2018/06/aa32675-18/aa32675-18-eq13.png) (11)
(11)
where m is the mass coordinate of the ejecta and MNi is the total 56Ni mass in M⊙. The scaling parameter, s, is used to alter the shape of the 56Ni distribution; smaller values have a more shallow 56Ni distribution, while larger values produce a distribution that sharply transitions between 56Ni-rich and 56Ni-poor regions. We present three values of s (3, 9.7, and 100), representing models with an extended, intermediate, and compact 56Ni distribution, respectively (see Fig. 4c). We have also fixed the
total 56Ni mass to be 0.6 M⊙ for all models discussed here. Future work will test the effects of varying 56Ni masses, as well as other forms for the 56Ni distributions.
As we wish to test only the effects from different distributions of 56Ni, we have taken a simplified approach to the ejecta composition. In each zone, 56Ni constitutes 100% of the total iron group elements immediately after explosion. This is unlikely to be realised in nature but nevertheless allows us to easily test 56Ni distributions in our simple parameter study. The outer ~0.1 M⊙ of the ejecta is dominated by carbon and oxygen, while the remaining material is intermediate mass elements. Relative abundance ratios are determined by the W7 model (Nomoto et al. 1984). Future work will test other composition arrangements. Figure 4 shows the density and 56Ni profiles discussed and representative composition for one model (v12500_d0_n8_s9.7).
Ejecta model parameters and properties.
 |
Fig. 4 Ejecta models used in this work. Panel a: density profiles for our model sequence. Transition velocity, delta, and n parameters are given for each model. Densities for a sample of explosion models are shown for comparison: W7 (Nomoto et al. 1984), DDT N100 (Seitenzahl et al. 2013), DEF N1600 (Fink et al. 2014), VM (Pakmor et al. 2012). Panel b: illustrative composition profile for one model (v12500_d0_n8_s9.7). The three zone structure is clearly demonstrated, with representative species shown. Panel c: 56Ni distributionsfor one density profile (v12500_d0_n8). 56Ni distributions for a sample of explosion models are also shown. |
 |
Fig. 5 Bolometric, Swift U, and JohnsonBV RI light curves for our v7500_d0_n8 density profile, with various scaling parameters (s = 3, 9.7, and 100), and the UBV RI light curves of SN 2009ig. Light curves of SN 2009ig are shown assuming μ = 32.6 ± 0.4, negligible host extinction, and an explosion epoch of JD = 2455063.41 ± 0.08 (Foley et al. 2012). Filled points represent KAIT light curves, while unfilled points show Swift light curves. We note that for our s = 3 model tstart = 0.5 days, hence we have omitted the light curve for t < 1 days. For s = 9.7 and 100, tstart = 1.5 days, and wehave omitted the light curve for t < 2 days in these cases. |
6 Model light curves
We perform simulations for the models discussed in Sect. 5 and presented in Table 1. We first consider the influence of the 56Ni distribution for a fixed density profile (Sect. 6.1) and then the effects of different density profiles (Sect. 6.2).
6.1 Effects of the 56Ni distribution for a fixed density profile
In Fig. 5, we show the light curves for our v7500_d0_n8_s3, 9.7, 100 models. Similar to Piro & Morozova (2016), we show that extended models (e.g. s3) exhibit very different light curves to compact models (e.g. s9.7 and s100). Our s3 model is much brighter than either the s9.7 or s100 models immediately following explosion (by ≳2 mag in the B-band at three days post-explosion), and shows a shallower rise to maximum. Between three and ten days after explosion, the B-band light curve increases by an average rate of 0.30, 0.49, and 0.54 mag day−1 for s3, s9.7, and s100, respectively. In the case of s3, there is a relatively large 56Ni mass in the outer ejecta – the outer ~50% of the ejecta mass contains ~20% of the 56Ni mass. As this 56Ni decays to 56Co, emitted γ-rays (and subsequent UV OIR photons) experience fewer interactions and escape more easily, hence the light curve is brighter at earlier times. The s9.7 and s100 models have 56Ni distributions more concentrated towards the ejecta centre – the outer ~50% of the ejecta contains ≲5% of the 56Ni mass in these cases. Therefore, in these models, emitted light has a higher probability of interaction, due to the larger ejecta mass through which it must travel before escaping, hence the light curves are fainter.
The s3, s9.7, and s100 models also show significant variation in their colour evolution, again for a fixed density profile. This is shown in Fig. 7 for our v12500_d0_n8 models. At very early times, the s3 model shows a bluer B− V colour (by ≲ 0.3 mag at three days post-explosion) than s9.7 and s100. During the next few days, the s3 model becomes slightly bluer (by ≲ 0.2 mag until approximately one week post-explosion) before gradually becoming redder until the end of our simulation – at 20 days, the B− V colour of s3 has increased to ~0.75 mag. Overall, the s9.7 and s100 models follow a broadly similar trend, although at different times. At three days, both models show redder colours than s3 (B−V ~ 0.3 mag) and continually become bluer until approximately two weeks post-explosion – reaching their most blue colours approximately one week after the s3 model. Following this, both models gradually become redder until the end of our simulations (B−V ~ 0.3 mag at 20 days).
That s3 is bluer at early times and redder at later times may be understood by considering the effects of 56Ni heating within the ejecta. The s3 model has a significant amount of 56Ni present in the outer ejecta that heats its surroundings as it decays to 56Co. The outer regions are therefore locally heated at all times. The outer regions of the s9.7 and s100 models lack 56Ni, hence they rely on diffusion of heat from the hotter inner layers and are relatively cool at early times. This produces an initially redder colour than s3, that gradually becomes bluer as light emitted in the inner regions diffuses outwards. As time increases, the outer ejecta become increasingly optically thin, exposing deeper and deeper layers of the ejecta. The more extended 56Ni distribution in s3 results in less 56Ni heating of the ejecta interior. Hence the temperature in these regions is lower than in s9.7 and s100, and the colour appears redder.
6.2 Effects of varying density profiles
The 56Ni distribution is affected not only by the scaling parameter s, but also the shape of the density profile (controlled by vt, δ, and n). Having shown how the light curves vary for the same density profiles but different scaling parameters, we now discuss the broad features of all of our models, and investigate the effects of each density parameter in turn.
Our models show a complicated behaviour with varying 56Ni distributions and density profiles. In Table 1 we list the light curve parameters for these models. We fit the light curves from each model with a sixth order polynomial between 10 and 25 days post-explosion. This was chosen simply to produce the best match to all of the model light curves after the initial rising phase but before the end of our simulations. From these model fits, we determine rise times and peak magnitudes in each band. These are given for bolometric, B-, and V -band light in Table 1. Table 1 also lists B−V colours at an early time (t = 2.5 days) and at B-band maximum. We note that, to determine the colour at 2.5 days, we fit the light curve between two and ten days.
The choice of transition velocity significantly affects the shape of the density profile. A higher transition velocity, vt, results in a larger and less dense inner region, and a smaller and more dense outer region (see Fig. 4). Typically this creates a brighter light curve before maximum light and a shorter rise time. Models with vt = 7500 km s−1 show a median bolometric rise time of 20.1 ± 1.2 days. For models with vt = 12 500 km s−1, the rise time is typically shorter (median ~16.7 ± 0.9 days). Indeed, all vt = 7500 km s−1 models have V -band rise times ≥23.7 days (most have rise times ≳25 days) – higher than the typical rise time for vt = 12 500 km s−1 (median ~19.7 ± 1.2 days). Higher vt will spread out more 56Ni to higher velocities, therefore light will be allowed to escape more easily in these cases. Similarly, vt has a significant effect on the colour evolution. For ≲3–7 days after explosion, higher vt models generally appear bluer as they produce more high frequency photons – resulting from the increased density in the outer regions, and hence higher temperature. These regions quickly become optically thin, however, exposing the inner regions. Models with higher vt will produce cooler inner regions, appearing redder at later times in both U− B and B− V. Despite differences in rise times and colour evolutions, models with different vt generally produce similar peak absolute magnitudes (within ~0.2 ± 0.2 mag).
The effect of a steeper inner density profile (larger δ) is less pronounced at times up to maximum light. A larger δ shifts mass to lower velocities, causing a decrease in density at higher velocities. This change in density is relatively small everywhere except the very centre of the ejecta (Fig. 4). This generally produces a delay in the rise of the light curve, a slightly longer rise time (by ≲1.5 days in all but one case), and a small decrease in peak magnitude (within typical photometric uncertainties of ~0.02 for the B- and V -band). Higher δ values may become more significant at later times, as the deepest layers of the ejecta are exposed, but this is beyond the scope of this work.
For steeper outer density profiles (larger n), again, more of the ejecta mass is shifted to lower velocities. The result is similar to that of a larger δ: the light curve is generally fainter in the optical bands during the pre-maximum phase and shows a slightly longer rise time. The U-band, however, is brighter for larger n. This is likely due to the fact that the inner regions are hotter for higher values of n, and the lower density outer region allows photons to escape more easily. Hence, more of the light escapes as higher frequency photons and the other optical bandlight curves, although fainter, also appear bluer. The effect is less significant in models with higher s values, as most of the 56Ni is already concentrated in the inner regions for these models.
We have shown how the model light curves respond to different density and 56Ni distributions. Our models broadly reproduce the peak magnitudes and rise times observed in SNe Ia. The exact shape of the light curves and colours, however, may not agree exactly. With an understanding of each parameter, tweaks may be made to produce light curves that better match observations. Model light curves will also be affected by changes in composition, but this will be investigated in future work.
7 Importance of a non-grey opacity
Given the complicated behaviour displayed by our models, here we demonstrate the importance of a frequency-dependent opacity in effectively capturing the evolution of the light curves and colours. We take one density profile (v12500_d0_n8) and perform new simulations using a grey, mean opacity for each of the 56Ni distributions discussed in Sect. 5 (i.e. extended, intermediate, and compact).
During each simulation, we calculated expansion and Thomson scattering opacities using TARDIS, as described in Sect. 2.4.2. We added the additional step of calculating either the Planck or Rosseland mean opacity, which is then used during the next time step. We calculate the Planck mean opacity as:
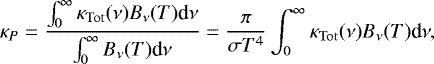 (12)
(12)
while the Rosseland mean opacity is given as:
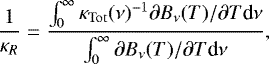 (13)
(13)
where Bν(T) is the Planck function. κTot(ν) is the total opacity, given by κTot(ν) = κexp(ν) + κTh, where κexp(ν) is the Eastman & Pinto (1993) expansion opacity (given in Eq. (5)) and κTh is the Thomson scattering opacity. The Planck mean opacity is more appropriate for optically thin plasmas (such as the diffuse outer regions of the SN ejecta) and is dominated by frequency intervals with high opacity, while the Rosseland mean opacity is more applicable for optically thick plasmas (such as the inner regions of the ejecta) and is dominated by frequency intervals with low opacity.
For these simulations, as we use a grey opacity, escaping packets are no longer binned by frequency and only contribute to the observed bolometric luminosity. To convert our bolometric luminosity to observed colours, we find the position of the photosphere (τ = 2/3), and calculate an effective black-body temperature, following the Stefan–Boltzmann law. We then calculate bolometric corrections for the desired filters using this effective temperature. This is repeated for each point in the light curve.
Figure 6 shows the effect of both approximations on the model opacity for three ejecta velocities at different times. As the Rosseland mean opacity is dominated by low opacity frequency intervals, it typically under-estimates the opacity for UV and near-UV photons (ν ≳ 1015 Hz). Conversely, the opacity is over-estimated for optical photons (ν ≲ 1015 Hz). Figure 7 demonstrates how the light curves are affected by this approximation, and presents light curves calculated using our full non-grey opacity, and the Planck and Rosseland means. It is clear from Fig. 7 that the Rosseland mean opacity produces light curves that are overall fainter in optical light, while being brighter in UV and near-UV light. Most photons are injected with UV or near-UV frequencies and therefore experience fewer interactions than in the non-grey opacity case. These photons then escape the ejecta more easily and produce a brighter U-band light curve. The optical light curves are directly affected by this also, as fewer photons are reprocessed to lower frequencies. In combination with this is the fact that the optical opacities themselves are also higher, which will further contribute to fainter optical light curves.
The Planck mean opacity produces an overall similar effect to that of the Rosseland mean opacity. From Fig. 6, the Planck mean opacity is significantly higher than both the Rosseland mean and non-grey opacities for all frequencies (with the exceptions of a narrow frequency window centred around ν ~ 2 × 1015 Hz and ν > 5 × 1015 Hz). As a consequence, packets experience more interactions, hence fewer photons escape and the light curves are fainter (Fig. 7).
From Fig. 7 it is clear that grey opacities and a colour correction are insufficient to capture the full evolution of the model light curves, and they become increasingly poor at later times and for models with extended 56Ni distributions. This is unsurprising, given that in models with more extended 56Ni distributions, there may be a relatively large 56Ni mass above the photosphere. Assuming these models operate as a black-body with a well defined photosphere is therefore a rather poor approximation. Even in models with 56Ni concentrated more towards the ejecta centre, the photosphere approximation becomes increasingly poor at later times, as the photosphere recedes into deeper layers of the ejecta where 56Ni is more prominent.
Having investigated each opacity approximation, we have shown that the Rosseland mean opacity can serve as a moderately good approximation for the early light curves in some regards. However, this grey opacity approximation is not suitable for cases where there is a large source of energy external to the photosphere – in other words, it has significant limitations when applied to models with extended 56Ni distributions (at all times) or if applied later than the first few days (all models). Therefore, complete quantification of the effects of the 56Ni distribution does need a full non-grey radiative transfer treatment.
 |
Fig. 6 Comparison of opacities used in simulations of our v12500_d0_n8_s3 model for three ejecta positions, at three different times. The Rosseland and Planck mean opacities are shown compared to the expansion and Thomson scattering opacities used in the non-grey case. |
 |
Fig. 7 Light curves obtained for various opacity treatments. Top: light curves of v12500_d0_n8 models using grey opacities and using our full, non-grey opacity treatment. Light curves have been offset vertically from each other for clarity. Bottom: B− V colours for v12500_d0_n8 models using grey opacities and using our full, non-grey opacity treatment. |
8 Relevance of surface 56Ni to light curve properties
Although the total ejecta mass is fixed for each model, the shape of the density profile is controlled by three parameters (vt, δ, n), with an additional parameter, s, controlling the distribution of 56Ni within the density profile. We have shown how each parameter affects the light curve, however they may also may be combined into a single parameter, column density. This gives an overall estimation of the amount of 56Ni present in the outer ejecta, or the proximity of the majority of 56Ni to the ejecta surface (i.e. higher column densities indicate the majority of the 56Ni mass is more deeply embedded within the ejecta). Following Noebauer et al. (2017), we investigate correlations between column density (measured at 104 s after explosion) and the light curve properties given in Table 1. The column density is given by:
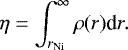 (14)
(14)
Noebauer et al. (2017) define rNi to be the outermost point at which 56Ni constitutes 1% of the ejecta composition. As the mass fraction of 56Ni does not drop to 1% in some of our models (see Fig. 4), we instead define rNi as the point at which the majorityof 56Ni is enclosed – in other words, the radius at which 90% (or 99%; see Table 1 for further details) of the total 56Ni mass is contained. Table 2 gives the column densities measured for our models. In determining the significance of trends, we use the Spearman rank correlation coefficient, 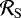 – a measure of whether any possible monotonic correlation (but not necessarily linear) exists between two variables. We note that
– a measure of whether any possible monotonic correlation (but not necessarily linear) exists between two variables. We note that 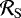 = ±1 indicates the variables are completely correlated, while zero indicates no monotonic correlation.
= ±1 indicates the variables are completely correlated, while zero indicates no monotonic correlation.
Figure 8a shows the rise times for our bolometric, B-, and V -band light curves as a function of column density. We find evidence for a strong correlation between bolometric rise time and column density, with 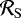 = 0.90 (p-value ~ 4 × 10−9). The column density defined here is simply a measure of the amount of surface 56Ni, therefore it is unsurprising that models with 56Ni close to the ejecta surface (i.e. the column density is low) have significantly shorter rise times. Correlations in the B- and V -bands are less significant, with
= 0.90 (p-value ~ 4 × 10−9). The column density defined here is simply a measure of the amount of surface 56Ni, therefore it is unsurprising that models with 56Ni close to the ejecta surface (i.e. the column density is low) have significantly shorter rise times. Correlations in the B- and V -bands are less significant, with 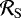 = 0.57 (p-value ~ 4 × 10−3) and
= 0.57 (p-value ~ 4 × 10−3) and 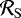 = 0.73 (p-value ~ 2 × 10−3), respectively. The strength of the correlation in the V -band is likely affected by the fact that a large number of our models peak after or close to the end of the simulations, and hence are not included. While the correlation between column density and rise time is fairly strong in bolometric light, it is less so in the B- and V -bands. This would indicate that there are more subtle effects determining the colour light curves than purely the 56Ni distribution. The v7500_d0,1_n8_s100 models, for example, are noticeable outliers in the B-band – their rise times are significantly shorter than models with similar column densities. Hence, we caution against attempts to determine the levels of surface 56Ni simply by measuring rise times in individual observed bands.
= 0.73 (p-value ~ 2 × 10−3), respectively. The strength of the correlation in the V -band is likely affected by the fact that a large number of our models peak after or close to the end of the simulations, and hence are not included. While the correlation between column density and rise time is fairly strong in bolometric light, it is less so in the B- and V -bands. This would indicate that there are more subtle effects determining the colour light curves than purely the 56Ni distribution. The v7500_d0,1_n8_s100 models, for example, are noticeable outliers in the B-band – their rise times are significantly shorter than models with similar column densities. Hence, we caution against attempts to determine the levels of surface 56Ni simply by measuring rise times in individual observed bands.
Similarly, we test for correlations between the column density and peak absolute magnitude. For the bolometric, B-, and V -band light curves we find 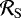 = 0.82 (p-value ~ 9 × 10−7), 0.88 (p-value ~ 4 × 10−8), and 0.88 (p-value ~ 1 × 10−5), respectively. The primary factor in determining the peak brightness of SNe Ia is the total amount of 56Ni produced during the explosion. Our results indicate that the distribution of 56Ni itself adds a further complication. Future models with varying 56Ni masses will allow for an investigation into the degeneracy between the total amount of 56Ni and its distribution.
= 0.82 (p-value ~ 9 × 10−7), 0.88 (p-value ~ 4 × 10−8), and 0.88 (p-value ~ 1 × 10−5), respectively. The primary factor in determining the peak brightness of SNe Ia is the total amount of 56Ni produced during the explosion. Our results indicate that the distribution of 56Ni itself adds a further complication. Future models with varying 56Ni masses will allow for an investigation into the degeneracy between the total amount of 56Ni and its distribution.
Finally, we investigate column density and colour. We find that models with higher levels of surface 56Ni (low column densities) tend to show redder colours at B-band maximum (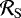 = −0.84; p-value ~ 3 × 10−7). Conversely, these models produce bluer colours very shortly after explosion (
= −0.84; p-value ~ 3 × 10−7). Conversely, these models produce bluer colours very shortly after explosion (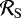 = 0.82; p-value ~ 9 × 10−7). As in the case for fixed density profiles, these trends demonstrate that models with extended 56Ni distributions (lower column densities) are typically hotter at early times and cooler at later times. Again, this is a result of the amount of 56Ni heating being probed at different points within the ejecta.
= 0.82; p-value ~ 9 × 10−7). As in the case for fixed density profiles, these trends demonstrate that models with extended 56Ni distributions (lower column densities) are typically hotter at early times and cooler at later times. Again, this is a result of the amount of 56Ni heating being probed at different points within the ejecta.
Our analysis shows the complicated sensitivity of the light curves to the parameters describing the ejecta, and general trends among the models. Although we find relatively strong correlations with colour and column density, these do not capture the shape of the light curves. For example, our v7500_d0_n12_s3 and v12500_d1_n12_s3 models show similar colours shortly after explosion, however, their colours and light curve shapes quickly diverge. Therefore, while colours and peak magnitudes, for example, may give a general sense of the level of surface 56Ni, caution is to be advised if one attempts to quantitatively infer the 56Ni distribution.Fully characterising the 56Ni distribution requires comprehensive comparisons with complete model light curves and colours.
Ejecta model rise indices and column densities.
 |
Fig. 8 Correlations between model column density and light curve parameters. Panel a: rise time as a function of column density for bolometric, B-, and V -band light curves. Panel b: peak absolute magnitude as a function of column density for bolometric, B-, and V -band light curves. Panel c: B−V colour at time of B-band maximum. Panel d: B−V colour at 2.5 d after explosion. For panels a–c, we first find the radius that encloses 90% of the total 56Ni mass. We then integrate density over radius (at 10 000 s) outwards from this point to calculate the column density. For panel d, we follow the same procedure but instead calculate the column density above the radius at which 99% of the total 56Ni mass is enclosed. We find evidence for correlations (of varying significance) between column density, rise time, peak magnitude, and colour. |
9 Rise index
Having investigated the light curve parameters, we now quantify the overall shape of the rising phase for our models. We perform fits for the rise index (z) in the same manner as Firth et al. (2015). For each model, we normalise the light curves using the peak absolute magnitudes from our polynomial fits (Table 1). We then fit the rising phase using:
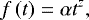 (15)
(15)
where f is flux, t is the time since explosion, α is a normalising factor, and z is the rise index. As in Firth et al. (2015), we define the rising phase as times where f < 0.5fPeak. Table 2 shows our fitted rise indices in each band, along with the median rise index.
Firth et al. (2015) show how the rise index of SNe Ia covers a broad range, from ~1.5 to ~3.7 for the PTF R-band and the broadband LSQ filter (which covers approximately the range of the SDSS gr filters). Our model rise indices are consistent with those of Firth et al. (2015), with fits to bolometric light curves producing rise indices ranging from 1.54 to 3.02. Based on the work of Piro & Nakar (2014), Firth et al. (2015) argue that the observed distribution of rise indices can be explained by differences in the 56Ni distribution. Our models support this conclusion and show that various 56Ni distributions can produce a wide range of rise indices. For a fixed density profile, our models show that an increasingly extended 56Ni distribution generally produces a more shallow rising light curve (lower rise index). However, the rising behaviour shows additional complexities. For a given value of s, the 56Ni distribution is fixed in terms of mass coordinate, yet changing the density parameters also affects the rise index. Therefore, although useful, the rise index is not a perfect indicator of the 56Ni mass depth probed by the light curves: the effects of the density and its overall shape must also be considered.
10 Comparison with the SN Ia SN 2009ig
In Fig. 5, we show the light curve of a SNe Ia, SN 2009ig (Foley et al. 2012), and demonstrate how our models may be used to constrain the 56Ni distribution in SNe Ia. The light curve of SN 2009ig shows remarkably good agreement with our v7500_d0_n8_s3 model light curve, despite the relatively simple, parametrised approach to our model setup (e.g. broken power law density profile, simple composition). It is clear from Fig. 5 that the early rise of SN 2009ig is too shallow to result from a compact 56Ni distribution.
Despite very good agreement in the BV R light curves, there are notable differences between the model and observed U- and I-band light curves. Our model U-band light curve shows a shallower rise to maximum than SN 2009ig, and is generally brighter (by between ~0.2 and 0.8 mag). The U-band is strongly affected by line blanketing from iron group elements (IGE), and even trace amounts of IGE may have a dramatic effect. We have assumed that 56Ni is 100% of the total IGE mass (as a means of testing purely the effects from the 56Ni distribution), while explosion models typically predict that this is not the case. For example, for the set of deflagration-to-detonation transition models presented by Seitenzahl et al. (2013), 56Ni constitutes between ~60 and 90% of the total IGE mass. Therefore, our models likely underestimate the total IGE mass in SNe Ia, hence the U-band light curve in particular appears brighter than what is observed. In addition, trace amounts of IGE may also be present in the progenitor WD, and therefore affect the U-band light curves (Höflich et al. 1998; Lentz et al. 2000). Future work will test different compositions for our models.
SN 2009ig shows a relatively flat I-band light curve from approximately seven days after explosion. The model light curve instead shows a smooth rise over the same period. This is likely a consequence of our LTE assumption. The recombination of IGE results in a strong secondary maximum in the NIR light curves of SNe Ia, and a slight “shoulder” in some of the optical bands (e.g. R and, to a much lesser extent, V; Kasen 2006). As discussed by Kromer & Sim (2009), the assumption of LTE has important implications for this effect. Kromer & Sim (2009) show that when using a detailed ionisation treatment, as opposed to LTE, the iron group elements in the ejecta remain more highly ionised for longer. This generally results in the recombination of Fe III to Fe II happening at earlier times in LTE. Hence, the first and secondary maxima blend together, forming a single peak that is broader than is observed in SNe Ia. This could explain why the model I-band in particular is most discrepant with SN 2009ig.
Figure 5 shows a comparison of our model light curves to SN 2009ig assuming an explosion epoch of JD = 2455063.41. Foley et al. (2012) infer this explosion epoch for SN 2009ig following the method of Riess et al. (1999a), where L ∝ t2. Piro & Nakar (2014), however, infer an explosion epoch 1.6 days earlier (JD = 2455061.8) by fitting the velocity evolution of absorption features (where v ∝ t−0.22). We compared all of our models to SN 2009ig using both explosion epochs and found best agreement with our v7500_d0_n8_s3 model and the explosion epoch of Foley et al. (2012). As an additional test, we fit this model to SN 2009ig by varying the explosion epoch. We find a best match explosion time to be consistent with that of Foley et al. (2012), JD = 2455063.34. We stress, however, that the model agreement with SN 2009ig is not perfect, and therefore could affect our explosion time estimate.
11 Conclusions
We presented a new Monte Carlo code, purpose built for modelling the early light curves of radioactively driven transients. Light curves computed by our code for the well-studied W7 explosion model (Nomoto et al. 1984) are consistent with those from other radiative transfer codes.
We performed an extensive parameter study of the 56Ni distribution and density profile, and explored their effects on model light curves. Similar to Piro & Morozova (2016) and Noebauer et al. (2017), we find that the light curve is strongly affected by the 56Ni distribution. For a given density profile, models with 56Ni extending throughout the ejecta are typically brighter and bluer at earlier times than models in which 56Ni is embedded deep within the ejecta. The density profile, however, also has significant effects on the model light curves.
We demonstrated the importance of a full radiative transfer treatment through comparisons with models thatuse grey opacities. We show how a grey (Rosseland) opacity is typically only applicable for times less than approximately one week after explosion and for models that do not have extended 56Ni distributions, and hence may produce inaccurate estimations of the 56Ni distribution.
Relations between the amount of surface 56Ni (or column density) and rise time, peak magnitude, and colour were investigated. We found that while correlations do exist, the scatter is sufficiently large that significant caution must be applied if individual light curve parameters (e.g. rise time to B-band maximum) are used to infer56Ni distributions. A comprehensive comparison of full colour light curves is necessary to quantify the 56Ni distribution in individual objects.
Finally, we compared our series of models to observations of the SNe Ia SN 2009ig (Foley et al. 2012). We find remarkably good agreement with a model that has 56Ni extending tothe outer ejecta, despite the relatively simple approach we have taken with, for example, the composition. It is clear that SN 2009ig is inconsistent with a 56Ni distribution that is concentrated towards the ejecta centre, and likely had a significant amount of 56Ni present in the outer ejecta. Piro & Nakar (2014) conclude that SN 2009ig must have had a 56Ni mass fraction, X56 of ~0.1 at ~ 0.1 M⊙ from the ejecta surface. All of our models with s = 3 have similar compositions to this (i.e. X56 = 0.1 at ~ 0.1 M⊙ from the ejecta surface), however, only our v7500_d0_n8_s3 model matches the light curve shape of SN 2009ig. This demonstrates the considerable power of early-phase light curve analysis to constrain a range of ejecta properties (such as the density profile) in addition to the 56Ni mass depth. Future work will focus on models with varying 56Ni and ejecta masses, as well as different compositions and more complex 56Ni distributions.
Our models clearly demonstrate that colour information is necessary to characterise the 56Ni distribution. In the case of SN 2009ig, our models show a preference for an extended 56Ni distribution, similar to detonation-to-deflagration and pure deflagration models. Whether other explosion models can induce similar degrees of mixing remains to be seen. Upcoming surveys will discover tens of thousands of SNe Ia. The high cadence and large field of view of the Large Synoptic Survey Telescope (Ivezic et al. 2008; LSST Science Collaboration 2009) for example, means that many of these discoveries will occur shortly after explosion. Comparison to a
larger observed sample will demonstrate whether the majority of SNe Ia typically show similar 56Ni distributions and place greater constraints on the explosion mechanism(s) of this class of supernovae.
Acknowledgements
We are grateful to U. Nöbauer for providing TARDIS analysis tools and STELLA light curves, L. Shingles for providing W7 model files, and C. Inserra for providing filter sets. We thank the anonymous referee for suggestions to improve our manuscript. This work made use of the Heidelberg Supernova Model Archive (HESMA), https://hesma.h-its.org. RK and SAS acknowledge support from STFC via grants ST/L000709/1 and ST/P000312/1. WEK was supported by an ESO fellowship.
References
- Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Ambwani, K., & Sutherland, P. 1988, ApJ, 325, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Arnett, W. D. 1982, ApJ, 253, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Bersten, M. C., Benvenuto, O., & Hamuy, M. 2011, ApJ, 729, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., Eastman, R., Bartunov, O. S., Popolitov, V. A., & Woosley, S. E. 1998, ApJ, 496, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., Röpke, F. K., Sorokina, E. I., et al. 2006, A&A, 453, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botyánszki, J., & Kasen, D. 2017, ApJ, 845, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., Mazzali, P. A., Benetti, S., et al. 1997, A&A, 328, 203 [NASA ADS] [Google Scholar]
- Carter, L. L., & Cashwell, E. D. 1975, Particle Transport Simulation with the Monte Carlo Method [Google Scholar]
- Cartier, R., Förster, F., Coppi, P., et al. 2011, A&A, 534, L15 [CrossRef] [EDP Sciences] [Google Scholar]
- Castor, J. I. 1972, ApJ, 178, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., Hillier, D. J., Blondin, S., & Khokhlov, A. 2014, MNRAS, 441, 3249 [Google Scholar]
- Eastman, R. G., & Pinto, P. A. 1993, ApJ, 412, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Fink, M., Kromer, M., Seitenzahl, I. R., et al. 2014, MNRAS, 438, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Firth, R. E., Sullivan, M., Gal-Yam, A., et al. 2015, MNRAS, 446, 3895 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Challis, P. J., Filippenko, A. V., et al. 2012, ApJ, 744, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J., & Dessart, L. 2012, MNRAS, 424, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P. 1995, ApJ, 443, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 185 [Google Scholar]
- Höflich, P., Wheeler, J. C., & Thielemann, F. K. 1998, ApJ, 495, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., Tyson, J. A., Abel, B., et al. 2008, ArXiv e-prints [arXiv:0805.2366] [Google Scholar]
- Kasen, D. 2006, ApJ, 649, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Thomas, R. C., & Nugent, P. 2006, ApJ, 651, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Röpke, F. K., & Woosley, S. E. 2009, Nature, 460, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kerzendorf, W. E., & Sim, S. A. 2014, MNRAS, 440, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Kromer, M., & Sim, S. A. 2009, MNRAS, 398, 1809 [Google Scholar]
- Kuhlen, M., Woosley, S. E., & Glatzmaier, G. A. 2006, ApJ, 640, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L., & Bell, B. 1995, Atomic Line Data, Kurucz CD-ROM No 23, (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Lentz, E. J., Baron, E., Branch, D., Hauschildt, P. H., & Nugent, P. E. 2000, ApJ, 530, 966 [Google Scholar]
- Livne, E., Asida, S. M., & Höflich, P. 2005, ApJ, 632, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Long, K. S., & Knigge, C. 2002, ApJ, 579, 725 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration (Abell, P. A., et al.) 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Lucy, L. B. 2002, A&A, 384, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2003, A&A, 403, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2005, A&A, 429, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B., & Abbott, D. C. 1993, ApJ, 405, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Benetti, S., Stritzinger, M., et al. 2010a, Nature, 466, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maeda, K., Taubenberger, S., Sollerman, J., et al. 2010b, ApJ, 708, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Maeda, K., Leloudas, G., Taubenberger, S., et al. 2011, MNRAS, 413, 3075 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., & Lucy, L. B. 1993, A&A, 279, 447 [NASA ADS] [Google Scholar]
- Morozova, V., Piro, A. L., Renzo, M., et al. 2015, ApJ, 814, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Noebauer, U. M., Kromer, M., Taubenberger, S., et al. 2017, MNRAS, 472, 2787 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Nugent, P. E., Sullivan, M., Cenko, S. B., et al. 2011, Nature, 480, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
- Piro, A. L., & Morozova, V. S. 2016, ApJ, 826, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Nakar, E. 2013, ApJ, 769, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Nakar, E. 2014, ApJ, 784, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Li, W., & Schmidt, B. P. 1999a, AJ, 118, 2668 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Li, W., et al. 1999b, AJ, 118, 2675 [NASA ADS] [CrossRef] [Google Scholar]
- Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2013, MNRAS, 429, 1156 [Google Scholar]
- van Rossum, D. R. 2012, ApJ, 756, 31 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Bolometric light curve and γ-ray deposition curve for the model presented by Lucy (2005) compared to a calculation performed in this work. Our code reproduces the results of Lucy (2005). |
| In the text | |
 |
Fig. 2 Wavelength at which packets are absorbed and re-emitted following their last interaction, and before exiting the simulation. Three values of the redistribution parameter are shown from left to right: scattering dominated (ϵ = 0.1), equal probability for scattering and redistribution (ϵ = 0.5), and redistribution dominated (ϵ = 0.9). |
| In the text | |
 |
Fig. 3 Comparison of bolometric and UBV RI light curves for the W7 explosion model generated by different light curve codes. ARTIS and STELLA light curves are from by Kromer & Sim (2009) and Noebauer et al. (2017), respectively. |
| In the text | |
 |
Fig. 4 Ejecta models used in this work. Panel a: density profiles for our model sequence. Transition velocity, delta, and n parameters are given for each model. Densities for a sample of explosion models are shown for comparison: W7 (Nomoto et al. 1984), DDT N100 (Seitenzahl et al. 2013), DEF N1600 (Fink et al. 2014), VM (Pakmor et al. 2012). Panel b: illustrative composition profile for one model (v12500_d0_n8_s9.7). The three zone structure is clearly demonstrated, with representative species shown. Panel c: 56Ni distributionsfor one density profile (v12500_d0_n8). 56Ni distributions for a sample of explosion models are also shown. |
| In the text | |
 |
Fig. 5 Bolometric, Swift U, and JohnsonBV RI light curves for our v7500_d0_n8 density profile, with various scaling parameters (s = 3, 9.7, and 100), and the UBV RI light curves of SN 2009ig. Light curves of SN 2009ig are shown assuming μ = 32.6 ± 0.4, negligible host extinction, and an explosion epoch of JD = 2455063.41 ± 0.08 (Foley et al. 2012). Filled points represent KAIT light curves, while unfilled points show Swift light curves. We note that for our s = 3 model tstart = 0.5 days, hence we have omitted the light curve for t < 1 days. For s = 9.7 and 100, tstart = 1.5 days, and wehave omitted the light curve for t < 2 days in these cases. |
| In the text | |
 |
Fig. 6 Comparison of opacities used in simulations of our v12500_d0_n8_s3 model for three ejecta positions, at three different times. The Rosseland and Planck mean opacities are shown compared to the expansion and Thomson scattering opacities used in the non-grey case. |
| In the text | |
 |
Fig. 7 Light curves obtained for various opacity treatments. Top: light curves of v12500_d0_n8 models using grey opacities and using our full, non-grey opacity treatment. Light curves have been offset vertically from each other for clarity. Bottom: B− V colours for v12500_d0_n8 models using grey opacities and using our full, non-grey opacity treatment. |
| In the text | |
 |
Fig. 8 Correlations between model column density and light curve parameters. Panel a: rise time as a function of column density for bolometric, B-, and V -band light curves. Panel b: peak absolute magnitude as a function of column density for bolometric, B-, and V -band light curves. Panel c: B−V colour at time of B-band maximum. Panel d: B−V colour at 2.5 d after explosion. For panels a–c, we first find the radius that encloses 90% of the total 56Ni mass. We then integrate density over radius (at 10 000 s) outwards from this point to calculate the column density. For panel d, we follow the same procedure but instead calculate the column density above the radius at which 99% of the total 56Ni mass is enclosed. We find evidence for correlations (of varying significance) between column density, rise time, peak magnitude, and colour. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


