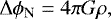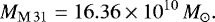| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731939 | |
| Published online | 13 June 2018 | |
MOND simulation suggests an origin for some peculiarities in the Local Group★
1
Astronomical Institute, Czech Academy of Sciences,
Boční II 1401/1a,
141 00
Praha, Czech Republic
e-mail: bilek@asu.cas.cz
2
Helmholtz-Institut für Strahlen- und Kernphysik,
Nussallee 14-16,
53115
Bonn, Germany
3
Charles University in Prague, Faculty of Mathematics and Physics, Astronomical Institute,
V Holešovičkách 2,
180 00
Praha 8, Czech Republic
4
Université de Strasbourg, CNRS UMR 7550, Observatoire Astronomique de Strasbourg,
11 rue de l’Université,
67000
Strasbourg, France
Received:
12
September
2017
Accepted:
6
February
2018
Context. The Milky Way (MW) and Andromeda (M 31) galaxies possess rotating planes of satellites. The formation of these planes has not been explained satisfactorily so far. It has been suggested that the MW and M 31 satellites are ancient tidal dwarf galaxies; this might explain their configuration. This suggestion gained support by an analytic backward-calculation of the relative MW–M 31 orbit in the MOND modified dynamics paradigm. The result implied that the galaxies experienced a close flyby 7–11 Gyr ago.
Aims. Here we explore the Local Group history in MOND in more detail using a simplified first-ever self-consistent simulation. We describe the features induced by the encounter in the simulation and identify possible real counterparts of these features.
Methods. The initial conditions were set to eventually roughly reproduce the observed MW and M 31 masses, effective radii, separation, relative velocity, and disk inclinations. We used the publicly available adaptive-mesh-refinement code Phantom of RAMSES.
Results. Matter was transferred from the MW to M 31 along a tidal tail in the simulation. The encounter induced the formation of several structures resembling the peculiarities of the Local Group. Most notably are that 1) a rotating planar structure formed around M 31 from the transferred material. It had a size similar to the observed satellite plane and was oriented edge-on to the simulated MW, just as the real plane. 2) The same structure also resembled the tidal features observed around M 31 by its size and morphology. 3) A warp in the MW developed with an amplitude and orientation similar to that observed. 4) A cloud of particles formed around the simulated MW, with the extent of the actual MW satellite system. The encounter did not end by merging in a Hubble time. The simulated stellar disks also thickened as a result of the encounter.
Conclusions. The simulation demonstrated that MOND might explain many peculiarities of the Local Group; this needs to be verified with additional simulations. The simulation moreover showed that tidal features observed in galaxies, usually interpreted as merger remnants, could have been formed by matter exchange during non-merging galactic flybys in some cases.
Key words: local group / galaxies: interactions / galaxies: formation / galaxies: kinematics and dynamics / galaxies: structure / gravitation
Three movies are available at http://www.aanda.org
© ESO 2018
1 Introduction
The satellites of the Milky Way (MW) have a remarkable spatial distribution (Lynden-Bell 1976; Kroupa et al. 2005; Metz et al. 2007): their positions define a flattened body (a satellite plane, SP, called the vast polar structure, VPOS, in the case of the MW) with a root-mean-square (RMS) half-thickness of around 15 kpc and an RMS radius of around 40 kpc (Pawlowski et al. 2015b). The most distant satellite lies 365 kpc away from the MW center. The central plane of this cloud is almost perpendicular to the MW disk and almost passes through the MW center (Kroupa et al. 2005). The angle between the VPOS and the line connecting the centers of the MW and the Andromeda galaxy (M 31) is around 40–50° (Pawlowski et al. 2013). The velocities of the satellites are mostly consistent with orbiting within the SP (Metz et al. 2008). Pawlowski & Kroupa (2013) found that 9 of the 11 brightest MW satellites orbit within the SP. Of these, 8 orbit the MW in the same sense and 1 in the opposite sense. Not only the satellites, but also stellar streams and outer halo globular clusters are concentrated within the VPOS (Pawlowski et al. 2012). The classical, bright satellites are more concentrated toward the midplane of the VPOS than the ultra-faint dwarfs (Kroupa 2012).
These discoveries motivated the search for SPs in other galaxies. A spectacular example was found in M 31, called the Great Plane of Andromeda, GPoA, (Metz et al. 2007, 2009a; Ibata et al. 2013). Ibata et al. (2013) revealed that 15 out of the 27 satellites with distances known at that time formed a plane whose edge points to the MW. This orientation enabled determining, without the knowledge of the tangential velocities, that 13 of the 15 satellites in the plane were consistent with corotating around M 31. This GPoA rotates in the same sense as the VPOS. Pawlowski et al. (2013) used a newer data set to conclude that up to 19 out of 34 M 31 satellites contribute to the plane. From the values given by Pawlowski et al. (2013), we were able to calculate that the inclination of this plane with respect to the line joining M 31 with the MW is just 2°. This SP has an RMS half-thickness of 14 kpc and an RMS radius of around 130 kpc along its long axis and 25 kpc along its intermediate axis (Pawlowski et al. 2013). It is nearly perpendicular to the MW galactic disk. Most of the M 31 satellites belonging to the GPoA lie on the side of M 31 closer to the MW, i.e., their distribution is lopsided. This remarkable property of the M 31 satellites is not exceptional: Libeskind et al. (2016) stacked images of many observed galaxy pairs and their satellites. They found a significant tendency for the satellites to lie between the pair.
There are also non-satellite dwarfs in the Local Group (LG) whose distances to the MW and M 31 are comparable. Pawlowski et al. (2013) looked for planes in the whole LG and found that 14 of the 15 non-satellite dwarfs lie on two very large and thin planes (RMS half-thickness of around 60 kpc, and RMS half-length of around 600 kpc along the longest axis). They are both parallel to the line connecting MW and M 31, and they have equal distances to it of around 150 kpc. The galactic disk of M 31 lies on the symmetry plane between the non-satellite dwarf planes. The LG thus has a high and unexplained symmetry.
Some of the LG dwarfs have even another kind of a special configuration. Pawlowski et al. (2013) found that they lie in near the plane of the M 31 galactic disk. Others possibly lie near the plane of the galactic disk of the MW.
The nearest large galaxy outside the LG is Centaurus A (Cen A, NGC 5128). Tully et al. (2015) reported a discovery of two almost parallel SPs here seen edge-on from the MW, both with an RMS half-thickness of 60 kpc and an RMS radius of 350 kpc. Müller et al. (2016) made another analysis of this satellite system that also took newly discovered faint satellites into account. They concluded that it cannot be excluded that there is only one single thick SP. Müller et al. (2018) has recently confirmed that most satellites in this plane corotate. A tidal stream extends from one of the Cen A satellites. The distance to several spots in the stream was measured by Crnojević et al. (2016). Müller et al. (2016) revealed that the stream lies almost in one of the original SPs by Tully et al. (2015).
The next nearest galaxy group is the M 81 group. Here Chiboucas et al. (2013) noted that the early-type dwarf galaxies are distributed in a flattened formation that is tilted toward the line of sight, while the distribution of the late-type dwarfs is more isotropic.
The last SP known to us has recently been reported by Müller et al. (2017) to lie around M 101. It is also seen edge-on from the MW.
Ibata et al. (2014a) statistically estimated the occurrence of rotating SPs in more distant galaxies in the SDSS database. A galaxy was counted as a candidate for having a rotating SP if the positions and radial velocities of its satellites were consistent with this hypothesis. The authors found that the frequency of these candidates is greater than would be expected if the galaxy satellites were distributed isotropically. This result is consistent with a fraction of about 50% of satellites residing in SPs around M31- and MW-like hosts at redshift z < 0.05. Ibata et al. (2015) made a similar analysis: they counted a galaxy as a candidate for having a rotating SP if for some of its spectroscopically confirmed satellites there was a satellite lying on the opposite side of the galaxy. Again, a 3σ overabundance of such candidates was detected.
Previous attempts to explain the existence of SPs in the cosmological Λ cold dark matter (CDM) model were not satisfactory (e.g., Pawlowski et al. 2015a, 2017). Cosmological ΛCDM dark-matter-only simulations result in a nearly isotropic satellite distribution around the host galaxy with only a mild degree of ellipticity and no preferred orbital direction. Kroupa et al. (2005) calculated that the probability is 0.5% that the positions of the 11 then-known MW satellites are consistent with cosmological dark-matter-only simulations. Using the most updated data, Pawlowski (2016) found that the spatial structure is a ≈5σ event with respect to an isotropic distribution. Including the clustering of the orbital momentum vectors of the satellites increases the significance of the VPOS even more. The probability that an SP like the GPoA is found among satellites with an isotropic distribution of positions and velocities is 0.002% (Ibata et al. 2013). It was suggested that satellites that accreted along a cosmological dark matter filament or accreted in a compact group would form SPs, but these effects are included naturally in cosmological simulations. Metz et al. (2009b) showed that the infall of groups of satellites cannot produce the VPOS. Pawlowski et al. (2015a) concluded that including baryons into cosmological simulation does not help to remove the problem. Dwarf galaxies in these simulations reside predominantly in primordial dark matter halos.
Another type of dwarf galaxies does not possess appreciable dark matter halos according to ΛCDM. These are tidal dwarf galaxies (TDGs), which are gravitationally bound objects formed in tidal tails of interacting galaxies (see, e.g., Bournaud 2010; Ploeckinger et al. 2018). They have been observed many times. Simulations showed two mechanisms of their formation: by the Jeans instability of the gas in tidal tail, or by accumulating a great amount of gas at the tip of a tidal tail. Since the material in the tidal tail was stretched from an originally small volume in a dynamically cold disk of the parent galaxy, the TDGs have to occupy a small volume in the phase-space according to Liouville’s theorem and form phase-space-correlated structures. This is exactly what is observed in the rotating SPs. Simulations showed that TDGs are free of dark matter (Barnes & Hernquist 1992), which seems to contradict the high dynamical mass-to-light ratios of the LG dwarfs. However, simulations by Kroupa (1997) demonstrated that dark-matter-free satellites in Newtoniangravity could appear as dark matter rich if they were not in dynamical equilibrium (see also Casas et al. 2012).
Hammer et al. (2013) presented a simulation where a galaxy accreted by M 31 produced TDGs that formed an SP around M 31. Fouquet et al. (2012) used hydrodynamical simulations and found that if the Giant Stream at M 31 is to be reproduced by an accreted satellite, then collision formed a tidal tail pointing toward the MW, which could form the VPOS. This scenario accounts for many properties of the LG galaxies. To account for the observed high dynamical masses of the satellites, they relied on the argument by Kroupa (1997).
Another possibility to explain the high dynamical masses of the LG dwarfs if they are TDGs is to assume MOND (Milgrom 1983, 2015b), a paradigm suggesting that the commonly used laws of gravitational dynamics (at least) have to be modified for low accelerations rather than to extend the well-proven standard model of particle physics by new particles of dark matter. Galaxy observations usually agree well with MOND in various situations (see, e.g., Famaey & McGaugh 2012 for a review). For example, MOND successfully explains the internal dynamics of most regular early- and late-type galaxies (Begeman et al. 1991; Sanders 1996; de Blok & McGaugh 1998; Milgrom & Sanders 2003, 2007; Tiret et al. 2007; Richtler et al. 2011; Gentile et al. 2011; Angus et al. 2012; Milgrom 2012; Samurović 2014; McGaugh et al. 2016; Dabringhausen et al. 2016; Lelli et al. 2017), the rotation curves of polar rings (Lüghausen et al. 2013), the properties of the Sagittarius stream (Thomas et al. 2017), or the galaxy-galaxy weak gravitational lensing (Milgrom 2013).
Zhao et al. (2013; Z13 hereafter) used the MOND two-body-force formula to calculate the history of the MW–M 31 relative orbit. They used the best estimates on the current baryonic masses, separation, and radial velocity. Despite some recent debates on the exact value of the tangential velocity (Salomon et al. 2016), the value they adopted from van der Marel et al. (2012b) is still the best direct value based on the Hubble Space Telescope. With this low tangential velocity, they found that the MW and M31 had to have had a close encounter 7–11 Gyr ago. This opens the possibility that TDGs formed and are observed as the LG dwarfs now. When integrated backward, the orbits of the Large and Small Magellanic Clouds were close to pericenter almost at the time when the MW and M 31 were at the pericenter. Dynamical friction during encounters of comparable galaxies is known to be weaker in MOND than in ΛCDM from the simulations by Tiret & Combes (2007), Nipoti et al. (2008), and Combes (2016; see also, Renaud et al. 2016 or Vakili et al. 2017) because of the absence of the large and massive dark matter halos (Kroupa 2015). A close MW–M 31 encounter in MOND would therefore be more likely to avoid ending in a merger than in ΛCDM. Simulated galaxy encounters in MOND also produce TDGs more easily than their ΛCDM counterparts (Tiret & Combes 2007; Renaud et al. 2016). By employing MOND, the equivalent Newtonian dynamical masses of most MW and M 31 satellites increase so that they match the observed values (Angus 2008; Serra et al. 2010; McGaugh & Milgrom 2013a,b). The remaining discrepancies for the least massive objects might be explained if these objects are not in dynamical equilibrium (e.g., McGaugh & Wolf 2010; Dabringhausen et al. 2016), as suggested by Kroupa (1997), but using Newtonian simulations. The rotation curves of the MW (Famaey & Binney 2005; McGaugh 2008; Iocco et al. 2015), M 31, and M 33 (Famaey & McGaugh 2012) are also reproduced well. When we assume that some TDGs formed during the MW–M 31 encounter and remained bound to one of the large galaxies, they would form at least a temporal (Fernando et al. 2017) SP in the case that the orbital planes of individual satellites around their hosts nearly coincide by chance. The non-satellite LG dwarfs with their planar distribution could be ejected TDGs. Further observational evidence for this scenario is given in Sect. 4. We might be seeing a formation of an SP in progress in the interacting disk galaxy pair ARP 87. Here one of the tidal tails seems to be wrapped around the other galaxy to form a disk-like structure1.
These findings have inspired our present work. In this paper, we proceed beyond the qualitative considerations and analytic calculations and explore the history of the LG in MOND using a first-ever self-consistent simulation. We describe the features induced by the encounter and compare the simulation to the observations. The simulation was set so that it approximately reproduced the observed MW–M 31 masses, disk radii, separation, relative radial and tangential velocity, and disk inclinations. The approximately correct rotation curves of our galaxy models were ensured by using MOND and their approximately correct mass distributions, since MOND works well for the real MW and M 31. The simulation shows a close encounter of the MW and M 31. The separation between the galaxies is 24 kpc at the pericenter, occurring around 7 Gyr ago. Mass is transferred from the MW to M 31. The encounter induced features around the simulated MW and M 31 similar to the observed tidal features by their morphology and spatial extent. A rotating planar structure resembling the GPoA formed at the simulated M 31, which was visible edge-on from the position of the Sun in the simulation. The encounter induced a warp in the simulated MW disk similar to the observed warp, and it increased the thicknesses of the galactic disks of the MW and M 31. Future more elaborate simulations are required to verify whether the features formed by an encounter between MW and M 31 in MOND can be tuned to closely match the observations.
This paper is organized as follows: in Sect. 2 we describe our computational methods and the choice of the input parameters. The outcome of the simulation is described in Sect. 3. We compare the outcome with observations and list some limitations of our approach in Sect. 4. We summarize the paper in Sect. 5.
2 Description of the simulation
2.1 Equations we solved
According to the modern formulation (Milgrom 2009), a non-relativistic MOND is any theory obeying these tenets: 1) it contains a constant with the dimension of acceleration a0, 2) in the limit a0 → 0 (all quantities with the dimension of acceleration are much greater than a0), the equations of the theory reduce to Newtonian dynamics, and 3) in the limit of a0 →∞ and G → 0 (all quantities with the dimension of acceleration are much smaller than a0), keeping the product a0G constant, the dynamics of purely gravitationally interacting systems is space-time scaling invariant, that is, if the equations of the theory allow the bodies to move on the trajectories (ri, t), then they also have to allow them to move on the trajectories expanded in time and space by a constant factor, λ(ri, t), where λ is a real number greater than 1. Consequently, the accelerations of bodies are enhanced compared to Newtonian dynamics in the low-acceleration regime that is called the deep-MOND regime.
All MOND theories are nonlinear (Milgrom 2014). This has the external field effect (EFE) as a consequence: the internal dynamics of a system is affected if the center of mass of the system is accelerating. In a wide class of modified-gravity-type MOND theories (Milgrom 2014), the gravitational force of a system in the deep-MOND weakens when the system is exposed to an external gravitational field. This differs from the tidal forces because the EFE occurs even for a homogeneous external field or for arbitrarily small systems. In the case of the LG, the gravitational attraction between the MW and M 31 is weaker when we take into account the external field caused by the nearby cosmic structures such as nearby galaxy clusters. With a zero external field, the model by Z13 gives the MW–M 31 pericenter around 7 Gyr ago, and around 10 Gyr ago with a more realistic external-field strength of 0.03 a0.
So far, two fully fledged non-relativistic MOND theories have been published, both of which are modified gravity theories (AQUAL, Bekenstein & Milgrom 1984; QUMOND, Milgrom 2010). Their differences are still not explored well (Zhao & Famaey 2010). For spherically symmetric matter density distributions, the theories give equal gravitational accelerations, but in other configurations, the accelerations can differ by some tens of percent, see an example in Banik & Zhao (2015). As Candlish et al. (2015) cautioned, the small difference in gravitational acceleration can accumulate over time and affect the evolution of the investigated system. Nevertheless, the existing comparative simulations seem to be little dependent on the particular MOND theory as far as we can judge from the figures in Banik & Zhao (2015), Candlish et al. (2015), or Candlish (2016).
Our simulations employed the QUMOND theory (Milgrom 2010). For a matter density distribution ρ, the QUMOND gravitational potential ϕ is given by the generalized Poisson equation
![\begin{equation*} {\mathrm\Delta}\phi= \vec{\nabla}\cdot [\nu (|\vec{\nabla}\phi_{\textrm{N}} |/a_0)\vec{\nabla}\phi_{\textrm{N}}], \end{equation*}](/articles/aa/full_html/2018/06/aa31939-17/aa31939-17-eq1.png) (1)
(1)
is the Newtonian gravitational potential and ν is the interpolation function, in our simulations chosen as
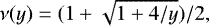 (3)
(3)
which is known to produce a good fit to galaxy rotation curves (Famaey & Binney 2005; Gentile et al. 2011) and for strong gravitational lenses (Sanders & Land 2008)2. Point masses move in this gravitational field according to the usual equation of motion 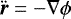 .
.
We solved these equations with the publicly available Phantom of RAMSES adaptive-mesh-refinement code (PoR, Lüghausen et al. 2015). The simulations contained only point masses in an invariable number. Cosmic expansion and an external field were not implemented. The computational parameters of this simulation are listed in Table 1. They lead to a spatial resolution of 120 pc. The PoR/RAMSES parameters not listed here were left as the default settings.
Simulation setup.
2.2 Choice of free physical parameters and coordinate system
When choosing the physical parameters of our simulation, we were motivated by observations, and where applicable, we roughly followed the fiducial model by Z13. We used a0 = 1.2 × 10−10 m s−2.
The galaxy masses approximately follow the baryonic Tully–Fisher relation, 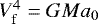 , which is precise in all MOND theories. Here Vf is the rotational velocity at the asymptotically flat part of the rotational curve. This formula gives M = 6.6 × 1010 M⊙ for Vf =180 km s−1 of the MW(Fig. 4 of Wu et al. 2008, following Z13) and M = 1.6 × 1011 M⊙ for Vf =225 km s−1 of M 31 (Carignan et al. 2006). In the simulation, we used
, which is precise in all MOND theories. Here Vf is the rotational velocity at the asymptotically flat part of the rotational curve. This formula gives M = 6.6 × 1010 M⊙ for Vf =180 km s−1 of the MW(Fig. 4 of Wu et al. 2008, following Z13) and M = 1.6 × 1011 M⊙ for Vf =225 km s−1 of M 31 (Carignan et al. 2006). In the simulation, we used
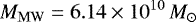 (4)
(4)
The galaxies were modeled as truncated exponential disks with a density distribution of the form
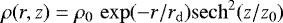 (6)
(6)
for r ≤ rt and ρ(r, z) = 0 for r > rt with the truncation radius rt of 20 kpc. The central density ρ0 was scaled to obtain the required disk masses. The real scale length of the MW is around 2.1 kpc (Bovy & Rix 2013) and that of M 31 is around 5.3 kpc (Courteau et al. 2011). In the simulation, we implemented the scale length rd of 3.5 kpc and the scale height z0 of 0.3 kpc for both galaxies (i.e. the half-mass radius, rh = 1.67 rd, of 5.8 kpc). The velocity dispersion was set to obtain the Toomre Q parameter of 1 at all radii according to Eqs. (20)–(22) of Lüghausen et al. (2015). The initial models for both galaxies were set up by the method and code described in Sect. 5.1 of Lüghausen et al. (2015). We show the evolution of our galaxy models in isolation in Appendix A. In short, they quickly develop bars and increase the effective radii by at most 25% between the simulation start and the time when the observed separation and relative velocity were reproduced. Figures 1 and 2 show the rotation curves of the simulated MW and M 31.
We used the same axes directions as van der Marel et al. (2012b), who measured the proper motion of M 31 using the Hubble Space Telescope: the Z axis pointed from the observed MW center to its northern pole, the X axis pointed from the current observed position of the Sun to the MW center, and Y axis pointed in the direction of the Sun motion around the MW center. We adopted the MW–M 31 barycenter as the origin of our coordinate system. Then, following van der Marel et al. (2012b), the vector from the MW center to the M 31 center is (their Eq. (2))
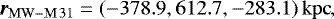 (7)
(7)
and the most probable relative velocity of M 31 with respect to the MW measured by van der Marel et al. (2012b) is (their Eq. (3))
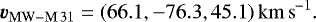 (8)
(8)
We adopted the current spin directions of the disks from Pawlowski et al. (2013), who used the same axes directions

The position of the Sun in our coordinate system was
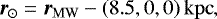 (11)
(11)
where we assumed the same distance of the Sun from the MW center as van der Marel et al. (2012b).
We assumed a zero external field, that is, the LG in our simulation is not subject to an EFE from neighboring objects.
None of these parameters was tuned to achieve the results described in Sect. 3.
 |
Fig. 1 Rotation curve of the simulated MW at the simulation start (0.0 Gyr) and at the current time (7.4 Gyr). The model was initiallytruncated at 20 kpc, but the particles spread outward as the galaxies developed bars and interacted, such that the rotation could be traced to larger distances at the later times. |
 |
Fig. 2 Rotation curve of the simulated M 31 at the simulation start (0.0 Gyr) and at the current time (7.4 Gyr). The model was initially truncated at 20 kpc, but the particles spread outward as the galaxies developed bars and interacted, such that the rotation could be traced to larger distances at the later times. |
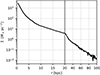 |
Fig. 3 Surface density profile of the simulated MW at the current time. |
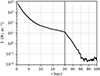 |
Fig. 4 Surface density profile of the simulated M 31 at the current time. |
2.3 Defining the basic galaxy properties in the simulation
To obtain the position and velocity of a galaxy in the simulation, we proceeded in the following way. Each particle had an identifier assigned according to its parent galaxy. To define a position of the galaxy i in the later time steps, we applied 60 passes of the sigma-clipping algorithm to the particles that originally belonged to the galaxy i. This means that we first calculated the center of mass of the particles in consideration, x, and the root-mean-square of the particle distances from x, σ; and for the next iteration, we considered the particles whose distance from x was smaller than 3σ. These steps were repeated iteratively. The velocity of a galaxy was calculated as the average velocity of the particles considered in the last iteration of the sigma-clipping algorithm.
We defined the galaxy spins in the simulation using the principal component method applied to the positions of the particles closer than 15 kpc from the respective galaxy center and chose the orientation according to the galaxy rotation sense. The disk midplanes of the galaxies were considered to be perpendicular to the spins and to pass through the galaxy positions.
With particles belonging to a galaxy, we mean the particles that were closer to it than to the other galaxy at the given simulation time.
2.4 Finding the orbital parameters
We aimed to find initial conditions so that the MW and M 31 in the simulation reproduced the observed MW–M 31 distance, relative velocity, and disk inclinations at some simulation time.
To determine the initial positions, we integrated the motion of the MW and M 31 analytically backward, starting from the observed state (Eqs. (7) and (8)) in the coordinate system defined in Sect. 2.2. We modified the prescription for the two-body force in MOND (Milgrom 1994; Zhao et al. 2010),
![\begin{align*} &F=\frac{Gm_1m_2}{r^2}+\frac{{\mathrm\Xi}\sqrt{G(m_1+m_2)^3a_0}}{r},\\ &{\mathrm\Xi}\equiv \frac{2}{3}\left[1-\sum_{i = 1}^2\left(\frac{m_i}{m_1+m_2}\right)^{3/2}\right], \end{align*}](/articles/aa/full_html/2018/06/aa31939-17/aa31939-17-eq13.png)
to account for the internal sizes of the galaxies by replacing the distance between the point masses r in Eq. (12) by 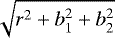 . Here bi = 1.28rd,i is the Plummer radius of a Plummer sphere with the same half-mass radius as an exponential disk with the scale length rd,i (in our case, rd,1 = rd,2 = 3.5 kpc, see Sect. 2.2). We integrated the motion of the galaxies backward until they reached the pericenter and then receded to 300 kpc from each other.
. Here bi = 1.28rd,i is the Plummer radius of a Plummer sphere with the same half-mass radius as an exponential disk with the scale length rd,i (in our case, rd,1 = rd,2 = 3.5 kpc, see Sect. 2.2). We integrated the motion of the galaxies backward until they reached the pericenter and then receded to 300 kpc from each other.
The initial spin vectors of the simulated galaxies were chosen as the observed spin vectors (Eqs. (9) and (10)): we assumed that the spins would not change much by the encounter and that the MW–M 31 orbit in the self-consistent simulation would not change substantially by dynamical friction compared to the analytic orbit. This is assessed in Table 2.
Then we searched for the initial velocities required to reproduce the observed relative MW–M 31 velocity and separation (but not necessarily the observed positions given by Eq. (7)). We proceeded iteratively. In the first iteration, the initial galaxy velocities were taken from the analytical orbit. We then ran a self-consistent simulation while checking its output every 20 Myr. When the galaxies reached the apocenter and when their separation dropped below the observed value, the simulation was stopped and the relative radial and tangential galaxy velocities were compared to the observed values. Then we adjusted the initial velocities for the next iteration by changing the initial relative radial and tangential velocity magnitudes (i.e., the plane of the encounter stayed fixed). This was repeated until the final relative radial and tangential velocities differed by less than 3 km s−1 from the observed values. The final simulation was continued to cover a time of 14 Gyr.
The complete setup of the final simulation is summarized in Table 1.
Comparison of the real and simulated LG properties.
Important orbital events in the simulated LG.
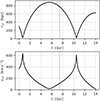 |
Fig. 5 Top: evolution of the galaxy separation, r12, with the simulation time, t. Bottom: evolution of the galaxy relative velocity magnitude, v12, with the simulation time. The vertical dashed line indicates the current time (7411 Myr). |
3 Results
As described above, our simulation was set up so that it approximately reproduced the observed MW–M 31 separation, radial and tangential velocity, disk spin direction, masses, and scale lengths. We stress that the results described in this section are a consequence of this setup; no other tuning was used.
We denote by the term “the current time” the moment when the simulated MW and M 31 reached the observed separation for the first time after coming through their first relative apocenter (and the observed radial and tangential velocities are also reproduced by design, see Sect. 2.4). The current time occurred 7411 Myr after the simulation start. In Table 2 we compare the main galaxy and orbital characteristic in the simulation at the current time to the adopted real values.
The time evolution of the galaxy separation and relative velocity magnitude are drawn in Fig. 5. The vertical dashed line indicates the current time. The first pericentric passage in our simulation occurred 6.8 Gyr before the current time when the galaxy separation was 24 kpc and the relative velocity reached 637 km s−1. To make a comparison to the method used by Z13, we analytically integrated the orbit backward using the two-body-force formula Eq. (12) and the galaxy masses as in our simulation. This resulted in a pericentric passage that surprisingly was closer to today by only 0.06 Gyr compared to the self-consistent simulation. The next pericentric passage in the self-consistent simulation occurred 3.1 Gyr after the current time. For comparison, the ΛCDM simulation by van der Marel et al. (2012a) gives the first future pericentric approach of the MW and M 31 in around 3.9 Gyr and the final merger in 5.9 Gyr from now. The galaxies were still far from merging at that time in our MOND simulation because of the reduced dynamical friction; the reason is that no particle dark matter halos occur. The times of the important orbital events in the simulation are listed in Table 3 along with the respective galaxy separations and relative velocity magnitudes. We recall that these times would change significantly if the EFE and the cosmic expansion were taken into account (see Z13).
We plot in Fig. 10 the ratio of the relative acceleration magnitude of the galaxies measured from their velocity change in the simulation to the acceleration calculated using the two-body-force formula Eq. (12) as a function of the galaxy separation color-coded according to the simulation time. Only the period between the first and second pericentric passage is plotted. The initial galaxy masses were assumed for the analytic calculation. Here we note several unexpected facts: 1) the acceleration ratio was different for the receding (blue) and approaching (green and yellow) partof the orbit, 2) the major up-wiggles in the receding part were followed by similar down-wiggles in the approachingpart when the galaxies had the same separation, and 3) the acceleration ratio evolved in time even in the apocenter when the separation changed only slightly. We leave the explanation of these effects for future investigations.
Figure 6 shows a few snapshots from our simulation at different simulation times. The videos showing the simulation projected along the X, Y, and Z axes are available online3. The projections of the simulation along the X, Y, and Z axes at the current time show Figs. 7, 8, and 6d, respectively. It might appear from these plots that the simulated galaxies are too large at the current time compared to the real MW and M 31, but this is an effect of the logarithmic color scale we used. The surface density profiles of the simulated galaxies at the current time are shown in Figs. 3 and 4. A comparison with the second row of Fig. 5 by Yin et al. (2009) shows that the surface density profiles are correct within an order of magnitude. Whether the real MW disk has a break beyond around 12 kpc is a matter of ongoing debate (Bland-Hawthorn & Gerhard 2016; Carraro 2015).
We can see that the encounter induced the formation of tidal tails in the MW (see Bournaud 2010 for an explanation of the tidal tail formation mechanism). One of the tidal tails in our simulation was ejected from the MW toward M 31, where part of it was captured. The remaining part was captured by the MW. This formed tidal structures visible in the simulation at the current time around both galaxies. The bridge connecting the MW and M 31 has been visible for around 4 Gyr. The other tidal tail was completely captured by the MW. There were no particles receding from the LG barycenter by more than a few hundred kiloparsec (no escaping particles were possible because the escape speed from isolated objects in MOND is infinite). Only minor hints of tidal tails were induced in M 31. When we define the transferred matter as the particles that belonged to one galaxy at the beginning of the simulation and belonged to the other galaxy at the current time, 3.2% of MW mass was transferred to M 31 and no mass was transferred in the opposite direction.
Three or four temporal TDGs could be visually detected to form in the tidal tails in the simulation (Fig. 9 is a magnified version of Fig. 6c, providing a detailed view of the TDGs). We note that the number of TDGs formed in the simulation would most probably increase if gas and star formation were included since the gas cooling facilitates the formation of gravitationally bound objects. The two TDGs in the tail pointing to M 31 were captured to become satellites of M 31. One or two TDGs formed in the tidal arm that initially pointed away from M 31 and stayed bound to the MW. This simulation therefore confirms the earlier finding that TDGs easily form during galaxy interactions in MOND. However, Wetzstein et al. (2007) found that in Newtonian gravity, the formation of the TDGs should be studied only in simulations containing gas (see Sect. 4 for more details). Nevertheless, MOND simulations with gas indeed show TDGs forming in tidal tails (see, e.g., Figs. 2 and 3 in Renaud et al. 2016), so that the MW and M 31 could be enriched by new satellites in the way suggested by our simulation. The relation of the satellites to the tidal streams here is partly opposite to the classical view: here the streams existed first and collapsed temporarily into the TDGs before the TDGs were disrupted into streams again when the tidal forces and the EFE increased (the satellite disruption in MOND was detailed by Brada & Milgrom 2000a).
To assess how the galaxy radial profiles, including the half-mass radii, evolved from the initial state to the current time, we made Figs. 11 and 12 for the MW and for M 31, respectively. These plots show the ratio of the Lagrangian radius for the current time to the Lagrangian radius at the simulation start for every mass on the horizontal axis for the respective galaxy (a Lagrangian radius is the radius enclosing a given mass). These plots imply for both galaxies that the half-mass radii almost did not change, while the galaxy centers shrunk and the outer parts expanded. This might be related to bulge formation.
The rotation curves of the MW and M 31 at the beginning of the simulation and at the current time are displayed in Figs. 1 and 2. To obtain the rotation velocity v at some galactocentric radius r, we chose all particles with a galactocentric distance between r − 0.5 kpc and r + 0.5 kpc and with a distance from the galaxy midplane shorter than 0.5 kpc. Then we calculated their average radial acceleration arad from their velocity change between the subsequent time steps and calculated the rotational speed 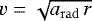 . The rotation curves can be compared toobservations in Bland-Hawthorn & Gerhard (2016) for the MW and in Carignan et al. (2006) for M 31. The difference is typically 10–20%.
. The rotation curves can be compared toobservations in Bland-Hawthorn & Gerhard (2016) for the MW and in Carignan et al. (2006) for M 31. The difference is typically 10–20%.
For what follows, we needed to define in the simulation at the current time the position and velocity of the Sun and analogs of the equatorial and the Galactic coordinate systems. The Sun lay at the point meeting the following conditions: 1) it lay in the MW midplane, 2) its distance from the MW center was 8.5 kpc, and 3) in the obvious analog of the Galactic coordinate system in the simulation, M 31 had the observed Galactic longitude. The MW north pole direction in the simulation was defined as the opposite vector to the MW spin, just as in the real MW. We defined the equatorial coordinate system connected with the Sun so that the MW center and its pole had the observed coordinates in it. We assumed that the Sun’s orbital velocity vector lay in the MW disk midplane, was perpendicular to the direction to the MW center, and agreed with the net rotation sense of the galaxy.
Figure 13 shows the projection of the particles belonging to M 31 as seen from the Sun at the current time. It is colored according to the average line-of-sight velocity with the systemic velocity subtracted. Here north is up and west is right to facilitate the comparison to real images of M 31, such as Fig. 14 or Fig. 15. We note several interesting features here: 1) the tidal structures around M 31, formed exclusively by the material coming from the MW, contain a pronounced planar sub-structure seen edge-on from the Sun that resembles the GPoA. A remnant of a dissolved TDG lies in this plane. 2) The radial extent of this plane, as seen in this projection, is 200–400 kpc. This corresponds to the radial extent of the GPoA (Fig. 14, see also Fig. 3 by Kroupa 2015 for a projection where it appears larger). 3) The receding part of the M 31 disk lies in the northern half of the galaxy. This is a trivial consequence of our simulation being set to approximately reproduce the galaxy inclinations. 4) The approaching part of the planar feature in the simulation lies in the same half of M 31 as its projected spin. This is also the case for the GPoA (Fig. 14). 5) There are clouds of high-velocity particles near the M 31 disk. They are probably particles on eccentric orbits near their pericenters. The angle between the planar feature and the simulated MW disk was around 40°, while the GPoA is perpendicular to the MW disk. The simulation thus shows that an MW–M 31 encounter can produce a planar feature in M 31 that easily resembles the GPoA in several aspects. On the other hand, we will demonstratein a next paper using restricted three-body simulations that the morphology of the tidal structures formed by such an encounter depends sensitively on the choice of free parameters.
It is thus possible that a change of some free parameters would affect the morphology of the tidal structures similarly to viewing the simulated M 31 from another direction. This is shown in Figs. 6d–8. We highlight the similarity of the tidal structures around the simulated M 31 in Fig. 6d to the tidal features in the real M 31 (Fig. 15), which have a similar size and stream-like morphology, and are joined to some of the satellites.
The tidal material formed a less distinct planar substructure around the MW at the current time. Figure 16 shows an edge-on view of both the flattened feature and the modeled MW disk. The radial extent of this feature is around 200 kpc. The radial extent of the VPOS is also around 200 kpc, see Fig. 3 by Pawlowski et al. (2015b). Unlike the VPOS, this SP candidate is not polar. There are no polar structures in our simulated MW. The angle between the SP candidate around the MW and the MW–M 31 connecting line was around 10° in our simulation, meaning that it was oriented almost edge-on toward M 31. This alignment is even better than that for the real objects. TheSP candidate here rotates in the opposite sense to the SP in the simulated M 31. In the real case, the VPOS and the GPoA rotate in the same sense.
Figure 17 shows the Aitoff projection of our simulation from the position of the Sun in our Galactic coordinate system at the current time (compare to Fig. 1 of Pawlowski et al. 2015b). The particles belonging to M 31 are shown in green. The red particles belong to the MW and have a vertical distance from its midplane higher than 50 kpc. They mostly belong to our SP candidate (compare to Fig. 16). The remaining MW particles are shown in blue. We also plot the velocities of the red particles projected on the plane of the sky using the assumed orbital velocity of the Sun. Figure 17 shows that most of the red particles form a coherent structures in phase space (i.e., nearby particles have similar velocities). In this regard, our SP candidate was similar to the VPOS.
The mass transferred in the simulation to M 31 was 2 × 109 M⊙. This matches the mass of the real M 31 streams by an order of magnitude, 8 × 109 M⊙, or the total mass of its halo, 11 × 109 M⊙ (Ibata et al. 2014b). This is a surprisingly good match given that the simulation was not tuned for this. The structures around the simulated MW could be morphologically classified as streams, several of which appear around the real MW (Fig. 5 by Pawlowski et al. 2012 shows several examples and their sizes). To obtain the mass of the MW halo in the simulation, we counted the particles that lay farther than 50 kpc off the MW disk midplane. This limit was chosen as the height of what visually appeared as the warped disk, see Fig. 16. We found that these particles constitute only 0.086% of the total MW mass. The real baryonic halo mass fraction of the MW is around ten times higher, around 1% (Bland-Hawthorn & Gerhard 2016). Another choice of the free parameters or a less simplified simulation might lead to a better match. This result can also mean that the MW halo was formed by a mechanism unrelated to the MW–M 31 encounter. That the galaxy halo formation mechanism is not universal is suggested by the observational finding by Merritt et al. (2016), who reported that galaxies with an MW luminosity have a wide variety of halo mass fractions.
The outer regions of our simulated MW were warped as shown in Fig. 19. This figure shows the median elevation of particles above the MW midplane calculated using the bins indicated in the figure by the colored annular sectors. The MW is seen from the north Galactic pole here. The Sun lies at 0° and 8.5 kpc. An edge-on view maximizing the visibility of the warp is shown in Fig. 20. The disk of the real MW is also warped, see Fig. 18, showing the elevation of its H I disk. The position of the Sun is marked by its symbol. The elevation here is measured above the agreed Galactic midplane having the Galactic latitude of b = 0°. We note several similarities to our simulation here. 1) The Sun lies approximately on the line dividing the raised and lowered halves of the disk, and these halves lie on the correct sides of the galaxy. We recall that the position of the Sun in the simulation was defined using the position of M 31. 2) The range of elevation in the simulation, about − 3 to 2 kpc, was surprisingly close to the real range, which is about −1 to 6 kpc. We note that this elevation was reached in the simulation at somewhat larger radii. In the context of MOND, the MW warp has previously been suggested to originate from the EFE exerted by the Large Magellanic Cloud, which can explain both its orientation and approximate magnitude (Brada & Milgrom 2000b). The EFE and the encounter therefore probably shape the warp together in the context of MOND.
It was suggested by Z13 that the MW–M 31 encounter could have contributed to the growth of the MW thick disk (but it was probably not the only contribution since thick disks are observed in most disk galaxies, see, e.g., Yoachim & Dalcanton 2006 or Comerón et al. 2012). We thus studied the evolution of the thicknesses of the galaxies in our simulation. We defined the thickness of a disk as the height of a layer centered on the galaxy midplane enclosing a given fraction of particles. We considered only the particles whose projections to the galactic midplane were near to the solar radius, namely with a distance between 7.5 and 9.5 kpc from the galactic center. Figure 21 (resp. Fig. 22) shows the evolution of the MW (M 31) thickness for the threshold heights enclosing 25, 50, or 75% of the particles. The thickness was divided for every time by the analogous thickness extracted from a simulation where the respective galaxy evolved in isolation in order to filter out the secular thickness growth. Only the time period between the simulation start and the current time is displayed. The vertical dashed line marks the time of the closest approach. A galaxy encounter thus adds to the list of mechanisms that can cause a growth in disk thickness (a review of thick-disk formation mechanisms is given in Minchev et al. 2012; see also Kroupa 2002 for a mechanism that may play a role when the star-formation rate of a thin disk is elevated, e.g. through an encounter). Greater details of this mechanism are beyond the scope of this paper.
 |
Fig. 6 Simulation snapshots. Projection along the Z-axis. The time since the beginning of the simulation is marked. Panel a: simulation starts. Panel b: galaxies are in the relative pericenter. Panel c: matter is being transferred from the MW to M 31. Panel d: the current time (the observed state is reproduced). Panel e: simulation ends. |
 |
Fig. 7 Current time. Projection along the X-axis. Simulation time of 7.4 Gyr. The MW is on the left and M 31 on the right. |
 |
Fig. 8 Current time. Projection along the Y -axis. Simulation time of 7.4 Gyr. The MW is on the right and M 31 on the left. |
 |
Fig. 9 Zoom-in of the tidal dwarf galaxies (TDGs) in the simulation at the simulation time of 2.2 Gyr. |
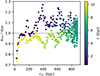 |
Fig. 10 Ratio of the relative accelerations that the galaxies have in the simulation, asim, to the acceleration calculated using the two-body-force formula (Eq. (12)), a2BF, as a function of the galaxy separation, r12. If the accelerations asim and a2BF were equal, the points would lie on the horizontal dashed line. The points are colored with respect to simulation time, t. Only the period between the first and second pericenter is displayed. |
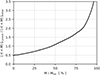 |
Fig. 11 Ratio of the radius enclosing the mass on the horizontal axis at the current time to the radius enclosing the same mass at the simulation start for the MW. |
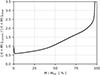 |
Fig. 12 Ratio of the radius enclosing the mass on the horizontal axis at the current time to the radius enclosing the same mass at the simulation start for the M 31. |
 |
Fig. 13 Viewof M 31 from the Sun in the simulation. The color codes the average line-of-sight velocity with the systemic velocity subtracted. Note the pronounced linear feature resembling the GPoA (Fig. 14) and the dissolving satellite in the right part (better visible in Fig. 8) similar to the dissolving satellite in Fig. 15. |
 |
Fig. 14 Satellites of M 31 (circles). The blue and red satellites belong to the GPoA. The satellites in blue are approaching Earth from the coordinate system connected with M 31, the satellites in red are receding. The arrow indicates the spin of the M 31 galactic disk. Compare to the model shown in Fig. 13. The area covered by the PAndAS survey is shown in gray to facilitate the comparison with the image of the galaxy in Fig. 15. Image courtesy Marcel Pawlowski (adapted from Fig. 11 in Bullock & Boylan-Kolchin 2017). |
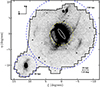 |
Fig. 15 Stellar streams around M 31 as observed by the PAndAS survey. Note the similarity to the tidal features around the simulated M 31 in Figs. 6d and 8. Image courtesy Dougal Mackey (adapted from Fig. 3 in Ferguson & Mackey 2016). |
 |
Fig. 16 Cloud of particles that formed around the simulated MW. The SP candidate is seen edge-on here. An SP that would be perpendicular to the MW galactic disk, just as the VPOS (see, e.g., Fig. 2 of Kroupa 2015) was not formed in this simulation, but the extent of the particle cloud here matches the extent of the VPOS well. |
 |
Fig. 17 Aitoff projection of all particles in the simulation seen from the position of the Sun in the Galactic coordinate system. TheM 31 particles are shown in green. The particles belonging to MW and farther than 50 kpc from the MW disk plane are plotted in red. The other MW particles are shown in blue. The arrows show the proper motions of the red particles as observed from the Sun in the simulation. This figure can be compared to Fig. 1 of Pawlowski et al. (2015b). |
 |
Fig. 18 Observed warp in the outer MW H I disk. The color indicates the elevation of the disk above the MW midplane (b = 0°). The ⊙ symbol marks the position of the Sun. Image courtesy of Leo Blitz (adapted from Fig. 2 of Levine et al. 2006). |
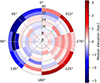 |
Fig. 19 Vertical elevation of the MW particles above the plane fitted to the inner 15 kpc of the galaxy. The Sun lies at 0° and 8.5 kpc. The radial scale in kiloparsecs is indicated on the vertical axis. The simulated MW disk is warped similarly to the disk of the real MW, see Fig. 18. |
4 Discussion
4.1 Simplifications in the simulation
We discuss some simplifications of our simulation and estimate their consequences.
The effect of a large-scale external field on the encounter can be estimated by considering the radii where the external acceleration is comparable to the acceleration from our galaxies. For a point mass M, the deep-MOND limit acceleration is 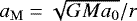 (Milgrom 1983). This is equal to the external acceleration ae at the isolation radius
(Milgrom 1983). This is equal to the external acceleration ae at the isolation radius
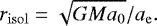 (14)
(14)
Within this radius, the dynamics of a galaxy is relatively unaffected by the external field (Bekenstein & Milgrom 1984; Milgrom 2013, 2014). The external field acting on the LG is likely a few hundredths of a0 (Famaey et al. 2007; Wu et al. 2008) and comes mostly from the Virgo and Coma galaxy clusters and from the Great Attractor. The value of risol could, of course, vary with cosmic time – partly because of the growth of structure and partly because of the possible variations of a0 (Milgrom 1983, 2015a, 2017). For the value ae = 0.03 a0, used by Z13, and our masses of the MW and M 31 (Eqs. (4) and (5)), Eq. (14) gives the MW and M 31 isolation radii of 280 and 460 kpc, respectively. These values are comparable with the sizes of the tidal structures in our simulation so that the large-scale gravitational field could affect the formation of TDGs, for instance. According to Table 1 by Z13, including a realistic external field shifts the pericentric passage into the past by 2–4 Gyr since the EFE reduces the gravitational attraction between the galaxies. A qualitatively similar effect is achieved by the including the cosmic expansion. The change in pericentric velocity and distance would influence the formation of tidal tails. We note that in order to study whether high-velocity galaxies of the LG could be reproduced (Banik & Zhao 2017, 2018), the external field should not be neglected.
A few TDGs formed in our simulation. Wetzstein et al. (2007) found that TDGs formed in their Newtonian gas-less N-body simulations only if the number of particles was too low as a consequence of particle noise. When gas was included in their simulations, TDGs formed even with a high number of particles. While the situation can be different in MOND, we recommend considering the TDGs in our simulation with reservation for the moment. Nevertheless, probably allsimulations of galaxy encounters in MOND with gas published so far produced several TDGs (Tiret & Combes 2007; Renaud et al. 2016; Thies et al. 2016). There was likely enough gas in the MW and M 31 around 10 Gyr ago. For example, Tacconi et al. (2010) found that the galaxies at z = 1.2 with masses of around 1011 M⊙ contained 34% of their baryonic mass in molecular gas on average.
Further dwarf galaxies could be descendants of the large gas clouds with masses of up to 109 M⊙ that are observed in galaxies at redshifts greater than about one (e.g., Dessauges-Zavadsky et al. 2017; Soto et al. 2017; Fisher et al. 2017). If some of these clouds were ejected into the tidal tails without being destroyed, they could evolve into dwarf galaxies.
For the models of our galaxies, we approximately used their current masses, disk sizes, inclinations, and density distributions. These quantities were likely different at the time when the pericentric passage is supposed to have occurred. There is evidence that galaxies gain mass by accretion of intergalactic gas (e.g., Sancisi et al. 2008). Assuming that the MW and M 31 evolved along the main star-forming sequence, we can estimate their masses in the past. Then it follows from Fig. 3 of Leitner (2012) that the MW and M 31 masses were lower by 30% than today 7 Gyr ago and that these masses were lower by more than 80% than today before 10 Gyr. These numbers apply if the ΛCDM relation between the redshift and the look-back time works well. It is questionable how this acquired mass and the momentum it brought influenced the trajectories of the galaxies and the inclinations of the disks. Effective radii of galactic disks seem to have evolved only little since the redshift of z = 1, while the disk outskirts, as measured by the Petrosian radius, seem to expand substantially with the cosmic time (van Dokkum et al. 2013; Sachdeva et al. 2015). If the galaxies had a greater extent, we expect the tidal arms to be more massive and to be forming more TDGs.
It is of course possible that several galaxy interactions, or other mechanisms, formed the observed SPs in the LG. For example, some of them could have been formed by the mechanism suggested by Hammer et al. (2013) and Fouquet et al. (2012).
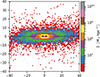 |
Fig. 20 Edge-on view of the warp in the simulated MW. The horizontal line marks the MW midplane. |
 |
Fig. 21 Thickness growth of the MW with time in the simulation of the encounter. The thickness is displayed normalized to the thickness of the MW in the simulation in isolation. The disk height was defined as enclosing either 25, 50, or 75% of the particlesin the vertical direction. Only particles close to the solar radius (8.5 kpc) were considered in the calculation. The dashed line marks the instant of the closest approach of MW and M 31. |
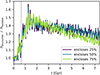 |
Fig. 22 Thickness growth of M 31 with time in the simulation of the encounter. The thickness is displayed normalized to the thickness of M 31 in the simulation in isolation. The disk height was defined as enclosing either 25, 50, or 75% of the particles in the vertical direction. Only particles close to the solar radius (8.5 kpc) were considered in the calculation. The dashed line marks the instant of the closest approach of MW and M 31. |
4.2 Comparison to observations
We described in Sect. 3 that the simulation reproduced some of the features observed in the LG without being tuned for this. To repeat, they were that the encounter led to the formation of tidal structures around the MW and M 31 that resembled the VPOS and GPoA in their sizes and in that they formed continuous structures in phase space. The tidal structure around the simulated M 31 contained a distinct planar substructure. This substructure is similar to the GPoA in that it points toward the MW by its edge, in its size, and in its the sense of rotation. The tidal structures at the simulated M 31 could be alternatively matched with the tidal features at the real M 31 because they have a similar extent and stream-like morphology, and, to within an order of magnitude, also the mass. The simulated MW disk was warped just like the real one. The nodal line had a similar orientation with respectto the MW–M 31 connecting line, and the amplitude of the warp was comparable. The encounter caused a vertical thickening of the galactic disks in the simulation. This might have contributed to the thick-disk formation, as suggested by Z13.
One of the driving questions for our work was whether the observed SPs in the LG and their special properties are a simple consequence of the MW–M 31 encounter in MOND. The VPOS and GPoA have four special properties: 1) the VPOS is perpendicular to the MW disk, 2) the edge of the GPoA points toward the MW, 3) the GPoA is perpendicular to the MW disk, and 4) the VPOS and GPoA rotate in the same sense. Of these properties, our simulation reproduced only property 2). We do not know how the simulation would need to be modified to guarantee that the remaining points are reproduced. The SP candidate around our simulated MW is also much less distinct than the VPOS. The two non-satellite dwarf galaxy planes discovered by Pawlowski et al. (2013) were not reproduced at all. Our simulation thus demonstrates that the MW–M 31 encounter in MOND does not lead to the formation of all observed properties generically. Future attempts to reproduce them by the MW–M 31 encounter in MOND will have to tune the free parameters.
Here we summarize the other observations that are consistent with the past MW–M 31 encounter that do not relate directly to our simulation. Deep optical imaging of nearby galaxies with stellar masses similar to that of the MW by Merritt et al. (2016) revealed that the MW and M 31 stellar halos are unusually massive and that the halo of M 31 is exceptionally structured. It was calculated by Z13 that when the MW–M 31 encounter was supposed to have occurred, the Large and Small Magellanic Clouds were almost in the pericenter of their orbit with respect to the MW. The classical bulge possessed by M 31 could be another encounter sign. In ΛCDM, classical bulges are supposed to mostly be merger products or to form from giant gas clouds that are transported to the galaxy center by dynamical friction against the dark matter halo (Gadotti 2012). We suggest that the bulge could form by the inward gas flow produced by gravity torques during galaxy encounters that accompanies the formation of tidal tails (Mihos & Hernquist 1996; Bournaud 2010). Bernard et al. (2015) found that while the stellar populations older than 8 Gyr constitute over 50% of the stellar mass in the stream-like structures in M 31, stellar populations of this age constitute only 38% of the disk regions. This fact is consistent with the encounter hypothesis since star formation in the tidal material would probably be reduced after diluting a small portion of the mother galaxy to a large space. The same can be said about the result by Tenjes et al. (2017) that the spiral structure in M 31 has an external origin. The star clusters associated with the VPOS (the young halo globular clusters) are around 9–12 Gyr old (Pawlowski et al. 2012), which agrees with the time since the encounter of 7–11 Gyr estimated by Z13. A past encounter between the MW and another galaxy, such as M 31, can naturally explain the satellites orbiting in the VPOS, but in the opposite sense as the majority of the VPOS members (Pawlowski et al. 2011). The TDGs likely form from a mix of gas and the stars of the mother galaxy. The metal-enriched gas can cool, collapsing into a compact core of new stars. The pre-existing stars cannot dynamically cool, and their apocenters stay far away from the core. We thus expect an age and metallicity gradient in TDGs with the younger and more metal rich stars atthe center. This is indeed observed (e.g., Battaglia et al. 2012; Kacharov et al. 2017; Okamoto et al. 2017).
We know of one observation that may be inconsistent with some of the MW satellites being TDGs. We expect that TDGs cannot capture many globular clusters (GCs) of their mother galaxies for the same reason as they cannot contain much dark matter, that is, the GCs move so fast in the mother galaxy, in equilibrium with its strong gravitational field, that they would quickly escape from the shallow potential wells of the TDGs. Thus, if the observed satellites are TDGs, then they should not contain many GCs that are older than the encounter that formed the TDGs. According to Z13, the MW–M 31 encounter in MOND occurred 7–11 Gyr ago. Mackey & Gilmore (2003) compiled the age estimates of the GCs of the Fornax and Sagittarius dwarfs based on stellar population models. In their Table 3, all five Fornax GCs and three of four Sagittarius GCs are older than 11 Gyr, and six of all these nine GCs are older than 14 Gyr. The youngest age estimates of the Fornax GCs that we were able to find were published by de Boer & Fraser (2016), who derived that the star formation peaked around 12 Gyr ago for four Fornax GCs and 11 Gyr for the remaining one. We can see that the age estimates have a substantial scatter. Another possibility might be that the MW and M 31 had lower masses in the past, which is probable (Sancisi et al. 2008). The effect of mass growth was not taken into account by Z13. With lower masses, the galaxies would have the encounter a longer time ago.
There is of course the possibility that some of the observed peculiarities in the LG might have an origin unrelated to the MW–M 31 encounter, even if MOND holds true.
The question remains whether the MOND encounter mechanism is able to produce all the observed satellite planes (Sect. 1). If it is the case, then we should be able to find another galaxy for every galaxy with a satellite plane that has experienced a close encounter with it. As Kroupa (2015) has pointed out, galaxies that have experienced an encounter in the early universe might appear unrelated today. For example, if the galaxies interacted 10 Gyr ago and their average relative velocity was 100 km s−1 (compare toFig. 5), then they would be separated by 1.0 Mpc today. Another requirement for producing a satellite plane might be a suitable orbit and inclination of the encountering galaxies. Whether this is a serious restriction for forming satellite planes is to be clarified by future work.
To discuss the formation of the SPs beyond the LG by the encounter mechanism, it might be important that the planar structure that formed around the simulated M 31 was a transient feature in the current model (as can be seen in the video of the simulation): the tidal arm captured by M 31 formed streams around M 31 whose shape evolved with time as their particles moved along their Rosetta orbits.
4.3 Tidal features in galaxies as encounter remnants
In the hierarchical galaxy formation scenario, massive galaxies are assembled by the merging of lighter galaxies. The observed tidal features in galaxies are often claimed to support this scenario. Our simulation demonstrated at least in the MOND framework that some of these tidal features can be formed by galaxy encounters that do not end by a merger in a Hubble time. These tidal features are formed by the material exchanged between the encountering galaxies. This material can likely transform into TDGs, some of which might then be accreted onto the original galaxies in minor mergers. Thus, observing tidal features and dwarf galaxies being disrupted cannot be considered as unambiguous evidence for the hierarchical galaxy formation scenario. If MOND holds true, a substantial fraction of tidal features might have been produced by this mechanism because, as our simulation proved, dynamical friction can be insufficient for the merging of closely encountering galaxies, and numerous close galaxy pairs are observed (see, e.g., Fig. 4 by Chou et al. 2012). This mechanism seems to be much more favored in MOND than in ΛCDM since the effective dynamical friction in the latter would probably soon cause any galaxies to merge that were able to exchange their baryons (see Sect. 4.4). A possible insufficiency of this consideration is that cosmological simulations in MOND have to be made to see what typical galaxy encounter velocities this framework implies: if the encounter velocity is too high, then no material can gain enough momentum to leave its mother galaxy.
4.4 MW–M 31 encounter in ΛCDM?
It seems unlikely in ΛCDM that the MW and M 31 could have had an encounter that would have any significant effect on their galactic disk because of the efficient dynamical friction. Many if not all simulations reproducing the morphology of observed interacting galaxies in ΛCDM lead to a merger in a few Gyr after the first pericenter (see, e.g., Fig. 1 of Privon et al. 2013). This fast merging is confirmed when we use Eq. (6) by Jiang et al. (2014), which gives the average merging time of two galaxies with given properties according to ΛCDM cosmological simulations. To obtain a rough estimate of the merging time for the hypothesized MW–M 31 past encounter, a redshift of 1, virial masses of both galaxies of 1011 M⊙, and a separation of 70 kpc can be substituted. This leads to the merging time of only 0.9 Gyr. To make sure that this equation is applicable to the LG, we used it to obtain the time to the future MW–M 31 merger. Substituting the redshift of zero, the virial masses of 1012 M⊙, and the current distance of 774 kpc, the equation gave the merging time of 6.6 Gyr, which agrees well with the MW–M 31 merger in 5.9 Gyr in the simulation by van der Marel et al. (2012a).
The fast merging is grounded in the classical timing argument for the LG (originally proposed by Kahn & Woltjer 1959). It states that the MW and M 31 had to have exactly one close encounter in the past, and this is at the Big Bang. Then the galaxies were exposed to the Hubble flow and mutual gravitational attraction. If we assume that the masses of the galaxies did not change over time and require that the current galaxy separation and relative velocity are reproduced, the total mass of the LG can be deduced. This provided one of the first indications of the missing-mass problem.
It is interesting to note here that the relative trajectory of the MW and M 31 is surprisingly different in MOND and ΛCDM, even if both frameworks have to account for the observed dynamics of the galactic disks. When we analytically integrated the MW–M 31 backward assuming the MOND two-body-force formula Eq. (12), we obtained the pericenter 7 Gyr ago (Sect. 3). When we replaced Eq. (12) by Newton’s law and assumed point masses of 2.1 × 1012 M⊙ (more than most of the recent estimates on the MW and M 31 virial masses), we obtained the pericenter 14 Gyr ago. The reason is that the gravitational field is different far away from the galaxy centers.
5 Summary
The paradigm of MOND proved that it can predict the dynamics of galaxies from the baryonic matter distribution (see Famaey & McGaugh 2012 for a review). When applied to the Local Group (LG), Zhao et al. (2013) found using an analytic calculation that the Milky Way (MW) and Andromeda (M 31) galaxies had a close encounter 7-11 Gyr ago. Such an encounter can potentially explain many observed phenomena in the LG. It was suggested that the encounter could explain why many dwarf satellites in the LG are concentrated on several planes (the satellite planes, SPs) which have special orientations with respect to the MW, M 31, and each other. The satellites lying in the planes around the MW and M 31 (called the VPOS and the GPoA, respectively) moreover orbit in these planes, and most of them in the same sense. Such a configuration has so far not been satisfactorily explained in the standard ΛCDM cosmology model.
Here we explored the history of the LG in MOND by performing the first-ever self-consistent collisionless simulation of the MW–M 31 encounter in MOND using the publicly available adaptive-mesh-refinement code Phantom of RAMSES (Lüghausen et al. 2015). We set up the initial condition so that the simulation approximately reproduces at a certain time the observed separation of the galaxies, their relative velocity, effective radii, masses, and inclinations (Sect. 2). Table 2 shows the deviations of these quantities from the observed values, and Table 1 the initial conditions we found. The galaxies came through pericenter 6.8 Gyr before reproducing the observed state (Sect. 3). At the pericenter, their separation reached 24 kpc and had a relative flyby velocity of 636 km s−1. The encounter did not come even close to merging after more than 13 Gyr after the first encounter when our simulation ends. The reason is that extensive and massive dark matter halos do not exist in MOND.
The simulated encounter led to the transfer of 3% of the MW mass to M 31 along a tidal tail (Sect. 3 and Fig. 6c). The other parts of the tidal tails were captured by the MW. No particles escaped, possibly because we neglected to include the external field acting on the Local Group such that the escape speed is infinite. The encounter formed clouds of particles around the simulated MW and M 31. The mass of the cloud that formed at the simulated M 31 was close to the real baryonic halo mass of M 31. The baryonic halo mass fraction came out ten times smaller than observed for the simulated MW. The clouds of particles around the simulated galaxies had a stream-like structure. They could be interpreted as the tidal streams observed around the MW and M 31 (Fig. 15) because their extent and morphology are similar (compare Fig. 6d and Figs. 8–15).
At the time when the simulation reproduced the observed MW–M 31 separation and relative velocity, the matter transferred to the simulated M 31 was forming a planar structure that resembled the GPoA (Figs. 13 and 14) in size, in being oriented by its edge toward the simulated MW, and in the same sense of rotation. A less distinct flattened structure formed at the simulated MW with the extent of the VPOS (Fig. 16).
The encounter induced a disk warp in the simulated MW that is very similar to the observed warp (Figs. 18 and 19): the zero-elevation line had the correct orientation with respect to the direction toward M 31 and the warp had the correct magnitude. The encounter induced a thickening of the galaxies in the simulation. The real encounter thus might have contributed to the formation of the thick disks in the MW and M 31.
On the other hand, not all properties of the VPOS and the GPoA were reproduced, for example, a distinct SP around the MW perpendicular to its galactic disk was missing, or the planar feature around the simulated M 31 was not perpendicular to the MW galactic disk, as it is the case with the GPoA. The two planes formed by non-satellite LG dwarfs discovered by Pawlowski et al. (2013) were not reproduced at all.
Here we see that the MW–M 31 encounter in MOND has the potential to explain many peculiarities of the LG, but the match is not perfect at this point. Our simulation included various simplifications (Sect. 4.1, e.g., we neglected the cosmic expansion, the mass growth of the galaxies, or the gas in the galaxies). Future investigations should address whether the simulations of the MW–M 31 encounter in MOND can be made to reproduce the observationsprecisely. A recent work by Banik et al. (2018) has shown that planes of rotating tidal debris can be produced by the encounter in restricted three-body simulations with correct orbital poles. Some peculiarities of the LG may be unrelated to the MW–M 31 encounter, even if MOND is correct.
In addition to the main line of our investigation, the simulation revealed the unexpected possibility that tidal features in galaxies (not only in the LG) can be formed by mass exchange between encountering non-merging galaxies (Sect. 4.3). Tidal features observed in galaxies thus cannot be considered as unambiguous proof that galaxies grow predominantly by merging.
Movies
Movie of Fig. 6: LGx Access here
Movie of Fig. 6: LGy Access here
Movie of Fig. 6: LGz Access here
Acknowledgements
The authors thank Marcel Pawlowski, Leo Blitz, Dougal Mackey, and Annette Ferguson for the provided figures. We appreciate the help by Guillaume Thomas with processing the RAMSES output. We thank Indranil Banik and Mordehai Milgrom for their useful comments and suggestions.
Appendix A Stability of our models
In order to explore the stability of our initial galaxy models, we let them evolve in isolation using the same computational setup as the main simulation, which is the same setup as is summarized in Table 1. Figures A.1–A.4 show the evolution of the MW model in isolation: Fig. A.1 is the start of the simulation (0.0 Gyr), Fig. A.2 shows the model at the time when the galaxies were in pericenter in the main simulation (0.65 Gyr), and Fig. A.3 after twice as much time (1.3 Gyr). A stable state was established approximately there, so that the galaxy did not evolve much until the time corresponding to the current time in the main simulation (7.4 Gyr); see
Fig. A.4. Figures A.5–A.8 display the same for M 31, whose evolution was qualitatively similar. We constructed the plots of the Lagrangian radii at these moments in Fig. A.9 for the MW and in Fig. A.10 for M 31.
To summarize, there was a short period of disk virialization that lasted for about 1 Gyr for both the MW and M 31 model. During this time, a bar developed, and spiral arms appeared and disappeared. The galaxies subsequently evolved only little. Importantly, there were no escaping particles, and the galaxy half-mass radii changed negligibly.
 |
Fig. A.1 Milky Way model simulated in isolation at the simulation start (0.0 Gyr). |
 |
Fig. A.2 Milky Way model simulated in isolation at the time when the MW and M 31 came through the pericenter in the main simulation (0.65 Gyr). |
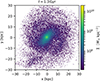 |
Fig. A.3 Milky Way model simulated in isolation at twice the time when the MW and M 31 came through the pericenter in the main simulation (1.3 Gyr). |
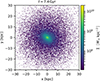 |
Fig. A.4 Milky Way model simulated in isolation at the time corresponding the current time in the main simulation (7.4 Gyr). |
 |
Fig. A.5 M 31 model simulated in isolation at the simulation start (0.0 Gyr). |
 |
Fig. A.6 M 31 model simulated in isolation at the time when the MW and M 31 came through the pericenter in the main simulation (0.65 Gyr). |
 |
Fig. A.7 M 31 model simulated in isolation at twice the time when the MW and M 31 came through the pericenter in the main simulation (1.3 Gyr). |
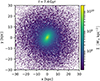 |
Fig. A.8 M 31 model simulated in isolation at the time corresponding the current time in the main simulation (7.4 Gyr). |
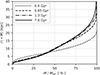 |
Fig. A.9 Lagrangian radius for the model of the MW evolving in isolation as a function of the enclosed mass. Each line corresponds to the time indicated in the figure legend. |
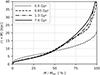 |
Fig. A.10 Lagrangian radius for the model of M 31 evolving in isolation as a function of the enclosed mass. Each line corresponds to the time indicated in the figure legend. |
References
- Angus, G. W. 2008, MNRAS, 387, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., van der Heyden, K. J., Famaey, B., et al. 2012, MNRAS, 421, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Banik, I., & Zhao, H. 2015, ArXiv e-prints [arXiv:1509.08457] [Google Scholar]
- Banik, I., & Zhao, H. 2017, MNRAS, 467, 2180 [NASA ADS] [Google Scholar]
- Banik, I., & Zhao, H. 2018, MNRAS, 473, 4033 [NASA ADS] [CrossRef] [Google Scholar]
- Banik, I., O’Ryan, D., & Zhao, H. 2018, MNRAS, 477, 4768 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1992, Nature, 360, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, G., Irwin, M., Tolstoy, E., de Boer, T., & Mateo, M. 2012, ApJ, 761, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Begeman, K. G., Broeils, A. H., & Sanders, R. H. 1991, MNRAS, 249, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Bekenstein, J.,& Milgrom, M. 1984, ApJ, 286, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Richardson, J. C., et al. 2015, MNRAS, 446, 2789 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F. 2010, in Galaxy Wars: Stellar Populations and Star Formation in Interacting Galaxies, eds. B. Smith, N. Bastian, S. J. U. Higdon, & J. L. Higdon, ASP Conf. Ser. (San Francisco: ASP), 423, 177 [NASA ADS] [Google Scholar]
- Bovy, J., & Rix, H.-W. 2013, ApJ, 779, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Brada, R., & Milgrom, M. 2000a, ApJ, 541, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Brada, R., & Milgrom, M. 2000b, ApJ, 531, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., & Boylan-Kolchin, M. 2017, ARA&A, 55, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Candlish, G. N. 2016, MNRAS, 460, 2571 [NASA ADS] [CrossRef] [Google Scholar]
- Candlish, G. N., Smith, R., & Fellhauer, M. 2015, MNRAS, 446, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Carignan, C., Chemin, L., Huchtmeier, W. K., & Lockman, F. J. 2006, ApJ, 641, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G. 2015, Boletín de la Asociación Argentina de Astronomía, 57, 138 [NASA ADS] [Google Scholar]
- Casas, R. A., Arias, V., Peña Ramírez, K., & Kroupa, P. 2012, MNRAS, 424, 1941 [NASA ADS] [CrossRef] [Google Scholar]
- Chiboucas, K., Jacobs, B. A., Tully, R. B., & Karachentsev, I. D. 2013, AJ, 146, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, R. C. Y., Bridge, C. R., & Abraham, R. G. 2012, ApJ, 760, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F. 2016, in Galactic Bulges (Basel: Springer International Publishing), ASSL, 418, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, S., Elmegreen, B. G., Salo, H., et al. 2012, ApJ, 759, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Widrow, L. M., McDonald, M., et al. 2011, ApJ, 739, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Crnojević, D., Sand, D. J., Spekkens, K., et al. 2016, ApJ, 823, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Dabringhausen, J., Kroupa, P., Famaey, B., & Fellhauer, M. 2016, MNRAS, 463, 1865 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., & McGaugh, S. S. 1998, ApJ, 508, 132 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, T. J. L., & Fraser, M. 2016, A&A, 590, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dessauges-Zavadsky, M., Schaerer, D., Cava, A., Mayer, L., & Tamburello, V. 2017, ApJ, 836, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & McGaugh, S. S. 2012, Liv. Rev. Rel., 15, 10 [Google Scholar]
- Famaey, B., Bruneton, J.-P., & Zhao, H. 2007, MNRAS, 377, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., & Mackey, A. D. 2016, Tidal Streams in the Local Group and Beyond (Basel: Springer International Publishing), 420, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Fernando, N., Arias, V., Guglielmo, M., et al. 2017, MNRAS, 465, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., Glazebrook, K., Abraham, R. G., et al. 2017, ApJ, 839, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Fouquet, S., Hammer, F., Yang, Y., Puech, M., & Flores, H. 2012, MNRAS, 427, 1769 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A. 2012, ArXiv e-prints [arXiv:1208.2295] [Google Scholar]
- Gentile, G., Famaey, B., & de Blok W. J. G. 2011, A&A, 527, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, F., Yang, Y., Fouquet, S., et al. 2013, MNRAS, 431, 3543 [NASA ADS] [CrossRef] [Google Scholar]
- Hees, A., Famaey, B., Angus, G. W., & Gentile, G. 2016, MNRAS, 455, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., Conn, A. R., et al. 2013, Nature, 493, 62 [CrossRef] [Google Scholar]
- Ibata, N. G., Ibata, R. A., Famaey, B., & Lewis, G. F. 2014a, Nature, 511, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., McConnachie, A. W., et al. 2014b, ApJ, 780, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Famaey, B., Lewis, G. F., Ibata, N. G., & Martin, N. 2015, ApJ, 805, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Iocco, F., Pato, M., & Bertone, G. 2015, Phys. Rev. D, 92, 084046 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, C. Y., Jing, Y. P., & Han, J. 2014, ApJ, 790, 7 [Google Scholar]
- Kacharov, N., Battaglia, G., Rejkuba, M., et al. 2017, MNRAS, 466, 2006 [NASA ADS] [CrossRef] [Google Scholar]
- Kahn, F. D., & Woltjer, L. 1959, ApJ, 130, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 1997, New Ast., 2, 139 [Google Scholar]
- Kroupa, P. 2002, MNRAS, 330, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2012, PASA, 29, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2015, Can. J. Phys., 93, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Theis, C., & Boily, C. M. 2005, A&A, 431, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitner, S. N. 2012, ApJ, 745, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., Schombert, J. M., & Pawlowski, M. S. 2017, ApJ, 836, 152 [Google Scholar]
- Levine, E. S., Blitz, L., & Heiles, C. 2006, ApJ, 643, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Libeskind, N. I., Guo, Q., Tempel, E., & Ibata, R. 2016, ApJ, 830, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Lüghausen, F., Famaey, B., Kroupa, P., et al. 2013, MNRAS, 432, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Lüghausen, F., Famaey, B., & Kroupa, P. 2015, Can. J. Phys., 93, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1976, MNRAS, 174, 695 [NASA ADS] [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2003, MNRAS, 340, 175 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2008, ApJ, 683, 137 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S., & Milgrom, M. 2013a, ApJ, 766, 22 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S., & Milgrom, M. 2013b, ApJ, 775, 139 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., & Wolf, J. 2010, ApJ, 722, 248 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Lelli, F., & Schombert, J. M. 2016, Phys. Rev. Lett., 117, 201101 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, A., van Dokkum, P., Abraham, R., & Zhang, J. 2016, ApJ, 830, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Metz, M., Kroupa, P., & Jerjen, H. 2007, MNRAS, 374, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Metz, M., Kroupa, P., & Libeskind, N. I. 2008, ApJ, 680, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Metz, M., Kroupa, P., & Jerjen, H. 2009a, MNRAS, 394, 2223 [NASA ADS] [CrossRef] [Google Scholar]
- Metz, M., Kroupa, P., Theis, C., Hensler, G., & Jerjen, H. 2009b, ApJ, 697, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1994, ApJ, 429, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2009, ApJ, 698, 1630 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2010, MNRAS, 403, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2012, Phys. Rev. Lett., 109, 131101 [Google Scholar]
- Milgrom, M. 2013, Phys. Rev. Lett., 111, 041105 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2014, MNRAS, 437, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2015a, Phys. Rev. D, 91, 044009 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2015b, Can. J. Phys., 93, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2017, ArXiv e-prints [arXiv:1703.06110] [Google Scholar]
- Milgrom, M., & Sanders, R. H. 2003, ApJ, 599, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M., & Sanders, R. H. 2007, ApJ, 658, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Jerjen, H., Pawlowski, M. S., & Binggeli, B. 2016, A&A, 595, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Scalera, R., Binggeli, B., & Jerjen, H. 2017, A&A, 602, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, O., Pawlowski, M. S., Jerjen, H., & Lelli, F. 2018, Science, 359, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Ciotti, L., Binney, J., & Londrillo, P. 2008, MNRAS, 386, 2194 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, S., Arimoto, N., Tolstoy, E., et al. 2017, MNRAS, 467, 208 [NASA ADS] [Google Scholar]
- Pawlowski, M. S. 2016, MNRAS, 456, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., & Kroupa, P. 2013, MNRAS, 435, 2116 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Kroupa, P., & de Boer K. S. 2011, A&A, 532, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pawlowski, M. S., Pflamm-Altenburg, J., & Kroupa, P. 2012, MNRAS, 423, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Kroupa, P., & Jerjen, H. 2013, MNRAS, 435, 1928 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Famaey, B., Merritt, D., & Kroupa, P. 2015a, ApJ, 815, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., McGaugh, S. S., & Jerjen, H. 2015b, MNRAS, 453, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Dabringhausen, J., Famaey, B., et al. 2017, Astron. Nachr., 338, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Ploeckinger, S., Sharma, K., Schaye, J., et al. 2018, MNRAS, 474, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Privon, G. C., Barnes, J. E., Evans, A. S., et al. 2013, ApJ, 771, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Famaey, B., & Kroupa, P. 2016, MNRAS, 463, 3637 [NASA ADS] [CrossRef] [Google Scholar]
- Richtler, T., Famaey, B., Gentile, G., & Schuberth, Y. 2011, A&A, 531, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sachdeva, S., Gadotti, D. A., Saha, K., & Singh, H. P. 2015, MNRAS, 451, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Salomon, J.-B., Ibata, R. A., Famaey, B., Martin, N. F., & Lewis, G. F. 2016, MNRAS, 456, 4432 [CrossRef] [Google Scholar]
- Samurović, S. 2014, A&A, 570, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sancisi, R., Fraternali, F., Oosterloo, T., & van der Hulst, T. 2008, A&ARv, 15, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, R. H. 1996, ApJ, 473, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H., & Land, D. D. 2008, MNRAS, 389, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, A. L., Angus, G. W., & Diaferio, A. 2010, A&A, 524, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soto, E., de Mello, D. F., Rafelski, M., et al. 2017, ApJ, 837, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Tenjes, P., Tuvikene, T., Tamm, A., Kipper, R., & Tempel, E. 2017, A&A, 600, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thies, I., Kroupa, P., & Famaey, B. 2016, ArXiv e-prints [arXiv:1606.04942] [Google Scholar]
- Thomas, G. F., Famaey, B., Ibata, R., Lüghausen, F., & Kroupa, P. 2017, A&A, 603, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiret, O., & Combes, F. 2007, A&A, 464, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiret, O., Combes, F., Angus, G. W., Famaey, B., & Zhao, H. S. 2007, A&A, 476, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B., Libeskind, N. I., Karachentsev, I. D., et al. 2015, ApJ, 802, L25 [Google Scholar]
- Vakili, H., Kroupa, P., & Rahvar, S. 2017, ApJ, 848, 55 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel,R. P., Besla, G., Cox, T. J., Sohn, S. T., & Anderson, J. 2012a, ApJ, 753, 9 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel,R. P., Fardal, M., Besla, G., et al. 2012b, ApJ, 753, 8 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Leja, J., Nelson, E. J., et al. 2013, ApJ, 771, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzstein, M., Naab, T., & Burkert, A. 2007, MNRAS, 375, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., Famaey, B., Gentile, G., Perets, H., & Zhao, H. 2008, MNRAS, 386, 2199 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2006, AJ, 131, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., & Famaey, B. 2010, Phys. Rev. D, 81, 087304 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., Li, B., & Bienaymé, O. 2010, Phys. Rev. D, 82, 103001 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H., Famaey, B., Lüghausen, F., & Kroupa, P. 2013, A&A, 557, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
An image of ARP 87 is available at https://apod.nasa.gov/apod/ap151209.html
However, see also Hees et al. (2016) for constraints in the solar system, showing that this function, as well as many others, does not approach the Newtonian regime quickly enough in strong gravitational fields.
The videos from our simulation are also available at http://galaxy.asu.cas.cz/~bilek/LGindex.html
All Tables
All Figures
 |
Fig. 1 Rotation curve of the simulated MW at the simulation start (0.0 Gyr) and at the current time (7.4 Gyr). The model was initiallytruncated at 20 kpc, but the particles spread outward as the galaxies developed bars and interacted, such that the rotation could be traced to larger distances at the later times. |
| In the text | |
 |
Fig. 2 Rotation curve of the simulated M 31 at the simulation start (0.0 Gyr) and at the current time (7.4 Gyr). The model was initially truncated at 20 kpc, but the particles spread outward as the galaxies developed bars and interacted, such that the rotation could be traced to larger distances at the later times. |
| In the text | |
 |
Fig. 3 Surface density profile of the simulated MW at the current time. |
| In the text | |
 |
Fig. 4 Surface density profile of the simulated M 31 at the current time. |
| In the text | |
 |
Fig. 5 Top: evolution of the galaxy separation, r12, with the simulation time, t. Bottom: evolution of the galaxy relative velocity magnitude, v12, with the simulation time. The vertical dashed line indicates the current time (7411 Myr). |
| In the text | |
 |
Fig. 6 Simulation snapshots. Projection along the Z-axis. The time since the beginning of the simulation is marked. Panel a: simulation starts. Panel b: galaxies are in the relative pericenter. Panel c: matter is being transferred from the MW to M 31. Panel d: the current time (the observed state is reproduced). Panel e: simulation ends. |
| In the text | |
 |
Fig. 7 Current time. Projection along the X-axis. Simulation time of 7.4 Gyr. The MW is on the left and M 31 on the right. |
| In the text | |
 |
Fig. 8 Current time. Projection along the Y -axis. Simulation time of 7.4 Gyr. The MW is on the right and M 31 on the left. |
| In the text | |
 |
Fig. 9 Zoom-in of the tidal dwarf galaxies (TDGs) in the simulation at the simulation time of 2.2 Gyr. |
| In the text | |
 |
Fig. 10 Ratio of the relative accelerations that the galaxies have in the simulation, asim, to the acceleration calculated using the two-body-force formula (Eq. (12)), a2BF, as a function of the galaxy separation, r12. If the accelerations asim and a2BF were equal, the points would lie on the horizontal dashed line. The points are colored with respect to simulation time, t. Only the period between the first and second pericenter is displayed. |
| In the text | |
 |
Fig. 11 Ratio of the radius enclosing the mass on the horizontal axis at the current time to the radius enclosing the same mass at the simulation start for the MW. |
| In the text | |
 |
Fig. 12 Ratio of the radius enclosing the mass on the horizontal axis at the current time to the radius enclosing the same mass at the simulation start for the M 31. |
| In the text | |
 |
Fig. 13 Viewof M 31 from the Sun in the simulation. The color codes the average line-of-sight velocity with the systemic velocity subtracted. Note the pronounced linear feature resembling the GPoA (Fig. 14) and the dissolving satellite in the right part (better visible in Fig. 8) similar to the dissolving satellite in Fig. 15. |
| In the text | |
 |
Fig. 14 Satellites of M 31 (circles). The blue and red satellites belong to the GPoA. The satellites in blue are approaching Earth from the coordinate system connected with M 31, the satellites in red are receding. The arrow indicates the spin of the M 31 galactic disk. Compare to the model shown in Fig. 13. The area covered by the PAndAS survey is shown in gray to facilitate the comparison with the image of the galaxy in Fig. 15. Image courtesy Marcel Pawlowski (adapted from Fig. 11 in Bullock & Boylan-Kolchin 2017). |
| In the text | |
 |
Fig. 15 Stellar streams around M 31 as observed by the PAndAS survey. Note the similarity to the tidal features around the simulated M 31 in Figs. 6d and 8. Image courtesy Dougal Mackey (adapted from Fig. 3 in Ferguson & Mackey 2016). |
| In the text | |
 |
Fig. 16 Cloud of particles that formed around the simulated MW. The SP candidate is seen edge-on here. An SP that would be perpendicular to the MW galactic disk, just as the VPOS (see, e.g., Fig. 2 of Kroupa 2015) was not formed in this simulation, but the extent of the particle cloud here matches the extent of the VPOS well. |
| In the text | |
 |
Fig. 17 Aitoff projection of all particles in the simulation seen from the position of the Sun in the Galactic coordinate system. TheM 31 particles are shown in green. The particles belonging to MW and farther than 50 kpc from the MW disk plane are plotted in red. The other MW particles are shown in blue. The arrows show the proper motions of the red particles as observed from the Sun in the simulation. This figure can be compared to Fig. 1 of Pawlowski et al. (2015b). |
| In the text | |
 |
Fig. 18 Observed warp in the outer MW H I disk. The color indicates the elevation of the disk above the MW midplane (b = 0°). The ⊙ symbol marks the position of the Sun. Image courtesy of Leo Blitz (adapted from Fig. 2 of Levine et al. 2006). |
| In the text | |
 |
Fig. 19 Vertical elevation of the MW particles above the plane fitted to the inner 15 kpc of the galaxy. The Sun lies at 0° and 8.5 kpc. The radial scale in kiloparsecs is indicated on the vertical axis. The simulated MW disk is warped similarly to the disk of the real MW, see Fig. 18. |
| In the text | |
 |
Fig. 20 Edge-on view of the warp in the simulated MW. The horizontal line marks the MW midplane. |
| In the text | |
 |
Fig. 21 Thickness growth of the MW with time in the simulation of the encounter. The thickness is displayed normalized to the thickness of the MW in the simulation in isolation. The disk height was defined as enclosing either 25, 50, or 75% of the particlesin the vertical direction. Only particles close to the solar radius (8.5 kpc) were considered in the calculation. The dashed line marks the instant of the closest approach of MW and M 31. |
| In the text | |
 |
Fig. 22 Thickness growth of M 31 with time in the simulation of the encounter. The thickness is displayed normalized to the thickness of M 31 in the simulation in isolation. The disk height was defined as enclosing either 25, 50, or 75% of the particles in the vertical direction. Only particles close to the solar radius (8.5 kpc) were considered in the calculation. The dashed line marks the instant of the closest approach of MW and M 31. |
| In the text | |
 |
Fig. A.1 Milky Way model simulated in isolation at the simulation start (0.0 Gyr). |
| In the text | |
 |
Fig. A.2 Milky Way model simulated in isolation at the time when the MW and M 31 came through the pericenter in the main simulation (0.65 Gyr). |
| In the text | |
 |
Fig. A.3 Milky Way model simulated in isolation at twice the time when the MW and M 31 came through the pericenter in the main simulation (1.3 Gyr). |
| In the text | |
 |
Fig. A.4 Milky Way model simulated in isolation at the time corresponding the current time in the main simulation (7.4 Gyr). |
| In the text | |
 |
Fig. A.5 M 31 model simulated in isolation at the simulation start (0.0 Gyr). |
| In the text | |
 |
Fig. A.6 M 31 model simulated in isolation at the time when the MW and M 31 came through the pericenter in the main simulation (0.65 Gyr). |
| In the text | |
 |
Fig. A.7 M 31 model simulated in isolation at twice the time when the MW and M 31 came through the pericenter in the main simulation (1.3 Gyr). |
| In the text | |
 |
Fig. A.8 M 31 model simulated in isolation at the time corresponding the current time in the main simulation (7.4 Gyr). |
| In the text | |
 |
Fig. A.9 Lagrangian radius for the model of the MW evolving in isolation as a function of the enclosed mass. Each line corresponds to the time indicated in the figure legend. |
| In the text | |
 |
Fig. A.10 Lagrangian radius for the model of M 31 evolving in isolation as a function of the enclosed mass. Each line corresponds to the time indicated in the figure legend. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.