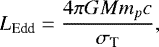| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201732235 | |
| Published online | 30 May 2018 | |
NGC 4051: Black hole mass and photon index-mass accretion rate correlation
1
LAPTh, Université Savoie-Mont-Blanc, CNRS,
B.P. 110,
74941
Annecy-le-Vieux,
France
2
Lomonosov Moscow State University/Sternberg Astronomical Institute, Universitetsky Prospect 13,
Moscow
119992,
Russia
e-mail: seif@sai.msu.ru
3
George Mason University, College of Science, 4400 University Drive,
Fairfax,
VA 22030,
USA
e-mail: achekhtm@gmu.edu
4
Dipartimento di Fisica, Università di Ferrara,
Via Saragat 1,
44122
Ferrara,
Italy
e-mail: titarchuk@fe.infn.it
Received:
4
November
2017
Accepted:
28
January
2018
We present a discovery of the correlation between the X-ray spectral (photon) index and mass accretion rate observed in an active galactic nucleus, NGC 4051. We analyzed spectral transition episodes observed in NGC 4051 using XMM-Newton, Suzaku and RXTE. We applied a scaling technique for a black hole (BH) mass evaluation which uses a correlation between the photon index and normalization of the seed (disk) component, which is proportional to a mass accretion rate. We developed an analytical model that shows the spectral (photon) index of the BH emergent spectrum undergoes an evolution from lower to higher values depending on a mass accretion rate in the accretion disk. We considered Cygnus X-1 and GRO J1550–564 as reference sources for which distances, inclination angles and the BH masses are evaluated by dynamical measurements. Application of the scaling technique for the photon index−mass accretion rate correlation provides an estimate of the black hole mass in NGC 4051 to be more than 6 × 105 solar masses.
Key words: accretion, accretion disks / black hole physics / radiation mechanisms: non-thermal / stars: black holes
© ESO 2018
1 Introduction
Determination of masses of Galactic black holes (BHs) is one of the most important tasks in modern astronomy. There are two methods for BH mass determination. One relies on determination of the mass function using optical observations. While the theoretical mass function is a function of the two masses and the inclination angle, the value of the observationally inferred mass function (the minimum possible mass of the compact object) depends only on the velocity half-amplitude K and the orbital period P and is independent of the inclination angle f(M) ∝ PK3. Orosz (2003) summarized the measurements of the rotational velocities and inclinations for 17 BH binaries.
However, this mass function method cannot be applied to active galactic nuclei (AGN) and for this case the second method of BH mass estimate using the photon index-mass accretion rate correlation (see Shaposhnikov & Titarchuk 2009, hereafter ST09) is potentially more promising because it applies only information on X-ray spectral characteristics of a compact object. It is worthwhile to point out that an evolution of the photon index for super-massive BH sources (AGN) was not systematically analyzed while the presence of fast evolution of X-ray spectral shape similar to one observed in a number of galactic BHs was reported also for AGNs (see Vaughan et al. 2011). In this paper we present a detailed analysis of X-ray spectral evolution in the AGN NGC 4051 and its application for a BH mass estimate.
Observational appearances of BHs in Galactic sources is conventionally described in terms of the BH spectral state classification (see Remillard & McClintock 2006; Belloni 2005; Klein-Wolt & van der Klis 2008, for different flavors of BH states definitions). A general BH state classification for five major BH states: quiescent, low-hard (LHS), intermediate (IS), high-soft (HSS) and very high states (VHS) is accepted by the community. When a BH transient goes into outburst it leaves the quiescent state and enters the LHS, a low luminosity state with the energy spectrum dominated by the thermal Comptonization component related to a weak thermal component. The photon spectrum in the LHS is presumably a result of the Comptonization (upscattering) of soft photons, that originated in a relatively weak inner part of the accretion disk, off electrons of the hot ambient plasma (see e.g., Sunyaev & Titarchuk 1980). Variability in the LHS is high (fractional root-mean-square variability is up to 40%) and presented by a flat-top broken power law (white-red noise) shape, accompanied by quasi-periodic oscillations (QPOs) in the range of 0.01–30 Hz, observed as narrow peaks in the power density spectrum (PDS). The HSS photon spectrum is characterized by a prominent thermal component which is probably a signature of a strong emission coming from a geometrically thin accretion disk. A weak power-law component is also present at a level of not more than 20% of the total source flux. In the HSS the flat-top variability ceases, QPOs disappear, and the PDS acquires a pure power-law shape. The total variability in the HSS is usually about 5% fractional rms. The IS is a transitional stage between the LHS and the HSS.
We have concentrated our efforts on a study of correlations between the photon index and the accretion disk (soft photon) luminosity. This correlation pattern carries the most direct information on a BH mass and a source distance. We also investigated a possibility that the shape of this correlation pattern can provide a direct signature of the bulk motion (converging) flow onto a BH, or in other words, the BH signature (see Titarchuk & Zannias 1998 and Laurent & Titarchuk 1999 for more details on this subject).
The authors of ST09 argue that that the saturation effect seen in the index-mass accretion rate correlation is a signature of a converging flow, when the mass accretion rate, Ṁ exceeds the Eddington limit, which can only exist in BH sources. We note that in the neutron star (NS) sources the mass accretion rate is, in most cases, less than the Eddington rate limit. As far as we know, in only Sco X-1 does it reaches the Eddington limit (compare Shaposhnikov & Titarchuk 2009; Titarchuk & Seifina 2009; Seifina & Titarchuk 2010, 2011, 2012; Seifina et al. 2013, 2014; and Titarchuk et al. 2013).
In the observed LHS and IS a small fraction of the disk emission component is seen directly. The Compton cloud almost fully covers the inner part of the disk. The energy spectrum is dominated by a Comptonized component seen as a power law at energies higher than the characteristic energy of the disk blackbody (BB) emission. To calculate the normalization of the seed (disk) BB component we modeled the spectrum using a generic Comptonization model (BMC; see Titarchuk et al. 1997) which consistently convolves a seed BB emission with the Green’s (response) function of the Compton corona (as a broken power law) to produce the Comptonized component (see details in Sect. 2). Calculated in this way the spectrum normalization is directly related to a BH mass, source distance and geometry. This allows us to apply the BB normalization as a scaling variable and to impose a constraint on a BH mass and distance ratios. Thus, we used the index-disk normalization correlation to constrain a BH mass for NGC 4051. As our reference values for the scaling measurements, we used the previously measured BH masses, source distances and inclinations for Galactic sources, Cygnus X-1 and GRO J1550-564. We also used a previous estimate of a BH mass for NGC 4051 obtained by Denney et al. (2009), (1.73 ± 0.55) × 106 solar massesin order to compare with our evaluation of it.
The descriptions of XMM-Newton, Suzaku and RXTE data are given in Sect. 2. We provide the details of the spectral state transitions analysis in Sect. 3. We describe a scaling method technique and present the results of interpretation of the data using the scaling method in Sect. 4. We discuss our results and emphasize on a BH mass estimate in NGC 4051 in Sect. 4. We make our final conclusions in Sect. 5
2 Observations and data reduction
For the study presented in this paper we have analyzed data for spectral transitions in NGC 4051 observed using XMM-Newton, Suzaku and RXTE. We analyzed a set of data taken during years when the source showed a transition from the LHS to the HSS. We used the archival XMM-Newton, Suzaku and RXTE data from the HEASARC1. For XMM-Newton there are 15 observations, 40 ks each collected in May–June 2009, two 50 ks observations collected on May 16, 2001 and on November 22, 2002 (see Table A.1). Data reduction was done using SAS software version 10.0.0. Four Chandra observations had much smaller observational time and thus, larger statistical errors and were used mainly to confirm the XMM-Newton results by an independent detector with different systematic errors. XMM-Newton and Chandra data have been extracted and analyzed in the 0.2–12 keV energy band.
We studied NGC 4051 using also the Suzaku data, for November 10 of 2005 as well as for November 6 and 23 of the 2008 observations (see Table A.2). We also used HEASOFT software package (version 6.13) and calibration database (CALDB) released on February 10, 2012 for XIS. Since the background is dominant inthe lower energy band, we used photons in the 1–10 keV (for XIS0, and 3) and 1–7 keV (for XIS 1) energy bands. The data reduction and spectral analysis are performed following the Suzaku Data Reduction Guide2. We obtained cleaned event files by re-running the Suzaku pipeline implementing the latest calibration database (CALDB) available since January 20 of 2013, and also applied the associated screening criteria files. We extracted our spectra from the cleaned event files using XSELEC and we generated responses for each detector utilizing the XISRESP script with a medium resolution. The spectral and response files for the front-illuminated detectors (XIS0, 1 and 3) were combined using the FTOOL ADDASCASPEC, after confirmation of their consistency. In addition, we grouped the spectra in order to have a minimum of 20 counts per energy bin.
We analyzed available data using the public archive (Bradt et al. 1993) using the RXTE observations made from May, 1996 to May, 2001. In Fig. 1 we show the light curve evolution for the RXTE 1996–2009 observations of NGC 4051. Standard tasks of the LHEASOFT/FTOOLS 6.21 software package were applied for data processing. For spectral analysis we used PCA Standard 2 mode data, collected in the 3–30 keV energy range, using PCA response calibration (ftool pcarmf v11.7). The standard dead time correction procedure was applied to the data. We subtracted a background corrected in off-source observations. Systematic error of 0.5% was applied to all analyzed RXTE spectra. In Table A.3 we provide the necessary information on the RXTE observations. We modeled all energy spectra using the XSPEC astrophysical fitting software.
To fit XMM-Newton, and Suzaku (BMC) component, the Laor line component with the energies ~ 6.5 keV, which are presumably due to the iron emission line (see Fig. 2) and the recombination edge (redge) component modified by gabs absorption. All the RXTE spectra were fitted using our composite model consist of the BMC and Laor line components.
In particular, the BMC model describes the outgoing spectrum as a convolution of the seed BB spectrum where the model parameters are normalization Nbmc, a color temperature kTcol, using the Comptonization Green’s function. Similarly to the ordinary BB XSPEC model the normalization CN is a ratio of source luminosity to square of the distance d
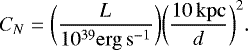 (1)
(1)
The resulting model spectrum is also characterized by a parameter log (A) related to a Comptonized (illumination) fraction, f = A∕(1 + A) and the Green’s function spectral index α = Γ − 1, where Γ is the photon index.
The two reasons for using the BMC model are firstly, the BMC, by the nature is a model which is applicable to a general case when soft (disk) photons gain energy not only due to the thermal Comptonization but also due to a dynamical or bulk motion Comptonization. Secondly, the BMC has normalization of the seed (disk) photons CN, which is proportional to the mass accretion rate in the disk.
The adopted spectral model well describes the most data sets used in our analysis. A value of the reduced 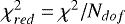 , where Ndof is a number of degrees of freedom for a given fit, is always around 1.0 for all of XMM, Suzaku and RXTE observations (see Tables A.4–A.6).
, where Ndof is a number of degrees of freedom for a given fit, is always around 1.0 for all of XMM, Suzaku and RXTE observations (see Tables A.4–A.6).
We incorporate the Laor-line profile to fit the line component. The line feature has a statistical significance of (3–10) σ depending on the spectral states. This line is variable and exhibits equivalent width (EW) in the range of 50–700 eV across the data, see Tables A.4–A.6. We found that an addition of the Laor-line component significantly improves the fit quality of the LHS and IS spectra.
We revealed absorption edges in the fits of the NGC 4051 spectra, which can be interpreted as an evidence of a clumpy, multi-temperature outflow around NGC 4051, particularly in the IS. We also applied the recombination edge emission model, redge3 for all Suzaku and XMM-Newton spectra, which considerably improves the fit quality of the LHS spectra. The parameters of the redge model are: Ec threshold energy; Tpl plasma temperature (keV), and Nredge, normalization in photons cm−2 s−1 in the line.
Thus, we identified a complete set of spectral transitions in a period when the source state changes from the LHS to the IS (or vice versa). We should establish that NGC 4051 does not reach the real HSS when the photon index of X-ray spectrum usually exceeds two (see e.g., ST09). The photon index saturation value is also determined by the electron temperature of the converging flow (see for example, Laurent & Titarchuk 1999, hereafter LT99). In Tables A.4–A.6 we present the details of the model fits to the spectral data for each of the observations related to a paricular spectral state defined by a value of the spectral (or photon) index.
As seen above we used all available XMM-Newton and Suzaku archived observations of NGC4051, which are distributed accordingly to the specific observation schedule. We also used all particular well-monitored RXTE observations of NGC 4051 where we observe the spectral changes, particularly changes of the spectral (or photon) indices. In these cases we established the correlation of the photon index, Γ vs normalization of the photon component which is identical to normalization of the soft (disk) component.
 |
Fig. 1 Evolution of ASM/RXTE count rate during 1996–2009 observations of NGC 4051. Vertical arrows (at the top of panel) indicate temporal distribution of the RXTE (pink), XMM-Newton (blue) and Suzaku (black) data sets listed in Tables A.1−A.3. |
 |
Fig. 2 Representative EF(E) spectral diagrams for the low-hard state (left panel) and for the intermediate state (right panel). Dataare taken from the XMM-Newton observations 0157560101 (left panel, X2 data set), and 0109141401 (right panel, X1 data set). The data are shown by black crosses and the spectral model components are displayed by dashed green, purple and blue lines for the BMC, Laor, and redge components, respectively. |
3 Correlations between the spectral (photon) index and mass accretion rate during spectral state transitions
3.1 Observations of spectral changes from the low-hard state to softer states
In Fig. 2 we show two representative EF(E) spectral diagrams for the LHS and the IS states (red lines). Data were taken from XMM-Newton observations 0157560101 (left panel, “X2” data set, LHS), and 0109141401 (right panel, “X1” data set, IS).
In Fig. 3 we demonstrate a spectral evolution using XMM-Newton data for the LHS (red curve) and IS (green curve) states (2001, 2009). It is worth pointing out a strength of the low energy component at ~ 0.5 keV in the IS and its weakness in the LHS. The XMM-Newton spectra, which are characterized by the highest energy resolution quality, clear demonstrate a number of additional emission and absorption features in the LHS (see Fig. 3, red line). However, these features are not well pronounced in the IS spectra (e.g., Fig. 3, green line). Thus, in this Figure we show the complete set of the spectra, which were detected during the spectral evolution.
We should emphasize the presence of the Laor line component and the recombination edge emission component, redge near 6.4 keV in all XMM-Newton spectra (see Figs. 2 and 3). For all spectra we also applied a Gaussian absorption line model, gabs using as parameters, the line energy, Eline, (in keV) the line width, σ (in keV) and the line optical depth at the line center. Our model for the data fits is gabsx(BMC + Laor + Redge).
In Fig. 4 we also show the spectra of NGC 4051 for the 2005 and 2008 outburst event epoches with another X-ray mission, Suzaku. The data cover two spectral states of the source, in our classification: the LHS (blue), the IS (red).
The normalization of the spectra (proportional to the mass accretion rate) positively correlates with the photon index. The correlation pattern for NGC 4051 presented in Fig. 5 demonstrate a clear saturation of the photon index which is also identified in several Galactic and extragalactic BH sources (see ST09, Seifina & Titarchuk 2011, 2012; Seifina et al. 2013, 2014, 2017; Titarchuk et al. 2013; Titarchuk & Seifina 2016a,b, 2017).
On the other hand (Farinelli & Titarchuk 2011; hereafter FT11) and later Seifina & Titarchuk (2011, 2012), Seifina et al. (2013, 2015, 2016), Titarchuk et al. (2013, 2014), Titarchuk & Seifina (2016a) show that the index stays the same in a number of NS sources independently of a mass accretion rate. One sees almost no change of the index when a particular NS source evolves fromthe low to high luminosity states. Thus, even phenomenologically the index evolves for BHs and stays around two for NSs. ST09 and FT11 present the strong theoretical arguments for such particular behaviors of the index in BH and NS sources, respectively.
The index saturation level for the spectral transition in NGC 4051 has values close to two. It can be due to the fact that at lower accretion rates in the disk the cooling of X-ray emission area [Compton cloud (CC)] by the disk photons is less efficient than that at high disk mass accretion rate Ṁ d. As a result, the electron temperature kTe of the converging flow (CF) is still relatively high (10−15 keV, see LT99) even when the total mass accretion Ṁsub + Ṁd rate is greater than 1. As a result this temperature effect leads to more efficient upscattering in CF and harder spectra. The direct connection between the electron temperature of the CC and the hardness of the emergent spectrum were shown by Laurent & Titarchuk (1999, 2011) using Monte-Carlo simulations. This type of the index-mass accretion rate correlation is also seen in Cygnus X-1 and in a number of other BHCs (see details in ST09).
As one can see that our definition of the spectral state is not arbitrary. Indeed, normalization of the soft component in the LHS is one order of magnitude less than that in the IS (see Figs. 2–4). The photon indices are also different; at about 1.5 in the LHS and 2 in the IS (see Figs. 2–6).
 |
Fig. 3 Spectral evolution using XMM-Newton data of NGC4051 for different spectral states: the LHS spectrum (May 11, 2009 – red points) and the IS spectrum (May 15, 2009 – green points). Curves are related to the best-fit model (see details in text). |
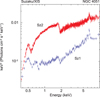 |
Fig. 4 Two EFE spectral diagrams during the LHS (2005 Nov, blue) and the IS [2008 Nov, 6–12 (red)]. Data taken from Suzaku observations700004010 (Sz1, low-hard) and 703023010 (Sz2, intermediate state). |
3.2 Analytical explanation of evolution of the spectral Index from the low-hard state to softer states in BHs
We then estimated a value of the spectral index in the low-hard state and its evolution to softer states. For this estimate we used the energy balance in the transition layer (TL) dictated by Coulomb collisions of protons (gravitational energy release), while inverse Compton and free-free emission are the main cooling channels (see a formulation of this problem in the pioneering work by Zel’dovich & Shakura 1969 and a similar consideration in Bisnovatyi et al. 1980). For the characteristic electron temperature (3 keV ≲kTe ≲ 50 keV) of these regions, Compton cooling dominates over free-free emission and the relation between the energy flux per unit surface area of the corona Qcor, the radiation energy density ε(τ) and electron temperature 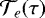 can be given by (see Zel’dovich & Shakura (1969) and Titarchuk et al. (1998), hereafter TLM98)
can be given by (see Zel’dovich & Shakura (1969) and Titarchuk et al. (1998), hereafter TLM98)
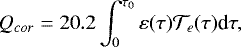 (2)
(2)
where τ is the Thomson optical depth in the transition layer (TL). The distribution ε(τ) is obtained as a solution of the diffusion equation
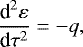 (3)
(3)
where q is a distribution of the sources in the corona due to the gravitational energy release of the accreted matter there and illumination of the corona by the soft flux of the disk. The parameter q can be presented as
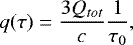 (4)
(4)
where Qtot = Qcor + Qdisk is the sum of the corona (TL) and intercepted disk fluxes, respectively. Combination of Eq. (3) with two boundary conditions at the outer and inner TL boundaries
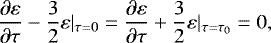 (5)
(5)
leads us to the formulation of the TL boundary problem.
The solution for ε(τ) is given by
![\begin{equation*} \varepsilon(\tau)=\frac{Q_{tot}}{c} \left[1+ \frac{3}{2}\tau_0\left(\frac{\tau}{\tau_0} - \frac{\tau^2}{\tau_0^2}\right)\right].\end{equation*}](/articles/aa/full_html/2018/05/aa32235-17/aa32235-17-eq8.png) (6)
(6)
We then rewrite the right-hand of Eq. (2) as
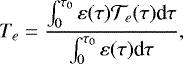 (7)
(7)
using the mean value theorem, where Te is the mean electron temperature.
The following integral of ε(τ) (see Eq. (6)) is
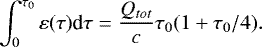 (8)
(8)
If we substitute Formula (8) into Eq. (2), after some straightforward algebra we obtain
![\begin{equation*} \frac{kT_e \tau_0 [1+\tau_0/4]}{m_e c^2}= \frac{0.25}{1+Q_{disk}/Q_{cor}}.\end{equation*}](/articles/aa/full_html/2018/05/aa32235-17/aa32235-17-eq11.png) (9)
(9)
To evaluate how the spectral (photon) index changes with ratio Qdisk ∕Qcor we use a formula for the spectral index α
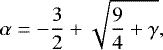 (10)
(10)
where γ = β∕Θ and β-parameter, Θ ≡ kTe∕mec2 defined in Titarchuk & Lyubarskij (1995). If we replace β by its diffusion limit βdiff
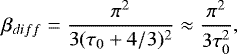 (11)
(11)
for τ0 ≫ 4∕3 using we obtain the diffusion spectral index as
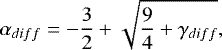 (12)
(12)
where 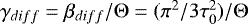 . Using this formula for γdiff and Eq. (9) we obtain that
. Using this formula for γdiff and Eq. (9) we obtain that
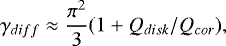 (13)
(13)
We can also rewrite Eq. (12) for αdiff in a more convenient form
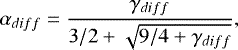 (14)
(14)
from which the following two asymptotic behaviors of αdiff are obvious: When Qdisk∕Qcor ≪ 1 it follows that γdiff ~ 3 and then
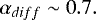 (15)
(15)
While for Qdisk∕Qcor ≫ 1 (or with a rise of the mass accretion rate) γdiff increases which leads to an increase of αdiff:
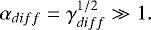 (16)
(16)
Thus, using formulas (13)−(16) one can see that αdiff rises when Qdisk∕Qcor increases.
The index evolution including its saturation with the mass accretion rate were analyzed observationally and numerically by ST09 and (Laurent & Titarchuk 2011; hereafter LT11). Here we estimate analytically that the spectral index α really rises from ~0.7 when Qdisk∕Qcor ≪ 1 and then the emergent spectrum becomes softer when the illumination of the innermost part of the accretion flow by the soft (disk) photons Qdisk increases (see e.g., Fig. 5).
Indeed, in Figs. 5 and 6 we demonstrate that the best-fit photon index really grows with a mass accretion rate, ṁ (or with 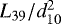 , see below Eq. (20)). But when ṁ increases the disk soft photon illumination of the transition layer, Qdisk increases too and thus, formulas (14)−(16) qualitatively describes the index rise with a mass accretion rate. The behavior of the photon index versus a mass accretion rate in the converging flow was studied in detail by LT99 and LT11 with taking into account all effects of General Relativity. Here, we describe the index increase qualitatively with the mass accretion rate.
, see below Eq. (20)). But when ṁ increases the disk soft photon illumination of the transition layer, Qdisk increases too and thus, formulas (14)−(16) qualitatively describes the index rise with a mass accretion rate. The behavior of the photon index versus a mass accretion rate in the converging flow was studied in detail by LT99 and LT11 with taking into account all effects of General Relativity. Here, we describe the index increase qualitatively with the mass accretion rate.
 |
Fig. 5 Photon index versus BMC normalization (proportional to mass accretion rate) for outburst transitions (1996–2009) in NGC 4051. Red triangles, and blue and black squares correspond to RXTE, XMM-Newton, and Suzaku observations, respectively. |
4 Discussion
The accretion process onto a BH is far from being completely understood. Theoretical models which are available for astronomers to explain observational phenomena usually deal with only narrow aspects of a broad observational picture. However, in recent years a concept of the transitional layer (TL) in the accretion flow has emerged. In the framework of this model several major observational aspects of accreting BHs find the natural explanation. We argue that this concept is a strong candidate to provide a basis for a theory of accretion process onto compact objects which would account for the current observational picture of BH sources. Moreover, this paradigm may provide us with a first direct BH signature observationally confirmed in multiple sources.
The starting point in the development of the TL paradigm is the notion of the necessary deviation of the rotational profile in the innermost part of the disk set by the conditions at (or near) a compact object for which rotation is presumed to be much slower than the Keplerian frequency near the object. This problem was first considered by Titarchuk et al. (1998) who showed that the adjustment of the Keplerian rotation in the accretion disk to the sub-Keplerian rotation of the central object leads to the formation of the inner hot Compton corona
Currently, BH identification in X-ray observational astronomy is based solely on a mass of compact object. Namely, a compact X-ray source is classified as a BH if it is well established that its mass exceeds the upper mass limit of a stable rotating neutron star, namely 3.2 M⊙ (see e.g., Rhoades & Ruffini 1974). To the date there is only one widely accepted method for mass determination related to the measurement of the mass function f(M) based on optical spectroscopy (see above). But this method the mass determination used for binaries cannot be applicable for AGNs.
We have evaluated a BH mass in NGC 4051 using scaling relationships in correlations between the index and mass accretion rate observed during the state transitions in Galactic and extragalactic accreting BHs. We applied a previously proposed technique for BH mass determination using scaling the index − X-ray spectrum normalization (see ST09) which contains information on source distance and BH mass.
4.1 The scaling technique and BH mass evaluation in NGC 4051
One of the goals of this study is to apply X-ray observational data for NGC 4051 to infer its fundamental characteristics. To do this we usedthe BH spectral state paradigm combined with the scaling laws expected to be observed in spectral and timing data during statetransitions.
The scaling law, which we have used as a basis for our mass determination analysis, relates a source flux F detected by an observer on the Earth, a disk flux L and distance d, namely
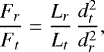 (17)
(17)
where subscripts r and t denote reference and target sources respectively, and F stands for the source flux detected by an observer on the Earth. The disk flux L can be represented as
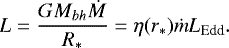 (18)
(18)
Here R* = r*RS is an effective radius at which the main energy release takes place, RS = 2GM∕c2 is the Schwarzschild radius, η = 1∕(2r*), ṁ = Ṁ∕Ṁcrit is dimensionless mass accretion rate in units of the critical mass accretion rate Ṁ crit = LEdd∕c2 and LEdd is the Eddington luminosity.
i.e., LEdd ∝ M and thus, using Eqs. (18) and (19) we have
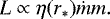 (20)
(20)
We assume that both ṁ and η are the same for two different sources in the same spectral state, which leads to Lr ∕Lt = Mr∕Mt. In our spectral analysis we determined the normalization of the seed photon radiation, which is supplied by an accretion flow (disk) prior to Comptonization. The ratio of these normalizations for target and reference sources in the same spectral state can be written as
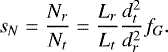 (21)
(21)
Here, fG is a geometrical factor which takes into account the difference in viewing angles of the seed photon emission area (the inner disk) by the Earth observer for these given sources. Therefore, in the case of radiation coming directly from the disk it has the value 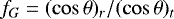 , where θ is the inclination angle of the inner disk. This formula for fG, however, may not be accurate because the geometry of both the inner disk and the corona can be different from the plane (disk) geometry. In BH states of interest (the LHS and the IS) they can be described, for instance, by quasi-spherical configuration. Despite this uncertainty in the determination of fG, we adopted the above form fG in which θ ~ i if the information on the system inclination angle i is available. In doing this we introduced an additional assumption that the inner accretion disk and the system inclination angles are the same. This assumption, however, proved to be in good agreement with this type of analysis.
, where θ is the inclination angle of the inner disk. This formula for fG, however, may not be accurate because the geometry of both the inner disk and the corona can be different from the plane (disk) geometry. In BH states of interest (the LHS and the IS) they can be described, for instance, by quasi-spherical configuration. Despite this uncertainty in the determination of fG, we adopted the above form fG in which θ ~ i if the information on the system inclination angle i is available. In doing this we introduced an additional assumption that the inner accretion disk and the system inclination angles are the same. This assumption, however, proved to be in good agreement with this type of analysis.
Using Eq. (21) and a relation Lr∕Lt = Mr∕Mt in hand, the task of BH mass measurement for a target source is reduced to the determination of scaling coefficients sN with respect to the data for a reference source. The appropriate technique has already been implemented in a number of BH sources (see ST09, Titarchuk & Seifina 2016a,b, 2017 hereafter TS16a, TS16b, TS17).
4.2 Estimate of a black hole mass
To estimate a BH mass, MBH of NGC 4051, we chose Galactic sources (GRO J1655–40 and Cyg X-1 (see ST09)) as the reference sources for which BH masses and distances were well established now (see Table A.7). For a BH mass estimate of NGC 4051 we used the BMC normalizations, NBMC of these reference sources. Thus, we scaled the index vs NBMC correlations for these reference sources with that of the target source NGC 4051 (see Fig. 6). The value of the index saturation in NGC 4051, 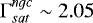 , is close to
, is close to 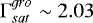 of GRO J1655–40 and to
of GRO J1655–40 and to 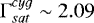 of Cyg X–1.The scaling procedure was implemented in a similar way as in ST09, TS16a, TS16b. We introduced an analytical approximation of the Γ(Nbmc) correlation, fitted by a formula
of Cyg X–1.The scaling procedure was implemented in a similar way as in ST09, TS16a, TS16b. We introduced an analytical approximation of the Γ(Nbmc) correlation, fitted by a formula
![\begin{equation*} {\mathcal{F}}(x)= {\mathcal{A}} - ({\mathcal{D}}\times {\mathcal{B}})\ln\{\exp[(1.0 - (x/x_{tr})^{\beta})/{\mathcal{D}}] + 1\},\end{equation*}](/articles/aa/full_html/2018/05/aa32235-17/aa32235-17-eq30.png) (22)
(22)
with x = Nbmc. Fitting of the observed correlation by this function 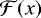 provide us a set of the best-fit parameters
provide us a set of the best-fit parameters 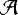 ,
, 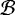 ,
, 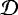 , xtr, and β. (see Table A.8). More detailed description of these parameters is given in TS16a.
, xtr, and β. (see Table A.8). More detailed description of these parameters is given in TS16a.
To implement this BH mass estimate for the target source one should rely on the same shape of the Γ − Nbmc correlations for the target source and those for the reference sources. To estimate a BH mass, Mt of NGC 4051 (target source) one should slide the reference source correlation along Nbmc-axis to that of the target source (see Fig. 6).
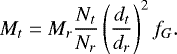 (23)
(23)
In Fig. 6 we demonstrate the Γ − Nbmc correlation for NGC 4051 using XMM-Newton (blue squares), Suzaku (black squares) and RXTE (red triangles) spectra (see Tables A.4–A.6) along with those for the Galactic reference sources, Cyg X–1 (black circles) and GRO 1655–40 (green squares). BH masses and distances for this target-reference pair are presented in Table A.7. We used values of Mr, Mt, dr, dt, and cos (i) from Table A.7 and then calculated the lowest limit of the mass, using the best fit value of Nt = (8.1 ± 0.1) × 10−3 taken them at the beginning of the index saturation (see Fig. 6) and measured in units of 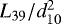 erg s−1 kpc−2 (see Table A.8 for values of the parameters of function
erg s−1 kpc−2 (see Table A.8 for values of the parameters of function 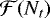 (see Eq. (22))). Finally, we obtained that Mngc≳6.1 × 105 M⊙ (Mngc = Mt) assuming dngc ~ 9.8 Mpc and fG ~ 1. To determine the distance to NGC 4051 we used the formula
(see Eq. (22))). Finally, we obtained that Mngc≳6.1 × 105 M⊙ (Mngc = Mt) assuming dngc ~ 9.8 Mpc and fG ~ 1. To determine the distance to NGC 4051 we used the formula
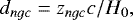 (24)
(24)
where the redshift zngc = 0.00234 for NGC 4051 (see Wright 2006), c is the speed of light and H0 = 70.8 ± 1.6 km s−1 Mpc−1 is the Hubble constant. We summarize these results in Table A.7.
Thus, we constructed the scaling which allowed us to obtain a BH mass of ≳6 × 105 solar masses in NGC 4051 which is our final evaluation of BH mass using the scaling method. The obtained BH mass estimate is in agreement with estimates of a variability time in optical Hβ line (Mngc ~ 1.1 × 106M⊙, Peterson et al. 2004). Furthermore, the lower limit of the BH mass for NGC 4051 from reverberation mapping method (6.13 × 105 M⊙, Kaspi et al. 2000) is close to that found in this paper. We also refer to the BH mass estimate in NGC 4051, (1.7 ± 0.5) × 106M⊙ obtained by Denney et al. (2009) and this BH mass interval indicates that our estimate does not contradict to the Denney et al. (2009) evaluation.
Our scaling method was effectively applied to evaluate BH masses of Galactic (e.g., ST09, STS13) and extragalactic black holes (TS16a,b; Sobolewska & Papadakis 2009; Giacche et al. 2014). Recently the scaling method was also successfully implemented to estimate BH masses of two ultraluminous X-ray (ULX) sources M101 ULX–1 (TS16a) and ESO 243–49 HLX–1 (TS16b). These findings suggest BH masses of order of 104 solar masses in these unique objects.
We then applied the scaling method and found the BH mass in another extragalactic source NGC 4051. Thus, the scaling technique provides a promising prospect for a BH mass evaluation for Galactic and extragalactic BHs, TDE, and ULX sources.
 |
Fig. 6 Scaling of the photon index versus normalization for NGC 4051 (red line – target source), and GRO J1655–40 and Cygnus X-1 (reference sources, green and black lines, respectively). Red triangles, black and blue squares correspond to RXTE, Suzaku and XMM-Newton data. Green squares and yellow-black circles correspond to RXTE data for GRO J1655–40 and Cygnus X-1, respectively. |
5 Conclusions
We performed a comprehensive study of a highly representative set of well observed spectral transitions in NGC 4051. The goal of the study is to explore the possibility of measuring the BH fundamental properties applying X-ray data and search for a BH signature in NGC 4051. We used the correlation between spectral and mass accretion rate properties during the state transitions as a main tool to estimate BH mass in NGC 4051.
We established the spectral state transition in this source collecting X-ray data from the Newton XMM, Suzaku and RXTE missions. We examined the correlation between the photon index of the Comptonized spectral component and its normalization. Analyzing the behavior of the correlation patterns we utilize three basic scaling laws: the observed disk flux is proportional to a BH mass, the mass accretion rate and inversely proportional to a square of distance to a particular source. We established that scalable correlation patterns do indeed contain information on BH mass.
Then we combined the correlation patterns in the normalization domain for Galactic X-ray BH binaries, Cygnus X-1, GRO 1655–40, forwhich BH masses and distances are known, and scaled them with that for NGC 4051. As a result we found that all of these correlations are self-similar for these three BHs. The application of the scaling technique for the high precision measurements of BH masses requires well sampled observations of the source evolution through the outbursts and careful consideration of scalability of correlation patterns.
We show that the photon index of the BH emergent spectra of NGC 4051, Γ undergoes an evolution from small to high values depending on a mass accretion rate in the source. Using this correlation along with scaling technique gives us an estimate of a BH mass in NGC 4051, Mbh≳6 × 105M⊙. We also note that the referee of this paper also emphasizes that NGC 4051 is one of the NLSy1s (narrow line Seyfert 1s), which are thought to have BHs with relatively low mass, of the order of 106 solar masses. This is why the Earth observer could even see the disk emission in X-rays (and is thus highly relevant to our model) (see Figs. 2 and 3).
Acknowledgements
E. S. acknowledges Pascal Chardonnet for useful discussions. L. T. thanks Filippo Frontera for wide discussion of the results of this paper and the referee for her/his interesting remarks on the content of the paper.
Appendix
XMM-Newton observations of NGC 4051 in the 0.2–10 keV range.
Suzaku observations of NGC 4051.
RXTE observations of NGC 4051 in the 3–20 keV range.
Best-fit parameters of spectral analysis for 2001, 2002 and 2009 with XMM-Newton observations of NGC 4051 in 0.2–10 keV energy rangea.
Best-fit parameters of spectral analysis for 2005 and 2008 with Suzaku observations of NGC 4051 in 0.2–10 keV energy rangea.
Best-fit parameters of spectral analysis for 1996 and 2001 with PCA/RXTE observations of NGC 4051 in 3–30 keV energy rangea.
BH masses and distances.
Parameterizations for the reference and target sources.
References
- Belloni, T. 2005, in AIP Conf. 797, Interacting Binaries: Accretion, Evolution, and Outcomes (New York: AIP), 197 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T., Homan, J., Casella, P., et al. 2005, A&A, 440, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, T., Parolin, I., Del Santo, M., Homan, J., & Casella, P. 2006, MNRAS, 367, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Bisnovatyi, G. S., Khlopov, M. Yu., Chechetkin, V. M., & Eramzhyan 1980, Sov. Astron., 24, 716 [Google Scholar]
- Borozdin, K., Revnivtsev, M., Trudolyubov, S., Shrader, C., & Titarchuk, L. 1999, ApJ, 517, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Bradt, H. V., Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] [Google Scholar]
- Casella, P., Belloni, T., Homan, J., & Stella, L. 2004, A&A, 426, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dennee, K. D., Watson, L. C., Peterson, B. M., et al. 2009, ApJ, 702, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Dewangan, G. C., Titarchuk, L., Griffiths, R. E. 2006, ApJ, 637, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARAA, 28, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Farinelli, R., & Titarchuk, L. 2011, A&A, 525, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinelli, R., Titarchuk, L., Paizis, A., & Frontera, F. 2008, ApJ, 680, 602, (F08) [NASA ADS] [CrossRef] [Google Scholar]
- Fiorito, R., & Titarchuk, L. 2004, ApJ, 614, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J., Bailyn, C. D., & Orosz, J. A. 2001, ApJ, 554, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Haba, Y., Liebmann, A. C., Fukumura, K., 2008, Publ. Astron. Soc. Japan, 60, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, J., Kudritzki, R. P., Gabler, R., Vilchez, J. M., & Gabler, A., 1995, A&A, 297, 556 [Google Scholar]
- Hjellming, R. M., & Rupen, M. P. 1995, Nature, 375, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., Wijnands, R., Kong, A., et al. 2006, MNRAS, 366, 235 [NASA ADS] [Google Scholar]
- Hynes, R. I., Steeghs, D., Casares, J., Charles, P. A., & O’Brien, K. 2004, ApJ, 609, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., & Nelemans, G. 2004, MNRAS, 354, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Kalemci, E., Tomsick, J. A., Buxton, M. M., et al. 2005, ApJ, 622, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Klein-Wolt, M., & van der Klis, M. 2008, ApJ, 675, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, K. R., 1998, Astrophysical Formulae, (Berlin: Springer) [Google Scholar]
- Laurent, P., & Titarchuk, L. 1999, ApJ, 511, 289 (LT99) [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., & Titarchuk, L. 2007, ApJ, 656, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Laurent, P., & Titarchuk, L. 2011, ApJ, 727, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Lobban, A. P., Reeves, J. N., Miller, L., 2011, MNRAS, 414, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Remillard, R. A., Rupen, M. P., et al. 2007, ApJ, 698, 1398 [Google Scholar]
- McHardy, I. M., Papadakis, I. E., Uttley, P. et al. 2004, MNRAS, 348, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Montanari, E., Titarchuk, L., & Frontera, F. 2009, ApJ, 692, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Darias, T., Casares, J., & Martínez-Pais, I. G. 2008, MNRAS, 385, 2205 [NASA ADS] [CrossRef] [Google Scholar]
- Ninkov, Z., Walker, G. A. H., & Yang, S. 1987, ApJ, 321, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A. 2003, in A Massive Star Odyssey: From Main Sequence to Supernova, eds. K. van der Hucht, A. Herrero, & E. Cesar (San Francisco, CA: ASP), in IAU Symp. 212, 365 [NASA ADS] [Google Scholar]
- Orosz, J. A., Groot, P. J., van der Klis, M., et al. 2002, ApJ, 568, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., McClintock, J. E., Remillard, R. A., & Corbel, S. 2004, ApJ, 616, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S. Q., Miller, J. M., McClintock, J. E., et al. 2004, ApJ, 610, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., McHardy, I. M., Wilkes, B. J., et al. 2000 ApJ, 542, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., & King, A. R., 2013, MNRAS, 433, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., Gilfanov, M., & Churazov, E. 2000, A&A, 363, 1013 [NASA ADS] [Google Scholar]
- Rhoades, Jr. C. E., & Ruffini, R., 1974, Phys. Rev. Lett., 32, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Corbel, S., & Tomsick, J. A. 2003, ApJ, 595, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J., Corbel, S., Kalemci, E., Tomsick, J. A., & Tagger, M. 2004, ApJ, 612, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, S., Homan, J., Miller, J. M., & Belloni, T. 2004, Nucl. Phys. B Proc. Suppl., 132, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics, (New York: Wiley-Interscience) [Google Scholar]
- Sánchez-Fernández, C., Castro-Tirado, A. J., Duerbeck, H. W., et al. 1999, A&A, 348, L9 [Google Scholar]
- Seifina, E., & Titarchuk, L. 2010, ApJ, 722, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., & Titarchuk, L. 2011, ApJ, 738, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., & Titarchuk, L. 2012, ApJ, 747, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., Titarchuk, L., & Frontera, F. 2013, ApJ, 766, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., Titarchuk, L., & Shaposhnikov, N. 2014, ApJ, 789, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., Titarchuk, L., Shrader, C., & Shaposhnikov, N. 2015, ApJ, 808, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., Titarchuk, L., & Shaposhnikov, N. 2016, ApJ, 821, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Seifina, E., Titarchuk, L., & Virgilli, E. 2017, A&A, 607, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shaposhnikov, N., & Titarchuk, L. 2006, ApJ, 643, 1098 (ST06) [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, N., & Titarchuk, L. 2007, ApJ, 663, 445 (ST07) [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov,N., & Titarchuk, L. 2008, AAS, HEAD #10, 1.08 [Google Scholar]
- Shaposhnikov,N., & Titarchuk, L. 2009, ApJ, 699, 453 (ST09) [NASA ADS] [CrossRef] [Google Scholar]
- Shimura, T., & Takahara, F. 1995, ApJ, 445, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Shrader, C., & Titarchuk, L. G. 1999, ApJ, 521, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Shrader, C., & Titarchuk, L. G. 2003, ApJ, 598, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. G. 1980, A&A, 86, 121 [NASA ADS] [Google Scholar]
- Sobczak, G. J., McClintock, J. E., Remillard, R. A., Levine, A. M., et al. 1999, ApJ, 517, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., Mushotzky, R, Winter, L., et al. ApJ, 660, 580 [Google Scholar]
- Terashima, Y., Gallo, L. C., Inoue, H., 2009, Publ. Astron. Soc. Japan, 61, S299 [Google Scholar]
- Titarchuk, L. G., & Fiorito, R. 2004, ApJ, 612, 988 (TF04) [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Lyubarskij, Y. 1995, ApJ, 450, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Seifina, E. 2009, ApJ, 706, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Seifina, E. 2016a, A&A, 595, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L., & Seifina, E. 2016b, A&A, 585, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L., & Seifina, E. 2017, A&A, 602, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L., & Shaposhnikov, N. 2008, ApJ, 678, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., & Zannias, T. 1998, ApJ, 493, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Mastichiadis, A., & Kylafis, N. D., 1997, ApJ, 487, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Lapidus, I. I., & Muslimov, A. 1998, ApJ, 499, 315 (TLM98) [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Bradshaw, C. F., & Wood, K. S. 2001, ApJ, 560, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Seifina, E. & Frontera, F. 2013, ApJ, 767, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Seifina, E. & Shrader, F. 2014, ApJ, 789, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Trudolyubov, S. P. 2001, ApJ, 558, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Trudolyubov, S. P., Borozdin, K. N., & Priedhorsky, W. C. 2001, MNRAS, 322, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Uttley, P., Pounds, K. A., Nandra, K., & Strohmayer, T. E. 2011, MNRAS, 413, 2489 [Google Scholar]
- Vignarca, F., Migliari, S., Belloni, T., Psaltis, D., & van der Klis, M. 2003, A&A, 397, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- Zel’dovich, Ya. B., & Shakura N. I. 1969, Sov. Astron. 13, 175 [Google Scholar]
- Zurita, C., Sánchez-Fernández, C., Casares, J., et al. 2002, MNRAS, 334, 999 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit parameters of spectral analysis for 2001, 2002 and 2009 with XMM-Newton observations of NGC 4051 in 0.2–10 keV energy rangea.
Best-fit parameters of spectral analysis for 2005 and 2008 with Suzaku observations of NGC 4051 in 0.2–10 keV energy rangea.
Best-fit parameters of spectral analysis for 1996 and 2001 with PCA/RXTE observations of NGC 4051 in 3–30 keV energy rangea.
All Figures
 |
Fig. 1 Evolution of ASM/RXTE count rate during 1996–2009 observations of NGC 4051. Vertical arrows (at the top of panel) indicate temporal distribution of the RXTE (pink), XMM-Newton (blue) and Suzaku (black) data sets listed in Tables A.1−A.3. |
| In the text | |
 |
Fig. 2 Representative EF(E) spectral diagrams for the low-hard state (left panel) and for the intermediate state (right panel). Dataare taken from the XMM-Newton observations 0157560101 (left panel, X2 data set), and 0109141401 (right panel, X1 data set). The data are shown by black crosses and the spectral model components are displayed by dashed green, purple and blue lines for the BMC, Laor, and redge components, respectively. |
| In the text | |
 |
Fig. 3 Spectral evolution using XMM-Newton data of NGC4051 for different spectral states: the LHS spectrum (May 11, 2009 – red points) and the IS spectrum (May 15, 2009 – green points). Curves are related to the best-fit model (see details in text). |
| In the text | |
 |
Fig. 4 Two EFE spectral diagrams during the LHS (2005 Nov, blue) and the IS [2008 Nov, 6–12 (red)]. Data taken from Suzaku observations700004010 (Sz1, low-hard) and 703023010 (Sz2, intermediate state). |
| In the text | |
 |
Fig. 5 Photon index versus BMC normalization (proportional to mass accretion rate) for outburst transitions (1996–2009) in NGC 4051. Red triangles, and blue and black squares correspond to RXTE, XMM-Newton, and Suzaku observations, respectively. |
| In the text | |
 |
Fig. 6 Scaling of the photon index versus normalization for NGC 4051 (red line – target source), and GRO J1655–40 and Cygnus X-1 (reference sources, green and black lines, respectively). Red triangles, black and blue squares correspond to RXTE, Suzaku and XMM-Newton data. Green squares and yellow-black circles correspond to RXTE data for GRO J1655–40 and Cygnus X-1, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.