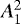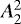| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 5 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201732032 | |
| Published online | 25 May 2018 | |
Timescales of starspot variability in slow rotators
1
Space Research Institute, Institut für Weltraumforschung (IWF), Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz, Austria
e-mail: oleksiy.arkhypov@oeaw.ac.at
2
Skobeltsyn Institute of Nuclear Physics, Moscow State University,
119992
Moscow, Russia
3
Institute for Astronomy (IfA), University of Vienna,
Türkenschanzstrasse 17,
1180
Vienna, Austria
e-mail: manuel.guedel@univie.ac.at
4
Karl-Franzens-Universität Graz (KFUG),
8010
Graz, Austria
Received:
3
October
2017
Accepted:
15
February
2018
There is an intriguing proximity between the turnover time τMLT of the standard mixing length theory of the Sun and the timescale τlam of solar activity patterns at the space scale of giant laminar convection assumed in deep layers of the Sun. To verify the reliability of this correspondence, we analyzed the light curves of 637 slowly rotating stars, observed by the Kepler mission, with periods from 16 to 30 days. The proximity τMLT ≈ τlam is confirmed. The performed study also confirms the manifestation of large scale turbulence in the dynamics of surface activity such as that in the Sun. These results open a new way to measure the key astrophysical parameter τMLT and to study deep convection that has been undetected with asteroseismology.
Key words: stars: activity / starspots / stars: interiors
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0;), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0;), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The mixing of plasma in deep layers of the solar convection zone (hereafter deep-mixing) plays a key role in calibration of the standard mixing length theory (MLT), which is a standard in modern astrophysics. In particular, the convective turnover time τMLT at the bottom of convection zone plays an important role in stellar modeling and rotation-activity relations. At the same time, this parameter cannot be measured directly. Only the relative variations of the convective turnover time with stellar color index or mass were found for main sequence stars using the rotation-activity relation. The absolute measure of the parameter requires a calibration with the theoretically calculated value of τMLT using the solar MLT model (e.g., Noyes et al. 1984; Wright et al. 2011).
However, the appropriateness of the MLT approach, based on the abstraction of identical convection cells (Böhm-Vitense 1958), is not obvious in a turbulent cascade of stellar convection (e.g., Li & Yang 2007). Nevertheless, the outcomes of such an approach look reasonable in the context of observational studies and are widely accepted in stellar physics. This paradox suggests a certain physical reality in the background of the MLT model with the supposed identical convective cells. In this paper we focus on an interesting formal proximity between τMLT and the timescale τlam of solar surface activity-pattern at the space scale of laminar convection (Arkhypov et al. 2013). The connection between starspot pattern and the deep convection was predicted in numerical models of magnetic tube emergence, which take into account the modulation effect from the convective flows (e.g., Weber et al. 2013). However, the solar proximity τMLT ≈ τlam needs extensive verification for other stars with various τMLT. The main sequence stars with rotation periods P < 16 days in the Kepler photometric survey are known to show manifestations of deep mixing (Arkhypov et al. 2015a, 2016). The subject of the present report is the verification of our previous results using another stellar set, consisting of rotators with the solar-type periods 16 < P < 30 days. Such slow rotators seem best indicators of deep mixing effects because of their relatively slight magnetism and, hence, the shortest lifetimes of starspots, which appear as a masking factor in this work.
The presented analysis became possible owing to an improved method explained below in Sect. 2. The obtained results are described in Sect. 3 and concluded in Sect. 4.
2 Method and stellar set
Detailed descriptions of the used spectral-autocorrelation method can be found in our previous papers (Arkhypov et al. 2015a,b, 2016). Therefore, we briefly describe only the key ideas.
We analyzed the rotational modulation of the stellar radiation flux F, which reflects the longitudinal distribution of spots (Fig. 1). The data used were already preprocessed to correct for the instrumental and environmental effects (PDCSAP_FLUX from the Kepler mission archive1). As in our previous studies (Arkhypov et al. 2015a,b, 2016), we considered the amplitudes A1 and A2 of the light-curve rotational Fourier harmonics with periods P and P∕2, respectively,where P is the period of stellar rotation. In Arkhypov et al. (2016) it was shown that the squared amplitudes 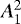 and
and 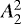 of these harmonics are statistically proportional to the sunspot number. In view of that, we used the values
of these harmonics are statistically proportional to the sunspot number. In view of that, we used the values 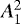 and
and 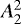 as activity indexes and found the timescales of their stochastic variability τ1 = −P∕ ln[r1(P)] and τ2 = −P∕ ln[r2(P)]. Here r1 (P) and r2 (P) are the autocorrelation functions of chronological series of the corresponding activity indexes (i.e.,
as activity indexes and found the timescales of their stochastic variability τ1 = −P∕ ln[r1(P)] and τ2 = −P∕ ln[r2(P)]. Here r1 (P) and r2 (P) are the autocorrelation functions of chronological series of the corresponding activity indexes (i.e., 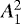 or
or 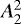 , respectively) at the time lag of one rotational period P. This approach is based on a simple approximation of the logarithm of autocorrelation function at the shortest lag: ln (rm) ≈−Δt∕τm (for details see in Arkhypov et al. 2016), where m = 1 or 2 is the harmonic number and Δt = P is the lag.
, respectively) at the time lag of one rotational period P. This approach is based on a simple approximation of the logarithm of autocorrelation function at the shortest lag: ln (rm) ≈−Δt∕τm (for details see in Arkhypov et al. 2016), where m = 1 or 2 is the harmonic number and Δt = P is the lag.
In fact, this approach is an adaptation of our method applied to the analysis of solar synoptic charts (Arkhypov et al. 2013). We used the same preprocessing of light curves as in our previous study in Arkhypov et al. (2016), aside from the improved later procedure for removing flares. In this work we approximated the one-period light curve, which covers a time interval of one rotation period P, with a sixth-order polynomial Fp = apδt6 + bpδt5 + cpδt4 + dpδt3 + epδt2 + fpδt + gp, where δt is the light curve running time and ap, bp, cp, dp, ep, fp, and gp are the fitted coefficients. This polynomial is used for the replacement of the measured flux F = Fp if |F − Fp| > 2σp, where 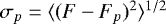 is the standard deviation in the considered one-period time interval.
is the standard deviation in the considered one-period time interval.
To exclude the artificial (e.g., instrumental) drifts and long period stellar nonrotational variability (i.e., with timescale ≫ P), we removed the linear trend in the one-period light curve using the following improved (as compared the method introduced in Arkhypov et al. 2015a) method. In the new algorithm we linearly approximated the first 0.05 P (i.e., the beginning) and last 0.05 P (i.e., the end) parts of the one-period light curve to be F = ab + bbδt and F = ae + beδt, respectively.Here ab, bb, ae, and be are fitted coefficients. Using these approximations, one can estimate the corresponding boundary fluxes Fb =ab and Fe = ae + beP for δt = 0 and P, respectively, and calculate the drift correction, i.e., F − [(Fe − Fb)∕P](δt − P∕2). As result, we obtained the light curve F(δt) with F(0) ≈ F(P), which we further analyzed to study its rotational Fourier harmonics. We note that this null trend rule is justified statistically. Indeed, although in reality the starspot evolution could generate slight accidental differences in F(0) and F(P), the average difference ⟨F(0) − F(P)⟩ should be negligible. Therefore, the main sense of the trend removing is a prevention of the residual instrumental trends.
Figure 2 shows the result of application of the above-mentioned procedures to a one-period light curve of the star KIC 5435923, including the flux interpolation in short gaps. Such prepared one-rotation light curves are further analyzed to study their rotational Fourier harmonics only.
For the study we selected the light curves of 637 slow rotators. This set includes the stars with rotation periods 16 < P < 30 days (according to measurements in Nielsen et al. 2013 and McQuillan et al. 2014) and effective temperatures 3337 ≤ Teff ≤ 7117 K from the Mikulski Archive for Space Telescopes (MAST)2). All the selected stars belong to the main sequence (surface gravity log (g[cm s−2]) > 4 in the catalogs used). These stars have high quality light curves without interferences (i.e., with no detectable short period pulsations or double periodicity from companions). The details of the star selection procedure are described in Arkhypov et al. (2015b, 2016).
Particularly, the value P, measured mainly in McQuillan et al. (2014), was visually reverified for the light curve of each selected star. In fact, this check does not reveal any misestimated periods by a factor 2. This result confirms our previous conclusion (Arkhypov et al. 2015b) on the reliability of the P catalogs (i.e., Nielsen et al. 2013 and McQuillan et al. 2014).
 |
Fig. 1 Typical light curve fragment (7% of the whole available record) of the star KIC 1027740 with starspot variability from the Kepler archive. Its rotation period P = 26.697 days (McQuillan et al. 2014) and effective temperature Teff = 5751 K (http://archive.stsci.edu/kepler/ stellar17/search.php) are close to the solar values (25.38 days and 5772 K, respectively). The time BJD here is the differential barycentric Julian days counted from the mission starting time. The plot was prepared using NASA Exoplanet Archives service (http://exoplanetarchive.ipac.caltech.edu/). |
 |
Fig. 2 Example of one-period light curve for the star KIC 5435923 before (a) and after (b) the flare removing procedure. In both curves, the trend is also removed and the flux is normalized F∕Fo, where Fo is the average flux for the considered time interval P. The interpolated gap is seen at 8.0 < δt < 8.8 days. |
3 Results
According to Arkhypov et al. (2015a, 2016), a kind of a gradient-like function is a useful diagnostic tool for starspot variability, that is,
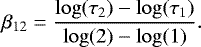 (1)
(1)
For example, the Kolmogorov theory of turbulence (e. g., Lang 1974) predicts a universal relation between the characteristic size of turbulent eddies (L) and the timescale of their variability (τL), i.e., τL ∝ L2∕3. Taking into account that L ∝ m−1, we obtain, for the timescale of rotational harmonics, τm ∝ m−2∕3, where m is the harmonic number. Substitution of this proportionality in Equation (1) gives β12 = −2∕3 = 0.6(6).
Figure 3 shows β12 estimate histograms for individual stars from the considered set of slow rotating objects. One can see the proximity of the histogram maxima to the predicted values –2/3. In particular, Fig. 3b is constructed with the bin width 0.09 localizing the histogram maximum at β = −0.68 ± 0.045, i.e., with 7% precision. The significance of this main peak is verified considering the binomial distribution of the near-maximum estimates in the limited interval − 1.8 < β12 < 0.4 (Fig. 3c). We calculated the probability of the main histogram peak, or a higher one, supposing a random distribution of β12 estimates
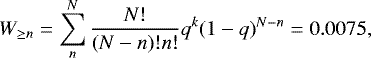 (2)
(2)
where n = 26 is the maximal number of β12 estimates in one bin of the histogram,N = 367 is the total number of the considered β12 estimates, and q = 1∕25 is the probability for one estimate to be in a certain bin from the set of 25 bins. Since the obtained probability W≥n is one chance of 1∕0.0075 ≈ 133, the considered histogram maximum at β12 ≈−0.67 is apparently not a statistical fluctuation, but is an indication of the turbulence manifestation. This is consistent with the analogous results for the stars with 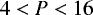 days (Arkhypov et al. 2016) and an outcome of the corresponding study for the Sun in Arkhypov et al. (2013) for the higher order harmonics 1 ≤ m ≤ 20.
days (Arkhypov et al. 2016) and an outcome of the corresponding study for the Sun in Arkhypov et al. (2013) for the higher order harmonics 1 ≤ m ≤ 20.
The turbulent convection generates irregular subphotospheric flows at the local height scale (m >> 1). For example, in the solar photosphere the turbulent cascade has been described at scales smaller than that of supergranules, i.e., m > 200 (Abramenkoet al. 2001; Stenflo 2012). However, Fig. 3 provides an argument for the turbulence manifestation (β12 ≈−0.67) at m = 1 and 2. Hence, the global (m = 1 and 2) character of the revealed turbulence contradicts to the small-scale photospheric and subphotospheric turbulent vortices. However, the deep large-scale convection is predicted in numerical modeling (e.g., Miesch et al. 2008) and found experimentally as a regular drift of supergranules (Hathaway et al. 2013). It is natural to connect the global turbulent effect in the starspot pattern with the giant convection in deep layers of a star.
This probable connection could be additionally verified by a comparison between the found timescales τ1, τ2 and the theoretical timescale of deep mixing τMLT of the MLT. Figure 4 shows that these values are different. But there is certain proximity between τMLT and the reductions of τ1 and τ2 to the spatial scale Dlam ≈ 23∕2Hcz (Dibaj & Kaplan 1976) of laminar convection based on the confirmed values for the deep turbulence time scaling, τm ∝ m−2∕3 (see Fig. 3), that is,
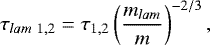 (3)
(3)
where mlam = 2πRstar∕Dlam; Rstar is the stellar radius from MAST and Hcz is the convective zone depth (van Saders & Pinsonneault 2012). This proximity is shown in Fig. 5.
 |
Fig. 3 Histograms of the the gradient-like function β12 for 637 stars with 16 < P < 30 days obtained with bin widths 0.468 and 0.090 in (panel a) and (panel b), respectively. Panel c: shows the histogram features at the distribution maxima in (panel b) with the labeled probability of exceeding the specified levels (pointed lines), according to the binomial distribution (Eq. (2)). The vertical dashed line indicates the prediction of Kolmogorov’s theory of turbulence β12 = −2∕3. The value n is the number of β12 estimates in one bin of the histogram. |
 |
Fig. 4 Timescales of variability of |
 |
Fig. 5 Averaged in temperature bins values of (a): log(τlam1) and (b): log(τlam2), defined by Eq. (3), vs. Teff. For comparison, the estimates of the τMLT turnover time by Noyes et al. (1984), are depicted by dashed line, and Wright et al. (2011) as error bar crosses, are given. |
4 Discussion and conclusions
Although the turbulent convection generates irregular subphotospheric flows smaller than supergranules at m ≫ 1, nevertheless the manifestation of turbulence (β12 ≈−2∕3) at global scales (m = 1 and 2) is confirmed also in stars with the solar-type rotational periods 16 < P < 30 days (Sect. 3). This means that the emersion of magnetic tubes in such stars including solar-like objects could be modulated by global turbulent vortices, which have vanishingly small direct manifestation in the solar photosphere. At the same time such global motions are predicted in deep layers of the convective zone (e.g., Miesch et al. 2008). Alternative interpretations of the starspot pattern dynamics in terms of magnetic dynamo or starspot decaying predict other values of the parameter β12, which are not supported by the histograms in Fig. 3. In particular:
- (a)
A stellar activity cycle modulates the total spot number with the identical period or timescale for all rotational harmonics of a light curve. This means β12 = 0 according to Eq. (1).
- (b)
The horizontal diffusion of magnetic elements in photosphere effectively decreases our activity indexes
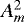 (m = 1, 2), when the average displacement of magnetic elements is about the longitudinal period of harmonic
2π∕m. For the normal diffusion this happens during the characteristic time,
(m = 1, 2), when the average displacement of magnetic elements is about the longitudinal period of harmonic
2π∕m. For the normal diffusion this happens during the characteristic time, 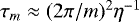 , where η
is the diffusion coefficient, i.e., τm ∝ m−2. In this case Eq. (1) gives β12 = −2.
, where η
is the diffusion coefficient, i.e., τm ∝ m−2. In this case Eq. (1) gives β12 = −2. - (c)
In highlymagnetized subphotospheric plasma, such as porous media, or in a network flow, the dependence of an average squared displacement of magnetic element ⟨x2⟩ on time t can differ from the linear relation. In a general case it may be represented as ⟨x2⟩∝ tα, where α < 1 is a constant. Therefore the squared displacement
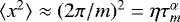 corresponds to the noticeable decrease of the activity index
corresponds to the noticeable decrease of the activity index 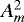 during the harmonic timescale τm. In this case τm ∝ m−2∕α
and, according Eq. (1), β12 = −2∕α. For example, the subdiffusion of magnetic elements with α = 0.6 ± 0.2 was found in the solar photoshere at the spatial scale of supergranulation (~104
km), which is related to the material network flow that traps these elements in the conjunction points (Iida 2016).
during the harmonic timescale τm. In this case τm ∝ m−2∕α
and, according Eq. (1), β12 = −2∕α. For example, the subdiffusion of magnetic elements with α = 0.6 ± 0.2 was found in the solar photoshere at the spatial scale of supergranulation (~104
km), which is related to the material network flow that traps these elements in the conjunction points (Iida 2016). - (d)
The differential rotation of a star stretches an activity region, or a complex of active regions, over the longitudinal harmonic scale Λm = 2π∕m during the time τm = Λm∕ΔΩ, where ΔΩ is a typical variation of angular velocity Ω over the latitudinal extension of the activity region or complex. Hence, the timescale of the considered feature blurring (i.e.,
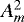 damping) is τm ∝ m−1, which corresponds to β12 = −1 in Eq. (1). However, the corresponding peak at n = 19 in Fig. 3c is rather insignificant because its W≥n = 0.22 according to Eq. (2).
damping) is τm ∝ m−1, which corresponds to β12 = −1 in Eq. (1). However, the corresponding peak at n = 19 in Fig. 3c is rather insignificant because its W≥n = 0.22 according to Eq. (2).
The aforementioned alternative predictions (i.e., β12 ≈ 0, − 2, < −2, and − 1, respectively) significantly (no less than than a half-width of the histogram bin) deviate from the histogram maxima at the prediction β12 ≈−2∕3 of the Kolmogorov’s turbulence theory. This fact is an argument for the deep-convective modulation of starspot pattern.
Such modulation is observable if its timescale is longer than the typical lifetime of starspots. If it were otherwise, the starspot pattern dynamics are controlled by the long lifetime of spots, which smooths the shorter living effects from deep mixing. In this case, the maximum of β12 -histogram should correspond to the spot decay process. Detailed studies (Arkhypov et al. 2016, 2018) have confirmed that stars with saturated magnetism have the histogram maximum at β12 ≈−2, corresponding to the diffusive decay of long-living spots. However, the slow rotators considered in this study have nonsaturated magnetism (see Fig. 2a in Arkhypov et al. 2018), sufficiently short-living spots, and the most frequent β12 = −2∕3, corresponding to the giant turbulence of deep-mixing.
Another possible manifestation of deep mixing appears to be the confirmed proximity of our timescale τlam for laminar giant convective cells to the turnover time τMLT (Fig. 5). In the successful MLT this turnover time is attributed to the standard (i.e., laminar) convective cells at the bottom of the convection zone (e.g., Gilliland 1985). The decaying giant (~ 45o) cells of laminar convection in turbulence were modeled in the solar convection zone (e.g., Brun & Toomre 2002) and indirectly detected in solar activity patterns (Arkhypov et al. 2012, 2013) and in the regular drift of supergranules (Hathaway et al. 2013). However, the directly observed solar photospheric granulation and even subphotospheric supergranules have much smaller diameters (≲ 0.4o) and shorter lifetimes (≲ 1.8 day; Rieutord & Rincon 2010) than the scales τMLT and τlam1,2 (> 10 days) in Fig. 5. Hence, the obtained scales τlam1,2 ≈ τMLT support the hypothesis regarding the starspot manifestation of plasma mixing in deeper layers of convective zones.
Since we confirmed the deep-mixing manifestations in the solar-like stars, such phenomena are additionally justified in the Sun as well. In particular, the found proximity β12 ≈−2∕3 suggests that some deep global flows generate the turbulent cascade at maximal scales. This raises a question on the source of such flows.
The standard MLT describes mixing in a range of situations, from planetary interiors to stars and the interstellar medium. However, its applicability to turbulence in astrophysical problems is often questionable. Nevertheless, MLT is acceptable for turbulence in stars. The confirmed proximity τMLT ≈ τlam1,2 suggests a way to resolve this paradox in terms of laminar contribution in the deep mixing.
The confirmed proximity τMLT ≈ τlam1,2 opens a new way to measure the key astrophysical parameter τMLT, which has so far only been calculated theoretically or estimated semiempirically using the MLT paradigm. Correspondingly, our results seem promising for related fields such as stellar activity and evolution.
Acknowledgements
This work was performed as a part of the project P25587-N27 of the Fonds zur Förderung der wissenschaftlichen Forschung, FWF. M.L.K. acknowledges the projects S11606-N16 and I2939-N27 of the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (FWF), Leverhulme Trust grant IN-2014-016, and partial support by the Ministry of Education and Science of Russian Federation (Grant RFMEFI61617X0084). This research has made use of the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
References
- Abramenko, V., Yurchyshyn, V., Wang, H., & Goode, P. R. 2001, Sol. Phys., 201, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhypov, O. V., Antonov, O. V., & Khodachenko, M. L. 2012, Sol. Phys., 278, 285 [Google Scholar]
- Arkhypov, O. V., Antonov, O. V., & Khodachenko, M. L. 2013, Sol. Phys., 282, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhypov, O. V., Khodachenko, M. L., Güdel, M., Lüftinger, T., & Johnstone, C. P. 2015a, A&A, 576, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arkhypov, O. V., Khodachenko, M. L., Güdel, M., Lüftinger, T., & Johnstone, C. P. 2015b, ApJ, 807, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhypov, O. V., Khodachenko, M. L., Güdel, M., Lüftinger, T., & Johnstone, C. P. 2016, ApJ, 826, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhypov, O. V., Khodachenko, M. L., Güdel, M., Lüftinger, T., & Johnstone, C. P. 2018, MNRAS, 473, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys. 46, 108 [Google Scholar]
- Brun, A. S., & Toomre, J. 2002, ApJ, 570, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dibaj, E. A., & Kaplan, S. A. 1976, Dimensions and Similarity of Astrophysical Quantities (Moscow: Nauka), 239 [Google Scholar]
- Gilliland, R. L. 1985, ApJ, 299, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H., Upton, L., & Colegrove, O. 2013, Science, 342, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Iida, Y., 2016, J. Space Weather Space Clim., 6, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lang, K. R. 1974, Astrophysical Formulae (Berlin: Springer) Chapter 3.5.12 [CrossRef] [Google Scholar]
- Li, Y., & Yang, J. Y. 2007, MNRAS, 375, 388 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Miesch, M. S., Brun, A. S., DeRosa, M. L., & Toomre, J. 2008, ApJ, 673, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, M. B., Gizon, L., Schunker, H., & Karoff, C. 2013, A&A, 557, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys., 7, 1 [NASA ADS] [Google Scholar]
- Stenflo, J. O. 2012, A&A, 541, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Saders, J. L., & Pinsonneault, M. H. 2012, ApJ, 746, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M. A., Fan, Y., & Miesch, M. S. 2013, ApJ, 770, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Typical light curve fragment (7% of the whole available record) of the star KIC 1027740 with starspot variability from the Kepler archive. Its rotation period P = 26.697 days (McQuillan et al. 2014) and effective temperature Teff = 5751 K (http://archive.stsci.edu/kepler/ stellar17/search.php) are close to the solar values (25.38 days and 5772 K, respectively). The time BJD here is the differential barycentric Julian days counted from the mission starting time. The plot was prepared using NASA Exoplanet Archives service (http://exoplanetarchive.ipac.caltech.edu/). |
| In the text | |
 |
Fig. 2 Example of one-period light curve for the star KIC 5435923 before (a) and after (b) the flare removing procedure. In both curves, the trend is also removed and the flux is normalized F∕Fo, where Fo is the average flux for the considered time interval P. The interpolated gap is seen at 8.0 < δt < 8.8 days. |
| In the text | |
 |
Fig. 3 Histograms of the the gradient-like function β12 for 637 stars with 16 < P < 30 days obtained with bin widths 0.468 and 0.090 in (panel a) and (panel b), respectively. Panel c: shows the histogram features at the distribution maxima in (panel b) with the labeled probability of exceeding the specified levels (pointed lines), according to the binomial distribution (Eq. (2)). The vertical dashed line indicates the prediction of Kolmogorov’s theory of turbulence β12 = −2∕3. The value n is the number of β12 estimates in one bin of the histogram. |
| In the text | |
 |
Fig. 4 Timescales of variability of |
| In the text | |
 |
Fig. 5 Averaged in temperature bins values of (a): log(τlam1) and (b): log(τlam2), defined by Eq. (3), vs. Teff. For comparison, the estimates of the τMLT turnover time by Noyes et al. (1984), are depicted by dashed line, and Wright et al. (2011) as error bar crosses, are given. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.