| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201425307 | |
| Published online | 01 April 2015 | |
Signs of deep mixing in starspot variability
1 Space Research Institute (IWF), Austrian Academy of Sciences, Schmiedlstrasse 6, 8042 Graz, Austria
e-mail: oleksiy.arkhypov@oeaw.ac.at
2 Skobeltsyn Institute of Nuclear Physics, Moscow State University, 119992 Moscow, Russia
3 Institute for Astronomy (IfA), University of Vienna, Türkenschanzstrasse 17, 1180 Vienna, Austria
e-mail: manuel.guedel@univie.ac.at
4 Karl-Franzens-Universität Graz (KFUG), 8010 Vienna, Austria
Received: 10 November 2014
Accepted: 14 January 2015
The current knowledge on plasma mixing in stellar interiors is based on theoretical modeling, which calibrates the empirical relations between the mixing and observable stellar parameters. Hence, a model-independent method of studying the mixing process is a desirable, but yet unfounded approach. Here, using a new spectral-correlation method, verified for the Sun, we show that deep mixing is manifested in stellar photometric light curves. We measure the timescales of the stochastic change in the spectral power of rotational variability of hundreds of main-sequence stars from the Kepler mission archive. The discovered proportionality of these timescales to the turnover time of the standard mixing length theory, their consistency with Kolmogorov’s theory of turbulence, and the relation with stellar activity provide a new approach to the probing of stellar interiors. This opens a broad perspective for experimental studies of deep mixing and magnetic dynamos in stars.
Key words: stars: activity / starspots / stars: interiors
© ESO, 2015
1. Introduction
The energy transport by convection in the deep layers of stars is a very important but insufficiently understood process. The standard “mixing length” theory or MLT (Böhm-Vitense 1958) used in modern astrophysics is a simplification of the convection process, since it replaces the wide spectrum of real turbulent eddies by standardized cells of identical size (the mixing length). The turnover time (τMLT) of a standard cell is a key parameter in modern theories of stellar evolution and magnetism. Until now, there have been two ways to estimate this parameter: using stellar models (e.g., Kim & Demarque 1996), or using empirical correlations between τMLT and average levels of stellar activity (Noyes et al. 1984; Wright et al. 2011). However, the real turnover times of convection cells with different diameters remain unknown.
The knowledge of plasma convection in the deep layers of stars is based on numerical modeling (Bessolaz & Brun 2011). Numerous attempts to detect the photospheric manifestations of predicted gigantic convective cells on the Sun, mainly with Doppler, astroseismic, and correlation tracking techniques, have been carried out with no conclusive results (Williams & Cuntz 2009; Hanasoge et al. 2010).
For the Sun, the vertical transport of the magnetic field has been used to probe the convective zone (CZ; Arkhypov et al. 2012). Active regions on the solar surface are generally thought to originate from a toroidal magnetic field generated by dynamo mechanisms operating at the base of the solar CZ (Tobias 2002). The magnetic field lines have to traverse the entire CZ before they reach the photosphere to form observable active regions. Numerical modeling shows that convective flows at deep layers control the rising of magnetic tubes, and hence the surface patterns of activity (Weber et al. 2013).
Chaotic convection or turbulence is typical in solar and stellar CZs. Its specific power spectrum and dynamics observed in activity patterns at the solar/stellar surface could be used as markers of deep mixing. These markers could manifest themselves as surface formations corresponding to the largest convective cells which involve material from the deepest layers below the photosphere.
Until recently, only relatively small-scale convective cells (from granules to supergranules with diameters of 30 Mm) had been detected in the solar photosphere (Rieutord & Rincon 2010). However, turbulent cascades have now been identified in the power spectra of variations of solar activity at scales up to 380 Mm (Arkhypov et al. 2013). Moreover, the timescales of variability for activity complexes of global sizes (>190 Mm) were shown to be consistent with the predictions of Kolmogorov’s theory of turbulence (Arkhypov et al. 2011, 2013). These features are the “fingerprints” of turbulence deep in the solar CZ. With a similar approach, we search for manifestations of deep mixing in stars with Kepler stellar photometry.
2. The method
Our method (Fig. 1) is based on the analysis of rotational modulation of radiation flux F, which reflects the longitudinal distribution of star spots.
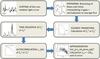 |
Fig. 1 General scheme of the used method of the light-curve processing. See the text for details. |
We selected for our analysis high-precision light curves of 513 main-sequence stars from the Kepler mission database1 with known rotation periods of 1 < P < 4 days (Nielsen et al. 2013), effective temperatures of 3504 < Teff < 6740 K (corresponding to spectral types of M1V to F5V), and clear spot variability.
These stars form the clear main sequence in the mass-temperature frame (Fig. 2). Since the stellar mass Mstar is scaled with the luminosity of a star, the mass-temperature plot may be considered a version of an HR-diagram. Some stars deviate from the main sequence at lower Teff. Note that we consider here only fast-rotating objects (with 1 < P < 4 days). These short periods are typical for G-stars (Mstar/Msun ≈ 1) in young stellar clusters of age ≲150 Myr. The periods P < 4 day are a rarity in old clusters (Meibom et al. 2011). Hence, the deviated stars may be interpreted as very young objects, which have not yet reached the main sequence.
 |
Fig. 2 Distribution of the selected stars (crosses) in the mass-temperature frame according to the reference catalog (Nielsen et al. 2013). The stellar mass, Mstar, is calculated as Mstar = (gR2) /γ, using the catalog values for the gravitation acceleration g in the photosphere and the stellar radius, R. Here γ is the gravitational constant. |
For each star, we processed all available data (data from quarters 0 to 16 in the Kepler archive) with long cadences. Each series of quarterly data contains 60 000 measurements per star of the radiation flux F (“PDCSAP_FLUX”) corrected for instrumental and environmental effects.
 |
Fig. 3 Major preparation steps of light curves: a) typical fragment of a raw light curve with starspot variability (the star KIC 7899309); b) normalized one-period light-curve for the star KIC 9019435 with flares; c) same b) renormalized curve after removal of the flares and the trend. |
The amplitude of such variability, normalized to the average flux over a rotation period P, is practically independent from residual instrumental trends in Kepler light curves, which have timescales much longer than the stellar rotation periods. We try to minimize the influence of stellar pulsations and instrumental trends on our results, which is why our study is focused on the rotational harmonics of the flux variability. Below we describe the main steps of the light curve analysis as shown in Fig. 1.
-
1.
-
CLIPPING. The first step in our analysis chain is the clipping ofone-period light curves from the whole data set for a particularstar. To deal mainly with the rotational variability, we divide theentire light curve of a star F(t), where t is time, into consecutive segments, each with durations of one stellar rotation period, P. These one-period light curves are analyzed separately further on.

Fig. 4 Influence of the error ΔP of the stellar rotation period P on the squared amplitudes of the first
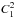 and second
and second 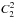 harmonics of rotational modulation of F (the analyzed parameters in our method). The variable
harmonics of rotational modulation of F (the analyzed parameters in our method). The variable 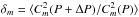 is the average ratio between the values
is the average ratio between the values 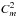 calculated for the same stellar rotation but using the adopted P and slightly modified P + ΔP rotation periods. The individual ratios were averaged using the whole stellar set (513 objects) for both harmonics with numbers m = 1 (squares and solid line) and m = 2 (diamonds and dashed line).
calculated for the same stellar rotation but using the adopted P and slightly modified P + ΔP rotation periods. The individual ratios were averaged using the whole stellar set (513 objects) for both harmonics with numbers m = 1 (squares and solid line) and m = 2 (diamonds and dashed line). We do not measure stellar rotation periods, but use the published average values of P (Nielsen et al. 2013). Typically, the differential rotation and the variability of spot latitudes could give a few percent variation in P (Reinhold et al. 2013). Figure 4 shows that the corresponding errors 1 − δm in squared amplitude of the first and second harmonics
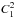 and
and 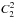 of rotational modulation of F, which are analyzed further on, are negligible values (| 1 − δm| < 10%) at ΔP/P ≲ 0.1. In the course of visual control of the light curves of all considered objects two stars (KIC 11349386 and KIC 12066633) were excluded from the analyzed set because of an erroneously estimated period (P/ 2 instead of P) in the catalog. The typical example of a one-period light curve is presented in (Fig. 3b).
of rotational modulation of F, which are analyzed further on, are negligible values (| 1 − δm| < 10%) at ΔP/P ≲ 0.1. In the course of visual control of the light curves of all considered objects two stars (KIC 11349386 and KIC 12066633) were excluded from the analyzed set because of an erroneously estimated period (P/ 2 instead of P) in the catalog. The typical example of a one-period light curve is presented in (Fig. 3b). -
2.
PREPARING. We also prepared each one-period light curve for the spectral analysis. To remove stellar flares in a one-period light curve (Fig. 3b), we calculate an average flux value, ⟨ F ⟩, and the dispersion, σ, at the same rotational phases, i.e. for F(t − P), F(t) and F(t + P). If the condition [F(t) − F(t − P)] /σ> 1 or [F(t) − F(t + P)] /σ> 1 is satisfied, then we replace the measured F(t) with the value [F(t − P) + F(t + P)] /2 (Fig. 3c). After this we remove the linear trend, so that F(t) = F(t + P). We filled the small (<0.1P) gaps in the light curves were filled using linear interpolation to provide equidistant counts of F. The periods with larger gaps were ignored. Then each of the one-period light-curve segments was normalized to its mean flux and processed with the standard Fourier method to obtain the power spectrum consisting of only rotational harmonics, which have periods P, P/ 2, P/ 3, etc.
-
3.
FOURIER TRANSFORM. For each one-period light curve, we calculate an individual squared amplitude
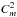 of spectral harmonics in the discrete Fourier transform:
of spectral harmonics in the discrete Fourier transform: 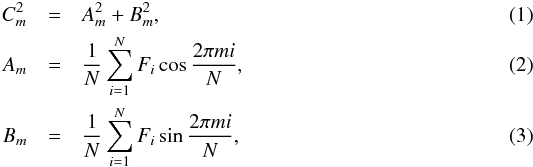 where m is the harmonic number; N is the number of all flux readings (Fi) in the one-period light-curve; i is the flux reading number in the one-period light curve. Breaking up the light curve in chunks of one rotation period length and calculation of individual
where m is the harmonic number; N is the number of all flux readings (Fi) in the one-period light-curve; i is the flux reading number in the one-period light curve. Breaking up the light curve in chunks of one rotation period length and calculation of individual 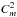 has the following advantages:
has the following advantages: -
a)
Decreasing the influence of long-period (>P) stellar variability and instrumental trends on
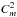 .
. -
b)
Decreasing the influence of short-period (≪P) stellar pulsations and photon noise on low-m harmonics, e.g.,
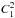 and
and 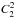 .
. -
c)
Monitoring the longitudinal distribution of starspots with maximal resolution in time (i.e., P).
The study of the longitudinal distribution of stellar activity helpsto reveal photospheric manifestations of deep convection. Thesemanifestations were found in the Sun (Arkhypovet al. 2011, 2013) and reproduced in numericalmodeling (Weber et al. 2013).
-
a)
-
4.
TIME SEQUENCES. Applying the above described sequence of procedures to all one-period light curves, we obtain the time sequences of values of
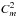 (Fig. 5, top panel). Although the summation of light from different parts of a stellar disk decreases the amplitude of a harmonic, the timescale of its variability is conserved. Hence, this should not distort the “size − timescale” relation. To investigate this relation, we analyzed the series of consecutive one-period light curves by constructing the chronological sequences of the power spectra of rotational variability.
(Fig. 5, top panel). Although the summation of light from different parts of a stellar disk decreases the amplitude of a harmonic, the timescale of its variability is conserved. Hence, this should not distort the “size − timescale” relation. To investigate this relation, we analyzed the series of consecutive one-period light curves by constructing the chronological sequences of the power spectra of rotational variability. -
5.
AUTOCORRELATION. The obtained time sequences of
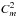 were processed with the autocorrelation analysis method to extract information on the timescale of the harmonic variability. We pay particular attention to the temporal behavior of the squared amplitudes,
were processed with the autocorrelation analysis method to extract information on the timescale of the harmonic variability. We pay particular attention to the temporal behavior of the squared amplitudes, 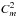 , of the most reliably measured harmonics, i.e. those with the number m< 3.
, of the most reliably measured harmonics, i.e. those with the number m< 3. 
Fig. 5 Example of a chronological sequence of
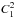 of the star KIC 7294867 (top plot) and the corresponding autocorrelation functions (bottom) against lag Δt for m = 1 (squares) and m = 2 (crosses). The quadratic trinomial approximations of ln(rm) at short lags (1 ≤ Δt/P ≤ 4) are shown as the dashed (m = 1) and dotted (m = 2) curves. The timescale ΔJD = JD − 2 454 833 in the top panel is the difference of barycentric Julian days (JD).
of the star KIC 7294867 (top plot) and the corresponding autocorrelation functions (bottom) against lag Δt for m = 1 (squares) and m = 2 (crosses). The quadratic trinomial approximations of ln(rm) at short lags (1 ≤ Δt/P ≤ 4) are shown as the dashed (m = 1) and dotted (m = 2) curves. The timescale ΔJD = JD − 2 454 833 in the top panel is the difference of barycentric Julian days (JD).The autocorrelation coefficient rm(Δt) in the chronological sequence of
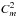 was calculated for the standard set of time lags Δt = nP, where n = 1,2,3,4 (Fig. 5):
was calculated for the standard set of time lags Δt = nP, where n = 1,2,3,4 (Fig. 5): ![\begin{equation} \label{autocorrelation} r_{m}(\Delta t) = \frac{1}{N}\frac{\sum_{i=0}^{N-1}\left\{\left[C_{m}^{2}(t_i)-\langle C_{m}^{2} \rangle\right] \left[C_{m}^{2}(t_i + \Delta t)-\langle C_{m}^{2} \rangle\right]\right \}}{\sigma_{1} \sigma_{2}}, \end{equation}](/articles/aa/full_html/2015/04/aa25307-14/aa25307-14-eq61.png) (4)where
(4)where ![\begin{eqnarray} \label{sigma1} && \sigma_{1} = \sqrt{\frac{1}{N}\sum_{j=0}^{N-1} \left[C_{m}^{2}(t_j)-\langle C_{m}^{2}(t)\rangle \right]^{2}},\\ \label{sigma2} && \sigma_{2} = \sqrt{\frac{1}{N}\sum_{k=0}^{N-1} \left[C_{m}^{2}(t_k+\Delta t)-\langle C_{m}^{2}(t+\Delta t)\rangle \right]^{2}}. \end{eqnarray}](/articles/aa/full_html/2015/04/aa25307-14/aa25307-14-eq62.png) Here
Here 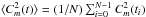 and
and 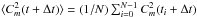 are the average values; N is the number of pairs
are the average values; N is the number of pairs 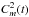 and
and 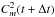 , which were found in the chronological sequence. The subscripts i, j and k at the time t are the number of stellar rotations.
, which were found in the chronological sequence. The subscripts i, j and k at the time t are the number of stellar rotations. -
6.
APPROXIMATION. To extract the information on the timescale of the harmonic variability (i.e., the dynamics of the activity pattern in stellar photosphere), the natural logarithm of rm(Δt) is approximated at short lags (1 ≤ Δt/P ≤ 4), as shown in Fig. 5, using the quadratic trinomial
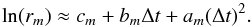 (7)For calculation of the coefficients am,bm,cm and their standard errors, we use the least square method and the minimal set of the lags Δt/P = 1,2,3, and 4 in the normal Eqs. (7). Only these short lags are considered to minimize the influence of non-quadratic terms of higher orders. We ignore the null lag to avoid the decorrelation jump between Δt/P = 0 and 1 due to processes with timescales shorter than P (photon noise, micro-flares, pulsations, granulation variability, etc.). These decorrelation jumps are well visible in Fig. 5 for both harmonics, where the extrapolation of approximating curves at Δt/P = 0 give log (rm) < 0 instead of the real value log (1) = 0. Since the dimension of the coefficient bm in Eq. (7) is the inverted time, and bm< 0, one can introduce the timescale τm = −1 /bm. In view of the fact that the manifestation of deep mixing was found in the linear term of the logarithmic approximation of the solar activity autocorrelation (Arkhypov et al. 2011, 2013), below we check whether the analogous stellar parameter τm = −1 /bm is related to τMLT.
(7)For calculation of the coefficients am,bm,cm and their standard errors, we use the least square method and the minimal set of the lags Δt/P = 1,2,3, and 4 in the normal Eqs. (7). Only these short lags are considered to minimize the influence of non-quadratic terms of higher orders. We ignore the null lag to avoid the decorrelation jump between Δt/P = 0 and 1 due to processes with timescales shorter than P (photon noise, micro-flares, pulsations, granulation variability, etc.). These decorrelation jumps are well visible in Fig. 5 for both harmonics, where the extrapolation of approximating curves at Δt/P = 0 give log (rm) < 0 instead of the real value log (1) = 0. Since the dimension of the coefficient bm in Eq. (7) is the inverted time, and bm< 0, one can introduce the timescale τm = −1 /bm. In view of the fact that the manifestation of deep mixing was found in the linear term of the logarithmic approximation of the solar activity autocorrelation (Arkhypov et al. 2011, 2013), below we check whether the analogous stellar parameter τm = −1 /bm is related to τMLT.
3. Results
With approach described above, we estimate τ1 and τ2 from the chronological sequences of 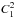 and
and 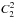 , respectively. The first and second (most powerful) harmonics are measured with maximal accuracy. Moreover, these harmonics could be connected with the nests of locally enhanced convection, revealed in numerical models of fast-rotating stars (Brown et al. 2008). The top panel in Fig. 6 shows that our τ1, as a function of stellar effective temperature, behaves similar to the theoretical τMLT from Eq. (4) in the classical paper (Noyes et al. 1984) after a transformation from the color scale into Teff (Flower 1996). The average shift 0.82 ± 0.02 between log (τ1) and log (τMLT) is because τMLT was calculated for moderate convective cells, while the considered (best measured) harmonic (m = 1) is related to larger scales. In the bottom panel of Fig. 6, we show that there is a linear relation between τ1 and τMLT, with a linear regression index of ∂ [log (τ1)] /∂ [log (τMLT)] = 1.13 ± 0.06, and hence, we conclude that τ1 is proportional to the timescale of deep mixing.
, respectively. The first and second (most powerful) harmonics are measured with maximal accuracy. Moreover, these harmonics could be connected with the nests of locally enhanced convection, revealed in numerical models of fast-rotating stars (Brown et al. 2008). The top panel in Fig. 6 shows that our τ1, as a function of stellar effective temperature, behaves similar to the theoretical τMLT from Eq. (4) in the classical paper (Noyes et al. 1984) after a transformation from the color scale into Teff (Flower 1996). The average shift 0.82 ± 0.02 between log (τ1) and log (τMLT) is because τMLT was calculated for moderate convective cells, while the considered (best measured) harmonic (m = 1) is related to larger scales. In the bottom panel of Fig. 6, we show that there is a linear relation between τ1 and τMLT, with a linear regression index of ∂ [log (τ1)] /∂ [log (τMLT)] = 1.13 ± 0.06, and hence, we conclude that τ1 is proportional to the timescale of deep mixing.
 |
Fig. 6 Experimental estimates of τ1 are compared with the model τMLT (Noyes et al. 1984). Top panel: relation of individual estimates of log (τ1) (crosses), their average values in the 300 K-intervals of Teff (squares with error bars), and log (τMLT) (dashed curve) with stellar effective temperature Teff. The solid line of log (τMLT) + 0.82 well approximates the experimental data. Bottom panel: comparison between log (τ1) and log (τMLT) shows a near-linear relation. The slope of the linear regression line (solid) is 1.13 ± 0.06. |
The second harmonic shows even better proximity to the MLT curve (Fig. 7, top panel), however, the value 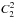 is systematically less than
is systematically less than 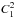 , which explains why τ2 is more scattered because of difficulties of measurement. In Fig. 7(bottom) its linear regression with τMLT has reduced index ∂ [log (τ2)] /∂ [log (τMLT)] = 0.56 ± 0.07 suggesting the interference from a non-deep-mixing process.
, which explains why τ2 is more scattered because of difficulties of measurement. In Fig. 7(bottom) its linear regression with τMLT has reduced index ∂ [log (τ2)] /∂ [log (τMLT)] = 0.56 ± 0.07 suggesting the interference from a non-deep-mixing process.
Apparently, this interference, the damping of 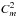 by the summation of light from different parts of a stellar disk, and the stellar microvariability are responsible for the disappearance of MLT-analogy in the behavior of τm at m ≥ 3.
by the summation of light from different parts of a stellar disk, and the stellar microvariability are responsible for the disappearance of MLT-analogy in the behavior of τm at m ≥ 3.
 |
Fig. 7 Same as in Fig. 6, for m = 2. The average shift between log (τ2) and log (τMLT) is 0.29 ± 0.03. |
 |
Fig. 8 Histograms of the parameter β = [log (τ2) − log (τ1)] /log (2), constructed using the best 108 pairs of τ1 and τ2 estimates with errors below 17% using different bin resolutions (gray and dark, respectively). The dashed line shows the prediction of Kolmogorov’s theory of turbulence β = −0.67 (Lang 1974). The vertical parameter n is the number of β estimates in one bin of a histogram. |
Kolmogorov’s theory of turbulence (Lang 1974) predicts a universal relation between the characteristic size of turbulent eddies (L) and the timescale of their variability (τL) as τL ∝ L2/3 or τL ∝ m-0.67 (taking into account that L = 360°/m). To check this relationship, we built a histogram (Fig. 8) of the derivative β = ∂ [log (τm)] /∂ [log (m)] ≈ [log (τ2) − log (τ1)] /log (2) using 108 stars from the analyzed sample with the most precise (errors below 17%) estimates of τ1 and τ2. The histogram peak agrees with the prediction of the theory of turbulence (β = −0.67; dashed line in Fig. 8), whereas the residual manifestations of nonrotational variability decrease β in some cases. We interpret this result as an indication that our measurements are statistically consistent with Kolmogorov turbulence at the super-large scales of deep mixing, since other effects (addressed below) cannot explain the main peak in Fig. 8.
The horizontal diffusion effectively decreases the harmonic amplitude, when the average displacement of magnetic elements is about the longitudinal period of harmonic 360°/m during the time tm = (360°/m)2η-1 (η is the diffusion coefficient). In this case one can obtain β = ∂ [log (tm)] /∂ [log (m)] ≈ [log (t2) − log (t1)] /log (2) = −2.
The differential rotation of a star stretches the activity complex area over the longitudinal harmonic scale Λm = 360°/m during the time Tm = Λm/ ΔΩ, where ΔΩ ≈ εΛm/ 2 is a typical difference of angular velocity Ω in the complex, and ε is an average latitudinal gradient of Ω. Hence, the timescale of the complex blurring (i.e., 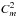 damping) is Tm = 2 /ε, which corresponds to β = ∂ [log (Tm)] /∂ [log (m)] = 0.
damping) is Tm = 2 /ε, which corresponds to β = ∂ [log (Tm)] /∂ [log (m)] = 0.
Therefore, the decay processes, such as horizontal diffusion and differential rotation should produce histogram peaks in at β = −2 and β = 0, respectively, which are not readily visible in Fig. 8. Apparently, as in the Sun (Arkhypov et al. 2011), the evolution of supergiant complexes of stellar activity is more related with deep mixing than that of smaller active regions.
Stellar magnetic activity is another source of information on deep mixing. It is expected (Noyes et al. 1984) that the stellar activity level is proportional to Roγ, where Ro = P/τMLT is the Rossby number, and γ = −2. Experimental studies confirm that Ro is much better than P as a predictor of stellar activity (Noyes et al. 1984; Wright 2011). Similarly, we investigated the dependence of stellar activity on Ro, defined using τ1 instead of τMLT.
We determine the activity index 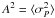 by averaging over all one-period light curves, where
by averaging over all one-period light curves, where 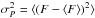 is a variance of an individual one-period light curve, which is a sum of variances of flux fluctuations from particular star spots. Thus, A2 is proportional to the average spot number, which is the classical index of solar activity (the Wolf number).
is a variance of an individual one-period light curve, which is a sum of variances of flux fluctuations from particular star spots. Thus, A2 is proportional to the average spot number, which is the classical index of solar activity (the Wolf number).
 |
Fig. 9 Our estimated activity parameter, A2, against rotation period Pa) and Rossby number P/τ1b). |
Figure 9 shows the effect of using τ1 instead of τMLT to construct the Rossby number P/τ1. In the same way as τMLT, τ1 turns the noncorrelated distribution of data points in A2 − P space (Fig. 9a) into a sharp cluster (Fig. 9b). The most reliable approximation for this cluster is the regression log (P/τ1) = h + qlog (A2), with h = −3.34 ± 0.10 and q = −0.41 ± 0.02 (solid line in Fig. 9b). The derivative ∂ [log (A2)] /∂ [log (P/τ1)] = 1 /q = −2.42 ± 0.13 is not far from the canonical value γ = −2 and in accordance with the estimates (γ ≈ − 2.18 to −2.70) based on X-ray data and τMLT (Wright et al. 2011).
 |
Fig. 10 Laminar convective timescale τlam (crosses) and its averaged estimates (squares) with the standard error bars as compared with the averaged τMLT curve (Noyes et al. 1984; solid) for m = 1 (top panel) and m = 2 (bottom). |
A surprising result is obtained, when we reduce the timescale τm to the laminar convective scale according to the Kolmogorov’s turbulence index τlam = τm(mlam/m)− 2/3, where mlam = 2πRstar/Dlam, Rstar is the stellar radius, and Dlam ≈ 23/2H is the typical diameter of a laminar convective cell (Dibaj & Kaplan 1976) with H as the CZ depth (van Saders & Pinsonneault 2012). Figure 10 shows that τlam approaches τMLT, especially at m = 2. This confirms the special role of the laminar scale in deep turbulence, demonstrated in particular for the Sun (Arkhypov et al. 2012, 2013).
4. Conclusions
The applied method is applicable for a mass measurement of the timescale of stochastic changes in the evolution of stellar activity complexes of a selected dimension.
Based on observational data, we found the correspondences between the measured timescales τ1, τ2 and the properties of deep mixing in main-sequence stars. Hence, the deep convection of global scale is manifested in stellar photometric light curves. This result opens the way for direct measurement of the turnover time in stellar convective zones. The turnover time plays a key role in theories of stellar structuring, evolution and magnetism.
The detection of turbulence manifestation (the histogram peak at β ≈ − 2/3 in Fig. 8) at the maximal scales (harmonics m = 1 and 2) suggests the existence of global convective flows in CZs of the fast-rotating stars that we studied. However, the numerical simulations predict the short-scale (m ~ 20; Brown et al. 2008) columnar convection cells, clustered in “nests” in equatorial CZs of fast-rotating sun-like stars. Apparently, the Coriolis force, as a driver of the columnar convection, is less important for the slow, super-large-scale flows between the convective nests, especially near tachocline. The nest modulation of convective pattern at m = 1 and 2 (Brown et al. 2008) may indicate that global flows trigger the development of enhanced columnar convection. Our result is an argument for this connection.
The indication of an important role of the laminar scale in stellar deep turbulence, found initially for the Sun (Arkhypov et al. 2013), has been confirmed in the context of Fig. 10. This effect could explain the astrophysical success of MLT, which is based on the abstraction of standard convection cells.
Acknowledgments
This work was performed as a part of the project P25587-N27 of the Fonds zur Förderung der wissenschaftlichen Forschung, FWF. The authors also acknowledge the FWF projects S11606-N16, S11604-N16, S11607-N16.
References
- Arkhypov, O. V., Antonov, O. V., & Khodachenko, M. L. 2011, Sol. Phys., 270, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhypov, O. V., Antonov, O. V., & Khodachenko, M. L. 2012, Sol. Phys., 278, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Arkhypov, O. V., Antonov, O. V., & Khodachenko, M. L. 2013, Sol. Phys., 282, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Bessolaz, N., & Brun, A. S. 2011, ApJ, 728, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Brown, D. P., Browning, M. K., Brun, A. S., Miesch, M. S., & Toomre, J. 2008, ApJ, 689, 1354 [CrossRef] [Google Scholar]
- Dibaj, Eh. A., & Kaplan, S. A. 1976, Dimensions and Similarity of Astrophysical Quantities (Moscow: Nauka), 239 [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355, Table 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hanasoge, S. M., Duvall, T. L., & DeRosa, M. L. 2010, ApJ, 712, L98 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y.-C., Demarque, P. 1996, ApJ, 457, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, K. R. 1974, Astrophysical Formulae (Berlin: Springer), Chap 3.5.12 [Google Scholar]
- Meibom, S., Mathieu, R. D., Stassun, K. G.,Liebesny, P., & Saar, S. H. 2011, ApJ, 733, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, M. B., Gizon, L., Schunker, H., & Karoff, C. 2013, A&A, 557, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhold, T., Reiners, A., & Basri, G. 2013, A&A, 560, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys. 7, 1 [NASA ADS] [Google Scholar]
- van Saders, J. L., & Pinsonneault, M. H. 2012, ApJ, 746, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Tobias, S. M. 2002, Phil. Trans. R. Soc. London, Ser. A., 360, 2741 [Google Scholar]
- Weber, M. A., Fan, Y., & Miesch, M. S. 2013, ApJ, 770, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. E., & Cuntz, M. A., 2009, A&A, 505, 1265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 General scheme of the used method of the light-curve processing. See the text for details. |
| In the text | |
 |
Fig. 2 Distribution of the selected stars (crosses) in the mass-temperature frame according to the reference catalog (Nielsen et al. 2013). The stellar mass, Mstar, is calculated as Mstar = (gR2) /γ, using the catalog values for the gravitation acceleration g in the photosphere and the stellar radius, R. Here γ is the gravitational constant. |
| In the text | |
 |
Fig. 3 Major preparation steps of light curves: a) typical fragment of a raw light curve with starspot variability (the star KIC 7899309); b) normalized one-period light-curve for the star KIC 9019435 with flares; c) same b) renormalized curve after removal of the flares and the trend. |
| In the text | |
 |
Fig. 4 Influence of the error ΔP of the stellar rotation period P on the squared amplitudes of the first |
| In the text | |
 |
Fig. 5 Example of a chronological sequence of |
| In the text | |
 |
Fig. 6 Experimental estimates of τ1 are compared with the model τMLT (Noyes et al. 1984). Top panel: relation of individual estimates of log (τ1) (crosses), their average values in the 300 K-intervals of Teff (squares with error bars), and log (τMLT) (dashed curve) with stellar effective temperature Teff. The solid line of log (τMLT) + 0.82 well approximates the experimental data. Bottom panel: comparison between log (τ1) and log (τMLT) shows a near-linear relation. The slope of the linear regression line (solid) is 1.13 ± 0.06. |
| In the text | |
 |
Fig. 7 Same as in Fig. 6, for m = 2. The average shift between log (τ2) and log (τMLT) is 0.29 ± 0.03. |
| In the text | |
 |
Fig. 8 Histograms of the parameter β = [log (τ2) − log (τ1)] /log (2), constructed using the best 108 pairs of τ1 and τ2 estimates with errors below 17% using different bin resolutions (gray and dark, respectively). The dashed line shows the prediction of Kolmogorov’s theory of turbulence β = −0.67 (Lang 1974). The vertical parameter n is the number of β estimates in one bin of a histogram. |
| In the text | |
 |
Fig. 9 Our estimated activity parameter, A2, against rotation period Pa) and Rossby number P/τ1b). |
| In the text | |
 |
Fig. 10 Laminar convective timescale τlam (crosses) and its averaged estimates (squares) with the standard error bars as compared with the averaged τMLT curve (Noyes et al. 1984; solid) for m = 1 (top panel) and m = 2 (bottom). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


