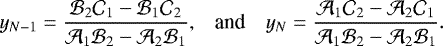| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 23 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731683 | |
| Published online | 31 May 2018 | |
Semidiurnal thermal tides in asynchronously rotating hot Jupiters
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N,
allée Geoffroy Saint-Hilaire,
33615
Pessac,
France
e-mail: pierre.auclair-desrotour@u-bordeaux.fr, jeremy.leconte@u-bordeaux.fr
Received:
31
July
2017
Accepted:
21
January
2018
Context. Thermal tides can torque the atmosphere of hot Jupiters into asynchronous rotation, while these planets are usually assumed to be locked into spin-orbit synchronization with their host star.
Aims. In this work, our goal is to characterize the tidal response of a rotating hot Jupiter to the tidal semidiurnal thermal forcing of its host star by identifying the structure of tidal waves responsible for variation of mass distribution, their dependence on the tidal frequency, and their ability to generate strong zonal flows.
Methods. We develop an ab initio global modelling that generalizes the early approach of Arras & Socrates (2010, ApJ, 714, 1) to rotating and non-adiabatic planets. We analytically derive the torque exerted on the body and the associated timescales of evolution, as well as the equilibrium tidal response of the atmosphere in the zero-frequency limit. Finally, we numerically integrate the equations of thermal tides for three cases, including dissipation and rotation step by step.
Results. The resonances associated with tidally generated gravito-inertial waves significantly amplify the resulting tidal torque in the range 1–30 days. This torque can globally drive the atmosphere into asynchronous rotation, as its sign depends on the tidal frequency. The resonant behaviour of the tidal response is enhanced by rotation, which couples the forcing to several Hough modes in the general case, while the radiative cooling tends to regularize it and diminish its amplitude.
Key words: hydrodynamics / planet-star interactions / waves / planets and satellites: atmospheres / planets and satellites: gaseous planets
© ESO 2018
1 Introduction
Modelling the general circulation of hot Jupiters is a key element in observationally constraining their properties (temperature structure, day-night heat transport, circulation regime). In particular, it allows to establish a link between these properties and the Doppler shift in the transmission spectra of the planets that can be measured in orbital phase curves of secondary eclipses (e.g. Rauscher & Kempton 2014). Because of their proximity to their host star, hot Jupiters orbiting circularly are generally assumed to be locked into spin-orbit synchronous rotation, meaning that their rotation rate is exactly equal to their orbital frequency (see Showman et al. 2015, and references therein). The argument invoked for this assumption is the mechanism of gravitational tides, which torques the planet towards this state of equilibrium. Given the strength of the tidal torque, the timescale associated with this evolution (a few million years, see Showman & Guillot 2002; Ogilvie & Lin 2004) is short compared to that associated with the evolution of the planetary system. Thus, tidal forces should lock the planet into synchronous rotation before they circularize its orbit (e.g. Rasio et al. 1996). However, other arguments have been given in recent works in favour of an asynchronous rotation, leading some authors to consider this configuration (e.g., Showman et al. 2009, 2015; Rauscher & Kempton 2014; Tsai et al. 2014).
These arguments invoke the transport of angular momentum between the planet’s orbit and its atmosphere or interior Showman & Guillot (2002), the forcing of a fast super-rotating equatorial jet in the atmosphere by the strong day-night heating contrast (Showman et al. 2015), and the ability of thermal tides to generate asynchronous zonal flows (Gu & Ogilvie 2009; Arras & Socrates 2010). This latter mechanism was first introduced by Gold & Soter (1969) through an ad hoc approach to explain the locking of Venus at the observed retrograde rotation rate. It results from the incoming stellar flux, which submits the atmosphere to a day-night periodic forcing. This forcing, like the tidal gravitational potential, generates density fluctuations leading to a global variation of mass distribution. The tidal torque induced by thermal tides can be in opposition with that induced by the gravitational forcing. In this case, the rotation of Venus-like planets evolves toward the asynchronous state of equilibrium where solid and atmospheric tidal torques compensate each other exactly (see Ingersoll & Dobrovolskis 1978; Dobrovolskis & Ingersoll 1980; Correia & Laskar 2001, 2003; Auclair-Desrotour et al. 2017b). These arguments have recently been reinforced by results obtained with ab initio models showing that the internal structure of the fluid layer and timescale associated with dissipative processes directly affect its tidal response (Leconte et al. 2015; Auclair-Desrotour et al. 2017a).
However, as discussed by Gu & Ogilvie (2009), there is no solid surface in hot Jupiters to support the load of a mass surplus in the atmosphere of the planet as in telluric Venus-like planets. As a consequence, it would seem that no net tidal bulge could appear and the tidal torque exerted on the atmosphere should be negligible. This seems to be at odds with the conclusions of Arras & Socrates (2010) about semidiurnal thermal tides, who argue for a strong amplification of the tidal torque in the range of forcing periods 1–30 days due to the propagation of resonant internal waves (see also Lubow et al. 1997). In this early work, the dynamical effect of rotation of the planet was ignored, although it is directly related to the forcing frequency. Similarly, dissipative processes such as radiative cooling were not taken into account although they dissipate the energy of tidally generated gravity modes (Terquem et al. 1998). Thus, we propose here to revisit the study by Arras & Socrates (2010) by using a similar ab initio global modelling. In this linear approach, we include both the coupling induced by rotation between excited tidal modes and the tidal forcing, and the dissipation resulting from radiative/diffusive cooling, which is modeled by a Newtonian cooling. We aim at (1) clarifying the internal structure of the tidal response by identifying dominating modes, their characteristics and their behaviour; (2) quantifying the order of magnitude of timescales associated with the forcing of zonal-mean flows by the semidiurnal thermal tide; and (3) characterizing how the rotation and radiative cooling affect the thermal tidal response and the resulting tidal torque.
Hence, in Sect. 2, we detail the physical setup of the model, establish the equations describing the structure of forced tidal waves, and discuss the used boundary conditions and gravitational and thermal tidal forcings. In Sect. 3, the expressions of the tidal torques and quadrupoles are given, and the associated evolution timescales introduced. Then, in Sect. 4, we compute the tidal response of the planet due to the thermal component and the associated evolution timescales in three cases: (a) in a static and adiabatic planet (case treated by Arras & Socrates 2010), (b) in a static planet with radiative cooling, and (c) in a rotating planet with radiative cooling. We show that a resonant behaviour can arise from the reflection of gravity waves on the boundaries of the stably stratified radiative zone. The radiative cooling tends to attenuate the amplitude of the response, while rotation increases it in the zero-frequency limit. In Sect. 5, we compute the frequency spectra of the total tidal torque in the above three cases. In the static case, we reproduce the results previously obtained by Arras & Socrates (2010) and show that rotation amplifies the resonant behaviour of the tidal response. Synchronization timescales associated with the gravitational and thermal tidal components are computed in Sect. 6. We finally discuss the consequences of thermal tides on zonal-flows and the used approximations in Sect. 7, and give our conclusions in Sect. 8.
2 Tidal waves dynamics
In this section, we establish the equations describing the tidal response of a rotating Jupiter submitted to both gravitational and thermalforcings. Thermal tides have been examined before in different ways (Gu & Ogilvie 2009; Arras & Socrates 2010; Leconte et al. 2015). Here, we use the formalism developed by Auclair-Desrotour et al. (2017a) with the physical setup of Arras & Socrates (2010).
2.1 Physical setup and background distributions
We consider a Jovian planet of mass Mp and radius Rp, rotating on itself at the spin angular velocity Ω, and orbiting its host star at the dynamical frequency norb. In order to avoid mathematical complications related to internal circulation, we assume in this study that the planet is in uniform rotation (this simplification is discussed in Sect. 7). The associated co-rotating reference frame centred on the centre of inertia of the body is denoted 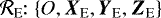 , where
, where 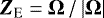 , Ω being the rotation vector of the planet, and XE and YE designate two directions of the equatorial plane. To locate a point M of the planet, we use the spherical vectorial basis
, Ω being the rotation vector of the planet, and XE and YE designate two directions of the equatorial plane. To locate a point M of the planet, we use the spherical vectorial basis 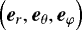 and coordinates
and coordinates 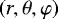 , which refer to the radius, the colatitude, and the longitude, respectively (see Fig. 1). Hence, the position vector is expressed as r = r er.
, which refer to the radius, the colatitude, and the longitude, respectively (see Fig. 1). Hence, the position vector is expressed as r = r er.
The internal structure of the planet is defined by spatial distributions of pressure p0, density ρ0, and gravity g. To simplify it, we ignoreday-night temperature gradients and the effect of the centrifugal acceleration. This approximation is appropriate provided that Ω ≪Ωc, 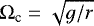 being the critical Keplerian angular velocity. The equation of hydrostatic balance is written
being the critical Keplerian angular velocity. The equation of hydrostatic balance is written
![\begin{equation*} \frac{{\textrm{d}}^2 p_0}{{\textrm{d}}r^2} + \left[ \frac{2}{r} - \left( \frac{{\textrm{d}} \ln \rho_0}{{\textrm{d}} p_0} \right) \frac{{\textrm{d}} p_0}{{\textrm{dr}}} \right] \frac{{\textrm{d}} p_0}{\textrm{dr}} + 4 \pi \mathscr{G} \rho_0^2 = 0,\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq6.png) (1)
(1)
the parameter "G" standing for the gravitational constant. Considering that the planet is basically composed of a deep convective envelope and a superficial, stably stratified atmosphere, we adopt the equation of state proposed by Arras & Socrates (2010) to fully characterize the internal structure. This equation writes
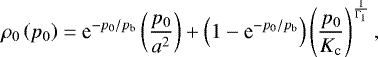 (2)
(2)
where we have introduced the adiabatic exponent Γ1 = 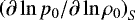 (the index S referring to specific macroscopic entropy), the pressure at the base of the stably stratified layer pb, the characteristic pressure specifying the entropy of the core
(the index S referring to specific macroscopic entropy), the pressure at the base of the stably stratified layer pb, the characteristic pressure specifying the entropy of the core 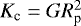 , and the isothermal sound speed of the envelope
, and the isothermal sound speed of the envelope 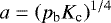 . The transition between the two layers thus occurs at p = pb. Equation (1) is then integrated upward using a Runge-Kutta scheme of the fourth order with the regularity condition dp0 ∕dr = 0 at r = 0. We deduce from the gravity profile the profile of mass contained within the sphere of radius r, expressed as
. The transition between the two layers thus occurs at p = pb. Equation (1) is then integrated upward using a Runge-Kutta scheme of the fourth order with the regularity condition dp0 ∕dr = 0 at r = 0. We deduce from the gravity profile the profile of mass contained within the sphere of radius r, expressed as
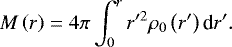 (3)
(3)
Hence, the pressure at the centre of the planet is iterated to make M converge toward Mp at the upper limit, denoted Re. We note that Re determines the pressure level at the upper limit of the atmosphere. It differs from Rp, which is the photospheric radius of the planet, and can be arbitrarily chosen as soon as Re >Rp. In this work, we set Re = 1.01 Rp in order to have 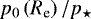 < 10−6 and avoid side effects at the upper boundary.
< 10−6 and avoid side effects at the upper boundary.
Other background distributions are deduced straight- forwardly from p0, ρ0 and g. The vertical profiles of pressure height and sound velocity are expressed as
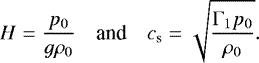 (4)
(4)
The stratification of the fluid with respect to convection is characterized by the Brunt-Väisälä frequency N, defined by
![\begin{equation*} N^2 = - g \left[ \frac{{\textrm{d}} \ln \rho_0}{{\textrm{d}} r} - \frac{1}{{\mathrm{\Gamma}}_1} \frac{{\textrm{d}} \ln p_0}{{\textrm{d}}r} \right].\vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq14.png) (5)
(5)
Finally, we assume that the fluid is a perfect gas uniform in composition, of molar mass 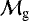 and specific gas constant
and specific gas constant 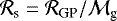 , the notation
, the notation 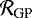 referring to the perfect gas constant. Denoting
referring to the perfect gas constant. Denoting 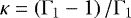 , we get the background profiles of temperature and heat capacity per unit mass,
, we get the background profiles of temperature and heat capacity per unit mass,
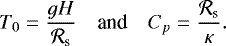 (6)
(6)
In this work, following Lindzen & McKenzie (1967; see also Dickinson & Geller 1968), we take into account the effect of internal dissipation on tidal waves by using a Newtonian cooling, that is, by considering that the local thermal losses Jd due to radiative and diffusive processes are proportional to the temperature variation Δ T. As demonstrated by Iro et al. (2005) with numerical simulations in the case HD 209458b, this approach is justified if Δ T∕T0 does not exceed 5%, which corresponds well to the framework of our linear modelling. The local dissipated power per unit mass can thus be written
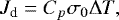 (7)
(7)
where σ0 designates the effective radiative frequency associated with diffusion and radiation. This parameter is the reciprocal of the thermal timescale τ0. The tidal response does not depend much on the vertical profile of τ0. However, it depends on its order of magnitude in the region where the stellar heating is absorbed, typically around the p⋆ pressure level. Therefore, to set τ0, we choose to use the vertical profile computed numerically by Iro et al. (2005) in the case of HD 209458b using an advanced model of thermal transfers (see Fig. 4 in their article). This profile shows two tendencies: 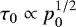 for p0 ≲ p⋆ and
for p0 ≲ p⋆ and 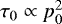 for p0 ≳ p⋆. We thus approximate it by the empirical scaling law
for p0 ≳ p⋆. We thus approximate it by the empirical scaling law
![\begin{equation*} \tau_0 = \frac{\tau_{\star}}{2} \left[ \left( \frac{p_0}{p_{\star}} \right)^{\frac{1}{2}} + \left( \frac{p_0}{p_{\star}} \right)^2 \right], \vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq23.png) (8)
(8)
the parameter τ⋆ standing for the radiative time at the base of the heated layer, at the characteristic pressure p⋆ (τ⋆ ~ 1 − 10 days and p⋆ ≈ 1 bar in the case of HD 209458b, see Showman & Guillot 2002; Cho et al. 2003; Iro et al. 2005). This modelling mimics the two regimes of thermal time, with a transition occurring at p0 ~ p⋆. For p0 < p⋆, τ0 increases slowly with pressure. Below the p⋆-level, pressure broadening increases the opacity rapidly. As a consequence, the effect of radiative cooling becomes negligible. Introducing σ⋆ = 2π∕τ⋆, we define the radiative frequency as
![\begin{equation*} \sigma_0 = 2 \sigma_{\star} \left[ \left( \frac{p_0}{p_{\star}} \right)^{\frac{1}{2}} + \left( \frac{p_0}{p_{\star}} \right)^2 \right]^{-1}.\vspace*{-3pt}\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq24.png) (9)
(9)
In the following, τ⋆ is used as acontrol parameter to specify the efficiency of the radiative cooling, the τ⋆ = +∞ limit corresponding to the adiabatic case.
As the thermal forcing generating thermal tides is absorbed in the upper layers of the atmosphere (in the case of HD 209458b, 99.99% of the incoming stellar flux is absorbed before reaching the 7 bar level, see Iro et al. 2005), the tidal perturbation mainly affects the stably stratified region. Therefore, it is convenient to choose as radial coordinate the reduced altitude defined by
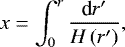 (10)
(10)
rather than the radius r (Chapman & Lindzen 1970). Indeed, this change of coordinates expands the domain of the stably stratified atmosphere (see Ioannou & Lindzen 1993a,b, 1994, for gravitational atmospheric tides in Jovian planets), which allows us to increase the vertical resolution in this region. Another way to expand the heated radiative zone would be to choose the optical depth zop measured from r = +∞ as radial coordinate, as done by Gu & Ogilvie (2009). With this coordinate, the upper limit of the atmosphere corresponds to zop = 0 and the centre of the planet to zop = +∞.
In order to compare our results to those obtained previously by Arras & Socrates (2010), we use the same values of physical parameters. Hence, denoting MJ and RJ the Jupiter’s mass and radius, we set the mass and radius of the planet to Mp = 0.7 MJ and Rp = 1.27 RJ, the core compressibility to 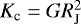 , the adiabatic exponent to Γ 1 = 1.4, the pressure at the base of the radiative atmosphere to pb = 100 bar and the pressure at the base of the heated layer to p⋆ = 1 bar. The corresponding background profiles are plotted in Fig. 2 as functions of r (left panel) and x (right panel) with τ⋆ = 1 day. By comparing the two plots, we observe that the proportion of the vertical domain occupied by the stably stratified atmosphere (N2 ≠ 0) switches from a few percents with r to almost a half of the total domain with x, as mentioned above. The base of the stably stratified layer thus corresponds approximately to x = 11.
, the adiabatic exponent to Γ 1 = 1.4, the pressure at the base of the radiative atmosphere to pb = 100 bar and the pressure at the base of the heated layer to p⋆ = 1 bar. The corresponding background profiles are plotted in Fig. 2 as functions of r (left panel) and x (right panel) with τ⋆ = 1 day. By comparing the two plots, we observe that the proportion of the vertical domain occupied by the stably stratified atmosphere (N2 ≠ 0) switches from a few percents with r to almost a half of the total domain with x, as mentioned above. The base of the stably stratified layer thus corresponds approximately to x = 11.
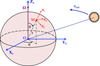 |
Fig. 1 Reference frames and systems of coordinates. The notations Ω and norb designate the rotation vector and the orbital angular velocity respectively. |
 |
Fig. 2 Background profiles normalized by their maxima as functions of the normalized radius r∕Rp (left panel) and of the pressure altitude x (right panel). Values of parameters are those given in Sect. 2.1, that is Mp = 0.7MJ, Rp = 1.27RJ, |
2.2 Structure and regimes of tidal waves
To establish the structure of tidal waves, we summarize the main lines of the formalism detailed in Auclair-Desrotour et al. (2017a). The planet is submitted to the tidal gravitational and thermal forcings of its host star. The gravitational forcing is due to the tidal gravitational potential U, such that the tidal force is defined by F = ∇U (we follow the convention of Zahn 1966), and the tidal heating to the heat power per unit mass J. These forcings generate tidal winds of velocity 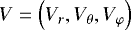 as well as fluctuations of pressure (δp), density (δρ) and temperature (δT), which are assumed to be small compared to background quantities in this linear approach. Thus, conserving only terms of the first order in V, δp, δρ and δT and neglecting the fluctuations of the self-gravitational potential (this is the so-called Cowling approximation, see Cowling 1941), we write the momentum equation (Auclair-Desrotour et al. 2017a)
as well as fluctuations of pressure (δp), density (δρ) and temperature (δT), which are assumed to be small compared to background quantities in this linear approach. Thus, conserving only terms of the first order in V, δp, δρ and δT and neglecting the fluctuations of the self-gravitational potential (this is the so-called Cowling approximation, see Cowling 1941), we write the momentum equation (Auclair-Desrotour et al. 2017a)
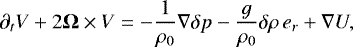 (11)
(11)
where t designates the time and ∂X = ∂∕∂X the partial derivative along the X coordinate. The dynamics are completed by the equation of mass conservation,
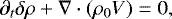 (12)
(12)
and the equation of perfect gas,
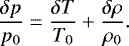 (14)
(14)
It should be noted that this set of primitive equations is very similar to that used by Arras & Socrates (2010). We have only added the effect of rotation by taking into account the Coriolis acceleration (2Ω× V) in the momentum equation, Eq. (11), and the effect of radiative/diffusive processes through the Newtonian cooling term (σ0 δT) in the equation of energy, Eq. (13).
We nowlook for solutions of Eqs. (11)–(14) both periodic in time and longitude. Thus, a perturbed quantity f is expanded into Fourier series,
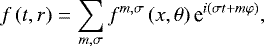 (15)
(15)
where we have introduced the imaginary number i, the tidal frequency σ and the longitudinal wavenumber m of a given mode (typically m = 2 and 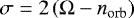 for the stellar semi-diurnal tide studied in the following section). In the following, the superscripts
for the stellar semi-diurnal tide studied in the following section). In the following, the superscripts 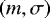 are omitted where no confusion arises.
are omitted where no confusion arises.
The latitudinal projection of the rotation vector in the Coriolis acceleration (Eq. (11)) induces a coupling between the horizontal and the vertical projections of the equation of dynamics. Deriving analytically the structure of the tidal response requires elimination of this coupling. Therefore, we assume the traditional approximation (e.g. Unno et al. 1989), which consists in ignoring 2Ωsinθ terms. This assumption is usually considered as appropriate in the regime of super-inertial waves, defined by 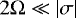 , where rotation hardly affects the fluid tidal response. In strongly stratified regions (
, where rotation hardly affects the fluid tidal response. In strongly stratified regions (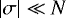 ), the previous condition becomes
), the previous condition becomes 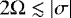 , (Mathis 2009; Prat et al. 2017), which allows us to treat sub-inertial waves in this case (see also Sect. 7). However, as discussed by Ogilvie & Lin (2004), the traditional approximation gives an inaccurate representation of the fluid tidal response within the inertial regime (
, (Mathis 2009; Prat et al. 2017), which allows us to treat sub-inertial waves in this case (see also Sect. 7). However, as discussed by Ogilvie & Lin (2004), the traditional approximation gives an inaccurate representation of the fluid tidal response within the inertial regime (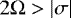 ) in convective regions, because it leads to an overestimated tidal dissipation. In this case, these authors argue that it is better to assume the static approximation, which consists in simply ignoring rotation, as Arras & Socrates (2010) do.
) in convective regions, because it leads to an overestimated tidal dissipation. In this case, these authors argue that it is better to assume the static approximation, which consists in simply ignoring rotation, as Arras & Socrates (2010) do.
In the following sections, we focus on thermal tides and ignore the component of the tidal response generated by the tidal potential. The traditional approximation can be assumed in this case because thermal tides only affect the thin stably stratified atmosphere of the planet, which approximately stands for ~ 2% of the planet radius (see Fig. 2, left panel). Tidal waves induced by the absorption of the stellar heating are expected to propagate within the stably stratified zone and not go through its threshold, as they are mainly restored by the Archimedean force. We verify this postulate a posteriori in Sect. 4 by plotting internal tidal density variations as a function of the latitude and pressure levels. The traditional approximation would lead to strongly inaccurate results if we considered the tidal component generated by the tidal gravitational potential because this forcing affect the whole planet, and particularly the thick convective region, where the assumptions mentioned above are violated. However, we choose to keep the terms associated with the gravitational tidal forcing in the following analytic development for the sake of generality, given that the present model can be applied to the case of the thin stably stratified atmospheric layers of a terrestrial planet, where the traditional approximation can be assumed.
Substituting Eq. (15) into Eqs. (11)–(14) and introducing the reduced pressure fluctuation y = δp∕ρ0, we obtain the set of equations defining the latitudinal and radial distributions of the perturbed quantities,

where ∇⊥ designates the horizontal part of the divergence operator.
The traditional approximation allows us to proceed to the separation of the x and θ coordinates in solutions, and to expand Fourier coefficients of Eq. (15) into series of Hough functions (Hough 1898). Thus, any Fourier coefficient fm,σ of the tidal gravitational potential, thermal forcing, pressure, density, temperature fluctuations and vertical velocity is written
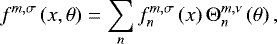 (21)
(21)
while Fourier co-efficients of horizontal velocities are expressed as
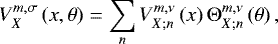 (22)
(22)
with X = θ, φ. In Eqs. (21) and (22), we have introduced the spin parameter ν defined by
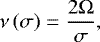 (23)
(23)
the latitudinal wavenumber n, such that 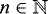 if
if 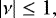 and
and 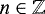 otherwise (with the notations of Lee & Saio 1997), the so-called Hough functions
otherwise (with the notations of Lee & Saio 1997), the so-called Hough functions 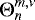 , and the associated horizontal functions
, and the associated horizontal functions 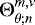 and
and 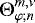 . Let us introduce the operator
. Let us introduce the operator
![\begin{align} \mathcal{L}^{m,\nu} = & \frac{1}{\sin \theta} \frac{{\textrm{d}}}{{\textrm{d}} \theta} \left( \frac{\sin \theta}{1 - \nu^2 \cos^2 \theta} \frac{{\textrm{d}}}{{\textrm{d}} \theta} \right) \\[6pt] & - \frac{1}{1 - \nu^2 \cos^2 \theta} \left( m \nu \frac{1 + \nu^2 \cos^2 \theta}{1 - \nu^2 \cos^2 \theta} + \frac{m^2}{\sin^2 \theta} \right). \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq49.png)
Hough functions are the solutions of the eigenvalue–eigenfunction problem defined by the Laplace’s tidal equation (Laplace 1798; Chapman & Lindzen 1970; Lee & Saio 1997; Wang et al. 2016),
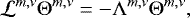 (26)
(26)
integrated with regularity boundary conditions. They are associated with the eigenvalues 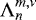 and constitute an orthogonal basis through the scalar product
and constitute an orthogonal basis through the scalar product
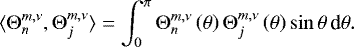 (27)
(27)
For convenience, we use the normalised Hough functions, such that 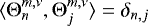 for any n and j, the notation δn,j standing for the Kronecker symbol. Moreover weuse the notation
for any n and j, the notation δn,j standing for the Kronecker symbol. Moreover weuse the notation 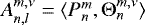 for the projection coefficients of Hough functions on the normalized associated Legendre polynomials, such that
for the projection coefficients of Hough functions on the normalized associated Legendre polynomials, such that
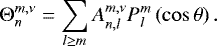 (28)
(28)
The associated horizontal functions intervening in Eq. (22) are straightforwardly deduced from the 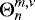 . They are defined by
. They are defined by
![\begin{align} & {\mathrm{\Theta}}_{\theta ; n}^{m,\nu} = \frac{1}{1 - \nu^2 \cos^2 \theta} \left( \frac{{\textrm{d}}}{{\textrm{d}} \theta} + m \nu \cot \theta \right) {\mathrm{\Theta}}_n^{m,\nu}, \\[3pt] & {\mathrm{\Theta}}_{\varphi ; n}^{m,\nu} = \frac{1}{1 - \nu^2 \cos^2 \theta} \left( \nu \cos \theta \frac{{\textrm{d}}}{{\textrm{d}} \theta} + \frac{m}{\sin \theta} \right) {\mathrm{\Theta}}_n^{m,\nu}. \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq57.png)
Symmetric Hough functions (n even) and the associated horizontal functions are plotted in Fig. 3 as functions of the colatitude for m = 2 (main component of the semidiurnal tide) for typical cases of the super-inertial ( ) and sub-inertial (
) and sub-inertial (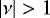 ) regimes, namely ν = 0.2 and ν = 2. We can observe on these graphs the two families of Hough modes characterizing the horizontal structure of tidal waves (e.g. Unno et al. 1989; Lee & Saio 1997):
) regimes, namely ν = 0.2 and ν = 2. We can observe on these graphs the two families of Hough modes characterizing the horizontal structure of tidal waves (e.g. Unno et al. 1989; Lee & Saio 1997):
- 1.
Gravity modes (n ≥ 0), also referred to as g modes. These modes are defined for
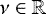 and associated with positive eigenvalues. When ν → 0, they converge toward the associated Legendre polynomials
and associated with positive eigenvalues. When ν → 0, they converge toward the associated Legendre polynomials 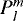 (with l = m + n), which are the solutions of the Laplace’s tidal equation in the non-rotating case. Similarly, the associated eigenvalues converge toward those of Legendre associated polynomials, that is
(with l = m + n), which are the solutions of the Laplace’s tidal equation in the non-rotating case. Similarly, the associated eigenvalues converge toward those of Legendre associated polynomials, that is 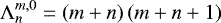 .
. - 2.
Rossby modes (n < 0), or r modes. These modes exist in the sub-inertial regime only (
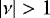 ). In this regime, gravity modes are confined within an equatorial band that becomes narrower while
). In this regime, gravity modes are confined within an equatorial band that becomes narrower while
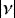 increases and Rossby modes spread from one pole to another (see Fig. 3, left panels).
increases and Rossby modes spread from one pole to another (see Fig. 3, left panels).
To obtain the vertical profiles of other perturbed quantities, we have to solve the system of Eqs. (18) to (20). After some manipulations and the introduction of the displacement ξ, such that V = ∂t ξ, this system is reduced to the system of ODEs
![\begin{align}& \frac{{\textrm{d}} y_n}{{\textrm{d}}x} = A_1 y_n + B_1 r^2 \xi_{r ; n} + C_1,\\[3pt]& \frac{{\textrm{d}}}{{\textrm{d}}x} \left( r^2 \xi_{r ; n} \right) = A_2 y_n + B_2 r^2 \xi_{r ; n} + C_2, \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq65.png)
The parameter εs; n that appears in Eq. (36) is an acoustic parameter comparing the tidal frequency to the Lamb frequency of the n-mode,
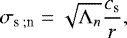 (39)
(39)
which is the characteristic cutoff frequency of horizontally propagating acoustic modes (we also introduce the general acoustic cutoff frequency σs = cs ∕ r); it writes
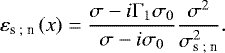 (40)
(40)
Therefore, εs; n weights the contribution of acoustic waves to the fluid tidal response; this contribution being negligible if 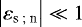 . Similarly, by considering Eqs. (34) and (23), we can note that the ratio N2 ∕ σ2 measures the contribution of internal gravity waves, that is, waves restored by the Archimedean force, and the spin parameter (ν), the contribution of inertial waves restored by the Coriolis acceleration. This draws up a global picture of possible tidal regimes. As shown by Fig. 4, where the frequency spectrum of these regimes is given, the nature of the tidal response is thus totally determined by the hierarchy of characteristic frequencies of the physical system (σ, σs, N, 2Ω and σ0).
. Similarly, by considering Eqs. (34) and (23), we can note that the ratio N2 ∕ σ2 measures the contribution of internal gravity waves, that is, waves restored by the Archimedean force, and the spin parameter (ν), the contribution of inertial waves restored by the Coriolis acceleration. This draws up a global picture of possible tidal regimes. As shown by Fig. 4, where the frequency spectrum of these regimes is given, the nature of the tidal response is thus totally determined by the hierarchy of characteristic frequencies of the physical system (σ, σs, N, 2Ω and σ0).
The last step consists in reducing the system of Eqs. (31)–(32) to a single vertical structure equation, which is first expressed as
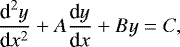 (41)
(41)
with the x-dependent coefficients (see Auclair-Desrotour et al. 2017a, Eq. (41))
![\begin{align} A \left( x \right) = & - \frac{\sigma - 2 i \sigma_0}{\sigma - i \sigma_0} \frac{H N^2}{g} - \frac{1}{{\mathrm{\Gamma}}_1} - K_{\circ},\\[6pt] B \left( x \right) = & H^2 \hat{k}_{\perp ; n}^2 \left( \frac{\sigma}{\sigma - i \sigma_0} \frac{N^2}{\sigma^2} - 1 \right) \left( 1 - \varepsilon_{\textrm{s ; n}} \right) \\[6pt] & - \left( \frac{{\textrm{d}}}{{\textrm{d}}x} + \frac{i \sigma_0}{\sigma - i \sigma_0} \frac{H N^2}{g} - \frac{1}{{\mathrm{\Gamma}}_1} - K_{\circ} \right) \left( \frac{H N^2}{g} + \frac{i \kappa \sigma_0}{\sigma - i \sigma_0} \right), \nonumber\\[6pt] C \left( x \right) = & \left( \frac{{\textrm{d}}}{{\textrm{d}}x} + \frac{i \sigma_0}{\sigma - i \sigma_0} \frac{H N^2}{g} - \frac{1}{{\mathrm{\Gamma}}_1} - K_{\circ} \right) \left( \frac{{\textrm{d}} U_n}{{\textrm{d}}x} - i \frac{\kappa}{\sigma - i \sigma_0} J_n \right) \nonumber \\[6pt] & + H^2 \hat{k}_{\perp ; n}^2 \left( \frac{\sigma }{\sigma - i \sigma_0} \frac{N^2}{\sigma^2} - 1 \right) \left[ U_n - i \frac{ \left({\mathrm{\Gamma}}_1 - 1 \right) \varepsilon_{\textrm{s ; n}} }{\sigma - i {\mathrm{\Gamma}}_1 \sigma_0} J_n \right] . \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq71.png)
In these expressions, we have identified the horizontal wavenumber 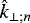 of the
of the 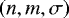 -mode, defined by
-mode, defined by
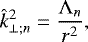 (45)
(45)
and a sphericity term, denoted K°, that is written
![\begin{equation*} K_{\circ} = \frac{r^2}{H} \left( \frac{\sigma}{\sigma - i \sigma_0} \frac{N^2}{\sigma^2} - 1 \right)^{-1} \frac{{\textrm{d}}}{{\textrm{d}}x} \left[ \frac{H}{r^2} \left( \frac{\sigma}{\sigma - i \sigma_0} \frac{N^2}{\sigma^2} - 1 \right) \right]. \vspace*{-5pt} \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq75.png) (46)
(46)
We finally introduce the change of variable yn = ΦnΨn, where Φn is the functiondefined by
![\begin{equation*} {\mathrm{\Phi}}_n \left( x \right) = \exp \left[ - \frac{1}{2} \int_0^x A \left( x' \right) \textrm{d} x' \right] .\vspace*{-5pt} \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq76.png) (47)
(47)
This allows us to write the vertical structure equation as a Schrödinger-like equation, which describes the forced response of a harmonic oscillator. Equation (41) thus becomes
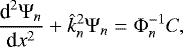 (48)
(48)
where 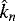 designates the normalized vertical wavenumber of the
designates the normalized vertical wavenumber of the 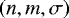 -mode (the vertical non-normalized wavenumber being
-mode (the vertical non-normalized wavenumber being 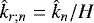 ) and is expressed as (see Auclair-Desrotour et al. 2017a, Eq. (47))
) and is expressed as (see Auclair-Desrotour et al. 2017a, Eq. (47))
![\begin{align}\hat{k}_n^2 = & H^2 \hat{k}_{\perp ; n}^2 \left( \frac{\sigma}{\sigma - i \sigma_0} \frac{N^2}{\sigma^2} - 1 \right) \left( 1 - \varepsilon_{\textrm{s ; n}} \right) \\ & - \left( \frac{{\textrm{d}}}{{\textrm{d}}x} + \frac{i \sigma_0}{\sigma - i \sigma_0} \frac{H N^2}{g} - \frac{1}{{\mathrm{\Gamma}}_1} - K_{\circ} \right) \left( \frac{H N^2}{g} + \frac{i \kappa \sigma_0}{\sigma - i \sigma_0} \right) \nonumber \\ & + \frac{1}{2} \frac{{\textrm{d}}}{{\textrm{d}}x} \left[ \frac{\sigma - 2 i \sigma_0}{\sigma - i \sigma_0} \frac{H N^2}{g} + K_{\circ} \right] \nonumber \\ & - \frac{1}{4} \left( \frac{\sigma - 2 i \sigma_0}{\sigma - i \sigma_0} \frac{H N^2}{g} - \frac{1}{{\mathrm{\Gamma}}_1} - K_{\circ} \right)^2. \nonumber\end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq81.png)
We recognize in the first term of  the vertical wavenumber of gravito-inertial waves propagating within a homogeneous fluid. This term predominates in the stably stratified radiative zone in the low-frequency asymptotic limit. It is responsible for the rapid increase of the vertical wavenumber, which scales as
the vertical wavenumber of gravito-inertial waves propagating within a homogeneous fluid. This term predominates in the stably stratified radiative zone in the low-frequency asymptotic limit. It is responsible for the rapid increase of the vertical wavenumber, which scales as 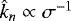 (if
(if 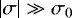 ) or
) or 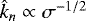 (if
(if 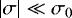 ) when
) when 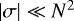 . Other terms result from radial variations of background distributions. They may be important around transition zones in the internal structure of the planet, such as the base of the atmosphere where the gradient of N2 is strong (see Fig. 2).
. Other terms result from radial variations of background distributions. They may be important around transition zones in the internal structure of the planet, such as the base of the atmosphere where the gradient of N2 is strong (see Fig. 2).
The tidally generated variation of mass distribution at the origin of the tidal torque is finally derived from Ψ n. It is written
![\begin{align*} \delta \rho_n = & - \frac{\rho_0}{gH} \frac{N^2}{N^2 - \sigma \left( \sigma - i \sigma_0 \right)} \left[{\mathrm{\Phi}}_n \left( \frac{{\textrm{d}} {\mathrm{\Psi}}_n}{{\textrm{d}}x} + \mathcal{B}_n {\mathrm{\Psi}}_n \right) \right. \\ & \left. - \frac{{\textrm{d}} U_n}{{\textrm{d}}x} + i \frac{\kappa \sigma}{N^2} J_n \right], \nonumber\vspace*{-2pt}\end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq88.png)
The polarization relations of other perturbed quantities are given in Appendix A. It shall be noted here that all of the results derived in this section remain true for any vertical profiles of background quantities as far as the fluid is a perfect gas at hydrostatic equilibrium.
 |
Fig. 3 Normalized symmetrical (n even) Hough functions (left) and associated horizontal functions (middle and right) as functions of latitude (degrees) for m = 2 and two values of ν = 2Ω ∕ σ representative of inertial regimes. Top: ν = 0.2 (super-inertial regime); weak impact of rotation on the tidal response. Bottom: ν = 2 (sub-inertial regime); strong impact of rotation. Gravity modes are designated by subscripts p ≥ 0 while Rossby modes correspond to p < 0. |
 |
Fig. 4 Frequency spectrum of tidal regimes and waves characterizing the fluid tidal response. The parameter σ designates the forcing frequency (Eq. (15)), σ0 the thermal frequency (Eq. (9)), 2Ω the inertia frequency, N the Brunt-Väisäl ä frequency (Eq. (5)), and σs the characteristic acoustic cutoff frequency (Eq. (39)). |
2.3 Thermal and gravitational forcings
As mentioned above, the incoming stellar flux is absorbed in the upper layers of the atmosphere.Thus, following Arras & Socrates (2010) and introducing the stellar zenith angle ϕ⋆, we define the distribution of total heat per unit mass as
![\begin{equation*} \left\{ \begin{array}{ll} \displaystyle J_{\star} \left( p_0 , \phi_{\star} \right) = \frac{g}{p_{\star}} F_{\star} {\textrm{e}}^{-p/p_{\star}} \cos \phi_{\star} & \displaystyle {\textrm{for}} \ \phi_{\star} \in \left[ 0 , \frac{\pi}{2} \right] , \\ \displaystyle J_{\star} \left( p_0 , \phi_{\star} \right) = 0 & \displaystyle {\textrm{for}} \ \phi_{\star} \in \left] \frac{\pi}{2} , \pi \right]. \end{array} \right.\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq90.png) (52)
(52)
In Eq. (52), F⋆ designates the incoming flux at the sub-stellar point, expressed as 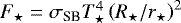 , where σSB is the Stefan-Boltzmann constant, r⋆ the star-planet distance, and R⋆ and T⋆ the stellar radius and mean surface temperature, respectively. If we assume that R⋆ ≪ r⋆, the gravitational potential generated by the star in the accelerated reference frame of the planet is written
, where σSB is the Stefan-Boltzmann constant, r⋆ the star-planet distance, and R⋆ and T⋆ the stellar radius and mean surface temperature, respectively. If we assume that R⋆ ≪ r⋆, the gravitational potential generated by the star in the accelerated reference frame of the planet is written
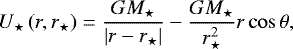 (53)
(53)
the vector r⋆ being the planet-star vector (such that 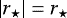 ) and M⋆ the mass of the star. In the general case, the stellar heating and gravitational forcing are expanded into Fourier series and spherical harmonics, that is
) and M⋆ the mass of the star. In the general case, the stellar heating and gravitational forcing are expanded into Fourier series and spherical harmonics, that is

the 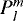 standing for the normalized associated Legendre polynomials1.
standing for the normalized associated Legendre polynomials1.
However, to simplify the forcing, we suppose that the planet orbits its host star circularly and that its equatorial plane is coplanar with the orbital plane. As a consequence, the expansion of the tidal gravitational potential in spherical harmonics is reduced to the semidiurnal quadrupolar component (l = m =2), expressed as (Arras & Socrates 2010, Mathis & Le Poncin-Lafitte 2009)
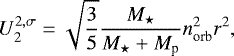 (56)
(56)
with 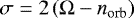 . Similarly, the quadrupolar component of the thermal forcing is given by
. Similarly, the quadrupolar component of the thermal forcing is given by
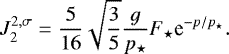 (57)
(57)
We note that the semidiurnal spin parameter is simply expressed as
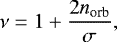 (58)
(58)
which highlights the parameter measuring the impact of rotation on the tidal response, 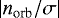 . For a sub-synchronous rotation (σ < 0), the inertial regime corresponds to
. For a sub-synchronous rotation (σ < 0), the inertial regime corresponds to 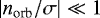 (see Fig. 5). In this case, the planet is rapidly rotating. The transition from the inertial regime to a sub-inertial one occurs for
(see Fig. 5). In this case, the planet is rapidly rotating. The transition from the inertial regime to a sub-inertial one occurs for 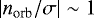 . Beyond this critical value, ν ∝ 2norb∕σ and diverges at the spin-orbit synchronousrotation (σ → 0), where the effects of rotation are stronger than the forcing. In the zero-frequency limit, the traditional approximation is only appropriate for strongly and stably stratified layers. Thus, the effects of rotation can be taken into account provided that the region where tidal waves propagate satisfies the condition 2Ω ≪ N (e.g., Mathis 2009; Auclair-Desrotour et al. 2017a).
. Beyond this critical value, ν ∝ 2norb∕σ and diverges at the spin-orbit synchronousrotation (σ → 0), where the effects of rotation are stronger than the forcing. In the zero-frequency limit, the traditional approximation is only appropriate for strongly and stably stratified layers. Thus, the effects of rotation can be taken into account provided that the region where tidal waves propagate satisfies the condition 2Ω ≪ N (e.g., Mathis 2009; Auclair-Desrotour et al. 2017a).
 |
Fig. 5 Logarithms of the spin parameter (ν) and stabilityratio |
2.4 Boundary conditions
To integrate the vertical structure equation, Eq. (48), two boundary conditions must be chosen. We set one condition at the lower boundary of the atmosphere, and one at its upper boundary. Arras & Socrates (2010) choose to set the lower boundary at the centre of the planet (x = 0). Hence, they use a standard regularity condition requiring all variables to be finite (e.g. Unno et al. 1989). In the static case, this condition writes
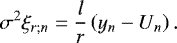 (59)
(59)
It can be adapted to the rotating case in the super-inertial regime (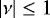 ), where the previous expression becomes
), where the previous expression becomes
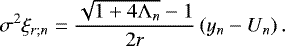 (60)
(60)
However, it cannot be applied for 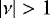 , Rossby modes being associated with negative Λn. Therefore, in this work, we choose to use a rigid-wall condition enforcing the fact that fluid particles cannot go through the lower boundary. It is simply expressed as ξr = 0, that is,
, Rossby modes being associated with negative Λn. Therefore, in this work, we choose to use a rigid-wall condition enforcing the fact that fluid particles cannot go through the lower boundary. It is simply expressed as ξr = 0, that is,
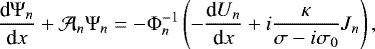 (61)
(61)
with (see Appendix A)
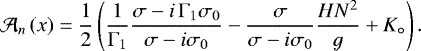 (62)
(62)
We notethat the lower boundary shall not necessarily be set at the centre of the planet since we focus on thermal tides, which only affect the stably stratified atmospheric layer of the planet. The convective region is not perturbed by the tidal thermal forcing. The lower boundary could thus be set at any pressure level greater than that corresponding to the base of the stably stratified region, that is pb ≈ 102 bar. Nevertheless, setting the lower limit of the atmosphere at pb would causereflections of waves and induce side effects, as discussed by Ogilvie & Lin (2004) and illustrated by Appendix B. This is the reason why this boundary shall be located at higher pressure levels. Here, considering that the tidal perturbation is confined to the atmosphere and does not affect the convective region, we set the lower boundary as far as possible from the basis of the stably stratified zone, that is at the centre of the planet. This allows us to avoid artefacts related to reflections. We verify a posteriori by checking other conditions that, in this case, the lower boundary condition has no repercussions on the tidal response generated by the thermal forcing.
The upper limit of the atmosphere is located in the tidally forced region. Thus, the associated boundary condition partly determines the frequency dependent behaviour of the fluid, as demonstrated by Arras & Socrates (2010). In the adiabatic case, it is possible to apply the radiation condition, that is to consider that waves carry energy upward without reflections (e.g. Wilkes 1949; Chapman & Lindzen 1970). This condition regularizes the tidal response by eliminating resonances due to gravity waves of short vertical wavelengths in the vicinity of spin-orbit synchronous rotation (e.g. Arras & Socrates 2010; Auclair-Desrotour et al. 2017a). The vertical energy flow associated with the 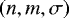 -mode is expressed as
-mode is expressed as
![\begin{align*} \mathfrak{F}_{r ; n} = & \frac{1}{2} \frac{\sigma \rho_0}{H} \Im \left\{ \left( \frac{\sigma}{\sigma - i \sigma_0} N^2 - \sigma^2 \right)^{-1} \left[ \left| {\mathrm{\Phi}}_n \right|^2 \left({\mathrm{\Psi}}_n^* \frac{{\textrm{d}} {\mathrm{\Psi}}_n}{{\textrm{d}}x} + \mathcal{A}_n \left| {\mathrm{\Psi}}_n \right|^2 \right) \right. \right. \nonumber \\ & \left. \left. + {\mathrm{\Phi}}_n^* {\mathrm{\Psi}}_n^* \left( - \frac{{\textrm{d}} U_n}{{\textrm{d}}x} + i \frac{\kappa}{\sigma - i \sigma_0} J_n \right) \right] \right\}. \end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq110.png) (63)
(63)
Assuming that the tidal sources are located below the altitude of the upper boundary (denoted Re or xe depending on the used vertical coordinate), we ignore the last term. For σ0 = 0, the only potentially negative term is thus 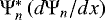 . We then suppose that the vertical wavelength of tidal waves is shorter than the length scale of background distributions, so that the solution of Eq. (48) writes
. We then suppose that the vertical wavelength of tidal waves is shorter than the length scale of background distributions, so that the solution of Eq. (48) writes 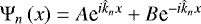 at the upper boundary (x = xe). The radiation condition hence consists in conserving only the first term of this solution associated with 𝔉r;n > 0, that is in setting
at the upper boundary (x = xe). The radiation condition hence consists in conserving only the first term of this solution associated with 𝔉r;n > 0, that is in setting
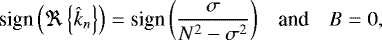 (64)
(64)
the symbol ℜ referring to the real part of a complex number.
As it may be noted, this condition is only convenient in the adiabatic case and for propagative modes 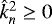 . If σ0 ≠ 0, both terms of the solution can contribute to a positive upward energy flux. Moreover, it is not appropriate to waves of wavelengths comparable to the pressure height scale. For these two reasons, we choose to apply at x = xe the standard free-surface condition, δp = gρ0ξr (e.g. Unno et al. 1989), which can be enforced for any
. If σ0 ≠ 0, both terms of the solution can contribute to a positive upward energy flux. Moreover, it is not appropriate to waves of wavelengths comparable to the pressure height scale. For these two reasons, we choose to apply at x = xe the standard free-surface condition, δp = gρ0ξr (e.g. Unno et al. 1989), which can be enforced for any 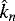 . This condition is formulated as
. This condition is formulated as
![\begin{equation*} \frac{{\textrm{d}} {\mathrm{\Psi}}_n}{{\textrm{d}}x} {+} \left[ \mathcal{A}_n + \frac{H}{g} \left( \frac{\sigma}{\sigma {-} i \sigma_0} N^2 - \sigma^2 \right) \right] {\mathrm{\Psi}}_n {\,=\,} {\mathrm{\Phi}}_n^{-1} \left( \frac{ i \kappa J_n}{\sigma - i \sigma_0} - \frac{{\textrm{d}} U_n}{{\textrm{d}}x} \right). \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq116.png) (65)
(65)
In the absence of dissipation, it leads to a highly frequency-resonant behaviour around σ = 0, given that gravity waves can be reflected backward at the upper boundary (Arras & Socrates 2010; Auclair-Desrotour et al. 2017a). In reality, due to the strong stellar heating, the energy given by the tidal forcing is partly radiated toward space, which makes internal tidal waves evanescent and consequently strongly attenuate the amplitude of the perturbation. This effect is modelled by Gu & Ogilvie (2009) with a Marshak condition, which enforces a radiative energy loss at the upper limit of the atmosphere. In our study, we model dissipative processes with the Newtonian cooling defined by Eqs. (7) and (9). As observed in Sect. 4, the frequency dependence of the tidal response is regularized by the damping for 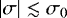 (see Fig. 4).
(see Fig. 4).
3 Tidal torque and quadrupole
As the goal of this work is to examine the ability of thermal tides to modify the planet’s rotation and to generate zonal flows, we introduce in this section the expressions used to compute the tidal torque exerted on the fluid shell with respect to the spin axis of the planet. This torque is obtained by projecting the tidally induced variation of mass distribution on the tidal force (F = ∇U). Thus, its 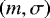 -component is defined by (Zahn 1966; Auclair-Desrotour et al. 2017a)
-component is defined by (Zahn 1966; Auclair-Desrotour et al. 2017a)
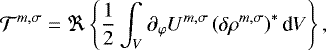 (66)
(66)
where V designates the volume of the fluid shell and * the conjugate of a complex number. By substituting in Eq. (66) the expansions of fluctuations in Hough functions given by Eq. (21), we end up with
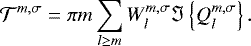 (67)
(67)
In this expression, we have introduced the imaginary part ℑ, the factors 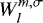 such that
such that 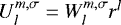 and the tidal multipole moments
and the tidal multipole moments 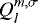 , which are expressed as
, which are expressed as
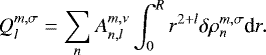 (68)
(68)
The coefficients 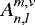 quantify the distortion of the tidal response caused by rotation. In the static case,
quantify the distortion of the tidal response caused by rotation. In the static case, 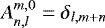 , and we retrieve the expression given by Arras & Socrates (2010). These authors propose an expansion of this expression in terms of other perturbed quantities in order to avoid numerical errors2. We adapt their formula to the rotating case in Appendices C and D, and get Eq. (D.3). In the following, in order to validate the obtained results, we compute the tidal quadrupole moment by using both Eqs. (68) and (D.3). The evolution timescale of the planet’s global rotation rate due to the
, and we retrieve the expression given by Arras & Socrates (2010). These authors propose an expansion of this expression in terms of other perturbed quantities in order to avoid numerical errors2. We adapt their formula to the rotating case in Appendices C and D, and get Eq. (D.3). In the following, in order to validate the obtained results, we compute the tidal quadrupole moment by using both Eqs. (68) and (D.3). The evolution timescale of the planet’s global rotation rate due to the 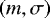 -mode is expressed as
-mode is expressed as
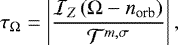 (69)
(69)
where 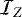 is the moment of inertia with respectto the Z-axis, that is written as
is the moment of inertia with respectto the Z-axis, that is written as
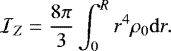 (70)
(70)
However, the global torque and timescale provide no information about the local strength of the thermal tidal forcing. To know which layers are forced and where strong jets can be generated, we use the longitudinal tidal force per unit volume averaged over the longitude,
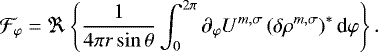 (71)
(71)
Hence, the characteristic timescale necessary to generate a jet of velocity V jet in the absence of viscous coupling writes
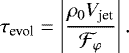 (72)
(72)
In the case of the quadrupolar semidiurnal tide, which is the object of this study, the perturbation is forced by the component defined by l = m = 2 and 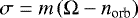 . Therefore, the total torque induced by the semi-diurnal tide reduces to (see (Eq. 56))
. Therefore, the total torque induced by the semi-diurnal tide reduces to (see (Eq. 56))
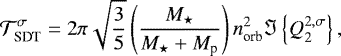 (73)
(73)
with the quadrupole moment
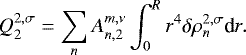 (74)
(74)
4 Properties of thermally forced tidal waves
We now explore the properties of the tidal response and its dependence on dissipative mechanisms and rotation by applying the linear analysis to three different configurations. The aim of this section is to investigate the consequences of the thermal tidal torque on the general circulation of the atmosphere, and particularly its ability to generate strong zonal flows. Thus, we isolate the thermal tide by setting U = 0 in the equations describing the vertical structure of the fluid tidal response (Sect. 2.2). The tidal gravitational potential given by Eq. (56) is nevertheless used to compute the induced gravitational tidal torque.
Using the values of parameters given by Table 1, we treat three cases:
- 1.
adiabatic without rotation. This is the case treated by Arras & Socrates (2010), where the rotation of the planet is ignored (Ω = 0, ν =0), as well asdissipative processes (τ⋆ = +∞);
- 2.
non-adiabatic without rotation. The thermal time at the base of the heated layer is set to τ⋆ = 1 d, which is the order of magnitude predicted by radiative transfer modellings for the hot Jupiter HD 209458b (Showman & Guillot 2002; Iro et al. 2005);
- 3.
non-adiabatic with rotation. The effect of rotation is taken into account by introducing the Coriolis acceleration in the framework of the traditional approximation.
Since the tidal torque is directly proportional to the imaginary part of the density fluctuation (see Eq. (74)), we use this quantity as a proxy to identify regions that are accelerated by the thermal tide. The imaginary part of δρ is thus plotted in Fig. 6 as a function of the latitude and pressure level in each case for a wide range of forcing periods (τtide = 10−1, 100, 101, 102, 103 days) in the regime of sub-synchronous rotation (σ < 0). Hence, a positive (negative) 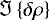 is associatedto an eastward (westward) accelerated zonal-mean flow. The corresponding timescale necessary to generate a jet of velocity V jet = 1 km s−1 (order of magnitude of velocities of atmospheric winds in HD 209458b, e.g. Showman & Guillot 2002) is plotted in Fig. 7 using Eq. (72).
is associatedto an eastward (westward) accelerated zonal-mean flow. The corresponding timescale necessary to generate a jet of velocity V jet = 1 km s−1 (order of magnitude of velocities of atmospheric winds in HD 209458b, e.g. Showman & Guillot 2002) is plotted in Fig. 7 using Eq. (72).
As may be observed, the thermal tide essentially affects the stably stratified region, where the Archimedean force restores internal gravity waves and allows them to propagate. We note here that the quality of the solution depends on the condition σ2 ≪ N2 mentioned above. This means that solutions involving density variations around the base of the stably stratified region (pb ≈ 102 bar) can be deteriorated given that the Brunt-Väisälä frequency falls down at this pressure level (see Fig. 2).
In addition to gravity waves, acoustic waves can also contribute to the tidal response, but only for forcing frequencies greater than acoustic cutoff frequencies of the horizontally propagating Lamb modes, defined by Eq. (39). Typically, in the non-rotating case, only one mode is forced by the quadrupolar thermal heating, the gravity mode of meridional degree n = 0 (black line in top panels of Fig. 3). This mode is associated with the eigenvalue 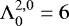 , which sets its characteristic Lamb period (τs; n = 2π ∕ σs;n) to τs;0 ≈ 1.4 days in the radiative zone. Hence, the tidal fluctuations that can be observed in the left panels of Figs. 6 and 7 are partly due to compressibility. However, the tidal frequency is not important enough to enable the propagation of internal waves in the convective region. We note that the propagation of internal waves in the convective region would not be realistic since the traditional approximation assumed in the present work is strongly violated in this region. Therefore, we do not compute solutions for tidal periods lower than 0.1 days.
, which sets its characteristic Lamb period (τs; n = 2π ∕ σs;n) to τs;0 ≈ 1.4 days in the radiative zone. Hence, the tidal fluctuations that can be observed in the left panels of Figs. 6 and 7 are partly due to compressibility. However, the tidal frequency is not important enough to enable the propagation of internal waves in the convective region. We note that the propagation of internal waves in the convective region would not be realistic since the traditional approximation assumed in the present work is strongly violated in this region. Therefore, we do not compute solutions for tidal periods lower than 0.1 days.
In the first case (top panels of Figs. 6 and 7), dissipation is ignored. Therefore, in the stably stratified region and for tidal periods τtide ≫ τs;0, the dispersion relation of internal waves associated with the n-mode given by Eq. (50) approximately reduces to
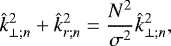 (75)
(75)
with n = 0. This highlights the two possible asymptotic regimes. On the one hand, if the forcing period is short, the vertical wavelength is of the same order of magnitude as the typical thickness of the atmosphere. The tidal response thus exhibits large scale patterns characterized by a small number of oscillations (top left panels in Figs. 6 and 7). On the other hand, when tidal periods are long (N2∕σ2 ≫ 1), 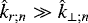 , which explains the wave-like oscillatory response that can be observed for τtide ≳ 10 days.
, which explains the wave-like oscillatory response that can be observed for τtide ≳ 10 days.
Without dissipation, waves reach the bottom of the radiative zone and the turning point N2 = σ2, where 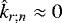 . The skin thickness of their penetration in the convective region decreases while the forcing period increases. Similarly, the vertical wavelength decays following the scaling law
. The skin thickness of their penetration in the convective region decreases while the forcing period increases. Similarly, the vertical wavelength decays following the scaling law 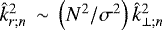 derived from Eq. (75). This leads to a highly oscillating response in the vicinity of spin-orbit synchronous rotation (see top right panels of Figs. 6 and 7). We note that such a behaviour is a source of complications for numerical calculations. Indeed, following the decay of wavelengths requires to increase the resolution by a factor 10 at each decade of τtide. This strong numerical constraint prevents us from computing solutions beyond a critical value of the forcing period. Here, with the 104 points mesh that we use for the vertical coordinate in the first case, this value approximately corresponds to τtide = 102 days, which means that solutions plotted in the top right panels of Figs. 6 and 7 are sub-resolved. However, this behaviour is not realistic because waves of such small scales are in reality damped by dissipative processes.
derived from Eq. (75). This leads to a highly oscillating response in the vicinity of spin-orbit synchronous rotation (see top right panels of Figs. 6 and 7). We note that such a behaviour is a source of complications for numerical calculations. Indeed, following the decay of wavelengths requires to increase the resolution by a factor 10 at each decade of τtide. This strong numerical constraint prevents us from computing solutions beyond a critical value of the forcing period. Here, with the 104 points mesh that we use for the vertical coordinate in the first case, this value approximately corresponds to τtide = 102 days, which means that solutions plotted in the top right panels of Figs. 6 and 7 are sub-resolved. However, this behaviour is not realistic because waves of such small scales are in reality damped by dissipative processes.
This is exactly what is observed in the second case, where the radiative cooling is introduced (middle panels of Figs. 6 and 7). Beyond the transition regime corresponding to τtide ~ τ⋆, tidal waves are first strongly damped. Second, their wavelengths remain rather large, which eliminates the numerical complications mentioned above. Third, their penetration in the atmosphere is limited by the damping. As in the previous case, the wavelikestructure of the tidal response implies that the thickness of regions where the tidal force is applied scales as half of the wavelength of the dominating mode. As a consequence, the forcing tends to generate superposed zonal-mean flows of alternate directions. Figure 7 shows the narrow separation there is between the convective envelope and the radiative atmosphere with respect to this forcing. The first layer is hardly affected by the thermal tidal torque, with time scales greater than 100 million years to generate jets, while the second one is submitted to a strong forcing. In this region, the time scale can reach values below 1 year. In the absence of dissipation, the linear response diverges, which explains why τevol is very short in the top right panels of Fig. 7. The observed contrast between the two layers is due to the fact that the whole energy of the semidiurnal thermal tide is deposited in the radiative zone, which is very thin compared to the planet radius (Fig. 2, left panel) and far less dense than the convective region (see Fig. 2).
As shown by the bottom panels of Figs. 6 and 7, introducing rotation distorts the regular structure associated with the quadrupolar mode, which was the only forced mode in the non-rotating cases. The fluid response is now formed by a series of Hough modes that describe the propagation of gravito-acoustic-inertial waves of different wavelengths. In order to facilitate the interpretation of results in the rotating case, we plot in Fig. 8 the eigenvalues associated to even Hough functions of degrees 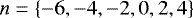 , the corresponding coupling coefficients with the quadrupolar forcing,
, the corresponding coupling coefficients with the quadrupolar forcing, 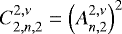 , and the ratios
, and the ratios 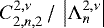 that will beidentified as amplification factors resulting from rotation in the following section. The values of spin parameters, computed using Eq. (58), and the associated
that will beidentified as amplification factors resulting from rotation in the following section. The values of spin parameters, computed using Eq. (58), and the associated 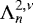 and
and 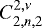 , are summarized in Table 2.
, are summarized in Table 2.
In the asymptotic case of rapid rotation, the predominant modes are the gravity modes of smallest horizontal wavenumbers. Hence, for τtide = 10−1 days (bottom left panel), the 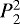 -like meridional variation of δρ and τevol corresponds to the gravity mode of degree n = 0. In the following case (τtide = 1 day), we note that the amplitude of the harmonic of degree 2 is of the same order of magnitude as that of degree 0, while
-like meridional variation of δρ and τevol corresponds to the gravity mode of degree n = 0. In the following case (τtide = 1 day), we note that the amplitude of the harmonic of degree 2 is of the same order of magnitude as that of degree 0, while 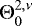 is far better coupled to
is far better coupled to 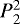 than
than 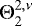 in this case (ν = 0.51). This results from a resonant amplification of the harmonic. While τtide increases, gravity modes tend to be confined equatorially. We observe this effect in the bottom middle panel of Figs. 6 and 7, where the meridional structure of the tidal response is essentially shaped by the main gravity mode (n = 0, see Fig. 3, top left panel). Because of the equatorial confinement, the coupling between gravity modes and the quadrupolar forcing decays. It follows that the family of modes composing the response switches from gravity modes to Rossby modes around τtide = 10 day, that is the transition between the inertial and the sub-inertial regimes illustrated by Fig. 5.
in this case (ν = 0.51). This results from a resonant amplification of the harmonic. While τtide increases, gravity modes tend to be confined equatorially. We observe this effect in the bottom middle panel of Figs. 6 and 7, where the meridional structure of the tidal response is essentially shaped by the main gravity mode (n = 0, see Fig. 3, top left panel). Because of the equatorial confinement, the coupling between gravity modes and the quadrupolar forcing decays. It follows that the family of modes composing the response switches from gravity modes to Rossby modes around τtide = 10 day, that is the transition between the inertial and the sub-inertial regimes illustrated by Fig. 5.
In the vicinity of spin-orbit synchronous rotation, the tidal response converges toward the asymptotic behaviour of the zero-frequency limit (τtide → +∞), that is the so-called equilibrium tide. The aspect of spatial distributions plotted in Figs. 6 and 7 does not evolve any more. This behaviour is studied analytically in Appendix C, where the vertical profiles of perturbed quantities associated with the equilibrium thermal tide are given. By comparing the dissipative cases with and without rotation (right panels of cases 1 and 2), we notice that rotation strongly affects this regime. In the static approximation (Ω = 0), the amplitude of the tidal response decreases while τtide increases, following the scaling law δρ ∝ σ. It is not the case any more when rotation is taken into account. Instead of decreasing, the amplitude of the density fluctuations saturates. Thus, the tidal response is enhanced by rotation. This saturation typically occurs for 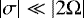 , that is, when the Coriolis effects exceed the thermally forced advection in the momentum equation. We will see in the following section that this results from the amplification of Rossby modes by the factor
, that is, when the Coriolis effects exceed the thermally forced advection in the momentum equation. We will see in the following section that this results from the amplification of Rossby modes by the factor 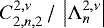 mentioned above. As shown by Fig. 8, this factor plummets for gravity modes in the limit ν →−∞, while it increases in the case of Rossby modes. Therefore, the coupling of the tidal response with Rossby modes is accentuated and the coupling with gravity modes annihilated. This explains why a gap can be observed at the equator, where gravity modes are confined (bottom right panels of Figs. 6 and 7).
mentioned above. As shown by Fig. 8, this factor plummets for gravity modes in the limit ν →−∞, while it increases in the case of Rossby modes. Therefore, the coupling of the tidal response with Rossby modes is accentuated and the coupling with gravity modes annihilated. This explains why a gap can be observed at the equator, where gravity modes are confined (bottom right panels of Figs. 6 and 7).
 |
Fig. 6 Imaginary part of density fluctuations generated by the quadrupolar semidiurnal thermal tide a functions of the latitude (horizontal axis, degrees) and background pressure in logarithmic scale (vertical axis, bars). Density fluctuations are plotted using Eq. (51) for several decades of the forcing period (τtide = 2π∕σ),
|
 |
Fig. 7 Characteristic time scale necessary for the quadrupolar semidiurnal thermal tide to generate an azimuthal jet of velocity V jet = 1 km s−1. The logarithm of τevol (yr) isplotted using Eq. (72) for several decades of the forcing period (τtide = 2π∕σ),
|
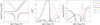 |
Fig. 8 Eigenvalues |
5 Frequency spectra of the tidal torque
We end this study by examining how the total tidal torque exerted on the planet depends on the tidal frequency and how it is affected by the radiative cooling and rotation. As done in the previous section, we isolate the component of the fluid response associated with the thermal tides by setting U = 0 in the equations of tidal waves, and use the parameters of Table 1. First, following Arras & Socrates (2010), we consider the static approximation (Ω = 0) and compute the tidal response for a strong radiative cooling (τ⋆ = 0.1 day) and a weaker one (τ⋆ = 10 day). Second, we compare the static (Ω = 0) and rotatingcases (Ω = norb + σ ∕ 2) for τ⋆ = 1 day. The obtained torques are plotted on Fig. 9 as functions of the tidal period.
In the static approximation (left panel of Fig. 9), we reproduce the results previously obtained by Arras & Socrates (2010). Three regimes can be observed. At small tidal periods, the spectrum of the tidal torque exhibits a resonance due to the propagation of internal gravito-acoustic waves in the radiative zone. For extremal values of the tidal period, tidal waves are mainly restored by the fluid compressibility, which allows them to cross the lower limit of the stably stratified atmosphere and propagate in the central convective region. We note however that these frequencies correspond to rotation rates greater than the critical Keplerian frequency (Ω c), meaning that the planet should be destroyed by centrifugal distortion in this frequency range. In the range τtide ≈ 1 − 30 days, a batch of resonances can be observed. It results from the excitation of the pure gravity waves observed in Figs. 6 and 7 (middle columns). Contrary to those associated with gravito-acoustic waves, these resonances are damped by the radiative cooling. Their amplitude decays while τ⋆ increases. The non-dissipative asymptotic case, τ⋆ = +∞ corresponds to the spectrum of Fig. 5 in the work by Arras & Socrates (2010).
Finally, in the limit of long tidal periods (zero-frequency limit), the tidal response converges toward the regime of the equilibrium thermal tide. For more details about solutions in this regime, we refer the reader to the analytic study detailed in Appendices C and D. Particularly, we derive in this study an analytic approximation of the tidal quadrupole moment 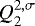 (Eq. (74)), which is expressed as (see Eq. (D.10))
(Eq. (74)), which is expressed as (see Eq. (D.10))
![\begin{align*}Q_{2}^{2,\sigma} = & \sum_n A_{n,2}^{2,\nu} \left\{ \left[ 1 - \frac{30}{{\mathrm{\Lambda}}_n^{m,\nu}} \right] \int_0^{R_{\textrm{e}}} \rho_0 r^{4} \left( \frac{\sigma^2}{N^2} \right) \frac{J_n}{i \sigma T_0 C_{\textrm{p}}} \textrm{d} r \right. \\ & \left. + \frac{R^{5}}{{\mathrm{\Lambda}}_n^{m,\nu}} \left[ \left( \frac{\sigma^2}{N^2} \right) \rho_0 \left( 6 + \frac{R}{H} \right) \frac{J_n}{i \sigma T_0 C_{\textrm{p}}} \right]_{r = R_{\textrm{e}}} \right\}, \nonumber \end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq154.png)
where Re designates the radius of the upper limit of the atmosphere introduced in Sect. 2.1. This formula is the generalization of the scaling law given by Arras & Socrates (2010) in (Eq. 45) to the rotating and dissipative case. This shows that the radiative cooling does not intervene in the asymptotic regime of the equilibrium thermal tide since the quadrupole moment does not depend on σ0. Hence, whatever the efficiency of the radiative cooling, the fluid tidal response associated with the thermal tide invariably converges towards the same asymptotic regime and the same spatial distributions of perturbed quantities. This corresponds to what is observed on Fig. 9 (left panel), where the equilibrium tidal torque is plotted by using Eq. (76) (dotted black line). In the asymptotic zero-frequency regime, the quadrupole scales as 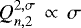 , a frequency-dependence corresponding to that described by the constant time lag model (Mignard 1979, 1980; Hut 1981). Moreover, we notice that the sign of the tidal torque varies with the tidal frequency depending on the internal variation of mass distribution generated by tidal waves (see Fig. 6, middle and top panels). As the rotation is sub-synchronous in the studied case (σ < 0), a positive torque (dashed line) pushes the planet toward spin-orbit synchronization in a global way while a negative torque (continuous line) tends to drive it away from this state of equilibrium. We note that this diagnosis is only valid as a zero-order approximation given that fluid layers are differentially forced by the thermal tide. The tidal forcing will generate zonal flows in the radiative zone as shown by early studies (e.g. Gu & Ogilvie 2009) and the previous section, rather than modify the mean solid rotation of the planet. These flows can nevertheless provide angular momentum to deeper layers through viscous coupling (e.g. Tsai et al. 2014).
, a frequency-dependence corresponding to that described by the constant time lag model (Mignard 1979, 1980; Hut 1981). Moreover, we notice that the sign of the tidal torque varies with the tidal frequency depending on the internal variation of mass distribution generated by tidal waves (see Fig. 6, middle and top panels). As the rotation is sub-synchronous in the studied case (σ < 0), a positive torque (dashed line) pushes the planet toward spin-orbit synchronization in a global way while a negative torque (continuous line) tends to drive it away from this state of equilibrium. We note that this diagnosis is only valid as a zero-order approximation given that fluid layers are differentially forced by the thermal tide. The tidal forcing will generate zonal flows in the radiative zone as shown by early studies (e.g. Gu & Ogilvie 2009) and the previous section, rather than modify the mean solid rotation of the planet. These flows can nevertheless provide angular momentum to deeper layers through viscous coupling (e.g. Tsai et al. 2014).
Let us now examine the effect of rotation on the frequency spectrum (Fig. 9, right panel). As seen in the previous section, the rotation increases the number of excited modes by inducing a coupling in the momentum equations of tidal waves through the Coriolis acceleration. The strength of this effect is related to the absolute value of the spin parameter (ν = 2Ω ∕ σ), the asymptotic limit ν → 0 corresponding to the static case. Thus, in the regime of rapid rotation ν ≈−1, and the number of resonances due to gravito-acoustic waves is increased. The transition between retrograde and prograde rotation occurs in the period range τtide ≈ 1–10 days (see Fig. 5). As a consequence, the regime of the fluid response is super-inertial and the quadrupolar forcing is essentially coupled with the gravity mode of degree n = 0 (Fig. 8, middle panel). This explains why the resonances associated with gravity waves in the range τtide ≈ 1 − 30 days are weakly modified by Coriolis effects.
It is not the case of the low-frequency range, where the tidal torque ceases to decay beyond τ ≈ 30 days. To interpret this behaviour, let us return to the analytic formula of the quadrupole, given by Eq. (76). Unlike dissipative processes, the rotation strongly affects the equilibrium thermal tide through the coupling coefficients 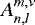 and the eigenvalues
and the eigenvalues 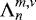 . In the regime of sub-inertial waves, where
. In the regime of sub-inertial waves, where 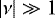 , the quadrupolar perturbation of the semidiurnal tide is mainly coupled with Rossby modes, characterized by very small eigenvalues in absolute value (see Fig. 8, left panel, and Townsend 2003, for scaling laws of the
, the quadrupolar perturbation of the semidiurnal tide is mainly coupled with Rossby modes, characterized by very small eigenvalues in absolute value (see Fig. 8, left panel, and Townsend 2003, for scaling laws of the 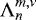 ). Therefore, the amplitude of the tidal response associated with the n-Hough mode is enhanced by a factor
). Therefore, the amplitude of the tidal response associated with the n-Hough mode is enhanced by a factor
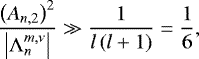 (77)
(77)
plotted in Fig. 8 (right panel). This corresponds to the fact that Coriolis effects dominate the forced advection terms in the momentum equation (Eq. (11)). As τtide → +∞, Ω → norb≠0, which lets time to the Coriolis force to affect tidal motions. As a consequence, the tidal response reaches the observed saturation plateau (Fig. 9, right panel, cyan curve) for 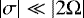 while the tidal frequency decreases. The global quadrupole does not scale as
while the tidal frequency decreases. The global quadrupole does not scale as 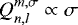 as in the static case.
as in the static case.
The analytic formula of Eq. (76) allows us to approximate this behaviour. We can notice however a factor 2 − 3 difference between the numerical results and the analytic approximation. This difference is due to limitations of the analytic study of Appendix C, where the eigenvalues associated with Hough modes are considered as weakly sensitive to the tidal frequency. Actually, these parameters strongly depend on σ in the sub-inertial regimes. Particularly, those associated with the Rossby modes decrease in absolute value while ν →−∞ (Fig. 8, left panel, see also Lee & Saio 1997; Townsend 2003). They thus tend to compensate the decay of the tidal frequency in the zero-frequency asymptotic limit. We however recover the correct functional form.
The observed behaviour of the tidal torque in the low-frequency range is due to the absence of friction in the model. This absence is responsible for the widening of the spectrum of Hough modes when σ → 0. In calculations, one has to take a large number of modes into account to compute the tidal response because their amplitude decays very slowly while the meridional degree (n) increases. As it is not possible to compute an infinite number of modes, this leads to truncation effects, which tends to degrade the obtained solution. In reality, friction modifies the tidal response in the low-frequency range by introducing an additional timescale, denoted τfriction. If τtide ≪ τfriction, the obtained solution is not modified. If τtide ≳ τfriction, it has a strong impact on the spectrum of excited Hough modes. In the asymptotic limit τtide∕τfriction → +∞, Rossby modes merge with gravity modes and converge toward the associated Legendre polynomials (see e.g. Volland & Mayr 1972; Volland 1974), which are the Hough functions in the absence of rotation. This means that the spectrum of Hough modes coupled with the quadrupolar thermal forcing tends to reduce to one function, as in the static case, when τtide ≳ τfriction, instead of broadening as observed in the present study. Hence, we expect that introducing friction in further works will change the aspect of the frequency-spectrum of the tidal torque in the low-frequency range.
 |
Fig. 9 Total tidal torque exerted of the planet (N.m) as a function of the tidal period (days). Left: for two extremal value of the thermal time (τ⋆ = 0.1, 10 days) in the static approximation (Ω = 0).
Right: for τ⋆ = 1 day in the static (Ω = 0) and traditional (Ω≠0) approximations (in this case, Ω is given by Ω = norb + σ ∕ 2 with |
6 Spin evolution
The tidal torque due to the semi-diurnal thermal tide is exerted on the radiative zone, where all of the tidal heating is absorbed. As showed by Sect. 4, there is a net separation between this zone and the convective interior as regards the direct impact of thermal tides on the dynamical evolution of the fluid. In this section, we investigate the possibility for thermal tides to generate a dynamical decoupling between the radiative zone and the convective interiors.
As a first step, let us compare the contributions of the tidal thermal and gravitational forcings in the radiative zone. For that, we introduce the ratio between the amplitude of the tidal thermal (Ctherm) and gravitational (Cgrav) components,η = Ctherm∕Cgrav. In the general case, these two components depend on the complex tidal response of the radiative zone and cannot be simply expressed. However, η can be derived analytically in the zero-frequency limit using the analysis detailed in Appendices C and D. In this case, the expression of the total multipole moment given by Eq. (D.3) shows that Ctherm and Cgrav are proportional to the two terms of the equilibrium vertical displacement, which reads for a given Hough mode (see Eq. (C.10))
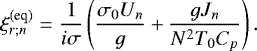 (78)
(78)
To simplify the problem, we consider the heated layer as isothermal, leading to N2 = g2∕CpT0, set the gravity to g = GMp∕R2, and assume 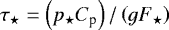 with
with 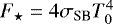 (e.g. Showman & Guillot 2002; Arras & Socrates 2010). Hence, by substituting in Eq. (78) the expressions of U2 and J2 given by Eqs. (56) and (57) and using the third Kepler law
(e.g. Showman & Guillot 2002; Arras & Socrates 2010). Hence, by substituting in Eq. (78) the expressions of U2 and J2 given by Eqs. (56) and (57) and using the third Kepler law 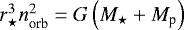 to eliminate norb, we finally obtain
to eliminate norb, we finally obtain
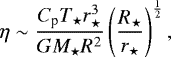 (79)
(79)
where the constant factor has been ignored.
The ratio η is plotted in Fig. 10 as a function of the star-planet distance. This figure shows the regions where the tidal response of the radiative layer is due to gravitational (η ≪ 1, blue area) and thermal(η ≫ 1, red area) forcings. In the case treated here, with the values of Table 1 and Cp = 7.49 × 103 J.kg−1. K−1, η ~ 1 corresponds to r⋆ ~ 0.03 AU, which means that the gravitational and thermal components are comparable in the zero-frequency limit. The thermal component can nevertheless be greater than the gravitational one in the frequency range of resonant internal gravity waves, where it is increased by two orders of magnitude (see Fig. 9). Moreover, one should bear in mind that η measures a mean ratio at the base of the heated layer. This ratio varies with the altitude from the base of the stably stratified layer, wheregravitational tides dominate, to the high levels of the atmosphere, mainly submitted to the stellar heating.
We nowcompare the global rotational evolution of the spin in the convective interior and radiative layer. The convective interior is submitted to the gravitational forcing of the star only, which generates an equilibrium elongation and a dynamical response taking the form of inertial waves (Ogilvie & Lin 2004). The lag due to the energy dissipated tidally by the factor, we obtain the global convective zone is thus specified by the tidal quality factor Q, and the corresponding tidal torque is given by (e.g. Goldreich & Soter 1966)
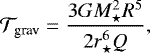 (80)
(80)
from which the synchronization time scale of the interior 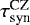 is deduced. Ignoring the constant factor, we get (e.g. Showman & Guillot 2002)
is deduced. Ignoring the constant factor, we get (e.g. Showman & Guillot 2002)
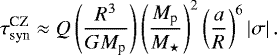 (81)
(81)
Similarly, by considering the radiative layer as a thin shell corresponding to the mass fraction fp of the planet and ignoring the constant factor, we obtain the global synchronization time scale of the spin due to semidiurnal thermal tides,
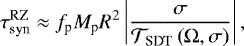 (82)
(82)
where 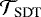 is the total tidal torque given by Eq. (73). The mass fraction of the radiative layer is determined by the pressure level at which the transition between neutral and stable stratification is located. Considering the background profiles computed in Sect. 2.2, we estimate it to fp ≈ 2 × 10−5 in the studied case.
is the total tidal torque given by Eq. (73). The mass fraction of the radiative layer is determined by the pressure level at which the transition between neutral and stable stratification is located. Considering the background profiles computed in Sect. 2.2, we estimate it to fp ≈ 2 × 10−5 in the studied case.
Hence, using Eqs. (81) and (82) with the values of parameters given by Table 1, we plot in Fig. 11 the synchronization time scale of the radiative and convective zones as a function of the tidal period. The tidal quality factor is not well constrained because it partly results from the dynamical tide within the convective region, which can vary over several orders of magnitude depending both on the properties of internal friction and on resonances associated with the propagation of inertial waves (Ogilvie & Lin 2004). For Jupiter, the magnitude of Q inferred from Io’s dissipation rate is in the range 6 × 104 < Q < 2 × 106 (Yoder & Peale 1981). For Saturn, Lainey et al. (2017) estimate the Love number to k2 = 0.390 ± 0.24 and the ratio k2∕Q to 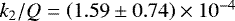 , which gives 1 × 10−3 < Q < 5 × 10−3. Therefore, to calculate the synchronization time scale of the convective interior, we employ a simplified constant-Q model, with two differentvalues of Q. In the first case, considered as weakly dissipative, the tidal quality factor is set to Q = 105 (blue dashed line). In the second case, which corresponds to a stronger tidal dissipation, Q = 103 (red dashed line). Concerning the radiative layer, we use the torque computed in the non-adiabatic case with rotation and its analytic approximation in the zero-frequency limit (see Fig. 9, right panel).
, which gives 1 × 10−3 < Q < 5 × 10−3. Therefore, to calculate the synchronization time scale of the convective interior, we employ a simplified constant-Q model, with two differentvalues of Q. In the first case, considered as weakly dissipative, the tidal quality factor is set to Q = 105 (blue dashed line). In the second case, which corresponds to a stronger tidal dissipation, Q = 103 (red dashed line). Concerning the radiative layer, we use the torque computed in the non-adiabatic case with rotation and its analytic approximation in the zero-frequency limit (see Fig. 9, right panel).
The figure shows that the synchronization time scale of the radiative layer forced by thermal tides is similar to that of the convective interior for Q = 105 (weak tidal dissipation) in the zero-frequency limit. In this case, thermal tides do not induce differential rotation between the radiative and convective regions. Resonances associated with the propagation of internal gravity waves can decrease the synchronization time scale of the radiative layer by two orders of magnitude in the period range 1–30 days. However, their effects on mean flows remain local, the high dissipation rate in the vicinity of a resonance tending to drive the rotation of the layer out of it. The time scale corresponding to a strong tidal dissipation in the radiative zone is of the same order of magnitude than that associated with Q = 103 in the convective interior.
 |
Fig. 10 Regions where the tidal response of the radiative layer is dominated by the gravitational (blue area) and thermal (red area) components of the forcing in the zero-frequency limit (σ → 0). The logarithm of the ratio η given by Eq. (79) (black solid line) is plotted as a function of the star-planet distance r⋆ (AU) in logarithmic scale. The blue dashed line designates the critical distance at which the two components are of the same order of magnitude (η ≈ 1). |
 |
Fig. 11 Synchronisation time scale (yr) of the radiative (RZ) and convective (CZ) zones as a function of the tidal period (days) in logarithmic scales. The cyan line designates the synchronization time scale computed numerically with the model of the uniformly rotating spherical shell using Eq. (82). This line is solid (dashed) in regions where the radiative layer is torqued away from (towards) synchronization. The dotted black line designates the synchronization time scale resulting from the torque derived analytically in the zero-frequency limit. Red and blue dashed lines correspond to the case of the convective interior with constant tidal quality factors set to Q = 103 and Q = 105, respectively.They are plotted using Eq. (81). |
7 Discussion
The linear analysis shows that semi-diurnal thermal tides are able to generate strong asynchronous zonal flows in the radiative zone, where all of the tidal heating is absorbed. Because of the propagation of internal waves, the fluid tidal response can be enhanced by several orders of magnitude. This reinforces the conclusions of Arras & Socrates (2010) for the semidiurnal tide, and of Gu & Ogilvie (2009) who demonstrated that the diurnal thermal tide could drive the upper layers of the atmosphere into asynchronous rotation by transporting angular momentum upward. Moreover, itemphasizes the necessity to consider the possibility of tidally driven asynchronous zonal flows in the modelling of the general circulation of hot Jupiters beyond a critical orbital radius, which is approximately r⋆ ≈ 0.03 AU in the treated case. Thermal tides can be difficult to take into account with GCMs for two reasons. First, they are negligible at time scales characterizing the global flows. Second, the atmospheric tidal response depends at the inner boundary condition on the distortion ofthe convective envelope. Thus, to properly compute the atmospheric tidal response, one should know how the system of coordinates is modified by the gravitationally excited distortion of the convective interior. However, owing to their ability to drive the radiative region into asynchronous rotation, the effects of thermal tides on the general circulation should be included in models when the thermally excited component of the tidal response is greater than the gravitationally excited component.
In the present work, it emerges that dissipative processes play a key role in the fluid tidal response. Firstly, they affect its magnitude, particularly for tidal periods τtide ≳ τ⋆. Secondly, they regularize the resonant behaviour obtained by Arras & Socrates (2010) in the vicinity of synchronous rotation, which is due to the reflection of internal gravity waves on the boundaries of the stably stratified layer (compare Fig. 9 with Fig. 4 of Arras & Socrates 2010). The radiative cooling drains away the energy injected by the tidal heating. In that sense, it acts similarly to the radiation condition used by Arras & Socrates (2010), which allows the energy to propagate upwards at the upper boundary. We thus retrieve qualitatively the spectrum plotted in Fig. 5 of their study in the static approximation. The effect of rotation on the tidal response is strong when 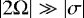 . It induces the excitation ofa large number of modes behaving in a frequency-resonant way. For this reason, the tidal response would be much more altered by rotation in the range 0.1 days < τtide < 1 day in the case of super-synchronous rotation than in the case of sub-synchronous rotation treated in this study.
. It induces the excitation ofa large number of modes behaving in a frequency-resonant way. For this reason, the tidal response would be much more altered by rotation in the range 0.1 days < τtide < 1 day in the case of super-synchronous rotation than in the case of sub-synchronous rotation treated in this study.
We shall discuss here the two approximations that we make concerning rotation to simplify calculations. As regards background flows, we consider that the planet rotates uniformly at the angular frequency Ω. Thus we ignore the coupling between tidal waves and mean flows. Nevertheless, this coupling could significantly modify the tidal response of the radiative region. Indeed, taking into account winds introduces an advection term in the momentum equation. This term is weighted by the Rossby number, that is, the parameter measuring the departure of the flow to solid rotation. Hence, in the regime of high Rossby numbers, the Coriolis acceleration is dominated by wind-driven advective accelerations, which implies a new tidal regime in Fig. 4. The effect of a vertical shear on internal waves has been studied in the framework of the Earth atmospheric tides (e.g. Chiu 1952; Booker & Bretherton 1967) and oceanic turbulence (e.g. Worthem et al. 1983). Beyond a critical value of the local Richardson number 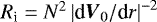 (V0 standing for the velocity vector of the wind), internal gravity are attenuated by the vertical shear at the level at which their horizontal phase speed is equal to the zonal velocity Vφ;0 (Booker & Bretherton 1967). As the horizontal phase speed scales as vφ ~ σR in the radiative zone, we expect that the vertical shear plays an important role in the low-frequency range. Typically, for R = 1.27 RJ and Vφ;0 = 1 km s−1, the frequency at which vφ ~Vφ,0 is σ = 1.1 × 10−5 s−1, which corresponds to the tidal period τtide = 6.5 days.
(V0 standing for the velocity vector of the wind), internal gravity are attenuated by the vertical shear at the level at which their horizontal phase speed is equal to the zonal velocity Vφ;0 (Booker & Bretherton 1967). As the horizontal phase speed scales as vφ ~ σR in the radiative zone, we expect that the vertical shear plays an important role in the low-frequency range. Typically, for R = 1.27 RJ and Vφ;0 = 1 km s−1, the frequency at which vφ ~Vφ,0 is σ = 1.1 × 10−5 s−1, which corresponds to the tidal period τtide = 6.5 days.
The second most important simplification as regards rotation is the traditional approximation (e.g. Unno et al. 1989). In this approximation, the horizontal component of the rotation vector, − Ωsinθ eθ, is neglected (see Eqs. (16) to (18)). Physically, this means that the we ignore the radial component of the Coriolis force and the horizontal component associated with radial motions. Therefore, the traditional approximation is appropriate in the case where the fluid displacement is dominated by horizontal motions. As the Archimedean force acts as a restoring force on fluid particles in the vertical direction, a sufficiently strong stable stratification limits vertical motions. The buoyancy thus dominates the radial component of the Coriolis force, and makes the horizontal component associated with radial motions negligible compared to that associated with horizontal motions. Given that the strengths of the Coriolis and Archimedean forces are measured by the inertia and Brunt-Väisälä frequencies, respectively, this condition is mathematically expressed by the hierarchy of frequencies  (e.g. Auclair-Desrotour et al. 2017a). The validity of the traditional approximation as regards the modelling of internal waves has been examined for various media, such as oceanic layers (e.g. Gerkema & Shrira 2005; Gerkema & Zimmerman 2008), planetary atmospheres and envelopes (e.g. Ogilvie & Lin 2004; Tort & Dubos 2014), and stellar interiors (e.g. Savonije et al. 1995; Mathis et al. 2008; Mathis 2009; Prat et al. 2017). The traditional approximation prevents us from extending the analytic approach used in this work to weakly of neutrally stratified layers, where radial and horizontal motions are of the same order of magnitude. In such cases, it is necessary to keep all of the components of the Coriolis force. This requires the use of numerical or semi-analytical methods like the Chebyshev pseudospectral method used by Ogilvie & Lin (2004).
(e.g. Auclair-Desrotour et al. 2017a). The validity of the traditional approximation as regards the modelling of internal waves has been examined for various media, such as oceanic layers (e.g. Gerkema & Shrira 2005; Gerkema & Zimmerman 2008), planetary atmospheres and envelopes (e.g. Ogilvie & Lin 2004; Tort & Dubos 2014), and stellar interiors (e.g. Savonije et al. 1995; Mathis et al. 2008; Mathis 2009; Prat et al. 2017). The traditional approximation prevents us from extending the analytic approach used in this work to weakly of neutrally stratified layers, where radial and horizontal motions are of the same order of magnitude. In such cases, it is necessary to keep all of the components of the Coriolis force. This requires the use of numerical or semi-analytical methods like the Chebyshev pseudospectral method used by Ogilvie & Lin (2004).
8 Conclusions
Motivated by the understanding of the effect of stellar semidiurnal thermal tides on the general circulation of hot Jupiters, we revisited theearly study by Arras & Socrates (2010) by including the effects of radiative cooling and rotation. We derived the equations describing the tidal response of a radially stratified fluid planet in the framework of the traditional approximation, where the horizontal and vertical structure of waves can be solved separately. For the background structure of the planet, we used the equation of state proposed by Arras & Socrates (2010), which mimics a bi-layer planet composed of a central neutrally stratified region and a thin superficial stably stratified radiative zone. As regards the radiative cooling, we applied the prescription given by Iro et al. (2005) to set the scaling law of the thermal time in the heated layer. We thus derived the equations of tidal waves forced both by the stellar incoming flux and the tidal gravitational potential of the star, as well as the associated tidal torque and time scale of evolution of tidally forced mean zonal flows. We then solved these equations numerically for the case treated by Arras & Socrates (2010) in three configurations: (a) in the static and adiabatic approximations (Arras & Socrates 2010), (b) in the static approximation with radiative cooling, (c) with rotation and radiative cooling. In each case, we computed both the internal structure of the tidal response due to the thermal forcing and the total tidal torque exerted on the planet.
The rotation strongly modifies the structure of the tidal waves by coupling the forcing with Hough modes of different wavenumbers. The better coupled modes can change depending on the frequency. In the super-inertial regime (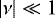 ), the main contributor is the gravity mode of degree n = 0. In the sub-inertial regime (
), the main contributor is the gravity mode of degree n = 0. In the sub-inertial regime (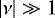 ), the structure of the tidal perturbation is shaped by a large number of Rossby modes. In the framework of the static and adiabatic approximations we recover the results obtained by Arras & Socrates (2010). The absence of dissipation allows gravito-acoustic waves to propagate over the whole thickness of the radiative zone and to be reflected by its boundaries, which amplify the tidal response and allows a strongly oscillating behaviour to arise in the vicinity of spin-orbit synchronous rotation. Introducing the radiative cooling leads to a regularized response where such oscillations do not exist any more. In this case, the response is characterized by large-scale patterns tending to generate zonal flows in alternate directions. However, the tidal response in the zero-frequency limit remains the same as in the adiabatic case. It does not depend on the thermal time of the radiative zone.
), the structure of the tidal perturbation is shaped by a large number of Rossby modes. In the framework of the static and adiabatic approximations we recover the results obtained by Arras & Socrates (2010). The absence of dissipation allows gravito-acoustic waves to propagate over the whole thickness of the radiative zone and to be reflected by its boundaries, which amplify the tidal response and allows a strongly oscillating behaviour to arise in the vicinity of spin-orbit synchronous rotation. Introducing the radiative cooling leads to a regularized response where such oscillations do not exist any more. In this case, the response is characterized by large-scale patterns tending to generate zonal flows in alternate directions. However, the tidal response in the zero-frequency limit remains the same as in the adiabatic case. It does not depend on the thermal time of the radiative zone.
In the zero-frequency limit, the obtained frequency spectrum of the tidal torque reaches a saturation plateau when rotation in included. It thus qualitatively differs from the static case treated by Arras & Socrates (2010). In their case, the torque follows the scaling law 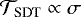 , which corresponds to the frequency behaviour described by the constant time lag model. Both behaviours are well approximated by the analytic formula derived for the equilibrium tide in this work, which generalizes that given by Arras & Socrates (2010) to non-adiabatic and rotating atmospheres. Particularly, this formula allows us to identify the amplification factors at the origin of the saturation in the rotating case. These amplification factors are due to the absence of friction in the model, which allows rotation to couple the perturbation with a large number of Rossby modes. In reality, friction would prevent this coupling in the low-frequency range and drive the perturbation toward a quadrupolar pattern, similarly to the forcing. As observed by Arras & Socrates (2010), the obtained spectra of the total tidal torque exhibit resonances corresponding to gravito-acoustic waves in the high-frequency range (τtide ≲ 1 day) and to gravity waves in the medium-frequency range (1 ≲ τtide ≲ 30 days).
, which corresponds to the frequency behaviour described by the constant time lag model. Both behaviours are well approximated by the analytic formula derived for the equilibrium tide in this work, which generalizes that given by Arras & Socrates (2010) to non-adiabatic and rotating atmospheres. Particularly, this formula allows us to identify the amplification factors at the origin of the saturation in the rotating case. These amplification factors are due to the absence of friction in the model, which allows rotation to couple the perturbation with a large number of Rossby modes. In reality, friction would prevent this coupling in the low-frequency range and drive the perturbation toward a quadrupolar pattern, similarly to the forcing. As observed by Arras & Socrates (2010), the obtained spectra of the total tidal torque exhibit resonances corresponding to gravito-acoustic waves in the high-frequency range (τtide ≲ 1 day) and to gravity waves in the medium-frequency range (1 ≲ τtide ≲ 30 days).
As the sign of the tidal torque varies with the tidal frequency, the semidiurnal tide is likely to drive strong asynchronous zonal flows over time scales comparable to the year in order of magnitude. This impact results from both the weak density of the radiative zone and the fact that it absorbs all of the incoming stellar flux. This highlights the fact that the dynamics of the radiative zone are far more sensitive to stellar thermal tides than the central convective region. However, the time scales associated with the growth of tidally forced jets remains larger than those characterizing the general circulation in the heated zone. In the zero-frequency limit, the thermal tidal response of the radiative layer dominate the gravitational component beyond a critical orbital radius, estimated to r⋆ ~ 0.03 AU in this work. The associated synchronization time scale is of the same order as that of the convective interior if this latter has a Jupiter-like tidal dissipation rate, Q = 105. It can be decreased by several orders of magnitude by resonances due to internal gravito-inertial waves in the period range 1–30 days.
A subject of interest for forthcoming works would be to investigate how winds affect the tidal response. The intense stellar heating to which hot Jupiters are submitted by their host star forces strong zonal jets inducing an important departure to the idealised solid rotation approximation. Therefore, the interplay between the general circulation and tidal waves appears as a key question in the understanding of the effect of tides on the dynamical evolution of hot Jupiters.
Acknowledgements
The authors acknowledge funding by the European Research Council through the ERC grant WHIPLASH 679030. They wish to thank the anonymous referee for helpful suggestions and remarks. P. Auclair-Desrotour acknowledges Anthony Caldas for his help with the use of Python plotting tools.
Appendix A Polarisation relations of the tidal response
The polarisation relations of the tidal response (Sect. 2.2) are computed by substituting Ψ n in primitive equations. Omitting the superscripts m and σ, we obtain, for latitudinal motions,

and for scalar quantities,
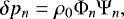 (A.7)
(A.7)
![\begin{align} \delta \rho_n = & - \frac{\rho_0}{gH} \frac{N^2}{N^2 - \sigma \left( \sigma - i \sigma_0 \right)} \left[{\mathrm{\Phi}}_n \left( \frac{{\textrm{d}} {\mathrm{\Psi}}_n}{{\textrm{d}}x} + \mathcal{B}_n {\mathrm{\Psi}}_n \right) \right. \\[9pt] & \left. - \frac{{\textrm{d}} U_n}{{\textrm{d}}x} + i \frac{\kappa \sigma}{N^2} J_n \right], \nonumber \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq185.png)
![\begin{equation*} \delta T_n = \frac{N^2}{N^2 - \sigma \left( \sigma - i \sigma_0 \right)} \left[{\mathrm{\Phi}}_n \left( \frac{{\textrm{d}} {\mathrm{\Psi}}_n}{{\textrm{d}}x} + \mathcal{C}_n {\mathrm{\Psi}}_n \right) - \frac{{\textrm{d}} U_n}{{\textrm{d}}x} + i \frac{\kappa \sigma}{N^2} J_n \right] , \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq186.png) (A.9)
(A.9)
]where we have introduced the co-efficients
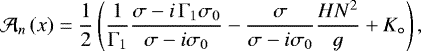 (A.10)
(A.10)
![\begin{align} \mathcal{B}_n \left( x \right) = & \frac{1}{2} \left[ \frac{1}{{\mathrm{\Gamma}}_1} \frac{\sigma - i \, {\mathrm{\Gamma}}_1 \sigma_0}{\sigma - i \sigma_0} \left( 2 \frac{\sigma \left( \sigma - i \sigma_0 \right)}{N^2} - 1 \right) \right. \\[6pt] & \left. - \frac{\sigma}{\sigma - i \sigma_0} \frac{H N^2}{g} + K_{\circ} \right], \nonumber \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq188.png)
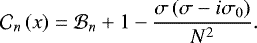 (A.12)
(A.12)
Appendix B Impact of the lower boundary condition on the solution
As discussed in Sect. 2.4, the lower limit of the fluid region where the tidal perturbation is computed can affect the obtained solution if it is set too close to the base of the stably stratified zone. We show here an example of the kind of artefacts that can occur in these cases. In plots displayed by Fig. 6, the lower limit is set as far as possible from the perturbed region, that is at the centre of the planet. This allows us to avoid artificial interactions of the perturbation with the lower boundary. In the present case, we set the lower limit of the fluid region at the pressure level p0 = 104 bar, much more closer to the basis of the stably stratified zone (the region now stands for 6% of the planet radius), and do the calculations again for two cases treated in Fig. 6: (i) τtide = 0.1 day and (ii) τtide = 10 days, with rotation and radiative cooling. The parameters used for this study are those given by Table 1. The lower boundary condition is a rigid-wall condition, as defined in Sect. 2.4. The obtained results are plotted in Fig. B.1.
 |
Fig. B.1 Imaginary part of density fluctuations in the case treated in Fig. 6 for a lower boundary located at the pressure level p0 = 104 bar instead of the centre of the planet as in Fig. 6. The density fluctuations are plotted as a function of latitude (degrees, horizontal axis) and pressure in logarithmic scale (bars, vertical axis) in the case with rotation and radiative cooling and for two different tidal periods, (i) τtide = 0.1 day (left) and (ii) τtide = 10 day (right). The corresponding rotation rates are given by Ω = σ∕2 + norb with |
In case (ii), we obtain exactly the same solution as in Fig. 6. Tidal density variations are not affected by the lower boundary. We cannot observe any artefact. The other case is different. In case (i), we clearly note that the solution exhibit a new pattern with respect the the plot of Fig. 6. This pattern corresponds to an artefact resulting from the interactions of the tidal perturbation with the lower boundary of the fluid region. It highlight the way this boundary can affects the solution and justifies that we set the lower limit of the fluid region “at the infinite”.
Appendix C Low-frequencies asymptotic regime
We derive here the asymptotic tidal response of the radiative zone in the low-frequency regime, which corresponds to σ ≪ σ0, 2Ω, N, σs (see Fig. 4). Following Arras & Socrates (2010), we first establish the zero-frequency limit, the so-called equilibrium tide, and then a finite frequency correction to obtain the trend in the vicinity of spin–orbit synchronous rotation. Our goal is study the role played by rotation and radiative cooling in this regime and to explain the results obtained numerically in Sects. 4 and 5.
C.1 The equilibrium tide (σ → 0)
The equilibrium tide is defined as the zero-frequency tidal response. We thus consider the primitive equations given by Eqs. (16) to (20) and let σ tend to zero. We begin with the equilibrium displacement. In the static case, the dis-placement associated with the  -mode can be expanded in the poloidal harmonics (e.g., Arras & Socrates 2010)
-mode can be expanded in the poloidal harmonics (e.g., Arras & Socrates 2010)
![\begin{equation*} \boldsymbol{\xi}_{l}^{m,\sigma} = \left[ \xi_{r ; l}^{m,\sigma} \left( r \right) {e}_r + \xi_{\perp ; l}^{m,\sigma} \left( r \right) r \boldsymbol{\nabla}_{\perp} \right] P_l^m \left( \cos \theta \right) \textrm{e}^{i \left( \sigma t + m \varphi \right)},\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq191.png) (C.1)
(C.1)
where  designates the vertical profile of the horizontal displacement and
designates the vertical profile of the horizontal displacement and 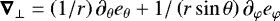 the horizontal gradient operator in spherical coordinates. When the rotation is introduced (using the traditional approximation), the solution is a series of Hough modes identified by the subscript n. The previous expression thus generalises into
the horizontal gradient operator in spherical coordinates. When the rotation is introduced (using the traditional approximation), the solution is a series of Hough modes identified by the subscript n. The previous expression thus generalises into
![\begin{equation*} \boldsymbol{\xi}_{n}^{m,\sigma} = \left[ \xi_{r ; n}^{m,\sigma} \left( r \right) + \xi_{\perp ; n}^{m,\sigma} \left( r \right) \boldsymbol{\mathcal{L}}_{\perp}^{m,\nu} \right] {\mathrm{\Theta}}_n^{m,\nu} \left( \theta \right) \textrm{e}^{i \left( \sigma t + m \varphi \right)}, \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq194.png) (C.2)
(C.2)
the notation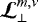 referring to the horizontal operator
referring to the horizontal operator
![\begin{align*} \boldsymbol{\mathcal{L}}_{\perp}^{m,\nu} = & \frac{1}{1 - \nu^2 \cos^2 \theta} \left[ \left( \frac{{\textrm{d}}}{{\textrm{d}} \theta} + m \nu \cot \theta \right) {e}_{\theta} \right. \\ & \left. + \left( \nu \cos \theta \frac{{\textrm{d}}}{{\textrm{d}} \theta} + \frac{m}{\sin \theta} \right) {e}_{\varphi} \right]. \nonumber \end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq196.png)
In the static case, 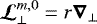 and we recover the expansion in poloidal harmonics given by Eq. (C.1). In the following, we omit the superscript
and we recover the expansion in poloidal harmonics given by Eq. (C.1). In the following, we omit the superscript  in order to lighten equations.
in order to lighten equations.
With the notations introduced above, the equation of conservation of the horizontal momentum is expressed as
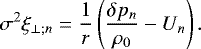 (C.4)
(C.4)
As a consequence, the equilibrium pressure fluctuation writes
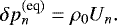 (C.5)
(C.5)
Substituting Eq. (C.5) in the equation of conservation of the vertical momentum,
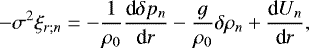 (C.6)
(C.6)
we get the density fluctuation associated with the equilibrium tide,
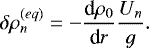 (C.7)
(C.7)
We then consider the equation of heat transport,
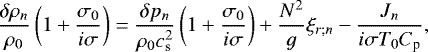 (C.8)
(C.8)
where we substitute the pressure and density fluctuations associated with the equilibrium tide, Eqs. (C.5) and (C.7). It follows that
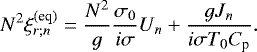 (C.9)
(C.9)
As discussed by Arras & Socrates (2010), we note that no solution exist in the central neutrally stratified region, since N2 → 0 while the thermal forcing is non-zero. This results from the vanishing of the Archimedean force, which is the only restoring force of the system in the vertical direction. In the neutrally stratified region, fluid particles can move freely along the vertical direction. As a consequence, no equilibrium can be reached when a forcing is applied. We shall also highlight here the fact that the traditional approximation is not valid in neutrally stratified region in the zero-frequency limit since 2Ω ≳ σ, N.
In the stably stratified radiative zone however, the vertical displacement associated with the equilibrium tide is expressed as
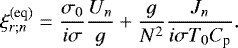 (C.10)
(C.10)
By substituting Eqs. (C.5), (C.7) and (C.10) in the equation of mass conservation,
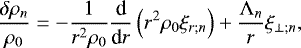 (C.11)
(C.11)
we finally get the horizontal displacement,
![\begin{equation*} r \rho_0 \xi_{\perp ; n}^{(\textrm{eq})} = \frac{1}{{\mathrm{\Lambda}}_n} \left[ \frac{{\textrm{d}}}{{\textrm{d}}r} \left( r^2 \rho_0 \xi_{r ; n}^{(\textrm{eq} )} \right) + r^2 \delta \rho_n^{(\textrm{eq})} \right].\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq207.png) (C.12)
(C.12)
Hence, the pressure and density fluctuations associated with the equilibrium tide are determined by the tidal gravitational potential only while the displacement results from both gravitational and thermal forcings. Looking at Eq. (C.10), we note that the radiative cooling only affects the gravitationally forced tidal component. This explains why the tidal torques computed for different thermal times all converge towards the same asymptotic law at τtide → +∞. The role played by rotation is of greater complexity. It is first expressed through the eigenvalues associated with Hough modes (Λ n), which take very different values from those of gravity modes in the static case. Typically, for 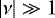 , predominant symmetric (n even) Rossby modes coupled with the quadrupolar forcing (m = 2) are characterized by
, predominant symmetric (n even) Rossby modes coupled with the quadrupolar forcing (m = 2) are characterized by 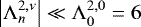 . Second, the rotation modifies the coupling coefficients weighting Hough modes (the
. Second, the rotation modifies the coupling coefficients weighting Hough modes (the 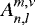 introduced in Eq. (28)) in a non-trivial way. Thus, predominant Hough modes can change depending on ν. In the super-inertial regime (
introduced in Eq. (28)) in a non-trivial way. Thus, predominant Hough modes can change depending on ν. In the super-inertial regime (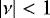 ) the predominant mode is the gravity mode of index n = 0. For ν = 10, it is the Rossby mode of index n = −2.
) the predominant mode is the gravity mode of index n = 0. For ν = 10, it is the Rossby mode of index n = −2.
C.2 Finite frequency correction
We now consider the first order correction in σ2, in order to derive scaling laws describing the behaviour of the density fluctuation as a function of σ in the asymptotic regime of low tidal frequencies. First, by identifying 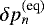 (Eq. (C.5)) in Eq. (C.4), we get
(Eq. (C.5)) in Eq. (C.4), we get
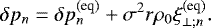 (C.13)
(C.13)
We then substitute this equation in the vertical momentum equation to obtain the density fluctuation,
![\begin{equation*} \delta \rho_n = \delta \rho_n^{(\textrm{eq})} + \frac{\sigma^2}{g} \left[ \rho_0 \xi_{r ; n}^{(\textrm{eq})} - \frac{{\textrm{d}}}{{\textrm{d}}r} \left( r \rho_0 \xi_{\perp ; n}^{(\textrm{eq}) } \right) \right]. \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq214.png) (C.14)
(C.14)
Finally, by using the expression of the horizontal dis-placement associated with the equilibrium tide (Eq. (C.12)) in this equation and ignoring the gravitational forcing, we end up with the expression of δρn as a function of 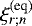 ,
,
![\begin{equation*} \delta \rho_n = \frac{\sigma^2}{g} \left[ \rho_0 \xi_{r ; n}^{(\textrm{eq})} - \frac{1}{{\mathrm{\Lambda}}_n} \frac{{\textrm{d}}^2}{{\textrm{d}}r^2} \left( r^2 \rho_0 \xi_{r ; n}^{(\textrm{eq})} \right) \right]. \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq216.png) (C.15)
(C.15)
Appendix D Tidal multipole moment
The tidal multipole moment 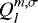 introduced in Eq. (68) stands for the global variation of mass distribution associated with the
introduced in Eq. (68) stands for the global variation of mass distribution associated with the 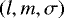 -mode. It quantifies the energy tidally dissipated by the mode and is defined by (e.g., Arras & Socrates 2010)
-mode. It quantifies the energy tidally dissipated by the mode and is defined by (e.g., Arras & Socrates 2010)
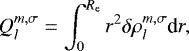 (D.1)
(D.1)
where 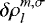 designates the projection of the distribution of density fluctuations on the
designates the projection of the distribution of density fluctuations on the  -harmonic, and Re the radius of the upper boundary introduced in Sect. 2.1. The tidal multipole moment is thus the sum of the contributions of Hough modes, denoted
-harmonic, and Re the radius of the upper boundary introduced in Sect. 2.1. The tidal multipole moment is thus the sum of the contributions of Hough modes, denoted 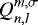 , weighted by the projections coefficients of Hough functions on the associated Legendre polynomials, that is,
, weighted by the projections coefficients of Hough functions on the associated Legendre polynomials, that is,
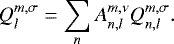 (D.2)
(D.2)
To improve the convergence of the numerical integration, Arras & Socrates (2010) separate the equilibrium and the dynamical tide (see Arras & Socrates 2010, Appendix A). Following their method, we substitute 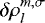 in Eq. (D.1) using Eq. (18). After two integrations by parts, and omitting the superscripts
in Eq. (D.1) using Eq. (18). After two integrations by parts, and omitting the superscripts 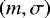 , we end up with
, we end up with
![\begin{align*} Q_{n,l}^{m,\sigma} = & \int_0^{R_{\textrm{e}}} r^{2+l} \delta \rho_n^{(\textrm{eq})} {\textrm{d}}r + \sigma^2 \left[ \frac{r^2}{{\mathrm{\Lambda}}_n} \frac{{\textrm{d}}}{{\textrm{d}}r} \left( \frac{r^{2+l}}{g} \right) \rho_0 \xi_{r ; n} - \frac{r^{3+l}}{g} \rho_0 \xi_{\perp ; n} \right]_0^{R_{\textrm{e}}} \nonumber \\ & + \sigma^2 \int_0^{R_{\textrm{e}}} \left\{ \rho_0 \xi_{r ; n} \left[ \frac{r^{2+l}}{g} - \frac{r^2}{{\mathrm{\Lambda}}_n} \frac{{\textrm{d}}^2}{{\textrm{d}}r^2} \left( \frac{r^{2+l}}{g} \right) \right] \right. \nonumber \\ & \left. + \frac{r^2}{{\mathrm{\Lambda}}_n} \frac{{\textrm{d}}}{{\textrm{d}}r} \left( \frac{r^{2+l}}{g} \right) \delta \rho_n \right\} \mathrm{d}r,\end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq226.png)
where ξ⊥;n and 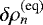 are defined by Eqs. (C.4) and (C.7), respectively. We recover here the multipole moment given by Arras & Socrates (2010) modified by rotation (the
are defined by Eqs. (C.4) and (C.7), respectively. We recover here the multipole moment given by Arras & Socrates (2010) modified by rotation (the 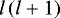 of Legendre polynomials have been replaced by the associated eigenvalues of Hough modes, Λ n). In Eq. (D.3), we have conserved the boundary term resulting from the integrations by part (second term of the right member). Arras & Socrates (2010) ignore this term by arguing that it is negligible with respect to the others. They thus compute the quadrupole moment associated with the l = m = 2 tidal component by using a simplified expression and find that it leads to a better convergence than integrating the density variations directly. However, we notice in our calculations that the boundary term is negligible in the zero-frequency limit and in the non-adiabatic case. In the adiabatic case, tidal waves can be reflected backward at the upper boundary, leading to a non-negligible boundary term. We verify that we obtain numerically the same results by using either Eq. (D.1) or Eq. (D.3), which suggests that writing the tidal quadrupole moment in the way of Eq. (D.3) does not improve the precision of the computation.
of Legendre polynomials have been replaced by the associated eigenvalues of Hough modes, Λ n). In Eq. (D.3), we have conserved the boundary term resulting from the integrations by part (second term of the right member). Arras & Socrates (2010) ignore this term by arguing that it is negligible with respect to the others. They thus compute the quadrupole moment associated with the l = m = 2 tidal component by using a simplified expression and find that it leads to a better convergence than integrating the density variations directly. However, we notice in our calculations that the boundary term is negligible in the zero-frequency limit and in the non-adiabatic case. In the adiabatic case, tidal waves can be reflected backward at the upper boundary, leading to a non-negligible boundary term. We verify that we obtain numerically the same results by using either Eq. (D.1) or Eq. (D.3), which suggests that writing the tidal quadrupole moment in the way of Eq. (D.3) does not improve the precision of the computation.
In the zero-frequency limit (σ → 0), the above expression can be simplified using the equations of the equilibrium thermal tide (Un = 0) established in Appendix C. First, let us note that 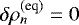 ,
, 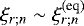 and
and 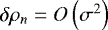 in this regime, which means that the term in δρn in Eq. (D.3) tends to become negligible compared to that in ξr;n while σ → 0. Moreover, as tidal waves cannot propagate in the central convective region, the perturbation at the lower boundary can be neglected. Itfollows that
in this regime, which means that the term in δρn in Eq. (D.3) tends to become negligible compared to that in ξr;n while σ → 0. Moreover, as tidal waves cannot propagate in the central convective region, the perturbation at the lower boundary can be neglected. Itfollows that
![\begin{align*}Q_{n,l}^{m,\sigma} = & \ \sigma^2 \int_0^{R_{\textrm{e}}} \rho_0 \xi_{r ; n} \left[ \frac{r^{2+l}}{g} - \frac{r^2}{{\mathrm{\Lambda}}_n} \frac{{\textrm{d}}^2}{{\textrm{d}}r^2} \left( \frac{r^{2 + l}}{g} \right) \right] \textrm{d} r \\ & + \sigma^2 \left[ \frac{1}{{\mathrm{\Lambda}}_n} \frac{{\textrm{d}}}{{\textrm{d}}r} \left( \frac{r^{2+l}}{g} \right) r^2 \rho_0 \xi_{r ; n} - \frac{r^{3+l}}{g} \rho_0 \xi_{\perp ; n} \right]_{r = R_{\textrm{e}}} . \nonumber \end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq232.png)
The thermal tide only affects a thin superficial layer of the planet. We thus approximate the internal mass by M ≈ Mp, which makes the gravity scale as g∝ r−2 in this region. This allows us to simplify the derivatives of r2+l∕g in Eq. (D.4) and to obtain for the integrand
![\begin{equation*} \frac{r^{2+l}}{g} - \frac{r^2}{{\mathrm{\Lambda}}_n} \frac{{\textrm{d}}^2}{{\textrm{d}}r^2} \left( \frac{r^{2+l}}{g} \right) = \frac{r^{2 + l}}{g} \left[ 1 - \frac{\left( l + 4 \right) \left( l + 3 \right) }{{\mathrm{\Lambda}}_n} \right]. \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq233.png) (D.5)
(D.5)
We now consider the boundary term of Eq. (D.4). Without the contribution of the gravitational tidal potential the horizontal displacement of the n-Hough mode given by Eq. (C.12) simplifies into
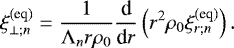 (D.6)
(D.6)
In this equation, the derivative can be expanded as
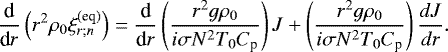 (D.7)
(D.7)
Firstly, with the approximation done above for the internal mass, r2 g is a constant. Secondly, the background structure that we use of the radiative zone corresponds to an isothermal atmosphere (see Fig. 2). As a consequence, T0 and Cp are constant and N2 = κg∕H varies slowly with the vertical coordinate compared to the density, which is approximated by the exponential law 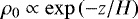 , the notation z standing for the altitude with respect to the base of the isothermal region. Besides,
, the notation z standing for the altitude with respect to the base of the isothermal region. Besides, ![$ J_n \propto J_{\star} \exp \left[ - \exp \left(- z / H \right) \right] $](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq237.png) , where J⋆ designates the tidal heating power per unit mass at z = +∞. It follows that
, where J⋆ designates the tidal heating power per unit mass at z = +∞. It follows that
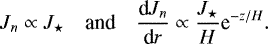 (D.8)
(D.8)
Therefore, the ratio between the second and the first term of Eq. (D.7), denoted ς, scales as ς ~ e−z∕H, which allows us to approximate  at r = Re by
at r = Re by
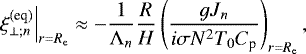 (D.9)
(D.9)
Appendix E Numerical scheme used to integrate the vertical structure equation of tidal waves
Integrating the vertical structure equation of tidal waves, Eq. (41), consists in seeking solutions of the boundary conditions problem defined by the equations
![\begin{equation*} \left\{ \begin{array}{ll} \displaystyle \frac{{\textrm{d}}^2 y}{{\textrm{d}}x^2} + P \frac{{\textrm{d}} y}{{\textrm{d}}x} + Q y = R, & \textrm{for} \ x \in \left[ x_{\textrm{inf}} , x_{\textrm{sup}} \right] , \\[0.3cm] \displaystyle a_{\textrm{inf}} \frac{{\textrm{d}}y}{{\textrm{d}}x} + b_{\textrm{inf}} y= c_{\textrm{inf}}, & \textrm{at} \ x = x_{\textrm{inf}}, \\[0.3cm] \displaystyle a_{\textrm{sup}} \frac{{\textrm{d}}y}{{\textrm{d}}x} + b_{\textrm{sup}} y = c_{\textrm{sup}}, & \textrm{at} \ x = x_{\textrm{sup}}, \end{array} \right.\end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq242.png) (E.1)
(E.1)
where P, Q, and R are r-dependent coefficients and  and
and 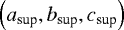 triplets of coefficients defining the lower and upper boundary conditions, respectively. To solve this system, we use a procedure of forward and backward substitution (cf. Press 2007, Sect. 2.4), also called Thomas’ algorithm. This method is interesting because it takes only
triplets of coefficients defining the lower and upper boundary conditions, respectively. To solve this system, we use a procedure of forward and backward substitution (cf. Press 2007, Sect. 2.4), also called Thomas’ algorithm. This method is interesting because it takes only 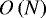 operations, the parameter N being the size of the mesh. It is used by Chapman & Lindzen (1970) with a finite difference scheme of the second order. Here, we adapt it to a finite difference numerical scheme of the fourth order. This allows us to improve the stability of the scheme, and thus the treatment of highly oscillating tidal waves3, for which the curvature terms can be very important.
operations, the parameter N being the size of the mesh. It is used by Chapman & Lindzen (1970) with a finite difference scheme of the second order. Here, we adapt it to a finite difference numerical scheme of the fourth order. This allows us to improve the stability of the scheme, and thus the treatment of highly oscillating tidal waves3, for which the curvature terms can be very important.
The domain ![$ \left[x_{\textrm{inf}} , x_{\textrm{sup}} \right] $](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq246.png) is divided into N intervals of size h. The points are indexed with the subscript n, such that 0 ≤ n ≤ N, n = 0 corresponding to the left boundary x = xinf and n = N to the upper boundary x = xsup. At the fourth order, the centred finite difference approximations of the first and second derivatives of f at the point of index n are expressed as
is divided into N intervals of size h. The points are indexed with the subscript n, such that 0 ≤ n ≤ N, n = 0 corresponding to the left boundary x = xinf and n = N to the upper boundary x = xsup. At the fourth order, the centred finite difference approximations of the first and second derivatives of f at the point of index n are expressed as
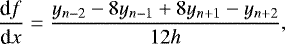 (E.2)
(E.2)
Therefore, by substituting Eqs. (E.2) and (E.3) into the differential equation given by Eq. (E.1), we obtain, for 2 ≤ n ≤ N − 2, the recurrence relation
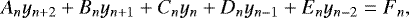 (E.4)
(E.4)
At the points n = 1 and n = N − 1, we use the centred finite difference scheme of the second order, where derivatives are written
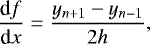 (E.6)
(E.6)
The recurrence relation is thus given by
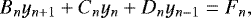 (E.8)
(E.8)
We introduce then the triplet 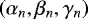 such that
such that
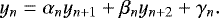 (E.10)
(E.10)
Substituting Eq. (E.10) into Eq. (E.4), we express the triplet 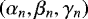 as a function of triplets of smaller indices (i.e. n − 1 and n − 2),
as a function of triplets of smaller indices (i.e. n − 1 and n − 2),
![\begin{align*} & \alpha_n = - K_n^{-1} \left( B_n + D_n \beta_{n-1} + E_n \alpha_{n-2} \beta_{n-1} \right), \\ & \beta_n = - K_n^{-1} A_n, \\ & \gamma_n = K_n^{-1} \left[ F_n - D_n \gamma_{n-1} - E_n \left( \alpha_{n-2} \gamma_{n-1} + \gamma_{n-2} \right) \right], \end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq258.png)
where Kn is expressed as
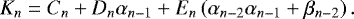 (E.14)
(E.14)
To initialise the series 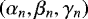 , we consider the left boundary condition. This condition implies that
, we consider the left boundary condition. This condition implies that
![\begin{equation*} \begin{array}{ll} \hspace*{-4pt} \displaystyle \alpha_0 = - \frac{2 a_{\textrm{inf}}}{h b_{\textrm{inf}} - \frac{3}{2} a_{\textrm{inf}}} , & \displaystyle \beta_0 = \frac{1}{2} \frac{a_{\textrm{inf}}}{h b_{\textrm{inf}} - \frac{3}{2} a_{\textrm{inf}}}, \\[0.3cm] \hspace*{-4pt} \displaystyle \gamma_0 = \frac{h c_{\textrm{inf}}}{h b_{\textrm{inf}} - \frac{3}{2} a_{\textrm{inf}}}. \end{array} \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq261.png) (E.15)
(E.15)
Besides, Eq. (E.8) expressed at n = 1 provides the co-efficients
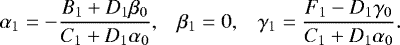 (E.16)
(E.16)
Hence, the co-efficients 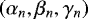 are computed forward from n = 2 to n = N − 2.
are computed forward from n = 2 to n = N − 2.
The terms yN−1 and yN of the series yn shall now be determined. We use the upper boundary condition and Eq. (E.8) at n = N − 1 to obtain the algebraic system
![\begin{equation*} \left\{ \begin{array}{l} \displaystyle \mathcal{A}_1 y_{N-1} + \mathcal{B}_1 y_N = \mathcal{C}_1 , \\[0.3cm] \displaystyle \mathcal{A}_2 y_{N-1} + \mathcal{B}_2 y_N = \mathcal{C}_2, \end{array} \right. \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq264.png) (E.17)
(E.17)
where the coefficients 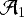 ,
, 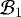 ,
, 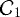 ,
, 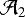 ,
, 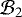 , and
, and 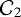 are given by
are given by
![\begin{equation*} \begin{array}{ll} \hspace*{-4pt} \displaystyle \mathcal{A}_1 = a_{\textrm{sup}} \left( \frac{1}{2} \alpha_{N-2} - 2 \right) , & \displaystyle \mathcal{A}_2 = C_{N-1} + D_{N-1} \alpha_{N-2}, \\[0.3cm] \hspace*{-4pt} \displaystyle \mathcal{B}_1 = \frac{1}{2} a_{\textrm{sup}} \left( 3 + \beta_{N-2} \right) + h b_{\textrm{sup}}, & \displaystyle \mathcal{B}_2 = B_{N-1} +D_{N-1} \beta_{N-2}, \\[0.3cm] \hspace*{-4pt} \displaystyle \mathcal{C}_1 = h c_{\textrm{sup}} - \frac{1}{2} a_{\textrm{sup}} \gamma_{N-2} , & \displaystyle \mathcal{C}_2 = F_{N-1} - D_{N-1} \gamma_{N-2}. \end{array} \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq271.png) (E.18)
(E.18)
The yn are finally integrated backward from n = N − 2 to n = 0 with the recurrence relation given by Eq. (E.10).
References
- Abramowitz, M., & Stegun, I. A. 1972, Handbook of Mathematical Functions (New York: Dover) [Google Scholar]
- Arras, P., & Socrates, A. 2010, ApJ, 714, 1 [Google Scholar]
- Auclair-Desrotour, P., Laskar, J., & Mathis, S. 2017a, A&A, 603, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auclair-Desrotour, P., Laskar, J., Mathis, S., & Correia, A. C. M. 2017b, A&A, 603, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Booker, J. R., & Bretherton, F. P. 1967, J. Fluid Mech., 27, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S., & Lindzen, R. 1970, Atmospheric Tides: Thermal and Gravitational. (Dordrecht: Reidel) [Google Scholar]
- Chiu, W.-C. 1952, Arch. Meteorol. Geophys. Bioklimatol., Ser. A., 5, 280 [Google Scholar]
- Cho, J. Y.-K., Menou, K., Hansen, B. M. S., & Seager, S. 2003, ApJ, 587, L117 [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2001, Nature, 411, 767 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Correia, A. C. M., & Laskar, J. 2003, J. Geophys. Res. (Planets), 108, 5123 [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- Dickinson, R. E., & Geller, M. A. 1968, J. Atm. Sci., 25, 932 [Google Scholar]
- Dobrovolskis, A. R., & Ingersoll, A. P. 1980, Icarus, 41, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Shrira, V. I. 2005, J. Fluid Mech., 529, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Gerkema, T., & Zimmerman, J. 2008, An introduction to internal wave, Lecture notes (Texel: Royal NIOZ) [Google Scholar]
- Gold, T., & Soter, S. 1969, Icarus, 11, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Soter, S. 1966, Icarus, 5, 375 [Google Scholar]
- Gu, P.-G., & Ogilvie, G. I. 2009, MNRAS, 395, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Hough, S. S. 1898, Roy. Soc. London Philos. Trans. Ser. A, 191, 139 [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Ingersoll, A. P., & Dobrovolskis, A. R. 1978, Nature, 275, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Ioannou, P. J., & Lindzen, R. S. 1993a, ApJ, 406, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Ioannou, P. J., & Lindzen, R. S. 1993b, ApJ, 406, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Ioannou, P. J., & Lindzen, R. S. 1994, ApJ, 424, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Iro, N., Bézard, B., & Guillot, T. 2005, A&A, 436, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lainey, V., Jacobson, R. A., Tajeddine, R., et al. 2017, Icarus, 281, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Laplace, P. S. 1798, Traité de mécanique céleste (Duprat J. B. M.) [Google Scholar]
- Leconte, J., Wu, H., Menou, K., & Murray, N. 2015, Science, 347, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, U., & Saio, H. 1997, ApJ, 491, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Lindzen, R. S., & McKenzie, D. J. 1967, Pure Appl. Geophys., 66, 90 [Google Scholar]
- Lubow, S. H., Tout, C. A., & Livio, M. 1997, ApJ, 484, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S. 2009, A&A, 506, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Le Poncin-Lafitte C. 2009, A&A, 497, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Talon, S., Pantillon, F.-P., & Zahn, J.-P. 2008, Sol. Phys., 251, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 1979, Moon Planets, 20, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 1980, Moon Planets, 23, 185 [Google Scholar]
- Ogilvie, G. I., & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Prat, V., Mathis, S., Lignières, F., Ballot, J., & Culpin, P.-M. 2017, A&A, 598, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H. 2007, Numerical Recipes 3rd edn.: The Art of Scientific Computing (Cambridge University Press) [Google Scholar]
- Rasio, F. A., Tout, C. A., Lubow, S. H., & Livio, M. 1996, ApJ, 470, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E., & Kempton, E. M. R. 2014, ApJ, 790, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Savonije, G. J., Papaloizou, J. C. B., & Alberts, F. 1995, MNRAS, 277, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showman, A. P., Fortney, J. J., Lian, Y., et al. 2009, ApJ, 699, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Lewis, N. K., & Fortney, J. J. 2015, ApJ, 801, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Terquem, C., Papaloizou, J. C. B., Nelson, R. P., & Lin, D. N. C. 1998, ApJ, 502, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Tort, M., & Dubos, T. 2014, QJRAS, 140, 2388 [Google Scholar]
- Townsend, R. H. D. 2003, MNRAS, 340, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Tsai, S.-M., Dobbs-Dixon, I., & Gu, P.-G. 2014, ApJ, 793, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial oscillations of stars 2nd edn. (Tokyo: University of Tokyo Press) [Google Scholar]
- Volland, H. 1974, J. Atm. Terr. Phys., 36, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Volland, H., & Mayr, H. G. 1972, J. Atm. Terr. Phys., 34, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Boyd, J. P., & Akmaev, R. A. 2016, Geosci. Model Dev., 9, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, M. V. 1949, Oscillations of the Earth’s Atmosphere (Cambridge University Press) [Google Scholar]
- Worthem, S., Mollo-Christensen, E., & Ostapoff, F. 1983, J. Fluid Mech., 133, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Yoder, C. F., & Peale, S. J. 1981, Icarus, 47, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1966, Annales d’Astrophysique, 29, 313 [Google Scholar]
The normalized associated Legendre polynomials are defined by (Abramowitz & Stegun 1972)![$ P_l^m \left( X \right) = \sqrt{\frac{\left( 2 l + 1 \right) \left( l - m \right) !}{2 \left( l + m \right) !}} \left( - 1 \right){}^m \left( 1 - X^2 \right){}^{m/2} \frac{{\textrm{d}}^m}{{\textrm{d}}X^m} \left[ P_l \left( X \right) \right], $](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq286.png) where the Pl stand for the Legendre polynomials,
where the Pl stand for the Legendre polynomials, ![$ P_l \left( X \right) = \frac{1}{2^l l !} \frac{{\textrm{d}}^l}{{\textrm{d}}X^l} \left[ \left( X^2 - 1 \right)^l \right]. $](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq287.png)
This point is discussed in Appendix D.
This regime typically corresponds to gravity waves propagating in a stably stratified radiative zone characterized by weak dissipative mechanisms (see e.g., Fig. 6, top right panels).
All Tables
All Figures
 |
Fig. 1 Reference frames and systems of coordinates. The notations Ω and norb designate the rotation vector and the orbital angular velocity respectively. |
| In the text | |
 |
Fig. 2 Background profiles normalized by their maxima as functions of the normalized radius r∕Rp (left panel) and of the pressure altitude x (right panel). Values of parameters are those given in Sect. 2.1, that is Mp = 0.7MJ, Rp = 1.27RJ, |
| In the text | |
 |
Fig. 3 Normalized symmetrical (n even) Hough functions (left) and associated horizontal functions (middle and right) as functions of latitude (degrees) for m = 2 and two values of ν = 2Ω ∕ σ representative of inertial regimes. Top: ν = 0.2 (super-inertial regime); weak impact of rotation on the tidal response. Bottom: ν = 2 (sub-inertial regime); strong impact of rotation. Gravity modes are designated by subscripts p ≥ 0 while Rossby modes correspond to p < 0. |
| In the text | |
 |
Fig. 4 Frequency spectrum of tidal regimes and waves characterizing the fluid tidal response. The parameter σ designates the forcing frequency (Eq. (15)), σ0 the thermal frequency (Eq. (9)), 2Ω the inertia frequency, N the Brunt-Väisäl ä frequency (Eq. (5)), and σs the characteristic acoustic cutoff frequency (Eq. (39)). |
| In the text | |
 |
Fig. 5 Logarithms of the spin parameter (ν) and stabilityratio |
| In the text | |
 |
Fig. 6 Imaginary part of density fluctuations generated by the quadrupolar semidiurnal thermal tide a functions of the latitude (horizontal axis, degrees) and background pressure in logarithmic scale (vertical axis, bars). Density fluctuations are plotted using Eq. (51) for several decades of the forcing period (τtide = 2π∕σ),
|
| In the text | |
 |
Fig. 7 Characteristic time scale necessary for the quadrupolar semidiurnal thermal tide to generate an azimuthal jet of velocity V jet = 1 km s−1. The logarithm of τevol (yr) isplotted using Eq. (72) for several decades of the forcing period (τtide = 2π∕σ),
|
| In the text | |
 |
Fig. 8 Eigenvalues |
| In the text | |
 |
Fig. 9 Total tidal torque exerted of the planet (N.m) as a function of the tidal period (days). Left: for two extremal value of the thermal time (τ⋆ = 0.1, 10 days) in the static approximation (Ω = 0).
Right: for τ⋆ = 1 day in the static (Ω = 0) and traditional (Ω≠0) approximations (in this case, Ω is given by Ω = norb + σ ∕ 2 with |
| In the text | |
 |
Fig. 10 Regions where the tidal response of the radiative layer is dominated by the gravitational (blue area) and thermal (red area) components of the forcing in the zero-frequency limit (σ → 0). The logarithm of the ratio η given by Eq. (79) (black solid line) is plotted as a function of the star-planet distance r⋆ (AU) in logarithmic scale. The blue dashed line designates the critical distance at which the two components are of the same order of magnitude (η ≈ 1). |
| In the text | |
 |
Fig. 11 Synchronisation time scale (yr) of the radiative (RZ) and convective (CZ) zones as a function of the tidal period (days) in logarithmic scales. The cyan line designates the synchronization time scale computed numerically with the model of the uniformly rotating spherical shell using Eq. (82). This line is solid (dashed) in regions where the radiative layer is torqued away from (towards) synchronization. The dotted black line designates the synchronization time scale resulting from the torque derived analytically in the zero-frequency limit. Red and blue dashed lines correspond to the case of the convective interior with constant tidal quality factors set to Q = 103 and Q = 105, respectively.They are plotted using Eq. (81). |
| In the text | |
 |
Fig. B.1 Imaginary part of density fluctuations in the case treated in Fig. 6 for a lower boundary located at the pressure level p0 = 104 bar instead of the centre of the planet as in Fig. 6. The density fluctuations are plotted as a function of latitude (degrees, horizontal axis) and pressure in logarithmic scale (bars, vertical axis) in the case with rotation and radiative cooling and for two different tidal periods, (i) τtide = 0.1 day (left) and (ii) τtide = 10 day (right). The corresponding rotation rates are given by Ω = σ∕2 + norb with |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



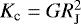
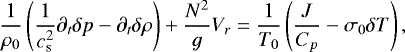
![\begin{align} & A_1 \left( x \right) = \frac{H N^2}{g} + \frac{i \kappa \sigma_0}{\sigma - i \sigma_0}, \\[3pt]& B_1 \left( x \right) = - \frac{H}{r^2} \left( \frac{\sigma}{\sigma - i \sigma_0} N^2 - \sigma^2 \right) , \\[3pt] & C_1 \left( x \right) = \frac{{\textrm{d}} U_n}{{\textrm{d}}x} - i \frac{\kappa}{\sigma - i \sigma_0} J_n ,\\[3pt]& A_2 \left( x \right) = \frac{H {\mathrm{\Lambda}}_n}{\sigma^2} \left( 1 - \varepsilon_{\textrm{s ; n}} \right), \\[3pt] & B_2 \left( x \right) =\frac{1}{{\mathrm{\Gamma}}_1} - \frac{i \sigma_0}{\sigma - i \sigma_0} \frac{H N^2}{g},\\ & C_2 \left( x \right) = - \frac{H {\mathrm{\Lambda}}_n}{\sigma^2} U_n - i \frac{\kappa r^2}{g \left( \sigma - i \sigma_0 \right)} J_n. \vspace*{-8pt} \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq66.png)
![\begin{align*} \mathcal{B}_n \left( x \right) = & \frac{1}{2} \left[ \frac{1}{{\mathrm{\Gamma}}_1} \frac{\sigma - i \, {\mathrm{\Gamma}}_1 \sigma_0}{\sigma - i \sigma_0} \left( 2 \frac{\sigma \left( \sigma - i \sigma_0 \right)}{N^2} - 1 \right) \right. \\ & \left. - \frac{\sigma}{\sigma - i \sigma_0} \frac{H N^2}{g} + K_{\circ} \right]. \nonumber \vspace*{-1pt}\end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq89.png)
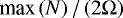
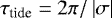
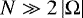
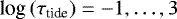
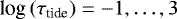
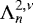
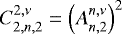
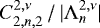
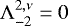
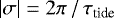

![\begin{align} \xi_{r ; n} = & - \frac{1}{H} \left( \frac{\sigma}{\sigma - i \sigma_0} N^2 - \sigma^2 \right)^{-1} \left[{\mathrm{\Phi}}_n \left( \frac{{\textrm{d}} {\mathrm{\Psi}}_n}{{\textrm{d}}x} + \mathcal{A}_n {\mathrm{\Psi}}_n \right) - \frac{\textrm{d} U_n}{\textrm{d}x} \right. \nonumber \\[4pt] & \left. + \,i \frac{\kappa}{\sigma - i \sigma_0} J_n \right], \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq182.png)
![\begin{align} V_{r ; n} = & - \frac{i \sigma}{H} \left( \frac{\sigma}{\sigma - i \sigma_0} N^2 - \sigma^2 \right)^{-1} \left[{\mathrm{\Phi}}_n \left( \frac{{\textrm{d}} {\mathrm{\Psi}}_n}{{\textrm{d}}x} + \mathcal{A}_n {\mathrm{\Psi}}_n \right) - \frac{\textrm{d} U_n}{\textrm{d}x} \right. \nonumber \\[6pt] & \left. + \,i \frac{\kappa}{\sigma - i \sigma_0} J_n \right], \end{align}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq183.png)
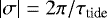
![\begin{align*}Q_{n,l}^{m,\sigma} = & \left[ 1 - \frac{\left( l + 3 \right) \left( l + 4 \right)}{ {\mathrm{\Lambda}}_n} \right] \int_0^{R_{\textrm{e}}} \rho_0 r^{2 + l} \left( \frac{\sigma^2}{N^2} \right) \frac{J_n}{i \sigma T_0 C_{\textrm{p}}} \textrm{d} r \\ & + \frac{R^{3+l}}{{\mathrm{\Lambda}}_n} \left[ \left( \frac{\sigma^2}{N^2} \right) \rho_0 \left( 4 + l + \frac{R}{H} \right) \frac{J_n}{i \sigma T_0 C_{\textrm{p}}} \right]_{r = R_{\textrm{e}}}. \nonumber \end{align*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq241.png)
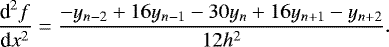
![\begin{equation*} \begin{array}{ll} \hspace*{-4pt} A_n = - 1 - h P_n, & B_n = 8 \left( 2 + h P_n \right), \\[0.3cm] \hspace*{-4pt} C_n = 6 \left( 2 h^2 Q_n - 5 \right), & D_n = 8 \left( 2 - h P_n \right), \\[0.3cm] \hspace*{-4pt} E_n = h P_n - 1 , & F_n = 12 h^2 R_n. \end{array} \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq250.png)
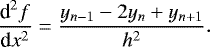
![\begin{equation*} \begin{array}{ll} \hspace*{-4pt} \displaystyle B_n = 1 + \frac{h}{2} P_n , & \displaystyle C_n = h^2 Q_n - 2, \\[0.3cm] \hspace*{-4pt} \displaystyle D_n = 1 - \frac{h}{2} P_n, & \displaystyle F_n = h^2 R_n. \end{array} \end{equation*}](/articles/aa/full_html/2018/05/aa31683-17/aa31683-17-eq254.png)