| Issue |
A&A
Volume 612, April 2018
H.E.S.S. phase-I observations of the plane of the Milky Way
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 14 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201630002 | |
| Published online | 09 April 2018 | |
Deeper H.E.S.S. observations of Vela Junior (RX J0852.0−4622): Morphology studies and resolved spectroscopy★
1
Centre for Space Research, North-West University,
2520 Potchefstroom,
South Africa
2
Universität Hamburg,
Institut für Experimentalphysik,
Luruper Chaussee 149,
22761 Hamburg,
Germany
3
Max-Planck-Institut für Kernphysik,
PO Box 103980,
69029 Heidelberg,
Germany
4
Dublin Institute for Advanced Studies,
31 Fitzwilliam Place,
Dublin 2,
Ireland
5
National Academy of Sciences of the Republic of Armenia,
Marshall Baghramian Avenue,
24, 0019 Yerevan,
Republic of Armenia
6
Yerevan Physics Institute,
2 Alikhanian Brothers St.,
375036 Yerevan,
Armenia
7
Institut für Physik,
Humboldt-Universität zu Berlin,
Newtonstr. 15,
12489 Berlin,
Germany
8
University of Namibia, Department of Physics,
13301 Private Bag,
Windhoek,
Namibia
9
GRAPPA, Anton Pannekoek Institute for Astronomy, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam,
The Netherlands
10
Department of Physics and Electrical Engineering, Linnaeus University,
351 95 Växjö,
Sweden
11
Institut für Theoretische Physik,
Lehrstuhl IV: Weltraum und Astrophysik, Ruhr-Universität Bochum,
44780 Bochum,
Germany
12
GRAPPA, Anton Pannekoek Institute for Astronomy and Institute of High-Energy Physics, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam,
The Netherlands
13
Institut für Astro- und Teilchenphysik,
Leopold-Franzens-Universität Innsbruck, 6020 Innsbruck,
Austria
14
School of Physical Sciences, University of Adelaide,
5005 Adelaide,
Australia
15
LUTH, Observatoire de Paris, PSL Research University, CNRS, Université Paris Diderot,
5 Place Jules Janssen,
92190 Meudon,
France
16
Sorbonne Universités, UPMC Université Paris 06, Université Paris Diderot, Sorbonne Paris Cité, CNRS, Laboratoire de Physique Nucléaire et de Hautes Energies (LPNHE),
4 place Jussieu,
75252 Paris Cedex 5,
France
17
Laboratoire Univers et Particules de Montpellier,
Université Montpellier,
CNRS/IN2P3,
CC 72, Place Eugène Bataillon,
34095 Montpellier Cedex 5,
France
18
DSM/Irfu,
CEA Saclay,
91191 Gif-Sur-Yvette Cedex,
France
19
Astronomical Observatory, The University of Warsaw,
Al. Ujazdowskie 4,
00-478 Warsaw,
Poland
20
Aix Marseille Université,
CNRS/IN2P3, CPPM UMR 7346,
13288 Marseille,
France
21
Instytut Fizyki Ja̧drowej PAN,
ul. Radzikowskiego 152,
31-342 Kraków,
Poland
22
Funded by EU FP7 Marie Curie, grant agreement No. PIEF-GA-2012-332350
23
School of Physics, University of the Witwatersrand,
1 Jan Smuts Avenue,
Braamfontein, 2050 Johannesburg,
South Africa
24
Laboratoire d’Annecy-le-Vieux de Physique des Particules,
Université Savoie Mont-Blanc, CNRS/IN2P3,
74941 Annecy-le-Vieux,
France
25
Landessternwarte,
Universität Heidelberg, Königstuhl,
69117 Heidelberg,
Germany
26
Université Bordeaux,
CNRS/IN2P3, Centre d’Études Nucléaires de Bordeaux Gradignan,
33175 Gradignan,
France
27
Oskar Klein Centre, Department of Physics, Stockholm University, Albanova University Center,
10691 Stockholm,
Sweden
28
Wallenberg Academy Fellow
29
Institut für Astronomie und Astrophysik,
Universität Tübingen,
Sand 1,
72076 Tübingen, Germany
30
Laboratoire Leprince-Ringuet,
Ecole Polytechnique, CNRS/IN2P3,
91128 Palaiseau,
France
31
APC,
AstroParticule et Cosmologie,
Université Paris Diderot, CNRS/IN2P3, CEA/Irfu,
Observatoire de Paris,
Sorbonne Paris Cité,
10,
rue Alice Domon et Léonie Duquet,
75205 Paris Cedex 13,
France
32
Univ. Grenoble Alpes,
IPAG,
38000 Grenoble,
France
CNRS, IPAG,
38000 Grenoble,
France
33
Department of Physics and Astronomy, The University of Leicester, University Road,
Leicester, LE1 7RH,
UK
34
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences,
ul. Bartycka 18,
00-716 Warsaw,
Poland
35
Institut für Physik und Astronomie,
Universität Potsdam,
Karl-Liebknecht-Strasse 24/25,
14476 Potsdam,
Germany
36
Friedrich-Alexander-Universität Erlangen-Nürnberg,
Erlangen Centre for Astroparticle Physics,
Erwin-Rommel-Str. 1,
91058 Erlangen,
Germany
37
DESY,
15738 Zeuthen,
Germany
38
Obserwatorium Astronomiczne,
Uniwersytet Jagielloński,
ul. Orla 171,
30-244 Kraków,
Poland
39
Centre for Astronomy, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University,
Grudziadzka 5,
87-100 Torun,
Poland
40
Department of Physics, University of the Free State,
PO Box 339,
9300 Bloemfontein,
South Africa
41
Heisenberg Fellow (DFG),
ITA Universität Heidelberg,
Germany
42
GRAPPA, Institute of High-Energy Physics, University of Amsterdam,
Science Park 904,
1098 XH Amsterdam,
The Netherlands
43
Department of Physics, Rikkyo University,
3-34-1 Nishi-Ikebukuro,
Toshima-ku,
171-8501 Tokyo,
Japan
44
Japan Aerospace Exploration Agency (JAXA), Institute of Space and Astronautical Science (ISAS),
3-1-1 Yoshinodai,
Chuo-ku, Sagamihara,
229-8510 Kanagawa,
Japan
45
Now at Santa Cruz Institute for Particle Physics and Department of Physics, University of California at Santa Cruz,
Santa Cruz,
CA 95064,
USA
★★ Corresponding authors: H.E.S.S. Collaboration,
e-mail: contact.hess@hess-experiment.eu
Received:
2
November
2016
Accepted:
5
April
2017
Aims. We study γ-ray emission from the shell-type supernova remnant (SNR) RX J0852.0−4622 to better characterize its spectral properties and its distribution over the SNR.
Methods. The analysis of an extended High Energy Spectroscopic System (H.E.S.S.) data set at very high energies (E > 100 GeV) permits detailed studies, as well as spatially resolved spectroscopy, of the morphology and spectrum of the whole RX J0852.0−4622 region. The H.E.S.S. data are combined with archival data from other wavebands and interpreted in the framework of leptonic and hadronic models. The joint Fermi-LAT-H.E.S.S. spectrum allows the direct determination of the spectral characteristics of the parent particle population in leptonic and hadronic scenarios using only GeV-TeV data.
Results. An updated analysis of the H.E.S.S. data shows that the spectrum of the entire SNR connects smoothly to the high-energy spectrum measured by Fermi-LAT. The increased data set makes it possible to demonstrate that the H.E.S.S. spectrum deviates significantly from a power law and is well described by both a curved power law and a power law with an exponential cutoff at an energy of Ecut = (6.7 ± 1.2stat ± 1.2syst) TeV. The joint Fermi-LAT-H.E.S.S. spectrum allows the unambiguous identification of the spectral shape as a power law with an exponential cutoff. No significant evidence is found for a variation of the spectral parameters across the SNR, suggesting similar conditions of particle acceleration across the remnant. A simple modeling using one particle population to model the SNR emission demonstrates that both leptonic and hadronic emission scenarios remain plausible. It is also shown that at least a part of the shell emission is likely due to the presence of a pulsar wind nebula around PSR J0855−4644.
Key words: astroparticle physics / gamma rays: general / acceleration of particles / cosmic rays / ISM: supernova remnants
A FITS image of the region of interest and two text files describing the H.E.S.S. spectrum of RX J0852.0–4622 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/612/A7
© ESO 2018
1 Introduction
RX J0852.0−4622 belongs to the class of young shell-type supernova remnants (SNRs) that display broadband nonthermal emission and have been detected at very high energies (photon energies E > 100 GeV; Katagiri et al. 2005; Aharonian et al. 2005, 2007); this SNR is listed in the Green SNR catalog (Green 2009) as SNR G266.2−1.2, as HESS J0852−463 in the High Energy Spectroscopic System (H.E.S.S.) catalog1, and is commonly referred to as Vela Junior. Its properties are similar to RX J1713.7−3946 (H.E.S.S. Collaboration 2018a) and, similar to this object, it has been extensively studied at multiple wavelengths (for an overview see Aharonian et al. 2007). The distance to the remnant and its age are still under debate in the literature but the range of possible values is narrowing. Studies of the shell expansion in X-rays, based on XMM-Newton data and the assumption of a shock velocity of 3000 km s−1 , have established a distance of ~ 750 pc and an age between 1700 yr and 4300 yr (Katsuda et al. 2008). Similar studies were also recently conducted with Chandra data from the years 2003 to 2008, placing a lower limit on the distance to the remnant at 500 pc (Allen et al. 2015). An upper limit is determined by the comparison of the detected 44Ti line emission with evolution models for different types of supernova (SN) explosions, yielding a highest allowed distance of 1 kpc (Iyudin et al. 2010). The distance estimate by Katsuda et al. (2008) is in the middle of the range of allowed values and is adopted hereafter.
The γ-ray emission from RX J0852.0−4622 has been interpreted in the framework of both hadronic (proton-proton interactions with subsequent π0 decay) and leptonic (inverse Compton (IC) scattering of relativistic electrons on ambient radiation fields) scenarios, without a definite answer so far. The high magnetic fields implied by hadronic scenarios are supported by the existence of sharp filamentary X-raystructures in the northwestern (NW) rim of the remnant, which have been resolved by Chandra (Bamba et al. 2005). The small effective width of these structures is explained by fast synchrotron cooling of relativistic electrons implying strong magnetic field amplification. The estimates of the amplified magnetic field strength range from ≳ 100 μG (Berezhko et al. 2009) to ~ 500 μG (Bamba et al. 2005). A softening of the X-ray spectrum of the remnant toward the interior of the SNR recently detected in the NW rim of RX J0852.0−4622 with XMM-Newton was interpreted as the gradual decrease of the cutoff energy of the electron spectrum due to fast synchrotron cooling (Kishishita et al. 2013). The authors have shown that the detected softening can be reproduced for a low magnetic field of a few μG, which would, however, require a high value of the electron cutoff energy of ~ 100 TeV near the shock front. For a lower value of the cutoff energy of about 20 TeV, a high magnetic field of ≳ 100 μG is required, still suggesting a strong magnetic field amplification in the rim. Alternatively, the sharp X-ray filaments can be explained by nonlinear damping of strong magnetic turbulence downstream from the shock, which creates thin regions with an enhanced magnetic field strength (see, e.g., Pohl et al. 2005). In this case the width of the filaments is limited by the extent of the regions with strong magnetic fields and the softening of the spectrum can be explained by the spatial variation of the magnetic field strength (Pohl et al. 2005; Rettig & Pohl 2012).
On the other hand, the hadronic scenario requires a relatively high density of the ambient medium of about ~ 1 cm −3 (Aharonian et al. 2007), which is in contradiction with the lack of detected thermal X-ray emission. The lack of thermal emission places an upper limit on the ambient density at ~ 0.01 cm−3 (Slane et al. 2001). Such a low density of the ambient medium is actually expected in the case of a core collapse SN explosion when the SNR is expanding inside the stellar bubble of the progenitor star. This scenario is argued to be the case for RX J0852.0−4622, as supported by the detection of the central compact object (CCO) AX J0851.9−4617.42 close to the center of the remnant (Aschenbach 1998; Aschenbach et al. 1999; Slane et al. 2001). However, no pulsations were detected from the CCO and, moreover, later it was suggested that the source might be an unrelated planetary nebula (Reynoso et al. 2006). An ambient density as low as 0.01 cm −3 leads to an unrealistically high value of the total energy in protons of ~ 1051 erg in the hadronic scenario (Tanaka et al. 2011). This would imply that all the energy from the SN explosion (~1051 erg) is used in accelerating particles, whereas normally this number is expected to be a factor ~10 lower. Several explanations were suggested to overcome the problem of the inconsistency of the hadronic model with the lack of thermal X-ray emission. Telezhinsky (2009) suggested that RX J0852.0−4622 might be older (17 500 yr) than usuallyassumed, which would place it in the transition phase between the adiabatic and radiative phases of SNR evolution. In this case the expected thermal X-ray flux decreases due to the formation of the dense shell and the cooling of the gas. The lack of thermal emission can only be claimed for the gas with a temperature above 1 keV because at lower energies RX J0852.0−4622 is completely obscured by the strong thermal emission from the Vela SNR. Another possible explanation was suggested by Inoue et al. (2012) and later by Gabici & Aharonian (2014) for the RX J1713.7−3946 SNR showing that a highly inhomogeneous clumpy environment significantly increases the expected γ-ray emission from hadronic interactions, while the thermal X-ray emission might remain at a very low level because denser cores of gas in clumps, which carry most of the mass, can survive the shock passing without being ionized. The environment of RX J0852.0−4622 exhibits a number of large clouds of atomic hydrogen, which are close to the current position of the main shock and coincident with the regions of enhanced emission from the remnant (see, e.g., Fukui 2013; Obergaulinger et al. 2014, and references therein). The lack of thermal X-ray emission is at the same time a strong argument in favor of a leptonic scenario. The leptonic scenario can naturally explain the correlation between the X-ray and γ-ray emitting regions (Aharonian et al. 2007) and is able to match the broadband emission from RX J0852.0−4622. This suggests, however, a very low average magnetic field of about 5–10 μG (Lee et al. 2013; Aharonian et al. 2007), which, in turn, seems to be in contradiction with the sharp filamentary structures detected in X-rays . Recent X-ray observations with Suzaku (Takeda et al. 2016) reveal a faint hard X-ray component in the NW rim of RX J0852.0−4622. X-rays are reported with a spectral index of 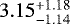 in the energy range from 12 keV to 22 keV. The absence of roll-off in the X-ray spectrum disfavors one-zone synchrotron models with electron spectra in the form of a power law with an exponential cutoff. However, the uncertainties on the spectral parameters are too large to draw strong conclusions.
in the energy range from 12 keV to 22 keV. The absence of roll-off in the X-ray spectrum disfavors one-zone synchrotron models with electron spectra in the form of a power law with an exponential cutoff. However, the uncertainties on the spectral parameters are too large to draw strong conclusions.
X-rayobservations with XMM-Newton (Acero et al. 2013) led to the discovery of a pulsar wind nebula (PWN) with an extension of 150 arcsec around the energetic (spin-down power Ė = 1.1 1036 erg/s) radio pulsar PSR J0855−4644 that coincides with the shell of RX J0852.0−4622. The pulsar is energetic enough to power a very high-energy PWN that is detectable by current generation Cherenkov telescopes (H.E.S.S. Collaboration 2018b, and references therein). Measurements of the column density toward the pulsar and RX J0852.0−4622 in X-rays with XMM-Newton data show that both objects are located at similar distances. Nevertheless, an association of PSR J0855−4644 with the SNR seems unlikely to be due to the age difference (the pulsar characteristic age is 140 kyr ) and the large speed (~3000 km s−1) needed by the pulsar to travel from the geometrical center of the SNR to its current position.
This paper reports new H.E.S.S. observations of RX J0852.0−4622. Section 2 describes the data set and the applied analysis techniques, and Sect. 3 presents the results of the conducted morphological and spectral studies. The results are discussed in the context of multiwavelength data and a simple modeling using one particle population for the entire SNR emission in Sect. 4.
2 H.E.S.S. observations and data analysis
H.E.S.S. is an array of five Cherenkov telescopes situated in the Khomas Highland of Namibia at an altitude of 1800 m above sea level. In its initial phase, it consisted of four 13 m diameter telescopes sensitive in the energy range of 100 GeV to 100 TeV. In 2012, a fifth, 28 m telescope was added at the center of the array that allows the threshold of the instrument to be lowered to several tens of GeV. All data presented in this work were taken in the initial phase of H.E.S.S. when only the 13 m telescopes were available. More details on the performance of H.E.S.S. in the four-telescope configuration are given in Aharonian et al. (2006) and references therein.
The data used for the analysis of RX J0852.0−4622 were taken between 2004 and 2009; the bulk of the observations were performed between 2004 and 2006. The analysis of the data up to the end of 2005 has already been published (Aharonian et al. 2005, 2007). This work presents a reanalysis ofthe source motivated by a rough doubling of the data set. The exposure times (normalized to an offset of 0.7°) available formorphological and spectral analyses amount to 60 h and 39 h, respectively. Thanks to the improved statistics more detailed studies of the morphology and spectrum are possible. In addition, a spatially resolved spectroscopy of the source can be performed.
The RX J0852.0−4622 data were analyzed with methods that are similar to the techniques discussed in Aharonian et al. (2006), however with two differences: gamma-hadron separation took advantage of a multivariate approach (Ohm et al. 2009, instead of box cuts based on scaled Hillas parameters), and a forward-folding method with a likelihood technique similar to that described in Piron et al. (2001) was used for spectrum derivation and flux measurements (instead of least-squares fitting). The results presented here were derived with the so-called HAP-HD analysis software and the corresponding instrument response tables. All results have been cross-checked with two independent software chains using an independent calibration of the data, yielding compatible results.
The extraction region or OFF-source region (short: ON region) selected for the analysis is a circle centered at the nominal position of RX J0852.0−4622 (in right ascension and declination 8h52m, − 46°22′12″, J2000) with a radius of 1.0°. This ON region is referred to as whole SNR in the following. To avoid any contamination from the nearby Vela X PWN (Abramowski et al. 2012) the region of the sky covering this source is excluded from the analysis, in particular in the estimation of cosmic-ray backgrounds from OFF-source regions (short: OFF regions).
Two different analysis configurations were applied to the data when studying the morphological and spectral properties of RX J0852.0−4622, respectively:
-
Spatial analysis was used to produce two-dimensional spatial skymaps to study the morphology of RX J0852.0−4622. This analysis is characterized by a loose (less stringent) data selection criterion in which data taken under optimal atmospherical conditions, but varying instrumental conditions, are acceptable. Hard image cuts were used for data filtering to improve the angular resolution at the expense of statistics. Cosmic-ray backgrounds were estimated with the ring background model (Berge et al. 2007).
-
Spectral analysis was used to produce flux measurements to study the photon spectrum of the entire SNR or of subregions (i.e., for spatially resolved spectroscopy). This analysis is characterized by a stringent (conservative) data selection criterion aiming at reducing systematic errors by selecting only data taken under optimal atmospherical and instrumental conditions. Standard cuts were used for data filtering, and the reflected region background model (Berge et al. 2007) was applied for cosmic-ray background estimation.
Details of the data selection criteria and the cut configurations (hard, standard) can be found in Aharonian et al. (2006). The analysis of RX J0852.0−4622 is challenging since the regions used for signal extraction and for excluding nearby sources from the analysis are large with respect to the field of view of the instrument, as compared to other sources. A careful study of the systematic uncertainties showed a larger than usual variation of spectral parameters when comparing the results derived with different analysis chains in use within the H.E.S.S. Collaboration. The dispersion of the results yielded a systematic error on flux measurements of 25% and an error on spectral indices of 0.2 for spectral indices in the range from 1.5 to 2.2. The error of cutoff energies was found to be 20%. These uncertainties are slightly larger than the typical systematic errors given for H.E.S.S. in Aharonian et al. (2006), and do not represent the general trend of H.E.S.S. measurements.
3 Results
Table 1 summarizes the event statistics of all analyses applied to the data using the ON region detailed above to encompass the entire SNR, and other smaller regions, to study spectral details of the different parts of RX J0852.0−4622 in the spatially resolved spectroscopy studies presented in Sect. 3.3. The specific parameters for all regions used are defined in Table A.1.
Statistics of the different analyses of the RX J0852.0−4622 data set.
3.1 Source morphology
The spatial analysis of RX J0852.0−4622 (cf. first row of Table 1) is based on a data set with a total livetime of 93.6 h and results in a total significance of 39.1σ. The difference between the livetime of the analysis and the exposure time previously quoted is because a large amount of the available observations were targeting nearby sources, had large offsets, and hence a small effective exposure time. The angular resolution attained in the morphological analysis is characterized by a PSF width (68% containment radius) of 0.08°. This angular resolution is larger than the 0.06° reported forthe morphological analysis in Aharonian et al. (2007) since the default telescope multiplicity ( ≥2 telescopes per event) was respected in the analysis presented here. This favors γ-ray efficiency at the expense of a somewhat larger angular resolution. Figure 1, left, shows the excess map corrected for the gradient of exposure across the field of view and smoothed with a Gaussian function with a width equal to the PSF width of 0.08°. The TeV emission matches the shape of the SNR shell well when compared to measurements in radio and X-rays; the brightest region is a semicircular arc in the NW (the NW rim), and there are two other bright regions toward the south and southeast. The contours of the ROSAT All Sky Survey for energies larger than 1.3 keV, smoothed to match the H.E.S.S. angular resolution, are shown in red in Fig. 1, right, together with the H.E.S.S. significance contours. The overall agreement is good. With an extension of ~ 2° in diameter, RX J0852.0−4622 is one of the largest known TeV sources in the sky.
The ON region (shown in Fig. 1, right) is in fact slightly too small since it barely encompasses the 5σ significance contour. This region was chosen because of the large extension of the source; an even larger ON region would make the determination of OFF regions within the same field of view very difficult, thereby reducing the effective data set available, especially for the spectral studies (cf. Sect. 3.2). The number of γ-rays left outside the ON region is small (~5%) compared to the signal inside and its systematic uncertainty. In the following, the effect is therefore neglected. Nevertheless, to avoid background contamination, a larger region covering the whole RX J0852.0−4622 emission was excluded for the determination of suitable OFF regions.
Projections of the skymap in Fig. 1 were calculated from the unsmoothed data and the resulting photon counts were normalized to the covered solid angle. Inspection of the radial profile (i.e., a skymap projection along the radial coordinate; profile not shown here) confirms the earlier result that the emission comes from a thin shell and not from a sphere (Aharonian et al. 2007). The azimuthal profile (i.e., skymap projection along the azimuthal coordinate) calculated for an annulus with inner and outer radius of 0.6° and 1.0° , respectively, around the center of RXJ0852.0−4622 is shown in Fig. 2. The azimuth angle is defined counterclockwise from north. Two periods separated by a dashed gray line are shown; green and black dashed lines at 121° and 168°, respectively, denote the position of PSR J0855−4644 and the center of the enhancement seen toward the south of the shell.
The azimuthal profile (blue points of Fig. 2, right) clearly shows that the emission is not homogeneous along the shell. In general, the NW rim (from 220° to 400°) is brighter than the southeastern part of the shell, where a region of high emission is observed between the southern (~160°) and the southeastern (~120°) enhancements. The emission in the southeast (cf. Fig. 2, left) is coincident with the position of the pulsar PSR J0855−4644. The emission roughly in the south is found to be coincident with the Fermi-LAT source 2FGL J0853.5−4711 and very close to the radio source PMN J0852−4712 (see Wright et al. 1994); 2FGL J0853.5−4711 is one of the three point-like sources in the 2FGL Fermi-LAT catalog3 associated with RX J0852.0−4622 as indicated in Lande et al. (2012) and Nolan et al. (2012). This morphology is also seen in radio and X-ray maps (Stupar et al. 2005)where most of the emission comes from the NW rim of the shell with some local enhancements toward the south. The azimuthal profile for the same region of the ROSAT All Sky Survey for energies larger than 1.3 keV was derived as well (red points of Fig. 2, right). The profiles of both instruments show a similar trend with a less pronounced enhancement toward PSR J0855−4644 in the case of the X-rays. In addition, the X-ray profile shows a clear local minimum at ~ 300°, marking a break in the NW rim region of the shell. This discontinuity of the shell is not as pronounced in the γ-ray emission.
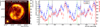 |
Fig. 2 Left: smoothed and exposure-corrected excess map with ROSAT X-ray contours, as in Fig. 1. The white annulus denotes the region used for extraction of the azimuthal profile; the white vertical line denotes the origin of the azimuthal angle (north), which increases in the counterclockwise direction. The green star indicates the position of PSR J0855−4644. The white dot-dashed line indicates a point-like region around the position of the southern enhancement. Right: azimuthal profile extracted from the annulus in the skymap on the left panel is shown in blue for the H.E.S.S. γ-ray data (left scale) and in red for the ROSAT X-ray data (right scale). For better visibility, two periods separated by a dashed gray line are shown. The azimuthal position of PSR J0855−4644 and the center of the region around the southern enhancement are indicated by green and black vertical dashed lines, respectively. The vertical error bars represent 1σ statistical uncertainties; the horizontal bars represent the bin widths. |
3.2 Gamma-ray spectrum of the whole supernova remnant
The increased data set for RX J0852.0−4622 enables a deeper study of the emission spectrum of the entire SNR. After data quality selection, the available exposure only amounts to 21.0 h since a sizable amount of the available observations is not usable for spectrum determination because of the large extent of the ON region and the exclusion region for Vela X. Many of the smaller ON regions used in the spatially resolved spectroscopy analysis in Sect. 3.3 achieve a better data efficiency. The statistics and properties of the ON region encompassing the whole SNR are shown in row 2 of Table 1. The spectrum was calculated in the energy range from 0.3 TeV to 30 TeV with the forward-folding technique assuming the three models listed in Table 2: a plain power law, a curved power law, and a power law with exponential cutoff. In the latter model, the parameter λ = 1∕Ecut is used in the fit because its error has a more Gaussian-like distribution than that of Ecut .
The best parameters found for all three models are presented in Table 3 (central section). A likelihood ratio test (based on the Wilks theorem from Wilks 1938) is used to select the model that describes the data best. The null hypothesis is the power law model and the alternative hypothesis is either the curved power law or power law with exponential cutoff model. Both alternative models are allowed to fall back into the power law during the fit, thereby fulfilling the nested hypotheses requirement for the test.
The results of the likelihood ratio tests are shown in the right section of Table 3. The power law model is rejected at the 7.3σ level by the curved power law model and at the 7.7σ level by the power law with exponential cutoff model. This demonstrates that a curved spectrum is clearly preferred over a plain power law, implying that an intrinsic curvature exists in the spectrum of RX J0852.0−4622. Since the power law with exponential cutoff model shows the highest significance, it will be used in the following as the model describing the data best. More complex models, such as power law with sub- or superexponential cutoff, were tested as well, but these models are not significantly better than any of the two curved models with three parameters.
The H.E.S.S. spectrum of RX J0852.0−4622 is shown in Fig. 3 together with the Fermi-LAT spectrum from Tanaka et al. (2011). The H.E.S.S. spectral points and fit parameters are shown in Tables A.2 and 4 (central column), respectively.The spectrum derived in this work represents a flux level that is 50% higher than that derived in previous publications (Aharonian et al. 2005, 2007). A careful study has revealed that the lower flux found in the earlier analyses was due to a lack of correction for the degradation of the telescope reflectivities when estimating γ-ray energies and fluxes. The revised flux makes RX J0852.0−4622 the brightest steady source in thesky above 1 TeV with F(E > 1 TeV) = (23.4 ± 0.7stat ± 4.9syst) × 10−12 cm-2 s-1 (a flux ~ 13% larger than the flux of the Crab nebula4 in the same energy range) and results in a smooth connection of the GeV (Fermi-LAT) and TeV (H.E.S.S.) spectra (cf. Fig. 3). Indeed, the spectral break that is visible at the 5.4σ level (statistical; or 1.6σ systematic) between the GeV (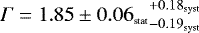 ) and the TeV(Γ = 2.24 ± 0.04stat ± 0.15syst) spectra in Tanaka et al. (2011) with the current measurement from Table 4 (central column) is only 0.4σ (statistical),i.e., nonexistent.
) and the TeV(Γ = 2.24 ± 0.04stat ± 0.15syst) spectra in Tanaka et al. (2011) with the current measurement from Table 4 (central column) is only 0.4σ (statistical),i.e., nonexistent.
Using both the Fermi-LAT and H.E.S.S. measurements, the ambiguity between the power law with exponential cutoff and curved power law models can be solved. Indeed, a simultaneous fit of the Fermi-LAT and H.E.S.S. data points yields a χ2 fit probability of 94% for a power law with exponential cutoff model, whereas the probability for the curved power law is 3.1 × 10−7. The simultaneous Fermi-LAT-H.E.S.S. fit using the power law with exponential cutoff model is shown in Fig. 3 with an orange dashed line and the fit parameters are shown in the rightmost column of Table 4. We determined the systematic uncertainties of the parameters of the simultaneous fit from the variations observed when moving the Fermi-LAT points down(up) and the H.E.S.S. points up (down) by one standard deviation of their respective systematic uncertainties, which tests the systematic uncertainty of the spectral index and cutoff energy. We also moved all data points down or up simultaneously to test the systematic uncertainty of the normalization.
A comparison of the parameter values of the simultaneous Fermi-LAT-H.E.S.S. fit and of the H.E.S.S. only spectrum (cf. Table 4) shows good agreement. The simultaneous fit shows smaller statistical uncertainties for all parameters (especially for the spectral index and cutoff energy), a smaller systematic uncertainty for the spectral index, a larger systematic uncertainty in the normalization, and a similar systematic uncertainty in the cutoff energy. Thus, the simultaneous fit is able to better determine the spectral index and cutoff energy at the cost of a higher systematic uncertainty in the flux. The latter is due to the larger systematic error in the Fermi-LAT flux measurement ( ~30–35%). The simultaneous fit also shows a smaller uncertainty for the low-energy part of the spectrum (E < 1 TeV), as shown by the smaller statistical uncertainty in the F(0.3−30 TeV) quantity, in contrast to the same uncertainty for the F(>1 TeV) quantity.
Spectrum models.
 |
Fig. 3 H.E.S.S. and Fermi-LAT spectra for RX J0852.0−4622 with statistical and systematic errors. The Fermi-LAT measurement was taken from Tanaka et al. (2011). The figure shows the spectral points with 1σ statistical (light and dark blue lines for Fermi-LAT and H.E.S.S., respectively) and systematic (red lines in both cases) uncertainties together with the spectral fits and their 1σ statistical uncertainty (shaded bands). In addition, the simultaneous Fermi-LAT-H.E.S.S. fit function is also shown (orange dashed line). |
Fit parameters for the H.E.S.S. spectrum (central column) and the simultaneous Fermi-LAT-H.E.S.S. spectral fit (right column) of RX J0852.0−4622.
3.3 Spatially resolved spectroscopy
The increased data set on RX J0852.0−4622 and the size of the SNR allow for the first time a spatially resolved spectroscopy, i.e., the derivation of spectra for subregions. For this purpose, we defined different subregions of RX J0852.0−4622 following its γ-ray morphology and the location of the PWN around PSR J0855−4644 and the southern enhancement. As shown in Fig. 4 (top left), we divided the SNR into a central part (region 0) and six regions (1–6) in the annulus covering the shell to test for spectral variations across the SNR. An additional region encompasses the 5σ significance contour around the bright NW rim (cf. Fig. 4, top center). Three circular regions around the position of PSR J0855−4644 (regions A, B, and C in Fig. 4, top center) are used to estimate a possible PWN flux. Region A supposes a point-like source centered at the pulsar position. Region B encompasses the 7σ contour around the pulsar excluding the elongation to the south. Region C roughly encompasses the 5σ contour around the pulsar. Region D (cf. Fig. 4, top center) is adapted to a hypothetical point-like source for the southern enhancement observed in the skymap and the azimuthal profile (cf. Fig. 2). In addition, the regions B ′ = B \A (i.e., region B, excluding region A) and C′ = C \B \D (i.e., region C, excluding regions B and D) are used to search for a softening of the spectrum of the possible TeV PWN around PSR J0855−4644 (shaded areas in Fig. 4, top right). The specific parameters for all regions used are defined in Table A.1.
Spectral analyses similar to those presented in Sect. 3.2 were performed for each of the regions. The event statistics of all analyses are presented in Table 1. All analyzed regions show a clear signal with significances between 7.7σ and 29.0σ. The spectral parameters of a power law with exponential cutoff fitted to the data of each analyzed region in the energy range from 0.3 TeV to 30 TeV are shown in Table 5. The significance of the cutoff is listed in the rightmost column.
The central part of the SNR (region 0) and the shell toward the bright NW rim show a preference for a cutoff in the spectrum (test significance greater than 3σ); for the enhancement toward PSR J0855−4644 the significance of the cutoff is only 1.8σ for the point-like region (region A) but it grows with the size of the integration region (regions B and C). As for spectral variations across the RX J0852.0−4622 region, the shape of the spectrum of the NW rim is compatible with the spectrum of the whole SNR.This spectrum is also compatible with the spectra of the rest of the SNR at the 2σ level when comparing to either regions C or 0, which largely cover the rest of the SNR emission. The spectra of the regions 0 to 6 do not show a clear deviation from the spectrum of the whole SNR (Γ ~ 1.8, λ ~ 0.15 TeV-1), as shown by the overlapping error contours in Fig. 4 (bottom left); the variations of the spectral index Γ are smaller than ±2σ. Although region 2 seems to deviate from regions 1, 4, and 6, the effect is not significant, and indeed the weighted average of (Γ, λ) for regions 0 to 6 still yields a χ2 probability of 4.8% (residual significance of 2.0σ), which shows that all regions are compatible with a single (Γ, λ) pair. The profile-likelihood method was applied to quantify the hypothesis that any of the seven regions 0 to 6 has a spectral index that differs by more than ± ΔΓ from the spectral index calculated from the remaining six regions. Depending on the region, the upper limits on ΔΓ calculated at the 95% confidence level are in the range of 0.25 to 0.40, which shows that the available statistics are not sufficient for a sensitive search for spectral variations. Similar values are found when using combinations of the regions from the top center and top right of Fig. 4. Also, spectral variations on angular scales comparable to or below the angular resolution of H.E.S.S. are not excluded. The spectra of the regions A and C also do not show a deviation from the spectra of either the whole SNR or the NW rim, as shown by the contour plot of Fig. 4 (bottom center). Region B shows some evidence of a harder spectrum with a larger cutoff energy compared to the NW rim (or the whole SNR); the significance for the cutoff in region B is not very high (only 2.7σ) and the deviation of index and cutoff energy is at the level of 3.5σ pretrials (2.6σ post-trials5 ). Figure 4 (bottom right) shows that the spectral index of the possible TeV PWN remains basically constant when moving farther away from PSR J0855−4644 (region A to B′ to C′ ): no significant change in the spectral parameters is observed across the mentioned regions. This plot also shows that the spectrum of region D is compatible with that of the NW rim. In addition, the spectrum of region B′, although it comprises a smaller exposure than that of region B, still shows marginal evidence for a difference with respect to the spectrum of the NW rim. The significance of the effect is 3.1σ pretrials (2.1σ post-trials). Nevertheless, the weighted average of (Γ, λ) for regions A, B′ , C′ , D, and the NW rim still yields a χ2 probability of 6.6% (residual significance of 1.8σ).
 |
Fig. 1 Left: exposure-corrected excess map for RX J0852.0−4622. The data were binned in bins of 0.01° on each coordinate and smoothed with a Gaussian function of width 0.08°. The white dashed line shows the position of the Galactic plane; the inset shows the PSF of the analysis at the same scale for comparison. Right: same as in the left panel, but additionally the boundary of the ON region is shown as a white circle and the significance contours at 3, 5, 7, 9, and 11σ are shown in black with increasing line width for increasing significance. In addition, X-ray contours from the ROSAT All Sky Survey for energies larger than 1.3 keV are shown in red. The X-ray data were smoothed in the same way as the γ-ray data to allow for a direct comparison. The X-ray contours were derived at 25, 50, 75, and 100 counts. The green star indicates theposition of PSR J0855−4644. |
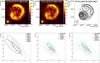 |
Fig. 4 Top figures represent skymaps (smoothed exposure-corrected excess map from Fig. 1 for the top left and center pads, significance contour map for the right pad) together with various regions used for the study of the spatially resolved spectroscopy of the RX J0852.0−4622 region. Top left: regions 0 for the central part of the SNR and 1–6 for the shell are shown in white. Center: regions A, B, and C around PSR J0855−4644, region D around the southern enhancement in the azimuthal profile, and the region used for the NW rim are shown in white. The H.E.S.S. significance contours at 5, 7, and 9σ are shown in black with increasing line width for increasing significance. The position of PSR J0855−4644 is denoted by the green star. Top right: regions B′ (dark gray shaded area) and C′ (light gray shaded area) around PSR J0855−4644 are shown. The H.E.S.S. significance contours at 3, 5, 7, and 9σ are shown in black with increasing line width for increasing significance. The position of PSR J0855−4644 is denoted by the black star. Bottom figures represent the error contour plots of λ = 1∕Ecut vs. Γ for the spectra of the regions in the excess maps assuming a power law with exponential cutoff model. For each region, the fitted value is indicated with a triangle, while the ellipse indicates the contour of the 3σ confidence level statistical uncertainty. Dashed lines are used for the regions where the cutoff significance is below 3σ. Bottom left: spectra of the regions 0 to 6 are represented. Bottom center: spectra of the regions A, B, and C are represented. In addition, the contours of the analysis of the whole SNR and NW rim are shown. Since the spectra of regions A–C are correlated because the regions overlap, the corresponding contours are not meant to be compared to each other, but to the contours of the NW rim. Bottom right: spectra of the regions A, B′ , C′ , and D are represented. In addition, the contours of the analysis of the whole SNR and the NW rim are shown. |
4 Discussion
In the following, we consider the implications of the new H.E.S.S. results on the understanding of the very high-energy γ-ray emission from RX J0852.0−4622. The multiwavelength (MWL) data used in this section consist of
-
Parkes radio data points from Duncan & Green (2000);
-
ASCA X-ray spectral fit from Aharonian et al. (2007);
-
Fermi-LAT GeV γ-ray points from Tanaka et al. (2011);
-
H.E.S.S. TeV γ-ray points from this work (cf. Fig. 3 and Table A.2).
The H.E.S.S. spectrum is not corrected for possible emission from a putative TeV PWN around PSR J0855−4644 (discussed in Sect. 4.3) since the expected flux contribution is smaller than the systematic error on the flux normalization.
4.1 Spectral variations
The spatially resolved spectroscopy analysis of RX J0852.0−4622 described in Sect. 3.3 does not show a significant variation of the spectral shape across the remnant. The regions that contain the PWN (cf. Fig. 4; discussed in Sect. 4.3) show some evidence for spectral variations but the effect is still below 3σ. This lack ofapparent spectral variations suggests that the parent particle population is essentially the same across the remnant; this in turn points to similar properties of the SNR shock and hence to similar properties of the medium in which the shock was formed and is expanding. The invariability of the γ-ray spectral shape across the remnant enables a simple treatment of the MWL emission from RX J0852.0−4622, using one particle population for the entire SNR emission. This modeling obtains the average properties of the SNR and its surrounding medium.
4.2 Parent particle population
The increased exposure and careful study of the systematic effects strongly improved the quality of the spectrum of the whole SNR, thereby resulting in a smooth connection to the spectrum in the GeV band and in the determination of a clear cutoff (cf. Sect. 3.2). The smooth connection to the Fermi-LAT spectrum enables the study of the combined GeV-TeV spectrum, which in turn provides an opportunity to extract directly from the observational data the present-time parent particle population that is responsible for the γ-ray emission in leptonic and hadronic scenarios. The advantage of this approach is that the spectral shape of the present-time parent particle population can be obtained without assumptions made on the SNR evolution, its hydrodynamics, properties of the local magnetic field, and energy losses that accelerated particles undergo. In this procedure we fit the Fermi-LAT and H.E.S.S. data points and their respective statistical errors (cf. Fig. 5, left) with the emission from parent electron or proton populations following a power law with an exponential cutoff
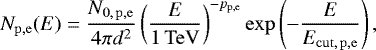 (1)
(1)
where N0, p,e is the normalization at 1 TeV, pp ,e is the spectral index, Ecut , p ,e is the cutoff energy, and d is the distance to the SNR. The subscripts p (for protons) and e (for electrons) denote the hadronic and leptonic scenarios, respectively. In order to evaluate the systematic uncertainty of our results, we also fit the model when we systematically shifted the Fermi-LAT and H.E.S.S. points in an analogous way to the simultaneous Fermi-LAT-H.E.S.S. spectral fit in Sect. 3.2. The distance of 750 pc is adopted in these calculations. Uncertainties on the distance estimate only impact flux normalization, and hence the estimate of the total energy in particles, but these uncertainties do not influence the spectral shape, i.e., the spectral index and cutoff energy. The spectral index is determined by the smooth connection of the Fermi-LAT and H.E.S.S. spectra, while the cutoff energy of the accelerated particles is constrained by the cutoff in the H.E.S.S. γ-ray spectrum. The derivation of the present-time parent particle population is very important for further modeling of the source. Hadronic and leptonic scenarios can be tested based on the attainability of the present-time particle population considering the physical properties of the SNR and its ambient medium.
 |
Fig. 5 Left: spectral energy distribution of SNR RX J0852.0−4622 in the GeV-TeV band. Filled squares reflect the emission detected by Fermi-LAT, while filled circles show the H.E.S.S. data. Error bars reflect statistical errors. The lines represent fits of the leptonic (dashed red) and hadronic (solid blue) γ-ray emission models to the data. Right: broadband spectral energy distribution of SNR RX J0852.0−4622 in the leptonic scenario. The MWL data are indicated as follows: radio data are denoted with filled blue triangles, X-ray are indicated with cyan bowties, GeV γ-rays are indicated with filled squares, TeV γ-rays are denoted with filled circles. The error bars of the Fermi-LAT and H.E.S.S. data points reflect statistical errors only. The filled blue bowtie represents the 90% confidence level statistical uncertainty band on the X-ray data; the open bowtie represents systematic uncertainties. Red lines represent the emission from the electron population as obtained from the fit of the GeV-TeV data (cf. left figure) and gray lines represent the emission from a modified electron population where all parameters were decreased by 0.6σ of the quadratically added statistical and systematic uncertainties. Dashed lines correspond to IC emission and dotted lines correspond to synchrotron radiation. |
4.2.1 Leptonic scenario
In the leptonic scenario, we assume that the GeV-TeV γ-ray emission from RX J0852.0−4622 is dominated by the IC emission from relativistic electrons scattered on ambient radiation fields. Besides the cosmic microwave background (CMB), local infrared (IR) and optical radiation fields might also contribute to the IC emission. However, it is often very difficult to estimate the spectrum of the local radiation fields owing to the poor knowledge of the environment. According to the interstellar radiation field model by Porter et al. (2006) the contributionof IR and optical radiation fields should be negligible because of the large distance between SNR RX J0852.0−4622 and the Galactic center (~ 9 kpc). Stars detected in the field of view of RX J0852.0−4622 are not powerful enough to provide a strong radiation field and, moreover, the high uncertainty on the determination of the distance to these stars makes it difficult to judge whether the stars are located in the proximity of the remnant or not (Iyudin et al. 2010). Therefore, we decided to adopt CMB as the only radiation field responsible for the IC scattering of relativistic electrons. The γ-ray emission is calculated according to Blumenthal & Gould (1970). The leptonic model (red dashed line in Fig. 5, left) provides a good fit to the Fermi-LAT-H.E.S.S. data with χ2 ∕NDF = 13.8∕13 (χ2 probability 0.39). The best-fit parameters are shown in Table 6. The integration of the electron spectrum above 100 GeV yields a total energy in electrons We = (4.1 ± 0.3stat ± 1.7syst) 1047 erg.
A magnetic field strength of 7 μG is needed to explain the observed X-ray flux by synchrotron emission from the obtained electron population (red dotted line in Fig. 5, right). The modeled synchrotron spectrum does not reproduce well the slope of the observed X-ray spectrum within its statistical uncertainty, but both agree within the systematics of the X-ray spectrum. The same synchrotron emission overpredicts the radio flux. However, a decrease in the values of all parameters by 0.6σ of the quadratically added statistical and systematic uncertainties allows us to accommodate the radio data within our leptonic model (gray dotted line in Fig. 5, right).
For such a low magnetic field, synchrotron cooling effects are negligible and do not have a significant impact on the energy spectrum of the electron population. Indeed, following Blumenthal & Gould (1970) and adopting an SNR age of 3000 yr, the break energy above which the synchrotron losses become important is
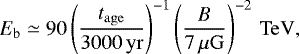
which is considerably higher than the obtained electron cutoff energy. This result suggests that the electron spectrum of RX J0852.0−4622 may be limited by the age of the SNR (see, e.g., Reynolds 1998) rather than by radiative losses or that the SNR is considerably younger than 3000 yr. A typical acceleration time for the electrons to reach the energy of 27 TeV in the magnetic field of 7 μG for the shock compression ratio of 4 is (Parizot et al. 2006)
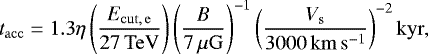
where V s is the shock velocity and η expresses the deviation of the diffusion coefficient from Bohm diffusion. However, the magnetic field could have been higher in the past, in which case synchrotron losses can still play a major role.
The obtained value of the magnetic field strength is in very good agreement with the values obtained in other leptonic models available in the literature (see, e.g., Lee et al. 2013). This value represents the average magnetic field across the remnant and does not exclude the existence of regions with higher or lower magnetic fields; it is, however, in conflict with the significantly amplified magnetic fields derived for the filamentary structures in the NW rim under the hypothesis that the filament width is limited by synchrotron cooling. Nevertheless, the good agreement in the morphology of the X-ray and γ-ray emissions, as shown by the contours of Fig. 1 and the azimuthal profiles of Fig. 2, still supports a leptonic nature of the γ-ray emission.
4.2.2 Hadronic scenario
In the hadronic scenario, we assume that the GeV-TeV γ-ray emission from RX J0852.0−4622 is dominated by γ-rays produced in hadronic interactions. The γ-ray emission is calculated according to Kelner et al. (2006). The hadronic model (solid blue line in Fig. 5, left) fits the Fermi-LAT-H.E.S.S. data very well with χ2∕NDF = 6.0∕13 (χ2 probability 0.95). The best-fit parameters are shown in Table 6. The integration of the proton spectrum above 1 GeV yields a total energy in protons ![$W_{\mathrm{p}} = (7.1 \pm 0.3{{_{\textrm{\tiny{stat}}}}} \pm 1.9{{_{\textrm{\tiny{syst}}}}})\,10^{49} \left[\frac{n}{1\,\mathrm{cm}^{-3}}\right]^{-1}$](/articles/aa/full_html/2018/04/aa30002-16/aa30002-16-eq6.png) erg, where n is the density of the ambient medium.
erg, where n is the density of the ambient medium.
The lack of thermal X-rays suggests a density of the ambient medium that is significantly lower than 1 cm −3 (Slane et al. 2001). This, in turn, would require an unrealistically high estimate of the energy transferred to protons, comparable to or even higher than the total energy of ~1051 erg provided bythe SN explosion. This problem, however, can be solved if the SNR is expanding in a very inhomogeneous clumpy environment with compact dense clouds as shown for RX J1713.7−3946 (Inoue et al. 2012; Gabici & Aharonian 2014). In this case the shock does not penetrate deep enough inside the clouds to heat up the gas and generate thermal X-rays, but at the same time relativistic protons can penetrate inside to interact with the cloud material and produce γ-ray emission. Indeed, RX J0852.0−4622 exhibits a good correspondence between the TeV γ-ray emission and the column density of interstellar medium proton distribution (see, e.g., Fukui 2013), which suggests a hadronic origin of at least a portion of the observed γ-ray emission. However, modeling such a scenario is beyond the scope of this paper.
The proton spectral index obtained in the GeV-TeV fit (1.83 ± 0.02stat ± 0.11syst) is slightly harder than the value of 2.0 expected in the diffusive shock acceleration for strong shocks with compression ratio of 4. However, from most of the SNRs detected at gamma-ray energies, an even steeper spectrum of protons is inferred (see, e.g., Caprioli 2011). The hard proton spectrum (index 1.8) implied by the fit of the GeV-TeV emission from RX J0852.0−4622 requires further theoretical investigation.
4.3 Pulsar wind nebula around PSR J0855−4644
The pulsar population studies by H.E.S.S. Collaboration (2018b), and references therein, show that wind nebulae of energetic pulsars are very likely to be detectable in γ-rays at TeV energies. Since PSR J0855−4644 falls into this category, it is likely that some of the emission attributed to RX J0852.0−4622 could come from a possible TeV PWN associated with PSR J0855−4644. The H.E.S.S. point spread function does not allow for a separation of the emissions due to the PWN and SNR. Nevertheless, the flux measurements in the regions A–C from Table 5 can be interpreted as flux upper limits on a possible TeV PWN associated with PSR J0855−4644 for different size assumptions of the PWN. Different sizes of the putative TeV PWN were assumed owing to the lack of knowledge of its potential size at TeV energies. For pulsars older than ~ 10 kyr the size of the TeV PWN can be up to 100–1000 times larger than the size of the X-ray PWN (Kargaltsev & Pavlov 2010) owing to particle propagation up to large distances from the pulsar through diffusion/advection processes and/or proper motion of the pulsar itself. In this context, the relatively small size of the X-ray PWN associated with PSR J0855−4644 (150 arcsec, slightly smaller than the marker used to mark the pulsar position in the skymaps, i.e., in Fig. 1, right) compared to the extension of RX J0852.0−4622 may be the reason for the smaller enhancement seen in the azimuthal profile (cf. Fig. 2) in X-rays compared to γ-rays toward the direction of PSR J0855−4644.
Region B is the only region with spectral parameters deviating more than 3σ (3.5σ pretrials, 2.6σ post-trials) from the spectrum of the NW rim, which might be suggestive of a PWN contribution to the flux in this region. The insignificant deviation of the spectra of the regions A and C from the rest of the remnant can be naturally explained by the sizes of these two regions. On the one hand, the small size of region A results in low statistics and hence high uncertainties in the spectral parameters. On the other hand, with its much larger size, region C comprises a significant part of the SNR interior and other parts of the shell, leading to the domination of the emission from the SNR over the emission from the PWN. Therefore, the deviation of the spectrum of region B from the spectrum of the rest of the SNR not only points to the contribution from the PWN but also constrains the size of the putative PWN. Moreover, the γ-ray spectrum of region B deviates from the spectrum of the rest of the SNR in the same way as the X-ray spectrum of the PWN differs from the spectrum of the SNR, which further supports the hypothesis of significant contribution of the PWN emission to the γ-ray flux in region B. The X-ray spectrum of the PWN is significantly harder than the spectrum of the SNR (Acero et al. 2013), which agrees well with an indication of increase of the cutoff energy of the γ-ray spectrum of region B with respect to the rest of the remnant. However, the significance of the increase of the cutoff energy in region B as well as of the existence of the cutoff feature is low. Setting the observed flux from region B as an upper limit on the flux from the PWN one can estimate the upper limit on the efficiency of the conversion of the pulsar spin-down luminosity to the γ-ray emission. The upper limit on the TeV efficiency defined as the ratio of the 1 − 10 TeV PWN luminosity to the spin-down power is 0.75 × 10−3, using for the distance to the pulsar the upper limit of 900 pc from Acero et al. (2013). This value of the γ-ray efficiency is compatible with that of other PWNe detected at TeV energies (H.E.S.S. Collaboration 2018b).
The γ-ray emission from the PWN might provide a substantial contribution to the overall flux from RX J0852.0−4622. Adopting the size of region B as a potential size of the putative TeV PWN, this contribution can be as large as ~ 8% of the total γ-ray flux from the SNR, considering the flux level measured for region B. However, the γ-ray emission from the remnant also contributes to the flux from region B and hence only a fraction of the γ-ray emission detected in that region is from the PWN. The azimuthal profile (cf. Fig. 2) exhibits approximately double the flux at the position coincident with the X-ray PWN compared to the regions around it. Therefore, a more plausible prediction for the fraction of the γ-ray emission from the PWN in the overall flux from RX J0852.0−4622 is about 4%. This was not taken into account in the modeling of the SNR presented above, assuming that all the detected γ-ray flux is coming from RX J0852.0−4622. However, if the contribution of the PWN is indeed only around 4% of the overall flux, it would be well covered by the systematic errors estimated for the GeV and TeV data. Even an 8% contribution would be covered by the 25% systematic error assigned to the overall flux.
5 Conclusions
The analysis of an enlarged H.E.S.S. data set, using approximately double the observation time compared to previous publications, comes to the following conclusions:
-
A revised flux measurement makes RX J0852.0−4622 the brightest steady source in the sky above 1 TeV with F(>1 TeV) = (23.4 ± 0.7stat ± 4.9syst) × 10−12 cm-2 s-1; this flux is ~ 13% larger than the flux of the Crab nebula in the same energy range.
-
The energy spectrum of RX J0852.0−4622 is clearly curved and has an exponential cutoff at Ecut = (6.7 ± 1.2stat ± 1.2syst) TeV. The determination of the cutoff helps to characterize the parent particle population better.
-
The new TeV spectrum connects well with the Fermi-LAT measurement at GeV energies without the need for a spectral break as in previous publications. This smooth connection of the GeV and TeV spectra together with the well-defined cutoff allows us to determine directly the characteristics of the parent particle population in both leptonic and hadronic scenarios.
-
The study of the spatially resolved spectroscopy reveals no clear spectral variation across the SNR, suggesting that the parent particle population can be assumed to be the same throughout the remnant, which in turn indicates that the conditions for particle acceleration, i.e., properties of the SNR shock and ambient medium, are similar everywhere.
-
The enhancement detected toward PSR J0855−4644 suggests that some of the emission might come from a possible TeV PWN associated with the pulsar. The contribution is estimated to be less than 8%.
Deeper H.E.S.S. observations of RX J0852.0−4622 thus provide a significant improvement of statistics revealing the existence of a cutoff in the TeV spectrum, which in turn considerably improves the characterization of the parent particle population and allows, for the first time, the estimation of the uncertainties of its parameters. Both leptonic and hadronic models remain plausible as both models provide a good fit of the data. Larger statistics at high energies (i.e., above 10 TeV), which provide a better characterization of the spectral cutoff, could give more insight into the nature of the parent particle population for this object. Such data could be obtained with even deeper H.E.S.S. observations and ultimately from the future CTA (Actis et al. 2011) observatory. In addition, larger statistics and better angular resolution should help in the search for clear spectral variations across the RX J0852.0−4622 region, such as a softening of the spectrum, when moving away from PSR J0855−4644. Moreover, smaller errors on the spectral parameters would also allow the establishment of spectral differences between region B and the NW rim. All this would help to separate the contributions from the PWN and SNR.
Acknowledgements
The support of the Namibian authorities and the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the U.K. Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, the University of Namibia, the Innsbruck University, the Austrian Science Fund (FWF), and the Austrian Federal Ministry for Science, Research and Economy, and by the University of Adelaide and the Australian Research Council. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment. This work benefitted from services provided by the H.E.S.S. Virtual Organisation, supported by the national resource providers of the EGI Federation.
Appendix A Region definitions and spectral points
Region definitions used for the analysis of RX J0852.0−4622.
H.E.S.S. flux points for the spectrum of RX J0852.0−4622.
References
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 548, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acero, F., Gallant, Y., Ballet, J., Renaud, M., & Terrier, R. 2013, A&A, 551, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [CrossRef] [Google Scholar]
- Actis, M., Agnetta, G., Aharonian, F., et al. 2011, Exp. Astron., 32, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2005, A&A, 437, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, ApJ, 661, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, G. E., Chow, K., DeLaney, T., et al. 2015, ApJ, 798, 82 [Google Scholar]
- Aschenbach, B. 1998, Nature, 396, 141 [CrossRef] [Google Scholar]
- Aschenbach, B., Iyudin, A. F., & Schönfelder, V. 1999, A&A, 350, 997 [NASA ADS] [Google Scholar]
- Bamba, A., Yamazaki, R., & Hiraga, J. S. 2005, ApJ, 632, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Berezhko, E. G., Pühlhofer, G., & Völk, H. J. 2009, A&A, 505, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D. 2011, J. Cosmol. Astropart. Phys., 5, 026 [Google Scholar]
- Duncan, A. R., & Green, D. A. 2000, A&A, 364, 732 [NASA ADS] [Google Scholar]
- Fukui, Y. 2013, in Cosmic Rays in Star-Forming Environments, eds. D. F. Torres, & O. Reimer, Astrophys. Space Sci. Proc., 34, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Gabici, S., & Aharonian, F. A. 2014, MNRAS, 445, L70 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2009, BASI, 37, 45 [NASA ADS] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018a, A&A, 612, A6 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., Abramowski, A., et al.) 2018b, A&A, 612, A2 (H.E.S.S. SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, T., Yamazaki, R., Inutsuka, S., & Fukui, Y. 2012, ApJ, 744, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Iyudin, A. F., Pakhomov, Y. V., Chugai, N. N., et al. 2010, A&A, 519, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kargaltsev, O., & Pavlov, G. G. 2010, in X-ray Astronomy 2009; Present Status, Multi-Wavelength Approach and Future Perspectives, AIP Conf. Proc., 1248, 25 [Google Scholar]
- Katagiri, H., Enomoto, R., Ksenofontov, L. T., et al. 2005, ApJ, 619, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Tsunemi, H., & Mori, K. 2008, ApJ, 678, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Kishishita, T., Hiraga, J., & Uchiyama, Y. 2013, A&A, 551, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lande, J., Ackermann, M., Allafort, A., et al. 2012, ApJ, 756, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S.-H., Slane, P. O., Ellison, D. C., Nagataki, S., & Patnaude, D. J. 2013, ApJ, 767, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, M., Horns, D., & Zechlin, H.-S. 2010, A&A, 523, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Obergaulinger, M., Iyudin, A. F., Müller, E., & Smoot, G. F. 2014, MNRAS, 437, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Ohm, S., van Eldik, C., & Egberts, K. 2009, Astropart. Phys., 31, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Parizot, E., Marcowith, A., Ballet, J., & Gallant, Y. A. 2006, A&A, 453, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piron, F., Djannati-Atai, A., Punch, M., et al. 2001, A&A, 374, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohl, M., Yan, H., & Lazarian, A. 2005, ApJ, 626, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, T. A., Moskalenko, I. V., & Strong, A. W. 2006, ApJ, 648, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rettig, R., & Pohl, M. 2012, A&A, 545, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, S. P. 1998, ApJ, 493, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Reynoso, E. M., Dubner, G., Giacani, E., Johnston, S., & Green, A. J. 2006, A&A, 449, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slane, P., Hughes, J. P., Edgar, R. J., et al. 2001, ApJ, 548, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Stupar, M., Filipović, M. D., Jones, P. A., & Parker, Q. A. 2005, Adv. Space Res., 35, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, S., Bamba, A., Terada, Y., et al. 2016, PASJ, 68, S10 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, T., Allafort, A., Ballet, J., et al. 2011, ApJ, 740, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Telezhinsky, I. 2009, Astropart. Phys., 31, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Wilks, S. S. 1938, Ann. Math. Stat., 9, 60 [Google Scholar]
- Wright, A. E., Griffith, M. R., Burke, B. F., & Ekers, R. D. 1994, ApJS, 91, 111 [NASA ADS] [CrossRef] [Google Scholar]
The subsequent 3FGL Fermi-LAT catalog (Acero et al. 2015) models RX J0852.0−4622 as an extended source (3FGL J0852.7−4631e) and does not list a counterpart.
Crab nebula fluxes in this work are calculated using the spectrum from Meyer et al. (2010).
All Tables
Fit parameters for the H.E.S.S. spectrum (central column) and the simultaneous Fermi-LAT-H.E.S.S. spectral fit (right column) of RX J0852.0−4622.
All Figures
 |
Fig. 2 Left: smoothed and exposure-corrected excess map with ROSAT X-ray contours, as in Fig. 1. The white annulus denotes the region used for extraction of the azimuthal profile; the white vertical line denotes the origin of the azimuthal angle (north), which increases in the counterclockwise direction. The green star indicates the position of PSR J0855−4644. The white dot-dashed line indicates a point-like region around the position of the southern enhancement. Right: azimuthal profile extracted from the annulus in the skymap on the left panel is shown in blue for the H.E.S.S. γ-ray data (left scale) and in red for the ROSAT X-ray data (right scale). For better visibility, two periods separated by a dashed gray line are shown. The azimuthal position of PSR J0855−4644 and the center of the region around the southern enhancement are indicated by green and black vertical dashed lines, respectively. The vertical error bars represent 1σ statistical uncertainties; the horizontal bars represent the bin widths. |
| In the text | |
 |
Fig. 3 H.E.S.S. and Fermi-LAT spectra for RX J0852.0−4622 with statistical and systematic errors. The Fermi-LAT measurement was taken from Tanaka et al. (2011). The figure shows the spectral points with 1σ statistical (light and dark blue lines for Fermi-LAT and H.E.S.S., respectively) and systematic (red lines in both cases) uncertainties together with the spectral fits and their 1σ statistical uncertainty (shaded bands). In addition, the simultaneous Fermi-LAT-H.E.S.S. fit function is also shown (orange dashed line). |
| In the text | |
 |
Fig. 1 Left: exposure-corrected excess map for RX J0852.0−4622. The data were binned in bins of 0.01° on each coordinate and smoothed with a Gaussian function of width 0.08°. The white dashed line shows the position of the Galactic plane; the inset shows the PSF of the analysis at the same scale for comparison. Right: same as in the left panel, but additionally the boundary of the ON region is shown as a white circle and the significance contours at 3, 5, 7, 9, and 11σ are shown in black with increasing line width for increasing significance. In addition, X-ray contours from the ROSAT All Sky Survey for energies larger than 1.3 keV are shown in red. The X-ray data were smoothed in the same way as the γ-ray data to allow for a direct comparison. The X-ray contours were derived at 25, 50, 75, and 100 counts. The green star indicates theposition of PSR J0855−4644. |
| In the text | |
 |
Fig. 4 Top figures represent skymaps (smoothed exposure-corrected excess map from Fig. 1 for the top left and center pads, significance contour map for the right pad) together with various regions used for the study of the spatially resolved spectroscopy of the RX J0852.0−4622 region. Top left: regions 0 for the central part of the SNR and 1–6 for the shell are shown in white. Center: regions A, B, and C around PSR J0855−4644, region D around the southern enhancement in the azimuthal profile, and the region used for the NW rim are shown in white. The H.E.S.S. significance contours at 5, 7, and 9σ are shown in black with increasing line width for increasing significance. The position of PSR J0855−4644 is denoted by the green star. Top right: regions B′ (dark gray shaded area) and C′ (light gray shaded area) around PSR J0855−4644 are shown. The H.E.S.S. significance contours at 3, 5, 7, and 9σ are shown in black with increasing line width for increasing significance. The position of PSR J0855−4644 is denoted by the black star. Bottom figures represent the error contour plots of λ = 1∕Ecut vs. Γ for the spectra of the regions in the excess maps assuming a power law with exponential cutoff model. For each region, the fitted value is indicated with a triangle, while the ellipse indicates the contour of the 3σ confidence level statistical uncertainty. Dashed lines are used for the regions where the cutoff significance is below 3σ. Bottom left: spectra of the regions 0 to 6 are represented. Bottom center: spectra of the regions A, B, and C are represented. In addition, the contours of the analysis of the whole SNR and NW rim are shown. Since the spectra of regions A–C are correlated because the regions overlap, the corresponding contours are not meant to be compared to each other, but to the contours of the NW rim. Bottom right: spectra of the regions A, B′ , C′ , and D are represented. In addition, the contours of the analysis of the whole SNR and the NW rim are shown. |
| In the text | |
 |
Fig. 5 Left: spectral energy distribution of SNR RX J0852.0−4622 in the GeV-TeV band. Filled squares reflect the emission detected by Fermi-LAT, while filled circles show the H.E.S.S. data. Error bars reflect statistical errors. The lines represent fits of the leptonic (dashed red) and hadronic (solid blue) γ-ray emission models to the data. Right: broadband spectral energy distribution of SNR RX J0852.0−4622 in the leptonic scenario. The MWL data are indicated as follows: radio data are denoted with filled blue triangles, X-ray are indicated with cyan bowties, GeV γ-rays are indicated with filled squares, TeV γ-rays are denoted with filled circles. The error bars of the Fermi-LAT and H.E.S.S. data points reflect statistical errors only. The filled blue bowtie represents the 90% confidence level statistical uncertainty band on the X-ray data; the open bowtie represents systematic uncertainties. Red lines represent the emission from the electron population as obtained from the fit of the GeV-TeV data (cf. left figure) and gray lines represent the emission from a modified electron population where all parameters were decreased by 0.6σ of the quadratically added statistical and systematic uncertainties. Dashed lines correspond to IC emission and dotted lines correspond to synchrotron radiation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


