EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 610 (February 2018) A&A, 610 (2018) A22 Full HTML
Free Access
Issue
A&A
Volume 610, February 2018
Article Number A22
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201731874
Published online 20 February 2018

© ESO 2018

1 Introduction

Type Ia supernovae (Ia-SNe) have played a pivotal role in our understanding of the structure of the universe and its rate of expansion through their use as standardizable candles (Phillips 1993; Riess et al. 1998; Perlmutter et al. 1999), as well as the chemical composition and evolution of galaxies (e.g. Pagel 1997). However, despite the significance, the origins of these SNe are still hotly debated (see e.g. Hillebrandt & Niemeyer 2000; Maoz et al. 2014, for reviews).

Regular Ia-SNe (there are several classes of peculiar Ia-SNe, which we do not discuss here, see e.g. Li et al. 2001; Graur et al. 2017; Taubenberger 2017) are powered by the thermonuclear explosion of a carbon-oxygen (CO) white dwarf (WD), and several astrophysical scenarios leading to Ia-SNe explosions have been proposed, and one or even multiple progenitor channels may exist (Hillebrandt & Niemeyer 2000; Maoz & Mannucci 2012). There are three classical progenitor channels of which two concern a WD reaching the Chandrasekhar mass limit. This happens either by accretion from a non-degenerate companion star in the single-degenerate (SD) channel (Whelan & Iben 1973; Nomoto 1982), or by a merger of two CO WDs in the double-degenerate (DD) channel (Iben & Tutukov 1984; Webbink 1984). Another Chandrasekhar-mass channel, concerns the merger of a WD and an AGB-star degenerate core (Kashi & Soker 2011; Ilkov & Soker 2012; Soker 2013). Additionally, sub-Chandrasekhar models have been considered through for example the double-detonation channel after He-accretion Woosley et al. (e.g. 1986); Livne (e.g. 1990). In recent years the DD scenario has been extended to include WD-WD collisions and not only mergers, but the former were thought to be extremely rare, and occur only in dense stellar clusters. For this reason they attracted relatively little attention compared with other WD explosion progenitors. Such collisions, however, are likely to be observable as type Ia SNe (Rosswog et al. 2009) and possibly non-standard SNe (Raskin et al. 2009, 2010; Papish & Perets 2016). Recently, it was shown that some triple systems may dynamically evolve through a quasi-secular process, reminiscent of Kozai-Lidov oscillations (Kozai 1962; Lidov 1962), but where significant pericentre changes can occur on a single orbit timescale (Antonini & Perets 2012), leading to extremely close pericentre approaches. In particular, it was suggested that such evolution in triples hosting an inner WD-WD binary could lead to physical collisions and the production of type Ia SNe (Katz & Dong 2012; Thompson 2011; Kushnir et al. 2013).

The WD-WD collision scenario has several advantages. In particular, the detonation mechanism (shock ignition) is well understood and robust compared with other progenitor models (Kushnir et al. 2013), and the model may provide a range of Ia-SNe with properties consistent with the observed ones. Physical collisions of WDs have been considered in the context of dense environments such as globular clusters and the Galactic centre (Hut & Inagaki 1985; Sigurdsson & Phinney 1993). However, the rates are expected to be several orders of magnitude below that of the observed Ia-SNe rate (Benz et al. 1989). The rate of collisions arising from a different channel, namely the evolution of isolated triples with quasi-secular evolution, however, was suggested tobe high (Katz & Dong 2012). Nevertheless, it was never self-consistently estimated and preliminary calculations suggested it is actually low (Hamers et al. 2013; Soker et al. 2014; Papish & Perets 2016). In particular, Hamers et al. (2013) studied the SNIa rate from isolated triples with secular evolution theory. They focus on wide inner binaries that do not interact in the absence of the tertiary star. They find a rate that is low compared to observations ( ~0.1%), which predominantly comes from triples with wide inner binaries that experience mass transfer (their “circular mergers”). Here we try to close our knowledge gap and calculate self-consistently the expected rate of collisions due to quasi-secular evolution, test the viabilityof the isolated-triples WD-WD collision model (hereafter the WD-collision model) in term of the progenitor production rates, and derive the delay time distribution (DTD) and collision components (masses) in such explosions. As we show in the following, we find that the SNe rate from WD-WD collisions is of the order of at most 0.1% of the observed Ia-SNe rate across all the models we explored, and the delay-time distribution is almost uniform in time, and is inconsistent with observations and unlikely to explain the origins of standard Ia-SNe.

We begin by describing the triple population synthesis we use (Sect. 2) and the method applied to couple it with quasi-secular triple evolution. We then lay out our assumptions and our criteria for identifying WD-WD collisions in our models and list the range of initial conditions explored. We then describe our detailed results for each of our models 3 and then discuss the results and summarize in Sect. 4.

2 Method

We studied the collision rate of WDs in triples by simulating the evolution of populations of triples. The first triple population synthesis studied were done in the context of destabilized triples due to stellar evolution (Perets & Kratter 2012), which did not account for secular dynamics. Later Hamers et al. (2013) and Naoz et al. (2016) developed population synthesis codes, which included secular evolution, but do not account for quasi-secular regime. Here we used a recently developed triple population synthesis code TRES (Toonen et al. 2016; see Sect. 2.2 for details) which we complement with a simplified treatment of the quasi-secular evolution implications for collisions.

The simulation of a triple system starts with three stars on the zero-age main-sequence in a specific orbital configuration. As the distribution of masses and orbital parameters of these primordial triples is not well known, we applied different model populations to assess the systematic error on our calculations (Sect. 2.1).

The evolution from the main-sequence onwards is simulated with the triple evolution code TRES (Sect. 2.2). We considered triples that avoid mass transfer and remain dynamically stable throughout their evolution. Our triples evolve into a triple WD (3WD), or a double WD in the inner binary with a stellar tertiary (2WD). Generally, the tertiary has a low mass (m3 < 0.95 M⊙) such that it does not evolve into a WD within a Hubble time. Subsequently, a collision occurs between the WDs in the inner binary that leads to the SNIa explosion. The collision can occur due to secular dynamics in three-body systems which drive the inner eccentricity to high values. However Katz & Dong (2012) demonstrated the collision rate may be significantly enhanced for marginally hierarchical systems due to a breakdown of the secular approximation in the quasi-secular regime. We applied two methods to extract the systems that have evolved to a marginal hierarchy (Sect. 2.3). For these systems, thetertiary can significantly change the angular momentum of the inner binary by order unity during a pericentre passage. Katz & Dong (2012) show that the angular momentum phase space is stochastically scanned, such that after a large number of pericentre passages a collision can be expected. Subsequently, the time to reach a collision tcol roughly follows a Poissonian distribution with a mean of: 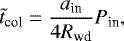t ˜ col = a in 4 R wd P in , \begin{equation*}\tilde{t}_{\textrm{col}}=\frac{a_{\textrm{in}}}{4R_{\textrm{wd}}}P_{\textrm{in}},\end{equation*}(1)

where Pin is the period of the inner binary, and Rwd is the radius of a WD here taken to be 109 cm. Throughout our analysis we assume that a triple entering into the quasi-secular regime leads to the inner binary direct collision on this given timescale.

2.1 Primordial triples

We performed simulations for six sets of primordial triples. These differ with respect to the distributions of stellar and orbital parameters (Table 1). In the standard model STD, we assume the mass (m1) of the initially most massive star in the inner binary (hereafter primary) follows the Kroupa initial mass function (IMF, Kroupa et al. 1993). The mass ratios of the inner binary (qinner ≡ m2∕m1, where m2 is the mass of the secondary) are distributed uniformly (Sana et al. 2012; Duchêne & Kraus 2013; Moe & Di Stefano 2017). We assumed that the mass m3 of the outer companion (hereafter tertiary) is uncorrelated to that of the inner stars. This is consistent with observations of binaries with wide orbits (Moe & Di Stefano 2017). Furthermore, in model STD the inner and outer semi-major axes (ainner and aouter) are distributed uniformly in log-space (N ∝ 1∕a), Abt (1983) between 5R⊙ and 5 × 106 R⊙. The eccentricities einner and eouter are distributed thermally (Heggie 1975) between 0 and 1. The mutual inclination follows a circular uniform distribution between 0 and π. We assumed that the arguments of pericentre and the lines of ascending nodes of both the inner and outer orbits are distributed uniformly between − π and π. We assumedthe stars have Solar metallicities. Finally, we adopted a constant binary fraction of 40% and triple fraction of 10% appropriate for Solar-mass stars (Raghavan et al. 2010; Duchêne & Kraus 2013; Tokovinin 2014; Moe & Di Stefano 2017). Systems that are dynamically unstable at initialization are rejected.

Our alternative models each differ from model STD in one aspect. In model Q_IN, we assumed that the masses of the inner binary are uncorrelated, as for the outer orbit of model STD. In model Q_OUT, we made the opposite assumption such that both the inner qinner and outer mass ratio qouter ≡ m3∕(m1 + m2) are distributed uniformly. In model A_SANA, the distribution of the inner and outer semi-major axes follow a power-law distribution N∝ (logP) −0.55 $N\propto(\log P)^{-0.55}$, as observed in binaries with O- and B-type primaries (Sana et al. 2012). For A-type primaries inbinaries, Rizzuto et al. (2013) found a log-normal distribution of semi-major axes (μ = 0.95 AU, σ = 1.35), which we adopted in model A_RIZ witha maximum separation of 5 × 108 R⊙. Lastly, in model E_CIRC we studied the effect of eccentricities on the collision rate. Initially these triples are circularized.

We considered stellar triples with m1 > 0.08 M⊙ and m2, m3 > 0.008 M⊙. When drawing a mass from the Kroupa IMF, we adopted a maximum mass of 100 M⊙. To speed up the simulations, we only simulated a subset of triples (comprising a fraction fparam.space of parameter space, see Table 2) that satisfy the following three requirements: 1) the inner binary can evolve into a double white dwarf within a Hubble time, that is 0.95 M⊙ < m1, m2 < 7.7 M⊙; 2) to avoid dissolution by the supernova m3 < 7.7 M⊙; 3) to avoid mass transfer a(1 − e2) > 2500 R⊙. The latter is a conservative limit that excludes even isolated binaries, as tides would circularize the binary to the semi-latus rectum. We implicitly assume that the parameter space that we do not consider does not give rise to Ia-SNe in the evolutionary channel considered here. The missing triples are taken into account in the normalization of the rates.

Table 1

Distributions of the initial binary masses and orbital parameters for the different models.

Table 2

Results of the population synthesis modelling.

2.2 Simulating triple evolution with TRES

TRES is an astrophysical code to simulate the evolution of stellar triples consistently (Toonen et al. 2016); the code couples three-body dynamics with stellar evolution including Kozai-Lidov oscillations, tides, gravitational wave emission, and the effects of precession and stellar winds. The dynamics is based on the secular approach up to and including octupole-order (e.g. Naoz 2016, for a review). Stellar evolution is simulated in a parametrized way through the binary population synthesis code SeBa (Portegies Zwart & Verbunt 1996; Toonen et al. 2012). TRES is valid for simulating isolated coeval stellar triples. Moreover, due to the usage of the secular approach, it is strictly only appropriate to simulate the evolution of hierarchical triples.

TRES is written in the Astrophysics Multipurpose Software Environment, or AMUSE (Portegies Zwart et al. 2009, 2013). It is a software framework that includes codes from different astrophysical domains, such as stellar dynamics, stellar evolution, hydrodynamics and radiative transfer. AMUSE provides the user with a homogeneous interface structure based on Python in which the community codes can be easily used and coupled. AMUSE can be downloaded for free at amusecode.org and github.com/amusecode/amuse.

2.3 Marginal hierarchical systems

We applied two methods to extract those triples that become marginally hierarchical during their evolution. In method 1, we tracked the level of hierarchy in the simulations with TRES. When a system enters the “quasi-secular” regime, the simulation is stopped1, according to the following boundary condition we implemented in TRES: 1− e 1 < 1− e crit ≡ f crit ×5π m 3 m 1 + m 2 [ a 1 a 2 (1− e 2 ) ] 3 , \begin{equation*}\sqrt{1-e_{1}}<\sqrt{1-e_{\textrm{crit}}}\equiv f_{\textrm{crit}}\times5\pi\frac{m_{3}}{m_{1}&#x002B;m_{2}}\left[\frac{a_{1}}{a_{2}(1-e_{2})}\right]^{3},\end{equation*}(2)

where fcrit is a numerical factor ≈1 (Antonini et al. 2014; see also Antonini & Perets 2012; Katz & Dong 2012). If the inner eccentricity becomes larger than ecrit, the angular momentum of the inner orbit can change by order of itself in one period. We note that with this criterion, the SNIa progenitors in our models predominantly fulfill the criterion (see Eq. (7) in Katz & Dong 2012) to experience a clean collision (see also Perets & Kratter 2012 for a similar clean collision criterion); all pericentre passages before the collision are large enough such that tidal or general relativistic effects are negligible. Cases where tidal interactions occur are treated by the regular secular evolution coupled to tidal evolution.

In method 2, the simulations with TRES were performed until time tform, which represents the time at which the triple WD forms, or the double WD if the tertiary star does not evolve to a WD in a Hubble time.

We calculated analytically the maximum eccentricity emax that the inner orbit can achieve afterwards based on the quadrupole approximation for ein ≥ 0 (e.g. Kinoshita & Nakai 2007; Perets & Naoz 2009; Naoz 2016). If emax > ecrit (Eq. (2)), we assumed the system enters the quasi-secular regime. Such a simplified criterion does not well capture the maximal eccentricity potentially reached due to octupole-level perturbations, however the latter typically become important for inner binaries with low-mass ratio, while WD-WD binaries in our study always have a high mass ratio (typically above 0.85). If a triple enters the quasi-secular regime before tform, the evolution of the system is evaluated based on the secular approach, which is not strictly valid in this regime. However, it is likely that the system reaches high eccentricities even within the secular approximation, such that Roche lobe overflow develops. Mass transferring systems are not taken into account in our rate estimates. Method 2 is less accurate than method 1, but allows for more flexibility by varying f.

3 Results

3.1 Formation

In order to calculate the rate of colliding WDs, we first study the formation rate of a DWD with an outer companion, either another WD (i.e. 3WD) or a low-mass stellar component (i.e. 2WD). In most of our models, about 6% of primordial triples evolve to a 3WD in a Hubble time, and about 70% to a 2WD (Table 2). An exception to this is model Q_OUT, in which the masses of the outer companion are correlated to those of the inner binaries and the average tertiary mass is therefore higher compared with the other models. In model Q_OUT 3WDs are formed more efficiently; about half of the primordial triples evolve to a 3WD and a fifth evolve to become a 2WD.

About 25% of triples do not become a 2WD or 3WD (Table 2). Mainly, these systems become dynamically unstable due to their stellar and orbital evolution or the systems experience mass transfer. Regarding the former, triples that become dynamically unstable due to mass loss in the stellar winds are studied by Perets & Kratter (2012). This evolutionary channel can lead to a stellar collision involving an (post-)AGB star. Perets & Kratter (2012) find that this channel could be the dominant form of stellar collisions in the field. Regarding the latter, double WDs that form through mass transfer are expected to have gone through a significant reduction of their orbit during the prior mass transfer phase between the primary WD and the hydrogen-rich progenitor of the secondary (Nelemans et al. 2000; van der Sluys et al. 2006). Assuming that the orbit of the tertiary does not shrink as well (a modest widening is expected if the mass loss from the inner binary acts as a fast non-interacting wind), the hierarchy of the triple has increased due to the mass transfer phase. This would make it less likely for triples with mass transfer to experience a collision in the inner double white dwarf due to quasi-secular evolution. In this paper we exclude triples that experience mass transfer. We note that overall the merger rate between WDs is enhanced if the binary has a tertiary companion, and some direct collisions may occur even outside the quasi-secular regime. Indeed, non-quasi-secular mergers and collisions in triples were studied by Hamers et al. (2013), however, such mergers and collisions do not contribute more than 10−3 of the Ia rate at any given time.

Next we consider those systems that become marginally hierarchical. In method 1, we track the level of hierarchy at every timestep in the simulations with TRES. We find that a few percent of all simulated triples reach sufficiently high inner eccentricities such that the systems enter the quasi-secular regime. The fraction is highest in model Q_OUT, which is related to the high average tertiary masses in this model. Of interest here are the 2WDs and 3WDs that become quasi-secular. All six models show that even though the formation of a 2WD or 3WD is common (in the part of parameter space simulated here), only a small percentage of the triples reach this state, that is 0.2− 0.5%. In method 2, we find similar percentages of 0.2−0.7%.

3.2 Supernovae rates and delay time distributions

We find that head-on collisions between carbon-oxygen WDs from wide isolated triples happen at a rate of a few times 10−7 per solar mass of created stars. The rates of the different models and methods are given in Table 3. In comparison, the observed rate of supernova Type Ia in field galaxies is about 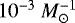10 −3   M ⊙ −1 $10^{-3}~M_{\odot}^{-1}$ (e.g. Maoz et al. 2014; Maoz & Graur 2017) and therefore the contribution the isolated-triples channel to the SNIa rate is of the order of 0.01−0.1%.

The different models of primordial triples give rise to up to an order of magnitude uncertainty in the synthetic Ia-SNe rates. The highest rates are expected if the inner and outer orbits are circularized (model E_CIRC). In this case fewer systems will undergo mass transfer, as indicated in Table 2 by the large fraction of parameter space that is simulated fparam.space, and the small fraction of systems experiencing mass transfer in the simulated triples. Consequently, these systems will follow a different evolutionary channel than considered here. The lowest rates are anticipated if the masses of the three stars are not correlated to one another (model Q_IN). In this case the average mass of the secondary is low, its evolutionary timescale is long, such that fewer triples will harbour two WDs in the inner binary (see fparam.space in Table 2). Furthermore, as the average mass of the tertiary is low, the dynamical effect of the tertiary on the inner binary is smaller, and fewer systems enter the quasi-secular regime.

Another aspect that affects the predicted collision rate is the extent of the quasi-secular regime. So far we have adopted a sharp boundary between the secular and quasi-secular regime, that is fcrit = 1. In reality, the reliability of the secular approximation deteriorates gradually when approaching the critical boundary. Assuming that the secular approximation falls short at fcrit = 2 (fcrit = 10 ) and using method 2, the collision rate increases by about a factor ~2−3 (~10−40).

The collision rate depends also on the abundance of triples, that is the triple fraction. Here we have assumed a triple fraction of 10% and a binary fraction of 40%. These values are based on observation of Solar-type stars (Raghavan et al. 2010; Duchêne & Kraus 2013; Tokovinin 2008, 2014). However, several studies have shown that the binary fraction varies with the stellar type of the primary (Raghavan et al. 2010; Duchêne & Kraus 2013; Klein & Katz 2017; Moe & Di Stefano 2017). The binary fraction increases with primary mass, and there are indications that the triple fraction follows a similar trend (Remage Evans 2011; Sana et al. 2014; Moe & Di Stefano 2017). Assuming a triple fraction of 25% and a binary fraction of 60% (appropriate for A-type stars), the collision rates in Table 3 increase by a factor of approximately two. Taking the most optimistic and likely not realistic assumptions, that is a high triple fraction, fcrit = 10 and model E_CIRC one can reach a level of ~6% of Ia-SNe from this channel. A more plausible fraction would of the order of 0.1− 1% of Ia-SNe.

The collision rate as a function of time since a single burst of star formation, that is the delay time distribution (DTD) is shown in Figs. 1 and 2. These shown DTDs are for all models in method 2. The predicted DTDs from method 1 (not shown) are in good agreement with those shown in the figures. We find that the DTDs of all models and methods have a very distinct shape, namely the delay times are distributed uniformly in time. On the other hand, the observed SNIa DTD decreases strongly with time. The characteristic shape of the observed DTD is d N∕dt ∝ tβ with β ≈−1 (Graur et al. 2011; Graur & Maoz 2013; Heringer et al. 2017).

Due to the shape of the predicted and observed DTD, the largest contribution from head-on collisions in isolated triples is expected at long delay times. At these times, the observed SNIa rate in field galaxies is about 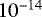10 −14   yr -1   M ⊙ −1 $10^{-14}~\textrm{yr^{-1}}~{M_{\odot}^{-1}}$ (Table 4), and our maximum predicted collision rate is about 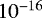10 −16   yr -1   M ⊙ −1 $10^{-16}~\textrm{yr^{-1}}~{M_{\odot}^{-1}}$ (model E_CIRC). At best, collisions in triples contribute about 1% to the SNIa rate at late times.

Table 3

Time-integrated collision rate of CO-CO WDs per solar mass of created stars.

Table 4

Delay time distribution at long delay times in field galaxies.

thumbnail Fig. 1

Delay time distribution of head-on collisions between white dwarfs in isolated triples. The rate of collisions is given per 1017 yr per solar mass of created stars. The different line-styles correspond to the different models in method 2. The DTD is approximately uniform in time. Both the normalization and the shape of the DTD is in clear contradiction with observations.
thumbnail Fig. 2

Cumulative delay time distribution of head-on collisions between white dwarfs in isolated triples. The collision rates are normalized to 1.

3.3 Masses and mass-ratios of colliding WDs

Now we turn to the masses of the colliding WDs. The combined mass of the colliding WDs and their mass ratios are shown in Figs. 3 and 4. These figures represent model STD using method 2, but all models show similar behaviours. The stellar evolution timescales are long for (single) low-mass stars that is low-mass WD progenitors. Therefore WD-WD systems with high total mass tend to form earlier, and therefore collide following a short delay time, while low-mass systems form later and thereby give rise to long delay times.

The individual masses of the colliding WDs are close to one another (Fig. 4). This is expected as the initial-to-final mass relation for WDs is fairly flat, for example Kalirai et al. (2008) who find Mfinal = (0.109 ± 0.007) Minitial (M⊙) + (0.394 ± 0.025) M⊙.

The masses of the colliding WDs are important for the amount of 56 Ni that can be synthesized in the collision (see e.g. García-Senz et al. 2013). Early works of hydrodynamical simulations of colliding WDs have found a minimum mass ratio (q≳0.6−0.7) and/or totalmass ≳1.0−1.2 M⊙ necessary for an explosion to take place. On the other hand, at higher resolution Kushnir et al. (2013) found all their collisions to produce enough 56Ni in order to appear as a SNIa. In our simulations, the mass ratios are typically ~ 0.9−1 (Fig. 4), such that a minimum mass ratio of ~0.6−0.7 does not effect the predicted collision rate significantly. On the other hand if the minimum total mass of the colliding WDs to produce a SNIa-like event is 1.2 M⊙, the synthetic rates given in this paper can be seen as an upper limit (Fig. 3).

Lastly, Piro et al. (2014) compared the distribution of 56 Ni derived from SNIa observations with the expected yields from colliding WDs (based on Kushnir et al. 2013). Piro et al. (2014) find that if colliding WDs are the main channel to form SNIa, the average mass of the WDs should be peaked around 0.75 M⊙. This is not reproduced by our models.

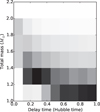thumbnail Fig. 3

Total mass of the colliding white dwarfs of the inner binary as a function of the delay time for model STD and method 2. Delay time is given as a fraction of the Hubble time, here taken as 13.5 Gyr. The grey scale is a density of objects on alinear scale.
thumbnail Fig. 4

Mass ratio of the colliding white dwarfs of the inner binary as a function of the delay time for model STD and method 2. Delay time is given as a fraction of the Hubble time, here taken as 13.5 Gyr. The grey scale is a density of objects on alinear scale.

4 Discussion and summary

In this paper we studied the rate of WD-WD direct collisions induced by secular and quasi-secular evolution in triple stellar systems, and their potential to explain the origin of typical type Ia SNe. Though triple secular evolution was shown to produce only low-rates of direct WD-WD collisions (Hamers et al. 2013), it was suggested that less hierarchical triple systems can evolve through quasi-secular evolution (Antonini & Perets 2012) leading to high rates of WD-WD collisions in triple (Katz & Dong 2012). In order to study this possibility we used a novel triple population synthesis models TRES, coupled to simplistic application of quasi-secular evolution, when relevant, and explored the properties of such triple-formed SNe, including their rates, total mass of the colliding WDs, the WDs mass-ratios and the expected delay time distribution. Given the many uncertainties in the properties and quasi-secular evolution of triple systems, we constructed a range of plausible models for the triple progenitor population, and employed several simplified models to account for the quasi-secular evolution involved. Though the predicted rates may range over an order of magnitude, depending on the chosen model, all models predict no more than ~ 0.1% of regular type Ia may arise from WD collisions in isolated triples. Moreover, the delay time distribution of SNe from this channel is distributed uniformly over time, and is therefore inconsistent with that inferred from observations (~t−1).

Many of the potential progenitors that initially have high inclinations and relatively weak hierarchy, that “active” triples susceptible to the quasi-secular evolution already dynamically evolve into mass-transfer, mergers or collisions during the main-sequence of giant-branch stages, and never produce WD-WD binaries for which collisions can be induced by the third stellar companion. Possible channels to introduce more active triples with WD-WD inner binaries in the relevant phase space could be through the perturbations of “non-active” triple, such as a triple with low-mutual inclination which would not quasi-secularly evolve significantly otherwise. In stellar clusters triples could be perturbed by other stars in the cluster and thereby change their orbital parameters. The evolution of such non-isolated perturbed triples is not considered here, however; the total number of triples in clusters is relatively small, both due to the total number of stars in clusters in general in addition to the small fraction of triples, which would need to be sufficiently compact (“hard”) as not to be disrupted by encounters with other stars. We therefore do not expect triples in cluster to contribute significantly to the formation of type Ia SNe.

Triples in the field might also be susceptible to flyby encounters by field stars. However, such flybys introduce negligible changes in the triple orbits, and at most minor changes in the orbits of the widest triples. Study of flybys in very wide triples will be explored elsewhere, but these too are not expected to contribute significantly. We conclude that triples, and in particular isolated field triples, are likely to produce only a small fraction (at most a percent) of type Ia SNe.

Acknowledgements

S.T. gratefully acknowledges support from the Netherlands Research Council NWO (grant VENI [No. 639.041.645]). H.B.P. and S.T. gratefully acknowledge support from the Israel science foundation I-CORE program 1829/12. A.S.H. gratefully acknowledges support from the Institute for Advanced Study, and from NASA grant NNX14AM24G.

References

  1. Abt, H. A. 1983, ARA&A, 21, 343 [Google Scholar]
  2. Antonini, F., Murray, N., & Mikkola, S. 2014, ApJ, 781, 45 [NASA ADS] [CrossRef] [Google Scholar]
  3. Antonini, F., & Perets, H. B. 2012, ApJ, 757, 27 [NASA ADS] [CrossRef] [Google Scholar]
  4. Benz, W., Thielemann, F.-K., & Hills, J. G. 1989, ApJ, 342, 986 [NASA ADS] [CrossRef] [Google Scholar]
  5. Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
  6. García-Senz, D., Cabezón, R. M., Arcones, A., Relano, A., & Thielemann, F. K. 2013, MNRAS, 436, 3413 [NASA ADS] [CrossRef] [Google Scholar]
  7. Graur, O., & Maoz, D. 2013, MNRAS, 430, 1746 [NASA ADS] [CrossRef] [Google Scholar]
  8. Graur, O., Poznanski, D., Maoz, D., et al. 2011, MNRAS, 417, 916 [NASA ADS] [CrossRef] [Google Scholar]
  9. Graur, O., Bianco, F. B., Modjaz, M., et al. 2017, ApJ, 837, 121 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hamers, A. S., Pols, O. R., Claeys, J. S. W., & Nelemans, G. 2013, MNRAS, 430, 2262 [NASA ADS] [CrossRef] [Google Scholar]
  11. Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
  12. Heringer, E., Pritchet, C., Kezwer, J., et al. 2017, ApJ, 834, 15 [NASA ADS] [CrossRef] [Google Scholar]
  13. Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hut, P., & Inagaki, S. 1985, ApJ, 298, 502 [NASA ADS] [CrossRef] [Google Scholar]
  15. Iben, Jr. I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ilkov, M., & Soker, N. 2012, MNRAS, 419, 1695 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kalirai, J. S., Hansen, B. M. S., Kelson, D. D., et al. 2008, ApJ, 676, 594 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
  19. Katz, B., & Dong, S. 2012, ArXiv e-prints [arXiv:1211.4584] [Google Scholar]
  20. Kinoshita, H., & Nakai, H. 2007, Celes. Mech. Dyn. Astron., 98, 67 [NASA ADS] [CrossRef] [Google Scholar]
  21. Klein, Y. Y., & Katz, B. 2017, MNRAS, 465, L44 [NASA ADS] [CrossRef] [Google Scholar]
  22. Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
  23. Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kushnir, D., Katz, B., Dong, S., Livne, E., & Fernández, R. 2013, ApJ, 778, L37 [NASA ADS] [CrossRef] [Google Scholar]
  25. Li, W., Filippenko, A. V., Treffers, R. R., et al. 2001, ApJ, 546, 734 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
  27. Livne, E. 1990, ApJ, 354, L53 [NASA ADS] [CrossRef] [Google Scholar]
  28. Maoz, D., & Graur, O. 2017, ApJ, 848, 25 [Google Scholar]
  29. Maoz, D., & Mannucci, F. 2012, PASA, 29, 447 [NASA ADS] [CrossRef] [Google Scholar]
  30. Maoz, D., Mannucci, F., Li, W., et al. 2011, MNRAS, 412, 1508 [NASA ADS] [CrossRef] [Google Scholar]
  31. Maoz, D., Mannucci, F., & Brandt, T. D. 2012, MNRAS, 426, 3282 [NASA ADS] [CrossRef] [Google Scholar]
  32. Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
  33. Moe, M., & Di Stefano R. 2017, ApJS, 230, 15 [Google Scholar]
  34. Naoz, S. 2016, ARA&A, 54, 441 [Google Scholar]
  35. Naoz, S., Fragos, T., Geller, A., Stephan, A. P., & Rasio, F. A. 2016, ApJ, 822, L24 [NASA ADS] [CrossRef] [Google Scholar]
  36. Nelemans, G., Verbunt, F., Yungelson, L. R., & Portegies Zwart S. F. 2000, A&A, 360, 1011 [NASA ADS] [Google Scholar]
  37. Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pagel, B. E. J. 1997, Nucleosynthesis and Chemical Evolution of Galaxies (Cambridge, UK: Cambridge University Press) [Google Scholar]
  39. Papish, O., & Perets, H. B. 2016, ApJ, 822, 19 [NASA ADS] [CrossRef] [Google Scholar]
  40. Perets, H. B., & Kratter, K. M. 2012, ApJ, 760, 99 [NASA ADS] [CrossRef] [Google Scholar]
  41. Perets, H. B., & Naoz, S. 2009, ApJ, 699, L17 [NASA ADS] [CrossRef] [Google Scholar]
  42. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
  43. Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
  44. Piro, A. L., Thompson, T. A., & Kochanek, C. S. 2014, MNRAS, 438, 3456 [NASA ADS] [CrossRef] [Google Scholar]
  45. Portegies Zwart, S., McMillan, S., Harfst, S., et al. 2009, New A, 14, 369 [NASA ADS] [CrossRef] [Google Scholar]
  46. Portegies Zwart, S., McMillan, S. L. W., van Elteren, E., Pelupessy, I., & de Vries N. 2013, Comput. Phys. Commun., 183, 456 [NASA ADS] [CrossRef] [Google Scholar]
  47. Portegies Zwart, S. F., & Verbunt, F. 1996, A&A, 309, 179 [NASA ADS] [Google Scholar]
  48. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Raskin, C., Timmes, F. X., Scannapieco, E., Diehl, S., & Fryer, C. 2009, MNRAS, 399, L156 [NASA ADS] [CrossRef] [Google Scholar]
  50. Raskin, C., Scannapieco, E., Rockefeller, G., et al. 2010, ApJ, 724, 111 [NASA ADS] [CrossRef] [Google Scholar]
  51. Remage Evans N. 2011, Bulletin de la Societe Royale des Sciences de Liege, 80, 663 [NASA ADS] [Google Scholar]
  52. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  53. Rizzuto, A. C., Ireland, M. J., Robertson, J. G., et al. 2013, MNRAS, 436, 1694 [NASA ADS] [CrossRef] [Google Scholar]
  54. Rosswog, S., Kasen, D., Guillochon, J., & Ramirez-Ruiz, E. 2009, ApJ, 705, L128 [NASA ADS] [CrossRef] [Google Scholar]
  55. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  56. Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, 215, 15 [NASA ADS] [CrossRef] [Google Scholar]
  57. Sigurdsson, S., & Phinney, E. S. 1993, ApJ, 415, 631 [NASA ADS] [CrossRef] [Google Scholar]
  58. Soker, N. 2013, in Binary Paths to Type Ia Supernovae Explosions, eds. R. Di Stefano, M. Orio, & M. Moe, IAU Symp., 281, 72 [NASA ADS] [Google Scholar]
  59. Soker, N., García-Berro, E., & Althaus, L. G. 2014, MNRAS, 437, L66 [NASA ADS] [CrossRef] [Google Scholar]
  60. Taubenberger, S. 2017, ArXiv e-prints [arXiv:1703.00528] [Google Scholar]
  61. Thompson, T. A. 2011, ApJ, 741, 82 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tokovinin, A. 2008, MNRAS, 389, 925 [NASA ADS] [CrossRef] [Google Scholar]
  63. Tokovinin, A. 2014, AJ, 147, 87 [NASA ADS] [CrossRef] [Google Scholar]
  64. Toonen, S., Hamers, A., & Portegies Zwart S. 2016, Comput. Astrophys. Cosmol., 3, 6 [CrossRef] [Google Scholar]
  65. Toonen, S., Nelemans, G., & Portegies Zwart S. 2012, A&A, 546, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. van der Sluys, M. V., Verbunt, F., & Pols, O. R. 2006, A&A, 460, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
  68. Whelan, J., & Iben, Jr. I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  69. Woosley, S. E., Taam, R. E., & Weaver, T. A. 1986, ApJ, 301, 601 [NASA ADS] [CrossRef] [Google Scholar]
1

We note that after a system enters the quasi-secular regime, it may still take a long time before the collision occurs (see Eq. (1)). If the triple is a 2WD with a relatively massive stellar tertiary, stellar evolution may still play a role for the evolution of the system. For all 2WDs in the quasi-secular regime ≲10% have a tertiary star with mass above 0.95 M⊙. An exception to this is model Q_OUT, in which 63% of quasi-secular 2WDs have a massive tertiary that will evolve of the main-sequence in a Hubble time. The treatment of the quasi-secular regime in this case is therefore not self-consistent. A better modelling is beyond the scope of this project and could be explored in the future.

All Tables

Table 1

Distributions of the initial binary masses and orbital parameters for the different models.

In the text
Table 2

Results of the population synthesis modelling.

In the text
Table 3

Time-integrated collision rate of CO-CO WDs per solar mass of created stars.

In the text
Table 4

Delay time distribution at long delay times in field galaxies.

In the text

All Figures

thumbnail Fig. 1

Delay time distribution of head-on collisions between white dwarfs in isolated triples. The rate of collisions is given per 1017 yr per solar mass of created stars. The different line-styles correspond to the different models in method 2. The DTD is approximately uniform in time. Both the normalization and the shape of the DTD is in clear contradiction with observations.
In the text
thumbnail Fig. 2

Cumulative delay time distribution of head-on collisions between white dwarfs in isolated triples. The collision rates are normalized to 1.
In the text
thumbnail Fig. 3

Total mass of the colliding white dwarfs of the inner binary as a function of the delay time for model STD and method 2. Delay time is given as a fraction of the Hubble time, here taken as 13.5 Gyr. The grey scale is a density of objects on alinear scale.
In the text
thumbnail Fig. 4

Mass ratio of the colliding white dwarfs of the inner binary as a function of the delay time for model STD and method 2. Delay time is given as a fraction of the Hubble time, here taken as 13.5 Gyr. The grey scale is a density of objects on alinear scale.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.