| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731290 | |
| Published online | 05 January 2018 | |
A deep X-ray view of the bare AGN Ark 120
IV. XMM-Newton and NuSTAR spectra dominated by two temperature (warm, hot) Comptonization processes
1 Université de Strasbourg, CNRS, Observatoire Astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
e-mail: delphine.porquet@astro.unistra.fr
2 Astrophysics Group, School of Physical & Geographical Sciences, Keele University, Keele ST5 5BG, UK
3 CSST, University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD 21250, USA
4 Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
5 INAF–Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
6 INAF–Osservatorio Astronomico di Brera, via Bianchi 46, 23807 Merate (LC), Italy
7 Center for Relativistic Astrophysics, School of Physics, Georgia Institute of Technology, 837 State Street, Atlanta, GA 30332-0430, USA
8 Space Sciences Laboratory, University of California, Berkeley, CA 94720, USA
9 DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Lyngby, Denmark
10 Dr Karl Remeis-Observatory and Erlangen Centre for Astroparticle Physics, Sternwartstr. 7, 96049 Bamberg, Germany
11 Department of Physics, Virginia Tech, Blacksburg, VA 24061, USA
12 Cahill Center for Astronomy and Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA
13 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
14 Columbia Astrophysics Laboratory, Columbia University, New York, New York 10027, USA
15 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
16 INAF – IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
17 NASA Goddard Space Flight Center, Code 662, Greenbelt, MD 20771, USA
Received: 1 June 2017
Accepted: 24 July 2017
Context. The physical characteristics of the material closest to supermassive black holes (SMBHs) are primarily studied through X-ray observations. However, the origins of the main X-ray components such as the soft X-ray excess, the Fe Kα line complex, and the hard X-ray excess are still hotly debated. This is particularly problematic for active galactic nuclei (AGN) showing a significant intrinsic absorption, either warm or neutral, which can severely distort the observed continuum. Therefore, AGN with no (or very weak) intrinsic absorption along the line of sight, so-called “bare AGN”, are the best targets to directly probe matter very close to the SMBH.
Aims. We perform an X-ray spectral analysis of the brightest and cleanest bare AGN known so far, Ark 120, in order to determine the process(es) at work in the vicinity of the SMBH.
Methods. We present spectral analyses of data from an extensive campaign observing Ark 120 in X-rays with XMM-Newton (4 × 120 ks, 2014 March 18–24), and NuSTAR (65.5 ks, 2014 March 22).
Results. During this very deep X-ray campaign, the source was caught in a high-flux state similar to the earlier 2003 XMM-Newton observation, and about twice as bright as the lower-flux observation in 2013. The spectral analysis confirms the “softer when brighter” behavior of Ark 120. The four XMM-Newton/pn spectra are characterized by the presence of a prominent soft X-ray excess and a significant Fe Kα complex. The continuum is very similar above about 3 keV, while significant variability is present for the soft X-ray excess. We find that relativistic reflection from a constant-density, flat accretion disk cannot simultaneously produce the soft excess, broad Fe Kα complex, and hard X-ray excess. Instead, Comptonization reproduces the broadband (0.3–79 keV) continuum well, together with a contribution from a mildly relativistic disk reflection spectrum.
Conclusions. During this 2014 observational campaign, the soft X-ray spectrum of Ark 120 below ~0.5 keV was found to be dominated by Comptonization of seed photons from the disk by a warm (kTe ~ 0.5 keV), optically-thick corona (τ ~ 9). Above this energy, the X-ray spectrum becomes dominated by Comptonization from electrons in a hot optically thin corona, while the broad Fe Kα line and the mild Compton hump result from reflection off the disk at several tens of gravitational radii.
Key words: X-rays: individuals: Ark 120 / galaxies: active / radiation mechanisms: general / accretion, accretion disks / quasars: general
© ESO, 2018
1. Introduction
In the standard picture, the emission of an active galactic nucleus (AGN) stems from an accretion disk around a supermassive black hole (SMBH) with mass spanning from a few million to billions of solar masses. X-ray spectra offer a unique potential to probe matter very close to the black hole and to measure the black hole spin. The X-ray spectra of AGN usually exhibit one or more of the following components: a soft excess below 2 keV, a power-law continuum up to about 10 keV, a Fe Kα line complex near 6.4 keV, and a Compton scattering hump near 20–30 keV.
Recent studies using XMM-Newton have shown that the soft X-ray excess component is commonly seen in AGN, and that for most AGN (the exception possibly being low-mass Narrow Line Seyfert 1 galaxies; Done et al. 2012) this soft excess is not the hard tail of the big blue bump observed in the UV coming from blackbody emission of the accretion disk (e.g., Gierliński & Done 2004; Porquet et al. 2004; Piconcelli et al. 2005). Different explanations have been proposed: for example, photo-ionized emission blurred by relativistic motion in the accretion disk (e.g., Crummy et al. 2006); Comptonization of soft (extreme UV) seed photons by the electrons of a corona above the disk (e.g., Czerny & Elvis 1987); and an artifact of strong, relativistically smeared, partially ionized absorption (Gierliński & Done 2004). These models can give a good representation of the soft excess, though the current simulations of line-driven AGN accretion disk winds cannot reproduce the smooth, soft X-ray excess (Schurch et al. 2009). Therefore, the origin of the soft excess is still an open issue.
Besides, the study of the Fe Kα complex emission can be used to provide fundamental diagnostics of the physical and dynamical conditions of the AGN central engine from the inner part of the accretion disk to the far-away molecular torus. Relativistic (or broad) Fe Kα lines have been studied in numerous AGN (e.g., Nandra et al. 2007; Brenneman & Reynolds 2009; Patrick et al. 2012), especially MCG-06-30-15 (e.g., Tanaka et al. 1995; Fabian et al. 2002; Marinucci et al. 2014), and other particular AGN thanks notably to XMM-Newton and/or NuSTAR data (NGC 1365: Risaliti et al. 2013; and Walton et al. 2014; Mrk 335: Parker et al. 2014; and SWIFT J2127.4+5654: Marinucci et al. 2014). However, the physical interpretation of the observed broad Fe Kα lines has been disputed due to the common presence of a warm absorber (Porquet et al. 2004; Piconcelli et al. 2005; Blustin et al. 2005), which has been proposed to explain in part the broadness of the lines (Turner & Miller 2009). Indeed, the presence of this hot gas on the line of sight could severely complexify the X-ray data analysis, in particular by distorting the underlying continuum of the Fe K line. However, arguments against this interpretation have been invoked by Reynolds et al. (2009).
Likewise, several origins for the hard X-ray spectrum above 10 keV for type 1 Seyferts have been proposed, such as relativistic reflection, complex absorption, and Comptonization, or a combination thereof (e.g., Nardini et al. 2011; Noda et al. 2011; Patrick et al. 2011, 2012; Risaliti et al. 2013; Walton et al. 2014; Ursini et al. 2015; Mehdipour et al. 2015). Therefore, AGN showing no (or very weak) presence of any X-ray warm absorber – so-called “bare AGN” – are the best targets to directly investigate the process(es) at work in the vicinity of SMBHs.
Ark 120 (z = 0.033, MBH = 1.50 ± 0.19 × 108 M⊙1) is the brightest and cleanest bare AGN known so far, that is, one displaying neither intrinsic reddening in its IR continuum nor evidence for absorption in UV and X-rays (e.g., Ward et al. 1987; Crenshaw et al. 1999; Reynolds 1997). The first XMM-Newton observation performed in August 2003 (~80 ks pn net exposure time) confirmed that its spectrum is warm absorption-free, with the smallest upper limit to the column density found among AGN (~3 × 1019 cm-2; Vaughan et al. 2004). Ark 120 therefore represents the best target to have the “purest” view of the properties of the accretion disk and of the black hole spin in AGN. This object displays a prominent soft excess observed down to 0.3 keV and a significant Fe Kα line complex (Vaughan et al. 2004). The width of the broad component of the Fe Kα line (Full width at half maximum (FWHM) ~30 000 km s-1) was much larger than that of the broad optical lines from the broad line region (BLR), with FWHM (Hβ) = 5850 ± 480 km s-1 (Wandel et al. 1999). Ark 120 was also observed with Suzaku in April 2007 (~100 ks) confirming the presence of a large soft excess and of a significant broad Fe Kα line (Nardini et al. 2011; Patrick et al. 2011). Recently, Matt et al. (2014) reported the first spectral analysis of a simultaneous XMM-Newton and NuSTAR observation performed in February 2013. They found that the smooth soft excess was more likely explained by Comptonization. In contrast with the 2003 XMM-Newton observation (Vaughan et al. 2004) and the 2007 Suzaku observation (Nardini et al. 2011), while a significant soft excess was also present, no obvious signature for relativistic reflection was found in the 2013 observation. It is worth mentioning that in 2013 the flux of Ark 120 was lower by about a factor of two than during the 2003 observation. Both this lower flux and the lack of any relativistic signature in this 2013 observation (“low-flux state”) may be explained by the presence of an extended optically-thick corona which hides most of the relativitic reflection from the accretion disk, while in 2003 (“high-flux state” ) and in 2007 (“intermediate-flux state”) this corona was likely less thick and/or less extended (Matt et al. 2014).
An extensive X-ray observational campaign was performed from 2014 March 18 to 24 to study Ark 120 in order to directly probe the accretion disk properties and the SMBH spin in this moderate Eddington ratio AGN (˙M ≳ 0.05 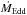 ; Vaughan et al. 2004). This campaign combined a deep XMM-Newton observation (480 ks split into four consecutive 120 ks observations from 2014 March 18 to 24; PI: D. Porquet) with a simultaneous 120 ks Chandra/HETG observation2 (PI: D. Porquet). Furthermore, a NuSTAR observation (65 ks; PI: NuSTAR AGN team) was performed during the third XMM-Newton observation, that is, on 2014 March 22.
; Vaughan et al. 2004). This campaign combined a deep XMM-Newton observation (480 ks split into four consecutive 120 ks observations from 2014 March 18 to 24; PI: D. Porquet) with a simultaneous 120 ks Chandra/HETG observation2 (PI: D. Porquet). Furthermore, a NuSTAR observation (65 ks; PI: NuSTAR AGN team) was performed during the third XMM-Newton observation, that is, on 2014 March 22.
In Reeves et al. (2016; hereafter Paper I), we reported on the analysis of the soft X-ray spectrum using the 480 ks XMM-Newton/RGS and 120 ks Chandra/HETG spectra. We confirmed that there were no detectable absorption lines due to the warm absorber in the deep RGS spectra, and that Ark 120 is the cleanest bare nucleus AGN known so far. Only absorption lines from the interstellar medium of our Galaxy were found. Interestingly, several soft X-ray emission lines from the He-like and H-like ions of N, O, Ne, and Mg were revealed for the first time thanks to this very high signal-to-noise (S/N) RGS spectrum. As a consequence, Ark 120 is not intrinsically bare since substantial X-ray emitting gas is present out of the direct line of sight towards this AGN. This result is very important in the framework of the unified scheme of AGN, which invokes the existence of wide scale obscuring and emitting gas (Antonucci 1993).
In Nardini et al. (2016; hereafter Paper II) we took advantage of the unprecedented depth of the new data sets to study the properties of the composite emission complex from iron fluorescence at 6–7 keV. The most prominent feature peaks around 6.4 keV, and can be plainly identified with the Kα transition from neutral iron. The profile of the narrow Fe Kα core is resolved in the Chandra/HETG spectrum with a FWHM of 4 700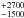 km s-1, consistent with a BLR origin (as was also found for the soft X-ray emission lines; Paper I). Excess components are systematically detected redwards (6.0–6.3 keV) and bluewards (6.5–7.0 keV) of the narrow Fe Kα core. The energy and equivalent width of the red wing rule out an interpretation in the form of the Compton shoulder of the 6.4 keV Kα feature. Moreover, its variability over timescales of about one year (February 2013 to March 2014) hints at the presence of an emission component from the accretion disk. Excess emission maps and time-resolved spectra based on the four consecutive orbits of XMM-Newton monitoring show that both the red and blue features are highly variable on short timescales (30–50 ks) but appear to be disconnected. Such a timescale suggests an origin for these two components at a few tens of gravitational radii from the central SMBH, potentially from discrete hot spots on the disk surface.
km s-1, consistent with a BLR origin (as was also found for the soft X-ray emission lines; Paper I). Excess components are systematically detected redwards (6.0–6.3 keV) and bluewards (6.5–7.0 keV) of the narrow Fe Kα core. The energy and equivalent width of the red wing rule out an interpretation in the form of the Compton shoulder of the 6.4 keV Kα feature. Moreover, its variability over timescales of about one year (February 2013 to March 2014) hints at the presence of an emission component from the accretion disk. Excess emission maps and time-resolved spectra based on the four consecutive orbits of XMM-Newton monitoring show that both the red and blue features are highly variable on short timescales (30–50 ks) but appear to be disconnected. Such a timescale suggests an origin for these two components at a few tens of gravitational radii from the central SMBH, potentially from discrete hot spots on the disk surface.
In Lobban et al. (2018; hereafter Paper III), we presented the spectral and timing properties of Ark 120 using all available XMM-Newton data (including this XMM-Newton Large Programme), a recent approximately six-month Swift monitoring campaign (Gliozzi et al. 2017), and data from RXTE obtained between 1998 and 2006. The spectral decomposition was investigated through fractional rms, covariance and difference spectra, where we found that the mid- to long-timescale (approximately day−year) variability is dominated by a relatively smooth, steep component, which peaks in the soft X-ray band. Additionally, we found evidence for a variable component of Fe Kα emission on the red side of the near-neutral Fe Kα core on long timescales, consistent with Paper II. We also measured the power spectrum and searched for frequency-dependent Fourier lags, obtaining the first detection of a high-frequency soft X-ray lag in this source. Finally, we found well-correlated optical/UV/X-ray variations with the Swift UVOT and searched for multi-wavelength time delays, finding evidence for the optical emission lagging behind the X-rays with a time delay of τ = 2.4 ± 1.8 days.
In this Paper IV, we report on the X-ray spectral analysis of the four 120 ks XMM-Newton/pn time-averaged spectra performed in March 2014, which represent the deepest and longest elapsed time X-ray observation for a bare AGN. We also report on a NuSTAR observation that was simultaneous with the third 2014 XMM-Newton observation (see Table 1 for details). In Sect. 2, we describe the observations, the data reduction, and the spectral analysis method. The spectral analysis of the four 2014 XMM-Newton/pn spectra is presented in Sect. 3, and the broadband X-ray spectrum (XMM-Newton and NuSTAR) of the 2014 March 22 observation in Sect. 4. In Sect. 5 our main results are summarized, before the discussion and conclusions in Sect. 6.
2. Observations, data reduction and analysis
2.1. XMM-Newton and NuSTAR data reduction
Observation log of the data analyzed in this work from the 2014 Ark 120 observational campaign.
During this observational campaign, Ark 120 was observed by XMM-Newton over four consecutive orbits between 2014 March 18 and March 24 (Table 1). As reported in Paper II, the event files were reprocessed with the science analysis system (SAS) v14.0, applying the latest calibrations available in 2015 February. Due to the high source brightness, the EPIC instruments were operated in small window mode. However, this observation mode was not sufficient to prevent pile-up in the MOS cameras, and therefore only the EPIC/pn (Strüder et al. 2001) data are taken into account (selecting the event patterns 0–4, that is, single and double pixels). The four pn spectra were extracted from a circular region centered on Ark 120, with a radius of 30″ to avoid the edge of the chip. The background spectra were extracted from a rectangular region in the lower part of the small window that contains no (or negligible) source photon. The latest part of each orbit was not used due to a high background flaring level. After the correction for dead time and background flaring, the total net exposure was about 330 ks. Redistribution matrices and ancillary response files for the four pn spectra were generated with the SAS tasks rmfgen and arfgen. As shown in Paper III, there is significant flux variability during each of the four XMM-Newton observations and between them. However, the spectral variability within any single orbit is slow and moderate, so we are able to use time-averaged spectra for each of the four observations. As detailed in Paper II, a gain shift has to be applied to take into account the known inaccuracy of the EPIC/pn energy scale likely due to inaccuracies in the long-term charge transfer (CTI) calibration3. The corresponding values for the xspec gain function are reported in Paper II. The 0.3–10 keV pn spectra were binned to give 50 counts per bin.
NuSTAR (Harrison et al. 2013) observed Ark 120 with its two co-aligned X-ray telescopes with corresponding focal plane modules A (FPMA) and B (FPMB) starting on 2014 March 22 for a total of ~131 ks of elapsed time. The level 1 data products were processed with the NuSTAR data analysis software (NuSTARDAS) package (v. 1.6.0). Cleaned event files (level 2 data products) were produced and calibrated using standard filtering criteria with the nupipeline task and the calibration files available in the NuSTAR calibration database (CALDB: 20170222). Extraction radii for both the source and the background spectra were 1.25 arcmin. After this process, the net exposure time for the observation was about 65 ks, with most of the time lost to Earth occultations. The pair of 3.5–79 keV NuSTAR spectra were binned in order to over-sample the instrumental resolution by at least a factor of 2.5 and to have a S/N greater than five in each spectral channel.
The summary log of the Ark 120 X-ray observations used in this work from the 2014 observational campaign are reported in Table 1.
2.2. Spectral analysis method
The xspec v12.9.0g software package (Arnaud 1996) was used for the spectral analysis. The Galactic column density is assumed to be NH = 9.78 × 1020 cm-2 as inferred from the weighted average NH value of the Leiden/Argentine/Bonn Survey of Galactic H i (Kalberla et al. 2005). Since there can be some additional contribution associated with molecular hydrogen (Willingale et al. 2013), we allow the value of Galactic NH to vary slightly (except for the fits above 3 keV, where the value is fixed to 9.78 × 1020 cm-2). However, we do not allow for any intrinsic absorption in the rest frame of Ark 120, since, as found in Paper I from the deep RGS spectrum, none is observed. We used the X-ray absorption model tbnew (v2.3.2) from Wilms et al. (2000), assuming throughout their interstellar medium (ISM) elemental abundances and the cross-sections from Verner et al. (1996).
As reported in Paper II, the narrow neutral core of the Fe Kα emission complex is consistent with being associated with the BLR, and so makes some contribution to the H-like line of iron. Consequently, throughout this work we take into account the contribution from the BLR to the Fe K complex using three Gaussian lines: the Fe KαBLR (E fixed at 6.40 keV) plus its associated Fe KβBLR line (E fixed at 7.05 keV), and the H-like iron line (E fixed at 6.97 keV). The normalization of Fe KβBLR is set to 0.135 times that of Fe KαBLR (Palmeri et al. 2003). The widths of these three lines are fixed to the value inferred in Paper II for the Fe Kα narrow core, that is, 43 eV, as determined from the simultaneous Chandra/HETG spectrum (Paper II). These three BLR emission lines are called hereafter “3 zgaussians(BLR)”.
Throughout this work, when considering relativistic reflection modeling, we use the relxill package (v0.4c4; released in May 2016). These reflection models calculate the proper emission angle of the radiation at each point on the accretion disk, and then take the corresponding reflection spectrum into account. This angle-dependent model connects self-consistently the xillver (Garcia & Kallman 2010; García et al. 2011, 2013, 2014) reflection models with the relativistic blurring code relline (Dauser et al. 2010, 2013, 2014, 2016). In this version the cosmological redshift is properly taken into account in the cut-off energy as well. The models used in this work assume a constant density profile of the accretion disk with ne = 1015 cm-3 (except when mentioned otherwise, see Sect. 4.1.2), and an exponentially broken power-law as the intrinsic continuum shape. Two main geometries are possible: the coronal one (relxill) and the lamppost one (relxilllp). Detailed descriptions of these models and their corresponding parameters are reported in Appendix A.
We use χ2 minimization throughout, quoting 90 percent errors for one interesting parameter (Δχ2 = 2.71) unless otherwise stated. Default values of H0 = 70 km s-1 Mpc-1, Ωm = 0.27, and ΩΛ = 0.73 are assumed. All figures are displayed in the AGN rest-frame.
3. Spectral analysis of the four 2014 XMM-Newton pn observations
In order to characterize the main X-ray components of the spectra, we fit the four XMM-Newton/pn spectra between 3–5 keV using a simple absorbed power-law model. The absorption column density has been fixed to the Galactic one, that is, 9.78 × 1020 cm-2. The power-law index is tied between the four spectra, while the normalization is allowed to vary between the observations (χ2/d.o.f. = 1656.8/1591). We find a photon index of 1.87 ± 0.02, which is typical of those found for radio-quiet quasars (e.g., Porquet et al. 2004; Piconcelli et al. 2005). The unabsorbed flux values between 3 and 5 keV are about 1.8–2.0 × 10-11 erg cm-2 s-1 and are similar to that found for the 2003 XMM-Newton observation, and about twice as bright as the 2013 observation. Then, we extrapolate over the whole 0.3–10 keV energy range. As illustrated in Fig. 1 (top panel), the four observations show a significant soft X-ray excess below 2 keV that is variable between the observations (see also Paper III) with the first observation (2014 March 18) exhibiting the largest soft X-ray excess. The prominent Fe K line profile is consistently seen in each of the observations (Fig. 1, bottom panel), though as shown in Paper II the red and blue sides of the Fe Kα complex are variable on a timescale of about 10–15 h, that is, faster than the total duration of each observation.
 |
Fig. 1 Data/model ratio of the four 2014 XMM-Newton/pn spectra of Ark 120 fitted with a Galactic absorbed power-law continuum model over the 3–5 keV energy range, and then extrapolated over the 0.3–10 keV energy range. Black: March 18, red: March 20, green: March 22, and blue: March 24. Top panel: 0.3–10 keV energy range. Bottom panel: zoom on the Fe Kα complex. |
3.1. Spectral analysis above 3 keV
In this section, we aim to characterize the disk component(s) above 3 keV, that is, without any bias from the soft excess contribution. This has been already investigated in Paper II, but here more general relativistic reflection configurations are probed (e.g, non-solar iron abundance, free inclination angle).
We use the baseline reflection model 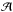 defined as tbnew × [relxill + 3 × zgaussians(BLR)]. The photon index (Γ), the reflection fraction (ℛ), and the normalization (norm) of the underlying continuum of the relativistic reflection component are allowed to vary between each observation. The high-energy cut-off (Ecut) is fixed to 1000 keV since it cannot be constrained from the pn energy range.
defined as tbnew × [relxill + 3 × zgaussians(BLR)]. The photon index (Γ), the reflection fraction (ℛ), and the normalization (norm) of the underlying continuum of the relativistic reflection component are allowed to vary between each observation. The high-energy cut-off (Ecut) is fixed to 1000 keV since it cannot be constrained from the pn energy range.
Simultaneous fit of the four 2014XMM-Newton/pn spectra with the baseline relativistic reflection model (model 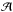 ) over the 3–10 keV energy range.
) over the 3–10 keV energy range.
We first consider a coronal geometry assuming a single power-law disk emissivity index q (ϵ ∝ R− q), tied between the four observations, and fixing the inner radius of the reflection component (Rin) at the innermost stable circular orbit (ISCO), which is self consistently determined from the spin value in the relxill models. We find a good fit (χ2/d.o.f. = 4461.7/4568) and infer a very flat emissivity index of ≤1.1 (see Table 2). The photon indices (Γ ~ 1.85–1.92) are typical of what is found in type-1 AGN (e.g., Porquet et al. 2004; Piconcelli et al. 2005). The extrapolation of the fit down to 0.3 keV shows that the soft excess is not accounted for by this model, which leaves a large positive residual below 2 keV (Fig. 2). If, instead, we fix the disk emissivity index to the standard value of three, the spin value to zero, and allow Rin (expressed in RISCO units) to vary, we also find a good fit in the 3–10 keV energy range and derive Rin = 17.8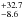 RISCO (see Table 2). If we fix the spin value to the maximal ones, we find Rin ≥ 56 RISCO and Rin = 11.9
RISCO (see Table 2). If we fix the spin value to the maximal ones, we find Rin ≥ 56 RISCO and Rin = 11.9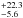 RISCO, for a = 0.998 and a = −0.998, respectively. This suggests that whatever the spin value is, the reflection component does not arise in the very inner part of the accretion disk, in agreement with the results discussed in Paper II. The extrapolation of the fit down to 0.3 keV shows that the soft excess is not accounted for, with a similarly large positive residual. The reflection fraction is found to be rather low, with ℛ = 0.4–0.5 in both cases.
RISCO, for a = 0.998 and a = −0.998, respectively. This suggests that whatever the spin value is, the reflection component does not arise in the very inner part of the accretion disk, in agreement with the results discussed in Paper II. The extrapolation of the fit down to 0.3 keV shows that the soft excess is not accounted for, with a similarly large positive residual. The reflection fraction is found to be rather low, with ℛ = 0.4–0.5 in both cases.
Then we adopt a lamppost geometry, where the primary source of radiation is modeled by a point source on the rotational axis of the black hole, using the relxilllp model. The reflection fraction is calculated directly from the lamppost geometry with the parameter fixReflFrac fixed to one. We find that the height of the X-ray source above the accretion disk is rather high (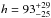 Rg, see Table 2). This suggests that the disk illumination is not centrally concentrated. As for the coronal geometry, a strong positive residual is found below 3 keV when the best fit is extrapolated down to 0.3 keV.
Rg, see Table 2). This suggests that the disk illumination is not centrally concentrated. As for the coronal geometry, a strong positive residual is found below 3 keV when the best fit is extrapolated down to 0.3 keV.
To summarize, good fits are found using a combination of a primary power-law and a relativistic reflection component when considering the 3–10 keV energy range, but they indicate that reflection does not arise in the very inner part of the accretion disk (flat disk emissivity index, large Rin or h), and has a moderate reflection fraction of about 0.4–0.5 (coronal geometry). These results are similar to those found in Paper II. Moreover, in all cases the soft excess is not accounted for, meaning that the soft excess may originate from another physical process.
3.2. Investigation of relativistic reflection modeling over the 0.3–10 keV energy range
We now consider the full 0.3–10 keV energy range to investigate whether reflection models can after all reproduce both the soft excess and the hard X-ray emission up to 10 keV.
We use model 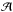 , but here we allow for a broken power-law disk emissivity index (q1, q2, and Rbr). We find a good fit statistic (χ2/d.o.f. = 7246.6/6728,
, but here we allow for a broken power-law disk emissivity index (q1, q2, and Rbr). We find a good fit statistic (χ2/d.o.f. = 7246.6/6728, 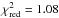 ) over the 0.3–10 keV energy range (Fig. 3, top panel), though there are positive residuals in the Fe K complex energy range (
) over the 0.3–10 keV energy range (Fig. 3, top panel), though there are positive residuals in the Fe K complex energy range (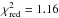 when considering only the 6–7 keV energy range). Since the fit is driven by the smooth soft X-ray emission, very high values for the spin and the disk emissivity indices, with a low inclination angle, are required to reproduce it (see Table 3). Large values (R ~ 7–10) for the reflection fraction are required as well. This would correspond to a scenario of a compact corona very close to the black hole, leading to strong gravitational light bending (Fabian et al. 2012; but see Dovciak & Done 2015). Moreover the primary photon index needed to reproduce the soft X-ray excess is much steeper (Γ ~ 2.4) than that associated to the Fe Kα features when fitting above 3 keV (Γ ~ 1.9). These extreme parameters are incompatible with those found to reproduce the 3–10 keV spectra (see Table 2).
when considering only the 6–7 keV energy range). Since the fit is driven by the smooth soft X-ray emission, very high values for the spin and the disk emissivity indices, with a low inclination angle, are required to reproduce it (see Table 3). Large values (R ~ 7–10) for the reflection fraction are required as well. This would correspond to a scenario of a compact corona very close to the black hole, leading to strong gravitational light bending (Fabian et al. 2012; but see Dovciak & Done 2015). Moreover the primary photon index needed to reproduce the soft X-ray excess is much steeper (Γ ~ 2.4) than that associated to the Fe Kα features when fitting above 3 keV (Γ ~ 1.9). These extreme parameters are incompatible with those found to reproduce the 3–10 keV spectra (see Table 2).
 |
Fig. 2 Extrapolation down to 0.3 keV of the fit over the 3–10 keV energy range of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model |
Moreover, as shown in Fig. 3 (bottom panel), there are still positive residuals with moderately broad line profiles from about 6–6.3 keV (red wing) and 6.6–6.9 keV (blue wing) in all the four spectra (AGN rest-frame), which cannot be reproduced by the extreme and very fine-tuned parameter values required to reproduce the smooth soft excess. The two emission features correspond to the red and blue Fe Kα features reported in Paper II, where the energy−time map showed that they both arise from the accretion disk. We therefore add two relativistic line components (relline, Dauser et al. 2013) that enable us to model these features for a small inclination angle5 as found for the soft excess (see Table 2). The inclination angle and the spin values are linked to those of the broadband blurred reflection component, but we allow the disk emissivity index to vary (Rin is fixed to the ISCO). We find a statistical improvement of the fit compared to the baseline model 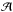 (Δχ2 ~ −238 for five additional parameters). We infer line energies of 6.47 ± 0.01 keV and 6.76
(Δχ2 ~ −238 for five additional parameters). We infer line energies of 6.47 ± 0.01 keV and 6.76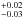 keV, and a disk emissivity index of 1.6
keV, and a disk emissivity index of 1.6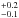 , much flatter than the ones found for the baseline reflection model
, much flatter than the ones found for the baseline reflection model 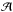 , that is, 7.5 ± 0.5 and 4.5 ± 0.4 for the 2014 March 18 observation (similar values are found for the three other sequences). If, instead, we force the disk emissivity index to be the same as the blurred component and allow the inner radius to vary, we also find a good fit (Δχ2 ~ −240 for five additional parameters) with
, that is, 7.5 ± 0.5 and 4.5 ± 0.4 for the 2014 March 18 observation (similar values are found for the three other sequences). If, instead, we force the disk emissivity index to be the same as the blurred component and allow the inner radius to vary, we also find a good fit (Δχ2 ~ −240 for five additional parameters) with 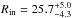 Rg and line energies6 of 6.45
Rg and line energies6 of 6.45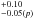 keV and 6.97
keV and 6.97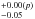 keV. Hence, in both cases, a flat disk emissivity index (q ~ 1.6) or a large inner radius (Rin ~ 25 Rg) are in conflict with the values required to account for the soft excess. This implies that this reflection model cannot self-consistently produce both the soft excess and the mildly relativistic Fe Kα line(s). We also notice that, in order to reproduce these Fe Kα features by means of another broadband reflection component (relxill), not only q (or Rin) and the disk inclination must be untied, but also the Γ value, which must be much harder, that is, below about 1.9.
keV. Hence, in both cases, a flat disk emissivity index (q ~ 1.6) or a large inner radius (Rin ~ 25 Rg) are in conflict with the values required to account for the soft excess. This implies that this reflection model cannot self-consistently produce both the soft excess and the mildly relativistic Fe Kα line(s). We also notice that, in order to reproduce these Fe Kα features by means of another broadband reflection component (relxill), not only q (or Rin) and the disk inclination must be untied, but also the Γ value, which must be much harder, that is, below about 1.9.
 |
Fig. 3 Data/model ratio of the fit over the 0.3–10 keV energy range of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model |
So it is worth investigating whether these accretion disk features (soft excess and Fe Kα residuals) can originate from a more complex disk emissivity shape such as a twice broken power-law, which allows for an intermediate region with a flat emissivity index as could be found for a co-rotating continuum point source or an extended corona (see Fig. 7 in Wilkins & Fabian 2012). However, even with this reflection model we cannot simultaneously reproduce these emission features. A disk ionization gradient (log ξ ∝ R− index) does not work either. The inferred parameters for these fits are reported in Table B.1. Then, we test a lamppost geometry, but a less good fit is found compared to the extended corona model (relxill), and significant residuals near 6.35 keV and 6.7 keV are still present and cannot be removed by allowing for an ionization gradient (assuming an α accretion disk or a power-law density profile (density ∝ R− index)). Table B.1 shows the inferred fit parameters.
In conclusion, these high S/N spectra of Ark 120 show that relativistic reflection models from a constant-density, geometrically-flat accretion disk, while leading to a reasonable χ2/d.o.f. value over 0.3–10 keV, are physically unsatisfactory, since they cannot simultaneously account for both the soft excess and the Fe Kα lines. Such residual Fe K features could have been missed or readily neglected in lower S/N spectra, thus leading to an interpretation of a relativistic reflection-dominated spectrum, with rather extreme and tuned parameters in terms of spin and emissivity.
Simultaneous fit of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model 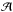 ) over the 0.3–10 keV energy range.
) over the 0.3–10 keV energy range.
3.3. Comptonization process as the origin of the soft excess
Simultaneous fit of the four 2014 XMM-Newton/pn data with the baseline Comptonization model with Comptt (model ℬ, Col. 2) over the 0.3–10 keV energy range.
In this section, we assume that the soft X-ray excess originates from the Comptonization of seed photons from the accretion disk by warm electrons from the corona (here using comptt), as found by Matt et al. (2014) for the February 2013 observation. For this, we use the baseline model ℬ defined as tbnew × [comptt + zpo+3 × zgaussians(BLR)]. The comptt model (Titarchuk 1994) is characterized by the input soft photon temperature (expressed in keV), the plasma temperature (kTe expressed in keV), the plasma optical depth (τ), and the geometry assumed (disk, sphere, analytical approximation). We assume a disk geometry, and an input soft photon temperature of 15 eV according to the black hole mass and the mean accretion rate of Ark 120. We note that the mean value of the input soft photon temperature (around 15 eV) has a negligible impact on the plasma temperature and optical depth values. The power-law component (zpo) is used to readily reproduce Comptonization by the hot electrons of the corona. We obtain an overall good fit with χ2/d.o.f. = 7384.1/6735 (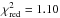 ) (see Table 4, Col. 2), except for the positive residuals at the Fe Kα complex energy range (see below and Fig. 4 top panel), as already found in the previous reflection-based models. We derive for the Comptonized plasma low temperature values of about 0.6–0.8 keV, and high optical depth values of about 7–8 for the four observations (the mean values and their associated errors bars for each observation are shown in Table 4). For illustration purposes, we display in Fig. 5 the 2D contour plot of the plasma temperature (kTe in keV) versus the plasma optical depth for the third XMM-Newton observation. The temperature value of the four observations seems to follow the soft excess strength, but the values between the four observations are consistent with each other within their errors bars. The primary photon indices of about 1.74–1.79 are much harder than those required to produce the soft excess from relativistic reflection modeling (Γ ~ 2.4).
) (see Table 4, Col. 2), except for the positive residuals at the Fe Kα complex energy range (see below and Fig. 4 top panel), as already found in the previous reflection-based models. We derive for the Comptonized plasma low temperature values of about 0.6–0.8 keV, and high optical depth values of about 7–8 for the four observations (the mean values and their associated errors bars for each observation are shown in Table 4). For illustration purposes, we display in Fig. 5 the 2D contour plot of the plasma temperature (kTe in keV) versus the plasma optical depth for the third XMM-Newton observation. The temperature value of the four observations seems to follow the soft excess strength, but the values between the four observations are consistent with each other within their errors bars. The primary photon indices of about 1.74–1.79 are much harder than those required to produce the soft excess from relativistic reflection modeling (Γ ~ 2.4).
 |
Fig. 4 Fit over the 0.3–10 keV energy range of the four 2014 XMM-Newton/pn spectra with the baseline Comptonization model (model ℬ). The fit parameters are reported in Table 4. Black: March 18, red: March 20, green: March 22, and blue: March 24. Top panel: data and data/model ratio. Bottom panel: unfolded spectra where the contributions of the model components are displayed. The following color code for the emission components (dot-dashed curves) is used: magenta for the soft Comptonization (comptt), blue for the cut-off power-law (hot Comptonization). For clarity purposes, we have not displayed the Fe K line components. |
 |
Fig. 5 2D contour plot of the plasma temperature (kTe in keV) versus the plasma optical depth for the third XMM-Newton observation inferred from the baseline Comptonization model (model ℬ). |
Not surprisingly with such a power-law continuum shape above 3 keV, the same red and blue components of Fe Kα residuals are still present. Indeed, they are known to be associated with the accretion disk (Paper II). Thanks to the high S/N of the present spectra and the ability to detect unambiguously these red and blue emission features, we are thus able to establish that even in this scenario, where the soft excess originates from Comptonization, a relativistic reflection component is still required. We therefore add a relativistic line profile (relline), fixing its emissivity index to the standard value of three and the inclination angle to 30 degrees (see Paper II). If Rin is allowed to vary, then the fit is significantly improved (see Table 4, Col. 3), and 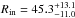 Rg is inferred. The relative contribution of the different model components is displayed in Fig. 4 (unfolded spectrum for illustration purposes only; bottom panel), and shows that Comptonization of seed disk photons by warm electrons of the corona is the dominant process below about 0.8 keV.
Rg is inferred. The relative contribution of the different model components is displayed in Fig. 4 (unfolded spectrum for illustration purposes only; bottom panel), and shows that Comptonization of seed disk photons by warm electrons of the corona is the dominant process below about 0.8 keV.
To summarize, the spectral analysis shows that Comptonization by a low-temperature (kTe ~ 0.6–0.8 keV) optically-thick (τ ~ 7–8) corona can reproduce well the soft excess below 1 keV. Above this energy, the power-law component dominates the continuum, which may represent Comptonization by the hot electrons in a thin corona (e.g., Haardt & Maraschi 1993; Zdziarski et al. 1995). We note that a contribution from disk reflection originating at tens of Rg is still required to account for a broad component of the FeK line, which was not the case for the low flux 2013 observation of Ark 120 (Matt et al. 2014).
4. Broadband X-ray view of Ark 120 observed on 2014 March 22
In this section, we investigate the simultaneous broadband XMM-Newton/pn and NuSTAR observations of Ark 120 performed on 2014 March 22.
First, we investigate the two NuSTAR spectra (FPMA and FPMB) by fitting them using a simple absorbed power-law model in the 3–10 keV energy range excluding the 5.5–7.5 keV energy range. We fix the absorption column density to 9.78×1020 cm-2, and tie the power-law parameters between both NuSTAR spectra. We allow for possible cross-calibration uncertainties between these two NuSTAR spectra. The resulting data/model ratio extrapolated up to 79 keV is reported in Fig. 6, where a significant hard X-ray excess is present in addition to the prominent Fe Kα complex.
4.1. Investigation of the relativistic reflection scenario
4.1.1. Spectral analysis above 3 keV
 |
Fig. 6 Data/model ratio of the NuSTAR spectra of Ark 120 obtained on 2014 March 22, fitted with a Galactic absorbed power-law continuum model (Γ = 1.92 ± 0.02) over the 3.5–10 keV energy range (excluding the 5.5–7.5 keV energy range, that is, the Fe K complex) and then extrapolated over the 3.5–79 keV energy range. In addition to the prominent Fe Kα complex, a significant hard X-ray excess is present. Red: NuSTAR FPMA, and green: NuSTAR FPMB. |
Simultaneous XMM-Newton/pn and NuSTAR spectral fit of the 2014 March 22 observation with the relativistic reflection model above 3 keV (model  ).
).
We start the simultaneous fit of the XMM-Newton/pn and of the two NuSTAR spectra in the 3–10 keV band using model 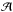 . We allow for cross-calibration uncertainties between the two NuSTAR spectra and the XMM-Newton/pn spectrum by including in the fit a cross-normalization constant corresponding to CNuSTAR A and CNuSTAR B for NuSTAR FPMA and FPMB spectra, respectively (see values in Table 5), related to the XMM-Newton/pn spectrum. The absorption column density has been fixed to the Galactic one, that is, 9.78 × 1020 cm-2. The fit parameters are similar (see Table 5, Col. 2) to those found when fitting simultaneously the four XMM-Newton/pn spectra over this energy range (see Table 2), showing a good match between XMM-Newton/pn and NuSTAR data. Only the inferred disk emissivity index q is larger and the inclination angle is lower due to the lower spectral resolution of the NuSTAR camera which broadens the apparent Fe K profile. We then extrapolate this fit up to 79 keV, and find that the data/model ratio is rather good, although the model slightly overpredicts the emission in the 10–40 keV energy range (see Fig. 7, top panel). The χ2/d.o.f. is 1698.1/1519 (
. We allow for cross-calibration uncertainties between the two NuSTAR spectra and the XMM-Newton/pn spectrum by including in the fit a cross-normalization constant corresponding to CNuSTAR A and CNuSTAR B for NuSTAR FPMA and FPMB spectra, respectively (see values in Table 5), related to the XMM-Newton/pn spectrum. The absorption column density has been fixed to the Galactic one, that is, 9.78 × 1020 cm-2. The fit parameters are similar (see Table 5, Col. 2) to those found when fitting simultaneously the four XMM-Newton/pn spectra over this energy range (see Table 2), showing a good match between XMM-Newton/pn and NuSTAR data. Only the inferred disk emissivity index q is larger and the inclination angle is lower due to the lower spectral resolution of the NuSTAR camera which broadens the apparent Fe K profile. We then extrapolate this fit up to 79 keV, and find that the data/model ratio is rather good, although the model slightly overpredicts the emission in the 10–40 keV energy range (see Fig. 7, top panel). The χ2/d.o.f. is 1698.1/1519 (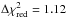 ) without any refitting. Now, we refit over the entire 3–79 keV energy range and find a very good fit (Fig. 7, bottom panel) with parameter values that are very similar to those found for the 3–10 keV energy range, except for the iron abundance which has increased from ≤0.8 to 3.3
) without any refitting. Now, we refit over the entire 3–79 keV energy range and find a very good fit (Fig. 7, bottom panel) with parameter values that are very similar to those found for the 3–10 keV energy range, except for the iron abundance which has increased from ≤0.8 to 3.3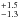 in order to better adjust the 10–40 keV emission (see Table 5). We find an upper limit of 0.6 for the spin value (at 90% confidence level), but we note that after the calculation of a 2D contour plot of the spin versus the inclination angle, the spin is actually unconstrained at the 90% confidence level. A power-law photon index of about 1.86 represents well the underlying continuum over the 3–79 keV energy range. This value is softer than that found for the 2013 observation (Γ ~ 1.73), when the source was in a low-flux state (Matt et al. 2014). Adding the possible contribution from a molecular torus7 does not improve the fit at all.
in order to better adjust the 10–40 keV emission (see Table 5). We find an upper limit of 0.6 for the spin value (at 90% confidence level), but we note that after the calculation of a 2D contour plot of the spin versus the inclination angle, the spin is actually unconstrained at the 90% confidence level. A power-law photon index of about 1.86 represents well the underlying continuum over the 3–79 keV energy range. This value is softer than that found for the 2013 observation (Γ ~ 1.73), when the source was in a low-flux state (Matt et al. 2014). Adding the possible contribution from a molecular torus7 does not improve the fit at all.
As illustrated in Fig. 8 (top panel), the extrapolation of the XMM-Newton/pn spectrum down to 0.3 keV shows that this model is not able to account for the soft X-ray excess, as might be expected given that the best fit is characterized by similar parameters as when considering the 3–10 keV band alone.
 |
Fig. 7 Simultaneous XMM-Newton/pn and NuSTAR spectra of Ark 120 obtained on 2014 March 22 fitted with model |
 |
Fig. 8 Simultaneous XMM-Newton/pn and NuSTAR spectra of Ark 120 obtained on 2014 March 22 fitted with model |
4.1.2. Spectral analysis over the 0.3–79 keV energy range
First, we note that if we try to reproduce the hard X-ray excess with a contribution from the torus using xillver,8 then the normalization of the Fe Kα line emitted by the BLR is consistent with zero. This is at odds with analysis of the Chandra/HETG spectra, where the narrow profile is resolved with a width compatible with the BLR (Paper II). We can therefore conclude, from both the 3–79 keV and 0.3–79 keV analysis, that any contribution from the torus is not significant, and therefore it is not considered from now on. However, we checked that the following results do not depend on the modeling of the narrow Fe Kα core either from the BLR (as established) in Paper II or by the common modeling of a molecular torus.
Simultaneous XMM-Newton/pn and NuSTAR spectral fit of the 2014 March 22 observation with the relativistic reflection model (model  ) over the broad 0.3–79 keV energy range.
) over the broad 0.3–79 keV energy range.
Using model  (and allowing for a single broken power-law emissivity index), we are able to find a satisfactory fit only up to 30 keV, with the parameters reported in Table 6 (χ2/d.o.f. = 2483.2/2058,
(and allowing for a single broken power-law emissivity index), we are able to find a satisfactory fit only up to 30 keV, with the parameters reported in Table 6 (χ2/d.o.f. = 2483.2/2058, 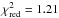 ). Indeed, as shown in Fig. 8 (bottom panel), above this energy there is a significant hard X-ray excess. Of course, as for the four XMM-Newton/pn spectra, there are still residuals present at Fe Kα, but these appear less apparent on the model/ratio plot due to the very significant positive residual observed above about 30 keV. As also found for the 0.3–10 keV spectral analysis, a large reflection fraction and a very steep disk emissivity shape (q1 ≳ 8 or h ~ 2 Rg) are required, as well as a very high (and strongly fine-tuned) value for the spin. Moreover, the inferred photon index is significantly steeper (Γ ~ 2.2) than that found considering only data above 3 keV (that is, Γ ~ 1.9), explaining the presence of the hard X-ray excess residual seen above about 30 keV. We also notice that this hard X-ray excess residual cannot be accounted for by any other alternative relxill models (that is, the ones tested in Sect. 3.2). The lamppost geometrical configuration leads to the worst fit of the data (see Table 6) We check whether such unsatisfactory fits are due to the specific model components and assumptions, still using the baseline model
). Indeed, as shown in Fig. 8 (bottom panel), above this energy there is a significant hard X-ray excess. Of course, as for the four XMM-Newton/pn spectra, there are still residuals present at Fe Kα, but these appear less apparent on the model/ratio plot due to the very significant positive residual observed above about 30 keV. As also found for the 0.3–10 keV spectral analysis, a large reflection fraction and a very steep disk emissivity shape (q1 ≳ 8 or h ~ 2 Rg) are required, as well as a very high (and strongly fine-tuned) value for the spin. Moreover, the inferred photon index is significantly steeper (Γ ~ 2.2) than that found considering only data above 3 keV (that is, Γ ~ 1.9), explaining the presence of the hard X-ray excess residual seen above about 30 keV. We also notice that this hard X-ray excess residual cannot be accounted for by any other alternative relxill models (that is, the ones tested in Sect. 3.2). The lamppost geometrical configuration leads to the worst fit of the data (see Table 6) We check whether such unsatisfactory fits are due to the specific model components and assumptions, still using the baseline model  , by alternatively:
, by alternatively:
-
Allowing the primary photon index of the NuSTAR spectra to bedifferent from that of the XMM-Newton/pn spectrum in order tocompensate for any possible calibration issues.
-
Replacing the relxill model with kyreflionx, which is a model combining the relativistic smearing (Dovčiak et al. 2004) and X-ray ionized reflection models reflionx (Ross & Fabian 2005) or xillver (García et al. 2013).
-
Allowing the incident continuum of the relativistic component to be different from the direct, observed one (see Appendix C.1 for details).
-
Assuming a larger accretion disk density of 1019 cm-3 (see Appendix C.2 for details).
However, none of these relativistic reflection-dominated scenarios allows us to account simultaneously for the three main components (soft excess, broad Fe Kα lines and Compton hump), or to obtain physically meaningful fit results. Furthermore, limiting the analysis to one or another energy range would lead to erroneous results on the physical condition of the disk-corona system (see a comparison of Tables 5 and 6).
To summarize, during this 2014 observational campaign of Ark 120, we can safely rule out relativistic reflection as the origin of both the soft and hard X-ray excesses, and the red and blue relativistic Fe Kα features.
4.2. Model combining Comptonization and relativistic reflection
Here we investigate if a combination of soft and hard Comptonization and mildly relativistic reflection can explain the whole 0.3–79 keV continuum shape, as found for the four XMM-Newton/pn spectra. To do this, we use model 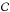 defined as tbnew×[comptt+cut-off PL+relxill+3×zgaussians(BLR)].
defined as tbnew×[comptt+cut-off PL+relxill+3×zgaussians(BLR)].
The cut-off power-law component is used here in order to merely parametrize Comptonization from hot electrons of the thin corona. This continuum shape is also the one used as the underlying hard X-ray continuum for the relativistic reflection component. Since the mildly relativistic Fe K component(s) does not appear to be formed in the very inner part of the accretion disk, as found previously in this work (see also Paper II), we allow Rin to vary and fix the emissivity index to three. We find a good fit (χ2/d.o.f. = 2197.6/2058,  ), as illustrated in Fig. 9 (top panel). The inferred fit parameters are reported in Table 7. We notice that the excess found above about 8 keV in the residuals for the pn spectrum is likely due to calibration issue between the pn spectrum using the small window mode and the NuSTAR spectra, and is particularly prominent for high S/N pn spectrum9. However, removing pn data above 8 keV leads to compatible fit parameters within their error bars (except for
), as illustrated in Fig. 9 (top panel). The inferred fit parameters are reported in Table 7. We notice that the excess found above about 8 keV in the residuals for the pn spectrum is likely due to calibration issue between the pn spectrum using the small window mode and the NuSTAR spectra, and is particularly prominent for high S/N pn spectrum9. However, removing pn data above 8 keV leads to compatible fit parameters within their error bars (except for 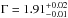 , the discrepancy, however, is marginal), with χ2/d.o.f. = 1972.9/1876 (
, the discrepancy, however, is marginal), with χ2/d.o.f. = 1972.9/1876 (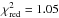 ).
).
We confirm that the Comptonizing plasma responsible for the soft excess has a low temperature (kTe ~ 0.5 keV) and a high optical depth (τ ~ 9). Another interesting result is that during this 2014 observation, the source spectrum above 3 keV shows a softer power-law index (Γ ~ 1.87) compared to the 2013 one (Γ ~ 1.73; Matt et al. 2014), in agreement with the recent study based on the Swift monitoring of Ark 120, which suggests that the source has a “steeper when brighter” behavior (Gliozzi et al. 2017, see also Paper III). The value of Rin of 25.5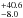 Rg is much larger than the innermost stable orbit even for a maximal retrograde spin of the black hole, that is, a = −0.998. This is another hint that the observed Fe K lines are not formed in the very inner part of the accretion disk.
Rg is much larger than the innermost stable orbit even for a maximal retrograde spin of the black hole, that is, a = −0.998. This is another hint that the observed Fe K lines are not formed in the very inner part of the accretion disk.
The relative contributions of the different model components is displayed in Fig. 9 (unfolded spectrum for illustration purposes only; bottom panel), and shows that the Comptonization process (including both warm and hot electrons of the corona) is the dominant one over the broadband X-ray range.
 |
Fig. 9 Fit over the 0.3–79 keV energy range of the 2014 March 22 XMM-Newton/pn and NuSTAR data with model |
Simultaneous fit of the 2014 March 22 XMM-Newton/pn and NuSTAR spectra over the 0.3–79 keV energy range with model  , which combines Comptonization and relativistic reflection contributions.
, which combines Comptonization and relativistic reflection contributions.
5. Summary
This paper is the fourth of a series of articles reporting on the study of an extensive X-ray (and also optical and UV) observational campaign of a bare AGN, targeting Ark 120. Here, we first performed the simultaneous spectral analysis of the four 120 ks XMM-Newton/pn spectra obtained in March 2014, and then we analyzed the broadband X-ray spectrum – combining pn and NuSTAR spectra – obtained on 2014 March 22. The main results are summarized below:
-
(i)
The four XMM-Newton observations of Ark 120 in 2014 reveal both a strong and variable soft excess and complex Fe Kα emission. Above 3 keV, both the continuum (with Γ ~ 1.9) and the iron-line complex are similar with limited variability between the XMM-Newton sequences.
-
(ii)
Above 3 keV, the four 2014 pn spectra can be well fitted with a disk reflection (relxill) model with moderate reflection fraction (ℛ ~ 0.4–0.5), which requires a flat emissivity profile or a large height of the X-ray source above the disk. Both of these interpretations suggest that the disk reflection emission originates much further away than the ISCO, at typical radii of tens of Rg.
-
(iii)
The extrapolation of the above reflection models leaves strong residuals due to the soft excess below 3 keV. To account for this, the reflection models tend to extreme, finely tuned values requiring a high degree of blurring and nearly maximal black hole spin, plus a steep (Γ ~ 2.4) continuum. However, such models produce a very smooth broadband spectrum, and do not account for the red and blue wings of the Fe Kα line, which require a flat emissivity index (or large Rin) and a harder continuum (Γ ~ 1.9).
-
(iv)
Likewise, when a reflection dominated model is applied to the 2014 NuSTAR data above 10 keV, simultaneous with the third XMM-Newton observation, it cannot fit the spectrum in the highest energy range, leaving a large excess of residual emission above 30 keV. Hence, reflection-only models from a constant-density, geometrically-flat accretion disk cannot simultaneously account for the soft excess, iron line and hard excess in the broadband 0.3–79 keV spectrum.
-
(v)
Instead, the X-ray broadband spectrum can be readily accounted for by a Comptonization model, whereby the soft and hard continuum components arise from a two temperature (warm, hot) disk corona. The warm part of the corona (kTe ~ 0.5 keV) produces the low energy part of the soft X-ray excess and is optically thick (τ ~ 9). A disk reflection component is still required, but it is less strong and originates at tens of gravitational radii from the ISCO of the black hole.
6. Discussion and conclusion
During this extensive X-ray observational campaign of the bare AGN Ark 120, carried out in March 2014, the source was caught in a high-flux state similar to the 2003 XMM-Newton observation (Vaughan et al. 2004), and about twice as bright as the 2013 low-flux observation (Matt et al. 2014). Based on the long-term Swift monitoring of Ark 120 (Gliozzi et al. 2017, Paper III), this large XMM-Newton program and the 2013 observation cover the typical high- to low-flux range observed in this source. Our spectral analysis confirms the “softer when brighter” behavior of Ark 120 (Gliozzi et al. 2017), as commonly found in AGN (e.g., Markowitz et al. 2003; Porquet et al. 2004; Sobolewska & Papadakis 2009; Soldi et al. 2014; Connolly et al. 2016; Ursini et al. 2016) and black-hole binaries systems (e.g., Remillard & McClintock 2006; Done et al. 2007; Wu & Gu 2008; Dong et al. 2014) with accretion rates above 0.01.
From the analysis of the four XMM-Newton/pn spectra (2014 March 18–24) and the March 22 XMM-Newton and NuSTAR observations, we find that relativistic reflection models from a constant-density, geometrically-flat accretion disk cannot self-consistently reproduce the soft excess, the mildly relativistic red and blue Fe Kα features, and the hard X-ray excess. We note that this shortcoming with relativistic reflection models is found in all four 120 ks XMM-Newton/pn spectra separately, thanks to the high-S/N spectra that can be obtained for a bright source like Ark 120. In order to form the large, smooth soft X-ray excess, extreme and tuned parameters are found for the “pure” relativistic reflection scenario: a maximally rotating black hole (a ~ 0.998), a very centrally peaked disk emissivity, a soft primary photon index (Γ ~ 2.4), and a very large reflection fraction (ℛ ~ 10), as reported in Table B.1. By contrast, the red and blue Fe Kα features require just a moderate reflection fraction (ℛ ~ 0.3), a flat emissivity index (q ~ 1.6) or large Rin (a few tens of Rg), and a harder power-law index (Γ ~ 1.9). The former case (reflection-dominated soft X-ray excess) would correspond to a compact corona located very close to the black hole, while the latter case (disk origin of the Fe Kα features) would correspond to an extended corona or a lamppost geometry with a large height of the X-ray source above the disk. Both conditions cannot be therefore explained
Instead, the whole 0.3–79 keV spectrum can be readily explained by a combination of Comptonization (dominating process) of the thermal optical-UV seed photons from the accretion disk by a warm (kTe ~ 0.5 keV) optically thick plasma (τ ~ 9) below about 0.5 keV, by a hot optically thin corona above 0.5 keV, and mildly relativistic reflection at a few ×10 Rg. As shown in Różańska et al. (2015), such a high optical depth of the warm corona could mean that either a strong magnetic field or vertical outflows to stabilize the system are required. An in-depth investigation of the physical properties of the warm and hot corona will be performed in a forthcoming paper (Marinucci et al. in prep.). Interestingly, such a soft X-ray excess origin (that is, enabling us to rule out a relativistic reflection scenario too) is similar to that found, for example, in some non-bare AGN like Mrk 509 (Mehdipour et al. 2011; Petrucci et al. 2013; Boissay et al. 2014) and NGC 5548 (Mehdipour et al. 2015), from deep X-ray (and multi-wavelength) observational campaigns. Such an origin has also been found for the lower-mass SMBH AGN NGC 4593, from high-energy monitoring with XMM-Newton and NuSTAR (Ursini et al. 2016).
Contrary to the 2013 observation, a relativistic reflection component is still required to explain part of the Fe Kα complex. This could be the signature that the optically thick corona is partly or totally hiding the inner accretion disk, as proposed by Matt et al. (2014) to explain the X-ray characteristics of the 2013 observation, which is a factor of two lower in hard X-ray flux and does not appear to show a broad Fe Kα line component. In March 2014, the optically thick part of the corona may have been less extended and/or have displayed a lower covering factor, allowing us to detect a larger part of the relativistic reflection emission. For example, as demonstrated by Wilkins & Gallo (2015), for a covering factor below about 85%, the blurred reflection features become more detectable. Moreover, a Comptonizing corona that covers the inner regions of the accretion disk can have a substantial impact on the observed reflection spectrum (Petrucci et al. 2001; Wilkins & Gallo 2015; Steiner et al. 2017). Furthermore, if the corona covers a sufficient fraction of the inner accretion disk so as to Comptonize the reflected emission, a low reflection fraction can be measured, as found during these March 2014 observations (ℛ ~ 0.3). This could support the presence of an extended corona in this object. The case of a receding, full covering corona between February 2013 and March 2014 will be investigated through the fitting of the spectral energy distribution from optical/UV to hard-X-rays in a forthcoming paper (Porquet et al., in prep.). The alternative scenario of a patchy corona will be tested in a future work too (Wilkins et al., in prep.).
In conclusion, the great advantage of a source like Ark 120 is that its “bare” properties remove any fit degeneracy due to warm absorption contributions. Thanks to both XMM-Newton (4 × ~ 120 ks) and NuSTAR (~65 ks), we are able to discriminate between Comptonization and relativistic reflection for the soft X-ray excess origin, as well as emission above about 2 keV. As revealed in Paper I thanks to the very deep 2014 RGS spectrum, a substantial number of X-ray emitting warm gas is present out of the direct line of sight. The presence of this warm gas (warm absorber) is seen in a very large number of type I AGN (e.g., Porquet et al. 2004; Piconcelli et al. 2005; Blustin et al. 2005) via mainly absorption lines, but also via emission lines (e.g., Bianchi & Matt 2002; Nucita et al. 2010; Wang et al. 2011; Ebrero et al. 2011; Reeves et al. 2013). Such a result demonstrates that Ark 120 is not a peculiar source but merely a source where the line of sight does not intercept the warm gas, and then broadly fits into the AGN unified scheme. Therefore, since Ark 120 has typical AGN properties, such as mass and accretion rate, it can be used as a prototype to perform an in-depth study of the X-ray corona and of its physical and geometrical properties over time, and of its possible impact on reflection spectra.
Black hole mass determined via reverberation mapping (Peterson et al. 2004).
We notice that we find similar results considering a single relativistic line, but in such case a larger inclination angle of about 30 degrees is required (see Paper II, and Table 2).
The same results are found if, instead of xillver, we use mytorus (Murphy & Yaqoob 2009) or pexmon (Nandra et al. 2007).
However, we note that Steiner et al. (2017) proposed that this hardening of reflection spectrum can be explained by Compton scattering in the corona.
Acknowledgments
The authors would like to deeply thank the anonymous referee for useful and constructive comments. The paper is based on observations obtained with the XMM-Newton, and ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). This work made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, and funded by NASA. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center and the California Institute of Technology. D.P. would like to acknowledge financial support from the French “Programme National Hautes Énergies” (PNHE). Part of the work was supported by the European Union Seventh Framework Program under the grant agreement No. 312789 (D.P., G.M., A.M., A.F.). J.N.R. acknowledges financial support via Chandra grant number GO4-15092X and NASA grant NNX15AF12G. J.N.R. and A.L. also acknowledge the support of the STFC, via the consolidated grant ST/M001040/1. G.M., A.M., A.T. and F.U. acknowledge financial support from the Italian Space Agency under grant ASI/INAF I/037/12/0-011/13. E.N. acknowledges funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement No. 664931.
References
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bianchi, S., & Matt, G. 2002, A&A, 387, 76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blustin, A. J., Page, M. J., Fuerst, S. V., Branduardi-Raymont, G., & Ashton, C. E. 2005, A&A, 431, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boissay, R., Paltani, S., Ponti, G., et al. 2014, A&A, 567, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brenneman, L. W., & Reynolds, C. S. 2009, ApJ, 702, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Connolly, S. D., McHardy, I. M., Skipper, C. J., & Emmanoulopoulos, D. 2016, MNRAS, 459, 3963 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Boggess, A., et al. 1999, ApJ, 516, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., & Elvis, M. 1987, ApJ, 321, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Wilms, J., Reynolds, C. S., & Brenneman, L. W. 2010, MNRAS, 409, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., Garcia, J., Wilms, J., et al. 2013, MNRAS, 430, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., García, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., García, J., Walton, D. J., et al. 2016, A&A, 590, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 2196 [Google Scholar]
- Dong, A.-J., Wu, Q., & Cao, X.-F. 2014, ApJ, 787, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Dovciak, M., & Done, C. 2015, in The Extremes of Black Hole Accretion, 26 [Google Scholar]
- Dovčiak, M., Karas, V., & Yaqoob, T. 2004, ApJS, 153, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Ebrero, J., Kriss, G. A., Kaastra, J. S., et al. 2011, A&A, 534, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Vaughan, S., Nandra, K., et al. 2002, MNRAS, 335, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Zoghbi, A., Wilkins, D., et al. 2012, MNRAS, 419, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Fürst, F., Nowak, M. A., Tomsick, J. A., et al. 2015, ApJ, 808, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, J., & Kallman, T. R. 2010, ApJ, 718, 695 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Kallman, T. R., & Mushotzky, R. F. 2011, ApJ, 731, 131 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Reynolds, C. S., et al. 2013, ApJ, 768, 146 [NASA ADS] [CrossRef] [Google Scholar]
- García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [NASA ADS] [CrossRef] [Google Scholar]
- García, J. A., Fabian, A. C., Kallman, T. R., et al. 2016, MNRAS, 462, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., & Done, C. 2004, MNRAS, 349, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Gliozzi, M., Papadakis, I. E., Grupe, D., Brinkmann, W. P., & Räth, C. 2017, MNRAS, 464, 3955 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobban, A., Porquet, D., Reeves, J., et al. 2018, MNRAS, 474, 3237 [NASA ADS] [CrossRef] [Google Scholar]
- Marinucci, A., Matt, G., Miniutti, G., et al. 2014, ApJ, 787, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A., Edelson, R., & Vaughan, S. 2003, ApJ, 598, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Marinucci, A., Guainazzi, M., et al. 2014, MNRAS, 439, 3016 [NASA ADS] [CrossRef] [Google Scholar]
- Mehdipour, M., Branduardi-Raymont, G., Kaastra, J. S., et al. 2011, A&A, 534, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mehdipour, M., Kaastra, J. S., Kriss, G. A., et al. 2015, A&A, 575, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, K. D., & Yaqoob, T. 2009, MNRAS, 397, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., O’Neill, P. M., George, I. M., & Reeves, J. N. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Fabian, A. C., Reis, R. C., & Walton, D. J. 2011, MNRAS, 410, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Porquet, D., Reeves, J. N., et al. 2016, ApJ, 832, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Noda, H., Makishima, K., Yamada, S., et al. 2011, PASJ, 63, S925 [NASA ADS] [CrossRef] [Google Scholar]
- Nucita, A. A., Guainazzi, M., Longinotti, A. L., et al. 2010, A&A, 515, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmeri, P., Mendoza, C., Kallman, T. R., Bautista, M. A., & Meléndez, M. 2003, A&A, 410, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, M. L., Wilkins, D. R., Fabian, A. C., et al. 2014, MNRAS, 443, 1723 [NASA ADS] [CrossRef] [Google Scholar]
- Patrick, A. R., Reeves, J. N., Porquet, D., et al. 2011, MNRAS, 411, 2353 [NASA ADS] [CrossRef] [Google Scholar]
- Patrick, A. R., Reeves, J. N., Porquet, D., et al. 2012, MNRAS, 426, 2522 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P. O., Merloni, A., Fabian, A., Haardt, F., & Gallo, E. 2001, MNRAS, 328, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porquet, D., Reeves, J. N., O’Brien, P., & Brinkmann, W. 2004, A&A, 422, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reeves, J. N., Porquet, D., Braito, V., et al. 2013, ApJ, 776, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Porquet, D., Braito, V., et al. 2016, ApJ, 828, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S. 1997, MNRAS, 286, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., Fabian, A. C., Brenneman, L. W., et al. 2009, MNRAS, 397, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Harrison, F. A., Madsen, K. K., et al. 2013, Nature, 494, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Różańska, A., Malzac, J., Belmont, R., Czerny, B., & Petrucci, P.-O. 2015, A&A, 580, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schurch, N. J., Done, C., & Proga, D. 2009, ApJ, 694, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Soldi, S., Beckmann, V., Baumgartner, W. H., et al. 2014, A&A, 563, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steiner, J. F., García, J. A., Eikmann, W., et al. 2017, ApJ, 836, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, T. J., & Miller, L. 2009, A&ARv, 17, 47 [Google Scholar]
- Ursini, F., Boissay, R., Petrucci, P.-O., et al. 2015, A&A, 577, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ursini, F., Petrucci, P.-O., Matt, G., et al. 2016, MNRAS, 463, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Fabian, A. C., Ballantyne, D. R., et al. 2004, MNRAS, 351, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Risaliti, G., Harrison, F. A., et al. 2014, ApJ, 788, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Wandel, A., Peterson, B. M., & Malkan, M. A. 1999, ApJ, 526, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fabbiano, G., Elvis, M., et al. 2011, ApJ, 742, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, M., Elvis, M., Fabbiano, G., et al. 1987, ApJ, 315, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, D. R., & Fabian, A. C. 2012, MNRAS, 424, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, D. R., & Gallo, L. C. 2015, MNRAS, 448, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Q., & Gu, M. 2008, ApJ, 682, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., Done, C., Smith, D., & McNaron-Brown, K. 1995, ApJ, 438, L63 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Description of the relativistic reflection package relxill
Appendix A.1: Coronal geometry
The relxill models are characterized by the following parameters: − the photon index of the illuminating radiation (identical for both the intrinsic cut-off power-law and the relativistic reflection spectrum): Γ; − the black hole spin: a; − the disk inclination angle: θ; − the inner and outer radii of the disk: Rin and Rout, respectively; − the broken power-law disk emissivity index: q1 (for R<Rbr), q2 (for R>Rbr) and the radius (Rbr) where emissivity changes from q1 to q2; − the reflection fraction as defined in Dauser et al. (2016): ℛ; − the ionization parameter (erg cm s-1, in log units) at the surface of the disk (that is, the ratio of the X-ray flux to the gas density): log ξ; − the iron abundance relative to the solar value (here Grevesse & Sauval 1998): AFe; − the high-energy cut-off (identical for both the intrinsic power-law and the relativistic reflection spectrum): Ecut.
The relxill_ion model is similar to the relxill one but allows us to calculate the reflection from the disk with several zones of different ionization (log ξ ∝ R− index). The number of the zones (which has to be high enough for a good physical representation, here taken at 15) and the ionization gradient versus the radius can be specified directly in the model.
Appendix A.2: Lamppost geometry
The relxill_lp models are defined for the lamppost geometry. The parameters q1, q2, and Rbr are replaced by the height of the primary source h, and the reflection fraction value is self-consistently determined by the lamppost geometry (fixReflFrac=1).
The relxill_lp_ion model takes into account an ionization gradient of the accretion disk as for the relxill_ion model, while the relxill_lp_alpha model calculates self-consistently the radial dependence of the ionization from the irradiation of the disk, using a certain mass accretion rate (ṁ) and assuming the density profile of an α accretion disk (Shakura & Sunyaev 1973).
Appendix B: Reflection models for the four 2014 XMM-Newton/pn spectra
Simultaneous fit of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model 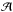 , n = 1015 cm-3) over the 0.3–10 keV energy range.
, n = 1015 cm-3) over the 0.3–10 keV energy range.
Table B.1 reports the spectral fits of the four 2014 XMM-Newton/pn spectra using the relxill models (see Sect. ).
Appendix C: Reflection modeling for the X-ray broadband spectra in 2014 March 22
Appendix C.1: Investigation of possible difference between the observed and incident photon indices
Following the results from Fürst et al. (2015) for the X-ray binary GX 339-4 (in low-luminosity, hard states), we then investigate if the inability of the relativistic reflection models to account for the broadband spectrum could be explained by a moderate difference in the spectral power-law indices. For GX 339–4 a ΔΓ ~ 0.3 were found10.
For the coronal geometry, we allow the blurred reflector to see a different continuum (Γ) with respect to the primary one. Since in the relxill model the intrinsic continuum is included in the model, not enabling us to have a different continuum shape for the direct and the reflected one, we modify the baseline model  as tbnew×(cutoffpl + relxill + 3 zgaussians), with the reflection fraction of the relxill model set to negative values to allow only the reflection component to be returned. cutoffpl is a power-law with a high-energy exponential cut-off. The fit statistic improves significantly with Δχ2 ~ −287 for only one additional parameter. However, this would mean an unlikely scenario with very different continua with ΔΓ ~ 1.0. We then investigate a scenario with two relativistic reflection models with different continuum shapes. This improves significantly the fit statistic compared to the single reflection component, with Δχ2 ~ 176 for three additional parameters. We find ΔΓ ~ 0.4, but a hard X-ray excess residual is still present above 35 keV.
as tbnew×(cutoffpl + relxill + 3 zgaussians), with the reflection fraction of the relxill model set to negative values to allow only the reflection component to be returned. cutoffpl is a power-law with a high-energy exponential cut-off. The fit statistic improves significantly with Δχ2 ~ −287 for only one additional parameter. However, this would mean an unlikely scenario with very different continua with ΔΓ ~ 1.0. We then investigate a scenario with two relativistic reflection models with different continuum shapes. This improves significantly the fit statistic compared to the single reflection component, with Δχ2 ~ 176 for three additional parameters. We find ΔΓ ~ 0.4, but a hard X-ray excess residual is still present above 35 keV.
We perform the same tests as above assuming a lamppost geometry, but we are unable to find satisfactory fits, even considering a vertically extended primary continuum source on the rotation axis (relxill_lp_ext⊗xillver) or a moving continuum source (relxilllp_velo).
Of course in all above fits, the Fe Kα red and blue residuals are still present.
Appendix C.2: High-density reflection modeling
The reflection models used in this work are calculated for a density of 1015 cm-3, for which it is assumed that the ionization state of the gas is identical for a given ξ value. But, as reported very recently by García et al. (2016), higher densities “are most relevant for low mass accreting black holes and when the coronal fraction is high”. Therefore, they computed the reflected spectra for densities larger than the commonly assumed density of 1015 cm-3, that is, up to n = 1019 cm-3. They showed that, for such higher density models, a very significant increase in the continuum flux at energies below about 2 keV occurs due to a large increase of thermal emission at soft X-ray energies. In other words, a high-density accretion disk leads to a larger soft excess compared to lower-density disks (such as 1015 cm-3). Therefore, since such a high density may be appropriate for Ark 120, a full grid of reflection models for n = 1019 cm-3 with high-energy cut-off fixed at 1000 keV has been produced (J. Garcia, priv. comm.). We apply this high-density model to the 2014 March 22 XMM-Newton/pn and NuSTAR spectra, for a coronal geometry. We find an unsatisfactory fit of the X-ray broadband energy (χ2/d.o.f. = 2513.3/2058; χred = 1.22). A weaker – though still significant – hard X-ray excess is found since a harder photon power-law index (Γ = 1.76 ± 0.01) can produce a larger soft excess emission, while a soft photon index is required for lower disk density (Γ = 2.22 ± 0.01, see Table 6). In addition, there are still significant model/data deviations below about 1 keV and in the Fe Kα energy range (see Fig. C.1). In conclusion, even a high-density disk cannot reproduce the broadband X-ray spectrum.
 |
Fig. C.1 Fit over the 0.3–79 keV energy range of the 2014 March 22 XMM-Newton/pn and NuSTAR data with a relativistic reflection baseline model using relxill (model |
All Tables
Observation log of the data analyzed in this work from the 2014 Ark 120 observational campaign.
Simultaneous fit of the four 2014XMM-Newton/pn spectra with the baseline relativistic reflection model (model  ) over the 3–10 keV energy range.
) over the 3–10 keV energy range.
Simultaneous fit of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model  ) over the 0.3–10 keV energy range.
) over the 0.3–10 keV energy range.
Simultaneous fit of the four 2014 XMM-Newton/pn data with the baseline Comptonization model with Comptt (model ℬ, Col. 2) over the 0.3–10 keV energy range.
Simultaneous XMM-Newton/pn and NuSTAR spectral fit of the 2014 March 22 observation with the relativistic reflection model above 3 keV (model  ).
).
Simultaneous XMM-Newton/pn and NuSTAR spectral fit of the 2014 March 22 observation with the relativistic reflection model (model  ) over the broad 0.3–79 keV energy range.
) over the broad 0.3–79 keV energy range.
Simultaneous fit of the 2014 March 22 XMM-Newton/pn and NuSTAR spectra over the 0.3–79 keV energy range with model  , which combines Comptonization and relativistic reflection contributions.
, which combines Comptonization and relativistic reflection contributions.
Simultaneous fit of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model 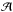 , n = 1015 cm-3) over the 0.3–10 keV energy range.
, n = 1015 cm-3) over the 0.3–10 keV energy range.
All Figures
 |
Fig. 1 Data/model ratio of the four 2014 XMM-Newton/pn spectra of Ark 120 fitted with a Galactic absorbed power-law continuum model over the 3–5 keV energy range, and then extrapolated over the 0.3–10 keV energy range. Black: March 18, red: March 20, green: March 22, and blue: March 24. Top panel: 0.3–10 keV energy range. Bottom panel: zoom on the Fe Kα complex. |
| In the text | |
 |
Fig. 2 Extrapolation down to 0.3 keV of the fit over the 3–10 keV energy range of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model |
| In the text | |
 |
Fig. 3 Data/model ratio of the fit over the 0.3–10 keV energy range of the four 2014 XMM-Newton/pn spectra with the baseline relativistic reflection model (model |
| In the text | |
 |
Fig. 4 Fit over the 0.3–10 keV energy range of the four 2014 XMM-Newton/pn spectra with the baseline Comptonization model (model ℬ). The fit parameters are reported in Table 4. Black: March 18, red: March 20, green: March 22, and blue: March 24. Top panel: data and data/model ratio. Bottom panel: unfolded spectra where the contributions of the model components are displayed. The following color code for the emission components (dot-dashed curves) is used: magenta for the soft Comptonization (comptt), blue for the cut-off power-law (hot Comptonization). For clarity purposes, we have not displayed the Fe K line components. |
| In the text | |
 |
Fig. 5 2D contour plot of the plasma temperature (kTe in keV) versus the plasma optical depth for the third XMM-Newton observation inferred from the baseline Comptonization model (model ℬ). |
| In the text | |
 |
Fig. 6 Data/model ratio of the NuSTAR spectra of Ark 120 obtained on 2014 March 22, fitted with a Galactic absorbed power-law continuum model (Γ = 1.92 ± 0.02) over the 3.5–10 keV energy range (excluding the 5.5–7.5 keV energy range, that is, the Fe K complex) and then extrapolated over the 3.5–79 keV energy range. In addition to the prominent Fe Kα complex, a significant hard X-ray excess is present. Red: NuSTAR FPMA, and green: NuSTAR FPMB. |
| In the text | |
 |
Fig. 7 Simultaneous XMM-Newton/pn and NuSTAR spectra of Ark 120 obtained on 2014 March 22 fitted with model |
| In the text | |
 |
Fig. 8 Simultaneous XMM-Newton/pn and NuSTAR spectra of Ark 120 obtained on 2014 March 22 fitted with model |
| In the text | |
 |
Fig. 9 Fit over the 0.3–79 keV energy range of the 2014 March 22 XMM-Newton/pn and NuSTAR data with model |
| In the text | |
 |
Fig. C.1 Fit over the 0.3–79 keV energy range of the 2014 March 22 XMM-Newton/pn and NuSTAR data with a relativistic reflection baseline model using relxill (model |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


