| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 6 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201730462 | |
| Published online | 22 December 2017 | |
The distribution of stars around the Milky Way’s central black hole
III. Comparison with simulations
1
School of Mathematics and Physics, University of Queensland,
St. Lucia,
QLD
4072, Australia
e-mail: h.baumgardt@uq.edu.au
2
Institute of Space Sciences (ICE, CSIC) & Institut d’Estudis Espacials de Catalunya (IEEC) at Campus UAB,
Carrer de Can Magrans s/n,
08193
Barcelona, Spain
e-mail: pau@ice.cat
3
Institute of Applied Mathematics, Academy of Mathematics and Systems Science, CAS,
Beijing
100190, PR China
4
Kavli Institute for Astronomy and Astrophysics,
Beijing
100871, PR China
5
Zentrum für Astronomie und Astrophysik, TU Berlin,
Hardenbergstraße 36,
10623
Berlin, Germany
6
Instituto de Astrofísica de Andalucía,
Glorieta de la Astronomía s/n,
18008
Granada, Spain
Received:
19
January
2017
Accepted:
11
October
2017
Context. The distribution of stars around a massive black hole (MBH) has been addressed in stellar dynamics for the last four decades by a number of authors. Because of its proximity, the centre of the Milky Way is the only observational test case where the stellar distribution can be accurately tested. Past observational work indicated that the brightest giants in the Galactic centre (GC) may show a density deficit around the central black hole, not a cusp-like distribution, while we theoretically expect the presence of a stellar cusp.
Aims. We here present a solution to this long-standing problem.
Methods. We performed direct-summation N-body simulations of star clusters around massive black holes and compared the results of our simulations with new observational data of the GC’s nuclear cluster.
Results. We find that after a Hubble time, the distribution of bright stars as well as the diffuse light follow power-law distributions in projection with slopes of Γ ≈ 0.3 in our simulations. This is in excellent agreement with what is seen in star counts and in the distribution of the diffuse stellar light extracted from adaptive-optics (AO) assisted near-infrared observations of the GC.
Conclusions. Our simulations also confirm that there exists a missing giant star population within a projected radius of a few arcsec around Sgr A*. Such a depletion of giant stars in the innermost 0.1 pc could be explained by a previously present gaseous disc and collisions, which means that a stellar cusp would also be present at the innermost radii, but in the form of degenerate compact cores.
Key words: methods: numerical / Hertzsprung–Russell and C-M diagrams / stars: kinematics and dynamics / Galaxy: centre / Galaxy: nucleus
© ESO, 2017
1. Introduction
The Galactic centre (GC) is the nucleus closest to us, offering the unique possibility of studying the interaction between a supermassive black hole (SMBH) and its surrounding star cluster using individual resolved stars. Adaptive-optics (AO) assisted near-infrared photometric and spectroscopic studies of the stars within about 1 pc of the SMBH have shown that the surface density of massive early-type stars is rising steeply towards Sagittarius A* (Sgr A*, the electromagnetic manifestation of the SMBH), while the density distribution of bright late-type stars down to the apparent median luminosity of the red clump (KS ≈ 15.5) – and therefore mostly old and lower mass stars – rises much more slowly and may even be flat within a few 0.1 pc of the black hole (Schödel et al. 2007; Do et al. 2009).
Typically, the projected stellar surface number density (and equivalently the 3D density) is described by a power law of the form Σ (R) ∝ RΓ, where R is the distance from Sgr A*. Buchholz et al. (2009) for example found that the surface density distribution within a projected radius R = 6′′ of Sgr A* can be described with an exponent Γ = 0.2 ± 0.1, which would correspond to a decreasing density within the innermost few arcseconds (1 arcsec corresponds to approximately 0.04 pc at the distance of the GC).
Since the relaxation time at the GC is of order of a Hubble time, old stars should have had enough time to settle into an equilibrium distribution around the black hole. Bahcall & Wolf (1976) found that a single-mass stellar population should settle into a power-law cusp ρ (r) ~ r-γ with a slope of γ = 1.75 within the influence radius of the central supermassive black hole, much steeper than what is observed. This has led to the so-called “missing giant star” problem. Moreover, the impact goes beyond stellar dynamics and the GC because these massive stars close to the MBH are the precursors of compact objects, which might eventually become a source of gravitational waves for a space-borne observatory such as LISA or Taiji (Amaro-Seoane et al. 2012; 2013; Gong et al. 2015). The gradual inspiral of a stellar-mass black hole has been coined an “extreme-mass ratio inspiral”, and it accumulates hundreds of thousands of cycles in the detector band, with impressive implications in fundamental physics and astrophysics (Amaro-Seoane et al. 2007; 2015; Amaro-Seoane 2012).
A number of works have tried to explain this conundrum with different ideas, which follow one of three possibilities. When Genzel et al. (1996) first discovered missing RGB stars, they proposed that this might be due to stellar collisions depleting giant stars in the innermost parts through the high stellar densities that are reached near the SMBH. Later, Davies et al. (1998), Alexander (1999), Bailey & Davies (1999), and Dale et al. (2009) addressed this idea in detail and came to the conclusion that it can only explain the absence of the brightest and most extended giant stars. A different suggested possibility to explain the missing stars is that our GC does not only have one, but a binary of two massive black holes. This hypothesised binary could indeed carve a core into the stellar distribution through three-body interactions, as shown by a number of authors (Baumgardt et al. 2006; Portegies Zwart et al. 2006; Matsubayashi et al. 2007; Löckmann & Baumgardt 2008; Gualandris & Merritt 2012). Nonetheless, the mass of the secondary needs to be of the order of 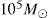 to explain the observed core. Such a massive secondary black hole would require the Milky Way to have experienced a major merger relatively recently, which is excluded by observations (see Hansen & Milosavljević 2003; Yu & Tremaine 2003; Chen & Liu 2013). Moreover, the existence of such a massive secondary black hole is largely ruled out from a number of other considerations, for instance, constraints on the proper motion of Sgr A* from radio interferometry (see Gualandris & Merritt 2009). A number of inspiraling smaller-mass black holes can also create a shallow stellar density profile in the centre, which would relax the major merger requirement, as has been shown by Mastrobuono-Battisti et al. (2014). It has also been put forward that a star cluster falling towards the GC could increase the density profile outside of 10′′ , so that within this distance the profile would be like a core (Kim & Morris 2003; Ernst et al. 2009; Antonini et al. 2012; Antonini 2014). However, mass segregation would rebuild a steeper profile in as fast as a quarter of the relaxation time (as shown by Preto & Amaro-Seoane 2010; Amaro-Seoane & Preto 2011). This requirement would hence need a steady inflow of clusters to maintain a weak cusp profile in the centre. Finally, Merritt (2010) and Antonini (2014) found that if the nuclear cluster in the GC formed with an extended enough initial core profile, the current stellar distribution would still not be dynamically relaxed. While this solution is possible, it requires fine-tuning in the initial conditions to produce the density distribution seen in the GC. Amaro-Seoane & Chen (2014) proposed that the discs of young stars observed at the GC (Paumard et al. 2006) are connected to the missing bright giants: the precursor gaseous discmust have gone through a fragmentation phase that produced dense enough clumps to ensure an efficient removal of the outer layers of the giants through collisions, rendering them invisible to observations. Their degenerate cores would nonetheless populate the same area of phase space where the missing bright giants should be. Kieffer & Bogdanović (2016) recently showed that in order to be viable, this scenario requires the total mass of the fragmenting disc to have been several orders of magnitude higher than that of the early-type stars in the stellar discs in the GC.
to explain the observed core. Such a massive secondary black hole would require the Milky Way to have experienced a major merger relatively recently, which is excluded by observations (see Hansen & Milosavljević 2003; Yu & Tremaine 2003; Chen & Liu 2013). Moreover, the existence of such a massive secondary black hole is largely ruled out from a number of other considerations, for instance, constraints on the proper motion of Sgr A* from radio interferometry (see Gualandris & Merritt 2009). A number of inspiraling smaller-mass black holes can also create a shallow stellar density profile in the centre, which would relax the major merger requirement, as has been shown by Mastrobuono-Battisti et al. (2014). It has also been put forward that a star cluster falling towards the GC could increase the density profile outside of 10′′ , so that within this distance the profile would be like a core (Kim & Morris 2003; Ernst et al. 2009; Antonini et al. 2012; Antonini 2014). However, mass segregation would rebuild a steeper profile in as fast as a quarter of the relaxation time (as shown by Preto & Amaro-Seoane 2010; Amaro-Seoane & Preto 2011). This requirement would hence need a steady inflow of clusters to maintain a weak cusp profile in the centre. Finally, Merritt (2010) and Antonini (2014) found that if the nuclear cluster in the GC formed with an extended enough initial core profile, the current stellar distribution would still not be dynamically relaxed. While this solution is possible, it requires fine-tuning in the initial conditions to produce the density distribution seen in the GC. Amaro-Seoane & Chen (2014) proposed that the discs of young stars observed at the GC (Paumard et al. 2006) are connected to the missing bright giants: the precursor gaseous discmust have gone through a fragmentation phase that produced dense enough clumps to ensure an efficient removal of the outer layers of the giants through collisions, rendering them invisible to observations. Their degenerate cores would nonetheless populate the same area of phase space where the missing bright giants should be. Kieffer & Bogdanović (2016) recently showed that in order to be viable, this scenario requires the total mass of the fragmenting disc to have been several orders of magnitude higher than that of the early-type stars in the stellar discs in the GC.
Owing to the extreme extinction and source crowding towards the GC, observational studies are complex, even with the power of AO assisted 10 m class telescopes. In particular, the spectroscopic identification of stars is limited to bright giants and massive young stars, while the crowding makes it almost impossible to detect main-sequence stars lower than two solar masses. Gallego Cano et al. (2018) and Schödel et al. (2018) have revisited the observational data with improved methods. On the one hand, they were able to push the completeness of the star counts one magnitude deeper than in previous studies. This means that not only bright giants down to the red clump (RC), but also fainter giants and sub-giants are included in the star counts. Thus we now have access to two stellar tracer populations, with different luminosities but similar masses, that can provide us with information on the structure of the nuclear star cluster (NSC). Furthermore, the authors also succeeded in deriving the surface brightness profile of the diffuse stellar light, which traces even fainter stars, probably sub-giants and main-sequence stars of 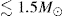 . The two new analyses provide fully consistent results. The spatial stellar density can be described by a power law with exponents between γ 1.15 to 1.40 inside 0.5 pc for three different tracers: resolved giant and sub-giant stars in the magnitude ranges 12.5 ≤ KS ≤ 16.0 and 17.5 ≤ KS ≤ 18.5 andthe diffuse light, which is created mainly by sub-giants and main-sequence stars. After combining the data on the central 1–2 pc with other measurements of the stellar distribution on scales 2–10 pc, the authors de-projected the surface density and determined a 3D power-law index γ between 1.15 to 1.40. For RC stars and brighter giants, Schödel et al. (2018) reproduced the findings of previous work, that is, a flattening of the stellar density distribution in the innermost 0.1–0.3 pc. The authors concluded that outside of this projected radius, the distribution of these stars is consistent with a stellar cusp, but that some process has probably altered the giant star distributions at smaller radii.
. The two new analyses provide fully consistent results. The spatial stellar density can be described by a power law with exponents between γ 1.15 to 1.40 inside 0.5 pc for three different tracers: resolved giant and sub-giant stars in the magnitude ranges 12.5 ≤ KS ≤ 16.0 and 17.5 ≤ KS ≤ 18.5 andthe diffuse light, which is created mainly by sub-giants and main-sequence stars. After combining the data on the central 1–2 pc with other measurements of the stellar distribution on scales 2–10 pc, the authors de-projected the surface density and determined a 3D power-law index γ between 1.15 to 1.40. For RC stars and brighter giants, Schödel et al. (2018) reproduced the findings of previous work, that is, a flattening of the stellar density distribution in the innermost 0.1–0.3 pc. The authors concluded that outside of this projected radius, the distribution of these stars is consistent with a stellar cusp, but that some process has probably altered the giant star distributions at smaller radii.
The masses of all tracer populations are very similar, between 1–2 M⊙. These stars can live for several Gyr and thus be old enough to be dynamically relaxed. If the faint stars and diffuse stellar light at the GC indeed trace an underlying old stellar population (of age ~ 109 to ~ 1010 yr), then the stellar cusp is surprisingly shallow. Here it becomes important to look at the theory in more detail. The steep power-law cusp solution found by Bahcall & Wolf (1976) only holds for a single-mass stellar population. If stars follow a distribution of masses, mass segregation causes stars of different masses to follow different density distributions with more massive components that have steeper central slopes (Bahcall & Wolf 1977; Baumgardt et al. 2004; Amaro-Seoane et al. 2004; Freitag et al. 2006). In particular, Alexander & Hopman (2009) and Preto & Amaro-Seoane (2010) independently derived the so-called “strong-mass segregation” solution for two stellar mass groups, which is more efficient than the solution expected from the theory of Bahcall & Wolf (1977), which is mathematically correct but physically inappropriate because of the number fractions they used.
Baumgardt et al. (2005) showed that in globular clusters containing intermediate-mass black holes, the surface density distribution of luminous stars can be described by a weak power-law cusp distribution, offering a new way to explain the missing-mass problem seen in the GC. However, their results cannot be directly applied to it, since in their simulations all stars formed at the same time, which is a valid assumption for a globular cluster, but not for the nuclear cluster at the centre of the Milky Way, where stars have formed continuously over a Hubble time (Pfuhl et al. 2011). In addition, while the GC has a relaxation time of the same order as its age, the star clusters in their simulations were simulated for about ten relaxation times.
In this paper we present results of direct N-body simulations aimed at studying the dynamics of the nuclear cluster in the Milky Way. In our simulations, we evolve a star cluster surrounding a central massive black hole over a Hubble time under the combined influence of two-body relaxation and continuous star formation. Our paper is organised as follows: in Sect. 2 we discuss our simulations and in Sect. 3 we compare the resulting distribution of stars with observations of the nuclear star cluster in the Galactic centre. Section 4 presents our conclusions.
2. Simulations
We have run N-body simulations of star clusters containing massive central black holes using the GPU enabled version of the collisional N-body code NBODY6 (Aarseth 1999; Nitadori & Aarseth 2012), and we followed the evolution of the star clusters under the combined influence of star formation, stellar evolution, and two-body relaxation. The mass distribution of stars in our simulations was given by a Kroupa (2001) mass function with lower and upper mass limits of 0.1 and 100 M⊙, respectively. This mass function is compatible with observations of the mass-to-light ratio of the nuclear cluster and the temperature and luminosity distribution of individual giant stars in the nuclear cluster (Löckmann et al. 2010; Pfuhl et al. 2015). Owing to the high escape velocity from the nuclear cluster, we assumed a 100% retention fraction for stellar-mass black holes and neutron stars upon their formation. We also assumed solar metallicity for the stars in our simulation, which is compatible with the average metallicity of stars in the GC (Ryde & Schultheis 2015; Do et al. 2015).
Because of the high computational cost of N-body simulations, we simulated clusters with smaller particle numbers but larger half-mass radius so that the relaxation time of the simulated clusters is the same as the relaxation time of the nuclear cluster in the GC. This approach is similar to the approach used by Baumgardt et al. (2003) to model the globular cluster G1 and Baumgardt (2017) to model Galactic globular clusters. It allows us to correctly model the effects of two-body relaxation, which is the main focus in this paper, but processes that do not occur on relaxation timescales like tidal disruption of stars cannot be modelled easily in scaled simulations. The nuclear cluster in the GC has a projected half-light radius of RhNC = 4.2 ± 0.4 pc and a mass of 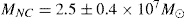 (Schödel et al. 2014). Using the definition of the half-mass relaxation time as given by Spitzer (1987) and assuming the 2D half-light radius to be 75% of the 3D half-light radius, this results in a half-light relaxation time of TRH ≈ 14 Gyr. We therefore used an initial projected half-mass radius of our simulated clusters of Rh = RhNC⋅(MNC∕MC)1∕3 = 26.9 pc, so that our simulated clusters have the same half-mass relaxation time as the nuclear cluster and evolve dynamically with the same rate per physical time. At the end of the simulations, we scaled our clusters down to a projected half-light radius of RhNC = 4.2 pc, so that we were able to directly compare with observational data. In total we performed three realisations using different random number seeds for each density profile and overlaid the results of five snapshots of each realisation centred on the MBH after scaling each cluster to the same half-mass radius.
(Schödel et al. 2014). Using the definition of the half-mass relaxation time as given by Spitzer (1987) and assuming the 2D half-light radius to be 75% of the 3D half-light radius, this results in a half-light relaxation time of TRH ≈ 14 Gyr. We therefore used an initial projected half-mass radius of our simulated clusters of Rh = RhNC⋅(MNC∕MC)1∕3 = 26.9 pc, so that our simulated clusters have the same half-mass relaxation time as the nuclear cluster and evolve dynamically with the same rate per physical time. At the end of the simulations, we scaled our clusters down to a projected half-light radius of RhNC = 4.2 pc, so that we were able to directly compare with observational data. In total we performed three realisations using different random number seeds for each density profile and overlaid the results of five snapshots of each realisation centred on the MBH after scaling each cluster to the same half-mass radius.
Pfuhl et al. (2011) found that most stars in the nuclear cluster are old, with about 80% of them having been born more than 5 Gyr ago. They also found that an exponentially decreasing star formation rate according to
 (1)
(1)
with a characteristic timescale τSFR = 5.5 Gyr matches the age distribution of old stars in the nuclear cluster. We therefore started our simulations with a star cluster containing N = 50 000 stars and an MBH that contained 15% of the cluster mass, similar to the mass ratio seen for the GC SMBH (see e.g. Genzel et al. 2010, and references therein). We then simulated the evolution of this cluster for 1 Gyr and added new stars to it after 1 Gyr with a rate given by Eq. (1). We evolved the new cluster for another Gyr before adding the next generation of stars and repeated this process until the cluster reached an age of T = 13 Gyr. Throughout the evolution, the mass ratio between the cluster and the central MBH was kept constant at 15%, that is, we assumed that the MBH grows at the same rate as the nuclear cluster. The new stars added to the simulation following a King (1966) model with dimensionless central potential of W0 = 5.0 initially. In order to study the influence of the initial density profile on the final results, we also ran simulations in which the initial density profiles had central potentials of W0 = 3.0 and W0 = 7.0, but found that the final slopes of the power-law profiles do not change by more than ΔΓ = ±0.1 in surface density, confirming that the GC nuclear star cluster is dynamically relaxed in its centre. When setting up the King (1966) models, we took the potential of the central black hole into account when calculating the stellar velocities. After 13 Gyr, we ended up with star clusters containing about ~255 000 stars and a final mass of 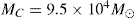 .
.
Figure 1 depicts a J KS vs. KS colour-magnitude diagram (CMD) of the stars in our simulation after T = 13 Gyr, calculated using the PARSEC isochrones (Bressan et al. 2012). In order to calculate the apparent KS band magnitudes,we assumed a distance of 8 kpc to the GC and a KS -band extinction of 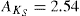 mag (Schödel et al. 2010) for all stars. The different generations of stars that were added to the star cluster during the simulation can clearly be distinguished in the CMD. In the following, we use stars with KS < 18.5 mag (shown in red) for the comparison with the number density profile of resolved stars from Gallego Cano et al. (2018). For the comparison with the diffuse light profile of Schödel et al. (2018), we used all stars fainter than this limit and summed their KS -band luminosities. With these limits, resolved stars have masses in the range
mag (Schödel et al. 2010) for all stars. The different generations of stars that were added to the star cluster during the simulation can clearly be distinguished in the CMD. In the following, we use stars with KS < 18.5 mag (shown in red) for the comparison with the number density profile of resolved stars from Gallego Cano et al. (2018). For the comparison with the diffuse light profile of Schödel et al. (2018), we used all stars fainter than this limit and summed their KS -band luminosities. With these limits, resolved stars have masses in the range 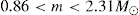 , while 90% of the diffuse light is created by stars with masses
, while 90% of the diffuse light is created by stars with masses 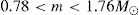 . On average,the resolved stars are about 0.25 M⊙ more massive than the brightest stars that contribute to the unresolved light.
. On average,the resolved stars are about 0.25 M⊙ more massive than the brightest stars that contribute to the unresolved light.
 |
Fig. 1 J KS CMD of the simulated nuclear clusters after 13 Gyr of evolution for a distance of 8 kpc to the GC and an average reddening of |
3. Results
Figure 2 shows the density distribution of different types of stars after 13 Gyr of evolution. Shown are the density distributions of stellar-mass black holes; giant stars, which we assume to be all stars with K-band luminosities KS < 18.5; upper main-sequence stars with masses between 0.6 and 0.8 M⊙ ; and lower main-sequence stars with masses between 0.1 and 0.3 M⊙ . For clarity we have shifted all curves vertically to separate the different curves from each other. We also scaled the final cluster to have a projected half-light radius of 4.2 pc to match the GC nuclear cluster. For this half-light radius, the influence radius of the central black hole, that is, the radius where the cumulated mass in stars becomes equal to the central black hole mass, is rBH = 2.8 pc. This value is close to the break radius seen in the surface density distributions of resolved stars and diffuse light as found by Gallego Cano et al. (2018) and Schödel et al. (2018) and depicted in Figs. 3 and 4.
Inside the influence radius, the density distribution of the differentstellar components can be well described by single-power-law distributions. Black holes and neutron stars follow a power-law distribution with the steepest slope of γ = 1.55, close to the theoretically predicted slope of γ = 1.75 for a single-mass stellar population around a massive black hole (Bahcall & Wolf 1976). Owing to mass segregation, all other components follow flatter density distributions. The slopes vary by only Δ γ = 0.16 between giant stars and the lowest-mass main-sequence stars, however. Overall, the power-law slopes of the different stellar mass groupsare flatter than what Baumgardt et al. (2004) found for a single-age stellar cluster with the same initial mass function after T = 12 Gyr of evolution (see their Fig. 7). This indicates that the GC starcluster is dynamically not yet completely relaxed because of its relatively long relaxation time (T ~ 14 Gyr). In addition, the continuous star formation reduces mass segregation between the different stellar components.
Because of the small amount of mass segregation, low-mass stars dominate the stellar mass profile for all radii outside 0.01 pc and the luminosity profile closely follows the mass profile in the nuclear cluster, that is, we do not predict a strong variation of the M ∕ L profile of the nuclear cluster with radius. When scaled to the GC, our simulations predict about ~ 300 stellar-mass black holes and a total mass of 7000 M⊙ in stars inside the central 0.1 pc. Our mass estimate is in good agreement with the approximate 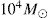 of total mass within this region that can be calculated with the Nuker model and the mass normalisations of Schödel et al. (2018), and it is also consistent with the upper limit of
of total mass within this region that can be calculated with the Nuker model and the mass normalisations of Schödel et al. (2018), and it is also consistent with the upper limit of 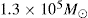 recently derived by Boehle et al. (2016). We note that these mass limits have been derived assuming a mass-to-light ratio that is independent of radius for the nuclear star cluster.
recently derived by Boehle et al. (2016). We note that these mass limits have been derived assuming a mass-to-light ratio that is independent of radius for the nuclear star cluster.
Figure 3 depicts the distribution of bright stars in the central parsec and compares it with the observed distribution of late-type giant stars within three different KS -band intervals as determined by Gallego Cano et al. (2018). In order to avoid uncertainties and systematic biases in mixing different observational data sets, we only depict the NACO data, that is, data in the radial range from 0.011 to 1 pc in Fig. 3. In order to increase the statistical significance of our results, we use all stars with KS < 18.5 in the simulations for the comparison with the observed distribution in the three magnitude intervals. This is justified since the observed stars are giant stars, which show only a small dependence of average mass and age with luminosity. Hence we expect the stars in the different magnitude bands to follow similar density distributions in our simulations. The observed and simulated density profiles agree very well with each other, the differences between the two profiles are usually less than 10% for all three magnitude intervals and are of the same order as the uncertainties of the observed profiles. The combined surface density distribution of the three simulations we have performed can be fitted by a power-law distribution Σ (R) ~ R-Γ with a slope Γ ~ 0.46 in the range 0.04 pc < R < 1.0 pc. This is in excellent agreement with the observed density distributions of bright stars, which have best-fitting slopes of Γ = 0.45 ± 0.01 for stars with 12.5 < KS < 16, Γ = 0.47 for stars with 16.5 < KS < 17.5 and Γ = 0.47 ± 0.02 for stars with 17.5 < KS < 18.5 over the same radial range (Gallego Cano et al. 2018). The observed data have almost the same slopes in the different bands, as expected from our simulations. While we compared our results only to the most recent results, we note that previous determinations of the surface density distribution of late-type giant stars (e.g. Schödel et al. 2007; Buchholz et al. 2009) are also compatible with our results, at least outside the central few arcsec. Stars with 12.5 < KS < 16 display a density deficit inside the innermost few arcsec, while their distribution at larger radii agrees with our simulations. This could indicate that some depletion process like giant star collisions or disc passages has altered their apparent distribution at the very centre.
Figure 4 compares the surface density profile of diffuse light in the GC from Schödel et al. (2018) with the results of our simulations. The black data points depict the KS -band surface luminosity derived by Schödel et al. (2018) after correction for differential extinction and combining their data inside 1.5 pc with the azimuthally averaged extinction-corrected near-infrared data by Fritz et al. (2016). The red lineshows the surface luminosity density of faint stars in our simulations. The simulated surface light distribution is well described by a single power-law profile with Σ (R) ~ R-0.37 inside 1.0 pc. This is close to the observed profile, which has Γ = 0.26 ± 0.02stat ± 0.05sys (Schödel et al. 2018). The slope predicted from our simulations is nearly the same as in the case of the resolved stars, again indicating that there was insufficient time for the nuclear cluster to develop significant mass segregation between main-sequence stars of different masses. The observed profile is slightly below our predicted data in the innermost few arcsec, but the differences are within the uncertainty with which we can determine the surface luminosity profile from our simulations and might therefore not be significant. In addition, the surface density of the diffuse light may show some systematic uncertainties at radii R = 1–2′′ because of the presence of very bright stars and the related difficulty of accurate point spread function subtraction in this region (see discussion in Schödel et al. 2018). We also see that our model somewhat over-predicts the surface density of diffuse light at radii R < 2′′ . However, the qualitative agreement, in particular the slope of the power-law at larger radii, is very good. There is a clear steepening of both the observed and simulated profiles beyond 20 arcsec, that is, outside the influence radius of the central black hole.
We conclude that the simulated and observed data agree excellently well with each other. In particular, the inferred power-law indices of the surface densities as well as the corresponding 3D power-law slopes (see caption of Fig. 2) agree well with the values estimated by Gallego Cano et al. (2018) and Schödel et al. (2018). The surface density profile of both resolved stars and diffuse light of the nuclear cluster are therefore entirely compatible with what we expect for a star cluster around a massive black hole that is evolving under the combined influence of dynamical relaxation and continuous star formation given the age and star formation history of the nuclear cluster.
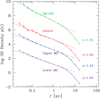 |
Fig. 2 Spatial density of different stellar components at the end ofour simulations. From top to bottom, we show the density distribution of black holes and neutron stars (green), giant stars with apparent magnitudes KS < 18.5 (red), upper main-sequence stars with masses 0.6 and 0.8 M⊙ (blue), and low-mass main-sequence stars with masses 0.1 and 0.3 M⊙ (orange). For clarity, curves are shifted vertically. Dashed lines show power-law density distributions ρ (r) ~ rγ fitted to the density distribution inside the influence radius of the black hole (rBH = 2.8 pc). Because of mass segregation, the slope steepens from γ = 1.04 for the lowest-mass main-sequence stars to γ = 1.55 for black holes. |
 |
Fig. 3 Surface density Σ (R) of old giant stars in the GC for three different KS -band intervals. The observed surface densities and associated error bars are taken from Gallego Cano et al. (2018) and are shown by circles for the different magnitude intervals. Black dashed lines and triangles show the profile that we obtain for giant stars at the end of our simulations. The profiles are in excellent agreement with each other in the different magnitude intervals, with the exception of the innermost density profile of stars in the magnitude interval 12.5 < KS < 16. |
 |
Fig. 4 KS -band surface luminosity profile Σ (R) of the diffuse light of the GC star cluster. The data points show the results of Schödel et al. (2018) corrected for differential extinction. Red line and data points show the surface luminosity profile of the simulated cluster, determined from all main-sequence stars fainter than KS > 18.5. Theoretical and observational profiles are in excellent agreement with each other outside the innermost few arcsec. |
4. Conclusions
The existence of stellar cusps in relaxed clusters around massive black holes is a long-standing prediction of theoretical stellar dynamics, but it has escaped confirmation for decades for several reasons, some observational and some theoretical. On the observational side, there is only a single target where the cusp theory can be tested with current instrumentation: the Galactic centre. Extragalactic nuclei are too far away for current instrumentation, and the existence of (intermediate-mass)massive black holes in globular clusters is still debated. However, the GC is not an easy target, and number counts and stellar classification both suffer from the very high and spatially highly variable interstellar extinction as well as from the extreme source crowding. Observational evidence has therefore been ambiguous for a long time. Recent new analyses, however, have found a stellar cusp around Sgr A*, with very consistent morphologies for different tracer populations that differ by several magnitudes in brightness. While the distribution of resolved giant stars with KS = 18 might be contaminated by young stars that formed within the last few 100 Myr, the contribution of such stars is much smaller for brighter giant stars with KS < 16 and the diffuse stellar light (Gallego Cano et al. 2018). The observations therefore imply the existence of a stellar cusp among the old and dynamically relaxed giant stars. This cusp has been found to be rather shallow, which is one of the reasons why it has so successfully escaped detection over a long time.
On the theoretical side, the main limitation was probably that the systems that were analysed were too simple. As we now know, the nuclear cluster around the SMBH at the GC is a highly complex system and has experienced many episodes of repeated star formation and/or cluster infall. As a result of the different physical and dynamical ages, stars that formed at different epochs will follow different radial distributions even if their masses are the same (Aharon & Perets 2014). This work presents an attempt to take the complex star formation history of the Milky Way’s NSC into account. As we have shown, two-body relaxation and repeated star formation across the lifetime of the Galaxy indeed results in a rather weak stellar cusp, consistent with the observations. It appears that this is the first time that theory and observations reach convergence on the question of the stellar cusp. Because we can be sure now that there is a power-law cusp around Sgr A*, the apparent deficit of giants within the innermost few arcsec of the central black hole also indicates that the latter do not trace the overall cluster structure. Either they do not have the same age structure as the fainter stars, or some process – such as a destruction of their envelopes via interactions with a fragmenting gaseous disc (the idea of Amaro-Seoane & Chen 2014) – has altered their apparent distribution.
The existence of a stellar cusp at the heart of the Milky Way implies that density cusps might also exist in many other galactic nuclei, especially smaller nuclei with relaxation times shorter than a Hubble time. This is of importance for gravitational wave astronomy because it means that extreme-mass ratio inspirals may be observed with significant frequency.
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. [614922]. PAS acknowledges support from the Ramón y Cajal Programme of the Ministry of Economy, Industry and Competitiveness of Spain. This work has been partially supported by the CAS President’s International Fellowship Initiative.
References
- Aarseth, S. J. 1999, PASP, 111, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Aharon, D., & Perets, H. B. 2014, ApJ, 799, 185 [Google Scholar]
- Alexander, T. 1999, ApJ, 527, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, T., & Hopman, C. 2009, ApJ, 697, 1861 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P. 2012, ArXiv e-prints [arXiv:1205.5240] [Google Scholar]
- Amaro-Seoane, P., & Chen, X. 2014, ApJ, 781, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., & Preto, M. 2011, Class. Quant. Grav., 28, 094017 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Freitag, M., & Spurzem, R. 2004, MNRAS, 352, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Gair, J. R., Freitag, M., et al. 2007, Class. Quant. Grav., 24, 113 [Google Scholar]
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2012, Class. Quant. Grav., 29, 124016 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2013, GW Notes, 6, 4 [Google Scholar]
- Amaro-Seoane, P., Gair, J. R., Pound, A., Hughes, S. A., & Sopuerta, C. F. 2015, J. Phys. Conf. Ser., 610, 012002 [CrossRef] [Google Scholar]
- Antonini, F. 2014, ApJ, 794, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Antonini, F., Capuzzo-Dolcetta, R., Mastrobuono-Battisti, A., & Merritt, D. 2012, ApJ, 750, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Wolf, R. A. 1976, ApJ, 209, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Wolf, R. A. 1977, ApJ, 216, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, V. C., & Davies, M. B. 1999, MNRAS, 308, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H. 2017, MNRAS, 464, 2174 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Makino, J., Hut, P., McMillan, S., & Portegies Zwart, S. 2003, ApJ, 582, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Makino, J., & Ebisuzaki, T. 2004, ApJ, 613, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Makino, J., & Hut, P. 2005, ApJ, 620, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Gualandris, A., & Portegies Zwart, S. 2006, MNRAS, 372, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Boehle, A., Ghez, A. M., Schödel, R., et al. 2016, ApJ, 830, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Buchholz, R. M., Schödel, R., & Eckart, A. 2009, A&A, 499, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, X., & Liu, F. K. 2013, ApJ, 762, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Davies, M. B., Church, R. P., & Freitag, M. 2009, MNRAS, 393, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, M. B., Blackwell, R., Bailey, V. C., & Sigurdsson, S. 1998, MNRAS, 301, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Do, T., Ghez, A. M., Morris, M. R., et al. 2009, ApJ, 703, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Do, T., Kerzendorf, W., Winsor, N., et al. 2015, ApJ, 809, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Ernst, A., Just, A., & Spurzem, R. 2009, MNRAS, 399, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Freitag, M., Amaro-Seoane, P., & Kalogera, V. 2006, ApJ, 649, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, R., Chatzopoulos, S., Gerhard, O., et al. 2016, ApJ, 821, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Gallego Cano, E., Schödel, R., Dong, H., et al. 2018, A&A, 609, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Thatte, N., Krabbe, A., Kroker, H., & Tacconi-Garman, L. E. 1996, ApJ, 472, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, X., Lau, Y.-K., Xu, S., et al. 2015, J. Phys. Conf. Ser., 610, 012011 [CrossRef] [Google Scholar]
- Gualandris, A., & Merritt, D. 2009, ApJ, 705, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Gualandris, A., & Merritt, D. 2012, ApJ, 744, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Milosavljević, M. 2003, ApJ, 593, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Kieffer, T. F., & Bogdanović, T. 2016, ApJ, 823, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S. S., & Morris, M. 2003, ApJ, 597, 312 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. R. 1966, AJ, 71, 64 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Löckmann, U., & Baumgardt, H. 2008, MNRAS, 384, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Löckmann, U., Baumgardt, H., & Kroupa, P. 2010, MNRAS, 402, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Mastrobuono-Battisti, A., Perets, H. B., & Loeb, A. 2014, ApJ, 796, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Matsubayashi,T., Makino, J., & Ebisuzaki, T. 2007, ApJ, 656, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D. 2010, ApJ, 718, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Nitadori, K., & Aarseth, S. J. 2012, MNRAS, 424, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Paumard, T., Genzel, R., Martins, F., et al. 2006, ApJ, 643, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Pfuhl, O., Fritz, T. K., Zilka, M., et al. 2011, ApJ, 741, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Pfuhl, O., Gillessen, S., Eisenhauer, F., et al. 2015, ApJ, 798, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., McMillan, S. L. W., et al. 2006, ApJ, 641, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Preto, M., & Amaro-Seoane, P. 2010, ApJ, 708, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Ryde, N., & Schultheis, M. 2015, A&A, 573, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schödel, R., Eckart, A., Alexander, T., et al. 2007, A&A, 469, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schödel, R., Najarro, F., Muzic, K., & Eckart, A. 2010, A&A, 511, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schödel, R., Feldmeier, A., Neumayer, N., Meyer, L., & Yelda, S. 2014, Class. Quant. Grav., 31, 244007 [NASA ADS] [CrossRef] [Google Scholar]
- Schödel, R., Gallego Cano, E., Dong, H., et al. 2018, A&A, 609, A27 [Google Scholar]
- Spitzer, L. 1987, Dynamical Evolution of Globular Clusters (Princeton, NJ: Princeton University Press) [Google Scholar]
- Yu, Q., & Tremaine, S. 2003, ApJ, 599, 1129 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 J KS CMD of the simulated nuclear clusters after 13 Gyr of evolution for a distance of 8 kpc to the GC and an average reddening of |
| In the text | |
 |
Fig. 2 Spatial density of different stellar components at the end ofour simulations. From top to bottom, we show the density distribution of black holes and neutron stars (green), giant stars with apparent magnitudes KS < 18.5 (red), upper main-sequence stars with masses 0.6 and 0.8 M⊙ (blue), and low-mass main-sequence stars with masses 0.1 and 0.3 M⊙ (orange). For clarity, curves are shifted vertically. Dashed lines show power-law density distributions ρ (r) ~ rγ fitted to the density distribution inside the influence radius of the black hole (rBH = 2.8 pc). Because of mass segregation, the slope steepens from γ = 1.04 for the lowest-mass main-sequence stars to γ = 1.55 for black holes. |
| In the text | |
 |
Fig. 3 Surface density Σ (R) of old giant stars in the GC for three different KS -band intervals. The observed surface densities and associated error bars are taken from Gallego Cano et al. (2018) and are shown by circles for the different magnitude intervals. Black dashed lines and triangles show the profile that we obtain for giant stars at the end of our simulations. The profiles are in excellent agreement with each other in the different magnitude intervals, with the exception of the innermost density profile of stars in the magnitude interval 12.5 < KS < 16. |
| In the text | |
 |
Fig. 4 KS -band surface luminosity profile Σ (R) of the diffuse light of the GC star cluster. The data points show the results of Schödel et al. (2018) corrected for differential extinction. Red line and data points show the surface luminosity profile of the simulated cluster, determined from all main-sequence stars fainter than KS > 18.5. Theoretical and observational profiles are in excellent agreement with each other outside the innermost few arcsec. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



