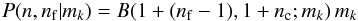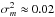| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201628568 | |
| Published online | 05 January 2018 | |
Determining open cluster membership
A Bayesian framework for quantitative member classification
Fairfield University, Department of Physics, Fairfield, CT 06824, USA
e-mail: jstott@fairfield.edu
Received: 21 March 2016
Accepted: 12 September 2016
Aims. My goal is to develop a quantitative algorithm for assessing open cluster membership probabilities. The algorithm is designed to work with single-epoch observations. In its simplest form, only one set of program images and one set of reference images are required.
Methods. The algorithm is based on a two-stage joint astrometric and photometric assessment of cluster membership probabilities. The probabilities were computed within a Bayesian framework using any available prior information. Where possible, the algorithm emphasizes simplicity over mathematical sophistication.
Results. The algorithm was implemented and tested against three observational fields using published survey data. M 67 and NGC 654 were selected as cluster examples while a third, cluster-free, field was used for the final test data set. The algorithm shows good quantitative agreement with the existing surveys and has a false-positive rate significantly lower than the astrometric or photometric methods used individually.
Key words: open clusters and associations: general / methods: data analysis / methods: statistical
© ESO, 2017
1. Introduction
Stellar formation begins with massive clouds of cold gas and dust. Under the force of gravity, these clouds collapse and fragment into smaller clumps. These clumps continue to collapse gravitationally and eventually form new stars (Hansen et al. 2004). As star formation accelerates, however, the light and heat of massive young stars quickly blows away the excess gas, leaving behind a gravitationally bound association of stars, which we call an open cluster. Open clusters are only weakly bound and evaporate on time scales of hundreds of millions to a few billion years, but until that happens they are one of our most important sources of knowledge about stellar evolution because we know that the stars in an open cluster all have about the same age and initial composition (Hansen et al. 2004). This makes open clusters attractive observational targets for stellar population and evolution studies.
2. Cluster membership
Before one can conduct a stellar population study, however, one must first identify which stars are actually members of the cluster and which stars are simply foreground or background stars that happen to appear in the same image. Especially in crowded galactic fields, the identification of cluster members is one of the most difficult aspects of the cluster study. There are two main approaches for identifying cluster membership: astrometric methods based on the position and motion of the stars and photometric methods derived from the color and brightness of stars.
2.1. Astrometric membership
The oldest approach to identifying cluster members is astrometric. Clusters are visible on the sky as an over-density of stars, as seen in Fig. 1, so the position of cluster stars must be spatially correlated – cluster stars are found near each other. Originally, cluster stars were identified by simply drawing a circle, centered on the cluster, that included the majority of the visible stars: stars within the circle were called cluster members and stars outside were not. In the modern era, numerical curve fitting has replaced hand-drawn circles, but still the goal is to separate the over-density from the background.
A more reliable way to identify clusters astrometrically is from their proper motions (or, equivalently, their radial velocities). Since clusters are gravitationally bound, all stars in a cluster share the same center-of-mass motion. If the proper motion of all the stars in a field are plotted, the cluster will form a distinct “clump” of co-moving stars. The most commonly used method for identifying cluster stars by their proper motions is based on Sanders (1971), which used maximum likelihood to infer cluster membership probabilities.
 |
Fig. 1 Open cluster NGC 609. The existence of a cluster in the center of the image cannot be doubted, but there is no obvious way to separate the cluster stars from the surrounding field stars. |
2.2. Photometric membership
What makes open clusters interesting, though, is not their spatial association but the fact that they formed out of the same gas cloud and thus represent a system of co-evolving stars. Because cluster stars follow the same evolutionary path, they can also be identified photometrically using color–color and color–magnitude diagrams. Photometric approaches all seek to somehow separate the cluster stars from the background stars using color and brightness information. Most commonly this is done using a two-step procedure. First, field stars are identified by comparing the program field (that contains the cluster) to a nearby reference image. Field stars are present in both color–magnitude diagrams while cluster stars are only in the program image. Often an empirical selection threshold is used to separate the two (Sarro et al. 2014). For faint or late-type stars, however, the field and cluster photometry overlap. In these cases some sort of statistical discrimination is required (Bica & Bonatto 2005; Bonatto & Bica 2007; Krone-Martins & Moitinho 2014). The classification can then be further refined by fitting a theoretical isochrone to the candidate cluster members and rejecting any final outliers.
2.3. Membership issues
Unfortunately, both of these approaches have deficiencies. Proper motions surveys, while generally reliable, are limited to nearby clusters and brighter stars (Krone-Martins & Moitinho 2014). Other astrometric methods (star counts, k-means, Voronoi tilings, etc.) are excellent for showing that a cluster is present, but they suffer from poor selectivity in that they do not distinguish between cluster members and field stars at the level of individual stars (Schmeja 2011).
Photometric studies, on the other hand, can have good selectivity but only after the background field stars have been scrubbed from the data set (Bonatto & Bica 2007; Sarro et al. 2014). In crowded fields it can be hard to separate the two: statistical subtraction methods may reject all but the strongest candidate stars and isochrones can become lost among the field stars at high extinctions or when looking for low-mass cluster members. Furthermore, purely photometric surveys ignore the spatial distribution of stars and can mis-identify as a cluster member any star in the general region of interest that happens to land near the best-fit isochrone.
2.4. Bayesian inference and estimation
Individually, astrometric and photometric selection methods struggle when pushed outside of their best-case scenarios. Some groups address this issue by adopting a two-step process: photometric and astrometric memberships are assessed independently and then stars which successfully pass both tests are accepted as cluster members. While mathematically justifiable, this approach is overly conservative and ends up rejecting many potential cluster members. What would be better is a single membership probability that properly incorporates photometric and spatial information at the same time.
In what follows, I will show that this is an example of a Bayesian inference problem where the final posterior probability density gives a single quantitative measure of the cluster probability, per star, incorporating all the available information and derived within a self-consistent statistical framework. Sarro et al. (2014) published a conceptually similar approach based on cluster proper motions; here I will focus specifically on the complementary case of single-epoch CCD observations. This approach assumes that two sets of measurements are available: a program field (with the putative cluster) and a nearby reference field that resembles the program field but does not contain any cluster stars. This could be either a subset of the same cluster image or a separate image; it makes no mathematical difference. Apart from the reference image, no additional information is required by the algorithm.
3. Bayesian cluster membership
My ultimate goal is to divide the stars in the image into two groups: field stars, which are randomly distributed across the image and follow the reference color–magnitude (CM) distribution, and cluster stars or non-field stars, which are spatially grouped and follow an unknown CM distribution. The final result will be the inferred star-by-star probability of belonging to the star cluster.
Before considering the full joint inference problem, I want to first show how to reinterpret conventional cluster membership approaches as Bayesian inference problems. I will then combine the two conventional approaches to derive the joint inference problem.
3.1. Photometric membership
Photometric cluster algorithms determine cluster membership based on the color and magnitude of stars as compared to some reference image. Thus, before making any measurements in the program field, we already know the distribution of field stars in one or more reference (CM) diagrams. The specific number of color–magnitude or color−color diagrams depends on the number of photometric filters used, but for simplicity I will limit the discussion to (B,V) photometry and a single color–magnitude plane. The CM distribution of field stars is then assumed to be the same for all images. This assumed uniformity also implies that the limiting magnitudes are the same for the program and the reference images. Under these conditions, the reference CM distribution becomes the prior probability for field stars in the program image.
The first task is to find the photometric distribution of field stars. Following Bica & Bonatto (2005), the photometric field star distribution is determined by dividing the color–magnitude space into bins (i,j) of width ΔC,i and height ΔM,j and counting the number of stars from the reference image that fall in each bin. There is no reason to require equal bin areas so long as the entire color–magnitude plane is covered.
The measurement, N(Ci,Mj), is the count of reference stars in the bin, but the count will not be equal to the true [population] distribution; there are always some associated statistical errors. To find cluster memberships, we need to know the probability of having a true background field star distribution, φi,j ≡ φ(Ci,Mj), given the measurements Ni,j (Loredo 1990). This probability is a type of posterior density, P(φi,j | Ni,j) and thus Bayes’ theorem gives its distribution. For every bin (i,j), 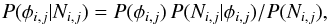 (1)where P(φi,j) is the prior probability for φi,j and P(Ni,j | φi,j) is the likelihood of counting Ni,j stars in that bin. Moreover, since every bin is an independent count, the probabilities are separable – we can treat each bin as an independent estimation problem. Because the equations will be the same for every bin, I will now drop the i,j subscripts except when needed for clarity.
(1)where P(φi,j) is the prior probability for φi,j and P(Ni,j | φi,j) is the likelihood of counting Ni,j stars in that bin. Moreover, since every bin is an independent count, the probabilities are separable – we can treat each bin as an independent estimation problem. Because the equations will be the same for every bin, I will now drop the i,j subscripts except when needed for clarity.
As a counting process, the natural distribution to describe the likelihood of counting a given number of stars is a Poisson distribution
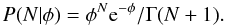 Nothing is known about φ before the measurement, so it must be assigned an uninformative prior. As a Poisson rate parameter, the Jeffreys’ prior for φ,
Nothing is known about φ before the measurement, so it must be assigned an uninformative prior. As a Poisson rate parameter, the Jeffreys’ prior for φ, 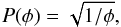 (2)is the least-informative prior (Jeffreys 1945). By least-informative, here and below, I mean that this is the prior which imposes the weakest prior assumptions and allows the data to determine the posterior to the maximum extent possible (as proven by Bernardo 1979; Berger et al. 2009, in their work on reference priors).
(2)is the least-informative prior (Jeffreys 1945). By least-informative, here and below, I mean that this is the prior which imposes the weakest prior assumptions and allows the data to determine the posterior to the maximum extent possible (as proven by Bernardo 1979; Berger et al. 2009, in their work on reference priors).
The marginal likelihood is then found by integrating over all possible background rates 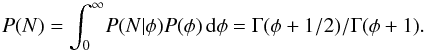 (3)Substituting Eq. (3)back into Eq. (1)gives the posterior density for the field distribution
(3)Substituting Eq. (3)back into Eq. (1)gives the posterior density for the field distribution 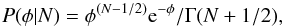 (4)which is equal to a gamma distribution with α = N + 1/2 and β = 1.
(4)which is equal to a gamma distribution with α = N + 1/2 and β = 1.
Now that we know the probability density for φ in terms of the measured reference image counts, the next step is to consider the program stars. First, the program data must be binned using the same bins as the reference data. Let ni,j be the number of program stars in the bin (i,j). Next, define mi,j to be the probability that any given program star in the bin (i,j) is member of the set of field stars (so the cluster probabilities will be 1−mi,j). These probabilities, together with the field star density φ, are the unknown parameters. Finally, the prior information is the counts of stars from the reference image, N. The initial posterior density for the m is found from Bayes’ theorem, 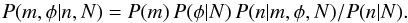 (5)
(5)
 |
Fig. 2 color–magnitude diagrams of the M67 reference (green) and program (blue) fields. The boxes show the adaptively sized bins used to calculate the photometric distribution. The reference field is significantly larger than the program field and thus has more stars, but otherwise the distributions look very similar to the eye. |
The prior for φ is given by Eq. (4). The prior for m represents whatever initial knowledge we have of the cluster probabilities. Since we have no such information to start, their prior is an uninformed uniform distribution,
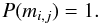 The likelihood will be easier to analyze if I introduce a new variable: nf, the actual number of field stars in a bin. For notational convenience, also define nc ≡ n−nf to be the actual number of cluster stars. The virtue of adding the variable nf is that now the likelihood can be factored into three separate parts. The first part gives the likelihood of having nf field stars given a background rate φ. This will be a Poisson distribution
The likelihood will be easier to analyze if I introduce a new variable: nf, the actual number of field stars in a bin. For notational convenience, also define nc ≡ n−nf to be the actual number of cluster stars. The virtue of adding the variable nf is that now the likelihood can be factored into three separate parts. The first part gives the likelihood of having nf field stars given a background rate φ. This will be a Poisson distribution 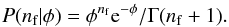 (6)This assumes that the total areas of the reference and program images are the same. If they differ, there will be proportionally more or fewer field stars in each bin and the rate φ must be scaled by the ratio of the areas, φ′ = φAimg/Aref. The second part of the likelihood gives the probability of finding nc cluster stars given an unknown cluster rate ψ. Again, this is a Poisson distribution
(6)This assumes that the total areas of the reference and program images are the same. If they differ, there will be proportionally more or fewer field stars in each bin and the rate φ must be scaled by the ratio of the areas, φ′ = φAimg/Aref. The second part of the likelihood gives the probability of finding nc cluster stars given an unknown cluster rate ψ. Again, this is a Poisson distribution 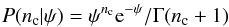 (7)and the prior for the rate ψ will be another Jeffreys’ prior for a Poisson rate
(7)and the prior for the rate ψ will be another Jeffreys’ prior for a Poisson rate 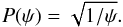 (8)The third term in the likelihood relates the division of n total stars into nf field and nc cluster stars given a field probability per star of m. This partitioning follows a binomial distribution
(8)The third term in the likelihood relates the division of n total stars into nf field and nc cluster stars given a field probability per star of m. This partitioning follows a binomial distribution 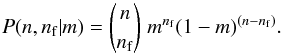 (9)Combining the three parts, Eqs. (6)–(9), gives me an initial likelihood in terms of n, nf, and ψ,
(9)Combining the three parts, Eqs. (6)–(9), gives me an initial likelihood in terms of n, nf, and ψ, 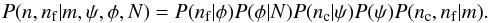 (10)The variable nf, however, is not a real measurement and the rates ψ and φ are unknown, so these cannot appear in the final likelihood. To eliminate them, we marginalize the variables by summing over the nf and integrating out the ψ and φ,
(10)The variable nf, however, is not a real measurement and the rates ψ and φ are unknown, so these cannot appear in the final likelihood. To eliminate them, we marginalize the variables by summing over the nf and integrating out the ψ and φ, ![\begin{eqnarray*} P(n|m,N) & = & \sum_{n_{\rm f}=0}^n\left[\vphantom{\int}P(n_{\rm c},n_{\rm f}|m) \right. \\ & & \times \int_0^\infty\! P(n_{\rm c}|\psi) P(\psi) \,\mathrm{d}\psi \int_0^\infty\! P(n_{\rm f}|\phi) P(\phi|N) \,\mathrm{d}\phi \left.\vphantom{\int}\right]. \end{eqnarray*}](/articles/aa/full_html/2018/01/aa28568-16/aa28568-16-eq42.png) The two integrals have exact solutions:
The two integrals have exact solutions: 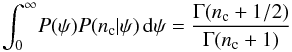 (11)and
(11)and 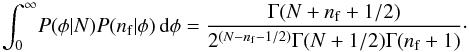 (12)The summation over nf could be simplified and written in terms of hypergeometric functions, but a numerical solution is more practical.
(12)The summation over nf could be simplified and written in terms of hypergeometric functions, but a numerical solution is more practical.
Substituting Eqs. (11), (12)back into Eq. (5)gives the marginalized posterior density 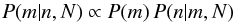 (13)from which we can estimate the membership probabilities for each bin,
(13)from which we can estimate the membership probabilities for each bin,
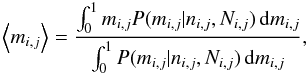 and any other desired moments of the distribution.
and any other desired moments of the distribution.
3.2. Astrometric membership
Astrometric cluster membership is determined from the positions of stars on a CCD image. As with the photometric case, we have some general a priori knowledge about the astrometric program data. First, there is a reference image so we know the average density of field stars (number of stars per unit solid angle), which we assume is uniform and constant. Second, the program image has a spatial structure: the field stars should be scattered randomly across the image while the cluster stars should be localized to a portion of the image.
As with the photometric inference, the first step is to estimate the true density of field stars. The reference image has some number of stars, Nref, scattered across an area of Aref, which gives a measured background density of 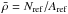 . As with the photometric case, this measured rate has an associated statistical error. The derivation of the astrometric rate probability is the same as the photometric derivation, with the analogous solution
. As with the photometric case, this measured rate has an associated statistical error. The derivation of the astrometric rate probability is the same as the photometric derivation, with the analogous solution 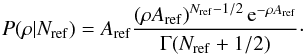 (14)As it was in the photometric case, this too is a gamma distribution for ρ with α = Nref + 1/2 and β = 1 /Aref.
(14)As it was in the photometric case, this too is a gamma distribution for ρ with α = Nref + 1/2 and β = 1 /Aref.
Open clusters appear on the sky as localized over-densities of stars. The program image, then, must be made up of stars from two sources: background stars that are uniformly distributed with a density ρ and cluster stars that have a non-uniform spatial density F(x,y). While any number of approaches exist for separating the two stellar populations, the simplest is to bin the data based on their positions; the more stars counted above the expected background rate, the more likely the stars in the bin are to be cluster stars.
The first task is to quantify the prior information about the counts. As with the photometric case, we have no advance knowledge of the membership probabilities, so their prior is the an uninformative constant, P(mi,j) = 1. For convenience, I will use vector notation to indicate the values at every bin
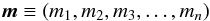 so the P(mi,j) can be written compactly as
so the P(mi,j) can be written compactly as
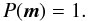 Next, we know that the density of background stars is the same as the density of the reference image. Thus, we have an informative prior for ρ, P(ρ | Nref), given by Eq. (14). The last piece of prior information we have is that the cluster stars are spatially localized with some distribution F(x,y). To make this concrete, we must decide what shape to use to model the distribution. While there are a variety of distributions available (King, Lorentzian, Moffat, etc.) the simplest choice is the symmetric Gaussian distribution
Next, we know that the density of background stars is the same as the density of the reference image. Thus, we have an informative prior for ρ, P(ρ | Nref), given by Eq. (14). The last piece of prior information we have is that the cluster stars are spatially localized with some distribution F(x,y). To make this concrete, we must decide what shape to use to model the distribution. While there are a variety of distributions available (King, Lorentzian, Moffat, etc.) the simplest choice is the symmetric Gaussian distribution 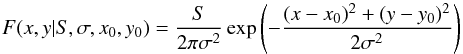 (15)which has four free parameters: S, σ, x0, and y0. The four parameters are independent, so the prior for the model distribution decomposes into a product
(15)which has four free parameters: S, σ, x0, and y0. The four parameters are independent, so the prior for the model distribution decomposes into a product
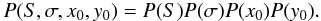 As there is no a priori information available about the cluster stars, all four parameters should have uninformative priors. The uninformed prior for the width of a Gaussian distribution is the Jeffreys’ prior, 1 /σ, so
As there is no a priori information available about the cluster stars, all four parameters should have uninformative priors. The uninformed prior for the width of a Gaussian distribution is the Jeffreys’ prior, 1 /σ, so 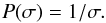 (16)S, the number of cluster stars per unit area, acts like the rate term of a Poisson distribution, so its uniformed prior is
(16)S, the number of cluster stars per unit area, acts like the rate term of a Poisson distribution, so its uniformed prior is 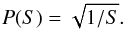 (17)The cluster centers (x0,y0) are positional parameters, so their prior probabilities are uniformly distributed across the image,
(17)The cluster centers (x0,y0) are positional parameters, so their prior probabilities are uniformly distributed across the image, 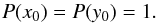 (18)The likelihood, P(n | m,S,σ,x0,y0,ρ,Nref) tells us how likely we are to have n stars in the bins given a background density ρ, a cluster density model F(x,y | S,σ,x0,y0), and the background probabilities m. For clarity, allow me to reparameterize the likelihood using two new variables: let b ≡ ρa be the expected number of background stars given bins of area a and let
(18)The likelihood, P(n | m,S,σ,x0,y0,ρ,Nref) tells us how likely we are to have n stars in the bins given a background density ρ, a cluster density model F(x,y | S,σ,x0,y0), and the background probabilities m. For clarity, allow me to reparameterize the likelihood using two new variables: let b ≡ ρa be the expected number of background stars given bins of area a and let
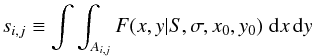 be the expected number of cluster stars in the same bin, which is equal to the integral of the cluster density model over the area of the bin. For the Gaussian model, Eq. (15), the integrals simplify to differences of error functions so si,j is a known function of the model parameters and the bin shape. In terms of these variables, the likelihood now becomes P(n | m,s,b).
be the expected number of cluster stars in the same bin, which is equal to the integral of the cluster density model over the area of the bin. For the Gaussian model, Eq. (15), the integrals simplify to differences of error functions so si,j is a known function of the model parameters and the bin shape. In terms of these variables, the likelihood now becomes P(n | m,s,b).
As with the photometric likelihood, the re-parameterized astrometric likelihood is again easier to derive if I introduce the additional variable f, the number of background stars per bin, whence c ≡ n−f are the number of cluster stars per bin. As in the photometric case, the likelihood of having f field stars out the of n measured stars given probabilities m follows a binomial distribution. At the same time, the actual number of background stars should be related to the expected number through a Poisson distribution. Unlike the photometric case, in the astrometric problem I also know the expected number of cluster stars per bin as a function of the model parameters: given s, the measured number of cluster stars in a bin should also be Poisson distributed. The initial likelihood is then equal to the product of individual binomial and Poisson distributions and the final likelihood is again found by summing over all possible values of fi,j![\begin{equation} \label{eq:alike} P(\vec{n}|\vec{m},\vec{s},\vec{b}) =\prod_{i,j}\left[\sum_{f=0}^{n_{i,j}} P(n_{i,j}-f,f|m_{i,j},s_{i,j},b_{i,j})\right]. \end{equation}](/articles/aa/full_html/2018/01/aa28568-16/aa28568-16-eq84.png) (19)Finally, the posterior is proportional to the product of the priors, Eqs. (14), (17)–(18), and the likelihood Eq. (19)
(19)Finally, the posterior is proportional to the product of the priors, Eqs. (14), (17)–(18), and the likelihood Eq. (19)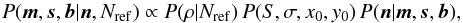 (20)where the s are implicitly functions of the model parameters and b are functions of the background density, ρ.
(20)where the s are implicitly functions of the model parameters and b are functions of the background density, ρ.
In the end, the expected value of the model parameters are not something we are interested in and so they should be marginalized away, leaving the final posterior probability distribution 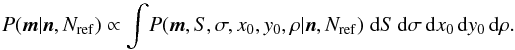 (21)This posterior gives us the probability density for the m as a function of the measurements n and N but it is un-normalized, so the expectation of the mi,j is given by
(21)This posterior gives us the probability density for the m as a function of the measurements n and N but it is un-normalized, so the expectation of the mi,j is given by
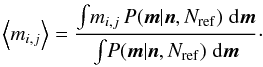 In practice, the posterior Eq. (21)is too complicated to solve analytically, so here we must resort to numerical solutions. One common approach is to find the most-probable values of m (the maximum a posteriori probability solution) by maximizing Eq. (21). Minimizing log P(m | n,Nref) is an equivalent problem, but one that is often preferred because all the products become sums which are easier to work with, particularly for algorithms that require calculating a Jacobian. A minimization such as this is, in essence, how clusters distributions are commonly found: a model cluster profile and a background density are fit to binned star counts (or some other proxy for the local stellar density) and the membership probability is set equal to the fraction of cluster stars in that bin, m ≈ si,j/ (si,j + bi,j). The chief difference between the approach here and conventional curve fitting is that this cost function is derived from a posterior density, P(m | n,Nref), which correctly reflects the Poisson statistics of the data and incorporates the measured background density.
In practice, the posterior Eq. (21)is too complicated to solve analytically, so here we must resort to numerical solutions. One common approach is to find the most-probable values of m (the maximum a posteriori probability solution) by maximizing Eq. (21). Minimizing log P(m | n,Nref) is an equivalent problem, but one that is often preferred because all the products become sums which are easier to work with, particularly for algorithms that require calculating a Jacobian. A minimization such as this is, in essence, how clusters distributions are commonly found: a model cluster profile and a background density are fit to binned star counts (or some other proxy for the local stellar density) and the membership probability is set equal to the fraction of cluster stars in that bin, m ≈ si,j/ (si,j + bi,j). The chief difference between the approach here and conventional curve fitting is that this cost function is derived from a posterior density, P(m | n,Nref), which correctly reflects the Poisson statistics of the data and incorporates the measured background density.
Because we have the full probability distribution, curve fitting is not the only possibility. Another option is to solve the integrals in Eq. (21)directly. The expected values of m are then found by calculating the moments of the posterior distribution (the norm, the mean, the variance, etc.). While multi-dimensional integrals are computationally inefficient, the direct integration approach has its attractions. First, it does not require calculating derivatives of the posterior, which are also computationally expensive for large problems. Second, there is no question of getting trapped in a local minimum due to an incorrect initial estimate, as can happen with some numerical minimization algorithms. Finally, because the shape of the distribution is known, confidence intervals can be assigned to all the expectations.
Furthermore, if the model parameters were already known then Eq. (21)would become separable by bins, significantly reducing the computational burden. This suggests a hybrid approach: first one finds the maximum a posteriori values of the model parameters by integrating over the posterior distribution
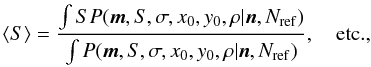 then the posterior is recomputed holding the model parameters fixed at their expectation values to determine the probabilities
then the posterior is recomputed holding the model parameters fixed at their expectation values to determine the probabilities 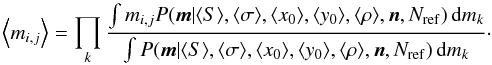 (22)Because the model parameters are now taken to be constants, the integrals Eq. (22)are separable and the cluster probability for each bin can be found very quickly.
(22)Because the model parameters are now taken to be constants, the integrals Eq. (22)are separable and the cluster probability for each bin can be found very quickly.
4. Bayesian joint cluster membership
Our ultimate goal is to find, for every star in the program field, the probability that it belongs to the cluster distributions and not to the field star distributions. To this end, there is one important piece of prior information we have left to apply: the astrometric and photometric cluster probabilities are linked in that being an astrometric cluster member necessarily implies that the star is also a photometric cluster member and vice versa. This means that a joint cluster estimation must do at least as well as a purely astrometric or purely photometric method and most of the time it ought to out-perform either of them.
In abstract terms, our goal is to find the cluster stars C, given the astrometric and photometric measurements A and P, and information from the reference images I. In Bayesian terms this becomes
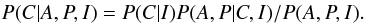 In practice, there are two approaches commonly used to find the posterior of this form. The first is to repeat the procedure we used with the astrometric and photometric data and solve for the posterior all at once. The second is to split the problem into two steps: a first step which looks at either the astrometric of photometric data in isolation followed by a second step which looks at the remaining data using the previous results as an informative prior. The two methods are formally equivalent, but the multi-stage problem is often easier to solve numerically due to its lower dimensionality.
In practice, there are two approaches commonly used to find the posterior of this form. The first is to repeat the procedure we used with the astrometric and photometric data and solve for the posterior all at once. The second is to split the problem into two steps: a first step which looks at either the astrometric of photometric data in isolation followed by a second step which looks at the remaining data using the previous results as an informative prior. The two methods are formally equivalent, but the multi-stage problem is often easier to solve numerically due to its lower dimensionality.
The process I will follow here is:
-
1.
Starting with the astrometric data, solve for the initial field starprobabilitiesP(m | n,Nref).
-
2.
Use this posterior as the [informative] prior probability of field star membership for the photometric data.
-
3.
Find the resulting joint astrometric-photometric posterior and, from that, the final expectation of the field star membership, ⟨m⟩, for every star.
-
4.
The cluster membership probability will be the complement, ⟨c⟩ = 1−⟨m⟩.
Splitting the problem up this way, the astrometric problem is unchanged from Sect. 3.2. To find the posterior, one finds the expected model parameters and then, fixing the model parameters at their expected values, uses the posterior Eq. (22)to find the astrometric cluster probability distribution P(m | n,N). This posterior then becomes the informative prior, P(m) for the second stage.
This new prior, unfortunately, complicates the joint posterior probabilities. In Sect. 3.1, the problem was separable by bin, the prior was a constant, and all stars in a bin were equally likely to be cluster members. With the prior Eq. (22), that will not be the case. While the problem remains separable, some stars are a priori probable cluster members, some are uncertain, and others are likely to be field stars. This means we can no longer assume a binomial distribution as in Eq. (9).
For now, leave the joint likelihood as some unspecified function of the probabilities m times the same poisson rates P(nf | φ) and P(nc | ψ) as before. Aside from the likelihood and the informative priors for m, the rest of the joint posterior follows the derivation of the photometric posterior in Sect. 3.1.
Equations (4)and (8)are again the prior for the background field star and cluster star densities and the posterior again has the form of Eq. (13)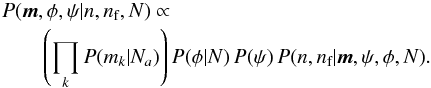 The subscript “a” indicates that these are from the previously solved astrometric problem and vector notation indicates the value at every star. As before, φ, ψ, and nf are nuisance parameters and need to be marginalized to eliminate them from the final posterior
The subscript “a” indicates that these are from the previously solved astrometric problem and vector notation indicates the value at every star. As before, φ, ψ, and nf are nuisance parameters and need to be marginalized to eliminate them from the final posterior 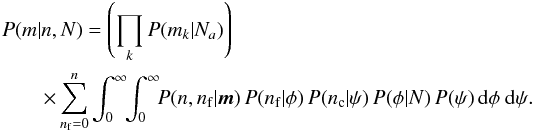 These are the same integrals we saw before and their solutions are given by Eqs. (11), (12). As with the photometric case, the summation is best handled numerically.
These are the same integrals we saw before and their solutions are given by Eqs. (11), (12). As with the photometric case, the summation is best handled numerically.
The final remaining term is the likelihood P(n,nf | m). This could be derived inductively as a very large combinatorial problem across all the possible combinations of m’s under the constraint n = nc + nf, but a less rigorous approach gives a more intuitive derivation. In the end, what we are trying to find is the average value of m for each star or, equivalently, the moments of the posterior with respect to a single star mk. Thus we do not need to know the full posterior, but rather the posterior after the contribution of every mj ≠ k has been marginalized out. This suggests that, for the purposes of finding its expected membership probability, each star can be treated as an independent Bernoulli random variable with some probability m that it is a field star and a probability (1−m) that it is a cluster star. For a given value of nf, that means that if a given star is a field star, then the other stars together contribute the remaining nf−1 field stars. Similarly, if it is a cluster star, then the other stars must sum to nf field stars. Since we am looking for a probability, this suggests using a beta distribution, B(α,β;p) to represent the rest of the likelihood where the parameters of the distribution, α and β, account for the contributions of all the other stars (the beta distribution is the conjugate prior for a Bernoulli likelihood, Fink 1997). That means that, for the k-th star, the likelihood becomes
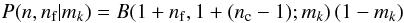 if it is a cluster star where B(α,β;x) is a beta distribution. Summing over all values of nf = 0,1,2,...,ni,j and all possible outcomes (either cluster or field) gives me the posterior distribution I am looking for
if it is a cluster star where B(α,β;x) is a beta distribution. Summing over all values of nf = 0,1,2,...,ni,j and all possible outcomes (either cluster or field) gives me the posterior distribution I am looking for 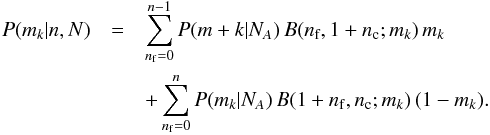 The first summation contains all the field star outcomes, the second has the cluster star outcomes. This posterior is simple to calculate, it contains the relevant statistics given the outcome of the measurement, and it allows one to calculate the expected membership probability ⟨m⟩k from its prior weighted moments.
The first summation contains all the field star outcomes, the second has the cluster star outcomes. This posterior is simple to calculate, it contains the relevant statistics given the outcome of the measurement, and it allows one to calculate the expected membership probability ⟨m⟩k from its prior weighted moments.
5. Results
To test the approach, I looked at two clusters, M 67 (NGC 2682) and NGC 654, and a third cluster-free region of the sky. M 67 is a well-studied open cluster with accurate proper motion data available as an independent cross-check on our cluster membership estimates (Sanders 1976; Girard et al. 1989; Montgomery et al. 1993; Boyle et al. 1998; Laugalys et al. 2004; Sandquist 2004; Balaguer-Núñez et al. 2007). NGC 654 is a fainter low galactic latitude cluster with a high density of background stars. While not as well studied as M 67, several photometric surveys have been made of NGC 654 as well (Pesch 1960; Hoag & Applequist 1965; Moffat 1972; Stone 1977, 1980; Mermilliod 1981; Joshi & Sagar 1983; Phelps & Janes 1994; Pietrzynski 1996; Shi & Hu 1999; Pandey et al. 2005). For my final test region, I used another patch of sky adjacent to my NGC 654 reference field which was made up entirely of field stars.
Photometric and positional data were downloaded from the NOMAD data set for all the fields (Zacharias et al. 2004) through the VIZIER web service (Ochsenbein et al. 2000). Only one set of image data was used per cluster. Each data set was then divided into an inner region with the cluster (the program data) and an outer boundary free of cluster stars (the reference data). To improve the statistics, the cluster reference images had roughly eight times as many stars as the program region. The non-cluster test used two smaller equal-sized images.
As a check, the purely photometric and purely astrometric probabilities were computed for each field, following the algorithms presented above in Sects. 3.1 and 3.2. In the astrometric case, the image region was subdivided into equal-area bins with an average of 12 program stars per bin. In the photometric case, an adaptive binning algorithm was used that recursively subdivided the bins until they held at most 24 stars per bin (the black boxes in Fig. 2 show the adaptive binning used for M 67). The adaptive binning was derived from the program data and then the same binning was used for the reference data. Finally, the probabilities were recalculated using the astrometric probabilities as a prior and following the joint posterior, as described in Sect. 4.
 |
Fig. 3 Cluster membership probabilities for M 67 (top), NGC 654 (middle), and a cluster-free section of sky (bottom). Blue circles are the astrometric probabilities, green circles are the photometric probabilities, and red circles are the inferred joint distribution; the x-axis is the star’s identifying index (sorted by increasing joint probability). Typical variances for the estimated probabilities are on the order of |
 |
Fig. 4 M67 membership probability as a function of position. Color indicates the individual probabilities: blue for astrometric, green for photometric, and red for joint estimation; the higher the probability, the stronger the color component(s). Colors are blended so, for example, light gray indicates uniformly high probabilities. The size of each star is proportional to the joint probability of its being a cluster star. Cluster members (stars with P> 0.5) are circled in black. |
 |
Fig. 5 M67 membership probabilities as a function of color and magnitude. The color scheme is the same as Fig. 4. Cluster stars (P> 0.5) have again been circled in black. |
Figure 3 shows a comparison of the results sorted by increasing joint membership probability. For each of the fields, the astrometric results are plotted in blue, the photometric in green, and the joint probabilities in red. As expected, the results data are broadly correlated: all three algorithms identified the same basic stars as likely [non-]cluster members. The joint result, however, incorporates the information from both of the other two curves and is thus a more reliable result; when the astrometric and photometric distributions agree the joint distribution gives an even higher probability, but where they disagree, the joint distribution reflects less certainty. While not plotted, the variance of the joint distribution is also consistently smaller than the other two distributions. Figures 4 and 5 show the same M 67 results using color to indicate where the astrometric and photometric classifications are taking place. The color scheme is the same as Fig. 3, but here the colors are blended, so a yellow star (red plus green) was identified by the photometric and joint algorithm as a cluster star but had a low astrometric probability, while a gray or white (red plus green plus blue) star was identified by all three distributions. Figure 6 has the same plots for NGC 654 and the cluster-free data sets.
The results of the three fields also corresponds well with the actual distribution of stars. M 67 is a large cluster with an apparent diameter of 20–30′. My program images are 30′ squares, so most of the stars visible will be cluster stars. Of the 452 stars observed, about 90% of them (412 in total) are identified as cluster members with a probability P> 50%. NGC 654 is a much smaller cluster (ca. 5′) and I identify only 95 probable cluster stars out of 292 in the field. This is consistent with other observations such as Pandey et al. (2005), who identified between 80 and 100 cluster members in their survey of the same cluster. Finally, the cluster-free field contained 805 stars and only two of them were mis-identified as a cluster star. All these results are summarized in Table 1.
The final check was to compare my results with two surveys of proper motions in M 67 by Zhao et al. (1993) and Sanders (1971). In all, 124 stars were reliably identified as being common to Zhao’s, Sanders’, and my own program data sets. Of these, Zhao identified 96 as being cluster members (P> 0.5), Sanders identified 106 (P> 0.5) and I identified 103 astrometric members, 116 photometric members, and 121 joint cluster members (all with P> 0.5). Thus, assuming the proper motion surveys are correct, the joint photometric-astrometric algorithms have a general tendency to over-estimate the probability of cluster membership (although that could be mitigated somewhat by either picking a higher threshold throughout, say P> 0.6, or incorporating the variance data to estimate confidence intervals). Table 2 summarizes the results. The astrometric algorithm produced large numbers of both false positives and false negatives. The photometric algorithm also generated large numbers of false positives, but relatively few false negatives. The joint algorithm, incorporating both astrometric and photometric information, produced the best results of the three. While the joint algorithm did not do anything for the false positive rate, its false negative rate was the best of the three. Similarly, while it is no better than the photometric algorithm at eliminating false cluster members, the number of true cluster members identified was the best of the three algorithms. Looking further at the data, while the main sequence stars were identified with generally high accuracy, the photometric algorithm had trouble with giant branch and blue straggler stars. The problem would seem to be statistical in origin – these areas of the color–magnitude diagram were sparsely populated and thus there was no statistical reason to reject one or two extra stars. The main sequence, in contrast, had a higher density of stars and the statistical selectivity was much higher there.
Total number of stars and the number of cluster stars in each field.
Final outcomes of the three different algorithms (photometric, astrometric, and joint) in analyzing the M 67 data, as compared with the two reference proper motion surveys.
 |
Fig. 6 Membership probabilities for NGC 654 (left) and the non-cluster field (right). Colors and sizes have the same meaning as Fig. 4. |
6. Discussion
As seen in the previous section, the Bayesian joint estimation of cluster membership is an improvement over either astrometric or photometric methods alone. Having said that, the method is not magic: while it makes more efficient use of it, this algorithm is still constrained by the information available from astrometric and photometric measurements and no algorithm can hope to do well when information is weak or lacking entirely. Overall, the algorithm performed best with main sequence stars because those parts of the color–magnitude diagram tended to be well populated. Other portions, such as the giant branch or white dwarfs, which did not contain many stars, had poor photometric statistics so the astrometric data tended to dominate the probability estimate (for better or for worse). In general, the algorithm performed best when the photometric reference image contained many stars, which improved the counting statistics in these less-populated areas of the color–magnitude diagram.
My goal in this paper was to demonstrate the algorithm, so I used the simplest and clearest approaches I could. As a consequence, my implementation was likely sub-optimal and there are a number of algorithmic improvements that could be made to further improve the accuracy of the results. First, the symmetric Gaussian is a poor choice for an astrometric model. Open clusters are only weakly gravitationally bound and many show signs of asymmetry due to tidal effects and other interactions with their local environment (Bonatto & Bica 2007). An elliptical Gaussian
![$$ f(x,y) = A \exp\left(-\frac{(x-x_0)^2}{2\sigma_x^2} - \frac{[(x-x_0)\sin\theta + (y-y_0)\cos\theta]^2}{2\sigma_y^2}\right) $$](/articles/aa/full_html/2018/01/aa28568-16/aa28568-16-eq149.png) would be a much better choice, although it requires estimating two additional parameters. King distributions are another more realistic possibility, although some authors have reported problems applying them to distorted clusters (Krone-Martins & Moitinho 2014).
would be a much better choice, although it requires estimating two additional parameters. King distributions are another more realistic possibility, although some authors have reported problems applying them to distorted clusters (Krone-Martins & Moitinho 2014).
Another area for improvement is the binning. I used a uniform binning for the astrometric data and a relatively crude divide-and-conquer adaptive binning for the photometric data. More sophisticated binning schemes that better reflect the structure of the data should yield better results. There is also the problem of determining the optimal bin size: too few stars per box and the statistical fluctuations become large but use too big a box and the spatial resolution suffers. This is of particular concern in the astrometric problem because if the cluster is not properly resolved by the bins then the model width, σ, cannot be determined.
The final improvement would be to incorporate external information into the priors. I set this problem up as a blind estimation using a single reference image and a single program image. In practice, however, pertinent information is often available from prior surveys. For example, estimates of the cluster center and size are often available before the observation is made, and these could be used as priors to improve the estimation of the astrometric model. If a library of isochrones and extinctions is available, these too could be used as photometric priors for the cluster rate ψ, although it does introduce the new problem of picking the most probable isochrone. Finally, other partial information, for example from a magnitude-limited spectroscopic or proper motion survey, can be used to improve the star-by-star priors for field star membership P(mk). This is true even if data are only available for a few stars; any extra information helps improve the results.
7. Conclusions
Because they represent a single star-formation event, open clusters are an important test-case for theories of stellar evolution. This raises the question, though, of which stars are cluster members and which stars are accidentally observed field stars? At low galactic latitudes this is an especially difficult problem, but unfortunately low galactic latitudes are also where the majority of open clusters are found. There are two common approaches for identifying cluster membership: astrometric methods based on the position and motion of the stars and photometric methods derived from the color and brightness of stars. While both can give satisfactory results, they also have their limitations.
In this paper I have sought to combine astrometric and photometric data into a single joint distribution. Working within a Bayesian statistical framework, I derived a posterior distribution for the cluster membership probability that incorporates information from both the astrometric and photometric data sets. The expected probability of cluster membership and its variance were then calculated from the moments of the posterior distribution. I then applied my prior to three different observational fields: M 67 (a well-studied cluster with good proper-motion membership surveys), NGC 654 (a cluster in a crowded field), and a third reference field with no cluster stars. In all three cases the joint algorithm performed better than either astrometric or photometric methods individually.
Unlike proper motion surveys, this method is very general and is designed for single-epoch observations. The algorithm requires only a pair of images per photometric filter, and even a single image will suffice if the cluster is much smaller than the field of view of the telescope. On the other hand, because this is a Bayesian estimation problem, one is not limited to just pairs of images. Bayesian priors allow one to naturally incorporate any and all a priori information (multi-color photometry, magnitude-limited proper motions, partial spectroscopy, data error estimates, etc.) into the estimation problem. As long as the information is given a proper statistical description, the algorithm will use incorporate the available information to estimate the distribution of cluster membership probabilities.
While there are a number of algorithmic improvements that could be added to this implementation, the joint Bayesian estimator has demonstrated itself to be a robust and reliable improvement over conventional purely astrometric or photometric techniques for identifying cluster membership.
Acknowledgments
This research was begun at the Vatican Observatory and has received additional support from Fairfield University startup funds. This research also made use of the VizieR catalog access tool (CDS, Strasbourg, France) and NASA’s Astrophysics Data System [ADS].
References
- Balaguer-Núñez, L., Galadì-Enriíque, D., & Jordi, C. 2007, A&A, 470, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, J. O., Bernardo, J. M., & Sun, D. 2009, Ann. Stat., 37, 905 [CrossRef] [Google Scholar]
- Bernardo, J. M. 1979, J. R. Stat. Soc. B, 41, 113 [Google Scholar]
- Bica, E., & Bonatto, C. 2005, A&A, 443, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonatto, C., & Bica, E. 2007, MNRAS, 377, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Boyle, R. P., Kazlauskas, A., Vansevivcius, V., et al. 1998, Balt. Astron., 7, 369 [NASA ADS] [Google Scholar]
- Fink, D. 1997, A compendium of conjugate priors, CiteSeer [Google Scholar]
- Girard, T. M., Grundy, W. M., López, C. E., & van Altena, W. F. 1989, AJ, 98, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, C. J., Kawaler, S. D., & Trimble, V. 2004, Stellar Interiors: Physical Principles, Structure, and Evolution, 2nd edn. (New York: Springer Science+Business Media) [Google Scholar]
- Hoag, A. A., & Applequist, L. N. 1965, Astron. J. Suppl. Ser., 12, 215 [Google Scholar]
- Jeffreys, H. 1945, Proc. Roy. Soc. A, Math. Phys. Sci., 186, 453 [Google Scholar]
- Joshi, U. C., & Sagar, R. 1983, MNRAS, 202, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Krone-Martins, A., & Moitinho, A. 2014, A&A, 561, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laugalys, V., Kazlauskas, A., Boyle, R. P., et al. 2004, Balt. Astron., 13, 1 [Google Scholar]
- Loredo, T. J. 1990, in Maximum entropy and Bayesian methods, ed. P. F. Fougère (Dordrecht, The Netherlands: Springer), 81 [Google Scholar]
- Mermilliod, J.-C. 1981, A&AS, 44, 467 [NASA ADS] [Google Scholar]
- Moffat, A. F. J. 1972, A&AS, 7, 355 [NASA ADS] [Google Scholar]
- Montgomery, K. A., Marschall, L. A., & Janes, K. A. 1993, AJ, 106, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, A. K., Upadhyay, K., Ogura, K., et al. 2005, MNRAS, 358, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Pesch, P. 1960, ApJ, 132, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Phelps, R. L., & Janes, K. A. 1994, ApJS, 90, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrzynski, G. 1996, Acta Astron., 46, 287 [NASA ADS] [Google Scholar]
- Sanders, W. L. 1971, A&A, 14, 226 [NASA ADS] [Google Scholar]
- Sanders, W. L. 1976, A&AS, 27, 89 [NASA ADS] [Google Scholar]
- Sandquist, E. L. 2004, MNRAS, 347, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Sarro, L. M., Bouy, H., Berihuete, A., et al. 2014, A&A, 563, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmeja, S. 2011, Astron. Nachr., 332, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, H. M., & Hu, J. Y. 1999, A&AS, 136, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stone, R. C. 1977, A&A, 54, 803 [NASA ADS] [Google Scholar]
- Stone, R. C. 1980, PASP, 92, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2004, BAAS, 36, 1418 [Google Scholar]
- Zhao, J. L., Tian, K. P., Pan, R. S., He, Y. P., & Shi, H. M. 1993, A&AS, 100, 243 [NASA ADS] [Google Scholar]
All Tables
Final outcomes of the three different algorithms (photometric, astrometric, and joint) in analyzing the M 67 data, as compared with the two reference proper motion surveys.
All Figures
 |
Fig. 1 Open cluster NGC 609. The existence of a cluster in the center of the image cannot be doubted, but there is no obvious way to separate the cluster stars from the surrounding field stars. |
| In the text | |
 |
Fig. 2 color–magnitude diagrams of the M67 reference (green) and program (blue) fields. The boxes show the adaptively sized bins used to calculate the photometric distribution. The reference field is significantly larger than the program field and thus has more stars, but otherwise the distributions look very similar to the eye. |
| In the text | |
 |
Fig. 3 Cluster membership probabilities for M 67 (top), NGC 654 (middle), and a cluster-free section of sky (bottom). Blue circles are the astrometric probabilities, green circles are the photometric probabilities, and red circles are the inferred joint distribution; the x-axis is the star’s identifying index (sorted by increasing joint probability). Typical variances for the estimated probabilities are on the order of |
| In the text | |
 |
Fig. 4 M67 membership probability as a function of position. Color indicates the individual probabilities: blue for astrometric, green for photometric, and red for joint estimation; the higher the probability, the stronger the color component(s). Colors are blended so, for example, light gray indicates uniformly high probabilities. The size of each star is proportional to the joint probability of its being a cluster star. Cluster members (stars with P> 0.5) are circled in black. |
| In the text | |
 |
Fig. 5 M67 membership probabilities as a function of color and magnitude. The color scheme is the same as Fig. 4. Cluster stars (P> 0.5) have again been circled in black. |
| In the text | |
 |
Fig. 6 Membership probabilities for NGC 654 (left) and the non-cluster field (right). Colors and sizes have the same meaning as Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.