| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A163 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202346569 | |
| Published online | 21 September 2023 | |
A Gaia astrometric view of the open clusters Pleiades, Praesepe, and Blanco 1⋆
Universidad de los Andes, Departamento de Física, Cra. 1 No. 18A-10, Bloque Ip, 4976 Bogotá, Colombia
e-mail: je.alfonso1@uniandes.edu.co; josegarc@uniandes.edu.co
Received:
31
March
2023
Accepted:
13
July
2023
Context. Nearby open clusters, such as Pleiades, Praesepe, and Blanco 1, have been extensively studied due to their proximity to the Sun. The Gaia data provide the opportunity to investigate these clusters, because they contain valuable astrometric and photometric information that can be used to update their kinematic and stellar properties.
Aims. Our goal is to carry out a star membership study in these nearby open clusters by employing an astrometric model with proper motions (PMs) and an unsupervised clustering machine learning algorithm that uses positions, PMs, and parallaxes. The star members are selected from the cross-matching between both methods. Once we know the members, we investigate the spatial distributions of these clusters and estimate their distances, ages, and metallicities.
Methods. We used the Gaia DR3 catalogue to determine star members using two approaches: a classical Bayesian model and the unsupervised machine learning algorithm DBSCAN. For star members, we built radial density profiles and spatial distributions, and computed the King parameters. The ages and metallicities were estimated using the BASE-9 Bayesian software.
Results. We identified 958, 744, and 488 star members for Pleiades, Praesepe, and Blanco 1, respectively. We corrected the distances and built the spatial distributions, finding that Praesepe and Blanco 1 have elongated shape structures. The distances, ages, and metallicities obtained were consistent with those reported in the literature.
Conclusions. We obtained catalogues of star members, and updated kinematic and stellar parameters for these open clusters. We find that the PMs model can find a similar number of members to the unsupervised clustering algorithm when the cluster population forms an overdensity in the vector point diagram. This allows us to select an adequate size of the PMs region with which to run these methods. Our analysis found stars that are being directed towards the outskirts of Praesepe and Blanco 1, which exhibit elongated shapes. These stars have high membership probabilities and similar PMs to those within the tidal radius.
Key words: astrometry / methods: data analysis / open clusters and associations: individual: Blanco 1 / open clusters and associations: individual: Pleiades / open clusters and associations: individual: Praesepe
Tables with cluster members are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/677/A163
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Open clusters (OCs) are groups of stars ranging in number from hundreds to thousands and held together by the gravitational force between their members. Such clusters have been found in spiral and irregular galaxies with active star formation processes (Reino et al. 2018). They are formed from the collapse of molecular clouds (Krumholz et al. 2019) and have unique age and metallicity parameters. The distribution of proper motions (PMs) and distances of cluster stars, which result from the initial conditions of position, velocity, and angular momentum of the stars and their interaction with the Galaxy’s potential over time, provide valuable information for studying stellar evolution.
The line of sight of OCs is often contaminated by background and foreground stars, making it challenging to determine which stars truly belong to any given cluster. Nowadays, overcoming this star membership problem is a mandatory task in the process of determining the ages, metallicities, distances, and rotational sequences of Milky Way OCs with the highest possible precision (Godoy-Rivera et al. 2021). To confront this problem, Vasilevskis et al. (1958) modelled the PM distribution of cluster and field stars using circular and elliptical bivariate density functions, respectively. By applying the Bayes rule, the probability that a star belongs to the cluster can be estimated based on its PMs. The PM model is effective in identifying stellar members, but becomes less effective when the cluster is far away and numerical issues arise in finding the PM centroid of the cluster. In such cases, the computed membership probabilities may not be accurate. However, for nearby OCs, their larger PMs compared to those of field stars make it easier to identify members using the vector point diagram (VPD). This is the case of Pleiades, Praesepe, and Blanco 1 OCs, whose PMs have a clear separation from the background stars.
The Density-Based Spatial Clustering of Applications with Noise (DBSCAN) algorithm forms the basis of another method used to identify the stars that belong to an OC (Ester et al. 1996). This unsupervised machine learning algorithm detects overdensities in a multi-dimensional space in order to find clusters. The definition of clusters is based on two hyperparameters: the ϵ radius, which defines the size of a neighbourhood around a point, and the minimum number of points (minPts) that a cluster must contain within the neighbourhood defined by the ϵ radius. By using the Gaia Data Release 3 (Gaia DR3) positions, PMs, and parallaxes, and applying the DBSCAN algorithm, it is possible to search for OCs in a specific sky area.
In this work, we aim to identify star members of Pleiades, Praesepe, and Blanco 1 using the Gaia DR3 catalogue. We employ both the PM model, which estimates star membership probabilities using maximum likelihood estimation (MLE) and a Markov chain Monte Carlo (MCMC) algorithm, and DBSCAN. We select the star members based on the cross-matching of the PM model and DBSCAN results. The distances are then corrected using the Bailer-Jones (2015) procedure. The structures of the clusters are analysed by building radial density profiles (RDPs) and spatial distributions, computing core and tidal radii from the King model fit, and estimating their ages and metallicities using color–magnitude diagrams (CMDs) and PARSEC isochrones (Bressan et al. 2012; Marigo et al. 2013).
The paper contains five sections. Section 2 describes the procedure to select the region of each cluster based on its average PM and distance. Section 3 is divided into three subsections, which describe the PM model implementation, the DBSCAN clustering algorithm and the estimation of parameters, and the density distribution used to compute the King model. Section 4 is divided into five subsections, two of which describe the results of star membership in each cluster and their implementation. The last three describe the RDPs with the estimation of King parameters, the spatial distributions, and the estimation of age and metallicity for each OC. The conclusions are presented in Sect. 5. Appendixes related to the Gaia data selection and the uncertainty estimation of parameters are presented.
2. Data
The European Space Agency (ESA) published the Gaia data release 3 (DR3) catalogue, which contains information on 1.8 billion sources collected over the first 34 months of the mission. The DR3 includes photometry in the G, GBP, and GRP pass-bands, radial velocities, and astrometric parameters including positions (α, δ), PMs (μα*1, μδ), and parallaxes (ϖ) (Gaia Collaboration 2016, 2023; Babusiaux et al. 2023). The data for the clusters studied here were downloaded from the Gaia archive using their centres in equatorial coordinates from SIMBAD and a search radius of 10 deg. We used astrometric and photometric errors filtered out to eliminate spurious sources as recommended by Lindegren et al. (2021; see Appendix A). These filters constrain the population of faintest stars. Nevertheless, further research is required to extend the cluster members using methodologies such as the one proposed by van Groeningen (2023) and thus extend the cluster membership lists. Our search was also limited to 500 pc through a parallax cutoff.
The clusters studied here are located in close proximity to the Sun. The PMs of Pleiades, Praesepe, and Blanco 1 as reported by Gaia Collaboration (2018) are centred at (19.9, −45.5) mas yr−1, ( − 36.1, −12.9) mas yr−1, and (18.7, 2.6) mas yr−1, respectively. This leads to the formation of overdensities in the VPDs due to their greater changes in coordinates when compared to distant stars. Consequently, it becomes possible to remove some of the background stars and reduce data contamination. However, finding the cluster and field centroids using the PM model can be limited when nf significantly exceeds nc. To address this, we fitted Gaussian densities around the average PMs of the clusters in each axis and chose stars within a range of 3σ to select a region in which to study the star membership. Radial velocities have been reported for around one-third of the stars outlined in the zoom plots in Fig. 1.
 |
Fig. 1. VPDs for Pleiades (left panel), Praesepe (middle panel), and Blanco 1 (right panel). The zoom plots show the selected regions in which we compute star membership with the PM model and the DBSCAN clustering algorithm. |
3. Methods
3.1. The proper motions model
The segregation problem in OCs involves identifying cluster and field stars, which overlap in the VPD due to their relative positions. Cluster stars are grouped around the centre of mass due to their gravitational interaction, while field stars are scattered in the foreground and background with weaker gravitational ties. One of the earliest studies regarding this problem was performed by Vasilevskis et al. (1958), who used PMs obtained from photographic plates to determine the probable members of the NGC 6633 cluster. To distinguish between the two populations, these authors model the PM distribution by two bivariate probability densities: a circular density for the cluster stars described by Eq. (1), and an elliptical density for the field stars described by Eqs. (2) and (3) (henceforth the subscripts c and f denote cluster and field). By combining these two probability densities, the joint probability distribution can be obtained, as expressed by Eq. (4) (Sanders 1971; Slovak 1977):
with
The joint probability distribution in Eq. (4) is a function of nine parameters represented by a θ vector; it includes the centroids of PM distributions for the cluster and field stars (μαc, μαc, μαf, μδf), the standard deviations (σc, σαf, σδf), the correlation coefficient (ρ) between PMs, and the fraction of cluster stars (nc) relative to the total number of stars (N = Nc + Nf). We employed the MLE to compute these parameters. This method uses the log-likelihood function in Eq. (5), which is defined from the joint probability distribution and gives the probability of the PM sample in the VPD as a function of the parameters (Uribe & Brieva 1994):
The log-likelihood function predicts the observed PMs based on the parameters, which are obtained through implementation of the MLE. The method maximises the log-likelihood function to find the nine parameters that generated the observed data. The initial guess was derived from the marginal densities provided by Sabogal-Martínez et al. (2001). To calculate the membership probabilities of each star, the bivariate probability densities given by Eqs. (1) and (2) are used in accordance with Bayes theorem. A priori probabilities of belonging to the cluster (nc) or the field (nf) are established for each population (Uribe & Brieva 1994). Finally, the membership probability of the ith star with PMs μα * ,i and μδ, i, is given by Eq. (6).
To determine if a star belongs to the cluster, we establish a threshold of P ≥ 0.5. If the membership probability of a star is greater than or equal to 0.5, it is considered to be part of the cluster.
3.2. The DBSCAN algorithm
The recent use of the unsupervised clustering algorithm DBSCAN by Castro-Ginard et al. (2018) with the Gaia DR2 catalogue involves identifying clusters through positions, PMs, and parallaxes. The algorithm identifies overdensities by computing distances between points in the data set. DBSCAN is dependent on two parameters: the ϵ radius of the hypersphere and the minimum number of points (minPts) that must be inside that hypersphere (Ester et al. 1996). In this algorithm, each point in the data set is assigned to one of the following three categories: (1) core points that contain at least minPts number of points – including the point itself – within their ϵ radius surrounding area in the dimensional space, (2) border points that are reachable from a core point and have less than minPts number of points within their ϵ radius surrounding area, and (3) outliers, which are points that are neither core nor border points.
To employ the clustering algorithm, we adopt a five-dimensional space composed of the equatorial coordinates, PMs, and parallaxes. We use the standard euclidean metric as expressed in Eq. (7) to measure the distances between the i and j stars:
In order to determine a unique scale for the data and avoid any weighting in Eq. (7), we standardised data using the equation z = (x − μ)/σ, where z is the standardised data, x is the raw data, and μ and σ are the mean and the standard deviation of the samples, respectively. This is a standard process that forms part of the data preparation procedure before applying machine learning models (Feigelson & Babu 2012); it transforms the data by removing the mean and scaling to unit variance.
3.3. Determination of the ϵ and minPts parameters
To optimise the results of the DBSCAN algorithm, an appropriate value of the ϵ parameter is essential. A procedure based on the one described by Castro-Ginard et al. (2018) was followed to determine an optimal ϵ. The first step was to compute the kth nearest-neighbour distance (k-NND) histogram of the data, and the median value was stored as ϵkNN. Next, a random sample of the same size as the data was generated using a Metropolis–Hastings algorithm from a Gaussian kernel. Then, the k-NND histogram of the simulated data was computed, and the median value was stored as ϵrand*. To reduce variation in ϵrand* due to sampling, an average of 30 repetitions was performed, and the result was stored as ϵrand. The final value of ϵ was determined as the average of ϵrand and ϵkNN, ϵ = (ϵrand + ϵkNN)/2.
The distribution of the 7th-NND for the Pleiades cluster region is shown in Fig. 2. The graph displays the 7th-NND for the Pleiades members selected from the PM model, the simulated data generated from a Gaussian kernel, and the selected ϵ value in that region. Unlike the approach used by Castro-Ginard et al. (2018), where the minimum value of the k-NND for the cluster and simulated data was chosen as the average, the distribution of the members and simulated data in the Pleiades cluster were found to be similar. Therefore, we chose the median value to improve the efficiency of the algorithm. Also, selecting the minimum value as Castro-Ginard et al. (2018) did, would result in classifying all data as outliers for any value of minPts.
 |
Fig. 2. Histogram of the 7th-NND for the region of Pleiades (red), simulated data (blue), and the Pleiades members selected from the PM model (orange). The grey dashed vertical line is the selected ϵ. |
To determine the minPts parameter in the algorithm, we need to take into account the size of the region being considered and the expected number of cluster members. Castro-Ginard et al. (2018) found that a range of minPts between 5 and 9 provides a good balance between minimising false positives and achieving good efficiency.
3.4. The density distribution
The analysis of the structure of an OC will benefit from the calculation of its stellar surface density. This latter provides information on the population of stars as a function of their projected distance from the centre of the cluster. To model this distribution, the empirical surface density function introduced by King (1962) is often used. This model was derived from a study of globular clusters in the Milky Way.
The King model accounts for both the inner and outer densities of the cluster and is described by two equations: ρ = ρ0/(1 + (r/rc)2) for the inner and ρ = ρ1(1/r − 1/rt)2 for the outer density. The normalisation constants ρ0 and ρ1 are used to scale the density values. Here, rc is the core radius, the distance from the centre in which the density falls to half its central value (ρ0). On the other hand, rt, the tidal radius, is the distance over which the cluster is tidally scattered by the Galaxy potential and the density reaches zero. These two equations can be condensed into a single expression, Eq. (8), to summarise the King model (Pinfield et al. 1998):
where ρ0, rc, and rt are the same as those described above. Even though the King model is not the physical solution of the collisionless Boltzmann equation, it is very useful to characterise the density profiles of star clusters (Binney & Tremaine 2008).
4. Results and discussion
In this study, we aim to perform the star membership in three nearby OCs using data from the Gaia DR3 catalogue. This is achieved through two methods: the astrometric PM model and an unsupervised clustering algorithm DBSCAN. The PM model is based on the Bayesian approach and uses PMs for membership determination (Vasilevskis et al. 1958). On the other hand, the DBSCAN algorithm takes into consideration five dimensions: equatorial coordinates, PMs, and parallaxes (Ester et al. 1996; Castro-Ginard et al. 2018). The final membership is determined by cross-matching the results from both methods2.
4.1. Star membership with the PM model
The PM model was implemented using two bivariate probability densities given by Eqs. (1) and (2). The MLE method was employed to determine the nine components of the vector parameter θ. The estimation was performed using the log-likelihood function given by Eq. (5), which maps the vector parameter space θ and gives a probability for the data. Subsequently, the vector parameter that maximises the probability for the observed data can be obtained, resulting in the maximum likelihood estimate θmax.
Aiming to determine the nine parameters of the PM model, we fitted a marginal density to the individual PM histograms. This tuning process resulted in the calculation of standard deviations and centroids for both the cluster and field stars, which served as the initial guess for the MLE method. Subsequently, we implemented the maximisation of the log-likelihood function considering the parameters previously determined as the initial guess. Additionally, we used an MCMC algorithm to estimate the uncertainty of the nine parameters (Foreman-Mackey et al. 2013; see the corner plot of the posterior probability function in the Pleiades region in Appendix B), using an uniform prior and computing the upper and lower error for each parameter as specified in Table 1. The convergence of the chains was validated by the Gelman & Rubin (1992) diagnostic; we found 0.9994, 0.9996 and 1.0000 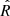 values for Pleiades, Praesepe, and Blanco 1, respectively, meaning that convergence has been reached.
values for Pleiades, Praesepe, and Blanco 1, respectively, meaning that convergence has been reached.
PM model parameters θmax computed using the MLE method for Pleiades, Praesepe, and Blanco 1 clusters.
The computed fraction of cluster star values (nc) were enough to offset the number of stars in the two populations, ensuring accurate membership probabilities. The correlation coefficients (ρ) were close to zero, indicating a lack of linear relationship between the PM distributions of cluster and field stars. The standard deviations of field stars were widely distributed compared to the cluster stars, as expected. Furthermore, the selected regions depicted in Fig. 1 allowed us to estimate the centroids of both cluster and field stars properly. The PM model uses two dimensions (μα*, μδ) to compute membership probabilities, and therefore cannot obtain information from coordinates (α, δ) and parallaxes (ϖ) as our clustering method can. However, it can find stars exhibiting PMs similar to the cluster mean, which may be helpful for observing the outskirts.
The membership probabilities were calculated according to Eq. (6) using the estimated parameters θmax reported in Table 1. A star was classified as a member of the cluster if its membership probability was greater than or equal to a predetermined threshold value of 0.5. The number of members identified by the PM model is presented in Table 2.
Number of members found with the PM model, the DBSCAN (DB) algorithm, the cross-matching, and parameters computed for the target clusters.
4.2. Star membership with the DBSCAN algorithm
The classification of OCs was also performed using the DBSCAN clustering algorithm (Ester et al. 1996) in five-dimensional astrometric space (α, δ, μα*, μδ, ϖ). We do not include the radial velocities as an additional dimension because only bright stars have this measurement in the catalogue (GRVS ⪅ 14 mag). The distances between standardised data were calculated using the metric given by Eq. (7). Our approach is similar in methodology to that established by Castro-Ginard et al. (2018) to determine the parameters minPts and ϵ. In accordance with Castro-Ginard et al. (2018), a reliable range for the value of minPts was determined to be 5–9 based on the size of the region being studied and by minimising the number of false positives in the clusters classified through the algorithm. We selected minPts = 8 and the corresponding equation k = minPts − 1 was used to calculate the k-NND. We also found that choosing a different value within the minPts range would not significantly impact the number of star members identified in the clusters by DBSCAN.
The methodology employed for determining the parameter ϵ in DBSCAN deviates moderately to some extent from that of Castro-Ginard et al. (2018). This is due to the fact that the original methodology results in the classification of all data points as outliers. To address this issue, we determined a reliable value of ϵ by calculating the average of the 7th-NND between the median value of the data and the average of 30 random resamplings, as described in Sect. 3.2. The values of ϵ determined for the Pleiades, Praesepe, and Blanco 1 regions are 0.404128, 0.370619, and 0.373202, respectively. These values remained almost unchanged even when the resampling was repeated several times. Figure 2 depicts the 7th-NND histograms for the entire Pleiades region, the simulated data from a Gaussian kernel, and the Pleiades members selected from the PM model. The distributions of the cluster and simulated distances are in a similar range to those of the Pleiades members selected by the PM model, and therefore the median value was used instead of the minimum, as was done by Castro-Ginard et al. (2018). The algorithm is based on finding overdensities in the dimensional space, and therefore tends to gather stars that minimise the population of stars in the surroundings. Despite the widespread use of HDBSCAN for detecting clusters in the Gaia catalogue (McInnes et al. 2017), we chose DBSCAN because this algorithm allows us to fine-tune the ϵ through sampling on the k-NND in the cluster regions. The number of members identified by the DBSCAN algorithm is presented in Table 2.
4.3. Radial density profile
The calculation of the RDPs depicted in Fig. 3 was performed by computing the stellar surface density in concentric rings. The formula used is 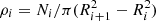 , where Ri and Ri + 1 represent the inner and outer radius, respectively. Ni is the number of stars in the ith ring. The distances of the clusters reported in Table 2 were estimated from a Gaussian fit to the distance histograms, incorporating the corrections outlined by Bailer-Jones (2015). We characterised the profiles using the King model for stellar density defined by Eq. (8). We also implemented the MLE method to determine the ρ0, rc, and rt parameters of the model using the log-likelihood function as
, where Ri and Ri + 1 represent the inner and outer radius, respectively. Ni is the number of stars in the ith ring. The distances of the clusters reported in Table 2 were estimated from a Gaussian fit to the distance histograms, incorporating the corrections outlined by Bailer-Jones (2015). We characterised the profiles using the King model for stellar density defined by Eq. (8). We also implemented the MLE method to determine the ρ0, rc, and rt parameters of the model using the log-likelihood function as
 |
Fig. 3. RDPs for Pleiades (left panel), Praesepe (middle panel) and Blanco 1 (right panel) OCs. The best-fit King model is shown by the solid red curves. The dashed vertical lines are the rc and rt values reported in Table 3. |
where ρi is the density computed at the ith ring, σρi is the Poissonian uncertainty and ρi, King is the density predicted by the model. The King model parameters derived from the fit are presented in Table 3 (see the corner plot of these parameters for Pleiades in Appendix C). The density profiles displayed in Fig. 3 indicate that all densities reach small values around 10 pc. This is further supported by the spatial distribution of members depicted in Fig. 4, which shows the presence of members at substantial distances from the cluster centre.
 |
Fig. 4. Spatial distributions in Galactic cartesian coordinates through the Astropy package (Astropy Collaboration 2022) for Pleiades (top row), Praesepe (middle row), and Blanco 1 (bottom row) after applying the distance corrections. The black arrow points to the Galactic centre. The red dashed circles are the tidal radii found in this work reported in Table 3. |
King model parameters.
In the following paragraphs, we compare the parameters and errors of the King model obtained in this work with those in the literature, if they are available.
The Pleiades profile depicted in Fig. 3 (left panel) exhibits a gradual decline in the inner region before reaching the core radius. The surface density decreases from 46 stars pc−2 at the centre of the cluster to approximately 0.01 stars pc−2 at the tidal radius. The King model provides a good fit to the projected radial distribution of stars because the Pleiades members are mainly within the tidal radius, as demonstrated by the spatial distribution in Fig. 4 (top panels). The ρ0, rc, and rt parameters obtained from the fit are presented in Table 3. The ρ0 computed in this study is slightly different from the values reported by Pinfield et al. (1998; 32.8 ± 2.3 stars pc−2) and is close to half of the value reported by Gao (2019a; 75.11 ± 1.66 stars pc−2). These differences may be due to variations in the number of star members used in the different studies. Additionally, both the core and tidal radii computed in this work match the estimates reported by Lodieu et al. (2019; 2.0 ± 0.25 pc and 11.6 pc) with a narrow difference of 2.2 pc in the core radius, and those of Meingast et al. (2021; 4.4 pc and 11.8 pc). They are also approximately 1 pc different from the values presented by Gao (2019a; 1.27 ± 0.04 pc and 12.3 ± 0.5 pc), which were also obtained through the King model.
The surface density profile for the Praesepe cluster shown in the middle panels of Fig. 3 displays a similar trend to the Pleiades profile. The King model provides a good match to the observed stellar density up to a distance of 10 pc from the core of the cluster; however, it fails to accurately reproduce the density beyond this point due to the distribution of members around the tidal radius and beyond. The limitations of the model are further highlighted by the fact that it does not account for tidal debris, as noted by Carrera et al. (2019). The King parameters ρ0, rc, and rt are reported in Table 3. The ρ0 obtained in this study is somewhat different from the value in Holland et al. (2000; 22.0 ± 3.9 stars pc−2), that is, there is a difference of 7.0 stars pc−2. Furthermore, the tidal radius differs by only 0.62 pc from the value reported by Kraus & Hillenbrand (2007; 11.5 ± 0.3 pc), and by 1.42 pc from the value reported by Lodieu et al. (2019; 10.7 pc).
Regarding the Blanco 1 cluster, its surface density profile, which is depicted in the right panel of Fig. 3, exhibits uniformity both before and after the core radius. The King model provides a good representation of the observed density until the tidal radius. Beyond this point, the number of star members decreases to low values, resulting in a reduction of the density in the surroundings and a flattening at around 0.01 stars pc−2. This discrepancy beyond the tidal radius is merely caused by the nature of the King model; it describes well the stellar surface density for clusters with spherical symmetry. On the other hand, when the OCs have elongated shapes, as in the case of Blanco 1, the King model cannot accurately reproduce the density of the surroundings. The rt parameter we obtain is considerably different from the values reported in Zhang et al. (2020; 10.0 ± 0.3 pc) and Pang et al. (2021; 10.2 pc), that is, by approximately 3.8 pc, and is smaller than the value of (20.0 ± 3.4) pc obtained by Piskunov et al. (2007). For ρ0, we see an increase compared to the value in Piskunov et al. (2007; 3.2 ± 0.4 stars pc−2), but our findings are consistent with the core radius found by these latter authors (1.5 ± 0.2 pc) based on the ASCC-2.5 catalogue.
The main discrepancies between the King model parameters reported in this work and those in the literature may be due to the methodology used to obtain member stars in these clusters. In previous studies, such as Gao (2019a), Lodieu et al. (2019), Zhang et al. (2020) and Pang et al. (2021), which used the Gaia catalogues, the number of stars inside or outside the tidal radius changes due to the method used to perform the membership, which is reflected in the values of ρ0, rc, and rt. In our case, although the PM model allows us to find more stars in the cluster surroundings, the unsupervised algorithm DBSCAN clusters the data in the space of positions, PMs, and parallaxes, detecting fewer stars in the cluster surroundings, which may be populated by low-mass stars because of the mass segregation effect. Consequently, these stars tend to be excluded from previous studies when the data is filtering. Efforts should therefore be made to include such stars using methodologies such as that proposed by van Groeningen (2023) in order to identify tidal tails.
4.4. Spatial distribution
Pleiades, Praesepe, and Blanco 1 are widely recognised as some of the most extensively studied star clusters. Because of their proximity to the Sun, these OCs provide a valuable opportunity to evaluate both stellar and dynamic models and to gain insight into the evolution of the Milky Way. From membership results, we constructed the spatial distributions of these clusters in Galactic cartesian coordinates, which are depicted in Fig. 4. The tidal radii reported in Table 3 for each cluster are also plotted.
The spatial distribution of the Pleiades cluster is shown in the top row of Fig. 4. Our analysis reveals the presence of 146 stars within the core radius, 806 stars between the core and tidal radii, and 6 stars beyond the tidal radius reaching 13.8 pc. The latter have high membership probability, indicating that they share similar PMs with those within the tidal radius. This is in agreement with Gao (2019a), who reported members up to 13.8 pc using probabilities. Our results do not support the detection of a tail-like structure in the (X, Z) plane as reported by Lodieu et al. (2019), but are consistent with the findings of Meingast et al. (2021), who found more than 80% of the mass of Pleiades to be within the tidal radius, without a prominent tail around it. The non-detection of the tidal tail may be explained by differences in the methodology used to find the cluster, which restricts the stars in the dimensional space.
As opposed to the case for Pleiades, the Praesepe members are distributed not only in the core but also in the surrounding area. The spatial distribution of Praesepe depicted in Fig. 4 (middle row) is characterised by a non-uniform distribution of its members. There are 707 stars within the tidal radius and 37 stars beyond it, forming an elongated shape reaching 24 pc in the (X, Y) and (X, Z) planes, as reported by previous studies (e.g., Lodieu et al. 2019; Röser & Schilbach 2019). This tail-like structure may be the result of an interaction between Praesepe and the Galaxy potential. Furthermore, because of its old age the cluster has had enough time to undergo stellar evolution processes that allow the formation of elongated structures. Also, the cluster is mass segregated, which allows low-mass stars to be ejected to the outskirts (Gao 2019b; Röser & Schilbach 2019). The bottom row of Fig. 4 shows the spatial distribution of the Blanco 1 cluster, which exhibits a total of 440 stars within the tidal radius and 48 stars beyond it. These latter are observed to extend up to a distance of 46 pc and form the most extended tail-like structure among the three clusters analysed. This structure is prominent along the line of sight of the cluster and may be the result of bias in the distance determination, which can produce an artificial elongation, as proposed by Zhang et al. (2020). Further research is required to identify how the Galactic potential affects the shape of clusters in order to distinguish between real and artificial stretching. In addition, Dinnbier et al. (2022) estimated tilt angles β of −32° and 22° for Pleiades and Blanco 1, respectively; the latter with a morphological age range from 91 Myr to 110 Myr. However, further investigation is necessary to compute this angle in the Praesepe cluster.
4.5. Age and metallicity
Two important parameters to understand the dynamics and stellar evolution of star clusters are age and metallicity. These provide insights into global properties and composition in regions of the Milky Way. Therefore, in order to estimate these parameters, we used the PARSEC tracks (Bressan et al. 2012; Marigo et al. 2013) and the Bayesian Analysis for Stellar Evolution with nine variables (BASE-9; von Hippel et al. 2006; Robinson et al. 2016) with photometry from the Gaia DR3 as inputs (see the corner plot of the age and metallicity computed via BASE-9 for the Pleiades in Appendix C). Because Gaia does not report magnitude errors, we incorporated uncertainties as σϖ, with a minimum value of 0.02 mag as done by Kounkel & Covey (2019). The best isochrones obtained through BASE-9 and the CMDs are depicted in Fig. 5.
 |
Fig. 5. CMDs for Pleiades (left panel), Praesepe (middle panel) and Blanco 1 (right panel) OCs. The best-fit isochrones are indicated with the solid red curves, with ages and metallicities estimated using BASE-9 (von Hippel et al. 2006; Robinson et al. 2016). |
The estimated age and metallicity values for Pleiades and Blanco 1 star clusters align with previous results reported by Gaia Collaboration (2018) and Bossini et al. (2019). In the case of Praesepe, while the computed metallicity is in agreement with the widely reported value of 0.020 dex, the estimated age differs from that in Gaia Collaboration (2018). Previous studies yielded a range of ages for Praesepe, from 662 Myr to 800 Myr (e.g., Mermilliod 1981; Salaris & Bedin 2019); however, our computed age is closest to the value of 741.0 Myr in Gossage et al. (2018).
The star population in the three clusters is mainly governed by main sequence stars, as expected. The brightest reddish stars in the Pleiades CMD depicted in Fig. 5 (left panel) – which split away from the upper side of the isochrone – could be fast rotators (Sun et al. 2019), and some of them might be Be stars. Optical spectroscopy is needed to confirm this assumption. Additionally, we did not find the previously confirmed Pleiades white dwarf LB 1497 (Eggen & Greenstein 1965). On the other hand, in the Praesepe cluster, we found 10 of the 11 white dwarfs reported by Lodieu et al. (2019). Further studies are needed to establish whether these white dwarfs are part of binary systems. These stars, as well three in the giant branch with colours around 1.0 mag, were not considered in the isochrone-fit analysis.
With regard to the Blanco 1 cluster, although there are two white dwarf candidates reported by Zhang et al. (2020), we did not detect them in our study. It is possible that the limitations of our method or data may have played a role in the non-detection of these white dwarfs. Further investigation is necessary to confirm their presence or absence.
5. Summary and conclusions
We used two methods to identify the star members in Pleiades, Praesepe, and Blanco 1 OCs using the Gaia DR3 data. The first method used the MLE and MCMC algorithms to compute the nine parameters of the PM model and their uncertainties. We then used the estimated parameters in conjunction with the PM model to calculate the membership probability for each star. A star was selected as a member if its membership probability was greater than or equal to 0.5. From our analysis, we note that the PM model has difficulty finding the cluster and field centroids when nf significantly exceeds nc. However, when the cluster kinematics shows mean PMs of greater than those of the background stars, its population can be seen as an overdensity in the VPD. The second method employed the DBSCAN clustering algorithm in a five-dimensional space of positions, PMs, and parallaxes. To find the optimal values for the parameters ϵ and minPts, we followed a similar procedure to that of Castro-Ginard et al. (2018). Our implementation differs in that we use the median value of ϵ instead of the minimum value in the k-NND. This significantly improves the efficiency of the algorithm in determining the star members in each cluster.
The RDPs were calculated considering Poissonian uncertainties in each ring. To characterise them, we fitted the King model, implementing the MLE method and the MCMC algorithm to estimate the ρ0, rc, and rt parameters and their uncertainties. The model matched the Pleiades cluster profile because its star members are confined mainly within the tidal radius. For this reason, there are no significant differences with previous works in the estimated radii for this cluster. On the contrary, the Praesepe and Blanco 1 clusters have members beyond their tidal radii, exhibiting extended structures, and the King model slightly disagrees beyond 10 pc from the centre of the clusters as a result of its limitations. We find substantial increments in the computed tidal radii for these clusters. The most noteworthy is found for the Blanco 1 cluster, whose radius increased compared to those reported by Zhang et al. (2020) and Pang et al. (2021), which may be due to the distribution of stars on the outskirts. On the other hand, the computed ρ0 values are larger than those previously estimated with other catalogues, because Gaia has observed these clusters in greater depth. For the Pleaides cluster, we find that the stars between the core and tidal radius are a little scattered. This may be a product of mass segregation in the cluster (van Leeuwen et al. 1980). Although a tidal tail was previously reported (Lodieu et al. 2019), we could not detect it. For Praesepe and Blanco 1, we identified elongated shapes and prominent tails containing stars that have high membership probabilities determined from the PM model. In particular, Blanco 1 is the most widespread, reaching a tidal tail almost twice the size of that of Praesepe. However, we found that only 5% and 10% of the members in Praesepe and Blanco 1 are on the outskirts of the clusters. In addition, the membership methods used in this work restrict the search region, limiting the possibility of observing tails. Further velocity space-based research is needed – similar to that presented by Röser & Schilbach (2019), Tang et al. (2019), Jerabkova et al. (2021), Tarricq et al. (2022) – in order to recover additional stars on the outskirts of these clusters.
Although the stellar population in these clusters is mostly dominated by main sequence stars, we found 10 of the 11 white dwarfs and 3 giant stars in Praesepe reported by Lodieu et al. (2019). On the contrary, the Pleiades white dwarf LB 1497 (Eggen & Greenstein 1965) was not detected in this work. We also estimated the ages and metallicities of the clusters using the BASE-9 method (von Hippel et al. 2006; Robinson et al. 2016) and the PARSEC tracks (Bressan et al. 2012; Marigo et al. 2013). The inputs for BASE-9 were the Gaia photometry values G, GBP, and GRP of the members that we classified using the cross-matching between the PM model and DBSCAN. Our age and metallicity results for Pleiades and Blanco 1 are in agreement with those reported by Gaia Collaboration (2018) and Bossini et al. (2019). The metallicity we calculate for Praesepe is in agreement with that obtained by Gaia Collaboration (2018), but the age we find is close to the value reported by Gossage et al. (2018).
Acknowledgments
The authors would like to thank the anonymous referee and Prof. Beatriz Sabogal for their valuable comments and suggestions to improve this manuscript. They also thank Prof. Ted von Hippel for his help in setting up BASE-9. The authors would like to thank the Vice Presidency of Research & Creation’s Publication Fund at Universidad de los Andes for its financial support and also the Fondo de Investigaciones de la Facultad de Ciencias de la Universidad de los Andes, Colombia, through programa de investigación código INV-2021-128-2295. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
References
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Fabricius, C., Khanna, S., et al. 2023, A&A, 674, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Bossini, D., Vallenari, A., Bragaglia, A., et al. 2019, A&A, 623, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, R., Pasquato, M., Vallenari, A., et al. 2019, A&A, 627, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Ginard, A., Jordi, C., Luri, X., et al. 2018, A&A, 618, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dinnbier, F., Kroupa, P., Šubr, L., & Jeřábková, T. 2022, ApJ, 925, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Eggen, O. J., & Greenstein, J. L. 1965, ApJ, 141, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. 1996, A Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. United States, 96, 226 [NASA ADS] [Google Scholar]
- Feigelson, E. D., & Babu, G. J. 2012, Modern Statistical Methods for Astronomy (Cambridge: Cambridge University Press) [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, X.-H. 2019a, PASP, 131, 044101 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, X.-H. 2019b, MNRAS, 486, 5405 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Statist. Sci., 7, 457 [NASA ADS] [Google Scholar]
- Godoy-Rivera, D., Pinsonneault, M. H., & Rebull, L. M. 2021, ApJS, 257, 46 [CrossRef] [Google Scholar]
- Gossage, S., Conroy, C., Dotter, A., et al. 2018, ApJ, 863, 67 [Google Scholar]
- Holland, K., Jameson, R. F., Hodgkin, S., Davies, M. B., & Pinfield, D. 2000, MNRAS, 319, 956 [Google Scholar]
- Jerabkova, T., Boffin, H. M. J., Beccari, G., et al. 2021, A&A, 647, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [Google Scholar]
- Kounkel, M., & Covey, K. 2019, AJ, 158, 122 [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2007, AJ, 134, 2340 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Bland-Hawthorn, J. 2019, ARA&A, 57, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Lodieu, N., Pérez-Garrido, A., Smart, R. L., & Silvotti, R. 2019, A&A, 628, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Bressan, A., Nanni, A., Girardi, L., & Pumo, M. L. 2013, MNRAS, 434, 488 [Google Scholar]
- McInnes, L., Healy, J., & Astels, S. 2017, J. Open Source Softw., 2 [Google Scholar]
- Meingast, S., Alves, J., & Rottensteiner, A. 2021, A&A, 645, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J. C. 1981, A&A, 97, 235 [NASA ADS] [Google Scholar]
- Pang, X., Li, Y., Yu, Z., et al. 2021, ApJ, 912, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Pinfield, D. J., Jameson, R. F., & Hodgkin, S. T. 1998, MNRAS, 299, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, A. E., Schilbach, E., Kharchenko, N. V., Röser, S., & Scholz, R. D. 2007, A&A, 468, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reino, S., de Bruijne, J., Zari, E., d’Antona, F., & Ventura, P. 2018, MNRAS, 477, 3197 [Google Scholar]
- Robinson, E., von Hippel, T., Stein, N., et al. 2016, Astrophysics Source Code Library [record ascl:1608.007] [Google Scholar]
- Röser, S., & Schilbach, E. 2019, A&A, 627, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabogal-Martínez, B. E., García-Varela, J. A., Higuera, G. M. A., Uribe, A., & Brieva, E., 2001, Rev. Mex. Astron. Astrofis., 37, 105 [Google Scholar]
- Salaris, M., & Bedin, L. R. 2019, MNRAS, 483, 3098 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, W. L. 1971, A&A, 14, 226 [NASA ADS] [Google Scholar]
- Slovak, M. H. 1977, AJ, 82, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, W., de Grijs, R., Deng, L., & Albrow, M. D. 2019, ApJ, 876, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, S.-Y., Pang, X., Yuan, Z., et al. 2019, ApJ, 877, 12 [Google Scholar]
- Tarricq, Y., Soubiran, C., Casamiquela, L., et al. 2022, A&A, 659, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uribe, A., & Brieva, E. 1994, Ap&SS, 214, 171 [NASA ADS] [CrossRef] [Google Scholar]
- van Groeningen, M. G. J., Castro-Ginard, A., Brown, A. G. A., Casamiquela, L., & Jordi, C. 2023, A&A, 675, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 1980, in Star Clusters, ed. J. E. Hesser, 85, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Vasilevskis, S., Klemola, A., & Preston, G. 1958, AJ, 63, 387 [NASA ADS] [CrossRef] [Google Scholar]
- von Hippel, T., Jefferys, W. H., Scott, J., et al. 2006, ApJ, 645, 1436 [Google Scholar]
- Zhang, Y., Tang, S.-Y., Chen, W. P., Pang, X., & Liu, J. Z. 2020, ApJ, 889, 99 [Google Scholar]
Appendix A: Gaia query
We selected data in the range of ϖ > ;2 mas. Also, to remove possible artifacts, we extracted sources by filtering the astrometric errors shown in the query below.
SELECT * FROM gaiadr3.gaia_source WHERE pmra IS NOT NULL AND pmra != 0 AND pmdec IS NOT NULL AND pmdec != 0 AND ruwe < 1.4 AND phot_g_mean_flux_over_error > 10 AND phot_rp_mean_flux_over_error > 10 AND phot_bp_mean_flux_over_error > 10 AND visibility_periods_used > 8 AND astrometric_excess_noise < 1 AND parallax_over_error > 10 AND parallax IS NOT NULL AND parallax > 2
Appendix B: Uncertainty estimation for the nine parameters in the PM model
We show a corner plot of the sampling of the posterior probability function using the MCMC algorithm for the PM model in the Pleiades region. The implementation uses 100 walkers and 5000 iterations, and converges to a good agreement with the MLE method result. The upper and lower uncertainties for each parameter correspond to the 16th and 84th percentiles of the samples, respectively.
 |
Fig. B.1. Corner plot of the posterior probability density function of the PM model for the Pleiades region. |
Appendix C: Estimation of the King and stellar parameters
We show corner plots of the King and stellar parameter sampling of the posterior probability functions using the MCMC algorithm for the Pleiades cluster. The upper and lower uncertainties for each parameter correspond to the 16th and 84th percentiles of the samples, respectively.
 |
Fig. C.1. Corner plots of the estimations of the King parameters (left panel) and stellar parameters using BASE-9 (right panel) for the Pleiades cluster. |
All Tables
PM model parameters θmax computed using the MLE method for Pleiades, Praesepe, and Blanco 1 clusters.
Number of members found with the PM model, the DBSCAN (DB) algorithm, the cross-matching, and parameters computed for the target clusters.
All Figures
 |
Fig. 1. VPDs for Pleiades (left panel), Praesepe (middle panel), and Blanco 1 (right panel). The zoom plots show the selected regions in which we compute star membership with the PM model and the DBSCAN clustering algorithm. |
| In the text | |
 |
Fig. 2. Histogram of the 7th-NND for the region of Pleiades (red), simulated data (blue), and the Pleiades members selected from the PM model (orange). The grey dashed vertical line is the selected ϵ. |
| In the text | |
 |
Fig. 3. RDPs for Pleiades (left panel), Praesepe (middle panel) and Blanco 1 (right panel) OCs. The best-fit King model is shown by the solid red curves. The dashed vertical lines are the rc and rt values reported in Table 3. |
| In the text | |
 |
Fig. 4. Spatial distributions in Galactic cartesian coordinates through the Astropy package (Astropy Collaboration 2022) for Pleiades (top row), Praesepe (middle row), and Blanco 1 (bottom row) after applying the distance corrections. The black arrow points to the Galactic centre. The red dashed circles are the tidal radii found in this work reported in Table 3. |
| In the text | |
 |
Fig. 5. CMDs for Pleiades (left panel), Praesepe (middle panel) and Blanco 1 (right panel) OCs. The best-fit isochrones are indicated with the solid red curves, with ages and metallicities estimated using BASE-9 (von Hippel et al. 2006; Robinson et al. 2016). |
| In the text | |
 |
Fig. B.1. Corner plot of the posterior probability density function of the PM model for the Pleiades region. |
| In the text | |
 |
Fig. C.1. Corner plots of the estimations of the King parameters (left panel) and stellar parameters using BASE-9 (right panel) for the Pleiades cluster. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&\psi _{\rm c}(\mu _{\alpha *, i},\mu _{\delta , i})=\frac{1}{2 \pi \sigma _{\rm c}^{2}} exp \left(-\frac{1}{2}\left[ \left(\frac{\mu _{\alpha *, i}-\mu _{\rm \alpha c}}{\sigma _{\rm c}}\right)^{2} +\left( \frac{\mu _{\delta , i}-\mu _{\rm \delta c}}{\sigma _{\rm c}}\right)^{2}\right] \right), \end{aligned} $$](/articles/aa/full_html/2023/09/aa46569-23/aa46569-23-eq1.gif)
![$$ \begin{aligned}&\psi _{\rm f}(\mu _{\alpha *, i},\mu _{\delta , i})=\frac{1}{2 \pi \sigma _{\rm \alpha f} \sigma _{\rm \delta f} \sqrt{1-\rho ^{2}}}\exp \left[-\frac{1}{2(1-\rho ^{2})} \Omega (\mu _{\alpha *, i},\mu _{\delta , i}) \right], \end{aligned} $$](/articles/aa/full_html/2023/09/aa46569-23/aa46569-23-eq2.gif)
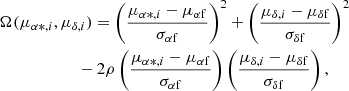
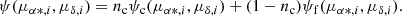
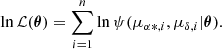
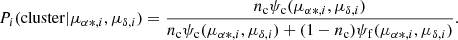

![$$ \begin{aligned} \rho (r) = \rho _0 \left[ \frac{1}{\sqrt{1 + (r/r_{\rm c})^2}} - \frac{1}{\sqrt{1 + (r_{\rm t}/r_{\rm c})^2}} \right]^2, \end{aligned} $$](/articles/aa/full_html/2023/09/aa46569-23/aa46569-23-eq8.gif)