| Issue |
A&A
Volume 608, December 2017
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201629878 | |
| Published online | 11 December 2017 | |
Chemical enrichment and accretion of nitrogen-loud quasars⋆,⋆⋆
1 Dipartimento di Fisica e Astronomia, Universitá degli Studi di Firenze, via G. Sansone 1, 50019 Sesto Fiorentino, Italy
e-mail: matsuoka@arcetri.astro.it
2 INAF–Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
3 Research Center for Space and Cosmic Evolution, Ehime University, 2–5 Bunkyo-cho, 790-8577 Matsuyama, Japan
4 Cavendish Laboratory, University of Cambridge, 19 J. J. Thomson Avenue, Cambridge CB3 0HE, UK
5 Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
6 Korea Astronomy and Space Science Institute, 776 Daedeok-daero, Yuseong-gu, 34055 Daejeon, Republic of Korea
7 The Open University of Japan, 2–11 Wakaba, Mihama-ku, 261-8586 Chiba, Japan
Received: 11 October 2016
Accepted: 18 September 2017
We present rest-frame optical spectra of 12 “nitrogen-loud” quasars at z ~ 2.2, whose rest-frame ultraviolet (UV) spectra show strong nitrogen broad emission lines. To investigate their narrow-line region (NLR) metallicities, we measure the equivalent width (EW) of the [O iii]λ5007 emission line: if the NLR metallicity is remarkably high, as suggested by the strong UV nitrogen lines, the [O iii]λ5007 line flux should be very weak due to the low equilibrium temperature of the ionized gas owing to significant metal cooling. In the result we found that our spectra show moderate EW of the [O iii]λ5007 line similar to general quasars. This indicates that nitrogen-loud quasars do not have extremely metal-rich gas clouds in NLRs. This suggests that strong nitrogen lines from broad-line regions (BLRs) originate from exceptionally high abundances of nitrogen relative to oxygen without very high BLR metallicities. This result indicates that broad emission lines of nitrogen are not good indicators of the BLR metallicity in some cases. On the other hand, we also investigate virial black hole masses and Eddington ratios by using the Hβ and C ivλ1549 lines for our sample. As a result, we found that black hole masses and Eddington ratios of nitrogen-loud quasars tend to be low and high relative to normal quasars, suggesting that nitrogen-loud quasars seem to be in a rapidly accreting phase. This can be explained in terms of a positive correlation between Eddington ratios and nitrogen abundances of quasars, which is probably caused by the connection between the mass accretion onto black holes and nuclear star formation.
Key words: galaxies: active / galaxies: nuclei / quasars: emission lines / quasars: general
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programme 088.B-0191(A), and at the Subaru Telescope, which is operated by the National Astronomical Observatory of Japan.
Reduced spectra (FITS files) are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/608/A90
© ESO, 2017
1. Introduction
Chemical evolution is one of the most crucial topics in extragalactic research because metal formations and its enrichments have close connections with the star formation in galaxies, corresponding to the galaxy evolution. The simplest way to investigate the chemical evolution of galaxies is by measuring metallicities or chemical abundances of galaxies at various redshifts and exploring its redshift evolution. Observationally, the gas-phase metallicity of star-forming galaxies in the local Universe can be measured by using optical emission-line spectra, e.g., [O ii]λ3727, Hβ, [O iii]λ4959, [O iii]λ5007, Hα, and [N ii] λ6584 (see Pagel et al. 1979; Kewley & Dopita 2002; Nagao et al. 2006a; Ly et al. 2016, and references therein), and even at z> 1 current near-infrared observations can cover these lines (e.g., Maiolino et al. 2008; Wuyts et al. 2016), with some caveats such as systematic errors in the calibration (see, e.g., Kewley & Ellison 2008). However, at z> 3, these diagnostics are more difficult because these emission lines are redshifted out of near-infrared wavelengths.
An alternative way to measure metallicities of galaxies in the early Universe is by focusing on the active Galactic nucleus (AGN). In fact, this approach has two main advantages in the high-z research. First, thanks to its huge luminosity we can obtain high quality spectra even at high redshift. Second, because of various emission lines shown in rest-frame ultraviolet (UV) wavelength we can extract chemical properties from observed-frame optical spectra. The prominent emission-line spectra of AGNs provide chemical properties of gas clouds illuminated by the central engine: it is possible to investigate chemical properties, even in the Galactic scale, if we focus on emission lines emitted from the narrow-line regions (NLRs) (RNLR ~ 102−4 pc; e.g., Bennert et al. 2006a,b), instead of broad-line regions (BLRs). Thus by using AGNs, we can reveal the chemical evolution in the early Universe, closely related to the formation and evolution of galaxies. In addition, we emphasize that only AGNs allow us to estimate black hole masses in the high-z Universe based on the kinematical state of BLR clouds. Therefore, AGN spectra are useful also in order to understand the co-evolution of galaxies and supermassive black holes (SMBHs) in the high-z epoch in addition to the chemical evolution.
In the diagnostics of AGN metallicities, we often recognize that nitrogen is one of the most useful elements since it is a secondary element and its abundance is expected to be proportional to the square of the metallicity, i.e., N/H ∝ (O/H)2. The spectra of AGN basically show some broad emission lines of nitrogen, e.g., N vλ1240, N iv]λ1486, and N iii]λ1749, in the UV wavelength. Hamann & Ferland (1992, 1993) used emission-line flux ratios of N vλ1240/C ivλ1549 and N vλ1240/He iiλ1640 as indicators of the BLR metallicity (see also Hamann & Ferland 1999; Hamann et al. 2002). Subsequently, many papers follow this method based on nitrogen lines to investigate BLR metallicities (e.g., Warner et al. 2004; Nagao et al. 2006b; Dietrich et al. 2009; Matsuoka et al. 2011; Shin et al. 2013).
In previous studies, emission-line flux ratios including nitrogen lines have mainly been used to estimate the BLR metallicity, ZBLR, as described above. Based on this method, it has been found that the BLR in the most luminous quasars show supersolar metallicities (e.g., Hamann & Ferland 1992; Dietrich et al. 2003; Nagao et al. 2006b), even for quasars at z> 6 (e.g., Kurk et al. 2007; Jiang et al. 2007; Juarez et al. 2009; Mortlock et al. 2011). Moreover, Osmer & Smith (1980) discovered an unusual quasar, Q0353−383, at z = 1.96 that has prominent broad emission lines of N iii]λ1749, N iv]λ1486, and N vλ1240: this is called the nitrogen-loud quasar (hereafter N-loud quasar). Baldwin et al. (2003b) claimed that these unusual nitrogen emissions in Q0353−383 are likely due to high metallicity in the BLR; the metallicity estimated by these nitrogen lines reaches ~ 15 Z⊙ (see also Osmer 1980) if we assume the relation of N/H ∝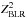 . However, we note that such extremely high metallicity is very hard to reconcile with galaxy chemical evolutionary models. Therefore, the N-loud quasars raise a question whether or not the broad nitrogen lines are really reliable for estimating ZBLR.
. However, we note that such extremely high metallicity is very hard to reconcile with galaxy chemical evolutionary models. Therefore, the N-loud quasars raise a question whether or not the broad nitrogen lines are really reliable for estimating ZBLR.
Motivated by this question, the rest-frame UV spectrum of N-loud quasars has been investigated. By using 293 N-loud quasars selected from the Sloan Digital Sky Survey (SDSS; York et al. 2000), Jiang et al. (2008) reported that N-loud quasars may not have such high BLR metallicities, but may just have unusually high relative abundances of nitrogen because their rest-frame UV spectra are not significantly different from those of typical normal quasars, except for the nitrogen lines; this means that metallicity-sensitive emission line flux ratios excluding nitrogen do not show the extremely high metallicity expected from nitrogen lines. This explanation throws a doubt on the use of nitrogen lines for BLR metallicity measurements for quasars, at least in some cases. On the other hand, Batra & Baldwin (2014) aimed to clarify this controversial point by estimating BLR metallicities of N-loud quasars, and claimed that strong nitrogen lines of N-loud quasars are caused by high BLR metallicities and not the high relative abundance of nitrogen. We note, however, that since this study was concluded only by using emission line flux ratios including nitrogen lines, i.e., N vλ1240, N iv]λ1486, and N iii]λ1750, it would be still unclear whether N-loud quasars have extremely metal-rich gas clouds in BLRs: we need to estimate BLR metallicities by using emission line flux ratios including nitrogen lines and also flux ratios excluding nitrogen lines, and comparing them with each other.
To solve this problem regarding the origin of strong nitrogen lines seen in quasar spectra, we focus on NLR metallicities instead of BLR ones. If BLR metallicities of N-loud quasars are extremely high, NLR values would be also relatively high, although both absolute values are not the same (e.g., Fu & Stockton 2007; Du et al. 2014). Recently, Araki et al. (2012) investigated the NLR metallicity of a N-loud quasar at z = 3.16, SDSS J1707+6443, by using the [O iii]λ5007 emission line shown in rest-frame optical wavelengths: if the NLR metallicity is remarkably high as suggested by strong UV nitrogen lines, the [O iii]λ5007 line flux should be very weak due to the low equilibrium temperature of the ionized gas owing to significant metal cooling. We also examined its other parameters (e.g., ionization parameter and hydrogen density of NLR gas clouds) by using fluxes of [Ne v]λ3426, [O ii]λ3727, and [Ne iii]λ3869, which are used to correctly estimate the NLR metallicity. In the result we found that the NLR in this N-loud quasar is not extremely metal rich, which is not consistent with the naive expectation from unusually strong nitrogen broad lines. We note, however, that it is difficult to conclude that the N-loud quasar is not extremely metal rich generally because this result was obtained only from one object. Therefore, additional data sets of rest-frame optical spectra of N-loud quasars are crucially needed to investigate whether or not BLR metallicities of N-loud quasars are universally extremely high.
Furthermore, if N-loud quasars do not have extremely high metallicities as Araki et al. (2012) claimed, unusually high nitrogen abundance relative to oxygen is required. Since the chemical properties of gas in Galactic nuclei are closely related to the past star formation history and the gas radial motion, we focus on the relation between the mass accretion to SMBHs and the nuclear star formation. Recently, by using optical spectra of 2383 SDSS quasars at 2.3 <z< 3.0, Matsuoka et al. (2011) investigated the dependence of the emission-line flux ratios (BLR metallicity indicators) on the Eddington ratio. They found that the Eddington ratio depends on the emission-line flux ratios involving N vλ1240, while it does not correlate with the other emission-line flux ratios without the nitrogen line (see Fig. 6 in Matsuoka et al. 2011). This result means that the relative nitrogen abundance seems to depend on the Eddington ratio. This indicates that a rapid mass accretion onto SMBHs is associated with a post-starburst phase when asymptotic giant branch (AGB) stars enrich the interstellar medium with nitrogen. By considering this relation, we can obtain one possible scenario that N-loud quasars are in an AGN active phase, i.e., a high accretion phase. This would be helpful in order to understand the connection between AGN and star formation activities, closely related to the co-evolution of galaxies and SMBHs. In this sense, therefore, it is also important to examine whether N-loud quasars show high Eddington ratios.
Journal of spectroscopic observations.
 |
Fig. 1 Near-infrared spectra of N-loud quasars obtained in our IRCS and SOFI runs, adopting the two-pixel binning in the wavelength direction. Gray dotted lines show the wavelengths of some rest-frame optical emission lines, i.e., [Ne v]λ3426, [O ii]λ3727, [Ne iii]λ3869, Hβ, [O iii]λ4959, and [O iii]λ5007 lines, expected from redshifts given in Shen et al. (2008). |
 |
Fig. 1 continued. |
In this paper, we present near-infrared spectra of 12 N-loud quasars and investigate their spectroscopic properties. Specifically, we estimate NLR metallicities, black hole masses, and Eddington ratios by using emission lines in the rest-frame optical wavelength. In Sect. 2, we describe our sample of N-loud quasars and observations. Section 3 shows the spectral measurements. We summarize our results in Sect. 4, and discuss the interpretation of results in Sect. 5. The summary is given in Sect. 6. Here, we adopt a concordance cosmology with (ΩM,ΩΛ) = (0.3,0.7) and H0 = 70 km s-1 Mpc-1.
2. Observations and data reduction
2.1. Target selection
We select our targets from the N-loud quasar catalogue of Jiang et al. (2008). They collected 293 N-loud quasars from the SDSS Fifth Data Release (Schneider et al. 2007) with the following criteria: (1) rest-frame equivalent widths (EW) of N iv]λ1486 or N iii]λ1750>3Å which are significantly higher than those of normal quasars, i.e., ~ 0.4 Å for N iii]λ1750 line and typically no detection for N iv]λ1486 line (see also Vanden Berk et al. 2001); (2) the redshift range 1.7 < z< 4.0 covering one or two broad nitrogen lines in SDSS optical spectra; and (3) i′ < 20.1. To obtain emission lines of [O iii]λ5007, Hβ, [Ne iii]λ3869, [O ii]λ3727, and [Ne v]λ3426 in the near-infrared wavelength range, in this study we select 12 quasars at 2.09 < z < 2.57 from the catalogue with the criteria of observable coordinates and apparent magnitudes given in Table 1.
2.2. Near-infrared spectroscopic observations
We observed our targets by using the Infrared Camera and Spectrograph (IRCS; Kobayashi et al. 2000) with the adaptive optics system with 188 elements (AO188; Hayano et al. 2008, 2010) on the Subaru Telescope, and with the Son of ISAAC (SOFI; Moorwood et al. 1998) on the New Technology Telescope (NTT). The observational logs are given in Table 1.
For the IRCS observation, we obtained J- and H-band spectra of three targets at z ~ 2.3 by using a 0.̋225 slit. Thanks to AO188 with the laser guide star (LGS) mode, we were able to achieve typical point-spread function sizes of ~0.25′′ around 13 000 Å and ~0.21′′ at 16 000 Å. In the H-band observation, we measured the emission lines of [O iii]λ5007 and Hβ, whose expected wavelength is 16 000 Å < λobs < 16 600 Å, to investigate NLR metallicities and black hole masses. On the other hand, in the J-band observation we focused on the emission lines of [O ii]λ3727 and [Ne iii]λ3869, redshifted to the range at 12 200 Å < λobs < 12 800 Å. These emission lines are used to investigate properties of NLR gases (e.g., ionization parameters and hydrogen densities of clouds). The spectral dispersion is ~ 4.68 Å pixel-1 and the spectral resolution estimated from OH emission lines was ~ 1000. The total exposure time for each target was roughly 7000 s for J band and 2500 s for H band. The unit exposure times were 300–600 s.
The SOFI observations were performed with the Grism Blue Filter (GBF) to cover the wavelength at 9500 Å < λobs < 16 400 Å, where we were able to cover five emission lines of the nine remaining N-loud quasars at 2.1 ≲ z ≲ 2.2 simultaneously. Typical seeing size was ~1.5′′. We used a long slit, 0.̋6 in width, and the dispersion was ~ 6.93 Å pixel-1. The spectral resolution was ~ 650. Total exposure times were ~ 7200 s for each target, adopting an unit exposure time of ~600 s.
2.3. Data reduction
For all spectra, standard data reduction procedures were performed using available IRAF1 tasks. By using dome-flat frames, object frames were flat-fielded and thus the first sky subtraction was performed with the A−B method; we subtracted pairs of subsequent frames with the target at different positions along the slit. Cosmic ray events were removed by using the lacos_spec task (van Dokkum 2001). We extracted the one-dimensional spectra with the apall task, using an 8-pixel (~0.4′′) aperture for IRCS and 11-pixel (~3.0′′) for SOFI. In this extraction, we fit the residuals of sky background and subtracted them. The wavelength calibration was executed with arc lamp frames. Finally, flux calibration and telluric absorption correction were carried out by using observed spectra of telluric standard stars. We took defocused data for bright standard star observations to avoid the saturation of the detector. This step affected the flux calibration: the obtained fluxes were overestimated due to the extensive slit loss of the defocused data.
 |
Fig. 2 Examples of spectral fittings in rest-frame optical spectra of two N-loud quasars (SDSS J1211+0449 and SDSS J0938+0900). Red lines show total fitting results. Gray dotted lines denote fits of continuum, and individual emission-line components are indicated as light gray Gaussian curves. Dark gray lines denote the residuals. |
To correct observational uncertainties, e.g., the slit loss, mainly in observations of standard stars and weather condition, we re-calibrated fluxes by using photometric magnitudes of the targets themselves. We obtained near-infrared magnitudes of the J and H bands from i-band magnitude using the color-z relation of SDSS-UKIDSS quasars in Wu & Jia (2010) since there is almost no near-infrared magnitude for our targets. We note that only two objects (SDSS J0938+0900 and SDSS J1308+1136) have been observed with J and H bands through the United Kingdom Infrared Telescope (UKIRT) Infrared Deep Sky Survey (UKIDSS; Lawrence et al. 2007), and we confirmed that these observed magnitudes are consistent with the estimated values describe above with uncertainties of ~ 2%. By comparing the extrapolated photometric magnitudes with spectroscopic magnitudes measured from our spectra, we scaled fluxes of the spectra; the mean value of the scaling factor is ~ 0.8. The final reduced spectra are shown in Fig. 1.
3. Spectral measurements
To measure line properties, we fit emission lines of Hβ and [O iii]λ4959, 5007 lines with Gaussian functions. In the multi-component fitting processes, we used a routine, mpcurvefit, in the Interactive Data Language (IDL). First, we converted our observed spectra to the rest frame. Second, we fit the continuum with a single power-law model. In this fitting, we ignored the host-galaxy starlight and the Fe ii emission blends due to low signal-to-noise ratios, S/N. The best continuum fit was determined based on the χ2 statistics in the wavelength ranges where there are no strong emission lines, e.g., 4600−4750 Å and 5050−5150 Å in the rest frame. From the power-law continuum model, we estimate the monochromatic luminosity at 5100 Å.
Results of spectral fitting.
After the pseudo-continuum model was subtracted from the original spectrum, we fit the emission of the Hβ, [O iii]λ4959, and [O iii]λ5007 lines. We used one or two Gaussians for the broad and narrow Hβ components. For the narrow [O iii]λ4959 and [O iii]λ5007 lines, we adopted the single-Gaussian fitting; their flux ratio is fixed as three. For all narrow components, we adopted the same velocity shift and width by assuming the same kinematics of NLR clouds. We measured the emission-line flux of [O iii]λ5007 and obtained the rest-frame equivalent width, EW[O iii], with the continuum flux at 5007 Å from the power-law model.
To estimate uncertainties of the line width and luminosity measurements, we adopted the Monte Carlo flux randomization method (e.g., Bentz et al. 2009; Shen et al. 2011; Park et al. 2012). We generated 1000 mock spectra for each observed spectrum by adding Gaussian random noise based on the flux errors. Then, we measured the line widths and AGN luminosities from the simulated spectra. We derived the standard deviation of their distribution as the measurement uncertainty. We also gave 3σ upper limits for the [Ne v]λ3426, [O ii]λ3727, and [Ne iii]λ3869 lines by adopting the average velocity width of the [O iii]λ5007 emission line (Δv ~ 1450 km s-1) since we could not detect these emission lines in our observations (see Fig. 1).
In Fig. 1, some objects (e.g., SDSS J1211+0449 and SDSS J1036+1247) seem to show blueshifted narrow lines compared to the expected central wavelength indicated by dotted vertical lines (Shen et al. 2008). Although these velocity shifts may be a sign of gas outflow (e.g., Rupke et al. 2005; Bae & Woo 2014; Woo et al. 2016; Bae et al. 2017), the accuracy of the redshift measurement needs to be considered carefully in order to discuss this topic, and this is beyond the scope of this paper. We note that this uncertainty of redshift does not affect our conclusion.
Figure 2 shows two examples of the fitting results. Measurement results, i.e., line fluxes and equivalent widths of the [O iii]λ5007 line, the full widths at half maximum (FWHM) of the broad Hβ line, and monochromatic luminosities at 5100 Å, are listed in Table 2, and 3σ upper limits of fluxes for the undetected emission lines, i.e., [Ne v]λ3426, [O ii]λ3727, and [Ne iii]λ3869 lines, are shown in Table 3.
4. Results
As described in Sect. 2, we obtained near-infrared (i.e., J- and H bands) spectra of 12 N-loud quasars as shown in Fig. 1. In J-band wavelength, there is no significant detection of emission lines, e.g., [Ne iii]λ3869, as Araki et al. (2012) found in the spectra of SDSS J1707+6443. On the other hand, H-band spectra show significant detections of Hβ, [O iii]λ4959, and [O iii]λ5007 lines for most of the objects in our sample.
Estimates of 3σ flux upper limits of undetected emission lines.
 |
Fig. 3 Distribution of rest-frame equivalent width of [O iii]λ5007 line. The black line histograms denote our sample of 13 N-loud quasars, the dark gray filled histogram shows our observed 11 N-loud quasars, and the open histogram shows the 3σ upper limit. The result of SDSS J1707+6443 (Araki et al. 2012) is shown as a light gray filled histogram. The gray line open histogram denotes the distribution of 232 SDSS quasars at 0 < z < 1 in a luminosity range at log λL5100 = 45.5–46.5 (Shen et al. 2011), which is divided by five to compare with our sample easily. |
Figure 3 shows distributions of observed rest-frame equivalent widths of the [O iii]λ5007 line of N-loud quasars, denoted as black-line filled histograms. Here, we added SDSS J1707+6443 in Araki et al. (2012) to our sample. In order to compare these N-loud quasars with general quasars, we also plot [O iii]λ5007 equivalent widths of SDSS quasars at 0 <z < 1 (Shen et al. 2011), shown as gray-line open histograms in Fig. 3. Moreover, since some previous studies reported the anti-correlation between the equivalent widths of narrow emission lines and the AGN luminosity (e.g., Steiner 1981; Zhang et al. 2013), for consistency in luminosities between N-loud and general quasars, we selected 232 general quasars at log λL5100 = 45.5–46.5 from the SDSS sample, which is almost the same range as our N-loud quasar sample. As shown in Fig. 3, we found that the equivalent widths of N-loud quasars are slightly larger than those of general SDSS quasars. The averaged equivalent widths (standard deviations) of N-loud and general quasars are 1.34 (0.22) and 0.99 (0.47), respectively. By using the Kolmogorov-Smirnov (KS) test, we checked that there is no significant difference of their EW[O iii] distributions (p = 0.004).
Measurements of rest-frame UV spectra obtained by SDSS observations.
In addition to measurements of emission lines, we also obtained black hole masses and Eddington ratios of our sample shown in Table 2, estimated based on the FWHM of the Hβ line and monochromatic luminosity at 5100 Å, which is well calibrated in the local Universe (e.g., Vestergaard & Peterson 2006; Ho & Kim 2015). Usually, the single-epoch estimation can be expressed as follows: 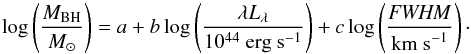 (1)In this study, we adopted a recipe of Hβ-based black hole masses in Vestergaard & Peterson (2006), i.e., a = 0.91, b = 0.50, and c = 2.00. Eddington ratios are provided through estimates of bolometric luminosities, using a bolometric correction of BC = 9.26 (Richards et al. 2006; Shen et al. 2011). Note that we gave only statistical errors of black hole masses and Eddington ratios in Table 2, excluding systematic ones originating from calibrations and virial parameters. In addition to the near-infrared spectra, our objects have observed optical spectra obtained with SDSS spectrographs (Shen et al. 2008, 2011). Thus, we collected the rest-frame UV measurements, i.e., FWHMC iv, log (λL1350), log (MBH,C iv), and log (L/LEdd)C iv, in Table 4. Here, C ivλ1549-based black hole masses are estimated with a recipe of a = 0.66, b = 0.53, and c = 2.00 (Vestergaard & Peterson 2006). In the estimation of bolometric luminosities from the monochromatic luminosity at 1350 Å, we adopted BC = 3.81 (Shen et al. 2011). For the 12 N-loud quasars in our sample, measurements of FWHMs of the C ivλ1549 line and monochromatic luminosities at 1350 Å are available from Shen et al. (2011).
(1)In this study, we adopted a recipe of Hβ-based black hole masses in Vestergaard & Peterson (2006), i.e., a = 0.91, b = 0.50, and c = 2.00. Eddington ratios are provided through estimates of bolometric luminosities, using a bolometric correction of BC = 9.26 (Richards et al. 2006; Shen et al. 2011). Note that we gave only statistical errors of black hole masses and Eddington ratios in Table 2, excluding systematic ones originating from calibrations and virial parameters. In addition to the near-infrared spectra, our objects have observed optical spectra obtained with SDSS spectrographs (Shen et al. 2008, 2011). Thus, we collected the rest-frame UV measurements, i.e., FWHMC iv, log (λL1350), log (MBH,C iv), and log (L/LEdd)C iv, in Table 4. Here, C ivλ1549-based black hole masses are estimated with a recipe of a = 0.66, b = 0.53, and c = 2.00 (Vestergaard & Peterson 2006). In the estimation of bolometric luminosities from the monochromatic luminosity at 1350 Å, we adopted BC = 3.81 (Shen et al. 2011). For the 12 N-loud quasars in our sample, measurements of FWHMs of the C ivλ1549 line and monochromatic luminosities at 1350 Å are available from Shen et al. (2011).
It is important to note that we ignore the effect of quasar variability on the results for black hole masses and Eddington ratios since a typical luminosity variability amplitude of quasars is only ~ 0.2 mag on timescales up to several years (e.g., Sesar et al. 2007; MacLeod et al. 2010, 2012) and the uncertainty of the single-epoch masses would be dominated by measurement errors (see Shen 2013, for more detail).
5. Discussion
In this section, we discuss chemical and physical parameters of N-loud quasars by using the measurements as described in Sects. 3 and 4. First, we investigate their NLR metallicities with a diagnostic method consisting of the equivalent width of the [O iii]λ5007 line (Araki et al. 2012). Second, we discuss the virial black hole mass of N-loud quasars estimated based on the Hβ line (see Sect. 4). We compare these black hole masses with those based on rest-frame ultraviolet spectra, e.g., the broad C ivλ1549 line. We also show their Eddington ratios, and discuss a possible connection between AGN and star formation.
5.1. NLR metallicities
The emission line of [O iii]λ5007 is a collisionally excited line and the emissivity depends strongly on the gas temperature. The equilibrium temperature of ionized gas clouds is significantly affected by gas metallicity because metal emission lines are main coolants of these clouds. Therefore, collisionally excited lines are good indicators of NLR metallicities; if the NLR metallicity is high, these emission lines should be faint.
To see the metallicity dependence of the [O iii]λ5007 equivalent width for NLR clouds, we used the photoionization code Cloudy (version 13.05; Ferland et al. 1998, 2013). In this calculation, we adopted the same parameters as those in Araki et al. (2012), i.e., the hydrogen densities of nH = 101.0 and 104.0 cm-3 and the ionization parameters of U = 10-3.5 and 10-1.5, whose parameter ranges are typical of low-z AGNs: Vaona et al. (2012) determined densities and ionization parameters of local Seyfert galaxies based on optical emission-line diagnostic diagrams (see also Bennert et al. 2006a,b; Nagao et al. 2001, 2002). For the spectral energy distribution (SED) of the photionizing continuum radiation (Mathews & Ferland 1987), we adopted the “table AGN” command, which reproduces the typical SED of AGNs. For the chemical composition of NLR gas, we assumed that dusty gas clouds contain Orion-type graphite and silicate grains, that all metals are changed with a solar abundance ratio, and we also consider the metal depletion onto dust grains (see Table 7.7 in Hazy, a brief introduction to Cloudy C13.05) except for helium and nitrogen. We used analytical expressions for He and N relative abundances as functions of metallicities given in Dopita et al. (2000): for helium, we consider both a primary nucleosynthesis component and the primordial value (Russell & Dopita 1992) and nitrogen is assumed to be a secondary nucleosynthesis element (e.g., van Zee et al. 1998). The metal depletion is also considered in these elements. We stopped the calculations when the hydrogen ionization fraction dropped below 15%.
Figure 4 shows the simulation result of EW[O iii] as a function of the NLR metallicity. This confirms that equivalent width of the [O iii]λ5007 line decreases rapidly as the metallicity increases, which is quite small at ZNLR> 5 Z⊙. These results are consistent with the predictions obtained by using the Cloudy version 08.00 in Araki et al. (2012). With this method, we can examine whether NLR metallicities of N-loud quasars are extremely high (ZNLR> 5 Z⊙) relative to general quasars, although we cannot estimate accurate metallicities only by using the [O iii]λ5007 equivalent width. As described in Sect. 4, we found that there is no significant difference between N-loud quasars and typical SDSS quasars in the same luminosity range. Since NLR metallicities show no significant redshift evolution (Nagao et al. 2006b; Matsuoka et al. 2009)2, we are able to compare our sample at z ~ 2.2 with the SDSS quasars at 0 <z< 1. This result, therefore, indicates that NLR metallicities of N-loud quasars are not extremely high relative to normal ones. This result confirms the result obtained by SDSS J1707+6443 in Araki et al. (2012).
 |
Fig. 4 Normalized equivalent widths of the [O iii]λ5007 line as a function of NLR metallicities, predicted by photoionization models. These are normalized at their respective peaks. Black solid, dashed, dot-dashed, and dotted lines are the photoionization model calculations with (log nH, log U) = (1.0, −1.5), (1.0, −3.5), (4.0, −1.5), and (4.0, −3.5), respectively. Given parameters are also labeled for each line. |
 |
Fig. 5 Model predictions of emission-line flux ratios, i.e., [Ne v]λ3426/[O iii]λ5007 (left, a), [O ii]λ3727/[O iii]λ5007 (middle, b), and [Ne iii]λ3869/[O iii]λ5007 (right, c), as a function of NLR metallicities. Black solid, dashed, dot-dashed, and dotted lines are the photoionization model calculations with (log nH, log U) = (1.0, −1.5), (1.0, −3.5), (4.0, −1.5), and (4.0, −3.5), respectively. The left panel shows only two high-U models because [Ne v]λ3426 line fluxes in low-U models are fainter than the [O iii]λ5007 fluxes. Horizontal lines show the 3σ upper limits of our sample. |
As described in Sect. 4, we also measured 3σ flux upper limits of undetected emission lines, i.e., [Ne v]λ3426, [O ii]λ3727, and [Ne iii]λ3869, listed in Table 3. Thus, to check whether the result obtained by the [O iii]λ5007 equivalent width is consistent with these upper limits, we compare the observational upper limits with model predictions obtained with the model calculations. Figure 5 shows the emission line flux ratios, i.e., [Ne v]λ3426/[O iii]λ5007, [O ii]λ3727/[O iii]λ5007, and [Ne iii]λ3869/[O iii]λ5007, as a function of NLR metallicities predicted by Cloudy. As shown in Fig. 5a, we find that the predicted emission line flux ratios of [Ne v]λ3426/[O iii]λ5007 are below the observational upper limits (gray horizontal lines) for all of the parameter sets examined in our calculations. We note that the predicted [Ne v]λ3426/[O iii]λ5007 flux ratio of the models with log U = −3.5 is far below the range shown in Fig. 5a. Figure 5b shows the line flux ratio of [O ii]λ3727/[O iii]λ5007 as a function of NLR metallicity; this line flux ratio is sensitive to ionization parameters. This figure implies that it is difficult to explain the observational results with low-U models, i.e., log U = −3.5. On the other hand, models with high ionization parameters satisfy most of observed upper limits at ZNLR< 4 Z⊙, whereas at ZNLR> 5 Z⊙, the low-nH and high-U model (a solid line) is restricted by all observational upper limits. This is consistent with the result of the [O iii]λ5007 equivalent width, namely that NLR metallicities of N-loud quasars are not extremely high. Moreover, in Fig. 5c we also confirmed that most objects can be explained with high-U model predictions of [Ne iii]λ3869/[O iii]λ5007 ratio instead of low-U models. It seems to be difficult to discuss hydrogen densities with the upper limits. As a result, we confirmed that these observational upper limits are consistent with the scenario that NLR metallicities of N-loud quasars are not extremely high.
In this section, we found that NLR clouds of N-loud quasars are not extremely metal rich generally. To interpret this observational result, we look at two possible scenarios. One is that the metallicity of N-loud quasars is not very high in BLRs and NLRs, assuming the correlation between ZBLR and ZNLR. In this case, our result indicates that BLR clouds of N-loud quasars are characterized by a very high nitrogen relative abundance without extremely high ZBLR. This means broad emission lines of nitrogen are unreliable indicators of the BLR metallicity in these cases. The second possibility is that ZBLR is determined by local enrichment at the BLR scale without an effect of global metallicity in their host galaxies traced by NLR metallicities because the total mass of BLR clouds is typically very low (MBLR ~ 102–104; Baldwin et al. 2003a). This picture can explain the situation that ZNLR is not very high while ZBLR is extremely high in N-loud quasars. In this case, since BLR metallicities do not trace chemical properties in Galactic scale, we should use metallicities of NLR gases instead of BLR metallicities if we want to investigate the chemical status in their host galaxies, especially at high redshift. We note, however, that Jiang et al. (2008) shows that emission line flux ratios excluding nitrogen lines of N-loud quasars do not seem to be different from those of normal quasars. This means that BLR metallicities do not have metal-rich gas clouds. Therefore, we conclude that BLR and NLR metallicities of N-loud quasars are not extremely high, and the nitrogen relative abundance is individually as high as in the former scenario. In the following sections we discuss a reason why N-loud quasars show BLR gas clouds containing high N relative abundance by considering a connection between BH growth and nitrogen enrichment via star formation.
 |
Fig. 6 Comparison of the monochromatic luminosities at 1350 Å and 5100 Å (left, a), the FWHM of the Hβ line and the C ivλ1549 line (middle, b), and virial black hole masses based on the C ivλ1549 line and Hβ line (right, c). Our sample of N-loud quasars are shown as red circles. Gray and yellow circles denote SDSS normal quasars at 1.5 < z < 2.2 in luminosity ranges of log λL1350 > 46.5 and log λL1350 < 46.5 from Shen & Liu (2012). Errors represent 1σ uncertainties of measurements, excluding systematic errors. The one-to-one relations are indicated by dashed lines for each panel. |
5.2. Black hole masses
As described in Sect. 4, we estimated black hole masses of N-loud quasars based on the rest-frame optical measurements, i.e., FWHM of Hβ line and continuum luminosities at 5100 Å, and the rest-frame UV measurements, i.e., FWHMC iv and L1350. In this section, we first examine the relation between L5100 and L1350, and the FWHMHβ and FWHMC iv relation. Then we compare the black hole masses of MBH,Hβ and MBH,C iv.
Figure 6a shows a relation of monochromatic luminosities at 5100 and 1350 Å of N-loud quasars, shown as red circles. For comparison, we also plotted SDSS general quasars at 1.5 <z< 2.2 in Shen & Liu (2012), represented with gray and yellow circles. In the result, we confirmed that N-loud quasars follow the L5100 Å and L1350 Å relation of general quasars. As shown in this figure, our N-loud quasars are distributed below the 1350 Å luminosity of log λL1350 ~ 46.5. Thus, to compare them to our N-loud quasars without possible luminosity effects, we colored the quasars at log λL1350> 46.5 and log λL1350< 46.5 with gray and yellow, respectively. Figure 6b shows the comparison of FWHMs of Hβ and C ivλ1549 lines. It is clear that the FWHMC iv of N-loud quasars is typically narrower than those of general quasars, although FWHMHβ seems not to show significant differences between N-loud and normal quasars: the mean values (standard deviations) of FWMHC iv and FWHMHβ are 3692 km s-1 (715 km s-1) and 5159 km s-1 (1992 km s-1) for N-loud quasars, whereas they are 5507 km s-1 (1229 km s-1) and 5652 km s-1 (1770 km s-1) for general quasars. This is consistent with the claim that the line widths of carbon broad emission lines of N-loud quasars are narrower than those of general quasars (Jiang et al. 2008; Bentz et al. 2004). Many studies claimed that highly ionized BLRs with C ivλ1549 line are affected by a non-virial component such as outflow, and would be a biased mass estimator (e.g., Shen & Liu 2012; Marziani & Sulentic 2012); however, the Hβ line widths obtained in this study also have uncertainties due to low S/N of near-infrared spectroscopies, implying that black hole masses estimated both with the Hβ and C ivλ1549 lines should involve respective uncertainties. Hence, hereafter, we regard mean black hole masses between them as their representative black hole masses. As shown in Fig. 6c, we found that black hole masses of N-loud quasars seem to be lower than those of general quasars even by focusing on the same luminosity objects shown as yellow circles: the averaged masses are 9.218 and 9.408 logarithmically for N-loud and general quasars, respectively: the averaged masses estimated by Hβ line are 9.214 and 9.327, and the averaged masses estimated by C ivλ1549 line are 8.965 and 9.320, respectively. This implies that N-loud quasars are situated in a BH growth phase, although we should keep their large uncertainties of BH masses in mind, and thus we discuss mass accretions into SMBHs with nitrogen enrichment of N-loud quasars.
 |
Fig. 7 Comparison of Eddington ratios estimated by the Hβ line with that by the C ivλ1549 line. Red, gray, and yellow circles are the same as those in Fig. 6. The one-to-one relation is indicated by the dashed line. Eddington ratios averaged from Hβ and C ivλ1549 lines are given as histograms in the small bottom panel. The red- and yellow-filled histograms show averaged Eddington ratios of our N-loud quasars and SDSS normal ones at log λL1350< 46.5 from Shen & Liu (2012), respectively. |
5.3. AGN activities of N-loud quasars
In Sect. 5.1, we found that NLR clouds in N-loud quasars are not extremely metal rich, indicating a picture in which only the nitrogen relative abundance of the BLR gas clouds is relatively high in the N-loud quasars (e.g., Jiang et al. 2008; Araki et al. 2012). In this section, we discuss an interpretation of this nitrogen excess by considering the connection between AGN activity and the nitrogen enrichment due to the nuclear star formation.
Previously, by using optical spectra of 2383 SDSS quasars at 2.3 <z< 3.0, we investigated the dependence of the BLR metallicity on the Eddington ratio (Matsuoka et al. 2011) where we utilized emission-line flux ratios of N vλ1240/C ivλ1549, N vλ1240/He iiλ1640, (Si ivλ1398+O iv]λ1402)/C ivλ1549, and Al iiiλ1857/C ivλ1549, which are sensitive to the BLR metallicity. In the result, we found that the Eddington ratio depends on the emission-line flux ratios involving the N vλ1240 line, while it does not correlate with the other emission-line flux ratios, i.e., (Si ivλ1398+O iv]λ1402)/C ivλ1549 and Al iiiλ1857/C ivλ1549 (see Fig. 6 in Matsuoka et al. 2011, for more detail). We suggested that the correlation between the Eddington ratio and the line ratios including nitrogen is tracing a delay of the mass accretion into SMBHs relative to the onset of nuclear star formation of about 108 yr reported by Davies et al. (2007), which is the timescale required for the nitrogen enrichment from AGB stars. In other words, this result indicates that the mass loss from AGB stars enriches BLR gas clouds with nitrogen and enhance the accretion into SMBHs.
By considering the relation between the Eddington ratio and nitrogen abundance described above, we suggest one possible scenario where N-loud quasars are situated in the AGN active phase, i.e., high accretion phase. If this scenario is correct, N-loud quasars should show relatively high Eddington ratios. Thus, we calculated Eddington ratios of N-loud quasars and plotted them in Fig. 7. For comparison, we also plotted the general quasar sample of Shen & Liu (2012), as in Fig. 6. To examine the distribution of Eddington ratios of N-loud and general quasars, we calculated the averaged Eddington ratios from Hβ-based and C ivλ1549-based black hole masses. The distributions of averaged Eddington ratios of our N-loud sample are shown in Fig. 7 as red-filled histograms. Regarding the general quasars at log λL1350< 46.5, we derived averaged Eddington ratios in the same way and shown as the yellow histogram. The mean values (standard deviations) of their Eddington ratios are −0.28 (0.24) and −0.54 (0.22) for our N-loud quasars and general ones, respectively. It indicates that Eddington ratios of N-loud quasars are slightly higher than those of SDSS quasars: the KS test confirms the significant difference between their distributions with p = 0.006. This result means N-loud quasars are significantly situated in a rapid accretion phase, consistent with the scenario that AGB stars enrich BLRs with nitrogen and enhance the accretion into SMBHs.
6. Conclusions
We have performed near-infrared spectroscopic observations of 12 N-loud quasars at 2.09 <z< 2.57 to investigate their rest-frame optical properties. We find the following results:
-
1.
The rest-frame optical spectra show that[O iii]λ5007 equivalent widths of N-loud quasars are slightly larger than those of general quasars, suggesting that NLR metallicities of N-loud quasars are not extremely high, as was expected with strong broad nitrogen lines. If BLR metallicities are related to chemical properties in NLRs, this result indicates a scenario that nitrogen broad lines depend not only on the BLR metallicity, but also on other parameters in some cases.
-
2.
We found N-loud quasars seem to show higher Eddington ratios than those of general quasars, indicating that the N-loud quasars are in a high accretion phase. This result can be predicted from an observational positive correlation between Eddington ratios and nitrogen abundance found in Matsuoka et al. (2011), suggesting a possible connection between AGN activities and star formation where the mass accretion onto SMBH is associated with a post-starburst phase, when AGB stars enrich the interstellar medium with nitrogen.
To understand the chemical properties of high-z galaxies, and also the connection between SMBH growths and galaxy formations, investigating the chemical compositions of BLR gas is crucial. It is especially important to examine whether nitrogen broad lines actually are good indicators of BLR metallicities because they are often used as BLR metallicity indicators. In this sense, understanding the backgrounds of N-loud quasars would be helpful as a first step since N-loud quasars would show us an extreme case regarding chemical evolution and black hole growth.
It has sometimes been reported that the AGN metallicity shows no redshift evolution, which is inferred for BLRs (e.g., Nagao et al. 2006b) and not only for NLRs. Significant redshift evolution of the gas metallicity is reported for star-forming galaxies (e.g., Maiolino et al. 2008), damped Lyα (e.g., Rafelski et al. 2012), and sub-damped Lyα (e.g., Péroux et al. 2003; Som et al. 2015). The origin of the discrepancy in the metallicity evolution between galaxies and AGNs (or the lack of the significant metallicity evolution in AGNs) has been discussed in, e.g., Juarez et al. (2009).
Acknowledgments
We would like to thank the anonymous referee for the useful comments and suggestions. We are also grateful to Nobuo Araki and Yosuke Minowa for observational support, and we thank the NTT and Subaru telescope staff for their invaluable help during the observations. We would like to thank Gary J. Ferland for providing the great photoionization code Cloudy. K.M. acknowledges financial support from the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant No. 14J01811. T.N. is financially supported by the JGC-S Scholarship Foundation and JSPS KAKENHI Grant Nos. 25707010, 16H01101, and 16H03958. R.M. acknowledges ERC Advanced Grant 695671 “QUENCH” and support by the Science and Technology Facilities Council (STFC). D.P. acknowledges support through the EACOA Fellowship from The East Asian Core Observatories Association, which consists of the National Astronomical Observatories, Chinese Academy of Science (NAOC), the National Astronomical Observatory of Japan (NAOJ), Korean Astronomy and Space Science Institute (KASI), and Academia Sinica Institute of Astronomy and Astrophysics (ASIAA). Data analysis were in part carried out on a common-use data analysis computer system at the Astronomy Data Center, ADC, of the National Astronomical Observatory of Japan (NAOJ).
References
- Araki, N., Nagao, T., Matsuoka, K., et al. 2012, A&A, 543, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bae, H.-J., & Woo, J.-H. 2014, ApJ, 795, 30 [Google Scholar]
- Bae, H.-J., Woo, J.-H., Karouzos, M., et al. 2017, ApJ, 837, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Ferland, G. J., Korista, K. T., Hamann, F., & Dietrich, M. 2003a, ApJ, 582, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Hamann, F., Korista, K. T., et al. 2003b, ApJ, 583, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Batra, N. D., & Baldwin, J. A. 2014, MNRAS, 439, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006a, A&A, 456, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006b, A&A, 459, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bentz, M. C., Hall, P. B., & Osmer, P. S. 2004, AJ, 128, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2009, ApJ, 705, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Müller Sánchez, F., Genzel, R., et al. 2007, ApJ, 671, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Hamann, F., Shields, J. C., et al. 2003, ApJ, 589, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Mathur, S., Grupe, D., & Komossa, S. 2009, ApJ, 696, 1998 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Kewley, L. J., Heisler, C. A., & Sutherland, R. S. 2000, ApJ, 542, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Du, P., Wang, J.-M., Hu, C., et al. 2014, MNRAS, 438, 2828 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Fu, H., & Stockton, A. 2007, ApJ, 664, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Ferland, G. 1992, ApJ, 391, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Ferland, G. 1993, ApJ, 418, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Ferland, G. 1999, ARA&A, 37, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., Korista, K. T., Ferland, G. J., Warner, C., & Baldwin, J. 2002, ApJ, 564, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Hayano, Y., Takami, H., Guyon, O., et al. 2008, Proc. SPIE, 7015 [Google Scholar]
- Hayano, Y., Takami, H., Oya, S., et al. 2010, Proc. SPIE, 7736 [Google Scholar]
- Ho, L. C., & Kim, M. 2015, ApJ, 809, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Fan, X., Vestergaard, M., et al. 2007, AJ, 134, 1150 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Fan, X., & Vestergaard, M. 2008, ApJ, 679, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Juarez, Y., Maiolino, R., Mujica, R., et al. 2009, A&A, 494, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, N., Tokunaga, A. T., Terada, H., et al. 2000, Proc. SPIE, 4008, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Kurk, J. D., Walter, F., Fan, X., et al. 2007, ApJ, 669, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ly, C., Malkan, M. A., Rigby, J. R., & Nagao, T. 2016, ApJ, 828, 67 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, C. L., Ivezić, Ž., Kochanek, C. S., et al. 2010, ApJ, 721, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, C. L., Ivezić, Ž., Sesar, B., et al. 2012, ApJ, 753, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marziani, P., & Sulentic, J. W. 2012, New Astron. Rev., 56, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, W. G., & Ferland, G. J. 1987, ApJ, 323, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, K., Nagao, T., Maiolino, R., et al. 2009, A&A, 503, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuoka, K., Nagao, T., Marconi, A., et al. 2011, A&A, 527, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moorwood, A., Cuby, J.-G., & Lidman, C. 1998, The Messenger, 91, 9 [NASA ADS] [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nagao, T., Murayama, T., & Taniguchi, Y. 2001, ApJ, 546, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Murayama, T., Shioya, Y., & Taniguchi, Y. 2002, ApJ, 575, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Maiolino, R., & Marconi, A. 2006a, A&A, 459, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagao, T., Marconi, A., & Maiolino, R. 2006b, A&A, 447, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osmer, P. S. 1980, ApJ, 237, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Osmer, P. S., & Smith, M. G. 1980, ApJS, 42, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Park, D., Woo, J.-H., Treu, T., et al. 2012, ApJ, 747, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Dessauges-Zavadsky, M., D’Odorico, S., Kim, T.-S., & McMahon, R. G. 2003, MNRAS, 345, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., Wolfe, A. M., Prochaska, J. X., Neeleman, M., & Mendez, A. J. 2012, ApJ, 755, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S., Veilleux, S., & Sanders, D. B. 2005, ApJ, 632, 751 [Google Scholar]
- Russell, S. C., & Dopita, M. A. 1992, ApJ, 384, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Hall, P. B., Richards, G. T., et al. 2007, AJ, 134, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Sesar, B., Ivezić, Ž., Lupton, R. H., et al. 2007, AJ, 134, 2236 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y. 2013, Bull. Astron. Soc. India, 41, 61 [NASA ADS] [Google Scholar]
- Shen, Y., & Liu, X. 2012, ApJ, 753, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Greene, J. E., Strauss, M. A., et al. 2008, ApJ, 680, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Shin, J., Woo, J.-H., Nagao, T., & Kim, S. C. 2013, ApJ, 763, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Som, D., Kulkarni, V. P., Meiring, J., et al. 2015, ApJ, 806, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, J. E. 1981, ApJ, 250, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L., Salzer, J. J., & Haynes, M. P. 1998, ApJ, 497, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Vaona, L., Ciroi, S., Di Mille, F., et al. 2012, MNRAS, 427, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, C., Hamann, F., & Dietrich, M. 2004, ApJ, 608, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Bae, H.-J., Son, D., & Karouzos, M. 2016, ApJ, 817, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X.-B., & Jia, Z. 2010, MNRAS, 406, 1583 [NASA ADS] [Google Scholar]
- Wuyts, E., Wisnioski, E., Fossati, M., et al. 2016, ApJ, 827, 74 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Zhang, K., Wang, T.-G., Gaskell, C. M., & Dong, X.-B. 2013, ApJ, 762, 51 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Near-infrared spectra of N-loud quasars obtained in our IRCS and SOFI runs, adopting the two-pixel binning in the wavelength direction. Gray dotted lines show the wavelengths of some rest-frame optical emission lines, i.e., [Ne v]λ3426, [O ii]λ3727, [Ne iii]λ3869, Hβ, [O iii]λ4959, and [O iii]λ5007 lines, expected from redshifts given in Shen et al. (2008). |
| In the text | |
 |
Fig. 1 continued. |
| In the text | |
 |
Fig. 2 Examples of spectral fittings in rest-frame optical spectra of two N-loud quasars (SDSS J1211+0449 and SDSS J0938+0900). Red lines show total fitting results. Gray dotted lines denote fits of continuum, and individual emission-line components are indicated as light gray Gaussian curves. Dark gray lines denote the residuals. |
| In the text | |
 |
Fig. 3 Distribution of rest-frame equivalent width of [O iii]λ5007 line. The black line histograms denote our sample of 13 N-loud quasars, the dark gray filled histogram shows our observed 11 N-loud quasars, and the open histogram shows the 3σ upper limit. The result of SDSS J1707+6443 (Araki et al. 2012) is shown as a light gray filled histogram. The gray line open histogram denotes the distribution of 232 SDSS quasars at 0 < z < 1 in a luminosity range at log λL5100 = 45.5–46.5 (Shen et al. 2011), which is divided by five to compare with our sample easily. |
| In the text | |
 |
Fig. 4 Normalized equivalent widths of the [O iii]λ5007 line as a function of NLR metallicities, predicted by photoionization models. These are normalized at their respective peaks. Black solid, dashed, dot-dashed, and dotted lines are the photoionization model calculations with (log nH, log U) = (1.0, −1.5), (1.0, −3.5), (4.0, −1.5), and (4.0, −3.5), respectively. Given parameters are also labeled for each line. |
| In the text | |
 |
Fig. 5 Model predictions of emission-line flux ratios, i.e., [Ne v]λ3426/[O iii]λ5007 (left, a), [O ii]λ3727/[O iii]λ5007 (middle, b), and [Ne iii]λ3869/[O iii]λ5007 (right, c), as a function of NLR metallicities. Black solid, dashed, dot-dashed, and dotted lines are the photoionization model calculations with (log nH, log U) = (1.0, −1.5), (1.0, −3.5), (4.0, −1.5), and (4.0, −3.5), respectively. The left panel shows only two high-U models because [Ne v]λ3426 line fluxes in low-U models are fainter than the [O iii]λ5007 fluxes. Horizontal lines show the 3σ upper limits of our sample. |
| In the text | |
 |
Fig. 6 Comparison of the monochromatic luminosities at 1350 Å and 5100 Å (left, a), the FWHM of the Hβ line and the C ivλ1549 line (middle, b), and virial black hole masses based on the C ivλ1549 line and Hβ line (right, c). Our sample of N-loud quasars are shown as red circles. Gray and yellow circles denote SDSS normal quasars at 1.5 < z < 2.2 in luminosity ranges of log λL1350 > 46.5 and log λL1350 < 46.5 from Shen & Liu (2012). Errors represent 1σ uncertainties of measurements, excluding systematic errors. The one-to-one relations are indicated by dashed lines for each panel. |
| In the text | |
 |
Fig. 7 Comparison of Eddington ratios estimated by the Hβ line with that by the C ivλ1549 line. Red, gray, and yellow circles are the same as those in Fig. 6. The one-to-one relation is indicated by the dashed line. Eddington ratios averaged from Hβ and C ivλ1549 lines are given as histograms in the small bottom panel. The red- and yellow-filled histograms show averaged Eddington ratios of our N-loud quasars and SDSS normal ones at log λL1350< 46.5 from Shen & Liu (2012), respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


