| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A8 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201730915 | |
| Published online | 30 October 2017 | |
Seismology of contracting and expanding coronal loops using damping of kink oscillations by mode coupling
1 Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, CV4 7AL, UK
e-mail: D.J.Pascoe@warwick.ac.uk
2 Division of Mathematics, University of Dundee, Nethergate, Dundee, DD1 4HN, Scotland, UK
e-mail: arussell@maths.dundee.ac.uk
3 Institute of Solar-Terrestrial Physics SB RAS, Lermontov St. 126, Irkutsk 664033, Russia
4 SUPA School of Physics and Astronomy, University of Glasgow, University Avenue, Glasgow, G12 8QQ, Scotland, UK
e-mail: paulo.simoes@glasgow.ac.uk
Received: 2 April 2017
Accepted: 11 August 2017
Aims. We extend recently developed seismological methods to analyse oscillating loops which feature a large initial shift in the equilibrium position and investigate additional observational signatures related to the loop environment and oscillation driver.
Methods. We model the motion of coronal loops as a kink oscillation damped by mode coupling, accounting for any change in loop length and the possible presence of parallel harmonics in addition to the fundamental mode. We apply our model to a loop which rapidly contracts due to a post-flare implosion (SOL2012-03-09) and a loop with a large lateral displacement (SOL2012-10-20).
Results. The seismological method is used to calculate plasma parameters of the oscillating loops including the transverse density profile, magnetic field strength, and phase mixing timescale. For SOL2012-03-09 the period of oscillation has a linear correlation with the contracting motion and suggests the kink speed remains constant during the oscillation. The implosion excitation mechanism is found to be associated with an absence of additional parallel harmonics.
Conclusions. The improved Bayesian analysis of the coronal loop motion allows for accurate seismology of plasma parameters, and the evolution of the period of oscillation compared with the background trend can be used to distinguish between loop motions in the plane of the loop and those perpendicular to it. The seismologically inferred kink speed and density contrast imply sub-Alfvénic (MA = 0.16 ± 0.03) propagation of the magnetic reconfiguration associated with the implosion, as opposed to triggering by a wave propagating at the Alfvén speed.
Key words: magnetohydrodynamics (MHD) / Sun: atmosphere / Sun: corona / Sun: magnetic fields / Sun: oscillations / waves
© ESO, 2017
1. Introduction
Standing transverse oscillations of coronal loops were first observed using the Transition Region And Coronal Explorer (TRACE; Aschwanden et al. 1999; Nakariakov et al. 1999). They are interpreted as kink oscillations for which the period of oscillation depends on the length of the coronal loop and the kink speed, which itself depends on the transverse profiles of magnetic field strength and plasma density (Edwin & Roberts 1983), and so can be used to estimate the coronal magnetic field strength (e.g. Nakariakov & Ofman 2001; Aschwanden et al. 2002; Van Doorsselaere et al. 2008; White & Verwichte 2012; Verwichte et al. 2013; Pascoe et al. 2016b). Improved measurement of oscillations provided by Atmospheric Imaging Assembly (AIA; Lemen et al. 2012; Boerner et al. 2012) onboard the Solar Dynamics Observatory (SDO) has significantly increased the number of detected events (e.g. Zimovets & Nakariakov 2015; Goddard et al. 2016), has improved the quality of the data (e.g. White & Verwichte 2012; Pascoe et al. 2016c), and has led to the discovery of low amplitude decayless oscillations (Nisticò et al. 2013; Anfinogentov et al. 2013, 2015), which require a continuous input of energy, such as self-oscillations generated by a quasi-steady flow (Nakariakov et al. 2016).
The damping of kink waves is explained by the process of mode coupling by resonant absorption (e.g. Hollweg & Yang 1988; Ruderman & Roberts 2002; Goossens et al. 2002), which occurs for any overdense coronal loop with a transition layer between the loop interior and external medium. This inhomogeneous layer provides a continuous variation in the local Alfvén speed and a transfer of wave energy from the kink to the Alfvén mode where the local Alfvén speed matches the kink speed (the phase speed of the collective transverse oscillation). The damping envelope for kink oscillations decaying due to mode coupling was initially approximated using an exponential profile (e.g. Ruderman & Roberts 2002; Goossens et al. 2002), corresponding to the asymptotic state of the system. Numerical simulations (Pascoe et al. 2012, 2013a; Ruderman & Terradas 2013; Pascoe et al. 2015; Magyar & Van Doorsselaere 2016) and an analytical treatment (Hood et al. 2013) have revealed that the initial stage is well-described by a Gaussian damping profile. Pascoe et al. (2013a) report how the Gaussian or exponential shape of the damping envelope depends on the coronal loop density contrast and hence can be used as a seismological tool (Arregui et al. 2013; Pascoe 2014; De Moortel et al. 2016). Observational evidence for the Gaussian damping regime has also been revealed by studying the shape of the damping envelope using data from TRACE (De Moortel et al. 2002; Ireland & De Moortel 2002) and SDO (Pascoe et al. 2016c; Morton & Mooroogen 2016). The seismological method proposed by Pascoe et al. (2013a) was first used to calculate the transverse density profile of coronal loops by Pascoe et al. (2016b), and further developed by Pascoe et al. (2017a) to account for additional physical effects including a time-dependent loop length and the presence of the second and third parallel harmonics of the kink mode. The seismological estimate of the inhomogeneous layer width of Loop #3 in Pascoe et al. (2017a) was found to be consistent with an independent estimate based on forward modelling of the transverse intensity profile (Pascoe et al. 2017b), while a statistical study of 233 coronal loops found that 75% exhibit evidence for an inhomogeneous layer (Goddard et al. 2017).
Another trove from SDO/AIA has been a significant number of observations in which solar flares and coronal mass ejections (CMEs) displace coronal loops that are not directly involved in magnetic reconnection. The loops remain at pre-flare temperatures and the most pronounced displacements are contractions of peripheral loops in the “elbows” of the active region (e.g. Sun et al. 2012; Gosain 2012; Liu et al. 2012; Simões et al. 2013; Shen et al. 2014; and Wang et al. 2016; also see earlier observations by Liu et al. 2009 and Liu & Wang 2009 using TRACE). These implosions begin abruptly at the start of the impulsive phase of a flare or the transition of a CME from slow rise to fast rise, often following much slower expansion or contraction of the same loops. Furthermore, individual loops begin contracting in a specific order that is consistent with a signal propagating outwards from the inner active region with a projected speed of ~ 0.3 Mm/s (Simões et al. 2013). The observed properties agree with the implosion hypothesis of Hudson (2000), who first pointed out that a reduction in the total magnetic energy in the corona should lead to inward motions. Nowadays, this effect is usually explained as a consequence of the relation between the magnetic energy and magnetic pressure, Em = ∫Vpm dV where pm = B2/ (2μ0), with the essence of the argument being that when magnetic energy in the low-altitude active region corona is converted to other forms of energy or transported elsewhere, this alters the magnetic pressure gradient and thus creates an unbalanced inward force on the loops. Therefore, peripheral loops must move inwards to dynamically maintain or restore force balance. Longer presentations of the energy-pressure argument and how it applies to confined flares and eruptions can be found in the papers by Janse & Low (2007), Liu et al. (2012), Shen et al. (2014), Russell et al. (2015) and Wang et al. (2016), with Fig. 3 of Russell et al. (2015) illustrating the basic concept.
Loop displacements and transverse oscillations were originally investigated separately, however Li & Gan (2006) first observed a kink oscillation in a contracting loop using TRACE 195 Å images. Loop oscillations were also noted in the implosions studied by Liu & Wang (2010), Sun et al. (2012), Gosain (2012) and Simões et al. (2013), which led Russell et al. (2015) to consider the possibility of a connection between these phenomena. Russell et al. (2015) concluded that when a loop’s environment changes in such a way as to change the location or shape in which the loop is in equilibrium, the loop responds in one of three ways (summarised in their Fig. 4). When the oscillation period is short compared to the time scale of the equilibrium change, loops move through a sequence of quasi-equilibria with no evident oscillation. When the loop’s period is much longer than the time scale for the equilibrium change, the result is an impulsively excited oscillation about the new equilibrium. Finally, in the intermediate case where the time scales are the same order of magnitude, oscillation and displacement occur in superposition as two parts of a single response. The different behaviours can be found in the same active region, ordered by oscillation period, as in the event studied by Simões et al. (2013) and Russell et al. (2015). More generally, comparison of observed implosion time scales (typically several minutes) with reported periods of transverse loop oscillations (from less than two minutes to longer than thirty minutes) suggests that transverse loop oscillations of contracting loops should be a common feature of implosions, with the caveat that Russell et al. (2015) also predicted that the largest amplitude oscillations require that the change in the equilibrium position be initially sharp. Implosions are potentially valuable as a source of transverse loop oscillations because they usually excite multiple loops, which raises the prospect of using them to build up a picture of properties across the active region periphery, and the opportunity to learn how loop properties evolve during the displacement.
It is now desirable to develop the tools of MHD seismology in order to exploit oscillations excited by implosions or other sharp displacements, such as the examples considered in Sect. 2. The main challenges being that one must disentangle the oscillation from the evolution of the equilibrium position and that displacements that produce large amplitude oscillations typically start sharply. In this paper we advance the seismological method developed by Pascoe et al. (2017a) by addressing the loop equilibrium evolution and the abrupt initiation of the oscillation, analysing an oscillation measured in a contracting coronal loop reported by Russell et al. (2015) and a loop with a large initial displacement reported by Goddard et al. (2016). The model for the background trend that allows us to account for a rapid shift in the loop equilibrium position is described in Sect. 3. Once we have an accurate model for the equilibrium position of the loop we may use the damping profile of the remaining oscillation to estimate the transverse density profile and other plasma parameters such as the magnetic field strength, presented in Sect. 4. The analysis also produces interesting new findings concerning the excitation of higher harmonics discussed in Sect. 5. Our conclusions are stated in Sect. 6.
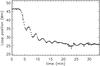 |
Fig. 1 Position of loop L3 of SOL2012-03-09 measured by Russell et al. (2015), which exhibits a damped oscillation as it rapidly contracts. |
2. Data
2.1. SOL2012-03-09
 |
Fig. 2 SDO/AIA 171 Å image of an oscillating loop during SOL2012-10-20 (GOES class M9.0) with its axis indicated by the dashed red line (top). The solid blue line shows the location of the slit used to generate the time-distance map (bottom) and time series for the loop position (crosses). |
Figure 1 shows the position of a contracting loop measured by Russell et al. (2015). This loop was observed by SDO/AIA on 9 March 2012 in active region NOAA 11429 and the dynamics of interest occur in response to a M6.4 class flare SOL2012-03-09 at 03:36:45 UT (Simões et al. 2013). The position of the loop’s axis was measured with sub-pixel accuracy by fitting the intensity in 171 Å along an artificial slit with a Gaussian plus linear background trend. Full details of the fitting and position uncertainty can be found in Russell et al. (2015), which refers to this loop as “L3”.
The plotted time series, which starts at 03:36:00 UT, shows that the loop begins contracting and oscillating approximately 3 min into the time series. The oscillation is damped, which we interpret as a kink oscillation decaying due to transfer of wave energy to Alfvén waves by mode coupling. We use this interpretation to obtain seismological estimates of the coronal loop parameters, in particular the transverse density profile derived from the shape of the damping envelope. Due to a secondary perturbation which impacts the loop, we limit our analysis to the first 18 min of the time series.
2.2. SOL2012-10-20
Another observation of an oscillating loop featuring a large initial displacement occurred after the M9.0 class flare SOL2012-10-20, also designated as “Event 40 Loop 2” in the catalogue by Goddard et al. (2016) and shown in Fig. 2. This loop was one of the six considered in Pascoe et al. (2016c), and was initially found to be better described by an exponential rather than Gaussian damping profile, although that analysis was based on a single damped sinusoid (fundamental standing kink mode) and did not include the start of the signal with the large displacement, which was too large to be accounted for by either a Gaussian or exponential damping profile and is the focus of this study. It was not one of the four loops analysed in further detail in Pascoe et al. (2017a) due to the inability of the slowly varying background trend in that study to account for the rapid shift in the equilibrium position, although we note it is generated by the same flare as Loop #4 of that paper, albeit in a different region.
3. Model
The seismological method used in this paper is an extension of that used by Pascoe et al. (2017a) which describes an oscillation in terms of a kink mode damped by mode coupling. Their model includes the effects of a time-dependent period of oscillation (3rd order polynomial), the presence of additional parallel harmonics (here we use the dispersionless approximation Pn = Pk/n corresponding to a thin loop without longitudinal structuring), and the decayless regime of standing kink oscillations (not considered in this paper) 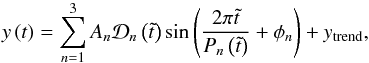 (1)where t0 is the start time of the oscillation (relative to the start time of the observational data) and
(1)where t0 is the start time of the oscillation (relative to the start time of the observational data) and 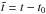 . We note that φ1 = 0 according to the definition of t0.
. We note that φ1 = 0 according to the definition of t0. 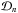 is the damping envelope for the nth harmonic given by the general damping profile
is the damping envelope for the nth harmonic given by the general damping profile 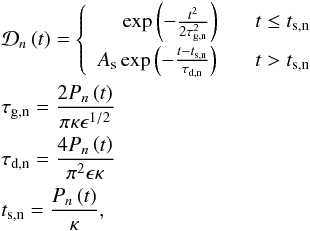 (2)where
(2)where 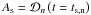 . The transverse density profile is described by the density contrast ratio ρ0/ρe and the width of the inhomogeneous layer ϵ, and κ = (ρ0 − ρe) / (ρ0 + ρe).
. The transverse density profile is described by the density contrast ratio ρ0/ρe and the width of the inhomogeneous layer ϵ, and κ = (ρ0 − ρe) / (ρ0 + ρe).
Changes in the period of oscillation of kink modes have previously been reported by several other authors (e.g. De Moortel et al. 2002; Ireland & De Moortel 2002; White et al. 2013). Nisticò et al. (2013) observed an increase in the period of decayless kink oscillations in an expanding loop, and the magnitude of the increase was found to be consistent with the assumption of the magnetic field remaining constant. Hayes et al. (2016) also related an increase in loop length during the decay phase of a flare to an increase in the timescale of quasi-periodic pulsations, although the increase in loop length was small compared with the increase in periods. The time-dependence of the period of oscillation used in Pascoe et al. (2017a) and followed in this paper is based on a 3rd order polynomial to allow both increases and decreases during the observation. Changes in the period are associated with a time-dependent loop length or internal Alfvén speed but with the assumption that the density contrast remains constant since the effect of a time-dependent density contrast on the damping envelope of the kink oscillation has not been studied. The time-dependent periods of oscillation are thus approximated by
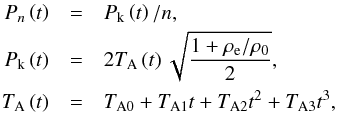 (3)where
(3)where 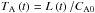 is the Alfvén transit time and the coefficients TAi are model parameters. In Pascoe et al. (2017a), the measured increases and decreases in the period of oscillation were much smaller than the event in this paper but were useful for keeping the modelled oscillation in phase with the data over the duration of the long time series required to accurately determine the transverse density profile.
is the Alfvén transit time and the coefficients TAi are model parameters. In Pascoe et al. (2017a), the measured increases and decreases in the period of oscillation were much smaller than the event in this paper but were useful for keeping the modelled oscillation in phase with the data over the duration of the long time series required to accurately determine the transverse density profile.
The background trend (ytrend) describes the evolution of the loop’s equilibrium position due to dynamics such as loop contraction, expansion, or lateral displacement, and about which the (kink) oscillation provides an additional periodic displacement. In Pascoe et al. (2017a), the background trend is described using spline interpolation, with the separation between interpolation points determined by the longest period of oscillation P1. This ensures the evolution of the background trend is accurately described but limits the timescale of the evolution to longer than the oscillation. However, the rapid change of the background is a key feature of the oscillation studied in this paper. Indeed for L3 the rapid contraction of the loop itself excites the oscillation. To allow our model to describe this behaviour, we include an additional term in the background trend based on Eq. (B.5) of Russell et al. (2015)
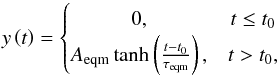 (4)where Aeqm is the amplitude of the equilibrium shift, and τeqm is the timescale of the shift. We note that this term describes a rapid change in the position of the loop (such as a contraction, expansion, or displacement) coinciding with the start time of the (kink) oscillation t0. The background trend itself is therefore now directly linked to the properties of the oscillation and must be considered simultaneously, that is, without detrending the time series of the loop position. As in Pascoe et al. (2017a), the model is tested against the observational data using Bayesian inference and Markov chain Monte Carlo sampling. Our results are based on 106 samples and posterior values are presented either as histograms (e.g. Fig. 5) or summarised by their median and 95% credible intervals as in Table 1.
(4)where Aeqm is the amplitude of the equilibrium shift, and τeqm is the timescale of the shift. We note that this term describes a rapid change in the position of the loop (such as a contraction, expansion, or displacement) coinciding with the start time of the (kink) oscillation t0. The background trend itself is therefore now directly linked to the properties of the oscillation and must be considered simultaneously, that is, without detrending the time series of the loop position. As in Pascoe et al. (2017a), the model is tested against the observational data using Bayesian inference and Markov chain Monte Carlo sampling. Our results are based on 106 samples and posterior values are presented either as histograms (e.g. Fig. 5) or summarised by their median and 95% credible intervals as in Table 1.
4. Results
 |
Fig. 3 Seismological analysis of the contracting loop. The top left panel shows the position of the contracting and oscillating loop as a function of time. The green and blue lines represent our model for the position and background trend alone, respectively, based on the median value of each model parameter. The dotted blue line represents the component of the background trend corresponding to the equilibrium shift given by Eq. (4). The rose shaded region represents the 99% credible intervals for the loop position predicted by the model, which includes an estimated noise σy. The dotted and dashed lines denote the median values of t0 and ts1, respectively. The top right panel shows a normalised 2D histogram approximating the marginalised posterior probability density function for the loop transverse density profile parameters, estimated using the oscillation damping envelope. The red bars indicate the median values and the 95% credible intervals, which are also shown by the dotted and dashed lines, respectively, in the 1D histograms (bottom panels). |
Figure 3 and Table 1 summarise the results of our seismological analysis for L3 of SOL2012-03-09. The behaviour of the background trend is indicated by the blue line and is comprised of a general component based on spline interpolation and the sudden shift in the equilibrium position (dotted blue line) given by Eq. (4). The rapid drop in the loop equilibrium is well-described by the inclusion of this additional term, although the contraction slows after t ≈ 5 min at which point the spline component becomes important.
Figure 4 compares the time-dependence of the period of oscillation Pk (dashed line) with the behaviour of the background trend ytrend (solid blue line), and indicates a strong relationship between the two. The linear Pearson correlation coefficient for Pk and ytrend (calculated over t ≥ t0) is 0.996. For comparison, the largest correlation coefficient for the loops in Pascoe et al. (2017a) was 0.89 for Loop #2. Since the observational slit is aligned with the direction of the loop contraction we associate the decrease in the position of the background trend with the decrease in the loop length, which is related to the period of oscillation by the kink speed Pk = 2L/Ck. Considering also that the relative size of the changes in Pk and ytrend is similar, our results support the kink speed remaining constant to a good approximation during the oscillation, as indicated by the red dash-dotted line in Fig. 4.
 |
Fig. 4 Evolution of the background trend ytrend (solid blue line), period of oscillation Pk (dashed line), and kink speed Ck (red dash-dotted line), each normalised to their initial value. The vertical dotted line denotes the start time of the oscillation t0. |
For a low-β plasma, the kink speed is 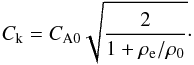 (5)Our model assumes ρ0/ρe is constant (since the effect of a time-dependent density contrast on the damping envelope is unknown) and the oscillation behaviour suggests Ck remains constant in time during the loop contraction. These conditions correspond to
(5)Our model assumes ρ0/ρe is constant (since the effect of a time-dependent density contrast on the damping envelope is unknown) and the oscillation behaviour suggests Ck remains constant in time during the loop contraction. These conditions correspond to 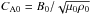 also remaining constant, implying
also remaining constant, implying 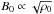 . Assuming also a conservation of mass (no inflows or outflows) for the loop with minor radius r leads to ρ0r2L remaining constant (a similar assumption was shown to be reasonable in Nisticò et al. 2013). We may also consider the conservation of magnetic flux, that is B0r2 , remaining constant, which then gives B0 ∝ 1 /L or, since L is proportional to the loop major radius rc, B0 ∝ 1 /rc. This suggests the magnetic geometry for the contracting loop’s environment is more similar to a 2.5D magnetic arcade with B ∝ 1 /rc (e.g. Brady et al. 2006; Pascoe et al. 2009a; Russell & Stackhouse 2013; Pascoe & De Moortel 2014) than to a dipolar field with
. Assuming also a conservation of mass (no inflows or outflows) for the loop with minor radius r leads to ρ0r2L remaining constant (a similar assumption was shown to be reasonable in Nisticò et al. 2013). We may also consider the conservation of magnetic flux, that is B0r2 , remaining constant, which then gives B0 ∝ 1 /L or, since L is proportional to the loop major radius rc, B0 ∝ 1 /rc. This suggests the magnetic geometry for the contracting loop’s environment is more similar to a 2.5D magnetic arcade with B ∝ 1 /rc (e.g. Brady et al. 2006; Pascoe et al. 2009a; Russell & Stackhouse 2013; Pascoe & De Moortel 2014) than to a dipolar field with 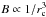 (e.g. McLaughlin & Ofman 2008), although this is subject to the model assumptions being valid and possibly also any changes in loop shape during contraction.
(e.g. McLaughlin & Ofman 2008), although this is subject to the model assumptions being valid and possibly also any changes in loop shape during contraction.
 |
Fig. 5 Histograms for the amplitudes of the fundamental (A1), second harmonic (A2), and third harmonic (A3) kink modes for the contracting loop. |
4.1. Estimate of magnetic field strength
At the start of the observation, the loop length is estimated as L(t = 0) = 234.5 ± 2.0 Mm. For the purpose of the following estimates we approximate the 1σ errors of model parameters as half the mean of the 95% credible intervals, obtaining ρ0/ρe = 2.93 ± 0.81 (ϵ = 0.35 ± 0.09), TA(t = 0) = 2.71 ± 0.20 min, and Pk(t = 0) = 4.44 ± 0.70 min. Using the approximation of a low-β plasma and untwisted magnetic field, corresponding to the fields being equal inside and outside the loop B0 = Be, we can then calculate the internal (CA0) and external (CAe) Alfvén speeds as 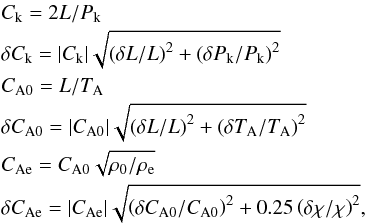 (6)where χ = ρ0/ρe. If we assume a typical coronal plasma density of ne = 1015 m-3 we can then estimate the magnetic field strength B0 as
(6)where χ = ρ0/ρe. If we assume a typical coronal plasma density of ne = 1015 m-3 we can then estimate the magnetic field strength B0 as 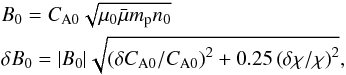 (7)where the vacuum permeability μ0 = 4π × 10-7 H/m, the mean atomic weight is
(7)where the vacuum permeability μ0 = 4π × 10-7 H/m, the mean atomic weight is 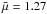 , mp = 1.6726 × 10-27 kg, and n0 = neρ0/ρe. These estimates return values of Ck = 1.76 ± 0.28 Mm/s, CA0 = 1.44 ± 0.11 Mm/s, CAe = 2.47 ± 0.39 Mm/s, and B0 = 12.8 ± 2.0 G (see also Table 1). These values (and those for SOL2012-10-20) are consistent with the typical values of the Alfvén speed in coronal active regions, estimated in Goddard et al. (2016). The inferred values of the loop density contrast ratio are also consistent with those reported in Pascoe et al. (2016b, 2017a) in terms of implying loops (or at least those observed supporting transverse oscillations) having low ratios of approximately two, rather than previous assumptions of approximately ten (e.g. Nakariakov et al. 1999; Ruderman & Roberts 2002; Goossens et al. 2002).
, mp = 1.6726 × 10-27 kg, and n0 = neρ0/ρe. These estimates return values of Ck = 1.76 ± 0.28 Mm/s, CA0 = 1.44 ± 0.11 Mm/s, CAe = 2.47 ± 0.39 Mm/s, and B0 = 12.8 ± 2.0 G (see also Table 1). These values (and those for SOL2012-10-20) are consistent with the typical values of the Alfvén speed in coronal active regions, estimated in Goddard et al. (2016). The inferred values of the loop density contrast ratio are also consistent with those reported in Pascoe et al. (2016b, 2017a) in terms of implying loops (or at least those observed supporting transverse oscillations) having low ratios of approximately two, rather than previous assumptions of approximately ten (e.g. Nakariakov et al. 1999; Ruderman & Roberts 2002; Goossens et al. 2002).
Alfvén waves generated by the mode coupling of kink waves form in the inhomogeneous layer, which has a continuously varying Alfvén speed, and so they will experience phase mixing (e.g. Heyvaerts & Priest 1983). This process generates large transverse gradients in the waves and so increases the efficiency of dissipative processes. Using the seismologically inferred information we can estimate the lifetime of the Alfvén waves (Mann & Wright 1995; Pascoe et al. 2016b) as 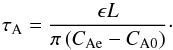 (8)
(8)
4.2. Analysis of loop with large lateral displacement
The results of our analysis for SOL2012-10-20 are summarised in Fig. 6 and Table 1. The density profile parameters are poorly constrained due to the small number of oscillation cycles used, but suggest a low-density contrast loop ρ0/ρe ≲ 2. The loop clearly moves to a new equilibrium position, which is approximately 3 Mm further along the observational slit, after the flare occurs and does so in a time comparable with the (kink mode) period of oscillation as discussed by Russell et al. (2015). However, since the observational slit for this loop is approximately perpendicular to the plane of the loop (see Fig. 2), the shift in the background trend is mainly associated with a lateral displacement. The correlation coefficient for the time-dependent period of oscillation and background trend is 0.561. This low correlation suggests that the small increase of approximately 10% in period during the oscillation is due to an expansion of the loop, but that a large component of the trend is also the expected lateral displacement. We also note that the background trend itself appears to oscillate (i.e. the equilibrium initially increases beyond its final position) as the loop settles into its new equilibrium, similar to the behaviour of Loops #1 and #3 in Pascoe et al. (2017a), and contrasted with the monotonic background trend of the contracting loop.
5. Discussion
The oscillation of the contracting loop studied in this paper is associated with a flare, but it is excited by the rapid change in the location of the loop’s equilibrium position rather than direct impact of the impulsive energy release (e.g. a CME or shock wave). The effect of this different excitation mechanism is evident not only in the strong downward background trend associated with the loop contraction, but also in the harmonic shape of the oscillation. The four loops studied in Pascoe et al. (2017a) had oscillations with fundamental kink mode amplitudes measured in the range 1.0–3.6 Mm and each had an aharmonic shape which was modelled in terms of the second and third parallel harmonics. The amplitudes of the fundamental, second, and third harmonics are plotted in Fig. 7. Each of the four loops had at least one additional harmonic with an amplitude of approximately 20% of the fundamental. SOL2012-10-20 (green datapoints) analysed in Sect. 4.2 is also consistent with this behaviour. Pascoe et al. (2016a) studied the case of a spatially-resolved second harmonic with an amplitude comparable to that of the fundamental mode (blue datapoint). This large-amplitude second harmonic was associated with the CME impacting one of the loop legs far more strongly than the other. The lower amplitude harmonics reported in Pascoe et al. (2017a) may be associated with loop perturbations that are only slightly asymmetric (generating even harmonics) and also spatially localised (generating odd harmonics in addition to the fundamental).
 |
Fig. 7 Amplitude of the second harmonic A2 (plus signs) and third harmonic A3 (circles) compared with the amplitude of the fundamental mode A1. The symbols represent the oscillations analysed by Pascoe et al. (2017a) (black), the contracting loop in this paper (red), and SOL2012-10-20 analysed in Sect. 4.2 (green). The blue datapoint is the strongly excited second harmonic reported in Pascoe et al. (2016a). The solid line denotes an amplitude of 0.2A1. |
The generation of these harmonics is also seen in numerical simulations of kink modes excited by external perturbations (Pascoe et al. 2009a; Pascoe & De Moortel 2014), and for sausage modes in loops with an expanding cross-section which causes coupling between different parallel harmonics (Pascoe et al. 2009b; Pascoe & Nakariakov 2016). The spatial and temporal localisation of the driver is also key to the generation of quasi-periodic fast wave trains in coronal loops (Roberts et al. 1984; Nakariakov et al. 2005), active regions (Nisticò et al. 2014), current sheets (Jelínek & Karlický 2012), funnels (Pascoe et al. 2013b), and coronal holes (Pascoe et al. 2014). In contrast, the oscillation of L3 examined in this paper exhibits a very harmonic shape, with the amplitude of the fundamental mode being approximately 2.4 Mm, but with amplitudes for the higher harmonics being negligible (Fig. 5 and Table 1).
As in Pascoe et al. (2017a), we performed the same seismological modelling without including the additional (second and third) parallel harmonics and compared the models using the Bayes factor (Jeffreys 1961; Kass & Raftery 1995). The calculated value of the Bayes factor is Kfd = 2lnBfd = 19.1, where model f contains the fundamental mode alone, and model d contains additional (dispersionless) harmonics. This indicates very strong evidence favouring the model without additional harmonics over the model with additional harmonics, consistent with the inclusion of additional model parameters (A2, A3, φ2, φ3) providing no significant improvement to the description of the observational data. In contrast, for SOL2012-10-20 we obtain Kfd = − 26.6, corresponding to very strong evidence in favour of the model with the additional harmonics. This can be understood in the context of the excitation mechanism for the contracting loop being the contraction itself, which effectively excites the entire loop simultaneously, and contrasted with more localised perturbations in the studies discussed above, and for SOL2012-10-20.
The spatial scale of the driver for the contracting loop being comparable with the loop length efficiently excites the fundamental mode alone. Furthermore, the oscillation having a large amplitude but a harmonic shape is consistent with the interpretation of Pascoe et al. (2017a) of the aharmonic shape being due to the simultaneous excitation of additional harmonics rather than a nonlinear effect of an initially harmonic oscillation generating higher harmonics by the nonlinear cascade. The large amplitude oscillation of the loop in this study shows no evidence of an aharmonic shape, while oscillations in Pascoe et al. (2017a) with lower amplitudes do have an aharmonic shape. This behaviour supports the nature of the excitation mechanism (particularly its spatial localisation) being more relevant than the amplitude of the oscillation in regards to the harmonic appearance.
We note that the decayless regime of kink oscillations is not considered in this study. A decayless component was included for Loop #3 in Pascoe et al. (2017a) based on prior evidence (Nisticò et al. 2013) and supported by Bayesian model comparison revealing very strong evidence for its existence; the Bayes factor comparing models with and without the decayless component being KD = 25.8. For the two oscillations analysed in the present paper, the equivalent Bayes factors are KD = − 22.7 and − 6.4 for the contracting and displaced loops, respectively, with negative values indicating evidence against the decayless component improving the description of the observational data by the model.
 |
Fig. 8 PFSS model for the magnetic field for SOL2012-03-09. The red field lines correspond to the contracting loops and have inclination angles 49–56 degrees relative to the line of sight. |
Analysis of the active region containing the contracting loop by Simões et al. (2013) demonstrated that surrounding loops also contracted, and did so at different times consistent with a signal propagating with a projected speed of vp = 0.304 Mm/s. This was initially assumed to correspond to the fast magnetoacoustic or Alfvén speed (Russell et al. 2015). However, our seismological estimate of the (external) Alfvén speed CA = 2.47 ± 0.39 Mm/s is significantly higher, which is unlikely to be accounted for by projection effects alone. Figure 8 shows the potential field source surface (PFSS) model for the magnetic field at 06:00:00UT, approximately 2.5 h after our observations. The inclination angle θ is taken as the angle between the line of sight vector and a vector joining the midpoint between the loop footpoints to the highest point of the loop, and has values of θ = 49–56 degrees for the contracting loops. Using these values we obtain an Alfvén Mach number MA = v/CA = 0.13–0.19 for the signal associated with the contraction, where v = vp/ sinθ. The signal appears to propagate at a constant speed indicating that no large scale structuring of the medium is affecting it, and deceleration by ubiquitous fine structuring can also be excluded (Yuan et al. 2015). Supra-arcade downward propagating disturbances interpreted as wakes generated by contracting loops (Savage et al. 2012) are also observed to have similarly low speeds (e.g. McKenzie 2000). Propagation at sub-Alfvénic speeds has also been considered in the context of EIT waves (e.g. recent review by Long et al. 2017). For example, the pseudo-wave model proposed by Chen et al. (2002) based on magnetic field reconfiguration suggests propagation speeds ≲ CA/ 3.
6. Conclusions
In this paper we have applied seismological methods based on kink oscillations to loops exhibiting large shifts in their equilibrium position for the first time, focusing on the best known observational examples as a demonstration of the technique and achievable results. These shifts are associated with large perturbations or changes to the equilibrium following impulsive energy releases. An additional term describing a rapid shift of the loop equilibrium (Russell et al. 2015) is combined with the more general but slowly evolving spline background trend to accurately reproduce the observed behaviour and distinguish between the changes in loop position due to the moving equilibrium and the oscillation about that equilibrium. This allows an accurate measurement of the oscillation damping envelope and the application of established seismological methods (Pascoe et al. 2013a, 2016b, 2017a) to calculate plasma parameters such as the transverse density profile and the magnetic field strength. Accurately measuring the initial amplitude and damping rate for the oscillation is also necessary to determine any dependence between these parameters (e.g. Goddard & Nakariakov 2016).
The background trend and time-dependent period of oscillation of the contracting loop are, to our knowledge, the most strongly correlated example reported, consistent with the expected behaviour of a standing kink mode with Pk = 2L/Ck. The relative changes in ytrend and Pk further suggest that Ck remains constant during the evolution, potentially revealing information about the structuring of the wider region, though it is unknown whether this is specific to this particular observation or a more general condition for the topology of flaring active regions. The same strong correlation is not present for the oscillating loop of SOL2012-10-20, which is viewed perpendicular to the plane of the loop and so the evolution of the background trend mainly corresponds to a lateral displacement. Hence, the relationship between the period of oscillation and the background trend provides us with information about whether observed motions are in the plane of the loop (contraction or expansion), or correspond to motions of the loop plane relative to the observer’s line of sight (displacement or rotation). This is related to the polarisation of the kink mode, being vertical or horizontal for perturbations in the loop plane or perpendicular to it, respectively (Wang & Solanki 2004). The difficulties of identifying the polarisation of kink modes have been discussed by Wang et al. (2008). For SOL2012-10-20, the loop is observed side-on and so the horizontal polarisation is readily identified, whereas there is potential ambiguity for SOL2012-03-09. However, since we have established that the loop is indeed undergoing contraction (and the rapid contracting motion excites the kink oscillation) it follows that the dominant polarisation will be vertical.
Unlike previously analysed loop oscillations (see Fig. 7), we do not find any evidence for additional parallel harmonics for the contracting loop. This is consistent with its excitation by an implosion most efficiently exciting the fundamental mode and supports the inward motion and oscillation being part of a single response as proposed by Russell et al. (2015). Our seismological calculation of plasma parameters also confirms that the reconfiguration associated with the implosion propagates outwards at a significantly sub-Alfvénic speed. Future studies may be able to derive additional information from this Alfvén Mach number.
We have proposed two observational signatures (ytrend-Pk correlation, and Bayesian model comparison for the presence of additional harmonics) which may be used to identify the excitation mechanism in future observations, that is, arising either from an externally generated perturbation or a locally generated change in equilibrium. Identifying the excitation mechanism in turn reveals the location of the driver. More generally, these examples demonstrate how detailed analysis of oscillation signals may be used to determine additional information about the evolution of coronal plasma.
Acknowledgments
This work is supported by the European Research Council under the SeismoSun Research Project No. 321141 (D.J.P., V.M.N., C.R.G.), the STFC grants ST/L000733/1 (V.M.N.) and ST/L000741/1 (P.J.A.S., L.F.), the Russian Foundation of Basic Research under grants 15-02-01089-a, 15-02-03835-a, 16-32-00315-mol-a (SAA), and by the Federal Agency for Scientific Organisations under project II.16.3.2 Non-stationary and wave processes in the solar atmosphere, CITIS No 01201281650 (S.A.A.). The data is used courtesy of the SDO/AIA team. This research has made use of NASA’s Astrophysics Data System.
References
- Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anfinogentov, S. A., Nakariakov, V. M., & Nisticò, G. 2015, A&A, 583, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Asensio Ramos, A., & Pascoe, D. J. 2013, ApJ, 769, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., de Pontieu, B., Schrijver, C. J., & Title, A. M. 2002, Sol. Phys., 206, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Brady, C. S., Verwichte, E., & Arber, T. D. 2006, A&A, 449, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, P. F., Wu, S. T., Shibata, K., & Fang, C. 2002, ApJ, 572, L99 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., Hood, A. W., & Ireland, J. 2002, A&A, 381, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., Pascoe, D. J., Wright, A. N., & Hood, A. W. 2016, Plasma Phys. Controll. Fusion, 58, 014001 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, C. R., & Nakariakov, V. M. 2016, A&A, 590, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goddard, C. R., Nisticò, G., Nakariakov, V. M., & Zimovets, I. V. 2016, A&A, 585, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goddard, C. R., Pascoe, D. J., Anfinogentov, S., & Nakariakov, V. M. 2017, A&A, 605, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goossens, M., Andries, J., & Aschwanden, M. J. 2002, A&A, 394, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gosain, S. 2012, ApJ, 749, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, L. A., Gallagher, P. T., Dennis, B. R., et al. 2016, ApJ, 827, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Hollweg, J. V., & Yang, G. 1988, J. Geophys. Res., 93, 5423 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., Ruderman, M., Pascoe, D. J., et al. 2013, A&A, 551, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hudson, H. S. 2000, ApJ, 531, L75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ireland, J., & De Moortel, I. 2002, A&A, 391, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janse, Å. M., & Low, B. C. 2007, A&A, 472, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability, 3rd edn. (Oxford) [Google Scholar]
- Jelínek, P., & Karlický, M. 2012, A&A, 537, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y. P., & Gan, W. Q. 2006, ApJ, 644, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R., & Wang, H. 2009, ApJ, 703, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R., & Wang, H. 2010, ApJ, 714, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R., Wang, H., & Alexander, D. 2009, ApJ, 696, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, R., Liu, C., Török, T., Wang, Y., & Wang, H. 2012, ApJ, 757, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Long, D. M., Bloomfield, D. S., Chen, P. F., et al. 2017, Sol. Phys., 292, 7 [Google Scholar]
- Magyar, N., & Van Doorsselaere, T. 2016, A&A, 595, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mann, I. R., & Wright, A. N. 1995, J. Geophys. Res., 100, 23677 [NASA ADS] [CrossRef] [Google Scholar]
- McKenzie, D. E. 2000, Sol. Phys., 195, 381 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., & Ofman, L. 2008, ApJ, 682, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, R. J., & Mooroogen, K. 2016, A&A, 593, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nakariakov, V. M., Pascoe, D. J., & Arber, T. D. 2005, Space Sci. Rev., 121, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Anfinogentov, S. A., Nisticò, G., & Lee, D.-H. 2016, A&A, 591, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Pascoe, D. J., & Nakariakov, V. M. 2014, A&A, 569, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J. 2014, Res. Astron. Astrophys., 14, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., & De Moortel, I. 2014, ApJ, 784, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., & Nakariakov, V. M. 2016, A&A, 593, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., de Moortel, I., & McLaughlin, J. A. 2009a, A&A, 505, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., Arber, T. D., & Murawski, K. 2009b, A&A, 494, 1119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Hood, A. W., de Moortel, I., & Wright, A. N. 2012, A&A, 539, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Hood, A. W., De Moortel, I., & Wright, A. N. 2013a, A&A, 551, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Kupriyanova, E. G. 2013b, A&A, 560, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Kupriyanova, E. G. 2014, A&A, 568, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Wright, A. N., De Moortel, I., & Hood, A. W. 2015, A&A, 578, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., & Nakariakov, V. M. 2016a, A&A, 593, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2016b, A&A, 589, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2016c, A&A, 585, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Anfinogentov, S., Nisticò, G., Goddard, C. R., & Nakariakov, V. M. 2017a, A&A, 600, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., Anfinogentov, S., & Nakariakov, V. M. 2017b, A&A, 600, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Terradas, J. 2013, A&A, 555, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russell, A. J. B., & Stackhouse, D. J. 2013, A&A, 558, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russell, A. J. B., Simões, P. J. A., & Fletcher, L. 2015, A&A, 581, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, S. L., McKenzie, D. E., & Reeves, K. K. 2012, ApJ, 747, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, J., Zhou, T., Ji, H., et al. 2014, ApJ, 791, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Simões, P. J. A., Fletcher, L., Hudson, H. S., & Russell, A. J. B. 2013, ApJ, 777, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X., Hoeksema, J. T., Liu, Y., et al. 2012, ApJ, 748, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., Young, P. R., & Verwichte, E. 2008, A&A, 487, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Van Doorsselaere, T., Foullon, C., & White, R. S. 2013, ApJ, 767, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., & Solanki, S. K. 2004, A&A, 421, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, T. J., Solanki, S. K., & Selwa, M. 2008, A&A, 489, 1307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, J., Simões, P. J. A., Fletcher, L., et al. 2016, ApJ, 833, 221 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. S., & Verwichte, E. 2012, A&A, 537, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. S., Verwichte, E., & Foullon, C. 2013, ApJ, 774, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, D., Pascoe, D. J., Nakariakov, V. M., Li, B., & Keppens, R. 2015, ApJ, 799, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Zimovets, I. V., & Nakariakov, V. M. 2015, A&A, 577, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Position of loop L3 of SOL2012-03-09 measured by Russell et al. (2015), which exhibits a damped oscillation as it rapidly contracts. |
| In the text | |
 |
Fig. 2 SDO/AIA 171 Å image of an oscillating loop during SOL2012-10-20 (GOES class M9.0) with its axis indicated by the dashed red line (top). The solid blue line shows the location of the slit used to generate the time-distance map (bottom) and time series for the loop position (crosses). |
| In the text | |
 |
Fig. 3 Seismological analysis of the contracting loop. The top left panel shows the position of the contracting and oscillating loop as a function of time. The green and blue lines represent our model for the position and background trend alone, respectively, based on the median value of each model parameter. The dotted blue line represents the component of the background trend corresponding to the equilibrium shift given by Eq. (4). The rose shaded region represents the 99% credible intervals for the loop position predicted by the model, which includes an estimated noise σy. The dotted and dashed lines denote the median values of t0 and ts1, respectively. The top right panel shows a normalised 2D histogram approximating the marginalised posterior probability density function for the loop transverse density profile parameters, estimated using the oscillation damping envelope. The red bars indicate the median values and the 95% credible intervals, which are also shown by the dotted and dashed lines, respectively, in the 1D histograms (bottom panels). |
| In the text | |
 |
Fig. 4 Evolution of the background trend ytrend (solid blue line), period of oscillation Pk (dashed line), and kink speed Ck (red dash-dotted line), each normalised to their initial value. The vertical dotted line denotes the start time of the oscillation t0. |
| In the text | |
 |
Fig. 5 Histograms for the amplitudes of the fundamental (A1), second harmonic (A2), and third harmonic (A3) kink modes for the contracting loop. |
| In the text | |
 |
Fig. 6 Seismological analysis for SOL2012-10-20 (panels as in Figs. 3–5). |
| In the text | |
 |
Fig. 7 Amplitude of the second harmonic A2 (plus signs) and third harmonic A3 (circles) compared with the amplitude of the fundamental mode A1. The symbols represent the oscillations analysed by Pascoe et al. (2017a) (black), the contracting loop in this paper (red), and SOL2012-10-20 analysed in Sect. 4.2 (green). The blue datapoint is the strongly excited second harmonic reported in Pascoe et al. (2016a). The solid line denotes an amplitude of 0.2A1. |
| In the text | |
 |
Fig. 8 PFSS model for the magnetic field for SOL2012-03-09. The red field lines correspond to the contracting loops and have inclination angles 49–56 degrees relative to the line of sight. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


