| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731226 | |
| Published online | 22 September 2017 | |
The disappearance and reformation of the accretion disc during a low state of FO Aquarii
1 Université de Strasbourg, CNRS, Observatoire astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
e-mail: jean-marie.hameury@astro.unistra.fr
2 Institut d’Astrophysique de Paris, CNRS et Sorbonne Universités, UPMC Paris 06, UMR 7095, 98bis Bd Arago, 75014 Paris, France
3 Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
4 Kavli Institute for Theoretical Physics, Kohn Hall, University of California, Santa Barbara, CA 93106, USA
Received: 23 May 2017
Accepted: 3 July 2017
Context. FO Aquarii, an asynchronous magnetic cataclysmic variable (intermediate polar) went into a low state in 2016, from which it slowly and steadily recovered without showing dwarf nova outbursts. This requires explanation since in a low state, the mass-transfer rate is in principle too low for the disc to be fully ionised and the disc should be subject to the standard thermal and viscous instability observed in dwarf novae.
Aims. We investigate the conditions under which an accretion disc in an intermediate polar could exhibit a luminosity drop of two magnitudes in the optical band without showing outbursts.
Methods. We use our numerical code for the time evolution of accretion discs, including other light sources from the system (primary, secondary, hot spot).
Results. We show that although it is marginally possible for the accretion disc in the low state to stay on the hot stable branch, the required mass-transfer rate in the normal state would then have to be extremely high, of the order of 1019 g s-1 or even larger. This would make the system so intrinsically bright that its distance should be much larger than allowed by all estimates. We show that observations of FO Aqr are well accounted for by the same mechanism that we have suggested as explaining the absence of outbursts during low states of VY Scl stars: during the decay, the magnetospheric radius exceeds the circularisation radius, so that the disc disappears before it enters the instability strip for dwarf nova outbursts.
Conclusions. Our results are unaffected, and even reinforced, if accretion proceeds both via the accretion disc and directly via the stream during some intermediate stages; the detailed process through which the disc disappears still requires investigation.
Key words: accretion, accretion disks / stars: dwarf novae / instabilities
© ESO, 2017
1. Introduction
Intermediate polars (IPs) are cataclysmic variables (CVs), in which a magnetic white dwarf accretes matter from a Roche-lobe-filling low-mass companion; the magnetic field of the white dwarf is strong enough to disrupt the disc and to channel the accretion flow onto the magnetic poles. As a result the luminosity is modulated at the white dwarf’s spin period. The strength of magnetic field, however, is not sufficient to synchronise the white dwarf spin with the orbital rotation as in AM Her stars (see Warner 1995, for a comprehensive description of cataclysmic variables; and Wickramasinghe 2014, for a review of magnetic CVs).
The existence of an accretion disc in IPs has been controversial. Hameury et al. (1986) argued that in some systems, the white dwarf magnetic field is large enough to prevent the formation of an accretion disc, and that the accretion stream originating from the L1 point would then impact directly onto the white dwarf’s magnetosphere. There is observational evidence that many IPs do posses accretion discs (Hellier 1991). In V2400 Oph (Hellier & Beardmore 2002), however, the emission is pulsed at the beat frequency ω−Ω between the orbital frequency Ω and the spin frequency ω, indicating that accretion flips from one pole to the other as expected when no disc is present and the stream directly interacts with the magnetosphere. Other systems, including FO Aqr (Hellier 1993), show pulsations both at the spin frequency and at the beat frequency. These systems have been interpreted as a mixture of disc and direct accretion resulting from the accretion stream overflowing the disc.
The existence of an accretion disc is also revealed by the presence of dwarf nova outbursts, which are due to a thermal-viscous instability occurring when, somewhere in the disc, the temperature is close to the hydrogen ionisation temperature and opacities become a steep function of temperature (see Lasota 2001, for a review of the disc instability model). In the disc instability model (DIM) describing dwarf-nova outbursts, the plot of the relation between the temperature at a given point in the disc, or equivalently the local mass-transfer rate, and the corresponding local surface density Σ has an S-shape; the upper, hot, and the lower, cool branches are stable, while the intermediate segment of the S-curve is thermally and viscously unstable. This intermediate branch corresponds to partial ionisation of hydrogen, and high sensitivity of the opacities to variations of the temperature. Only systems accreting at a rate high enough that hydrogen is ionised everywhere in the disc, or low enough that hydrogen is entirely neutral, can be steady. Whereas for non-magnetic CVs, the latter option requires very low, unrealistic accretion rates, it has been shown by Hameury & Lasota (2017) that this can explain why so few IPs exhibit dwarf-nova outbursts.
FO Aqr is an IP that underwent a low state in 2016 (decrease of the optical luminosity by 2 mag, from a normal state with V = 13.5 to a faint state with V = 15.5), from which it recovered slowly and steadily over a time scale of several months (Littlefield et al. 2016). X-ray observations (Kennedy et al. 2017) show that the mass-transfer rate decreased by about one order of magnitude. Due to solar conjunction, few data are available for the descent to the low state, which has been rapid (time scale of weeks) as compared to the recovery time. Interestingly, no dwarf nova outburst has been detected during the rise from the low state, which is analogous to the behaviour of VY Scl stars in a similar phase of their luminosity variations. VY Scl stars are bright cataclysmic variables that occasionally enter low states, fainter by one magnitude or more; although such drops in luminosity should bring these systems into the instability strip, they show no outbursts. This is puzzling, because one would expect that in the low state, the mass-transfer is low enough for the disc to become thermally and viscously unstable. Leach et al. (1999) suggested that irradiation of the accretion disc by a hot white dwarf prevents the occurrence of dwarf nova outbursts. However, Hameury & Lasota (2002) showed that irradiation cannot completely suppress the outbursts (especially during the long rise from minimum) and suggested instead that VY Scl stars are magnetic CVs, in which the magnetic field is strong enough to lead to disc disappearance during the low state. The required magnetic moments are comparable to that observed in IPs. It is therefore tempting to apply the same idea to confirmed IPs when they show no-outburst behaviour analogous to that of VY Scl stars.
In this paper, we consider the specific case of FO Aqr. This source possesses an accretion disc during the high state, as shown by its partial eclipses. We examine in turn the three possibilities that could account for the absence of dwarf nova outbursts in FO Aqr: a very high mass-transfer rate, for which the disc can stay on the hot branch during the low state, a very low mass-transfer for which the disc sits on the cool branch even during the high state, and finally the case of a mass-transfer rate corresponding to the system’s orbital period, and show that, in this latter case, the accretion disc, disrupted by the white dwarf’s magnetic field, vanishes in the low state before entering the instability strip.
We adopt the following parameters for FO Aqr:
-
Orbital period: 4.85 h; spin period: 1254 s(Patterson & Steiner 1983, Kennedy et al. 2016).
-
Orbital inclination i: FO Aqr has a grazing eclipse; we take i = 70° (Hellier et al. 1989).
-
Primary mass M1: this parameter is poorly constrained; values found in the literature range from 0.45 M⊙ (Yuasa et al. 2010) to 1.22 M⊙ (Cropper et al. 1998). Here, we adopt M1 = 0.7M⊙, close to the value of 0.61 M⊙ quoted by Brunschweiger et al. (2009) from the Swift/BAT survey.
-
Secondary mass M2: we take M2 = 0.4 M⊙, appropriate for a system with a period of 4.85 h in which the secondary is not evolved. This value is slightly smaller than the 0.46 M⊙ deduced from the empirical mass-period relation derived by Knigge (2006); deviations and scatter from this mass-period relation are expected as a result of differences in primary masses and in evolutionary tracks.
-
Secondary effective temperature: de Martino et al. (1994) found that the secondary effective temperature is in the range 3700–3900 K; here we adopt a value of 3800 K for the non-irradiated part of the secondary. This corresponds to an M0 star, typical of what is expected for a period of 4.85 h.
-
Distance d: this parameter is also poorly constrained. Pretorius & Mukai (2014) assume
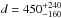 pc, which corresponds to an uncertainty by a factor 2–3 in the luminosity.
pc, which corresponds to an uncertainty by a factor 2–3 in the luminosity. -
Mass transfer rate: this can be estimated either by converting the X-ray luminosity into an accretion rate, or by using spectral models. The second method is model dependent, while the first one suffers from the uncertainty on the source distance, and from the uncertainty on the bolometric correction. There is indeed a large intrinsic absorption in IPs, and the total accretion luminosity is typically 50–100 times larger than the 2–10 keV luminosity (we refer to Warner 1995, for a discussion of this effect). The 2–10 keV X-ray flux given in Koji Mukai’s on-line catalogue1 is 3.5 × 10-11 erg cm-1 s-1. For the assumed primary mass and distance, this corresponds to accretion rates of the order of 4–8 × 1017 g s-1, with large uncertainties. Mukai et al. (1994) quote a small value of the bolometric luminosity (4.6 × 1033 erg s-1 for a distance of 400 pc). This would imply very low mass-transfer rates (4 × 1016 g s-1), too low to account for the properties of FO Aqr (see below). On the other hand, de Martino et al. (1994) estimate a mass accretion rate of 9.2 × 1017 g s-1 when fitting the fraction of the optical and infrared flux that is not modulated with the orbital period with a disc plus blackbody component, implying a larger absorption of the X-ray flux than estimated by Mukai et al. (1994). In the low state, one expects the mass-transfer rate to be reduced by about a factor 10 from the high state.
-
Magnetic moment: Butters et al. (2009) found some evidence for circular polarisation in the I band, and variation of this with spin phase. This detection is marginal, however, and assuming a surface magnetic field of a few MG as for other intermediate polars for which circular polarisation has been detected, one obtains a magnetic moment of a few 1032–1033 G cm3 for a 0.7 M⊙ white dwarf. Norton et al. (2004) suggested a magnetic moment of 1.2 × 1033 G cm3 for FO Aqr, under the assumption of spin equilibrium, when the rate at which angular momentum is accreted by the white dwarf is balanced by the braking effect of the magnetic torque on the disc at its inner edge.
2. The case for a low-accretion-rate system
A system will not undergo dwarf nova outbursts during decay to a low state if, in the normal, high state, the disc already sits on the cold, stable branch. For this to happen, the mass-accretion rate must be lower, homogeneously throughout the disc, than the maximum value ṀA allowed for a cold, stable disc. ṀA is an increasing function of radius, and reaches its minimum at the inner edge of the disc, given by the magnetospheric radius rmag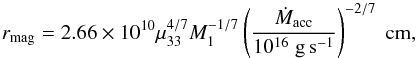 (1)where Ṁacc is the accretion rate onto the white dwarf, and μ33 is the white dwarf magnetic moment in units of 1033 G cm3; the white dwarf mass M1 is measured in solar units. This is possible if the mass-transfer from the secondary is less than some critical value (Hameury & Lasota 2017):
(1)where Ṁacc is the accretion rate onto the white dwarf, and μ33 is the white dwarf magnetic moment in units of 1033 G cm3; the white dwarf mass M1 is measured in solar units. This is possible if the mass-transfer from the secondary is less than some critical value (Hameury & Lasota 2017): 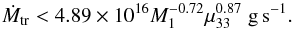 (2)Equation (2) must be satisfied both during the normal- and low state. We have used our DIM evolution code as described in Hameury et al. (2017) and Hameury & Lasota (2017) to estimate the visual magnitude of a steady disc. As we are interested in steady state solutions, we take arbitrary, large values for the time step. We include the contributions to the optical light from the primary star, for which we take a temperature T1 = 104 K. The secondary star is treated as described in Schreiber et al. (2003); it is divided in two hemispheres with different effective temperatures, a non-irradiated one with Teff,unirr = 3800 K, and an irradiated one for which
(2)Equation (2) must be satisfied both during the normal- and low state. We have used our DIM evolution code as described in Hameury et al. (2017) and Hameury & Lasota (2017) to estimate the visual magnitude of a steady disc. As we are interested in steady state solutions, we take arbitrary, large values for the time step. We include the contributions to the optical light from the primary star, for which we take a temperature T1 = 104 K. The secondary star is treated as described in Schreiber et al. (2003); it is divided in two hemispheres with different effective temperatures, a non-irradiated one with Teff,unirr = 3800 K, and an irradiated one for which 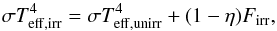 (3)where η is the albedo, taken to be 0.8, and Firr is the irradiation flux due to accretion onto the white dwarf, estimated at distance a; a being the orbital separation. Specifically, one has:
(3)where η is the albedo, taken to be 0.8, and Firr is the irradiation flux due to accretion onto the white dwarf, estimated at distance a; a being the orbital separation. Specifically, one has: 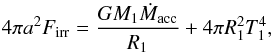 (4)where R1 is the white dwarf radius. Teff,unirr corresponds to an M0 star, typical of what is expected for a period of 4.85 h. For an accretion rate of 1018 g s-1, the effective temperature of the irradiated secondary is 7560 K; for an accretion rate of 6 × 1017 g s-1, this temperature is 6700 K. These compare well with the values obtained by de Martino et al. (1994); these authors fitted the spectrum of the optical and infrared light modulated at the orbital period and found that it can be fitted by a cool component, presumably representing the irradiated emission with a temperature of 6800 K, and by a hot component with a temperature ≥20 000 K, with a large uncertainty. This hot component is presumably due to the hot spot. Using HST and IUE observations, de Martino et al. (1999) were able to constrain this temperature to a more accurate value of 19 500 ± 500 K. The contribution of the hot spot is also included in our model; we assume a colour temperature of 104 K, typical of hot spots in CVs, but smaller than the value found by de Martino et al. (1999). This possibly overestimates the contribution from the hot spot in the optical, but, as will be seen below, the hot spot contribution to the optical light is small, meaning that this should not introduce any significant error.
(4)where R1 is the white dwarf radius. Teff,unirr corresponds to an M0 star, typical of what is expected for a period of 4.85 h. For an accretion rate of 1018 g s-1, the effective temperature of the irradiated secondary is 7560 K; for an accretion rate of 6 × 1017 g s-1, this temperature is 6700 K. These compare well with the values obtained by de Martino et al. (1994); these authors fitted the spectrum of the optical and infrared light modulated at the orbital period and found that it can be fitted by a cool component, presumably representing the irradiated emission with a temperature of 6800 K, and by a hot component with a temperature ≥20 000 K, with a large uncertainty. This hot component is presumably due to the hot spot. Using HST and IUE observations, de Martino et al. (1999) were able to constrain this temperature to a more accurate value of 19 500 ± 500 K. The contribution of the hot spot is also included in our model; we assume a colour temperature of 104 K, typical of hot spots in CVs, but smaller than the value found by de Martino et al. (1999). This possibly overestimates the contribution from the hot spot in the optical, but, as will be seen below, the hot spot contribution to the optical light is small, meaning that this should not introduce any significant error.
 |
Fig. 1 Visual magnitude for a system with the parameters of FO Aqr (see text), as a function of the mass-transfer rate from the secondary. The thick solid curve is the total luminosity; the thin red curve is the contribution from the disc, the blue curve is that of the secondary star, and the green curve is that of the hot spot. The white dwarf at a temperature of 104 K corresponds to a magnitude mV = 20.7. The dashed portion of these curves corresponds to unstable cases, in which a fraction of the disc sits on the intermediate branch of the S curve and is therefore not physical. |
Figure 1 shows the magnitude of a system with the parameters of FO Aqr, as a function of the mass-transfer from the secondary, for a magnetic moment of 1032 G cm3. The dashed portions of the curves correspond to unstable discs, and are therefore not physical; the curves are also interrupted at low mass-transfer rates, when the magnetospheric radius becomes equal to the circularisation radius and the disc can no longer exist. The circularisation radius is the radius of a Keplerian orbit with the same specific angular momentum as the transferred matter had when leaving L1 (Frank et al. 2002); for the parameters adopted here for FO Aqr, this is 0.107a ~ 1.12 × 1010 cm, a being the orbital separation. As can be seen, the system luminosity is dominated by the irradiated secondary at low mass-transfer rates, and the difference between the maximum possible brightness of a system with a disc on the cool branch and the minimum corresponding to very small accretion rates is only 1 mag for the orbital parameters of FO Aqr and for μ = 1032 G cm3. This conclusion is independent of the assumed source distance; the maximum amplitude depends only on the secondary luminosity and on the magnetic moment of the white dwarf. Figure 2 shows the same as Fig. 1 for different values of μ. As can be seen, the maximum amplitude increases with increasing μ, but is limited by the fact that the magnetospheric radius cannot exceed the circularisation radius. Variations as large as 2 mag cannot therefore be accounted for if the disc is to remain on the cool, stable branch. In addition, the visual magnitudes for a system on the cold branch are faint; the maximum brightness is 15.5–16, depending on μ, which is 2 mag fainter than FO Aqr in the normal state. In order to reconcile the predicted and observed values, one would have to reduce the distance by a factor 2.5 at least, which, despite the large uncertainty on the distance, is unlikely. In addition, at those low mass transfer rates, the effective temperature of the illuminated side of the secondary is small; for Ṁacc = 4 × 1016 g s-1, Teff,irr = 4270 K, much smaller than the value found by de Martino et al. (1994).
 |
Fig. 2 Visual magnitude for a system with the parameters of FO Aqr (see text), as a function of the mass-transfer rate from the secondary, for μ30 = 10 (red curve), 100 (black curve), and 1000 (blue curve). The dashed portion of these curves corresponds to unstable cases. |
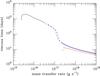 |
Fig. 3 Viscous time for a system with the parameters of FO Aqr (see text), as a function of the mass-transfer rate from the secondary, for μ30 = 10 (red curve), 100 (black curve), and 1000 (blue curve). The dashed portion of these curves corresponds to unstable cases. |
It is also worth noting that, for μ = 1032 G cm3, we find from Fig. 2 that the maximum mass-transfer rate for a system on the cold stable branch is 2.8 × 1016 g s-1, which is larger than the value given by Eq. (2)by a factor 3. This difference arises from the fact that the inner disc radius is not very different from the outer disc radius (a factor ~5); the boundary-condition term [1−(rmag/r)1/2] , which enters into the steady state solution, is important, and introduces significant corrections, which are not well captured by the fits in Hameury & Lasota (2017).
We assume that the disc is steady, which is valid only if the viscous time, 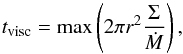 (5)is less than the time-scale on which the mass-transfer rate from the secondary evolves. Figure 3 shows tvisc as a function of the mass-transfer rate for a steady disc, for various values of the white dwarf magnetic moment. As can be seen, tvisc is of the order of 500–1000 days for μ = 1032 G cm3 on the cold branch of the S curve; longer than the duration of the low state in FO Aqr. We therefore expect the disc not to be steady. The disc will be slightly more luminous in the low state than a steady disc with the same mass-transfer rate, thereby reducing the amplitude of the luminosity variation. One should also note that the maximum of the viscous time is reached in the outer parts of the accretion disc, explaining why tvisc depends only weakly on μ. If μ becomes large, the effect of the inner boundary condition is felt throughout the entire disc, which explains why the curve calculated for μ = 1033 G cm3 deviates from the other two.
(5)is less than the time-scale on which the mass-transfer rate from the secondary evolves. Figure 3 shows tvisc as a function of the mass-transfer rate for a steady disc, for various values of the white dwarf magnetic moment. As can be seen, tvisc is of the order of 500–1000 days for μ = 1032 G cm3 on the cold branch of the S curve; longer than the duration of the low state in FO Aqr. We therefore expect the disc not to be steady. The disc will be slightly more luminous in the low state than a steady disc with the same mass-transfer rate, thereby reducing the amplitude of the luminosity variation. One should also note that the maximum of the viscous time is reached in the outer parts of the accretion disc, explaining why tvisc depends only weakly on μ. If μ becomes large, the effect of the inner boundary condition is felt throughout the entire disc, which explains why the curve calculated for μ = 1033 G cm3 deviates from the other two.
 |
Fig. 4 Light curve of a system remaining on the cold branch, in which the mass-transfer rate decreases exponentially by a factor 10 during the first 50 days, then recovers on a time scale of 250 days. The black curve is the actual V magnitude, while the red one corresponds to a steady state system. |
Figure 4 shows the evolution of a system with an initial mass-transfer rate of 2.64 × 1016 g s-1 that decreases exponentially by a factor 10 during 50 days, and then recovers on a 250-day time scale. As can be seen, the departure from steady state is significant, and the amplitude of the optical luminosity variations is smaller than expected from the steady-state assumption. It is also difficult to account for the rapid decline observed in FO Aqr.
We therefore conclude that the normal- and low states of FO Aqr cannot be accounted for by a disc residing permanently on the cold branch of the S-curve.
3. The case for a high-accretion-rate system
We now examine the possibility that the disc can be on the hot stable branch both during the normal- and the low states. This is possible if the mass-transfer rate from the secondary is always larger than the critical value for the disc to stay on the hot branch at the outer edge (Hameury & Lasota 2017) 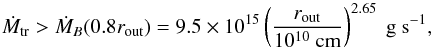 (6)where we have neglected the small dependence on the viscosity parameter α. The 0.8Rout term accounts for additional heating terms in the outer disc (heating due to the dissipation of tidal torques and by the stream impact on the disc edge, Buat-Ménard et al. 2001), so that the disc is stable for mass-transfer rates smaller than ṀB(rout). For FO Aqr, the outer disc radius is 3.7 × 1010 cm, and the critical rate is 3.2 × 1017 g s-1. We note that this rate depends only on the primary mass and is therefore accurate to more than a factor 2.
(6)where we have neglected the small dependence on the viscosity parameter α. The 0.8Rout term accounts for additional heating terms in the outer disc (heating due to the dissipation of tidal torques and by the stream impact on the disc edge, Buat-Ménard et al. 2001), so that the disc is stable for mass-transfer rates smaller than ṀB(rout). For FO Aqr, the outer disc radius is 3.7 × 1010 cm, and the critical rate is 3.2 × 1017 g s-1. We note that this rate depends only on the primary mass and is therefore accurate to more than a factor 2.
The examination of Fig. 2 again shows the maximum amplitude that one can expect for a disc on the hot branch. The mass transfer for which the disc becomes unstable depends slightly on the magnetic moment, whereas Eq. (6) does not depend on μ; the reason for this is that the inner boundary condition, νΣ = 0, where ν is the kinematic viscosity and Σ the surface density, introduces a term 1−(r/rin)1/2, rin being the inner disc radius, that slightly modifies the outer structure of the disc and becomes increasingly important as the magnetospheric truncation radius increases. Figure 2 shows that 2 mag amplitudes are possible if the mass-transfer rate in the normal state is at least of the order of a few times 1018 or 1019 g s-1, and of order of 5 × 1017 g s-1 in the low state. These lower limits are obtained for large values of μ and correspond to the case where the disc has almost disappeared in the low state, and therefore require some fine tuning. These rates are much higher than the rates expected from secular evolution models (Knigge et al. 2011), and would imply that the current mass-transfer deviates by 2 orders of magnitude from the secular mean; this is in principle possible, though. The system would also have to be brighter than observed for the fiducial distance of 450 pc by 2 mag; the distance would then have to be larger than 1 kpc to reconcile the model and the observations. Given the galactic latitude of FO Aqr (b = −49.16deg), this would put the source at a distance larger than 750 pc above the galactic plane.
Figure 3 shows that when the disc is on the hot, stable branch of the S-curve, viscous time is of the order of a few days, much shorter than the time scale on which the system luminosity has been observed to vary, and the steady state assumption is fully justified.
We therefore conclude that it is possible, but very unlikely, that the disc of FO Aqr was in the hot branch of the S curve during its low state.
4. The case for the disappearance of the accretion disc
 |
Fig. 5 Optical magnitude for a system with the parameters of FO Aqr (see text) and μ = 1.5 × 1033 G cm3, as a function of the mass-transfer rate. The thick solid line is the total optical luminosity; the thin dashed curve represents the disc contribution and the upper and lower thin solid curves represent the secondary and hot spot contributions, respectively. The red portion of the curve corresponds to discless accretion. The grey area corresponds to the optical luminosity variations between the normal- and low states. |
The last option is that the disc is on the hot branch of the S-curve during the normal state, and that, during decline, the magnetospheric radius exceeds the circularisation radius before the critical ṀB is reached. The mass-transfer rate in the normal state should then be of the order of 1018 g s-1 (the minimum value would be 5.5 × 1017 g s-1, but this would imply that the disc has almost disappeared in the normal state) and the visual magnitude should be ~13.5, as observed, and the magnetic moment should be somewhat larger than 1033 G cm3, so that the disc can vanish before entering the instability strip.
Because the disc, when it exists, sits on the hot stable branch, its viscous time is short, and the steady state assumption is fully justified.
Figure 5 shows the optical luminosity of a system in steady state with the parameters of FO Aqr, and a magnetic moment of 1.5 × 1033 G cm3 as a function of the mass-transfer rate from the secondary. The disc, when it exists, is always in the hot state; when the mass-transfer rate decreases below 5.5 × 1017 g s-1, the magnetospheric radius exceeds the circularisation radius, and the disc vanishes. The optical luminosity is then due to the contributions of the irradiated secondary, of the primary, and of the region where the stream of matter leaving the L1 point impacts the magnetosphere. For simplicity, we assume that the stream kinetic energy is dissipated entirely in this region and that the effective temperature is 104 K; when the disc vanishes, this contribution is thus equivalent to that of the hot spot, and then decreases as the mass-transfer rate decreases. The hot spot contribution increases slightly immediately before the disappearance of the disc; due to the fact that the outer disc radius decreases until reaching the circularisation radius, at which point the disc disappears. The heated secondary and the stream impact onto the magnetosphere dominate the optical light and have similar contributions, except for very low mass-transfer rates.
This scenario therefore provides a very reasonable explanation of the low state behaviour of FO Aqr.
5. Conclusions
We have shown that the absence of dwarf nova outbursts during the decline and slow recovery of FO Aqr is naturally accounted for if the magnetic moment of the white dwarf is large enough for the accretion disc to disappear before the mass-transfer rate enters the instability strip. It is, however, possible that the disc is always present and hot; but this would require mass-transfer rates much larger than expected, and would imply large luminosities which could only be reconciled with the observed optical magnitude if the distance to FO Aqr is larger than normally assumed by a factor of at least 2. Given the source position, this would put the source 750 pc above the galactic plane, which would be very difficult to account for.
The disappearance of the accretion disc has observable consequences. It is interesting to note that the partial eclipse shape changed during the low state; the eclipses became narrower and less deep, indicating that the accretion disc had shrunk (Littlefield et al. 2016). As the phased light curve over the orbital period was calculated by Littlefield et al. (2016) over their entire dataset, it is not possible to decide from these observations if the accretion disc completely disappeared at some point. One nevertheless expects, however, that material impacting the magnetosphere should form some structure in the orbital plane, possibly mimicking a ring whose size should be comparable to the magnetospheric radius, which is smaller by a factor ~2 than the disc size in the normal state; this is approximately the ratio of the eclipse full width at half maximum (FWHM) in the normal- and low states.
One also expects the power spectrum in the optical to change when the disc disappears. Wynn & King (1992) showed that discless accretion models produce a rich variety of power spectra, and that the presence of beat-frequency modulations is incompatible with dominant accretion via a disc. In the case of discless accretion, the power spectrum should be dominated by the beat frequency ω−Ω between the spin and orbital frequency and its first harmonic 2ω−2Ω, whereas in the case of disc accretion, the spin frequency should be dominant (Ferrario & Wickramasinghe 1999). Littlefield et al. (2016) found that, in the low state, the beat component amplitude is more than twice that of the spin component, while in the hight state, it is only 20% of the spin component. Although the modelling of the power spectrum is complex due to the complex geometry of the accretion flow and to the contribution of several sources to the optical light (see above), the change in the power spectrum clearly supports our finding that the disc disappears during the low state.
There have been suggestions that accretion in IPs can occur both via an accretion disc and directly onto the white dwarf; this would happen if, for example, the stream leaving the L1 point overflows the accretion disc after impacting its outer edge (Armitage & Livio 1996). This was found to occur in FO Aqr at some epochs (Hellier 1993). However, our conclusions that the disc must disappear during the faintest portion of the low state would still hold. The absence of dwarf nova outburst implies that the disc, when it exists, must remain on the hot branch. Since only a fraction of the accretion flow is processed through the accretion disc, this makes it even more difficult to account for an accretion disc in the low state: The system brightness in the high state would have to be even larger than estimated above. This does not rule out the possibility that the transition between disc and discless accretion could be gradual, and that both may happen at some time, but the amplitude of the observed variations makes it most likely that the disc has to vanish in the lowest state. The way the disc disappears has been treated in a very simplified manner in this paper. However, the study of the detailed precesses through which the disc disappears would require 3D simulations of the accretion flow which are clearly beyond the scope of this paper.
We finally note that the reasons for mass-transfer variations in cataclysmic variables are not understood at present. Low states are observed in magnetic CVs, and most notably in AM Her systems, which do not possess accretion discs, so that luminosity variations directly reflect variations in the mass-transfer rate from the secondary. Livio & Pringle (1994) proposed that variations in VY Scl stars could be due to star spots passing in the L1 region, and Hessman et al. (2000) later extended and developed this model to AM Her systems; but as noted by Littlefield et al. (2016), the unusually long duration of the recovery in FO Aqr remains somewhat mysterious.
Acknowledgments
This work was supported by a National Science Centre, Poland grant 2015/19/B/ST9/01099 and by the National Science Foundation under Grant No. NSF PHY-1125915. J.P.L. was supported by a grant from the French Space Agency CNES.
References
- Armitage, P. J., & Livio, M. 1996, ApJ, 470, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Brunschweiger, J., Greiner, J., Ajello, M., & Osborne, J. 2009, A&A, 496, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat-Ménard, V., Hameury, J.-M., & Lasota, J.-P. 2001, A&A, 366, 612 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butters, O. W., Katajainen, S., Norton, A. J., Lehto, H. J., & Piirola, V. 2009, A&A, 496, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cropper, M., Ramsay, G., & Wu, K. 1998, MNRAS, 293, 222 [NASA ADS] [CrossRef] [Google Scholar]
- de Martino, D., Buckley, D. A. H., Mouchet, M., & Mukai, K. 1994, A&A, 284, 125 [NASA ADS] [Google Scholar]
- de Martino, D., Silvotti, R., Buckley, D. A. H., et al. 1999, A&A, 350, 517 [NASA ADS] [Google Scholar]
- Ferrario, L., & Wickramasinghe, D. T. 1999, MNRAS, 309, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics, 3rd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Hameury, J. M., & Lasota, J. P. 2002, A&A, 394, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hameury, J. M., & Lasota, J. P. 2017, A&A, 602, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hameury, J.M., King, A.R., & Lasota, J.P. 1986, MNRAS, 218, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Hameury, J. M., Lasota, J. P., Knigge, C., & Körding, E. G. 2017, A&A, 600, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hellier, C. 1991, MNRAS, 251, 693 [Google Scholar]
- Hellier, C. 1993, MNRAS, 265, L35 [Google Scholar]
- Hellier, C., & Beardmore, A. P. 2002, MNRAS, 331, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Mason, K. O., & Cropper, M. 1989, MNRAS, 237, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Hessman, F. V., Gänsicke, B. T., & Mattei, J. A. 2000, A&A, 361, 952 [NASA ADS] [Google Scholar]
- Kennedy, M. R., Garnavich, P., Breedt, E., et al. 2016, MNRAS, 459, 3622 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, M. R., Garnavich, P. M., Littlefield, C. 2017, MNRAS, 469, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C. 2006, MNRAS, 373, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Lasota, J.-P. 2001, New Astron. Rev., 45, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, R., Hessman, F. V., King, A. R., Stehle, R., & Mattei, J. 1999, MNRAS, 305, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefield, C., Garnavich, P., Kennedy, M. R., et al. 2016, ApJ, 833, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Pringle, J. E. 1994, ApJ, 427, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K., Ishida, M., & Osborne, J. P. 1994, PASJ, 46, L87 [NASA ADS] [Google Scholar]
- Norton, A. J., Wynn, G. A., & Somerscales, R. V. 2004, ApJ, 614, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., & Steiner, J. E. 1983, ApJ, 264, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Pretorius, M. L., & Mukai, K. 2014, MNRAS, 442, 2580 [Google Scholar]
- Schreiber, M. R., Hameury, J. M., Lasota, J. P. 2003, A&A, 410, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warner, B. 1995, Cataclysmic variable stars, Camb. Astrophys. Ser., 28 [Google Scholar]
- Wickramasinghe, D. 2014, Eur. Phys. J. Web Conf., 64, 03001 [CrossRef] [EDP Sciences] [Google Scholar]
- Wynn, G. A., & King, A. R. 1992, MNRAS, 255, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Yuasa, T., Nakazawa, K., Makishima, K., et al. 2010, A&A, 520, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Visual magnitude for a system with the parameters of FO Aqr (see text), as a function of the mass-transfer rate from the secondary. The thick solid curve is the total luminosity; the thin red curve is the contribution from the disc, the blue curve is that of the secondary star, and the green curve is that of the hot spot. The white dwarf at a temperature of 104 K corresponds to a magnitude mV = 20.7. The dashed portion of these curves corresponds to unstable cases, in which a fraction of the disc sits on the intermediate branch of the S curve and is therefore not physical. |
| In the text | |
 |
Fig. 2 Visual magnitude for a system with the parameters of FO Aqr (see text), as a function of the mass-transfer rate from the secondary, for μ30 = 10 (red curve), 100 (black curve), and 1000 (blue curve). The dashed portion of these curves corresponds to unstable cases. |
| In the text | |
 |
Fig. 3 Viscous time for a system with the parameters of FO Aqr (see text), as a function of the mass-transfer rate from the secondary, for μ30 = 10 (red curve), 100 (black curve), and 1000 (blue curve). The dashed portion of these curves corresponds to unstable cases. |
| In the text | |
 |
Fig. 4 Light curve of a system remaining on the cold branch, in which the mass-transfer rate decreases exponentially by a factor 10 during the first 50 days, then recovers on a time scale of 250 days. The black curve is the actual V magnitude, while the red one corresponds to a steady state system. |
| In the text | |
 |
Fig. 5 Optical magnitude for a system with the parameters of FO Aqr (see text) and μ = 1.5 × 1033 G cm3, as a function of the mass-transfer rate. The thick solid line is the total optical luminosity; the thin dashed curve represents the disc contribution and the upper and lower thin solid curves represent the secondary and hot spot contributions, respectively. The red portion of the curve corresponds to discless accretion. The grey area corresponds to the optical luminosity variations between the normal- and low states. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


