| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A146 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731014 | |
| Published online | 27 October 2017 | |
Reduced gas accretion on super-Earths and ice giants
Laboratoire Lagrange, UMR7293, Université Côte d’Azur, CNRS, Observatoire de la Côte d’Azur, Boulevard de l’Observatoire, 06304 Nice Cedex 4, France
e-mail: michiel.lambrechts@oca.eu
Received: 21 April 2017
Accepted: 1 August 2017
A large fraction of giant planets have gaseous envelopes that are limited to about 10% of their total mass budget. Such planets are present in the solar system (Uranus, Neptune) and are frequently observed in short periods around other stars (the so-called super-Earths). In contrast to these observations, theoretical calculations based on the evolution of hydrostatic envelopes argue that such low-mass envelopes cannot be maintained around cores exceeding five Earth masses. Instead, under nominal disk conditions, these planets would acquire massive envelopes through runaway gas accretion within the lifetime of the protoplanetary disk. In this work we show that planetary envelopes are not in hydrostatic balance, which slows down envelope growth. A series of 3D global, radiative hydrodynamical simulations reveal a steady-state gas flow, which enters through the poles and exits in the disk midplane. Gas is pushed through the outer envelope in about ten orbital timescales. In regions of the disk that are not significantly dust-depleted, envelope accretion onto cores of about five Earth masses can get stalled as the gas flow enters the deep interior. Accreted solids sublimate deep in the convective interior, but small opacity-providing grains are trapped in the flow and do not settle, which further prevents rapid envelope accretion. The transition to runaway gas accretion can however be reached when cores grow larger than typical super-Earths, beyond 15 Earth masses, and preferably when disk opacities are below κ = 1 cm2/g. These findings offer an explanation for the typical low-mass envelopes around the cores of super-Earths.
Key words: planets and satellites: formation / planets and satellites: gaseous planets / hydrodynamics / methods: numerical
© ESO, 2017
1. Introduction
In the core accretion scenario, giant planets form by attracting a gaseous envelope onto a previously formed solid core (Pollack et al. 1996). These large cores of a few Earth masses (ME) form from planetary embryos that are able to accrete larger than km-sized planetesimals (Rafikov 2004) and sweep up cm-sized pebbles with high efficiency (Lambrechts & Johansen 2012). As the core grows large, the envelope is accreted from the gaseous component of the protoplanetary disk, which only remains present for a few million years around young stars (Ribas et al. 2015). Core formation must therefore proceed at a rate of several Earth masses per 106 yr.
The accretion of the gaseous atmosphere itself can be divided in two separate phases. Early on, the envelope slowly gains mass as it cools down, a process which can be further delayed by continued heat deposition from solid accretion. However, if the cooling process can proceed efficiently and for a sufficient amount of time, the envelope can grow as massive as the core. This process triggers a second phase of rapid gas accretion. The onset of a self-gravitating gas envelope facilitates continued envelope cooling and mass growth. Planets that enter this regime become gas giants with a high-mass envelope.
In this work we focus on planets in the process of attracting a gaseous envelope before they have reached the point of runaway gas accretion. This growth phase has been studied extensively with 1D numerical models that assume a spherical symmetric atmosphere and evolve the envelope assuming hydrostatic equilibrium at all times, a method that originated from stellar evolution calculations (Mizuno 1980; Ikoma et al. 2000; Piso & Youdin 2014). These models show that the timescale to reach runaway gas accretion is very sensitive to the solid accretion rate, the core mass, the dust opacity in the outer envelope, and the amount of dissolved solids (Stevenson 1982). Recent work has argued that the dust grains do not contribute much to opacity because they coagulate and settle rapidly (Ormel 2014). This reduces the timescale for which a completed ten-Earth mass core starts runaway gas accretion to ~ 1 Myr, which is shorter than the disk lifetime (Mordasini 2014). Similarly, the addition of sublimated solids raises the mean molecular weight of the envelope and even further reduces the time to runaway gas accretion (Hori & Ikoma 2011; Venturini et al. 2015, 2016). Together these findings hint that all cores above a few Earth masses should have massive gas envelopes.
These theoretical findings, however, are in conflict with the existence of the ice giants in the solar system: Uranus and Neptune. Both planets are larger than 10 ME, but have never accreted a massive gas envelope. This also does not agree with the characterized population of short-period exoplanets. Super-Earths, planets with sizes between 1–4 Earth radii (RE), are found around approximately half of the Sun-like stars (Winn & Fabrycky 2015). In addition, these planets, which have masses of up to 25 ME, typically have hydrogen/helium envelopes that do not exceed 10% of the total mass of the planet (Hadden & Lithwick 2017).
New hydrodynamical simulations challenge the standard assumptions used in envelope growth models. Previous evolution studies (Pollack et al. 1996; Ikoma et al. 2000; Piso & Youdin 2014) assumed envelopes in hydrostatic balance that are closed systems. Interaction with the protoplanetary disk would only occur through an imposed outer boundary condition that matches the unperturbed protoplanetary disk. Instead, hydrodynamical simulations performed in 3D show that gas continuously flows from the poles through the planetary envelope (Ayliffe & Bate 2012; Tanigawa et al. 2012; D’Angelo & Bodenheimer 2013). Moreover, recent simulations performed under the simplifying assumption of a constant temperature envelope and disk, have quantified that gas is continuously advected through the envelope on orbital timescales, implying that almost no gas accretion would occur (Ormel et al. 2015; Fung et al. 2015). However, the simplifying assumption of an isothermal envelope corresponds to the limit case of a completely cooled-down planet, which cannot be obtained for planets heated by the process of formation. Therefore, these new results are difficult to interpret. Furthermore, hydrodynamical studies in 3D that have a more complete thermodynamical treatment of the envelope claim results closely in line with envelope growth rates from standard hydrostatic models (D’Angelo & Bodenheimer 2013).
Here, we aim to find the quasi-static structure of a low-mass envelope around a massive core (5–15 ME). We do not make an isothermal approximation, but instead use a radiative treatment similar to D’Angelo & Bodenheimer (2013). Additionally, we model the heat deposited by solid accretion. In order to correctly describe disk-planet interaction, we model a full annulus of the protoplanetary disk around the planet. Hydrodynamical simulations covering the complete evolution of envelope growth in time are numerically unfeasible. Therefore, we make temporal snapshots at different growth stages that show how envelopes are structured and grow.
The paper is structured as follows. A technical description of the methods can be found in Sect. 2. We first study the case of a planet with a luminosity that is dominated by the heat released by the accretion of solids (Sect. 3). This case is investigated in detail to establish the dynamical and energetic structure of planetary envelopes in their formation stage. Then we proceed by studying planetary envelopes after solid accretion has come to a halt (Sect. 4). Our results depend on the opacity in the envelope and the mass of the solid core of the planet. High dust opacities tend to delay envelope growth (Sect. 5). Large cores facilitate the transition to runaway gas accretion (Sect. 6). In Sect. 7, we summarize the implications of our work on the growth of the envelope and the core. We place our results in the context of exoplanet observations that reveal a high occurrence rate of super-Earths, but argue for a low frequency of more massive gas giants (Sect. 8). Finally, a summary is presented (Sect. 9).
2. Methods
 |
Fig. 1 Global view on the vertically integrated density (Σgas in g/cm2) of the simulated annulus taken from run RADL27k0.01. We can identify the spiral arms originating from the planet located at coordinates (1,0) revealing a strong interaction between planet and disk. |
2.1. General description of the model
We model a full annulus encompassing the orbit of the planet, as illustrated in Fig. 1. This allows us to carefully analyze the exchange of gas between the envelope and the disk. The simulations are performed in 3D, as gas motion perpendicular to the midplane regulates the gas dynamics around the envelope. We use a nonuniform grid to be able to trace the flow of gas on small scales well inside the Hill sphere of the planet, following the approach by Fung et al. (2015). Additionally we include the heat deposited by the accretion of solids, and model energy transfer by radiation, similar to the method used by D’Angelo & Bodenheimer (2013). In order to do so, we make use of the FARGOCA code (Lega et al. 2014). This radiation-hydrodynamics code is designed for global 3D studies of planet-disk interaction. It is based on the finite difference code FARGO (Masset 2000). Below, we report in greater detail the methods used to model the planetary envelope.
2.2. Gas dynamics
We simulate a non-self-gravitating viscous gas on a fixed grid co-rotating with the planet. The standard continuity and momentum equations, 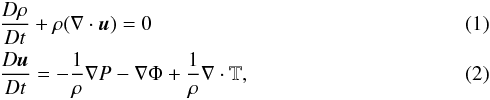 are solved using spherical coordinates (see Lega et al. 2014) for more details on the implementation in FARGOCA). Here, D/Dt is the Lagrangian time derivative, ρ is the density, P is the gas pressure, u is the velocity, and T is the viscous stress tensor.
are solved using spherical coordinates (see Lega et al. 2014) for more details on the implementation in FARGOCA). Here, D/Dt is the Lagrangian time derivative, ρ is the density, P is the gas pressure, u is the velocity, and T is the viscous stress tensor.
The gravitational potential Φ is the sum of the contribution of the stellar potential, the potential of the planet, and indirect terms that take into account the acceleration of the primary due to the gravity of the planet and the disk. The planetary potential is given by Φp = − GMc/r outside a radius rsm from the planet. Here G is the gravitational constant and Mc is the core mass. Within the smoothing length rsm, the central singularity is avoided by a cubic interpolation to Φp = − 2GMc/rsm (Klahr & Kley 2006). In Appendix A, we describe this prescription for the planetary potential in more detail and explore its influence on our results.
2.3. Gas thermodynamics
2.3.1. Energy equation
We separately evolve the thermal energy density (Egas) and radiative energy density (Erad). The evolution equations are given by (Kley 1989; Commerçon et al. 2011; Bitsch et al. 2013) 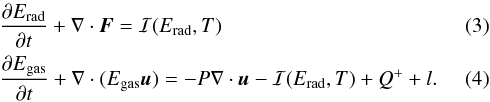 Here, F is the radiative flux. The fluid-radiation interaction term is described by ℐ = ρκ(4σSBT4 − cErad), where σSB is the Stefan-Boltzmann constant, κ is the Rosseland mean opacity, T is the temperature, and c is the speed of light. In the optical thick limit, this term reduces to energy diffusion of the form D∇2Egas. The diffusion coefficient,
Here, F is the radiative flux. The fluid-radiation interaction term is described by ℐ = ρκ(4σSBT4 − cErad), where σSB is the Stefan-Boltzmann constant, κ is the Rosseland mean opacity, T is the temperature, and c is the speed of light. In the optical thick limit, this term reduces to energy diffusion of the form D∇2Egas. The diffusion coefficient, 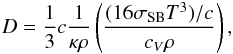 (5)corresponds to the product of the velocity and the mean free path of the photons and the last factor in brackets weights the expression with the ratio between the specific heat of the photons with respect to the gas (cV). The term P∇·u in Eq. (4) represents compressional heating and Q+ viscous heating (for further details, see Mihalas & Mihalas 1984). The final term, l, is a source term which represents the deposited heat per unit time by solid accretion. The implementation of this term is discussed in more detail in Appendix B.
(5)corresponds to the product of the velocity and the mean free path of the photons and the last factor in brackets weights the expression with the ratio between the specific heat of the photons with respect to the gas (cV). The term P∇·u in Eq. (4) represents compressional heating and Q+ viscous heating (for further details, see Mihalas & Mihalas 1984). The final term, l, is a source term which represents the deposited heat per unit time by solid accretion. The implementation of this term is discussed in more detail in Appendix B.
The radiative flux is calculated in the framework of the flux-limited diffusion approximation, 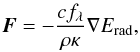 (6)where fλ is a flux-limiter (Levermore & Pomraning 1981). The implementation is described in more detail in Lega et al. (2014).
(6)where fλ is a flux-limiter (Levermore & Pomraning 1981). The implementation is described in more detail in Lega et al. (2014).
2.3.2. Opacity
Both gas and dust act as a source of opacity which absorbs and deflects radiation. Below temperatures of around 1700 K, dust particles are the predominant opacity source (Bell & Lin 1994). In this work, we purposely choose a simple constant opacity prescription for our envelope and gas disk. We then explore this free parameter in Sect. 5.
2.3.3. Equation of state
Similar to our choice of a constant opacity, we employ a simple equation of state. We use an ideal gas, where the pressure is given by 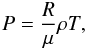 (7)where R is the gas constant. We used a fixed value for the mean molecular weight (μ = 2.35), corresponding to a solar H/He mixture. More realistic prescriptions would need to take into account the pollution of the envelope by heavy elements and the changes to the mean molecular weight and adiabatic index. Additionally, variables like the specific heat at constant volume cV are temperature sensitive and depend on the unknown ratio of ortho- to parahydrogen (D’Angelo & Bodenheimer 2013). These topics can be investigated in future work.
(7)where R is the gas constant. We used a fixed value for the mean molecular weight (μ = 2.35), corresponding to a solar H/He mixture. More realistic prescriptions would need to take into account the pollution of the envelope by heavy elements and the changes to the mean molecular weight and adiabatic index. Additionally, variables like the specific heat at constant volume cV are temperature sensitive and depend on the unknown ratio of ortho- to parahydrogen (D’Angelo & Bodenheimer 2013). These topics can be investigated in future work.
2.4. Numerical implementation
2.4.1. Coordinate system
We use spherical coordinates (r,θ,ϕ), where r is the radial distance from the origin, θ the polar angle measured from the z-axis, and ϕ is the azimuthal coordinate starting from the x-axis. The midplane of the disk is at the equator (θ = π/ 2) and the origin of the coordinates is centered on the star. We work in a coordinate system which rotates with angular velocity, 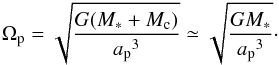 (8)The code operates in code units with the stellar mass M∗, the semi-major axis of the planet ap and the Keplerian frequency set to unity.
(8)The code operates in code units with the stellar mass M∗, the semi-major axis of the planet ap and the Keplerian frequency set to unity.
2.4.2. Simulation domain and boundary conditions
Radially, the disk extends from amin/ap = 0.7 to amax/ap = 1.3. In the vertical direction the disk extends from the midplane (θ ≃ 90° to 6° above the midplane, i.e., θ ≃ 84°). We do not study inclined planets orbits; therefore, we do not need to extend the disk below the midplane.
We use periodic boundary conditions in the azimuthal direction as we aim to simulate the full 2π-annulus. We use a reflective boundary on the midplane. This is appropriate for non-inclined planets, where mirror symmetry can safely be assumed between the upper and lower hemisphere of the disk. The upper boundary condition is also reflective in order to prevent mass outflow. In the radial direction we use evanescent boundaries with a wave suppression zone covering 10% of the inner and outer radius to prevent the reflection of density waves (de Val-Borro et al. 2006).
2.4.3. Disk model
Before inserting the planet, we bring the disk into radiative equilibrium (Lega et al. 2015). This equilibrium is obtained for a 2D (r,z) axisymmetric disk with resolution (Nr,Nθ,Nϕ) = (200,52,2) in about 100  .
.
Viscous stresses are the only heating source as we ignore stellar heating. This is a good description for the inner disk, where viscous heating dominates. We have used a constant viscosity 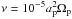 (code units). This low viscosity will be necessary to properly capture the 3D flow. We noticed that higher values of viscosity (on the order of
(code units). This low viscosity will be necessary to properly capture the 3D flow. We noticed that higher values of viscosity (on the order of 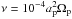 ) effectively force 2D flow, in agreement with Fung et al. (2015). We also verified that extremely low values of
) effectively force 2D flow, in agreement with Fung et al. (2015). We also verified that extremely low values of 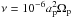 do not alter our results significantly, but at times they may produce unsteady fluctuations.
do not alter our results significantly, but at times they may produce unsteady fluctuations.
The gas surface density follows a power law profile, Σgas = Σp(a/ap)− 1 / 2 g/cm2, which gives an equilibrium disk without radial gas motion. At the location of the planet, we record a surface density of Σp = 1.3 × 10-3 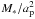 , corresponding to Σp = 400 g/cm2 at a distance of 5.2 AU. The aspect ratio is the result of the equilibrium between viscous heating and radiative cooling. Depending on the choice of the opacity, we find a gas scale aspect ratio of H/ap = 0.03 for κ = 0.01 cm2/g or H/ap = 0.05 for κ = 1 cm2/g at the position of the planet. We note, however, that our results on the small scale of planetary envelopes only weakly depend on the exact choice of the large-scale disk structure.
, corresponding to Σp = 400 g/cm2 at a distance of 5.2 AU. The aspect ratio is the result of the equilibrium between viscous heating and radiative cooling. Depending on the choice of the opacity, we find a gas scale aspect ratio of H/ap = 0.03 for κ = 0.01 cm2/g or H/ap = 0.05 for κ = 1 cm2/g at the position of the planet. We note, however, that our results on the small scale of planetary envelopes only weakly depend on the exact choice of the large-scale disk structure.
Simulation parameters.
2.4.4. Introduction of the planet
After the procedure to generate an equilibrium disk, we refine the grid azimuthally and work in 3D. Planets of 5 or 15 Earth masses are then embedded in the equilibrium disk and held on fixed circular orbits in the midplane, with code units rp = 1, ϕp = 0, θp = π/ 2. Our mesh is chosen so that the planet is at the intersection between cell’s surfaces in the three directions, i.e., at the corner of eight grid cells.
Since hydrodynamical 3D calculations of fully radiative disks are expensive in computational time, we split our simulations into two phases. In the first phase we employ a uniform grid so that we can use the Fast Advection in Rotating Gaseous Objects algorithm (FARGO; Masset 2000) and benefit from large time steps. We recall that in a Keplerian disk the traditional Courant condition provides very small time steps due to the fast orbital motion at the inner boundary of the disk. In the FARGO algorithm, the time step is instead limited by the perturbed azimuthal velocity with respect to the Keplerian one. We run each simulation with the uniform grid until the disk relaxes to the presence of the planet. This occurs after approximately 30 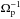 . Figure 1 shows the gas surface density when the stationary state is reached. For this uniform grid, our nominal resolution corresponds to (Nr,Nθ,Nϕ) = (200,52,2048) grid cells. This choice provides a resolution of 0.003 ap, corresponding to ten grid cells in the Hill sphere of a 5 ME planet.
. Figure 1 shows the gas surface density when the stationary state is reached. For this uniform grid, our nominal resolution corresponds to (Nr,Nθ,Nϕ) = (200,52,2048) grid cells. This choice provides a resolution of 0.003 ap, corresponding to ten grid cells in the Hill sphere of a 5 ME planet.
2.4.5. Increased resolution around the planet
In the second phase, we use a nonuniform grid with increasing resolution towards the planet to more accurately model the planetary envelope. The grid layout is based on the formulation by Fung et al. (2015), which gives small, nearly uniform grid cells in the Hill sphere around the planet and large grid cell sizes farther out.
Our medium resolution corresponds to a width of the inner grid cells of 0.00135 ap, which resolves the Hill sphere of a 5 ME planet by about 24 grid cells. In total the grid has (Nr,Nθ,Nϕ) = (200,52,1512) cells in the radial, polar, and azimuthal directions. At this resolution we have about 1 orbit in 8 h of computation with 60 cores using hybrid MPI+OpenMP parallelization. We typically run the code for at least 8 orbits to relax the system into equilibrium.
In high-resolution runs, we use inner grid cells of width 4.27 × 10-4 ap, corresponding to about 84 grid cells across a Hill sphere for a 5 ME planet. This finer grid has (Nr,Nθ,Nϕ) = (300,76,2268) cells in the radial, polar, and azimuthal directions. At this resolution we have about 1 orbit in 50 h of computation with 60 cores. In this final step, we simulate 4 planetary orbits, which we found to be sufficient to capture the interior structure of the planet.
Finally, we note that the FARGO advection algorithm cannot be used on the nonuniform grid; instead, the time step is set by the usual Courant condition (Stone & Norman 1992).
2.5. Simulations
Our main numerical experiments are described in detail in Sects. 3–6. Table 1 gives an overview of the performed simulations and the parameter space covered. Additionally, we performed several performance tests of the code. In Appendix A we present several convergence tests. We investigate the dependency on the resolution in the code with a focus on properly resolving the planetary potential. Additionally, long-term integrations are performed to demonstrate steady-state stability.
3. Results: the envelope around a core accreting solids
3.1. Overview
We start with a presentation of our results on the envelope around a planetary core in the process of accreting solids (run RADL27k0.01). The structure of the envelope is discussed in detail. This allows us to compare, to this reference case, results from following sections where we explore the influence of key parameters. In particular, we discuss the role of interior heating by solid accretion in Sect. 4 (run RADL0k0.01). We then proceed to investigate the role of the opacity in Sect. 5, when accreting solids (run RADL27k1) or not (run RADL0k1). We leave the discussion of the role of the core mass itself to Sect. 6 (runs RADL27k1M15 and RADL0k1M15).
3.2. Luminosity from accreting solids
The structure of the envelope is set by the balance between the central gravitational attraction of the planetary core and outward pressure from the heated interior. We now consider a planet where the interior heat generation is dominated by energy deposition from solids sinking towards the core. For such a planet, in the process of forming its 5 ME core, the accretion luminosity is on the order of 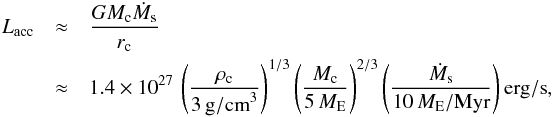 (9)where Ṁs is the solid accretion rate, and rc and ρc the core radius and density. Here, we have assumed that most heat is ultimately deposited deep down in the interior of the envelope (Lambrechts et al. 2014).
(9)where Ṁs is the solid accretion rate, and rc and ρc the core radius and density. Here, we have assumed that most heat is ultimately deposited deep down in the interior of the envelope (Lambrechts et al. 2014).
The magnitude of the solid accretion rate Ṁs is poorly constrained. It depends on the unknown amount of solids available in the protoplanetary disk, but must be on the order of 10 ME/Myr in order to grow the core to completion before disk dissipation. In Appendix E, we motivate the solid accretion rate in more detail.
3.3. Envelope structure
 |
Fig. 2 Averaged envelope structure for an envelope undergoing solid accretion at a rate of 10 ME/Myr (black) and an envelope not undergoing solid accretion (blue). Shown are the azimuthally averaged temperature and density in the planetary midplane (RADL27k0.01,RADL0k0.01). The diamond indicates the gas scale height H of the protoplanetary disk at the location of the planet, the circle the Hill radius rH of the 5 ME core, the square the Bondi radius rB, and the triangle the estimated position of the radiative-convective boundary rrcb. The top panel (A) displays the temperature. The bottom panel (B) shows the azimuthally averaged density in the midplane. In the background we also show the density structure for a cooled-down isothermal planet with a gray dotted curve. An adiabatic convective interior, a polytrope with γ = 1.4, is shown with the purple dotted line up to rrcb. |
Figure 2 shows the azimuthally averaged temperature and density profile of the envelope together with characteristic length scales. We first note that gas is perturbed up to a scale height, 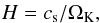 (10)away from the core. Here cs is assumed to be the unperturbed sound speed. Therefore, the gas is affected by the presence of the core even outside the gravitational reach of the core, given by the Hill radius,
(10)away from the core. Here cs is assumed to be the unperturbed sound speed. Therefore, the gas is affected by the presence of the core even outside the gravitational reach of the core, given by the Hill radius, 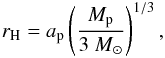 (11)where M⊙ is the stellar mass. Outside this radius, the stellar tidal field starts dominating over the gravity of the core. Since we consider low-mass envelopes, we make the approximation that the core dominates the potential (Mp ≈ Mc).
(11)where M⊙ is the stellar mass. Outside this radius, the stellar tidal field starts dominating over the gravity of the core. Since we consider low-mass envelopes, we make the approximation that the core dominates the potential (Mp ≈ Mc).
The Bondi radius, 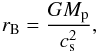 (12)corresponds to the radius where the pressure is perturbed by the gravitational force from the planet, assuming no temperature perturbation. This assumption makes this length scale, often used in envelope studies, impractical in the context of our radiative hydrodynamical calculations. We therefore prefer to scale our results with respect to the Hill sphere. However, for completeness we have indicated the Bondi radius with a square symbol in Fig. 2.
(12)corresponds to the radius where the pressure is perturbed by the gravitational force from the planet, assuming no temperature perturbation. This assumption makes this length scale, often used in envelope studies, impractical in the context of our radiative hydrodynamical calculations. We therefore prefer to scale our results with respect to the Hill sphere. However, for completeness we have indicated the Bondi radius with a square symbol in Fig. 2.
Interior to these outer length scales, spherical hydrostatic models predict the existence of a radiative-convective boundary (Appendix D). This corresponds to the location in the envelope where heat transfer goes from being convection-dominated in the interior to radiation-dominated in the outer envelope. The depth of this radiative shell, rrcb, is given by ![\begin{eqnarray} \frac{r_{\rm rcb}}{r_{\rm B}} \approx \left[ \ln \left( \frac{64 \pi G \sigma_{\rm SB} \nabla_{\rm ad} T_{\rm mid}^4 M_{\rm c}}{3 \kappa L P_{\rm mid}} \right) \right]^{-1} , \end{eqnarray}](/articles/aa/full_html/2017/10/aa31014-17/aa31014-17-eq125.png) (13)where Tmid and Pmid are the midplane temperature and pressure, and ∇ad the adiabatic temperature gradient. We discuss this expression in more detail in Appendix D.
(13)where Tmid and Pmid are the midplane temperature and pressure, and ∇ad the adiabatic temperature gradient. We discuss this expression in more detail in Appendix D.
The radius of the core itself is located deep inside the envelope, at about 10-3 Hill radii, and cannot be resolved.
In this paper, we consider low-mass planets embedded in the gas disk. Therefore, the above length scales are typically ordered as rrcb ≲ rB ≲ rH ≲ H, as can be seen in Fig. 2. The ordering depends on the planetary mass and solid accretion rate. Figure 3 illustrates these various length scales as functions of planetary mass. We indicate the depth of the radiative zone with the black curve, assuming a luminosity provided by the core accreting pebbles (see Fig. E.1). Cores with masses above about 20 ME are typically not embedded in disks with aspect ratios below H/ap = 0.05. Then the Bondi radius exceeds the Hill radius, which has become larger than the local gas scale height of the disk.
 |
Fig. 3 Relevant length scales for a low-mass envelope, expressed with respect to the disk scale height, as a function of planetary mass. The yellow line represents the Hill radius (rH), the blue line the Bondi radius (rB), and the black curve the radius above which radiative energy transfer is possible (rrcb) assuming κ = 0.01 cm2/g and H/ap = 0.03. |
Taken together the panels of Fig. 2 indicate a good qualitative agreement with the expected thermodynamical structure of a planet, based on 1D analytical calculations. Overall, we note little temperature increase in the part of the envelope we model (Panel A of Fig. 2). The outer region of the envelope remains nearly isothermal, while interior to approximately 0.2 rH the temperature slope steepens. This transition occurs around rrcb, which we calculated for the given accretion luminosity. This gives a first hint that heat transport in the interior of the planet does not occur radiatively. This result is thus in line with standard 1D models. We note that the turnover of the slope at the smallest scales towards 0.01 rH is largely an artifact of the necessary smoothing of the potential.
Panel B of Fig. 2 shows the azimuthally averaged density structure in the envelope (black curve), as measured in the midplane. We recover the characteristic exponential increase in the nearly isothermal outer layer. This can be seen by comparison to the gray dotted line in panel B of Fig. 2, which gives the density profile for a purely isothermal envelope (an isotherm). Interior to approximately 0.2 rH, corresponding to the location of rrcb, we observe a turnover to a power law slope. This turnover qualitatively agrees with a polytropic interior, with adiabatic index γ = 1.4, which we would expect from an inner convective interior. This is illustrated by the purple dotted curve in Fig. 2, where we have taken into account the smoothing of the potential, which is responsible for the flat slope at the smallest radii.
3.4. Flow through the envelope
 |
Fig. 4 Sample of gas streamlines arriving from the upstream direction with respect to the planet (run RADL27k0.01). The core is located at x = r − ap = 0, y = ap(φ − φp) = 0, z = 0, as indicated by the black circle, and surrounded by a transparent purple sphere with radius r = rH. Results are shown in the frame co-rotating with the planet. Blue and green streamlines make a perturbed horseshoe orbit. Gas parcels arrive well above the midplane (z >rH), enter the Hill sphere, and subsequently exit closer to the midplane (z < rH). The red and orange curves are examples of streamlines that interact strongly with the core. The orange streamline circulates closely around the core (within r < 0.5 rH), while the red streamline indicates a gas parcel that remains trapped for the duration of the integration. |
3.4.1. Overview
A large fraction of the gas inside the envelope, both in mass and volume, is not bound to the core. Instead, gas parcels enter and leave the planetary atmosphere in a complex fashion on orbital timescales. We find these flows reach a (nearly) steady-state pattern and do not exceed the sound speed.
Figure 4 illustrates the characteristic orbits of gas parcels that enter the Hill sphere of the planetary core. At high latitudes above the disk midplane, fluid elements are only weakly perturbed by the planetary core, and perform the expected U-turn associated with horseshoe orbits. However, at lower latitudes, streamlines bend significantly when they enter the Hill sphere and exit the atmosphere closer to the midplane (blue and green curves in Fig. 4). Closest to the core, we note that field lines (red curve in Fig. 4) remain trapped and perform a circumplanetary motion with a weak retrograde tendency.
3.4.2. Force balance
We now inspect the force balance on the fluid elements that approach the core. Assuming the Coriolis term dominates over advection (small Rossby number approximation), the momentum equation in the rotating frame takes the form 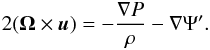 (14)Here we ignored the viscosity term and assumed steady state. This expression is similar to geostrophic balance, but with the addition of an effective potential term, which is the sum of the gravity terms and the centrifugal force (∇Ψ′). By multiplying Eq. (14) by ρ and taking the curl, we find the form
(14)Here we ignored the viscosity term and assumed steady state. This expression is similar to geostrophic balance, but with the addition of an effective potential term, which is the sum of the gravity terms and the centrifugal force (∇Ψ′). By multiplying Eq. (14) by ρ and taking the curl, we find the form ![\begin{eqnarray} 2 \left[ \nabla \times (\vec \Omega \times \rho \vec u ) \right] = - \nabla \times (\rho \nabla \Psi' ) . \end{eqnarray}](/articles/aa/full_html/2017/10/aa31014-17/aa31014-17-eq145.png) (15)We can further rewrite this expression by expanding both terms
(15)We can further rewrite this expression by expanding both terms ![\begin{eqnarray} 2 \left[ - (\Omega \cdot \nabla ) (\rho \vec u ) + (\nabla \cdot \rho \vec u ) \vec \Omega \right] = - \nabla \rho \times \nabla \Psi' - \rho \nabla \times \nabla \Psi'. \end{eqnarray}](/articles/aa/full_html/2017/10/aa31014-17/aa31014-17-eq146.png) (16)By making use of the steady-state continuity equation, we can reduce this expression to
(16)By making use of the steady-state continuity equation, we can reduce this expression to 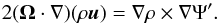 (17)Here, the directional derivative on the left-hand term expresses the vertical gradients in the mass flux.
(17)Here, the directional derivative on the left-hand term expresses the vertical gradients in the mass flux.
Outside the Hill radius, densities are nearly uniform within a gas scale height from the midplane. Therefore, the above expression reduces to ∂u/∂z = 0, which corresponds to the Taylor-Proudman theorem. As uz = 0 is zero in the midplane, it remains so at higher altitudes as well. Distant horseshoe orbits do not develop vertical motion and appear approximately identical from the midplane up to higher altitudes.
However, the planetary potential perturbs densities and the above approximation breaks down near the planet. From Eq. (17), it is nevertheless clear that a vertical mass flux gradient (∂(ρuz) /∂z) requires special nonaligned density gradients with respect to the gravity force term that are perpendicular to axis of rotation. This situation occurs when horseshoe-like streamlines come close to the planet and hit the spiral density perturbation triggered by the planet. Indeed, we note a sudden drop in altitude towards the second quadrant (x < 0,y > 0) for the blue, green, and orange streamlines of Fig. 4. As Eq. (17) is general in nature, similar vertical motions are present in the isothermal approximation (Fung et al. 2015; Ormel et al. 2015).
We can also see that streamlines that get very close to the core and approach the midplane, rotate in a retrograde fashion. This hints that the pressure term slightly dominates the gravity terms towards the midplane, as can be seen from Eq. (14). This resulting retrograde motion, as seen in our prograde rotating frame, is reminiscent of vortices with high pressure centers in protoplanetary disks.
Closer to the core we can expect hydrostatic balance to set in. By definition this corresponds to the left-hand terms of Eq. (14), or equivalently the left-hand term of Eq. (17), being equal to zero. Assuming again no vertical velocities in the midplane, Eq. (17) implies that there can be no significant vertical mass flux into an innermost hydrostatic region.
 |
Fig. 5 Energy balance along streamlines as a function of time in units of orbital period T. Each panel traces the energy budget for the different streamlines depicted in Fig. 4, with panels A to D decreasing in height above the midplane. Magenta curves show the kinetic energy contribution, which is negligible. The purple curve is the effective potential term (see main text for full description). The green curve gives the thermal energy along the streamline. The black curve is the sum of the energy contributions, the Bernoulli parameter. Circles mark the points where the field line enters and exits the Hill sphere. The square symbol indicates the point where the fluid parcel crosses the x = 0 plane, which corresponds to the orbit of the planet. When multiple crossings occur the point closest to the core is selected. |
3.4.3. Energy balance
As fluid elements enter the envelope, they convert part of the liberated potential energy to thermal energy and exchange energy with the atmosphere. The energy budget on a streamline is given by 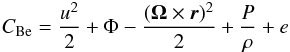 (18)for steady flow in a non-time-dependent potential, while ignoring heat exchange. Here, the term (Ω × r)2/ 2 comes from the centrifugal force in the rotating frame and e is the internal energy per unit mass. Together the last two terms of the expression form the enthalpy. If no heat exchange is assumed and the inviscid limit is taken, the quantity CBe is conserved along the field line (Bernoulli’s constant). However, heat is exchanged between the disk and the planet through compressional heating and radiative exchange.
(18)for steady flow in a non-time-dependent potential, while ignoring heat exchange. Here, the term (Ω × r)2/ 2 comes from the centrifugal force in the rotating frame and e is the internal energy per unit mass. Together the last two terms of the expression form the enthalpy. If no heat exchange is assumed and the inviscid limit is taken, the quantity CBe is conserved along the field line (Bernoulli’s constant). However, heat is exchanged between the disk and the planet through compressional heating and radiative exchange.
We carefully investigate the energy balance for the streamlines depicted in Fig. 4. This analysis is presented with one panel for each streamline of Fig. 5. First, we note that the kinetic energy contribution is negligible for all streamlines. This may look surprising given the short timescales, on the order of ten orbital timescales, on which fluid elements cross the Hill sphere, as can be read from the horizontal time axis. However, from an energetic viewpoint, they can be safely ignored. The potential term depicted here is the sum of stellar potential, the potential of the planet, and the centrifugal term Ψ = Ψgrav − Ω2r2/ 2. For clarity, in Fig. 5 we only show the deviation from the background state at the orbital radius of the planet (Ψback = − Ωr − Ω2r2/ 2 = − 1.5 in code units).
As fluid elements approach the core, the combination of compressional heating and irradiation increase the thermal energy (Eth = e + P/ρ). The peak value occurs in the point closest to the planetary core. The panels of Fig. 5 show that in general internal energy increases as the potential component diminishes. However, this balance is not perfect, as can be seen in the change in the Bernoulli parameter during envelope crossing. Fluid parcels lose gravitational energy as they approach the point closest to the core, but pick up energy on the way out of the envelope. Overall, the tendency for streamlines is to produce a net deposit of energy, as can be seen by comparing the Bernoulli parameter at the entry and exit points of the Hill sphere (dot symbols in Fig. 5).
So far, we can conclude the following. The inspection of the averaged density and temperature structure reveals a planet that appears to be in near hydrostatic equilibrium, confirming our standard picture of planetary envelopes. In contrast, the analysis of the streamlines paints a more complex picture. There is no spherical symmetry. Moreover, streamlines reveal a strong steady-state flow through the planetary envelope, which explicitly relies on breaking hydrostatic equilibrium. Little gas is bound to the envelope. Additionally, the flow leaves an imprint on the energy transport in the envelope, which we investigate in more depth in Sect. 3.7.
3.4.4. Midplane
For completeness, we also show the flow morphology in the midplane in Fig. 6, as is often done (Tanigawa et al. 2012; D’Angelo & Bodenheimer 2013; Fung et al. 2015; Ormel et al. 2015). Care has to be taken to not overinterpret these midplane streamlines as being a complete representation of the flow because of the strong vertical flow component that is present (Tanigawa et al. 2012). Additionally, because we forced mirror symmetry, we force uz = 0 in the inner turbulent region where this condition does not necessarily need to hold. In Fig. 6, we recognize the horseshoe orbits, depicted by the orange curves. The horseshoe orbits are strongly asymmetric across the y-axis, compared to standard 2D results (Fung et al. 2015). Keplerian shear enters deeply within the Hill sphere, as indicated here by the gray curves. The streamlines closest to the planet are unsteady close to the planetary core. This is in line with the notion that the inner envelope is convective. Farther from the planet, we note the two channels in the midplane that are aligned with the density wave perturbations launched by the planet, through which flow can escape from the planet and the horseshoe region.
Figure 6 can be compared to the velocity field in an isothermal midplane, as depicted in Fig. C.2. The velocity field is characterized by two broad arms with flow escaping from the planet, as depicted by the white curves, in line with Fung et al. (2015) and Ormel et al. (2015). In our non-isothermal calculation, the width of these two arms is reduced, but the overall flow morphology is similar.
3.5. Angular momentum
 |
Fig. 6 Streamlines and gas density in the midplane of the planet, shown in a co-rotating frame centered on a planet. Here the core is accreting solids at rate of about 10 ME/Myr. (RUNHIGHRESL27). The x-axis points radially, the y-axis follows the azimuthal direction. Significant advection of mass occurs through the Hill sphere (marked by the white dashed line). The inner (left) and outer (right) circulating streamlines are shown in gray. Orange streamlines indicate the horseshoe region. The white streamlines show infalling gas from the poles being deflected outwards. Inside this region gas is unsteady in nature but nearly bound. A slow retrograde rotation can be seen, with respect to the rotating frame. The midplane gas density is shown in the background (in g/cm3). |
Isothermal simulations show the emergence of prograde disks around planetary cores (Machida et al. 2008; Tanigawa et al. 2012). In our isothermal simulations we indeed recover prograde rotation (Fig. C.2). Gas is orbiting close to Keplerian velocity, consistent with the results by Tanigawa et al. (2012; their Fig. 8). In contrast, our non-isothermal simulations show the atmosphere does not build up significant angular momentum. Only a weak retrograde motion is measured with respect to our prograde rotating frame. This is illustrated in Fig. 7, which shows the azimuthally averaged specific angular momentum, normalized by the Keplerian value, 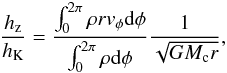 (19)for our reference simulations (runs RADL27k0.01, RADL0k0.01, ISO). Here, r and φ are radial and azimuthal coordinates centered on the planet.
(19)for our reference simulations (runs RADL27k0.01, RADL0k0.01, ISO). Here, r and φ are radial and azimuthal coordinates centered on the planet.
We have thus found that envelopes are supported by a strong pressure force compared to the gravitational force, as opposed to results in the isothermal approximation. This change in the radial force balance altered the rotation direction from prograde to retrograde, as can be understood from Eq. (14). The planet thus only attracts low angular momentum accretion through the planetary poles. We do not see the development of a flattened disk, as the thermal energy contained in the envelope is non-negligible compared to the gravitational potential. In fact, we find a result more consistent with Keplerian shear motion persisting throughout the envelope. In such a case, the angular momentum distribution takes the form, 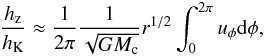 (20)by ignoring azimuthal variations in the density. We can further linearize the velocity field to
(20)by ignoring azimuthal variations in the density. We can further linearize the velocity field to 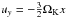 , as in the shearing sheet approximation, to find
, as in the shearing sheet approximation, to find 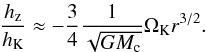 (21)Finally, by making use of the definition of the Hill radius (Eq. (11)), we obtain
(21)Finally, by making use of the definition of the Hill radius (Eq. (11)), we obtain 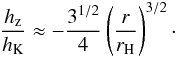 (22)This relation is shown in gray in Fig. 7. The scaling is approximately maintained inside the Hill sphere, although averaged velocities do become slower closer to the core.
(22)This relation is shown in gray in Fig. 7. The scaling is approximately maintained inside the Hill sphere, although averaged velocities do become slower closer to the core.
3.6. Mass flux through the envelope
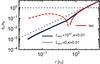 |
Fig. 7 Azimuthally averaged specific angular momentum, normalized by the Keplerian value, measured in the midplane. Full lines indicate retrograde motion, while dashed lines mark prograde motion. The red curve shows an isothermal simulation (run ISO) with prograde rotation inside the Hill sphere. The black and blue curve correspond to, respectively, the reference simulations RADL27k0.01 and RADL0k0.01. Gray dotted lines indicate two limit cases, gas purely in Keplerian rotation around the core (hz/hK = 1) and gas in purely Keplerian rotation around the star, as if no planet were present (Eq. (22)). |
 |
Fig. 8 Enclosed gas mass, as a function of envelope radius r, around a 5 ME core (runs RADL27k0.01, RADL0k0.01, RADL271, RADL0k1). The interior envelope mass decreases when solid accretion rates increase. Higher dust opacities (κ = 1 cm2/g) decrease the envelope mass. The circles indicate the total interior mass within the Hill sphere. |
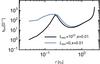 |
Fig. 9 Vertical mass flux through a shell with radius r. The quantity shown is the timescale tflux, over which the mass flux replenishes the mass interior to a radius r. The black curve corresponds to run RADL27k0.01, the blue curve to run RADL0k0.01. The total flow outside r ≳ 0.3 rH is dominated by vertical infall. The mass flow is on the order of 1% of the envelope per orbit. For the planet accreting solids, tflux decreases towards the core because of convective motions that are not present in run RADL0k0.01. Near the core interpretation is difficult because of poor resolution on these small scales. |
The advection of gas is significant. Gas flows on tens of orbital timescales through the Hill sphere and involves a significant mass fraction of the envelope. Figure 8 shows how mass is distributed in the envelope by displaying the cumulative mass as function of the planetary radius. The total mass inside the Hill sphere is about 0.5 ME, about 10% of the core mass, as shown by the black curve in Fig. 8. In our simulations we find the bulk of the envelope mass lays outside a radius of ≈0.2 rH. The steep slope in the cumulative mass function at smaller radii (≲0.1 rH) is influenced by potential smoothing, as shown in panel B of Fig. 2.
We now introduce a vertical mass flux timescale, 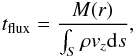 (23)where M(r) is the mass within a radius r, and the dominator is the inward directed vertical mass flux through the surface S of the sphere. This is a mass-weighted measure of how rapidly gas is transported through the envelope. It corresponds to the total vertical flow, which includes gas pushed into and then back out of a spherical shell. This quantity is displayed in Fig. 9 as a function of envelope radius.
(23)where M(r) is the mass within a radius r, and the dominator is the inward directed vertical mass flux through the surface S of the sphere. This is a mass-weighted measure of how rapidly gas is transported through the envelope. It corresponds to the total vertical flow, which includes gas pushed into and then back out of a spherical shell. This quantity is displayed in Fig. 9 as a function of envelope radius.
Outside ≈0.2 rH, we note gas is pushed through the envelope at a rate of about 10% of the envelope mass per orbit, up to a Hill radius from the core. These rates are consistent with previous measurements of isothermal simulations, which are on the order of 1% of the envelope per 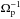 (Ormel et al. 2015) to 100% per
(Ormel et al. 2015) to 100% per 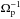 (Fung et al. 2015). At larger radii, outside the Hill radius, the vertical flux diminishes as gas comes in from directions perpendicular to the rotation axis.
(Fung et al. 2015). At larger radii, outside the Hill radius, the vertical flux diminishes as gas comes in from directions perpendicular to the rotation axis.
Closer to the core, around r ≲ 0.2 rH, we note a peak in tflux. It indicates that at this radius a large amount of the vertical mass flux is deviated away from the core. This transition is illustrated in more detail by the azimuthally averaged vector field displayed in Fig. 10. This location broadly corresponds to the location of the radiative-convective boundary.
At even closer radii to the core, we do not measure an increase in tflux, which would be expected from a clear transition to a static bound envelope. Instead, the opposite trend is seen where the vertical envelope mass flow becomes more efficient. We associate this with the emergence of convective flows, as can be seen in Fig. 10. At close distances to the core (r ≲ 0.05 rH), the analysis is complicated by poor resolution and future work will need to address the inner envelope in more detail.
 |
Fig. 10 Azimuthally averaged velocity field around an accreting 5 ME core, as seen in the co-rotating frame (run RADL27k0.01). The background shows the azimuthally averaged temperature (in units of K) around the core. The inset shows in greater detail the azimuthally averaged velocity field where overturning motions are driven by the heat release from solid accretion. |
3.7. Heating and cooling a three-layer envelope
 |
Fig. 11 Advection timescale (solid curves) and thermal diffusion timescale (dashed curves) as functions of the vertical depth in the envelope. Black curves show results from the accreting planet (run RADL27k0.01). Outside the Hill radius, at heights above the scale height of the disk, heat exchange by radiative diffusion is efficient. Inside the Hill radius, around 0.5 rH, we find a balance between advection and diffusion, as the timescales become comparable and are on the order of 10–100 |
The continuous flow of gas through the envelope also impacts heat transport. The outer shells, where gas flow is predominant, cannot be seen as parts of a static envelope that partake in secular cooling. Instead, they are dynamic regions where a complex interplay of advection, heat deposition by compression (vertical direction), and cooling (horizontal direction) take place.
In order to further investigate the modes of heat transport, we consider two timescales: an advection timescale, 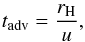 (24)and a timescale to diffuse heat through radiation over the characteristic length scale of the planetary envelope,
(24)and a timescale to diffuse heat through radiation over the characteristic length scale of the planetary envelope, 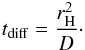 (25)Here D is the radiative diffusion coefficient (see Eq. (5), Sect. 2.3.1).
(25)Here D is the radiative diffusion coefficient (see Eq. (5), Sect. 2.3.1).
We find a three-layer envelope structure. In the outer layer, between 0.5 to 1 rH, advection of heat occurs on a similar timescale to radiative diffusion, as can be seen in Fig. 11. Outside of the envelope, at r ≳ 1 rH, radiative diffusion starts to dominate as we move the heights above the disk midplane.
In the middle layer, between 0.2 to 0.5 rH, we find that radiative diffusion is the primary heat transport mechanism. We can also identify this thin radiative shell in Fig. 10 as a region with little advection.
In the inner shell, within r ≲ 0.2 rH, advection is again clearly the most efficient channel for heat transport. This is consistent with an interior envelope, where convective motions transport heat outwards.
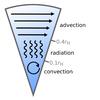 |
Fig. 12 Cartoon illustrating a three-layer envelope. Energy transport occurs in the interior by convection until a radiative shell is reached, situated between r ≈ 0.1 rH and r ≈ 0.4 rH. Fast gas advection takes place in the outer envelope (r ≳ 0.4 rH). |
3.8. Summary
So far, we have found that a planet in the process of accreting solids is not in hydrostatic equilibrium, but does reach a steady-state flow pattern. The envelope acquires a characteristic three-layer structure, made up of a convective interior, a radiative shell, and an advective outer envelope, which we illustrate in Fig. 12. We observe that the gas flux remains substantial, even through the deep interior where the mass flux is on the order of 10% of the enclosed mass per orbit (Fig. 9). At larger radii, rapid advection of gas and radiative diffusion both help transport heat away from the planet.
The envelope around the solid accreting planet we described is stable and maintains a steady state. However, on longer timescales the core mass increases and solid accretion rates change. As long as solid accretion dominates the luminosity budget, the cool-down process of the planet can be safely ignored. Then planetary envelopes move from one pseudo-equilibrium state (similar to the one described here) to the next. However, when solid accretion rates become too low or come to a complete standstill, this balance comes to an end. In the next section, we describe an envelope in this stage.
4. Results: after solid accretion
During the formation of a planet there is no guarantee that solid accretion onto the core continues during the whole life time of the gas disk. Cores can become isolated from planetesimals due to scattering (Tanaka & Ida 1999) and resonant trapping (Levison et al. 2010). Similarly, pebble accretion comes to a halt when cores grow sufficiently massive to perturb the disk enough to form a pressure bump that prevents inwards drift and accretion of pebbles (Lambrechts et al. 2014). Or pebble accretion simply comes to an end because radial drift has depleted the available solid reservoir before the onset of gas disk dissipation (Sato et al. 2016). Therefore, we now focus on the same planetary core placed in the same disk environment, but without interior heat generation by solid accretion (run RADL0k0.01).
4.1. Luminosity from compression
 |
Fig. 13 Azimuthally averaged velocity field around a 5 ME core, similar to Fig. 10, but without the addition of accretion luminosity (run RADL0k0.01). The background shows the azimuthally averaged compressional heating around the core. A large fraction of the gas that falls in from high elevation through the poles gets compressed above the inner planetary envelope, which gives rise to a mushroom-shaped compressional heat map. The inset zooms in on the vector field close to the core. A small amount of convergent motion can be identified, in contrast with the inset in Fig. 10 that shows convective overturn. |
When the accretion of solids starts winding down, the predominant form of heat generation becomes compressional heating of gas that enters the planetary potential. Figure 13 shows the azimuthally averaged compressional heating near the planetary center and a heated cloud at the poles of the envelope where gas gets compressed as it gets deflected from the more bound interior towards the midplane. The integrated net heating, as a function of the planetary radius, is shown in Fig. 14. We find a luminosity of about L ≈ 1027 erg/s from compressional heating.
It is important to note that we obtained this new equilibrium envelope and the corresponding luminosity profile without modeling the remnant interior heat in the envelope left by the formation of the core and the secular cooling of the envelope. We thus modeled a cooled-down planet that lost this heat contribution just before self-gravity became important. Later stages in the evolution of the envelope are not accessible in our simulations as we do not model self-gravity.
Compressional heating is also relevant even when solid accretion occurs. Figure 14 shows that the compression of gas generates a similar amount of luminosity to that generated by solid accretion. This energy is mostly liberated in the outer envelope. Therefore, the location and total amount of energy deposition between the runs with and without solid accretion are similar, but envelope structures are not identical.
4.2. Envelope structure
The thermodynamical structure of the envelope appears similar to the planet in the process of accreting solids, as can be seen in Fig. 2. The radial temperature profile is nearly identical. However, the density profile shows a sharper increase towards the center than in the solid-accreting case. This central density increase results in a slightly more massive inner envelope, as can be inspected in Fig. 8.
 |
Fig. 14 Luminosity generated around the core. The blue curve shows the integrated energy released by compressional heating as a function of radius r in the absence of heating by solid accretion (run RADL0k0.01). Black curves correspond to run RADL27k0.01. The solid line gives the sum of the accretion heat and the contribution by compressional heating (Lcomp = Lacc + Lcomp). This latter fraction is depicted by the black dashed line. |
 |
Fig. 15 Streamlines and gas density in the midplane of the planet, shown in a co-rotating frame centered on a planet, not accreting any solids (run RUNHIGHRESL0). The x-axis points radially, the y-axis follows the azimuthal direction. Significant advection of mass occurs through the Hill sphere (marked by the white dashed line). The inner (left) and outer (right) circulating streamlines are shown in gray. Orange streamlines indicate the horseshoe region. The white streamlines show infalling gas from the poles being deflected outwards. Inside this region gas is bound and rotates slowly retrograde. |
Inspection of the midplane streamlines (see Fig. 15) also illustrates a similar flow structure to that in the solid-accretion phase (Fig. 6). Rotation is again weakly retrograde, as also shown in Fig. 7. However, the interior streamlines do not reveal unsteady motion; instead, we see bound field lines in the midplane.
Indeed, the inner envelope shows little motion. The interior is in near-hydrostatic balance and only a small amount of radial flow can be identified. As can be seen in Fig. 11, the advection timescale becomes exceedingly long as we approach the core. Nevertheless, the advection timescale is still shorter that the radiative diffusion timescale in the inner optically thick envelope (r ≲ 2 rH).
4.3. Advection of gas
We again measure a strong mass flux through the outer envelope, on the order of 10% of the envelope mass per orbit, similar to the case of the solid accreting core (Fig. 9). Closer to the core, within r ≲ 2 rH, tflux, the less turbulent interior leads to a slower vertical mass flux timescale. Previous studies have argued that this mass flux through the envelope can be estimated as a modified Bondi flow, 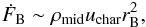 (26)where uchar is a characteristic velocity, often taken to be the Keplerian shear and the cross section is typically taken to be the Bondi radius (D’Angelo & Lubow 2008; Lissauer et al. 2009; Ormel et al. 2015). For the planet we consider, this corresponds to a mass flux on the order of 103 ME/Myr, which is indeed in reasonable agreement with our measurement of the flow through the outer envelope (Fig. 9). Previous studies (D’Angelo & Lubow 2008; Lissauer et al. 2009; Machida et al. 2010) have interpreted this mass flux as a measurement of the accretion rate, implying unrealistic fast envelope growth timescales. Instead, we show here that most of this mass flux is caused by an unbound flow through the envelope.
(26)where uchar is a characteristic velocity, often taken to be the Keplerian shear and the cross section is typically taken to be the Bondi radius (D’Angelo & Lubow 2008; Lissauer et al. 2009; Ormel et al. 2015). For the planet we consider, this corresponds to a mass flux on the order of 103 ME/Myr, which is indeed in reasonable agreement with our measurement of the flow through the outer envelope (Fig. 9). Previous studies (D’Angelo & Lubow 2008; Lissauer et al. 2009; Machida et al. 2010) have interpreted this mass flux as a measurement of the accretion rate, implying unrealistic fast envelope growth timescales. Instead, we show here that most of this mass flux is caused by an unbound flow through the envelope.
4.4. Accretion of gas
A direct measurement of the gas accretion rate, the net gas flux that remains bound to the core, is difficult to make. The flow of gas that transits the envelope dominates the much smaller fraction that is accreted. Directly measuring the mass growth of the envelope is difficult as this occurs on timescales that are numerically not feasible. In Appendix A, we show results of the longest integrations that are numerically feasible, on the order of 50 orbits. An accurate measure of any direct mass growth of the planetary envelope cannot be made.
We can, however, indirectly place a constraint on the gas accretion rate. The generation of heat requires a net divergence of the flow (− P∇·u), which we can link to the accretion flow (inset of Fig. 13). As the luminosity generated by compressional heating is ultimately the liberation of potential energy, we can estimate the gas accretion rate as 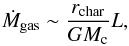 (27)where rchar is a characteristic radius corresponding to depth of the potential. Taking L ~ 5 × 1026 erg/s and rchar ~ rcore, we would find an accretion rate on the order of Ṁgas ~ 1 ME/Myr. This slow accretion estimate is in line with 1D models (Piso & Youdin 2014), and further illustrates the challenge of making direct measurements of the gas accretion rate.
(27)where rchar is a characteristic radius corresponding to depth of the potential. Taking L ~ 5 × 1026 erg/s and rchar ~ rcore, we would find an accretion rate on the order of Ṁgas ~ 1 ME/Myr. This slow accretion estimate is in line with 1D models (Piso & Youdin 2014), and further illustrates the challenge of making direct measurements of the gas accretion rate.
5. Dependency on opacity
5.1. Opacity in protoplanetary disks
Inside the planet-forming regions of protoplanetary disks, dust particles smaller than mm in radius are the predominant cause of absorption and scattering of radiation. The opacity caused by dust can be expressed as 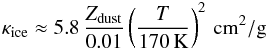 (28)just outside the ice line at approximately 170 K. Here we have taken a composition and dust-to-gas ratio Zdust similar to the interstellar medium (ISM) from which the star and protoplanetary disk formed. Inside the ice line, icy particles sublimate and opacities rapidly settle to the value provided by silicate grains,
(28)just outside the ice line at approximately 170 K. Here we have taken a composition and dust-to-gas ratio Zdust similar to the interstellar medium (ISM) from which the star and protoplanetary disk formed. Inside the ice line, icy particles sublimate and opacities rapidly settle to the value provided by silicate grains, 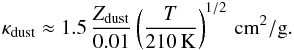 (29)A more complete description can be found in Bell & Lin (1994), D’Angelo & Bodenheimer (2013), Semenov et al. (2003).
(29)A more complete description can be found in Bell & Lin (1994), D’Angelo & Bodenheimer (2013), Semenov et al. (2003).
These values can best be interpreted as upper limits. As dust grows by collisions into larger particles, the ratio of small dust to gas, Zdust, will decrease. Nevertheless, in some special regions in the disk, for example around ice lines, the complex interplay of growth, fragmentation, and sublimation may lead again to higher values.
Inside the envelopes of planets, the evolution of the dust opacity is poorly constrained. As a first approximation, we can assume the envelope inherits the same opacity as the disk, valid when coagulation proceeds more slowly then advection and settling of dust inside the envelope. Alternatively, we can estimate how the dust opacity can be reduced by grain growth inside the planetary envelope (Movshovitz et al. 2010; Ormel 2014; Mordasini 2014). These models find atmospheres with ISM-like opacities in the outer parts of the envelope that decrease radially inwards to values around 10-3 cm2/g. Nevertheless, these models do not take into account bouncing and fragmentation of grains or the large gas advection flows through the atmosphere that will incorporate dust grains.
In the deep interiors of planetary envelopes within the sublimation line for dust Tdust ~ 1000 K, opacities are set by the gas component. Such high temperatures are only reached very close to the core within about 10 core radii (Piso & Youdin 2014; Lambrechts et al. 2014). Our simulations do not resolve such short distances. Therefore, we do not reach dust sublimation temperatures in the envelope, as can also be seen in the top panel of Fig. 2. Consequently, we are not required to include gas opacities in our calculations.
Given these uncertainties on dust opacity values, we have limited this study to opacities that are constant throughout the envelope. The previous results we showed were obtained for envelopes with κ = 0.01 cm2/g, which corresponds to an envelope with moderate grain growth (as used in standard works such as Hubickyj et al. 2005). We now will present envelopes where we assume no significant growth of dust has occurred and opacities are close to an ISM-like opacity for silicate grains (κ = 1 cm2/g). These unreduced opacities thus assume no significant dust depletion. We will again consider two cases, the case of a planet accreting solids (run RADL27k1) and the case where solid accretion has come to a halt (run RADL0k1).
 |
Fig. 16 Azimuthally averaged velocity field around an accreting planet in a high-opacity environment (run RADL27k1). The gas flux from the poles also enters the deep interior, as seen in greater detail in the inset. This stands in contrast to the low-opacity case (run RADL27k0.01, Fig. 10) where rapid advection was limited to the outer envelope. |
5.2. Solid-accreting planet with unreduced opacity
In a higher opacity environment (κ = 1 cm2/g), gas flows through the entire envelope of a solid-accreting planet (Lacc = 1027 erg/s). This can be seen in Fig. 16, which shows the azimuthally averaged velocity field, and can be compared directly to Fig. 10. Clearly, there is no trace left of the three-layer envelope discussed in Sect. 3.7. Instead gas circulates through the planet even at depths close to the core.
There is thus no development of a more bound interior shielded by a thin radiative shell where tadv>tdiff, as was the case in the reduced opacity models. Instead, radiative diffusion timescales remain of the same order as the advection timescales, as can be seen from the red curves in Fig. 17. Radiative diffusion is generally much more efficient than in the low-opacity case presented in Fig. 11 (run RADL27k0.01). It might appear counterintuitive that higher opacities promote more efficient radiative diffusion. However, the improved radiative transport is mostly just a consequence of the lower central densities. Indeed, the envelope has a much smaller mass in the interior, as can be seen in Fig. 8.
It is worth reflecting on this unexpected critical transition obtained by simply increasing the opacity. A new equilibrium state emerges where the envelope is dominated by the advection of gas that enter from the poles. This stands in contrast to spherical hydrostatic models, which would have predicted that increasing the opacity results in the envelope becoming simply more convection dominated. In these models the depth of the radiative zone is approximately inversely proportional to the opacity (Prcb ∝ (κLacc)-1, Eq. (D.3)). Indeed, we verified that this scaling approximately holds in the low κ-regime by recovering equivalent envelopes between run RADL27k0.01 and a run with κ = 0.1 cm2/g and Lacc = 1026 erg/s, which holds the product κLacc constant. However, as we have shown here, when the opacity increases enough the radiative outer zone starts to shrink until a sudden transition occurs. Then the envelope opens up and becomes advection-dominated.
Finally, we verified this result once more by analyzing a simulation with an initial condition that was different from the standard procedure obtained by gradually introducing the planet in the disk, as outlined in Sect. 2.4. Instead, the equilibrium state of RADL0k1 was used as the initial condition. After initialization, the envelope gradually became heated by accretion heating and we found an equivalent envelope structure this way as well. Therefore, the fast advection result is not dependent on the method used to initialize the simulation.
 |
Fig. 17 Advection and thermal diffusion timescales through the envelope, similar to Fig. 11, but for an unreduced opacity κ = 1 cm2/g. Red curves show the results from run RADL27k1, which is the model of a solid-accreting core. Advection timescales are short, on the order of 10 |
5.3. After solid accretion with unreduced opacity
 |
Fig. 18 Integrated energy delivery and removal respectively by compression and expansion for the unreduced opacity environment (κ = 1 cm2/g). Red curves show the case where solids are accreted (run RADL27k1). Inside the Hill sphere, we see that the inner envelope mostly acts as a sink of energy that helps gas parcels to expand as they move through the envelope. Green curves represent the energy deposition from compressional heating after solid accretion (run RADL0k1). Compressional heating now provides the luminosity that supports the envelope. The y-axis has been cut to represent the negative values on the log axis. |
We now consider the case without solid accretion in an unreduced opacity environment (κ = 1 cm2/g) corresponding to run RADL0k1. We recover an envelope similar to the case with lower opacity (run RADL0K0.01). Diffusion and advection timescales throughout the envelope are indeed similar, as can be seen by comparing the diffusion and advection timescales (green curves in Fig. 17) with those shown previously for run RADL0K0.01 in Fig. 11.
The luminosity released by compressional heating in the interior envelope is approximately Lcomp = 5 × 1025 erg/s, as shown by the green curve in Fig. 18. This is an order of magnitude lower than the case with κ = 0.01 cm2/g. This reduction can be understood approximatively because we recover a similar depth of the radiative-convective boundary rrcb/rB, or equivalently Prcb/Pmid when we force no accretion heat. From Eq. (D.3), we find 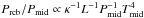 (for more details see Appendix D). Therefore, we would expect L ∝ 1 /κ and a reduction of the luminosity by a factor 100. However, changing the opacity also changes the disk structure, and therefore the values for the temperature and pressure. This softens the reduction in the luminosity by a factor of 10. It also explains why the deposition Lacc = 1027 erg/s onto the same 5 ME planet with k = 1 cm2/g is a significant contribution that drastically changes the envelope structure, as discussed in Sect. 5.2. The addition of solid accretion does not generate an envelope-supporting luminosity, but instead heats gas up such that it expands and leads to a net cooling effect, as can be seen from the red curve in Fig. 18.
(for more details see Appendix D). Therefore, we would expect L ∝ 1 /κ and a reduction of the luminosity by a factor 100. However, changing the opacity also changes the disk structure, and therefore the values for the temperature and pressure. This softens the reduction in the luminosity by a factor of 10. It also explains why the deposition Lacc = 1027 erg/s onto the same 5 ME planet with k = 1 cm2/g is a significant contribution that drastically changes the envelope structure, as discussed in Sect. 5.2. The addition of solid accretion does not generate an envelope-supporting luminosity, but instead heats gas up such that it expands and leads to a net cooling effect, as can be seen from the red curve in Fig. 18.
The lower luminosity we measure implies slower gas accretion rates. Repeating the order of magnitude analysis in Sect. 4.4, we would find a gas accretion rate of Ṁgas ~ 0.1 ME/Myr, for a luminosity of L ~ 5 × 1025 erg/s, and rchar ~ rcore. This would lead to the formation of planets that have envelopes up to ~10% of the total planetary mass, similar to the known super-Earths and ice-giants.
6. Dependency on core mass
The mass of the core is, in addition to the accretion rate and the opacity, an important quantity that regulates the structure of the envelope. We have now seen that in environments where it is difficult for heat to diffuse out of the envelope, the atmosphere can become advection-dominated. We identified this effect around a low-mass core of 5 ME. Increasing the mass of the core should suppress this effect as the potential of the planet becomes too deep to allow the flow of gas to go through unhindered.
 |
Fig. 19 Azimuthally averaged velocity field around an accreting planet with a 15 ME core in an unreduced opacity environment (run RADL27k1M15). As opposed to the 5 ME case, the bulk of gas that enters through the poles does not enter the deep interior. The deepened potential compensates for the higher opacity (κ = 1 cm2/g). |
Indeed, around a core of 15 ME placed in the same unreduced opacity environment with κ = 1 cm2/g (run RADL27k1M15), we recover a flow profile that shows great similarity to the one we observed around a 5 ME core in the low-opacity environment. Figure 19 shows the azimuthally averaged flow profile around a core in the process of accreting solids. Clearly, we no longer see the large-scale advecting flows seen in Fig. 10 that occurred around the 5 ME core in a similar κ = 1 cm2/g environment.
The envelope recovers an exterior radiative-advective region and an interior shell where radiative transport dominates. Close to the center, overturning motions become the predominant mode for energy transport. This can also be seen when inspecting the advection and diffusion timescales presented in Fig. 20.
Without the contribution of solid accretion, we also note that gas accretion speeds up again (run RADL0k1M15). In this case, we measure a luminosity from compressional heating of approximately 5 × 1026 erg/s. Following the order of magnitude analysis of Eq. (27), we find a gas accretion rate of around 1 ME/Myr, about an order of magnitude higher than around the 5 ME core in a similar unreduced opacity region. This facilities the transition to runaway gas accretion, but the growth rate is still modest and disk dissipation might occur before growing a massive envelope.
 |
Fig. 20 Advection and thermal diffusion timescales through the envelope, similar to Fig. 11, but measured now around a 15 ME core in an unreduced opacity environment with κ = 1 cm2/g (runs RADL27k1M15 and RADL0k1M15). |
7. Implications: delaying runaway gas accretion
Previous studies (Mizuno 1980; Pollack et al. 1996; Ikoma et al. 2000; Rafikov 2006; Piso & Youdin 2014) investigated the role of the core mass, opacity, solid accretion rate, and envelope composition, but assumed hydrostatic envelopes. Here we have seen that envelopes are not in hydrostatic balance, and large flows of gas enter and leave the planetary atmosphere. This result has several significant implications on the growth of the envelope.
7.1. Dust opacity
Previous studies have speculated that envelopes could acquire atmospheres enriched up to 100 times in opacity-providing grains with respect to the star and the disk (Lee et al. 2014; Venturini et al. 2016). Such high opacities would delay the contraction of the envelope. However, this pathway can now be dismissed on three grounds. High dust-to-gas ratios do not remain homogeneously mixed (Lambrechts et al. 2016), coagulation aids the rain out of solids from dust-rich atmospheres (Ormel 2014; Mordasini 2014), and here we add that the rapid flux of gas through the atmosphere does not allow for such dust pileups in the first place. Conversely, extremely low dust opacities are also ruled out because fresh dust is continuously transported through the outer envelope. Therefore, we expect dust opacities in the radiative-advective outer region of planets to be, to a good approximation, comparable to the dust opacity in the disk at the location of the planet. A more precise determination of the opacity at the radiative-convective boundary would require solving self-consistently for the transport of dust particles and the opacity dependent depth of the advective outer shell.
7.2. Accretion of solids and envelope pollution
We expect that the gas flows through the envelope will only have a moderate effect on the accretion rate of solids. Large planetesimals feel little gas drag because of their large size. Smaller pebbles, on the other hand could, see their trajectories changed. However, the accretion of pebbles predominantly occurs close to the disk midplane from a direction diagonal to the direction of outflow along the spiral density waves (Lambrechts & Johansen 2012). Additionally, pebbles have friction and crossing times that are comparable, on the order of the orbital timescale, while the flux through the atmosphere occurs on timescales that are 10 times as long in the outer envelope. Nevertheless, we plan to study this in more detail in an upcoming work, which will also allow us to study at which depths in the envelope the accretion heat is released.
As solids sink in the envelope they can evaporate and pollute the envelope. Particles with a silicate composition only vaporize at high temperatures exceeding 1000 K that are found close to the core. Therefore, these dust species settle in the inner nearly hydrostatic envelope and will be accreted. Ices on the other hand can deposit water vapor at much shallower depths in the envelope. If the sublimation point is located in the highly advective outer regions of the atmosphere, vapor will simply be transported away in tens of orbital timescales. However, in our simulations where the planet is located outside of the water ice line of the disk, we can see that this is not the case. In fact, the water ice sublimation point, at about 170 K, is located deep inside the convective interior, shielded from the outer layers where rapid gas advection takes place (Fig. 2). Therefore, not all water vapor will be immediately lost. Instead, the solid accretion rate, the redistribution of vapor by convection, and the advection rate will set the fraction of solids that settle to the core, the fraction that is deposited in the envelope, and the vapor fraction that is lost. It will be important to quantify this in more detail because this balance influences core growth, and the accretion of gas as well, since the deposition of high mean molecular weight material speeds up gas accretion (Hori & Ikoma 2011; Lambrechts et al. 2014; Venturini et al. 2016).
7.3. Cooling the envelope
Finally, there is the impact on the secular cooling of the envelope. Gas in spherical hydrostatic models is bound. Therefore, the outward transport of heat is paired with the cooling of the envelope and the increase in the envelope mass. In this way, a hydrostatic growth sequence can be constructed for planets (Pollack et al. 1996; Ikoma et al. 2000; Piso & Youdin 2014).
Rapid advection of gas through the envelope challenges this paradigm (Ormel 2014; Fung et al. 2015). The outward transport of heat is not extracted from a bound reservoir of gas, which slows down envelope cooling and associated mass growth to a greater extent than in spherical hydrostatic models. However, the picture is complicated. After the solid-accretion phase, we have shown that planets have their strong advecting flows limited to the outer envelope (Sect. 4). In the inner envelope, we see mass advection diminish as we get closer to the core. Therefore, gas close to the core is in approximate hydrostatic balance and future modified 1D models may be suitable for long-term integrations, following the approach used in D’Angelo & Bodenheimer (2013).
A more quantitative analysis determining the bound envelope will require an improved resolution in the inner shells. Resolving this region close to the core would also necessitate the use of a more accurate, nonconstant opacity prescription that takes the high temperatures in the inner envelope into account. An improved equation of state may also be necessary. Such improved measurements would help make secular cooling histories of young planets more accurate. Furthermore, it would also be of great value to explore a broader planetary mass range since even planets as large as Jupiter see a large gas flux transit through their atmospheres (Gressel et al. 2013; Morbidelli et al. 2014; Szulágyi et al. 2014).
7.4. Summary
In summary, we have identified three different effects that stall envelope accretion. Dust opacity values will be similar to the disk, water pollution can be inefficient, and cooling times are delayed by the delivery of fresh gas.
8. Interpreting exoplanet super-Earths and gas giants
Why do some planets build up massive envelopes and others do not? We have argued that the formation of gas giants with large atmospheres requires specific conditions: the rapid formation of cores larger than 15 ME in a disk environment with reduced opacities. These requirements can be met in the outer regions of the protoplanetary disk, where particles have grown to cm sizes and radially drift inwards through the disk. Such rocky/icy pebbles can be efficiently accreted by planetary embryos (Ormel & Klahr 2010; Lambrechts & Johansen 2012) allowing for cores approximately 20 ME in size to form outside of the iceline within disk lifetimes (Lambrechts et al. 2014). Such fast core growth generally requires initial dust-to-gas ratios in the disk that are solar-like or higher (Lambrechts & Johansen 2014; Bitsch et al. 2015). This requirement seems to be in line with the observed lack of close-in gas giant planets around stars with subsolar metallicities (Buchhave et al. 2012). We note that the required solar or higher initial dust-to-gas ratio does not imply that densities of opacity-providing grains must have been high as well. Particle growth outside the ice line reduces the opacity and local pebble surface densities fall rapidly by a factor of 10 below initial values because of radial drift (Lambrechts & Johansen 2014).
Super-Earths and ice giants did not accrete such massive gas envelopes. Their smaller core masses helped prevent rapid gas accretion. Additionally, they may have formed predominantly in regions where disk opacities were not significantly reduced.
Ice giants have cores that formed slowly in very wide orbits and likely never experienced strongly reduced opacities, as particle sizes generally remain small in the outer disk (Brauer et al. 2008). Super-Earths, on the other hand, are commonly found in short orbits. They thus formed in situ or the cores migrated into this inner disk region. Possibly, they predominantly formed in a part of the disk where solids piled up, which would explain why multiple super-Earths are common (Winn & Fabrycky 2015) and occurrence rates are only weakly dependent on stellar metallicity (Buchhave et al. 2012). Such a pileup of solids would likely have been associated with a high-opacity environment because of dust delivery by radial drift and possibly collisional fragmentation, which would further limit gas accretion.
In summary, we propose that gas giant planets predominantly form outside of the ice line where particles grew to pebble sizes, allowing the formation of large cores. Models of exoplanet compositions support that gas giants typically have substantial cores exceeding 10 ME (Thorngren et al. 2016). Reduced opacities may then have further facilitated rapid gas accretion. Super-Earths, on the other hand, have smaller cores, and may additionally have formed in high-opacity environments associated with pileups of solids in the inner disk. This prevented rapid gas accretion. The specific conditions for the formation of massive gas envelopes may explain in part why occurrence rates for gas giants are below super-Earths by about a factor five (Winn & Fabrycky 2015).
9. Summary
Atmospheres around growing planets in the super-Earth to ice giant regime are not spherically symmetric envelopes in hydrostatic balance. Here, we presented global 3D radiative hydrodynamical simulations that show a steady-state flow through planetary envelopes. Large amounts of gas enter through the poles of the envelopes and exit near the disk midplane. This is the result of density perturbations with gradients that are not aligned with the gravitational potential.
Our results imply that (1) opacities in the outer envelope are similar to disk opacities; (2) icy solids will sublimate in the convective interior; and (3) the flow of gas delays the secular cooling of the envelope. We numerically investigated the dependency of our results on three key parameters: the accretion rate, the dust opacity, and the mass of the core.
Dust opacities can fluctuate widely in the protoplanetary disk because of particle growth and drift. In regions of the disk with dust opacities of κ = 0.01 cm2/g, below the initial ISM-like opacity of about κ ≈ 1 cm2/g, planets develop a three-layer atmosphere. The envelope consists of an advective outer shell, a radiative shell around a radius of 0.3 Hill radii, and an interior that shows convection-like overturning motions that transfer the heat of solid accretion. When solid accretion comes to a halt, gas close to the core slowly settles in the potential. The liberated heat from this convergent motion supports the envelope. Measurements of the accretion rate are challenging, but our estimates are on the order of 1 ME per Myr. Improved measurements will require simulations that exceed the advection timescale and that are performed at high resolution in order to allow smoothing lengths down to the core surface.
We also explored unreduced dust opacities that are comparable to values found in the ISM (κ = 1 cm2/g) in the disk and envelope, motivated by the the high gas advection rates in the outer atmosphere. For planets in the process of accreting solids, we identify a previously unreported transition into an advection-dominated envelope. Hydrostatic models would have predicted a nearly completely convective atmosphere. Instead, we found an envelope where advection of gas, from the poles to the deep interior, becomes the predominant mode of energy transport. After solid accretion comes to an end, gas accretion rates are low, on the order of 0.1 ME per Myr. Under these conditions, a 5 ME core would not go into runaway gas accretion and therefore remain a super-Earth.
However, a larger core leads to a more bound interior envelope and an increase in the gas accretion rate. We found that around massive solid-accreting cores (Mc ≳ 15 ME) envelopes are no longer advection-dominated in a κ = 1 cm2/g environment. After solid accretion, the increase in the core mass boosts the envelope growth rate by a factor 10 compared to the 5 ME case. Therefore, a transition to runaway gas accretion becomes possible again.
These findings deserve further attention and future models of envelope evolution would benefit from a more quantitative analysis. However, based on our current results we can already argue that super-Earths did not accrete massive gas envelopes because their cores are sufficiently small, provided they formed in disk environments where dust opacities were not strongly reduced below κ ~ 0.01 cm2/g.
Acknowledgments
We would like to thank Aurélien Crida and Alessandro Morbidelli for the insightful comments. We also benefited from helpful discussions with Bertram Bitsch, Matthäus Schulik, Julia Venturini, Seth Jacobson, Anders Johansen, and Tristan Guillot. The authors are grateful for the constructive feedback by an anonymous referee. We are thankful to ANR for supporting the MOJO project (ANR-13-BS05-0003-01). This work was performed using HPC resources from GENCI [IDRIS] (Grant 2016, [i2016047233]) and from “Mesocentre SIGAMM”, hosted by the Observatoire de la Côte d’Azur.
References
- Ayliffe, B. A., & Bate, M. R. 2012, MNRAS, 427, 2597 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez-Llambay, P., Masset, F., Koenigsberger, G., & Szulágyi, J. 2015, Nature, 520, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., & Bodenheimer, P. 2013, ApJ, 778, 77 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, G., & Lubow, S. H. 2008, ApJ, 685, 560 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., Artymowicz, P., & Wu, Y. 2015, ApJ, 811, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Gressel, O., Nelson, R. P., Turner, N. J., & Ziegler, U. 2013, ApJ, 779, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hadden, S., & Lithwick, Y. 2017, AJ, 154, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, Y., & Ikoma, M. 2011, MNRAS, 416, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Icarus, 179, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H., & Kley, W. 2006, A&A, 445, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W. 1989, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., Capelo, H. L., Blum, J., & Bodenschatz, E. 2016, A&A, 591, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E. J., Chiang, E., & Ormel, C. W. 2014, ApJ, 797, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Lega, E., Crida, A., Bitsch, B., & Morbidelli, A. 2014, MNRAS, 440, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Lega, E., Morbidelli, A., Bitsch, B., Crida, A., & Szulágyi, J. 2015, MNRAS, 452, 1717 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Thommes, E., & Duncan, M. J. 2010, AJ, 139, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Hubickyj, O., D’Angelo, G., & Bodenheimer, P. 2009, Icarus, 199, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Kokubo, E., Inutsuka, S.-I., & Matsumoto, T. 2008, ApJ, 685, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Kokubo, E., Inutsuka, S.-I., & Matsumoto, T. 2010, MNRAS, 405, 1227 [NASA ADS] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
- Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [Google Scholar]
- Morbidelli, A., Szulágyi, J., Crida, A., et al. 2014, Icarus, 232, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C. 2014, A&A, 572, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Movshovitz, N., Bodenheimer, P., Podolak, M., & Lissauer, J. J. 2010, Icarus, 209, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2014, ApJ, 789, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Shi, J.-M., & Kuiper, R. 2015, MNRAS, 447, 3512 [NASA ADS] [CrossRef] [Google Scholar]
- Piso, A.-M. A., & Youdin, A. N. 2014, ApJ, 786, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2004, AJ, 128, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2006, ApJ, 648, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, Á., Bouy, H., & Merín, B. 2015, A&A, 576, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sato, T., Okuzumi, S., & Ida, S. 2016, A&A, 589, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., Henning, T., Helling, C., Ilgner, M., & Sedlmayr, E. 2003, A&A, 410, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevenson, D. J. 1982, Planet. Space Sci., 30, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Szulágyi, J., Morbidelli, A., Crida, A., & Masset, F. 2014, ApJ, 782, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., & Ida, S. 1999, Icarus, 139, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Tanigawa, T., Ohtsuki, K., & Machida, M. N. 2012, ApJ, 747, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Venturini, J., Alibert, Y., Benz, W., & Ikoma, M. 2015, A&A, 576, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturini, J., Alibert, Y., & Benz, W. 2016, A&A, 596, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Convergence tests
 |
Fig. A.1 Azimuthally averaged density profile in the midplane for different smoothing lengths and resolutions. The legend indicates the used smoothing length parameter ϵ = rsm/rH and the characteristic grid cell width inside the envelope (dx/rH). Only in our highest resolution runs with a small smoothing length do we correctly capture the envelope structure to within a radius of 0.1 rH. Inside this radius, we start to see the influence of the smoothing length that reduces gas densities towards the core. |
We model the presence of a planetary core through an imposed gravitational potential for the gas. Figure A.1 illustrates the dependency of our results on the resolution across the Hill sphere and the employed smoothing length. The planetary potential is given by 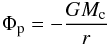 (A.1)outside a smoothing radius rsm away form the planet. Within the smoothing length, the central singularity is avoided by a cubic interpolation to Φp = − 2GMc/rsm, using
(A.1)outside a smoothing radius rsm away form the planet. Within the smoothing length, the central singularity is avoided by a cubic interpolation to Φp = − 2GMc/rsm, using ![\appendix \setcounter{section}{1} \begin{eqnarray} \Phi_{\rm p, sm} = -\frac{GM_{\rm core}}{r_{\rm sm}} \left[ 2 - 2 \left( \frac{r}{r_{\rm sm}} \right)^2 + \left( \frac{r}{r_{\rm sm}} \right)^3 \right] , \end{eqnarray}](/articles/aa/full_html/2017/10/aa31014-17/aa31014-17-eq236.png) (A.2)following Klahr & Kley (2006). The mass of the envelope is ignored in the calculation of the potential, which is a valid approximation for the low-mass envelopes we consider.
(A.2)following Klahr & Kley (2006). The mass of the envelope is ignored in the calculation of the potential, which is a valid approximation for the low-mass envelopes we consider.
 |
Fig. A.2 Enclosed envelope mass as a function of time. Orange lines corresponds to run RADL27k0.01LONG, blue lines to RADL0k0.01LONG. Short-dashed, dashed, and solid curves correspond to the mass within a radius of respectively 0.3,0.6, and 0.9 rH. Convergence is reached within approximately 10 orbits. The inner envelope shells take the longest time to settle, especially when the pressure balance is driven by compressional heating. The potential is introduced during one orbital period (Eq. (A.3)). |
The potential is centered between grid cells. We found the planetary potential to be well resolved with about ≳4 grid cells across a smoothing length. This avoids additional artificial smoothing of the potential, which can be seen in the low-resolution results in Fig. A.1. Finally, we introduce the potential gently over an orbital period T as ![\appendix \setcounter{section}{1} \begin{eqnarray} M = M_{\rm c} \left[\sin \left( \frac{\pi}{2} \frac{t}{T} \right) \right]^2 \cdot \label{eq:intropot} \end{eqnarray}](/articles/aa/full_html/2017/10/aa31014-17/aa31014-17-eq240.png) (A.3)We have verified that we obtain steady-state envelope structures. Figure A.2 shows the evolution of the envelope mass with time. We find an envelope structure that remains stable on timescales of around 50 orbits. We also verified this by inspecting the stability of the total torque. The long-term integrations presented in Fig. A.2 do not reveal any accretion of gas. Even longer simulations, exceeding 105 yr, would likely be necessary in order to capture the secular cooling process of the envelope and the resulting growth in envelope mass. Inspection of Fig. A.3 shows that about 8 orbits at medium resolution are sufficient to capture the thermal structure and advection flow inside the planetary envelope to sufficient precision. However, we note that high-resolution simulations are required to capture the flow structure around r ≈ 0.2 rH. Therefore, about 4 orbits at high resolution are required to capture the effect of a reduced vertical flux. Demonstrating full convergence in tadv would demand running a high-resolution simulation for a time t ≳ tadv, which is currently unfeasible. Nevertheless, since no qualitative changes are expected to occur physically at later times, a shorter run time is sufficient in the context of this work.
(A.3)We have verified that we obtain steady-state envelope structures. Figure A.2 shows the evolution of the envelope mass with time. We find an envelope structure that remains stable on timescales of around 50 orbits. We also verified this by inspecting the stability of the total torque. The long-term integrations presented in Fig. A.2 do not reveal any accretion of gas. Even longer simulations, exceeding 105 yr, would likely be necessary in order to capture the secular cooling process of the envelope and the resulting growth in envelope mass. Inspection of Fig. A.3 shows that about 8 orbits at medium resolution are sufficient to capture the thermal structure and advection flow inside the planetary envelope to sufficient precision. However, we note that high-resolution simulations are required to capture the flow structure around r ≈ 0.2 rH. Therefore, about 4 orbits at high resolution are required to capture the effect of a reduced vertical flux. Demonstrating full convergence in tadv would demand running a high-resolution simulation for a time t ≳ tadv, which is currently unfeasible. Nevertheless, since no qualitative changes are expected to occur physically at later times, a shorter run time is sufficient in the context of this work.
 |
Fig. A.3 Convergence of radiative and advective timescales. Radiative timescales in run RADL27k0.01LONG converge rapidly in about 4 orbits, outside the smoothing radius at 0.25 rH. Little change occurs between 8 to 50 orbits. After 8 medium resolution orbits, the restart at high resolution, labeled hr in the legend, does not alter tdiff outside 0.1 rH. Advective timescales also settle quickly. We note, however, that approximately 4 orbits at high resolution are required to capture the increased vertical advection timescale around 0.2 rH (run RADL27k0.01). |
Appendix B: Accretion luminosity
We use a simple prescription to model the accretion heat released at the interior of the planetary envelope (Benítez-Llambay et al. 2015). All accretion heat Lacc is assumed to be deposited uniformly in the volume prescribed by the inner grid cells around the planet core. Simulations are mirrored across the midplane, so we only prescribe the four cells of the upper midplane that are centered around the midpoint of the planetary potential. For each of the four cells, we set an energy deposit rate of 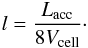 (B.1)Here, Vcell is the grid cell volume, which is well described by a constant since our nonuniform grids are to a very good accuracy equal-sized close to the position of the planet.
(B.1)Here, Vcell is the grid cell volume, which is well described by a constant since our nonuniform grids are to a very good accuracy equal-sized close to the position of the planet.
Appendix C: Isothermal equation of state
 |
Fig. C.1 Azimuthally averaged velocity field around a 5 ME core, seen in the co-rotating frame, with the use of an isothermal equation of state (run ISO). The background shows the azimuthally averaged gas density (⟨log ρ⟩p,azi in g/cm3). |
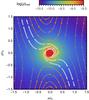 |
Fig. C.2 Velocity field around a 5 ME core in the co-rotating frame (run ISO). Displayed are the streamlines in the midplane (z = 0). Seen are the outer regions dominated by Keplerian shear, the horshoe orbits in front and behind the planet, and two distinct arms transporting mass away from the planet. The background shows the gas density in the midplane. |
In this section, we compare FARGOCA using an isothermal equation of state, with previous results obtained in the literature for the 3D flow in low-viscosity disks. In this way we test the code and more specifically the implementation of the 3D nonuniform grid.
We first compare the morphology of the flow field in the disk midplane around the planet. We use a parameter set very close to the one reported by Fung et al. (2015; simulation ISO). Figures C.2 and C.1 show the motion of gas around the planet. We find the same morphology as reported in Ormel et al. (2015) and Fung et al. (2015) for their 3D results in a low-viscosity disk. Gas enters the Hill sphere vertically (Fig. C.1) and escapes along the midplane through two channels in the second and fourth quadrant (white streamlines in Fig. C.2). This represents the transient horseshoe flow reported in Fung et al. (2015).
Appendix D: Hydrostatic model of a spherical atmosphere
In this appendix, we briefly discuss the structure of a planetary envelope in hydrostatic balance (Mizuno 1980; Rafikov 2006; Piso & Youdin 2014). In the outer shell, energy transport occurs through radiation. The temperature gradient with respect to the pressure takes the form 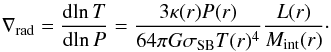 (D.1)We now assume a constant opacity and luminosity through the envelope, L(r) = L. We consider low-mass envelopes; therefore, the potential is dominated by the core, Mint(r) = Mc. Then the temperature remains nearly constant in the outer envelope, T(r) = Tout. Thus, the pressure and density exponentially increase,
(D.1)We now assume a constant opacity and luminosity through the envelope, L(r) = L. We consider low-mass envelopes; therefore, the potential is dominated by the core, Mint(r) = Mc. Then the temperature remains nearly constant in the outer envelope, T(r) = Tout. Thus, the pressure and density exponentially increase, ![\appendix \setcounter{section}{4} \begin{eqnarray} P = P_{\rm out} \exp \left[ r_{\rm B} \left(\frac{1}{r} - \frac{1}{r_{\rm out}} \right) \right] \cdot \label{eq:expP} \end{eqnarray}](/articles/aa/full_html/2017/10/aa31014-17/aa31014-17-eq254.png) (D.2)Here Pout is the pressure at an unperturbed point at rout, often taken to be the Bondi radius.
(D.2)Here Pout is the pressure at an unperturbed point at rout, often taken to be the Bondi radius.
The temperature gradient cannot grow unbounded towards the interior. Steep temperature gradients become unstable to convection. Energy transport starts occurring through the overturning motions of gas, which are assumed to maintain a critical temperature gradient 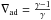 . Therefore, the depth of the radiative zone is set by the point where ∇ad = ∇rad. This allows us to rewrite Eq. (D.1) to find the pressure at the radiative convective boundary:
. Therefore, the depth of the radiative zone is set by the point where ∇ad = ∇rad. This allows us to rewrite Eq. (D.1) to find the pressure at the radiative convective boundary: 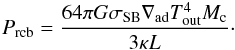 (D.3)Here the subscript “rcb” stands for values evaluated at the point where outward radiation transport starts at the radiative convective boundary. The depth of the radiative zone can be expressed, using Eq. (D.2), as
(D.3)Here the subscript “rcb” stands for values evaluated at the point where outward radiation transport starts at the radiative convective boundary. The depth of the radiative zone can be expressed, using Eq. (D.2), as ![\appendix \setcounter{section}{4} \begin{eqnarray} \frac{r_{\rm rcb}}{r_{\rm out}} &\approx& \left[ \ln \left( \frac{P_{\rm rcb}}{P_{\rm B}} \right) + \frac{r_{\rm B}}{r_{\rm out}} \right]^{-1} \\ &= &\left[ \ln \left( \frac{64 \pi G \sigma_{\rm SB} \nabla_{\rm ad} T_{\rm out}^4 M_{\rm core}}{3 \kappa L P_{\rm out} } \right) + \frac{r_{\rm B}}{r_{\rm out}} \right]^{-1} \cdot \end{eqnarray}](/articles/aa/full_html/2017/10/aa31014-17/aa31014-17-eq261.png) This expression represents a powerful relationship between the depth of the radiative zone, the opacity, and the luminosity of the planet. We also note that the depth of the radiative zone uniquely determines the energy stored in the envelope. Hot, nearly fully convective envelopes have rrcb close to the outer boundary edge of the atmosphere. The more the envelope cools, the deeper the radiative zone moves into the envelope.
This expression represents a powerful relationship between the depth of the radiative zone, the opacity, and the luminosity of the planet. We also note that the depth of the radiative zone uniquely determines the energy stored in the envelope. Hot, nearly fully convective envelopes have rrcb close to the outer boundary edge of the atmosphere. The more the envelope cools, the deeper the radiative zone moves into the envelope.
Appendix E: Pebble accretion
 |
Fig. E.1 Luminosity from the accretion of solids. The black curve corresponds to the luminosity by pebble accretion, which can be considered the maximum possible accretion rate. The red dashed line gives a lower bound on the accretion luminosity from the requirement in order to have sufficiently high accretion rates to finish core growth within the lifetime of the protoplanetary disk. The orange squares represent the accretion luminosities explored in this work. |
In Fig. E.1 we present the accretion luminosity for a core growing by the accretion of pebbles in a nominal pebble disk model (Lambrechts & Johansen 2014). The efficient accretion of drag-sensitive particles in the cm size range allows cores to grow to completion before gas disk dissipation. This growth rate can be considered to give an upper limit on the accretion luminosity because pebbles be can accreted from the full Hill sphere and the whole mass reservoir of inwards drifting pebbles is available. Conversely, accretion rates cannot have been much lower in order to meet the constraint that cores form before disk dissipation. The red curve in Fig. E.1 is constructed by assuming the upper bound on the growth timescale of Mc/Ṁmin = 10 Myr, which would correspond to a long-lived protoplanetary disk.
All Tables
All Figures
 |
Fig. 1 Global view on the vertically integrated density (Σgas in g/cm2) of the simulated annulus taken from run RADL27k0.01. We can identify the spiral arms originating from the planet located at coordinates (1,0) revealing a strong interaction between planet and disk. |
| In the text | |
 |
Fig. 2 Averaged envelope structure for an envelope undergoing solid accretion at a rate of 10 ME/Myr (black) and an envelope not undergoing solid accretion (blue). Shown are the azimuthally averaged temperature and density in the planetary midplane (RADL27k0.01,RADL0k0.01). The diamond indicates the gas scale height H of the protoplanetary disk at the location of the planet, the circle the Hill radius rH of the 5 ME core, the square the Bondi radius rB, and the triangle the estimated position of the radiative-convective boundary rrcb. The top panel (A) displays the temperature. The bottom panel (B) shows the azimuthally averaged density in the midplane. In the background we also show the density structure for a cooled-down isothermal planet with a gray dotted curve. An adiabatic convective interior, a polytrope with γ = 1.4, is shown with the purple dotted line up to rrcb. |
| In the text | |
 |
Fig. 3 Relevant length scales for a low-mass envelope, expressed with respect to the disk scale height, as a function of planetary mass. The yellow line represents the Hill radius (rH), the blue line the Bondi radius (rB), and the black curve the radius above which radiative energy transfer is possible (rrcb) assuming κ = 0.01 cm2/g and H/ap = 0.03. |
| In the text | |
 |
Fig. 4 Sample of gas streamlines arriving from the upstream direction with respect to the planet (run RADL27k0.01). The core is located at x = r − ap = 0, y = ap(φ − φp) = 0, z = 0, as indicated by the black circle, and surrounded by a transparent purple sphere with radius r = rH. Results are shown in the frame co-rotating with the planet. Blue and green streamlines make a perturbed horseshoe orbit. Gas parcels arrive well above the midplane (z >rH), enter the Hill sphere, and subsequently exit closer to the midplane (z < rH). The red and orange curves are examples of streamlines that interact strongly with the core. The orange streamline circulates closely around the core (within r < 0.5 rH), while the red streamline indicates a gas parcel that remains trapped for the duration of the integration. |
| In the text | |
 |
Fig. 5 Energy balance along streamlines as a function of time in units of orbital period T. Each panel traces the energy budget for the different streamlines depicted in Fig. 4, with panels A to D decreasing in height above the midplane. Magenta curves show the kinetic energy contribution, which is negligible. The purple curve is the effective potential term (see main text for full description). The green curve gives the thermal energy along the streamline. The black curve is the sum of the energy contributions, the Bernoulli parameter. Circles mark the points where the field line enters and exits the Hill sphere. The square symbol indicates the point where the fluid parcel crosses the x = 0 plane, which corresponds to the orbit of the planet. When multiple crossings occur the point closest to the core is selected. |
| In the text | |
 |
Fig. 6 Streamlines and gas density in the midplane of the planet, shown in a co-rotating frame centered on a planet. Here the core is accreting solids at rate of about 10 ME/Myr. (RUNHIGHRESL27). The x-axis points radially, the y-axis follows the azimuthal direction. Significant advection of mass occurs through the Hill sphere (marked by the white dashed line). The inner (left) and outer (right) circulating streamlines are shown in gray. Orange streamlines indicate the horseshoe region. The white streamlines show infalling gas from the poles being deflected outwards. Inside this region gas is unsteady in nature but nearly bound. A slow retrograde rotation can be seen, with respect to the rotating frame. The midplane gas density is shown in the background (in g/cm3). |
| In the text | |
 |
Fig. 7 Azimuthally averaged specific angular momentum, normalized by the Keplerian value, measured in the midplane. Full lines indicate retrograde motion, while dashed lines mark prograde motion. The red curve shows an isothermal simulation (run ISO) with prograde rotation inside the Hill sphere. The black and blue curve correspond to, respectively, the reference simulations RADL27k0.01 and RADL0k0.01. Gray dotted lines indicate two limit cases, gas purely in Keplerian rotation around the core (hz/hK = 1) and gas in purely Keplerian rotation around the star, as if no planet were present (Eq. (22)). |
| In the text | |
 |
Fig. 8 Enclosed gas mass, as a function of envelope radius r, around a 5 ME core (runs RADL27k0.01, RADL0k0.01, RADL271, RADL0k1). The interior envelope mass decreases when solid accretion rates increase. Higher dust opacities (κ = 1 cm2/g) decrease the envelope mass. The circles indicate the total interior mass within the Hill sphere. |
| In the text | |
 |
Fig. 9 Vertical mass flux through a shell with radius r. The quantity shown is the timescale tflux, over which the mass flux replenishes the mass interior to a radius r. The black curve corresponds to run RADL27k0.01, the blue curve to run RADL0k0.01. The total flow outside r ≳ 0.3 rH is dominated by vertical infall. The mass flow is on the order of 1% of the envelope per orbit. For the planet accreting solids, tflux decreases towards the core because of convective motions that are not present in run RADL0k0.01. Near the core interpretation is difficult because of poor resolution on these small scales. |
| In the text | |
 |
Fig. 10 Azimuthally averaged velocity field around an accreting 5 ME core, as seen in the co-rotating frame (run RADL27k0.01). The background shows the azimuthally averaged temperature (in units of K) around the core. The inset shows in greater detail the azimuthally averaged velocity field where overturning motions are driven by the heat release from solid accretion. |
| In the text | |
 |
Fig. 11 Advection timescale (solid curves) and thermal diffusion timescale (dashed curves) as functions of the vertical depth in the envelope. Black curves show results from the accreting planet (run RADL27k0.01). Outside the Hill radius, at heights above the scale height of the disk, heat exchange by radiative diffusion is efficient. Inside the Hill radius, around 0.5 rH, we find a balance between advection and diffusion, as the timescales become comparable and are on the order of 10–100 |
| In the text | |
 |
Fig. 12 Cartoon illustrating a three-layer envelope. Energy transport occurs in the interior by convection until a radiative shell is reached, situated between r ≈ 0.1 rH and r ≈ 0.4 rH. Fast gas advection takes place in the outer envelope (r ≳ 0.4 rH). |
| In the text | |
 |
Fig. 13 Azimuthally averaged velocity field around a 5 ME core, similar to Fig. 10, but without the addition of accretion luminosity (run RADL0k0.01). The background shows the azimuthally averaged compressional heating around the core. A large fraction of the gas that falls in from high elevation through the poles gets compressed above the inner planetary envelope, which gives rise to a mushroom-shaped compressional heat map. The inset zooms in on the vector field close to the core. A small amount of convergent motion can be identified, in contrast with the inset in Fig. 10 that shows convective overturn. |
| In the text | |
 |
Fig. 14 Luminosity generated around the core. The blue curve shows the integrated energy released by compressional heating as a function of radius r in the absence of heating by solid accretion (run RADL0k0.01). Black curves correspond to run RADL27k0.01. The solid line gives the sum of the accretion heat and the contribution by compressional heating (Lcomp = Lacc + Lcomp). This latter fraction is depicted by the black dashed line. |
| In the text | |
 |
Fig. 15 Streamlines and gas density in the midplane of the planet, shown in a co-rotating frame centered on a planet, not accreting any solids (run RUNHIGHRESL0). The x-axis points radially, the y-axis follows the azimuthal direction. Significant advection of mass occurs through the Hill sphere (marked by the white dashed line). The inner (left) and outer (right) circulating streamlines are shown in gray. Orange streamlines indicate the horseshoe region. The white streamlines show infalling gas from the poles being deflected outwards. Inside this region gas is bound and rotates slowly retrograde. |
| In the text | |
 |
Fig. 16 Azimuthally averaged velocity field around an accreting planet in a high-opacity environment (run RADL27k1). The gas flux from the poles also enters the deep interior, as seen in greater detail in the inset. This stands in contrast to the low-opacity case (run RADL27k0.01, Fig. 10) where rapid advection was limited to the outer envelope. |
| In the text | |
 |
Fig. 17 Advection and thermal diffusion timescales through the envelope, similar to Fig. 11, but for an unreduced opacity κ = 1 cm2/g. Red curves show the results from run RADL27k1, which is the model of a solid-accreting core. Advection timescales are short, on the order of 10 |
| In the text | |
 |
Fig. 18 Integrated energy delivery and removal respectively by compression and expansion for the unreduced opacity environment (κ = 1 cm2/g). Red curves show the case where solids are accreted (run RADL27k1). Inside the Hill sphere, we see that the inner envelope mostly acts as a sink of energy that helps gas parcels to expand as they move through the envelope. Green curves represent the energy deposition from compressional heating after solid accretion (run RADL0k1). Compressional heating now provides the luminosity that supports the envelope. The y-axis has been cut to represent the negative values on the log axis. |
| In the text | |
 |
Fig. 19 Azimuthally averaged velocity field around an accreting planet with a 15 ME core in an unreduced opacity environment (run RADL27k1M15). As opposed to the 5 ME case, the bulk of gas that enters through the poles does not enter the deep interior. The deepened potential compensates for the higher opacity (κ = 1 cm2/g). |
| In the text | |
 |
Fig. 20 Advection and thermal diffusion timescales through the envelope, similar to Fig. 11, but measured now around a 15 ME core in an unreduced opacity environment with κ = 1 cm2/g (runs RADL27k1M15 and RADL0k1M15). |
| In the text | |
 |
Fig. A.1 Azimuthally averaged density profile in the midplane for different smoothing lengths and resolutions. The legend indicates the used smoothing length parameter ϵ = rsm/rH and the characteristic grid cell width inside the envelope (dx/rH). Only in our highest resolution runs with a small smoothing length do we correctly capture the envelope structure to within a radius of 0.1 rH. Inside this radius, we start to see the influence of the smoothing length that reduces gas densities towards the core. |
| In the text | |
 |
Fig. A.2 Enclosed envelope mass as a function of time. Orange lines corresponds to run RADL27k0.01LONG, blue lines to RADL0k0.01LONG. Short-dashed, dashed, and solid curves correspond to the mass within a radius of respectively 0.3,0.6, and 0.9 rH. Convergence is reached within approximately 10 orbits. The inner envelope shells take the longest time to settle, especially when the pressure balance is driven by compressional heating. The potential is introduced during one orbital period (Eq. (A.3)). |
| In the text | |
 |
Fig. A.3 Convergence of radiative and advective timescales. Radiative timescales in run RADL27k0.01LONG converge rapidly in about 4 orbits, outside the smoothing radius at 0.25 rH. Little change occurs between 8 to 50 orbits. After 8 medium resolution orbits, the restart at high resolution, labeled hr in the legend, does not alter tdiff outside 0.1 rH. Advective timescales also settle quickly. We note, however, that approximately 4 orbits at high resolution are required to capture the increased vertical advection timescale around 0.2 rH (run RADL27k0.01). |
| In the text | |
 |
Fig. C.1 Azimuthally averaged velocity field around a 5 ME core, seen in the co-rotating frame, with the use of an isothermal equation of state (run ISO). The background shows the azimuthally averaged gas density (⟨log ρ⟩p,azi in g/cm3). |
| In the text | |
 |
Fig. C.2 Velocity field around a 5 ME core in the co-rotating frame (run ISO). Displayed are the streamlines in the midplane (z = 0). Seen are the outer regions dominated by Keplerian shear, the horshoe orbits in front and behind the planet, and two distinct arms transporting mass away from the planet. The background shows the gas density in the midplane. |
| In the text | |
 |
Fig. E.1 Luminosity from the accretion of solids. The black curve corresponds to the luminosity by pebble accretion, which can be considered the maximum possible accretion rate. The red dashed line gives a lower bound on the accretion luminosity from the requirement in order to have sufficiently high accretion rates to finish core growth within the lifetime of the protoplanetary disk. The orange squares represent the accretion luminosities explored in this work. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


