| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201730849 | |
| Published online | 19 September 2017 | |
Cliffs versus plains: Can ROSINA/COPS and OSIRIS data of comet 67P/Churyumov-Gerasimenko in autumn 2014 constrain inhomogeneous outgassing?
1 Physikalisches Institut, Universität Bern, Sidlerstrasse 5, 3012 Bern, Switzerland
e-mail: raphael.marschall@space.unibe.ch
2 NCCR PlanetS, Sidlerstrasse 5, 3012 Bern, Switzerland
3 Deutsches Zentrum für Luft- und Raumfahrt (DLR), Institut für Planetenforschung, Asteroiden und Kometen, Rutherfordstrasse 2, 12489 Berlin, Germany
4 Department of Mechanical Engineering, National Chiao Tung University, 1001 Ta-Hsueh Road, 30010 Hsinchu, Taiwan
5 National Central University, Graduate Institute of Astronomy, 300 Chung-Da Rd, 32054 Chung-Li, Taiwan
6 Institute for Geophysics and Extraterrestrial Physics, TU Braunschweig, 38106 Braunschweig, Germany
7 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg, 3, 37077 Göttingen, Germany
8 Laboratoire d’Astrophysique de Marseille, 38 rue de Frédéric Joliot-Curie, 13388 Marseille Cedex 13, France
Received: 22 March 2017
Accepted: 26 June 2017
Context. This paper describes the modelling of gas and dust data acquired in the period August to October 2014 from the European Space Agency’s Rosetta spacecraft when it was in close proximity to the nucleus of comet 67P/Churyumov-Gerasimenko.
Aims. With our 3D gas and dust comae models this work attempts to test the hypothesis that cliff activity on comet 67P/Churyumov-Gerasimenko can solely account for the local gas density data observed by the Rosetta Orbiter Spectrometer for Ion and Neutral Analysis (ROSINA) and the dust brightnesses seen by the Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS) in the considered time span.
Methods. The model uses a previously developed shape model of the nucleus. From this, the water sublimation rates and gas temperatures at the surface are computed. The gas expansion is modelled with a 3D Direct Simulation Monte Carlo algorithm. A dust drag algorithm is then used to compute dust volume number densities in the coma, which are then converted to brightnesses using Mie theory and a line-of-sight integration. Furthermore we have studied the impact of topographic re-radiation on the models.
Results. We show that gas activity from only cliff areas produces a fit to the ROSINA/COPS data that is as statistically good as a purely insolation-driven model. In contrast, pure cliff activity does not reproduce the dust brightness observed by OSIRIS and can thus be ruled out. On the other hand, gas activity from the Hapi region in addition to cliff activity produces a statistically better fit to the ROSINA/COPS data than purely insolation-driven outgassing and also fits the OSIRIS observations rather well. We found that topographic re-radiation does not contribute significantly to the sublimation behaviour of H2O but plays an important role in how the gas flux interacts with the irregular shape of the nucleus.
Conclusions. We demonstrate that fits to the observations are non-unique. We can conclude however that gas and dust activity from cliffs and the Hapi region are consistent with the ROSINA/COPS and OSIRIS data sets for the considered time span and are thus a plausible solution. Models with activity from low gravitational slopes alone provide a statistically inferior solution.
Key words: comets: individual: 67P/Churyumov-Gerasimenko / methods: numerical / methods: data analysis
© ESO, 2017
1. Introduction
The European Space Agency’s Rosetta spacecraft entered an irregular orbit around the Jupiter family comet 67P/Churyumov-Gerasimenko (hereafter 67P) on 2014-08-06. Rosetta carried 11 instruments to investigate the comet and its environment (Glassmeier et al. 2007; Schulz 2010). In particular, the payload was designed to comprehensively investigate the gas and dust emission from the nucleus as the comet approached the Sun. In this work, we focus on observations of the nucleus and the innermost dust coma using the Optical, Spectroscopic, and Infrared Remote Imaging System (OSIRIS; Keller et al. 2007) and observations of the in situ gas density at the spacecraft position using the Rosetta Orbiter Spectrometer for Ion and Neutral Analysis (ROSINA; Balsiger et al. 2007). Specifically, we use the cometary gas pressure (density) sensor, COPS.
The sublimation of surface ices leads to the production of the gas and dust comae of comets (e.g. Huebner et al. 2006). However, to what degree outgassing from cometary surfaces is inhomogeneous has been the subject of intense debate for many years (Keller et al. 1987; Crifo et al. 2002). The Rosetta data from autumn 2014 are particularly suited to the task of searching for inhomogeneity of outgassing because the spacecraft was relatively close to the nucleus at this time. Expansion of the gas (both radially and laterally) into the inner coma tends to smooth out inhomogeneities at larger distances. Previous work on modelling the gas emission from 67P during autumn 2014 and subsequent comparisons with the neutral gas density measured in situ at Rosetta by COPS (Bieler et al. 2015; Marschall et al. 2016) have suggested that a reasonably good fit to the data could be obtained by models assuming purely insolation-driven activity at the nucleus. However, in both published papers, Bieler et al. (2015) and Marschall et al. (2016) showed that better fits required higher levels of outgassing from the “neck” of the nucleus, now referred to by its regional name, Hapi. We will be referring to regions on the cometary surface as defined by Thomas et al. (2015a) and El-Maarry et al. (2015). It has been noted however (e.g. Marschall et al. 2016), that solutions are non-unique. At the smallest scales, it is obvious that small relative changes in activity in highly localised areas will have no statistically significant effect on the gas density 20 km from the source. Indeed, one can argue that any variations in activity on scale lengths less than the mean free path will have little measurable effect on the density seen relatively far from the surface assuming that the bulk parameters (total production rate, initial temperature, etc.) are similar to the insolation-driven case.
When reviewing the diverse morphology of the surface (Thomas et al. 2015a), insolation-driven outgassing appears to be counter-intuitive. There are regions of very different surface structure and appearance. Therefore it is not necessarily evident that a uniform distribution of ice over the entire comet is appropriate. Knowing that fits to the gas measurements are non-unique, one can then ask whether or not specific structurally related inhomogeneities can reproduce the gas measurements from COPS. The OSIRIS observations of dust in the inner coma provide further constraints.
A study by Vincent et al. (2016) proposed that the cometary dust jets in the northern hemisphere of 67P arise mainly from rough cliff-like terrain. Using our 3D gas and dust dynamics coma model described in detail in Marschall et al. (2016) we have run simulations with the aim of deciphering whether or not areas with high gravitational slopes alone can account for both the ROSINA/COPS and the OSIRIS data obtained from the period between mid August and the end of October 2014.
In Sect. 2, we summarise the gas and dust models. In Sects. 3 and 4, we compare the results with COPS and OSIRIS data, respectively. Motivated by these results we finally look into the impact that topographic re-radiation plays in our models in Sect. 5. We then draw some conclusions on the basis of a statistical comparison of the model calculations and their goodness of fit to the observational data.
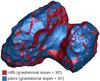 |
Fig. 1 Shape model SHAP4S with surface coloured according to gravitational slopes: cliffs (gravitational slopes >30°) in red and plains (gravitational slopes <30°) in blue. This view shows the northern hemisphere. |
 |
Fig. 2 Left panel: cosine of the incidence angle in a north polar view for a sub-solar longitude of 140° and a sub-solar latitude of 42.5°. This solar geometry is the one used to produce the results shown in Fig. 4, 8, and 9 and also corresponds to the illumination of OSIRIS image A presented in Sect. 4. Centre panel: north polar view of the comet overlaid with the longitude. Right panel: view onto the equator overlaid with latitude used in this work. |
2. The gas and dust model
Our 3D gas and dust dynamics model is described in detail in Marschall et al. (2016) but we summarise the main steps in the model here and provide the necessary information on the different set-ups studied in this work.
The basis of our simulations is the shape model “SHAP4S” of Preusker et al. (2015). The choice to neglect thermal conduction at this point seems to be justified due to the low thermal inertia found by Gulkis et al. (2015) and Schloerb et al. (2015). A preliminary test by Liao (2017) with a thermal inertia of 50 J m-2 K-1 s−1/2 has shown no significant effect on the gas dynamics. Furthermore, our focus here is to include all dominant physical effects with the least number of free parameters. Surface temperatures have been defined using a simple thermal model (including insolation, shadowing, thermal emission, and sublimation, but neglecting conduction) computed for each facet of the shape model allowing a consistent and known description of the gas flux and its initial temperature. Due to an improvement of the ray tracing method we were also able to enhance the fits to the models presented in Marschall et al. (2016). In the following step we use the DSMC program PDSC++ (Su 2013) to calculate the gas properties in 3D space. The gas solution can be compared with the in situ gas measurements of ROSINA/COPS. In a subsequent step dust particles are introduced into the gas flow to determine dust volume number densities. We assume the dust to be spherical and with zero initial velocity at the surface. The two forces acting on the dust particles are gravity and the drag force from the gas flow. The dust follows, though in a complex way, the gas flow from the nucleus. If the gas flow is perpendicular to the surface, so is the motion of the dust particles within the first meters above the surface. But lateral flows in areas with large gas production rate gradients (e.g. close to the terminator) are possible and thus also result in lateral dust flows close to the surface. A column integrator and Mie theory code are then used to produce dust brightnesses that can be compared to OSIRIS data. We had found in Marschall et al. (2016) that for the first months of the mission at the comet, inhomogeneous outgassing with dominant emission from the Hapi region in the neck part of the comet significantly increases the quality of fit to the ROSINA/COPS and the OSIRIS data. In all cases, the gas production rate from each surface facet is, as far as we know, far below the corresponding free sublimation rate into vacuum of water ice. We control the power of the emission from a specific area or region via the effective active fraction (fraction of a surface element that is emitting gas). An effective active fraction of 1 corresponds to the entire facet area emitting at a rate corresponding to the free sublimation rate. An effective active fraction of 0 on the other hand corresponds to an inert facet. The effective active fraction is usually on the order of a few percent and has been selected to match to the best extent possible, the observed gas densities at Rosetta.
To examine cliff activity, we have separated the surface facets into two categories – one with gravitational slopes larger than 30° which we call cliffs and one with slopes less than 30° which we shall call plains. Figure 1 shows the northern hemisphere of the shape model SHAP4S. The surface is coloured according to our cliff/plains criterion. We have chosen 30° as it is close to the angle of repose for granular material – the minimum angle of an inclined plane that causes an object to slide down the plane. This value is consistent with the range of 20°–30° found by Vincent et al. (2016).
We compare five models in this work. The first two models have already been presented in Marschall et al. (2016) but we shall recall their set-ups. The other three models are the main focus of this paper and thus their set-ups depend on the gravitational slopes as discussed in the previous section.
-
1.
Insolation-driven model: the gas emission of a surface elementis solely driven by the incident power of the sun light. This modelprovides a small improvement to the one presented in Marschallet al. (2016) resulting from a betterself-shadowing algorithm. The effective active fraction of thismodel is 1.2% for the entire cometary surface.
-
2.
Inhomogeneous model: different regions exhibit different effective active fractions. The effective active fractions for the different regions are as follows:
-
(a)
Hapi: 7.50%.
-
(b)
Hathor: 4.00%.
-
(c)
Hatmehit, and Imhotep: 0.50%.
-
(d)
Remaining regions: 0.95%.
-
(a)
-
3.
Plains-only model: only surface areas with gravitational slopes less than 30° are active with an effective active fraction of 4.95%.
-
4.
Cliffs-only model: only surface areas with gravitational slopes larger than 30° are active with an effective active fraction of 7.5%.
-
5.
Cliffs + Hapi model: only surface areas with gravitational slopes larger than 30° are active. In addition Hapi (a region with a low gravitational slope) is added as an active area. Both Hapi and Hathor – a cliff area – have been assigned higher effective active fractions. The following effective active fractions have been used in this model:
-
(a)
Hapi: 22.50%.
-
(b)
Hathor: 13.50%.
-
(c)
Cliffs in Anuket, and Bastet: 9.00%.
-
(d)
Cliffs in Ash, Babi, and Seth: 6.00%.
-
(e)
Cliffs in Hatmehit, and Ma’at: 3.75%.
-
(f)
Remaining cliffs: 1.50%.
-
(a)
Figure 3 shows the global gas production rate as a result of the illuminated hemisphere of the comet as a function of sub-solar longitude. The values were calculated for the 2014-09-09 when the comet was at a heliocentric distance of 3.4 AU and the Sun was at a sub-solar latitude of 42.5°. We have defined the zero meridian along the negative x-axis in the Cheops frame. The equator is defined by the x − y-plane of the Cheops frame, and the north pole and rotation axis is along the positive z-axis. This definition of the latitude and longitude is illustrated in Fig. 2. Also shown in Fig. 2 is the cosine of the incidence angle in a north polar view for a sub-solar longitude of 140° and a sub-solar latitude of 42.5°. This solar geometry is the one used to produce the results shown in Figs. 4, 8, and 9 and also corresponds to the illumination of OSIRIS image A presented in Sect. 4. For the inhomogeneous and the cliffs + Hapi models, the effective active fractions have been adapted to optimise the fits to the data. In the other three cases, a single effective active fraction has been used, but again scaled to match, to the best extent possible, the observed gas densities at Rosetta.
 |
Fig. 3 Global gas production rates Qg in kg s-1 on 2014-09-09 for the different models as a function of the sub-solar longitude (vertical lines at 0°, 50°, 90°, 140°, 180°, 230°, 270°, 320° indicate the sub-solar longitudes that were run with our gas dynamics code). The Sun is at a sub-solar latitude of 42.5° and the comet is at a heliocentric distance of 3.4 AU pre-perihelion. |
 |
Fig. 4 View of a slice through the 3D gas solutions for the sub-solar longitude of 140°. The plane shown is normal to the terminator plane, and has been chosen such that the highest-activity regions can be seen. The views do not reflect the geometry of “image A” in Sect. 4. The direction of the Sun is in the shown plane, the rotation axis of the comet comes out of the plane but has the same projected direction as the Sun direction in this view. The top row shows the gas number density [log10(m-3)] for the five models (columns). The bottom row shows the gas speeds [m s-1] for the five models (columns). The 3D shape of the comet is also displayed. |
3. Results from the gas model and comparison with ROSINA/COPS
In this section we present the results from the DSMC gas simulations and how they compare with ROSINA/COPS data. We see that the cliffs + Hapi model fits the ROSINA/COPS data equally well as the inhomogeneous one and better than any of the other models. In addition, the cliffs-only model is statistically as equally good as our insolation-driven model. It is not surprising that the models with more free parameters perform better than the ones with less. But the important point is that the models with fewer free parameters do not seem to capture the complexity of this problem to a satisfactory degree, and thus require more variation in the outgassing distribution over the surface. This of course leads to the solutions possibly being even more degenerate.
Figure 4 shows a view of a slice through the 3D gas solutions for a sub-solar longitude of 140° plotting gas number densities and speeds. The plane that is shown is normal to the terminator plane and contains the direction of the Sun. The plane has been chosen such that the highest-activity regions can be seen. Looking at the gas number density we can observe that the direction of the coma is generally in the direction of the Sun but does vary depending on the model. In the cliffs + Hapi model, the coma direction is most strongly skewed towards the “head” lobe of the nucleus. The inhomogeneous model on the other hand exhibits a coma with the largest bend towards the “body” lobe of the nucleus. The plains-only and cliffs-only models mainly differ in the direction of the gas coma. When looking at the gas speeds we can see that the inhomogeneous and cliffs + Hapi models differ significantly from the other three models. Due to their higher activity in the Hapi region, these two models also produce higher gas speeds of over 700 m s-1. Furthermore, the high gas speeds are reached very close to the surface.
So how do these models compare to the data collected by ROSINA/COPS? Figure 5 shows the comparison of the insolation-driven and inhomogeneous models with the in situ measured number density by ROSINA/COPS over the period from the 2014-08-21 to 2014-09-22. This figure is an updated version of that shown in Marschall et al. (2016) because of the improved self shadowing algorithm. We have drawn lines between the model results solely for the purpose of readability. They are not interpolations of the model results. This must be kept in mind especially when we have no simulated data point at the centre of a peak, and thus the line will not show the actual maximum of the peak on that particular cycle.
The error bars drawn are ±10% of the value and correspond to our estimate for the accuracy of our DSMC code and the applied extrapolation. We also truncated the time axis to show the main time periods of interest that are, to the greatest extent, representative of the entire time interval. Specifically, we have omitted data with high southern spacecraft latitudes where CO2 was a significant contributor to the measured COPS density. We only consider H2O herein. Compared to Marschall et al. (2016) we see that the time shift in Zone C is now resolved and we get a very high agreement of the inhomogeneous model with the data.
 |
Fig. 5 Top panel: comparison of the COPS NG (blue points) data with our insolation-driven (red points), and inhomogeneous (green points) outgassing models over the period from 2014-08-21 to 2014-09-22. Upper middle panel: the cometocentric distance and the phase angle of the observations on the same scale showing how the spacecraft approached the comet towards Zone D but at relatively high phase. Middle lower panel: the sub-spacecraft latitude (left axis) and longitude (right axis) showing how in Zone C the spacecraft was moving towards the northern pole, which is located in the Hapi region. Bottom panel: the sub-spacecraft local time (SCLT) and the local time at the position of the zero longitude meridian (CLT) that runs through Imhotep. |
Figure 6 is an equivalent figure to the previous one but comparing the plains-only (red circles), cliffs-only (orange triangles), and cliffs + Hapi (green squares) outgassing models with the in situ measured number density by ROSINA/COPS. We can see that the plains-only model falls short especially in Zones B, C, and D where the diurnal structure is not reproduced at all. The cliffs-only model is an improvement in the respect that it reproduces the diurnal periodicity of the data. But we also see that this model falls short especially in Zone E as it does not reproduce the correct relative peak height. The cliffs + Hapi model on the other hand reproduces the data substantially better. Not only is the diurnal structure of the data reproduced (seen especially in Zones B and C) but also the relative height of the peaks (seen especially in Zones D and E).
 |
Fig. 6 Top panel: comparison of the COPS NG (blue points) data with our plains-only (red circles), cliffs-only (orange triangles), and cliffs + Hapi (green squares) outgassing models over the period from the 2014-08-21 to 2014-09-22. The lower three panels are the same as in Fig. 5. |
To obtain a more objective view on how well each of the models performs, we have followed the basic approach of Bieler et al. (2015) and use two measures of the Pearson product-moment correlation coefficient (PPMCC). The first one considers the entire period from 2014-08-20 through to 2014-10-31 as a whole, and we call this the “total PPMCC”. It does factor in diurnal variations but is mainly dominated by long-term variations in the data. The second metric we have chosen should give an understanding of how well we match the diurnal variations. To do this we have calculated the PPMCC for all intervals where we have a full cometary day of data and then averaged over all days. We call this metric the diurnal PPMCC. The results are presented in Fig. 7. The error bars represent a 2σ (or 95%) confidence interval. We can see that our five models split into three groups. These are in ascending order of goodness of fit:
-
1.
Worst fit: the plains-only model is statistically inferior to allother models.
-
2.
Intermediate fit: the insolation-driven and cliffs-only models are statistically indistinguishable and fit the data better than the plains-only model. Hence the ROSINA/COPS data cannot differentiate between the two.
-
3.
Best fit: the inhomogeneous and the cliffs + Hapi models are statistically indistinguishable and fit the data the best; ROSINA/COPS cannot differentiate between these two either.
We have thus seen that eliminating all plains surfaces except for Hapi from an inhomogeneous model does not worsen the fit to the ROSINA/COPS data in our considered time span. It is thus plausible that cliffs play an important role in the gas emission from the stand point of ROSINA/COPS.
 |
Fig. 7 “Total” and “diurnal” Pearson product-moment correlation coefficient for the period 2014-08-20 through to 2014-10-31 for the five models. The error bars represent a 2σ confidence interval. |
4. Results from the dust model and comparison with OSIRIS
As a following step, we are interested in whether or not the results we have seen in the gas are consistent with the dust dynamics. As in Marschall et al. (2016) we compare with the OSIRIS image WAC_2014-09-05T09.19. 13.810Z_ID30_1397549700_F18 taken with the wide angle camera (WAC) on 2014-09-05 at 9:20:23 UTC with filter 18 (central wavelength: 612.6 nm; bandwidth: 9.8 nm) from a distance of 42.5 km to the nucleus centre, a phase angle of 59°, and an exposure time of 0.469 s. The sub-solar longitude at the time the image was taken was 140°. We refer to this image as “image A”. The second image (“image B”) we present here is WAC_2014-12-02T09.19.03.915Z_IDB0_1397549800_F18 taken with the WAC on 2014-12-02 at 9:19:04 UTC with filter 18 with a cometocentric distance of 30.2 km, a phase angle of 89°, and an exposure time of 0.648 s. The sun in this image is at a longitude of 218°. These images represent well our considered time span and show the prominent dust feature originating from the Hapi region. Additionally, image B shows a second dust feature originating around the Hatmehit and Ma’at region on the head lobe (we refer to Fig. 10 at polar angle 250°). The peak intensity of that feature is 40% less than the peak intensity of the dust feature originating in the Hapi region.
 |
Fig. 8 View of a slice through the 3D dust solutions for the sub-solar longitude of 140°. The plane shown is normal to the terminator plane. The direction to the Sun is in the plane shown; the rotation axis of the comet comes out of the plane but has the same projected direction as the Sun direction in this view. The top row shows the dust number density [log10(m-3)] for the five models (columns). The bottom row shows the dust speeds [m s-1] for the five models (columns). The results are given for a dust radius of rd = 1.6 μm and assuming a dust to gas production rate ratio of Qd/Qg = 1. The latter only affects the number density values. The 3D shape of the comet is also displayed. |
 |
Fig. 9 View of a slice through the 3D dust solutions for the sub-solar longitude of 140° for different dust size radii, starting from 1.6E− 8 to 1.6E− 4 m. The plane shown is normal to the terminator plane. The direction of the Sun is in the plane shown; the rotation axis of the comet comes out of the plane but has the same projected direction as the Sun direction in this view. All results assume the gas solution of the cliffs + Hapi model as an input for the dust model. The top row shows the logarithmic relative dust number density for each dust size. To convert to absolute units of log (m-3) the corresponding value needs to be added. For each dust size, a dust to gas ratio of unity was assumed for these plots. The centre row shows the relative dust speeds of each dust size. For the absolute values the corresponding values need to be multiplied by the given scaling. The bottom row shows the fraction of the dust velocity that is in the direction of the Sun with 100% being sunward and − 100% anti sunward. Also the fraction of ballistic particles is given. The 3D shape of the comet is also displayed. |
 |
Fig. 10 Artificial dust brightness images of our five models compared to the OSIRIS images WAC_2014-09-05T09.19.13.810Z (image A) with a sub-solar longitude of 140° and WAC_2014-12-02T09.19.03.915Z (image B) with a sub-solar longitude of 218°. The second and fourth rows show polar profiles of the relative dust brightness radially integrated from the inner to the outer circles drawn multiplied by the radial distance for the OSIRIS images and the respective model. The profile of image A shows an increase starting at a polar angle of 320° and maximum at 345°. This increase is due to a ghost image as described in Tubiana et al. (2015b). The crosses in the images mark the centre of the nucleus. |
For our dust model, we run 40 dust sizes in the range of rd ∈ [ 8 × 10-9 m; 3.2 × 10-4 m]. The lower bound of the size range has been chosen to be safely below the efficient scattering regime. The upper bound is mainly constrained by the speed of the dust particles. When dust particles become too big and thus don’t accelerate to high enough speeds, our assumption that the solution is time independent breaks down. Each size bin simulates the trajectory of approximately four million spherical test particles to determine the dust number densities and dust speeds in 3D space as described in Marschall et al. (2016). For the final composition of an artificial dust brightness image, the dust size distribution, n(rd), and the dust to gas mass production rate ratio, Qd/Qg, are the dominant variables controlling the overall brightness as explained in Marschall et al. (2016). The activity distribution of the dust is the same as that of the gas.
Figure 8 shows a view of a slice through the 3D dust solutions for sub-solar longitude of 140° plotting dust number densities and speeds for dust with radius rd = 1.6 μm and assuming a dust to gas production rate ratio of Qd/Qg = 1. The latter only affects the number density values and thus the overall dust brightness. Because we are only interested in the relative brightness (which is proportional to the number density), assuming an optically thin coma, this assumption is well justified. As the dust dynamics is primarily driven by the gas motion, the dust number densities reflect similar trends as the gas solutions we have seen in Sect. 3. Comparing especially the plains-only and cliffs-only models, we see that the main coma structure in the plains-only model is in the sunward direction, whereas in the cliffs-only model, the main direction of the dust coma is clearly skewed towards the “head” lobe of the comet and thus slightly away from the sun direction. Also, the cliffs-only and cliffs + Hapi models are missing the prominent feature originating around the Aten regions (this feature can be very clearly seen in the insolation-driven case). The emission (or lack of it) from the Hatmehit (primarily plains) region can also clearly be seen when comparing the plains-only to the cliffs-only model. There are also stark differences in the dust speeds. As with the gas, the inhomogeneous and cliffs + Hapi models exhibit the largest speeds. This can be mainly attributed to the higher gas production rates and hence gas drag on the dust in the Hapi. The maximum dust speed of the inhomogeneous and cliffs + Hapi models is almost double that of the other three models. Additionally the inhomogeneous and cliffs + Hapi models illustrate nicely how, in this geometry, the dust coma is blocked from expansion by the Hathor cliff. As the dust size increases, the dust speeds decrease and gradually particles start falling back to the night side of the comet. This is illustrated in Fig. 9. For increasing dust sizes from left to right, this figure shows in the bottom row the fraction of the dust velocity that is in the direction of the sun with 100% being sunward and − 100% anti sunward. Unsurprisingly, the main direction of the dust is sunwards for the main dust activity. Particles close to the terminator are emitted primarily normal to the surface, which in that case is transverse to the direction of the sun. When the gas density drops enough, gravity will redirect the dust into the anti-sunward direction and if the dust was not accelerated past escape speed, it will finally be redeposited on the surface. As the dust size increases, this process becomes favoured. This can especially be seen for the 1.6 × 10-4 m particles where 7.6% of ejected particles return to the surface, thus being on ballistic trajectories. Most particles on ballistic trajectories are gravitationally bound particles. The rest of the ballistic particles are emitted in the neck regions and collide with the opposing region. For a sub-solar longitude of 140° as shown in the figure, some particles emitted in the Hapi region collide shortly afterwards with the Hathor region. When particles are redeposited on the southern hemisphere, their velocity is towards the surface and thus in that specific case also sunwards. Figure 9 also shows the relative dust number densities and relative dust speed for the different dust sizes. The smaller the dust particles, the higher the speed in a larger part of the slice shown. This is mainly due to the fact that for small particles gravity is a significant force, thus reducing the speed. For the largest dust size shown, values of 0.15 (dark blue) correspond to the escape speed of 0.8 m s-1. Thus in a large part of the simulation domain, particles are on ballistic trajectories. This can also be seen in the relative number densities. Whereas the night side is almost devoid of small particles, the largest dust size shows non-negligible dust densities. In this case there is dust-mass transport from the northern to the southern hemisphere.
In the end we want to compare our dust model with the OSIRIS images and we have thus produced the respective artificial dust brightness images. The results for our five models can be seen in Fig. 10. There are large differences in the structure of the dust coma that can be observed qualitatively by comparing the artificial images to the OSIRIS images. What stands out immediately is that the insolation and plains-only models both exhibit the most dust filaments across the entire day side of the comet in both image A and B. Of special interest is a pronounced dust feature originating in the Hatmehit and Ma’at region on the “head” lobe seen in the models but not at all visible in image A. Considering this, we can exclude these two models as a match for the OSIRIS data and hence confirm the conclusion we had already seen in Sect. 3 regarding these models. In the cliffs-only model we clearly see the suppression of the dust feature coming from Hatmehit and Ma’at as this region mainly has low gravitational slopes. More predominantly, this model exhibits a very different direction of the dust structure. It is originating primarily from the Seth region rather than Hapi and is directed very clearly away from the “body” lobe. The direction is almost normal to the projected surface of Seth. Based on this we can exclude the cliffs-only model as a viable candidate.
To obtain a more qualitative view on the fit of the models to the data we have performed polar profiles as shown in the graphs of Fig. 10 to study the brightness as a function of the polar angle in a specific distance interval. As the OSIRIS images are relatively noisy, we have decided to radially integrate the brightness for each polar angle to get a clearer signal. The minimum distance is given by the comet’s nucleus not being within the integration zone and the maximum distance by the field of view of the OSIRIS image itself. For an easier comparison with the data, all profiles have been scaled such that the main peak takes the value of 1. Image A shows only one peak and the rest of the profile shows no features. However the peak is not much above the noise level. In principle there could be more features that are simply hidden in the noise. The profile of image A also shows an increase starting at a polar angle of 320° and maximum at 345°. This increase is due to a ghost image as described in Tubiana et al. (2015b). We can clearly see what we were already able to observe qualitatively in Fig. 10. The plains-only model exhibits at least four very pronounced peaks for image A and a very pronounced feature on the head lobe for image B. The cliffs-only model does indeed only have one dust peak for image A but the direction is off by approximately 20°. For image B the model profile is very far from the one of the data. The insolation-driven model also produces too many dust peaks, which are not observed at this stage of the mission. For the inhomogeneous and cliffs + Hapi models, the main peak is close to the one in the data of image A. The main difference between these two models is that only the cliffs + Hapi model produces only the main peak and is featureless along the rest of the profile. For image B, the profile of the cliffs + Hapi model comes very close to the actual profile compared to the inhomogeneous model that does not. The cliffs + Hapi model is hence a very plausible candidate.
However even the cliffs + Hapi model’s peak is shifted by approximately 7° and the Hatmehit and Ma’at dust feature is not well reproduced. The latter indicates some emission from the Hatmehit and Ma’at regions. Regarding the direction of the Hapi jet, there are three possible explanations for this. First, due to the fact that we are using a decimated-shape model it is possible that the actual surface and the model surface facets are inclined to each other by just a few degrees; second, we could be dealing with non-orthogonal emission from the surface. In our model the dust leaves the surface primarily normal to the respective surface and subsequently goes over to a radial flow; and third, additional gas emission from Hathor during local night would push the gas and thus the dust coma away from the head lobe. Such night-time activity is conceivable when considering topographic re-radiation. A test with night activity from Hathor has shown that this can indeed push the jet in the right direction but does not account for the full shift.
There are several explanations as to why we do not reproduce the dust data perfectly. For one, we are assuming the dust production rate to be proportional to the gas production rate; using a globally defined dust to gas ratio. Furthermore, we have used the same dust-size distribution across the entire surface, only letting it change naturally due to particles not being lifted. But the dust activity might also vary regionally or locally as we have seen for the gas activity distribution. The dust activity would in that case not be directly correlated with the gas activity, which has been suggested by Tenishev et al. (2016).
5. The role of topographic re-radiation
Non-illuminated surfaces can be heated by illuminated surfaces that are facing them as shown by Keller et al. (2015). Calculating the surface temperature taking this into consideration (according to Keller et al. 2015) has shown that we do not reach the sublimation regime in shadowed areas of the comet. In our simple thermal model neglecting topographic re-radiation and heat conduction, shadowed surface areas receive no energy input (therefore no temperature can be calculated) and thus do not lead to sublimation. Including topographic re-radiation into the thermal model for a 2.87 AU pre-perihelion model shows that the temperatures in shadowed areas in the neck reach temperatures of between 120 and 140 K and thus do not lead to additional sublimation. This is shown in Fig. 11. The resulting global production rates are within 2%. Locally, production rates close to the terminator, especially with proximity to illuminated facets that are face to face, are as expected boosted more strongly.
More essentially though, topographic re-radiation is important for understanding the behaviour of the surface with respect to the back flux of gas. When a surface is cold enough, gas is adsorbed by it, and thus such surfaces act like a vacuum boundary in our model. Previously we have set the entire cometary surface as a diffusely reflecting boundary without giving physical justification. As illustrated in Fig. 12 where we have compared three insolation-driven models to the ROSINA/COPS data in the time span from 2014-09-01 to 2015-01-01. This assumption provides a slightly better fit to the data. The red and blue models both do not account for topographic re-radiation and differ only in the reflectivity of the surface. In the red model, the entire nucleus surface is absorbing, and in the blue one, the entire surface reflects gas back flux diffusely. The green model on the other hand takes topographic re-radiation into account. Additionally surface facets with temperatures above 130 K are set to reflect, and those below 130 K absorb any gas back flux. This threshold has been chosen according to a study by Sandford & Allamandola (1993) who have determined residence times for different molecules on various icy surfaces for different temperatures. At 130 K, water molecules will be trapped on a water ice surface for no longer than 1.7 h (i.e. <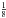 of a rotation period). Figure 12 shows that the fit to the ROSINA/COPS data is improved when going from an absorbing to a reflecting surface even without taking topographic re-radiation into account, though the correlation coefficients are within the margin of error of each other. The fit further improves when we include topographic re-radiation, and is statistically better than the absorbing model without topographic re-radiation. Thus topographic re-radiation not only provides for better fits to the ROSINA/COPS data but more importantly provides a framework with a solid physical foundation for setting the surface boundary condition. In our previous models without topographic re-radiation, no temperature could be determined for shadowed surfaces and thus their reflectivity could not be determined physically.
of a rotation period). Figure 12 shows that the fit to the ROSINA/COPS data is improved when going from an absorbing to a reflecting surface even without taking topographic re-radiation into account, though the correlation coefficients are within the margin of error of each other. The fit further improves when we include topographic re-radiation, and is statistically better than the absorbing model without topographic re-radiation. Thus topographic re-radiation not only provides for better fits to the ROSINA/COPS data but more importantly provides a framework with a solid physical foundation for setting the surface boundary condition. In our previous models without topographic re-radiation, no temperature could be determined for shadowed surfaces and thus their reflectivity could not be determined physically.
Even though we do not reach the free sublimation temperature of water in shadowed areas due to topographic re-radiation, the temperatures in these areas are high enough for the sublimation of CO2. Because a preliminary test with night side activity has shown that the direction of the jet in OSIRIS image A can be shifted by such activity it is possible that the cause of this shift is due to the sublimation of CO2.
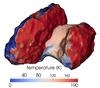 |
Fig. 11 Surface temperature including topographic re-radiation in the thermal model for 2.87 AU pre-perihelion. The sun in the figure is at 185° longitude. |
 |
Fig. 12 Pearson product-moment correlation coefficient (PPMCC) for ROSINA/COPS data for three insolation-driven models for 2.87 AU pre-perihelion in the period 2014-09-01 to 2015-01-01. The three models only differ in the thermal model and surface reflectivity applied. In red, no topographic re-radiation is included and the surface is assumed to be absorbing. In blue, no topographic re-radiation was assumed but the surface was set to be diffusely reflecting. Lastly, in green, topographic re-radiation is included and all surfaces above 130 K are assumed to be diffusely reflecting. |
6. Conclusions
We have set out to test the hypothesis of whether activity originating solely from cliff areas on comet 67P can account for the measurements seen in the ROSINA/COPS and OSIRIS data sets in the early phase of the Rosetta mission. We have also included the opposite assumption of activity solely from plains. From the analysis of the gas and dust model results, we can clearly conclude that a plains-only model of cometary activity is not a feasible option. Regarding the gas, the cliffs-only model performs as well as a purely insolation-driven model and cannot be statistically differentiated from such a model. On the other hand, a cliffs-only model does not reproduce the dust coma structure and can, on these grounds, be discarded as a valid model. We have also seen that a cliffs + Hapi model performs equally well with respect to the ROSINA/COPS data as our inhomogeneous model presented in Marschall et al. (2016). It is not possible to differentiate between them solely on the basis of the ROSINA/COPS observations. When looking at the OSIRIS image, the cliffs + Hapi model has a slight advantage over the inhomogeneous model as the latter still exhibits too many dust features, as shown in Fig. 10. We must stress at this point though that this only means that a cliffs + Hapi model is plausible. We have clearly seen that the solution is non-unique. Nevertheless, it is remarkable that we can reduce activity of large parts of the comet (all plains except for Hapi) to zero and yet still get good agreement with OSIRIS and ROSINA/COPS data. It must also be noted that these results represent the studied epoch only. The relative contributions of the different areas might (and probably will) change with time, as heliocentric distance and seasons change. It would be valuable to compare our models to the data towards the end of the Rosetta mission in September 2016, even though the sub-solar latitude never reached the values seen in the early part of the mission considered here. Furthermore we have found that topographic re-radiation provides a solid physical framework to determine the surface boundary condition regarding reflectivity, which leads to an improvement of the fits. Also, topographic re-radiation could be a source of CO2 activity in shadowed areas. Finally we have seen the advantages of multi-instrument analysis helping to distinguish between plausible and implausible solutions.
Acknowledgments
The team from the University of Bern is supported through the Swiss National Science Foundation, and through the NCCR PlanetS. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 686709. (MiARD project, www.miard.eu). This work was supported by the Swiss State Secretariat for Education, Research and Innovation (SERI) under contract number 16.0008-2. The opinions expressed and arguments employed herein do not necessarily reflect the official view of the Swiss Government. OSIRIS was built by a consortium of the Max-Planck-Institut für Sonnensystemforschung in Göttingen, Germany; CISAS-University of Padova, Italy; the Laboratoire d’Astrophysique de Marseille, France; the Instituto de Astrofisica de Andalucia, CSIC, Granada, Spain, the Research and Scientific Support Department of the European Space Agency, Noordwijk, The Netherlands; the Instituto Nacional de Tecnica Aeroespacial, Madrid, Spain; the Universidad Politechnica de Madrid, Spain the Department of Physics and Astronomy of Uppsala University, Sweden; and the Institut für Datentechnik und Kommunikationsnetze der Technischen Universität Braunschweig, Germany. The support of the national funding agencies of Germany (DLR), France (CNES), Italy (ASI), Spain (MEC), Sweden (SNSB), and the ESA Technical Directorate is gratefully acknowledged. Work on ROSINA at the University of Bern was funded by the State of Bern, the Swiss National Science Foundation, and the ESA PRODEX Programme.
References
- Balsiger, H., Altwegg, K., Bochsler, P., et al. 2007, Space Sci. Rev., 128, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crifo, J. F., Lukianov, G. A., Rodionov, A. V., Khanlarov, G. O., & Zakharov, V. V. 2002, Icarus, 156, 249 [NASA ADS] [CrossRef] [Google Scholar]
- El-Maarry, M. R., Thomas, N., Giacomini, L., et al. 2015, A&A, 583, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glassmeier, K.-H., Boehnhardt, H., Koschny, D., Kührt, E., & Richter, I. 2007, Space Sci. Rev., 128, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, 709 [CrossRef] [Google Scholar]
- Huebner, W. F., Benkhoff, J., Capria, M.-T., et al. 2006, Heat and Gas Diffusion in Comet Nuclei (Noordwijk, The Netherlands: ESA Publications Division) [Google Scholar]
- Keller, H. U., Delamere, W. A., Reitsema, H. J., Huebner, W. F., & Schmidt, H. U. 1987, A&A, 187, 807 [NASA ADS] [Google Scholar]
- Keller, H. U., Barbieri, C., Lamy, P., et al. 2007, Space Sci. Rev., 128, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H. U., Mottola, S., Davidsson, B., et al. 2015, A&A, 583, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liao, Y. 2017, Ph.D. Thesis, Universität Bern, Switzerland [Google Scholar]
- Marschall, R., Su, C. C., Liao, Y., et al. 2016, A&A, 589, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2015, A&A, 583, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandford, S. A., & Allamandola, L. J. 1993, Icarus, 106, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Schloerb, F. P., Keihm, S., von Allmen, P., et al. 2015, A&A, 583, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulz, R. 2010, IAU Symp. 263, eds. J. A. Fernandez, D. Lazzaro, D. Prialnik, & R. Schulz, 312 [Google Scholar]
- Su, C. C. 2013, Ph.D. Thesis (Taiwan: National Chiao Tung Univ.) [Google Scholar]
- Tenishev, V., Fougere, N., Borovikov, D., et al. 2016, MNRAS, 462, S370 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, N., Sierks, H., Barbieri, C., et al. 2015a, Science, 347, 440 [Google Scholar]
- Tubiana, C., Güttler, C., Kovacs, G., et al. 2015b, A&A, 583, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vincent, J.-B., Oklay, N., Pajola, M., et al. 2016, A&A, 587, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Shape model SHAP4S with surface coloured according to gravitational slopes: cliffs (gravitational slopes >30°) in red and plains (gravitational slopes <30°) in blue. This view shows the northern hemisphere. |
| In the text | |
 |
Fig. 2 Left panel: cosine of the incidence angle in a north polar view for a sub-solar longitude of 140° and a sub-solar latitude of 42.5°. This solar geometry is the one used to produce the results shown in Fig. 4, 8, and 9 and also corresponds to the illumination of OSIRIS image A presented in Sect. 4. Centre panel: north polar view of the comet overlaid with the longitude. Right panel: view onto the equator overlaid with latitude used in this work. |
| In the text | |
 |
Fig. 3 Global gas production rates Qg in kg s-1 on 2014-09-09 for the different models as a function of the sub-solar longitude (vertical lines at 0°, 50°, 90°, 140°, 180°, 230°, 270°, 320° indicate the sub-solar longitudes that were run with our gas dynamics code). The Sun is at a sub-solar latitude of 42.5° and the comet is at a heliocentric distance of 3.4 AU pre-perihelion. |
| In the text | |
 |
Fig. 4 View of a slice through the 3D gas solutions for the sub-solar longitude of 140°. The plane shown is normal to the terminator plane, and has been chosen such that the highest-activity regions can be seen. The views do not reflect the geometry of “image A” in Sect. 4. The direction of the Sun is in the shown plane, the rotation axis of the comet comes out of the plane but has the same projected direction as the Sun direction in this view. The top row shows the gas number density [log10(m-3)] for the five models (columns). The bottom row shows the gas speeds [m s-1] for the five models (columns). The 3D shape of the comet is also displayed. |
| In the text | |
 |
Fig. 5 Top panel: comparison of the COPS NG (blue points) data with our insolation-driven (red points), and inhomogeneous (green points) outgassing models over the period from 2014-08-21 to 2014-09-22. Upper middle panel: the cometocentric distance and the phase angle of the observations on the same scale showing how the spacecraft approached the comet towards Zone D but at relatively high phase. Middle lower panel: the sub-spacecraft latitude (left axis) and longitude (right axis) showing how in Zone C the spacecraft was moving towards the northern pole, which is located in the Hapi region. Bottom panel: the sub-spacecraft local time (SCLT) and the local time at the position of the zero longitude meridian (CLT) that runs through Imhotep. |
| In the text | |
 |
Fig. 6 Top panel: comparison of the COPS NG (blue points) data with our plains-only (red circles), cliffs-only (orange triangles), and cliffs + Hapi (green squares) outgassing models over the period from the 2014-08-21 to 2014-09-22. The lower three panels are the same as in Fig. 5. |
| In the text | |
 |
Fig. 7 “Total” and “diurnal” Pearson product-moment correlation coefficient for the period 2014-08-20 through to 2014-10-31 for the five models. The error bars represent a 2σ confidence interval. |
| In the text | |
 |
Fig. 8 View of a slice through the 3D dust solutions for the sub-solar longitude of 140°. The plane shown is normal to the terminator plane. The direction to the Sun is in the plane shown; the rotation axis of the comet comes out of the plane but has the same projected direction as the Sun direction in this view. The top row shows the dust number density [log10(m-3)] for the five models (columns). The bottom row shows the dust speeds [m s-1] for the five models (columns). The results are given for a dust radius of rd = 1.6 μm and assuming a dust to gas production rate ratio of Qd/Qg = 1. The latter only affects the number density values. The 3D shape of the comet is also displayed. |
| In the text | |
 |
Fig. 9 View of a slice through the 3D dust solutions for the sub-solar longitude of 140° for different dust size radii, starting from 1.6E− 8 to 1.6E− 4 m. The plane shown is normal to the terminator plane. The direction of the Sun is in the plane shown; the rotation axis of the comet comes out of the plane but has the same projected direction as the Sun direction in this view. All results assume the gas solution of the cliffs + Hapi model as an input for the dust model. The top row shows the logarithmic relative dust number density for each dust size. To convert to absolute units of log (m-3) the corresponding value needs to be added. For each dust size, a dust to gas ratio of unity was assumed for these plots. The centre row shows the relative dust speeds of each dust size. For the absolute values the corresponding values need to be multiplied by the given scaling. The bottom row shows the fraction of the dust velocity that is in the direction of the Sun with 100% being sunward and − 100% anti sunward. Also the fraction of ballistic particles is given. The 3D shape of the comet is also displayed. |
| In the text | |
 |
Fig. 10 Artificial dust brightness images of our five models compared to the OSIRIS images WAC_2014-09-05T09.19.13.810Z (image A) with a sub-solar longitude of 140° and WAC_2014-12-02T09.19.03.915Z (image B) with a sub-solar longitude of 218°. The second and fourth rows show polar profiles of the relative dust brightness radially integrated from the inner to the outer circles drawn multiplied by the radial distance for the OSIRIS images and the respective model. The profile of image A shows an increase starting at a polar angle of 320° and maximum at 345°. This increase is due to a ghost image as described in Tubiana et al. (2015b). The crosses in the images mark the centre of the nucleus. |
| In the text | |
 |
Fig. 11 Surface temperature including topographic re-radiation in the thermal model for 2.87 AU pre-perihelion. The sun in the figure is at 185° longitude. |
| In the text | |
 |
Fig. 12 Pearson product-moment correlation coefficient (PPMCC) for ROSINA/COPS data for three insolation-driven models for 2.87 AU pre-perihelion in the period 2014-09-01 to 2015-01-01. The three models only differ in the thermal model and surface reflectivity applied. In red, no topographic re-radiation is included and the surface is assumed to be absorbing. In blue, no topographic re-radiation was assumed but the surface was set to be diffusely reflecting. Lastly, in green, topographic re-radiation is included and all surfaces above 130 K are assumed to be diffusely reflecting. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


