| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201730607 | |
| Published online | 20 September 2017 | |
Impact of a star formation efficiency profile on the evolution of open clusters
1 Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12-14, 69120 Heidelberg, Germany
e-mail: beks@ari.uni-heidelberg.de
2 Fesenkov Astrophysical Institute, Observatory 23, 050020 Almaty, Kazakhstan
3 The International Center of Future Science of the Jilin University, 2699 Qianjin St., 130012 Changchun City, PR China
4 National Astronomical Observatories of China and Key Laboratory for Computational Astrophysics, Chinese Academy of Sciences, 20A Datun Rd, Chaoyang District, 100012 Beijing, PR China
5 Main Astronomical Observatory, National Academy of Sciences of Ukraine, 27 Akademika Zabolotnoho St, 03680 Kyiv, Ukraine
Received: 13 February 2017
Accepted: 5 June 2017
Aims. We study the effect of the instantaneous expulsion of residual star-forming gas on star clusters in which the residual gas has a density profile that is shallower than that of the embedded cluster. This configuration is expected if star formation proceeds with a given star-formation efficiency per free-fall time in a centrally concentrated molecular gas clump.
Methods. We performed direct N-body simulations whose initial conditions were generated by the program “mkhalo” from the package “falcON”, adapted for our models. Our model clusters initially had a Plummer profile and are in virial equilibrium with the gravitational potential of the cluster-forming clump. The residual gas contribution was computed based on a local-density driven clustered star formation model. Our simulations included mass loss by stellar evolution and the tidal field of a host galaxy.
Results. We find that a star cluster with a minimum global star formation efficiency (SFE) of 15 percent is able to survive instantaneous gas expulsion and to produce a bound cluster. Its violent relaxation lasts no longer than 20 Myr, independently of its global SFE and initial stellar mass. At the end of violent relaxation, the bound fractions of the surviving clusters with the same global SFEs are similar, regardless of their initial stellar mass. Their subsequent lifetime in the gravitational field of the Galaxy depends on their bound stellar masses.
Conclusions. We therefore conclude that the critical SFE needed to produce a bound cluster is 15 percent, which is roughly half the earlier estimates of 33 percent. Thus we have improved the survival likelihood of young clusters after instantaneous gas expulsion. Young clusters can now survive instantaneous gas expulsion with a global SFEs as low as the SFEs observed for embedded clusters in the solar neighborhood (15–30 percent). The reason is that the star cluster density profile is steeper than that of the residual gas. However, in terms of the effective SFE, measured by the virial ratio of the cluster at gas expulsion, our results are in agreement with previous studies.
Key words: galaxies: star clusters: general / stars: kinematics and dynamics / methods: numerical / stars: formation
© ESO, 2017
1. Introduction
The formation of bound star clusters can be divided into three phases: 1) star formation (SF); 2) expulsion of the residual star-forming gas; and 3) violent relaxation, that is, the cluster dynamical response to gas expulsion. The dynamics of stars in young clusters during their formation and after gas expulsion is not fully understood yet. It has been the object of intense scrutiny over the past years, with the applied methods ranging from pure N-body simulations (Tutukov 1978; Lada et al. 1984; Boily & Kroupa 2003b; Baumgardt & Kroupa 2007; Goodwin 2009; Proszkow & Adams 2009; Smith et al. 2011; Lee & Goodwin 2016) and combined hydrodynamical and N-body simulations (Bonnell et al. 2011; Girichidis et al. 2012; Moeckel et al. 2012; Fujii & Portegies Zwart 2016) to analytical and semi-analytical models (Hills 1980; Adams 2000; Boily & Kroupa 2003a; Parmentier & Pfalzner 2013).
Star clusters form in dense (>5–10 × 103 cm-3) clumps of gas inside giant molecular clouds (GMC; Lada & Lada 2003; Lada et al. 2010; Kainulainen et al. 2014). The global star formation efficiency (SFEgl), the mass fraction of a star-forming region converted into stars, is defined as 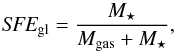 (1)where M⋆ is the total stellar mass and Mgas is the mass of unprocessed gas.
(1)where M⋆ is the total stellar mass and Mgas is the mass of unprocessed gas.
The star formation efficiencies (SFEs) measured from observations vary from a few to 30 percent for the dense clumps of molecular clouds (Lada & Lada 2003; Higuchi et al. 2009), and from 0.1 percent to a few percent for their host GMCs (Evans et al. 2009; Murray 2011).
Several mechanisms (stellar winds, ionizing radiation, radiation pressure, Type II supernova explosions) interrupt the SF process and blow up the unprocessed gas out of the cluster (Krumholz & Matzner 2009; Murray et al. 2010; Dib et al. 2013; Hopkins et al. 2013). The observed open clusters older than 10 Myr are already gas free (Leisawitz et al. 1989; Lada & Lada 2003). The duration of SF is on order of 1 Myr, with observations of young star clusters revealing stellar age spreads ranging approximately between 0.3 Myr and 5.0 Myr (Reggiani et al. 2011; Kudryavtseva et al. 2012).
The combination of the SF duration with the SFE per free-fall time determines the global SFE achieved by a cluster-forming clump at the time of gas expulsion. The SFE per free-fall time, the fraction of gas mass converted into stars over one free-fall time, was estimated to be 0.01 by Krumholz & Tan (2007), while Murray (2011) suggested that it varies between 0.01 and 0.50 depending on the GMC mass.
Baumgardt & Kroupa (2007) performed a grid of simulations assuming an embedded cluster in virial equilibrium with the residual gas, where both mass density profiles have identical shape. From these N-body simulations (see also Fig. 1 in Parmentier & Gilmore 2007, for an overview of earlier works) it was concluded that a global SFE of at least 33 percent is needed to form a bound cluster after instantaneous gas expulsion. This minimum global SFE is slightly higher than the SFEs observed for molecular clumps, which vary by up to 30 percent and are frequently estimated to be around 10 percent (Higuchi et al. 2009; Murray 2011; Kainulainen et al. 2014). To address this discrepancy between theoretical works and observations, different solutions exist: adiabatic gas expulsion(Lada et al. 1984; Geyer & Burkert 2001; Baumgardt & Kroupa 2007; Brinkmann et al. 2017), a subvirial cluster at the time of gas expulsion (Verschueren & David 1989; Goodwin 2009; Farias et al. 2015), or hierarchically formed clusters (Smith et al. 2011; Lee & Goodwin 2016).
Goodwin (2009) stressed that the critical factor for a cluster to survive gas expulsion is its dynamical state (as measured by its virial ratio) at the onset of gas expulsion, and not its global SFE. Because star clusters are not necessarily in equilibrium, he introduced an alternative SFE derived from the virial ratio of a star cluster measured immediately after instantaneous gas expulsion and called effective SFE (eSFE; see also Goodwin & Bastian 2006): 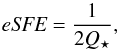 (2)with the virial ratio defined by
(2)with the virial ratio defined by 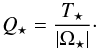 (3)Here T⋆ and Ω⋆ are the total kinetic and potential energies of a star cluster immediately after gas expulsion, and Q⋆ = 0.5 corresponds to virial equilibrium. The eSFE is equivalent to the global SFE for these models, where the SFE is constant with the distance to the center of the star-forming clump (i.e., stars and gas follow the same density profiles shape), and stars are in virial equilibrium with the gravitational potential of residual gas. According to Goodwin (2009), clusters whose virial ratio is Q⋆< 1.5 (equivalent to eSFE> 0.33) can survive the instantaneous gas expulsion.
(3)Here T⋆ and Ω⋆ are the total kinetic and potential energies of a star cluster immediately after gas expulsion, and Q⋆ = 0.5 corresponds to virial equilibrium. The eSFE is equivalent to the global SFE for these models, where the SFE is constant with the distance to the center of the star-forming clump (i.e., stars and gas follow the same density profiles shape), and stars are in virial equilibrium with the gravitational potential of residual gas. According to Goodwin (2009), clusters whose virial ratio is Q⋆< 1.5 (equivalent to eSFE> 0.33) can survive the instantaneous gas expulsion.
Smith et al. (2011, 2013) and Farias et al. (2015) studied this problem by proposing a hierarchical merging scenario of substructured embedded clusters. They also concluded that the dynamical state of a cluster at the time of gas expulsion is important to cluster survival, while the global SFE is not. However, their distributions of stars and star-forming gas are different, while not depending on each other.
The more recent work by Lee & Goodwin (2016) proposed different dynamical states for the subclusters, which are in virial equilibrium with each other within the cluster-forming region. The authors also concluded that the total dynamical state of the whole cluster at gas expulsion onset is the most important factor in predicting whether the cluster survives gas expulsion. They did not link the formation of a bound cluster to its global SFE, however, and, considered only eSFEs. One could nevertheless map their virial ratio to a subcluster mean SFE, assuming that in each subcluster, stars and gas present the same density profile shape.
Parmentier & Pfalzner (2013), however, proposed a semi-analytical model of cluster formation in which the density profile of the embedded cluster is steeper than that of the cluster-forming gas. That is, the SFE varies locally, as it steadily increases from the clump outskirts to the clump inner regions (see Fig. 10 in Parmentier & Pfalzner 2013). The reason is that the cluster-forming clump is denser and therefore experiences faster SF in its central regions than in its outskirts. The response to the gas expulsion of a cluster like this differs from the most often investigated case, that is, the case where the gas and stars density profiles have identical shapes. This was first investigated by Adams (2000) with a semi-analytical method. His choice for different gas and star density profiles was not physically motivated, however. Adams (2000) showed that if the stellar mass is more concentrated in the cluster center than the gas mass, the cluster survival probability is significantly increased (see his Fig. 3). The reason is a gas-poor region in the cluster central regions, which promotes the formation of a bound cluster, even when the global SFE is low. In addition, Pfalzner et al. (2014) performed N-body simulations whose initial conditions build on the model of Parmentier & Pfalzner (2013) for a global SFE of about 18 percent.
In this contribution, we revisit this problem by means of direct N-body simulations. Specifically, we build on the model of Parmentier & Pfalzner (2013) to generate the initial conditions of our N-body simulations, thereby physically motivating our choice for the stars and gas density profiles of the embedded cluster at the time of the gas expulsion. Our simulations also take into account stellar evolution and the tidal field of a Milky Way-like galaxy.
The outline of the paper is as follows. In Sect. 2 we build on the model of Parmentier & Pfalzner (2013) to relate the density profiles of the embedding gas and of the cluster at the onset of gas expulsion. Section 3 presents the technical setup and the initial conditions of our N-body simulations.
In Sect. 4 we discuss the results of our simulations and compare them to earlier works. Finally, we present our conclusions in Sect. 5.
2. Star-formation efficiency and density profiles
A semi-analytical model of star cluster formation from centrally concentrated spherically symmetric gas clumps with a constant SFE per free-fall time, ϵff, was developed by Parmentier & Pfalzner (2013). Because the free-fall time is shorter in the clump inner (denser) regions than in the clump outer (less dense) regions, the density profile of the formed star cluster is steeper than the density profiles of the initial and residual gas. The authors considered that the total density profile ρ0 of the system remains constant.
The total density profile is the sum of the density profiles of the embedded cluster, ρ⋆, and the residual gas, ρgas, at any time t after SF onset: 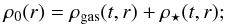 (4)here r is the distance to the clump center. The density profile of the unprocessed gas at time t is described with Eq. (19) from Parmentier & Pfalzner (2013), which we reproduce here for the sake of clarity:
(4)here r is the distance to the clump center. The density profile of the unprocessed gas at time t is described with Eq. (19) from Parmentier & Pfalzner (2013), which we reproduce here for the sake of clarity: 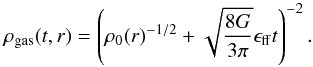 (5)G is the gravitational constant and ϵff is the SFE per free-fall time. The mass of the embedded cluster at time t is distributed according to Eq. (20) in Parmentier & Pfalzner (2013):
(5)G is the gravitational constant and ϵff is the SFE per free-fall time. The mass of the embedded cluster at time t is distributed according to Eq. (20) in Parmentier & Pfalzner (2013): 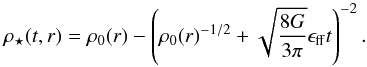 (6)Our aim is to investigate the dynamical evolution of such star clusters after instantaneous gas expulsion and to estimate their survival likelihood. The instantaneous gas expulsion corresponds to the case when the timescale of the gas expulsion is significantly shorter than the dynamical timescale of the system. In terms of cluster survivability, it is the worst scenario we can envision. If a star cluster survives instantaneous gas expulsion, it is also able to survive a longer gas expulsion timescale.
(6)Our aim is to investigate the dynamical evolution of such star clusters after instantaneous gas expulsion and to estimate their survival likelihood. The instantaneous gas expulsion corresponds to the case when the timescale of the gas expulsion is significantly shorter than the dynamical timescale of the system. In terms of cluster survivability, it is the worst scenario we can envision. If a star cluster survives instantaneous gas expulsion, it is also able to survive a longer gas expulsion timescale.
We can adopt two different approaches to study this problem.
-
A.
Either the starting point is a molecular clump, with a givendensity profile ρ0(r), and we obtain the density profile of the star cluster that formed after some SF time span based on Parmentier & Pfalzner (2013).
-
B.
Alternatively, the starting point is an embedded cluster with a well-known profile (e.g., Plummer or King), and assuming an SF time span, we recover the initial gas density profile of the molecular clump out of which the cluster has formed.
In case (A) we start with the initial spherically symmetric gas clump that has a certain density profile ρ0(r) at time t = 0. Then we assume that a star cluster forms within a time interval t = tSF called SF duration with a constant SFE per free-fall time ϵff = const. Its density profile is then given by Eq. (6). Depending on how long the SF process lasts, star clusters with different SFEgl are formed (see Fig. 9 in Parmentier & Pfalzner 2013). At time t = tSF (corresponding to a certain value of SFEgl), we set the instantaneous gas expulsion, that is, we remove the unprocessed gas from the system. A star cluster then becomes super-virial because it has lost part of the gravitational potential within which it was in virial equilibrium. This would define the initial conditions of our direct N-body simulations to study the effect of instantaneous gas expulsion.
Because model (A) depends on the SF duration, it results in star clusters with different global SFEs, masses, and spatial and velocity distributions, which makes it difficult to compare the results of the N-body simulations to each other. Additionally, generating the initial conditions of such models for N-body simulations is not trivial.
Our main point is to study the effect of instantaneous gas expulsion on a star cluster in dependence of its global SFE, therefore we can simplify the problem and consider clusters with a fixed stellar mass and spatial distribution while varying the global SFE at gas expulsion. This leads us to our case (B), on which we focus in this paper.
In case (B), we thus assume a fixed density profile and a fixed stellar mass for the embedded clusters at gas expulsion. Then the initial clumps that formed such clusters have therefore different total masses and spatial distributions depending on the assumed global SFE.
As we wish to study the response of a star cluster to gas expulsion as a function of the global SFE, we have to find the cluster velocity distribution for any given global SFE assuming it is in virial equilibrium with the gravitational potential of the residual gas. To find this distribution, which depends on the SF duration, we need to solve the inverse problem to that presented in case (A). That is, having the density distribution of a star cluster ρ⋆(r), we determine the density profile of the residual gas at gas expulsion ρgas(r,tSF), and following from this, the density profile of the whole cluster-forming clump, ρ0(r,tSF). Then we modify the cluster velocity distribution function so as to account for its virial equilibrium with the gravitational potential of the residual gas.
The model developed by Parmentier & Pfalzner (2013) can be applied to any clump density profile. So we can choose a well-known density profile ρ⋆ for the embedded cluster and define the density profile of the residual gas corresponding to an SF duration tSF by modifying Eqs. (4) and (5) and setting t = tSF: 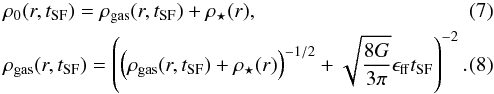 In this equation, we note that the SF duration tSF is given in units of Myr if densities ρ(⋆, gas) are expressed in M⊙ pc-3 and the gravitational constant
In this equation, we note that the SF duration tSF is given in units of Myr if densities ρ(⋆, gas) are expressed in M⊙ pc-3 and the gravitational constant 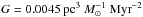 . Introducing the parameter
. Introducing the parameter 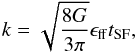 (9)which depends on the SFE per free-fall time ϵff and SF duration tSF, we can rewrite Eq. (8) as
(9)which depends on the SFE per free-fall time ϵff and SF duration tSF, we can rewrite Eq. (8) as 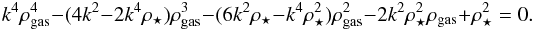 (10)Solving this equation provides us with the residual gas density profile ρgas as a function of the stellar density profile ρ⋆, SFE per free-fall time, ϵff, and SF duration tSF. The stellar density profile, ρ⋆, can be any centrally concentrated spherically symmetric density profile. We find that two of the four roots of Eq. (10) are complex. The other two roots are real, one increasing and one decreasing function of stellar density. Since we consider a centrally concentrated clump, where the stellar density decreases with increasing radius, the gas density should follow the stellar density and decrease as well. Thus we choose the root that is an increasing function of stellar density. The mathematical expressions and a short analysis of these roots are provided in Appendix A.
(10)Solving this equation provides us with the residual gas density profile ρgas as a function of the stellar density profile ρ⋆, SFE per free-fall time, ϵff, and SF duration tSF. The stellar density profile, ρ⋆, can be any centrally concentrated spherically symmetric density profile. We find that two of the four roots of Eq. (10) are complex. The other two roots are real, one increasing and one decreasing function of stellar density. Since we consider a centrally concentrated clump, where the stellar density decreases with increasing radius, the gas density should follow the stellar density and decrease as well. Thus we choose the root that is an increasing function of stellar density. The mathematical expressions and a short analysis of these roots are provided in Appendix A.
Parmentier & Pfalzner (2013) used a power-law density profile with a slope of −2 for their cluster-forming clumps. This yields a power-law density profile with a slope of about −3 for a star cluster. Such initial conditions are not ideal for N-body simulations because of their infinite stellar and gas masses. We need either to truncate these power-law profiles, or choose steeper profiles with finite masses. Thus we decide to use one of the well-known spatial density distribution functions for an embedded cluster, that is, the Plummer profile (Plummer 1911), 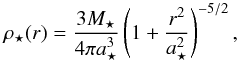 (11)where M⋆ is the cluster total mass and a⋆ is the Plummer radius, which corresponds to the projected half-mass radius of a star cluster.
(11)where M⋆ is the cluster total mass and a⋆ is the Plummer radius, which corresponds to the projected half-mass radius of a star cluster.
Choosing a Plummer profile has many advantages, for instance, a finite mass for both gas and stars, and an analytical expression. It is also supported by almost all N-body codes, which makes it possible to compare the results of different works.
3. Technical setup
3.1. Initial conditions
Since our aim is to perform N-body simulations, we adopted dimensionless N-body ([NB]) units. They are associated with the star cluster parameters, not with the cluster-forming clump parameters: 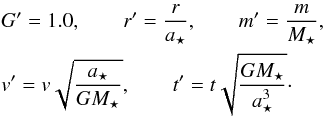 (12)The N-body units can be converted into physical units when G,a⋆,M⋆ are assigned numerical values in their respective units. Here we note that our “N-body” time unit depends on the cluster stellar mass M⋆ and Plummer radius a⋆ at the time of the instantaneous gas expulsion. It does not represent the dynamical timescale of the cluster (stars only) because the cluster is super-virial and its dynamics bears the imprint of the cluster-forming clump mass at the time of the gas expulsion. Neither does it represent the dynamical timescale of the clump (stars+gas) since the total mass and half-mass radius of the cluster-forming clump differ from the stellar mass and stellar half-mass radius because their density profiles have different shapes. We applied these N-body units for (i) to recover the density profile of the residual cluster-forming gas with Eq. (10); and (ii) to perform the subsequent N-body integration of the gas-free cluster after instantaneous gas expulsion.
(12)The N-body units can be converted into physical units when G,a⋆,M⋆ are assigned numerical values in their respective units. Here we note that our “N-body” time unit depends on the cluster stellar mass M⋆ and Plummer radius a⋆ at the time of the instantaneous gas expulsion. It does not represent the dynamical timescale of the cluster (stars only) because the cluster is super-virial and its dynamics bears the imprint of the cluster-forming clump mass at the time of the gas expulsion. Neither does it represent the dynamical timescale of the clump (stars+gas) since the total mass and half-mass radius of the cluster-forming clump differ from the stellar mass and stellar half-mass radius because their density profiles have different shapes. We applied these N-body units for (i) to recover the density profile of the residual cluster-forming gas with Eq. (10); and (ii) to perform the subsequent N-body integration of the gas-free cluster after instantaneous gas expulsion.
To generate the initial conditions of our N-body simulations is not trivial because we need a star cluster in virial equilibrium with the gravitational potential of the residual gas, where the shapes of the gas and star distributions differ. In that respect, our case differs from most previous N-body simulations, as radial variations of the SFE increase the degree of complexity of the problem.
We used the falcON program mkhalo by McMillan & Dehnen (2007), which produces a spherically symmetric star cluster in virial equilibrium with an external potential as the initial conditions of direct N-body simulations. External potential means a gravitational potential produced by anything but the stars of the cluster. In this framework, the gravitational potential produced by the residual gas constitutes an external potential.
To use mkhalo for our purpose, we wrote an additional acceleration plugin, that is, an additional code, which takes into account the new external potential of our models. In this plugin we calculated the gravitational potential and the forces produced by the residual gas knowing its density profile. For this, we used Eq. (3.15′) from Duboshin (1968): 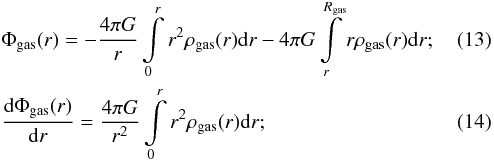 where ρgas was obtained by solving Eq. (10) (see Sect. 2), and Rgas is the adopted outer edge of the clump of residual gas. We used Rgas = 32a⋆, which is the smallest radius possible to use in mkhalo. Because the gas density profile, ρgas, is not a simple function of r, the distance to the clump center, Eqs. (13) and (14) were integrated numerically using the Simpson method.
where ρgas was obtained by solving Eq. (10) (see Sect. 2), and Rgas is the adopted outer edge of the clump of residual gas. We used Rgas = 32a⋆, which is the smallest radius possible to use in mkhalo. Because the gas density profile, ρgas, is not a simple function of r, the distance to the clump center, Eqs. (13) and (14) were integrated numerically using the Simpson method.
In the framework of this study, we adopted a fixed SFE per free-fall time of ϵff = 0.05. Then the only parameter we varied in our acceleration plugin to produce the initial conditions is the SF duration tSF. To allow a comparison of our results with other works, however, it is better to use as a main parameter the SFEgl than tSF. To develop a grid of models with a given SFEgl (0.05, 0.10, ...), we still need to infer the corresponding tSF and add them to the models.
We defined the global SFE as the ratio between the stellar and total (stellar + gas) masses residing inside a chosen outer limit, Rcl. Because a Plummer model has no finite outer limit, we adopted Rcl = 10a⋆, which is the radius inside which about 98 per cent of the stellar mass resides. Here we note that because of the slope difference between the density profiles of the embedded cluster and the residual (as well as total) gas, a larger outer limit would imply a lower global SFE, and vice versa.
The relation between the SFEgl and the corresponding SF duration tSF calculated in N-body units is presented in Fig. 1. In our study we concentrated on models with an SFEgl< 0.50. The corresponding values of SFEgl and tSF for different models are presented in Table 1. Using these values, we produced the initial conditions of our simulations with mkhalo. Then, using the generated positions and velocities of the stars, we calculated the initial potential (Ω⋆) and kinetic (T⋆) energies of our model clusters at the moment of instantaneous gas expulsion, as well as their initial virial ratios and effective SFEs, using Eqs. (3) and (2). The corresponding values are also presented in Table 1.
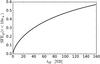 |
Fig. 1 Relation between the SF duration (tSF) (given in N-body units according to Eq. (12)) and the global SFE (SFEgl), measured inside Rcl = 10a⋆. The lowest value of the global SFE here in this plot is SFEgl = 0.007, which corresponds to an SF duration tSF = 0.01 [NB]. |
We find that in our models the effective and global SFEs are different, unlike the models that used the same density profile for both the stars and gas (see Boily & Kroupa 2003a; Goodwin & Bastian 2006; Goodwin 2009). Varying the outer edge Rcl of the cluster, we infer that these eSFEs are almost the same as the global SFEs measured inside 1.5a⋆, that is, similar within 2–3 percent to the global SFEs measured inside a cluster half-mass radius. The latter also measures the local stellar fraction (LSF) as defined by Smith et al. (2011). Goodwin (2009) noted that star clusters with an initial virial ratio lower than 1.5 are able to survive the instantaneous gas expulsion (in the case of Plummer profiles for both stars and gas), which corresponds to an effective SFE of 33 percent. Taking this into account, we can expect the minimum SFE needed to form a bound cluster to be SFEgl = 0.15, as it corresponds to Q⋆ ≈ 1.5 for our models (see Table 1). This is indeed what we show in Sect. 4.
The density profiles of the embedded cluster, its residual gas before instantaneous gas expulsion, and the initial clump gas for different global SFEs are shown in Fig. 2. The models were scaled to physical units assuming a star cluster mass of M⋆ = 3000 M⊙ and a 3D half-mass radius of rh = 1 pc. The density units are given in M⊙ pc3 (right y-axis) and molecules per cm3 (left y-axis). Gas densities on this scale vary within the observed range of dense clumps (≲105 cm-3). The SF durations tSF for these three models are 0.39 Myr, 2.21 Myr, and 12.77 Myr. As we see, some of our models are inconsistent with observations in the sense that the inferred SF duration is longer than what is observed.
 |
Fig. 2 Density profiles of the star cluster (black dashed line), of the residual (solid lines), and initial (dash-dotted lines) gas for different SFEgl in scaled physical units. A total stellar mass M⋆ = 3000 M⊙ and a 3D half-mass radius rh = 1 pc are assumed. Note that the stellar density profile is a Plummer profile. |
For our high-resolution direct N-body simulations we have chosen the φgrape-gpu code developed by Berczik et al. (2011). As a check of the stability of the initial conditions generated by the code mkhalo, we added our newly created external potential to the φgrape-gpu code and tested the dynamics of the embedded cluster within the residual gas potential. We ran a few simulations with external potentials corresponding to different tSF. The test runs were performed for isolated clusters with N = 10k single-mass particles over a time interval of up to 1000 N-body time units, which is slightly shorter than three relaxation times of the same cluster in virial equilibrium without external potential. We checked the evolution of the Lagrangian radii and cumulative mass profiles for two models with low and high values of tSF. These exercises showed that our newly generated initial conditions are indeed in virial equilibrium with the external gas potential.
3.2. Setting up the simulations
We performed two types of N-body simulations. First, we simulated isolated single-mass clusters without stellar evolution to observe the pure dynamical effect of an instantaneous gas expulsion. We ran these simulations with N = 104 particles and covered global SFEs ranging from 5 to 50 percent.
Second, we studied a more realistic scenario of violent relaxation by considering star clusters consisting of multi-mass stars that evolve in a Galactic tidal field. We refer to these two sets of simulations as “isolated” and “non-isolated” models.
For the stellar initial mass function (IMF) of our non-isolated models we adopted the IMF of Kroupa (2001) with the lower and upper mass limits of Mlow = 0.08 M⊙ and Mup = 100 M⊙, respectively.
To account for the tidal field of the Galaxy, we used an axisymmetric three-component model that consists of a bulge, disk, and halo, as described by the Plummer-Kuzmin model (Miyamoto & Nagai 1975). This was added to the φgrape-gpu code by Just et al. (2009), and we used it keeping their parameters.
We considered that our clusters move on a circular orbit in the plane of the Galactic disk, at a distance of R0 = 8 kpc from the Galactic center.
We normalized our N-body units to the real physical units in order to assign the correct timescale to the stellar evolution routines (SSE; Hurley et al. 2000) implemented in the φgrape-gpu code. This means that we assigned certain values to the cluster mass (M⋆) and the initial Plummer radius (a⋆).
Our simulations encompass five different initial cluster stellar masses: M⋆ = 3000, 6000, 10 000, 15 000, and 30 000 M⊙. Then knowing the distance of the cluster to the Galactic center, we can calculate the cluster tidal (Jacobi) radius rt for a given mass M⋆ using Eq. (13) from Just et al. (2009), which we reproduce here for the sake of clarity: 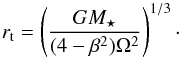 (15)Here β = 1.37 is the normalized epicyclic frequency and Ω = V0/R0 is the angular speed of a star cluster on a circular orbit at a distance R0 from the Galactic center. For R0 = 8000 pc, the orbital speed recovered from the rotation curve of the Galaxy model provided in Just et al. (2009) is V0 = 234.24 km s-1.
(15)Here β = 1.37 is the normalized epicyclic frequency and Ω = V0/R0 is the angular speed of a star cluster on a circular orbit at a distance R0 from the Galactic center. For R0 = 8000 pc, the orbital speed recovered from the rotation curve of the Galaxy model provided in Just et al. (2009) is V0 = 234.24 km s-1.
To make the models comparable with each other, we fixed the half-mass radius to the tidal radius ratio. We calculated it for a cluster mass M⋆ = 3000 M⊙ with a half-mass radius of rh = 1 pc. This means that we considered clusters with different stellar masses, but the same mean stellar volume densities. The tidal radius of a cluster with M⋆ = 3000 M⊙ and rh = 1 pc is rt = 19.2 pc, and therefore 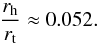 (16)Thus we normalized the N-body length unit into physical units of pc knowing that in a Plummer model rh ≈ 1.3a⋆,
(16)Thus we normalized the N-body length unit into physical units of pc knowing that in a Plummer model rh ≈ 1.3a⋆, 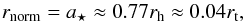 (17)where the tidal radius is calculated using Eq. (15). For the models with an initial stellar mass M⋆ = 3000 M⊙, for instance, the normalized length is equal to rnorm = 0.77 pc. With our definition of the outer limit Rcl of our cluster-forming clumps (see Sect. 3.1), star clusters initially fill their tidal radius up to 40 percent. This means that the total radius of a star cluster is initially smaller than its tidal radius: Rcl = 10a⋆ = 0.4rt. The properties of a star cluster as a function of its stellar mass are presented in Table 2.
(17)where the tidal radius is calculated using Eq. (15). For the models with an initial stellar mass M⋆ = 3000 M⊙, for instance, the normalized length is equal to rnorm = 0.77 pc. With our definition of the outer limit Rcl of our cluster-forming clumps (see Sect. 3.1), star clusters initially fill their tidal radius up to 40 percent. This means that the total radius of a star cluster is initially smaller than its tidal radius: Rcl = 10a⋆ = 0.4rt. The properties of a star cluster as a function of its stellar mass are presented in Table 2.
Set of models corresponding to different initial stellar masses.
The scale factor of time units, as shown in Eq. (12), can be found as 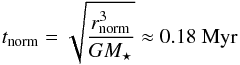 (18)when rh/rt = 0.052. Given our assumption of a fixed ratio of the half-mass to tidal radius (see Eqs. (16) and (17)), rnorm ∝ rt ∝ (GM⋆)1/3, tnorm is the same for all models as well as the mean stellar volume densities.
(18)when rh/rt = 0.052. Given our assumption of a fixed ratio of the half-mass to tidal radius (see Eqs. (16) and (17)), rnorm ∝ rt ∝ (GM⋆)1/3, tnorm is the same for all models as well as the mean stellar volume densities.
The corresponding values of SF duration and total (stars + gas) volume densities averaged within the initial stellar 3D half-mass radius are provided in Table 3. This table shows that the models are consistent with the observations in terms of SF duration and clump mean densities. It is thought that star cluster formation takes between one half and roughly 5 Myr in the solar neighborhood. We therefore consider the models in these limits to make our simulations as consistent with reality as possible. This limits the SF duration of our models between 2.7 and 27 N-body time units, which corresponds to 0.5 and 5 Myr for our chosen scale factor of rh/rt. Consequently, this also limits us in the range of achievable SFEgl. According to these limits, we decided to calculate models with SFEgl between 10 percent and 25 percent for ϵff = 0.05, which corresponds to an SF duration tSF between 1.15 and 5.25 Myr for all initial cluster masses M⋆. To cover still higher SFEs, we ran two additional models with global SFEs of 30 and 35 percent for M⋆ = 6000 M⊙. To make these runs consistent with the observations in terms of SF duration, we built on the following feature of Eq. (10): because the parameter k in Eq. (10) is proportional to ϵfftSF, our results stand for any model where the product ϵfftSF is conserved (e.g., a twice higher SFE per free-fall time with a twice shorter SF duration). In our two additional runs the SF durations can therefore be considered as tSF = 3.64 Myr and 4.88 Myr, respectively, if ϵff = 0.1. For comparison, additional models with the same spatial distribution of stars initially in virial equilibrium within a Galactic tidal field, but without any residual star-forming gas, (i.e., equivalent to SFEgl = 1.0), were run for M⋆ = 3000, 6000, and 10 000 M⊙.
The mean (total and stellar) volume densities of models are also consistent with observations of star-forming molecular clumps, where an SF density threshold has been suggested (≳104 cm-3 in Lada et al. 2010 and >5 × 103 cm-3 in Kainulainen et al. 2014) and with stellar densities in embedded clusters, which vary from 100–200 to 1–2 × 104 stars pc-3 (Lada et al. 1991; Hillenbrand & Carpenter 2000).
Based on these simulations, we now study the evolution of the bound fraction of star clusters. We present the results of isolated models scaled to physical units such that M⋆ = 6000 M⊙ and rh = 1.26 pc (see Table 2) to compare them with M⋆ = 6000 M⊙ non-isolated models, which consist of 10 455 stars.
4. Results and discussions
4.1. Cluster-bound fraction evolution
In the classical way, the bound fraction of isolated clusters in virial equilibrium is defined as the fraction of stars whose total energy is negative, that is, the potential energy dominates the kinetic energy. Our model isolated clusters become supervirial and start to expand quickly after instantaneous gas expulsion, however. Thus it is not trivial to distinguish between bound and unbound stars in such systems during their expansion. This process can take quite a long time in isolated systems, especially if the final bound fraction is small. For instance, the cluster with SFEgl = 0.15 needs 1 Gyr to approach the final bound fraction if this is defined in the “classical” way. We therefore developed the following technique to determine the final bound fraction. We recalculated the total energies of stars, removing the unbound stars (i.e., stars whose total energy is positive) from the cluster even if they were located in the center of the cluster. We iterated until no unbound star remained in the cluster. Doing so, we excluded the contribution of unbound stars to the cluster potential. The final bound fraction of our isolated models is defined as the final fraction of stars that remained bound to the cluster – if any – at the end of the iterations. We emphasize that removing the unbound stars does not mean that we removed them from the simulations, but that we removed them from our selected sample at each snapshot for the purpose of our analysis only. For each snapshot in time, we always started the iterative process with the total number of stars. More discussion about this technique and its relevance can be found in Appendix B.
For the non-isolated clusters, that is, those evolving within a Galactic tidal field, the bound fraction is defined as the stellar mass residing inside the instantaneous tidal radius normalized to the initial stellar mass, 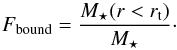 (19)In the top panel of Fig. 3 we present the time evolution of the bound fractions of our non-isolated (solid lines) and isolated (dashed lines) models.
(19)In the top panel of Fig. 3 we present the time evolution of the bound fractions of our non-isolated (solid lines) and isolated (dashed lines) models.
 |
Fig. 3 Evolution of the bound fraction of clusters obtained in our simulations. Different colors correspond to different global SFEs (see the key). The gray lines show the impact of mass loss caused by stellar evolution alone. The vertical dotted line corresponds to t = 20 Myr.Top panel: comparison of the bound fraction evolution of isolated (dashed lines) and non-isolated (solid lines) models for M⋆ = 6000 M⊙ with N ≈ 104 stars. Note that the isolated models are the single-mass models without stellar evolution and scaled to the same physical units as the non-isolated models (i.e., M⋆ = 6000 M⊙ and rh = 1.26 pc). Bottom panel: bound fraction (instantaneous tidal mass as a fraction of initial stellar mass) evolution for non-isolated models with different initial stellar masses (see the key for the line-coding). |
We note that for the isolated clusters we present the final bound fraction defined with the technique described above, and not the fraction of stars with negative total energy. This clearly provides a method for determining the bound mass very early (see Appendix B ). For our non-isolated models, we also show the imprint of stellar-evolution mass loss as the gray lines. The model clusters with SFEgl = 1.0, that is, those that are initially in virial equilibrium without any residual star-forming gas, are depicted as sky-blue lines. To better visualize both the very fast evolution shortly after gas expulsion and the cluster long-term evolution, the scale of the x-axis (time) is logarithmic. The plateau at the very beginning of the bound mass evolution results from our definition of the bound mass fraction, which does not account for the high-velocity unbound stars within the tidal radius. Because the cluster initial size is smaller than its tidal radius (rh/rt = 0.052), almost all stars reside within the tidal radius during the first few Myr of evolution even when the cluster starts to expand. The bound mass fraction starts to decrease as the escaping stars reach the tidal radius and become unbound by our definition.
From the bound fraction evolution of our non-isolated model clusters we can identify two regimes of mass loss (the solid lines in the top panel of Fig. 3), in addition to the mass loss driven by stellar evolution. During the first 20 Myr after gas expulsion, clusters intensively lose their mass (top panel of Fig. 3: the solid lines on the left-hand side of the vertical dotted line). During this time span, the cluster evolution is dominated by the consequences of gas expulsion, and their response is mostly determined by the cluster initial virial ratio.More or less flat plateaus can be seen in between two identified mass-loss regimes around 20 Myr after gas expulsion. This means that the surviving part of the cluster is not expanding anymore.
The bound fraction then decreases more slowly with time. It is now mostly affected by stellar evolution and the tidal field of the host galaxy (top panel of Fig. 3: the solid lines on the right-hand side of the vertical dotted line).
The bottom panel of Fig. 3 presents results for the non-isolated models alone for the global SFEs and initial cluster stellar masses quoted in the key. The color-coding is identical to the coding used in the top panel. We find that the models with identical global SFE show similar evolutionary tracks within the first 20 Myr (i.e., during the violent relaxation) independently of their initial stellar mass (bottom panel of Fig. 3). In particular, the models with a low global SFE dissolve on similar timescales independently of the initial star cluster mass, M⋆ (see the black curves). Here we recall that the ratio rh/rt is kept constant for now. The model with a global SFE of 13 percent and M⋆ = 6000 M⊙ does survive as a bound cluster, although with a very small bound fraction, around 2 percent (the blue lines in the top panel of Fig. 3). All other stellar mass models with a global SFE of 13 percent dissolve, however, except for the M⋆ = 30 000 M⊙ model, which barely survives with a 0.17 percent bound fraction, which corresponds to a bound mass of about 52 M⊙. Therefore we adopt the models with SFEgl = 0.13 as the limit between survival and dissolution following cluster gas expulsion for our adopted tidal field impact rh/rt = 0.052. Cluster models with a global SFE of 0.15 and higher can survive instantaneous gas expulsion, as expected from their initial virial ratios (see Table 1). We note that SFEgl = 0.13 is about 2.5 times lower than the SFE threshold for cluster survival when (i) the density profiles of the stars and residual gas have the same shape; (ii) gas expulsion is instantaneous; and (iii) the tidal field impact is negligible.
We performed a few simulations for a given parameter set but different random seeds to explore the bound fraction variations that are due to random realizations. Figure 4 shows that the bound mass fraction at t = 20 Myr displays a range of variations of about 10 percent for a cluster with N = 10 455 stars (i.e., M⋆ = 6000 M⊙ cluster). For a cluster with a higher number of stars (N = 26 138, M⋆ = 15 000 M⊙), the range of bound mass fraction variations is about 6 percent. The duration of cluster mass-loss in response to gas expulsion remains shorter than 20 Myr for different random realizations.
 |
Fig. 4 Different random realizations (see line types in the key) of the model clusters with M⋆ = 6000 M⊙ (N = 10 455 stars) for rh/rt = 0.052. |
After violent relaxation, the cluster life-expectancy depends on its stellar mass, as expected (red lines in the bottom panel of Fig. 3). A higher stellar mass implies a higher probability to survive a longer time (but see Ernst et al. 2015). The models corresponding to the high global SFEs in this set of simulations show long-term evolutionary patterns similar to the pure Plummer models (i.e., initially in virial equilibrium without any external potential).
This study shows us that the mass loss of the cluster in response to gas expulsion is completed within 20 Myr, independently of its initial stellar mass and global SFE, and that its dynamical evolution is mostly affected by the tidal field of the host galaxy thereafter (Fig. 3). Since we focus on the cluster bound mass evolution, we consider the violent relaxation as the time span when the cluster loses its mass intensively in response to an instantaneous gas expulsion. We therefore used t = 20 Myr to measure the final bound fraction of clusters. We note, however, that the outer shells of surviving clusters need a longer time-span to return to virial equilibrium, as shown by Fig. 5 (see below; see also Brinkmann et al. 2017). We note therefore that the violent relaxation duration, as defined here, does not strictly equate with the cluster revirialization time.
An example of the Lagrange radius Rf evolution of a non-isolated cluster with SFEgl = 0.20 and M⋆ = 6000 M⊙ is presented in Fig. 5.
 |
Fig. 5 Evolution of a non-isolated cluster of the solar neighborhood with SFEgl = 0.20, M⋆ = 6000 M⊙ and rh/rt = 0.052 over 50 Myr after gas expulsion. We show 49 Lagrange radii, ranging from 2 percent to 98 percent in intervals of 2 percent (solid and dashed lines). The instantaneous tidal radius rt of the cluster is shown as the dotted line. Thick solid lines correspond to every 10 percent of the Lagrange radius, and the dashed line corresponds to 50 percent of the Lagrange radius. |
The Lagrange radii are defined based on the fraction of initial stellar mass, not on the number fraction of stars. The dotted line in this figure represents the instantaneous tidal radius. This figure shows that the inner parts of a cluster recede, form a bound cluster, and return to virial equilibrium within 20–30 Myr after gas expulsion. The inner shells of a cluster revirialize faster than the outer shells, as also found in Brinkmann et al. (2017), for example. The cluster tidal radius stays roughly constant after 20 Myr.
4.2. Influence of the cluster initial stellar density
To quantify the effect of the tidal field impact, three additional sets of simulations were performed for cluster masses M⋆ = 6000 M⊙ and 15 000 M⊙: one with a weaker tidal field impact (rh/rt = 0.025), and two with stronger tidal field impact corresponding to rh/rt = 0.07 and 0.10. That is, we varied the half-mass radius of our model clusters, keeping them in the solar neighborhood (i.e., keeping the same tidal radius for a given stellar mass). Because we varied the initial density of the cluster, we varied the normalization factor of time units as shown in Table 4. For denser clusters (smaller rh/rt), a given physical time-span represents a higher number of N-body time units.
Scaling factors to the physical time and duration of 20 Myr in N-body units corresponding to different ratios of the cluster half-mass to tidal radius.
We present the bound mass fraction evolution of M⋆ = 15 000 M⊙ clusters with different initial densities in Fig. 6.
 |
Fig. 6 Evolution of the bound fraction of M⋆ = 15 000 M⊙ clusters with different impact of the tidal field (see the key for the line-coding). Different colors correspond to different global SFEs (see the key for the color-coding). |
We find that the dense clusters evolve quicker than the less dense clusters within the first 20 Myr after gas expulsion. The violent relaxation duration of clusters and their bound mass fraction at t = 20 Myr depend on the initial cluster mean densities. This is consistent with Parmentier & Baumgardt (2012) and Banerjee & Kroupa (2013), who showed that dense clusters have shorter revirialization times than less dense clusters. However, we find the cluster violent relaxation to depend fairly weakly on the initial stellar density. The difference during the first 10 Myr results from our definition of the bound mass fraction. That is, the most compact cluster (rh/rt = 0.025) loses mass in response to gas expulsion faster than the most diffuse cluster (rh/rt = 0.100). Its escaping stars reach the tidal radius twice faster because their velocity dispersions differ by a factor of 2. Although it is not obvious how to define the duration of violent relaxation accurately, Fig. 6 shows that it remains shorter than 20–25 Myr regardless of the cluster initial density. The key to understanding the violent relaxation duration may reside in the mean stellar density within the tidal radius, which is the same for all considered clusters since they all have the same orbit.
We note that stars that would be bound to the cluster if the cluster is isolated now become unbound once they cross the tidal radius of the cluster. Additionally, they are taken away from the cluster by the Galactic tidal field (see the different behaviors of the 30 percent Lagrange radius in Figs. 5 and 7).
In Fig. 7 we present an example of Lagrange radii evolution of a most compact cluster with M⋆ = 6000 M⊙,SFEgl = 0.20. We can see that the inner shells of the cluster with rh/rt = 0.025 revirialize faster than those of a more diffuse cluster with rh/rt = 0.052.
Figure 6 shows the differences in bound mass fraction at t = 20 Myr to be around 10 percent between the most compact and the most diffuse clusters. More diffuse clusters have a lower bound fraction since their outer shells expand beyond their instantaneous tidal radius. We have checked that a higher number of particles (M⋆ = 15 000 M⊙) does not affect our results.
 |
Fig. 7 Evolution of the cluster with M⋆ = 6000 M⊙, SFEgl = 0.20 and rh/rt = 0.025 over the first 50 Myr after the instantaneous gas expulsion. |
4.3. Final bound mass fraction in dependence of SFE
We compare our results (represented by the mean values taken from the model clusters with rh/rt = 0.052 and different stellar masses) with previous works (Adams 2000; Lada et al. 1984; Geyer & Burkert 2001; Boily & Kroupa 2003b; Fellhauer & Kroupa 2005; Baumgardt & Kroupa 2007) in the top panel of Fig. 8, which shows the bound fraction as a function of global SFE.
 |
Fig. 8 Bound fraction as a function of global or effective SFE. We compare our results (red lines) with previous works. The isolated models are depicted by the red diamonds, and non-isolated models by red crosses. In the top panel we use our global SFE (SFEgl) and in the bottom panel, the effective SFE, eSFE = 1 /Q⋆ (which is almost the same as the LSF, the local stellar fraction of our models). |
We note here the improved survival likelihood of star clusters after instantaneous gas expulsion, and that although the tidal field is included in our models. Our model star clusters whose global SFE is lower than 30 percent, but higher than 15 percent, survive and retain a significant fraction of their stars after violent relaxation.
The global SFEs required by our model clusters to survive gas expulsion provide a good match to the SFEs observed in embedded clusters, which are lower than 30 percent (Higuchi et al. 2009; Murray 2011; Kainulainen et al. 2014). Star clusters are now able to survive instantaneous gas expulsion despite a global SFE as low as 15−20 percent. We now have four avenues to understand the presence of star clusters with ages older than few Myr in the solar neighborhood despite the low SFE observed: adiabatic gas expulsion (Lada et al. 1984; Geyer & Burkert 2001; Baumgardt & Kroupa 2007; Brinkmann et al. 2017), sub-virial clusters (Verschueren & David 1989; Goodwin 2009; Farias et al. 2015), hierarchically formed clusters (Smith et al. 2011; Lee & Goodwin 2016), and centrally concentrated cluster formation (this contribution).
We argue that the improved survivability of our model clusters is mostly caused by the difference in density profiles between the embedded cluster and its residual gas, as postulated by Parmentier & Pfalzner (2013), namely, the stars have a density profile steeper than that of the residual and initial gas. This is the consequence of SF taking place with a constant SFE per free-fall time in a centrally concentrated molecular clump.
We reproduce similar results to previous works when we plot the bound fraction as a function of the effective SFE (eSFE) instead of the global SFE (see the bottom panel of Fig. 8). We note here again that in our models the eSFE and the local stellar fraction (LSF) are almost the same. Our study thus agrees with all present works, including the most recent paper of Lee & Goodwin (2016), who concluded that the effective SFE is the most important parameter in predicting the cluster survivability. Our study allows us to compare model SFEs to those achieved in observed forming clusters, however.
5. Conclusions
We have performed N-body simulations of violent relaxation and bound cluster formation after instantaneous gas expulsion. The key point of our study is that we used special initial conditions built on the model of Parmentier & Pfalzner (2013). This means that the density profile of our model star cluster is steeper than the density profile of the star-forming gas at the time of instantaneous gas expulsion. If this cluster is in virial equilibrium, including the gravitational potential of residual gas, it should be able to survive gas expulsion despite low SFEs, as shown by Adams (2000) based on a semi-analytical model.
Since our N-body simulations start from the time of instantaneous gas expulsion and do not cover the SF phase, we started with a well-known star cluster model, namely the Plummer model, instead of starting from the star-free molecular clump. For this we obtained the dependency of the residual gas density profile on stellar density profile at the time of instantaneous gas expulsion under the assumptions of Parmentier & Pfalzner (2013). In their cluster-formation model, the density profile of a clump (i.e., stars + gas) is constant during SF, and SF takes place with a constant SFE per free-fall time. Using this, we produced the initial conditions of embedded clusters for our N-body simulations, which depend on the product of two parameters (SFE per free-fall time and SF duration). With the equations we provide in the Appendix A, one can use any centrally concentrated spherically symmetric density profile for the embedded cluster and recover the initial and residual gas density profiles.
We adapted the falcON program mkhalo by McMillan & Dehnen (2007) to our problem and have written an additional acceleration plug-in, which represents the gravitational potential of the residual gas in dependence on the SF duration and SFE per free-fall time for a Plummer embedded cluster. Building on this adapted version of mkhalo, we produced the initial conditions of our simulations, that is, a Plummer star cluster in virial equilibrium with its residual gas with their respective density profiles obeying Eqs. (18) and (19) of Parmentier & Pfalzner (2013). We related the SF duration to the global SFE to make our set of simulations comparable to earlier works, in which the bound fraction is often presented in dependence on the global SFE.
We performed two types of cluster simulations, each time covering different global SFEs: 1) isolated single-mass clusters; and 2) non-isolated models, that is, star clusters with stellar evolution and dissolving within a Milky Way-like galaxy. We studied the effect of different initial cluster stellar masses as well as of different cluster densities on the evolution of our non-isolated models. The latter are implemented by varying the cluster half-mass to tidal-radius ratio, rh/rt = 0.025, 0.052, 0.07, and0.10.
Based on the performed simulations, we quantified the bound fraction evolution and the violent relaxation duration of young clusters. We defined the violent relaxation duration as the time span of cluster mass-loss in response to instantaneous gas expulsion. We note that with our definition, the violent relaxation duration differs from the cluster revirialization time. Our models for isolated single-mass clusters allowed us to define an upper limit to the bound fraction as a function of the global SFE. For the models considered in our work with their specific parameters – the stellar density profile (Plummer model), the cluster orbit (with a circular velocity, in the solar neighborhood in the Galactic disk plane), the stellar evolutionary mass-loss from the SSE routine (Hurley et al. 2000) and for the cluster mean volume density range (rh/rt = [0.025:0.100]) – we conclude that the violent relaxation is not longer than 20 Myr, and its duration depends weakly on the initial stellar density of a cluster. We found that the violent relaxation duration of non-isolated model clusters depends neither on the cluster initial stellar mass nor on the global SFE, keeping the same initial stellar density. Varying the tidal field impact, that is, varying the cluster size while retaining the cluster mass, does not affect the cluster mass-loss in response to instantaneous gas expulsion much.
We also found that the minimum global SFE necessary to form a bound cluster after instantaneous gas expulsion is SFEgl = 0.15 for a cluster with a circular orbit in the Galactic disk plane at a distance of R0 = 8 kpc from the Galactic center. If the tidal field is stronger, that is, the cluster is closer to the Galactic center, the minimum SFEgl needed to survive instantaneous gas expulsion may be different. For the given rh/rt ratio, the bound fraction of surviving clusters that achieved the same global SFE does not depend on the cluster initial stellar mass. The bound mass fraction at the end of violent relaxation for clusters with rh/rt of 0.025 and 0.10 differs by only about 10 percent, with denser clusters retaining a higher bound fraction than more diffuse clusters. The evolution of bound clusters after violent relaxation is mostly driven by the tidal field of the host galaxy, and their life expectancy then depends on their stellar mass.
We compared our results with earlier works. Our final bound fractions are similar to those found in previous works only when the bound fraction is plotted in dependence of the effective SFE. Thus we agree with Goodwin (2009) that the virial ratio of a cluster at the time of gas expulsion is a key parameter for predicting whether it survives gas expulsion. However, when working in terms of the global SFE, that is, the SFE that can be measured by observers as the ratio between the stellar mass and the total (gas+star) mass of a star-forming region, the models proposed in this paper improve the survival likelihood of star clusters after instantaneous gas expulsion. This is caused by the difference in density profiles between the embedded cluster and its residual gas, namely, the stellar density profile has a steeper slope than that of the residual gas, which is a consequence of SF taking place with a constant star-formation efficiency per free-fall time in a centrally concentrated molecular clump.
Acknowledgments
We thank the referee for the helpful comments. This work was supported by Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject B2) of the German Research Foundation (DFG). The authors gratefully acknowledge Walter Dehnen for his support and discussions in connection with implementing the code mkhalo for our purposes. The authors gratefully acknowledge the computing time granted by the John von Neumann Institute for Computing (NIC) and provided on the supercomputer JURECA at Jülich Supercomputing Centre (JSC), under application No. 10341 (hhd28). We also used the smaller GPU cluster KEPLER, funded under the grants I/80 041-043 and I/81 396 of the Volkswagen Foundation, and the special GPU accelerated supercomputer LAOHU at the Center of Information and Computing at National Astronomical Observatories, Chinese Academy of Sciences, funded by the Ministry of Finance of the People’s Republic of China under the grant ZDYZ2008-2. B.S. gratefully acknowledges Rainer Spurzem for providing computing time on the high-performance computing clusters JURECA and LAOHU.
B.S. acknowledges the support within program N0073-10/PCF-15-MON by the Ministry of Education and Science of the Republic of Kazakhstan.
P.B. acknowledges the support by the Chinese Academy of Sciences through the Silk Road Project at NAOC, through the “Qianren” special foreign experts program, and the President’s International Fellowship for Visiting Scientists program of CAS and also the Strategic Priority Research Program (Pilot B) “Multi-wavelength gravitational wave universe” of the Chinese Academy of Sciences (No. XDB23040100).
P.B. acknowledges the support of the Volkswagen Foundation under the Trilateral Partnerships grant No. 90411 and the special support by the NASU under the Main Astronomical Observatory GRID/GPU computing cluster project.
References
- Adams, F. C. 2000, ApJ, 542, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., & Kroupa, P. 2013, ApJ, 764, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] [Google Scholar]
- Berczik, P., Nitadori, K., Zhong, S., et al. 2011, in International conference on High Performance Computing, Kyiv, Ukraine, October 8–10, 8 [Google Scholar]
- Boily, C. M., & Kroupa, P. 2003a, MNRAS, 338, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Boily, C. M., & Kroupa, P. 2003b, MNRAS, 338, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., Smith, R. J., Clark, P. C., & Bate, M. R. 2011, MNRAS, 410, 2339 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkmann, N., Banerjee, S., Motwani, B., & Kroupa, P. 2017, A&A, 600, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S., Gutkin, J., Brandner, W., & Basu, S. 2013, MNRAS, 436, 3727 [NASA ADS] [CrossRef] [Google Scholar]
- Duboshin, G. N. 1968, Nebesnaia mekhanika, Osnovnuye zadachi i metody (Moscow: Nauka) [Google Scholar]
- Ernst, A., Berczik, P., Just, A., & Noel, T. 2015, Astron. Nachr., 336, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, II, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Farias, J. P., Smith, R., Fellhauer, M., et al. 2015, MNRAS, 450, 2451 [NASA ADS] [CrossRef] [Google Scholar]
- Fellhauer, M., & Kroupa, P. 2005, ApJ, 630, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., & Portegies Zwart, S. 2016, ApJ, 817, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Geyer, M. P., & Burkert, A. 2001, MNRAS, 323, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Federrath, C., Allison, R., Banerjee, R., & Klessen, R. S. 2012, MNRAS, 420, 3264 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P. 2009, Ap&SS, 324, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S. P., & Bastian, N. 2006, MNRAS, 373, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Higuchi, A. E., Kurono, Y., Saito, M., & Kawabe, R. 2009, ApJ, 705, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., & Carpenter, J. M. 2000, ApJ, 540, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1980, ApJ, 235, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Narayanan, D., Murray, N., & Quataert, E. 2013, MNRAS, 433, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Just, A., Berczik, P., Petrov, M. I., & Ernst, A. 2009, MNRAS, 392, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Federrath, C., & Henning, T. 2014, Science, 344, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Matzner, C. D. 2009, ApJ, 703, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Tan, J. C. 2007, ApJ, 654, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Kudryavtseva, N., Brandner, W., Gennaro, M., et al. 2012, ApJ, 750, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Margulis, M., & Dearborn, D. 1984, ApJ, 285, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, E. A., Depoy, D. L., Evans, II, N. J., & Gatley, I. 1991, ApJ, 371, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, P. L., & Goodwin, S. P. 2016, MNRAS, 460, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- Leisawitz, D., Bash, F. N., & Thaddeus, P. 1989, ApJS, 70, 731 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J., & Dehnen, W. 2007, MNRAS, 378, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
- Moeckel, N., Holland, C., Clarke, C. J., & Bonnell, I. A. 2012, MNRAS, 425, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N. 2011, ApJ, 729, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., Quataert, E., & Thompson, T. A. 2010, ApJ, 709, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, G., & Baumgardt, H. 2012, MNRAS, 427, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, G., & Gilmore, G. 2007, MNRAS, 377, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Parmentier, G., & Pfalzner, S. 2013, A&A, 549, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S., Parmentier, G., Steinhausen, M., Vincke, K., & Menten, K. 2014, ApJ, 794, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Proszkow, E.-M., & Adams, F. C. 2009, ApJS, 185, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Reggiani, M., Robberto, M., Da Rio, N., et al. 2011, A&A, 534, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R., Fellhauer, M., Goodwin, S., & Assmann, P. 2011, MNRAS, 414, 3036 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R., Goodwin, S., Fellhauer, M., & Assmann, P. 2013, MNRAS, 428, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V. 1978, A&A, 70, 57 [NASA ADS] [Google Scholar]
- Verschueren, W., & David, M. 1989, A&A, 219, 105 [NASA ADS] [Google Scholar]
Appendix A: Expression of the density profile of unprocessed gas
Equation (10) can be easily solved using software such as mathematica. Since the roots of this equation obtained with mathematica are very long, we made them more compact by introducing the following intermediate terms: ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\alpha = k^{4}\rho_\star^2;\\[4mm] &&K_0=\sqrt[3]{\alpha^3+36 \alpha^2+216 \alpha +24 \alpha \sqrt{3 \left(\alpha+27\right)}} ; \\[4mm] &&K_1=\sqrt{\frac{\alpha^2+\alpha(K_0+24)+K_0 (K_0+12)}{12 k^4 K_0}}; \\[4mm] &&K_2=\frac{\left(\alpha-K_0+24\right) \left(K_0-\alpha\right)}{3 k^4 K_0}\cdot \end{eqnarray}](/articles/aa/full_html/2017/09/aa30607-17/aa30607-17-eq159.png) Then we can write the four roots of Eq. (10) as
Then we can write the four roots of Eq. (10) as 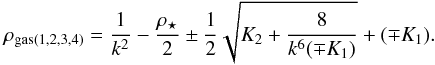 (A.5)The following relation is true for all real values of k and ρ⋆
(A.5)The following relation is true for all real values of k and ρ⋆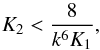 (A.6)which gives complex numbers for two of the roots in case of (− K1). The other two roots are real, with one decreasing and the other increasing with ρ⋆.
(A.6)which gives complex numbers for two of the roots in case of (− K1). The other two roots are real, with one decreasing and the other increasing with ρ⋆.
In our case, we expect the residual gas density profile to be a decreasing function of the radius, as the stellar density profile. Thus we choose the root that increases together with stellar density toward the clump center with the following expression: 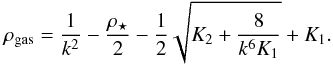 (A.7)
(A.7)
Appendix B: Bound fraction of isolated models
For isolated models we first defined the bound fraction based on the total (i.e., kinetic + potential) energy of stars, that is, as the fraction of stars with a negative total energy (solid lines in Fig. B.1).
 |
Fig. B.1 Time evolution of the bound fraction Fb of isolated models (N = 104) as defined by two methods: defined by the fraction of stars with a negative total energy (solid lines), and defined by recalculating the total energy of stars in an iterative process (see text for details; dashed lines). The vertical dotted line corresponds to t = 20 Myr when we scale the isolated models with the same scale factor as for a non-isolated model with M⋆ = 6000 M⊙, which also has N ≈ 104. |
 |
Fig. B.2 Top panel: bound and final bound fraction evolution of an isolated cluster with SFEgl = 0.15 (solid and dashed lines, respectively). Bottom panel: Lagrange radius evolution of the same model. Lagrange radii are given in units of the initial stellar half-mass radius. |
Since our model clusters become super-virial after instantaneous gas expulsion, the unbound stars can be located anywhere inside the cluster and make a significant contribution to its gravitational potential depending on global SFE. Thus the bound fraction remains overestimated until bound and unbound stars are clearly spatially separated from each other. For instance, model clusters with global SFEs of 0.05 and 0.10 do not survive the instantaneous gas expulsion. In Fig. B.1, however, they retain a significant bound fraction for several Myr. For clusters with global SFEs of 0.13 and 0.15, we need to wait for a long time to reach the final bound fraction, that is, for the unbound stars to have evacuated the cluster region and to no longer contribute to the cluster gravitational potential.
These reasons motivated us to develop another technique to define the final bound fraction early on in the evolution of clusters. To do so, we recalculated the total energy of each star after removing the unbound stars. Some of these recalculated energies are now positive (i.e., some previously bound stars are now unbound) since the cluster gravitational potential is now shallower. We removed this new sample of unbound stars, and continued to iterate until only bound stars were left within our selection. The fraction of stars left in this selection determines the final bound fraction.
Figure B.2 presents an example of the evolution of the bound fraction and Lagrange radii of an isolated cluster with a global SFE of 15 percent. As we see when comparing the top and bottom panels, the bound fraction decreases during the cluster expansion and reaches its final value when its bound stars have collapsed back and form a bound cluster. With the new technique, however, we can predict the final bound fraction already after 2 Myr, when the cluster is still in the expansion phase. Figure B.1 and the top panel of Fig. B.2 show that the instantaneous bound fraction converges toward the final bound fraction determined with our technique by the end of the simulations. This shows that with our calculation method we can estimate the final bound fraction even before the inner part of the cluster starts to collapse back and return to virial equilibrium. We caution, however, that with this method we underestimate the final bound fraction of a cluster with a low global SFE during their early evolution after instantaneous gas expulsion. This is caused by removing all unbound stars, including the centrally concentrated ones, which contribute the most to the gravitational field of the cluster (see Fig. B.2). This is the reason for the unusual behavior of the final bound fractions of isolated clusters with a global SFE of 0.13 and 0.15, which is 0 at t ≲ 1 Myr, and why they rise at an early time in the evolution instead of decreasing.
All Tables
Scaling factors to the physical time and duration of 20 Myr in N-body units corresponding to different ratios of the cluster half-mass to tidal radius.
All Figures
 |
Fig. 1 Relation between the SF duration (tSF) (given in N-body units according to Eq. (12)) and the global SFE (SFEgl), measured inside Rcl = 10a⋆. The lowest value of the global SFE here in this plot is SFEgl = 0.007, which corresponds to an SF duration tSF = 0.01 [NB]. |
| In the text | |
 |
Fig. 2 Density profiles of the star cluster (black dashed line), of the residual (solid lines), and initial (dash-dotted lines) gas for different SFEgl in scaled physical units. A total stellar mass M⋆ = 3000 M⊙ and a 3D half-mass radius rh = 1 pc are assumed. Note that the stellar density profile is a Plummer profile. |
| In the text | |
 |
Fig. 3 Evolution of the bound fraction of clusters obtained in our simulations. Different colors correspond to different global SFEs (see the key). The gray lines show the impact of mass loss caused by stellar evolution alone. The vertical dotted line corresponds to t = 20 Myr.Top panel: comparison of the bound fraction evolution of isolated (dashed lines) and non-isolated (solid lines) models for M⋆ = 6000 M⊙ with N ≈ 104 stars. Note that the isolated models are the single-mass models without stellar evolution and scaled to the same physical units as the non-isolated models (i.e., M⋆ = 6000 M⊙ and rh = 1.26 pc). Bottom panel: bound fraction (instantaneous tidal mass as a fraction of initial stellar mass) evolution for non-isolated models with different initial stellar masses (see the key for the line-coding). |
| In the text | |
 |
Fig. 4 Different random realizations (see line types in the key) of the model clusters with M⋆ = 6000 M⊙ (N = 10 455 stars) for rh/rt = 0.052. |
| In the text | |
 |
Fig. 5 Evolution of a non-isolated cluster of the solar neighborhood with SFEgl = 0.20, M⋆ = 6000 M⊙ and rh/rt = 0.052 over 50 Myr after gas expulsion. We show 49 Lagrange radii, ranging from 2 percent to 98 percent in intervals of 2 percent (solid and dashed lines). The instantaneous tidal radius rt of the cluster is shown as the dotted line. Thick solid lines correspond to every 10 percent of the Lagrange radius, and the dashed line corresponds to 50 percent of the Lagrange radius. |
| In the text | |
 |
Fig. 6 Evolution of the bound fraction of M⋆ = 15 000 M⊙ clusters with different impact of the tidal field (see the key for the line-coding). Different colors correspond to different global SFEs (see the key for the color-coding). |
| In the text | |
 |
Fig. 7 Evolution of the cluster with M⋆ = 6000 M⊙, SFEgl = 0.20 and rh/rt = 0.025 over the first 50 Myr after the instantaneous gas expulsion. |
| In the text | |
 |
Fig. 8 Bound fraction as a function of global or effective SFE. We compare our results (red lines) with previous works. The isolated models are depicted by the red diamonds, and non-isolated models by red crosses. In the top panel we use our global SFE (SFEgl) and in the bottom panel, the effective SFE, eSFE = 1 /Q⋆ (which is almost the same as the LSF, the local stellar fraction of our models). |
| In the text | |
 |
Fig. B.1 Time evolution of the bound fraction Fb of isolated models (N = 104) as defined by two methods: defined by the fraction of stars with a negative total energy (solid lines), and defined by recalculating the total energy of stars in an iterative process (see text for details; dashed lines). The vertical dotted line corresponds to t = 20 Myr when we scale the isolated models with the same scale factor as for a non-isolated model with M⋆ = 6000 M⊙, which also has N ≈ 104. |
| In the text | |
 |
Fig. B.2 Top panel: bound and final bound fraction evolution of an isolated cluster with SFEgl = 0.15 (solid and dashed lines, respectively). Bottom panel: Lagrange radius evolution of the same model. Lagrange radii are given in units of the initial stellar half-mass radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


