| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 12 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201630338 | |
| Published online | 06 September 2017 | |
Optical monitoring of BL Lac object S5 0716+714 and FSRQ 3C 273 from 2000 to 2014⋆
1 Center for Astrophysics, Guangzhou University, Guangzhou, 510006, Guangdong, PR China
e-mail: yh_yuan@gzhu.edu.cn
2 Astronomy Science and Technology Research Laboratory of Department of Education of Guangdong Province, 510006 Guangzhou, PR China
3 Shanghai Astronomical Observatory, CAS, 80 Nandan Road, 200030 Shanghai, PR China
4 Joint Institute for Galaxies and Cosmology, ShAO and USTC, CAS, Shanghai, PR China
Received: 23 December 2016
Accepted: 15 May 2017
Context. Using the 1.56 m telescope at the Shanghai Observatory (ShAO), China, we monitored two sources, BL Lac object S5 0716+714 and flat spectrum radio quasar (FSRQ) 3C 273. For S5 0716+714, we report 4969 sets of CCD (Charge-coupled Device) photometrical optical observations (1369 for V band, 1861 for R band and 1739 for I band) in the monitoring time from Dec. 4, 2000 to Apr. 5, 2014. For 3C 273, we report 460 observations (138 for V band, 146 for R band and 176 for I band) in the monitoring time from Mar. 28, 2006 to Apr. 9, 2014.
Aims. The observations provide us with a large amount of data to analyze the short-term and long-term optical variabilities. Based on the variable timescales, we can estimate the central black hole mass and the Doppler factor. An abundance of multi-band observations can help us to analyze the relations between the brightness and spectrum.
Methods. We use Gaussian fitting to analyze the intra-day light curves and obtain the intra-day variability (IDV) timescales. We use the discrete correlation function (DCF) method and Jurkevich method to analyze the quasi-periodic variability. Based on the VRI observations, we use the linear fitting to analyze the relations between brightness and spectrum.
Results. The two sources both show IDV properties for S5 0716+714. The timescales are in the range from 17.3 min to 4.82 h; for 3C 273, the timescale is ΔT = 35.6 min. Based on the periodic analysis methods, we find the periods PV = 24.24 ± 1.09 days, PR = 24.12 ± 0.76 days, PI = 24.82 ± 0.73 days for S5 0716+714, and P = 12.99 ± 0.72, 21.76 ± 1.45 yr for 3C 273. The two sources displayed the “bluer-when-brighter” spectral evolution properties.
Conclusions. S5 0716+714 and 3C 273 are frequently studied objects. The violent optical variability and IDV may come from the jet. Gaussian fitting can be used to analyze IDVs. The relations between brightness (flux density) and spectrum are strongly influenced by the frequency.
Key words: BL Lacertae objects: individual: S5 0716+714
A table of the individual photometry measurements is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/605/A43
© ESO, 2017
1. Introduction
Blazars show some extreme properties, such as violently optical variability, core dominance, superluminal motion, and so on (Urry & Padovani 1995; Ulrich et al. 1997). The optical variations of blazars last from minutes to years, and can be divided into two types: short-term and long-term variations. Being a special short-term variation, intra-day variabilities (IDV) show timescales from minutes to hours, and have been analyzed by many studies (Oke 1967; Miller 1975; Gupta et al. 2008; Fan et al. 2009a,b,c, 2014; Dai et al. 2009; Poon et al. 2009; Yuan et al. 2015a).
Blazars can be divided into two subclasses, BL Lacs and flat spectrum radio quasars (FSRQs), the former being characterized by featureless optical spectra or weak emission lines (Stickel et al. 1991), and the latter showing flat-spectrum radio spectra and typical broad emission lines (Urry & Padovani 1995). Generally, the division between the two subclasses is based on the equivalent width (EW) of the optical broad emission; BL Lacs show EW< 5 Å (Urry & Padovani 1995; Ghisellini et al. 2011; Sbarrato et al. 2012; Ghisellini & Tavecchio 2015).
Time-scale is an important physical quantity, which is often used to probe the physical process of blazars. While the short-term variations, including intra-day variations, are usually non-periodic, the long-term ones are quasi-periodic. In particular the first ones may come from the jets or the accretion disc. There are many theoretical models used to explain these variations, such as the shocks propagating from the relativistic jets (Marscher & Gear 1985; Wagner & Witzel 1995), hotspots or disturbances on or above accretion discs surrounding black holes (Chakrabarti & Wiita 1993; Mangalam & Wiita 1993).
With an estimated redshift z = 0.31 ± 0.08 from the photometric detection of the host galaxy (Nisson et al. 2008), S5 0716+714 is a well known and frequently studied BL Lac object. It shows optical variabilities in the whole electromagnetic band with timescales from minutes to years. Intra-day variabilities (IDVs) have been studied by many authors (Poon et al. 2009; Liu et al. 2012; Gupta et al. 2012; Bhatta et al. 2013; Man et al. 2016; Lee et al. 2016, etc.). Gupta et al. (2009) obtained timescales of 25 min; Rani et al. (2010) obtained timescales of 15 min; Man et al. (2016) obtained timescales of 17.6 min; and Bhatta et al. (2016) displayed the variability based on the peak-to-peak variations of 30% and “bluer-when-brighter” spectral evolution.
For this particular BL Lac object, many works have studied the time delays among different optical bands (Poon et al. 2009; Zhang 2010; Wu et al. 2012; Man et al. 2016). For example, Poon et al. (2009) found that the time delay between B and I band was τBI = 11 min; Zhang (2010) obtained time-delay values of a few minutes at different optical bands; Wu et al. (2012) got a time delay of 30 min between B and V bands and Man et al. (2016) obtained values of 1.308 ± 0.603 min between R and I bands and 1.445 ± 0.511 min between B and I bands.
Discovered in 1963 by Smith & Hoffleit (1963), 3C 273, with a redshift z = 0.158, is one of the widely studied FSRQs and exhibits super-luminal motions (Unwin et al. 1985). Asada et al. (2002) reported that 3C 273 has helical magnetic structure. Dai et al. (2009) presented the long-term B,V,R,I (BVRI) observations and discussed the correlations between color index and brightness. Beaklini & Abraham (2014) used the variability at 7 mm band to find evidence of shocks and precession in the jet. Fan et al. (2014) analyzed the correlation between V-band flux density (FV) and spectral index (α), and found that FV = 28 mJy, suggesting two different correlations. When FV< 28 mJy, FV and α show anti-correlation, when FV> 28 mJy, FV and α show positive correlation. Yuan & Fan (2015c) found an elliptic structure in the distribution of flux density and spectral indices, and that the time-span of the elliptic circle was consistent with the long-term optical periodicity of this source.
On the subject of blazars, there are many papers exploring the relationship between the spectrum and brightness (Edelson et al. 1990; Trevese & Vagnetti 2002; Vagnetti et al. 2003; Dai et al. 2009; Poon et al. 2009; Yuan et al. 2015; Yuan & Fan 2015). Stevens & Gear (1999) analyzed the distributions of αro and αrx (r, o, x, represents radio band, optical band and X-ray band, respectively), and obtained a correlation between the two spectral indices. Trevese et al. (2001) underlined a linear correlation between the variance of spectral index and the logarithmic flux density.
Generally, BL Lacs shows that the spectrum becomes flatter when the sources become brighter, and becomes steeper when the sources become fainter. However, FSRQs show a very complicated structure; some sources show a similar variation tendency to BL Lacs, and some sources show no variation tendency or flatter when the sources become fainter (Brown et al. 1989; Carini & Miller 1992; Fan et al. 1998; Massaro et al. 1998; Nesci et al. 1998; Speziali & Natali 1998; Webb et al. 1998; Fan 1999; Xie et al. 1999, 2002; Villata et al. 2002; Gu et al. 2006; Papadakis et al. 2007; Dai et al. 2009; Poon et al. 2009; Yuan et al. 2015a; Yuan & Fan 2015b). In particular S5 0716+714 shows strong “bluer when brighter” correlations were not only found on timescales of one night but also during longer-term observations (Poon et al. 2009; Chandra et al. 2011; Wu et al. 2012; Man et al. 2016, etc.).
This paper is arranged as follow: Sect. 2, presents our observations and data reductions; Sect. 3, presents our findings in terms of optical variability; Sect. 4, presents a discussion of our results in the context of current literature; and in Sects. 5 we present our conclusions.
2. Observations and data reductions
Observations were carried out using the Sheshan 1.56 m optical telescope at the Shanghai Astronomical Observatory (ShAO), which is equipped with a cooled CCD camera (1024 × 1024 pixels, 1 pixel = 0.019 mm). The telescope view field is about 4′17′′ (1 pixel = 0.̋25) and 13′ (1 pixel = 0.̋25) for a focal reducer. Another new liquid-nitrogen-cooled CCD camera (2048 × 2048 pixels) has been used since August, 2002. The chip subtends to 11′ × 11′ in the sky and the scale is 0.31 arcsec per pixel (1 pixel = 0.024 mm). The filters are standard Johnson B, V and Cousins R, I.
The bias images are taken at the beginning and the end of the night’s observation. The flat-field images are taken at dusk and dawn. The data reduction is carried out by the standard IRAF procedures based on the Linux system. Photometry is obtained after the bias, dark and flat-field correlations.
Given K, the number of comparison stars, for each of them (Si, i = 1, 2,...K), we calculate the ith target magnitude (mi): mi = mi | o + mi | c−mi | oc, here mi | oc is the observed comparison star magnitude, mi | o is the observed target magnitude, mi | c is the standard comparison star magnitude. Considering the whole comparison stars, the target magnitude (m) can be calculated as 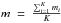 with a standard error
with a standard error 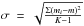 .
.
In this work, for S5 0716+714, the VR comparison stars are from Villata et al. (1998) and the I comparison stars are from Ghisellini et al. (1997), and for 3C 273, the comparison stars are from Smith et al. (1985). All the comparison stars have been listed in Table 1, in which, Col. 1 is signed label of comparison stars, Col. 2 is comparison stars at V band, Col. 3 is comparison stars at R band, and Col. 4 is comparison stars at I band.
Comparison stars of S5 0716+714 and 3C 273.
3. Optical variability
 |
Fig. 1 VRI light curves of S5 0716+714 (the upper sub-picture) and 3C 273 (the lower sub-picture). The black dots signify I band, the red dots signify R band and the green dots signify V band. |
For S5 0716+714 and 3C 273, the V, R, I (VRI) light curves are shown in Fig. 1, in which the upper panel displays S5 0716+714 and the lower panel 3C 273. For S5 0716+714, there are 4969 observations. At V band, there are 1369 observations, which cover 12.44 ± 0.02 mag to 15.11 ± 0.01 mag, with the averaged value 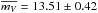 mag. At R band, there are 1861 observations, which cover 11.67 ± 0.04 mag to 14.59 ± 0.08 mag, with the averaged value
mag. At R band, there are 1861 observations, which cover 11.67 ± 0.04 mag to 14.59 ± 0.08 mag, with the averaged value 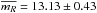 mag. At I band, there are 1739 observations, which cover 11.31 ± 0.03 mag to 14.09 ± 0.02 mag, with the averaged value
mag. At I band, there are 1739 observations, which cover 11.31 ± 0.03 mag to 14.09 ± 0.02 mag, with the averaged value 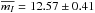 mag.
mag.
For 3C 273, there are 460 observations. At V band, there are 138 observations, which cover 12.40 ± 0.07 mag to 13.38 ± 0.07 mag, with the averaged value 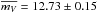 mag. At R band, there are 146 observations, which cover 12.31 ± 0.09 mag to 12.88 ± 0.12 mag, with the averaged value
mag. At R band, there are 146 observations, which cover 12.31 ± 0.09 mag to 12.88 ± 0.12 mag, with the averaged value 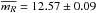 mag. At I band, there are 176 observations, which cover 11.78 ± 0.06 mag to 12.40 ± 0.08 mag, with the averaged value
mag. At I band, there are 176 observations, which cover 11.78 ± 0.06 mag to 12.40 ± 0.08 mag, with the averaged value 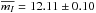 mag.
mag.
3.1. Intra-day optical variabilities
In the intra-day light curves, if the optical variability Δm> 3σ, we use the Gaussian function to analyze the intra-day light curves, which can be explained by the following,
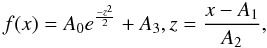 where A0, A1, A2, A3 are the fitting parameter between x and f(x). In order to explain the four parameters, we take an example when A0 = 0.2, A1 = 0.3, A2 = 0.025, and A3 = 13.5. Figure 2 represents the change trend of f(x) with x (A0, A1, A2, A3 are known). If the change trend of f(x) with x can be fitted by a full Gaussian function, we identify this fitting profile as “w”; otherwise we identify it as “p”. If the intra-day light curves can be fitted by a full Gaussian function, the variable timescales ΔT can be calculated as: ΔT = 4 × A2. Otherwise we take the actual span (Δt) of optical variability as the variable timescales ΔT: ΔT = Δt.
where A0, A1, A2, A3 are the fitting parameter between x and f(x). In order to explain the four parameters, we take an example when A0 = 0.2, A1 = 0.3, A2 = 0.025, and A3 = 13.5. Figure 2 represents the change trend of f(x) with x (A0, A1, A2, A3 are known). If the change trend of f(x) with x can be fitted by a full Gaussian function, we identify this fitting profile as “w”; otherwise we identify it as “p”. If the intra-day light curves can be fitted by a full Gaussian function, the variable timescales ΔT can be calculated as: ΔT = 4 × A2. Otherwise we take the actual span (Δt) of optical variability as the variable timescales ΔT: ΔT = Δt.
 |
Fig. 2 Change trend of f(x) with x. A0, A1, A2 and A3 have been noted. |
For S5 0716+714, the IDV analyzed results are plotted in Fig. 3 (I band), Fig. 4 (R band), and Fig. 5 (V band), in which, the red, blue, and green lines stand for the Gaussian fitting. Table 2 lists the main results, in which Col. 1 is JD (+2 450 000); Col. 2 is band; Col. 3 is A0; Col. 4 is A1; Col. 5 is A2; Col. 6 is A3; Col. 7 is intra-day optical variability (in units of mag); Col. 8 is error, corresponding to Col. 7 (in units of mag); Col. 9 is Gaussian function profile, “w”: full Gaussian function, “p”: part Gaussian function; and Col. 10 is the IDV timescales.
Our results show that the IDV timescales are in the range 0.48 to 4.82 h at I band, in the range 0.29 to 2.56 h at R band, and in the range 0.38 to 2.56 h at V band. The minimum timescales with the optical variability are ΔTI = 0.48 h with Δm = 0.73 ± 0.04 mag on JD 2 453 388 at I band; ΔTR = 0.29 h with Δm = 0.46 ± 0.11 mag on JD 2 453 774 at R band; and ΔTV = 0.38 h with Δm = 0.35 ± 0.10 mag on JD 2 453 779 at V band.
 |
Fig. 3 For S5 0716+714, at I band, the results of intra-day light curves based on the Gaussian function. The red, green, and blue lines represent the Gaussian fitting curve. |
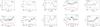 |
Fig. 4 For S5 0716+714, at R band, results of intra-day light curves based on the Gaussian function. The red, green, and blue lines represent the Gaussian fitting curve. |
 |
Fig. 5 For S5 0716+714, at V band, results of intra-day light curves based on the Gaussian function. The red, green, and blue lines represent the Gaussian fitting curve. |
Result of IDV light curves analyzed by the Gaussian function of S5 0716+714.
For 3C 273, on Dec. 20, 2013 (JD 2 456 647), within 34.6 min, the optical variability is ΔmI = 0.36 ± 0.09 mag, which is an obvious IDV; we refer to Fig. 6, in which, the upper parts stand for the intra-day light curves and the lower parts stand for the magnitude difference between comparison stars “C” and “D”.
3.2. Quasi-periodic optical variability
It’s very important to choose suitable methods to analyze the long-term optical variability. Considering the uneven light curve, we use the discrete correlation function (DCF) method and the Jurkevich method to deal with this question, and choose the common part as the quasi-periodicity.
The DCF method (Edelson & Krolik 1988; Hufnagel & Bregman 1992) can explore the correlation from two variable temporal sets with a given time lag. If we only input one set, we can calculate the period of the set. In order to achieve this outcome, firstly we calculate the unbinned correlation (UDCF) of the two data streams a and b, that is, 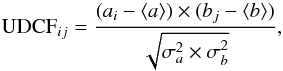 (1)where ai, bj are two data streams, ⟨ a ⟩ and ⟨ b ⟩ are the average values of the data sets, σa and σb are the corresponding standard deviations. Secondly, we average the points through sharing the same time lag by binning the UDCFij in suitably sized time-bins in order to get the DCF for each time lag τ,
(1)where ai, bj are two data streams, ⟨ a ⟩ and ⟨ b ⟩ are the average values of the data sets, σa and σb are the corresponding standard deviations. Secondly, we average the points through sharing the same time lag by binning the UDCFij in suitably sized time-bins in order to get the DCF for each time lag τ, 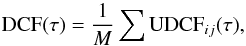 (2)where M is the total number of pairs. The standard error of each bin is
(2)where M is the total number of pairs. The standard error of each bin is ![\begin{equation} \sigma(\tau)=\frac{1}{M} \left(\sum[{\rm UDCF}_{ij}-{\rm DCF}(\tau)]^{2}\right)^{0.5}\!. \end{equation}](/articles/aa/full_html/2017/09/aa30338-16/aa30338-16-eq121.png) (3)The Jurkevich method (Jurkevich et al. 1971) is based on the expected mean square deviation. It tests a run of trial periods around which the data are folded. All data are assigned to m groups according to their phases around each bin, and the whole
(3)The Jurkevich method (Jurkevich et al. 1971) is based on the expected mean square deviation. It tests a run of trial periods around which the data are folded. All data are assigned to m groups according to their phases around each bin, and the whole 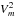 for each bin is computed;
for each bin is computed; 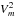 is the mean square deviation calculated by the square deviation of m groups. If the trial period is equal to the true one, then
is the mean square deviation calculated by the square deviation of m groups. If the trial period is equal to the true one, then 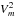 reaches its minimum. A “good” period will give a much reduced variance relative to those given by “false” trial periods and with almost constant values. The error can be determined by the half width at half-maximum (HWHM) of the minimum in the
reaches its minimum. A “good” period will give a much reduced variance relative to those given by “false” trial periods and with almost constant values. The error can be determined by the half width at half-maximum (HWHM) of the minimum in the 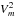 , and m = 5 is used in the following calculation.
, and m = 5 is used in the following calculation.
 |
Fig. 6 For 3C 273 at I band; results of intra-day light curves based on the Gaussian function. The red lines represent the Gaussian fitting curve. |
For S5 0716+714, we use the DCF method to analyze the results, which are PD | I = 24.82 ± 0.73 days, PD | R = 24.12 ± 0.76 days, PD | V = 24.24 ± 1.09 days (Fig. 7 the upper three sub-pictures). The results based on the Jurkevich method are PJ | I = 27.28 ± 2.68 days, PJ | R = 27.28 ± 2.33 days, PJ | V = 26.62 ± 2.01 day (Fig. 7 the lower three sub-pictures). Considering the common parts, we can obtain the quasi-periods, PV = 24.24 ± 1.09 days (V band), PR = 24.12 ± 0.76 days (R band), and PI = 24.82 ± 0.73 days (I band).
 |
Fig. 7 Using the Jurkevich and DCF methods to analyze the periodicities of VRI light curves. The left three panels show the DCF results and the right three panels show the Jurkevich results. |
Figure 8 shows our results from the use of the DCF and Jurkevich methods to analyze the long-term variability for 3C 273. We cannot, however, obtain the periodic properties from these results. In order to analyze the long-term variability more comprehensively, we collected the available data from the literature (Angione & Smith 1985; Fan et al. 2009, 2014; Dai et al. 2009), supplemented our observations and then built the light curves, which are shown in Fig. 9. Based on the DCF method, the results are as follows: PD | 1 = 13.20 ± 1.63 yr and PD | 2 = 22.69 ± 2.28 yr. Based on the Jurkevich method, the results are PJ | 1 = 0.99 ± 0.13 yr, PJ | 2 = 2.05 ± 0.23 yr, PJ | 3 = 12.99 ± 0.72 yr, and PJ | 4 = 21.76 ± 1.45 yr. The calculated results are shown in Fig. 10. Considering the common parts, we can obtain the quasi-periods, P1 = 12.99 ± 0.72 yr and P2 = 21.76 ± 1.45 yr.
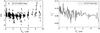 |
Fig. 8 Calculation of the long-term periodicity of 3C 273 based on our data. The upper panel shows the DCF result and the lower panel shows the Jurkevich result. |
 |
Fig. 9 Light curves of 3C 273. The black dots represent the literature data, and the red dots represent our observations. |
 |
Fig. 10 Periodic results of 3C 273. The first panel shows the DCF result with the red line being Gaussian fitting. The second panel shows the Jurkevich result. |
 |
Fig. 11 Correlations between α and FIRV. The upper three panels show results for S5 0716+714, and the lower three panels shoiw results for 3C 273. The red line represents the linear correlation between α and FIRV. |
3.3. Optical spectral indices
In order to obtain the optical spectral index (α), firstly, we make the Galactic extinction correction; then, we convert the magnitude (mν) into flux density (Fν); and lastly, we use the relation Fν ∝ ν− α to calculate the spectral index (α). Here ν is frequency.
-
1.
We made the Galactic Extinction correction from NED(http://ned.ipac.caltech.edu/). For S5 0716+714, we use AV = 0.085 mag, AR = 0.067 mag, and AI = 0.047 mag; and for 3C 273, we use AV = 0.057 mag, AR = 0.045 mag, and AI = 0.031 mag.
-
2.
To obtain the spectral index, we convert the magnitude (mν) into flux density (Fν), here ν is frequency (ν = VRI, V: 6.17 × 1014 Hz, R: 4.78 × 1014 Hz, I:3.89 × 1014 Hz).
-
3.
VRI bands cannot expose at the same time; they in fact expose in turn. Considering the total exposure time of ~1 min for S5 0714+714, and ~2 min for 3C 273, we respectively choose 2 min for S5 0714+714 and 4 min for 3C 273 as the maximum time span among three bands, and adopt the relation Fν ∝ ν− α to calculate the spectral index (α).
Converting the upper relation into the more convenient linear fitting form log (Fν) = −αlog (ν) + const., we input the VRI observations and calculate from this formula the α parameter. After calculation, there are 1095 spectral indices(α) in the range 0.16 ± 0.09 to 2.99 ± 0.09, with the averaged value 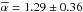 for S5 0716+714. There are 85 spectral indices in the range 0.17 ± 0.09 to 1.82 ± 0.04, with the averaged value
for S5 0716+714. There are 85 spectral indices in the range 0.17 ± 0.09 to 1.82 ± 0.04, with the averaged value 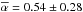 for 3C 273.
for 3C 273.
We use the linear fitting to analyze the relation between α and Fν (ν = V, R, I): Fν = k × α + b. In this process, p is the chance probability of linear fitting, and r is the Pearson’s correlation coefficient, which is expressed as (Press et al. 1994; Pavlidou et al. 2012; Fan et al. 2013):
where, xi is FV,R,I, yi is α, 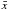 is the averaged value of α, and
is the averaged value of α, and 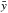 is the averaged value of Fν (ν = V, R, I).
is the averaged value of Fν (ν = V, R, I).
For S5 0716+714, the correlations between Fν (ν = V, R, I) and α are shown in Fig. 11. At I band, rI = 0.01 and p = 83.8%; this result shows that there is no correlation. At R band, α = (−1.70 ± 0.001) × 10-2FR + (1.62 ± 0.006), with rR = −0.26, p = 4.51 × 10-6; this result shows a strong anti-correlation. At V band, α = (−3.51 ± 0.001) × 10-2FV + (1.88 ± 0.005), with rV = −0.48, and p = 2.56 × 10-18; this result also shows a strong anti-correlation. With the frequency increasing (I → V), the correlation shows the following variation: no correlation → strong anti-correlation.
For 3C 273, the relations between Fν and α are shown in Fig. 11 (the upper three panels.) At I band, α = (3.22 ± 0.008) × 10-2FI−(0.65 ± 0.11), with rI = 0.37, p = 5.18 × 10-4; this result shows a positive correlation. At R band, rR = −0.004 and p = 96.9%; this result shows no correlation. At V band, α = −(5.64 ± 0.004) × 10-2FV + (2.24 ± 0.04), with rV = −0.68, p = 4.94 × 10-13; this result shows a strong anti-correlation. With the frequency increasing (I → R → V), the correlations show the following variations: a positive correlation → no correlation → a strong anti-correlation.
4. Discussion
4.1. IDV optical variability
From the intra-day light curves of S5 0716+714 and 3C 273, we can see that on individual days, the differences between the comparison stars are far from being random (Fig. 3–6 (red dots)). The reason for this could be the strong atmosphere agitation during those days.
The IDV timescales of S5 0716+714 are in the range 17.3 min to 4.82 h. We refer to Table 2, which can be divided into four parts, T1, T2, T3 and T4, as well as Fig. 12. We use the Gaussian function to fit T1, T2, and T3 and to obtain the averaged values 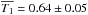 h,
h, 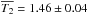 h, and
h, and 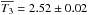 h. T4 has only one value, T4 = 4.82 h.
h. T4 has only one value, T4 = 4.82 h.
A large telescope on board the Fermi (Fermi-LAT) supplies us with abundant γ-ray data of blazars, among which there are many sources that show lares with variability timescales of about 104 s (Abdo et al. 2009, 2010a,b; Ackermann et al. 2010; Tavecchio et al. 2010; Foschini et al. 2011). Our timescales are in the range of 0.64 ~ 4.82 h (2.3 × 103 ~ 1.7 × 105 s). These are consistent with the γ-ray flare timescales, which suggests that the optical IDVs and γ-ray flares might come from the same place in the jet of S5 0716+714.
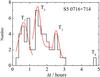 |
Fig. 12 ΔT distributions of S5 0716+714, which can be divided into three parts, fitted by Gaussian function (red lines). |
4.2. The central-black-hole mass
In blazars, the central black holes play a very important role in the observational properties and attract great attention. The black hole mass might shed some light on the evolution of active galactic nuclei (AGNs; Fan 2005) and there are many methods to calculate this parameter, such as velocity dispersion (Wu et al. 2002; Woo & Urry 2002; Woo et al. 2005; Sbarrato et al. 2012), reverberation mapping (Woo & Urry 2002), optical luminosity (Kawakatu et al. 2007; Zhou & Cao 2009), and so on.
The origin of short timescales are probably produced in the innermost part of the blazar and the region near the black hole, such as the accretion disc, the broad line region, etc. In this sense, the short-term timescale can be used to estimate the mass (Abramowicz & Nobili 1982; Miller et al. 1989). For S5 0716+714, we use the Gaussian function to analyze the intra-day light curves, and obtain a minimum timescale of ΔT = 17.3 min. For 3C 273, the IDV timescale obtained is ΔT = 35.6 min.
If in the center of the thin accretion disks lies a Schwarzschild black hole, the radius is 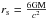 . But if there lies a Kerr black hole, the radius is
. But if there lies a Kerr black hole, the radius is 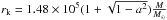 , where a is the angular momentum parameter (Witta 1985). Consider the period
, where a is the angular momentum parameter (Witta 1985). Consider the period 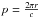 , that is,
, that is, 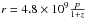 , p in units of second. For a Schwarzschild black hole, the mass can be
, p in units of second. For a Schwarzschild black hole, the mass can be 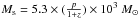 (M⊙: the Solar mass). For a Kerr black hole (a = 1), the mass can be
(M⊙: the Solar mass). For a Kerr black hole (a = 1), the mass can be 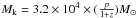 . We use the short-term timescale Δt to indicate the period “p”.
. We use the short-term timescale Δt to indicate the period “p”.
For S5 0716+714, the redshift z = 0.31 ± 0.08 (Nisson et al. 2008) and ΔT = 17.3 min. Furthermore, we obtained the central black hole: Ms = 4.2 × 106M⊙ for a Schwarzschild black hole and Mk = 2.56 × 107M⊙ for a Kerr black hole. Gupta et al. (2009) used IDV timescale to obtain the mass 2.5 × 106M⊙, which is very consistent with our results. Liang & Liu (2003) used the optical luminosity to obtain M = 1.25 × 108M⊙, which is heavier than our results. The reason for this might be that our value gives the lower limit.
For 3C 273, z = 0.158, and therefore the black hole mass is 9.5 × 106M⊙ for a Schwarzschild black hole and 5.74 × 107M⊙ for a Kerr black hole. Espaillat et al. (2008) obtained a black hole mass of about 8.1 × 107M⊙, which is consistent with our result. Paltani & Turler (2005) applied the reverberation method to find a maximum-likelihood mass of about 6.59 × 109M⊙, which is heavier than ours and Espaillat et al. (2008)’s results.
 |
Fig. 13 Spectral variation of 3C 273 and S5 0716+714. The denser distributions are indicated by the rectangle regions. |
Linear correlations between α and FIRV of S5 0716+714 and 3C 273.
 |
Fig. 14 For S5 0716+714, the relations between α and FVRI at the five denser regions. The black dots and the red dots represent the different parts of the same regions. The green lines stand for the linear fitting between α and FVRI. |
 |
Fig. 15 For 3C 273, the relations between α and FVRI at the three denser regions. The black dots and the red dots stand for the different parts of the same regions. The green lines show the linear fitting between α and FVRI. |
4.3. Doppler factor
The Doppler factors of S5 0716+714 and 3C 273 have been studied by many authors (Ghisellini et al. 1993; Hartman et al. 1999; Fan et al. 2009a, 2014; Hovatta et al. 2009; Savolainen et al. 2010).
Based on the relativistic beaming model, the optical depth can be calculated from the pair-production. Based on the work of Mattox et al. (1993), Fan et al. (2013) deduced the lower limit of the Doppler factor (δ),
where FkeV is X-ray flux at 1 keV (in unit of μJy), αX is X-ray spectral index, dL is luminosity distance (in unit of Mpc), ΔT is timescale (in unit of hour), and Eγ is averaged γ-ray photon energy (in unit of GeV).
For S5 0716+714, dL = 1499 Mpc (NED, http://ned.ipac.caltech.edu/), FkeV = 0.99 μJy, αX = 1.77 (Donato et al. 2001), and Eγ = 4.59 GeV (Fan et al. 2014b). Our minimum ΔT is 0.64 hours, so we can obtain δ ≥ 5.89. There are many works dealing with the Doppler factor of S5 0716+714, for example, Ghisellini et al. (1993): δ = 2.1, Hovatta et al. (2009): δ = 10.9, Fan et al. (2009d): δ = 8.76 and Savolainen et al. (2010): δ = 10.8. Our results are consistent with those by Fan et al. (2009d), Hovatta et al. (2009), and Savolainen et al. (2010).
For 3C 273, dL = 734 Mpc (NED), FkeV = 10.921 μ Jy, αX = 2.11 (Brinkmann et al. 1997), Eγ = 2.82 GeV (Fan et al. 2014b), and ΔT = 34.6 / 60 h, so we can obtain δ ≥ 6.64. Hartman et al. (1999) obtained δ = 6. Fan et al. (2009c) used the radio optical timescales and obtain δ = 6.05. Zhang et al. (2013) obtained δ = 7.4 ± 0.9; Hovatta et al. (2009) obtained δ = 17; and Savolainen et al. (2010) obtained δ = 16.8. Our results are consistent with those works.
4.4. Relations between brightness and spectrum
4.4.1. S5 0716+714
For S5 0716+714, at different bands, α and FVRI show different relations. At V and R band, there exists strong anti-correlation; at I band, there exists no-correlation. We check the spectral variation, and find that there are five denser regions, which have been noted by the rectangular boxes 1, 2, 3, 4 and 5 (Fig. 13 the left panel).
For the five regions, we analyzed their correlations (Fig. 14). The analyzed results have been listed in Table 3 (Col. 5 displays the intercept, b, Col. 6 the correlation coefficient, and Col. 7: the chance probability. At I band, on most of the regions, α and FI show no correlation or weak anti-correlation (except for region-3), and α and FI show anti-correlation. At R band, on Regions 1 and 5 there is anti-correlation, and on Regions 2, 3, and 4, α and FR show strong anti-correlation. At V band, on the whole five Regions, α and FV show strong anti-correlations. Comparison with the correlations at three bands shows that with the frequency increasing (I → R → V), the correlations tend to be strong anti-correlation, which is consistent with the variation tendency from the gross sample.
In some regions, with the flux densities increasing, α and FVRI show different relations. For example, in Region-2, at I band, there is a break point, FI | b = 27 mJy. When FI< 27 mJy, no correlation exists between α and FI; but when FI> 27 mJy, there is strong correlation, α = (0.09 ± 0.01)FI−(1.68 ± 0.66), with r = 0.68, p = 1.0 × 10-4. In Region-3, the break points are FI | b = 29 mJy, FR | b = 23 mJy and FV | b = 14.5 mJy. In Region-4, the break points at three bands are FI | b = 31.5 mJy, FR | b = 19.3 mJy, FV | b = 20 mJy. In Region-5, the break points at three bands are FI | b = 24 mJy, FR | b = 16 mJy, and FV | b = 12 mJy. The break points at each region have been noted in Fig. 14. The upper results show that the relations between spectrum and brightness can be influenced by the brightness of the source.
4.4.2. 3C 273
For 3C 273, at different bands, α and FVRI show different relations. From I to V band, the relations are from strong correlation to no correlation to strong anti-correlation. The spectral variation of this source has been shown in Fig. 13 (the right panel), based on which, we can find three denser regions, noted by the rectangular boxes 1, 2, and 3.
The analyzed results concerning the three regions are listed in Table 3 and shown in Fig. 15. At I and R band, there exist different relations, from strong correlation to strong anti-correlation. At V band, in each of these three Regions, α and FV show strong anti-correlations. Comparing these results with the whole sample, we find that with increasing frequency (I → R → V), the correlations tend to be strong anti-correlation, which is consistent with the variation tendency of the sample as a whole.
S5 0716+714 and 3C 273 belong to different subclasses of Blazars. At V band, both objects show “bluer-when-brighter” evolution properties. At R and I band, the relations between brightness and spectrum are not fixed. Fiorucci et al. (2004) pointed out that the optical spectrum of QSOs consists of two components; one variable (αv, with a flatter slope), which comes from synchrotron emission, and the other part stable (αs), which might come from the thermal emission. For S5 0716+714 and 3C 273, at V band, most emissions could possibly come from synchrotron emission, and the relations between FV and α show anti-correlation. With decreasing detection frequency, the near IR emission becomes important, and α−FRI show complicated results.
4.5. Quasi-periods
There are many sources showing quasi-periods, such as 3C 273, 3C 279, 3C 454.3, Mrk335, Mrk 421, Mrk 501, OJ287, 0109+224, 0735+178, 2200+420, and so on (Kunkel 1967; Sillanpaa et al. 1988; Chertoprud et al. 1973; Liu et al. 1995; Stickel et al. 1993; Fan et al. 1998, 2007, 2014; Fan & Lin 2000; Xie et al. 2002; Raiteri et al. 2001; Ciprini et al. 2003). Explanation of the long-term variations could be based on the binary black-hole model, the thermal instability model or the perturbation model, and so on (Fan et al. 2007).
The quasi-periods of 3C 273 have been studied frequently. Smith & Hoffleit (1963) analyzed the optical light curve of 1887–1963 and obtained a period of 12.7 ~ 15.2 yr. Babadzhanyants & Belokon (1993) found a period of 13.4 yr. Based on 110 yr of optical data, Fan et al. (2001) obtained periods of ~2.0, 13.65 ± 0.20, and 22.5 ± 0.2 yr. Vol’vach et al. (2013) claimed periods of 2.8 ± 0.3, 4.9 ± 0.3 yr, 7.2 ± 0.8, 11.2 ± 2.3 yr in optical band. Our result P1 = 12.99 ± 0.72 yr is consistent with Smith & Hoffleit (1963), Babadzhanyants & Belokon (1993), Fan et al. (2001), Vol’vach et al. (2013), and the other result of P2 = 21.76 ± 1.46 yr was also found by Fan et al. (2001).
When we use the Jurkevich method to analyze the long-term variation, we find the other two results PJ = 0.99 ± 0.13, 2.05 ± 0.23. These results, however, are not shown when using DCF methods, and therefore should not be taken as quasi-periods. The Jurkevich results might be influenced by the sampling because 3C 273 is close to the ecliptic and cannot be observed all year round as the Sun is sometimes too close.
5. Conclusion
In this work, we present VRI photometric results of S5 0716+714 and 3C 273, which were obtained using the 1.56 m telescope at the Shanghai Observatory. Based on these observations, we come to the following conclusions.
Although S5 0716+714 and 3C 273 belong to different sub-classes of Blazars, both sources show complex dependency on the spectral index and flux density. The relations between these two parameters can be strongly influenced by the frequency and brightness.
Furthermore, the timescales provided here could be used to constrain some important physical parameters, such as the black hole, Doppler factor, emitting region, and so on. The causes of IDV and long-term optical periodicity are not clear and definite. To answer this question, further observations and improvement of the emitting theory are required. Gaussian function fitting is very useful when we calculate the timescales and study the whole variation trend of optical variability.
Acknowledgments
We thank the anonymous referee for useful comments. The work is partially supported by the National Natural Science Foundation of China (NSFC 11403006, USFC U1531245, NSFC 10633010, NSFC 11173009 and NSFC U1431112), Science and Technology Program of Guangzhou (201707010401), Guangdong Province Universities and Colleges Pearl River Scholar Funded Scheme (GDUPS 2009), Yangcheng Scholar Funded Scheme (10A027S), Innovation team in Guangdong Province (2014KCXD014) and the finaincial support for the Key subject of Guangzhou City.
References
- Abdo, A. A., Ackermann, M., Atwood, W. B., et al. 2009, ApJ, 697, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 710, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 714, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowicz, M. A., & Nobili, L. 1982, Nature, 300, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2010, ApJ, 721, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Angione, R. J., & Smith, H. J. 1985, ApJ, 90, 12 [CrossRef] [Google Scholar]
- Asada, K., Inone, M., & Uchida, Y. 2002, PASJ, 54, 39 [CrossRef] [Google Scholar]
- Beaklini, P. P. B., & Abraham, Z. 2014, MNRAS, 437, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatta, G., Webb, J. R., Hollingsworth, H., et al. 2013, A&A, 558, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhatta, G., Stawarz, L., Ostrowski, M., et al. 2016, ApJ, 831, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkmann, W., Yuan, W., & Siebert, J. 1997, A&A, 319, 413 [NASA ADS] [Google Scholar]
- Chakrabarti, S. K., & Wiita Paul, J. 1993, ApJ, 411, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, S., Baliyan, K. S., Ganesh, S., & Joshi, U. C. 2011, ApJ, 731, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Chertoprud, V. E., Gudzenko, L. I., & Ozernoy, L. M. 1973, ApJ, 182, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Carini, M. T., & Miller, H. R. 1992, ApJ, 385, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Ciprini, S., Tosti, G., Raiteri, C. M., et al. 2003, A&A, 400, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dai, B. Z., Li, X. H., Liu, Z. M., et al. 2009, MNRAS, 392, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., Krolik, J. H., & Pike, G. F. 1990, ApJ, 359, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Bregman, J., Hughes, P., & Lloyd-Davies, E. 2008, ApJ, 679, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., & Lin, R. G. 2000, ApJ, 537, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., Xie, G. Z., Pecontal, E., et al. 1998, ApJ, 507, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., Liu, Y., & Yuan, Y. H. 2007, A&A, 462, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, J. H., Huang, Y., Yuan, Y. H., et al. 2009a, RA&A, 9, 538 [Google Scholar]
- Fan, J. H., Zhang, Y. W., Qian, B. C., et al. 2009b, ApJS, 181, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., Peng, Q. S., Tao, J., Qian, B. C., & Shen, Z. Q. 2009c, AJ, 138, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., Huang, Y., He, T. M., et al. 2009d, PASJ, 61, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, J. H., Yang, J. H., Liu, Y., & Zhang, J. Y., et al. 2013, RA&A, 13, 259 [Google Scholar]
- Fan, J. H., Kurtanidze, O., Liu, Y., et al. 2014, ApJS, 213, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Fiorucci, M., Ciprini, S., & Tosti, G. 2004, A&A, 419, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foschini, L., Ghisellini, G., Tavecchio, F., Bonnoli, G., & Stamerra, A. 2011, A&A, 530, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2015, MNRAS, 448, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Ghisellini, G., Villata, M., Raiteri, C. M., et al. 1997, A&A, 327, 61 [NASA ADS] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., & Ghirlanda, G. 2011, MNRAS, 414, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F., Lee, C. U., Pak, S., Yim, H. S., & Fletcher, A. B. 2006, A&A, 450, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, A. C., Fan, J. H., Bai, J. M., & Wagner, S. J. 2008, AJ, 135, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Srivastava, A. K., & Wiita Paul, J. 2009, ApJ, 690, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Krichbaum, T. P., Wiita, P. J., et al. 2012, MNRAS, 425, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hovatta, T., Valtaoja, E., Tornikoski, M., et al. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hufnagel, B. R., & Bregman, J. N. 1992, ApJ, 386, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Jurkevich, I., Usher, P. D., & Shen, B. S. P. 1971, Ap&SS, 10, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Kunkel, W. E. 1967, AJ, 72, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. W., Lee, S. S., & Kang, S. 2016, A&A, 592, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, E. W., & Liu, H. T. 2003, MNRAS, 340, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F. K., & Chen, X. 1995, ApJ, 671, 1272 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, F. K., Xie, G. Z., & Bai, J. M. 1995, A&A, 295, 1 [NASA ADS] [Google Scholar]
- Man, Z. Y., Zhang, Z. Y., Wu, J. H., et al. 2016, MNRAS, 456, 3168 [NASA ADS] [CrossRef] [Google Scholar]
- Mangalam, A. V., & Wiita, P. J. 1993, ApJ, 406, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1993, ApJ, 410, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, H. R. 1975, ApJ, 201, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, H. R., Carini, M. T., & Goodrich, B. D. 1989, Nature, 337, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B. 1967, ApJ, 147, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Paltani, S., & Turler, M. 2005, A&A, 435, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlidou, V., Richards, J. L., Max-Moerbeck, W., et al. 2012, ApJ, 751, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Poon, K., Fan, J. H., & Fu, J. N. 2009, ApJS, 185, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1994, Numerical Recipes in Fortran, The art of Scientific Computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Raiteri, C. M., Villata, M., Aller, H. D., et al. 2001, A&A, 377, 396 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Gupta, A. C., Joshi, U. C., et al. 2010, ApJ, 719, 153 [Google Scholar]
- Savolainen, T., Homan, D. C., Hovatta, T., et al. 2010, A&A, 512, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Maraschi, L., & Colpi, M. 2012, MNRAS, 421, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Sillanpaa, A., Haarala, S., Valtonen, M. J., Sundelius, B., & Byrd, G. G. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H. J., & Hoffleit, D. 1963, Nature, 198, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, P. S., Balonek, T. J., Heckert, P. A., et al. 1985, AJ, 90, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Stickel, M., Fried, J. W., & Kuhr, H. 1993, A&A, 98, 393 [Google Scholar]
- Stevens, J. A., & Gear, W. K. 1999, MNRAS, 307, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Ghisellini, G., Bonnoli, G., & Ghirlanda, G. 2010, MNRAS, 405, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Trevese, D., & Vagnetti, F. 2002, ApJ, 564, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Trevese, D., Kron, R. D., & Bunone, A. 2001, ApJ, 551, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich Marie-Helene, M. L., & Urry, C. M. 1997, ARA&A, 35, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Unwin, S. C., Cohen, M. H., Biretta, J. A., et al. 1985, ApJ, 289, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vagnetti, F., Trevese, D., & Nesci, R. 2003, ApJ, 590, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Villata, M., Raiteri, C. M., Lanteri, L., et al. 1998, A&AS, 130, 305 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Vol’vach, A. E., Kutkin, A. M., Vol’vach, L. N., et al. 2013, Astron. Rep., 57, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, G. Z., Zhou, S. B., Dai, B. Z., et al. 2002, MNRAS, 329, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Y. H., & Fan, J. H. 2015, Ap&SS, 357, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Y. H., Fan, J. H., & Pan, H. J. 2015a, AJ, 150, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Y. H., Fan, J. H., Pan, H. J., et al. 2015b, Ap&SS, 360, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Liang, E. W., Sun, X. N., et al. 2013, ApJ, 774, 5 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 VRI light curves of S5 0716+714 (the upper sub-picture) and 3C 273 (the lower sub-picture). The black dots signify I band, the red dots signify R band and the green dots signify V band. |
| In the text | |
 |
Fig. 2 Change trend of f(x) with x. A0, A1, A2 and A3 have been noted. |
| In the text | |
 |
Fig. 3 For S5 0716+714, at I band, the results of intra-day light curves based on the Gaussian function. The red, green, and blue lines represent the Gaussian fitting curve. |
| In the text | |
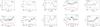 |
Fig. 4 For S5 0716+714, at R band, results of intra-day light curves based on the Gaussian function. The red, green, and blue lines represent the Gaussian fitting curve. |
| In the text | |
 |
Fig. 5 For S5 0716+714, at V band, results of intra-day light curves based on the Gaussian function. The red, green, and blue lines represent the Gaussian fitting curve. |
| In the text | |
 |
Fig. 6 For 3C 273 at I band; results of intra-day light curves based on the Gaussian function. The red lines represent the Gaussian fitting curve. |
| In the text | |
 |
Fig. 7 Using the Jurkevich and DCF methods to analyze the periodicities of VRI light curves. The left three panels show the DCF results and the right three panels show the Jurkevich results. |
| In the text | |
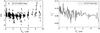 |
Fig. 8 Calculation of the long-term periodicity of 3C 273 based on our data. The upper panel shows the DCF result and the lower panel shows the Jurkevich result. |
| In the text | |
 |
Fig. 9 Light curves of 3C 273. The black dots represent the literature data, and the red dots represent our observations. |
| In the text | |
 |
Fig. 10 Periodic results of 3C 273. The first panel shows the DCF result with the red line being Gaussian fitting. The second panel shows the Jurkevich result. |
| In the text | |
 |
Fig. 11 Correlations between α and FIRV. The upper three panels show results for S5 0716+714, and the lower three panels shoiw results for 3C 273. The red line represents the linear correlation between α and FIRV. |
| In the text | |
 |
Fig. 12 ΔT distributions of S5 0716+714, which can be divided into three parts, fitted by Gaussian function (red lines). |
| In the text | |
 |
Fig. 13 Spectral variation of 3C 273 and S5 0716+714. The denser distributions are indicated by the rectangle regions. |
| In the text | |
 |
Fig. 14 For S5 0716+714, the relations between α and FVRI at the five denser regions. The black dots and the red dots represent the different parts of the same regions. The green lines stand for the linear fitting between α and FVRI. |
| In the text | |
 |
Fig. 15 For 3C 273, the relations between α and FVRI at the three denser regions. The black dots and the red dots stand for the different parts of the same regions. The green lines show the linear fitting between α and FVRI. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



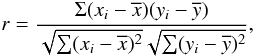
![\begin{eqnarray} &&\delta\geq\left[1.54\times10^{-3}(1+z)^{4+2\alpha_{\rm X}}\left(\frac{d_L}{{\rm Mpc}}\right)^2 \right. \nonumber \\ &&\qquad\qquad \left.\times \left(\frac{\Delta T}{h}\right)^{-1}\left(\frac{F_{\rm keV}}{\mu{{\rm Jy}}}\right)\left(\frac{E_{\gamma}}{{\rm GeV}}\right)^{\alpha_{\rm X}}\right]^{\frac{1}{4+2\alpha_{\rm X}}}, \end{eqnarray}](/articles/aa/full_html/2017/09/aa30338-16/aa30338-16-eq308.png)