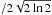| Issue |
A&A
Volume 604, August 2017
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201630186 | |
| Published online | 23 August 2017 | |
Planck’s dusty GEMS
IV. Star formation and feedback in a maximum starburst at z = 3 seen at 60-pc resolution⋆
1 Institut d’Astrophysique Spatiale, CNRS, Univ. Paris-Sud, Université Paris-Saclay, Bât. 121, 91405 Orsay Cedex, France
2 European Southern Observatory, ESO Vitacura, Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago, Chile
3 Atacama Large Millimeter/submillimeter Array, ALMA Santiago Central Offices, Alonso de Cordova 3107, Vitacura, Casilla 763-0355, Santiago, Chile
4 Steward Observatory, University of Arizona, Tucson, AZ 85721, USA
5 Institut d’Astrophysique de Paris, 75014 Paris, UPMC Université Paris 6, UMR7095, France
6 Chalmers University of Technology, Onsala Space Observatory, Onsala, Sweden
7 Laboratoire AIM, CEA/DSM/IRFU, CNRS, Universite Paris-Diderot, Bat. 709, 91191 Gif-sur-Yvette, France
8 Aix Marseille Univ, CNRS, LAM, Laboratoire d’Astrophysique de Marseille, 13013 Marseille, France
9 Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ, UK
10 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
11 Department of Physics and Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, 6658 British Columbia, Canada
⋆⋆ Corresponding author: R. Cañameras, canameras@dark-cosmology.dk
Received: 2 December 2016
Accepted: 24 March 2017
We present an analysis of high-resolution ALMA interferometry of CO(4–3) line emission and dust continuum in the “Ruby” (PLCK_G244.8+54.9), a bright, gravitationally lensed galaxy at z = 3.0 discovered with the Planck all-sky survey. The Ruby is the brightest of Planck’s dusty GEMS, a sample of 11 of the brightest gravitationally lensed high-redshift galaxies on the extragalactic sub-mm sky. We resolve the high-surface-brightness continuum and CO line emission of the Ruby in several extended clumps along a partial, nearly circular Einstein ring with 1.4′′ diameter around a massive galaxy at z = 1.5. Local star-formation intensities are up to 2000 M⊙ yr-1 kpc-2, amongst the highest observed at high redshift, and clearly in the range of maximal starbursts. Gas-mass surface densities are a few × 104M⊙ pc-2. The Ruby lies at, and in part even above, the starburst sequence in the Schmidt-Kennicutt diagram, and at the limit expected for star formation that is self-regulated through the kinetic energy injection from radiation pressure, stellar winds, and supernovae. We show that these processes can also inject sufficient kinetic energy and momentum into the gas to explain the turbulent line widths, which are consistent with marginally gravitationally bound molecular clouds embedded in a critically Toomre-stable disk. The star-formation efficiency is in the range 1–10% per free-fall time, consistent with the notion that the pressure balance that sets the local star-formation law in the Milky Way may well be universal out to the highest star-formation intensities. AGN feedback is not necessary to regulate the star formation in the Ruby, in agreement with the absence of a bright AGN component in the infrared and radio regimes.
Key words: galaxies: starburst / galaxies: high-redshift / submillimeter: galaxies / galaxies: evolution / galaxies: star formation / galaxies: ISM
© ESO, 2017
1. Introduction
Vigorous star formation in high-redshift galaxies occurred in environments with higher gas and stellar mass surface densities, higher gas fractions, and strong turbulence compared to nearby galaxies, with no obvious local kin. Elmegreen (1999) already recognized that massive, dense galaxy bulges must form most of their stars in one to a few dynamical times (“maximal starburst”), in accordance with the presence of a universal upper threshold of stellar mass surface density (Hopkins et al. 2010). How this limit is set is still a matter of active debate; alternatives are either related to gas fragmentation on kpc scales, or to the local kinetic energy injection from star formation through radiation pressure or thermalized supernova ejecta, and perhaps active galactic nuclei (AGN). Andrews & Thompson (2011) argued that radiation pressure could explain the upper envelope of the far-infrared luminosity of galaxies in the Schmidt-Kennicutt diagram with a dependence on optical depth, and Riechers et al. (2013) characterized such a maximal burst in an exceptional dusty starburst at z ~ 6.
Observers have stressed that rotation seems to be able to maintain the gas marginally Toomre-stable (e.g., Förster Schreiber et al. 2009), but centrifugal support cannot be dominant on scales smaller than approximately 100 pc (Toomre 1964; Escala & Larson 2008). Studying the local environments and regulation mechanisms in the most intensely star-forming galaxies at high redshift on small scales is particularly interesting in this regard, and is now becoming feasible with ALMA for the most strongly gravitationally lensed systems, such as SDP 81, for example (e.g., ALMA Partnership et al. 2015; Dye et al. 2015; Rybak et al. 2015; Hatsukade et al. 2015; Swinbank et al. 2015; Oteo et al. 2017). Existing observations of the resolved Schmidt-Kennicutt law in massive, dusty, gravitationally lensed high-redshift galaxies with intense star formation and specific star-formation rates that fall above those along the “main sequence” (“starburst galaxies”, e.g., Elbaz et al. 2011) suggest that star-formation intensities at a given gas mass surface density are generally as high as, or factors of a few greater than, those of galaxies near the high-redshift main sequence (Swinbank et al. 2011; Hatsukade et al. 2015). Investigating how high the star-formation intensity (star-formation rate density) in such galaxies can be is particularly interesting, because it allows us to infer the mechanism that sets the upper boundary to how intensely galaxies may form their stars. Currently known high-redshift galaxies generally fall factors of a few below the limit expected for galaxies that form stars at rates near the Eddington limit as quantified by, for example, Andrews & Thompson (2011); however, suitable observations are still very rare.
 |
Fig. 1 Morphology and kinematics of CO(4–3) line emission in the Ruby. Left to right: continuum and gas-mass surface brightness, velocities (in km s-1) and Gaussian line widths (FWHM |
Here we report on ALMA 0.1′′ resolution observations from the first long-baseline observing cycle of ALMA of the strongly lensed z = 3 galaxy PLCK G244.8+54.9, the “Ruby”. The Ruby is the brightest source in our set of 11 gravitationally enhanced submillimeter sources at redshifts z = 2.2–3.6 (Planck’s dusty GEMS), discovered with the Planck all-sky survey. The modified blackbody fits to the Herschel/SPIRE photometry of Cañameras et al. (2015, C15 indicates an observed peak flux density in the far-infrared of μSFIR = 1135 ± 2 mJy at 300 μm, which, when integrating over 8–1000 μm, corresponds to μLFIR = 2.65 ± 0.02 × 1014L⊙ at z = 3.0. SMA-850 μm and ALMA-3 mm interferometry show a near-complete Einstein ring with 1.4′′ diameter, encircling a massive galaxy with a spectroscopic redshift z = 1.52, one of the highest-redshift lenses currently known (Cañameras et al. 2017, C17 hereafter), which itself does however not contribute significantly to the bright far-infrared emission. Detailed lens modeling with LENSTOOL (Jullo et al. 2007) suggests typical gravitational magnification factors between 10 and 40 for the different clumps along the ring (C17). An AGN may contribute at most 10% to the FIR luminosity, and the source falls near the local far-infrared radio correlation (C15); AGN feedback is therefore unlikely to play a major role in the gas dynamics or regulation of star formation. Here we focus on the first part of our ALMA program, high-resolution interferometry of the CO(4–3) line with the long baseline array, which allows us to probe the local star-formation law on scales below 100 pc, even at long wavelengths of ~ 3 mm, which are best suited to probe relatively low-J CO transitions. We also present a first discussion of how feedback from star formation leaves its imprint on the resolved star-formation law and kinematic properties of the gas.
The outline of the paper is as follows: in Sect. 2 we present our observations and describe the data reduction. In Sect. 3 we describe the gas and dust morphology of the Ruby and the kinematic properties of the molecular gas as probed by the CO(4–3) line. We also investigate the impact of differential lensing. In Sect. 4 we discuss the intrinsic properties of the two independent regions within the same galaxy, which give rise to the two systems of multiple, gravitationally lensed images seen in the Ruby. In Sect. 5 we present the resolved Schmidt-Kennicutt law between gas-mass surface density and star-formation intensity. In Sect. 6 we discuss the energy and momentum injection from star formation into the gas, and investigate whether this can drive the gas turbulence, and regulate star formation in the way suggested by the Schmidt-Kennicutt diagram. We summarize our results in Sect. 7.
Throughout the paper, we adopt the flat ΛCDM cosmology from Planck Collaboration XVI (2014), with H0 = 68 km s-1 Mpc-1, Ωm = 0.31, and ΩΛ = 1 − Ωm. At z = 3.005 this implies a luminosity distance of 26.0 Gpc, and a projected physical scale of 7.85 kpc arcsec-1. Where appropriate, we explicitly mention the magnification factor μ to mark results that have not been corrected for the gravitational magnification, unless we refer to surface densities which are conserved by the lens.
2. Observations and data reduction
2.1. ALMA band 3 interferometry of CO(4-3) and dust
These ALMA Cycle 3 data (2015.1.01518.S, PI Nesvadba) were taken on October 23 2015 in the long baseline configuration C36-8 with maximum baselines of over 10 km. The target was observed for 58 min with 35 antennas in excellent conditions with precipitable water vapor PWV of around 0.6–1.0 mm and high phase stability (95–100 μm rms on baselines of 6500 m). We had centered baseband 1 on the redshifted CO(4–3) line at 114.888 GHz, and the remaining three spectral windows onto the continuum at frequencies of 100.908 GHz, 102.783 GHz, and 112.897 GHz, respectively.
For the reduction of the ALMA data we used the standard manual scripts with the Common Astronomy Software Application (CASA), applying automatic and manual flagging of visibilities, calibrating bandpass, phase and amplitude/flux, and using CLEAN to construct the synthesized beam de-convolved images of the frequency data cubes and continuum images. For antenna positions we used the best estimates available from the entire campaign of baseline monitoring throughout the long baseline observing in October and November 2015.
The data were imaged into cubes using the “channel” and “velocity” modes, “briggs” weighting with robust = 0.5, and custom cleaning masks using 1000 iterations. The rms in the final continuum image is 0.014 mJy beam-1, and 0.34 mJy beam-1 in the CO(4–3) cube for a spectral channel width of 24.4 MHz (63.7 km s-1). The beam size is 0.14′′ × 0.06′′ along PA = 55°.
3. Results
3.1. Continuum and gas morphology and gas kinematics
In the left panel of Fig. 1 we show the continuum morphology extracted from the two line-free windows 1 and 2 at 100.9 and 102.8 GHz as both gray-scale and contours. These frequencies correspond to 404 GHz and 412 GHz in the rest-frame, respectively (and to wavelengths of 742 μm and 728 μm, respectively).
Image-plane properties of individual counter images.
The Ruby consists of several clumps belonging to two image systems identified in C17, which form a partial Einstein ring around a massive galaxy at z = 1.52, with 1.4′′ diameter. The intervening lensing source was not detected in our ALMA data cube down to the rms of our continuum image. The continuum shows several clumps with maximal surface brightness levels between (63 ± 14) μJy beam-1 and (130 ± 14) μJy beam-1, that is, clumps are detected at 4.5σ to 9σ. Individual clumps are spatially resolved, at least along the major axis, with sizes between 0.25′′ and 0.4′′, seen with a beam of 0.14′′ × 0.06′′. The projected sizes in the image plane, and maximal continuum surface brightnesses of each clump are listed in Table 1.
We extrapolate the dust SED from C15 to find an expected source-integrated continuum flux density at the frequency of our ALMA observations of 2.75 mJy. Integrating the continuum flux over the entire ring of the Ruby, we recover 73% of this flux density, that is, 2.00 ± 0.05 mJy (not correcting for lensing). Most of the missing flux is likely to be in the extended diffuse regions along the Einstein ring seen with the Submillimeter Array at 850 μm (C17); these regions are not too extended to be seen with ALMA with the long baselines that we used, but are too faint to be significantly detected with our small beam size at 3 mm. In the following analysis we focus on the properties of the intensely star-forming clumps, so that the missing flux will not significantly affect our analysis.
We construct maps of the CO(4–3) line observed in spectral window 3 by fitting single Gaussian profiles to each spatial pixel with a custom IDL routine based on the MPFIT algorithm of Markwardt (2009). Figure 1 shows the resulting gas morphology, velocity maps, and maps of Gaussian line widths, with the continuum morphology overplotted as contours. The line emission is dominated by several bright clumps, some of which are resolved into a few resolution elements. Maximal CO line surface brightness levels are between 200 and 600 mJy km s-1 beam-1, with typical uncertainties of 20–40 mJy km s-1 beam-1. Velocities measured locally in each pixel span a range between − 600 and 200 km s-1 relative to z = 3.005, with typical uncertainties of 30–40 km s-1. The velocity gradients in the northern and southern clumps are nearly perpendicular to the magnification direction, which shows that we resolve the source also along that direction. To our knowledge, this is the first time that this has been achieved in the millimeter for a gravitationally lensed image.
Velocity dispersions (Gaussian widths) are between 25 km s-1 and 200 km s-1, with typical uncertainties of 40–50 km s-1, and with a few smaller regions between clumps having widths up to approximately 330 km s-1. This could be a signature of blending of line emission from multiple sources. For a sound speed 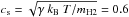 km s-1, with Boltzmann constant kB, temperature T = 50 K (C15), and molecular mass of H2 = 3.24 × 10-24 g, these widths correspond to highly supersonic velocities with Mach numbers between ℳ = 40 and 550.
km s-1, with Boltzmann constant kB, temperature T = 50 K (C15), and molecular mass of H2 = 3.24 × 10-24 g, these widths correspond to highly supersonic velocities with Mach numbers between ℳ = 40 and 550.
3.2. Morphological and kinematic substructure of the Ruby
The morphology and kinematics of the Ruby are complex. C17 identify multiple lensed images of two physically distinct regions, which partially overlap. In order to examine the morphological and kinematic substructure in the Ruby in a robust, reproducible way, we analyzed the CO(4–3) data cube with the Clumpfind algorithm (Williams et al. 1994). Clumpfind identifies contiguous regions of line emission in three-dimensional data cubes taking all spatial and velocity information into account, and returns the position, size, aspect ratio, and integrated emission line properties of each clump.
We ran Clumpfind in steps of 2σ, starting at 2σ, as suggested by Williams et al. (1994), where σ = 2 mJy is the root mean square of the CO(4–3) data set measured from a cube that was smoothed by three pixels along the two spatial axes, and five pixels along the spectral axis. This is comparable to the size of the beam and the line width, respectively, and hence does not lead to a loss in spatial resolution while marginalizing over the details of the line profile per pixel, and hence maximizing the signal-to-noise along the spectral axis.
With Clumpfind we identified a total of 12 clumps at ≥5σ. We also inverted the cube, to provide another constraint on the potential number of spurious clumps, finding none with >4σ significance. Visual inspection of these clumps in the CO data cube showed that 11 of them are extended over at least the size of the beam, and their peak is detected at significances of up to 14σ. All can be associated with the multiple images identified visually by C17 from the peaks of the flux map and orientation of the velocity gradients. However, blueshifted and redshifted gas in a given counter image was typically identified as two individual clumps. The 12th and faintest clump appears to be spurious, and was discarded from the subsequent analysis.
 |
Fig. 2 Spectra of individual counter images as assembled from clouds identified with Clumpfind, as labeled in Fig. 1. Images #1.2 and #1.3 are blended and identified as a single clump by Clumpfind. The dark blue and red lines show fits with Gaussian functions to the total line profile of each image system shown in Fig. 2, scaled to the total flux in each image. The mismatch between the blue component in image #1.4 can be explained with partial overlap with image #2.2. |
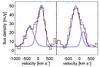 |
Fig. 3 Integrated spectra of image system 1 (left) and 2 (right), summed over images #1.1 and #1.2, and #2.1, and #2.2, respectively. Solid blue lines show individual Gaussian components of the line profiles, while the red dashed line shows the sum of both components. |
To provide an independent verification of the previous identification of image systems by C17 we reassembled clumps into individual lens images, which are labeled in the left panel of Fig. 1. Figure 2 shows the resulting spectra integrated over all images. This would not be the case, if, for example, Clumpfind had missed significant parts of the flux. Images #1.2 and #1.3 are strongly blended, and were not identified as separate clumps by Clumpfind. Discrepancies between the line profile of image #1.4 and the other images of system 1 can be explained with partial overlap of images #1.3 and #2.2, or potentially different magnification factors for the blueshifted and redshifted gas. Note that the blue and red lines in Fig. 2 are not fits of Gaussian functions to the spectra of individual counter images, but rescaled versions of the sum of all counter images in a given image system shown in Fig. 1, keeping the same line width and redshift as in the total image of each system, and also the same ratio between the two line components. The fluxes of these spectra are listed in Table 2. The similarity of these line profiles confirms the previous assignment of individual images to image systems, which C17 did based on the lens modeling. The combined spectrum of each image system is shown in Fig. 3.
4. Intrinsic properties of regions 1 and 2
We will now focus on two of the brightest, most isolated images, #1.1 and #2.1, to analyze the properties of the two regions in the source plane that are magnified by the gravitational lens in front of the Ruby. Since all other images are either from system 1 or 2, they would provide the same physical constraints at lower signal-to-noise ratio. Images #1.2 and #2.2 are somewhat brighter, but are also contaminated with partially overlapping adjacent images, and their morphology and gas kinematics is therefore more difficult to interpret. Images #1.1 and #2.1 are also least affected by systematic uncertainties from the lens reconstruction.
Redshifts, centroid velocities relative to z = 3.005, FWHM line widths, and integrated line fluxes in individual counter images of the Ruby.
 |
Fig. 4 Reconstructed source-plane morphology of the integrated and beam-convolved CO(4–3) line image of regions 1 (left) and 2 (right) as obtained with LENSTOOL. Both regions are spatially well resolved by our ALMA data. Blue diamond-shaped lines indicate the position of the internal caustic line at z = 3.005. The solid and dotted brown lines shows the 3-sigma positional uncertainty on the luminosity-weighted centroid of each region, for the line and continuum emission, respectively. |
The source-plane reconstruction of C17 obtained with LENSTOOL suggests that these two image systems trace two independent regions that are separated by 470 pc in the source plane (Fig. 4). Region 1 samples a region with intrinsic maximal side lengths in the source plane of approximately 1.4 kpc and 0.7 kpc along the major and minor axis, respectively, while these lengths in region 2 amount to 1.2 kpc and 0.3 kpc along the major and minor axis, respectively. Both regions are well spatially resolved in our ALMA data, and likely extend beyond the part of the galaxy which is most strongly magnified by the gravitational lens. The sizes were measured from the reconstructed source-plane morphology determined through the CleanLens algorithm within LENSTOOL (Sharon et al. 2012), and correspond to 3σ isophotal sizes in the image plane. Corresponding areas are 0.5 kpc2 and 0.3 kpc2, respectively, and were derived by summing over the area of all pixels in the reconstructed source-plane image (Fig. 4). Taking into account their gravitational magnification factor and the beam shape, we reach maximal spatial resolutions of 64 pc and 160 pc along the caustic line in region 1 and 2, respectively.
4.1. Dynamical mass and mass surface densities
The angular separation of 470 pc between these two regions is smaller than the size of each region, which suggests that both are within the gravitational potential of the same galaxy or an advanced galaxy merger near coalescence. This is also suggested by the excellent agreement in velocity between the two regions, which are within 200 km s-1 of one another. The velocity difference between these two regions (measured from the peak of the Gaussian line profiles in their integrated spectra) is less than the range of velocities, Δv, which we measure in the velocity maps of each individual region, and which are given relative to a single reference redshift of z = 3.005. In region 1, we find a total velocity range of Δv1 = 550 ± 35 km s-1, and in region 2, this range is Δv2 = 260 ± 27 km s-1. Integrated luminosity-weighted Gaussian line widths, 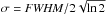 , in each clump are between approximately 130 ± 38 km s-1 and 330 ± 45 km s-1.
, in each clump are between approximately 130 ± 38 km s-1 and 330 ± 45 km s-1.
We measured minimal and maximal velocities directly from the map, without the use of a model. Commonly used algorithms, such as, for example, kinemetry (Krajnović et al. 2006) rely on fitting up to 15 free parameters internally, which we cannot provide with our data set, which is resolved to only 2–4 independent resolution elements along the kinematic major axis.
If these gradients approximately sample gravitational motion within a rotating disk, we can provide dynamical mass estimates by setting Mdyn = v2R/G. Here v is the circular velocity, which we approximate as Δv/ 2 sini, R the radius, and G the gravitational constant. The small spatial sizes we probe in the source plane make it unlikely that the gas kinematics probe two fairly isolated, approximately virialized galaxies in the early stage of a merger. Using the above measurements, and with intrinsic sizes R1 = 700 pc and R2 = 600 pc for regions 1 and 2, we find dynamical mass estimates of (1.2 ± 0.3) and (0.24 ± 0.05) × 1010sini-2M⊙, respectively, and corresponding mass surface densities of (8 ± 1.7) × 109sini-2M⊙ kpc-2 and (2 ± 0.4) × 109sini-2M⊙ kpc-2. We calculated mass surface densities by dividing the above dynamical mass estimates by the surface of circular regions of radius R1 and R2, respectively. Note that these estimates are not corrected for inclination effects and potential offsets between rotation and magnification direction; together, these typically lower the observed relative to the intrinsic mass by factors of 2–4, which would imply intrinsic dynamical masses of regions 1 and 2 of approximately (3.6 ± 0.8) and (0.8 ± 0.2) × 1010M⊙, respectively, and mass surface density estimates of (3.7 ± 0.8) and (0.6 ± 0.1) × 1010M⊙ kpc-2, respectively. The greater of these values is close to the highest stellar mass surface densities observed in massive early-type galaxies and globular clusters at low redshift (e.g., Hopkins et al. 2010), ~ 5 − 10 × 1010M⊙ kpc-2. Kauffmann et al. (2003) argued that high mass surface densities are a signature predominantly of very massive galaxies, so that this finding adds another piece to the considerable body of evidence of the evolutionary link between massive low-z elliptical galaxies and the most intense starbursts at redshifts 2–3, (e.g., Blain et al. 2002; Tecza et al. 2004; Swinbank et al. 2006; Amblard et al. 2011).
4.2. Global gas stability and fragmentation scale
Similar to galaxies in the field, the disk in the Ruby appears to be overall Toomre-stable. A number of parametrizations of the Toomre parameter, Q, have been proposed in the literature, depending on gas configuration, and whether stellar or gas mass surface density dominates. Here we use the parametrization of Genzel et al. (2014) to set Q = avcσ/πRG Σgas, with a = 2 as is appropriate for the monotonically rising part of a rotation curve. vc is the rotational velocity, σT the turbulent velocity dispersion. R is the disk radius (we adopt the 700 pc in #1.1, i.e., the largest radius magnified by the lens) and G is the gravitational constant. For the gas-mass surface density, Σgas, we use a typical value for the Ruby of 1 × 104M⊙ pc-2 (Sect. 5.1). This gives Q = 1.0 ± 0.3. Hence the gas in the Ruby appears to be globally marginally Toomre-stable.
Clumpfind identifies only a single contiguous component associated with image #1.1, with a FWHM size of 0.2′′ × 0.12′′, corresponding to an (averaged) diameter of 0.16′′. In image #2.1, the algorithm identifies four individual clumps with sizes between 0.1′′ and 0.2′′. Corrected for the luminosity-weighted average magnifications, this corresponds to source-plane diameters between approximately 40 pc and 200 pc in the two images at z = 3.005. These sizes are comparable to or smaller than the sizes of individual small clumps identified in unlensed dusty starburst galaxies at similar redshifts, which have typical diameters of 200 pc (Iono et al. 2016).
 |
Fig. 5 Zoom onto the southern part of the Ruby, showing the CO(4–3) morphology as color image, and the dust morphology as contours. We note the small offset between the emission-line and continuum peak. |
This range also corresponds to the range of sizes expected for gas clouds in a fragmenting disk. Expected fragmentation scales, LJ, expected from a classical Jeans analysis at these mass surface densities scale as 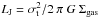 , where σt is the velocity dispersion of the gas, G the gravitational constant, and Σgas the gas-mass surface density. The corresponding mass for a uniform-density sphere, MJ, can be written as
, where σt is the velocity dispersion of the gas, G the gravitational constant, and Σgas the gas-mass surface density. The corresponding mass for a uniform-density sphere, MJ, can be written as 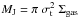 . For Gaussian widths between 100 and 170 km s-1 and mass surface densities of approximately 104M⊙ pc-2, we find cloud sizes of approximately 40–100 pc, and masses between 1 and 3 × 108M⊙. These are smaller than the gas masses we see in individual regions of the Ruby. Cloud overlaps or a larger fragmentation scale in clumpy high-z galaxies than suggested by this simple analysis (Romeo & Agertz 2014) might cause this difference.
. For Gaussian widths between 100 and 170 km s-1 and mass surface densities of approximately 104M⊙ pc-2, we find cloud sizes of approximately 40–100 pc, and masses between 1 and 3 × 108M⊙. These are smaller than the gas masses we see in individual regions of the Ruby. Cloud overlaps or a larger fragmentation scale in clumpy high-z galaxies than suggested by this simple analysis (Romeo & Agertz 2014) might cause this difference.
4.3. A note on differential lensing
Depending on the relative morphology of dust and gas, differential lensing may produce major biases in studies of strongly lensed galaxies at low spatial resolution (e.g., Serjeant 2012). However, these estimates were made on toy models, which is unavoidable given our limited knowledge of the internal structure of dusty high-redshift starburst galaxies. The exceptionally high spatial resolution of our ALMA data allows us to quantify the potential biases from differential lensing in a direct way.
We do find small positional offsets between the peaks of the dust and the CO line emission (Figs. 1 and 5) of up to 0.2′′ in two clumps seen in the image plane, which correspond to an intrinsic offset in the source plane (Fig. 4). For the other clumps, we do not find a measurable offset between the intrinsic dust and gas morphology in the source plane. Since dust and gas morphologies were derived with the same observations and are at almost the same frequencies, these offsets must be intrinsic, and show that we are resolving the internal structure of the star-forming regions in the Ruby.
We use luminosity-weighted maps of CO and continuum emission to infer the impact of the differences in gravitational magnification on the total estimates of the gas and dust luminosity. When summing over all pixels that are seen in both gas and dust, we find luminosity-weighted average magnification factors of 33.8 ± 6.4 and 43.6 ± 8.2 for the FIR continuum luminosity and CO(4–3) line luminosity, respectively. This corresponds to a difference of approximately 22% for the integrated values, and is not greater than other systematic and measurement uncertainties in this kind of study.
For image #1.1, a similar analysis gives luminosity-weighted average magnification factors of 21.7 ± 4.2 and 19.8 ± 3.3 for the continuum and line luminosities, respectively, while for #2.1 we find factors of 10.7 ± 2.6 and 9.0 ± 2.2, respectively. This corresponds to approximately 10% for image #1.1, and 20% for image #2.1. Again, these differences are not very large compared to other systematic and measurement uncertainties, and reflect the intrinsic offsets between gas and dust on the small spatial scales on which we resolve the Ruby in the source plane.
5. Resolved star-formation law and self regulation
5.1. Schmidt-Kennicutt law
 |
Fig. 6 Left: spatially resolved Schmidt-Kennicutt law in PLCK G244.8+54.9 (red stars) and best fit relation (solid black line). The lower and upper black star indicate the luminosity-weighted average position of images #2.1 and #1.1, respectively. Other symbols indicate: submillimeter galaxies at z ~ 2 (green upside-down triangles, Bothwell et al. 2010), local starbursts (black circles, Kennicutt 1998), spatially-resolved data from the Eyelash (dark green triangles Swinbank et al. 2011) and SDP.81 (yellow squares, Hatsukade et al. 2015). The green and dark blue dashed lines indicate the Schmidt-Kennicutt relationship for high-z starburst galaxies and main sequence galaxies of Daddi et al. (2010), respectively. All star-formation rates are given for a Chabrier initial mass function, and are a factor 1.8 lower than in many other figures showing the Schmidt-Kennicutt relationship (see text for details). Right: same Schmidt-Kennicutt diagram, showing the position of maximum starbursts in several models, and the position of the Ruby relative to them. Light blue circles indicate nearby Eddington-limited starbursts (Andrews & Thompson 2011). The dark green solid lines show the mechanical input from stellar winds and supernova remnants for 100% and 50% efficiency, respectively. The dark blue lines and yellow hatched region show the models of Andrews & Thompson (2011) for an Eddington-limited starburst with a range of opacities between 10 and 30 cm2 g-1. Solid lines show the optically thick limit above the critical gas-mass surface density for the optically thick case, dashed lines the optically thin case below that limit. The solid blue line shows the relationship of Ostriker & Shetty (2011), also for optically thick and optically thin gas. The red line shows the model of Faucher-Giguère et al. (2013). |
Star-formation intensity (projected star-formation rate density) is closely related to the local gas-mass surface density in galaxies over more than six orders of magnitude in star-formation intensity, and this relationship seems to be linear for gas-mass surface densities above approximately 10 M⊙ pc-2 (Bigiel et al. 2008). The zero point of this relationship is a measure of the efficiency with which galaxies turn their gas into stars. Most studies of star-forming regions in the Milky Way and nearby galaxies suggest this efficiency is around 1% per gas free-fall time (e.g., Krumholz & Tan 2007). The reasons for this are not yet fully understood, although there is a growing consensus in the literature that the turbulence within molecular clouds and filaments plays a major role in establishing this parameter (Klessen et al. 2000; Krumholz & McKee 2005; Li et al. 2005; Hennebelle & Audit 2007; Bournaud et al. 2010; Audit & Hennebelle 2010).
At high redshift, it has been suggested that galaxies falling onto the main sequence of star-forming galaxies could have a lower star-formation efficiency than starburst galaxies that fall above this relationship (e.g., Daddi et al. 2010; Genzel et al. 2010), perhaps a consequence of the higher pressures reached in the dense gas that is filling the deep gravitational potential wells of the most intensely star-forming high-redshift galaxies (Swinbank et al. 2011, 2015). Likewise, the energy injection from intense star formation should limit the maximal rate with which gas can be turned into stars (e.g., Heckman et al. 1990; Lehnert & Heckman 1996b,a; Veilleux et al. 2005; Andrews & Thompson 2011; Murray et al. 2005).
The Schmidt-Kennicutt diagram plotted in the left panel of Fig. 6 shows the local star-formation intensities as a function of the local gas mass surface densities extracted from each spatial pixel (Kennicutt 1989). To estimate the star-formation rates, we measured the average continuum flux density in each 0.04′′ × 0.04′′ pixel in our line-free ALMA spectral windows 1 and 2, and extrapolated along a modified black body curve with a global temperature, T = 50 K, and β = 2.0 (as used by Cañameras et al. 2015, for the Ruby), to translate these monochromatic flux densities into FIR luminosities.
We follow Kennicutt (1989) in estimating the star-formation rates by setting SFR = 4.5 × 10-44LFIR, where SFR is given in M⊙ yr-1. LFIR is in erg s-1, integrated between 8 μm and 1000 μm in the rest frame. Resulting star-formation rates are then corrected by a factor 1.8 downward to adopt the now more commonly used Chabrier initial mass function instead of the Salpeter initial mass function originally adopted by Kennicutt (1989). Tacconi et al. (2008) showed that Salpeter initial mass functions would lead to stellar mass estimates for high redshift sub-millimeter galaxies that are inconsistent with gas and dynamical mass estimates.
This estimation procedure results in local star-formation intensities of 220–2200 M⊙ yr-1 kpc-2, which is higher by approximately two orders of magnitude than in low-redshift starburst galaxies (e.g., Kennicutt 1998). It is also higher by factors of a few than in typical high-redshift galaxies that are closer to the main sequence. For example, star-formation intensities in H-ATLAS J09011.6 + 003906 (SDP.81) are below 200 M⊙ yr-1 kpc-2, as found by Rybak et al. (2015) with an analysis that was also based on star-formation rates measured pixel by pixel.
Such values are akin to those measured in the brightest, not gravitationally lensed dusty starburst galaxies at high redshifts, for which measurements of the dust morphology have been obtained at resolutions ≲0.5′′ (Ikarashi et al. 2015; Iono et al. 2016). Total sizes of the most actively star-forming regions in these galaxies are approximately 1–4 kpc (Ikarashi et al. 2015; Iono et al. 2016), compared to major axis sizes of approximately 1.4 kpc and 1.2 kpc, respectively, for regions 1 and 2 seen in the Ruby (Sect. 4). We can therefore assume that the star-formation properties as probed in the Ruby are representative of the most intense high-redshift starbursts. Oteo et al. (2017) recently reported comparable star-formation intensities of up to 3000 M⊙ yr-1 kpc-2, over scales of approximately 200 pc, in a pair of strongly lensed galaxies at z = 3.4 discovered in ALMA calibration data, but also point out that parts of the FIR continuum could potentially come from an AGN, which is not the case here (C15).
The abscissa of Fig. 6 shows the molecular gas mass surface density, which we derived from the CO(4–3) surface brightness. The linearity of the relationship between CO and FIR luminosity of high-z galaxies suggests that the brightness of the J = 4–3 transition is dominated by gas-mass surface density, not gas excitation (Greve et al. 2014). We follow Solomon et al. (1997) to estimate molecular gas masses from the CO line flux of each spatial pixel, and adopt a CO-to-H2 conversion factor of αCO = 0.8M⊙ [K km s-1 pc2]-1, which is a commonly adopted value in studies of dusty, intensely star-forming high-redshift galaxies (e.g., Tacconi et al. 2008; Bothwell et al. 2010; Hatsukade et al. 2015), and also agrees with the global dust-to-gas ratio estimates of C15 from the FIR-to-millimeter dust photometry of the GEMS. Less intensely star-forming high-redshift galaxies appear to be better characterized by a factor that is closer to the standard conversion factor found in the Milky Way, which is approximately five times greater (see Bolatto et al. 2013, for a recent review), but any correction by more than a factor of approximately two would lead to gas masses and gas mass surface densities in the Ruby that are greater than the dynamical mass estimate and derived surface densities, which would therefore be unphysical.
A correction factor for which no consensus has yet been reached is the flux ratio between mid-J CO lines and CO(1–0), for which the Schmidt-Kennicutt law has initially been calibrated. For CO(4–3), Carilli & Walter (2013) and Bothwell et al. (2013) found 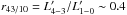 in high redshift starburst galaxies, however, these have on average much lower star-formation intensities. Galaxy-integrated measurements can also be contaminated with CO(1-0) emission from diffuse gas not associated with star-forming clouds (Ivison et al. 2010), thereby preferentially increasing the apparent CO(1-0) flux, so that estimates of molecular gas masses associated with star formation from mid-J CO lines might be more reliable than those from CO(1-0). This could happen to a different degree in unlensed galaxies in the field compared to the Ruby, which samples a small, intensely star-forming region.
in high redshift starburst galaxies, however, these have on average much lower star-formation intensities. Galaxy-integrated measurements can also be contaminated with CO(1-0) emission from diffuse gas not associated with star-forming clouds (Ivison et al. 2010), thereby preferentially increasing the apparent CO(1-0) flux, so that estimates of molecular gas masses associated with star formation from mid-J CO lines might be more reliable than those from CO(1-0). This could happen to a different degree in unlensed galaxies in the field compared to the Ruby, which samples a small, intensely star-forming region.
In the following, we therefore adopt r43 / 10 = 0.6, which corresponds to the measured value in the Eyelash (Danielson et al. 2011) and a stack of lensed galaxies from the South Pole Telescope sample (Spilker et al. 2014) and falls between the values adopted by Tacconi et al. (2008) and Carilli & Walter (2013).
With these assumptions and corrections, resulting gas-mass surface densities are within 103.7 − 4.7M⊙ pc-2, and most apertures fall between 104.1 and 104.5M⊙ pc-2. The Ruby falls therefore well above the locus of main sequence galaxies at high redshifts in the left panel of Fig. 6, and for some apertures even above the typical sequence of intense starbursts found from galaxy-integrated measurements (Daddi et al. 2010), which could at least partially be due to the lower physical resolution in observations of unlensed galaxies.
5.2. Self regulation in a maximum starburst
The high star-formation intensities we find in the Ruby are consistent with the extreme values of ≳1000–2000 M⊙ yr-1 kpc-2 expected for galaxies that form the bulk of their stars within one or a few crossing times (“maximal starbursts” Elmegreen 1999; Tacconi et al. 2006; Riechers et al. 2013). They are also greater by factors of a few than the intensities measured previously in strongly gravitationally lensed dusty starburst galaxies at high redshift (Fig. 6), meaning that our observations of the Ruby allow us to push even further towards probing the most intensely star-forming systems.
Several theoretical studies have proposed that galaxies in this part of the Schmidt-Kennicutt diagram should be self-regulated by stellar feedback. In such galaxies, hydrostatic mid-plane pressure should be balanced by the injection of kinetic energy from star formation, either through radiation pressure or the kinetic energy from stellar winds and supernovae remnants, or a mix of both. We compare the star-formation intensity with the models of Andrews & Thompson (2011) and Ostriker & Shetty (2011), who determined which region in this diagram should be populated by an Eddington-limited starburst. Feedback in this case is dominated by radiation pressure in (optically thin and optically thick) clouds with a range of dust opacities, κ. In both models, clouds with gas-mass surface densities as observed in the Ruby lie in the optically thick regime.
The relationship of Ostriker & Shetty (2011) is shown as a dark blue solid line in Fig. 6 in the optically thick regime, and as a dotted line at surface densities where the clouds are still optically thin. The yellow dashed band in the same figure shows the range of locations expected in the model of Andrews & Thompson (2011), for their warm starburst scenario. They account for ranges in gas-to-dust ratio and dust temperature, which are akin to those we find in the Ruby. Both agree very well with the location of the Ruby. We caution that systematic effects can blur this result. For example, uncertainties in the CO-to-H2 conversion factor and gas excitation (the r43 / 10 factor in Sect. 5.1) make gas mass surface density estimates uncertain by a few tenths of a dex. The accuracy of our data therefore does not allow us to distinguish between the detailed assumptions of each feedback model. Nonetheless, the range covered by radiation pressure and mechanical feedback from star formation in this diagram is large enough that our basic result, namely, that the Ruby falls well within the regime dominated by feedback, is robust in spite of these uncertainties.
Likewise, the Ruby falls into the self-limited regime if stellar winds and supernovae are the main channel through which kinetic energy is injected into the gas. We use Starburst99 (Leitherer et al. 1999) to estimate the energy and momentum injection rates for a starburst with an age of 10 Myr (Sect. 6.1), and equate the pressure created by the star formation with the hydrostatic midplane pressure. The resulting relationship is shown as the two solid dark green lines in the right panel of Fig. 6. The lower line is the limit for galaxies where 100% of the kinetic energy is thermalized into the wind, the upper line is for galaxies where this happens with an efficiency of 50%. Both estimates provide very similar limits to those implied by radiation pressure, suggesting that these mechanisms are about equally important in the most intensely star-forming systems. We stress that radiation pressure and winds should be considered as two co-existing, not competing processes, because the photon flux from the young stellar population is emitted in parallel to the mechanical energy and momentum carried by outflows from supernovae and young stars. A somewhat steeper relationship is produced when using the star-formation law of Faucher-Giguère et al. (2013), who combined the momentum input from radiation pressure, winds, and supernovae in an ansatz that explicitly accounts for the formation of giant molecular clouds in a marginally Toomre-stable disk supported by the turbulent pressure from the starburst itself. Figure 6 shows that the Ruby falls into the regime expected from a self-regulated starburst for all these approaches.
5.3. Star-formation efficiency
Our high-resolution data of the Ruby also allow us to estimate the star-formation efficiency on scales that are comparable to those probed in nearby galaxies (e.g., Bigiel et al. 2008). As argued by Daddi et al. (2010) and Genzel et al. (2010), high redshift starburst galaxies fall above the ridge line of main sequence galaxies in the Schmidt-Kennicutt diagram, which could imply that they convert their gas into stars at higher efficiencies (e.g., Hodge et al. 2015; Usero et al. 2015). We now estimate the star-formation rate per free-fall time to investigate if the position of the Ruby well above the main sequence is also matched by higher star-formation efficiencies per free-fall time.
The free-fall time, tff, is set by 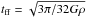 , where G is the gravitational constant and ρ the gas density. We estimate the three-dimensional gas density from the observed range of (projected) gas mass surface densities of approximately 104.1 − 4.5M⊙ pc-2, by assuming cloud sizes between 50 pc and 100 pc, corresponding to their Jeans lengths (Sect. 4). Resulting densities are between 8.5 × 10-21 and 4.3 × 10-20 g cm-3. This suggests free-fall times between 3 and 7 × 105 yr. Over such timescales, approximately 150–1400 M⊙ pc-2 of stars form, corresponding to a range of approximately 1–9% of the available gas-mass. This does not suggest significantly higher star-formation efficiencies per free-fall time than in more moderately star-forming galaxies, and is consistent with the theoretical arguments of Krumholz & Thompson (2012), who attributed the offset between the two populations in the Schmidt-Kennicutt diagram to differences in the formation and survival time of molecular clouds rather than intrinsic offsets in the efficiency of converting gas into stars. Star-formation in the Ruby is therefore consistent with the presence of a universal star-formation law out to the most intense starbursts.
, where G is the gravitational constant and ρ the gas density. We estimate the three-dimensional gas density from the observed range of (projected) gas mass surface densities of approximately 104.1 − 4.5M⊙ pc-2, by assuming cloud sizes between 50 pc and 100 pc, corresponding to their Jeans lengths (Sect. 4). Resulting densities are between 8.5 × 10-21 and 4.3 × 10-20 g cm-3. This suggests free-fall times between 3 and 7 × 105 yr. Over such timescales, approximately 150–1400 M⊙ pc-2 of stars form, corresponding to a range of approximately 1–9% of the available gas-mass. This does not suggest significantly higher star-formation efficiencies per free-fall time than in more moderately star-forming galaxies, and is consistent with the theoretical arguments of Krumholz & Thompson (2012), who attributed the offset between the two populations in the Schmidt-Kennicutt diagram to differences in the formation and survival time of molecular clouds rather than intrinsic offsets in the efficiency of converting gas into stars. Star-formation in the Ruby is therefore consistent with the presence of a universal star-formation law out to the most intense starbursts.
 |
Fig. 7 Turbulent scaling (“Larson”) relationship (Larson 1981) between gas velocity dispersion and cloud size in the source plane. Empty red stars show the sizes and line widths of the redshifted and blueshifted components seen in the Ruby within images #1 and #2, respectively. Green and yellow filled circles show similar observations of SDP.81 and the Eyelash from Swinbank et al. (2015) and Swinbank et al. (2011). Empty black circles show giant molecular clouds in the Milky Way. We also show expected line-width size relationships for gas mass surface densities, Σgas = 50M⊙ pc-2 characteristic for the Milky Way, and for 5000 M⊙ and 16 000M⊙ pc-2, which correspond to the lowest and highest values for the Ruby, respectively (Fig. 6). For each density we show the relationship for virial parameters αvir = 1 and 5, that is, clouds where turbulent energy either balances gravitational binding energy (solid line), or where it exceeds it by a factor 5 (dashed-dotted lines). |
6. Gas energetics and turbulent support
6.1. Kinetic energy and momentum
The previous section shows that the Ruby falls into a regime of gas-mass surface density and star-formation intensity, where star formation should be self-regulated through the energy and momentum injection from young stellar populations into the gas. Whether this occurs primarily through radiation pressure or ejecta from supernovae and young massive stars, it should leave an imprint on the gas kinematics, through driving turbulence and perhaps causing outflows. We will in the following analysis use our kinematic maps of the Ruby to quantify the possible effect of feedback from star formation onto the gas kinematics. This is particularly interesting here, because the Ruby is the most extreme starburst observed today with resolutions of ≲100 pc in the source plane.
We will now use the gas kinematics to further constrain the impact of feedback. We note that we have not found clear evidence of outflows in our data; this could be due to the faintness of the line emission as seen in our high-resolution data. Spectra which do show outflow signatures, typically also show a prominent systemic component, which dominates the overall line profile. Moreover, it is possible that a wind component would predominantly be in lower column density gas, which would not necessarily lead to bright line emission (Sturm et al. 2011), or in lower density, and perhaps atomic rather than molecular gas (e.g., Hayward & Hopkins 2017; Nesvadba et al. 2011). We also caution that the blue and redshifted components in the integrated spectra of individual counter images, which could be taken as line wings from outflowing gas in unresolved spectra (Fig. 2), arise from multiple gas clouds, as seen in Fig. 1.
We used the maps of CO surface brightness, velocity dispersion, and gravitational magnification to estimate the kinetic energy, Ekin,turb, and momentum, p, corresponding to each spatial pixel in regions 1 and 2, by setting 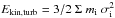 and p = Σ miσi, where mi and σi are the molecular gas mass and Gaussian velocity dispersion measured in each individual pixel. We find gas kinetic energies of Eturb,#1.1 = (1.8 ± 0.5) × 1057 erg s-1 and (2.5 ± 0.3) × 1057 erg s-1 in regions 1 and 2, respectively, and momenta of p#1.1 = (7.0 ± 1.8) × 1049 dyn s and p#2.1 = (6.3 ± 0.6) × 1049 dyn s, respectively (all values are corrected for gravitational magnification).
and p = Σ miσi, where mi and σi are the molecular gas mass and Gaussian velocity dispersion measured in each individual pixel. We find gas kinetic energies of Eturb,#1.1 = (1.8 ± 0.5) × 1057 erg s-1 and (2.5 ± 0.3) × 1057 erg s-1 in regions 1 and 2, respectively, and momenta of p#1.1 = (7.0 ± 1.8) × 1049 dyn s and p#2.1 = (6.3 ± 0.6) × 1049 dyn s, respectively (all values are corrected for gravitational magnification).
Given that the Ruby is strongly obscured in the rest-frame UV and optical, we have no direct constraints on the stellar population, which makes it difficult to infer the age of the starburst. Our main purpose here, however, is to investigate whether or not the star formation is sufficient to power the observed gas kinematics. For this work, a lower limit on the age of the stellar population is sufficient, and this can be obtained from the ratio of far-infrared luminosity and GHz radio continuum. C15 showed that the Ruby falls near the ratio q = 2.4 typical for low-redshift galaxies, which implies that star formation has already reached an equilibrium between the production of massive stars and the explosion of supernovae (Bressan et al. 2002). This equilibrium is reached approximately 1 to a few times 107 yr after the onset of star formation (Bressan et al. 2002). Adopting a lower limit on the starburst age in the Ruby of 10 Myr, this suggests that we need energy injection rates of approximately 6 × 1042 erg s-1 and 8 × 1042 erg s-1 to explain the kinetic energy in images #1.1 and #2.1, and approximately 2.1 × 1035 dyn and 3.3 × 1035 dyn in momentum injection rate.
In the following, we rely on Starburst99 (Leitherer et al. 1999) to estimate the energy and momentum injection rates from supernovae and stellar winds. For continuous star formation over a few times 107 yr and solar metallicity, with a Chabrier IMF, they find mechanical luminosities of 1041.8 erg s-1 for each solar mass of star formation. This corresponds to a momentum injection rate of approximately 2.1 × 1033 dyn per solar mass formed. For image #1.1 with an intrinsic, magnification-corrected SFR = 335 ± 2M⊙ yr-1, this implies an energy injection rate of (2.1 ± 0.2) × 1044 erg s-1 and a momentum deposition rate of (7.0 ± 0.6) × 1035 dyn. For image #2.1, intrinsic energy and momentum injection rates are 1.5 ± 0.2 × 1044 erg s-1 and 4.9 ± 0.5 × 1035 dyn, respectively. From radiation pressure, we expect 1.5 × 1036 dyn in image #1.1, and 1.1 × 1036 dyn in image #2.1.
We follow Murray et al. (2005) to estimate the momentum injection rate from radiation pressure by setting LSB/c ~ 4.6 × 1033ϵ3 SFR dyn. Note that we used a low-mass cutoff of 1 M⊙ instead of 0.1 M⊙ (as would be implied by the Salpeter initial mass function adopted by Murray et al. 2005), which approximates the Chabrier initial mass function we adopted earlier, and increases our momentum estimate by a factor 2.3 compared to that of Murray et al. (2005).
6.2. Turbulent support
The above suggests that mechanical feedback from supernovae and stellar winds can provide the kinetic energy in the gas, and either these sources or radiation pressure can also provide sufficient momentum to explain the observed broad line widths. As a complementary test, we now investigate whether the observed line widths are also consistent with those expected to keep the gas marginally gravitationally bound, as is found in giant molecular clouds (e.g., Krumholz & McKee 2005).
A central quantity for turbulence-regulated star formation is the virial parameter, αvir, the ratio of turbulent and gravitational binding energy, 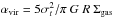 , where σt is the Gaussian line width, G, the gravitational constant, R the cloud radius, and Σgas the gas-mass surface density (Bertoldi & McKee 1992). Clouds are gravitationally bound if αvir< 1. Star-forming giant molecular clouds in the Milky Way typically have αvir ≳ 1, that is, they are marginally bound (e.g., Heyer et al. 2009).
, where σt is the Gaussian line width, G, the gravitational constant, R the cloud radius, and Σgas the gas-mass surface density (Bertoldi & McKee 1992). Clouds are gravitationally bound if αvir< 1. Star-forming giant molecular clouds in the Milky Way typically have αvir ≳ 1, that is, they are marginally bound (e.g., Heyer et al. 2009).
In Fig. 7 we show where the Ruby falls relative to the line-width size relationship of giant molecular clouds that are kept marginally gravitationally stable by supersonic turbulence. We show the location of clouds with αvir = 1 and αvir = 5, virial parameters that roughly straddle the velocity dispersions of giant molecular clouds in the Milky Way. We show this relationship for these virial parameters at three different gas mass surface densities, at 50M⊙ pc-2 as found in the Milky Way (Heyer et al. 2009), and at 5000 and 16 000 M⊙ pc-2, respectively, which represent the lower and higher ranges of gas-mass surface densities found in the Ruby. The Ruby falls into the region expected for gas-mass surface densities as observed.
Figure 7 resembles the line-width size diagrams shown by Swinbank et al. (2011) for the Cosmic Eyelash and by Swinbank et al. (2015) for SDP.81, and we also show these two galaxies for comparison here. The offsets of these two galaxies from the local line-width size relationship of nearby giant molecular clouds are somewhat smaller than that of the Ruby, consistent with their somewhat lower gas-mass surface densities. The more extreme position of the Ruby in the Schmidt-Kennicutt diagram suggests that the same equilibrium conditions hold up to the highest star-formation intensities expected for maximal starbursts.
Swinbank et al. also interpreted these offsets in terms of the hydrostatic mid-plane pressure of the disks in these galaxies, arguing that the higher pressures in high-redshift galaxies are at the origin of the higher star-formation intensities. This is not in contradiction with our work; however, by parameterizing this offset in terms of αvir, Fig. 7 highlights that it is the balance between turbulent and hydrostatic pressure that determines the regime where molecular clouds are marginally gravitationally stable. Star-forming clouds are not only found for a single equilibrium pressure, but scatter around a range of ratios of turbulent and gravitational energy. Generally speaking, the clouds in the Ruby do not seem to span a wider range than nearby GMCs. This shows that the interaction between the energy and momentum injection from star formation and the depth of the potential wells in high-redshift galaxies together set the efficiency at which stars form, an efficiency that appears to vary much less than the diversity of the environments in which it occurs might suggest.
7. Summary
We presented an analysis of ALMA extended-baseline observations of CO(4–3) and the 3-mm continuum in the z = 3.0 dusty starburst galaxy PLCK G244.8+54.9, the “Ruby” at 0.1′′ spatial resolution, probing spatial scales down to approximately 60 pc in the source plane. This galaxy is the brightest of Planck’s dusty GEMS, a set of exceptionally bright high-redshift galaxies discovered with the Planck and Herschel satellites. The Ruby forms a small Einstein ring around a distant, massive galaxy at z = 1.52 (C17), magnifying two regions of the same galaxy into two sets of multiple images. Differential lensing is not a concern for the present analysis, however, we used the high spatial resolution to infer what the impact of differential lensing between gas and dust would be for unresolved data, finding shifts of approximately 10–30% at most, much less than what is sometimes proposed based on toy models (but the effects in other wavebands might of course be more important).
These images sample two individual regions within a single galaxy that are apart by roughly 470 pc in the source plane, and are spatially resolved along, and also perpendicular to the lensing direction, with sizes of 1.4 kpc × 0.7 kpc, and 1.2 kpc × 0.6 kpc, respectively. Velocity gradients within individual images are larger than the velocity difference between the two regions. Interpreting these velocity gradients as rotational motion, we find mass surface densities of a few 1010M⊙ kpc-2, and a Toomre parameter Q = 1.0 ± 0.3, consistent with a critically Toomre-stable disk on large scales.
The high star-formation intensities of up to 2200 M⊙ yr-1 kpc-2 are clearly in the range of a maximal starburst, and the location of the Ruby in the Schmidt-Kennicutt diagram suggests that star formation is self-regulated by the energy and momentum injection from radiation pressure (“Eddington-limited starburst”) and supernova and wind ejecta from young stellar populations. Both contribute by very similar amounts to balancing the hydrostatic mid-plane pressure. The star-formation efficiency is approximately 1–10%, and we have no reason to suspect that the star-formation law as found in the Milky Way would not be universal even in the most intense starbursts.
We investigate whether kinetic energy from star formation could also explain the gas kinematics, which is a direct probe of the physical link between the energy output from young stars and the processes that determine the star-formation efficiency in scenarios of turbulence-regulated star formation. We find that both radiation pressure and supernovae and winds can provide sufficient feedback to keep molecular clouds in the Ruby marginally gravitationally stable, akin to star-forming clouds in the Milky Way, although at much higher mass surface densities and turbulent pressures. Additional feedback from an AGN is not necessary, in agreement with the absence of a bright AGN in the infrared and radio.
Acknowledgments
We thank the anonymous referee for comments that helped improve the paper. We also thank the ALMA Regional Center in Grenoble for their support with preparing these observations and the ALMA staff in Chile for carrying out the observations. R.C. would like to thank Claudio Grillo for useful discussions and comments. NPHN acknowledges support through a JAO visitor grant, and wishes to thank the ALMA staff in Vitacura for interesting scientific discussions and their great hospitality during an extended stay in early 2016. She also wishes to thank Matt Lehnert for having pointed out that the Kennicutt relation of star formation and FIR luminosity has initially been derived for a Salpeter, not a Chabrier IMF. M.L. acknowledges CNRS and CNES for support. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.1.01518.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. I.O. acknowledges support from the European Research Council in the form of the Advanced Investigator Programme, 321302, cosmicism.
References
- ALMA Partnership,Vlahakis, C., Hunter, T. R., et al. 2015, ApJ, 808, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Amblard, A., Cooray, A., Serra, P., et al. 2011, Nature, 470, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, B. H., & Thompson, T. A. 2011, ApJ, 727, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Audit, E., & Hennebelle, P. 2010, A&A, 511, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Blain, A. W., Smail, I., Ivison, R. J., Kneib, J.-P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bothwell, M. S., Chapman, S. C., Tacconi, L., et al. 2010, MNRAS, 405, 219 [NASA ADS] [Google Scholar]
- Bothwell, M. S., Aguirre, J. E., Chapman, S. C., et al. 2013, ApJ, 779, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., Teyssier, R., Block, D. L., & Puerari, I. 2010, MNRAS, 409, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Silva, L., & Granato, G. L. 2002, A&A, 392, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cañameras, R., Nesvadba, N. P. H., Guery, D., et al. 2015, A&A, 581, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cañameras, R., Nesvadba, N. P. H., Kneissl, R., et al. 2017, A&A, 600, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [Google Scholar]
- Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2011, MNRAS, 410, 1687 [NASA ADS] [Google Scholar]
- Dye, S., Furlanetto, C., Swinbank, A. M., et al. 2015, MNRAS, 452, 2258 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G. 1999, ApJ, 517, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Escala, A., & Larson, R. B. 2008, ApJ, 685, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., Quataert, E., & Hopkins, P. F. 2013, MNRAS, 433, 1970 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Förster Schreiber, N. M., Rosario, D., et al. 2014, ApJ, 796, 7 [Google Scholar]
- Greve, T. R., Leonidaki, I., Xilouris, E. M., et al. 2014, ApJ, 794, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Hatsukade, B., Tamura, Y., Iono, D., et al. 2015, PASJ, 67, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Hayward, C. C., & Hopkins, P. F. 2017, MNRAS, 465, 1682 [Google Scholar]
- Heckman, T. M., Armus, L., & Miley, G. K. 1990, ApJS, 74, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Audit, E. 2007, A&A, 465, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Hodge, J. A., Riechers, D., Decarli, R., et al. 2015, ApJ, 798, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Murray, N., Quataert, E., & Thompson, T. A. 2010, MNRAS, 401, L19 [NASA ADS] [Google Scholar]
- Ikarashi, S., Ivison, R. J., Caputi, K. I., et al. 2015, ApJ, 810, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Iono, D., Yun, M. S., Aretxaga, I., et al. 2016, ApJ, 829, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Swinbank, A. M., Swinyard, B., et al. 2010, A&A, 518, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
- Kennicutt, Jr., R. C. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Tan, J. C. 2007, ApJ, 654, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Thompson, T. A. 2012, ApJ, 760, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996a, ApJ, 462, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996b, ApJ, 472, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [Google Scholar]
- Li, Y., Mac Low, M.-M., & Klessen, R. S. 2005, ApJ, 620, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Murray, N., Quataert, E., & Thompson, T. A. 2005, ApJ, 618, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Polletta, M., Lehnert, M. D., et al. 2011, MNRAS, 415, 2359 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, E. C., & Shetty, R. 2011, ApJ, 731, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Oteo, I., Zwaan, M. A., Ivison, R. J., Smail, I., & Biggs, A. D. 2017, ApJ, 837, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration, XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Romeo, A. B., & Agertz, O. 2014, MNRAS, 442, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Rybak, M., McKean, J. P., Vegetti, S., Andreani, P., & White, S. D. M. 2015, MNRAS, 451, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Serjeant, S. 2012, MNRAS, 424, 2429 [NASA ADS] [CrossRef] [Google Scholar]
- Sharon, K., Gladders, M. D., Rigby, J. R., et al. 2012, ApJ, 746, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Downes, D., Radford, S. J. E., & Barrett, J. W. 1997, ApJ, 478, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Spilker, J. S., Marrone, D. P., Aguirre, J. E., et al. 2014, ApJ, 785, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, E., González-Alfonso, E., Veilleux, S., et al. 2011, ApJ, 733, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Chapman, S. C., Smail, I., et al. 2006, MNRAS, 371, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Papadopoulos, P. P., Cox, P., et al. 2011, ApJ, 742, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Dye, S., Nightingale, J. W., et al. 2015, ApJ, 806, L17 [Google Scholar]
- Tacconi, L. J., Neri, R., Chapman, S. C., et al. 2006, ApJ, 640, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Smail, I., et al. 2008, ApJ, 680, 246 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tecza, M., Baker, A. J., Davies, R. I., et al. 2004, ApJ, 605, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Usero, A., Leroy, A. K., Walter, F., et al. 2015, AJ, 150, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Redshifts, centroid velocities relative to z = 3.005, FWHM line widths, and integrated line fluxes in individual counter images of the Ruby.
All Figures
 |
Fig. 1 Morphology and kinematics of CO(4–3) line emission in the Ruby. Left to right: continuum and gas-mass surface brightness, velocities (in km s-1) and Gaussian line widths (FWHM |
| In the text | |
 |
Fig. 2 Spectra of individual counter images as assembled from clouds identified with Clumpfind, as labeled in Fig. 1. Images #1.2 and #1.3 are blended and identified as a single clump by Clumpfind. The dark blue and red lines show fits with Gaussian functions to the total line profile of each image system shown in Fig. 2, scaled to the total flux in each image. The mismatch between the blue component in image #1.4 can be explained with partial overlap with image #2.2. |
| In the text | |
 |
Fig. 3 Integrated spectra of image system 1 (left) and 2 (right), summed over images #1.1 and #1.2, and #2.1, and #2.2, respectively. Solid blue lines show individual Gaussian components of the line profiles, while the red dashed line shows the sum of both components. |
| In the text | |
 |
Fig. 4 Reconstructed source-plane morphology of the integrated and beam-convolved CO(4–3) line image of regions 1 (left) and 2 (right) as obtained with LENSTOOL. Both regions are spatially well resolved by our ALMA data. Blue diamond-shaped lines indicate the position of the internal caustic line at z = 3.005. The solid and dotted brown lines shows the 3-sigma positional uncertainty on the luminosity-weighted centroid of each region, for the line and continuum emission, respectively. |
| In the text | |
 |
Fig. 5 Zoom onto the southern part of the Ruby, showing the CO(4–3) morphology as color image, and the dust morphology as contours. We note the small offset between the emission-line and continuum peak. |
| In the text | |
 |
Fig. 6 Left: spatially resolved Schmidt-Kennicutt law in PLCK G244.8+54.9 (red stars) and best fit relation (solid black line). The lower and upper black star indicate the luminosity-weighted average position of images #2.1 and #1.1, respectively. Other symbols indicate: submillimeter galaxies at z ~ 2 (green upside-down triangles, Bothwell et al. 2010), local starbursts (black circles, Kennicutt 1998), spatially-resolved data from the Eyelash (dark green triangles Swinbank et al. 2011) and SDP.81 (yellow squares, Hatsukade et al. 2015). The green and dark blue dashed lines indicate the Schmidt-Kennicutt relationship for high-z starburst galaxies and main sequence galaxies of Daddi et al. (2010), respectively. All star-formation rates are given for a Chabrier initial mass function, and are a factor 1.8 lower than in many other figures showing the Schmidt-Kennicutt relationship (see text for details). Right: same Schmidt-Kennicutt diagram, showing the position of maximum starbursts in several models, and the position of the Ruby relative to them. Light blue circles indicate nearby Eddington-limited starbursts (Andrews & Thompson 2011). The dark green solid lines show the mechanical input from stellar winds and supernova remnants for 100% and 50% efficiency, respectively. The dark blue lines and yellow hatched region show the models of Andrews & Thompson (2011) for an Eddington-limited starburst with a range of opacities between 10 and 30 cm2 g-1. Solid lines show the optically thick limit above the critical gas-mass surface density for the optically thick case, dashed lines the optically thin case below that limit. The solid blue line shows the relationship of Ostriker & Shetty (2011), also for optically thick and optically thin gas. The red line shows the model of Faucher-Giguère et al. (2013). |
| In the text | |
 |
Fig. 7 Turbulent scaling (“Larson”) relationship (Larson 1981) between gas velocity dispersion and cloud size in the source plane. Empty red stars show the sizes and line widths of the redshifted and blueshifted components seen in the Ruby within images #1 and #2, respectively. Green and yellow filled circles show similar observations of SDP.81 and the Eyelash from Swinbank et al. (2015) and Swinbank et al. (2011). Empty black circles show giant molecular clouds in the Milky Way. We also show expected line-width size relationships for gas mass surface densities, Σgas = 50M⊙ pc-2 characteristic for the Milky Way, and for 5000 M⊙ and 16 000M⊙ pc-2, which correspond to the lowest and highest values for the Ruby, respectively (Fig. 6). For each density we show the relationship for virial parameters αvir = 1 and 5, that is, clouds where turbulent energy either balances gravitational binding energy (solid line), or where it exceeds it by a factor 5 (dashed-dotted lines). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.