EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 603 (July 2017) A&A, 603 (2017) A121 Full HTML
Free Access
Issue
A&A
Volume 603, July 2017
Article Number A121
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201730690
Published online 19 July 2017

© ESO, 2017

1. Introduction

The interstellar medium (ISM) is pervaded with magnetic fields of energy similar to other ISM species, generated by small-scale and large-scale (α − Ω) dynamo processes and transported with the bulk motion of interstellar plasma (Beck 2016). Observational evidence suggests that magnetic fields in galaxies play an important role in regulating the ISM by confining cosmic ray electrons (Berezinskii et al. 1990) and providing vertical support to the interstellar gas (Fletcher & Shukurov 2001), and regulating angular momentum transfer in gas clouds that eventually collapse to form stars (Zweibel & Heiles 1997). A study of individual nearby galaxies provides us with data on topology and strength of magnetic fields in various galactic environments. Revealing statistical relations between the various observational parameters to describe the galaxies and the magnetic field strength is a helpful tool in recognising, modelling, and understanding the impact of various physical processes involved in the formation and evolution of magnetic fields in the galaxies.

There are objective obstacles encountered in such studies, like difficulties in observing optically and radio-weak dwarf galaxies and distant protogalaxies. For example, a systematic study of low-mass galaxies in the Local Group revealed surprisingly little information concerning magnetic fields in these objects as only three out of 12 dwarfs were detected in the radio domain (Chyży et al. 2011). The results obtained indicated that magnetic fields in the dwarf galaxies are rather weak, with a mean value of total field strength of only 4 μG. Basing on the radio-detected low-mass galaxies (from the Local Group as well as from outside it) a power-law relation of the magnetic field strength and the surface density of star formation rate (SSFR) with an index of 0.30 ± 0.04 was determined. Some other relationships of magnetic fields with galaxy parameters were also found. To what extent the relationships obtained for the low-mass galaxies remain valid also for the massive galaxies and starbursts, is not known.

Recently, Tabatabaei et al. (2016) indicated that the large-scale (ordered) magnetic field in a sample of 26 galaxies is proportional to their rotational speed. The enhanced field in this case could be due to gas compression and shearing flows in fast rotating systems. In another work, Van Eck et al. (2015) used 20 well-observed nearby galaxies to present a statistically important relation of the total magnetic field strength with the SSFR (with the power-law index n = 0.19 ± 0.03) as well as with the density of molecular gas (n = 0.21 ± 0.04). The magnetic pitch angle appeared to be associated with the total gas density, star formation rate, and strength of the axisymmetric component of the large-scale part of magnetic field. A steeper relation between the total field and the SSFR was found by Heesen et al. (2014) for 17 galaxies, containing two dwarfs. Performing similar studies for a much larger sample of different galaxies is much needed.

In order to investigate importance of various correlations of observed parameters of galaxies, Disney et al. (2008) used the principal component analysis (PCA) to statistically analyse a sample of 200 galaxies, showing that the galaxies can be described in a much simpler way than suggested by the hierarchical structure formation theory and are actually controlled by a small number of dominating parameters. In later studies, Li & Mao (2013) reproduced the results of Disney et al. for a sample of 2000 SDSS galaxies and used PCA to construct parameters to better differentiate the galaxies than the original observables, like colour, stellar age, or stellar mass. They also proved that the galaxy environment did not affect galaxy morphology to a greater extent, while significantly changing galactic colours.

In this paper, we explore how the statistical relationships determined for the low-mass objects concern the general population of galaxies, probing relations of magnetic field with a number of properties describing galaxies in a sample of 55 objects. Our sample includes faint dwarf galaxies, normal spirals, and several massive starbursts, in order to cover a wide range of star formation processes and to find out possible interrelations for all the objects. We use our radio observations of low-mass objects and acquire information on the other galaxies from the available publications. The sample’s size allows us to inspect magnetic fields across the Hubble sequence. The radio-faintest dwarf galaxies, for which stacking experiments of their radio maps were performed, are also analysed. The investigation involves a statistical analysis of the galaxy sample basing on two methods, PCA and regression modelling.

2. Galaxy sample

2.1. Low-mass objects

In our low-mass sample, we included low-mass galaxies from our radio observations made with the 100-m Effelsberg telescope: three dwarf galaxies from Chyży et al. (2011) observed at 2.64 GHz (NGC 6822, IC 10, IC 1613), five low-mass, Magellanic-type galaxies observed at 4.85 GHz and/or 8.35 GHz (NGC 3239, NGC 4027, NGC 4618, NGC 5204, UGC 11861), peculiar, “pure disk” objects (NGC 2976 and NGC 4605) (Jurusik et al. 2014), as well as three galaxies (NGC 4236, NGC 4656, IC 2574) from Chyży et al. (2007). For all these galaxies we calculated the total magnetic field strength B assuming energy equipartition between magnetic fields and cosmic rays (Beck & Krause 2005). The separation of thermal emission from the radio total flux was achieved with the help of Hα fluxes. In the case of Magellanic and peculiar objects, we corrected the Hα fluxes for dust attenuation using information on the infrared (dust) emission (see Jurusik et al. 2014). The sizes and masses of these objects are between the dwarf and typical spiral galaxies.

In order to have the best possible representation of radio-faint star-forming dwarf galaxies, we included into the sample UGC 5456 and analysed the “common” sample of dwarfs from the stack experiment from Roychowdhury & Chengalur (2012), while performing a similar stack experiments for the dwarf galaxies of the Local Group which went undetected in the work of Chyży et al. (2011). Using NVSS (1.4 GHz) maps for these nine dwarfs from the Local Group (Aquarius, GR 8, WLM, LGS 3, SagDIG, Sextant A, Sextant B, Leo A, and Pegasus), we were able to estimate only the upper limit of B = 5 ± 1 μG. Presumably, the number of our stacked objects was too small for the signal to be detected. Our Effelsberg observations (Chyży et al. 2011) at 2.64 GHz provided a better estimation of this upper limit with B< 3.8 ± 0.6 μG.

We also added five galaxies from the available work: LMC, SMC, NGC 4449, NGC 1569, NGC 4214. The sources of the data for these objects are given in Table A.1.

2.2. Massive galaxies

Our sample contained well-researched normal spiral galaxies for which we were able to find proper data in the literature. To work with the most uniform dataset possible, we used radio continuum data from the WSRT survey of SINGS galaxies (Braun et al. 2007) to estimate the equipartition magnetic field strength for 14 objects from the nonthermal emission, taking the thermal fractions from Heesen et al. (2014) and the galaxy inclination values from HyperLeda or NED. For other 14 galaxies we used estimations of B (for the entire galaxies) from the compilation of Van Eck (2015). We also added seven well-known spirals from other studies (Table A.1). Our sample involved massive starbursts (NGC 253, M 81) as well as luminous infrared radio galaxies (LIRGs: NGC 3256 and Arp 220).

2.3. Construction of extensive and intensive parameters

For each galaxy in the sample, we searched the literature for information on their global properties: morphological (Hubble) type T, inclination i, distance D, the optical angular radius, which was transformed to the linear one R, rotational velocity V, global SFR, the total H i mass MHI, the total mass of molecular gas MH2, the near-infrared luminosity LK in Ks band, which is related to the total galactic stellar mass. We also calculated “tentative” total masses of galaxies, estimating them from the formula: M ∝ RV2. The parameters: SFR, LK, MHI, MH2, M, R are all extensive properties of galaxies and depend on the object size: splitting a galaxy in half would result in decreasing the values of these parameters to half of the original ones.

The mean magnetic field strength, calculated as an average value over the galaxy, is directly related to the volume density of magnetic energy and calculated from the radio emission, taking into account the synchrotron pathlength. This is an intensive property, independent of galaxy size. Therefore, we constructed other parameters describing the intensive properties of galaxies, free from the influence of their sizes and masses (see e.g. Lara-López et al. 2013). The analysis which global or intensive parameters are mainly related to the magnetic field, and which are less important is one of the purposes of our analysis. We constructed the following set of intensive parameters: the (mean) surface density of star formation rate SSFR = SFR/A, the density of hydrogen gas SMHI = MHI/A, the density of H2 gas SMH2 = MH2/A, near-infrared surface brightness SLK = LK/A, where A is the observed surface area of the galaxy. Moreover, we calculated the star formation efficiency with reference to the neutral gas SFE = SFR/MHI and the similar efficiency for the H2 gas SFEH2 = SFR/MH2. The intensive parameters involving the magnetic field strength and the surface densities are derived for the entire galaxies using their optical or radio extents.

We note that in some literature (e.g. Thompson et al. 2006) the magnetic field strength and gas densities are calculated for restricted regions of strong star formation, which obviously yields different estimates (e.g. in the extreme cases of M 82 and Arp 220, the values of B obtained by us are by an order of magnitude lower than those in Thompson et al. 2006 calculated for compact starbursts). The main properties of all 55 galaxies are summarised in Table A.1.

3. Results

The investigation of our galaxy sample is performed by applying two statistical methods: PCA and two-dimensional regression.

3.1. Principal component analysis

Table 1

Eigenvalues, variances explained by the principal components, and eigenvectors from PCA of global parameters and B (see Sect. 3.1).

Table 2

Eigenvalues, variances explained by the principal components, and eigenvectors of PCA of intensive parameters and B (see Sect. 3.1).

PCA is an exploratory technique useful for finding patterns or structure in a multivariate dataset. This method combines variables (parameters) that redundantly measure the same property, and reduces the importance of variables that contribute little information to the data. It is also useful as a more general statistical tool for describing and understanding the data structure. PCA models the covariance or correlation matrix of the data to find relationships to best account for the data variance. As a result, it produces a number of new, statistically independent variables, called the principal components (PCs), which are linear combination of the original variables.

The problem of determining new variables to maximize information (data variance) is equivalent to finding eigenvectors and eigenvalues of the data covariance (or correlation) matrix. The ith PC is the line in the data parameter space that follows the eigenvector associated with the ith largest eigenvalue measuring the variance in the direction of the ith PC. Therefore the first PC is aligned with the direction of maximum variance in the entire dataset, the second one shows the highest variability for all directions orthogonal to the first PC, and so forth. The number of derived PCs equals the number of the original parameters considered in the analysis and the original observations can be expressed in the new coordinates (by projecting onto the PCs). We performed such PCA basing on the correlation matrix of logarithmised parameters describing our sample of galaxies.

In our first PCA approach, we analysed only the global parameters of galaxies (SFR, MHI, MH2, LK, R, V, and M). It turned out that all the parameters are correlated, allowing for descripting the entire sample by just one principal component (PC1), which can account for 82% of variance in the galaxy parameters. All the global parameters contribute to PC1 to roughly the same extent and with the same sign. The second and next PCs have eigenvalues smaller than 1 and are considered insignificant.

Additionally, introducing B to the global parameters in the subsequent PCA distributes the information on galaxies essentially into two PC components. This is illustrated in Table 1, where the first row gives the eigenvalues that measure the variance in the direction of associated PCs. The sum of eigenvalues gives the total variance in the data, which in our approach is just the number of PCs, as the original variables were standarised. The second row shows the proportion of eigenvalues to the total data variance and determines how big a fraction of the total variance is accounted for by the subsequent PCs. The next part of the table shows in respective columns the components of eigenvectors associated with individual PCs, which can be understood as to what extent each original variable contributed to building a PC. On examining the values presented in Table 1 one can see that PC1 contains mostly information from the global parameters, as in the previous analysis, but involves also a contribution from some (systematic) part of magnetic field B, which is less than in the case of the global parameters. In contrast, most of the information about magnetism is independent of the other parameters and constitutes the next component, PC2. Both PCs account for 75% and 14% of the variability in the data, respectively, which suggests that in this description of galaxies, the global parameters carry much more information than the magnetic field strength.

In our third approach to PCA, we analysed the intensive parameters (SSFR, SFE, SFEH2, SMHI, SMH2, SLK). Here, only four (SSFR, SFE, SMH2, SLK) out of six variables significantly contribute to PC1, which accounts for 51% of the population variability. The other parameters, SFEH2 and SMHI, dominate the components PC2 and PC3, respectively.

Subsequently, we added information about B, which passed almost completely into PC1, where it constituted a factor comparable to the other intensive parameters (see Table 2). The next two primary components are dominated again by SFEH2 and SMHI. The first three components combined describe 91% of the data variance. Contrary to PCA performed on global parameters the magnetic field thus appears equally important as SSFR, SMH2, and SLK, in accounting for the intensive properties of galaxies.

In the final analysis, we took into account all the intensive parameters, including B, and the global ones. From the comparison of eigenvector components, it is clear that the strength of magnetic field is connected mainly to the intensive parameters, while the global parameters have only weak relationships with B.

This is apparent in the correlation vector diagram (biplot in Fig. 1), which shows two-dimensional projections of each data point onto the first two PCs and the components of eigenvectors (shown as arrows) representing the original variables as projected into the PC1-PC2 plane. The elements of the vectors correspond to the correlations of each variable with each PC. As the cosines of the angles between the different vectors are a measure of correlation between the respective variables, the vectors pointing in the same direction represent the perfectly correlated variables, while the perpendicular ones indicate a complete lack of correlation. In our plot the vector corresponding to B is surrounded solely by the vectors of intensive parameters, which suggests that they are closely related. The angles between vectors representing the intensive parameters (including B) and the global ones are large, indicating just weak associations.

Galaxies appear to be well grouped in the PC1-PC2 plane (Fig. 1). In particular, the low-mass objects acquire the highest value of the component PC1 and are located to the right on the graph. More massive objects exhibiting the strongest star formation (LIRGs, M 82) occupy the bottom-left part of the chart and have a small value of the PC1. The starbursting dwarfs NGC 1569 and IC 10 lie between them, while the normal spirals are on the other side of the plot.

thumbnail Fig. 1

Biplot obtained from PCA of all galaxy parameters, showing the positions of individual galaxies and the directions of the original variables (arrows) as projected into the plane of the first two PCs. The horizontal axis is the most varying direction of the data-set. The positions of galaxies were scaled down by the standard deviation of the corresponding PCs multiplied by the square root of the number of observations (bottom and left-hand axes), while the vectors were scaled up by the same values (top and right-hand axes).

3.2. Regressions

The influence of galaxy extensive and intensive properties on magnetic field can be quantitatively assessed by regression methods and expressed in functional form. Following some earlier attempts (e.g. Chyży et al. 2011; Heesen et al. 2014; Van Eck 2015; Tabatabaei et al. 2016, 2017), we approximated the data using power-law functions, which correspond to linear fits after converting to the logarithmic scale. To remove possible data outliers, we used a robust M-estimation of two-dimensional (Y/X) regression by the means of iterated re-weighted least squares. The method was used instead of the ordinary (Y/X) least squares regression, but actually in all cases the results obtained from both the methods were very similar. We also applied bisector regression, that treats the variables in a symmetrical way. For finding the strength of relationship between the parameters, the Spearman’s rank correlation coefficient was determined.

Table 3

Parameters of statistical fits.

The most significant correlation found in the relationship of magnetic field with the galaxy parameters is the relation B − SSFR (ρ = 0.78, Table 3 and Fig. 2a). The fitted index of the power law n = 0.33 ± 0.03 is almost identical with the one obtained for the dwarf irregular galaxies only: 0.30 ± 0.04 (Chyży et al. 2011). The magnetic field is also associated with the global SFR but to a smaller extent (ρ = 0.68, n = 0.21 ± 0.02).

thumbnail Fig. 2

Relations between various galaxy parameters for sample galaxies of different categories: dwarfs – rectangles, Magellanic and peculiar low-mass galaxies – triangles, spiral galaxies – circles, massive starbursts and LIRGs – diamonds. The solid line represents the M-estimation of Y/X regression and the dashed line denotes the bisector fit.

We found that the total magnetic field strength B is significantly correlated (ρ = 0.65) with the surface density of molecular (H2) gas but not correlated with neutral gas SMHI (ρ = − 0.03) (see Figs. 2d, e). As B is closely associated with SSFR , the difference could presumably have arisen from the observed different linking of SSFR with the density of neutral gas (ρ = 0.15) and of molecular gas (ρ = 0.78) (see Fig. 2h). We checked that B − SMHI and B − SMH2 relationships for our sample are similar to those observed for the sample of Van Eck et al. (2015). In our previous work, we found a distinct B − SMHI relation for a group of low-mass (dwarf) galaxies (Chyży et al. 2011). This makes for a remarkable difference with our current study. We think that this can be possibly related to galactic mass (or SFR), since the more massive galaxies we took into consideration, the smaller B − SMHI correlation was observed. When we restricted our sample so as to not include massive starbursts, just a weak correlation emerged (Table 3). The work of Bigiel et al. (2008) can further support this view as it shows that SSFR − SMH2 relation for H i dominated dwarf irregular galaxies resemble the coupling found in outer parts of spiral galaxies, but galaxies with higher fraction of H2 gas or inner parts of spiral galaxies can show slightly different relationship. Bigiel et al. received n = 1.0 ± 0.2 for SSFR − SMH2 relation for galaxies in the regime where SMH2 = 3 − 50 M⊙ pc-2. When our sample was restricted to this range we obtain similar relation with an index of 0.96 ± 0.20.

The relation of B with the total gas density (SMgas = SMHI + SMH2) is also statistically significant for our sample showing a power-law index n = 0.41 ± 0.10 and ρ = 0.52. We note that within regions in M 31 B was found even to be best coupled to the volume density of the total gas rather than to a specific component (Berhhuijsen et al. 1993). For more H2 dominated galaxies we expect B − SMH2 relation to be the strongest one due to a clear, monotonic SSFR − SMH2 relationship shown by Bigiel et al. (2008).

For our sample the magnetic field does not show any significant relation with the star formation efficiency based on H2 (ρ = 0.07). We notice strong association of B with the star formation efficiency based on neutral gas (SFE ) with ρ = 0.75, but this did not provide us with any new information. We explain this association as a result of the mentioned strong B − SSFR correlation and the lack of significant relationships between SSFR and SMHI (Table 3).

The comparison of the strength of correlation of B with global MHI, MH2, and M, shows that B is not closely connected with the total mass M, which is the largest source of gravitational force. Actually, the strongest relation occurs with the molecular mass – that part of the galactic mass which is most related with production of stars. Therefore, we interpret the dependence of B on M (as well as on V) as an indirect one, resulting from the B − SFR coupling and the observed connection of global SFR with the available total molecular mass in galaxies. The association we find between B and LK (ρ = 0.49), a rough estimator of stellar mass in galaxies and stellar activity, may support this line of reasoning.

We checked whether the galaxy inclination is related to any other parameters and whether it could have affected our results. The calculated correlation coefficient between the inclination and the other parameters turned out to be statistically non-significant. We then applied a simple correction for the inclination in calculating the surface density of the SFR: instead of the galaxy observed surface area, we scaled the SFR by the area of a circle with the radius equal to the galaxy major axis. We repeated the regression analysis for the magnetic field and thus obtained the surface density of the star formation rate SSFRcor. The fitted index of the power law n = 0.31 ± 0.03 is very similar to the original one (Table 3), which proves once again that inclination does not change the calculated relationships by more than statistical uncertainties.

4. Discussion and conclusions

The PCA allowed us to compare the significance of relations of B with various galaxy parameters, demonstrating that the global galaxy parameters are all mutually correlated and can be represented by a single principal component. Thus our sample reproduces the result of Disney et al. (2008), who had used almost 200 galaxies (Sect. 1). According to our analysis, the values of magnetic field are not too closely related to the global parameters, hence the latter cannot be a major drivers of magnetic fields. Nevertheless, the PCA and regression analysis do reveal weak correlations of B with the global parameters, for example, the global SFR (Sect. 3.2).

In order to probe these connections and spotting in Fig. 2a that the locations of galaxies depend on their category, we constructed a graph of B along the Hubble sequence (Fig. 3). There is a large diversity of observed strengths of magnetic field for almost each Hubble type. The maximum values of B are not restricted by the morphological type and even dwarf galaxies (those which are in the starburst phase) are able to produce strong total magnetic fields. However, it can be noticed that the lower envelope of field strength varies with the type in a systematic way. Weaker fields appear exclusively in later Hubble types (T> 8) and the mean strength as low as about 5 μG is not observed in the normal spiral galaxies. We suspect these differences are due to density waves, which in the typical spiral galaxies always force some minimal level of star forming activity and in turn, subsequent production of magnetic fields by the small-scale dynamo.

We also notice relatively weak fields for early types of galaxies (Fig. 3), although this part of the diagram requires more data to verify this observation. A systematic decrease of B towards the early-type galaxies is expected: in the Sa (T = 1) galaxies, massive stars form usually in small clusters, while in the Sc-d (5 ≤ T ≤ 7) objects H ii associations containing hundreds or thousands of OB stars are found (Kennicutt 1998b). As the stellar activity modifies the structure and dynamics of ISM, we can suppose that magnetic field topologies and strengths are accordingly changed and weaker fields occur in more quiet ISM.

We find that the closest relationship of B is with SSFR (ρ = 0.78), which is described by a power-law with an index n = 0.33 ± 0.03. As this relation is in excellent correspondence to the one determined for low-mass galaxies alone (0.30 ± 0.04, Chyży et al. 2011) it shows that the processes of generating magnetic field in the dwarf and Magellanic-type galaxies are similar to those in the massive spirals. In the present analysis the statistical sample (of 55 objects) is several times larger than the previous one and not only supports but also even strengthens the results obtained from the Local Group dwarfs. This trend is observed over three orders of magnitude in SSFR for galaxies, while the global SFR spreads over more than four orders of magnitude. Also the three starburst galaxies with highest SSFR (Fig. 2a) fit the trend. Hence, we can reasonably suspect that the distant galaxies with extremely high SFR (like Ultra LIRGs) would also follow this relationship. Deep radio surveys, for example with LOFAR (Hardcastle et al. 2016), can potentially provide appropriate observational evidence.

thumbnail Fig. 3

Magnetic field strength B along the Hubble sequence. Symbolic markers are the same as in Fig. 2.

Our sample is large enough to statistically compare for the first time the production levels of magnetic fields in the spirals, dwarf and irregular galaxies having similar SSFR. The relevant data can be seen in the categorial plot of B against SSFR in Fig. 2a. It appears that the spiral galaxies have slightly stronger fields than dwarfs (in agreement with Fig. 3). Different galaxy mixes can thus lead to different power-law indices in B − SSFR relation, which may explain the slightly different results reported in previous published works (see e.g. Van Eck et al. 2015 and Sect. 1).

In our sample, the total magnetic field is correlated with the density of cold molecular (H2) gas but not with warm neutral (H i) medium (Figs. 2d, e). This is supported by similar results obtained by Bigiel et al. (2008) and Van Eck et al. (2015) for different galaxy samples. According to our work, a best-fit Schmidt law (SSFR − SMgas) shows an exponent n = 1.39±0.20 (Table 3) whereas Kennicutt (1998a) found n = 1.40 ± 0.15 for actively star-forming galaxies.

Considering the above we propose two possibilities to simply interpret the observed B − SSFR relation. According to the first idea this relation partly results from a tight correlation between radio luminosity LR and the infrared luminosity which is closely connected to the global SFR. Modelling of this relation which can be described by a power-law with an index β (LR ∝ SFRβ) usually assumes proportionality of radio luminosity to the CRs production rate, which itself is proportional to the supernova rate and hence to the SFR. Different galaxy properties and environment may further involve other processes as CRs and dust-heating UV-photons escape or synchrotron emission from secondary CR electrons produced by interaction of CRs protons with dense molecular clouds. Assuming further energy equipartition between magnetic fields and CRs yields a formula for radio intensity I ∝ B3 + α where α is the radio spectral index, which allow us to re-write the radio-infrared relation to the form: B ∝ SSFRβ/ (3 + α). The observed relation B ∝ SSFR0.33 and typical value of α = 0.9 results in the radio-infrared relation with β = 1.29. This value is in a good agreement with observations (see e.g. Heesen et al. 2014; Beck 2016).

The second interpretation of the B − SSFR relation we base on the SSFR − SMgas coupling (the Schmidt law with the observed exponent n = 1.39 ± 0.20) which leads to 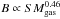. Then we assume turbulent magnetic field amplification, for example by a small-scale dynamo, which results in scaling of the magnetic energy with the turbulent energy of the gas: B2 ∝ SMgasv2 where v ≈ 10 km s-1 is the turbulent gas velocity. This results in scaling 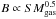which well corresponds with the derived exponent 0.46 and the observed exponent 0.41 ± 0.10 (Table 3). More detailed description of physical processes involved in amplification of magnetic fields by a small-scale dynamo by Schleicher & Beck (2013) leads to the relationship (B ∝ SSFR1 / 3) which is very similar to the observed one.

The results from the stack experiment involving the radio-faint dwarf galaxies (the “common” sample, Sect. 2.1) from Roychowdhury & Chengalur (2012), can also be compared with our B − SSFR relation. The value B = 1.4 μG and SSFR = 9.8×10-4M⊙ yr-1 kpc2 locates these objects significantly (≈ 1 μG) below the trend (Fig. 2a). This difference is not likely due to errors. The value of B is lower than the magnetic field equivalent, due to inverse Compton losses of relativistic electrons in the cosmic microwave background. Hence, the strength estimated from the presumably reduced synchrotron emission can be undervalued. Additionally, at such low SSFR the turbulence injection timescale (or timescale of massive star formation) can become longer than the dissipation timescale of CR electrons and brake the equipartition between magnetic fields and CRs resulting in decrease in synchrotron emission and B (see Schleicher & Beck 2016).

In the case of faint, radio-undetected dwarf galaxies of the Local Group, instead of using results from the stack experiments (Sect. 2.1), we take for the purpose of analysis the upper limit of B = 4 μG from Chyży et al. (2011) and determine SSFR = 7.3 × 10-5M⊙ yr-1 kpc2 from the data presented in that work. The obtained position for these dwarfs is deflected slightly above the global B − SSFR trend. Therefore, these objects and those from the “common” sample were not included in other statistical analyses.

Differential rotation and large-scale dynamo are indispensable to account for the ordered part of magnetic field in galaxies. In the work of Tabatabaei et al. (2016), mainly the ordered part of magnetic field was investigated for a sample of 26 galaxies and found to be correlated with the dynamic mass and the rotational velocities of galaxies. In our sample, only the total field was analysed, but it also showed the relationships with V and M of roughly similar strength (ρ = 0.30 − 035). As the ordered field contributes just little to the total field, the argument of Tabatabaei et al. (2016) that the massive, faster-rotating galaxies compress and share turbulent magnetic field leading to stronger ordered fields is not valid for our B − M and B − V relations (see Fig. 2i). As shown in Sect. 3.2, the total magnetic field B in our objects is strongly associated with the star formation rate (ρ = 0.68), and even more strongly with the SSFR (ρ = 0.78). Such relationships can be explained by the turbulent energy injected to the ISM through supernova explosions and amplification of magnetic fields by a small-scale dynamo (Schleicher & Beck 2016). Hence, we suspect that B is directly related to the SSFR or SMH2, while, since the amount of molecular gas available for star formation is related to the total mass of galaxies (Sect. 3.2), the relation of B with galactic mass or rotation is only an indirect one.

In our sample, the B − SSFR relation is also fulfilled by dwarf galaxies and massive starbursts, which usually manifest slow or disordered rotation. We have shown that even dwarf galaxies with slow rotation and low mass (as e.g. IC 10) can develop strong magnetic fields in the starburst phase. Therefore, for our sample of galaxies, it is the small-scale dynamo mechanism rather than the large-scale one that decisively determines the magnetic field strength.

We note that some relations beween B and intensive variables presented throughout this work could be stronger if they were determined only over the regions of high star-forming activity. In our approach, we applied the average values, based on the full extent of galaxies. Further investigation of these different approaches involving a larger sample of galaxies, from the upcoming large area radio continuum survey with the LOFAR (Shimwell et al. 2017) and the APERTIF (Verheijen et al. 2009) radio telescopes, are highly desirable.

Acknowledgments

This research was supported by Polish National Science Centre through grant 2012/07/B/ST9/04404. We thank Dr. Rainer Beck and the anonymous referee for the detailed and constructive comments. We acknowledge the use of the HyperLeda (http://leda.univ-lyon1.fr) and NED (http://nedwww.ipac.caltech.edu) databases.

References

  1. Adebahr, B., Krause, M., Klein, U., et al. 2013, A&A, 555, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bajaja, E., van der Burg, G., Faber, S. M., et al. 1984, A&A, 141, 309 [NASA ADS] [Google Scholar]
  3. Baan, W. A., van Gorkom, J. H., Schmelz, J. T., & Mirabel, I. F. 1987, ApJ, 313, 102 [NASA ADS] [CrossRef] [Google Scholar]
  4. Beck, R. 2016, A&ARv, 24, 7 [NASA ADS] [CrossRef] [Google Scholar]
  5. Beck, R., & Krause, M. 2005, Aston. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
  6. Berezinskii, V. S., Bulanov, S. V., Dogiel, V. A., & Ptuskin, V. S. 1990, Astrophysics of cosmic rays (Amsterdam: North-Holland), ed. V. L. Ginzburg [Google Scholar]
  7. Berkhuijsen, E. M., Bajaja, E., & Beck, R. 1993, A&A, 279, 359 [NASA ADS] [Google Scholar]
  8. Berkhuijsen, E. M., Urbanik, M., Beck, R., & Han, J. L. 2016, A&A, 588, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
  10. Braun, R., Oosterloo, T. A., Morganti, R., Klein, U., & Beck, R. 2007, A&A, 461, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Calzetti, D., Wu, S.-Y., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
  12. Casasola, V., Bettoni, D., & Galletta, G. 2004, A&A, 422, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Chynoweth, K. M., Langston, G. I., Yun, M. S., et al. 2008, AJ, 135, 1983 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chyży, K. T., Bomans, D. J., Krause, M., et al. 2007, A&A, 462, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Chyży, K. T., Weżgowiec, M., Beck, R., & Bomans, D. 2011, A&A, 529, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Chyży, K. T., Drzazga, R. T., Beck, R., et al. 2016, ApJ, 819, 39 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cohen, R. S., Dame, T. M., Garay, G., et al. 1988, ApJ, 331, L95 [NASA ADS] [CrossRef] [Google Scholar]
  18. Combes, F., García-Burillo, S., Casasola, V., et al. 2014, A&A, 565, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Cram, T. R., Roberts, M. S., & Whitehurst, R. N. 1980, A&AS, 40, 215 [NASA ADS] [Google Scholar]
  20. Crosthwaite, L. P. 2001, Ph.D. Thesis, Univ. California, USA [Google Scholar]
  21. Dame, T. M., Koper, E., Israel, F. P., & Thaddeus, P. 1993, ApJ, 418, 730 [NASA ADS] [CrossRef] [Google Scholar]
  22. de Blok, W. J. G., Józsa, G. I. G., Patterson, M., et al. 2014, A&A, 566, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Disney, M. J., Romano, J. D., Garcia-Appadoo, D. A., et al. 2008, Nature, 455, 1082 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Drzazga, R. T., Chyży, K. T., Jurusik, W., & Wiórkiewicz, K. 2011, A&A, 533, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Dumke, M., Braine, J., Krause, M., et al. 1997, A&A, 325, 124 [NASA ADS] [Google Scholar]
  26. English, J., Norris, R. P., Freeman, K. C., & Booth, F. S. 2003, AJ, 125, 1134 [NASA ADS] [CrossRef] [Google Scholar]
  27. Fletcher, A., & Shukurov, A. 2001, A&A, 325, 312 [Google Scholar]
  28. Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2010, A&A, 522, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Hardcastle, M. J., Gürkan, G., van Weeren, R. J., et al. 2016, MNRAS, 462, 1910 [NASA ADS] [CrossRef] [Google Scholar]
  30. Heald, G., de Blok, W. J. G., Lucero, D., et al. 2016, MNRAS, 462, 1238 [NASA ADS] [CrossRef] [Google Scholar]
  31. Heesen, V., Brinks, E., Leroy, A. K., et al. 2014, AJ, 147, 103 [NASA ADS] [CrossRef] [Google Scholar]
  32. Huchtmeier, W. K., & Seiradakis, J. H. 1985, A&A, 143, 216 [NASA ADS] [Google Scholar]
  33. Irvin, A. J. 1994, AJ, 429, 618 [NASA ADS] [CrossRef] [Google Scholar]
  34. Israel, F. P. 1988, A&A, 194, 24 [NASA ADS] [Google Scholar]
  35. Jarrett, T. H., Chester, T., & Cutri, R. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
  36. Jurusik, W., Drzazga, R. T., Jableka, M., et al. 2014, A&A, 567, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Karachentsev, I. D., & Kaisin, S. S. 2007, AJ, 133, 1883 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kenney, J. D. P., Scoville, N. Z., & Wilson, C. D. 1991, ApJ, 366, 432 [NASA ADS] [CrossRef] [Google Scholar]
  39. Kennicutt, R. C. 1998a, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kennicutt, R. C., Jr. 1998b, ARA&A, 36, 189 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kepley, A. A., Zweibel, E. G., Wilcots, E. M., Johnson, K. E., & Robishaw, T. 2011, ApJ, 736, 139 [NASA ADS] [CrossRef] [Google Scholar]
  42. Koribalski, B. S., Staveley-Smith, L., Kilborn, V. A., et al. 2004, AJ, 128, 16 [NASA ADS] [CrossRef] [Google Scholar]
  43. Lara-López, M. A., Hopkins, A. M., López-Sánchez, A. R., et al. 2013, MNRAS, 433, L35 [NASA ADS] [CrossRef] [Google Scholar]
  44. Leroy, A. K., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]
  45. Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
  46. Li, Z., & Mao, C. 2013, ApJS, 207, 8 [NASA ADS] [CrossRef] [Google Scholar]
  47. Lindblad, P. O. 1999, A&ARv, 9, 221 [NASA ADS] [CrossRef] [Google Scholar]
  48. Liu, L., Gao, Y., & Greve, T. R. 2015, AJ, 805, 31 [NASA ADS] [CrossRef] [Google Scholar]
  49. Martinet, L., & Friedli, D. 1997, A&A, 323, 363 [NASA ADS] [Google Scholar]
  50. Mateo, M. 1998, ARA&A, 36, 435 [NASA ADS] [CrossRef] [Google Scholar]
  51. Misiriotis, A., Popescu, C. C., Tuffs, R., & Kylafis, N. D. 2001, A&A, 372, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Neininger, N., Beck, R., Sukumar, S., & Allen, R. J. 1993, A&A, 274, 687 [NASA ADS] [Google Scholar]
  53. Nikiel-Wroczyński, B., Soida, M., Urbanik, M., et al. 2013, A&A, 553, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Papadopoulos, P. P., van der Werf, P., Xilouris, E., Isaak, K. G., & Gao, Yu 2012, ApJ, 751, 10 [NASA ADS] [CrossRef] [Google Scholar]
  55. Pence, W. D., Taylor, K., & Atherton, P. 1990, ApJ, 347, 415 [NASA ADS] [CrossRef] [Google Scholar]
  56. Rots, A. H. 1979, A&A, 80, 255 [NASA ADS] [Google Scholar]
  57. Roychowdhury, S., & Chengalur, J. N. 2012, MNRAS, 423, L127 [NASA ADS] [CrossRef] [Google Scholar]
  58. Sancisi, R., & Allen, R. J. 1979, A&A, 74, 73 [NASA ADS] [Google Scholar]
  59. Sargent, A. I., Sanders, D. B., & Phillips, T. G. 1989, ApJ, 346, L9 [NASA ADS] [CrossRef] [Google Scholar]
  60. Schleicher, D. R. G., & Beck, R. 2013, A&A, 556, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Schleicher, D. R. G., & Beck, R. 2016, A&A, 593, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Sofue, Y., Tutui, Y., Honma, M., et al. 1999, ApJ, 523, 136 [NASA ADS] [CrossRef] [Google Scholar]
  64. Tabatabaei, F. S., Martinsson, T. P. K., Knapen, J. H., et al. 2016, ApJ, 818, L10 [NASA ADS] [CrossRef] [Google Scholar]
  65. Tabatabaei, F. S., Schinnerer, E., Krause, M., et al. 2017, ApJ, 836, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Thompson, T. A., Quataert, E., Waxman, E., Murray, N., & Martin, C. L. 2006, ApJ, 645, 186 [NASA ADS] [CrossRef] [Google Scholar]
  67. Throson, H. A. , Jr., & Bally, J. 1987, NASCP, 2466, 267 [Google Scholar]
  68. van der Marel, R. P., Rix, H. W., Carter, D., et al. 1994, MNRAS, 268, 521 [NASA ADS] [CrossRef] [Google Scholar]
  69. Van Eck, C. L., Brown, J. C., Shukurov, A., & Fletcher, A. 2015, ApJ, 799, 35 [NASA ADS] [CrossRef] [Google Scholar]
  70. Verheijen, M., Oosterloo, T., Heald, G., & van Cappellen, W. 2009, in Proc. Panoramic Radio Astronomy: Wide-field 1–2 GHz Research on Galaxy Evolution, 10 [Google Scholar]
  71. Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
  72. Wilson, C. D., Warren, B. E., Israel, F. P., et al. 2012, MNRAS, 424, 3050 [NASA ADS] [CrossRef] [Google Scholar]
  73. Woo, J., Courteau, S., & Dekel, A. 2008, MNRAS, 390, 1453 [NASA ADS] [Google Scholar]
  74. Young, J. S., & Scoville, N. Z. 1984, ApJ, 287, 153 [NASA ADS] [CrossRef] [Google Scholar]
  75. Zweibel, E. G., & Heiles, C. 1997, Nature, 385, 131 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Information on galaxies

Table A.1

Breakdown of basic properties of the galaxy sample by category.

All Tables

Table 1

Eigenvalues, variances explained by the principal components, and eigenvectors from PCA of global parameters and B (see Sect. 3.1).

In the text
Table 2

Eigenvalues, variances explained by the principal components, and eigenvectors of PCA of intensive parameters and B (see Sect. 3.1).

In the text
Table 3

Parameters of statistical fits.

In the text
Table A.1

Breakdown of basic properties of the galaxy sample by category.

In the text

All Figures

thumbnail Fig. 1

Biplot obtained from PCA of all galaxy parameters, showing the positions of individual galaxies and the directions of the original variables (arrows) as projected into the plane of the first two PCs. The horizontal axis is the most varying direction of the data-set. The positions of galaxies were scaled down by the standard deviation of the corresponding PCs multiplied by the square root of the number of observations (bottom and left-hand axes), while the vectors were scaled up by the same values (top and right-hand axes).
In the text
thumbnail Fig. 2

Relations between various galaxy parameters for sample galaxies of different categories: dwarfs – rectangles, Magellanic and peculiar low-mass galaxies – triangles, spiral galaxies – circles, massive starbursts and LIRGs – diamonds. The solid line represents the M-estimation of Y/X regression and the dashed line denotes the bisector fit.

In the text
thumbnail Fig. 3

Magnetic field strength B along the Hubble sequence. Symbolic markers are the same as in Fig. 2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.