| Issue |
A&A
Volume 603, July 2017
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201730554 | |
| Published online | 19 July 2017 | |
Search for rings and satellites around the exoplanet CoRoT-9b using Spitzer photometry
1 Institut d’astrophysique de Paris, CNRS, UMR 7095 & Sorbonne Universités, UPMC Paris 6, 98bis Bd Arago, 75014 Paris, France
e-mail: lecaveli@iap.fr
2 Observatoire de Haute-Provence, CNRS/OAMP, 04870 Saint-Michel-l’ Observatoire, France
3 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
4 Universidad de La Laguna, Dept. de Astrofísica, 38206 La Laguna, Tenerife, Spain
5 INAF–Osservatorio Astrofisico di Torino, via Osservatorio 20, 10025 Pino Torinese, Italy
6 Observatoire de l’Université de Genève, 51 chemin des Maillettes, 1290 Sauverny, Switzerland
7 Anton Pannekoek Institute for Astronomy, University of Amsterdam, 1090 GE Amsterdam, The Netherlands
8 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
9 Universidad de Buenos Aires, Facultad de Ciencias Exactas y Naturales, 1053 Buenos Aires, Argentina
10 CONICET – Universidad de Buenos Aires, Instituto de Astronomía y Física del Espacio (IAFE), 1053 Buenos Aires, Argentina
11 Canada-France-Hawaii Telescope Corporation, CNRS, 65-1238 Mamalahoa Hwy, Kamuela, HI 96743, USA
Received: 3 February 2017
Accepted: 29 April 2017
Using Spitzer photometry at 4.5 microns, we search for rings and satellites around the long period transiting planet CoRoT-9b. We observed two transits in 2010 and 2011. From their non-detection, we derive upper limits on the plausible physical characteristics of these objects in the planet environment. We show that a satellite larger than about 2.5 Earth radii is excluded at 3σ for a wide range of elongations at the two epochs of observations. Combining the two observations, we conclude that rings are excluded for a wide variety of sizes and inclination. We find that for a ring extending up to the Roche limit, its inclination angle from the edge-on configuration as seen from the Earth must be lower than 13° in the case of silicate composition and lower than 3° in the case of material with water ice density.
Key words: planetary systems / stars: individual: CoRoT-9 / techniques: photometric
© ESO, 2017
1. Introduction
Satellites and rings are common features in the solar system. All the solar system planets apart from Mercury and Venus host satellites; more than 80 satellites with diameters larger than 10 km are known today, including the six largest ones with diameters between 3000 and 5300 km. Some dwarf planets (Pluto, Eris, and Haumea) also host satellites. Rings are also present around the four giant planets Jupiter, Saturn, Uranus, and Neptune; recently, narrow and dense rings have been discovered around Chariklo, a small Centaur object beyond Saturn. Further, the Cassini spacecraft revealed evidence for the possible past presence of rings around the Saturnian satellites Rhea and Iapetus (Sicardy et al. 2017).
The detection of thousands of exoplanets since the mid 90’s has triggered the search for extrasolar satellites and rings around them. Exomoons and exorings are expected to allow constraints to be put on small body formation and evolution processes in planetary systems. Many models describe the formation of solar system satellites (e.g., Ogihara & Ida 2012); some implying impacts or captures (e.g., Agnor et al. 2004, 2006; see also Barr & Syal 2017; and Barr 2016). Satellites are also found to play a key role in the evolution of the orbital parameters of some planets, as in the case of Uranus (Morbidelli et al. 2012). In addition to allowing similar studies for exoplanetary systems, exomoons could also provoke interest in terms of potential habitability (e.g., Williams et al. 1997; Heller 2012; Heller et al. 2014). Indeed, whereas only a few habitable rocky planets are known, numerous giant exoplanets are known and characterized in the habitable zone of their host stars (Díaz et al. 2016). The detection of a satellite around one of them would have a particularly high impact. In addition to the question of habitable moons, the presence of satellites could also play a role in the habitability of their planets. A famous case is the Moon, which is known to stabilize the Earth’s obliquity and thus helps to avoid dramatic climate changes, which impact the evolution of life (Laskar et al. 1993). Finally, the detection of satellites and rings could be a way to probe the nature of transiting planets, their formation, and evolution history. So the detection of exomoons and exorings would be of high interest.
Several detection methods have been proposed. All are challenging as the expected signals are extremely small. The first of them is the transit method in photometry, which is well adapted to searching for material in the close environment of transiting planets. Transits of satellites and rings would present clear signatures in light curves (e.g., Sartoretti & Schneider 1999; Barnes & Fortney 2004; Arnold 2005; Ohta et al. 2009; Heller 2017). More elaborated methods based on transits could improve the sensitivity for exomoon detection; they include variation scatter peak (Simon et al. 2012) or the orbital sampling effect (Heller 2014). Still based on transits, dynamical effects could also reveal the presence of satellites; they would produce TTV (transit timing variations: Simon et al. 2007; Lewis et al. 2008; Kipping 2009a; Lewis 2013) and/or TDV (transit duration variations: Kipping 2009a,b; Awiphan & Kerins 2013). Other proposed methods to detect exomoons include microlensing (Han & Han 2002; Bennett et al. 2014), spectroscopy (Simon et al. 2010; Kaltenegger 2010), and even direct imaging (Agol et al. 2015). Reflected light and spectroscopy have also been proposed in the search for exorings (Arnold & Schneider 2004; Santos et al. 2015).
Despite several attempts, neither exomoon nor exoring detections have been clearly established up to now. One of the deepest searches for satellites was presented by Kipping et al. (2015) who reported no compelling detection in a survey of tens of systems using Kepler data and a photodynamical model using both the transit method and dynamical effects. Bennett et al. (2014) reported the detection of the microlensing event MOA-2011-BLG-262Lb, which could be due to a sub-Earth-mass satellite orbiting a free-floating gas giant planet, but another scenario with no satellite cannot be excluded. A deep search for exorings surrounding 21 planets, mostly hot-jupiters, using Kepler photometry also yields non-detection (Heising et al. 2015). Solid surrounding material has been proposed around some exoplanets, including β Pictoris b (Lecavelier des Etangs et al. 1995, 2016) and Fomalhaut b (Kalas et al. 2013). The case of 1SWASP J140747.93-394542.6 is particularly rich but uncertain, as the possible ring around the unseen planet J1407b could be sculpted by the presence of a satellite (Kenworthy & Mamajek 2015). So, whereas the existence of exomoons is more than likely, their existence is not demonstrated up to now. Their occurrence rate and their properties remain unknown.
CoRoT-9b (Deeg et al. 2010) is a particularly favorable case for satellite and ring exploration. Indeed, it was the first discovered planet to present all the properties of being transiting, giant, and far enough from its host star to have an extended sphere of gravitational influence (Hill sphere). CoRoT-9b is a 0.84 Jupiter-mass planet orbiting a G3 main sequence star on a nearly circular orbit with a semi-major axis of 0.402 au (a Mercury-like orbit). The orbital period is 95.3 days, and the impact parameter of the transits is almost zero, resulting in an 8-h transit duration. To have stable orbits, the rings and satellites must be included well within the Hill sphere where the gravity of the planet dominates the gravity of the star. The stable prograde orbits are typically within about 0.4 times the radius of the Hill sphere (Hinse et al. 2010 and reference therein). The size of the Hill sphere is proportional to the periastron distance (Lecavelier des Etangs et al. 1995). Most of the transiting planets known before CoRoT-9b were hot-Jupiter types, or pass close to their star at the short periastron distance of their orbit, like HD 80606b, causing them to be strongly irradiated and to have confined Hill spheres. For instance, the radius of the Hill sphere around HD 209458b is about 0.4 × 106 km, or four planetary radii. In contrast, CoRoT-9b is a much cooler planet, with a periastron not shorter than 0.33 au (Bonomo et al. 2017). As a consequence, CoRoT-9b has an extended Hill sphere ![\hbox{$R_{\rm Hill} \approx a (1-e) \sqrt[3]{\frac{M_{\rm p}}{3 M_\star}} \approx 3.5 \times 10^{6} $}](/articles/aa/full_html/2017/07/aa30554-17/aa30554-17-eq5.png) km, where a and e are the semi-major axis and the eccentricity of its orbit and Mp and M⋆ the planetary and stellar masses, respectively. This Hill sphere radius is two to three times larger than the orbit of the major Jupiter and Saturn satellites like Callisto and Titan, which have orbital distances of 1.8 and 1.2 × 106 km, respectively. We highlight also that all satellites of Jupiter and Saturn, including minor satellites, are within half of the Hill sphere radius of their planet. By analogy, CoRoT-9b presents good prospects for having rings and satellites in the inner part of its Hill sphere. Moreover, the brightness of the CoRoT-9b host star (V = 13.7) is high enough to allow accurate photometry. Consequently, this giant planet is one of the most favorable cases to search for transiting solid material such as rings and satellites in its environment.
km, where a and e are the semi-major axis and the eccentricity of its orbit and Mp and M⋆ the planetary and stellar masses, respectively. This Hill sphere radius is two to three times larger than the orbit of the major Jupiter and Saturn satellites like Callisto and Titan, which have orbital distances of 1.8 and 1.2 × 106 km, respectively. We highlight also that all satellites of Jupiter and Saturn, including minor satellites, are within half of the Hill sphere radius of their planet. By analogy, CoRoT-9b presents good prospects for having rings and satellites in the inner part of its Hill sphere. Moreover, the brightness of the CoRoT-9b host star (V = 13.7) is high enough to allow accurate photometry. Consequently, this giant planet is one of the most favorable cases to search for transiting solid material such as rings and satellites in its environment.
With that in mind we observed photometric transits of CoRoT-9b with the Spitzer space observatory using the IRAC camera at 4.5 μm on the post-cryogenic mission. A sufficiently large satellite around CoRoT-9b would have a clear signature in the transit light curve with a duration similar to the planetary transit, that is, about 8 h. A 2-REarth satellite would produce a transit depth of ~ 4 × 10-4. Rings would have signatures in the shape of the light curve during ingress and egress, with a transit depth that could be up to 10-3. Thanks to its high sensitivity and its Earth-trailing heliocentric orbit allowing long-duration continuous observations, Spitzer is particularly well adapted for the search of tiny signals in a light curve of a planetary transit.
Observations have been carried out in 2010 and in 2011. These observations are presented in Sect. 2, and the data analysis is described in Sect. 3. The search for satellites and rings are presented in Sects. 4 and 5 together with the derived upper limits, before concluding in Sect. 6.
2. Observations
The long orbital period of the planet and the observability windows make CoRoT-9b transits observable with Spitzer particularly rare. Only two transits were observable between 2010 and 2013; we observed both of them.
We first observed1 the transit centered on June 18, 2010 at 01h (UT) with the IRAC camera of Spitzer (Fazio et al. 2004). Only two infrared channels of the IRAC camera are available in the post-cryogenic Spitzer. We chose to observe with only one of the two channels in order to avoid repointing the telescope during the transit, thus reducing overheads. This allows the target to be located on the same part of the detector during all the observation sequence and thus to reduce systematic effects due to imperfect flat-field corrections and intra-pixel sensitivity variations. We chose the Channel 2 at 4.5 μm for the observation since it has the best noise properties. This wavelength also has a lower limb-darkening effect than Channel 1 at 3.6 μm. This, as well as the lower uncertainty on the limb darkening effect, favors the search for ring signatures in the ingress and egress light curves. The observations were executed using IRACs stellar mode. While planning the observation in the Astronomical Observing Request (AOR) format, we carefully selected a pixel area avoiding dead pixels. We also purposely did not dither the pointing in order to keep the source on a given pixel of the detector, and increase the photometric accuracy. This common observational strategy matched that of our previous Spitzer observations of HD 189733 (Ehrenreich et al. 2007; Désert et al. 2009, 2011a).
The run #1 observation was secured between June 17 at 10 h and June 18 at 15 h (UT), 2010. We acquired 3338 consecutive images, each of them obtained in whole array with a 30-s integration time (26.8-s effective integration time per pixel). Such exposure time clearly avoids saturation of the pixels. The 29-h total duration of the sequence covers the transit of the half inner part of the planetary Hill sphere where the rings and large satellites are supposed to be located. This includes 10.5 h before and 10.5 h after the transit to cover ~ 1.7 × 106 km around the planet.
The second transit observed during run #2 was centered on July 04, 2011 at 03h (UT)2. We acquired 4376 consecutive images between July 03 at 8 h and July 04 at 21 h (UT), with the same IRAC setting as for the first transit. This provides more than 37 h’ coverage corresponding to ~ 2.2 × 106 km around the planet. The longer duration of this second observation run was chosen to improve the coverage of the out-of transit light curve and increase the chance of detecting a putative satellite at large distance from the planet: the ingress/egress of the satellite at large elongation may require the observation at about ~15 h before/after the central time of the transit of the planet (see Sect. 4).
3. Data analysis
3.1. Spitzer photometry
The analysis was done using the Spitzer/IRAC Basic Calibrated Data (BCD) of the 7714 frames. These frames are produced by the standard IRAC calibration pipeline and include corrections for dark current, detector nonlinearity, flat fielding, and conversion to flux units. To extract the light curves, we first find the center of the point-spread function (PSF) of the star to a precision of 0.01 pixels by computing the weighted centroid of the star. To obtain the photometric measurement, we then used the APER routine of the IDL Astronomy Library3 to perform a weighted photometry within an aperture of a given radius (Horne 1986; Naylor 1998). After various tests, we decided to use a radius of 2.3 pixels, which minimizes the final rms of the light curves. The background level for each image was determined with APER by the median value of the pixels inside an annulus, centered on the star, with an inner and outer radius of 10 and 15 pixels, respectively. The PSF, used for weighting, is estimated as the median of the background-subtracted fluxes. The estimated error on the weighted integrated flux is calculated as the square root of the photon-noise quadratic sum (Horne 1986; Naylor 1998). After producing a time series for each observation, we iteratively select and trim outliers by comparing the measurements to a transit light curve model. Doing so, we remove any remaining points affected by transient phenomena. At the end, we discarded 170 exposures in run #1 and 522 in run #2; we ended up with a total of 3168 photometric measurements in run #1 and 3854 in run #2. The decrease of the measured rms when binning the measurements up to 100 pixels showed that the red noise is negligible at least on a timescale of one hour.
For the 2010 data, we considered the time given in barycentric modified Julian Date (BMJD), from which we removed a constant value of 55 364. This yields a zero reference time on June 17, 2010 at 0h00 UT. For the 2011 data, we removed a constant value of 55 745, which yields a zero reference time on July 3, 2011 at 0h00 UT.
3.2. Correction of systematics
 |
Fig. 1 Light curve of CoRoT-9 during the transit of CoRoT-9b on June 18, 2010. Each dot represents an individual photometric measurement. Large squares show the data measurements rebinned by 40. The thick red line shows the best fit with an exoplanet transit model. The bottom panel gives the residual of the measurements after subtraction of the best fit model. The two vertical dashed lines represent the time range of the estimated time of the photometric bump that could be due to the transit in front of a stellar spot. The data taken within this time range have been excluded from the analysis. |
The Spitzer/IRAC photometry is known to be systematically affected by the so-called pixel-phase effect. This effect produces an oscillation of the measured fluxes due to the Spitzer telescope jitter and the intra-pixel sensitivity variations on the IRAC detector (see e.g., Charbonneau et al. 2005; Désert et al. 2009; 2011b). To correct for these systematics, we used the method developed by Ballard et al. (2010). A map of the sensitivity function is calculated using the residuals of the measurements in a non-corrected light curve compared to a theoretical light curve in the neighborhood of each pixel (see Eq. (1) in Ballard et al. 2010). For each measurement, we obtained a weighted-sensitivity correction factor W, which is used to correct the measurements as a function of the barycenter position of the target. The typical length scale of the Gaussian used to smooth the sensitivity map is characterized by σx and σy in the x and y direction. The values of σx and σy are obtained by minimizing the rms in the final light curve.
We also implemented the BLISS algorithm, which uses a bilinear interpolation on a grid to map the sensitivity variation as a function of the position of the target on the detector (Stevenson et al. 2012). We concluded that the BLISS algorithm does not provide significant improvement compared to the Ballard et al. algorithm: we found that the improvement in the rms vanished if, for each corrected measurement, the residual of that measurement was excluded from the map calculation. We therefore decided to use the Ballard et al. algorithm for all our photometric measurement extractions.
3.3. Light curves
The final light curves for run #1 (2010) and run #2 (2011) observations are plotted in Figs. 1 and 2. The flux measurements are fitted using a theoretical transit light curve given by the equations of Mandell & Agol (2002) in the small planet approximation. The limb darkening coefficients for the bandpass of the Spitzer Channel 2 at 4.5 μm are obtained from the table of Sing (2010). For a star with T = 5630 K, [Fe/H] = 0, and log g = 4.5 and fixing c1 = 0, interpolation of Sing’s Table gives c2 = 0.8071, c3 = −0.9785, and c4 = 0.3973.
A first fit reveals a bump in the light curve of run #1 (Fig. 1). It could be due to an instrumental artifact or to the planet transiting in front of a stellar spot, however we make no conclusions as CoRoT-9 is not known to be particularly active. The bump is seen from t = 24 h to t = 25.5 h, and hereafter the corresponding data have been excluded for the analysis presented here.
The fits to the light curves have six free parameters: b, the impact parameter in units of stellar radius, T0, the central time of the transit, Rp/R∗, the planet to star radius ratio, v the tangential transit velocity in stellar radius per unit of time, and A0,1 the two parameters of the first degree polynomial fitting the light curve baseline. The tangential transit velocity v is related to the semi-major axis a by the equation 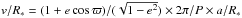 , where e, ϖ, and P are the eccentricity, the longitude of periastron, and the period of the orbit, respectively. The eccentricity is not a parameter of the model because it does not affect the shape of the light curve (see Hébrard et al. 2010); it is only needed to convert the measured v/R∗ into an estimate of a/R∗. We also let the weighted-sensitivity W free to vary in calculating the parameter and its error bar estimates. This ensures that the error bars are not underestimated by a bias introduced by a miscalculation of W.
, where e, ϖ, and P are the eccentricity, the longitude of periastron, and the period of the orbit, respectively. The eccentricity is not a parameter of the model because it does not affect the shape of the light curve (see Hébrard et al. 2010); it is only needed to convert the measured v/R∗ into an estimate of a/R∗. We also let the weighted-sensitivity W free to vary in calculating the parameter and its error bar estimates. This ensures that the error bars are not underestimated by a bias introduced by a miscalculation of W.
We found that these light curves are well fitted by b = 0.00 ± 0.25, T0run#1 = 24.645 ± 0.020 h, T0run#2 = 26.795 ± 0.025 h, 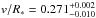 h-1. We found a slightly different Rp/R∗ radius ratio in the two light curves: Rp/R∗ run#1 = 0.1167 ± 0.0011 and Rp/R∗ run#2 = 0.1140 ± 0.0015. This small difference (1.5σ) could be linked to the bump seen in run #1. If the bump is due to an occulted spot, this would yield a higher relative surface brightness of the spot-free transited part of the stellar disk used in the fit (we recall that we excluded from the fit the measurements obtained during the bump, see Fig. 1) and therefore a bias towards a higher transit depth.
h-1. We found a slightly different Rp/R∗ radius ratio in the two light curves: Rp/R∗ run#1 = 0.1167 ± 0.0011 and Rp/R∗ run#2 = 0.1140 ± 0.0015. This small difference (1.5σ) could be linked to the bump seen in run #1. If the bump is due to an occulted spot, this would yield a higher relative surface brightness of the spot-free transited part of the stellar disk used in the fit (we recall that we excluded from the fit the measurements obtained during the bump, see Fig. 1) and therefore a bias towards a higher transit depth.
The determination of refined parameters for the CoRoT-9 planetary system is beyond the scope of the present paper. This is done by Bonomo et al. (2017), who use the present Spitzer data as well as other datasets.
 |
Fig. 3 Difference of the χ2 between the best fit with a satellite and without a satellite as a function of the satellite size and central time of transit, measured in the light curve of the 2010 transit. The red iso-curves are for negative values of Δχ2, where the fit with a satellite is better than the fit without satellite. The vertical lines show the central time (short-dashed) and the time of first and fourth contact (long-dashed lines) for the transit of the planet. The upper x-axis provides the projected distance of the satellite to the planet (elongation) for the corresponding central time of the satellite transit (T0s). |
4. Search for satellites
4.1. Method
In all of the following, we search in the light curves for the signature of the transit of an additional body in front of the star, which could be a satellite. If a satellite is present in the environment of the planet, it will produce an additional occultation when it transits the star. The satellite transit depth depends on the satellite to star radius ratio Rsat/R∗. The transit epochs or central time of the satellite (T0s) depend on the elongation of the satellite relative to the planet projected on the sky and on the direction of the planet’s trajectory.
To perform the search for the satellite, we fitted the light curves of 2010 and 2011 observations with theoretical light curves including a satellite with the two additional fixed parameters defined above (Rsat/R∗ and T0s) whilst keeping the other parameters describing the planet and its orbit free to vary. For each satellite configuration, we calculated the resulting χ2(Rsat/R∗,T0s) and its difference with the best 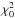 of the fit without a satellite:
of the fit without a satellite: 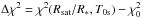 . Although the light curve noise may not be exactly Gaussian, this Δχ2 can be used to quantify the improvement in the fit when introducing a satellite in the model. A more rigorous treatment would require modeling the data covariance matrix, which is also beyond the scope of this paper. Furthermore, we estimate that the effect on our results would be small. Moreover, to see if the possible improvement of the χ2 (when Δχ2< 0) could be due to features in the light curve that are not related to a satellite (i.e., correlated red-noise on transit duration timescale, or simply the decrease of the number of degrees of freedom with the addition of two parameters in the model), we also considered the theoretical light curves with an increase of the flux with the same shape as the flux decrease due to a satellite of a given size and elongation: we parametrize those test light curves (“bright-satellite”) with a negative planet size Rsat/R∗< 0.
. Although the light curve noise may not be exactly Gaussian, this Δχ2 can be used to quantify the improvement in the fit when introducing a satellite in the model. A more rigorous treatment would require modeling the data covariance matrix, which is also beyond the scope of this paper. Furthermore, we estimate that the effect on our results would be small. Moreover, to see if the possible improvement of the χ2 (when Δχ2< 0) could be due to features in the light curve that are not related to a satellite (i.e., correlated red-noise on transit duration timescale, or simply the decrease of the number of degrees of freedom with the addition of two parameters in the model), we also considered the theoretical light curves with an increase of the flux with the same shape as the flux decrease due to a satellite of a given size and elongation: we parametrize those test light curves (“bright-satellite”) with a negative planet size Rsat/R∗< 0.
In these calculations to search for a perturbation in the light curve due to a satellite (or a ring in the Sect. 5), we also left the sensitivity correction factors W free to vary. This ensures that if a ring or a satellite is detected it cannot be due to a bias introduced by a miscalculation of W.
4.2. Results
The resulting Δχ2 difference as a function of the satellite size and elongation are plotted in Figs. 3 and 4 for the 2010 and 2011 observations, respectively.
In the fit to the 2010 data, an improved χ2 is found with Δχ2 ≲ −4 for Rsat/R∗ ~ 0.026 and T0s ~ 36.5 h, and for Rsat/R∗ ~ 0.025 and T0s in the range 16 h-21 h (Fig. 5). However, it can be seen in Fig. 3 that similar Δχ2 can be found for negative values of Rsat/R∗, with even Δχ2 < −9 for Rsat/R∗ ~ −0.028 and T0s ~ 27.6 h. We conclude that in the cases where there is an improvement in the fit by including a satellite in the transit model, this improvement is likely due to correlated noise and other features in the light curves that are not related to the transit of a satellite in front of the star. We note that although Bonomo et al. (2017) stated that the correlated noise is practically negligible, here we are considering correlated noise on the very long timescale of the transit duration, which cannot be quantified within the present data.
The observations of 2011 yield similar results (Fig. 4). The χ2 improvement is Δχ2 ~ −3.4 at the best for Rsat/R∗ ~ 0.020 and T0s ~ 20.5 h (Fig. 6). Again this is not a significantly better fit to the data compared to the fits that include a (fake) “bright-satellite” like the one at, for instance, Rsat/R∗ ~ −0.020 and T0s ~ 35 h, which yields Δχ2 ~ −5. Therefore, we conclude that this best fit including a satellite is most likely a false positive signature for a satellite transit in the light curve.
Nonetheless, we can derive upper limits on the size of a satellite that can be detected in the present data. Using 2010 data (Fig. 3), we derive an upper limit at 3σ (Δχ2> 9) for the radius ratio of Rsat/R∗< 0.025 (Rsat< 2.5 R⊕) if T0s ranges from 8 h to 12 h and from 27 h to 31.5 h. These T0s correspond to projected distances to the planet of 3.0−2.2 × 106 km (0.9−0.6 Hill radius) ahead of the planet and 0.4−1.2 × 106 km (0.1−0.3 Hill radius) after the planet at the epoch of observation. For other elongations, correlated noise leading to a fake positive signature significantly increases the upper limit, and the transit of the planet itself hides the possible signature of a satellite for | T0s−T0p | < 2.0 h, corresponding to a projected distance lower than 0.35 × 106 km (0.1 Hill radius).
The 2011 data yields approximately similar upper limits: we derive the same upper limit of 2.5 R⊕ for T0s ranging from 29 h to 38 h, that is for a projected distance of 0.4−2.0 × 106 km (0.1−0.6 Hill radius) after the planet at the epoch of observation.
We did not compute upper limits using the 2010 and 2011 transits simultaneously as any potential satellite is expected to have a different position at different epochs.
 |
Fig. 5 Light curve of the transit on June 18, 2010, and the fit including a satellite with a radius of 0.026 times the planet radius, and with a central time of transit 16.0 h after June 17, 2010, 0h00 UT (blue solid line). This fit has a χ2 of 3162.4, that is smaller by ~6.4 than the χ2 = 3168.8 of the fit without a satellite. The data have been rebinned by 31 into 100 individual measurements. The red dashed line shows the transit model without a satellite. The model light curve with the satellite has an additional occultation starting at about 12 h and ending at about 20 h. The bottom panel shows the residuals of the data (filled squares) and the light curve of the model including the satellite, after subtraction of the best fit without a satellite. |
 |
Fig. 6 Same as Fig. 5 for the transit of 2011 and the fit including a satellite with a radius of 0.020 times the planet radius, and with a central time of transit 19.0 h after July 3, 2011, 0h00 UT. This fit has a χ2 of 3938.8, that is smaller by ~2.5 than the χ2 = 3941.3 of the fit without a satellite. Here the additional occultation by the satellite starts at about 15 h. |
5. Search for rings
5.1. Method
We also searched in the light curves for the signature of the transit of rings surrounding the planet. If rings are present in the environment of the planet, they affect the shape of the light curve observed during the ingress and the egress: at first order, the rings, which are elongated occulting bodies, make the ingress/egress last longer than a spherical body producing the same occultation depth. To avoid an additional degree of freedom in the considered ring models, we hypothesize that the ring has an ascending node close to the plane of the sky and thus is oriented such that, as seen from the Earth, the main axis of the elliptic ring shadow is in the direction of the planet trajectory. For a ring that has a different orientation, at first order, a ring configuration with the same extension and thickness would produce a very similar light curve. In the case of a positive detection, it would be interesting to explore various inclination configurations in the three-dimensional space that match the detection. But with no detection, this is not the purpose of the work presented here.
In the light curve, the ring transit depth and transit duration depend on the apparent thickness and size of the elliptic shadow of the ring. The ellipse figure of the ring is characterized by its extension from the planet limb (Lr) and its apparent thickness or height (Hr), both expressed in units of stellar radius. From these parameters, we can derive the semi-major and semi-minor axis of the shadow ellipse occulting the stellar disk to be ar = Lr + Rp and br = Hr/ 2. Therefore, the inclination of the ring axis relative to the plane of the sky, ir, is given by Hr/ 2/(Lr + Rp) = sin(90°−ir).
To perform the search for rings, we fitted the light curves of 2010 and 2011 observations with theoretical light curves including a ring with the two additional parameters defined above (Lr/R∗ and Hr/R∗). The area of the rings shadow occulting the stellar disk was calculated using a generalization of equations given by Zuluaga et al. (2015) and equations for the sector and segment areas of an ellipse given by Cavalieri’s Principle4 to obtain an analytical derivation of the area of the intersection of the stellar disk, the planetary disk, and the ring’s shadow. For each ring configuration, we calculated the resulting χ2(Lr/R∗,Hr/R∗) of the fit with the given ring and the corresponding difference with the best 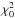 of the fit without a ring:
of the fit without a ring: 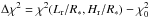 . To see if the possible improvement of the χ2 (when Δχ2< 0) could be due to features that are not a ring, we also considered the theoretical light curves with an increase of the flux as we have done in the search for a satellite. We parametrize those test light curves (“bright-ring”) with a negative ring thickness Hr/R∗< 0.
. To see if the possible improvement of the χ2 (when Δχ2< 0) could be due to features that are not a ring, we also considered the theoretical light curves with an increase of the flux as we have done in the search for a satellite. We parametrize those test light curves (“bright-ring”) with a negative ring thickness Hr/R∗< 0.
5.2. Results
The resulting Δχ2 difference as a function of the ring size and ring thickness is plotted for the 2010 and 2011 observations in Figs. 7 and 8. Because the rings are not expected to have changed between the two observations, we also produced the same plot obtained by combining the two sets of data (Fig. 9). A plot of the light curve and the corresponding fit including a ring is given in Fig. 10.
None of the fits including rings yield a significantly better fit to the light curves (2010, 2011 or combined) than the best fit without a ring. The best improvement in the χ2 is lower than a unity: Δχ2> −1. The Δχ2 is found to be closely related to the equivalent occulting area of the ring, which is proportional to Lr × Hr (light blue curves in Figs. 7–9).
As for the satellite, despite a non-detection, we can derive upper limits on the size of a ring that could have been detected in the present data as a function of its thickness. Using the combined data set (Fig. 9), we derive an upper limit at 3σ (Δχ2> 9) for the ring size. For thickness of Hr/R∗ = 0.015, the 3σ upper limit is Lr/R∗< 0.25; for Hr/R∗ = 0.030 and Hr/R∗ = 0.050, the upper limits are Lr/R∗< 0.16 and Lr/R∗< 0.12, respectively.
 |
Fig. 7 Difference of the χ2 between the best fit with a ring and without a ring as a function of the ring size and thickness, which is obtained using the light curve of the 2010 transit. Blue thin lines show the iso-curves of the equivalent occulting area of the ring Lr × Hr. |
The Roche limit for the ring size in the fluid approximation is about 2.4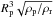 , where Rp is the planet radius, and ρp and ρr are the density of the planet and the ring material5, respectively. For a ring composed of silicates (ρr ~ 2.6 g cm-3) or water ices (ρr ~ 1 g cm-3), we have a Roche limit of 1.7Rp and 2.4Rp, respectively. Because here the ring size, Lr, is counted from the planet limb, these latter values correspond to the ring sizes of Lr = 0.7 Rp = 0.08 R∗ and Lr = 1.4 Rp = 0.16 R∗. For these ring sizes, the combined data set yields 3σ upper limits on the thickness that are Hr/R∗< 0.090 and Hr/R∗< 0.030, respectively (Fig. 9). The ring thickness Hr is related to ir the ring inclination to the line of sight by Hr/ 2/(Lr + Rp) = sin(90°−ir); we therefore conclude that in the case of a ring extending up to the Roche limit, our non-detection constrains its inclination to be | ir−90° | < 13° in the case of silicates and | ir−90° | < 3° in the case of material with water ice density.
, where Rp is the planet radius, and ρp and ρr are the density of the planet and the ring material5, respectively. For a ring composed of silicates (ρr ~ 2.6 g cm-3) or water ices (ρr ~ 1 g cm-3), we have a Roche limit of 1.7Rp and 2.4Rp, respectively. Because here the ring size, Lr, is counted from the planet limb, these latter values correspond to the ring sizes of Lr = 0.7 Rp = 0.08 R∗ and Lr = 1.4 Rp = 0.16 R∗. For these ring sizes, the combined data set yields 3σ upper limits on the thickness that are Hr/R∗< 0.090 and Hr/R∗< 0.030, respectively (Fig. 9). The ring thickness Hr is related to ir the ring inclination to the line of sight by Hr/ 2/(Lr + Rp) = sin(90°−ir); we therefore conclude that in the case of a ring extending up to the Roche limit, our non-detection constrains its inclination to be | ir−90° | < 13° in the case of silicates and | ir−90° | < 3° in the case of material with water ice density.
It is also interesting to know if rings similar to Saturn’s and not fully opaque could be detected. Here forward scattering is negligible because observable signals require scattering surfaces that subtend a significant angle as seen from the star, as would be the case for objects on shorter orbital distances. An example for an observable scattering signal is from KIC 12557548 (Rappaport et al. 2012), an evaporating transiting planet on a 16-h orbit, but scattering cannot be observable for a ring around CoRoT-9b at 0.33 au from the star (see also the marginal scattering amplitude compared to the extinction for a comet-like object at 0.3 au from the star, in Fig. 4 of Lecavelier et al. 1999). Saturn’s inner A-D rings extend to a distance of 137 000 km from Saturn’s center. This corresponds to Lr = 1.3 RSaturn, where we use a Saturn equatorial radius of 60 000 km. For a corresponding value of Lr = 1.3 Rp = 0.15 R∗, we have a 3σ upper limit for the thickness of Hr/R∗< 0.032 or Hr< 0.28 Rp. Based on profiles of the Saturn rings’ optical transmission at 0.9 microns (Nicholson et al. 2000), we use an average optical depth of τ = 0.3. The transmittance Ti of the rings at a given inclination ir (where 0° inclination is for face-on rings) is given by the usual equation Ti = e(− τ/ cosir). For a face-on disk, we obtain a transmittance Ti = 0 = 0.75. For inclined translucent rings, we have an occultation similar to rings with Hr = 2 × (1−Ti) × (Lr + Rp)sin(90°−ir). Assuming an optical depth of τ = 0.3 and a ring size Lr = 1.3 Rp, from the 3σ upper limit of Hr< 0.28 Rp we therefore derive that Saturn-like rings with inclination as large as 4° could still have been detected around CoRoT-9b. The chance of missing a Saturn-like ring system is therefore relatively low.
 |
Fig. 10 Light curve of the transit on June 18, 2010, and the fit including a ring with a size Lr = 0.2 R∗ and a thickness Hr = 0.07 R∗, where R∗ is the star radius (blue line). This fit has a χ2 of 3204, that is larger by ~35 than the χ2 of the best fit without a ring (thin red line). Such ring is thus excluded at about 6σ confidence level. The bottom panel shows the residuals after subtraction of the best fit without ring. |
6. Conclusion
Through detailed analysis of two transit light curves of CoRoT-9b, we searched for the signature of a satellite and rings in the planet’s environment. Despite the non-detection, we have been able to derive upper limits for the satellite and the ring sizes. The upper limits on the satellite size are not very constraining, nonetheless the presence of satellites may have been jeopardized by the dynamical instability, which could be at the origin of the planet eccentricity (Bonomo et al. 2017). Since the discovery of CoRoT-9b, a few other exoplanets have been discovered in transit at large orbital distances. To enlarge the exploration of the giant exoplanets’ environment, these targets deserve to be observed at high photometric accuracy. In this spirit, it is expected that the forthcoming new space facilities, such as the ESA/Cheops photometric observatory, will allow a deeper search of perturbation in the light curves that can be due to small bodies in orbit around those planets.
Alexander Bogomolny, Area, Sector Area, and Segment Area of an Ellipse, from Interactive Mathematics Miscellany and Puzzles, http://www.cut-the-knot.org/Generalization/Cavalieri2.shtml
We note that rings may be larger than the Roche limit, as is known from the presence of Saturn’s E ring and the still wider Phoebe ring. However, these rings are very tenuous (the denser E Ring has an optical depth of ≲10-5, Showalter et al. 1991), making the detection of such wide rings in transit observations highly unlikely.
Acknowledgments
This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Support for this work was provided by the CNES and by an award from the Fondation Simone et Cino Del Duca. We acknowledge the support of the French Agence Nationale de la Recherche (ANR), under program ANR-12-BS05-0012 “Exo-Atmos”. A.S.B. acknowledges funding from the European Union Seventh Framework programme (FP7/2007-2013) under grant agreement No. 313014 (ETAEARTH). HD acknowledges support by grant ESP2015-65712-C5-4-R of the Spanish Secretary of State for R&D&i (MINECO). D.E. acknowledges the financial support of the National Centre for Competence in Research “Planets” supported by the Swiss National Science Foundation (SNSF).
References
- Agnor, C., & Asphaug, E. 2004, ApJ, 613, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Agnor, C. B., & Hamilton, D. P. 2006, Nature, 441, 192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Agol, E., Jansen, T., Lacy, B., Robinson, T. D., & Meadows, V. 2015, ApJ, 812, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, L. F. A. 2005, ApJ, 627, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, L., & Schneider, J. 2004, A&A, 420, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Awiphan, S., & Kerins, E. 2013, MNRAS, 432, 2549 [NASA ADS] [CrossRef] [Google Scholar]
- Ballard, S., Charbonneau, D., Deming, D., et al. 2010, PASP, 122, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. W., & Fortney, J. J. 2004, ApJ, 616, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Barr, A. C. 2016, Astron. Rev., 12, 24 [Google Scholar]
- Barr, A. C., & Syal, M. B. 2017, MNRAS, 466, 4868 [NASA ADS] [Google Scholar]
- Bennett, D. P., Batista, V., Bond, I. A., et al. 2014, ApJ, 785, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bonomo, A. S., Hébrard, G., Raymond, S. N., et al. 2017, A&A, 603, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, D., Allen, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Deeg, H. J., Moutou, C., Erikson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Désert, J.-M., Lecavelier des Etangs, A., Hébrard, G., et al. 2009, ApJ, 699, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Désert, J.-M., Sing, D. K., Vidal-Madjar, A., et al. 2011a, A&A, 526, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Désert, J.-M., Bean, J., Miller-Ricci Kempton, E., et al. 2011b, ApJ, 731, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, R. F., Rey, J., Demangeon, O., et al. 2016, A&A, 591, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Hébrard, G., Lecavelier des Etangs, A., et al. 2007, ApJ, 668, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., & Han, W. 2002, ApJ, 580, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Désert, J.-M., Díaz, R. F., et al. 2010, A&A, 516, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heising, M. Z., Marcy, G. W., & Schlichting, H. E. 2015, ApJ, 814, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Heller, R. 2012, A&A, 545, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heller, R. 2014, ApJ, 787, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Heller, R. 2017, ArXiv e-prints [arXiv:1701.04706] [Google Scholar]
- Heller, R., Williams, D., Kipping, D., et al. 2014, Astrobiology, 14, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Hinse, T. C., Christou, A. A., Alvarellos, J. L. A., & Goździewski, K. 2010, MNRAS, 404, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Kalas, P., Graham, J. R., Fitzgerald, M. P., & Clampin, M. 2013, ApJ, 775, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L. 2010, ApJ, 712, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Kenworthy, M. A., & Mamajek, E. E. 2015, ApJ, 800, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009a, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009b, MNRAS, 396, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M., Schmitt, A. R., Huang, X., et al. 2015, ApJ, 813, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., Joutel, F., & Robutel, P. 1993, Nature, 361, L615 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier des Etangs, A., Deleuil, M., Vidal-Madjar, A., et al. 1995, A&A, 299, 557 [Google Scholar]
- Lecavelier des Etangs, A., Vidal-Madjar, A., & Ferlet, R. 1999, A&A, 343, 916 [Google Scholar]
- Lecavelier des Etangs, A., & Vidal-Madjar, A. 2016, A&A, 588, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, K. M. 2013, MNRAS, 430, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, K. M., Sackett, P. D., & Mardling, R. A. 2008, ApJ, 685, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., Tsiganis, K., Batygin, K., Crida, A., & Gomes, R. 2012, Icarus, 219, 737 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholson, P. D., French, R. G., Tollestrup, E., et al. 2000, Icarus, 145, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Ogihara, M., & Ida, S. 2012, ApJ, 753, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Ohta, Y., Taruya, A., & Suto, Y. 2009, ApJ, 690, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Levine, A., Chiang, E., et al. 2012, ApJ, 752, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Martins, J. H. C., Boué, G., et al. 2015, A&A, 583, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sartoretti, P., & Schneider, J. 1999, A&AS, 134, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showalter, M. R., Cuzzi, J. N., & Larson, S. M. 1991, Icarus, 94, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., El Moutamid, M., Quillen, A. C., et al. 2017, in Planetary Ring Systems, eds. M. Tiscareno, & C. Murray (Cambridge University Press) [arXiv:1612.03321] [Google Scholar]
- Simon, A. E., Szatmàry, K., & Szabó, G. M. 2007, A&A, 470, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, A. E., Szabó, G. M., Szatmàry, K., & Kiss, L. L. 2010, MNRAS, 406, 2038 [Google Scholar]
- Simon, A. E., Szabó, G. M., Kiss, L. L., & Szatmàry, K. 2012, MNRAS, 419, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K. 2010, A&A, 510, A21 [Google Scholar]
- Stevenson, K. B., Harrington, J., Fortney, J. J., et al. 2012, ApJ, 754, 136 [Google Scholar]
- Williams, D. M., Kasting, J. F., & Wade, R. A. 1997, Nature, 385, 234 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zuluaga, J. I., Kipping, D. M., Sucerquia, M., & Alvarado, J. A. 2015, ApJ, 803, L14 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Light curve of CoRoT-9 during the transit of CoRoT-9b on June 18, 2010. Each dot represents an individual photometric measurement. Large squares show the data measurements rebinned by 40. The thick red line shows the best fit with an exoplanet transit model. The bottom panel gives the residual of the measurements after subtraction of the best fit model. The two vertical dashed lines represent the time range of the estimated time of the photometric bump that could be due to the transit in front of a stellar spot. The data taken within this time range have been excluded from the analysis. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 for the light curve of CoRoT-9 during the transit of CoRoT-9b on July 4, 2011. |
| In the text | |
 |
Fig. 3 Difference of the χ2 between the best fit with a satellite and without a satellite as a function of the satellite size and central time of transit, measured in the light curve of the 2010 transit. The red iso-curves are for negative values of Δχ2, where the fit with a satellite is better than the fit without satellite. The vertical lines show the central time (short-dashed) and the time of first and fourth contact (long-dashed lines) for the transit of the planet. The upper x-axis provides the projected distance of the satellite to the planet (elongation) for the corresponding central time of the satellite transit (T0s). |
| In the text | |
 |
Fig. 4 Same as Fig. 3 using the light curve of the 2011 transit. |
| In the text | |
 |
Fig. 5 Light curve of the transit on June 18, 2010, and the fit including a satellite with a radius of 0.026 times the planet radius, and with a central time of transit 16.0 h after June 17, 2010, 0h00 UT (blue solid line). This fit has a χ2 of 3162.4, that is smaller by ~6.4 than the χ2 = 3168.8 of the fit without a satellite. The data have been rebinned by 31 into 100 individual measurements. The red dashed line shows the transit model without a satellite. The model light curve with the satellite has an additional occultation starting at about 12 h and ending at about 20 h. The bottom panel shows the residuals of the data (filled squares) and the light curve of the model including the satellite, after subtraction of the best fit without a satellite. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 for the transit of 2011 and the fit including a satellite with a radius of 0.020 times the planet radius, and with a central time of transit 19.0 h after July 3, 2011, 0h00 UT. This fit has a χ2 of 3938.8, that is smaller by ~2.5 than the χ2 = 3941.3 of the fit without a satellite. Here the additional occultation by the satellite starts at about 15 h. |
| In the text | |
 |
Fig. 7 Difference of the χ2 between the best fit with a ring and without a ring as a function of the ring size and thickness, which is obtained using the light curve of the 2010 transit. Blue thin lines show the iso-curves of the equivalent occulting area of the ring Lr × Hr. |
| In the text | |
 |
Fig. 8 Same as Fig. 7 for the light curve of the 2011 transit. |
| In the text | |
 |
Fig. 9 Same as Fig. 7 using the combination of both the light curves of the 2010 and 2011 transits. |
| In the text | |
 |
Fig. 10 Light curve of the transit on June 18, 2010, and the fit including a ring with a size Lr = 0.2 R∗ and a thickness Hr = 0.07 R∗, where R∗ is the star radius (blue line). This fit has a χ2 of 3204, that is larger by ~35 than the χ2 of the best fit without a ring (thin red line). Such ring is thus excluded at about 6σ confidence level. The bottom panel shows the residuals after subtraction of the best fit without ring. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


