| Issue |
A&A
Volume 601, May 2017
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201630233 | |
| Published online | 22 May 2017 | |
BD-19 5044L: discovery of a short-period SB2 system with a magnetic Bp primary in the open cluster IC 4725 ⋆
1 Armagh Observatory, College Hill, Armagh, BT61 9DG, UK
e-mail: jlandstr@uwo.ca; jls@arm.ac.uk
2 Department of Physics & Astronomy, University of Western Ontario, London, Ontario N6A 3K7, Canada
3 Department of Physics and Astronomy, Uppsala University, Box 516, 75120 Uppsala, Sweden
4 UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble, France
5 CNRS-IPAG, 38000 Grenoble, France
6 LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. Paris 06, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
7 Max Planck Insitut für Extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
8 Laboratoire AIM Paris-Saclay, CEA/DRF, CNRS, Université Paris Diderot, IRFU/SAp Centre de Saclay, 91191 Gif-sur-Yvette, France
9 Department of Physics, Royal Military College of Canada, PO Box 17000, Stn Forces, Kingston, Ontario K7K 7B4, Canada
Received: 12 December 2016
Accepted: 23 January 2017
Context. Until recently almost nothing was known about the evolution of magnetic fields found in upper main sequence Ap/Bp stars during their long main sequence lifetime. We are thus studying magnetic Ap/Bp stars in open clusters in order to obtain observational evidence of how the properties of Ap/Bp magnetic stars, such as field strength and structure, evolve with age during the main sequence. One important aspect of this study is to search for the very rare examples of hot magnetic stars in short-period binary systems among magnetic cluster members.
Aims. In this paper we characterise the object BD-19 5044L, which is both a member of the open cluster IC 4725 = M 25, and a short-period SB2 system containing a magnetic primary star.
Methods. We have obtained a series of intensity and circular polarisation spectra distributed through the orbital and rotation cycles of BD-19 5044L with the ESPaDOnS spectropolarimeter at CFHT. From these data we determine the orbital and stellar properties of each component.
Results. We find that the orbit of BD-19 5044L AB is quite eccentric (e = 0.477), with a period of 17.63 d. The primary is a magnetic Bp star with a variable longitudinal magnetic field, a polar field strength of ~1400 G and a low obliquity, while the secondary is probably a hot Am star and does not appear to be magnetic. The rotation period of the primary (5.04 d) is not synchronised with the orbit, but the rotation angular velocity is close to being synchronised with the orbital angular velocity of the secondary at periastron, perhaps as a result of tidal interactions. Because this system is a member of IC 4725, the two stars have a common age of log t = 8.02 ± 0.05 dex.
Conclusions. The periastron separation is small enough (about 12 times the radius of the primary star) that BD-19 5044L may be one of the very rare known cases of a tidally interacting SB2 binary system containing a magnetic Ap/Bp star.
Key words: binaries: spectroscopic / stars: chemically peculiar / stars: evolution / stars: magnetic field / stars: individual: BD-19 5044L
© ESO, 2017
1. Introduction
Magnetic fields have been found in a small percentage of upper main sequence stars (mostly chemically peculiar or Ap/Bp stars) since the 1940s. It is possible to detect quite small fields, down to mean longitudinal field values ⟨ Bz ⟩ of a few G, and to establish the surface magnetic field geometry and to map the anomalous and patchy atmospheric chemical abundances that often accompany magnetism (see for example reviews by Mestel & Landstreet 2005; Donati & Landstreet 2009; Bagnulo & Landstreet 2015).
However, although a lot is now known about magnetism in field stars near the Sun, it has not been possible from these data to establish clearly how the observed fields and accompanying chemical peculiarities evolve during the long main sequence lifetime, because it has been very difficult to obtain accurate ages for field stars. In the past decade, major improvements in the sensitivity and wavelength coverage of spectropolarimeters have made it possible to search for and study magnetic fields in considerably fainter Ap/Bp stars than in the past, and it has become practical to study magnetic stars in open clusters of known age. Data for magnetic stars in clusters of various ages have established clearly that the surface magnetic fields of upper main sequence late B stars are largest (typically several kG) early in the main sequence life, and that these fields decline quite strongly during the main sequence, so that almost all magnetic stars near the terminal-age main sequence have relatively weak surface fields, typically a factor of ten or more smaller than their values close to the zero-age main sequence (Landstreet et al. 2008).
The sample of cluster magnetic stars used to study the evolution of surface field strength is made up largely of stars that have not been studied very much until recently, as many are fainter than mV = 10. The observations of Bagnulo et al. (2006) and Landstreet et al. (2008) were the first magnetic measurements made of most of them. In order to complete a first survey of a statistically interesting sample of stars in a reasonable amount of time, early magnetic measurements of the peculiar open cluster stars were mostly snapshots of one or two measurements.
Following the early survey, a second stage of investigation currently in progress is to study in detail a fraction of the open cluster magnetic stars, and to map their field geometries and surface abundances, in order to discover how these evolve as a function of main sequence age. This has led to observing programmes obtaining a number of observations per star, which in turn has led (among other things) to the discovery of a small number of open cluster spectroscopic binary systems containing a magnetic Ap/Bp star.
One such object has turned out to be extremely interesting. The Bp object BD-19 5044L in the open cluster IC 4725 (log age ≈ 8.02, Landstreet et al. 2007) is shown to be a double-lined spectroscopic binary made up of two upper main sequence stars (as suspected by Paunzen et al. 2011). The more massive of the two stars shows a clear magnetic field, while the less massive star is apparently non-magnetic. We find the orbital period of the system to be 17.6 day, with rather high eccentricity, suggesting that the two stars may have interacted significantly during their main sequence lifetimes. Such close binaries containing a magnetic upper main sequence star are very rare (Carrier et al. 2002; Alecian et al. 2015; Neiner et al. 2015a,b), and so this system is well worth studying in detail.
In this paper we report our extensive spectropolarimetric observations of BD-19 5044L AB, which we analyse and model to provide a first detailed description of this system.
2. Observations
The object BD-19 5044L = CPD-19 6897 is a probable member of the open cluster IC 4725 = Messier 25, a small cluster at about 620 pc from the Sun (Kharchenko et al. 2005). BD-19 5044L has V = 10.18 and, based on the single-star photometric calibration of available uvby photometry, has an effective temperature of about Teff = 12 800 K. No high-precision astrometry is available, but membership is supported by the good agreement of stellar effective temperature and luminosity log L/L⊙ with evolution tracks fitted to other cluster stars (Bagnulo et al. 2006; Landstreet et al. 2007). A further test of membership is to compare the systemic mean radial velocity V0 = 5.30 ± 0.18 km s-1 of BD-19 5044L (see below) with the cluster mean radial velocity. The situation in the literature concerning the radial velocity of IC 4725 is quite confused, but we may compare the mean radial velocity of BD-19 5044L directly with our own (unpublished) measured radial velocities of two other cluster stars, HD 170836 (VR = 3.80 ± 0.5 km s-1) and HD 170860 (VR = 6.20 ± 0.5 km s-1); the close agreement supports cluster membership (and suggests a cluster mean velocity close to + 5 km s-1).
Photometric and spectral classification (Maitzen 1985; Paunzen et al. 2011) agree that the star is chemically peculiar, but a first effort in 2004 to measure the field using ESO’s FORS1 low-resolution spectropolarimeter did not detect a magnetic field (Bagnulo et al. 2006). However, two further field measurements with the ESPaDOnS spectropolarimeter at the Canada-France-Hawaii Telescope (CFHT) successfully detected a mean longitudinal field of ⟨ Bz ⟩ ≈ −250 ± 40 G. The field strength was evaluated using the method of least-squares deconvolution (LSD, Donati et al. 1997) as discussed by Landstreet et al. (2008). The field measurements were obtained on two successive nights. On the first night the mean Stokes I LSD line profile was fairly symmetric, while on the second it appeared quite lumpy, which is not uncommon for magnetic stars with highly non-uniform surface abundances. Neither spectrum strongly suggested that the object is a binary star system.
When the campaign to obtain rotationally phased field measurements was started on the CFHT in semester 2015A, BD-19 5044L was included in the programme. On the first night of 2015A observations (MJD 57 200.320), the star showed a clearly separated SB2 spectrum, with a magnetic field detected in the primary star only. As no rotation or other period was known for this system, it was observed on ten nights in 2015A and six more nights in 2015B, after which BD-19 5044L moved too close to the Sun for further observation. Two more ESPaDOnS observations were obtained during semester 2016A, and three during 2016B.
The observations reported here were all made with the ESPaDOnS spectropolarimeter. This instrument obtains Stokes (intensity or flux) I and (circularly polarised) V spectra covering almost all of the spectral window between 3800 Å and 1.04 μm with spectral resolution of about 65 000. The spectra were typically exposed for about an hour, and signal-to-noise ratios (S/N) of about 200 per pixel were achieved near 5000 Å. The circularly polarised spectra acquired were reduced at the CFHT using Libre-Esprit, a dedicated software package based on Esprit (Donati et al. 1997). We retrieved the combined polarised spectra, both normalised and non-normalised. The presence of the two components of the SB2, separated by some tens of km s-1, were clearly visible in most of the spectra. Both stars are quite sharp-lined. No signature of a magnetic field was visible in the V spectra of individual spectral lines.
For each spectrum we then created a mean of all significant spectral lines and a similar mean of the circular polarisation spectrum over the same lines, using the LSD technique. This produced mean line and polarisation profiles with S/N of the order of 2000. An example of such a profile is shown in Fig. 1. We also created for each mean spectrum another mean polarisation spectrum with the subexposures added in such a way as to cancel out any real polarisation signal (a null or N spectrum), in order to look for spurious instrumental polarisation signals. In every case the N spectrum shows nothing but photon noise.
The LSD plots gave us mean stellar absorption lines whose radial velocities could be measured quite accurately, and revealed in every spectrum the clear S-shaped signature of a magnetic field, always of approximately the same shape, and always associated with the spectrum of the primary star. Thus this SB2 system is composed of a brighter star with a magnetic field, and a fainter one that shows no sign at all of magnetism.
The radial velocities of both stellar components of the system were measured using the “e” (equivalent width, integrated flux, and centre) function of the IRAF1 “splot” command. Repeated radial velocity measurements suggest that (except when the two lines overlap) the internal precision of the measurements is about ± 0.5 km s-1. The scatter observed in repeated measurements near the same orbital phase in different orbits (see below, Sect. 3) suggests that this precision estimate is realistic for the secondary (except when the two spectra begin to overlap). However, the LSD profiles of the primary star are variable in shape and equivalent width, a normal situation for a magnetic Ap or Bp star. As a result, repeated velocity measurements at the same orbital phase (see below) do not repeat to better than about ± 2 km s-1. This strongly suggests that the rotation period of the magnetic primary star is not yet synchronised with the orbital period.
 |
Fig. 1 An example of an LSD plot, for the spectrum from CFHT file 1822453pn.s. The lower curve is the mean Stokes I spectral line, with the primary star at −45 km s-1 and the secondary at + 70 km s-1. The lack of symmetry about the line centre of the mean primary line is clearly visible, while the secondary line is both constant in shape and symmetric. The upper curve is the mean Stokes V circular polarisation, multiplied by 20 and shifted upward to + 1.04 for ease of comparison. This Stokes component clearly shows that a field is present in the primary, while no evidence of a field is seen in the secondary. |
The mean longitudinal magnetic field ⟨ Bz ⟩ (the mean line-of-sight field component, averaged over the visible hemisphere) was also estimated from the LSD spectra, using the expression 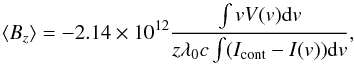 (1)where the intensity I and circular polarisation V are expressed as functions of velocity v relative to the heliocentric standard of rest, Icont is the continuum intensity, λ0 is the mean wavelength of the lines contributing to the LSD mean (in Å), z is the mean Landé factor of the lines, and c is the speed of light (Mathys 1989). Because this measurement is mathematically equivalent to the measurement of the centroid separation of the two circularly polarised components of the mean spectral line, no correction needs to be applied to the measurements because of dilution of the spectrum by the unpolarised secondary spectrum when the two stellar lines are clearly separated. No field is detected in the secondary star with measurement uncertainty of typically 100 G.
(1)where the intensity I and circular polarisation V are expressed as functions of velocity v relative to the heliocentric standard of rest, Icont is the continuum intensity, λ0 is the mean wavelength of the lines contributing to the LSD mean (in Å), z is the mean Landé factor of the lines, and c is the speed of light (Mathys 1989). Because this measurement is mathematically equivalent to the measurement of the centroid separation of the two circularly polarised components of the mean spectral line, no correction needs to be applied to the measurements because of dilution of the spectrum by the unpolarised secondary spectrum when the two stellar lines are clearly separated. No field is detected in the secondary star with measurement uncertainty of typically 100 G.
The measured radial velocities of the two components and the measured values of ⟨ Bz ⟩ of the primary star, starting with the first two measurements from 2008, are listed in Table 1. Note that ⟨ Bz ⟩ was not measured for phases at which the primary and secondary LSD lines are blended with one another.
CFHT exposure identification (odometer) number, modified Julian date at mid-exposure, radial velocities of primary and secondary (VR1 and VR2 respectively), and measured longitudinal field ⟨ Bz ⟩ of the primary star with uncertainty σBz.
3. Orbit of the SB2
 |
Fig. 2 Radial velocity curves as a function of orbital phase measured relative to the velocity extremum, using the best period of 17.63011 d. The velocities of the primary are plotted with blue circles, those of the secondary as red diamonds. Smooth curves are from the model discussed in the text. |
Seventeen spectra were obtained in 2015 spanning about four months with a variety of time intervals between spectra. When the radial velocity data from 2015 are plotted against time, it is clear from the data on MJD 57 207 and 57 225 (when the radial velocities of the two components of the SB2 system are approximately equal and the velocity of the primary is becoming negative) that the orbital period is approximately 17 or 18 d. Plotting all 2015 data on periods around these values, and requiring smooth variation of the orbital velocities, the period was quickly refined to about 17.62 ± 0.04 d. We then considered the two data points from 2008, on MJD 54 650 and 54 651. Fortunately these two data points, by chance, identify the same velocity crossover phase as the two dates mentioned above, and limit the allowed periods to 17.510, 17.631, and 17.753 d. With the restrictions derived from the 2015 data alone, we find an orbital period of 17.630 ± 0.005 d. Adding five new ESPaDOnS radial velocities from 2016, the final best fit orbital period becomes Porb = 17.63011 ± 0.00035 d.
The radial velocity curves have been modelled in detail using the Liege Orbital Solution Package (LOSP; Sana et al. 2006), a set of FORTRAN programmes that fit the radial velocity data and provide model values of the important parameters of the SB2 system. They were also modelled using a programme created by one of us (O. Kochukhov). This code, written in IDL, performs non-linear least-squares fitting of the orbital radial velocity variations, based on the Astrolib helio_rv routine. Both programmes provided very similar orbital solutions. As the orbit computed with Kochukhov’s programme fits the observations somewhat better than the orbit produced by LOSP, we have adopted the orbital solution found by this programme.
The full set of radial velocities is plotted in Fig. 2, using T0 = 54 653.915 as origin. It is clear from the figure that the adopted period describes the radial velocity variations very well, but that there is a significant phase gap of about 0.20 in the available radial velocity data. However, this missing phase interval does not introduce significant uncertainties into the analysis of the orbit of the SB2 system. The fit to the two sets of radial velocities generated by Kochukhov’s programme are also shown in the figure.
The SB2 system parameters derived from the binary orbit fit are listed in Table 2. In this table, the rms values are the dispersions of the individual data points around the fitted orbital solution, Porb is the orbital period, T0 is an MJD of maximum velocity difference, K1 and K2 are the velocity semi-amplitudes of the two stars, V0 is the system velocity, e is the orbital eccentricity, ω is argument of perihelion, M1 and M2 are the masses of the primary and secondary stars, a1 and a2 are the orbital semi-major axes of the individual stars around their common centre of mass, and i is the orbital inclination relative to the plane of the sky. (Subscripts 1 refer to component A, subscripts 2 to component B.)
The dispersion of radial velocities about the best-fit orbit allows us to estimate the total uncertainties of our radial velocity measurements as rms(A) = 0.9 and rms(B) = 1.4 km s-1. These values are somewhat larger than the internal measurement uncertainties estimated above, but presumably include such additional effects as physical scatter in the line positions (e.g. due to spectrum variability of the primary) and small wavelength calibration uncertainties in the spectra.
Note that the radial velocities of the primary star show an apparent jump near phase 0.50. This is probably a symptom of intrinsic variability of the primary spectrum, together with the lack of synchronism of the orbital and rotational periods of the primary, as mentioned in the previous section.
Orbital elements and uncertainties of the SB2 system BD-19 5044L computed as described in the text.
4. Magnetic field of the Bp star
Table 1 shows that the magnetic field of the primary star never changes sign, and it is not immediately obvious that the apparent mild variations are significant. In fact the dispersion of the ⟨ Bz ⟩ values is about 85 G, 2 × larger than the median ⟨ Bz ⟩ uncertainty. We have tested these data for (rotational) periodic variability with a periodogram programme, dchi.f, that was used to fit a sine wave for all significantly different periods between 100 and 1 d by minimising the reduced chi-squared statistic of the best fit for each of the many frequencies. The resulting chi-squared fit spectrum, somewhat surprisingly, shows only two significant periods: 5.040 ± 0.026 d, and its one-day alias 1.2433 ± 0.0023 d. The best fit with the longer period has χ2/ν = 0.61, while for the shorter period the best value is 1.22. Thus both periods fit the data quite acceptably. In view of the obviously small vsini seen in Fig. 1 (about 14 km s-1, see next section), which would allow a rotation period as long as about 2 wk), the shorter period is rather unlikely, so this results strongly suggests a rotation period of 5.04 d. The variation of the magnetic field on this period is shown in Fig. 3.
We have tested this period by computing the sine wave chi-squared fit spectrum for the equivalent width of the primary star’s LSD line, which is found to vary between about 0.54 and 0.74 km s-1, with uncertainties of about 0.02 km s-1. This second periodogram reveals exactly the same periods, 5.041 ± 0.011 d and 1.2435 ± 0.0007 d. The periods determined from equivalent width variations are more precise than those from ⟨ Bz ⟩ variations because the full amplitude of equivalent widths variations is about 8σ while that of ⟨ Bz ⟩ measurements is only about 5.5σ, where σ is a typical measurement uncertainty. The minimum values of χ2/ν = 0.79 for the 5 d period while that of the 1.24 d period is 1.66. This difference favours the longer period but is not conclusive. However, on physical grounds we again prefer the longer period. The variations of equivalent width of the primary LSD line is shown in Fig. 4. (The small value of the χ2/ν statistic, and the obviously small scatter around the mean curve in Fig. 3, suggest that our LSD ⟨ Bz ⟩ measurements have rather conservative uncertainties.)
We conclude that the rotation period of BD-19 5044L A is very probably P1 = 5.041 ± 0.011 d. It is notable that the rotation period is about 3.5 times shorter than the orbital period. The system is clearly widely enough separated that synchronism of orbital and rotational motions has not been achieved in the 1.0 × 108 yr since the cluster (and presumably the binary system) formed. (See the discussion of this issue in Sect. 6.)
It is obvious from the plotted variations of ⟨ Bz ⟩ and equivalent width with phase on the 5.041 d period that the largest value of the primary’s equivalent width occurs close to the largest absolute value of ⟨ Bz ⟩, or at the point where the line of sight to the star passes closest to the visible magnetic pole, while the equivalent width is smallest where the line of sight is near the magnetic equator. The LSD line is dominated by even-Z iron peak elements, particularly by Fe, and this result suggests that the iron abundance on this star increases from the equator towards the visible magnetic pole. A visual comparison of the equivalent widths of a number of lines of He, Mg, Si, Ti, Cr and Fe, made by overplotting a primary star spectrum obtained near minimum line strength (magnetic phase 0.0) with one obtained near maximum line strength (magnetic phase 0.5) shows that He and Mg vary rather little, while the lines of Si and the three iron peak elements all vary together in the same sense as the LSD line. It appears that on the surface of BD-19 5044L the elements Si, Ti, Cr and Fe all have higher abundance near the magnetic pole than near the equator. This provisional conclusion should be confirmed by detailed mapping, but in any case it is clear that the abundances of several spectroscopically important elements vary strongly over the stellar surface.
 |
Fig. 3 Variations of the magnetic moment ⟨ Bz ⟩ of BD-19 5044L A phased with a rotational period of 5.041 d. The origin of the rotational phase system is the first ⟨ Bz ⟩ measurement in 2015, from Table 1. The smooth curve is the best sine wave fit to the data. |
 |
Fig. 4 Variations of equivalent width of the LSD line of the primary star of BD-19 5044L, phased with a rotational period of 5.041 d. The origin of the phase system is the first ⟨ Bz ⟩ measurement in 2015, from Table 1. The smooth curve is the best sine wave fit to the data. |
Comparing Fig. 3 to 4, it is also clear that there is a small phase shift between the extrema of about 0.1 cycle – the largest absolute value of ⟨ Bz ⟩ occurs about 0.1 cycle before maximum equivalent width of the LSD spectral line. This situation clearly points to a distribution of abundances over the visible surface of BD-19 5044L A that is not cylindrically symmetic around the magnetic field axis of symmetry (if indeed the field itelf is approximately axisymmetric, which is unknown). This situation is commonly observed in detailed mapping studies (e.g. Kochukhov & Wade 2010; Kochukhov et al. 2011).
5. Physical properties of the component stars of the system
Properties of primary and secondary stars of BD-19 5044L as derived from this study.
The Strömgren uvby colours of BD-19 5044L were used to determine a temperature, Teff = 12 800 K, and luminosity, log L/L⊙ = 2.25, of the system treated as a single star. Using the single-star parameters, the position of BD-19 5044L in the theoretical HR Diagram lies essentially on the isochrone for the cluster age. The position in the HR diagram provides a single-star mass of M = 3.5 M⊙. The deduced value of the fractional age (the fraction of main sequence lifetime already elapsed) is 0.46 (Landstreet et al. 2007). (The isochrones used for HR diagram comparisons are those of the Padova group, described by Fagotto et al. 1994; for Z = 0.02. The methods used to obtain accurate cluster ages are described in detail by Silaj & Landstreet 2014.)
Because the secondary star contributes to the spectrum and to the photometric magnitudes, we anticipate that the primary is slightly bluer than the observed colours, but about 0.1 dex less luminous (see below), log (L1/L⊙) = 2.15 ± 0.1. The result is that the best estimate of the mass of the primary changes only slightly, to about (3.40 ± 0.2) M⊙. The estimated effective temperature of the primary, from its position in the HR diagram, is about log Teff = 4.12 ± 0.02, or Teff = 13200 ± 500 K.
Using the well-determined binary mass ratio of 1.479, we deduce that the secondary star has a mass of (2.30 ± 0.15)M⊙. When we place the secondary on the cluster isochrone, we deduce a luminosity of about log (L2/L⊙) = 1.5 ± 0.1. This means that the secondary contributes about 18% of the total light from the system, which is equivalent to the 0.1 dex assumed above. The luminosity ratio is L1/L2 ≈ 4.5. The secondary lies very close to the cluster ZAMS, with Teff ≈ 10 000 ± 500 K.
Because the secondary contributes only a rather small fraction of the light, the single star parameters are approximately representative of the primary star of BD-19 5044L, and the mass and other properties of the primary are determined securely with reasonably good precision. (Moreover, because the primary is a chemically peculiar star, a more refined estimate of its parameters is not likely to be significantly more accurate than our first simple estimate.) Similarly, the properties of the secondary are rather accurately determined from the mass ratio and the fact that both stars are members of the open cluster IC 4725 and thus have well-determined age, distance and positions in the cluster HR diagram.
In order to investigate further the properties of the two stars in the BD-19 5044L AB system, we have carried out spectral disentangling using a programme developed by one of us (O. Kochukhov). This code was previously applied to SB2 systems containing CP star components by Folsom et al. (2010, 2013). The reader can find more details about our disentangling procedure in those publications.
The result of disentangling is two high S/N spectra, one for each star, which when added together with appropriate radial velocity shifts, match closely the (rather noisy) individual observed binary spectra. However, the disentanglement itself does not provide information about the fraction of the light contributed at each wavelength by each of the two stars; each of the two solution spectra is still normalised to the total light of the system at each wavelength.
For abundance determinations, we need to determine the flux ratio in the wavelength region to be modelled (or equivalently the zero level of each spectrum). Since component A of BD-19 5044L is significantly hotter than component B, and thus has substantially higher flux in the UV, we suspect that the light ratio in the visible window will probably be less than 4.5. In fact there is one spectral window, around 4500 Å, where the local flux ratio is quite closely constrained, by the depth of the Mg ii triplet of lines at 4481.13, 4481.15, and 4481.33 Å. The feature produced by this group is so strong that the central depth of the line is set essentially (in LTE) by the surface temperature at the top of atmosphere. Furthermore, because the feature is a blend of lines about 0.2 Å apart, the observed central depth of the line is almost independent of (small) microturbulent velocity, and of rotational velocity provided that vsini is less than about 10 km s-1. In addition this central depth varies little with Teff for small excursions around Teff = 10 000 K.
We have available high resolution spectra of spectral windows including the Mg ii feature for several stars which have parameters close to those deduced for BD-19 5044L B, obtained using the ESPaDOnS spectrograph (R ≈ 65 000) at the CFHT or the Aurélie spectrograph (R ≈ 50 000) at the Observatoire de Haute-Provence. The available spectra include HD 114330 (minimum normalised flux = 0.270), HD 72 660 (0.260), HD 214994 (0.270), HD 209459 (0.297), and HD 19805 (0.267). All have Teff = 9700 ± 600 K, 3.4 ≤ log g ≤ 4.3, and vsini ≤ 7 km s-1.
From these observed values in similar stars, we adopt a typical minimum normalised flux of 0.27 ± 0.01 for BD-19 5044L B. When we experiment with various values of flux ratio for normalising the two disentangled spectra, this constraint on the central depth of the Mg ii feature sets the zero point of the disentangled spectrum of BD-19 5044L B, which results in a flux ratio f1/f2 at 4481 Å of 3.6 ± 0.1. We assume that this ratio is valid over at least ~102 Å in either direction from the Mg ii blend, and normalise both disentangled spectra in this region appropriately.
The disentangled, renormalised spectra around 4500 Å were then fit using the line synthesis programme zeeman.f (Landstreet 1988; Wade et al. 2001). This programme assumes a given value of Teff and log g, interpolates within a grid of ATLAS solar abundance models, and computes a synthetic spectrum using a line list from the Vienna Atomic Line Database (VALD: Piskunov et al. 1995; Ryabchikova et al. 1997; Kupka et al. 1999, 2000). The computation is fully in LTE, and the effects of a magnetic field on radiative transfer in each spectral line can be included (or omitted if the star is non-magnetic). An initial abundance table is assumed, and one element at a time is iterated to a best fit of all the largely unblended lines of a single element found within the window under study. This process can be iterated (for a non-magnetic atmosphere) over various values of assumed microturbulence in order to select the microturbulence parameter that leads to the best concordance between abundances from weak and strong lines. At the end, the programme reports the best fit abundance of the element varied, the best fit value of vsini, and the best microturbulent parameter ξ, and produces a set of plottable synthetic spectra with the lines used for the fitting marked. The process is then repeated for other elements, and iterated to convergence.
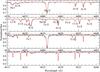 |
Fig. 5 Small sections of the best fits found by zeeman.f to the disentangled mean spectrum of BD-19 5044L A (upper two panels) and BD-19 5044L B (lower two panels). The observed spectra are the (black) curves with noise; the computed spectra (red) have no noise. Ion identifications are provided for the stronger lines in the upper two panels; these generally apply to the corresponding lines in the lower two panels. |
We start spectrum fitting with BD-19 5044L B, as the lack of a magnetic field makes this the simpler of the two stars to model. Our fitting process was first carried out for Fe in windows about 75 Å wide in the range 4438−4652 Å. Because iron has numerous lines in these windows, some weak and others strong, our spectrum synthesis yields a robust non-zero value of the microturbulence parameter of ξ = 1.2 ± 0.2 km s-1. This value was held fixed for further calculations of other elements for which, in general, not enough lines are available to provide an accurate value of this parameter. The best fit value of projected rotational velocity is found to be about vsini = 6.3 ± 0.2 km s-1, and the abundance of iron is found to be log NFe/NH = −4.32, an overabundance of almost a factor of two relative to solar abundance ratios. The dispersion of values suggests an uncertainty in the derived iron abundance of about 0.1 dex.
This fitting process was repeated for a window at 4998−5072 Å, where the normalisation of the two disentangled spectra was assumed to still be given by f1/f2 = 3.6, and the microturbulence was held at 1.2 km s-1. For this window a best fit abundance of iron of log NFe/NH = −4.15 ± 0.1 was found. This is not significantly different from the value found around 4500 Å, and we conclude that the normalisation in this window is not greatly different from that at 4500 Å, so we use the same flux ratio of 3.6 for all spectra modelled in these two windows.
Experiments varying the effective temperature Teff between the 1σ limits of 9500 and 10 500 K indicate that the abundance uncertainty due to Teff is about ± 0.20 dex. This uncertainty dominates the total error budget for iron. We find that the situation is similar for other iron peak elements.
The fitting process was then repeated for the elements He, Mg, Si, Ca, Ti, Cr, and Ba. The deduced abundance ratios are given in Table 4, together with the solar ratios. The final fit of the synthetic spectrum to two small segments of the renormalised mean spectrum of the secondary is shown in Fig. 5. It is clear that a reasonable fit has been achieved for most of the lines in the illustrated spectrum segment shown in the figure.
The underabundance of Ca relative to the solar abundance, and the overabundance of Ba, strongly suggest that BD-19 5044L B is a hot Am star. With Teff ≈ 10 000 K, it is near the upper temperature limit of this class.
Atmospheric abundances of BD-19 5044L A and B.
For BD-19 5044L A, which has a magnetic field, we need to make an assumption about what field strength and geometry to include in the spectrum synthesis. We first note that the dipolar field large enough to produce the maximum mean longitudinal field absolute value observed, a little larger than 400 G, has a polar field strength below about 1500 G. Since the actual field configuration may depart significantly from that of a simple dipolar field, the local field strength may exceed this value in places on the stellar surface. Even allowing for this possibility, it is reasonable to suppose that the field locally is generally below 2 kG. Such a weak field has very little effect on the observed flux line profiles (about as large an effect as a microturbulence of 1 km s-1). Thus we can derive an accurate value of vsini = (13.8 ± 0.4) km s-1 by fitting line profiles of some of the stronger lines, including a magnetic field of 1.5 kG.
Using the expression for the equatorial velocity of the primary star veq = 50.6(R/R⊙) /Prot (e.g. Preston 1971), together with the inferred radius of the primary star, we find that v1,eq = (22.8 ± 3.6) km s-1, and with v1sini1 = 13.8 km s-1, we deduce that the inclination of the rotation axis of the primary star to the line of sight is i1 = 37° ± 9°.
The magnetic field of the primary is expected to have a roughly dipolar morphology. The observed V/I signatures are generally rather simple, like the one shown in Fig. 1, consistent with this assumption. Assuming that the field can be usefully modelled by a simple dipolar field, the angle β of the dipole axis with respect to the stellar rotation axis can be estimated using Eq. (3) of Preston (1971) to be about β = 26° ± 9°. That is, in order for the field moment ⟨ Bz ⟩ not to change sign as the primary rotates, the field axis cannot make a large angle with respect to the rotation axis. With the deduced angles, the line of sight passes very close to the visible magnetic pole, and we can estimate that the polar field strength of the model dipole is of the order of 1400 G (Preston 1971, Eq. (9)).
The disentangled spectrum of BD-19 5044L A is an average over observed phases, so we have taken the field to be a dipole plus octupole (chosen to reduce the dipolar contrast between polar and equatorial field strengths) with a typical strength of ⟨ B ⟩ ~ 1200 G in the fitting process. The exact configuration of the field, and its exact value, make very little difference to the deduced abundance values. Proceeding as for the secondary star, we find the abundance values listed in Table 4. Again the uncertainties in the abundance values include estimates of the scatter in values deduced from different spectral windows, but are usually dominated by the uncertainty in the value of Teff. The derived abundances are compared to solar abundance ratios from Grevesse & Sauval (1998).
Note that this star (like many other magnetic Bp stars) shows a large discrepancy between the abundance values deduced from Si ii and Si iii. We suspect that this arises from strong variation of the abundance of Si with height in the atmosphere, as argued by Bailey & Landstreet (2013).
BD-19 5044L A is clearly strongly underabundant in He, by a factor of 20 or more. Mg is also strongly underabundant. The iron peak elements Ti, Cr and Fe are near solar or slightly overabundant. From the definite identification of several weak lines, the rare Earth Nd is clearly present, and is overabundant by about 3.2 dex. These are abundance values that clearly identify BD-19 5044L A as a chemically peculiar (Bp) star, consistent with its magnetic field. As expected for a star of mass of about 3.4 M⊙ that has an age of about 1.0 × 108 yr and is about half way through its main sequence evolution, the root-mean-square magnetic field ⟨ Bz ⟩ rms is below 1 kG (Landstreet et al. 2008), and some of the chemical abundances are approaching solar values, a result discovered for a sample of magnetic Bp stars of similar mass by Bailey et al. (2014). Note that Bailey et al. included BD-19 5044L in their study as a single star, finding abundances in broad agreement with those found here, given the slightly different fundamental parameters and the significantly different zero-point choice adopted by them.
6. The orbit again
With estimates of the masses of the two stars in the BD-19 5044L system, we return to the geometry of the orbit. From the value of M1sin3i = 0.435 M⊙, and M1 ≈ (3.40 ± 0.20) M⊙, we deduce that the orbital inclination is given by sini = 0.504 ± 0.010 or i = 30.3° ± 0.6°.
In turn the value of i allows us to deduce (see Table 2) that a1 = 20.5 R⊙ and a2 = 30.4 R⊙. The semi-major axis of the relative orbit is a = a1 + a2 = 50.9 R⊙ = 3.54 × 1012 cm. In the relative orbit of the two stars, periastron occurs with a separation of rpa = (a1 + a2)(1−e) = 26.8 R⊙ while apoastron occurs with a separation of raa = (a1 + a2)(1 + e) = 75.0 R⊙.
Using the parameters we have estimated in the previous section for the two stars of BD-19 5044L, we find that the radius of the primary is R1 ≈ 2.3 R⊙. Thus the semi-major axis of the relative orbit is about 22.4 R1 and the separation of the two stars at periastron is about rpa ≈ 12 R1.
The two components of BD-19 5044L are both stars with external radiative envelopes and convective cores. For such stars, tidal friction is driven by thermal diffusion applied on tidal gravity waves (the so-called dynamical tide) excited in the radiative zones of the two stars (Zahn 1975). For this situation, the ratio a/R1 is substantially above the critical value of the ratio required for circularisation and synchronisation according to Zahn (1977). Thus it is not expected that this system should be able to reach a state of a circularised orbit and synchronous stellar rotation during its main sequence lifetime (see also North & Zahn 2003).
Although the separation of the components is too large to have produced either orbital circularisation or rotational synchronisation, the rather small minimum separation suggests that the two stars may nevertheless have undergone some tidal interaction in the 108 yr during which they have presumably orbited one another.
One consequence of tidal interaction (or of initial conditions during formation of the binary) could be that the rotation axis of the primary would be aligned to the orbital axis. If this situation occurs, then the inclination angle of the stellar rotation to the line of sight should be the same as that of the orbit, 30° ± 1°. The derived inclination angle of the primary, 37° ± 9°, is within the uncertainties the same as the orbital inclination. Although the (near) equality of the two inclinations does not prove that the primary star has its rotation axis normal to the orbital plane, this result is consistent with that situation.
This computation strengthens the identification of 5.04 d rather than the 1.245 d alias as the correct value of the rotation period of the primary (see Sect. 4), since the 5 d period leads to a “reasonable” value of i1, while the shorter period would require i1 ≈ 8°, a value which has no obvious relationship to the binary orbit.
Another consequence of the tidal interaction could be to alter or even regulate the rotation period of the primary. Clearly the stellar rotation is not synchronous with the mean orbital velocity. In fact, the primary rotates with a period of only 5.04 d, less than 1/3 of the orbital period. Thus we are led to consider the possibility that the primary star has its rotation period locked to the orbital motion, not with respect to the average orbit period, but to the relative motion of the secondary star at periastron, when the tidal interaction is most intense. This possibility is related to the “pseudo-synchronous states” introduced and discussed by Hut (1981). We can test this idea by comparing the rotational angular velocity of the primary star to the orbital angular velocity of the secondary star at its closest approach to the primary.
With a rotational period of P1 = 5.04 d, the angular velocity of the primary is Ω1 = 2π/P1 = 1.44 × 10-5 rad s-1.
The maximum velocity of the secondary star relative to the primary star is given by 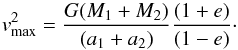 (2)Using the estimates of the masses from the previous section, of the orbital inclination i = 30°, and of e, a1sini and a2sini from Table 2, we find that vmax = 245 km s-1. This is very close to the maximum observed velocity difference between the two stars of about 123 km s-1 divided by sini, or 244 km s-1. This is what is expected from the value of the argument of perihelion ω = 187°, which indicates that our line of sight is almost perpendicular to the major axis of the relative orbit of the two stars. From this result, the angular velocity of the secondary star relative to the primary at periastron is given by
(2)Using the estimates of the masses from the previous section, of the orbital inclination i = 30°, and of e, a1sini and a2sini from Table 2, we find that vmax = 245 km s-1. This is very close to the maximum observed velocity difference between the two stars of about 123 km s-1 divided by sini, or 244 km s-1. This is what is expected from the value of the argument of perihelion ω = 187°, which indicates that our line of sight is almost perpendicular to the major axis of the relative orbit of the two stars. From this result, the angular velocity of the secondary star relative to the primary at periastron is given by 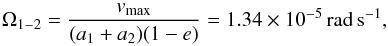 (3)which corresponds to a period of 5.4 days.
(3)which corresponds to a period of 5.4 days.
Properties of known short-period (Porb< 20 d) SB2 systems containing a magnetic upper main sequence star.
The two values of angular velocity are not equal but they are remarkably similar. It does not appear that the uncertainty of either angular velocity is large enough to make the two values equal. However, their very similar values suggest that tidal interaction at periastron may very well be affecting the rotation of the primary, and that this effect is close to forcing the primary star to rotate at the same angular rate as the orbital angular velocity of the secondary star at periastron2.
Another peculiarity of the primary star is that the inclination angle β of the magnetic field with respect to the stellar rotation axis (see Sect. 5) is small, of the order of 26°. Since magnetic Ap/Bp stars having rotation periods shorter than a few weeks usually have large β angles (e.g. Landstreet & Mathys 2000), we can wonder whether the small β value is another consequence of tidal interactions. Interestingly, two other close binary systems containing magnetic Ap/Bp stars, ϵ Lup (Shultz et al. 2015) and HD 5550 (Alecian et al. 2016), also share the characteristic of magnetic fields having small values of β.
7. Conclusions
During the course of a project to obtain repeated spectropolarimetric observations of magnetic Ap/Bp stars in open clusters, we discovered that the magnetic Bp star BD-19 5044L, a member of the open cluster IC 4725, is a short-period double-lined spectroscopic binary system. Because short-period main sequence SB systems only very rarely contain a magnetic Ap/Bp star, we have systematically observed this system to determine the main characteristics of the individual stars composing it, and the orbital parameters, and tried to identify ways in which the binary nature may have interacted with the magnetic field of the primary star. A particular interest of this system is that, in addition to being an intrinsically rare type of close binary, its membership in IC 4725 independently tells us that its age is approximately 1.0 × 108 yr.
The system is found to have an orbital period of 17.630 ± 0.005 d. The orbit is quite eccentric, with e = 0.474. The mass ratio is 1.479. The primary star can be securely identified as a late B star of mass about 3.4 M⊙ and Teff = 13 200 K. The secondary has a mass of about 2.3 M⊙ and an effective temperature of about 10 000 K. We have disentangled the two spectra (obtaining mean spectra for both stars), and used spectrum synthesis to carry out an approximate abundance analysis of each of the two components. These results (Table 4) show that component A is clearly a magnetic Bp star with typical abundance anomalies for its age, and that component B appears to be a (non-magnetic) hot Am star.
With these data and a model of the double-lined binary velocity curve, we determine that the orbit is inclined to the line of sight at i = 30°, and that the semi-major axis of the relative orbit has a length of a = 3.58 × 1012 cm = 51.4 R⊙. The closest approach of the secondary to the primary occurs with a separation of only about 12 R1.
The magnetic field of the primary star is observed to vary periodically with the stellar rotation period of 5.04 d. From the observed variations we deduce that the rotation axis of the star is probably perpendicular to the binary orbit, and that the field is roughly dipolar, with an axis inclined to the rotation axis by roughly β = 26°. The field of the primary star has a polar field strength of the order of 1400 G, while no field is detected in the secondary.
The angular velocity of the primary star is almost, but not quite, equal to the angular velocity with which the secondary orbits relative to the primary at periastron, and angular momentum exchanges between orbit and rotation may have led to this situation.
This SB2 system is of considerable interest in the context of stellar magnetic fields. It is a new member of the tiny class of known close binary stars containing a magnetic Ap/Bp star. Because the system is a member of the open cluster IC 4725, the system age is known independently. Unusually as well, enough is known about the basic parameters of both stars to fully characterise the orbit of the system, and to demonstrate that significant interactions of several kinds may have occurred between the system members during 108 yr.
A table of all known short-period (Porb< 20 d) SB2 systems containing (at least) one magnetic star is shown in Table 5. For each star, the table lists the period Porb, inclination i, and eccentricity e of the orbit; the mass M1, rotation period P1, projected rotation velocity v1sini1, the inclination i1 of the rotation axis of the star to the line of sight, the estimated dipolar field strength Bd1 of the field, and the obliquity of the dipole axis to the stellar rotation axis of the primary star; and the mass, vsini value, and estimated dipole field strength of the secondary star. These data are incomplete, and ... indicate missing values. Many values are at least somewhat uncertain; colons “:” indicate particularly uncertain values.
The data in the table are derived mainly from the following publications. The discovery of the field of HD 5550, and the data in the table, were reported by Alecian et al. (2016). The field of HD 37017 was discovered by Borra & Landstreet (1979) while most of the tabular data were taken from Bohlender et al. (1987). The masses were estimated from Teff values. Petit et al. (2011) discovered the field of HD 37061, and the data are from that paper and from Abt et al. (1991). All data on HD 47129 are from the discovery paper by Grunhut et al. (2013). The field of HD 98088 was predicted by Abt (1953), who observed Ap-like spectrum variations, and confirmed directly by Babcock (1958); other tabular data were taken from the substantial study by Folsom et al. (2013). A field was claimed on the basis of a single marginal observation of HD 136504 by Hubrig et al. (2009) and clearly detected by Shultz et al. (2012); other data were taken from the paper by Shultz et al. (2015) announcing the discovery of a field in the secondary star of this system and analysing the system. The magnetic field of the secondary star in the HD 161701 system was discovered by Hubrig et al. (2014), and their analysis of this system was described in more detail by González et al. (2014). All data concerning BD-19 5044L are from the present paper.
In addition to the systems with periods shorter than 20 d that are listed in Table 5, several longer-period SB2 systems have high eccentricity and may possibly have undergone significant tidal interactions. These include HD 1976 (Neiner et al. 2014), HD 34736 (Semenko et al. 2014), HD 36485 (Petit et al. 2013), HD 55719 (Bonsack 1976), and HD 135728 (Freyhammer et al. 2008).
The most striking feature of Table 5 is its shortness. It contains only three systems with orbital periods less than about 10 days, short enough that synchronised rotation is expected and (mostly) observed, and even for these systems only one orbit (and one of a system with Porb = 12.45 d) have been circularised by tidal friction (see Zahn 1977). A second feature is the wide range of primary masses, from 2.2 M⊙ to 45 M⊙. In five of the systems, the primary star is magnetic; in two systems (HD 47129 and HD 161701), it is the secondary which is magnetic, and one system (ϵ Lup) actually contains two magnetic stars. The typical field strengths ⟨ B ⟩ (estimated as the polar field strength of a dipolar field Bd large enough to lead to the observed values of ⟨ Bz ⟩), vary from less than one hundred to several thousand G.
A third point of interest in connection in particular with BD-19 5044L is the fact that the system HD 161720, with stars similar to those of BD-19 5044L, and a period of 12.45 days, not much shorter than that of BD-19 5044L, has achieved a state of both circularisation of its orbit and synchronism of the primary rotation with the orbital period. The existence of this system strongly suggests that significant effects of tidal interaction may be present in the BD-19 5044L AB system.
However, no obvious global regularities emerge immediately from Table 5. It appears that the main empirical path to understanding the origin and evolution of such rare binary stars will have to rely mainly on detailed studies of individual systems, like the present study, until a larger sample of such magnetic short period systems is available.
If we compute the pseudo-synchronous rotation following the formalism of Hut (1981, Eqs. (42) and (45)), we obtain a rotation of 6.9 days for a constant time lag friction model. This shows that the dynamical tide in intermediate and massive stars cannot be modelled using such a simplified model.
Acknowledgments
Work by J.D.L. and G.A.W. has been supported by the Natural Sciences and Engineering Research Council of Canada. O.K. acknowledges financial support from the Knut and Alice Wallenberg Foundation, the Swedish Research Council, and the Swedish National Space Board. S.M. acknowledges funding by the European Research Council through ERC grant SPIRE 647383. S.M. thanks E. Bolmont for fruitful discussions on pseudo-synchronous states.
References
- Abt, H. A. 1953, PASP, 65, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Abt, H. A., Wang, R., & Cardona, O. 1991, ApJ, 367, 155 [Google Scholar]
- Alecian, E., Neiner, C., Wade, G. A., et al. 2015, in New Windows on Massive Stars, eds. G. Meynet, C. Georgy, J. Groh, & P. Stee, IAU Symp., 307, 330 [Google Scholar]
- Alecian, E., Tkachenko, A., Neiner, C., Folsom, C. P., & Leroy, B. 2016, A&A, 589, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babcock, H. W. 1958, ApJS, 3, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., & Landstreet, J. D. 2015, in Polarimetry of Stars and Planetary Systems, eds. L. Kolokolova, J. Hough, & A.-C. Levasseur-Regourd (Cambridge University Press), 224 [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Mason, E., et al. 2006, A&A, 450, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailey, J. D., & Landstreet, J. D. 2013, A&A, 551, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailey, J. D., Landstreet, J. D., & Bagnulo, S. 2014, A&A, 561, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlender, D. A., Landstreet, J. D., Brown, D. N., & Thompson, I. B. 1987, ApJ, 323, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Bonsack, W. K. 1976, ApJ, 209, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Borra, E. F., & Landstreet, J. D. 1979, ApJ, 228, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Carrier, F., North, P., Udry, S., & Babel, J. 2002, A&A, 394, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Collier Cameron, A. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Fagotto, F., Bressan, A., Bertelli, G., & Chiosi, C. 1994, A&AS, 105, 39 [NASA ADS] [Google Scholar]
- Folsom, C. P., Kochukhov, O., Wade, G. A., Silvester, J., & Bagnulo, S. 2010, MNRAS, 407, 2383 [NASA ADS] [CrossRef] [Google Scholar]
- Folsom, C. P., Likuski, K., Wade, G. A., et al. 2013, MNRAS, 431, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Freyhammer, L. M., Elkin, V. G., Kurtz, D. W., Mathys, G., & Martinez, P. 2008, MNRAS, 389, 441 [NASA ADS] [CrossRef] [Google Scholar]
- González, J. F., Saffe, C., Castelli, F., et al. 2014, A&A, 561, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grunhut, J. H., Wade, G. A., Leutenegger, M., et al. 2013, MNRAS, 428, 1686 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Briquet, M., De Cat, P., et al. 2009, Astron. Nachr., 330, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Carroll, T. A., González, J. F., et al. 2014, MNRAS, 440, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Kochukhov, O., & Wade, G. A. 2010, A&A, 513, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kochukhov, O., Lundin, A., Romanyuk, I., & Kudryavtsev, D. 2011, ApJ, 726, 24 [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Baltic Astron., 9, 590 [Google Scholar]
- Landstreet, J. D. 1988, ApJ, 326, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D., & Mathys, G. 2000, A&A, 359, 213 [NASA ADS] [Google Scholar]
- Landstreet, J. D., Bagnulo, S., Andretta, V., et al. 2007, A&A, 470, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landstreet, J. D., Silaj, J., Andretta, V., et al. 2008, A&A, 481, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maitzen, H. M. 1985, A&AS, 62, 129 [NASA ADS] [Google Scholar]
- Mathys, G. 1989, Fund. Cosmic Phys., 13, 143 [Google Scholar]
- Mestel, L., & Landstreet, J. D. 2005, in Cosmic Magnetic Fields, eds. R. Wielebinski, & R. Beck, Lecture Notes in Physics (Berlin: Springer Verlag), 664, 183 [Google Scholar]
- Neiner, C., Tkachenko, A., & MiMeS Collaboration 2014, A&A, 563, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., Mathis, S., Alecian, E., et al. 2015a, in Polarimetry, eds. K. N. Nagendra, S. Bagnulo, R. Centeno, & M. Jesús Martínez González, IAU Symp., 305, 61 [Google Scholar]
- Neiner, C., Morin, J., & Alecian, E. 2015b, in SF2A-2015: Proc. Annual meeting French Soc. Astron. Astrophys., eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 213 [Google Scholar]
- North, P., & Zahn, J.-P. 2003, A&A, 405, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E., Netopil, M., Pintado, O. I., & Rode-Paunzen, M. 2011, Astron. Nachr., 332, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, V., Wade, G., Drissen, L., Montmerle, T., & Alecian, E. 2011, in Astronomical Polarimetry 2008: Science from Small to Large Telescopes, eds. P. Bastien, N. Manset, D. P. Clemens, & N. St-Louis, ASP Conf. Ser., 449, 290 [Google Scholar]
- Petit, V., Owocki, S. P., Wade, G. A., et al. 2013, MNRAS, 429, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Preston, G. W. 1971, PASP, 83, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Balt. Astron., 6, 244 [NASA ADS] [Google Scholar]
- Sana, H., Gosset, E., & Rauw, G. 2006, MNRAS, 371, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Semenko, E. A., Romanyuk, I. I., Kudryavtsev, D. O., & Yakunin, I. A. 2014, Astrophys. Bull., 69, 191 [Google Scholar]
- Shultz, M., Wade, G. A., Grunhut, J., et al. 2012, ApJ, 750, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Shultz, M., Wade, G. A., Alecian, E., & BinaMIcS Collaboration 2015, MNRAS, 454, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Silaj, J., & Landstreet, J. D. 2014, A&A, 566, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wade, G. A., Bagnulo, S., Kochukhov, O., et al. 2001, A&A, 374, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
All Tables
CFHT exposure identification (odometer) number, modified Julian date at mid-exposure, radial velocities of primary and secondary (VR1 and VR2 respectively), and measured longitudinal field ⟨ Bz ⟩ of the primary star with uncertainty σBz.
Orbital elements and uncertainties of the SB2 system BD-19 5044L computed as described in the text.
Properties of primary and secondary stars of BD-19 5044L as derived from this study.
Properties of known short-period (Porb< 20 d) SB2 systems containing a magnetic upper main sequence star.
All Figures
 |
Fig. 1 An example of an LSD plot, for the spectrum from CFHT file 1822453pn.s. The lower curve is the mean Stokes I spectral line, with the primary star at −45 km s-1 and the secondary at + 70 km s-1. The lack of symmetry about the line centre of the mean primary line is clearly visible, while the secondary line is both constant in shape and symmetric. The upper curve is the mean Stokes V circular polarisation, multiplied by 20 and shifted upward to + 1.04 for ease of comparison. This Stokes component clearly shows that a field is present in the primary, while no evidence of a field is seen in the secondary. |
| In the text | |
 |
Fig. 2 Radial velocity curves as a function of orbital phase measured relative to the velocity extremum, using the best period of 17.63011 d. The velocities of the primary are plotted with blue circles, those of the secondary as red diamonds. Smooth curves are from the model discussed in the text. |
| In the text | |
 |
Fig. 3 Variations of the magnetic moment ⟨ Bz ⟩ of BD-19 5044L A phased with a rotational period of 5.041 d. The origin of the rotational phase system is the first ⟨ Bz ⟩ measurement in 2015, from Table 1. The smooth curve is the best sine wave fit to the data. |
| In the text | |
 |
Fig. 4 Variations of equivalent width of the LSD line of the primary star of BD-19 5044L, phased with a rotational period of 5.041 d. The origin of the phase system is the first ⟨ Bz ⟩ measurement in 2015, from Table 1. The smooth curve is the best sine wave fit to the data. |
| In the text | |
 |
Fig. 5 Small sections of the best fits found by zeeman.f to the disentangled mean spectrum of BD-19 5044L A (upper two panels) and BD-19 5044L B (lower two panels). The observed spectra are the (black) curves with noise; the computed spectra (red) have no noise. Ion identifications are provided for the stronger lines in the upper two panels; these generally apply to the corresponding lines in the lower two panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


