| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 12 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201629312 | |
| Published online | 29 March 2017 | |
The bound fraction of young star clusters
1 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: brinkmann@mpifr-bonn.mpg.de
2 Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
3 Helmholz-Institut für Strahlen-und Kernphysik, Auf dem Hügel 71, 53121 Bonn, Germany
4 California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA
5 Charles University in Prague, Faculty of Mathematics and Physics, Astronomical Institute, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
Received: 14 July 2016
Accepted: 20 October 2016
Context. The residual gas within newly formed star clusters is expelled through stellar feedback on timescales ≲ 1 Myr. The subsequent expansion of the cluster results in an unbinding of a fraction of stars, before the remaining cluster members can re-virialize and form a surviving cluster.
Aims. We investigate the bound fraction after gas expulsion as a function of initial cluster mass in stars Mecl and gauge the influence of primordial mass segregation, stellar evolution and the tidal field at solar distance. We also assess the impact of the star-formation efficiency εSFE and gas expulsion velocity vg.
Methods. We perform N-body simulations using Sverre Aarseth’s NBODY7 code, starting with compact clusters in their embedded phase and approximate the gas expulsion by means of an exponentially depleting external gravitational field. We follow the process of re-virialization through detailed monitoring of different Lagrange radii over several Myr, examining initial half-mass radii of 0.1 pc, 0.3 pc and 0.5 pc and Mecl usually ranging from 5 × 103M⊙ to 5 × 104M⊙.
Results. The strong impact of the relation between the gas expulsion timescale and the crossing time means that clusters with the same initial core density can have very different bound fractions. The adopted εSFE = 0.33 in the cluster volume results in a distinct sensitivity to vg over a wide mass range, while a variation of εSFE can make the cluster robust to the rapidly decreasing external potential. We confirm that primordial mass segregation leads to a smaller bound fraction, its influence possibly decreasing with mass. Stellar evolution has a higher impact on lower mass clusters, but heating through dynamical friction could expand the cluster to a similar extent. The examined clusters expand well within their tidal radii and would survive gas expulsion even in a strong tidal field.
Key words: galaxies: star clusters: general / methods: numerical
© ESO, 2017
1. Introduction
Star clusters form within the dense cores of giant molecular clouds (Lada & Lada 2003; Alves & Bouy 2012; Megeath et al. 2016). Within proto-cluster cloud cores, individual proto-stellar cores approach their hydrogen-burning main sequences to form an infant star cluster, still embedded in residual gas. Both observational and numerical studies (Adams & Fatuzzo 1996) indicate that star formation process may be self-regulatory, due to mechanical and radiation feedback from the proto-stars and O/B main-sequence stars, leading to a partial conversion of gas into stars. This means that all newborn clusters begin their lives in a gas-embedded phase. The incomplete conversion from gas into stars can be quantified through the star-formation efficiency (εSFE) 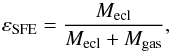 (1)where Mecl and Mgas describe the total mass in stars and gas respectively, right after star formation ceases within the proto-cluster clump. This assumes star cluster formation over a “single” starburst within the dense gas clump. A lack of age spread in young massive star clusters in the Milky Way and the Magellanic Clouds support episodic formation of star clusters. Also, as demonstrated in Banerjee & Kroupa (2015b), a short-duration cluster assembly implies formation of either a monolithic stellar distribution or close to monolithic one. In the latter case, a substructured stellar distribution is formed, where the stellar overdensities (sub-clusters) are located closely at birth (due to triggering) and merge into a single cluster in ≲ 1 Myr.
(1)where Mecl and Mgas describe the total mass in stars and gas respectively, right after star formation ceases within the proto-cluster clump. This assumes star cluster formation over a “single” starburst within the dense gas clump. A lack of age spread in young massive star clusters in the Milky Way and the Magellanic Clouds support episodic formation of star clusters. Also, as demonstrated in Banerjee & Kroupa (2015b), a short-duration cluster assembly implies formation of either a monolithic stellar distribution or close to monolithic one. In the latter case, a substructured stellar distribution is formed, where the stellar overdensities (sub-clusters) are located closely at birth (due to triggering) and merge into a single cluster in ≲ 1 Myr.
Both, observational (Lada & Lada 2003; Megeath et al. 2016) and computational studies (Machida & Matsumoto 2012) suggest εSFE ≲ 30% within dense star-forming gas clumps, which are typically of parsec scale. Over molecular clouds of ≳ 10 pc, εSFE is only a few percent. The newly-formed cluster remains gas embedded until a substantial portion of the gas is ionized by the UV radiation from the O/B stars. Once ionized, the radiation couples efficiently and pressurizes the gas over the entire proto-cluster, ultimately blowing it off the cluster. The properties of radiation propagation in ultra-compact H ii (UCH ii) regions dictate a relatively brief phase of τd ≲ 1 Myr, until the residual gas is expelled (Banerjee & Kroupa 2013). Indeed, the existence of few-Myr old, well-exposed massive starburst clusters, e.g., ≈ 1 Myr-old NGC 3603, suggests that the gas-embedded phase lasts for ≲ 1 Myr. Such radiative gas expulsion would take place at least with the sound speed in ionized hydrogen (≈ 10 km s-1), and hence can be expected to happen promptly, typically faster than or similar to the dynamical time or crossing time, τcr, of the embedded cluster (Banerjee & Kroupa 2013; Lada & Lada 2003). The corresponding dilution of the potential well causes the cluster to expand in its dynamical timescale. In this process, a fraction of the originally bound stars becomes unbound and leaves the cluster, before the latter may reach a new equilibrium state (e.g., Adams 2000; Kroupa et al. 2001; Boily & Kroupa 2002; Baumgardt & Kroupa 2007; Pfalzner & Kaczmarek 2013; Banerjee & Kroupa 2013; Smith et al. 2013).
The timescale of gas expulsion, τg, and εSFE are the two key parameters that determine the evolution of a given embedded cluster (Lada et al. 1984; Lada & Lada 2003; Adams 2000). For a collisionless system, gas removal should unbind a cluster (or any gravitationally self-bound system) if εSFE ≤ 0.3. The survivability of star clusters, for εSFE ≤ 0.3, relies solely on energy exchange among stellar orbits over a dynamical timescale in the expanding cluster. This causes a fraction of the stars, preferentially from the cluster’s central region with highest stellar density, to lose orbital energy and eventually fall back to form a remaining bound cluster which is in dynamical equilibrium, i.e., “re-virialized” (Banerjee & Kroupa 2013; Kroupa et al. 2001). A longer τg, therefore, allows for a longer time for violent relaxation, resulting in a larger remnant cluster. This mechanism plays a crucial role for a cluster’s survival, since both observations and theoretical studies support clump εSFE of ≲ 0.3 (Lada & Lada 2003; Machida & Matsumoto 2012; Megeath et al. 2016).
In this study, we consider initially massive, compact clusters and investigate the mass bound fraction, i.e., the mass fraction of stars that remain gravitationally bound after the gas dispersal, to form a surviving cluster. While this is a basic question which has already been explored in the literature (Lada et al. 1984), its importance is renovated as an increasing number of young massive and open clusters, with a variety of dynamical conditions, are being observed in detail. This issue is directly connected to the question of the contribution of clustered star formation to the field star population in a galaxy. Despite several notable contributions over the past decade, a systematic study of the bound fraction of star clusters with realistic conditions is still pending. Assuming a canonical initial mass function (IMF), there are four primary parameters that control an embedded cluster’s bound fraction after its re-virialization, viz., its initial mass, Mecl, its initial size (half-mass radius), rh, εSFE, and gas dispersal timescale, τg.
2. Initial conditions and gas expulsion
The starting point for all our simulations is a star cluster in its gas-embedded phase. The total initial stellar mass, Mecl, is compounded by stars following the canonical optimal IMF (Kroupa et al. 2013), whose spatial and velocity distributions are described by a Plummer sphere in dynamical equilibrium (Heggie & Hut 2003; Plummer 1911). Initially dense spherical Plummer conditions are a good approximation given the structure of well observed very young clusters (Kroupa et al. 2001; Banerjee & Kroupa 2013). Initially hierarchical sub-clump configurations are limited to be near-monolithic systems formed in a single-burst, given its youth (Banerjee & Kroupa 2015b). The residual gas is mimicked by a time-dependent external potential of a spherically-symmetric mass distribution of total mass Mgas following the same Plummer radial density profile as the stars, enabling us to effectively adopt an εSFE as defined by Eq. (1). The essential dynamical effect of gas dispersal is mimicked by depleting the total gas mass Mgas (and hence its potential), exponentially: 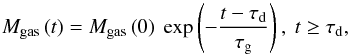 (2)thus allowing the embedded cluster to evolve secularly for time τd, before Mgas decreases in a timescale τg. This timescale, which is given by
(2)thus allowing the embedded cluster to evolve secularly for time τd, before Mgas decreases in a timescale τg. This timescale, which is given by 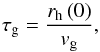 (3)depends on the initial half-mass radius (HMR),
(3)depends on the initial half-mass radius (HMR), 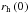 , of the stellar cluster and the gas, and the average radial velocity of gas expulsion, vg. The latter is taken to be vg ≈ 10 km s-1, the sound speed in an H ii region (e.g., Kroupa et al. 2001; Banerjee & Kroupa 2013). This simplifying assumption neglects the possible radiation-pressure dominated (RPD) initial phase of gas expansion, during which the gas blow-out velocity might exceed the speed of sound (which is essential for massive clusters with large escape velocities), as shown by Krumholz & Matzner (2009), thereby denoting our choice of τg as an upper limit.
, of the stellar cluster and the gas, and the average radial velocity of gas expulsion, vg. The latter is taken to be vg ≈ 10 km s-1, the sound speed in an H ii region (e.g., Kroupa et al. 2001; Banerjee & Kroupa 2013). This simplifying assumption neglects the possible radiation-pressure dominated (RPD) initial phase of gas expansion, during which the gas blow-out velocity might exceed the speed of sound (which is essential for massive clusters with large escape velocities), as shown by Krumholz & Matzner (2009), thereby denoting our choice of τg as an upper limit.
The time until the commencement of gas expulsion is estimated to be τd ≈ 0.6 Myr (see Kroupa et al. 2001; Banerjee & Kroupa 2013 and references therein), by considering the lifetimes of ultra-compact (≈ 0.1 pc) H ii regions of up to ≈ 0.1 Myr and scaling them to the radii investigated in our simulations (Banerjee & Kroupa 2014). During the time until termination of star formation, several generations of stars can condense out of the gas (Wuchterl & Tscharnuter 2003) in a real cluster and orbit the potential for several crossing times, thereby nearing equilibrium (see also Kroupa 2005).
Admittedly, the process of gas dispersal, especially from massive clusters, is still a poorly understood process and the quantities, vg(τg) and τd, as adopted above to describe this process have to be treated essentially as model parameters, with their plausible representative values chosen based on the present knowledge. If not stated otherwise, we treat the models computed here as isolated clusters with no primordial mass segregation; stellar evolution is taken into account and the initial HMR is 0.3 pc and εSFE = 0.33. The above mentioned values for vg and τd are used for the time evolution of the gas potential.
3. Bound fraction and its dependence on cluster parameters
The effect of gas expulsion from an embedded cluster is an interplay between the rapid (in timescale comparable to the dynamical time of the cluster) dilution of the gas potential that tends to unbind the cluster and orbital energy exchange among the stars (in a rapidly-changing gravitational field) resulting in “violent relaxation” that helps a fraction of the expanding stellar population to dissipate energy and fall back and retain a (lower-mass) bound cluster (see Banerjee & Kroupa 2015a, for a discussion). A self-consistent and accurate treatment of this violent relaxation is crucial for a reliable estimate of the bound fraction left after the gas removal. This is why we need to resort to direct N-body simulations in this work.
The dynamical relaxation of a self-gravitating many body system is most realistically calculated using star-by-star direct N-body integration. In this study we use the state-of-the-art direct N-body code NBODY7 (formerly NBODY6; Aarseth 2003, 2012) to compute the evolution of star clusters before, during and following gas expulsion. In addition to tracking the individual stars’ orbits using the highly-accurate fourth-order Hermite scheme and dealing with the diverging gravitational forces, during, e.g., close encounters and hard binaries, through two-body and many-body regularizations, NBODY7 also includes well-tested analytical stellar and binary evolution recipes viz., the SSE and the BSE schemes (Hurley et al. 2000, 2002), that is employed simultaneously with the dynamical integration. The above stellar-evolutionary schemes include mass loss due to stellar winds and supernovae and stellar masses and other parameters are updated accordingly during the N-body integration. Over the early ages considered in this study (≲ 20 Myr), the stellar mass loss happens predominantly due to very fast winds from O-type stars (~ 103 km s-1) and supernova ejecta (~ 104 km s-1), which would escape from the cluster immediately. Hence, in these calculations, any stellar mass loss is simply removed from the system, contributing to the dilution of the cluster’s gravitational potential accordingly. Furthermore, mergers among stars and remnant formation are treated through analytic recipes. Most importantly, no softening of gravitational forces is employed at any stage, making sure that the energetics of general two-body interactions and close encounters, that plays a key role in the dynamical relaxation of the cluster, is accurately computed. This numerical code, therefore, naturally and best suits the purpose of this study.
A straightforward way to calculate the bound fraction of a computed model cluster, as a result of its early gas expulsion, is to follow its Lagrange radii over time. In this study, we use Lagrange radii at 2% intervals of mass fraction, reaching from 2% to 99%. This allows for the tracking of the different layers of an evolving cluster fairly closely and hence the calculation of the bound fraction with reasonable accuracy, for a particular simulation (see, e.g., Fig. 6 below). Here, the bound fraction after gas expulsion is determined by the outermost Lagrange radius displaying a reversal of its expansion, though we also take the slope of the radii in comparison to the bound inner layers into account. The re-collapse of a particular Lagrange radius can be easily identified by eye estimation (cf. Fig. 6; except perhaps for the innermost few). That way the “inherent” bound fraction, as a result of the loss of stars due to gas expulsion (plus any stellar-evolutionary mass loss), is estimated. The fact that one does get consistent results, as shown below, justifies this approach.
Note that this approach does not strictly take into account the stars’ gravitational boundedness to the cluster. This is because it can, in principle, include a small fraction of stars whose velocities are higher than the escape velocity and which are on their way of escaping the system. We plot the bound fraction as a function of Mecl for most considered parameters. The functions tracing the bound fractions are basic arctan functions which are fitted to the data to provide visual aid only.
Notably, the relative bound mass after 20 Myr, as a function of εSFE and initial cluster density, is studied by Pfalzner & Kaczmarek (2013), whereas our results give an upper limit on the bound fraction for a given initial condition, without focusing on a certain point in time. Their bound fractions after 20 Myr would consequently be smaller than those determined with our method. In addition to the overall bound fraction of a computed cluster, we also note the re-virialization time for 10%, 20%, etc. Lagrange radii. The realized simulations are intended to give an impression of the impact of various physical parameters on the bound fraction, providing a base for further studies. The error bars in bound fractions, for most plots here, are derived using the 2% error in determining the bound fraction in an individual simulation; they are sometimes larger due to fluctuations in the Lagrange radii, especially for lower mass clusters. When multiple runs are available for a particular set of parameters, we use the mean values and standard deviation.
3.1. Half-mass radii and re-virialization times
To examine the influence of certain key cluster parameters on the bound fraction after gas expulsion, we consider massive and initially very compact clusters with a HMR of ≲ 0.3 pc. Such compact initial conditions are consistent with the sizes of the observed proto-cluster cores and filament junctions in molecular clouds (Malinen et al. 2012; André et al. 2014), where massive clusters are likely to form. In order to make estimations for differently sized clusters, we typically take initial HMRs of rh = 0.1 pc, 0.3 pc and 0.5 pc and plot their bound fraction as a function of initial cluster mass. This is shown in Fig. 1. Here, the arctan funcions used for fitting suggest a theoretical maximum bound fraction of roughly 83% for the compact 0.1 pc, and 77% for the 0.5 pc clusters. Over the whole mass range, the initial HMR seems to have a distinct effect on the bound fraction. This dependency also shows up when plotting the bound fraction as a function of initial core density (see Kroupa 2008, particularly pages 28 and 31), 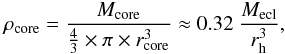 as shown in Fig. 2: the same initial core density can lead to very different bound fractions, depending on the initial HMR.
as shown in Fig. 2: the same initial core density can lead to very different bound fractions, depending on the initial HMR.
 |
Fig. 1 Bound fraction for initial HMR of 0.1 pc, 0.3 pc and 0.5 pc as a function of initial cluster mass. The data points for 0.1 pc and 0.3 pc correspond to one run per mass, for 0.5 pc 3−6 are averaged. |
 |
Fig. 2 Bound fraction as a function of initial core density for initial HMR of 0.1 pc, 0.3 pc and 0.5 pc. |
This is mostly owed to the influence of the HMR on the important relation τg/tcross (Baumgardt & Kroupa 2007). With εSFE and gas expulsion velocity vg both set and the definitions given in Kroupa (2008), we can estimate 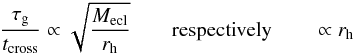 for a fixed density: although a smaller cluster can re-virialize faster, the timescale for gas expulsion decreases even quicker, deteriorating the above relation and reducing the bound fraction. This is emphasized when plotting (Fig. 3) the bound fraction against
for a fixed density: although a smaller cluster can re-virialize faster, the timescale for gas expulsion decreases even quicker, deteriorating the above relation and reducing the bound fraction. This is emphasized when plotting (Fig. 3) the bound fraction against 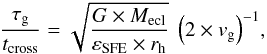 G being the gravitational constant. A specific value of τg/tcross seems to result in a corresponding bound fraction, a stronger correlation than observed for the other parameters.
G being the gravitational constant. A specific value of τg/tcross seems to result in a corresponding bound fraction, a stronger correlation than observed for the other parameters.
 |
Fig. 3 Bound fraction as a function of the ratio between gas expulsion timescale and crossing time. A certain bound fraction may be traced back to a specific value of τg/tcross. |
The re-virialization time, here defined as the moment a given Lagrange radius no longer shrinks, is more difficult to determine. Specifically in the lower mass clusters, we find ambiguity due to the effects of stellar evolution setting in and “overlaying” the contraction of the Lagrange radii. The inner radii also pose difficulties caused by fluctuations due to strong stellar encounters. The re-virialization times plotted in Fig. 4, therefore, give only a rough estimate and are only adoptable for an initial HMR of 0.5 pc. The more compact 0.1 pc and 0.3 pc clusters show considerably shorter re-virialization times (<1 Myr for most Lagrange radii for the HMR 0.1 pc clusters).
 |
Fig. 4 Re-virialization times for clusters with an initial HMR of 0.5 pc and Mecl of 104M⊙ to 6 × 104M⊙. The values are averaged over 3−6 simulations and include the τd ≈ 0.6 Myr equilibrium (embedded) phase of the cluster. |
3.2. Gas expulsion velocity
The impact of the gas expulsion velocity, vg, on the bound fraction is examined for two clusters with initial stellar component masses Mecl of 104M⊙ and 105M⊙, by varying vg from 5 km s-1 to 100 km s-1. The high sensitivity of the clusters’ survival to the changing velocity (see Sect. 1) is illustrated in Fig. 5. Infant mass loss differs strongly over a comparatively short range of vg, suggesting that a 104M⊙ cluster, with εSFE = 0.33, would not survive the gas expulsion phase, should the average gas velocity exceed 30 km s-1.
 |
Fig. 5 Influence of the gas expulsion velocity on the bound fraction for initially unsegregated, isolated clusters with stellar masses of 104M⊙ and 105M⊙, considering a εSFE of 0.33 and an initial HMR of 0.3 pc, one simulation per data point. |
 |
Fig. 6 Evolution over 7 Myr for 104M⊙ clusters with an initial HMR of 0.3 pc for εSFE = 0.33 (left panel), εSFE = 0.50 (middle panel) and εSFE = 0.66 (right panel). Pictured are 50 Lagrange radii, reaching from 2% to 99% in 2% intervals. As a visual aid, the prominent dashed curve refers to the HMR, the other prominent curves mark 10% steps. |
3.3. Varying star-formation efficiency
With the notable impact of the gas removal velocity on the bound fraction as shown in the previous section, the variation of εSFE seems to be the only way to produce clusters that survive their gas expulsion phase when considering higher gas velocities, the often-assumed instantaneous gas removal being the extreme case. The rest of the parameters, that are examined in our simulations, do not seem to have comparable effects on the infant weight loss.
The effect of variation of εSFE, to reduce infant weight loss or even to prevent the complete dissolution of a cluster of intermediate mass, is summarized in Fig. 7, where we look upon unsegregated 104M⊙ clusters. Progressing towards higher velocities, while εSFE = 0.33 will not result in a surviving cluster, the bound fraction reaches a plateau for εSFE = 0.50 and εSFE = 0.66, rendering a cluster tolerant against any gas loss. Simulations of early cluster evolution (e.g., Pfalzner & Kaczmarek 2013) with instantaneous gas removal, therefore, necessitates a high εSFE, with possible consequences for other cluster parameters.
A higher εSFE will result in a larger number of massive stars, and hence more mass as massive stellar members, compared to the primordial gas mass, for a given initial mass of the cluster-forming gas clump. This would, e.g., influence the clusters reaction to the effects of stellar evolution, once the first SN occurs or result in a smaller re-virialization time (as the disturbance caused by the rapid potential drop is smaller). This is demonstrated in Fig. 6. Additionally, the radial outgoing velocities of the unbound outer layers also seem to be strongly affected by a change of εSFE, i.e., the radial velocities are smaller for larger εSFE.
 |
Fig. 7 Bound fraction as a function of gas removal velocity for different εSFE, here for clusters with an initial stellar mass of 104M⊙ and a HMR of 0.3 pc. Approximating the gas removal to be instantaneous might make the assumption of an unusually high εSFE necessary, as otherwise simulations might not have any surviving cluster after gas expulsion. Every data point corresponds to a single simulation. |
3.4. Primordial mass segregation
Observations suggest that massive stars are preferentially located in the inner parts of star clusters, both for young, exposed and embedded ones. Mass segregation is, of course, expected in dynamically-evolved clusters as a consequence of two-body relaxation leading toward equipartition of energy among stellar populations with different masses (Meylan 2000). However, mass segregation is also observed in a number of young, not yet relaxed systems, suggesting primordial mass segregation (de Grijs et al. 2002; Littlefair et al. 2003; Bontemps et al. 2010) in them. Alternatively, diminished two-body relaxation times in initially sub-structured stellar configurations may offer another explanation for mass segregation in young clusters (McMillan et al. 2007).
The influence of primordial mass segregation on the bound fraction is examined here by a series of simulations with Mecl ranging from 2 × 103M⊙ to 5 × 104M⊙. In these computed models, the initial mass segregation is implemented using the method of Baumgardt et al. (2008). For lower to intermediate mass clusters, the bound fraction changes by around 7% to 10% (even more for the lowest regarded mass), and by ≲ 3 % for the high masses.
 |
Fig. 8 Influence of primordial mass segregation on the bound fraction as a function of initial cluster mass Mecl, based on one simulation per data point. An impact in lower mass clusters is observable, but the effect seems to lessen with increasing mass. This may be due to segregation in the heavy clusters in the equilibrium phase before gas expulsion. |
 |
Fig. 9 Effect of primordial mass segregation. Tracking the first 8 Myr (respectively 7.4 Myr after the beginning of gas expulsion) for two 2.5 × 104M⊙ clusters, without (left) and with (right) primordial mass segregation. Their differences begin to show after stellar evolution produces the first SN, the subsequent mass loss being more destructive for the initially segregated cluster. |
Figure 8 shows that the impact of primordial mass segregation becomes less pronounced with increasing cluster mass, possibly due to the evolution during the embedded ultra-compact H ii phase in the 0.6 Myr prior to gas expulsion: the massive members would dynamically segregate (mostly due to dynamical friction) to a greater extent with increasing cluster mass and hence central density within this time, resulting in a mass segregated initial condition anyway at the onset of gas expulsion. However, the segregated clusters, where stellar evolutionary mass loss is generally more pronounced in the inner regions, should have a smaller bound fraction than their unsegregated counterpart. This aspect is demonstrated in Fig. 9 for two 2.5 × 104M⊙ clusters; while the evolution of their Lagrange radii is comparable right after gas expulsion, the differences show up after ≈ 3 Myr, when the supernovae begin. From the inner layers to outwards, the initially-segregated cluster shows an ongoing expansion with a higher rate than the unsegregated cluster. Consequently, primordial mass segregation would lead to a less concentrated cluster than that without it, for the same initial mass.
The consequence of primordial mass segregation on low mass and massive clusters is considered in the simulations illustrated in Fig. 10. For the lower mass 5 × 103M⊙ cluster, the process of re-virialization is still ongoing at t ≈ 4.5 Myr, making it more vulnerable to the additional mass loss through stellar evolution. This aspect is more profound for the segregated cluster, where the additional stellar mass loss leads to re-expansion of the cluster. The influence of primordial mass segregation is subtle for more massive clusters, which largely re-virialize before the supernovae commence. The less concentrated structure in the primordially-segregated case, as discussed above, is still perceivable though, and it shows similar re-expansion as the lower mass cluster.
 |
Fig. 10 Effect of primordial mass segregation for masses of 5 × 103M⊙ (upper panels) and 5 × 104M⊙ (lower panels). The plots on the left are unsegregated, the ones on the right segregated. The strong dependence of the re-virialization time on the cluster mass is obvious, but also the more destructive impact of stellar evolution on segregated clusters can be seen over the whole mass range. |
3.5. Stellar evolution
It is intuitively clear that mass loss through stellar evolution will cause the cluster potential to dilute, aiding the loss of stars from the cluster. Although including stellar evolution is physically realistic, we do additional simulations without it, so that we can assess its impact. These simulations cover initially mass-segregated clusters with masses between 5 × 103M⊙ and 5 × 104M⊙.
The difference caused by stellar evolution is demonstrated in Fig. 11 for lower mass clusters, most notably when the stellar mass loss boosts after the first SN at ≈ 4 Myr. After 9.5 Myr, even the innermost layers of the model cluster including stellar evolution are still expanding considerably, having only ≈ 2% of the initial cluster mass left within a radius of ≈ 1 pc. All layers, including those which initially rebound after gas expulsion, show an ongoing expansion. In contrast, the inner layers of the model without stellar evolution are still within that radius and do not expand significantly.
 |
Fig. 11 Effect of stellar evolution. Covering the first 9.5 Myr (respectively 8.9 Myr after the beginning of gas expulsion) for two 5 × 103M⊙ clusters. While the reversion process after gas expulsion is ongoing for the cluster without stellar evolution (left panel), the first SN disturb the process of re-virialization in the more realistic scenario including stellar evolution (right panel). The effect is more distinct in these lower mass clusters. |
The overall influence of stellar evolution is summarized in Fig. 12, it illustrates that stellar evolution reduces the bound fraction over the whole examined mass range. The impact on the lower mass clusters seems to be larger, due to their longer re-virialization time and thereby higher sensitivity to the additional stellar mass loss. Consequently, not only the bound fraction, but the structure of the inner parts of the surviving cluster can be strongly influenced by stellar evolution. For the regarded HMR 0.3 pc clusters, stellar evolution reduces the bound fraction for about 10% in the lower mass regime, and stagnates just under 5% for higher masses.
3.6. Stellar evolution vs. dynamical friction
It would be worthwhile to consider how the bound fraction is affected by the dynamical heating effect alone, arising from the dynamical friction of the most massive stars. Without the stellar evolution and hence the additional potential drop through stellar mass loss, the bound fraction would tend to increase. However, without the mass loss (in other words, if the stars were point masses) the most massive stars, which are ≳ 100 M⊙, would as well deposit energy preferentially to the central part of the cluster, due to their repeated scattering from and sinking back to the core via dynamical friction. The importance of the above effect can be assessed in models that maximize it, i.e., in initially mass-segregated clusters without stellar evolution.
This is summarized in Fig. 13 which shows that the maximal effect of heating of the cluster through dynamical friction alone could be of the same order as that due to stellar evolution has on the bound fraction for an unsegregated cluster.
 |
Fig. 12 Influence of stellar evolution on the bound fraction as a function of initial cluster mass. The effect lessens with increasing mass, but is noticeable over the whole examined mass range. The differences are most likely due to the different re-virialization times after gas expulsion. The values for the clusters without stellar evolution are averaged over 3 simulations per mass, while one simulation per mass is used for those including stellar evolution. |
 |
Fig. 13 Impact of dynamical friction, estimated through minimization and maximization of its effect. The overlap over large parts of the mass range suggests that its heating of the cluster might be of the same order of magnitude as the influence of stellar evolution. The simulations maximizing dynamical friction are averaged over 3 runs per mass, the data points for minimized dynamical friction correspond to one realization per mass. |
A comparison between two 3 × 104M⊙ clusters is shown in Fig. 14, illustrating that neither the overall expansion nor the bound fraction is notably different. The expansion due to stellar mass loss via supernovae in one cluster (left panel), starting at ≈ 3.5 Myr, and the flattening at about 7 Myr when the cluster is close to dynamical equilibrium again, are of the same order as the heating through dynamical friction alone. The innermost parts of the model cluster with maximized dynamical friction (right panel) show stronger fluctuations, the interactions with the still existing most massive particles providing a persistent source of heating.
3.7. The tidal field at solar distance
The clusters simulated so far were assumed to be isolated, i.e., without the influence of an external galactic tidal field. Their corresponding bound fractions therefore represent an upper limit to that for the more realistic scenario that includes the external forces.
Here we consider the tidal field at the solar distance, approximated by the field of a point mass of 2 × 1010M⊙ at a distance of 8.5 kpc, orbited by the model clusters with a circular velocity of 220 km s-1.
The results are shown in Fig. 15 which suggest that the clusters remain well within their tidal radii at all times, for solar-like Galactocentric distance, making the influence of the tidal field negligible for the range of cluster mass and HMR and the εSFE considered here.
3.7.1. Removing escaped stars
Unlike the question concerning the importance of incorporating stellar evolution discussed in 3.5, the removal of stars which are no longer bound to the cluster from the calculations is of a more technical interest. If the bound fraction after gas expulsion does not change either way, it is more economical to remove them from the calculations. The results for a tidal field at solar distance shown in Fig. 16 indicate that the removal of escapers is indeed viable, assuming our examined mass range and HMR.
3.8. Strong tidal field: a simple model of the Arches Cluster
While a Galactic tidal field does not seem to have a significant impact on the bound fraction at the solar distance, clusters much closer to the Galactic center could be influenced due to the much stronger tidal field there and hence smaller tidal radii. In order to estimate the effect of a strong tidal field, we compute a simplified model of the Arches cluster and try to reconstruct its initial mass and HMR.
The cluster is set to orbit the Galactic center at a distance of 100 pc (an estimate between the 30 pc projected distance from Nagata et al. 1995 and the upper limit of 200 pc suggested by Stolte et al. 2008) with an orbital velocity of 200 km s-1, comparable to the values mentioned in Stolte et al. (2008) or Clarkson et al. (2012). It encloses a point mass of 109M⊙ (a rough estimate, accounting for the central SMBH and parts of the nuclear bulge with a total mass of ≈ (1.4 ± 0.6) × 109M⊙, Launhardt et al. 2002). The previous simulations here show an expansion of the inner Lagrange radii by a factor of about 3 to 4 after re-virialization for high-mass, compact clusters, in quite good agreement with the theoretical estimate (Kroupa 2008) for adiabatic gas removal 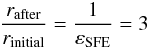 for εSFE 0.33. So from the measured HMR of around 0.4 pc (Olczak et al. 2012 and references therein) one can estimate the approximate initial HMR being 0.1−0.15 pc. We vary the initial mass and compare the resulting HMR after 2.5 Myr, which corresponds to the current age of the Arches Cluster (Figer et al. 2002).
for εSFE 0.33. So from the measured HMR of around 0.4 pc (Olczak et al. 2012 and references therein) one can estimate the approximate initial HMR being 0.1−0.15 pc. We vary the initial mass and compare the resulting HMR after 2.5 Myr, which corresponds to the current age of the Arches Cluster (Figer et al. 2002).
 |
Fig. 14 Impact of dynamical friction, gauged with exemplary plots, tracking the first 10 Myr (respectively 9.4 Myr after the beginning of gas expulsion) for two 3 × 104M⊙ clusters. The bound fraction and overall extension are of the same order of magnitude at that time. The expansion of the cluster with minimized dynamical friction (left panel) is driven primarily by stellar evolution, whereas the interactions through dynamical friction provide a constant source of heating for the other cluster (right panel). |
As to be expected, the computed clusters show a reaction to the strong tidal field (see Fig. 17), the slope of their outer Langrange radii being steeper, their overall expansion after gas expulsion bigger. The inner structure of both clusters looks similar though, suggesting that the influence of the external field can be regarded as being limited to the outer layers in good approximation. Outer parts of the cluster which initially reverse within 1 Myr experience a strong outward acceleration once their distance to the cluster center exceeds ≈3 to 4 pc (representing the tidal radius of the cluster, illustrated in Fig. 18). It is noteworthy though that the bound fraction does not differ over more than ≈10% with or without the tidal field, which is most likely due to the very compact initial size of the clusters. However, the ongoing albeit moderate overall expansion after gas expulsion results in a HMR over 0.4 pc after just 2.5 Myr, even for the heaviest simulated clusters of 3.5 × 104M⊙. This means that one would need a more massive, but preferably an even more compact cluster with an initial HMR smaller than 0.1 pc to match the parameters of the Arches cluster given further below.
As an approximation of the bound fraction, we now look at the Lagrange radii after 2.5 Myr and determine what layers are within 4 pc (a rough estimate of the tidal radius, which will slightly overestimate the bound fraction). So in this case, we will not determine the maximum bound fraction, but the mass fraction within a certain radius at a given time. The results are shown in Fig. 19. To make comparisons with observational data easier, Fig. 20 contains the same information as Fig. 19, but shows the current mass instead of the bound fraction. The current mass measured within 3′ (respective extent for an observer from Earth) would then point directly to the initial cluster mass, should the other parameters (initial HMR, εSFE, etc.) be realistic.
 |
Fig. 15 Impact of the tidal field at solar distance on the bound fraction as a function of initial cluster mass. With their relatively compact initial HMR of 0.3 pc, the clusters show no distinct reaction to the field. Every data point corresponds to one simulation for the isolated clusters, the data points for the clusters in a tidal field consider 2 simulations per mass. |
 |
Fig. 16 Comparison between removing and keeping escaped stars in the calculations. Removing escapers from clusters situated in a tidal field at the solar distance does not seem to have a significant impact on the bound fraction over the considered mass range. The overlap with the comparison plot including the escapers in the total cluster mass is notable in wide parts. For the clusters with removed stars, one simulation per mass is used, while the data points for the clusters keeping escapers consider 2 runs per mass. |
Estimates for the current mass and possible initial mass vary for different studies. A current mass of (3.1 ± 0.6) × 104M⊙ (Espinoza et al. 2009) suggests an initial mass of just over 4 × 104M⊙ from our simulations, whereas a current mass of (1.9 ± 0.3) × 104M⊙ suggested by Habibi et al. (2013) prompts an initial mass of around 2.7 × 104M⊙. The aforementioned underestimated growth of the HMR in 2.5 Myr would still warrant the assumption of a smaller initial HMR, but the already carried out simulations portray a reasonable approximation. Estimates of the initial mass vary from around 2 × 104M⊙ (Kim et al. 2000), over (4.9 ± 0.8) × 104M⊙ (Harfst et al. 2010) to the upper mass limit of ~ 7 × 104M⊙ (within 0.23 pc) of Figer et al. (2002).
Our result seems to agree quite well with the above values, although we make several approximations. The actual environment around Arches is much more complex, but nevertheless the incorporation of a strong tidal field shows that an Arches-like cluster can readily survive gas expulsion even under these conditions.
 |
Fig. 17 Comparing two 3 × 104M⊙ clusters, both with an initial HMR of 0.1 pc. The left panel shows a simplified model of Arches in a strong Galactic tidal field, the right model is considered to be in isolation. |
 |
Fig. 18 The tidal radius in the strong tidal field is emphasized by the removal of escaped stars from the calculations. The plot shows a 3 × 104M⊙ cluster with an initial HMR of 0.1 pc. |
 |
Fig. 19 Mass fraction within 4 pc as an estimate of the bound fraction for the Arches Cluster at its current age of 2.5 Myr and an initial HMR of 0.1 pc. |
 |
Fig. 20 Mass within 4 pc for more convenient comparisons with observational data of the Arches cluster. Measurements of the current mass point to the initial mass Mecl, provided the other parameters match the actual conditions close enough. |
3.9. Radial velocities
Apart from determining the bound fraction after gas expulsion, our simulations enable a rough estimate for the radial velocities of the unbound outer layers. Determining those velocities might help to understand the heating of the Galactic thick disc (Kroupa 2002; Assmann et al. 2011). If one can find a relation between the radial velocity and the initial mass, it may be possible to constrain values for cluster masses responsible for properties of the Galactic thick disc. The observed chain galaxies at high redshift (Elmegreen & Elmegreen 2006) suggest that this model of star-cluster-birth induced heating of galactic discs may indeed be relevant.
Figure 21 gives an impression of the radial velocities of inner and outer layers, right after gas expulsion and at a cluster age around 6 Myr. The velocities right after gas expulsion are averaged over a cluster age of 0.6 Myr to 0.7 Myr, the later velocities are averaged over 6 Myr to 6.5 Myr. The latter point in time is somewhat arbitrary and chosen because the re-virialization process is completed for most clusters, yet the low mass clusters are not yet totally disrupted by stellar evolution.
One can see that the expansion of the inner layers (10% and 50%) has slowed down or even stopped after 6 Myr, whereas the outer 90% layer accelerated further. The latter may be caused by stellar evolution: the few two-body encounters in the outer parts with low density can not slow down the expansion effectively, so that the additional mass loss through stellar evolution causes an outward acceleration (see Fig. 21). A viable estimate of a sufficiently high cluster mass to explain properties of the thick disc will need more simulations and should be addressed in future studies. Kroupa (2002) suggests a cluster mass of 106M⊙, which is currently too massive for direct N-body calculations. The required radial velocity (or velocity dispersion perpendicular to the Galactic disc plane) of around 40 km s-1 is not reached by any of our simulated clusters, but lies well beyond 105M⊙. With the importance of εSFE implied by Fig. 6, the required mass could be reduced for clusters with lower star-formation efficiency. Additionally, external fields could accelerate the outer layers yet more, thus also implying a time dependence of the radial velocities even at later cluster age.
 |
Fig. 21 Left panel: radial velocities right after gas expulsion and at a cluster age around 6 Myr as a function of Mecl. The simulations are for clusters with εSFE = 0.33 and initial HMR of 0.3 pc. They consider stellar evolution, no primordial mass segregation and no Galactic tidal field, one simulation per mass. Right panel: evolution of Lagrange radii for a 105M⊙ cluster (this time not in logarithmic scale, resulting in a clear visibility of only the outermost radii) to explain the acceleration of the outer layers: at a cluster age around 3.8 Myr, stellar evolution causes noticeable mass loss. The outer low density regions have not yet slowed down from the initial expansion due to gas expulsion, because the stars have little chance to interact. Further mass loss through stellar evolution can therefore not be compensated, resulting in an accelerated expansion. |
4. Discussion and conclusions
Several commonly used approximations are made in our simulations. For instance, the system is in equilibrium at the start of gas expulsion, we do not consider sub-structures, there are no primordial binaries and εSFE is constant over the whole cluster.
The self-consistent formation of a bound cluster from a giant molecular cloud carried out by Hurley & Bekki (2008) shows that equilibrium is reached in the order of a few crossing times, with said timescale being fairly short for our compact configurations and well within the adopted τd ≈ 0.6 Myr.
Furthermore, this simplifying assumption is necessary to make the models computable, because simulating a forming cluster of mass larger than about 100 M⊙ magneto-hydrodynamically with feedback is beyond the current technological capabilities. In reality the earliest phases of embedded cluster assembly are given by the simultaneous inward flow of gas, driven by the deepening potential well of the embryonic embedded cluster, and by the nearly-simultaneous outflow of gas driven by the increasing stellar feedback and magnetic fields generated in the proto-stellar accretion disks (a single proto-star taking ≈ 105 Myr to assemble ≈ 95% of its mass, see Wuchterl & Tscharnuter 2003). At any particular time the existing proto-stellar population virialises within several crossing times which is very short in the embryonic embedded cluster such that the approximation of a virialised stellar population embedded in gas is more accurate than assuming the entire final population is in a free fall as if the stars formed instantaneously with little motions. For example Dale et al. (2015) perform a set of hydrodynamical plus feedback simulations but without magnetic fields to test the general evolution of clusters of different mass. They conclude that feedback has little disruptive effect on the forming clusters. However, in contrast to their statements, the resolution achieved is not adequate to address the issue of cluster survival or disruption adequately, because for example at the high-mass end (their initial clouds near 106M⊙), their stellar particles have masses of 100 M⊙ thereby constituting unresolved substantial sub-clusters. The least massive clouds simulated (104M⊙) have a resolution of 1 M⊙ such that the embedded clusters form from unresolved sub-clusters of 1 M⊙ each. Especially at the low-mass end, where the dynamics is heavily relaxation driven, very high precission integration techniques are required to account for the interparticle forces. Dale et al. (2015) write that in their simulations locally, where stellar particles are formed, the star-formation efficiency is near 100%. This contradicts our assumption that εSFE is typically 0.33 throughout the embedded cluster volume. However, it is also in contradiction with the results of the high-resolution magnetohydrodyamical calculations by Machida & Matsumoto (2012; see also Bate et al. 2014) of forming individual proto-stars. Machida & Matsumoto (2012) find that the magnetic fields induced in the evolving circum-stellar disk drives a bi-polar outflow such that the star-formation efficiency is about 0.26−0.54 only. Therefore, the Nbody models of embedded clusters used here capture the important physical processes. Despite the shortcomings of either approach, the models presented here agree broadly with those of Dale et al. (2015; their Fig. 9) since for embedded cluster masses larger than 104M⊙ the fraction of stars which become unbound to the removal of residual gas becomes 0.30 or less for star formation-efficiencies of 0.30 or more. The reason for this high fraction of bound stars despite the low star-formation efficiency, even in the present Nbody models, is that the velocity of gas expulsion is comparable to the pre-gas expulsion velocity dispersion in our models. The overall conclusion, in broad but not in detail agreement with those of Dale et al. (2015), is thus that embedded clusters more massive than about 104M⊙ loose a minor fraction of their stars as a result of residual gas expulsion. For less-massive clusters, such as the Orion Nebula Cluster, residual gas expulsion is more destructive with a larger expansion and leaving a smaller fraction of the initial stellar population in a bound open-cluster (Kroupa et al. 2001). Assuming an analytical time changing gas potential as used here can be consistent with simulations including heated gas, as demonstrated by Geyer & Burkert (2001).
Sub-structures are examined in the studies of Banerjee & Kroupa (2015b) or Fellhauer et al. (2009), which indicate that the timescale for clump-merging may be shorter than the time for residual gas expulsion. As we consider high-mass clusters, the omission of sub-structures also seems reasonable. Neglecting primordial binaries could underestimate ejections from the cluster due to the missing of very tight binaries (see also Pfalzner & Kaczmarek 2013, and references therein), again making clear that our results point to the upper limit of the bound fraction. On the other hand, primordial binaries can cause a brief initial contraction of the cluster as described in Banerjee & Kroupa (2014) due to “binary cooling”. Soft binaries can absorb kinetic energy to become unbound, the cooling therefor being a result of the chosen binary distribution. If the cluster re-virializes fast enough after this initial collapse, binary activity should have no major effect on the following gas expulsion phase. The influence of εSFE varying over the cluster is related to the density profile. Should εSFE be higher in the central regions, we could expect a higher stellar density compared to a constant εSFE over the whole cluster. Simulations discussed in Pfalzner & Kaczmarek (2013) compare King-type and Plummer-type clusters, showing a significant difference for the bound fraction around εSFE = 0.33, whereas other εSFE has matching results. This high sensitivity to the density profile, and more generally to the phase-space density function (Boily & Kroupa 2002, 2003), should be addressed in future studies.
Summarizing our main results:
-
1.
The bound fraction is extremely sensitive to the timescale of gasexpulsion for the consideredεSFE, or more precisely to the relation τg/tcross. Clusters with the same initial core density can have very different bound fractions.
-
2.
The variation of εSFE or the timescale of gas expulsion can result in the same bound fraction. It would be desirable to have more observational constraints, especially regarding the gas expulsion velocity.
-
3.
We can confirm that primordially mass segregated clusters have a smaller bound fraction. The effect lessens with increasing mass, possibly due to our models segregating during the early equilibrium phase, thus not actually depicting unsegregated heavy clusters at the beginning of gas expulsion.
-
4.
Stellar evolution reduces the bound fraction over the whole considered mass range. In the lower mass clusters, the first SN disturb the process of re-virialization, resulting in a more pronounced mass loss.
-
5.
Heating through dynamical friction could be of the same order of magnitude as the expansion caused by stellar evolution in unsegregated clusters.
-
6.
The massive, very compact clusters considered in our simulations seem to expand well within their tidal radii. The impact of a Galactic tidal field at solar distance is negligible, as is the more technical aspect of keeping or removing escaped stars from the simulated cluster in this case.
-
7.
An Arches-like cluster can survive gas expulsion in the presence of a strong Galactic tidal field.
-
8.
The bound fraction increases from 20% to 80% for Mecl ≈ 5 × 103M⊙ to 105M⊙ for the canonical combination of gas expulsion parameters εSFE = 0.33, τd = 0.6 Myr and vg = 10 km s-1.
Acknowledgments
We acknowledge the support of the Argelander-Institut für Astronomie computing team.
References
- Aarseth, S. J. 2003, in Gravitational N-Body Simulations (Cambridge University Press), 430 [Google Scholar]
- Aarseth, S. J. 2012, MNRAS, 422, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C. 2000, ApJ, 542, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., & Fatuzzo, M. 1996, ApJ, 464, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J., & Bouy, H. 2012, A&A, 547, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, 27 [Google Scholar]
- Assmann, P., Fellhauer, M., Kroupa, P., Brüns, R. C., & Smith, R. 2011, MNRAS, 415, 1280 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., & Kroupa, P. 2013, ApJ, 764, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., & Kroupa, P. 2014, ApJ, 787, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, S., & Kroupa, P. 2015a, ArXiv e-prints [arXiv:1512.03074] [Google Scholar]
- Banerjee, S., & Kroupa, P. 2015b, MNRAS, 447, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Tricco, T. S., & Price, D. J. 2014, MNRAS, 437, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., De Marchi, G., & Kroupa, P. 2008, ApJ, 685, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Boily, C., & Kroupa, P. 2002, in Modes of Star Formation and the Origin of Field Populations, eds. E. K. Grebel, & W. Brandner, ASP Conf. Ser., 285, 141 [Google Scholar]
- Boily, C. M., & Kroupa, P. 2003, MNRAS, 338, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Bontemps, S., Motte, F., Csengeri, T., & Schneider, N. 2010, A&A, 524, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clarkson, W. I., Ghez, A. M., Morris, M. R., et al. 2012, ApJ, 751, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ercolano, B., & Bonnell, I. A. 2015, MNRAS, 451, 987 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., Gilmore, G. F., Johnson, R. A., & Mackey, A. D. 2002, MNRAS, 331, 245 [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Elmegreen, D. M. 2006, ApJ, 650, 644 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Espinoza, P., Selman, F. J., & Melnick, J. 2009, A&A, 501, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fellhauer, M., Wilkinson, M. I., & Kroupa, P. 2009, MNRAS, 397, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F., Najarro, F., Gilmore, D., et al. 2002, ApJ, 581, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Geyer, M. P., & Burkert, A. 2001, MNRAS, 323, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Habibi, M., Stolte, A., Brandner, W., Hußmann, B., & Motohara, K. 2013, A&A, 556, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harfst, S., Portegies Zwart, S., & Stolte, A. 2010, MNRAS, 409, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D., & Hut, P. 2003, The Gravitational Million-Body Problem: A Multidisciplinary Approach to Star Cluster Dynamics (Cambridge University Press) [Google Scholar]
- Hurley, J. R., & Bekki, K. 2008, MNRAS, 389, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S. S., Figer, D. F., Lee, H. M., & Morris, M. 2000, ApJ, 545, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, MNRAS, 330, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2005, in The Three-Dimensional Universe with Gaia, eds. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 629 [Google Scholar]
- Kroupa, P. 2008, in The Cambridge N-Body Lectures, eds. S. J. Aarseth, C. A. Tout, & R. A. Mardling, Lect. Notes Phys. (Berlin: Springer Verlag) 760, 181 [Google Scholar]
- Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, in The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations, eds. T. D. Oswalt, & G. Gilmore, 115 [Google Scholar]
- Krumholz, M. R., & Matzner, C. D. 2009, ApJ, 703, 1352 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Margulis, M., & Dearborn, D. 1984, ApJ, 285, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., Zylka, R., & Mezger, P. G. 2002, A&A, 384, 112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Littlefair, S. P., Naylor, T., Jeffries, R. D., Devey, C. R., & Vine, S. 2003, MNRAS, 345, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., & Matsumoto, T. 2012, MNRAS, 421, 588 [NASA ADS] [Google Scholar]
- Malinen, J., Juvela, M., Rawlings, M. G., et al. 2012, A&A, 544, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMillan, S. L. W., Vesperini, E., & Portegies Zwart, S. F. 2007, ApJ, 655, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2016, AJ, 151, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, G. 2000, in Massive Stellar Clusters, ed. A. Lançon & C. M. Boily, ASP Conf. Ser., 211, 215 [Google Scholar]
- Nagata, T., Woodward, C. E., Shure, M., & Kobayashi, N. 1995, AJ, 109, 1676 [NASA ADS] [CrossRef] [Google Scholar]
- Olczak, C., Kaczmarek, T., Harfst, S., Pfalzner, S., & Portegies Zwart, S. 2012, ApJ, 756, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Pfalzner, S., & Kaczmarek, T. 2013, A&A, 555, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Smith, R., Goodwin, S., Fellhauer, M., & Assmann, P. 2013, MNRAS, 428, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Stolte, A., Ghez, A. M., Morris, M., et al. 2008, ApJ, 675, 1278 [NASA ADS] [CrossRef] [Google Scholar]
- Wuchterl, G., & Tscharnuter, W. M. 2003, A&A, 398, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Bound fraction for initial HMR of 0.1 pc, 0.3 pc and 0.5 pc as a function of initial cluster mass. The data points for 0.1 pc and 0.3 pc correspond to one run per mass, for 0.5 pc 3−6 are averaged. |
| In the text | |
 |
Fig. 2 Bound fraction as a function of initial core density for initial HMR of 0.1 pc, 0.3 pc and 0.5 pc. |
| In the text | |
 |
Fig. 3 Bound fraction as a function of the ratio between gas expulsion timescale and crossing time. A certain bound fraction may be traced back to a specific value of τg/tcross. |
| In the text | |
 |
Fig. 4 Re-virialization times for clusters with an initial HMR of 0.5 pc and Mecl of 104M⊙ to 6 × 104M⊙. The values are averaged over 3−6 simulations and include the τd ≈ 0.6 Myr equilibrium (embedded) phase of the cluster. |
| In the text | |
 |
Fig. 5 Influence of the gas expulsion velocity on the bound fraction for initially unsegregated, isolated clusters with stellar masses of 104M⊙ and 105M⊙, considering a εSFE of 0.33 and an initial HMR of 0.3 pc, one simulation per data point. |
| In the text | |
 |
Fig. 6 Evolution over 7 Myr for 104M⊙ clusters with an initial HMR of 0.3 pc for εSFE = 0.33 (left panel), εSFE = 0.50 (middle panel) and εSFE = 0.66 (right panel). Pictured are 50 Lagrange radii, reaching from 2% to 99% in 2% intervals. As a visual aid, the prominent dashed curve refers to the HMR, the other prominent curves mark 10% steps. |
| In the text | |
 |
Fig. 7 Bound fraction as a function of gas removal velocity for different εSFE, here for clusters with an initial stellar mass of 104M⊙ and a HMR of 0.3 pc. Approximating the gas removal to be instantaneous might make the assumption of an unusually high εSFE necessary, as otherwise simulations might not have any surviving cluster after gas expulsion. Every data point corresponds to a single simulation. |
| In the text | |
 |
Fig. 8 Influence of primordial mass segregation on the bound fraction as a function of initial cluster mass Mecl, based on one simulation per data point. An impact in lower mass clusters is observable, but the effect seems to lessen with increasing mass. This may be due to segregation in the heavy clusters in the equilibrium phase before gas expulsion. |
| In the text | |
 |
Fig. 9 Effect of primordial mass segregation. Tracking the first 8 Myr (respectively 7.4 Myr after the beginning of gas expulsion) for two 2.5 × 104M⊙ clusters, without (left) and with (right) primordial mass segregation. Their differences begin to show after stellar evolution produces the first SN, the subsequent mass loss being more destructive for the initially segregated cluster. |
| In the text | |
 |
Fig. 10 Effect of primordial mass segregation for masses of 5 × 103M⊙ (upper panels) and 5 × 104M⊙ (lower panels). The plots on the left are unsegregated, the ones on the right segregated. The strong dependence of the re-virialization time on the cluster mass is obvious, but also the more destructive impact of stellar evolution on segregated clusters can be seen over the whole mass range. |
| In the text | |
 |
Fig. 11 Effect of stellar evolution. Covering the first 9.5 Myr (respectively 8.9 Myr after the beginning of gas expulsion) for two 5 × 103M⊙ clusters. While the reversion process after gas expulsion is ongoing for the cluster without stellar evolution (left panel), the first SN disturb the process of re-virialization in the more realistic scenario including stellar evolution (right panel). The effect is more distinct in these lower mass clusters. |
| In the text | |
 |
Fig. 12 Influence of stellar evolution on the bound fraction as a function of initial cluster mass. The effect lessens with increasing mass, but is noticeable over the whole examined mass range. The differences are most likely due to the different re-virialization times after gas expulsion. The values for the clusters without stellar evolution are averaged over 3 simulations per mass, while one simulation per mass is used for those including stellar evolution. |
| In the text | |
 |
Fig. 13 Impact of dynamical friction, estimated through minimization and maximization of its effect. The overlap over large parts of the mass range suggests that its heating of the cluster might be of the same order of magnitude as the influence of stellar evolution. The simulations maximizing dynamical friction are averaged over 3 runs per mass, the data points for minimized dynamical friction correspond to one realization per mass. |
| In the text | |
 |
Fig. 14 Impact of dynamical friction, gauged with exemplary plots, tracking the first 10 Myr (respectively 9.4 Myr after the beginning of gas expulsion) for two 3 × 104M⊙ clusters. The bound fraction and overall extension are of the same order of magnitude at that time. The expansion of the cluster with minimized dynamical friction (left panel) is driven primarily by stellar evolution, whereas the interactions through dynamical friction provide a constant source of heating for the other cluster (right panel). |
| In the text | |
 |
Fig. 15 Impact of the tidal field at solar distance on the bound fraction as a function of initial cluster mass. With their relatively compact initial HMR of 0.3 pc, the clusters show no distinct reaction to the field. Every data point corresponds to one simulation for the isolated clusters, the data points for the clusters in a tidal field consider 2 simulations per mass. |
| In the text | |
 |
Fig. 16 Comparison between removing and keeping escaped stars in the calculations. Removing escapers from clusters situated in a tidal field at the solar distance does not seem to have a significant impact on the bound fraction over the considered mass range. The overlap with the comparison plot including the escapers in the total cluster mass is notable in wide parts. For the clusters with removed stars, one simulation per mass is used, while the data points for the clusters keeping escapers consider 2 runs per mass. |
| In the text | |
 |
Fig. 17 Comparing two 3 × 104M⊙ clusters, both with an initial HMR of 0.1 pc. The left panel shows a simplified model of Arches in a strong Galactic tidal field, the right model is considered to be in isolation. |
| In the text | |
 |
Fig. 18 The tidal radius in the strong tidal field is emphasized by the removal of escaped stars from the calculations. The plot shows a 3 × 104M⊙ cluster with an initial HMR of 0.1 pc. |
| In the text | |
 |
Fig. 19 Mass fraction within 4 pc as an estimate of the bound fraction for the Arches Cluster at its current age of 2.5 Myr and an initial HMR of 0.1 pc. |
| In the text | |
 |
Fig. 20 Mass within 4 pc for more convenient comparisons with observational data of the Arches cluster. Measurements of the current mass point to the initial mass Mecl, provided the other parameters match the actual conditions close enough. |
| In the text | |
 |
Fig. 21 Left panel: radial velocities right after gas expulsion and at a cluster age around 6 Myr as a function of Mecl. The simulations are for clusters with εSFE = 0.33 and initial HMR of 0.3 pc. They consider stellar evolution, no primordial mass segregation and no Galactic tidal field, one simulation per mass. Right panel: evolution of Lagrange radii for a 105M⊙ cluster (this time not in logarithmic scale, resulting in a clear visibility of only the outermost radii) to explain the acceleration of the outer layers: at a cluster age around 3.8 Myr, stellar evolution causes noticeable mass loss. The outer low density regions have not yet slowed down from the initial expansion due to gas expulsion, because the stars have little chance to interact. Further mass loss through stellar evolution can therefore not be compensated, resulting in an accelerated expansion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


