| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527922 | |
| Published online | 04 April 2017 | |
Spatially resolved star formation relation in two HI-rich galaxies with central post-starburst signature
1 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
e-mail: aklitsch@eso.org
2 Ludwig-Maximilians-Universität München, Faculty of Physics, Schellingstraße 4, 80799 München, Germany
3 Australian Astronomical Observatory, PO Box 915, North Ryde, NSW 1670, Australia
4 Sydney Institute for Astronomy, School of Physics, University of Sydney, NSW 2006, Australia
5 Department of Physics and Astronomy, Macquarie University, NSW 2109, Australia
6 The Australian Astronomical Observatory, PO Box 915, North Ryde, NSW 1670, Australia
Received: 8 December 2015
Accepted: 18 November 2016
Context. E+A galaxies are post-starburst systems that are identified based on their optical spectra. These galaxies contain a substantial young A-type stellar component but display no emission lines, which indicates only little ongoing star formation (SF). HI 21 cm line emission is found in approximately half of the nearby E+A galaxies, indicating that they contain a reservoir of gas that could fuel active SF.
Aims. We study the distribution and kinematics of atomic and molecular gas in two HI-rich galaxies, which show a typical E+A spectrum at the centre and SF at larger radii. From our results we aim to infer whether the SF activity of these galaxies is consistent with the activity seen in disc galaxies, or if it indicates a transition towards another evolutionary phase.
Methods. We present newly obtained high spatial resolution radio interferometric observations of the HI 21 cm emission line using the Karl Jansky Very Large Array (VLA) and of the CO(1–0) emission line using the Atacama Large Millimeter/submillimeter Array (ALMA). We combine these data sets to predict the star formation rate (SFR) using a pressure-based SF relation and show that it does not correlate well with the SFR derived from Hα on sub-kpc scales. We apply a recently developed statistical model for the small-scale behaviour of the SF relation to predict and interpret the observed scatter.
Results. We find regularly rotating HI gas that is smoothly distributed across the entire disc. The CO(1–0) emission line is not detected for either of the two galaxies. The derived upper limit on the CO mass implies a molecular gas depletion time of tdepl ≲ 20 Myr. However, because of the low metallicity, the CO-to-H2 conversion factor is highly uncertain. In the relations between the Hα-based SFR and the HI mass, we observe a substantial scatter we demonstrate results from small-number statistics of independent SF regions on sub-kpc scales.
Conclusions. We confirm the HI-richness of ESO534-G001 and 2dFRS S833Z022, and find that the scale dependence of the atomic SF relation in these galaxies is consistent with the predicted increase in the scatter towards small size scales. This is due to the incomplete sampling of independent HI clouds and SF regions. This finding adds to the existing literature, which has reported a scale dependence of the molecular SF relation, showing that the atomic and molecular phases are both susceptible to the evolutionary cycling of individual regions. This suggests that the atomic gas reservoirs host substantial substructure, which should be observable with future high-resolution observations.
Key words: stars: formation / galaxies: evolution / galaxies: ISM
© ESO, 2017
1. Introduction
Summary of galaxy properties.
The bimodal distribution of galaxies in the colour-magnitude diagram is well established up to redshift z ~ 2 (Williams et al. 2009). Red-sequence galaxies are generally characterized by a spheroidal shape, quiescence, no ongoing star formation (SF), and a low gas mass fraction. Galaxies in the blue cloud, in contrast, are disc dominated, star forming, and gas rich (e.g. Blanton & Moustakas 2009). The red sequence shows a mass growth by at least a factor of 2 since z ~ 1 (Bell et al. 2004). This bimodality suggests that SF is quenched and galaxies evolve from the blue cloud onto the red sequence. In this evolutionary phase, they pass through the so-called green valley.
Post-starburst galaxies (or more specifically, E + A galaxies) are a useful tool to study the quenching mechanism, as these galaxies are thought to be part of this transitional phase (e.g. Zabludoff et al. 1996; Norton et al. 2001; Pracy et al. 2009).
E+A galaxies are identified based on their optical spectra. The spectra show strong Balmer absorption lines, indicating a relatively young A-type stellar population, and only little or no [OII] 3727 Åand Hα emission. The combination of these characteristics suggests that the galaxies are post-starburst galaxies and that no significant SF occurred in the last ~1 Gyr (Couch & Sharples 1987). This indicates that E+A galaxies are snapshots of galaxies that move from the blue cloud onto the red sequence. However, it is still unclear whether this is the final transition. Half of the nearby E+A galaxies have HI 21 cm emission line detections (Buyle et al. 2006; Zwaan et al. 2013), suggesting that the galaxies may host further SF at a later time that is due to newly accessible gas reservoirs. The total number of known E+A galaxies is small at low redshift.
In this study, we present high spatial resolution follow-up observations of two HI-rich nearby low-mass E+A galaxies: ESO534-G001 (hereafter referred to as GalA) and 2dFGRS S833Z022 (hereafter referred to as GalB) from Zwaan et al. (2013). These galaxies were identified as E+A galaxies based on their central optical spectra. The stellar masses of these galaxies are log(M⋆/M⊙) = 9.1 and log(M⋆/M⊙) = 9.3, respectively (Zwaan et al. 2013). These stellar masses are lower than or comparable to that of the Large Magellanic Cloud, which has a stellar mass of log(M⋆/M⊙) = 9.3 (Skibba et al. 2012). The absolute B-band luminosity of GaIA is MB = −15.8 mag and of GalB is MB = −16.1 mag. These are several magnitudes fainter than the characteristic break in the galaxy luminosity function, which in the B band is 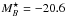 mag (Marzke et al. 1998). Based on the mass and luminosity, these galaxies are therefore characterized as dwarf galaxies.
mag (Marzke et al. 1998). Based on the mass and luminosity, these galaxies are therefore characterized as dwarf galaxies.
The distance to these galaxies is 20 Mpc for GalA and 31 Mpc for GalB, which is sufficiently nearby to study the gas properties with high physical resolution. The careful selection process, which restricts the observations to the southern hemisphere, is described in detail by Zwaan et al. (2013). The atomic hydrogen mass is determined from previous single-dish observations to be 9.63 × 108M⊙ for GalA and 14.7 × 108M⊙ for GalB (Zwaan et al. 2013). We present high spatial resolution HI 21 cm line observation and CO(1–0) emission line observations as a tracer of molecular hydrogen. Furthermore, optical integral field unit (IFU) spectra were obtained (Pracy et al. 2014). In these IFU spectra, Pracy et al. (2014) observed that the E+A signature is restricted to the central region and that SF is found at larger radii. Furthermore, extended UV emission is seen in the GALEX UV images. The total NUV-r colour of the galaxies is 1.5 ± 0.2 and 1.7 ± 0.2 for GalA and GalB, respectively. In the total NUV-r versus stellar mass plane this places these galaxies in the blue cloud. The centre, however, behaves differently from the rest of the galaxy. We did not use the GALEX data for our further analysis because of a lack of a solid estimate of dust extinction.
The goal is to determine whether the SF activity of these galaxies is consistent with the activity seen in normal spiral galaxies, or if it shows signs of a transition towards another evolutionary phase.
This paper is structured as follows. In Sect. 2 we present newly obtained observations of neutral hydrogen using the NRAO Karl G. Jansky Very Large Array (VLA) and observations of CO(1–0) using the Atacama Large Millimeter/submillimeter Array (ALMA). Additionally, a brief summary of the integral field unit spectra presented by Pracy et al. (2014) is given. The analysis of these data sets is shown in Sect. 3. In Sect. 4 we summarize the results and discuss our conclusions. For distance-related quantities, we assume H0 = 70kms-1Mpc-1 . We use the following conversion from angular to physical size scales: 1″ ≈ 97 pc (GalA) and 1″ ≈ 150 pc (GalB).
2. Data
Details of the VLA and ALMA observations.
We present newly obtained high spatial resolution VLA and ALMA line observations of the HI 21 cm and the CO J = 1−0 (vrest = 115.27 GHz) line of the two selected HI-rich galaxies from Zwaan et al. (2013) that have an E+A like spectrum in their central region. In our analysis we also make use of the optical IFU data that were presented by Pracy et al. (2014). These latter observations showed that the typical E+A signature is only seen in the centre of the two galaxies, whereas clumpy SF was detected at larger radii. A summary of the galaxy properties is given in Table 1. The details of the observations are discussed below and summarized in Table 2.
2.1. HI 21 cm line observations
To study the three-dimensional structure of the atomic gas, we observed the two galaxies in the HI 21 cm emission line using the VLA in its hybrid BnA and CnB configurations. In this configuration the northern arm of the array is in a more extended setup, so as to observe targets at low declination with a nearly circular beam. The observations were carried out using the WIDAR correlator in dual polarization mode, giving 7.8 kHz wide channels. The resulting channel separation is ~1.7 km s-1 and the resolution after Hanning smoothing is 3.3 km s-1. The total bandwidth of 4 MHz translates into a total velocity range of 860 km s-1, sufficiently wide to include all the HI emission, as can be seen from the Green Bank Telescope (GBT) spectra. The details of the observations are summarized in Table 2.
The calibration and data reduction was carried out using the Common Astronomy Software Applications (CASA 4.2.2) software package. The editing was done interactively, allowing us to remove parts of the data that suffered from radio frequency interference (RFI) or other obvious technical issues. The calibration was done using appropriate flux and bandpass calibrator sources and standard procedures. The time-variable complex gain was calibrated using frequent observations of a standard unresolved calibrator source in the same region on the sky. The flux scale was set using an observation of the source 3C147. Before imaging, the continuum emission was removed from the u,v data set by fitting a constant to the real and imaginary parts of the line-free channels.
The imaging was done using the standard clean algorithm. The multi-scale option was used, which is optimized for high spatial resolution observations of extended sources. A “robust” weighting scheme was applied, using a Briggs parameter of 0.5, which guarantees a nearly optimal sensitivity while still providing a high spatial resolution and a well-behaved synthesized beam. The resulting mean rms noise level is measured to be ~0.7 mJy beam-1 per 3.3 km s-1. The angular resolution of the HI data cube is ~4′′, and the largest angular scale observable is ~16′.
To ensure that only real emission is taken into account in the subsequent analysis, we define masking regions based on lower resolution data cubes. To that end, we use only the data from observations in the CnB configuration and convolve the resulting image cube with a Gaussian kernel with a full width at half maximum of 25′′. We define the masking regions as those regions that correspond to HI emission above a 2σ noise level. For the moment analysis of the high-resolution data cubes, these masking cubes are used to separate real emission from noise.
2.2. CO(1–0) observations
We use the CO(1–0) emission line at rest frequency of 115.27 GHz to trace the molecular hydrogen content and kinematics of our sample galaxies. ALMA Cycle 1 observations in Band 3 were obtained, the characteristics of which are summarized in Table 2. A phase calibrator was observed every ~8 min, and a bandpass calibrator was observed for 15 min at the beginning of the observations. The absolute flux scale was obtained through observing unresolved targets whose flux scale is regularly monitored by the ALMA observatory. The total on-source integration times were 100 min for GalA and 40 min for GalB. The data were taken with four basebands, one with a velocity resolution of 2.5 km s-1 centred on the expected CO line, and the other three in low-resolution mode at lower frequencies. For these observations, 32 antennas were available, but 5 of these had to be flagged during the data reduction procedure. The full reduction of the VLA data was carried out with CASA.
Cubes were made using a slight tapering of the longest baseline data and a “robust” weighting scheme with a Briggs parameter of 0.5 to obtain a spatial resolution of 3 arcsec. The velocity resolution of the cubes was set at 10 km s-1. The largest observable scale with the array configuration we used is ~20′′. The measured rms noise level is ~1.5 mJy beam-1 per 10 km s-1.
2.3. Integral field spectra
Pracy et al. (2014) present the optical IFU observations used in this study. The target galaxies were observed on 2012 November 12 using the Wide Field Spectrograph (WiFeS). It is operated on Mount Stromlo with the 2.3 m telescope of the Siding Spring Observatory. The average seeing was 1.7′′. The spaxel size is 1″ × 1″ and the total field of view is 25″ × 38″. The spectra span a wavelength range from ~3500 to 9000 Å with a spectral resolution of R ~ 3000. In this paper, we use the fully reduced and flux-calibrated data cubes from Pracy et al. (2014).
3. Analysis and results
 |
Fig. 1 Results for GalA. a) HI surface density in M⊙ pc-2 from the combined VLA observations. The spacing between the contours is 5 M⊙ pc-2. b) Line-of-sight velocity map of HI observed using the VLA. The Δv spacing between the contours is 14 km s-1. c) Velocity dispersion map. The spacing between the contours is 5 km s-1. d) Rotation curve of the HI disc observed with the VLA. The curves are obtained from the tilted ring model described in the text. e): HI residual velocity field. The contours are at −10, 0 and 10 km s-1. f) Stellar surface density map obtained from the B-band luminosity determined from IFU observations and a colour-dependent mass-to-light ratio (Bell et al. 2003). In these maps, north is at the top and east is on the left-hand side. |
 |
Fig. 2 Analysis results for GalB. For a description of each plot see the caption of Fig. 1. The differences with Fig. 1 are that for the HI surface densities the contours are at 5, 15, and 25 M⊙ pc-2. For the line-of-sight velocity the Δv spacing between the contours is 26 km s-1. |
3.1. Neutral hydrogen
From the 21 cm line observations we infer the HI distribution as well as the kinematics. The HI mass surface density is calculated by integration of the spectrum over the frequency axis. High spatial resolution surface density maps are shown in Figs. 1a and 2a. For the conversion from spectral flux densities to HI mass surface densities, we use ![\begin{equation} \Sigma_{{\rm HI}}\;[{\rm \textit{M}}_{\odot} \,{\rm pc^{-2}}]= 0.020 \cos i \; I\;[{\rm K \; km \; s^{-1}}] \end{equation}](/articles/aa/full_html/2017/04/aa27922-15/aa27922-15-eq54.png) (1)deprojecting and including a factor of 1.36 to account for the presence of helium (Leroy et al. 2008). The gas mass surface densities have peak values of 16.79 M⊙ pc-2 (GalA) and 30.23 M⊙ pc-2 (GalB). The gas is distributed relatively regularly over each galaxy with a mean HI mass surface density of 3.37 M⊙ pc-2 (GalA) and 5.3 M⊙ pc-2 (GalB), measured over the entire observed HI discs. The total neutral hydrogen masses we determine are MHI = (10.1 ± 0.2) × 108M⊙ (GalA) and MHI = (11.3 ± 0.6) × 108M⊙ (GalB). A summary of the properties derived from the surface density maps is given in Table 3. These results are consistent within the uncertainties with the results from the single-dish observations that are listed in Table 1 based on Zwaan et al. (2013), where lower observed fluxes result from the fact that only flux on certain scales is visible with an interferometer.
(1)deprojecting and including a factor of 1.36 to account for the presence of helium (Leroy et al. 2008). The gas mass surface densities have peak values of 16.79 M⊙ pc-2 (GalA) and 30.23 M⊙ pc-2 (GalB). The gas is distributed relatively regularly over each galaxy with a mean HI mass surface density of 3.37 M⊙ pc-2 (GalA) and 5.3 M⊙ pc-2 (GalB), measured over the entire observed HI discs. The total neutral hydrogen masses we determine are MHI = (10.1 ± 0.2) × 108M⊙ (GalA) and MHI = (11.3 ± 0.6) × 108M⊙ (GalB). A summary of the properties derived from the surface density maps is given in Table 3. These results are consistent within the uncertainties with the results from the single-dish observations that are listed in Table 1 based on Zwaan et al. (2013), where lower observed fluxes result from the fact that only flux on certain scales is visible with an interferometer.
The rotational velocity is determined based on the intensity-weighted mean velocity maps, which are shown in Figs. 1b and 2b. For the creation of these maps an additional 3σ noise level cut is applied to the masked data cube to ensure a high signal-to-noise ratio (S/N). The observed line-of-sight velocities are consistent with a rotating disc. To determine the deprojected rotation curves, we use the tilted ring model of Begeman (1989), which describes a galaxy as a set of concentric rings with the following parameters: position of the centre (x0, y0), systemic velocity Vsys, rotation velocity vrot, inclination i, position angle (PA) measured anti-clockwise between north on the sky and the semi-major axis of the receding part of the galaxy. For the application of the tilted ring model, we use the GIPSY task ROTCUR. We subsequently fix the parameters in a four-step procedure following Noordermeer et al. (2007). In this way, we can infer the radial dependence of the parameters and exclude warps in the discs, which would be observed as radius-dependent inclination or position angle. The resulting rotation curves are plotted in Figs. 1d and 2d. An approximately constant slope is observed in the inner part for both galaxies, which is consistent with a rotating solid body. At larger radii the slope of the rotation curves starts to decrease. For GalB in Fig. 2d we even observe a flat rotation curve at large radii. For GalA in Fig. 1d, however, a flat rotation curve is not reached within the maximum radius that can be observed. For dwarf galaxies, the flat part of the rotation curve is not necessarily seen, as we do not observe the HI disc to large enough radii. (Swaters et al. 2009). The rotation velocity increases to (69 ± 3) km s-1 (GalA) and (75 ± 13) km s-1 (GalB), where we use the dispersion of velocities along each tilted ring as the error of the rotation velocity.
The accuracy of the model velocity field is assessed from the residual velocity field, which is defined as the difference between observed and model velocity field. The residual velocity maps are shown in Figs. 1e and 2e. The plots demonstrate that there are no systematic deviations. The mean deviation is (0 ± 3) km s-1 for GalA and (1 ± 7) km s-1 for GalB.
The velocity dispersion is determined based on the intensity-weighted velocity dispersion maps, which are shown in Figs. 1c and 2c. For the calculation of these maps, the same 3σ cut is applied as for the rotational velocity maps. The velocity dispersion increases to maximum values of 20 km s-1 (GalA) and 22 km s-1 (GalB) in the galaxy centres. Overall, the velocity dispersion decreases from the centre to larger radii, which is most clearly visible for GalA. The mean velocity dispersion observed over the entire observed HI discs is 4.4 km s-1 (GalA) and 4.6 km s-1 (GalB). These values are on the low end of the range observed in nearby star-forming spiral galaxies (Walter et al. 2008; Ianjamasimanana et al. 2012) and dwarf galaxies (Hunter et al. 2012).
Summary of galaxy gas properties determined from the HI 21 cm line observations and the CO(1–0) emission line observations presented in this work.
3.2. Molecular hydrogen
After scrutinising the ALMA CO(1–0) cubes, we do not detect any CO(1–0) emission in either of the two galaxies. Therefore, we can only determine upper limits to the total CO(1–0) flux, and hence to the total molecular hydrogen present in the two galaxies. We note here that the ALMA observations that we obtained are only sensitive to observable scales below ~20′′, which correspond to physical scales of 1.94 kpc for GalA and 3.01 kpc for GalB. Any coherent emission on spatial scales larger than these values would generallly escape detection by our observations.
For the calculation of upper limits, we stack CO spectra over as large a region as possible in an attempt to enhance the S/N. To this end, we first de-rotate the CO(1–0) data cubes, making sure that all CO spectra are aligned in velocity space, with zero-velocity being equal to the local radial component of the rotational velocity. We use the measured HI velocity at each pixel and shift all the corresponding spectra accordingly. To set the spatial region over which we average, we use as a criterion an HI surface density exceeding a threshold of 1 M⊙ pc-2. The CO spectra at all positions fulfilling that criterion are then added up to a total spectrum from which we determine the upper limit to the integral CO flux. To calculate this total flux, we sum the spectra over a velocity range corresponding to plus or minus the measured HI velocity dispersion. Since CO velocity dispersions in galaxy discs are typically lower than those measured in HI (see Mogotsi et al. 2016), this choice of velocity limits ensures that no CO flux is missed. The uncertainty on the flux measurement is calculated by repeating the same exercise 60 times, but each time offsetting the central velocity by at most 300 km s-1.
Using this procedure, we evaluate 3σ upper limits to the total CO(1–0) luminosity of LCO = 1.9Kkms-1pc2 and 4.6Kkms-1pc2 for GalA and GalB, respectively. We convert these values into total molecular gas masses using the following equation: 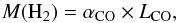 (2)where αCO is the conversion factor between the CO line intensity and the molecular gas surface density (see below).
(2)where αCO is the conversion factor between the CO line intensity and the molecular gas surface density (see below).
The CO-to-H2 conversion factor is strongly dependent on the metallicity. For low metallicities, Schruba et al. (2012) found that αCO increases by more than an order of magnitude.
Using the spatially integrated spectra from Pracy et al. (2014), we determine the gas metallicity with the R23 method (see e.g. Pagel et al. 1979; Kewley & Ellison 2008): ![\begin{equation} \text{R}_{23} = ([\text{OII}] + [\text{OIII}])/\text{H}_{\beta}. \end{equation}](/articles/aa/full_html/2017/04/aa27922-15/aa27922-15-eq79.png) (3)We correct the spectra for stellar contribution by fitting and removing an optimal template from the MILES library (v9.1; Sánchez-Blázquez et al. 2006) with ppxf (Cappellari & Emsellem 2004). Then, following Domínguez et al. (2013), we calculate E(B−V) = 1.97log 10 [ (Hα/ Hβ)obs/ 2.86 ] assuming Case B recombination (Osterbrock 1989) from the measured Balmer decrement. The galaxy spectra are then de-reddened with the Calzetti et al. (2000) procedure.
(3)We correct the spectra for stellar contribution by fitting and removing an optimal template from the MILES library (v9.1; Sánchez-Blázquez et al. 2006) with ppxf (Cappellari & Emsellem 2004). Then, following Domínguez et al. (2013), we calculate E(B−V) = 1.97log 10 [ (Hα/ Hβ)obs/ 2.86 ] assuming Case B recombination (Osterbrock 1989) from the measured Balmer decrement. The galaxy spectra are then de-reddened with the Calzetti et al. (2000) procedure.
We measure log (R23) = 0.65 and 0.73 for GalA and GalB, respectively. To determine whether we are on the lower or upper branch of R23, we also determine the log ([ NII ] / [ OII ]) and log ([ NII ] / [ Hα ]) values. They amount to − 1.27 and − 0.91 for GalA and − 1.24 and − 1.18 for GalB. The [NII]/[OII] ratios indicate the upper branch of R23, whereas for [NII]/Hα we are in the intermediate regime. We assume the upper branch in the metallicity estimates.
Using the Kobulnicky & Kewley (2004) equations as described in Kewley & Ellison (2008, Appendix A2.3,) we calculate a gas metallicity of 12 + log (O/H) = 8.81 and 8.81 for GalA and GalB, respectively. However, if we use the equations by Pettini & Pagel (2004) as described in Kewley & Ellison (2008, Appendix A4) for the N2 ratio, we obtain 12 + log (O/H) = 8.13 and 8.16 for GalA and GalB, respectively. Given the large uncertainty in measuring the gas metallicity, we adopt 12 + log (O/H) = 8.2 for this paper.
Based on the work by Elmegreen et al. (2013), we estimate that αCO ≈ 70M⊙ (Kkms-1pc2)-1 is an appropriate conversion factor. This would lead to an upper limit for the molecular hydrogen mass of 1.3 × 106M⊙ (GalA) and 3.3 × 106M⊙ (GalB). These masses are extremely low compared to molecular hydrogen masses of 107.7–109.8M⊙ found for E+A galaxies by French et al. (2015). However, the galaxies observed by French et al. (2015) have stellar masses of log (M⋆/M⊙) ≥ 9.96. Thus, previous studies did detect CO(1–0) line emission in E+A galaxies that are about an order of magnitude more massive than GalA and GalB.
Even with a value of αCO appropriate for the low metallicity of these galaxies, the molecular hydrogen mass is very low. This could be explained by the low gas densities and possibly a strong radiation field that would destroy the CO molecules. In that case, the molecular hydrogen would not be well traced by CO.
 |
Fig. 3 Total CO(1–0) luminosity as a function of B-band luminosity for normal spirals and dwarf galaxies presented by Schruba et al. (2012) in black and our galaxies in red. The black line is a linear fit to the bright galaxies (MB< −18) also taken from Schruba et al. (2012). |
Finally, we compare the upper limits in LCO with a literature sample of normal spirals and dwarf galaxies from Schruba et al. (2012), shown in Fig. 3. In their study, Schruba et al. (2012) found that in spirals with MB ≤ −18, MB and LCO trace each other nicely. Dwarf galaxies are found to be under-luminous in CO compared to this relation. The two galaxies presented in this study add further evidence to this. However, most of the low optical luminosity galaxies have only upper limits in LCO. With our ALMA observations we reach a higher sensitivity and therefore a lower upper limit than Schruba et al. (2012), but it clearly indicates that to constrain this relation for dwarf galaxies, observations of LCO with higher sensitivity in dwarf galaxies are needed.
3.3. Integral field spectra
In the original optical study the IFU was aligned with the major axis of the galaxies (Pracy et al. 2014). For this work, however, we use the rotated data cubes to have all data sets aligned. The coverage of GalA is limited, but GalB is covered in its entirety.
From the IFU spectra we derive the stellar mass surface density using a colour-dependent mass-to-light ratio (Bell et al. 2003): 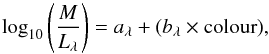 (4)where Lλ is the luminosity in a specific passband, aλ and bλ are passband-specific parameters, and the colour can be chosen among six different colours listed by Bell et al. (2003). To determine the stellar mass surface density, we use the luminosity in the B band and the B−R colour. To determine the B−R colour, we use the conversion given by Couch & Newell (1980). The corresponding parameters are given as aB = −1.224, bB = 1.251. Figures 1f and 2f show the stellar mass surface density maps for GalA and GalB, respectively.
(4)where Lλ is the luminosity in a specific passband, aλ and bλ are passband-specific parameters, and the colour can be chosen among six different colours listed by Bell et al. (2003). To determine the stellar mass surface density, we use the luminosity in the B band and the B−R colour. To determine the B−R colour, we use the conversion given by Couch & Newell (1980). The corresponding parameters are given as aB = −1.224, bB = 1.251. Figures 1f and 2f show the stellar mass surface density maps for GalA and GalB, respectively.
Using the spatially integrated spectra from Pracy et al. (2014), we determine the stellar velocity dispersions with ppxf (Cappellari & Emsellem 2004) and the MILES library (v9.1; Sánchez-Blázquez et al.2006). The galaxies’ spectral resolution was adjusted to the MILES library (Beifiori et al. 2011), and emission lines were masked out in the fit. These fits result in σ = (146 ± 11) km s-1 andσ< 100 km s-1 for GalA and GalB, respectively. Because the spectra are dominated by the Balmer absorption lines, the fits are somewhat unstable and the error might be even larger than the above-quoted formal error.
 |
Fig. 4 Maps of the pressure-based relative SFR of GalA (left) and GalB (right) and indicated by colour maps. Top: contours of the Hα emission at 3 × 10-16ergs-1cm-2 and from 5 to 20 × 10-16ergs-1cm-2 in steps of 5 × 10-16ergs-1cm-2 for GalA and at 5, 10, and 15 × 10-16ergs-1cm-2 for GalB over-plotted. Bottom: contours of the NUV emission from GALEX over-plotted on the same pressure-based SFR colour maps as in the top panels. The optical data cubes are aligned using the DSS observations and are therefore correct to ~1–2″. |
 |
Fig. 5 ΣSFR vs. ΣHI of GalA (left) and GalB (right). The solid line shows a power-law fit to the data. The spatial resolution for each plot is given in the lower left corner. r is the correlation coefficient, std is the corrected sample standard deviation, and a is the power-law index. From top to bottom, the spatial resolution decreases in steps of ~100 pc for GalA and ~150 pc for GalB. The highest spatial resolution presented is ~280 pc for GalA and ~440 pc for GalB. |
 |
Fig. 5 continued. |
Furthermore, we use the Hα emission observed in the IFU spectra as a comparison for the star formation rate (SFR) predictions calculated in Sect. 4.
4. Star formation rate prediction
In this section we calculate SFRs based on the previously calculated quantities. We derive the SFR by two different approaches.
The first is based on the observed Hα emission. Even though these galaxies are E+A galaxies, which should not show Hα emission by definition, Pracy et al. (2014) observed clumpy Hα emission at larger radii. For the original classification this emission was not known because it was based on a single-fiber spectrum of the central region. We determine the SFR from the Hα emission from the outer regions of the galaxies. Murphy et al. (2011) found the following relation between Hα luminosity LHα and SFR: ![\begin{equation} {\rm SFR}_{\rm H\alpha}[{\rm \textit{M}}_{\odot} \; {\rm yr}^{-1}] = 5.37 \times 10^{-42} L_{\rm H\alpha}[{\rm erg \; s^{-1}}], \end{equation}](/articles/aa/full_html/2017/04/aa27922-15/aa27922-15-eq120.png) (5)where LHα is corrected for dust extinction. From this we obtain integrated SFRs of 0.07 M⊙ yr-1 for GalA and 0.3 M⊙ yr-1 for GalB. Based on the upper limits of the H2 mass (within the region covered by the IFU observations), the corresponding gas depletion times tdepl are 18 Myr and 11 Myr. In comparison, nearby main-sequence galaxies have molecular depletion times of ~2 Gyr (e.g. Leroy et al. 2008; Bigiel et al. 2008). The computation of tdepl depends on αCO, which is poorly constrained in dwarf galaxies (see above). It is therefore possible that our assumed estimate of αCO is too small. On the other hand, gas depletion times of ~2 Gyr may only hold for main-sequence galaxies in equilibrium. GalA and GalB are dwarf galaxies, and Hunt et al. (2015) have shown that the molecular gas depletion times in such galaxies can differ by a factor of ~200. They found a decreasing tdepl with decreasing stellar mass, consistent with other studies (e.g. Huang & Kauffmann 2014).
(5)where LHα is corrected for dust extinction. From this we obtain integrated SFRs of 0.07 M⊙ yr-1 for GalA and 0.3 M⊙ yr-1 for GalB. Based on the upper limits of the H2 mass (within the region covered by the IFU observations), the corresponding gas depletion times tdepl are 18 Myr and 11 Myr. In comparison, nearby main-sequence galaxies have molecular depletion times of ~2 Gyr (e.g. Leroy et al. 2008; Bigiel et al. 2008). The computation of tdepl depends on αCO, which is poorly constrained in dwarf galaxies (see above). It is therefore possible that our assumed estimate of αCO is too small. On the other hand, gas depletion times of ~2 Gyr may only hold for main-sequence galaxies in equilibrium. GalA and GalB are dwarf galaxies, and Hunt et al. (2015) have shown that the molecular gas depletion times in such galaxies can differ by a factor of ~200. They found a decreasing tdepl with decreasing stellar mass, consistent with other studies (e.g. Huang & Kauffmann 2014).
The second approach we use for estimating the SFR is indirect and was introduced by Elmegreen (1989, 1993). It is based on the atomic gas maps and assumes that the hydrostatic pressure has an impact on both the formation and destruction rate of H2 and a probability of an overdensity gravitationally collapsing in a turbulent ISM. We use the empirical law determined by Blitz & Rosolowsky (2006) with the updated values from Leroy et al. (2008): 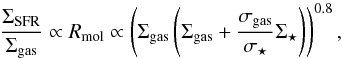 (6)where Rmol = ΣH2/ ΣHI, Σgas is the gas mass surface density, Σ⋆ is the stellar mass surface density, σgas is the velocity dispersion of the gas, and σ⋆ is the velocity dispersion of the stars. We use Σgas and σgas maps shown in Figs. 1a and c and Figs. 2a and c, respectively. The spatial resolution of these maps is 390 pc and 600 pc for GalA and GalB, respectively. The velocity resolution of the corresponding HI data cube is 3.3 km s-1. Furthermore, we use Σ⋆ maps shown in Figs. 1f and 2f, respectively. For σ⋆ we use the values determined from the spatially integrated central spectra as global values because of the low S/N. The velocity resolution of the optical spectra used to determine the velocity dispersion is 190 km s-1 (FWHM). We use the HI maps as well as the IFU spectra to predict the SFR maps if Eq. (6) holds. The SFR surface density predictions are shown in Fig. 4. The contours in these plots represent the Hα emission (top panels) and the NUV emission, which are both linearly proportional to the SFR, but trace different timescales. In all plots in this figure, a mismatch between predicted and observed SFR is visible. The predicted SFR maps peak at different positions than the Hα and NUV maps. The Hα and NUV maps look similar, but are not entirely consistent, which might be caused by the two indicators probing different SF-timescales, and/or by dust extinction. If the SF law applies independently of the spatial averaging scale, a mismatch between the SFR prediction and the observed SFR should not occur. This observation shows that in HI-dominated regions the pressure-based SF law can only be used as a global SF law (see Sect. 4.1).
(6)where Rmol = ΣH2/ ΣHI, Σgas is the gas mass surface density, Σ⋆ is the stellar mass surface density, σgas is the velocity dispersion of the gas, and σ⋆ is the velocity dispersion of the stars. We use Σgas and σgas maps shown in Figs. 1a and c and Figs. 2a and c, respectively. The spatial resolution of these maps is 390 pc and 600 pc for GalA and GalB, respectively. The velocity resolution of the corresponding HI data cube is 3.3 km s-1. Furthermore, we use Σ⋆ maps shown in Figs. 1f and 2f, respectively. For σ⋆ we use the values determined from the spatially integrated central spectra as global values because of the low S/N. The velocity resolution of the optical spectra used to determine the velocity dispersion is 190 km s-1 (FWHM). We use the HI maps as well as the IFU spectra to predict the SFR maps if Eq. (6) holds. The SFR surface density predictions are shown in Fig. 4. The contours in these plots represent the Hα emission (top panels) and the NUV emission, which are both linearly proportional to the SFR, but trace different timescales. In all plots in this figure, a mismatch between predicted and observed SFR is visible. The predicted SFR maps peak at different positions than the Hα and NUV maps. The Hα and NUV maps look similar, but are not entirely consistent, which might be caused by the two indicators probing different SF-timescales, and/or by dust extinction. If the SF law applies independently of the spatial averaging scale, a mismatch between the SFR prediction and the observed SFR should not occur. This observation shows that in HI-dominated regions the pressure-based SF law can only be used as a global SF law (see Sect. 4.1).
 |
Fig. 6 Schmidt-Kennicutt plot for the total amount of gas. The green triangles are the average ΣSFR within ΣHI bins of 400 pc sized regions within a sample of dwarf galaxies presented by Roychowdhury et al. (2015), the magenta diamond shows data from the LMC (Staveley-Smith et al. 2003), the cyan stars are disc averages of local dwarf galaxies from the LITTLE THINGS Survey (Zhang et al. 2012), the grey shaded area represents the region in which the bulk of the spatially resolved data points from local spiral galaxies presented by Bigiel et al. (2008) at a resolution of 750 pc lie, and the blue and red squares are the spatially resolved data points of GalA and GalB at the highest resolution, respectively. The solid and dashed lines represent lines of constant atomic gas depletion times, where solid is 1 Gyr and dashed 10 Gyr. |
Since the pressure-based SFR traces the HI distribution, we investigate this mismatch by a closer look at the relation between the HI distribution and Hα flux. To show this, we plot in Fig. 5 the observed ΣHI versus the observed ΣSFR for each resolution element. In addition, we fit a power law to the data. To determine whether the mismatch depends on the spatial resolution and to estimate at which scale the pressure-based SF law is applicable, we show the same plots for a decreasing spatial resolution. For GalA starting at a maximum spatial resolution of ~280 pc, the resolution elements are increased in size in steps of ~100 pc to a maximum edge length of ~680 pc. For GalB starting at a maximum resolution of ~440 pc, the resolution elements are increased in size in steps of ~150 pc to a maximum edge length of ~1060 pc. The correlation coefficient slightly increases with decreasing resolution, except for the lowest resolution plots. The fits show that the power-law index first increases and then decreases again for a decreasing resolution. This is comparable to what was found by Bigiel et al. (2008). Furthermore, a large scatter in atomic gas depletion time is observed for the original spatial resolution. In this figure no evolution of the scatter around the respective best fit is seen when comparing the corrected sample standard deviation. To further study the deviation from a linear relation and the corresponding scatter, we apply a recently developed theoretical model in the following subsection.
We note that based on previous studies (e.g. Bigiel et al. 2008), the gas is expected to be molecular at the ΣHI presented in Fig. 5 (highest resolution). However, these studies were carried out at a lower spatial resolution. When we take the spatial resolution into account and compare the spatially resolved data points from Bigiel et al. (2008) with our data at a spatial resolution of ~750 pc, the two results agree better. Furthermore, the extremely low molecular gas mass is inferred from the CO(1–0) emission line, which might not be tracing the molecular gas well in this case.
To determine whether the ΣSFR we show in Fig. 5 is atypical for local dwarf galaxies, we plot the spatially resolved data with the highest resolution onto the atomic gas Schmidt-Kennicutt relation together with a sample of spatially resolved local spiral galaxies compiled by Bigiel et al. (2008), disc-average values from local dwarf galaxies from the LITTLE THINGS Survey (Zhang et al. 2012), the LMC (Staveley-Smith et al. 2003), and data from a sample of spatially resolved ultra-faint dwarf galaxies presented by Roychowdhury et al. (2015). The corresponding plot is shown in Fig. 6. Compared to the ultra-faint dwarfs, GalA and GalB have higher SFR surface densities. However, the mean stellar mass of the ultra-faint dwarf galaxies is ~107M⊙, which is two orders of magnitude lower than our galaxies. Compared to the dwarf galaxies in the same mass range from the LITTLE THINGS survey, the SFR surface densities are comparable and the LMC also has a comparable ΣSFR. Furthermore, when we compare our galaxies with a spatially resolved sample of local spiral galaxies from Bigiel et al. (2008), we also find comparable ΣSFR. Therefore, we conclude that the ΣSFR is not only comparable to disc-averaged values of dwarf galaxies with comparable mass, but also to spatially resolved data of spiral galaxies. Furthermore, we over-plot in Fig. 6 lines of constant gas depletion times. The atomic gas depletion time is mostly between 1 and 10 Gyr for both galaxies, which is not atypical, as can be seen by comparison to other data sets. As we have pointed out, the extremely short molecular gas depletion times result most likely from the uncertainty of the CO-to-H2 conversion factor.
4.1. Understanding the scale-dependence of the star formation relation
 |
Fig. 7 Scatter in gas depletion time σ(log tdepl) as a function of aperture size for GalA (top) and GalB (bottom). The solid curves are least-squares fits. The red lines are two-parameter fits, and the blue solid curves are three-parameter fits, where the determined parameters and uncertainties are given in the legend. For the red curves tgas is kept fixed at 25 Myr. For the dashed curves the minimum/maximum parameter values of each fit are used to give an error interval. |
We compare the scale-dependence of the SF relation (i.e. the mismatch between the HI-predicted and observed Hα maps) to a theoretical model for the multi-scale nature of the SF relation (the “uncertainty principle for star formation” of Kruijssen & Longmore 2014, hereafter referred to as KL principle). Galactic SF relations assume that all phases of the SF timeline are well sampled within each aperture. However, the KL principle shows that this assumption is no longer valid on small-size scales. In small apertures, the sampling of the SF process is incomplete, as it matters when a region is observed. The corresponding prediction is that the scatter on the SF relation increases towards smaller aperture sizes. We note that the model of KL14 is entirely independent of the tracers used and only assumes that both tracers each occupy their own part of the evolutionary timeline (even though the model allows them to be completely coincident; in that case, there is no small-scale breakdown of the SF relation).
The KL principle models the scale dependence of the SF relation as a Poisson process. It assumes a random distribution of points (“regions”) in two-dimensions with a typical separation length 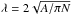 , where A is the total area and N indicates the total number of points. Each of these points represents an independent star-forming region and resides at a random moment on the evolutionary timeline. For simplicity, we assume a simple two-phase SF process, where during the first phase only the gas tracer can be observed, and during the second phase only the SF tracer can be observed, meaning that the possible overlap time of the two phases is set to zero. While the overlap is obviously non-zero in nature, it has been shown by Kruijssen & Longmore (2014) that this assumption does not affect the results on the size scales lap>λ considered here (see below).
, where A is the total area and N indicates the total number of points. Each of these points represents an independent star-forming region and resides at a random moment on the evolutionary timeline. For simplicity, we assume a simple two-phase SF process, where during the first phase only the gas tracer can be observed, and during the second phase only the SF tracer can be observed, meaning that the possible overlap time of the two phases is set to zero. While the overlap is obviously non-zero in nature, it has been shown by Kruijssen & Longmore (2014) that this assumption does not affect the results on the size scales lap>λ considered here (see below).
The Kruijssen & Longmore (2014) model for the scatter as a function of the aperture size is described in their Appendix B and is publicly available at http://www.mpa-garching.mpg.de/KL14principle. To compare its predictions to our observations, we first derive the observed scatter in the gas depletion time (tdepl ≡ Mgas/ SFR) as a function of aperture size. To do so, we convolve the observed maps with a top-hat kernel from the original spatial resolution of ~280 pc in steps of ~100 pc (GalA) and ~440 pc in steps of ~150 pc (GalB). The final resolution is limited to 0.5 times the minor axis of the galaxies, which is ~680 pc for GalA and ~1060 pc for GalB. For each convolved map, we calculate the scatter according to σlog (tdepl) = σlog (LHI/LHα), where we use the standard deviation σ of the quotient of the observed HI emission LHI and the observed Hα emission LHα. This is the scatter orthogonal to a linear relation between the HI surface density and the Hα emission.
Plots comparing the observed scatter σ(log (tdepl)) for increasing aperture size with the model predictions are shown in Fig. 7. For the KL principle predictions, we adopt the parameters given in Kruijssen & Longmore (2014). The model has four parameters, of which one is fixed in advance: tgas is the duration of the gas phase, tstar is the duration of the young stellar phase, λ is the separation length of independent regions, and σMF1 is the scatter induced by the fact that the mass spectrum of star-forming regions is not a delta function. Of these parameters, we fix tstar to a value of 6 Myr because we use Hα to trace the SF (cf. Leroy et al. 2013). The other three parameters are left free and specified in the legend of Fig. 7. As shown in Fig. 3 of KL14, the size scale of the knee in the curves in Fig. 7 is typically ~2.5 times larger than λ. As a result, it is possible to constrain the separation length between independent cloud and star-forming regions using Fig. 7. We attempt to constrain the free parameters by performing a least-squares fit of the KL14 model to the data, where the weights are the inverse errors of the observed scatter. We perform both a two- and a three-parameter fit, where tgas is either fixed to 25 Myr or left free. We find that tgas only has an impact on the predicted scatter at large aperture sizes. Because of the small angular size of the observed galaxies, we cannot trace size scales large enough to constrain tgas. On the other hand, λ and σMF1 can both be determined quite accurately from the fits, although we caution against overinterpreting these numbers as the parameters are strongly correlated, with correlation coefficients larger than 0.7. This confirms the finding of Kruijssen & Longmore (2014) that the scatter as a function of size scale is a degenerate result of (most of) the underlying parameters that describe the cloud-scale SF process. The authors showed that these parameters can be constrained to very high accuracy by instead considering the bias of the depletion time when focusing apertures on gas peaks or young stellar peaks. Even though such an analysis could in principle be carried out for the two galaxies considered here, it would require a larger number of peaks than can be identified at the current resolution of our maps (Kruijssen, in prep.).
5. Summary and conclusion
We presented a multi-tracer study of the two galaxies ESO534-G001 and 2dFGRS S833Z022, covering atomic, molecular, and Hα emission. These galaxies are known to have an E+A-like optical spectrum in the centre and SF at larger radii observed in optical IFU data as well as in GALEX NUV emission images. The goal was to study the SF relation in these systems, in which SF might proceed differently than in main-sequence galaxies. The results of our analysis are as follows.
The observations of the HI 21 cm emission line show that the neutral hydrogen gas is distributed as expected for typical spiral galaxies throughout the entire discs of both galaxies. In the velocity maps we observe a regularly rotating disc. The velocity dispersion maps reveal no peculiarities. The observed velocities and dispersions are comparable with regular star-forming spiral galaxies.
We did not detect the CO(1–0) emission line. This implies either that the H2 mass is low, or, alternatively, that the H2 is not well traced by CO in these galaxies. From the detection limit, it is only possible to calculate upper limits of 1.3 × 106M⊙ (ESO534-G001) and 3.3 × 106M⊙ (2dFGRS S833Z022). These upper limits are only valid for molecular hydrogen structures on angular scales smaller than ~20′′or ~2 kpc. To confirm the low molecular hydrogen mass, single-dish observations of CO or other dense gas tracers have to be obtained.
We found short molecular gas depletion times of ≲20 Myr in these galaxies with an E+A galaxy-like spectrum in the center. This result is strongly influenced by the uncertainty of the CO-to-H2 conversion factor. Furthermore, we propose an additional explanation. These gas depletion times are in the lower range of the observed scatter in low-mass galaxies, which reaches <50 Myr (Hunt et al. 2015) and is possibly due to the bursty nature of SF in low-mass galaxies.
We used the HI maps to calculate the predicted SFR following the pressure-based law of Blitz & Rosolowsky (2006). We compared this to the observed SFR based on the Hα and NUV emission. In these maps we found a clear mismatch between predictions and observations, in that the predicted and observed SF peaks are at different positions. This indicates that the pressure-based SF relation in HI-dominated regions only applies globally and does not describe SF on the cloud scale.
We studied the small-scale breakdown of the atomic SF relation further by deriving it for different size scales. We found that the scatter around a power-law fit decreases with decreasing resolution for both galaxies. Furthermore, the power-law index increases towards the lowest resolution. These findings indicate that galactic SF relations do not apply on sub-galactic scales.
We compared the observed scatter in gas depletion time with the predictions from the “uncertainty principle for star formation” of Kruijssen & Longmore (2014) and found that our observations agree with the predictions. This shows that the scale dependence of the atomic SF relation in these galaxies is consistent with the predicted increase of the scatter towards small size scales that is due to the incomplete sampling of independent HI clouds and star-forming regions. This finding adds to the existing literature reporting a scale dependence of the molecular SF relation, showing that the atomic and molecular phases are both susceptible to the evolutionary cycling of individual regions. This suggests that the atomic gas reservoirs host substantial substructure, which should be observable with future high-resolution observations.
We found short molecular tdepl, which could suggest that the two galaxies are in a transitioning phase in which SF may proceed at a different rate than in main-sequence galaxies. However, the observed total SFRs are not atypical, and the previously observed E+A-like spectrum is only a central feature. Furthermore, the galaxies lie in the blue cloud regime of the NUV-r vs. stellar mass diagram. Owing to the limited flux recovery of interferometric observations, our depletion time measurements should be confirmed with single-dish observations. Despite the non-detection of CO, we have found a substantial reservoir of atomic hydrogen in these galaxies, suggesting that the central region may be rejuvenated and experience multiple presumably bursty SF cycles before being quenched.
Acknowledgments
The authors would like to thank Diederik Kruijssen for assistance with the application of the “uncertainty principle for star formation” and further comments that greatly improved the paper. We thank Andreas Schruba for very interesting discussions about molecular gas depletion times. We thank Achim Weiss for suggestions and discussions during this project. We would like to thank the anonymous referee for insightful comments that helped to improve the paper. This paper makes use of the following VLA data: 13B-106 and 12A-400. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This paper makes use of the following ALMA data: ADS/JAO.ALMA# 2012.1.00293.S ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Begeman, K. 1989, A&A, 223, 47 [NASA ADS] [Google Scholar]
- Beifiori, A., Maraston, C., Thomas, D., & Johansson, J. 2011, A&A, 531, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Wolf, C., Meisenheimer, K., et al. 2004, ApJ, 608, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., & Moustakas, J. 2009, ARA&A, 47, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Rosolowsky, E. 2006, ApJ, 650, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Buyle, P., Michielsen, D., De Rijcke, S., et al. 2006, ApJ, 649, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, W. J., & Newell, E. B. 1980, PASP, 92, 746 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, W. J., & Sharples, R. 1987, MNRAS, 229, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, A., Siana, B., Henry, A. L., et al. 2013, ApJ, 763, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. 1993, ApJ, 411, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 1989, ApJ, 344, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Rubio, M., Hunter, D. A., et al. 2013, Nature, 495, 487 [NASA ADS] [CrossRef] [Google Scholar]
- French, K. D., Yang, Y., Zabludoff, A., et al. 2015, ApJ, 801, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, M.-L., & Kauffmann, G. 2014, MNRAS, 443, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., García-Burillo, S., Casasola, V., et al. 2015, A&A, 583, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, D. A., Ficut-Vicas, D., Ashley, T., et al. 2012, AJ, 144, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Ianjamasimanana, R., De Blok, W., Walter, F., & Heald, G. H. 2012, AJ, 144, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., & Longmore, S. N. 2014, MNRAS, 439, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Marzke, R. O., da Costa, L. N., Pellegrini, P. S., Willmer, C. N. A., & Geller, M. J. 1998, ApJ, 503, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Mogotsi, K. M., de Blok, W. J. G., Caldú-Primo, A., et al. 2016, AJ, 151, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Noordermeer, E., Van Der Hulst, J., Sancisi, R., Swaters, R., & Van Albada, T. 2007, MNRAS, 376, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, S. A., Gebhardt, K., Zabludoff, A. I., & Zaritsky, D. 2001, ApJ, 557, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of gaseous nebulae and active galactic nuclei (Mill Valley, CA: University Science Books) [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pracy, M. B., Kuntschner, H., Couch, W. J., et al. 2009, MNRAS, 396, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Pracy, M. B., Owers, M. S., Zwaan, M., et al. 2014, MNRAS, 443, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Roychowdhury, S., Huang, M.-L., Kauffmann, G., Wang, J., & Chengalur, J. N. 2015, MNRAS, 449, 3700 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2012, AJ, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., Engelbracht, C. W., Aniano, G., et al. 2012, ApJ, 761, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Staveley-Smith, L., Kim, S., Calabretta, M. R., Haynes, R. F., & Kesteven, M. J. 2003, MNRAS, 339, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Swaters, R., Sancisi, R., Van Albada, T., & Van Der Hulst, J. 2009, A&A, 493, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, F., Brinks, E., De Blok, W., et al. 2008, AJ, 136, 2563 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., Van Dokkum, P., & Labbé, I. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Zabludoff, A. I., Zaritsky, D., Lin, H., et al. 1996, ApJ, 466, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H.-X., Hunter, D. A., & Elmegreen, B. G. 2012, ApJ, 754, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Zwaan, M. A., Kuntschner, H., Pracy, M. B., & Couch, W. J. 2013, MNRAS, 432, 492 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of galaxy gas properties determined from the HI 21 cm line observations and the CO(1–0) emission line observations presented in this work.
All Figures
 |
Fig. 1 Results for GalA. a) HI surface density in M⊙ pc-2 from the combined VLA observations. The spacing between the contours is 5 M⊙ pc-2. b) Line-of-sight velocity map of HI observed using the VLA. The Δv spacing between the contours is 14 km s-1. c) Velocity dispersion map. The spacing between the contours is 5 km s-1. d) Rotation curve of the HI disc observed with the VLA. The curves are obtained from the tilted ring model described in the text. e): HI residual velocity field. The contours are at −10, 0 and 10 km s-1. f) Stellar surface density map obtained from the B-band luminosity determined from IFU observations and a colour-dependent mass-to-light ratio (Bell et al. 2003). In these maps, north is at the top and east is on the left-hand side. |
| In the text | |
 |
Fig. 2 Analysis results for GalB. For a description of each plot see the caption of Fig. 1. The differences with Fig. 1 are that for the HI surface densities the contours are at 5, 15, and 25 M⊙ pc-2. For the line-of-sight velocity the Δv spacing between the contours is 26 km s-1. |
| In the text | |
 |
Fig. 3 Total CO(1–0) luminosity as a function of B-band luminosity for normal spirals and dwarf galaxies presented by Schruba et al. (2012) in black and our galaxies in red. The black line is a linear fit to the bright galaxies (MB< −18) also taken from Schruba et al. (2012). |
| In the text | |
 |
Fig. 4 Maps of the pressure-based relative SFR of GalA (left) and GalB (right) and indicated by colour maps. Top: contours of the Hα emission at 3 × 10-16ergs-1cm-2 and from 5 to 20 × 10-16ergs-1cm-2 in steps of 5 × 10-16ergs-1cm-2 for GalA and at 5, 10, and 15 × 10-16ergs-1cm-2 for GalB over-plotted. Bottom: contours of the NUV emission from GALEX over-plotted on the same pressure-based SFR colour maps as in the top panels. The optical data cubes are aligned using the DSS observations and are therefore correct to ~1–2″. |
| In the text | |
 |
Fig. 5 ΣSFR vs. ΣHI of GalA (left) and GalB (right). The solid line shows a power-law fit to the data. The spatial resolution for each plot is given in the lower left corner. r is the correlation coefficient, std is the corrected sample standard deviation, and a is the power-law index. From top to bottom, the spatial resolution decreases in steps of ~100 pc for GalA and ~150 pc for GalB. The highest spatial resolution presented is ~280 pc for GalA and ~440 pc for GalB. |
| In the text | |
 |
Fig. 5 continued. |
| In the text | |
 |
Fig. 6 Schmidt-Kennicutt plot for the total amount of gas. The green triangles are the average ΣSFR within ΣHI bins of 400 pc sized regions within a sample of dwarf galaxies presented by Roychowdhury et al. (2015), the magenta diamond shows data from the LMC (Staveley-Smith et al. 2003), the cyan stars are disc averages of local dwarf galaxies from the LITTLE THINGS Survey (Zhang et al. 2012), the grey shaded area represents the region in which the bulk of the spatially resolved data points from local spiral galaxies presented by Bigiel et al. (2008) at a resolution of 750 pc lie, and the blue and red squares are the spatially resolved data points of GalA and GalB at the highest resolution, respectively. The solid and dashed lines represent lines of constant atomic gas depletion times, where solid is 1 Gyr and dashed 10 Gyr. |
| In the text | |
 |
Fig. 7 Scatter in gas depletion time σ(log tdepl) as a function of aperture size for GalA (top) and GalB (bottom). The solid curves are least-squares fits. The red lines are two-parameter fits, and the blue solid curves are three-parameter fits, where the determined parameters and uncertainties are given in the legend. For the red curves tgas is kept fixed at 25 Myr. For the dashed curves the minimum/maximum parameter values of each fit are used to give an error interval. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


