| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201629760 | |
| Published online | 10 March 2017 | |
Catastrophic rotational braking among Sun-like stars
A model of the Sun’s rotation evolution
European Space Agency, ESTEC − Postbus 299, 2200 AG Noordwijk, The Netherlands
e-mail: pgondoin@cosmos.esa.int
Received: 20 September 2016
Accepted: 16 December 2016
Context. Observations of young open clusters show a bimodal distribution of stellar rotation. In those clusters, Sun-like stars group into two main populations of fast and slow rotators. Beyond an age of approximately 600 Myr, the two populations converge towards a single sequence of slow rotators.
Aims. The present study addresses the origin of this bimodal distribution and the cause of its observed evolution.
Methods. New prescriptions of mass-loss rate and Alfven radius dependences on Rossby number suggested by observations are implemented in a phenomenological model of angular-momentum loss and redistribution. The obtained model is used to calculate the time evolution of a rotation-period distribution of solar-mass stars similar to that observed in the 5 Myr-old NGC 2362 open cluster. The simulated distributions at subsequent ages are compared with those of h Per, the Pleiades, M 50, M 35, and M 37.
Results. The model is able to reproduce the appearance and disappearance of a bimodal rotation-period distribution in open clusters providing that a brief episode of large-angular-momentum loss is included in the early evolution of Sun-like stars.
Conclusions. I argue that a transitory episode of large-angular-momentum loss occurs on Sun-like stars with Rossby numbers between 0.13 and 0.3. This phenomenon of enhanced magnetic braking by stellar wind would be mainly driven by a rapid increase of mass loss at a critical rotation rate. This scenario accounts for the bimodal distribution of stellar rotation in open clusters with ages between 20−30 Myr and approximately 600 Myr. The mass-loss rate increase could account for a significant fraction of the X-ray luminosity decay of Sun-like stars in the 0.13−0.3 Rossby number range where a transition from the saturated to the non-saturated regime of X-ray emission is observed. Observed correlations between Li abundance and rotation sequences in the Pleiades and M 34 clusters support this scenario.
Key words: open clusters and associations: general / stars: rotation / stars: evolution / stars: solar-type / stars: mass-loss / Sun: rotation
© ESO, 2017
1. Introduction
Open clusters provide essential calibration for rotation-age-activity relations (Hawley et al. 2016), since each cluster gives a snapshot of stellar evolution at a single age for all masses (e.g., Giampapa et al. 2006; Gondoin et al. 2012; Gondoin 2013; Meibom et al. 2015; Wright et al. 2011). In the past decade, many photometric surveys of open clusters have monitored the modulation of stellar brightness induced by the rotation of starspots (see e.g., Affer et al. 2013; Delorme et al. 2011; Hartman et al. 2009, 2010; Henderson & Stassun 2012; Irwin et al. 2008a, 2009; Meibom et al. 2009, 2011). These surveys have produced extensive rotation period measurements on Sun-like stars of different ages. The results indicate a spin-up phase during pre-main sequence contraction, a rapid spin-down during early main-sequence evolution, and a pause where surface rotation does not change significantly (Brun et al. 2015). Older stars then resume spinning down with the square root of time (Skumanich 1972).
The results also show (e.g., Barnes 2003; Meibom et al. 2009, 2011) a bimodal distribution of stellar rotation in young open clusters. Young Sun-like stars tend to group into two distinct populations of fast and slow rotators. These populations lie on narrow sequences in diagrams where the measured rotation periods of the members of a stellar cluster are plotted against their B−V colors. Beyond the age of approximately 600 Myr, the two populations converge towards a unique sequence of slow rotators.
Understanding the observed evolution of stellar rotation has been the subject of many studies (e.g., MacGregor & Brenner 1991; Keppens et al. 1995; MacGregor & Charbonneau 1994; Krishnamurthi et al. 1997; Allain 1998; Dennissenkov et al. 2010; Reiners & Mohanty 2012; Gallet & Bouvier 2013, 2015). These works mainly focussed in improving angular momentum evolution models by testing different prescriptions of the stellar wind torque and of the core/envelope coupling. The obtained models reproduce the spin-up during pre-main sequence contraction followed by a rapid spin-down during early evolution on the main sequence. They fit the narrowing of the dispersion of rotation periods among solar-type stars reasonably well as these reach the age of the Hyades. However, very few studies (Brown 2014) have intended to account for the bimodal distribution of stellar rotation observed in young open clusters.
 |
Fig. 1 Left: moment of inertia (from Siess et al. 2000) of the outer convective envelope and inner radiative core (in units of total MR2). Middle: radius at the bottom of the convective envelope relative to the total stellar radius. Right: total surface radius at optical depth 0.005 (in solar unit). |
The present paper reports on an attempt to build a model of stellar angular momentum evolution that accounts for this bimodal distribution. Section 2 describes a phenomenological model of stellar rotation. It proposes empirical laws for a mass-loss rate and Alfven radius dependence on the Rossby number that are suggested by observations. Section 3 presents simulation results of the rotation evolution of a Sun-like star as a function of its initial rotation rate. It also compares the simulated evolution of a normal distribution of rotation periods with rotation-period histograms measured in open clusters of various ages. The implications for the rotation history of Sun-like stars are discussed in Sect. 4.
2. Model of stellar rotation evolution
2.1. The double zone and magnetic torque models
Studies of the rotation evolution of Sun-like stars often use a phenomenological model of angular momentum redistribution in stellar interiors, the so-called Double Zone model (DZM). This model assumes that the radiative core and the convective envelope rotate rigidly at all ages (MacGregor & Brenner 1991; Keppens et al. 1995; Allain 1998). These hypotheses are justified (Spada et al. 2011) by the facts that (i) the envelope is expected to be strongly coupled by the very efficient angular momentum redistribution associated with turbulent convection; and (ii) a large-scale magnetic field, even as weak as 1 G, can maintain a condition of rigid rotation in most of the core.
At any given time, t, the angular momenta Jc of the core, and Je of the envelope can thus be expressed as Jc(t) = Ic(t)Ωc(t) and Je(t) = Ie(t)Ωe(t) where Ic, Ie, Ωc, and Ωe are the moments of inertia and the angular velocities of the core and the envelope, respectively. Assuming that the angular momentum redistribution between the two regions occurs on a timescale τc, the evolution of their angular momenta is governed by two coupled differential equations (e.g., Spada et al. 2011; Oglethorpe & Garaud 2013):
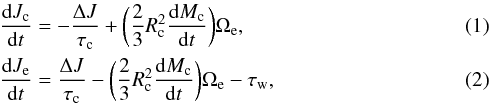 where
where 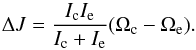 (3)τw is the torque exerted by the wind on the convective envelope. For weak core-envelope coupling (large τc), the region spun-down by the wind is first limited to the convection zone, while the radiation zone feels the braking effect later, when ΔJ has grown sufficiently.
(3)τw is the torque exerted by the wind on the convective envelope. For weak core-envelope coupling (large τc), the region spun-down by the wind is first limited to the convection zone, while the radiation zone feels the braking effect later, when ΔJ has grown sufficiently.
Regarding the torque exerted on the convective envelope, Weber & Davis (1967) used a simple one dimensional model to quantify the angular momentum carried by the stellar wind. They demonstrated that the loss rate of angular momentum by the star is expressed in a steady state as the product of the mass-loss rate and the specific angular momentum carried by the outflow, such that: 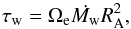 (4)where
(4)where  is the average mass-loss rate and RA is the average Alfven radius.
is the average mass-loss rate and RA is the average Alfven radius.
During pre-main sequence evolution, the growth of the core at the expense of the envelope produces an angular momentum transfer. This is accounted for by the second term in the right-hand side of both Eqs. (1) and (2) where Rc and Mc are the radius and mass of the radiative core, respectively. Assuming that the internal stellar structure is not modified by rotation or mass loss, these stellar quantities and their time derivatives are taken from the evolutionary track of a solar mass star established by Siess et al. (2000) with a metallicity Z = 0.02 and a moderate overshoot parameter d = 0.20 Hp where Hp is the pressure scale height (see Fig. 1).
According to the simple model described above, the angular momentum evolution of a Sun-like star depends on the time evolution of its internal structure and on three parameters describing the angular-momentum loss and its redistribution within the stellar interior. These three parameters are the mass-loss rate 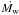 , the mean Alfven radius RA, and the core-envelope coupling timescale τc.
, the mean Alfven radius RA, and the core-envelope coupling timescale τc.
2.2. Core-envelope coupling
A number of physical processes act to redistribute angular momentum throughout the stellar interior (Bouvier et al. 2013). These include various classes of hydrodynamical instabilities (e.g., Decressin et al. 2009; 2010; Lagarde et al. 2012; Eggenberger et al. 2012), magnetic fields (e.g., Denissenkov & Pinsonneault 2007; Spada et al. 2010; Strugarek et al. 2011), and gravity waves (Charbonnel et al. 2013; Mathis 2013). In the absence of a consistent model of angular momentum exchange between the core and the envelope, empirical prescriptions are most often used for the core-envelope coupling timescale τc that parametrizes the exchange rate of angular momentum within the stellar interior.
This parameter was initially found to be constant throughout the evolution of a 1 M⊙ star with a magnitude ranging from 10 Myr (MacGregor & Brenner 1991) to a few tens of millions of years (Keppens et al. 1995). In order to account for new observational results, recent studies suggested that the coupling timescale may be different for fast and slow rotators (Irwin et al. 2007; Bouvier 2008; Irwin & Bouvier 2009). Denissenkov et al. (2010) assumed that the rotation dependent coupling timescale is a step function, where the coupling timescale is short at high velocity and suddenly increases below some critical velocity. Spada et al. (2011) explored a power law dependence of the coupling timescale on the differential angular rotation velocity between the core and the envelope.
Based on the argument that the derived dependency is weak, Gallet & Bouvier (2013) assumed that the core-envelope coupling time scale is constant over the evolution of a Sun-like star with a given initial rotation period. Implementing the wind braking prescription of Matt et al. (2012), they found that the core-envelope coupling timescale is longer for stars that are initially slow rotators (τc ≈ 30 Myr for initial periods of 7 and 10 days) than for stars that are initially fast rotators (τc ≈ 12 Myr for initial rotation periods of 1.4 days). The present study assumes that the core-envelope coupling timescale of a Sun-like star is constant over time and independent of its initial rotation rate.
2.3. Mass-loss rate
Johnstone et al. (2015) pointed out that the lack of direct observational constraints means that it remains unclear which, if any, of the existing wind models of Sun-like stars are reliable. These authors divided wind models into two categories: those that try to apply existing knowledge of the physics of the solar wind to other stars (e.g., Cranmer & Saar 2011; Suzuki et al. 2013), and those that scale the solar wind to other stars by applying scaling relations between wind properties and stellar parameters, such as age, rotation rate, or coronal X-ray properties (e.g., Badalyan & Livshits 1992; Grießmeier et al. 2004; Holzwarth & Jardine 2007; See et al. 2014).
I followed this second approach based on observational indications by Wood et al. (2005, 2014) that the mass-loss rate of Sun-like stars increases as a power law of their X-ray surface flux. The interpretation of these observations with the assistance of hydrodynamic models also suggests that, beyond a certain flux, the mass-loss rate of young stars drops to weaker values.
Since the X-ray surface flux of cool stars is a function of their Rossby number, I formulated this scaling law as follows: 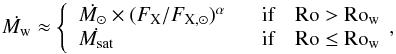 (5)where FX and FX ⊙ are the stellar and solar X-ray surface flux, respectively. Ro = 2π/ (Ωe × τc) is the Rossby number and τc is the convective turnover time. Row is the Rossby number at a so-called wind dividing line below which the mass-loss rate saturates at a constant value
(5)where FX and FX ⊙ are the stellar and solar X-ray surface flux, respectively. Ro = 2π/ (Ωe × τc) is the Rossby number and τc is the convective turnover time. Row is the Rossby number at a so-called wind dividing line below which the mass-loss rate saturates at a constant value 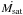 .
.
Equation (5) is justified by the fact that the wind driving is related to coronal heating, which itself is a consequence of magnetic activity, and of which coronal X-ray emission is a reliable indicator (e.g., Fisher et al. 1998; Schrijver & Zwaan 2000; Pevtsov et al. 2003). Johnstone et al. (2015) also noted that, in view of the slow rotation evolution of young stars, it is reasonable to assume that the mass-loss rate saturates at fast rotation. This statement is supported by numerical experiments for Alfven wave-driven stellar winds with a wide range of input Poynting flux from the photosphere (Suzuki et al. 2013).
X-ray observations of late-type stars have shown that their X-ray to bolometric luminosity ratios can be parametrized as a function of their Rossby number Ro. In this study, I used the formulation proposed by Pizzolato et al. (2003): 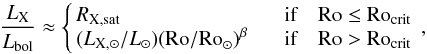 (6)with log (LX, ⊙/L⊙) = −6.24 (Judge et al. 2003). In this equation, Lbol is the stellar bolometric luminosity and Rocrit is the Rossby number above which the saturation of X-ray emission occurs. RX,sat = 0.74 × 10-3 is the saturation level of the X-ray to bolometric luminosity ratio. Pizzolato et al. (2003) found a power index β = −2 while Wright et al. (2011) argued that a value β = −2.70 ± 0.13 provides a better fit to the Sun’s X-ray luminosity. Based on this parametrization, these authors empirically derived the relationship:
(6)with log (LX, ⊙/L⊙) = −6.24 (Judge et al. 2003). In this equation, Lbol is the stellar bolometric luminosity and Rocrit is the Rossby number above which the saturation of X-ray emission occurs. RX,sat = 0.74 × 10-3 is the saturation level of the X-ray to bolometric luminosity ratio. Pizzolato et al. (2003) found a power index β = −2 while Wright et al. (2011) argued that a value β = −2.70 ± 0.13 provides a better fit to the Sun’s X-ray luminosity. Based on this parametrization, these authors empirically derived the relationship: 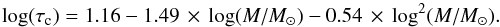 (7)I combined Eqs. (5) and (6) to parametrize the mass-loss rate of Sun-like stars as a function of their Rossby number. Since the study uses the Wright et al. (2011) parametrization of the X-ray luminosity vs. Rossby number, the associated turnover-time vs. mass relationship is also adopted for consistency. It gives τc = 14.45 days for a 1 M⊙ star independently from the age of the star.
(7)I combined Eqs. (5) and (6) to parametrize the mass-loss rate of Sun-like stars as a function of their Rossby number. Since the study uses the Wright et al. (2011) parametrization of the X-ray luminosity vs. Rossby number, the associated turnover-time vs. mass relationship is also adopted for consistency. It gives τc = 14.45 days for a 1 M⊙ star independently from the age of the star.
Simulations show that the increase of τc during the pre-main sequence phase (see e.g. Landin et al. 2010) has a negligible effect on the modeled evolution of stellar rotation. During this phase, indeed, the rotation evolution is dominated by the contraction of the star and by the transfer of angular momentum between its core and its envelope. Rotational braking effects by stellar winds are limited by the large moment of inertia of the convective envelope (see Fig. 1).
2.4. Alfven radius
One observational constraint on the rotation evolution of Sun-like stars comes from the well-known result of Skumanich (1972) that stars older than approximately 1 Gyr spin down with the inverse of the square root of time. This law imposes τw ≈ τw, ⊙ × {Ωe/ Ω⊙}3, where τw, ⊙ is the average braking torque of the solar wind and Ω⊙ the angular velocity of the Sun.
Combining this relation with Eqs. (4)−(6) gives 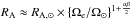 for slow rotators. In the absence of any constraint on the angular-momentum loss of young stars, I assumed that the Alfven radius of rapid rotators saturates at a constant value RA,sat. The Alfven radius can thus be expressed as follows:
for slow rotators. In the absence of any constraint on the angular-momentum loss of young stars, I assumed that the Alfven radius of rapid rotators saturates at a constant value RA,sat. The Alfven radius can thus be expressed as follows: 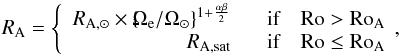 (8)where RoA is the Rossby number below which the Alfven radius remains equal to a constant value RA,sat.
(8)where RoA is the Rossby number below which the Alfven radius remains equal to a constant value RA,sat.
Imposing a continuous decay of the Alfven radius with increasing rotation rate until a saturation value (i.e., without any discontinuity at RoA) implies that: 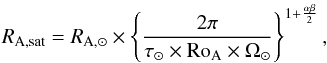 (9)where τ⊙ is the convective turnover time of a Sun-like star.
(9)where τ⊙ is the convective turnover time of a Sun-like star.
Based on two-dimensional axisymmetric magneto-hydrodynamic simulations to compute steady-state solutions for solar-like stellar winds from rotating stars with dipolar magnetic fields, Matt et al. (2012) found that the Alfven radius scales approximately as 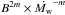 with m ≈ 0.22 where B is the global magnetic field strength. A comparable value of the exponent m between 0.2 and 0.25 was found in the wind simulations of Washimi & Shibata (1993) and Pinto et al. (2011). Assuming Row = Rocrit = 0.13 and RoA = 0.4 (see Sect. 3.1), a comparison of this scaling law with the mass-loss rate and Alfven radius prescriptions used in the present model (see Eqs. (5), (6), and (8)) suggests that B is independent of rotation in the saturated regime (Ro ≤ 0.13) and scales approximately with Ro-1.8 for 0.13 < Ro ≤ 0.4 and with Ro-0.2 for Ro > 0.4. Mean large-scale magnetic field strengths derived from spectro-polarimetric observations (Vidotto et al. 2014; See et al. 2015; Folsom et al. 2016) indicate a similar dependence on the Rossby number with tentative evidence that the total field saturates for Ro ≤ 0.1 in stars with radiative cores. In the non-saturated regime, Vidotto et al. (2014) found a power-law slope of approximately −1.4 for the radial component of the surface field while See et al. (2015) noted that the slope is steeper for the toroidal component. Both studies use measurements obtained with the Zeeman-Doppler imaging technique that favors rapidly rotating objects.
with m ≈ 0.22 where B is the global magnetic field strength. A comparable value of the exponent m between 0.2 and 0.25 was found in the wind simulations of Washimi & Shibata (1993) and Pinto et al. (2011). Assuming Row = Rocrit = 0.13 and RoA = 0.4 (see Sect. 3.1), a comparison of this scaling law with the mass-loss rate and Alfven radius prescriptions used in the present model (see Eqs. (5), (6), and (8)) suggests that B is independent of rotation in the saturated regime (Ro ≤ 0.13) and scales approximately with Ro-1.8 for 0.13 < Ro ≤ 0.4 and with Ro-0.2 for Ro > 0.4. Mean large-scale magnetic field strengths derived from spectro-polarimetric observations (Vidotto et al. 2014; See et al. 2015; Folsom et al. 2016) indicate a similar dependence on the Rossby number with tentative evidence that the total field saturates for Ro ≤ 0.1 in stars with radiative cores. In the non-saturated regime, Vidotto et al. (2014) found a power-law slope of approximately −1.4 for the radial component of the surface field while See et al. (2015) noted that the slope is steeper for the toroidal component. Both studies use measurements obtained with the Zeeman-Doppler imaging technique that favors rapidly rotating objects.
3. Simulations
3.1. Rotation evolution of a Sun-like star
In order to simulate the rotation evolution of a solar-mass star, I first used the empirical parametrizations of the mass-loss rate vs. X-ray surface flux proposed by Wood et al. (2014) and that of the X-ray luminosity vs. Rossby number formulated by Wright et al. (2011). When imposing those relationships, the rotation evolution model has only three free parameters, namely the initial rotation period after circumstellar disk dispersion, the core-envelope coupling timescale, and the Rossby number RoA below which the Alfven radius saturates at its lowest value. For various distributions of initial rotation periods, I could not find a set of parameters that reproduces the measured distributions of rotation periods in open clusters of different ages. In particular, the simulations could not reproduce the bi-modal distribution of stellar rotation observed in young open clusters.
 |
Fig. 2 Assumed braking torque of a Sun-like star as a function of its Rossby number. |
Model parameters used to simulate the angular momentum evolution of solar-mass stars.
I thus let the mass-loss rate at saturation 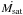 vary since this parameter is poorly constrained by observations. I also imposed that the saturation of the wind occurs at Row = 0.13 and that the saturation of the Alfven radius occurs at RoA = 0.4. These constraints are suggested by the observations that the transition from the fast to the slow rotation sequence in the M 34 open cluster and in the Pleiades occurs on stars with 0.13 ≤ Ro < 0.4 (Gondoin 2012, 2015).
vary since this parameter is poorly constrained by observations. I also imposed that the saturation of the wind occurs at Row = 0.13 and that the saturation of the Alfven radius occurs at RoA = 0.4. These constraints are suggested by the observations that the transition from the fast to the slow rotation sequence in the M 34 open cluster and in the Pleiades occurs on stars with 0.13 ≤ Ro < 0.4 (Gondoin 2012, 2015).
Figure 2 shows the braking torque of a 1 M⊙ star as a function of its Rossby number resulting from these hypothesis and assuming 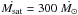 . The angular-momentum loss of the star dramatically increases at Ro = 0.13, that is, at a rotation period of 1.9 days for a 1 M⊙ star. The time at which this abrupt enhancement of the braking torque occurs depends on the initial rotation period of the stars after dispersion of its circumstellar disk. It never happens for stars that initially rotate too slowly.
. The angular-momentum loss of the star dramatically increases at Ro = 0.13, that is, at a rotation period of 1.9 days for a 1 M⊙ star. The time at which this abrupt enhancement of the braking torque occurs depends on the initial rotation period of the stars after dispersion of its circumstellar disk. It never happens for stars that initially rotate too slowly.
Cranmer (2008) pointed out that the Sun-integrated mass-loss rate 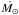 is a quantity that is not often considered by solar physicists since both remote sensing observations and in-situ measurements resolve small volumes of solar plasma at a time. It is nevertheless possible to use in-situ measurements of the solar plasma density and flow speed to estimate a time dependent mass flux. Wang (1998) used empirical correlations between the plasma properties measured at 1 AU and the coronal magnetic field geometry extrapolated from photospheric fields to reconstruct a sphere-integrated value of
is a quantity that is not often considered by solar physicists since both remote sensing observations and in-situ measurements resolve small volumes of solar plasma at a time. It is nevertheless possible to use in-situ measurements of the solar plasma density and flow speed to estimate a time dependent mass flux. Wang (1998) used empirical correlations between the plasma properties measured at 1 AU and the coronal magnetic field geometry extrapolated from photospheric fields to reconstruct a sphere-integrated value of 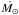 over two solar cycles. This author estimated that the solar mass-loss rate varied from 2 to 3 × 10-14M⊙/yr over that period, with higher value at solar maximum.
over two solar cycles. This author estimated that the solar mass-loss rate varied from 2 to 3 × 10-14M⊙/yr over that period, with higher value at solar maximum.
Using an average solar mass-loss rate 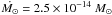 /yr, an Alfven radius RA, ⊙ = 7.0 R⊙ leads to rotation periods in the range 22−28 days at an age of 4.5 Gyr (i.e., similar to the Sun) for initial periods ranging from 0.6 to 30 days at 5 Myr. This value of the mean solar Alfven radius is higher than the one derived by Reville et al. (2015) from realistic magnetic field topology simulations. It is lower than the one derived by Pizzo et al. (1983) from the analysis of Helios data for equatorial regions near solar minimum. The Ulysses data indicate an even higher value of 16 R⊙ at high latitudes (Li 1999). However, Pizzo et al. (1983) noted that these values vary depending on the corona model. Isothermal models tend to give lower limits for RA, ⊙ (e.g., Pneuman & Kopp 1971), whereas conductive models give the highest estimates (e.g., Durney & Pneuman 1975).
/yr, an Alfven radius RA, ⊙ = 7.0 R⊙ leads to rotation periods in the range 22−28 days at an age of 4.5 Gyr (i.e., similar to the Sun) for initial periods ranging from 0.6 to 30 days at 5 Myr. This value of the mean solar Alfven radius is higher than the one derived by Reville et al. (2015) from realistic magnetic field topology simulations. It is lower than the one derived by Pizzo et al. (1983) from the analysis of Helios data for equatorial regions near solar minimum. The Ulysses data indicate an even higher value of 16 R⊙ at high latitudes (Li 1999). However, Pizzo et al. (1983) noted that these values vary depending on the corona model. Isothermal models tend to give lower limits for RA, ⊙ (e.g., Pneuman & Kopp 1971), whereas conductive models give the highest estimates (e.g., Durney & Pneuman 1975).
 |
Fig. 3 Simulated angular velocity evolution of a solar-mass star with initial rotation periods (at 5 Myr age) of 0.6 (upper curve), 1, 2, 3, 6, 10, 20, and 30 days (lower curve). The simulated angular velocity curves are compared with rotation measurements in h Per (13 Myr; Moraux et al. 2013), the Pleiades (125 Myr; Hartman et al. 2010), M 50 (130 Myr; Irwin et al. 2009), M 35 (133 Myr; Meibom et al. 2009), and M 37 (550 Myr; Hartman et al. 2009). |
Table 1 lists the model parameters that I used to simulate the angular momentum evolution of a solar-mass star. Figure 3 plots the results for initial rotation periods ranging from 0.6 (upper curve) to 30 days (lower curve) at an age of 5 Myr. It shows a spin-up phase during pre-main sequence contraction followed by a spin-down near the ZAMS and during further evolution on the main sequence.
Measurements of stellar angular velocities in several open clusters (see Table 2) are also plotted in Fig. 3. The simulated angular velocity curves fit the dispersion of rotation periods among solar-type stars in young open clusters reasonably well. The narrowing of their distribution between the age of M 37 (~550 Myr) and that of the Sun is also reproduced.
Figure 3 shows that stars with low initial angular velocities (i.e. P0 > 6 days) converge rapidly towards similar rotation rates, even before they reach the main sequence. It takes much longer, that is, several hundred Myr, for stars with large initial angular velocities (i.e., P0 < 3 days) to converge towards similar values. This dichotomy in the rotation evolution results from the assumed angular momentum loss (see Fig. 2). Stars that are initially slow rotators are submitted to a strong braking torque during their early evolution that limit the increase of their angular velocity up to the ZAMS. On the contrary, stars that are initially fast rotators experience a moderate braking torque that barely affects their spin-up due to pre-main sequence contraction. It then takes a significant amount of time for this moderate torque to slow them down on the main sequence until they reach the critical Rossby number Row = 0.13 where a burst of angular-momentum loss is assumed to be triggered. Their rotation rate then decreases rapidly catching up with the angular velocity of the initially slow rotators.
 |
Fig. 4 Simulated evolution of a normal distribution of rotation periods (upper left) emulating that of a 5 Myr-old cluster (see text) at subsequent ages of 13 Myr (upper middle), 25 Myr (upper right), 55 Myr (center left), 130 Myr (center middle), 250 Myr (center right), 550 Myr (lower left), 1.25 Gyr (lower middle), and 2.5 Gyr (lower right). |
3.2. Early distribution of stellar rotation in open clusters
Understanding whether or not such an evolutionary behavior could explain the observed distribution of stellar rotation in open clusters requires some information on the early distribution of rotation periods in young open clusters. The time series photometric survey of NGC 2362 by Irwin et al. (2008b) provides a measurement of such a distribution.
Mayne et al. (2007) estimated the age of NGC 2362 to 3−4 Myr consistent with the ages of 1.8 Myr derived by Dahm (2005) using the isochrones of D’Antona & Mazzitelli (1997), and of 3.5−5 Myr from the isochrones of Baraffe et al. (1998). I extracted a sample of 91 NGC 2362 stars with masses included between 0.7 and 1.1 M⊙ stars from the list of Irwin et al. (2008a). This sample shows a broad distribution of rotation periods between 0.4 and 25 days with a maximum around 7 days (see upper left plot in Fig. 5). The histogram exhibits no evidence of a bimodal behaviour with distinct populations of slow and fast rotators.
Only a few stars in the parent sample have mid-infrared excesses indicative of the presence of circumstellar disks (Irwin et al. 2008b). Dahm & Hillenbrand (2007) derived an upper limit for the primordial, optically thick disk fraction in NGC 2362 of ~7 ± 2%, with another ~12 ± 3% of suspected members exhibiting infrared excesses indicative of a weak or optically thin disk emission. I assumed that the disk accretion process has ceased for most of the stars in NGC 2362 and will not affect the subsequent evolution of their angular momentum. The measured distribution of stellar angular velocities among the 91 sample stars is used as an example of a distribution of stellar rotation in an open cluster immediately after dispersion of circumstellar disks. It is worth noting that Bell et al. (2013) derived ages for 13 young (<30 Myr) star-forming regions including NGC 2362 that are up to a factor of two older than the ages typically adopted in the literature. NGC 2362 would be 12 Myr old instead of the <5 Myr previously assumed. This result has wide-ranging implications, including that circumstellar discs could survive longer.
The NGC 2362 sample of 0.7 to 1.1 M⊙ stars with known rotation periods has a small size compared with those of Sun-like star samples in some older clusters (see Table 2). I thus emulated a larger distribution of stellar angular velocities in NGC 2362 by generating a normal distribution of 1000 rotation periods with a maximum around 7 days. The distribution was truncated below 0.3 days to mimic the distribution of rotation periods in NGC 2362 that covers the range 0.3 to 30 days. This obtained distribution of rotation periods is plotted in the upper left graph of Fig. 4.
The evolution of each initial rotation period of this reference distribution was then calculated using the angular momentum evolution model described in Sect. 2 with the parameter listed in Table 1. Figure 4 shows the simulated evolution of this 5 Myr reference distribution at subsequent ages of 13, 25, 55, 130, 250, 550, 1250, and 2500 Myr.
Figure 4 indicates that during the first 13 Myr the broad initial distribution is shifted towards shorter rotation periods due to the effect of stellar contraction. At an age of approximately 25 Myr, a double peak distribution appears that lasts until the age of approximately 550 Myr. At later ages, the simulation produces a single peak distribution that sharpens and moves with time towards longer rotation periods.
3.3. Distributions of stellar rotation in open clusters
 |
Fig. 5 Measured rotation period histogram of 0.7−1.1 M⊙ stars in NGC 2362 (5 Myr; Irwin et al. 2008a), h Per (13 Myr; Moraux et al. 2013), Pleiades (125 Myr; Hartman et al. 2010), M 50 (130 Myr; Irwin et al. 2009), M 35 (150 Myr; Meibom et al. 2009), and M 37 (550 Myr; Hartman et al. 2009). |
In order to compare the simulated evolution of the reference NGC 2362-like distribution with observations, I looked for open clusters with a large enough number of Sun-like stars with known rotation periods. Open clusters with 100 such stars are estimated to be of a reasonable size for establishing rotation period distributions with large enough statistical significance. I initially defined Sun-like stars as stars within the 0.9 to 1.1 M⊙ mass range. However, since large enough samples could only be found in two clusters, namely h Per and M 35, I extended the mass bin to the 0.7−1.1 M⊙ range. Three additional clusters were found that have large enough samples of 0.7−1.1 M⊙ stars with known rotation periods. These are the Pleiades, M 50, and M 37. The names of these clusters, their ages, the number of sample stars, and the references to the parent surveys are given in Table 2.
Large samples of 0.7−1.1 M⊙ stars with measured rotation periods used for comparisons with simulated rotation period distributions.
All rotation periods were derived by monitoring the modulation of the stars brightnesses due to the rotation of surface spots. This method is free from projection effects and provides a direct measurement. The study assumes that the rotation period distributions derived from the photometric surveys are representative of the cluster distribution and are not significantly affected by observational biases, such as selection effects, rapid rotation in tidally synchronised binaries, slow rotation from contaminating field stars, or aliases and harmonics of the true stellar period resulting from incomplete or uneven temporal sampling.
Figure 5 shows the rotation period histograms of the 0.7−1.1 M⊙ stars extracted from the selected surveys. A logarithmic scale is used on the x-axis such that the shapes of the histograms are the same when using rotation period or angular velocity bins.
The upper middle graph in Fig. 5 shows the measured rotation period distribution of 0.7−1.1 M⊙ stars in h Per (NGC 869). This cluster is the westernmost member of the Perseus double cluster whose age has been estimated to be 13 Myr (Mayne & Naylor 2008). A sample of 207 0.7−1.1 M⊙ stars with known rotation periods was selected from the output catalog of a recent photometric monitoring survey (Moraux et al. 2013). By the age of this cluster, the disk accretion process has ceased on all stars that freely evolve towards the ZAMS. The h Per sample shows a bi-modal distribution with a fast rotator group having rotation periods of approximately 0.3−0.4 days, a slow rotator group with periods of approximately 5−6 days, and a number of stars within the intermediate 1−2 day period range. The simulated rotation evolution of the NGC 2362-like reference sample does not show a bimodal distribution by the age of 13 Myr (see upper middle graph in Fig. 4) as observed in h Per, but only 10 Myr later (see upper right graph in Fig. 4).
The Pleiades, M 50, and M 35 open clusters have similar ages estimated to be ~125 Myr (e.g., Stauffer et al. 1998), ~130 Myr (Kalirai et al. 2003), and ~133 Myr (e.g., McNamara et al. 2011), respectively. They have been the subject of extensive photometric time-series survey by Hartman et al. (2010), Irwin et al. (2009), and Meibom et al. (2009), respectively. The results of these surveys provide well populated samples of 0.7−1.1 M⊙ stars with known rotation periods. By the age of these clusters, stars within the 0.7−1.1 M⊙ mass range have reached the main sequence.
The three stellar samples show similar rotation period distributions (see upper right, lower left, and lower middle graphs in Fig. 5). These include an important group of slow rotators with periods ranging between 2.5 and 10 days but concentrated around 5−8 days. A smaller group of fast rotators is also visible between 0.25 and 1.5 days in the Pleiades and M 35 histograms. They represent 19% and 27% of the overall Pleiades and M 35 sample sizes, respectively. In M 50, the fast rotators group appears as a long tail in the rotation period distribution.
The fact that three open clusters of similar age have similar rotation period distributions is not expected a priori. This suggests that solar-mass stars in open clusters have similar rotation distributions at a given age and that the distributions of their rotation periods at different ages form a coherent sequence of evolution. This conclusion is supported by the simulated evolution of the NGC 2362-like rotation period distribution at an age of 130 Myr (see middle plot in Fig. 4). The simulation reproduces the bimodal distribution of rotation periods observed in the Pleiades and M 35 reasonably well, with 34% of the stars in the fast rotator group.
The M 37 open cluster has an age of 550 Myr (Hartman et al. 2008) comparable to that of the Hyades (625 Myr; Perryman et al. 1998). It is the oldest cluster for which a large number of stellar rotation periods have been measured. I found 284 0.7−1.1 M⊙ stars within the Hartman et al. (2009) catalog of candidate cluster members having known rotation periods. The distribution of rotation periods in M 37 is narrower than in younger clusters. The histogram exhibits a strong peak of slow rotators with periods of between 6 and 10 days.
This distribution is consistent with the view that Sun-like stars in old clusters such as M 37 and the Hyades are slow rotators while younger open clusters such as the Pleiades, M 50, and M 35 show a wide spread of their rotation distribution. The bimodal distribution of stellar rotation observed in those clusters has almost fully disappeared in M 37.
This evolutionary trend is accounted for in the simulated evolution of the NGC 2362-like rotation period distribution (see graphs in the lower row of Fig. 4). The simulated distribution at 550 Myr and the measured rotation periods histogram in M 37 both show a peak in the 6−10 days interval.
The measured rotation period histogram of M 37 is however broader than that of the simulation at 550 Myr since the spread in mass of the M 37 sample stars is not taken into account in the simulation. The origin of this effect is illustrated in Fig. 6 that compares the rotation period histograms of M 37 sample stars in the 0.7−0.9 M⊙ and 0.9−1.1 M⊙ mass bins. The rotation period distribution in the 0.9−1.1 M⊙ range is shifted by approximately 25% in rotation period towards slower rotation compared with the distribution in the 0.7−0.9 M⊙ range thus broadening the measured distribution in the 0.7−1.1 M⊙ range (see lower left graph in Fig. 4). The actual rotation period distribution of 1 M⊙ stars in M 37 should thus be narrower than the simulated distribution that is comparable in width to the measured rotation period distribution of M 37 stars in the 0.9−1.1 M⊙ range. Also, the simulation suggests a broadening of the slow rotator distribution between the ages of 130 Myr and 550 Myr (see Fig. 4), which is not observed when comparing the rotation period histograms of 0.9−1.1 M⊙ stars in M 35 and M 37. These differences between measurements and simulation results are indicative of the predictive accuracy of the model. The comparison is also limited by the fact that different clusters have evolved from initial rotation period distributions that may not be fully identical.
 |
Fig. 6 Measured rotation period histograms of 0.7−0.9 M⊙ stars (top) and 0.9−1.1 M⊙ stars (middle) in M 37 (550 Myr; Hartman et al. 2009) compared with the simulated histogram of solar-mass stars at 550 Myr (bottom). |
4. Discussion
The present study uses a phenomenological model of angular momentum loss and redistribution in stellar interiors. The model is implemented with new prescriptions of mass-loss rate and Alfven radius dependences on the Rossby number that are suggested by observations. It is used to calculate the evolution of an initial distribution of rotation periods of Sun-like stars.
A normal distribution truncated below 0.3 days is selected as an input since it emulates the distribution of rotation periods of 0.7−1.1 M⊙ stars in the 5 Myr-old NGC 2362 open cluster. The calculated distributions of rotation periods at subsequent ages are compared with those observed in h Per, the Pleiades, M 50, M 35, and M 37. They reproduce the main features of the distributions observed in those open clusters. In particular, they account for the bimodal distribution of stellar rotation that is observed among Sun-like stars in the Pleiades, M 50, and M 35. The model also simulates the appearance of a bimodal rotation period distribution at an early stage of the cluster evolution, though slightly later than observed in h Per. The bimodal distribution has almost disappeared by the age of M 37.
These results suggest that the rotation distributions of Sun-like stars in open clusters of increasing age form a coherent sequence of evolution determined by some common property of the angular momentum evolution of individual stars. This is supported by the similitude of the measured rotation distributions of Sun-like stars in the Pleiades, M 50, and M 35 open clusters that have similar ages. The slight difference between the fraction of stars in the fast and slow rotation sequences of those clusters could be related to some differences in their early distributions of stellar rotation just after the dispersion of circumstellar disks.
In order to reproduce the bimodal distribution of stellar rotation observed in young open clusters, the model requires that a brief episode of large-angular-momentum loss is included in the early evolution of Sun-like stars. This catastrophic event would occur in Sun-like stars with Rossby numbers in the range 0.13−0.3 (see Fig. 2). This corresponds to rotation periods between 1.9 and 4.3 days for a 1 M⊙ star. During stellar contraction on the main sequence, this episode of enhanced rotational braking would limit the spin-up of stars with rotation rates that are initially moderate. For main-sequence stars that are initially fast rotators, a strong deceleration of stellar rotation is induced much later, which explains the bimodal distribution of stellar rotation observed in young clusters. According to the model, the 0.13−0.3 Rossby number range is reached by stars with ages between 20-30 and approximately 600 Myr depending on their initial rotation rate. This accounts for the transition between the fast- and the slow-rotator sequence that is observed in clusters with those ages (Barnes 2003; Meibom et al. 2011).
The model assumes that the brief episode of enhanced angular momentum loss is due to a sudden rise of the mass-loss rate at a critical rotation rate combined with a continuous and moderate increase of the Alfven radius with decreasing rotation rate. This scenario is suggested by measurements of astrospheric Lyα absorptions interpreted with the support of hydrodynamic models (Wood et al. 2005, 2014). These observations indicate that the mass-loss rates of G-K dwarfs increase with the X-ray surface flux up to a wind dividing line beyond which the mass-loss rate of active young stars would be significantly lower.
Although the model assumes that the episode of enhanced rotational braking is driven by a sudden increase in the mass-loss rate, alternative scenarios producing a similar evolution of the angular momentum loss are a priori equally plausible. This includes, for example, the sudden change in the coupling between the wind and the large-scale magnetic fields of the stars proposed in the metastable dynamo model described by Brown (2014). This scenario, however, does not seems to be consistent with spectro-polarimetric observations of solar-type stars (Donati & Landstreet 2009). Folsom et al. (2016) found no strong difference in their sample of young Sun-like stars between the magnetic geometry of fast rotators (P< 2 days) and that of moderate rotators, which would essentially correspond to the transition between the fast and slow rotation sequence of Barnes (2003). Their observations rather indicate a continuous evolution from strong, toroidal, and non-axisymmetric magnetic fields on stars with small Rossby number to a more poloidal and axisymmetric configuration of large-scale magnetic fields on moderate rotators.
Remarkably, the rapid evolution of stellar rotation in the 0.13−0.3 Rossby number range is correlated with a change in the evolution of the stellar X-ray emission level. A steep transition in X-ray to bolometric luminosity ratio has been observed in the M 34 open cluster (Gondoin 2012) between stars on the fast rotator sequence that emit close to the 10-3 saturation level, and stars on the slow rotator sequence, whose LX/Lbol ratio is significantly lower. Correlations between the saturated, respectively non-saturated X-ray emission regimes and the fast, respectively slow rotator sequences are also observed in the Pleiades (Gondoin 2015).
Based on these observations, Gondoin (2013) argued that the transition from the saturated to the non-saturated regime of X-ray emission among main-sequence stars may be the result of a transition between different dynamo regimes. The present study suggests an alternative explanation. The onset of strong stellar winds at a Rossby number of 0.13 is expected to affect the energy balance of stellar coronae between heating mechanisms and energy losses by radiation (mainly in the X-ray domain), by conduction to the lower atmosphere, and by mass flowing outward as stellar wind and downward into the chromosphere (e.g., Withbroe & Noyes 1977; Aschwanden 2005). The measured decay of the X-ray luminosity of Sun-like stars between Rossby numbers 0.13 and 0.3 (i.e., ~2.7 × 1030 erg s-1 according to Eq. (6)) is equivalent to the kinetic energy flux of a 900 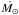 flow having the escape velocity of a solar-mass star. According to the model (see Eqs. (5) and (6)), this value is comparable to the average increase of mass-loss rate (~1600
flow having the escape velocity of a solar-mass star. According to the model (see Eqs. (5) and (6)), this value is comparable to the average increase of mass-loss rate (~1600 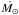 ) in the 0.13−0.3 Rossby number interval above the wind saturation level (~300
) in the 0.13−0.3 Rossby number interval above the wind saturation level (~300 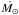 ; see Table 1). This similitude suggests that the onset of a large mass-loss rate in the 0.13−0.3 Rossby number range could account for a significant fraction of the X-ray luminosity decay of Sun-like stars observed in this Rossby number interval (e.g., Patten & Simon 1996; Pizzolato et al. 2003; Wright et al. 2011; Gondoin 2012). This scenario, however, does not identify the process that would trigger an abrupt change of mass-loss rate at a given rotation rate. The hypothesis of a transition between different dynamo regimes is not excluded.
; see Table 1). This similitude suggests that the onset of a large mass-loss rate in the 0.13−0.3 Rossby number range could account for a significant fraction of the X-ray luminosity decay of Sun-like stars observed in this Rossby number interval (e.g., Patten & Simon 1996; Pizzolato et al. 2003; Wright et al. 2011; Gondoin 2012). This scenario, however, does not identify the process that would trigger an abrupt change of mass-loss rate at a given rotation rate. The hypothesis of a transition between different dynamo regimes is not excluded.
An episode of enhanced angular momentum loss due to a more efficient magnetic braking by stellar winds should increase the differential rotation between the core and the envelope of the star. Since the magnetic field lines that sling charged particles from the wind into space are rooted in the photosphere, a strong wind torque is expected to decelerate the envelope rotation while the conservation of angular momentum should keep the radiative core in rapid rotation. A large shear should develop at the base of the convection zone and trigger various instabilities. These instabilities are expected to drive mass motions or gravity waves that redistribute angular momentum and mix the stellar material enhancing light-element depletion (e.g., Chaboyer et al. 1995; Charbonnel & Talon 2005; Talon 2008). Such an effect was observed in the Pleaides and M 34 by Gondoin (2014) who noted that K stars on the fast rotator sequence have significantly higher lithium abundances than stars with similar masses and ages located on the slow rotator sequence. This observed depletion of Li among stars that evolve from the fast to the slow rotator sequence supports the occurrence of a brief episode of enhanced magnetic braking by stellar wind in the early evolution of Sun-like stars.
The possible causes of such a catastrophic event remain to be determined. However, the observed correlations between X-ray emission regimes, rotation sequences, and Li abundance in young Sun-like stars suggest that differential rotation, dynamo processes, coronal heating by magnetic field related processes, large scale magnetic field topologies, and coronal cooling by stellar wind are most likely involved.
In conclusion, the appearance of a bimodal distribution of rotation periods in young open clusters and the correlation of the rotation sequences with X-ray emission and Li abundance point toward a scenario where Sun-like stars with a rapid enough rotation after circumstellar disk dispersion experience a short episode of large rotational braking by stellar wind in their early evolution. This catastrophic event is driven by a sudden increase in mass loss at a critical rotation rate and induces a large rotational shear at the bottom of the convective zone. It occurs on stars with ages between 20−30 Myr and approximately 600 Myr depending on their initial rotation rate after the dispersion of circumstellar disks. The mass-loss rate increase could account for a significant fraction of the X-ray luminosity decay of Sun-like stars observed in the 0.13−0.3 Rossby number range where a transition from the saturated to the non-saturated regime of X-ray emission is observed. Observed correlations between Li abundance and rotation sequence in M 34 and the Pleiades also supports this scenario.
Acknowledgments
I am grateful to the anonymous referee for the helpful comments that allowed me to improve the paper.
References
- Affer, L., Micela, G., Favata, F., et al. 2013, MNRAS, 430, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Allain, S. 1998, A&A, 333, 629 [NASA ADS] [Google Scholar]
- Aschwanden, M., J. 2005, Physics of the Solar Corona. Praxis Publishing Ltd., Chichester, UK (New York, Berlin: Springer) [Google Scholar]
- Badalyan, O. G., & Livshits, M. A. 1992, Soviet Astron., 36, 70 [NASA ADS] [Google Scholar]
- Barnes, S. A. 2003, ApJ, 586, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschild, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., et al. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bouvier, J. 2008, A&A, 489, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., Matt, S., Mohanty, S., et al. 2013, Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 433 [Google Scholar]
- Brown, T. M. 2014, ApJ, 796, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Brun, A. S., Garcia, R. A., Houdek, G., et al. 2015, Space Sci. Rev., 196, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Chaboyer, B., Demarque, P., & Pinsonneault, M. H. 1995, ApJ, 441, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charbonnel, C., Decressin, T., Amard, L., et al. 2013, A&A, 554, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cranmer, S. R. 2008, Proc. 14th Cambridge Workshop on Cool Stars, Stellar, System, and the Sun, ASP Conf. Ser. 384, ed. G. T. van Belle, 317 [Google Scholar]
- Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E. 2005, AJ, 130, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E., & Hillenbrand, L. A. 2007, AJ, 133, 2072 [NASA ADS] [CrossRef] [Google Scholar]
- D’Antona, F., & Mazzitelli, I. 1997, Mem. Soc. Astron. It., 68, 807 [Google Scholar]
- Decressin, T, Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., & Pinsonneault, M. 2007, ApJ, 655, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Pinsonneault, M., Terndrup, D. M., & Newsham, G. 2010, ApJ, 716, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Delorme, P., Collier Cameron, A., Hebb, L., et al. 2011, MNRAS, 413, 2218 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Durney, B. R., & Pneuman, G. W. 1975, Sol. Phys., 40, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Montalban, J., & Migglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fisher, G., Longcope, D., Metcalf, T., et al. 1998, ApJ, 508, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Folsom, C. P., Petit, P., Bouvier, J., et al. 2016, MNRAS, 457, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giampapa, M. S., Hall, J. C., Radick, R. R., & Baliunas, S. L. 2006, ApJ, 651, 444 [Google Scholar]
- Gondoin, P. 2012, A&A, 546, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gondoin, P. 2013, A&A, 556, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gondoin, P. 2014, A&A, 566, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gondoin, P. 2015, Proc. 2nd Solarnet meet.: solar and stellar magnetic activity, http://www.astropa.inaf.it /Solarnet2015/Proceedings/ Proceedings.html [Google Scholar]
- Gondoin, P., Gandolfi, D., Fridlund, M., et al. 2012, A&A, 548, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grießmeier, J. M., Stadelmann, A., Penz, T., et al. 2004, A&A, 425, 753 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Gaudi, B. S., Holman, M. J., et al. 2008, ApJ, 675, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Gaudi, B. S., Pinsonneault, M. H., et al. 2009, ApJ, 691, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Kovács, G., & Noyes, R. W. 2010, MNRAS, 408, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., Angus, R., Buzasi, D., et al. 2016, to appear in Kavli workshop report (see NOAO website, http://www.noao.edu/meetings/lsst-oir-study/ [Google Scholar]
- Henderson, C. B., & Stassun, K. G. 2012, ApJ, 747, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Holzwarth, V., & Jardine, M. 2007, A&A, 463, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2008a, MNRAS, 377, 741 [Google Scholar]
- Irwin, J., Hodgkin, S., Aigrain, S., et al. 2008b, MNRAS, 384, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., & Bouvier, J. 2009, Proc. IAU Symp., 258, 363 [NASA ADS] [Google Scholar]
- Irwin, J., Aigrain, S., Bouvier, J., et al. 2009, MNRAS, 392, 1456 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Johnstone, C. P., Güdel, M., Brott, I., & Lüftinger, T. 2015, A&A, 577, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalirai, J. S., Fahlman, G. G., Richer, H. B., & Ventura, P. 2003, AJ, 126, 1402 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., MacGregor, K. B., & Charbonneau, P. 1995, A&A, 294, 469 [NASA ADS] [Google Scholar]
- Krishnamurthi, A., Pinsonneault, M. H., Barnes, S., & Sofia, S. 1997, ApJ, 480, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landin, N. R., Mendes, L. T. S., & Vaz, L. P. R. 2010, A&A, 510, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, J. 1999, MNRAS, 302, 203 [NASA ADS] [CrossRef] [Google Scholar]
- MacGregor, K. B., & Brenner, M. 1991, ApJ, 376, 204 [NASA ADS] [CrossRef] [Google Scholar]
- MacGregor, K. B., & Charbonneau, P. 1994, Cool Stars; Stellar Systems; and the Sun; Eighth Cambridge Workshop, ASP Conf. Ser., 64, 174 [Google Scholar]
- Mathis, S. 2013, Lect. Notes Phys. (Berlin Heidelberg: Springer-Verlag), 64, 23 [NASA ADS] [Google Scholar]
- Matt, S. P., MacGregor, K. B., Pinsonneault, M. H., & Greene, T. P. 2012, ApJ, 754, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., & Naylor, T. 2008, MNRAS, 386, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Mayne, N. J., Naylor, T., Littlefair, S., et al. 2007, MNRAS, 375, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. J., Harrison, T. E., McArthur, B. E., & Benedict, G. F. 2011, AJ, 142, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Mathieu, R. D., & Stassun, K. G. 2009, ApJ, 695, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Matthieu, R. D., Stassun, K. G., et al. 2011, ApJ, 733, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Meibom, S., Barnes, S. A., Platais, I., et al. 2015, Nature, 517, 589 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Moraux, E., Artemenko, S., Bouvier, J., et al. 2013, A&A, 560, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oglethorpe, R. L. F., & Garaud, P. 2013, ApJ, 778, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Patten, B. M., & Simon, T. 1996, ApJS, 106, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., Brown, A. G. A., Lebreton, Y., et al. 1998, A&A, 331, 81 [NASA ADS] [Google Scholar]
- Pevtsov, A. A., Fisher, G. H., Acton, L. W., et al. 2003, ApJ, 598, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H. 2010, Proc. IAU Symp. 268, eds. C. Charbonnel, M. Tosi, F. Primas, & C. Chiappini, 375 [Google Scholar]
- Pinto, R. F., Brun, A. S., Jouve, L., et al. 2011, ApJ, 737, 72 [Google Scholar]
- Pizzo, V., Schwenn, R., Marsch, E., et al. 1983, ApJ, 271, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pneuman, G. W., & Kopp, R. A. 1971, Sol. Phys., 18, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Mohanty, S. 2012, ApJ, 746, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Reville, V., Brun, A. S., Matt, S. P., et al. 2015, ApJ, 798, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, in Solar and Stellar Magnetic Activity (Cambridge University Press) [Google Scholar]
- See, V., Jardine, M., Vidotto, A. A., et al. 2014, A&A, 570, A99 [Google Scholar]
- See, V., Jardine, M., Vidotto, A. A., et al. 2015, MNRAS, 453, 4301 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Skumanich, A. 1972, ApJ, 171, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., Lanzafame, A. C., & Lanza, A. F. 2010, MNRAS, 404, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, F., Lanzafame, A. C., Lanza, A. F., et al. 2011, MNRAS, 416, 447 [NASA ADS] [Google Scholar]
- Stauffer, J. R., Schild, R., Barrado y Navascues, D., et al. 1998, ApJ, 504, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Strugarek, A., Brun, A. S., & Zahn, J.-P. 2011, A&A, 532, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suzuki, T. K., Imada, S., Kataoka, R., et al. 2013, PASJ, 65, 98 [NASA ADS] [Google Scholar]
- Talon, S. 2008, Memo. Soc. Astron. It., 79, 569 [Google Scholar]
- Vidotto, A. A., Gregory, S. G., Jardine, M., et al. 2014, MNRAS, 441, 2361 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M. 1998, Proc. 10th Cambridge Workshop on Cool Stars, Stellar, System, and the Sun, eds. R. A. Donahue & J. A. Bookbinder, ASP Conf. Ser., 154, 131 [Google Scholar]
- Washimi, H., & Shibata, S. 1993, MNRAS, 262, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, E. J., & Davis, L., Jr. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Withbroe, G. L., & Noyes, R. W. 1977, ARA&A, 15, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H.-R., Zank, G. P., et al. 2005, ApJ, 628, L143 [Google Scholar]
- Wood, B. E., Müller, H.-R., Redfield, S., & Edelaman, E. 2014, ApJ, 781, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Model parameters used to simulate the angular momentum evolution of solar-mass stars.
Large samples of 0.7−1.1 M⊙ stars with measured rotation periods used for comparisons with simulated rotation period distributions.
All Figures
 |
Fig. 1 Left: moment of inertia (from Siess et al. 2000) of the outer convective envelope and inner radiative core (in units of total MR2). Middle: radius at the bottom of the convective envelope relative to the total stellar radius. Right: total surface radius at optical depth 0.005 (in solar unit). |
| In the text | |
 |
Fig. 2 Assumed braking torque of a Sun-like star as a function of its Rossby number. |
| In the text | |
 |
Fig. 3 Simulated angular velocity evolution of a solar-mass star with initial rotation periods (at 5 Myr age) of 0.6 (upper curve), 1, 2, 3, 6, 10, 20, and 30 days (lower curve). The simulated angular velocity curves are compared with rotation measurements in h Per (13 Myr; Moraux et al. 2013), the Pleiades (125 Myr; Hartman et al. 2010), M 50 (130 Myr; Irwin et al. 2009), M 35 (133 Myr; Meibom et al. 2009), and M 37 (550 Myr; Hartman et al. 2009). |
| In the text | |
 |
Fig. 4 Simulated evolution of a normal distribution of rotation periods (upper left) emulating that of a 5 Myr-old cluster (see text) at subsequent ages of 13 Myr (upper middle), 25 Myr (upper right), 55 Myr (center left), 130 Myr (center middle), 250 Myr (center right), 550 Myr (lower left), 1.25 Gyr (lower middle), and 2.5 Gyr (lower right). |
| In the text | |
 |
Fig. 5 Measured rotation period histogram of 0.7−1.1 M⊙ stars in NGC 2362 (5 Myr; Irwin et al. 2008a), h Per (13 Myr; Moraux et al. 2013), Pleiades (125 Myr; Hartman et al. 2010), M 50 (130 Myr; Irwin et al. 2009), M 35 (150 Myr; Meibom et al. 2009), and M 37 (550 Myr; Hartman et al. 2009). |
| In the text | |
 |
Fig. 6 Measured rotation period histograms of 0.7−0.9 M⊙ stars (top) and 0.9−1.1 M⊙ stars (middle) in M 37 (550 Myr; Hartman et al. 2009) compared with the simulated histogram of solar-mass stars at 550 Myr (bottom). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


